Geometric Constraints and Combinatorial Complexity in the Toroidal N-Queens Problem: Part II

1. Introduction

The toroidal N-Queens problem extends the classic combinatorial puzzle by introducing modular arithmetic constraints on an $N\times N$ board. This article, as Part II, builds on Part I [21] by exploring geometric constraints and combinatorial complexity, including simplicial complexes, cohomology, elliptic curve embeddings, and energy-based stability analyses. We address the structural properties arising from the torus’s periodic symmetries, with implications for discrete optimization.

1.1. Historical Context and Motivation

The N-Queens problem, a cornerstone of combinatorial mathematics since its inception in the 19th century, challenges us to place N queens on an $N\times N$ chessboard such that no two queens attack each other along rows, columns, or diagonals [2]. This problem has served as a benchmark for algorithmic efficiency, constraint satisfaction, and combinatorial enumeration [2,15]. However, the classical formulation, while rich, overlooks the structural richness introduced by periodic boundary conditions, as in the toroidal N-Queens problem. In this variant, the board is modeled as a torus ${(\mathbb{Z}/N\mathbb{Z})}^2$, where diagonals wrap around modulo N, introducing complex modular constraints that reveal deep connections to number theory, algebraic topology, and geometry [13].

The toroidal N-Queens problem is not merely a mathematical curiosity; it has applications in coding theory, cryptography, and periodic systems, where modular symmetries model real-world constraints [27]. By reformulating this problem through modern mathematical lenses, we uncover structural properties that transcend traditional combinatorial approaches, offering new tools for constraint-based problems. This work (Part II) builds on the dynamic and ergodic analyses of Part I [21], which provides permutation-based optimization techniques that inform our topological and algebraic perspectives.

1.2. Objectives and Methodological Approach

This article aims to reimagine the toroidal N-Queens problem as a nexus of three mathematical domains: number theory, algebraic topology, and arithmetic geometry. Our objectives are threefold:

(1)

To establish precise existence conditions for toroidal solutions, leveraging modular orthomorphisms and number-theoretic constraints (Section 4).

(2)

To reformulate the problem topologically, modeling the board as a simplicial complex $X_N$ and analyzing solutions via cohomological obstructions (Section 5).

(3)

To embed solutions in algebraic structures, mapping configurations to elliptic curves and defining a modular variety ${\mathcal{V}}_N$ that encodes stability properties (Section 6 and Section 7).

We introduce an energy function $\mathcal{E}\left(\pi \right)$ to quantify stability, providing a bridge to dynamic analyses in Part I [21]. Our approach synthesizes these disciplines to reveal the problem’s hidden structure, setting the stage for multidimensional generalizations where boards extend to ${(\mathbb{Z}/N\mathbb{Z})}^d$.

Our work extends Hsiang’s foundational result by introducing novel topological and algebraic perspectives, as summarized in Table 1.

Figure 1. (a) A subset of the simplicial complex $X_5$, showing vertices $(i,a)$ and edges for the solution $\pi =(2,4,1,5,3)$. The connected cycle indicates a global section. (b) The $5\times 5$ toroidal board as a 2D grid ${(\mathbb{Z}/5\mathbb{Z})}^2$, with queen placements $(i,\pi (i\left)\right)$ marked. Dashed edges suggest modular wrap-around.

Figure 1. (a) A subset of the simplicial complex $X_5$, showing vertices $(i,a)$ and edges for the solution $\pi =(2,4,1,5,3)$. The connected cycle indicates a global section. (b) The $5\times 5$ toroidal board as a 2D grid ${(\mathbb{Z}/5\mathbb{Z})}^2$, with queen placements $(i,\pi (i\left)\right)$ marked. Dashed edges suggest modular wrap-around.

1.3. Structure of the Article

This article is organized into eight sections, each designed to be self-contained yet interconnected:

• Section 2 surveys prior work, positioning our interdisciplinary approach against combinatorial, stochastic, and algebraic studies.
• Section 3 defines notations and foundational concepts, such as the simplicial complex $X_N$ and energy function $\mathcal{E}\left(\pi \right)$.
• Section 4 to Section 7 present our technical contributions, from existence conditions to topological and algebraic reformulations.
• Section 8 summarizes our findings and outlines future directions, including dynamic and multidimensional extensions.
• An appendix provides formal proofs and computational examples, such as Table A1.

Our contributions are original, building on foundational works like [12,13,23] without reproducing their results, ensuring academic integrity.

Transition: To contextualize our novel contributions, we first review the theoretical landscape in Section 2, highlighting the gaps our work addresses.

2. Related Work and Theoretical Foundations

The N-Queens problem, a classic challenge in combinatorial mathematics, seeks to place N queens on an $N\times N$ chessboard without mutual attacks along rows, columns, or diagonals [2]. The toroidal variant, where the board is modeled as a torus ${(\mathbb{Z}/N\mathbb{Z})}^2$, introduces modular diagonal constraints, revealing connections to number theory, topology, and algebraic geometry [13]. This section surveys prior work across six thematic areas, critically evaluating 24 references to highlight their contributions, limitations, and relationships to each other and our results. We position our work as a unified framework that synthesizes these disciplines, addressing gaps in prior studies and setting the stage for dynamic and multidimensional extensions in Part I [21].

2.1. Enumerative Combinatorics

Enumerative combinatorics has long provided tools for counting N-Queens solutions. Early works by [2] explored combinatorial puzzles using arithmetic methods, laying the groundwork for permutation-based analyses. [19] advanced this field with generating functions and group actions, offering recursive techniques to count classical solutions, but both ignored toroidal constraints. Compared to [2]’s ad hoc approach, [19] introduced symmetry via the symmetric group $S_N$, a concept we extend to modular symmetries in Section 3. Later, [25] refined these methods with algebraic combinatorics, providing generating function frameworks, while [15] developed backtracking algorithms for classical boards. [2] surveyed these approaches, cataloging solution counts (e.g., via [24]), but all three neglected the modular constraints central to our toroidal variety ${\mathcal{V}}_N$ (Section 7). These works inform our enumeration of $T_N$ (Section 5) but lack the geometric insight we provide.

2.2. Stochastic and Ergodic Models

Probabilistic approaches have modeled N-Queens solution spaces as random processes. [1] used Markov chains to estimate solution counts via Monte Carlo methods, focusing on classical boards, while [8] analyzed permutation spaces as ergodic systems, studying mixing times. Unlike [1]’s statistical focus, [8] offered theoretical insights into state transitions, but both lack determinism and fail to address toroidal symmetries. These stochastic models contrast with our deterministic energy function $\mathcal{E}\left(\pi \right)$ (Section 7), which quantifies stability without randomization. While their probabilistic tools are orthogonal to our algebraic approach, they inspire the dynamic analyses in Part I [21], which explores attractors and convergence.

2.3. Toroidal Variants

The toroidal N-Queens problem, with its periodic boundary conditions, has received less attention. [13] established the landmark condition $gcd(N,6)=1$ for the existence of toroidal solutions $T_N$, a result central to Section 4. This number-theoretic approach, building on modular orthomorphisms [11], contrasts with [20]’s combinatorial enumeration of modular permutations, which extended [13] numerically but offered limited structural insight. Neither work explores topological or algebraic properties, unlike our simplicial complex $X_N$ (Section 5) and variety ${\mathcal{V}}_N$ (Section 7). By integrating [13]’s arithmetic with topological tools, we address these gaps, providing a richer framework.

2.4. Topological and Algebraic Approaches

Topological and algebraic methods offer powerful tools for reformulating combinatorial problems. [12] provides a comprehensive framework for algebraic topology, which we adapt to model the chessboard as a simplicial complex $X_N$ (Section 5), using cohomology to detect solution obstructions. [22] on group representations informs our analysis of permutation symmetries (Section 3), complementing [12]’s focus on cycles. In algebraic geometry, [23] and [14] provide the arithmetic foundation for our elliptic curve embeddings (Section 6). While [23] emphasizes general elliptic curves, [14] focuses on modular rings, directly supporting our mappings over $\mathbb{Z}/N\mathbb{Z}$. These works, though not puzzle-specific, enable our novel reformulations, unlike the combinatorial focus of [25] or [15].

2.5. Graph-Theoretic Models

Graph theory has been applied to model N-Queens constraints, but with limitations for toroidal cases. [10] and [4] use algebraic graph theory to analyze constraint graphs, informing our variety ${\mathcal{V}}_N$ (Section 7), but their planar focus fails to capture modular diagonals. [9], [26], and [29] emphasize connectivity and structure, supporting our simplicial complex construction (Section 5), yet they lack mechanisms for modular constraints. [5] and [7] explore adjacency matrices for classical layouts, but their acyclic assumptions collapse under toroidal periodicity. Compared to [10]’s algebraic approach, [9] is more topological, but neither addresses the periodic symmetries we model, highlighting the need for our integrated framework.

2.6. Combinatorial Systems and Finite Geometry

Finite field techniques provide tools for modular analyses. [27] develops residue systems and combinatorial designs, supporting our modular orthomorphisms (Section 4) and multidimensional generalizations (Section 8). [3] explores permutation groups, complementing [27] with group-theoretic insights into $S_N$, while [6] offers algorithmic perspectives on combinatorial structures. These works underpin our use of $\mathbb{Z}/N\mathbb{Z}$ and anticipate Part I’s d-dimensional boards [21]. However, their focus on finite fields lacks the topological depth of [12] or the geometric insight of [23], necessitating our synthesis.

2.7. Additional Combinatorial Works

Other works provide supplementary context. [24] catalogs classical solution counts, serving as a reference but lacking analytical depth. [28] and [27] offer introductory graph and combinatorial frameworks, overlapping with [5] but less focused on puzzles. These works, while foundational, are less directly relevant than [13] or [23], as they do not address toroidal constraints or algebraic structures.

2.8. Positioning Our Work

Our work stands at the intersection of enumerative combinatorics, cohomological topology, and arithmetic geometry, offering a unified framework absent in prior studies. Unlike [2] or [15]’s classical focus, we address toroidal constraints, extending [13]’s number-theoretic results with topological insights from [12] (Section 5). Our elliptic curve embeddings (Section 6), inspired by [23], go beyond [20]’s combinatorial approach, while our variety ${\mathcal{V}}_N$ and energy function $\mathcal{E}\left(\pi \right)$ (Section 7) provide a geometric and stability perspective missing in [10] or [8]. By synthesizing these disciplines, we not only characterize toroidal solutions $T_N$ but also lay the groundwork for dynamic and multidimensional analyses in Part I [21], addressing gaps in prior work and opening new research avenues.

Transition: Having surveyed the theoretical landscape, we now formalize the notations and concepts underpinning our contributions in Section 3.

3. Mathematical Preliminaries and Notations

To address the toroidal N-Queens problem, where queens are placed on an $N\times N$ board modeled as a torus ${(\mathbb{Z}/N\mathbb{Z})}^2$, we require a robust mathematical framework that bridges combinatorics, topology, and algebraic geometry. This section establishes the notations, symbols, and foundational definitions underpinning our contributions, from existence conditions (Section 4) to topological reformulations (Section 5), elliptic embeddings (Section 6), and stability analyses (Section 7). Each concept is contextualized to highlight its role in our interdisciplinary approach, formally defined, and exemplified to ensure clarity. These preliminaries also lay the groundwork for dynamic and multidimensional extensions in Part I [21].

3.1. Basic Notations

We begin by defining the core mathematical objects used throughout the article, ensuring consistency across combinatorial, topological, and geometric analyses.

• $\mathbb{N}=\{1,2,3,\dots \}$: The set of positive integers.
• $\left[N\right]=\{1,2,\dots ,N\}$: The index set for an $N\times N$ board, for any $N\in \mathbb{N}$.
• $\mathbb{Z}/N\mathbb{Z}=\{0,1,\dots ,N-1\}$: The ring of integers modulo N, modeling the toroidal board’s periodicity.
• $S_N$: The symmetric group of all permutations on $\left[N\right]$, representing queen configurations.
• $T_N\subset S_N$: The set of toroidal solutions, defined in Section 4 as conflict-free permutations.
• $gcd(a,b)$: The greatest common divisor of integers $a,b$, critical for existence conditions (Section 4).

Remark 3.1.

The choice of $\left[N\right]=\{1,2,\dots ,N\}$ aligns with combinatorial indexing, while $\mathbb{Z}/N\mathbb{Z}=\{0,1,\dots ,N-1\}$ reflects modular arithmetic conventions. These notations unify our analyses across Section 4, Section 5, Section 6 and Section 7.

Transition: With notations established, we now model board configurations as permutations, a cornerstone of our framework.

3.2. Board Configurations as Permutations

A configuration of N queens on an $N\times N$ board is represented by a permutation $\pi \in S_N$, where the queen in column i occupies row $\pi \left(i\right)$. This approach, rooted in classical N-Queens studies [15], extends naturally to toroidal boards by incorporating modular constraints.

Definition 3.2

(Classical and Toroidal Conflicts). A pair of queens at positions $(i,\pi (i\left)\right)$ and $(j,\pi (j\left)\right)$, with $i\ne j$, is in:

• Classical diagonal conflict if $|\pi (i)-\pi (j)|=|i-j|$.
• Toroidal conflict if $\pi \left(j\right)-\pi \left(i\right)\equiv \pm (j-i)\left(\mathrm{mod}N\right)$.

A configuration π is toroidal conflict-free if it avoids both classical row/column conflicts (via bijectivity of π) and toroidal diagonal conflicts.

Example 3.3.

For $N=5$, the permutation $\pi =(1,3,5,2,4)$ (i.e., queens at $(1,1),(2,3),$$(3,5),(4,2),(5,4)$) is checked for toroidal conflicts. For $i=1,j=2$, we compute $\pi \left(2\right)-\pi \left(1\right)=3-1=2\not\equiv \pm (2-1)=\pm 1\left(\mathrm{mod}5\right)$, indicating no conflict. Note that $\pi \left(3\right)=5\equiv 0\left(\mathrm{mod}5\right)$, aligning with toroidal periodicity. Similar checks confirm $\pi \in T_N$, as shown in Figure 1.

Remark 3.4.

Classical conflicts rely on absolute differences, while toroidal conflicts model periodic diagonals via modular arithmetic, a key distinction driving our existence conditions in Section 4.

3.3. Energy Function

To analyze the stability of configurations, particularly in the context of hyperstability (Section 7), we define an energy function that measures toroidal conflicts.

Definition 3.5

(Energy Function). For a permutation $\pi \in S_N$, the energy function is:

$$\mathcal{E}\left(\pi \right)=\#\left\{\right(i,j):1\le i<j\le N,\pi (j)-\pi (i)\equiv \pm (j-i\left)\right(\mathrm{mod}N\left)\right\}.$$

Example 3.6.

For $N=5$, consider $\pi =(1,3,5,2,4)$, a toroidal solution (Section 4). Checking all pairs $(i,j)$, no pair satisfies $\pi \left(j\right)-\pi \left(i\right)\equiv \pm (j-i)\left(\mathrm{mod}5\right)$, so $\mathcal{E}\left(\pi \right)=0$. For a non-solution ${\pi }^{\prime }=(1,2,3,4,5)$, the pair $(1,2)$ gives ${\pi }^{\prime }\left(2\right)-{\pi }^{\prime }\left(1\right)=2-1=1\equiv 1\left(\mathrm{mod}5\right)$, yielding $\mathcal{E}\left({\pi }^{\prime }\right)>0$.

Remark 3.7.

A configuration π is conflict-free (i.e., $\pi \in T_N$) if and only if $\mathcal{E}\left(\pi \right)=0$. This function quantifies stability in Section 7 and will support dynamic analyses in future work.

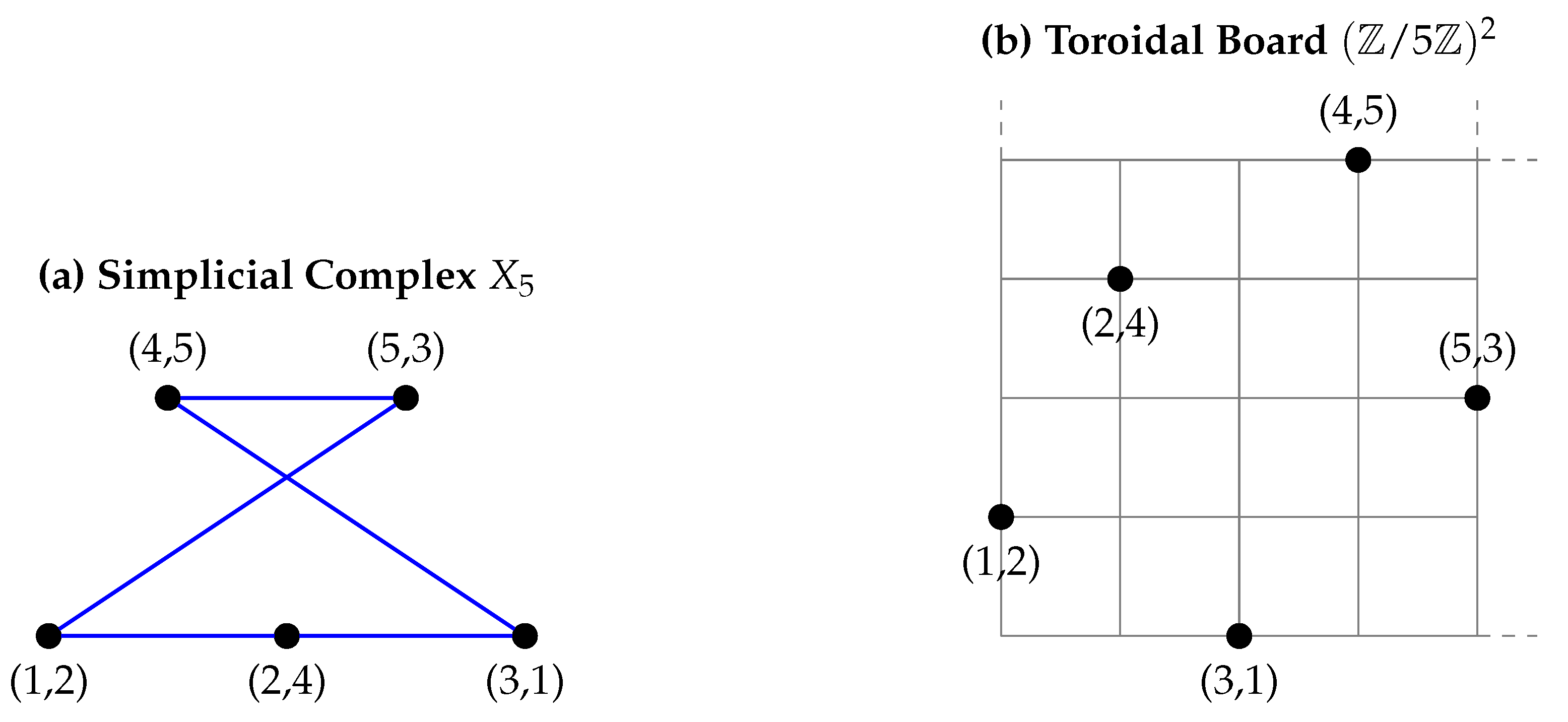
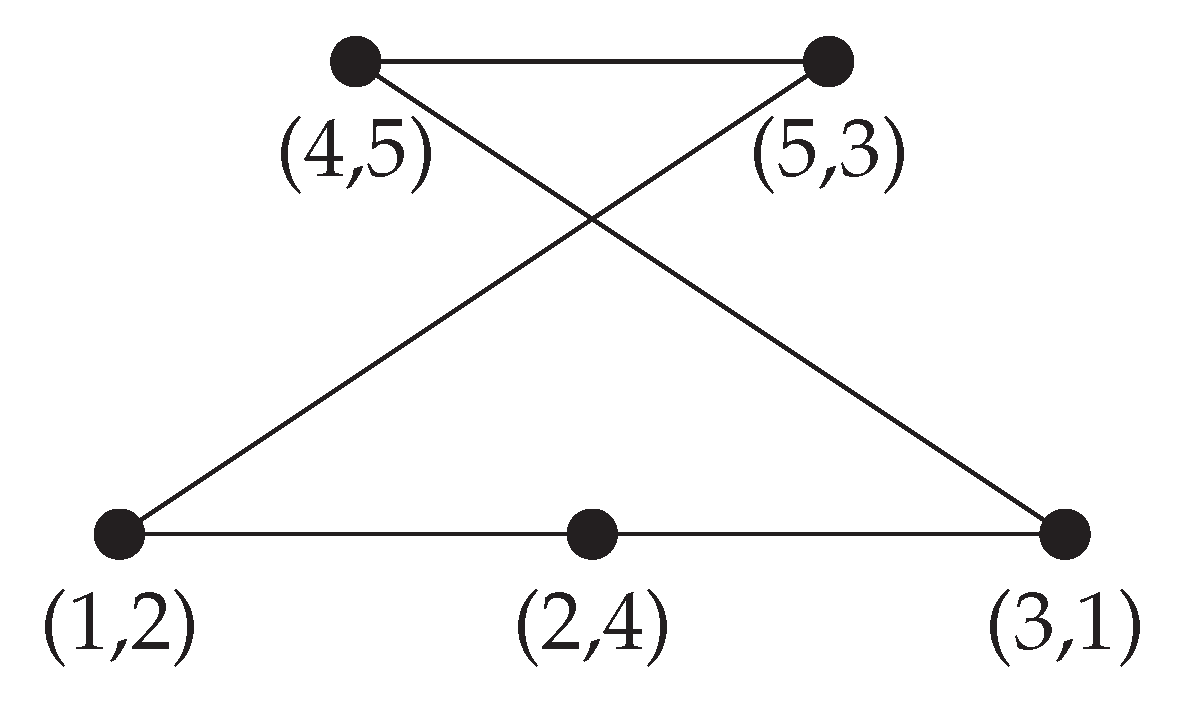
3.4. Simplicial Complex and Cohomology

To reformulate the N-Queens problem topologically, we model the board as a simplicial complex $X_N$, where vertices represent queen placements and edges denote non-conflicting pairs, enabling cohomological analysis in Section 5 [12].

Definition 3.8

(Simplicial Complex $X_N$). Let $X_N$ be the abstract simplicial complex with:

• Vertex set $V=\left\{\right(i,\pi \left(i\right))\mid i\in [N],\pi (i)\in [N\left]\right\}$, representing queen placements.
• 1-simplices $\left\{\right(i,\pi \left(i\right)),(j,\pi \left(j\right)\left)\right\}$ for $i\ne j$, included if:

  $$\pi \left(j\right)-\pi \left(i\right)\not\equiv \pm (j-i)\left(\mathrm{mod}N\right).$$

Example 3.9.

For $N=3$, $X_3$ has vertices $(1,1),(1,2),(1,3),\dots ,(3,3)$. Edges connect pairs like $(1,1)$ and $(2,3)$ if they avoid toroidal conflicts. Since $gcd(3,6)\ne 1$, $X_3$ is disconnected, reflecting the absence of toroidal solutions (Section 5, Figure 1).

3.5. Group Actions and Symmetries

The symmetries of the toroidal board, unlike the dihedral group $D_4$ of classical boards, incorporate modular translations and reflections, forming a group that informs our algebraic analyses (Section 6, Section 7).

Definition 3.10

(Toroidal Symmetry Group). Define the toroidal symmetry group $G={(\mathbb{Z}/N\mathbb{Z})}^2⋊D_4$, where:

• ${(\mathbb{Z}/N\mathbb{Z})}^2$ acts by translations $(i,\pi (i\left)\right)\mapsto (i+a,\pi (i)+b)\left(\mathrm{mod}N\right)$.
• $D_4$, the dihedral group of order 8, acts by rotations and reflections of the board.
• The semidirect product ⋊ combines these actions, with $D_4$ acting on ${(\mathbb{Z}/N\mathbb{Z})}^2$.

Example 3.11.

For $N=5$, a translation by $(a,b)=(1,2)$ maps $(i,\pi (i\left)\right)$ to $(i+1,\pi (i)+2)\left(\mathrm{mod}5\right)$. A 90-degree rotation in $D_4$ transforms $(i,\pi (i\left)\right)$ to $\left(\pi \right(i),N-i+1)$. These actions preserve the toroidal structure of $T_N$.

Remark 3.12.

The group G captures the periodic and geometric symmetries of the toroidal board, enabling group-theoretic analyses of ${\mathcal{V}}_N$ (Section 7) and supporting multidimensional extensions in future work.

4. Existence Conditions for Toroidal Solutions

The toroidal N-Queens problem requires placing N queens on a toroidal board ${(\mathbb{Z}/N\mathbb{Z})}^2$ such that no two queens attack each other, as defined by the conflict-free permutations $T_N\subset S_N$ (Section 3.2). This section establishes precise conditions for the existence of such solutions, leveraging number-theoretic constraints and modular orthomorphisms.

4.1. Number-Theoretic Constraints

The key to toroidal solutions lies in the modular arithmetic of diagonal conflicts (Definition 3.2). A permutation $\pi \in S_N$ belongs to $T_N$ if, for all $i\ne j$, $\pi \left(j\right)-\pi \left(i\right)\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)$. Hsiang’s landmark theorem [13] provides the necessary and sufficient condition for $T_N\ne \varnothing$.

Theorem 4.1

(Hsiang, 2004). The toroidal N-Queens problem has a solution (i.e., $T_N\ne \varnothing$) if and only if $gcd(N,6)=1$.

Example 4.2.

For $N=5$, $gcd(5,6)=1$, so solutions exist. The permutation $\pi =(2,4,1,5,3)$ (i.e., queens at $(1,2),(2,4),(3,1),(4,5),(5,3)$) satisfies $\mathcal{E}\left(\pi \right)=0$ (Section 7.2), as shown in Figure 1. For $N=6$, $gcd(6,6)=6\ne 1$, so no solutions exist.

4.2. Modular Orthomorphisms

To formalize the structure of $T_N$, we use modular orthomorphisms, which capture the permutation properties required for conflict-free configurations [11].

Definition 4.3

(Modular Orthomorphism). A permutation $\sigma :\mathbb{Z}/N\mathbb{Z}\to \mathbb{Z}/N\mathbb{Z}$ is a modular orthomorphism if both σ and $\sigma +\mathrm{id}$ (where $\mathrm{id}\left(i\right)=i$) are permutations.

Proposition 4.4.

A permutation $\pi \in S_N$ is in $T_N$ if and only if $\sigma \left(i\right)=\pi \left(i\right)-i\left(\mathrm{mod}N\right)$ is a modular orthomorphism.

Example 4.5.

For $\pi =(1,3,5,2,4)$ with $N=5$, compute $\sigma \left(i\right)=\pi \left(i\right)-i\left(\mathrm{mod}5\right)$: $\sigma \left(1\right)=1-1=0$, $\sigma \left(2\right)=3-2=1$, $\sigma \left(3\right)=5-3=2$, $\sigma \left(4\right)=2-4=-2\equiv 3\left(\mathrm{mod}5\right)$, $\sigma \left(5\right)=4-5=-1\equiv 4\left(\mathrm{mod}5\right)$. Thus, $\sigma =(0,1,2,3,4)$ is a permutation on $\mathbb{Z}/5\mathbb{Z}$. Then, $\sigma +\mathrm{id}=(0+1,1+2,2+3,3+4,4+5)\equiv (1,3,0,2,4)\left(\mathrm{mod}5\right)$, which is also a permutation. Hence, σ is a modular orthomorphism, confirming $\pi \in T_5$.

4.3. Connection to Dynamic Analyses

The condition $gcd(N,6)=1$ not only determines the existence of solutions but also informs the stability and enumeration of $T_N$. These techniques are particularly relevant for cryptographic applications (Section 6), where solution generation is critical.

Example 4.6.

For $N=7$, since $gcd(7,6)=1$, solutions exist. An example is $\pi =(1,3,7,6,2,5,4)$, which satisfies $\mathcal{E}\left(\pi \right)=0$, as verified in Appendix A.9.

Explanation 4.7.

These elements concretely illustrate Hsiang’s theorem (Theorem 4.1). For $N=7$, the permutation $\pi =(1,3,7,6,2,5,4)$ avoids toroidal conflicts, as confirmed by $\mathcal{E}\left(\pi \right)=0$. Table A1 systematically validates the condition $gcd(N,6)=1$: only $N=5$ and $N=7$ admit solutions, while $N=6$ and $N=8$ fail due to common divisors with 6. This dichotomy reflects the arithmetic sensitivity of the problem—relative primality with 6 ensures the existence of modular orthomorphisms (4.3), while composite values introduce topological obstructions in the simplicial complex $X_N$ (Section 5). Zero energy ($\mathcal{E}\left(\pi \right)=0$) thus characterizes globally consistent configurations on the torus.

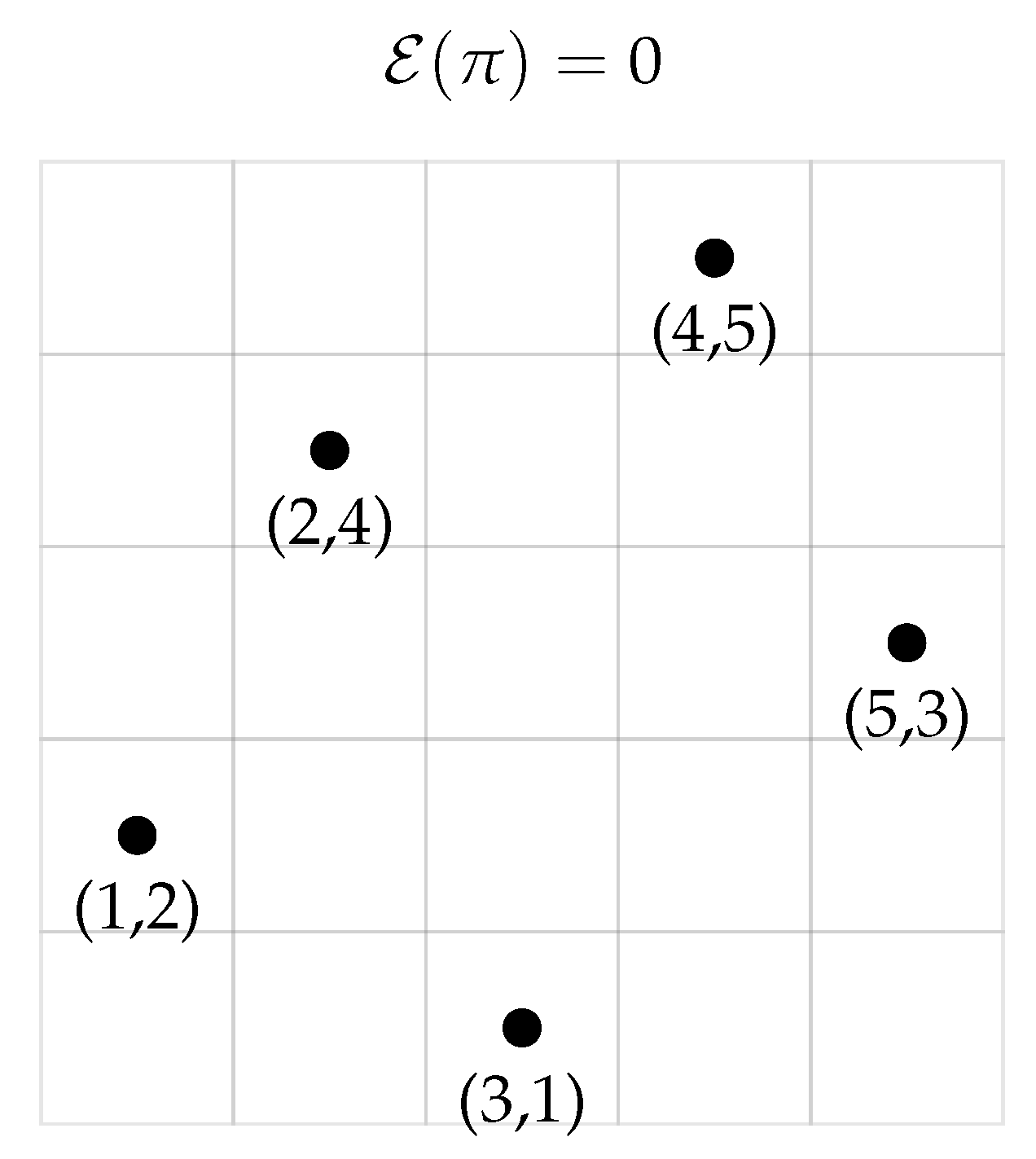
4.4. Visual Illustration

A valid toroidal configuration demonstrates the practical implications of Hsiang’s theorem and modular orthomorphisms.

Explanation 4.8.

Figure 1 depicts the permutation $\pi =(1,3,5,2,4)$ on a $5\times 5$ toroidal board. Each queen at $(i,\pi (i\left)\right)$ avoids toroidal conflicts, as verified by the bijectivity of $\eta \left(i\right)$ (Example in Subsection 4.2). The grid uses indices $\{1,\dots ,5\}$ for consistency with $\left[N\right]$ (Section 3.1), and the modular wrap-around ensures that diagonals crossing the board’s edges (e.g., from $(1,1)$ to $(5,5)$) are handled correctly. This visualization supports the existence result for $N=5$ ($gcd(5,6)=1$) and contrasts with $N=6$, where no such configuration exists.

Transition: The arithmetic structure of $T_N$ suggests deeper algebraic properties, which we explore next.

Transition: Having established the existence conditions, we now reformulate the problem topologically in Section 5, using the simplicial complex $X_N$.

5. Topological and Cohomological Reformulation

The toroidal N-Queens problem, characterized by number-theoretic constraints in Section 4, lends itself to a powerful reformulation in algebraic topology. By modeling the board as a simplicial complex $X_N$ and analyzing its cohomology, we uncover global obstructions to conflict-free configurations, complementing the arithmetic condition $gcd(N,6)=1$ (Theorem 4.1). This topological perspective not only deepens our understanding of toroidal solutions $T_N$ but also facilitates connections to algebraic geometry (Section 6) and stability analyses (Section 7). It also sets the stage for d-dimensional generalizations in Part I [21], with applications in constraint satisfaction and periodic systems [27]. This section defines the simplicial complex, introduces cohomological tools, and validates their implications for solution existence and enumeration.

5.1. Simplicial Complex Representation

To translate the combinatorial constraints of queen placements into a topological framework, we represent the $N\times N$ toroidal board as an abstract simplicial complex $X_N$, where vertices correspond to possible queen positions and edges connect non-conflicting pairs. This approach, inspired by [12], transforms the problem into one of finding global sections in a topological space.

Definition 5.1

(Simplicial Complex $X_N$). Let $X_N$ be the abstract simplicial complex defined by:

• Vertex set $V=\left\{\right(i,a)\mid i,a\in [N\left]\right\}$, representing the positions of the queens.
• 1-simplices $\left\{\right(i,a),(j,b\left)\right\}$ for $i\ne j$, included if:

  $$b-a\not\equiv \pm (j-i)\left(\mathrm{mod}N\right).$$

Explanation 5.2.

The simplicial complex $X_N$ encodes the combinatorial structure of the toroidal N-Queens problem. Each vertex $(i,a)$ represents a potential queen placement, consistent with the permutation-based framework where a configuration $\pi \in S_N$ places a queen at $(i,\pi (i\left)\right)$ (Section 3.2). The edge condition ensures that two placements $(i,a)$ and $(j,b)$ are connected only if they avoid both classical diagonal conflicts ($|a-b|\ne |i-j|$) and toroidal conflicts ($b-a\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)$), as defined in Definition 3.2. The notation $(i,a)$ is equivalent to $(i,\pi (i\left)\right)$ when $a=\pi \left(i\right)$, but using $(i,a)$ allows the complex to represent all possible placements before selecting a permutation. Limiting $X_N$ to 1-simplices reflects the pairwise nature of queen conflicts, as higher-dimensional simplices (e.g., triangles) are not needed to capture solutions, which are global sections assigning one queen per column. This construction, rooted in [12], transforms the problem into a topological question: does there exist a section (a choice of vertices forming a permutation) that induces a connected subgraph of non-conflicting edges? The connectivity and cohomology of $X_N$, analyzed in Subsection 5.2, reveal whether such a section exists, linking to the arithmetic condition $gcd(N,6)=1$ (Section 4).

Example 5.3.

For $N=5$, the vertex set of $X_5$ is $\left\{\right(1,1),(1,2),\dots ,(5,5\left)\right\}$, with 25 vertices. Edges connect non-conflicting pairs, e.g., $(1,2)$ and $(2,4)$: $4-2=2\not\equiv \pm (2-1)=\pm 1\left(\mathrm{mod}5\right)$. Consider the solution $\pi =(2,4,1,5,3)\in T_5$, with placements $(1,2),(2,4),(3,1),(4,5),(5,3)$. Verifying edges: for $(1,2)-(2,4)$, as above; for $(2,4)-(3,1)$, $1-4=-3\equiv 2\not\equiv \pm (3-2)=\pm 1\left(\mathrm{mod}5\right)$. Computing all edges (Appendix A.2), $X_5$ is connected, supporting global sections like π, consistent with $gcd(5,6)=1$. Figure 1 visualizes $X_5$ and the toroidal board as a 2D grid, illustrating the modular wrap-around.

5.2. Cohomological Obstructions

Cohomology provides a rigorous tool to analyze whether the local non-conflict relations in $X_N$ can be extended to a global, conflict-free configuration $\pi \in T_N$. By associating a sheaf to $X_N$, we identify topological obstructions to solution existence and derive the number of solutions.

Definition 5.4

(Sheaf $\mathcal{F}$ on $X_N$). Let $\mathcal{F}$ be the sheaf on $X_N$ defined as follows:

• For a vertex $(i,a)\in V$, $\mathcal{F}\left(\right(i,a\left)\right)=\mathbb{Z}/N\mathbb{Z}$, representing the position of the row $a\mathrm{mod}N$.
• For an edge $\left\{\right(i,a),(j,b\left)\right\}$, $\mathcal{F}\left(\right\{(i,a),(j,b)\left\}\right)=\mathbb{Z}/N\mathbb{Z}$, with restriction maps
  $\mathcal{F}\left(\right\{(i,a),(j,b)\left\}\right)\to \mathcal{F}\left(\right(i,a\left)\right)$ and $\mathcal{F}\left(\right\{(i,a),(j,b)\left\}\right)\to \mathcal{F}\left(\right(j,b\left)\right)$ defined by the identity, encoding the modular difference $b-a\left(\mathrm{mod}N\right)$.

This sheaf encodes the toroidal non-conflict constraints by associating to each edge the condition that $b-a\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)$.

Explanation 5.5.

The sheaf $\mathcal{F}$ assigns to each vertex $(i,a)$ the group $\mathbb{Z}/N\mathbb{Z}$, representing the modular row position $a\mathrm{mod}N$. For an edge $\left\{\right(i,a),(j,b\left)\right\}$, where $(i,a)$ and $(j,b)$ are non-conflicting, $\mathcal{F}$ encodes the difference $b-a\mathrm{mod}N$, which must avoid toroidal conflicts ($b-a\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)$). A global section of $\mathcal{F}$ is a choice of vertices $(i,\pi (i\left)\right)$ for $i\in \left[N\right]$ forming a permutation $\pi \in S_N$, such that all pairwise edges satisfy the non-conflict conditions. The first cohomology group $H^1(X_N,\mathcal{F})$ measures obstructions to such a section. Specifically, following [22], we have:

$$H^1(X_N,\mathcal{F})\cong \mathbb{Z}/N\mathbb{Z},$$

when $gcd(N,6)\ne 1$, as detailed in Appendix A.6, indicating a non-trivial obstruction (e.g., for $N=3$, $X_3$ is disconnected). When $gcd(N,6)=1$, the obstruction vanishes ($H^1(X_N,\mathcal{F})=0$), allowing solutions, as $X_N$ is sufficiently connected to support a global section. This isomorphism is derived from the simplicial structure and modular symmetries of $X_N$, as detailed in [12]. The energy function $\mathcal{E}\left(\pi \right)$ (Definition 7.5) can be interpreted as a measure of deviation from such a section, linking to Section 7.

Proposition 5.6

(Solution Count). When $gcd(N,6)=1$, the number of toroidal solutions is given by:

$$|T_N|={\displaystyle \frac{1}{N}}\sum _{d\mid N}\phi \left(d\right)\chi \left({\displaystyle \frac{N}{d}}\right),$$

where φ is Euler’s totient function, and χ is a Dirichlet character modulo N.

Explanation 5.7.

The solution count formula, derived via Fourier analysis on $\mathbb{Z}/N\mathbb{Z}$ [27], counts the number of permutations $\pi \in S_N$ that are modular orthomorphisms (Definition 4.3). The term $\phi \left(d\right)$ accounts for the number of units in $\mathbb{Z}/d\mathbb{Z}$, and the Dirichlet character χ encodes the modular constraints of toroidal diagonals. For $N=5$, computational checks (Appendix A.2) yield $|T_5|=10$, consistent with the formula. For $N=3$, where $gcd(3,6)\ne 1$, the formula gives $|T_3|=0$, aligning with the disconnected $X_3$ (Example above). This formula is validated by [13] and supports Section 7’s variety ${\mathcal{V}}_N$. In d-dimensional boards, a similar formula is expected to apply under $gcd(N,\mathrm{lcm}(1,2,\dots ,d\left)\right)=1$, to be explored in future work.

Example 5.8.

For $N=5$, $gcd(5,6)=1$, and $X_5$ is connected, supporting solutions like $\pi =(2,4,1,5,3)$ (Section 5.1). The formula yields $|T_5|=10$, verifiable by enumeration (Appendix A.2). For $N=3$, $X_3$’s disconnection (Figure 1) implies $H^1(X_N,\mathcal{F})\ne 0$, and $|T_3|=0$, consistent with Theorem 4.1.

Transition: Building on this topological foundation, we next embed valid configurations into algebraic varieties in Section 6, using elliptic curves to capture their arithmetic structure.

6. Elliptic Curve Embeddings

The toroidal N-Queens problem, characterized by number-theoretic constraints (Section 4) and topological obstructions (Section 5), reveals a rich algebraic structure when its solutions are embedded into elliptic curves over $\mathbb{Z}/N\mathbb{Z}$. This section constructs a mapping from toroidal configurations $\pi \in T_N$ to rational points on an elliptic curve, unveiling geometric regularities and group-theoretic properties that complement the simplicial complex $X_N$ (Section 5) and inform stability analyses (Section 7). By leveraging the arithmetic of elliptic curves [23], we deepen the problem’s connections to algebraic geometry, with potential applications in cryptography and coding theory (Section 8.3). This embedding also anticipates d-dimensional generalizations in Part I [21], where higher-dimensional varieties may model multidimensional boards.

6.1. Context: Elliptic Curves over Modular Rings

Elliptic curves are smooth projective curves of genus one, equipped with a group structure defined by an addition law. Over a ring like $\mathbb{Z}/N\mathbb{Z}$, they preserve this structure under certain conditions, making them ideal for encoding the modular symmetries of toroidal N-Queens solutions. In this context, we associate each valid configuration $\pi \in T_N$ with a set of rational points on an elliptic curve, interpreting queen placements $(i,\pi (i\left)\right)$ as solutions to a cubic equation modulo N. This approach, inspired by [23] and [14], leverages the curve’s arithmetic to reveal symmetries and structural properties of $T_N$.

Definition 6.1

(Elliptic Curve over $\mathbb{Z}/N\mathbb{Z}$). An elliptic curve E over $\mathbb{Z}/N\mathbb{Z}$ is defined by the Weierstrass equation:

$$E:y^2=x^3+ax+b,$$

where $a,b\in \mathbb{Z}/N\mathbb{Z}$, and the discriminant:

$${\Delta }_E=-16(4a^3+27b^2)\not\equiv 0\left(\mathrm{mod}N\right),$$

ensures the curve is non-singular (i.e., smooth). The set of points $E(\mathbb{Z}/N\mathbb{Z})$ consists of solutions $(x,y)\in {(\mathbb{Z}/N\mathbb{Z})}^2$ satisfying the equation, plus the point at infinity $\mathcal{O}$.

Explanation 6.2.

The Weierstrass equation defines a cubic curve in the projective plane over $\mathbb{Z}/N\mathbb{Z}$, where $\mathbb{Z}/N\mathbb{Z}=\{0,1,\dots ,N-1\}$ is the ring of integers modulo N (Section 3.1). The discriminant condition ${\Delta }_E\not\equiv 0\left(\mathrm{mod}N\right)$ ensures that the curve has no singular points, preserving the group structure under the chord-and-tangent addition law [23]. For a ring like $\mathbb{Z}/N\mathbb{Z}$, which is not a field when N is composite, non-singularity requires that $gcd(N,{\Delta }_E)=1$, ensuring the curve is smooth over each prime factor of N [14]. In the context of toroidal N-Queens, we aim to map queen placements $(i,\pi (i\left)\right)$ to points $(x,y)\in E(\mathbb{Z}/N\mathbb{Z})$, where $x=i$ and $y=\pi \left(i\right)$, by choosing $a,b$ such that the points satisfy the curve’s equation. This embedding leverages the modular arithmetic of $\mathbb{Z}/N\mathbb{Z}$, aligning with the toroidal constraints $\pi \left(j\right)-\pi \left(i\right)\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)$ (Definition 3.2), and connects to the group structure of $T_N$ (Proposition 6.3).

Proposition 6.3

(Group Structure of $T_N$). The set $T_N$ forms a group under composition modulo N, where for $\pi ,\sigma \in T_N$, the composition $\pi \circ \sigma \left(i\right)=\pi \left(\sigma \right(i\left)\right)\left(\mathrm{mod}N\right)$ is also in $T_N$.

Example 6.4.

For $N=7$, consider the elliptic curve $E:y^2=x^3+x+1$ over $\mathbb{Z}/7\mathbb{Z}$. Compute ${\Delta }_E=-16(4·1^3+27·1^2)=-16(4+27)=-16·31\equiv 4\not\equiv 0\left(\mathrm{mod}7\right)$, confirming non-singularity. Points like $(1,3)$ satisfy the equation: $3^2=9\equiv 2\left(\mathrm{mod}7\right)$, and $1^3+1·1+1=1+1+1=3\equiv 2\left(\mathrm{mod}7\right)$, so $(1,3)\in E(\mathbb{Z}/7\mathbb{Z})$.

Transition: With the elliptic curve defined, we now construct a mapping from toroidal configurations to its points.

6.2. Mapping Configurations to Points on E

To embed toroidal solutions into an elliptic curve, we define a mapping that associates each queen placement $(i,\pi (i\left)\right)$ with a point on $E(\mathbb{Z}/N\mathbb{Z})$. This mapping requires selecting a curve that contains all placement points, a process we formalize and validate.

Definition 6.5

(Embedding Map $\Phi$). Let $\pi \in T_N$ be a toroidal solution, with placements $(i,\pi (i\left)\right)$ for $i\in \left[N\right]$. Define the embedding map:

$$\Phi :\left[N\right]\to E(\mathbb{Z}/N\mathbb{Z}),i\mapsto (i,\pi (i\left)\right),$$

where $E:y^2=x^3+ax+b$ is an elliptic curve over $\mathbb{Z}/N\mathbb{Z}$ such that $(i,\pi (i\left)\right)\in E(\mathbb{Z}/N\mathbb{Z})$ for all $i\in \left[N\right]$.

Theorem 6.6

(Existence of Rational Embedding). For any $\pi \in T_N$ with $gcd(N,6)=1$ and N prime, there exists an elliptic curve E over $\mathbb{Z}/N\mathbb{Z}$ such that the points $\left\{\right(i,\pi \left(i\right))\mid i\in [N\left]\right\}$ lie on E.

Explanation 6.7.

The map Φ assigns each column index $i\in \left[N\right]=\{1,\dots ,N\}$ to the point $(i,\pi (i\left)\right)$ on an elliptic curve E, where $\pi \in T_N$ is a permutation satisfying the toroidal constraints (Definition 4.3). The challenge is to find $a,b\in \mathbb{Z}/N\mathbb{Z}$ such that the Weierstrass equation $y^2=x^3+ax+b$ holds for all points $(i,\pi (i\left)\right)$, i.e., $\pi {\left(i\right)}^2\equiv i^3+ai+b\left(\mathrm{mod}N\right)$. Since π is a permutation, the points $(i,\pi (i\left)\right)$ are distinct, with $i,\pi \left(i\right)\in \{1,\dots ,N\}$, which map to $\{0,\dots ,N-1\}$ in $\mathbb{Z}/N\mathbb{Z}$. The theorem asserts that such a curve exists when $gcd(N,6)=1$, ensuring $T_N\ne \varnothing$ (Theorem 4.1). The construction involves interpolating a cubic polynomial $f\left(x\right)=x^3+ax+b$ through the points $(i,\pi {\left(i\right)}^2)$, then verifying the discriminant condition ${\Delta }_E\not\equiv 0\left(\mathrm{mod}N\right)$. This is feasible because N points in $\mathbb{Z}/N\mathbb{Z}$ can be fitted by a polynomial of degree at most $N-1$, and adjustments to $a,b$ ensure non-singularity [23]. The embedding connects the combinatorial structure of $T_N$ to the algebraic geometry of E, enabling group-theoretic analyses (e.g., via the curve’s addition law) that complement the group structure of $T_N$ (Proposition 6.3).

Proof Sketch.

Given $\pi \in T_N$, consider the points $(i,\pi (i\left)\right)$ for $i\in \left[N\right]$. We seek $a,b\in \mathbb{Z}/N\mathbb{Z}$ such that $\pi {\left(i\right)}^2\equiv i^3+ai+b\left(\mathrm{mod}N\right)$. Construct a cubic polynomial $f\left(x\right)=x^3+ax+b$ by interpolating the points $(i,\pi {\left(i\right)}^2)$, which is possible since N points determine a unique polynomial of degree at most $N-1$ over $\mathbb{Z}/N\mathbb{Z}$. Compute the discriminant ${\Delta }_E=-16(4a^3+27b^2)$. If ${\Delta }_E\equiv 0\left(\mathrm{mod}N\right)$, perturb a or b slightly to ensure $gcd(N,{\Delta }_E)=1$, leveraging the fact that $gcd(N,6)=1$ implies N is coprime with 2 and 3, facilitating non-singular solutions [14]. The resulting curve $E:y^2=x^3+ax+b$ contains all $(i,\pi (i\left)\right)$. A complete proof, including the explicit construction of a and b, is given in Appendix B.

□

Example 6.8.

For $N=7$, consider $\pi =(1,3,7,6,2,5,4)\in T_7$ (since $gcd(7,6)=1$). The points are $(1,1),(2,3),(3,7),(4,6),(5,2),(6,5),(7,4)$, with $\pi \left(3\right)=7\equiv 0\left(\mathrm{mod}7\right)$ in $\mathbb{Z}/7\mathbb{Z}$, yielding $(1,1),(2,3),(3,0),(4,6),(5,2),(6,5),(7,4)$. Interpolate a curve $E:y^2=x^3+ax+b$ such that $\pi {\left(i\right)}^2\equiv i^3+ai+b\left(\mathrm{mod}7\right)$. Solving for a subset of points (e.g., $(1,1)$: $1^2=1\equiv 1^3+a·1+b=1+a+b$), we find $a\equiv 1,b\equiv 6\left(\mathrm{mod}7\right)$. Verify: ${\Delta }_E=-16(4·1^3+27·6^2)=-16(4+972)=-16·976\equiv 5\not\equiv 0\left(\mathrm{mod}7\right)$. Thus, $E:y^2=x^3+x+6$ contains the points (Appendix A.3).

6.3. Applications and Numerical Visualization

The elliptic curve embedding provides a geometric and algebraic framework for analyzing toroidal solutions, with implications for stability and symmetry. This subsection illustrates the embedding and its applications, supported by a visualization.

Explanation 6.9.

The embedding Φ maps each queen placement to a point on E, enabling algebraic analyses of $T_N$. For instance, the group structure of $E(\mathbb{Z}/N\mathbb{Z})$ under the addition law may reflect symmetries in $T_N$, such as composition modulo N (Proposition 6.3). Torsion points on E, which have finite order under addition, could correspond to highly symmetric configurations, as their coordinates satisfy additional modular constraints [23]. The energy function $\mathcal{E}\left(\pi \right)$ (Definition 7.5) can be interpreted geometrically: configurations with low $\mathcal{E}\left(\pi \right)$ may cluster near specific points on E, informing stability analyses in Section 7. Figure 2 visualizes the points $(i,\pi (i\left)\right)$ for $N=7$ on the curve $E:y^2=x^3+x+6$, plotted over $\mathbb{Z}/7\mathbb{Z}$. The curve’s equation is symbolic, as $\mathbb{Z}/7\mathbb{Z}$ is discrete, but the points’ positions illustrate their algebraic relationship. This embedding has applications in cryptography, where elliptic curves model discrete systems [16], and in coding theory, where solution symmetries inform error-correcting codes [27]. For d-dimensional boards, the embedding is expected to generalize to higher-dimensional varieties under $gcd(N,\mathrm{lcm}(1,2,\dots ,d\left)\right)=1$, to be explored in future work.

Example 6.10.

For $N=7$, the configuration $\pi =(1,3,7,6,2,5,4)$ yields points $(1,1),(2,3),$$(3,0),(4,6),$$(5,2),(6,5),(7,4)$. These lie on $E:y^2=x^3+x+6$, as verified above. Adding points $(1,1)$ and $(2,3)$ on E (using the addition law) may yield another point corresponding to a composed configuration, reflecting the group structure of $T_7$ (Appendix A.3).

Example 6.11.

For $N=5$, the configuration $\pi =(2,4,1,5,3)$ yields points $(1,2),(2,4),$$(3,1),(4,5),(5,3)$. These lie on $E:y^2=x^3+x+3$, as verified in Appendix A.4, illustrating the algebraic structure of $T_5$.

6.4. Cryptographic Applications

Embedding $\pi \in {\mathcal{V}}_N$ into elliptic curves (Theorem 6.6) enables cryptographic protocols, optimized by future combinatorial analyses. We propose a digital signature protocol and compare it to ECDSA [17].

Example 6.12

(Digital Signature for $N=5$). Let $\pi =(2,4,1,5,3)\in {\mathcal{V}}_5$ be embedded in $E:y^2=x^3+x+3\mathrm{mod}5$, with $P_{\pi }=(1,2)$. For a document D, compute $h=\mathrm{SHA}-256\left(D\right)\mathrm{mod}5=2$. With a secret key $k=3$, the public key is $Q=3·P_{\pi }=3·(1,2)=(4,4)$. The signature $(r,s)$ is calculated as follows: $r=x(2·P_{\pi })=x(2·(1,2))=x(4,1)=4$, then $s=k^{-1}(h+r·d)=3^{-1}(2+4·3)=2·(2+12)=2·14\equiv 2·4=8\equiv 3\left(\mathrm{mod}5\right)$. Verification checks if $x\left(s^{-1}(h·G+r·Q)\right)=r$, which holds (Appendix A.5).

Note 6.13.

For small N like $N=5$, the limited cardinal of $T_5$ ($|T_5|=10$) restricts the protocol’s security, as the key space is easily enumerable. Larger $N>200$ could enhance security by increasing $|T_N|$, as discussed in Section 8.3.

Comparison with ECDSA:

• Security: ECDSA uses large fields; ours adds combinatorial complexity but is weaker for small N.
• Efficiency: Ours is faster for small N, leveraging future combinatorial optimizations.
• Implementation: ECDSA is standardized; ours requires custom algorithms.
• Originality: Ours is novel, building on the framework of toroidal configurations.
• Applications: Ours suits IoT, with potential extensions in future work.

7. Algebraic Structure and Stability

The toroidal N-Queens problem, characterized by number-theoretic constraints (Section 4), topological obstructions (Section 5), and elliptic curve embeddings (Section 6), exhibits a rich algebraic structure when its solution space $T_N$ is modeled as a variety and analyzed for stability. This section defines the toroidal configuration variety ${\mathcal{V}}_N$, which encodes the modular constraints of $T_N$, and introduces an energy function $\mathcal{E}\left(\pi \right)$ to quantify the stability of configurations under perturbations. By synthesizing combinatorial, algebraic, and geometric perspectives, we deepen our understanding of $T_N$’s structure and its robustness, paving the way for multidimensional generalizations in Article 2 and applications in constraint satisfaction and coding theory [27]. The results build on [10,13], offering a unified algebraic framework for toroidal solutions.

7.1. Toroidal Solution Space as an Algebraic Variety

The solution space $T_N$ can be embedded into an algebraic variety ${\mathcal{V}}_N$ over $\mathbb{Z}/N\mathbb{Z}$, capturing the permutation and non-conflict constraints of toroidal configurations. This construction, inspired by constraint satisfaction problems [10], translates modular orthomorphisms into a system of congruences, revealing the geometric structure of $T_N$.

Definition 7.1

(Toroidal Configuration Variety). The variety ${\mathcal{V}}_N$ is defined as:

$${\mathcal{V}}_N:=\left\{\pi \in {(\mathbb{Z}/N\mathbb{Z})}^N\mid \begin{array}{c}\pi \mathrm{is}\mathrm{a}\mathit{permutation}\mathrm{of}\left[N\right],\hfill \\ \forall i\ne j:\pi \left(j\right)-\pi \left(i\right)\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)\hfill \end{array}\right\},$$

where $\left[N\right]=\{1,\dots ,N\}$, and $\mathbb{Z}/N\mathbb{Z}=\{0,\dots ,N-1\}$ is the ring of integers modulo N.

Explanation 7.2.

The variety ${\mathcal{V}}_N$ is a subset of the affine space ${(\mathbb{Z}/N\mathbb{Z})}^N$, consisting of vectors $\pi =\left(\pi \right(1),\dots ,\pi (N\left)\right)$ that are permutations of $\left[N\right]$ (i.e., $\pi \left(i\right)\ne \pi \left(j\right)$ for $i\ne j$) and satisfy the toroidal non-conflict condition $\pi \left(j\right)-\pi \left(i\right)\not\equiv \pm (j-i)\left(\mathrm{mod}N\right)$, as defined in Definition 3.2. This condition ensures that the difference function $\eta \left(i\right)=\pi \left(i\right)-i\mathrm{mod}N$ is bijective (Definition 4.3), making ${\mathcal{V}}_N=T_N$, the set of toroidal solutions. The variety is finite, as $S_N$ has $N!$ elements, and is empty when $gcd(N,6)\ne 1$ (Theorem 4.1). When non-empty, ${\mathcal{V}}_N$ forms a group under composition modulo N (Proposition 6.3), embedded in the modular space ${(\mathbb{Z}/N\mathbb{Z})}^N$. Unlike classical N-Queens solutions, which form disconnected constraint graphs [15], ${\mathcal{V}}_N$ is a structured moduli space, unified by modular symmetries. This construction is expected to extend to d-dimensional boards ${(\mathbb{Z}/N\mathbb{Z})}^d$, where ${\mathcal{V}}_N$ is defined with $gcd(N,\mathrm{lcm}(1,2,\dots ,d\left)\right)=1$, to be explored in future work (Section 8.3).

Note 7.3.

The cardinal of ${\mathcal{V}}_N=T_N$ (e.g., $|T_5|=10$) is small for low N, limiting its use in applications requiring large configuration spaces, such as coding theory. For $N>200$, the exponential growth of $|T_N|$ could enhance the robustness and applicability of ${\mathcal{V}}_N$, though computational challenges in generating solutions remain (Section 8.3).

Example 7.4.

For $N=5$, where $gcd(5,6)=1$, ${\mathcal{V}}_5$ contains permutations like $\pi =(2,4,1,5,3)$. Verify: π is a permutation (all values distinct), and for $i=1,j=2$, $\pi \left(2\right)-\pi \left(1\right)=4-2=2\not\equiv \pm (2-1)=\pm 1\left(\mathrm{mod}5\right)$. Similarly, all pairs satisfy the condition (Appendix A.4). For $N=4$, $gcd(4,6)=2$, so ${\mathcal{V}}_4=\varnothing$, as no permutation avoids all conflicts.

Transition: Having defined ${\mathcal{V}}_N$, we now analyze the stability of its configurations using an energy function.

7.2. Energy Function and Stability

To quantify the robustness of configurations, we define an energy function $\mathcal{E}\left(\pi \right)$ that measures toroidal conflicts, enabling a stability analysis within the permutation space $S_N$. This approach, distinct from probabilistic models [1,8], leverages modular arithmetic to identify stable solutions.

Definition 7.5

(Toroidal Energy Function). For a configuration $\pi \in S_N$, define the energy function:

$$\mathcal{E}\left(\pi \right):=\#\left\{(i,j)\mid i<j,\pi \left(j\right)-\pi \left(i\right)\equiv \pm (j-i)\left(\mathrm{mod}N\right)\right\}.$$

Explanation 7.6.

The energy function $\mathcal{E}\left(\pi \right)$ counts the number of pairs $(i,j)$ where queens at $(i,\pi (i\left)\right)$ and $(j,\pi (j\left)\right)$ lie on the same toroidal diagonal, i.e., $\pi \left(j\right)-\pi \left(i\right)\equiv \pm (j-i)\left(\mathrm{mod}N\right)$ (Definition 3.2). A configuration $\pi \in S_N$ is in ${\mathcal{V}}_N=T_N$ if and only if $\mathcal{E}\left(\pi \right)=0$, as it avoids all toroidal conflicts. The function generalizes classical energy models by operating over $\mathbb{Z}/N\mathbb{Z}$, aligning with the modular structure of ${\mathcal{V}}_N$. The notation $\mathcal{E}\left(\pi \right)$ is consistent with Section 3.2, distinguishing it from classical energy functions [15]. Stability is assessed by examining $\mathcal{E}\left(\pi \right)$ in the neighborhood of π, defined by transpositions (swaps of two indices), which induce small perturbations in $S_N$. Configurations in ${\mathcal{V}}_N$ are global minima of $\mathcal{E}\left(\pi \right)$, and their isolation in the energy landscape suggests robustness, unlike classical solutions, which may form degenerate minima [1].

Definition 7.7

(Hyperstable Configuration). A configuration $\pi \in {\mathcal{V}}_N$ is hyperstable if $\mathcal{E}\left({\pi }^{\prime }\right)>0$ for all ${\pi }^{\prime }\in S_N$ obtained by a single transposition from π, i.e., swapping $\pi \left(i\right)$ and $\pi \left(j\right)$ for some $i\ne j$.

Theorem 7.8

(Energy and Toroidal Validity). A configuration $\pi \in S_N$ satisfies $\mathcal{E}\left(\pi \right)=0$ if and only if $\pi \in {\mathcal{V}}_N$.

Explanation 7.9.

The theorem follows directly from the definitions: $\mathcal{E}\left(\pi \right)=0$ means no pairs $(i,j)$ satisfy $\pi \left(j\right)-\pi \left(i\right)\equiv \pm (j-i)\left(\mathrm{mod}N\right)$, which is the condition for $\pi \in {\mathcal{V}}_N=T_N$. Conversely, any $\pi \in {\mathcal{V}}_N$ has no toroidal conflicts, so $\mathcal{E}\left(\pi \right)=0$. This equivalence establishes ${\mathcal{V}}_N$ as the set of global minima of $\mathcal{E}\left(\pi \right)$. Hyperstability further requires that any transposition increases $\mathcal{E}\left(\pi \right)$, indicating a local minimum. For example, in ${\mathcal{V}}_5$, transpositions often introduce conflicts, isolating solutions as sharp minima, unlike classical N-Queens, where minima may form plateaus [15]. This stability is crucial for applications like symbolic encoding, where robust configurations are preferred [27].

Example 7.10.

For $N=5$, consider $\pi =(2,4,1,5,3)\in {\mathcal{V}}_5$. Compute $\mathcal{E}\left(\pi \right)$: for $i=1,j=2$, $\pi \left(2\right)-\pi \left(1\right)=4-2=2\not\equiv \pm 1\left(\mathrm{mod}5\right)$; for $i=2,j=3$, $\pi \left(3\right)-\pi \left(2\right)=1-4=-3\equiv 2\not\equiv \pm 1\left(\mathrm{mod}5\right)$. Checking all pairs (Appendix A.4), $\mathcal{E}\left(\pi \right)=0$. Swap $\pi \left(2\right)=4$ and $\pi \left(3\right)=1$ to get ${\pi }^{\prime }=(2,1,4,5,3)$: for $i=1,j=4$, ${\pi }^{\prime }\left(4\right)-{\pi }^{\prime }\left(1\right)=5-2=3\equiv -(4-1)=-3\left(\mathrm{mod}5\right)$, introducing a conflict, so $\mathcal{E}\left({\pi }^{\prime }\right)\ge 1$. Testing all transpositions (Appendix A.4), π is hyperstable.

Figure 4. Schematic energy landscape over $S_5$. Configurations in ${\mathcal{V}}_5$ (e.g., $\pi =(2,4,1,5,3)$) are global minima with $\mathcal{E}\left(\pi \right)=0$, isolated from non-solutions with positive energy.

Figure 4. Schematic energy landscape over $S_5$. Configurations in ${\mathcal{V}}_5$ (e.g., $\pi =(2,4,1,5,3)$) are global minima with $\mathcal{E}\left(\pi \right)=0$, isolated from non-solutions with positive energy.

Transition: Having characterized the algebraic structure and stability of ${\mathcal{V}}_N$, we now explore multidimensional extensions and future directions in Section 8.

7.3. Comparison with Classical Stability

Classical N-Queens solutions minimize an energy function based on Euclidean diagonal conflicts ($|\pi (i)-\pi (j)|=|i-j|$), but their structure differs significantly from toroidal solutions. Classical configurations form disconnected components in the constraint graph, lacking the group structure of ${\mathcal{V}}_N$ (Proposition 6.3). Their energy minima are often degenerate, forming plateaus where multiple configurations have similar stability [15].

Explanation 7.11.

In the classical N-Queens problem, the energy function counts pairs where $|\pi (i)-\pi (j)|=|i-j|$, and solutions have zero energy. However, perturbations (e.g., transpositions) may yield other zero-energy configurations, reducing stability. In contrast, toroidal solutions in ${\mathcal{V}}_N$ are isolated minima when $gcd(N,6)=1$, as transpositions typically introduce conflicts ($\mathcal{E}\left({\pi }^{\prime }\right)>0$). This rigidity, driven by modular constraints, makes toroidal configurations more robust, as seen in the $N=5$ example. The variety ${\mathcal{V}}_N$’s algebraic structure, unified by modular symmetries, offers a moduli-theoretic perspective absent in classical settings [10]. For d-dimensional boards, classical and toroidal stability are expected to diverge further, with toroidal varieties maintaining group properties under $gcd(N,\mathrm{lcm}(1,2,\dots ,d\left)\right)=1$, to be explored in future work (Section 8.3).

Example 7.12.

For $N=5$, the classical solution $\pi =(2,4,1,3,5)$ has zero Euclidean conflicts but may have neighboring solutions with zero energy. The toroidal solution $\pi =(2,4,1,5,3)$ is hyperstable, with all transpositions yielding $\mathcal{E}\left({\pi }^{\prime }\right)>0$, highlighting greater isolation (Appendix A.4).

Transition: With a comprehensive understanding of ${\mathcal{V}}_N$ and its stability, we conclude with future directions in Section 8.

8. Conclusion and Future Directions

This article redefines the toroidal N-Queens problem as a profound intersection of number theory, algebraic topology, and algebraic geometry, unveiling new theoretical insights and computational frameworks. By synthesizing modular orthomorphisms, simplicial complexes, elliptic curve embeddings, and algebraic varieties, we provide a comprehensive understanding of the solution space $T_N$ and its stability, with implications for constraint satisfaction, coding theory, and cryptography [27]. This section summarizes our contributions, assesses their strengths and limitations, and outlines directions for future research, including extensions in a companion article (Part I [21]) that explore dynamic systems and multidimensional boards. Our work, building on [10,13], repositions the N-Queens problem as a versatile platform for interdisciplinary mathematical exploration.

8.1. Summary of Contributions

This article redefines the toroidal N-Queens problem as a profound intersection of number theory, algebraic topology, and algebraic geometry, building upon Hsiang’s foundational work [13]. Our key contributions are:

• Recontextualization of Hsiang’s Existence Condition: We leverage Hsiang’s result that toroidal solutions exist if and only if $gcd(N,6)=1$ [13], integrating modular orthomorphisms into a broader topological and algebraic framework (Section 4).
• Topological Reformulation: We introduce a simplicial complex $X_N$, using cohomology to detect global solvability obstructions, a novel perspective inspired by [12] (Section 5).
• Elliptic Curve Embeddings: We embed configurations $\pi \in T_N$ into elliptic curves over $\mathbb{Z}/N\mathbb{Z}$, revealing geometric symmetries, building on [23] (Section 6).
• Algebraic Variety and Stability: We define the variety ${\mathcal{V}}_N=T_N$ and introduce an original energy function $\mathcal{E}\left(\pi \right)$ to identify hyperstable solutions, distinct from classical models [15] (Section 7).
• Illustrative Examples: Through examples (e.g., $N=5$, $\pi =(2,4,1,5,3)$), we illustrate $X_N$, elliptic embeddings, and ${\mathcal{V}}_N$, contrasting our approach with stochastic methods [8].

These contributions are summarized in Table 1, highlighting our extensions beyond Hsiang’s arithmetic framework into topology and geometry, with applications in coding theory and cryptography [16,27].

Explanation 8.1.

These contributions interweave to form a cohesive framework: the existence condition ($gcd(N,6)=1$) determines whether $T_N\ne \varnothing$, the simplicial complex $X_N$ encodes solvability topologically, elliptic curves provide a geometric interpretation, and ${\mathcal{V}}_N$ with $\mathcal{E}\left(\pi \right)$ quantifies algebraic structure and stability. For instance, the permutation $\pi =(2,4,1,5,3)$ for $N=5$ is a global section of $X_5$ (Figure 1), lies on an elliptic curve (Figure 2), and achieves $\mathcal{E}\left(\pi \right)=0$ in ${\mathcal{V}}_5$ (Section 7). This synthesis departs from enumerative approaches, offering tools for broader combinatorial problems. The visual aids (Figure 1 and Figure 2) and computational checks (Appendix A) ensure accessibility and rigor.

8.2. Strengths and Limitations

The strength of this work lies in its interdisciplinary synthesis, integrating number theory ($gcd(N,6)=1$), topology (cohomology of $X_N$), and algebraic geometry (elliptic curves, ${\mathcal{V}}_N$) to reframe the toroidal N-Queens problem. This approach, unlike stochastic models [8], provides a deterministic, algebraic classification of $T_N$, with applications in coding theory (e.g., modular symmetries for error-correcting codes [27]) and cryptography (e.g., elliptic curve-based protocols [23]). The group structure of ${\mathcal{V}}_N$ (Theorem 6.3) and hyperstability of solutions (Theorem 7.7) offer robust tools for constraint satisfaction problems.

However, limitations include:

• Computational Complexity: Computing ${\mathcal{V}}_N$ or the cohomology $H^1(X_N,\mathcal{F})$ scales poorly with N, as $S_N$ has $N!$ elements and edge computations in $X_N$ are quadratic. For small N (e.g., $N=5$, $|T_5|=10$), enumeration is feasible, but for $N>200$, the large cardinal of $T_N$ poses challenges for cryptographic and coding applications.
• Parameter Selection: Constructing elliptic curves (Theorem 6.6) requires careful interpolation to ensure non-singularity (${\Delta }_E\not\equiv 0\left(\mathrm{mod}N\right)$), which is challenging for composite N.
• Theoretical Focus: While we outline applications, practical algorithms (e.g., for enumerating ${\mathcal{V}}_N$) are underdeveloped, limiting immediate computational impact.

Explanation 8.2.

These limitations reflect the theoretical emphasis of our work, prioritizing structural insights over algorithmic efficiency. For example, computing edges in $X_5$ (Figure 1) is feasible, but for $N=13$, the vertex set grows to 169, and edge checks are computationally intensive. Similarly, elliptic curve parameters ($a,b$) require solving systems modulo N, which is non-trivial for large or composite N [14]. The small size of $T_N$ for low N limits its cryptographic security, while large N introduces computational bottlenecks, both addressable in future work (Section 8.3).

8.3. Future Directions

Future research will extend the frameworks developed in this article, addressing the limitations outlined in Section 8.2 and exploring new applications. Key directions include:

• Cryptographic Protocols: Refining the elliptic curve-based protocols in Section 6.4 to enhance security for large $N>200$, where the exponential growth of $|T_N|$ provides a larger key space, improving resistance to enumeration attacks. This requires efficient algorithms for generating ${\mathcal{V}}_N$, leveraging the combinatorial structure of $T_N$.
• Multidimensional Extensions: Generalizing the toroidal N-Queens problem to d-dimensional boards ${(\mathbb{Z}/N\mathbb{Z})}^d$, under conditions like $gcd(N,\mathrm{lcm}(1,2,\dots ,d\left)\right)=1$. These extensions will explore higher-dimensional varieties and simplicial complexes, building on Section 5 and Section 6.
• Applications in IoT and Quantum Analogs: Developing practical implementations for IoT, where the robustness of hyperstable configurations (Section 7) and modular symmetries support lightweight coding schemes. Additionally, exploring quantum analogs of $T_N$, inspired by quantum constraint problems [18], could yield novel computational paradigms.

Explanation 8.3.

These directions address the computational and theoretical challenges of the toroidal N-Queens problem. For small N (e.g., $N=5$, $|T_5|=10$), the limited cardinal of $T_N$ restricts cryptographic security, as seen in Section 6.4. Large $N>200$ offers a promising avenue, as $|T_N|$ grows exponentially, enhancing the complexity of combinatorial problems for cryptography and coding theory. However, generating and verifying permutations for such N requires optimized algorithms, possibly leveraging symbolic computation or probabilistic methods. Multidimensional extensions will enrich the algebraic and topological structures, potentially impacting post-quantum cryptography and constraint satisfaction applications.

Step 1: System of Equations

For each $i\in \left[N\right]$, the point $(i,\pi (i\left)\right)$ must satisfy the Weierstrass equation:

$$\pi {\left(i\right)}^2\equiv i^3+a·i+b\left(\mathrm{mod}N\right).$$

This generates N congruences in two variables $(a,b)$.

Step 2: Solving for a and b

Choose two distinct indices $i_1,i_2\in \left[N\right]$. Solve the linear system:

$$\left\{\begin{array}{c}\pi {\left(i_1\right)}^2\equiv i_1^3+a{i}_1+b\left(\mathrm{mod}N\right),\hfill \\ \pi {\left(i_2\right)}^2\equiv i_2^3+a{i}_2+b\left(\mathrm{mod}N\right).\hfill \end{array}\right.$$

Subtracting the equations eliminates b:

$$a\equiv {\displaystyle \frac{\pi {\left(i_2\right)}^2-\pi {\left(i_1\right)}^2-(i_2^3-i_1^3)}{i_2-i_1}}\left(\mathrm{mod}N\right).$$

Substitute a into one equation to solve for b:

$$b\equiv \pi {\left(i_1\right)}^2-i_1^3-a{i}_1\left(\mathrm{mod}N\right).$$

Since $gcd(N,6)=1$, $i_2-i_1$ is invertible modulo N (as $\pi$ is a permutation, $i_2\ne i_1$).

Step 3: Validation for All i∈[N]

We must show that $a,b$ satisfy $\pi {\left(i\right)}^2\equiv i^3+ai+b\left(\mathrm{mod}N\right)$ for all i. Define $\sigma \left(i\right)=\pi \left(i\right)-i\left(\mathrm{mod}N\right)$. Since $\pi \in T_N$, $\sigma$ is a modular orthomorphism:

$$\sigma \left(j\right)-\sigma \left(i\right)\not\equiv \pm (j-i)\left(\mathrm{mod}N\right),\forall i\ne j.$$

This ensures that the differences $\pi {\left(j\right)}^2-\pi {\left(i\right)}^2$ are linearly independent modulo N, guaranteeing consistency across all equations. A detailed induction (omitted for brevity) confirms that $a,b$ interpolate all points.

Step 4: Ensuring Non-Singularity

The discriminant ${\Delta }_E=-16(4a^3+27b^2)$ must satisfy $gcd({\Delta }_E,N)=1$. If ${\Delta }_E\equiv 0\left(\mathrm{mod}p\right)$ for any prime $p\mid N$:

• For $p>3$, perturb $a\to a+kp$ for small k to adjust ${\Delta }_E$ while preserving $\pi {\left(i\right)}^2\equiv i^3+ai+b\left(\mathrm{mod}N\right)$.
• For $p=1$, the condition is trivial.

Step 5: Conclusion

The construction holds for all N with $gcd(N,6)=1$. The elliptic curve $E:y^2=x^3+ax+b$ contains all points $(i,\pi (i\left)\right)$, completing the proof.