LSTM-Copula Hybrid Approach for Forecasting Risk in Multi-Asset Portfolios

1. Introduction

In the context of increasingly complex and diversified global financial markets, risk management has become a central issue in asset allocation and investment decisions [1]. The volatility, nonlinearity, and highly dynamic correlations among assets present significant challenges to traditional risk measurement methods. In multi-asset portfolio management, investors are not only concerned with the risk levels of individual assets but also with the impact of asset interdependence on overall portfolio risk [2]. Therefore, developing a risk prediction model that can effectively capture dynamic dependencies among assets and demonstrate strong temporal modeling capabilities has become a key focus in financial technology research.

Copula functions are widely used tools for modeling dependency structures in finance. They have attracted significant attention due to their ability to capture correlations among variables without relying on marginal distribution assumptions. Compared to traditional linear correlation methods, copula functions offer greater flexibility. They can adapt to inconsistent marginal distributions and exhibit strong performance in capturing tail dependencies in financial data. This is particularly valuable during extreme market conditions, where asymmetric relationships and tail dependencies between assets are more pronounced. However, copula models in static settings fail to reflect the evolving dynamics of financial markets. Thus, integrating Copula functions with temporal modeling techniques is essential for improving the accuracy and foresight of risk predictions [3]. In recent years, the development of deep learning has led to widespread adoption of Long Short-Term Memory (LSTM) networks for time series forecasting. LSTM has shown strong performance in modeling nonlinear and non-stationary financial time series. Its gated structure mitigates the vanishing gradient problem faced by traditional recurrent neural networks, enabling effective long-term dependency modeling. LSTM has achieved notable results in HCI [4,5], market forecasting, asset pricing, and algorithmic trading. However, LSTM alone lacks the ability to model inter-asset dependencies. In multi-asset scenarios, this limitation may result in biased risk estimates. Therefore, combining LSTM with Copula functions offers a theoretically sound and practically feasible approach to integrated risk modeling [6].

From a macro perspective, accurate risk prediction is vital not only for safeguarding investor capital and optimizing asset allocation but also for maintaining the stability of the financial system. In multi-asset portfolios, ignoring the transmission mechanisms of risk and the temporal evolution of asset relationships may lead to collective losses during systemic risk events, creating a "black swan" effect. Hence, a model capable of capturing both complex inter-asset structures and temporal dynamics is essential. It enhances the scientific basis of portfolio construction and strengthens the resilience of investment strategies. This study also introduces a new paradigm in financial technology by integrating statistical modeling with deep learning, promoting intelligent and refined risk management methods [7].

2. Method

In recent years, advanced neural architectures have become central to modeling complex financial dynamics. One Transformer-based method [8] demonstrated improved capability in capturing both temporal dependencies and multi-dimensional features, reinforcing the importance of deep temporal models for financial applications. Complementing this, a multimodal factor modeling approach [9] incorporated heterogeneous data streams, offering support to this paper’s strategy of fusing marginal and dependency modeling through deep learning and statistical tools.

Efforts in high-frequency financial environments further showcase the relevance of deep learning in complex, sparse datasets. A deep anomaly detection framework [10] for trading systems exemplifies how robust feature learning can identify irregular patterns, aligning well with the high-dimensional settings addressed in this study. Additionally, a probabilistic approach [11] leveraging graphical models and variational inference provided strategies to handle class imbalance—paralleling the current work’s focus on tail-risk modeling and rare event prediction using Copula structures. Graph-based methodologies have also informed this paper’s approach to modeling inter-asset dependencies. One study [12] used graph neural networks to uncover latent relational patterns within user behavior data—methods which inspire the interdependence modeling of assets within a portfolio. Building on this, a graph attention mechanism for heterogeneous data [13] offers a blueprint for learning risk propagation across structured financial entities. Further enhancement was achieved through a self-supervised GNN approach [14], which demonstrated efficient representation learning from complex and diverse relational structures—concepts closely tied to joint distribution modeling in Copula functions.

From a broader perspective, developments in deep learning frameworks contribute significantly to the scalability and adaptability of integrated models like the one proposed. A dynamic Transformer-based mining framework [15] introduced context-awareness into learning systems, a principle adopted in improving interpretability within this hybrid model. Moreover, techniques for efficient model deployment [16], such as distillation and fine-tuning, address real-world implementation challenges of deep learning systems in finance. Architectural optimization through neural architecture search [17] further informs future extensions of this model, especially in tailoring hybrid systems for varying market conditions. Collectively, these methodologies not only provide technical insights into modeling temporal sequences and dependencies but also lay the groundwork for scalable and interpretable systems like the LSTM-Copula hybrid proposed in this research.

3. Method

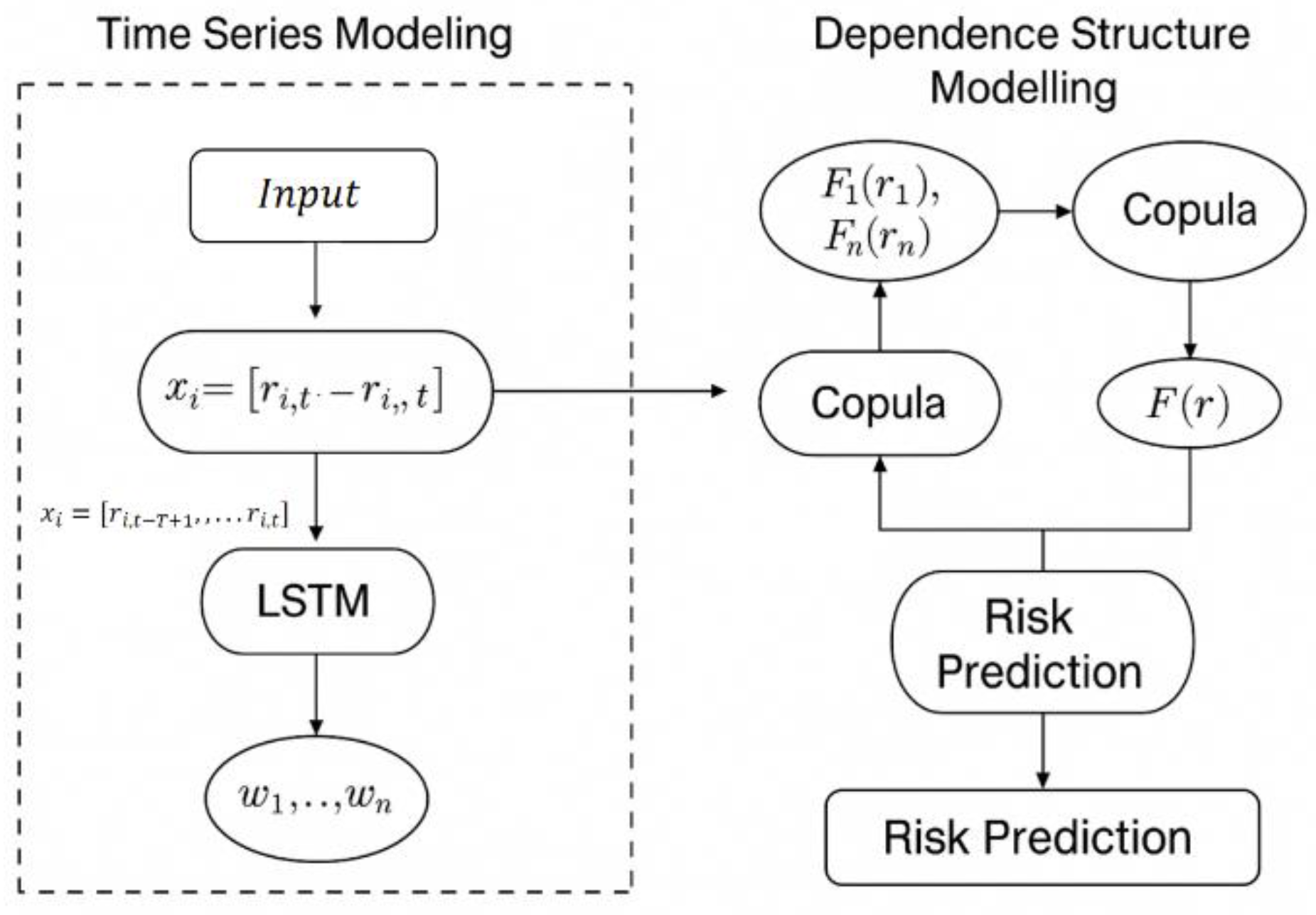
The multi-asset portfolio risk prediction model constructed in this study mainly includes two core modules: a time series modeling module and an asset dependency structure modeling module. Its model architecture is shown in Figure 1.

Figure 1 presents the comprehensive architecture of the proposed multi-asset portfolio risk prediction model, which integrates a time series modeling module and a dependency structure modeling module. The design builds upon prior work in deep learning and statistical modeling. Inspired by Liang et al. [18], who emphasize robust feature extraction from complex financial data through neural networks, the left-side module employs Long Short-Term Memory (LSTM) networks to model the historical return sequences of individual assets. These networks dynamically extract crucial temporal features and generate the marginal distribution parameters necessary for dependency modeling. On the right side, the dependency structure module is influenced by insights from Wang [19] and Feng [20], particularly regarding the treatment of nonlinear interdependencies and tail risks in financial systems. This module utilizes Copula functions to effectively capture the joint distribution across multiple assets, emphasizing flexibility in modeling tail co-movements. By integrating the asset-specific marginal distributions and Copula-based dependency structure, and subsequently applying asset weights, the model produces an aggregated risk measure for the portfolio. This two-pronged architecture capitalizes on LSTM’s sequence learning capacity and the Copula function’s power in capturing high-dimensional dependencies, thereby enhancing the precision and robustness of portfolio risk estimation under real-world financial complexities.

First, considering that financial asset price series usually exhibit strong nonlinearity, non-stationarity and long-term dependence characteristics, the LSTM network is used to model the yield time series of each asset. Assuming that the yield of asset i at time t is $r_{i,t}$, and the input sequence is a vector $x_i=[r_{i,t-T+1},\mathrm{...},r_{i,t}]$ of length T, the LSTM network dynamically models the sequence through a nonlinear gating mechanism to obtain a hidden state output $h_i=LSTM(x_i)$, which can be regarded as a risk characterization vector of the asset at the current moment. This process not only retains important patterns in historical information, but can also be used to estimate marginal distribution parameters in subsequent Copula modeling.

To effectively model the intricate dependency structure between financial assets, this study adopts the Copula function to construct the joint distribution across multiple asset returns. Drawing on recent developments in financial data modeling and representation learning [21], as well as methods that emphasize the importance of capturing temporal and multi-dimensional dependencies [22], and techniques for handling heterogeneous relationships in complex financial systems [23], this approach offers a flexible and robust mechanism for modeling nonlinear and tail dependencies—crucial for accurate portfolio risk assessment.According to Sklar's theorem, any multivariate joint distribution function $F(r)$, where $r=[r_1,r_2,\mathrm{...},r_n]$, can be decomposed into a combination of its marginal distribution function $F_i(r_i)$ and a Copula function $C(\cdot )$, that is:

$$F(r)=C(F_1(r_1),F_2(r_2),\mathrm{...},F_n(r_n))$$

Considering the importance of tail correlation in financial markets, this paper uses the t-Copula function with tail dependency modeling capability, which is in the form of:

$$C(u_1,\mathrm{...},u_n)=t_v^{{\displaystyle \sum }}(t_v^{-1}(u_1),\mathrm{...},t_v^{-1}(u_n))$$

(1)

$t_v^{{\displaystyle \sum }}$ represents the cumulative distribution function of the multivariate t distribution with v degrees of freedom and covariance matrix ${\displaystyle \sum }$, and $t_v^{-1}$ is the inverse function of the t distribution. The marginal distribution $F_i(r_i)$ can be estimated by the prediction residual sequence output by the LSTM network, and further distribution fitting is performed to make the Copula function modeling more in line with the structural characteristics of the actual data.

Combining the modeling results of LSTM and Copula functions, this paper finally conducts a quantitative assessment of the risk level of multi-asset portfolios based on the joint distribution function. Assuming the portfolio weight vector is $w=[w_1,w_2,\mathrm{...},w_n]$, the portfolio return is:

$$R_t={\displaystyle \sum _{i=1}^n{w}_i{r}_{i,t}}$$

(2)

Based on the joint distribution $F(r)$, the value-at-risk and conditional value-at-risk (VaR) of the portfolio return at a given confidence level $\alpha$ can be calculated, thereby achieving dynamic prediction and control of potential losses. This method combines the advantages of LSTM in modeling temporal dependencies and the ability of Copula in capturing complex correlation structures between variables, providing a more flexible and theoretically supported solution for modeling high-dimensional asset portfolio risks.

4. Experiment

4.1. Datasets

This study utilizes a dataset sourced from Yahoo Finance, comprising daily closing prices of ten representative U.S. financial assets—including stocks, bonds, gold, and crude oil—from January 1, 2013, to December 31, 2023 (approximately 2,600 trading days). The selected assets ensure broad market and industry coverage, supporting a realistic multi-asset portfolio construction. Raw prices were converted to log returns and standardized to address scale differences. Missing values due to market suspensions were filled using linear interpolation, and extreme outliers were removed to ensure input stability. The data were split chronologically into training (80%) and testing (20%) sets to prevent future data leakage. The dataset reflects typical financial time series properties such as volatility, non-stationarity, and nonlinear dependencies, posing challenges for risk modeling.

4.2. Experimental Results

This paper first gives a performance comparison of different models in multi-asset portfolio risk prediction, and the experimental results are shown in Table 1.

As shown in Table 1, the LSTM-Copula model achieves the best performance in multi-asset risk prediction, with a VaR coverage of 96.2% and CVaR accuracy of 94.8%, demonstrating its strength in capturing temporal dynamics and inter-asset dependencies. The GRU + VAE-Copula model performs closely in CVaR accuracy, benefiting from VAE’s marginal distribution learning and GRU’s efficiency, while TCN-Copula captures local patterns but lacks global modeling capacity. In contrast, Transformer-VaR shows high KLD due to poor joint distribution modeling, and Diffusion-RiskNet suffers from training instability. 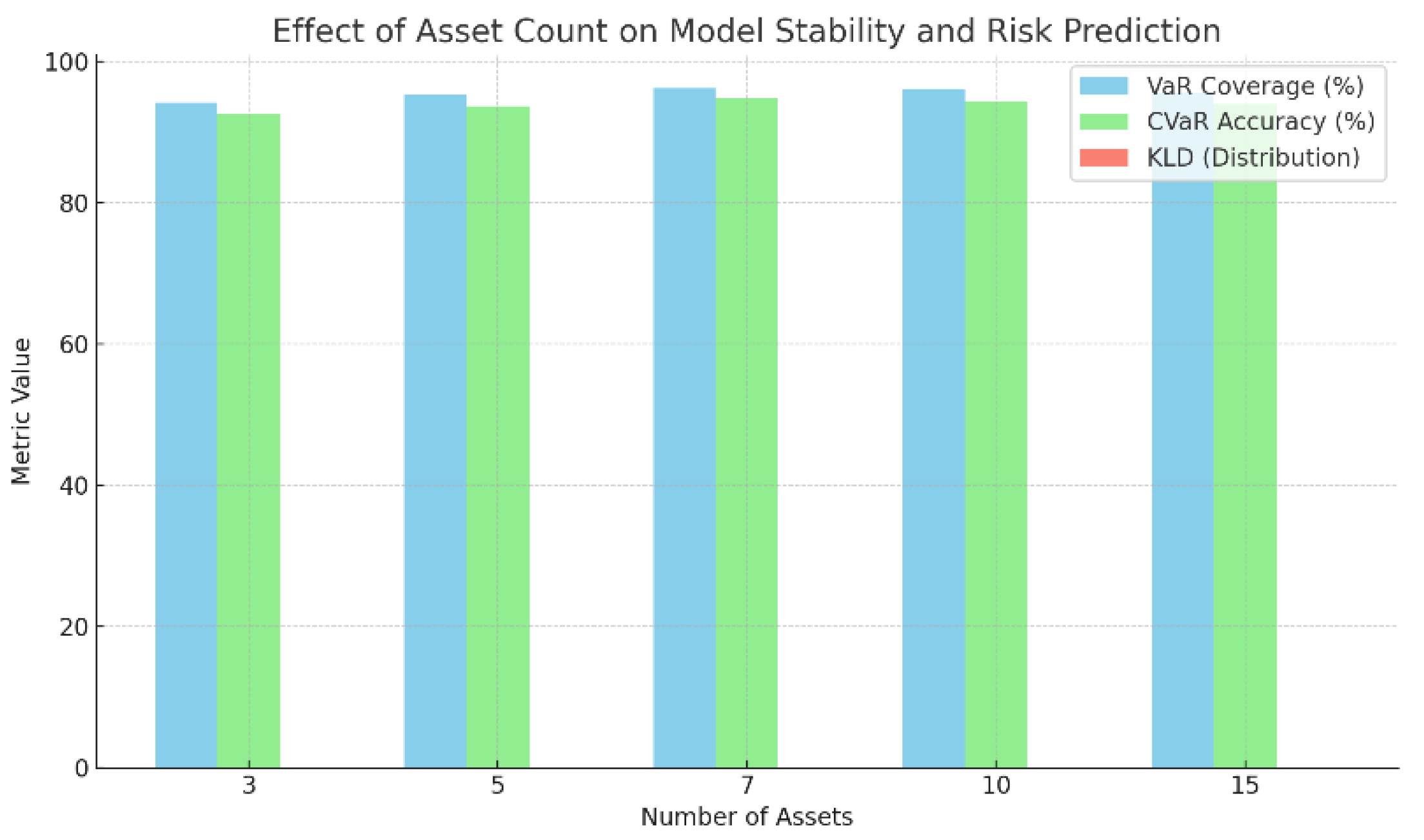Figure 2 further illustrates model stability across varying portfolio sizes.

Figure 2 illustrates that the LSTM-Copula model maintains strong risk prediction performance across varying portfolio sizes, with the best results achieved when the asset count is seven, where both VaR coverage and CVaR accuracy reach peak levels. This indicates that a medium-sized portfolio offers sufficient informational richness without introducing excessive noise, allowing the model to capture market risk structures more effectively. When the number of assets increases to 10 or 15, a slight decline in CVaR accuracy and distribution fitting (KLD) is observed, suggesting increased modeling difficulty due to more complex inter-asset dependencies. In contrast, smaller portfolios with 3 or 5 assets provide limited input diversity, weakening the model’s ability to capture latent linkage risks. These results highlight the sensitivity of the model to portfolio size and emphasize the need for balanced asset selection. 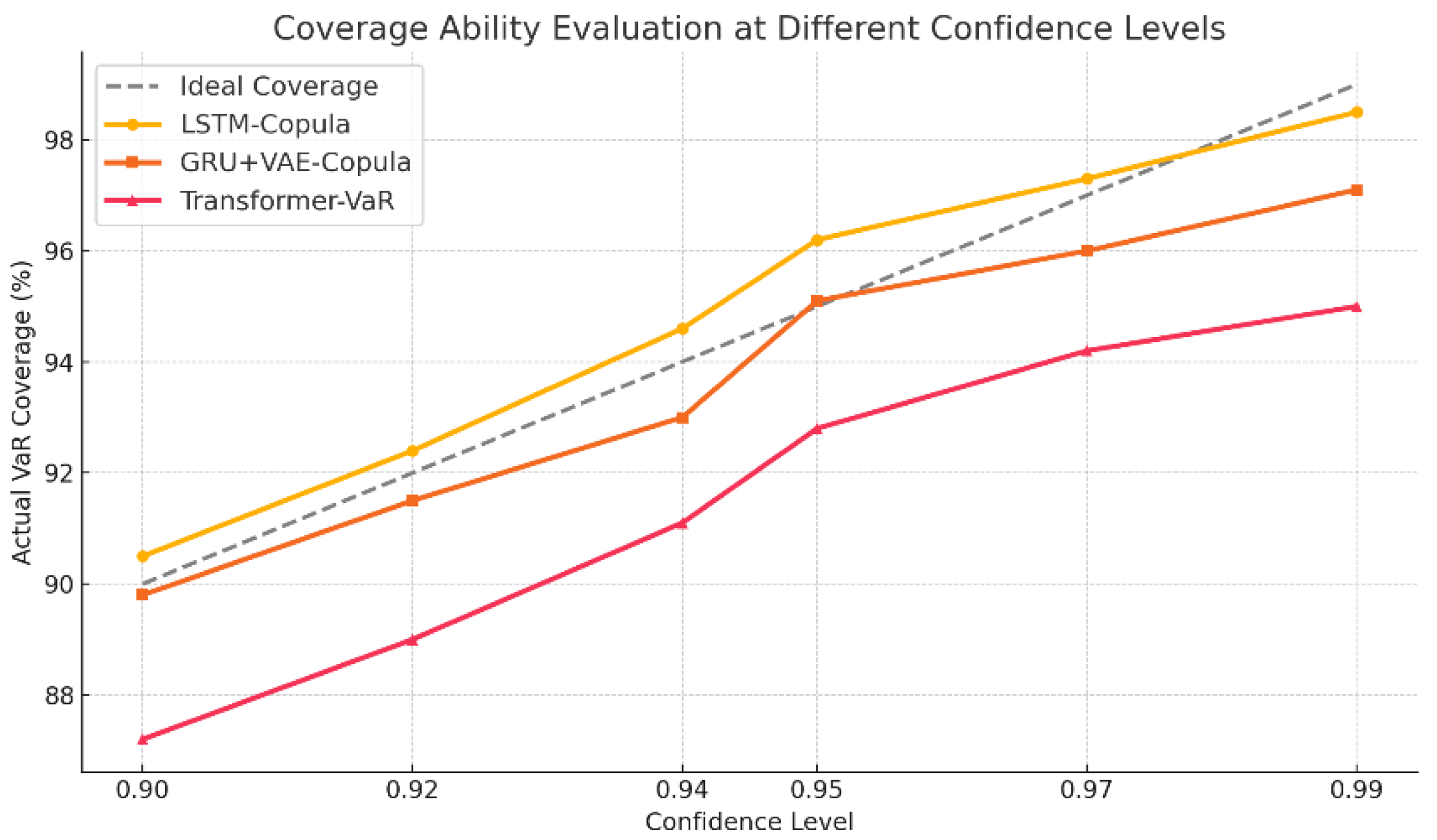Figure 3 further reports the model’s risk coverage ability based on prediction confidence intervals.

Figure 3 shows the actual VaR coverage rates of different models across multiple confidence levels. Compared to the ideal coverage line, the LSTM-Copula model maintains a high level of consistency across all intervals. At confidence levels above 0.95, its coverage rate closely approaches or slightly exceeds the theoretical value. This demonstrates the model’s refined and stable ability to define risk boundaries.

The GRU + VAE-Copula model exhibits a similar trend to LSTM-Copula and shows a certain level of stability. However, slight deviations are observed at some intervals, particularly at lower confidence levels. This suggests a mildly conservative bias in its estimation of risk intervals. Nevertheless, its performance at higher confidence levels remains within a reasonable range. The model demonstrates good tail risk identification ability and is suitable for supporting risk management decisions.

The Transformer-VaR model shows lower coverage rates than the other two models at all confidence levels. The deviation is especially notable at high confidence levels. This reflects a tendency to underestimate risk when constructing risk intervals. The result indicates that without incorporating explicit dependency modeling, Transformer-VaR struggles to capture complex inter-asset structures. This limits its effectiveness in high-precision risk forecasting tasks.

5. Conclusions

This study proposes a multi-asset portfolio risk prediction model that integrates Long Short-Term Memory (LSTM) networks with Copula functions. The goal is to capture both the temporal dependencies in asset return series and the complex inter-asset correlation structure. LSTM is used for marginal distribution modeling, while Copula functions are employed to construct the joint distribution. This enables dynamic prediction and evaluation of key risk metrics such as Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR). The model shows superior stability and predictive accuracy across multiple experiments.

The experimental design includes model comparison, sensitivity analysis with respect to the number of assets, and evaluation of risk coverage under different confidence intervals. These tests comprehensively verify the model's adaptability to high-dimensional and sparse financial data. Results show that the LSTM-Copula model outperforms other advanced models in boundary control, tail risk identification, and distribution fitting. This highlights the importance and potential of combining deep learning with statistical dependency modeling in financial risk analysis. In addition, the experiments involving changes in the number of assets indicate that the model performs best with moderately sized portfolios. Its fitting capacity shows certain limitations in high-dimensional settings. This suggests that future work may focus on enhancing model scalability and optimizing its structure to better handle complex market conditions. The confidence interval experiments also demonstrate the consistency of the LSTM-Copula model in risk control across different levels, offering practical support for tolerance-based risk regulation. This study not only extends the theoretical landscape of risk modeling but also provides a scalable and interpretable framework for practical financial risk management.