Submitted:
01 April 2025
Posted:
01 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
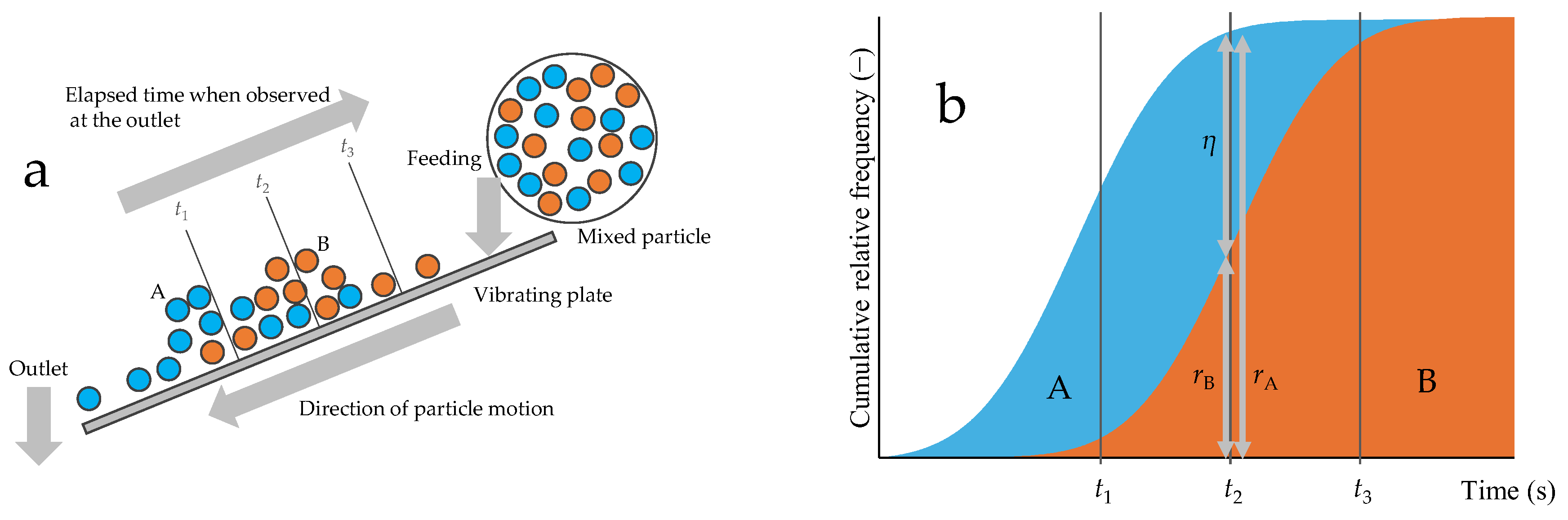
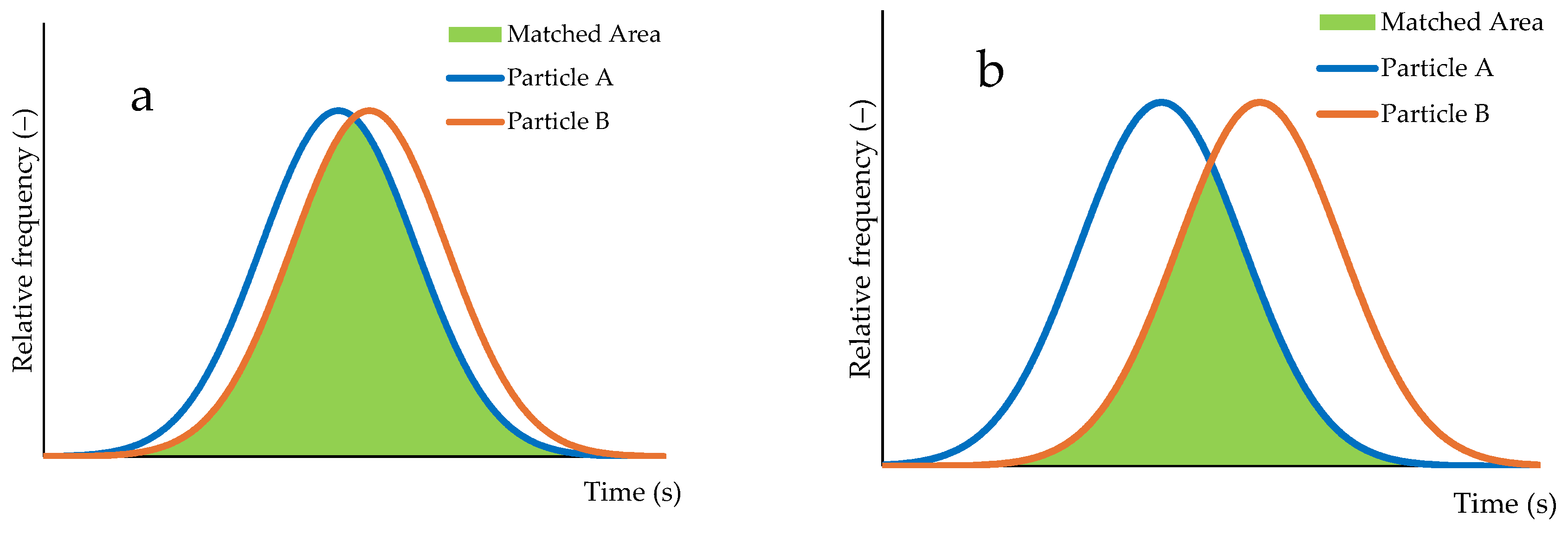
2.1. Sorting and Newton’s Efficiency
2.2. Instruments
2.3. Materials
2.4. Overview of Existing Sorting Experimental Procedures
2.4.1. Visual Sorting
2.4.2. Pumice Settling Process via Decompression Treatment
2.5. Procedure for Sorting Experiments Using a Vibratory Sorter
3. Results and Discussion
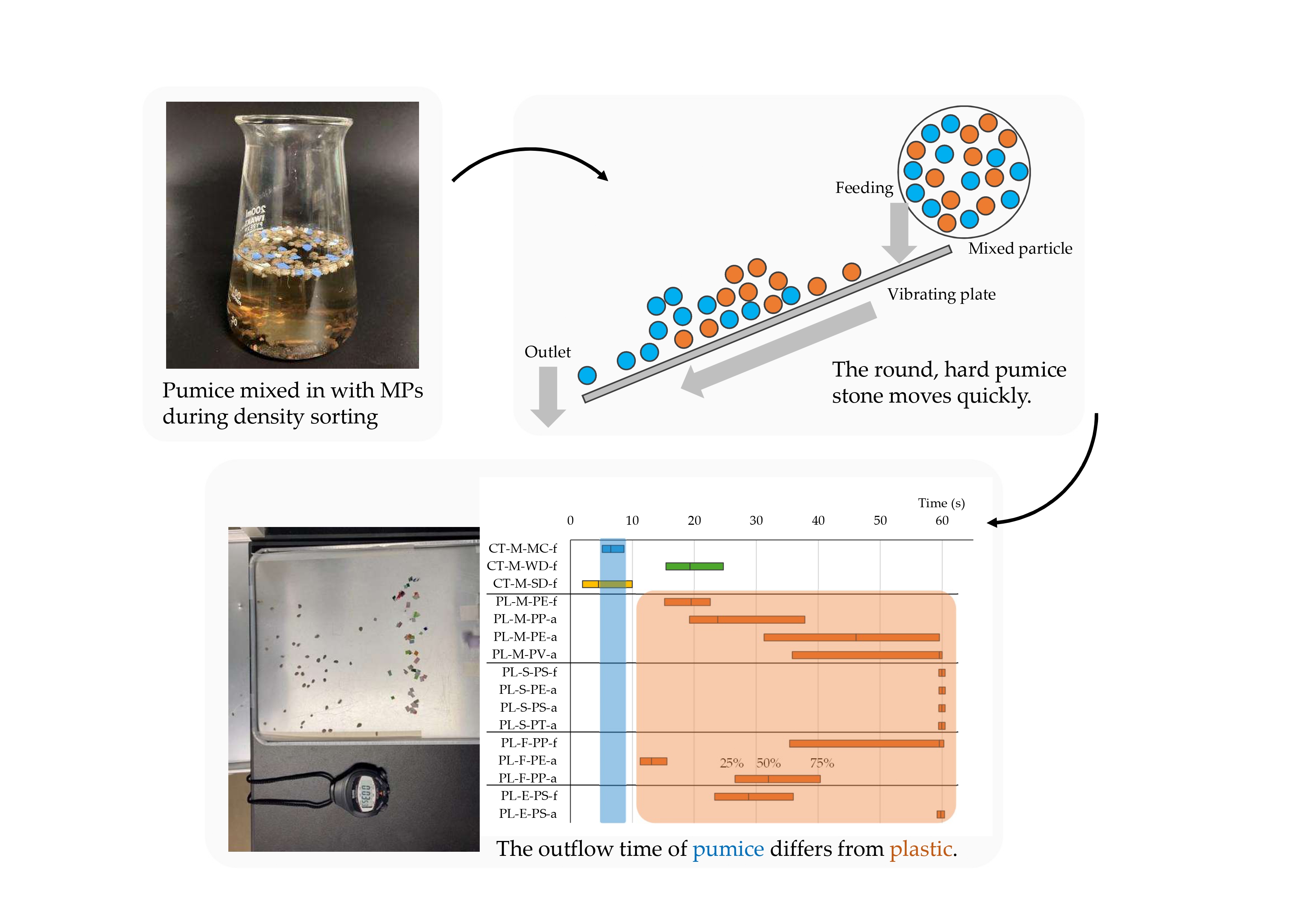
3.1. Sorting Experiments
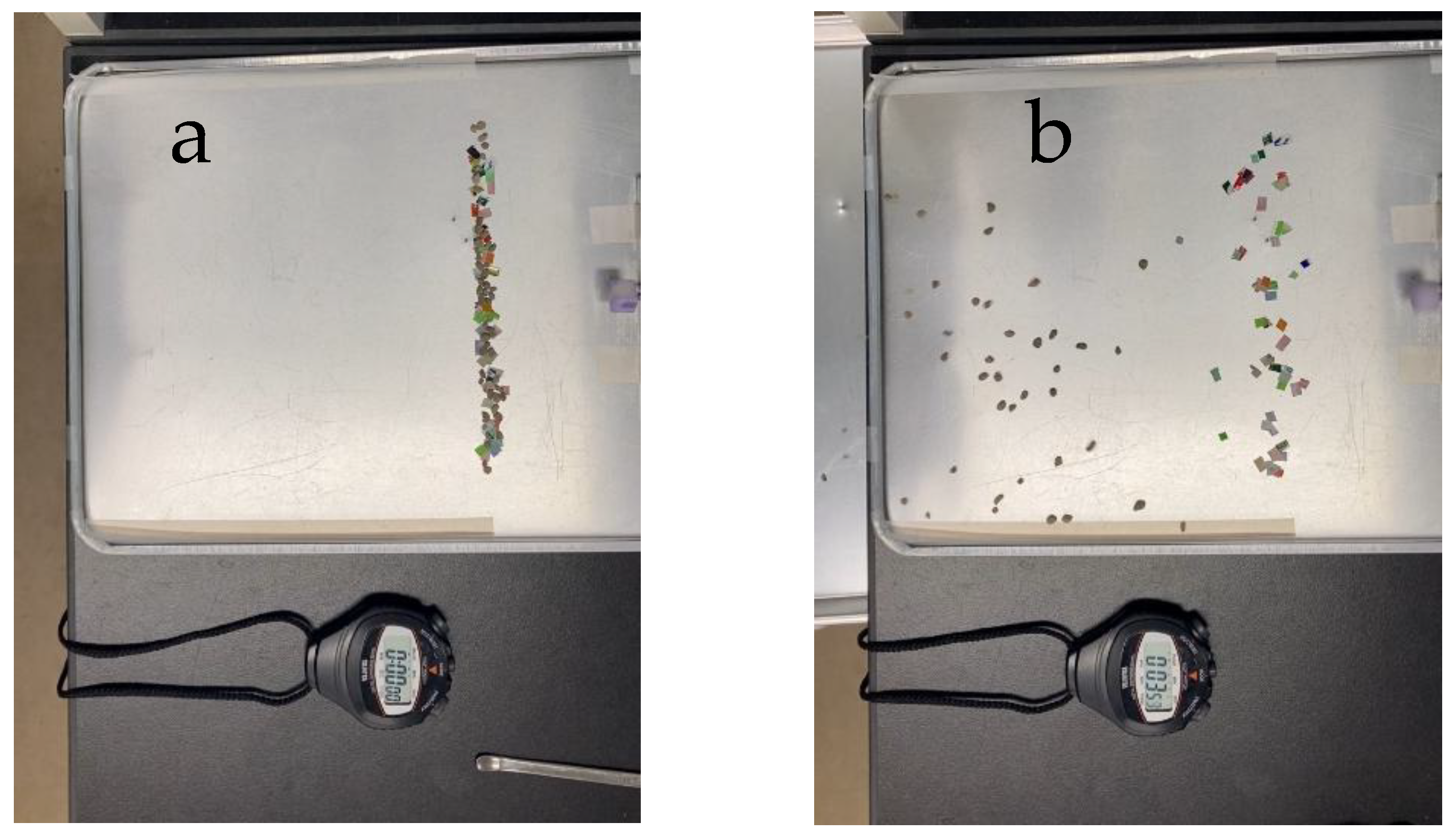
3.1.1. Visual Sorting
3.1.2. Pumice Settling Process via Decompression Treatment
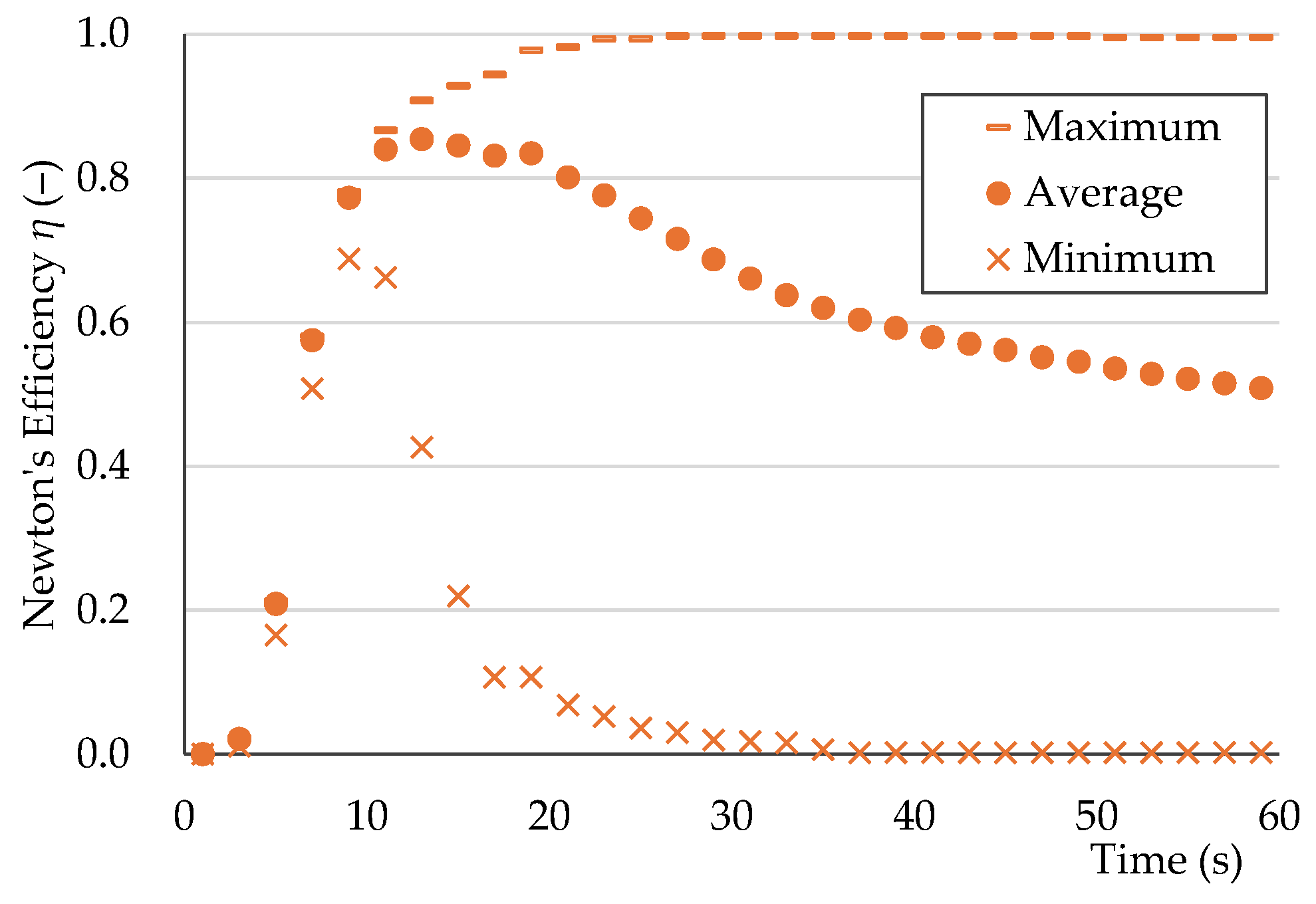
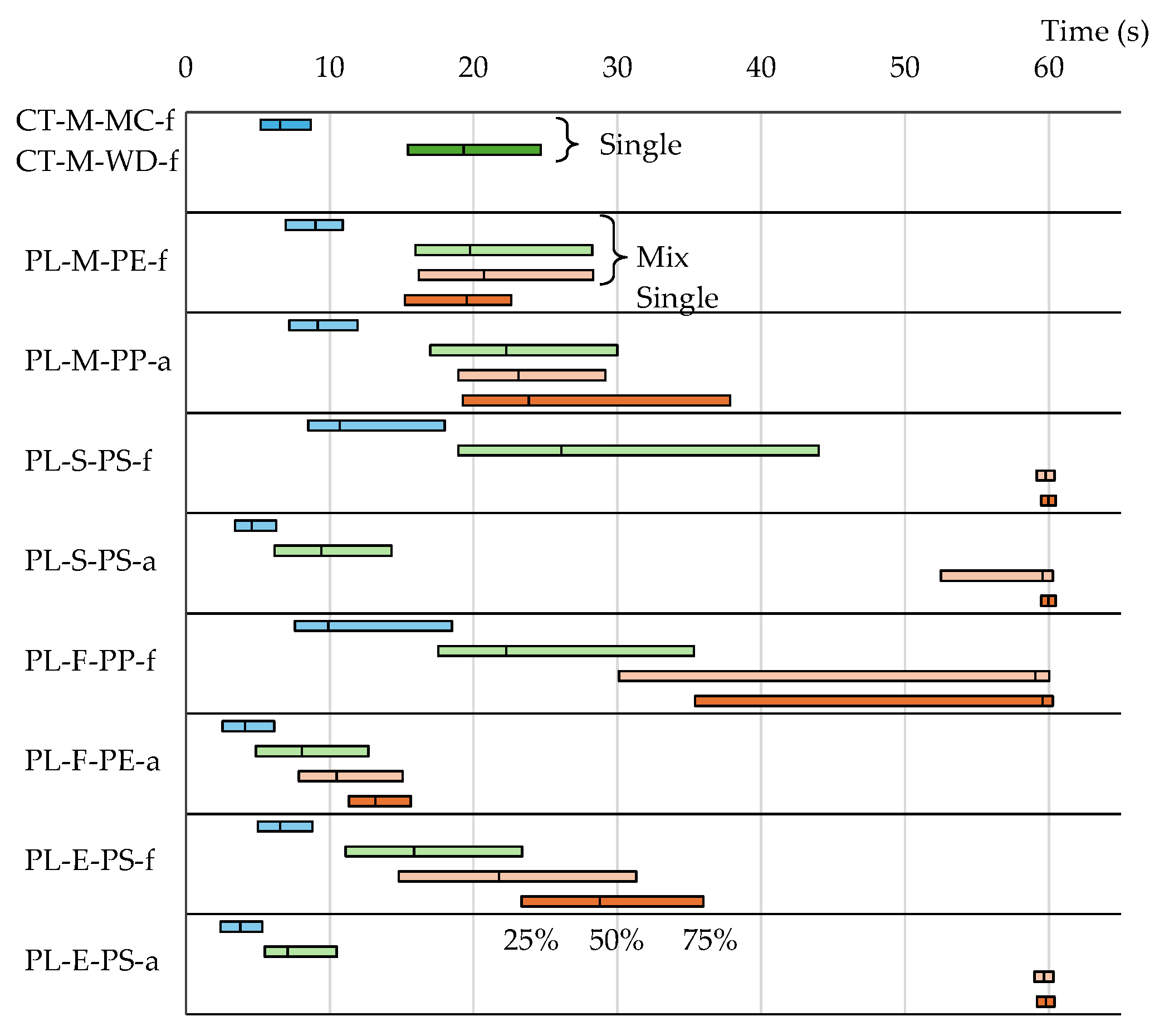
3.2. Large-Diameter Single Particle Behavior and Virtual Sorting Efficiency in a Vibratory Sorter
3.3. Medium-Diameter Single Particle Behavior and Virtual Sorting Efficiency in a Vibratory Sorter
3.4. Actual Vibratory Sorting of Large-Diameter Mixed Particles
3.5. Evaluation of Pumice Removal Efficiency Using a Vibratory Sorter
3.6. Significance of This Study
3.7. Limitations and Future Research Directions
5. Conclusions
- (1)
- The maximum Newton’s efficiency ηmax values for virtual sorting of large-diameter single pumice and plastic ranged from 0.74 to 1.00.
- (2)
- For virtual sorting of medium-diameter single pumice and plastic, ηmax values ranged from 0.74 to 0.97. Sorting efficiency tended to decline with smaller particles.
- (3)
- Actual sorting of large-diameter pumice and plastic mixtures produced ηmax values ranging from 0.68 to 1.00. The actual sorting efficiency of the mixed sample was lower than the virtual sorting efficiency of the single particles.
- (4)
- Based on Newton’s efficiencies, vibratory sorting cannot replace visual sorting. However, the time required for vibratory sorting is 21% of that required for visual sorting, making it advantageous for estimating coastal sediment MP levels. Moreover, the present study contributes to the development of efficient beach cleanup methods.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- Roland, G.; Jenna, R.J.; Kara, L.L. Production, use, and fate of all plastics ever made. Science Advances 2017, 3, e1700782. [Google Scholar]
- OECD. Global Plastics Outlook: Economic Drivers, Environmental Impacts and Policy Options. OECD Publishing, Paris. 2022. Available online: https://www.oecd.org/en/publications/global-plastics-outlook_de747aef-en.html (accessed on 28 February 2025).
- Andrady, A.L. Microplastics in the marine environment. Mar. Pollut. Bull. 2011, 62, 1596–1605. [Google Scholar] [CrossRef]
- Kuriyama, Y.; Konishi, K.; Kanehiro, H.; Otake, C.; Kaminuma, T.; Mato, Y.; Takada, H.; Kojima, A. Plastic pellets in the marine environment of Tokyo Bay and Sagami Bay. Nippon Suisan Gakkaishi 2002, 68, 164–171. (in Japanese). [Google Scholar] [CrossRef]
- Isobe, A.; Uchida, K.; Tokai, T.; Iwasaki, S. East Asian seas: A hot spot of pelagic microplastics. Mar. Pollut. Bull. 2015, 101, 618–623. [Google Scholar] [CrossRef]
- Isobe, A. Percentage of microbeads in pelagic microplastics within Japanese coastal waters. Mar. Pollut. Bull. 2016, 110, 432–437. [Google Scholar] [CrossRef] [PubMed]
- Boucher, J.; Friot, D. Primary Microplastics in the Oceans: A Global Evaluation of Sources. Gland, Switzerland: IUCN. 2017. Available online: https://portals.iucn.org/library/sites/library/files/documents/2017-002-En.pdf (accessed on 28 February 2025).
- Barrows, A.P.W.; Cathey, S.E.; Petersen, C.W. Marine environment microfiber contamination: Global patterns and the diversity of microparticle origins. Environ. Pollut. 2018, 237, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Jamieson, A.J.; Brooks, L.S.R.; Reid, W.D.K.; Piertney, S.B.; Narayanaswamy, B.E.; Linley, T.D. Microplastics and synthetic particles ingested by deep-sea amphipods in six of the deepest marine ecosystems on Earth. R. Soc. Open Sci. 2019, 6, 180667. [Google Scholar] [CrossRef]
- Louis, K.B.; Alan, E.B. Occurrence of plastic particles in seabirds from the eastern North Pacific. Mar. Pollut. Bull. 1997, 34, 323–325. [Google Scholar]
- Van Cauwenberghe, L.; Janssen, C.R. Microplastics in bivalves cultured for human consumption. Environ. Pollut. 2014, 193, 65–70. [Google Scholar] [CrossRef]
- Azad, S.M.O.; Towatana, P.; Pradit, S.; Patricia, B.G.; Hue, H.T.T.; Jualaong, S. First evidence of existence of microplastics in stomach of some commercial fishes in the lower Gulf of Thailand. Appl. Ecol. Environ. Res. 2018, 16, 7345–7360. [Google Scholar] [CrossRef]
- Leslie, H.A.; Van Velzen, M.J.M.; Brandsma, S.H.; Dick Vethaak, A.; Garcia-Vallejo, J.J.; Lamoree, M.H. Discovery and quantification of plastic particle pollution in human blood. Environ. Int. 2022, 163, 107199. [Google Scholar] [CrossRef] [PubMed]
- Nihart, A.J.; Garcia, M.A.; El Hayek, E.; et al. Bioaccumulation of microplastics in decedent human brains. Nat. Med. 2025. [Google Scholar] [CrossRef] [PubMed]
- Qiao, R.; Deng, Y.; Zhang, S.; Wolosker, M.B.; Zhu, Q.; Ren, H.; Zhang, Y. Accumulation of different shapes of microplastics initiates intestinal injury and gut microbiota dysbiosis in the gut of zebrafish. Chemosphere 2019, 236, 124334. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Fang, J.; Du, M.; Gao, Y.; Fang, J.; Jiang, Z. Microplastics influence physiological processes, growth and reproduction in the Manila clam, Ruditapes philippinarum. Environ. Pollut. 2022, 293, 18502. [Google Scholar] [CrossRef]
- Rios, L.M.; Moore, C.; Jones, P.R. Persistent organic pollutants carried by synthetic polymers in the ocean environment. Mar. Pollut. Bull. 2007, 54, 1230–1237. [Google Scholar] [CrossRef]
- Campanale, C.; Dierkes, G.; Massarelli, C.; Bagnuolo, G.; Uricchio, V.F. A Relevant Screening of Organic Contaminants Present on Freshwater and Pre-Production Microplastics. Toxics 2020, 8, 100. [Google Scholar] [CrossRef]
- Wardrop, P.; Shimeta, J.; Nugegoda, D.; Morrison, P.D.; Miranda, A.; Tang, M.; Clarke, B.O. Chemical Pollutants Sorbed to Ingested Microbeads from Personal Care Products Accumulate in Fish. Environ. Sci. & Tech. 2016, 50, 4037–4044. [Google Scholar]
- European Union. Directive - 2019/904 - EN - SUP Directive - EUR-Lex. 2019. Available online: https://eur-lex.europa.eu/eli/dir/2019/904/oj (accessed on 28 February 2025).
- U.S. Environmental Protection Agency. National Recycling Strategy Part One of a Series on Building a Circular Economy for All. Washington, U.S. 2021. Available online: https://www.epa.gov/system/files/documents/2021-11/final-national-recycling-strategy.pdf (accessed on 28 February 2025).
- Ministry of the Environment Government of Japan. Plastic Resource Recycling Strategy. Tokyo, Japan. 2019. Available online: https://www.env.go.jp/content/900513722.pdf (accessed on 28 February 2025). (in Japanese).
- Simantiris, N.; Vardaki, M.Z. A systematic review and scientometrics analysis on microplastic pollution on coastal beaches around the globe. Continental Shelf Research 2025, 286, 105424. [Google Scholar] [CrossRef]
- Luan, J.; Wang, Y. Abundance, morphology, spatial-temporal distribution and sources of microplastics in Shilaoren Beach, Qingdao, China. Regional Studies in Marine Science 2024, 71, 103422. [Google Scholar] [CrossRef]
- Borah, A.; Hande, O.M.; Jayakumar, S.; Devipriya, S.P. Microplastic pollution in beach sediments in the Dapoli coast, Maharashtra, the western peninsular region of India. Regional Studies in Marine Science 2024, 77, 103640. [Google Scholar] [CrossRef]
- Sagawa, N.; Kawaai, K.; Hinata, H. Abundance and size of microplastics in a coastal sea: Comparison among bottom sediment, beach sediment, and surface water. Mar. Pollut. Bull. 2018, 133, 532–542. [Google Scholar] [CrossRef] [PubMed]
- Dodson, G.Z.; Shotorban, A.K.; Hatcher, P.G.; Waggoner, D.C.; Ghosal, S.; Noffke, N. Microplastic fragment and fiber contamination of beach sediments from selected sites in Virginia and North Carolina, USA. Mar. Pollut. Bull. 2020, 151, 110869. [Google Scholar] [CrossRef]
- Esiukova, E. Plastic pollution on the Baltic beaches of Kaliningrad region, Russia. Mar. Pollut. Bull. 2017, 114, 1072–1080. [Google Scholar] [CrossRef] [PubMed]
- Expósito, N.; Rovira, J.; Sierra, J.; Folch, J.; Schuhmacher, M. Microplastics levels, size, morphology and composition in marine water, sediments and sand beaches. Case study of Tarragona coast (western Mediterranean). Sci. Total Environ. 2021, 786, 147453. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Arroyo-Olarte, H.; Trilleras, J.; Arana, V.A.; Mantilla-Barbosa, E.; Gracia, C.A.; Mendoza, A.V.; Neal, W.J.; Williams, A.T.; Micallef, A. Microplastics pollution on Colombian Central Caribbean beaches. Mar. Pollut. Bull. 2021, 170, 112685. [Google Scholar] [CrossRef]
- Mayoma, B.S.; Sørensen, C.; Shashoua, Y.; Khan, F.R. Microplastics in beach sediments and cockles (Anadara antiquata) along the Tanzanian coastline. Bull. Environ. Contam. Toxicol. 2020, 105, 513–521. [Google Scholar] [CrossRef] [PubMed]
- Hayes, H.; Kirkbride, K.P.; Leterme, S.C. Variation in polymer types and abundance of microplastics from two rivers and beaches in Adelaide, South Australia. Mar. Pollut. Bull. 2021, 172, 112842. [Google Scholar] [CrossRef]
- Tasnim, J.; Ahmed, M.K.; Hossain, K.B.; Islam, M.S. Spatiotemporal distribution of microplastic debris in the surface beach sediment of the southeastern coast of Bangladesh. Heliyon 2023, 9, e21864. [Google Scholar] [CrossRef]
- Claessens, M.; Van Cauwenberghe, L.; Vandegehuchte, M.B.; Janssen, C.R. New techniques for the detection of microplastics in sediments and field collected organisms. Mar. Pollut. Bull. 2013, 70, 227–233. [Google Scholar] [CrossRef]
- Asakura, H. Accuracy of a Simple Microplastics Investigation Method on Sandy Beaches. Microplastics 2023, 2, 304–321. [Google Scholar] [CrossRef]
- Masura, J.; Baker, J.; Foster, G.; Arthur, C. Laboratory Methods for the Analysis of Microplastics in the Marine Environment: Recommendations for Quantifying the Synthetic Particles in Water and Sediments. NOAA Marine Debris Division: Silver Spring, MA, USA, 2015.
- Imhof, H.K.; Schmid, J.; Niessner, R.; Ivleva, N.P.; Laforsch, C. A novel, highly efficient method for the separation and quantification of plastic particles in sediments of aquatic environments. Limnol. Oceanogr. Methods 2012, 10, 524–537. [Google Scholar] [CrossRef]
- Mani, T.; Frehland, S.; Kalberer, A.; Burkhardt-Holm, P. Using castor oil to separate microplastics from four different environmental matrices. Anal. Methods. 2019, 11, 1788–1794. [Google Scholar] [CrossRef]
- Kubo, T. Ocean dumping of pumice (volcanic products from Fukutoku-Oka-no-Ba or Hunga Tonga-Hunga Ha’apai Volcano). 2021. Available online: https://www.fit.ac.jp/~kubo/research_en.html (accessed on 28 February 2025).
- Felsing, S.; Kochleus, C.; Buchinger, S.; Brennholt, N.; Stock, F.; Reifferscheid, G. A new approach in separating microplastics from environmental samples based on their electrostatic behavior. Environ. Pollut. 2017, 234, 20–28. [Google Scholar] [CrossRef]
- Giani, H.; Borchers, B.; Kaufeld, S.; Feil, A.; Pretz, T. Fine grain separation for the production of biomass fuel from mixed municipal solid waste. Waste Management 2016, 47, 174–183. [Google Scholar] [CrossRef]
- Zhou, C.; Pan, Y.; Lu, M.; Yang, C. Liberation characteristics after cryogenic modification and air table separation of discarded printed circuit boards. J. Hazard. Mater. 2016, 311, 203–209. [Google Scholar] [CrossRef] [PubMed]
- Chalavadi, G.; Singh, R.K.; Das, A. Processing of coal fines using air fluidization in an air table. International Journal of Mineral Processing 2016, 149, 9–17. [Google Scholar] [CrossRef]
- Back, S.; Ueda, K.; Sakanakura, H. Determination of metal-abundant high-density particles in municipal solid waste incineration bottom ash by a series of processes: Sieving, magnetic separation, air table sorting, and milling. Waste Management 2020, 112, 11–19. [Google Scholar] [CrossRef]
- Komatsuzaki, M.; Endo, O.; Yoshizaki, S.; Osaki, K. Studies on the Relation between Persistence of Volunteer Cereals and Cropping System in Upland (VI) Separating characteristics of rough rice separaters to contaminated barley by mixing of volunteer wheat grain, Japanese Journal of Farm Work Research 1994, 29, 14–20.
- The Society of Powder Technology, Japan. Terminology Dictionary of powder Technology, 2nd Edition. Nikkan Kogyo Shinbunsha, 2000, Tokyo, Japan. (in Japanese).
- Ferdana, A.D.; Petrus, H.T.B.M.; Bendiyasa, I.M.; Prijambada, I.D.; Hamada, F.; Takahi, S. Optimization of gold ore Sumbawa separation using gravity method: Shaking table. AIP Conference Proceedings 2018, 1945, 020070. [Google Scholar] [CrossRef]
- Oi, E.; Arai, S.; Kikuchi, E.; Ito, S. Separation of metallic fragments from shredded electric devices using air table. Shigen to Sozai 1997, 113, 577–581. (in Japanese). [Google Scholar] [CrossRef]
- Dodbiba, G.; Sadaki, J.; Okaya, K.; Shibayama, A.; Fujita, T. The use of air tabling and triboelectric separation for separating a mixture of three plastics. Minerals Engineering 2005, 18, 1350–1360. [Google Scholar] [CrossRef]




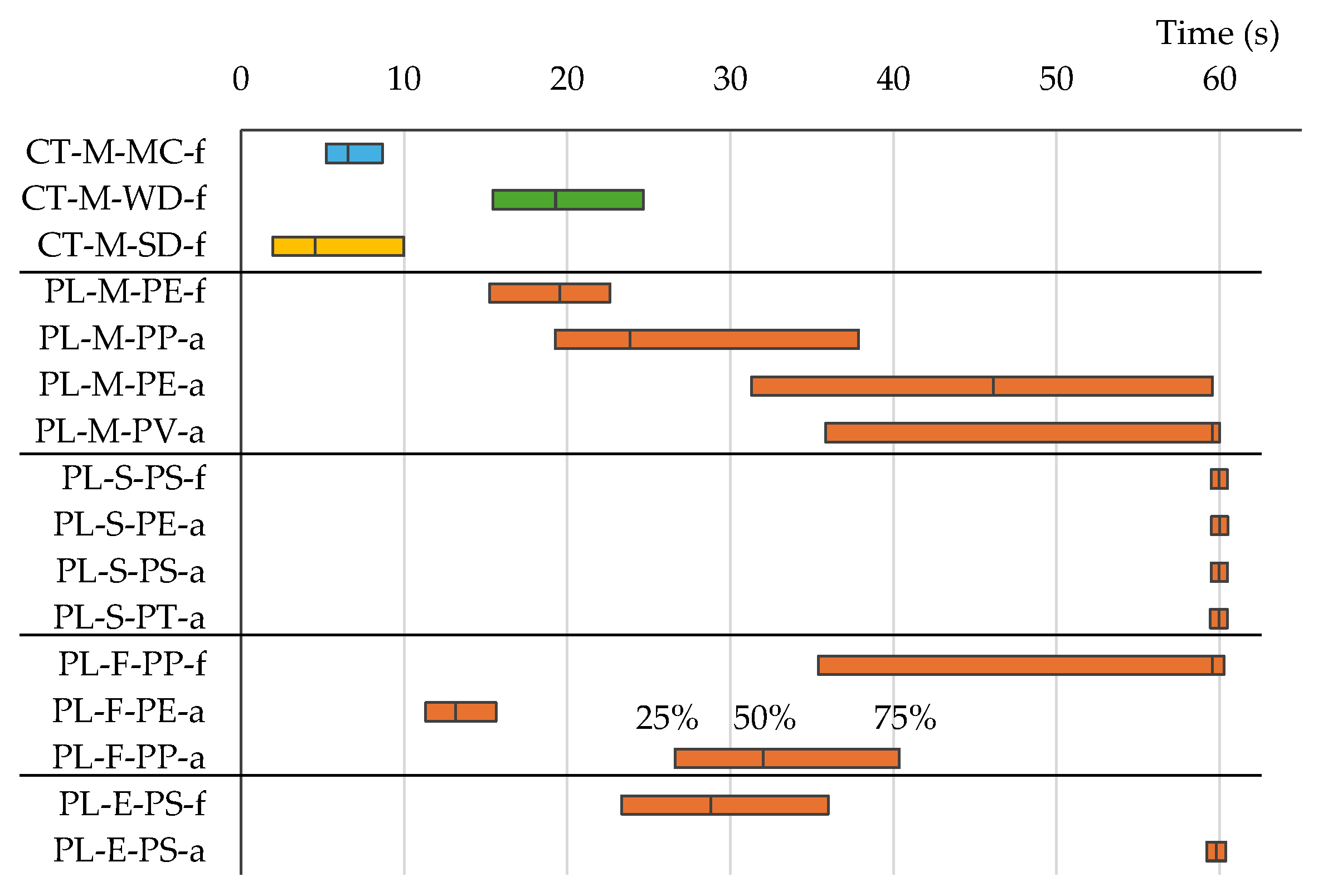
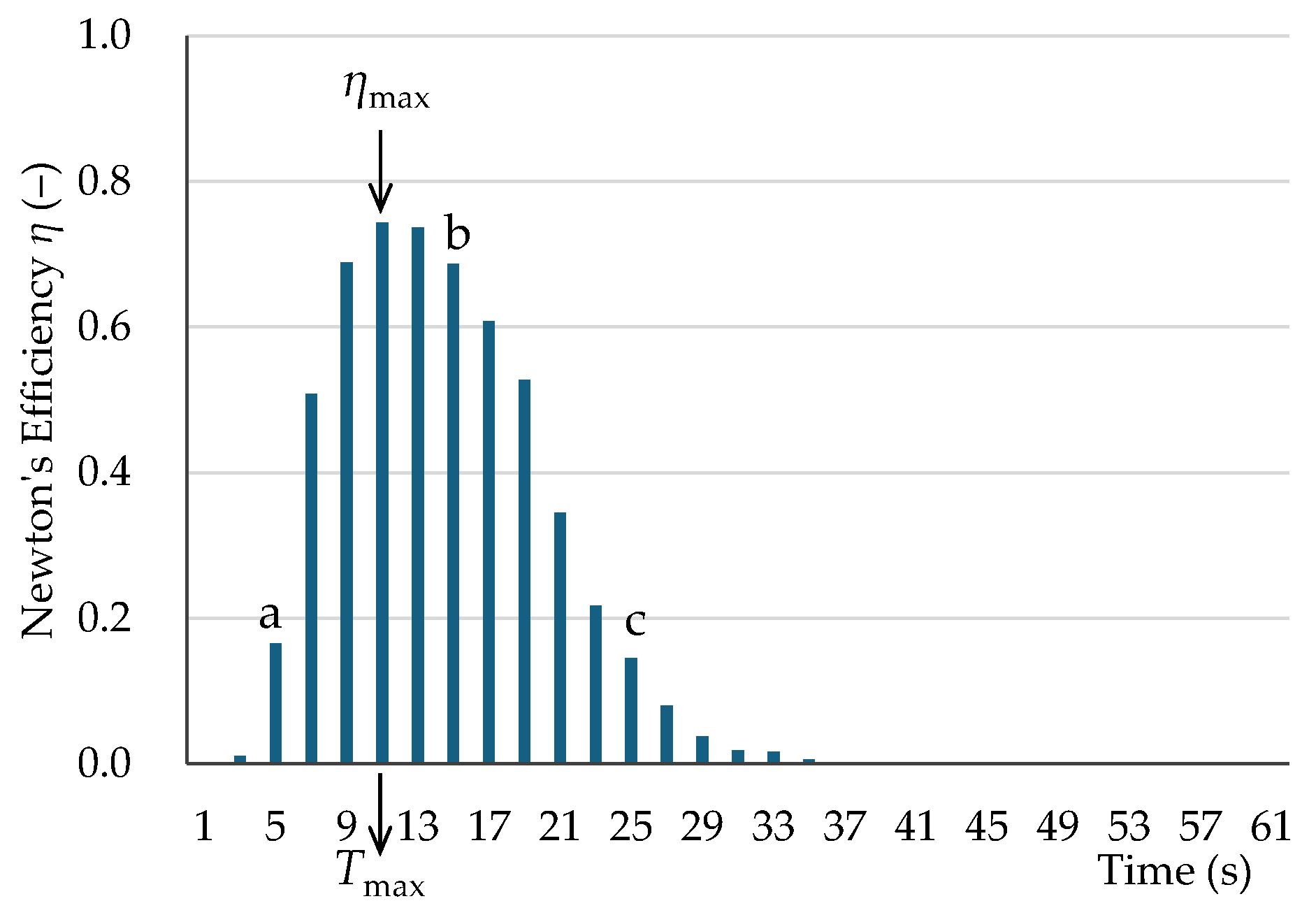
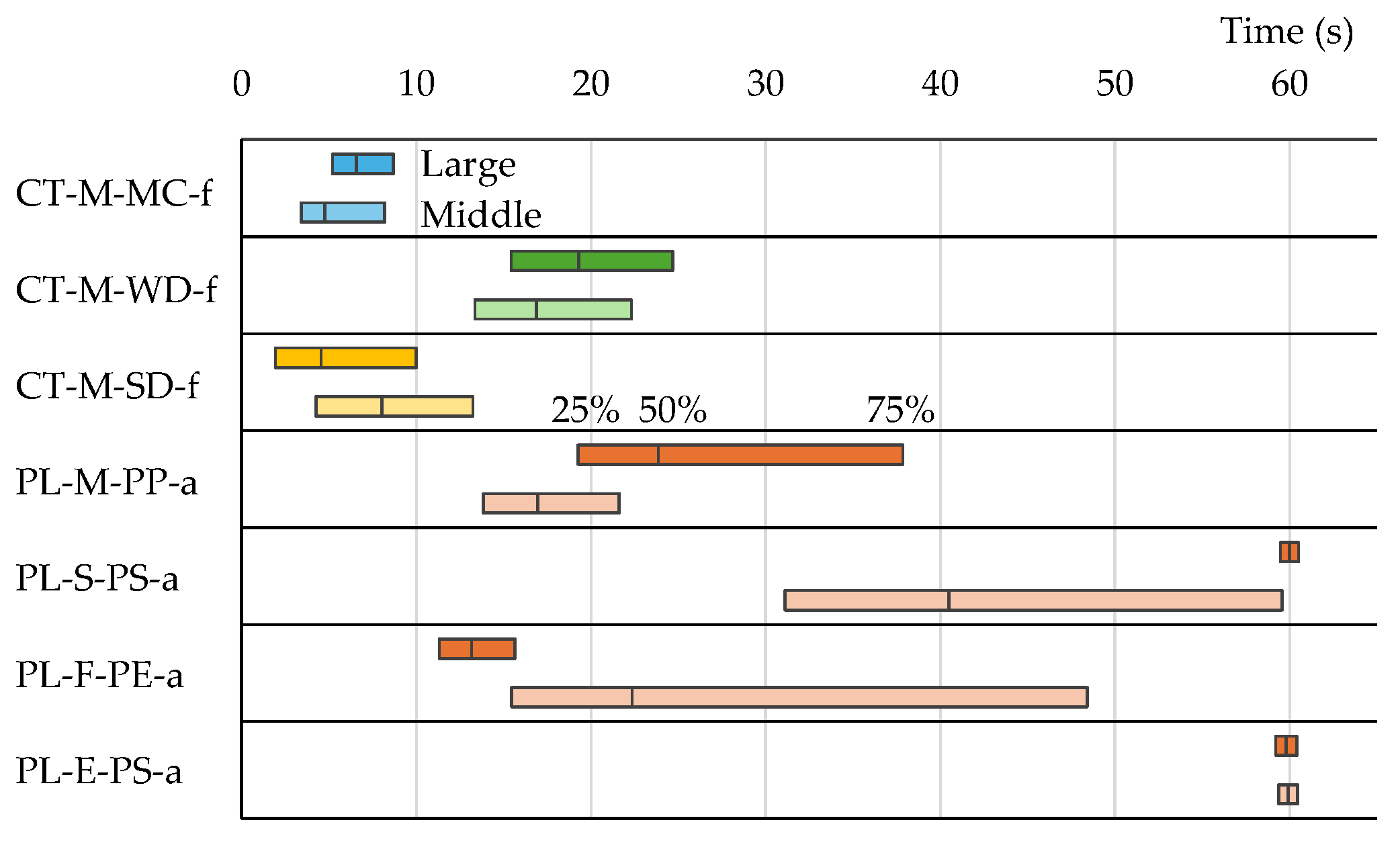
| Contaminants or Plastics |
Shape | Material | Origin*1 | Density*2 (g/cm3) |
Description | Size*3 | Mix*4 |
| Contaminant (CT) |
Mass (M) | Pumice (MC) | f | 0.89 | Pumice | LM | X |
| Wood (WD) | f | 0.98 | Wood | LM | X | ||
| Seed (SD) | f | 0.95 | Seed | LM | |||
| Plastic (PL) | Mass (M) | PE | f | 0.92 | Fertilize capsule | L | X |
| PP | a | 0.91 | Clothespin | LM | X | ||
| PE | a | 0.93 | Polybottle | L | |||
| PVC (PV) | a | 1.38 | Corrugated sheet | L | |||
| Sheet (S) | PS | f | 1.03 | Plastic bottle label | L | X | |
| PE | a | 0.91 | Shopping bag | L | |||
| PS | a | 1.03 | Plastic bottle label | LM | X | ||
| PET (PT) | a | 1.39 | Lumirror ® film | L | |||
| Fiber (F) | PP | f | 0.80 | Fishing rope | L | X | |
| PE | a | 0.75 | Construction rope | LM | X | ||
| PP | a | 0.49 | Construction rope | L | |||
| Expanded (E) |
PS | f | 0.02 | Expanded polystyrene | L | X | |
| PS | a | 0.02 | Expanded polystyrene | LM | X |
| η (‒) | Time (s) | |||
| Mean | S.D. | Mean | S.D. | |
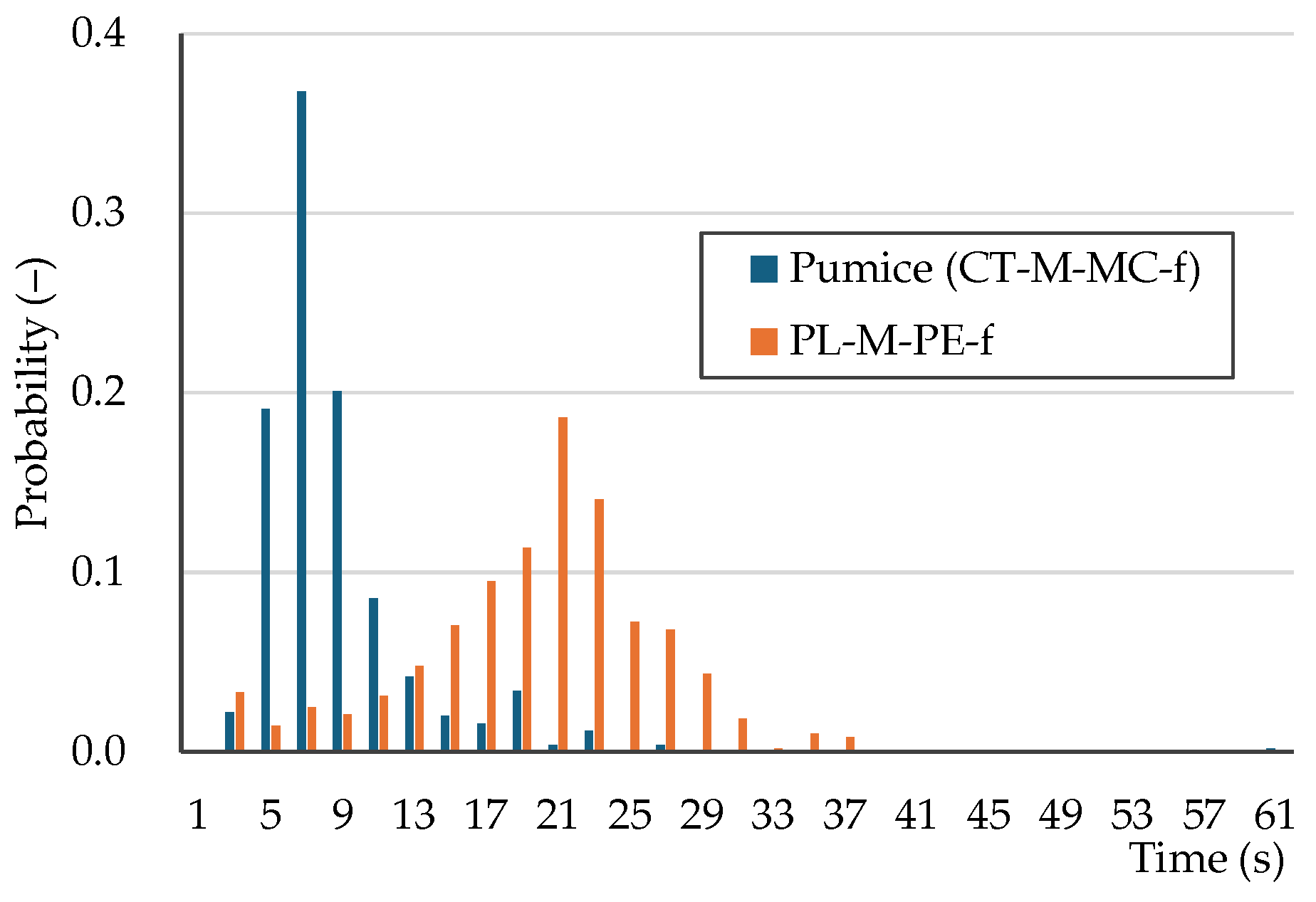
| PL-M-PE-f | 1.00 | 0.00 | 69 | 9.4 |
| PL-S-PS-f | 1.00 | 0.00 | 66 | 4.4 |
| PL-F-PP-f | 1.00 | 0.00 | 61 | 7.5 |
| PL-E-PS-f | 0.99 | 0.01 | 76 | 6.8 |
| Large-Single | Medium-Single | Large-Mix | ||||||
| E(T) | S.D. | E(T) | S.D. | E(T) | S.D. | |||
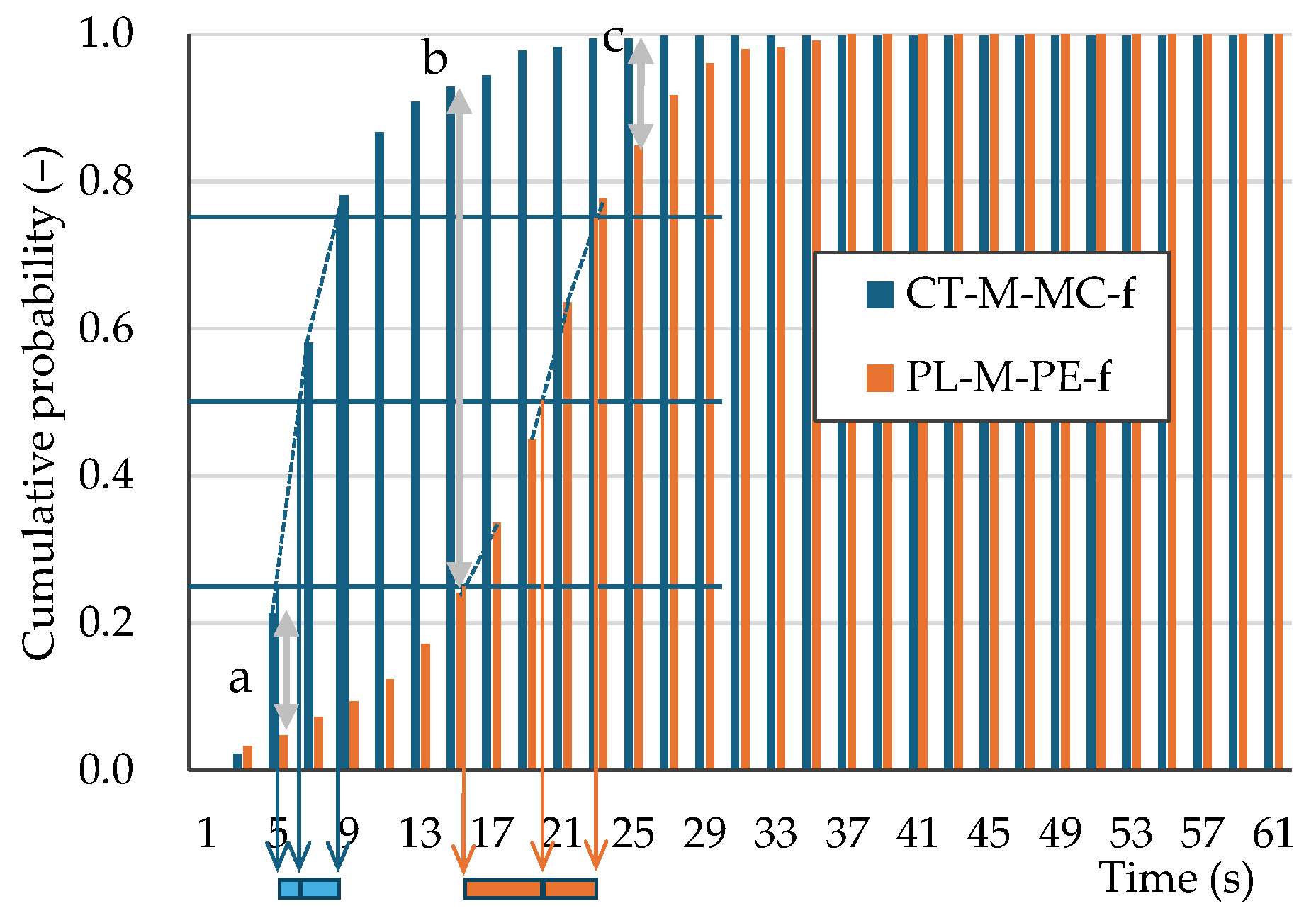
| CT-M-MC-f | 9 | 5 | 8 | 7 | 5‒16 | 3‒12 | ||
| CT-M-WD-f | 22 | 8 | 20 | 9 | 9‒33 | 5‒16 | ||
| CT-M-SD-f | 8 | 8 | 11 | 8 | ‒ | ‒ | ||
| PL-M-PE-f | 20 | 7 | ‒ | ‒ | 26 | 15 | ||
| PL-M-PP-a | 31 | 14 | 21 | 11 | 27 | 10 | ||
| PL-M-PE-a | 46 | 15 | ‒ | ‒ | ‒ | ‒ | ||
| PL-M-PV-a | 49 | 14 | ‒ | ‒ | ‒ | ‒ | ||
| PL-S-PS-f | 61 | 3 | ‒ | ‒ | 58 | 7 | ||
| PL-S-PE-a | 61 | 1 | ‒ | ‒ | ‒ | ‒ | ||
| PL-S-PS-a | 61 | 2 | 44 | 14 | 55 | 11 | ||
| PL-S-PT-a | 60 | 3 | ‒ | ‒ | ‒ | ‒ | ||
| PL-F-PP-f | 51 | 17 | ‒ | ‒ | 48 | 16 | ||
| PL-F-PE-a | 16 | 6 | 31 | 18 | 14 | 10 | ||
| PL-F-PP-a | 36 | 12 | ‒ | ‒ | ‒ | ‒ | ||
| PL-E-PS-f | 33 | 13 | ‒ | ‒ | 26 | 14 | ||
| PL-E-PS-a | 58 | 8 | 60 | 6 | 54 | 15 | ||
| ηmax (‒) | Tmax (s) | ||||||
| Pumice | Wood | Seed | Pumice | Wood | Seed | ||
| PL-M-PE-f | 0.74 | < | < | 11 | 29 | 11 | |
| PL-M-PP-a | 0.89 | < | 0.81 | 13 | 19 | 15 | |
| PL-M-PE-a | 0.95 | < | 0.89 | 19 | 27 | 21 | |
| PL-M-PV-a | 0.96 | 0.73 | 0.90 | 19 | 31 | 23 | |
| PL-S-PS-f | 0.99 | 0.98 | 0.99 | 27 | 51 | 37 | |
| PL-S-PE-a | 1.00 | 0.99 | 1.00 | 27 | 49 | 37 | |
| PL-S-PS-a | 1.00 | 0.98 | 1.00 | 27 | 49 | 37 | |
| PL-S-PT-a | 1.00 | 0.97 | 1.00 | 27 | 41 | 37 | |
| PL-F-PP-f | 0.90 | 0.72 | 0.83 | 15 | 41 | 15 | |
| PL-F-PE-a | 0.77 | < | 0.70 | 9 | 15 | 9 | |
| PL-F-PP-a | 0.94 | < | 0.88 | 19 | 25 | 17 | |
| PL-E-PS-f | 0.90 | < | 0.83 | 15 | 23 | 15 | |
| PL-E-PS-a | 0.99 | 0.90 | 0.96 | 23 | 35 | 25 | |
| DAD* (‒) | ηmax (‒) | Tmax (s) | rηM/L** (‒) | |
| CT-M-MC-f | 0.61 | ‒ | - | ‒ |
| PL-M-PP-a | 0.59 | 0.75 | 9 | 0.84 |
| PL-S-PS-a | 0.36 | 0.94 | 21 | 0.94 |
| PL-F-PE-a | 0.46 | 0.74 | 9 | 0.96 |
| PL-E-PS-a | 0.89 | 0.97 | 31 | 0.99 |
| DAD* (‒) | ηmax (‒) | Tmax (s) | rηMX/SG** (‒) | ||
| Pumice | Plastics | ||||
| PL-M-PE-f | 0.67 | 0.76 | 0.70 | 13 | 0.93 |
| PL-M-PP-a | 0.62 | 0.83 | 0.79 | 13 | 0.89 |
| PL-S-PS-f | 0.47 | 0.82 | 0.91 | 33 | 0.92 |
| PL-S-PS-a | 0.61 | 0.71 | 1.00 | 19 | 1.00 |
| PL-F-PP-f | 0.58 | 0.73 | 0.74 | 23 | 0.83 |
| PL-F-PE-a | 0.56 | 0.59 | 0.68 | 7 | 0.88 |
| PL-E-PS-f | 0.87 | 0.64 | 0.70 | 9 | 0.77 |
| PL-E-PS-a | 0.49 | 0.84 | 0.96 | 13 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





