Families of Non-Even Harmonious Graphs

1. Introduction

We follow Chartrand and Lesniak [2] and Gallian [4] for basic notations in graph theory and known results of graph labeling. In particular, we will consider a finite simple graph. For positive integers $a$ and $b$ with $a<b$, we denote $\{a,a+1,\mathrm{...},b\}$ by $[a,b]$ and the set $\{a,a+2,a+4,\mathrm{...},b\}$ by ${[a,b]}_2$, where $a$ and $b$ have the same parity, that is $a\equiv b(\mathrm{mod}\hspace{0.17em} 2)$, Let ${\mathbb{Z}}_m$ denote the group of integers modulo $m$. For a graph $G$ if $\left|V(G)\right|=p,\hspace{0.33em}\hspace{0.17em}\left|E(G)\right|=q$, we call $G$ is a $(p,q)-$graph. In this section, we mention some related definitions and some variations of the definition of the even harmonious labeling and expose some of the known results that we may use in the paper.

Definition 1.1. [8] A $(p,q)-$graph $G$with $p\le q$ is called harmonious if there is an injection function $f:V(G)\to {\mathbb{Z}}_q$ such that the induced function $f^{\ast }:E(G)\to {\mathbb{Z}}_q$ defined as $f^{\ast }(uv)=(f(u)+f(v))(\mathrm{mod}\hspace{0.33em}q)$ for all edge $uv\in E(G)$ is a bijection. If $G$ is a tree, exactly two vertices are having the same label. A labeling function $f$ is called a harmonious labeling of the graph $G$.

Graham and Sloane [8] proved the following.

Theorem 1.1. If $G$ is a harmonious of even size $q$ and $2^k\left|\mathrm{deg}(v)\right.$, $(k\ge 1)$, for every vertex $v\in V(G)$, then $2^{k+1}\left|q\right.$.

Since Graham and Sloane [8] proved that $C_n$ is harmonious if and only if $n$ is odd, it obvious that the necessary condition in Theorem 1.1 is not sufficient for cycles.

There are few general results on harmonious labeling. Most papers focused on classifications of the harmoniousness of some families of graphs. Youssef [11] proved the following results:

Theorem 1.2. If $G$ is a harmonious graph, then $mG$ is harmonious for all odd positive integer $m.$

Theorem 1.3. If $G$ is a harmonious graph, then $G^{(m)}$ (the graph consisting of disjoint union $n$ copies of $G$ with one fixed vertex in common) is harmonious for all odd positive integer $m$

Lee, Schmeichel and Shee [9] gave a generalization of the harmonious labeling in the following definition.

Definition 1.2. [9] A $(p,q)-$graph $G$ is called felicitous if there exists an injection $f:V(G)\to [0,q]$ such that the induced function $f^{\ast }:E(G)\to [0,q-1]$ defined as $f^{\ast }(uv)=(f(u)+f(v))(\mathrm{mod}\hspace{0.33em}q)$ for all edge $uv\in E(G)$ is a bijection.

Lee, Schmeichel and Shee [9] showed that the cycle graph $C_n$ is felicitous if and only if $n\cancel{\equiv }2(\mathrm{mod}4)$. Figueroa-Centeno et al. [3] conjectured that the disjoint union $C_m\cup C_n$ is felicitous if and only if $m+n\cancel{\equiv }2(\mathrm{mod}4)$and $m{C}_n$ is felicitous if and only if $mn\cancel{\equiv }2(\mathrm{mod}4).$

Chang, Hsu and Rogers [1] and independently Grace [7] have introduced subclasses of harmonious graphs and independently by Chang, Hsu and Rogers [1] have given a subclass of felicitous graphs as well in the following definition.

Definition 1.3. [1,7] A $(p,q)-$graph $G$ is called strongly $k$-harmonious (resp. strongly $k$-elegant) if there exists an injective function $f:V(G)\to [0,q-1]$ (resp. $f:V(G)\to [0,q]$) and a positive integer $k$ such that the induced function $f^{\ast }:E(G)\to [k,k+q-1]$ defined as $f^{\ast }(uv)=(f(u)+f(v))$ for all edge $uv\in E(G)$ is a bijection.

By taking the edge labels of a strongly $k$-harmonious labeled graph with $q$edges modulo $q$, we obviously obtain a harmoniously labeled graph. It is not known if there is a graph that can be harmoniously labeled but not strongly k-harmonious labeled.

Recently many variations of even harmonious labeling were introduced. We deal with the variation of the even harmonious labeling when the vertex labels of a graph of size $q$ are from the set ${\mathbb{Z}}_{2q}$.

Definition 1.4. [4] A graph $G$ with $q$ edges is called even harmonious if there exists an injective function $f$ from $V(G)$ to ${\mathbb{Z}}_{2q}$ such that the induced function $f^{\ast }:E(G)\to {[0,2(q-1)]}_2$ defined as $f^{\ast }(uv)=f(u)+f(v)\hspace{0.33em}\hspace{0.33em}(\mathrm{mod}2q)$ for all edge $uv\in E(G)$ is a bijection.

Note that in a connected even harmonious graph all the vertex labels must have the same parity, while in case of disconnected even harmonious graph of c components, the vertex labels of each competent must have the same parity, that is all are even or all are odd. As an example the graph $2K_3$is even harmonious via the vertex labels 0,2, and 10 for one copy of $2K_3$ and by the vertex labels 1,3, and 5 for the other copy.

The following theorem shows that we may change the parity of the vertex labels of connected even harmonious graphs from even to odd and vice versa.

Theorem 1.4. Let $G$ be a connected graph of $q$ edges. If $g$is an even harmonious labeling of $G$, then so is $ag+b$, where $a$is an invertible element of ${\mathbb{Z}}_{2q}$ and $b$ is any element of ${\mathbb{Z}}_{2q}$.

One consequences of the above theorem, is we can assume that in any connected even harmonious graph $G$, the vertex labels are all even and any vertex of $G$ can be assigned the label zero. We formulate this in the following result.

Corollary 1.5. Any vertex in an even harmonious graph can be assigned the label zero.

The following result gives a necessary condition for certain families of graphs to be even harmonious.

Theorem 1.6.[12] If $G$ is a connected even harmonious graph with $q=\left|E(G)\right|$ is even and $2^k\left|\mathrm{deg}(v)\right.$, $(k\ge 1)$, for every vertex $v\in V(G)$, then $2^{k+1}\left|q\right.$.

However, in the following theorem we give a necessary condition in case of disconnected graphs.

Theorem 1.7. [13] If $G$ is a disconnected even harmonious $2^k$-regular graph, $(k\ge 1)$ having an even number $q$ of edges and the order of each component of $G$ is even, then $q$ is divisible by $2^{k+1}$.

Youssef and Aljouiee [14] gave the following result.

Lemma 1.8. Every felicitous (resp. harmonious) graph $G$ is an even harmonious (resp. strictly even harmonious) and the converse is true if $G$ connected.

Definition 1.5. [5, 6, 13] A graph $G$ with $q$ edges is said to be strongly even $2k$-harmonious (resp. strongly even $2k$-sequential, strongly even $2k$-elegant) if there exists an injective function $f:V(G)\to [0,2q-2]$(resp. $f:V(G)\to [0,2q-1]$,$f:V(G)\to [0,2q]$) and a positive integer $k$ such that the induced function $f^{\ast }:E(G)\to {[2k,2k+2q-2]}_2$ defined as $f^{\ast }(uv)=f(u)+f(v)$ for all edge $uv\in E(G)$ is a bijection.

We observe that if $G$ is a connected strongly even $2k$-harmonious (resp. strongly even $2k$-sequential, strongly even $2k$-elegant), then all the vertex labels of $G$ are even or all are odd, while if $G$ is a disconnected graph, then the vertex labels of some components are even or are odd.

Youssef and Aljouiee [14] proved that$C_{2m}\cup C_n$ is even harmonious if and only if $2m+n\cancel{\equiv }2(\mathrm{mod}4)$ and showed also that if $m$ and $n$ are odd integers with $m,n\ge 3$, then $C_m\cup C_n$ is even harmonious if $m+n\equiv 2(\mathrm{mod}4)$.

Gallian and Schoenhard [5] conjectured that $C_{4n}$ is even harmonious for all positive integer $n.$ This conjecture was proved by Youssef [12]. Youssef and Aljouiee [14] showed the following results:

Theorem 1.9. $m{C}_{2n+1}$ is even harmonious for all $m,n\ge 1$.

Theorem 1.10. For all $m\ge 1$ and $n\ge 2$, $m{C}_{2n}$ is not even harmonious if $mn$ is odd.

Proving that a graph is not even harmonious is a hard problem. We have to show that no injective function satisfying the property of even harmoniousness. There are a huge number of injective functions as the number of edges increase. In the following section, we deal with giving some families of non-even harmonious graphs.

2. Non-Even Harmonious Graphs

For proving a specific connected graph is not even harmonious, we have only a parity condition in Theorem 1.6. For example, the cycles of order congruent to 2 modulo 4 are not even harmonious. Otherwise, for other graphs it is not an easy task to show that they are not even harmonious. In this section, we give some families which are not even harmonious.

The next result shows that the cycles of order congruent to 0 modulo 4 are not even harmonious besides the cycles of order congruent to 2 modulo 4 which comes from the parity condition in Theorem 1.6 and Theorem 1.7 shows that if a 2-regular graph consisting of disjoint union of cycles each of even order is even harmonious, then its size is congruent to 0 modulo 4.

Theorem 2.1. If $C_n$ is even harmonious, then $n$ is odd.

Proof. Let $f$ be an even harmonious labeling of $C_n$.We may assume that all vertex labels of $C_n$ are even. Then

$${\displaystyle \sum _{e\in E(C_n)}{f}^{*}(e)}\equiv 0+2+\cdots +2n-2\equiv n(n-1)(\mathrm{mod}2n)\cdots (1)$$

On the other hand,

$${\displaystyle \sum _{e\in E(C_n)}{f}^{*}(e)}=2{\displaystyle \sum _{v\in V(C_n)}f(v)}\equiv 2(0+2+\cdots +2n-2)\equiv n(2n-2)(\mathrm{mod}2n)\cdots (2)$$

Combining (1) and (2), we get

$n(2n-2)\equiv n(n-1)(\mathrm{mod}2n)$, which implies that $n(n-1)\equiv 0(\mathrm{mod}2n)$. Hence, $n$is odd. $\square$

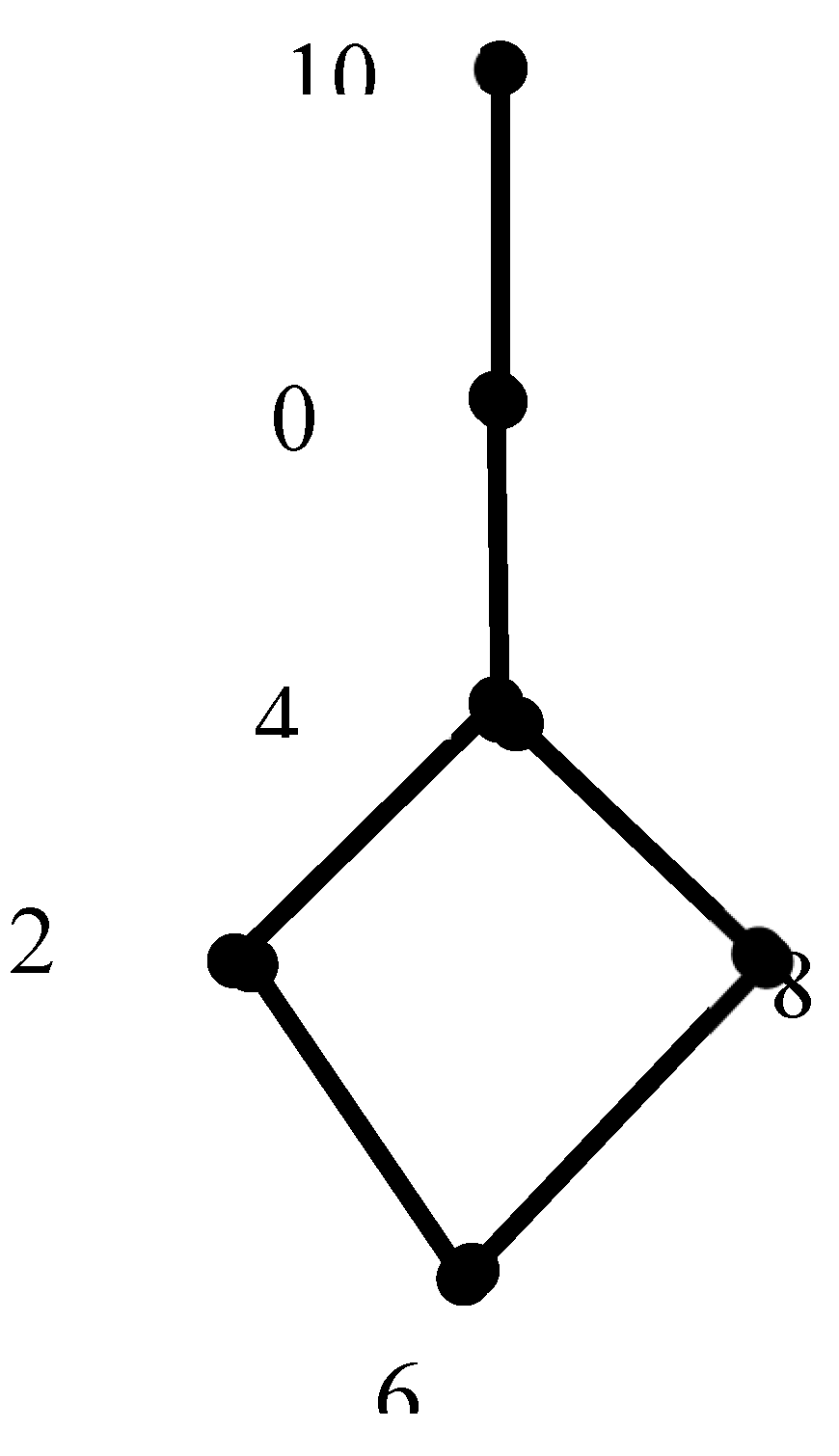
The dragon( also called ballon, kite, or tadpole) graph $D_{m,n}$ is the graph obtained by identifying an end vertex of the path of size $m$ to a vertex of the cycle $C_n$ as in the figure below.

Theorem 2.2. If $m+n$ is odd, then $D_{m,n}$ is not even harmonious.

Proof Let $D_{m,n}$ be described as in Figure 1. Suppose that $D_{m,n}$has an even harmonious labeling $f:V(D_{m,n})\to {\mathbb{Z}}_{2q},\hspace{1em}q=m+n$, then

$${\displaystyle \sum _{e\in E(D_{m,n})}{f}^{*}(e)}\equiv 0+2+\cdots +2q-2\equiv q(q-1)(\mathrm{mod}2q)\cdots (1)$$

On the other hand,

$$\begin{array}{l}{\displaystyle \sum _{e\in E(D_{m,n})}{f}^{*}(e)}\equiv f(u_1)+2f(u_2)+\cdots +2f(u_m)+3f(v_1)+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}2(f(v_2)+\cdots +f(v_n))\end{array}$$

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\equiv f(u_1)+3f(v_1)+2(f(u_2)+\cdots +f(u_m)+f(v_2)+\cdots +f(v_n))$$

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\equiv f(u_1)+3f(v_1)+2({\displaystyle \frac{q}{2}}(2q-2)-f(u_1)-f(v_1))$$

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\equiv f(v_1)-f(u_1)+q(2q-2)(\mathrm{mod}2q)\cdots (2)$$

Combining (1) and (2), we get

$$f(v_1)-f(u_1)\equiv q(q-1)(\mathrm{mod}2q)$$

If $q$ is odd, we will get $f(v_1)\equiv f(u_1)(\mathrm{mod}2q)$, which contradicts the assumption that $f$ is injective. Hence $D_{m,n}$ is not even harmonious when $q=m+n$ is odd. $\square$

Figure 2 shows an even harmonious labeling of $D_{2,4}$. We note that not all dragons of even order are even harmonious as we will show in Theorem 2.4. The following results show the even harmoniousness of some families of unicyclic graphs.

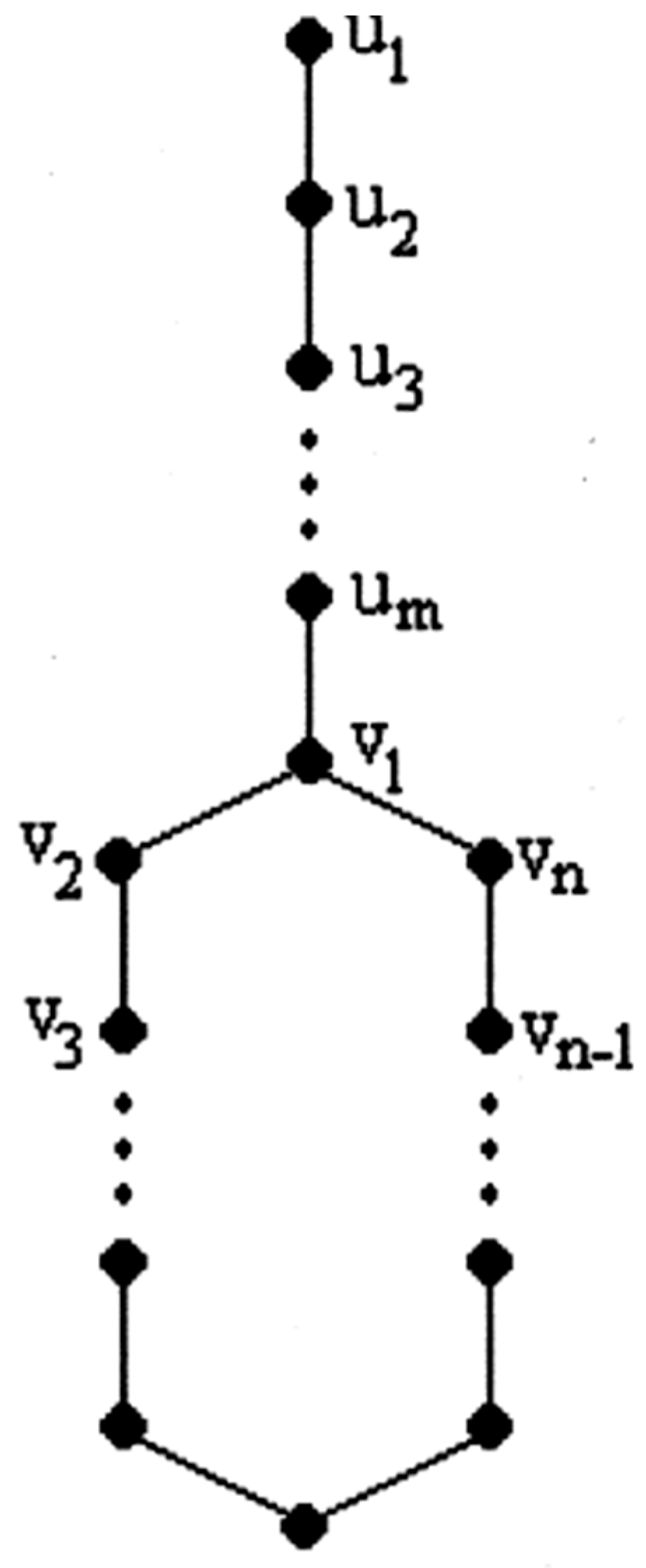
Theorem 2.3. Let $G$ be the graph

Figure 3. then G is even harmonious if and only if $n\equiv 0(\mathrm{mod}4)$.

Figure 3. then G is even harmonious if and only if $n\equiv 0(\mathrm{mod}4)$.

Proof Let $q=\left|E(G)\right|=n+4.$

$\Rightarrow$Suppose that $G$has an even harmonious labeling $f$ with $f(v_0)=0$, then there must exist distinct even positive integers $0<2x_1,2y_1,2z_1<2q$ such that

$2x_1+2y_1\equiv 0,\hspace{1em}2x_1+2z_1\equiv 2y_1,\hspace{1em}2y_1+2z_1\equiv 2x_1(\mathrm{mod}2q)$. Hence $4z_1\equiv 0(\mathrm{mod}2q)$ and $q=2z_1$. Therefore $x_1$ and $y_1$ have the same parity and $z_1$ must be even, then $n\equiv 0(\mathrm{mod}4)$.

$\Leftarrow$Suppose that $n\equiv 0(\mathrm{mod}4)$. Define a bijection $f:V(G)\to {\mathbb{Z}}_{2q}$ such that $f(v_0)=0,\hspace{1em}f(x)={\displaystyle \frac{q}{2}},\hspace{1em}f(y)={\displaystyle \frac{3}{2}}q,\hspace{1em}f(z)=q$. Then one can easily checks that $f^{\ast }$ is onto as well. $\square$

Theorem 2.4. Let $G$ be the graph

Figure 4. then G is not even harmonious for all $n\ge 0$.

Figure 4. then G is not even harmonious for all $n\ge 0$.

Proof Let $q=\left|E(G)\right|=n+4.$Suppose that $G$ has an even harmonious labeling $f$ with $f(v_0)=0$, then there exist distinct even positive integers $0<2x_1,2y_1,2z_1,2w_1<2q$ such that $\Rightarrow$ Suppose that $G$ has an even harmonious labeling $f$ with $f(v_0)=0$, then there must exist even positive integers $0<2x_1,2y_1,2z_1<2q$ such that

$$2x_1+2y_1\equiv 2z_1,\hspace{1em}2x_1+2z_1\equiv 2y_1,\hspace{1em}2z_1+2w_1\equiv 0,\hspace{1em}2z_1+2y_1\equiv 2x_1(\mathrm{mod}2q)$$

Or

$$2x_1+2y_1\equiv 2z_1,\hspace{1em}2x_1+2z_1\equiv 2y_1,\hspace{1em}2z_1+2w_1\equiv 2x_1,\hspace{1em}2z_1+2y_1\equiv 0(\mathrm{mod}2q).$$

The first line gives $4x_1\equiv 4z_1\equiv 0(\mathrm{mod}2q)$ which is absurd and the second line gives $2w_1\equiv 2z_1(\mathrm{mod}2q)$ which is absurd as well. $\square$

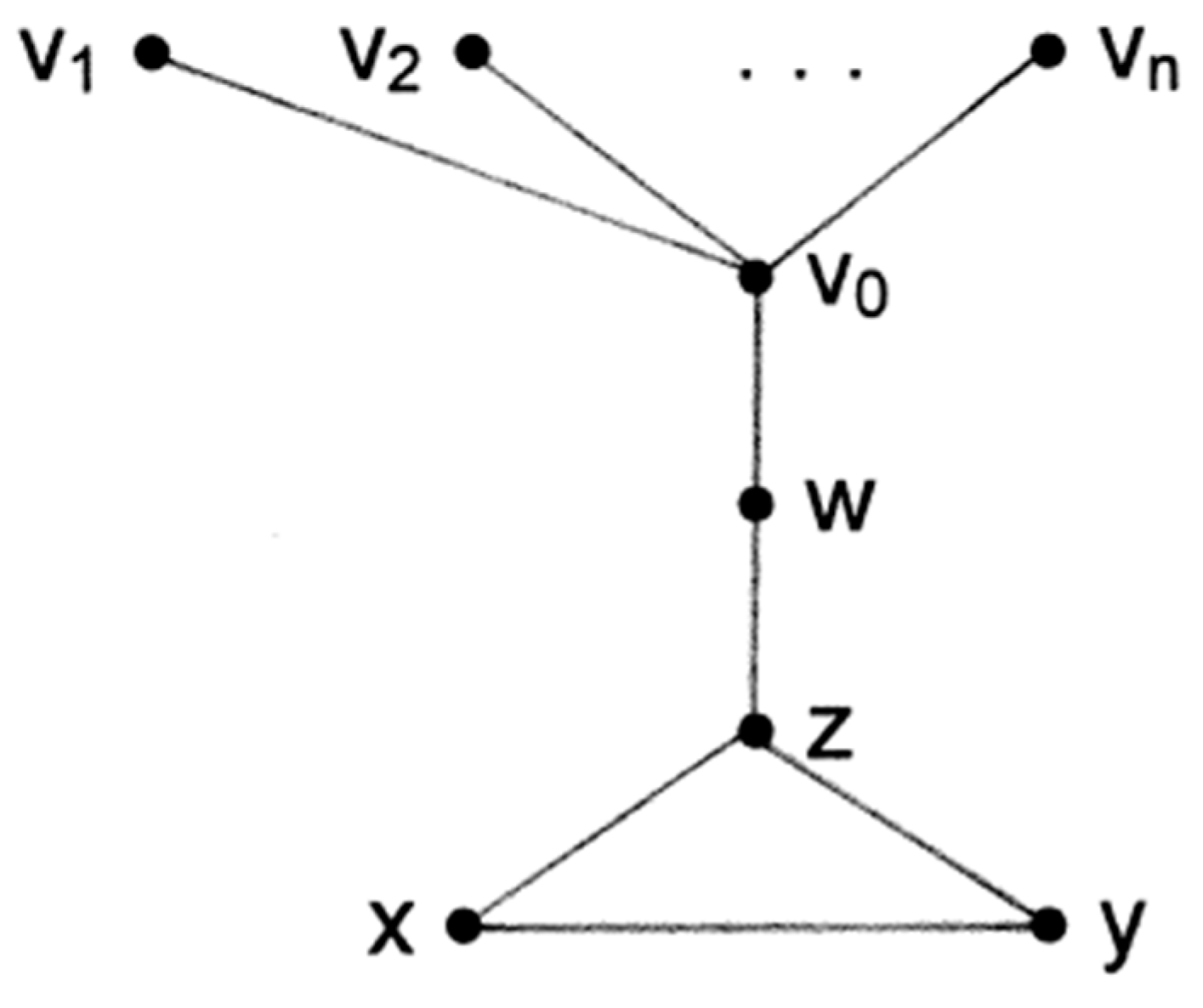
Let $C_{m,n}$ be the graph consisting of the two cycles of lengths $m$ and $n$with one vertex in common. The even harmonious property of such graphs is investigated in the next two theorems.

Theorem 2.5. If $C_{m,n}$ is even harmonious then $m+n\equiv 0(\mathrm{mod}\hspace{0.33em}4).$

Proof Suppose that $C_{m,n}$is even harmonious and let $u$be the common vertex of the two cycles. Then $G=C_{m,n}\cup K_1$ ia again even harmonious, where $V(K_1)=\left\{w\right\}.$Put $q=\left|E(G)\right|=m+n.$By Corollary ….. there exists a harmonious labeling $f$ with $f(u)=0$, so that

$$\begin{array}{l}q(q-1)\equiv {\displaystyle \sum _{e\in E(G)}{f}^{*}(e)}=(2({\displaystyle \sum _{v\in V(G)}f(v)})-f(w))(\mathrm{mod}\hspace{0.33em}2q)\\ \hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\equiv q(2q-2)-f(w))(\mathrm{mod}\hspace{0.33em}2q)\end{array}$$

If $q$is odd, we get $f(w)\equiv f(u)\equiv 0(\mathrm{mod}2q)$, which is absurd. Our result follows since $C_{m,n}$ is not even harmonious if $m+n\equiv 2(\mathrm{mod}4)$ by Theorem …..$\square$

Theorem 2.6.$C_{3,n}$ is even harmonious if and only if $n\equiv 1(\mathrm{mod}\hspace{0.33em}4).$

Proof Necessity follows from Theorem …. For sufficiency, suppose that $n\equiv 1(\mathrm{mod}\hspace{0.33em}4)$ and $V(C_{3,n})=\{u,v,v_1,v_2,\cdots ,v_n\}$where $u$ and $v$ are the two vertices of the cycles $C_3$ in $C_{3,n}$. Define the function

$$f:V(C_{3,n})\to {\mathbb{Z}}_{2n+6}$$

by

$$f(v_i)=\left\{\begin{array}{c}i-1,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}i\hspace{0.33em}odd\le {\displaystyle \frac{n+1}{2}}\\ i+1,\hspace{1em}\hspace{1em}{\displaystyle \frac{n+1}{2}}<i\le n\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ n+5+i,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}i\hspace{0.33em}even\le n-1,\end{array}\right.$$

$$f(u)=n+3,\hspace{1em}f(v)=n+5.$$

Clearly, $f$ is injective. We have

$$f^{\ast }(v_n{v}_1)=n+1,\hspace{1em}{f}^{\ast }(u{v}_1)=n+3,\hspace{1em}{f}^{\ast }(v{v}_1)=n+5,f^{\ast }(uv)=2.$$

$$\{f^{\ast }(v_i{v}_{i+1})\left|1\le i\le {\displaystyle \frac{n+1}{2}}\right.\}=\{n+5+2i\left|1\le i\le {\displaystyle \frac{n+1}{2}}\right.\}$$

and

$$\begin{array}{l}\{f^{\ast }(v_i{v}_{i+1})\left|{\displaystyle \frac{n+1}{2}}<i<\right.n\}=\{n+5+2i+2\left|\left|{\displaystyle \frac{n+1}{2}}<i<\right.n\right.\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left\{2j\left|2\le j\le \right.{\displaystyle \frac{n+1}{2}}\right\}(\mathrm{mod}2n+6).\end{array}$$

Hence $f^{\ast }$ is onto as desired. $\square$

The graph $n{K}_3$ is harmonious if and only if $n$ is odd [4], while it is even harmonious for every positive integer $n$[13]. Also the graph $n{K}_4$ is harmonious for odd $n$[11], but $n{K}_4$ is even harmonious for every positive integer $n$[13]. In the following theorem we show that the graph $K_4\cup K_2$ is not harmonious, although this graph is even harmonious by labeling the vertices of $K_4$ by the labels 0,2,4, and 8 and the vertices of $K_2$ by the labels 5 and 9. Also the graph $K_4\cup K_3$ is even harmonious by labeling the vertices of $K_4$ by the labels 0, 4, and 6, and 8 and the vertices of $K_3$ by the labels 7, 9, and 11.

Theorem 2.7. $K_4\cup K_2$ is not harmonious.

Proof Let $G=K_4\cup K_2$ and suppose that $f$ is an even harmonious of $G$where the labels of the vertices of $K_4$ are $x_1,x_2,x_3,x_4$ and of the vertices of $K_2$ are $a,b$. We may assume that $0\notin \mathrm{Im}(f)$, so that

$${\displaystyle \sum _{i=1}^4{x}_i}+a+b\equiv 0(\mathrm{mod}7)$$

and

$${\displaystyle \sum _{e\in E(G)}{f}^{*}(e)}\equiv 3{\displaystyle \sum _{i=1}^4{x}_i}+a+b\equiv 0(\mathrm{mod}7).$$

Hence $a+b\equiv 0(\mathrm{mod}7)$ and $x_i+x_j\equiv 0(\mathrm{mod}7)$ for some $1\le i,j\le 4,i\ne j$, which is absurd. $\square$

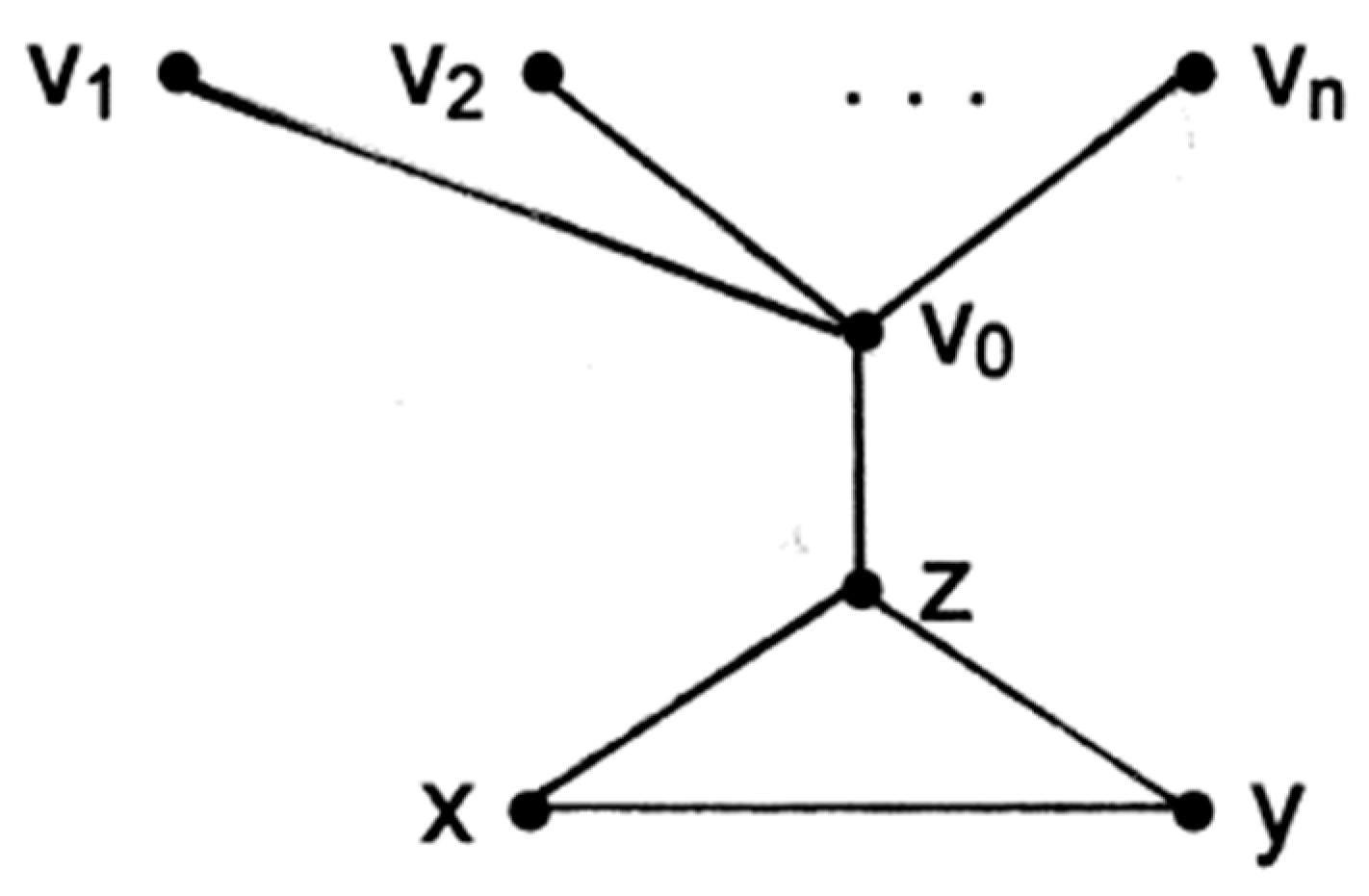
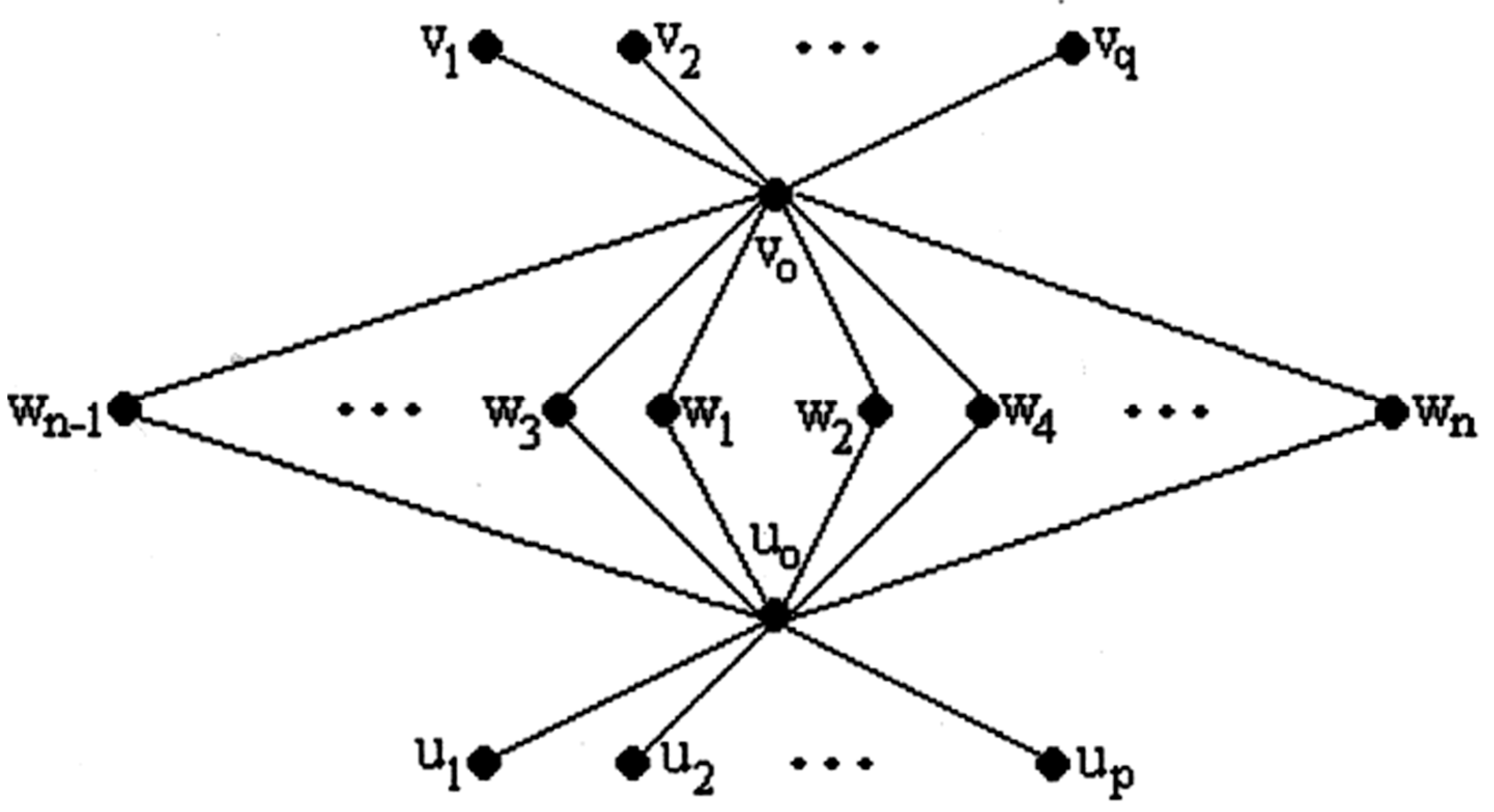
Theorem 2.8. The graph obtained by attaching $p$ and $q$$(p,q\ge 0)$pendant edges to the two vertices of degree $n$of the graph $K_{2,n}$$(n\ge 2)$is not even harmonious.

Proof Let $G$ be the graph appearing in Figure 5. The graph $G$ consisting of $e=2n+p+q$ edges. Suppose that $G$ is even harmonious, Since every vertex in even harmonious graph can delivered the label zero, we may label the vertex $v_0$ by 0, and we label all the remaining vertices of the graph with the labels from $2$ to $2e-2$ except the vertex $u_0$ which will be labeled $2s$. Now, the edge label $2s$ can never be obtained, since if we could obtain the label $2s$, then there would exist a vertex label $2x$ to one of the vertices $w_i$ or $u_j$ $(i\ge 1,j\ge 0)$ such that

$2s+2x\equiv 2s(\mathrm{mod}2e),$$2x\in \{2,4,\cdots ,eq-2\}\backslash \left\{2s\right\}$which is impossible, and hence the graph is not even harmonious. $\square$