1. Introduction
In the Lorentz transformation, light is directly chosen as the basis for derivation to obtain the spacetime coordinate transformation relationship. Based on this, Einstein proposed the renowned special relativity. One of the core ideas of special relativity is the spacetime correlation between time and space. It is believed that under high-speed motion, time and space are no longer independent but are interrelated. This spacetime correlation leads to spacetime effect phenomena such as time dilation, length contraction, and the relativity of simultaneity.[
2,
4,
5]
In fact, there is another implicit basic assumption in the Lorentz transformation. That is, the observer uses light as the means of observation, and light serves as the medium for measuring the motion of objects. All the results in the Lorentz transformation and special relativity are obtained on the premise that the observer uses light as the tool for observation and measurement.
However, why is light chosen? What role does light play in special relativity? Whether the spacetime effects obtained by using light as the measurement medium are universal has never been questioned.
Obviously, humans have diverse means of observing the world, and light is not the only observation medium. What results would be obtained if the observer uses other observation methods?
Therefore, a core question arises: how does the observer's choice of observation means, that is, the observation medium, affect the measurement results of moving objects? The Lorentz transformation and special relativity do not analyze this problem.
This paper proposes a new theory and method of the Extended Lorentz Transformation to analyze and study the above-mentioned problems.
2. Extended Lorentz Transformation
The Lorentz transformation is a mathematical tool in special relativity that describes the transformation of spacetime coordinates between different inertial reference frames[
1,
3]. The two basic postulates of the Lorentz transformation are as follows:
- i.
The principle of relativity: The laws of physics have the same form in all inertial reference frames.
- ii.
The principle of the constancy of the speed of light: The speed of light in a vacuum is constant in all inertial reference frames.
The above basic postulates use light as a specific observation medium, and the conclusions obtained have certain limitations.
This paper proposes a theory of the Extended Lorentz Transformation. Instead of taking light as a specific observation medium, it is assumed that there is a substance with a motion speed of , and its speed range is from zero to infinity. This substance satisfies the following two extended basic postulates:
- i.
The principle of relativity: The laws of physics have the same form in all inertial reference frames.
- ii.
The principle of the constancy of the observation medium's speed: The speed of the observation medium is constant in all inertial reference frames.
Through the above assumptions, the original Lorentz transformation with a specific light medium can be extended to the Extended Lorentz Transformation. The Extended Lorentz Transformation provides a mathematical tool with a wider scope of application, which can more comprehensively analyze the influence of the observation medium on the observation results.
Let there be two inertial reference frames
,
moves relative to
along the x-axis at a constant speed
. At the initial moment, the origins of the two reference frames coincide. The above - mentioned extended basic postulates meet the requirements of the Lorentz transformation. By following the derivation process of the Lorentz transformation, the corresponding solutions can be obtained in the same way:
where
and
is called the Lorentz factor.
According to special relativity, we can get
Relativity of simultaneity
3. Result Analysis
The following further discusses the influence of the speed of the observation medium on the measurement results:
3.1. When
According to special relativity
The measured and are both imaginary numbers and have no real - number solutions. This indicates that when the speed of the observation medium is less than the speed of the object's motion, the state of the measured object cannot be measured. Thus, it can be seen that the speed of the observation medium being greater than the speed of the object is a necessary condition for effective observation.
3.2. When
According to special relativity
The measured and are both infinite, indicating that when the speed of the observation medium is equal to the speed of the object's motion, the distance and time are both infinite. The moving clock runs infinitely slow, the length of the object in the direction of motion is zero, and there is a relativity of simultaneity.
3.3. When
According to special relativity
When the speed of the observation medium is infinite, the spacetime effects disappear, that is, time dilation and length contraction are zero, and the relativity of simultaneity also disappears.
3.4. When
The observation medium is light, the results of special relativity can be obtained. This shows that the results obtained by using light as the observation medium are just a special case.
3.5. When
According to special relativity
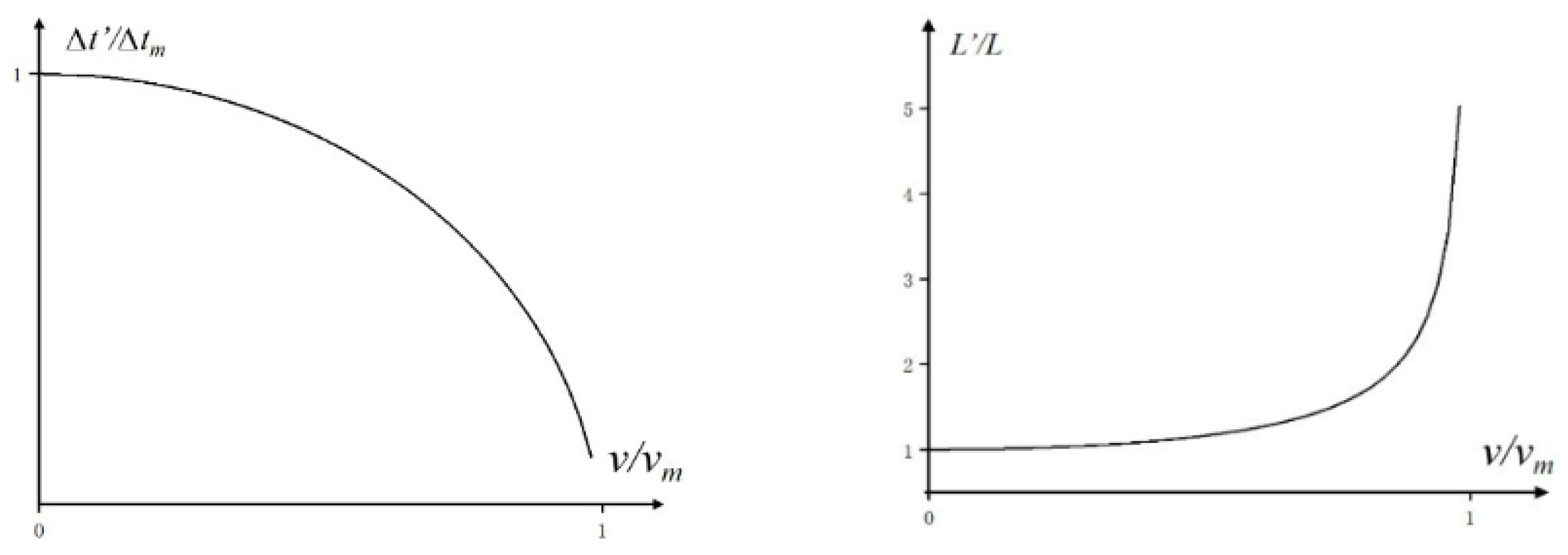
It can be seen from
Figure 1 that when
, the spacetime effects of the object are determined by
. Generally, the larger
is, the smaller the spacetime effects are; the smaller
is, the larger the spacetime effects are. A comprehensive analysis of the above results is as follows:
- 1).
In the Lorentz transformation, there is actually an implicit basic assumption that the observer uses light as the means of observation, and light is the medium for measuring the motion of objects. All the results in the Lorentz transformation and special relativity are obtained based on the observer using light as the tool for observation and measurement.
- 2).
From the analysis of the Extended Lorentz Transformation, since the motion speed of the reference frame is constant, the spacetime transformation of a moving object only depends on the value of . Different observation media yield different results of spacetime effects. The faster the speed of the observation medium, the smaller the spacetime effects. When is infinite, the spacetime effects miraculously disappear, and time and space are completely synchronized in the two coordinate systems. This fully shows that spacetime effects are related to the observer's choice of observation medium. The magnitude of spacetime effects is determined by the speed of the observation medium. This phenomenon reveals another important conclusion: spacetime effects are essentially measurement errors of the observer's observation method, which are independent of the reference frame and the motion characteristics of the moving object. The speed of the observation medium is the fundamental cause of measurement errors. The faster the speed, the more accurate the measurement. When the speed of the observation medium is infinite, the measurement error is zero.
- 3).
When light is selected as the observation medium, is a fixed value, which ignores the influence of the observation medium and mistakenly believes that spacetime effects are only related to the speed of the reference-frame motion, leading to the results of Einstein's special relativity spacetime effects. In fact, the light observation medium is only a special case of human subjective choice for observing the motion of objects, and the results of Einstein's special relativity are also a special case and not universal.
4. Spacetime Effects of the Medium for Acoustic Wave
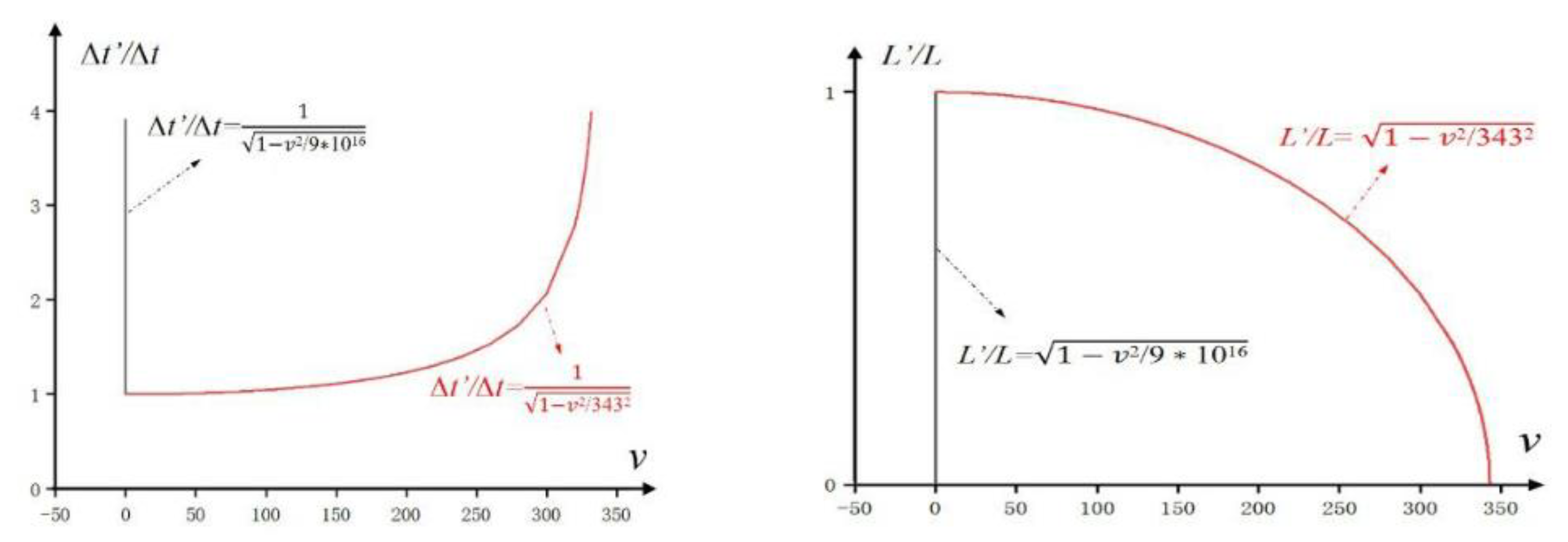
To verify the influence of the observation medium on measurement errors, acoustic waves are used as the observation medium. It is assumed that the air is completely uniform within the measurement space range, and the propagation speed of acoustic waves is the same. Since the speed of acoustic waves in different reference frames also remains unchanged, it meets the two basic conditions of the Lorentz transformation. The spacetime effects of acoustic wave and light observation media are compared.
Let the speed of light be approximately and the speed of sound be . Substitute into the formulas:
Figure 2 shows the calculation results of the two media. It can be seen that compared with the light medium, the measurement results of sound waves have strong spacetime effects and large measurement errors. When
, for sound waves, the time is dilated by 1.231 times, and the length is contracted to 0.8124 of the original. For light, its spacetime effects are extremely small, and the measurement error can be ignored.
5. Calculation of Spacetime Effect in Non-Inertial Reference Frames
In practical engineering applications, the reference frames and the motions of objects are not always uniform. Calculating the observation errors of non-uniform objects is of guiding significance for engineering applications. In variable-speed motion, the motion can be decomposed into multiple small time intervals. The motion in each time interval can be approximately regarded as a uniform linear motion, which satisfies the two basic conditions of the Lorentz transformation. Then, the solution can be obtained through integration.
Let there be two inertial reference frames
and
.
moves relative to
along the x-axis with a changing speed
. The running time period is
and the relationship between the motion speed
and time is
From the Extended Lorentz Transformation, we can get:
Length - contraction error:
Relativity - of - simultaneity error:
The above formulas can be used to calculate the cumulative spacetime errors generated by an observer when measuring a high-speed moving object within a certain period of time under variable-speed conditions.
6. Conclusions
The analysis of the Extended Lorentz Transformation excludes the influence of the special case of light-medium observation, analyzes the internal mechanism of the influence of the observation medium on spacetime, reveals the essence of spacetime effects, and expands the scope of application of relativity. The following conclusions are drawn:
- 1).
Spacetime effects are essentially subjective measurement errors caused by the observation method and are independent of the reference frame and the motion state of the object. Time and space are not interrelated.
- 2).
The speed of the observation medium is the fundamental cause of measurement errors. The faster the speed of the observation medium, the more accurate the measurement. When the speed is infinite, the measurement error is zero, and the spacetime effects completely disappear. It is a necessary condition that the speed of the observation medium is greater than that of the moving object.
- 3).
The light observation medium is only a special case of human subjective choice for observing the motion of objects, and the observation results do not have universal applicability. The acoustic-wave medium has more obvious spacetime effects.
- 4).
Under the condition of non-inertial reference frames, the calculation formula for spacetime effects is derived, which expands the scope of application of special relativity.
Einstein's special relativity holds that time and space are no longer independent but interrelated. This spacetime correlation leads to spacetime effect phenomena such as time dilation, length contraction, and the relativity of simultaneity. This paper theoretically proves that this conclusion is not valid and verifies it through the observation and analysis of the acoustic - wave medium.
To expand its scope of application, a method for calculating spacetime errors in non - uniformly moving reference frames is further proposed theoretically, providing a theoretical basis for the accurate measurement of high - speed moving objects.
Since quantum has the property of synchronous entanglement, its speed can be understood as infinite[
6]. If quantum is used as the observation medium, the measurement error is zero under any conditions. Quantum measurement may become one of the most important directions in future research on accurate measurement.
References
- Chen, F. Definition of simultaneity in general theory of relativity. Journal of Dalian University of Technology Retrieved from ://CSCD:4775852. 2013, 53, 1–3. [Google Scholar]
- Einstein, A. On the electrodynamics of moving bodies. Annalen Der Physik Retrieved from ://WOS:000201991700003. 1905, 17, 891–921. [Google Scholar]
- Garcia, J. A. (2007). “Doubly special relativity and canonical transformations:: Comment on "Lagrangian for doubly special relativity particle and the role of noncommutativity".” Physical Review D, 76(4). [CrossRef]
- Molski, M. (1995). “Special relativity and space-time geometry.” Physics Essays, 8(4), 601-604. [CrossRef]
- Gourgoulhon, ´ Eric. 2013. Special Relativity in General Frames. Graduate Texts in Physics Berlin: Springer Verlag. [CrossRef]
- Bacelar Valente, M. (2011). “The Relation between Classical and Quantum Electrodynamics.” Theoria-Revista De Teoria Historia Y Fundamentos De La Ciencia, 26(1), 51-68. Retrieved from ://CCC:000288692900003.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).