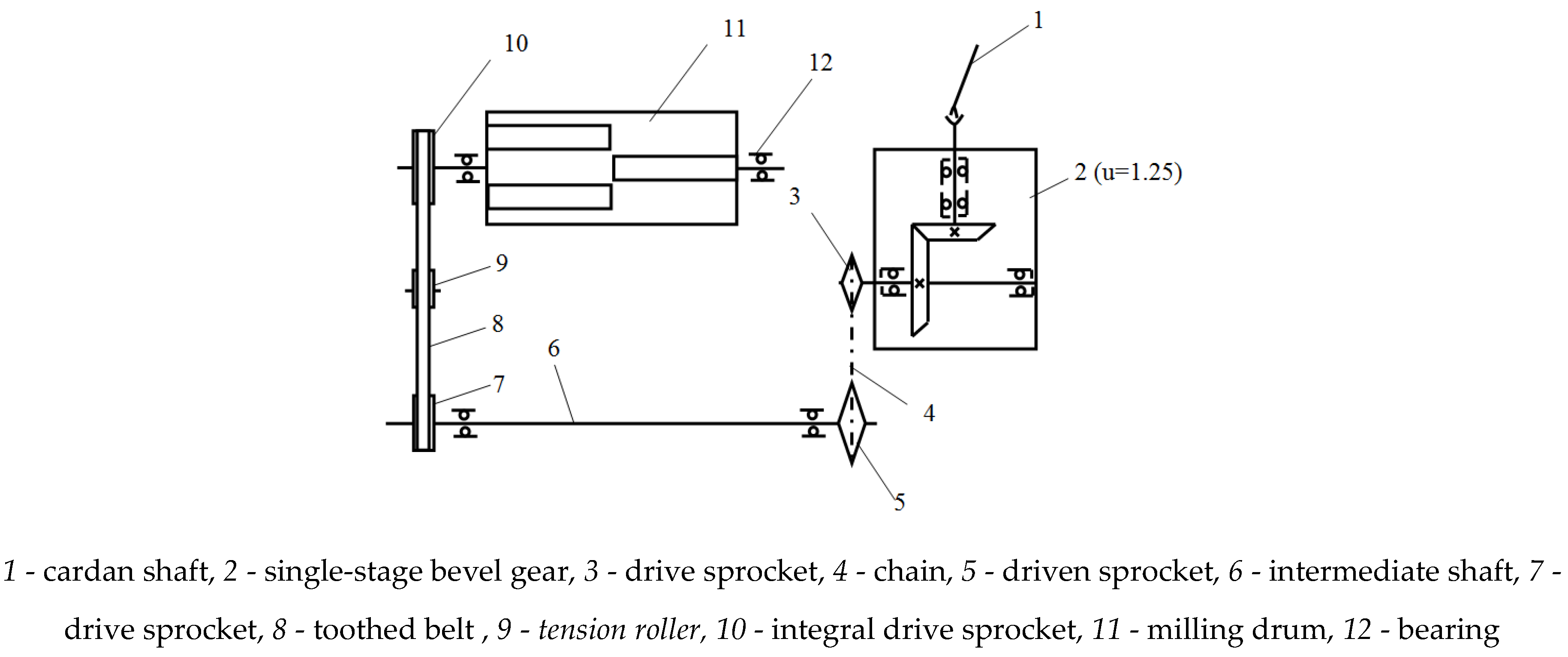
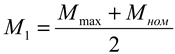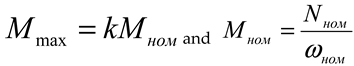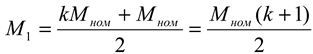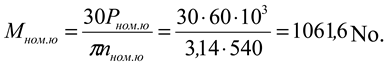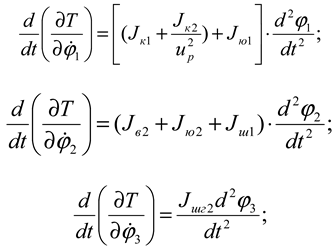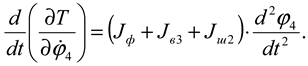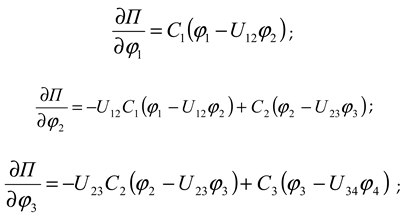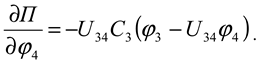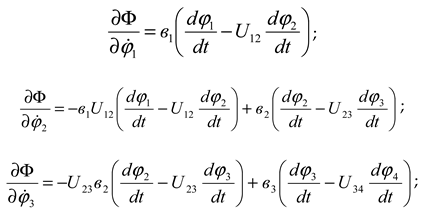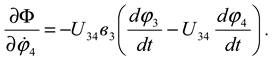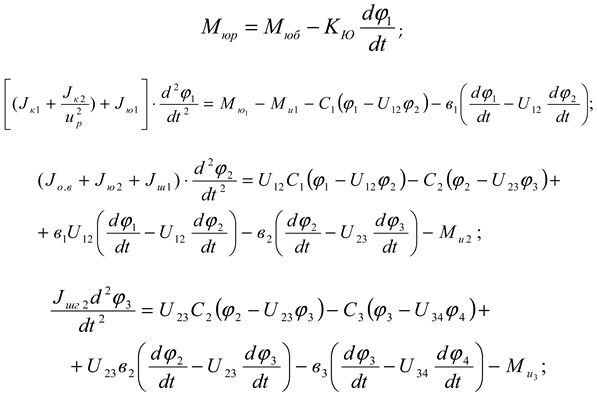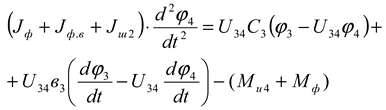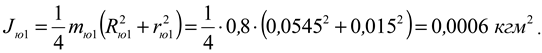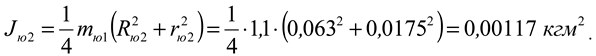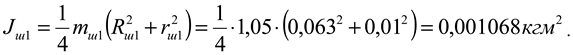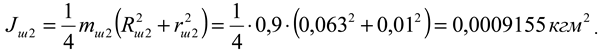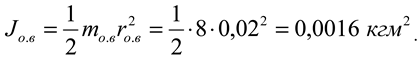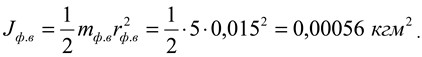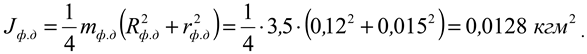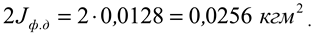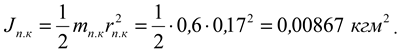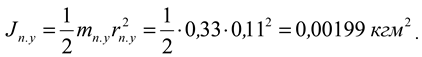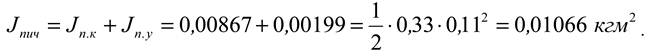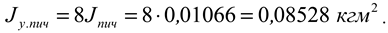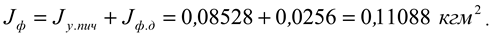Methodology
According to the calculation scheme presented in
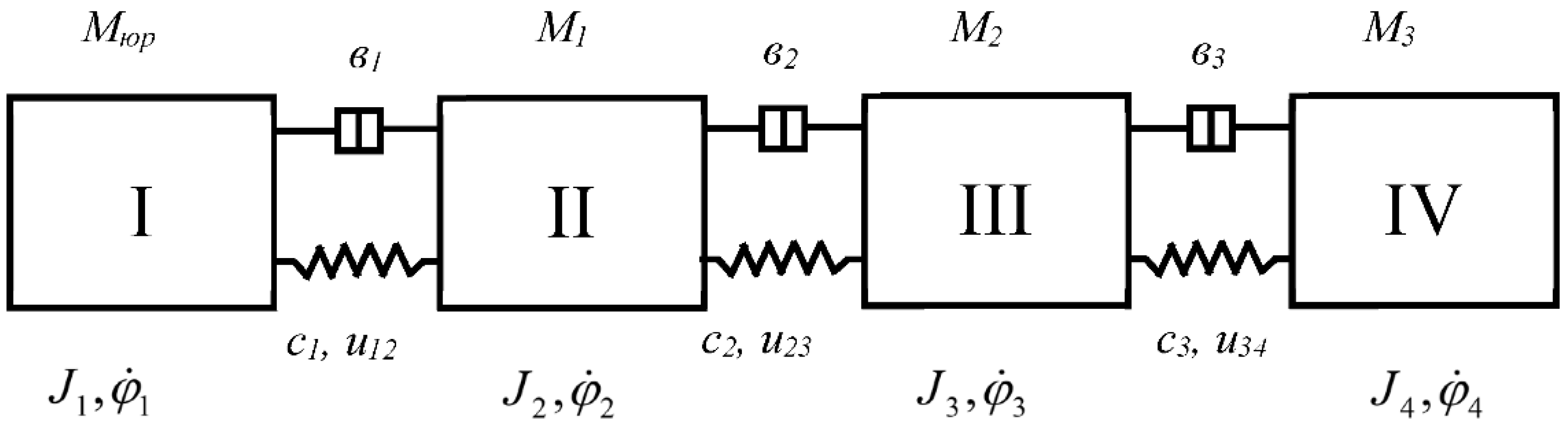
Figure 2, it is known that four masses are in rotational motion, therefore, 4 generalized coordinates can be defined. To derive the equation of motion of a four-mass machine unit for one section of the machine, we use Langrauge's equation of the second kind [
1,
2,
3,
4]
where
ϕi - generalized coordinates of masses for the
i- mass system, i.e. angles of rotation;
T - total kinetic energy of the
i -mass system, Nm; P - total potential energy of the system, Nm;
F - Rayleigh dissipative function in elastic and flexible joints, Nm;
M i ( ϕi ) -
i moment of the generalized force acting on the masses of the i-mass system, Nm.
According to the calculation scheme of the machine unit shown in
Figure 2, the expression for determining the total kinetic energy is as follows:
where
ϕ1 ,
ϕ2 ,
ϕ3 ,
ϕ4 are the generalized coordinates of the rotating masses of the machine unit, i.e. the angles of rotation;
J 1 ,
J 2 ,
J 3 ,
J 4 are the moments of inertia of the masses, kgm
2 .
The moment of inertia of a mass is determined by the following expressions
where
J ov ,
J fv - moments of inertia of the rotating shafts, kgm
2 ;
J k1 ,
J k2 - moments of inertia of the bevel gears of the reducer, kgm
2 ;
J yu1 ,
J yu2 - moments of inertia of the chain sprockets, kgm
2 ;
J f - moment of inertia of the milling drum, kgm
2 ;
J sh1 - moments of inertia of the driving pulley, kgm
2 ;
J shg2 - moments of inertia of the driven pulley flange, kgm
2 ;
J sh2 - moments of inertia of the driven pulley hub, kgm
2 ;
u r - gear ratio of the bevel gear.
In the four-mass machine unit under consideration, 1 chain transmission and 1 toothed belt transmission are used. Taking them into account, the expression for determining the total potential energy for the machine unit is as follows
where
S 1 ,
S 2 are the elastic coefficients of the chain and belt, respectively, Nm/rad;
S 3 is the elastic coefficient of the elastic element in the driven toothed pulley, Nm/rad;
U 12 ,
U 23 ,
U 34 are the transmission ratios between the rotating masses, respectively.
We write the expression for the Rayleigh dissipation function for the system as follows:
where
v 1 ,
v 3 are the dissipation coefficients of the corresponding chain and belt;
v 3 is the dissipation coefficient of the belt element in the driven toothed pulley.
Generalized torques in a machine unit
where
M u1 ,
M u2 ,
M u3 ,
M u4 are the moments of friction forces on the shafts, Nm;
M f are the moments of resistance forces from the crushed clod and soil on the milling drums, Nm.
If we take into account the number of blades on the milling drum and random values of the resistance moment,
M f will be equal to:
where
M f 1 is the value of the moments of resistance forces from the crushed pieces in the milling drum, without taking into account random values, Nm; Δ
M f is the random value of the moments of resistance forces, Nm.
To obtain the driving torque on the power take-off shaft of the base tractor, the mechanical characteristics of the shaft, i.e. the law of dependence of the driving torque M yu on the angular velocity of the shaft, are used. The MTZ-80 tractor has an internal combustion engine with a power of 500 kW and a rotation frequency of 1800 min -1 For the case where , we obtain its mechanical static characteristics.
Results and Discussion
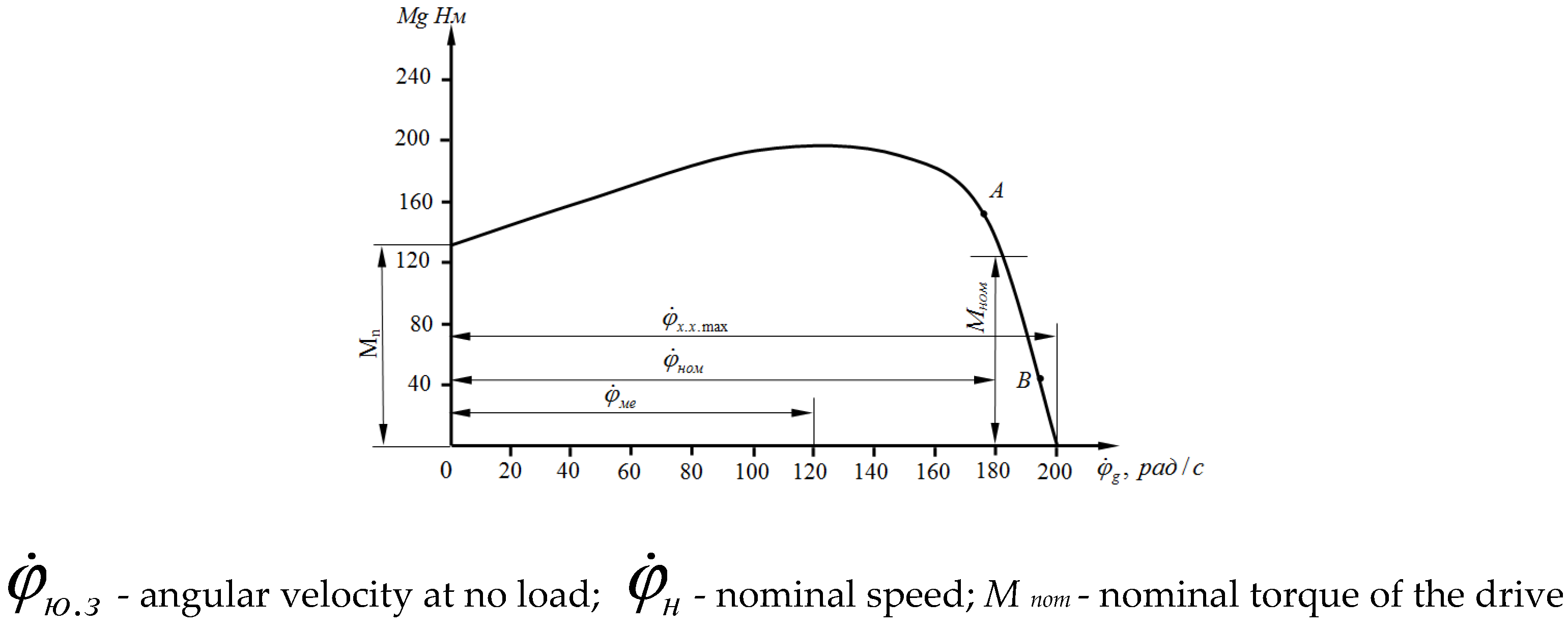
The operating modes of the tractor drive mainly include the processes of starting to move steadily, moving steadily and stopping. In the tractor, the drive is driven by a clutch. Therefore, the power take-off shaft mainly operates in the steady-state mode. In this case, the AV on the graph of the mechanical static characteristic of the drive (
Figure 3)
It is expected that there will be an operating mode between the points. In this case, the mechanical characteristic of the power take-off shaft
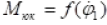
is expected to change along a straight line for the operating condition. In this case, if the rotational frequency of the crankshaft of the working drive is 1800
min -1 , the rotational frequency of the power take-off shaft is 540
min -1 1 ga, therefore, their mutual transmission number is 3.15 [
5,
6,
7,
8].
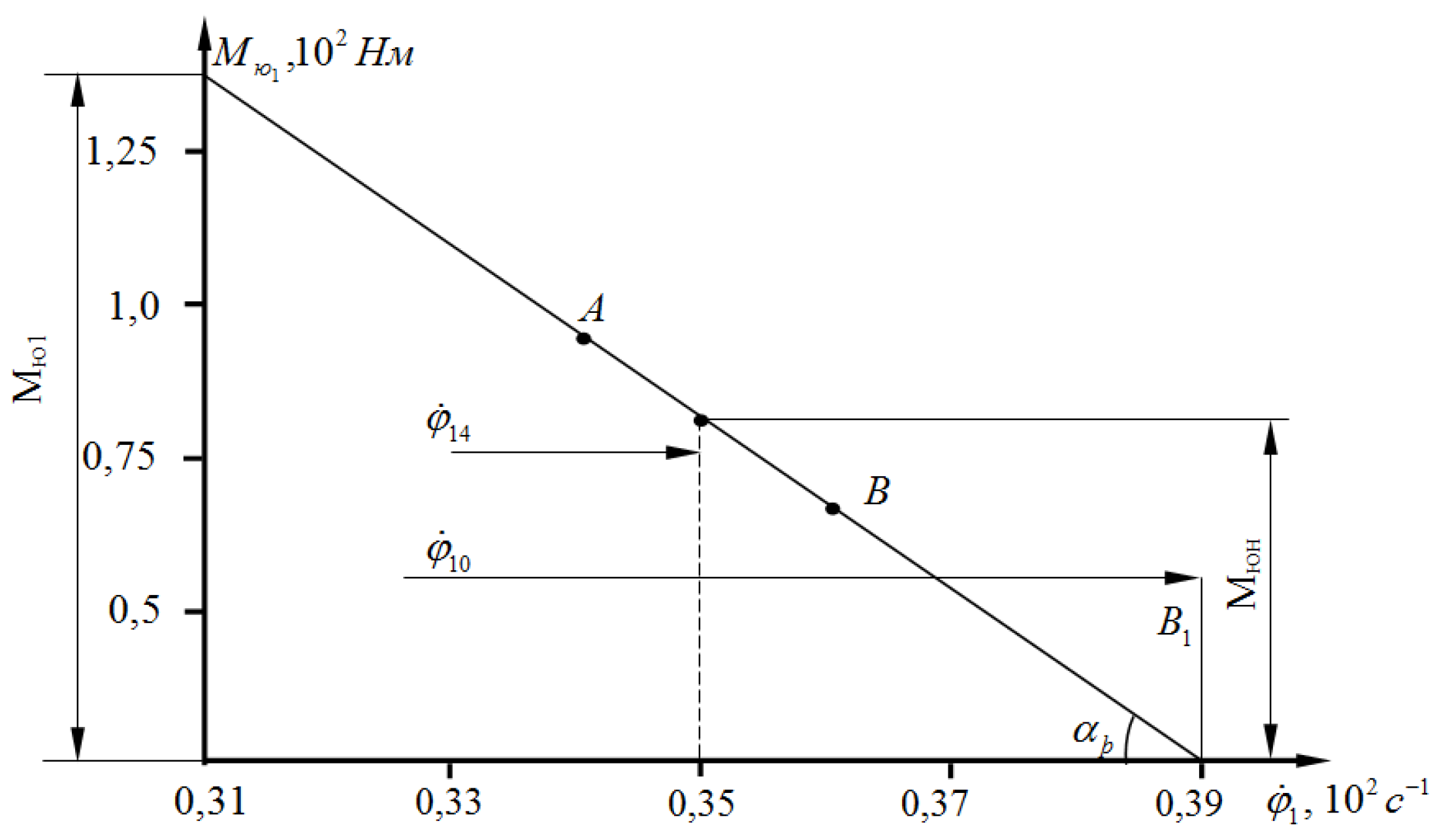
Taking into account the above, the mechanical characteristic of the power take-off shaft was considered for the operating mode (
Figure 4). It was taken as a straight line (when applied to shaft 1). In this mechanical characteristic,
A1B1 the zone is considered the main operating mode zone and it
AB corresponds to the operating mode zone of the drive mechanical characteristic in
Figure 4. In this case, the mechanical characteristic of the first shaft is:
where -
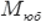
is the initial torque value on the shaft,
Nm ;
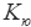
- is the slope coefficient of the mechanical characteristic, i.e. -
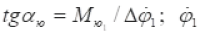
is the angular velocity of the first shaft.
The driving torque is determined as follows:
where
M max –maximum engine driving torque, Nm;
M nom – nominal driving torque of the engine, Nm.
in which
N is the name – nominal power of the power take-off shaft, kW;
ω nom – nominal angular velocity of the power take-off shaft, rad/s.
the nominal power of the MTZ-80 tractor engine is
R nom.yu =60 kW and the nominal number of revolutions of the power take-off shaft is
n nom.yu =540 rpm, the torque of the power take-off shaft is equal to:
The resistance moment on the milling drum is M f = 76.9 Nm.
second- order equation for each mass . The partial derivatives of the kinetic energy with respect to each generalized coordinate velocity and the derivatives with respect to additional time are as follows:
Coordinates generalized from the total potential energy of the system
The specific derivatives of will be as follows:
Similarly, we can derive the derivatives of the dissipation function with respect to the generalized coordinate velocities:
Substituting the obtained expressions (7), (11), (12) and (13) and expressions (4) and (5) into equation (1) for each mass, we obtain the system of differential equations representing the machine unit of a combined machine tool with a chain transmission consisting of a driven star in the transmission mechanism as follows:
The fixed parameters in the mechanical characteristics were taken as follows [
9,
10,
11] :
We determine the moments of inertia of rotating masses using an existing method [
12,
13].
The sprocket on the output shaft of the reducer: mass
m yu1 =0.8 kg; outer circle radius
R yu1 =0.0545 m; inner circle radius
r yu1 =0.015 m;
The sprocket on the intermediate shaft: mass
m yu2 =1.1 kg; outer circle radius
R yu2 =0.063 m; inner circle radius
r yu2 =0.0175 m;
The gear pulley on the shaft that transmits motion to the milling drum has: mass
m sh1 =1.05 kg; outer circle radius
R sh1 =0.063 m; inner circle radius
r sh1 =0.01 m;
The star on the milling drum shaft: mass
m ш2 =0.9 kg; outer circle radius
R ш2 =0.063 m; inner circle radius
r ш2 =0.01 m;
Moments of inertia of shafts:
Intermediate shafts: mass
m ov =8.0 kg; radius
r ov =0.02 m;
Milling drum shaft : mass
m fv =5.0 kg; radius
r fv =0.015 m;
The moment of inertia of the milling drum disk : mass m fd =3.5 kg;
The radius of the outer circle
R fd =0.12 m; the radius of the inner circle
r fd =0.015 m;
Since there are two discs in the milling drum, we multiply the output by two and get the following
mass of the milling drum blade is
m fp =0.93 kg . To simplify the calculation of the moment of inertia, we divide the blade into two parts. The first part 0,22 mis the cutting part, i.e. the blade part, with a mass of
m pk =0.6 kg, and the second part 0,12 mis the part mounted on the disk, i.e. the blade part, with a mass of
m pu =0.33 kg.
The moment of inertia of the cutting part of the blade: mass
m pk =0.6 kg; distance to the axis of rotation
r pk =0.17 m ;
of inertia of the part of the blade that is mounted on the disk: mass
m pu =0.33 kg; distance to the axis of rotation
r pu =0.1 1 m;
Total moment of inertia of the blade
Considering that 4 blades are installed on the milling drum disk, the total moment of inertia of the blades on the milling drum is
The total moment of inertia of the milling drum is equal to:
The determined values of the moments of inertia of the masses are given in
Table 1.
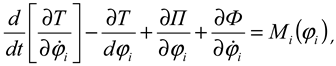
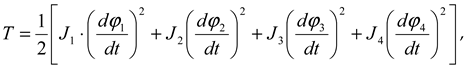
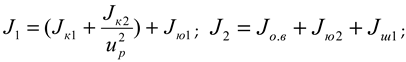
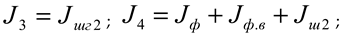
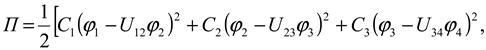
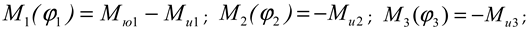
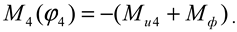
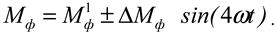
 is expected to change along a straight line for the operating condition. In this case, if the rotational frequency of the crankshaft of the working drive is 1800 min -1 , the rotational frequency of the power take-off shaft is 540 min -1 1 ga, therefore, their mutual transmission number is 3.15 [5,6,7,8].
is expected to change along a straight line for the operating condition. In this case, if the rotational frequency of the crankshaft of the working drive is 1800 min -1 , the rotational frequency of the power take-off shaft is 540 min -1 1 ga, therefore, their mutual transmission number is 3.15 [5,6,7,8].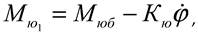
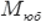 is the initial torque value on the shaft, Nm ;
is the initial torque value on the shaft, Nm ; 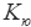 - is the slope coefficient of the mechanical characteristic, i.e. -
- is the slope coefficient of the mechanical characteristic, i.e. - 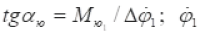 is the angular velocity of the first shaft.
is the angular velocity of the first shaft.