Prerpints.org logo
Preprint
Article

Analysis of the Reliability and Efficiency of Information Extraction Using AI-Based Chatbot: The More for Less Paradox

This version is not peer-reviewed.

Submitted:

18 March 2025

Posted:

19 March 2025

You are already at the latest version

Abstract
This paper addresses the following problem of information extraction using an AI-powered chatbot. An AI chatbot processes a natural language conversation with a human user using semantic search and human-chatbot interaction to extract the most relevant and contextually appropriate information from available databases. During a natural language conversation between a human and an AI, the human user can modify and refine queries until he/she is satisfied with the chatbot’s output. The reliability of an AI chatbot is defined as its ability to understand user queries and provide correct answers; in the current study, it is measured by the frequency (probability) of correct answers. The search efficiency of a chatbot indicates how accurate and relevant the information returned by the chatbot is; in this work, it is measured by the satisfaction level that the human user receives for a correct answer. We uncover a counterintuitive relationship between AI chatbot reliability and search efficiency: we demonstrate that, under fairly general conditions, a less reliable AI chatbot can have a higher expected search efficiency than a more reliable chatbot. This phenomenon aligns with a family of “more-for-less” paradoxes observed in various complex systems. Finally, we discuss the underlying mechanism of this paradox.
Keywords: 
information search
;  
stochastic search policy
;  
artificial intelligence (AI) chatbot
;  
chatbot reliability
;  
search efficiency
;  
more-for-less paradox
Subject: 
Computer Science and Mathematics  -   Robotics

1. Introduction

This paper addresses the problem of information extraction by an AI-powered chatbot that is not entirely reliable and may make mistakes in its responses. Unlike conventional search-and-rescue robots, which typically perform targeted searches using well-known pathfinding algorithms to autonomously navigate physical space, the AI chatbot processes a natural language conversation with a human user and extracts meaningful information using semantic search and human-AI interaction to generate the most relevant and contextually appropriate responses. During the user-AI natural language conversation, the human user can modify and refine queries until he/she is satisfied with the chatbot’s output.
We analyse two key characteristics of human-AI interaction, reliability and search efficiency [1,2,3]. The reliability of an AI-based chatbot is reflected in its ability to understand user queries and provide correct answers; it is measured by the frequency (probability) of correct answers [1,2]. The search efficiency of a chatbot [3] shows how accurate and relevant the information returned by the chatbot is. In this study, search efficiency is measured by the level of satisfaction that a human user receives for a correct answer from the chatbot on a 10-point Likert scale. This is a well-known IBM SPSS rating system for measuring customer satisfaction, in which the highest score of 1.0 signifies “very satisfied” on a 10-point scale ranging from 0.1 to 1.0, while the lowest score of 0.1 means “very dissatisfied” [4].
In this work, we uncover a counterintuitive relationship between the reliability of AI chatbots and their search efficiency. We demonstrate that, under fairly general conditions, reducing the reliability of deployed chatbots can improve the search efficiency. In particular, a less reliable chatbot that stops searching after extracting relevant information may have higher expected efficiency than a more reliable chatbot. This phenomenon aligns with the family of “more-for-less” paradoxes observed in various complex systems. Finally, we discuss the underlying mechanism of this paradox.
The main contributions of this paper are as follows: (i) we present and formalize a multi-stage (multi-round) conversation process between a human user and AI chatbot, such as ChatGPT, which serves to extract relevant information and consists of multiple rounds of query modification/refinement during the conversation; (ii) the optimization information-extraction problem for the imperfect AI chatbot is formulated as a sequential discrete search problem with probabilistic parameters; (iii) a new efficient index-based algorithm for determining the optimal search policy is developed, which extends the known fast scheduling algorithms of Ross [5], Sweat [6] and Chew [7] for sequential discrete search problems; and finally (iv) the counterintuitive relationship between the AI chatbot reliability and search efficiency characteristics in the multi-round informational search process is analyzed and explained.
The remainder of the paper is organized as follows. In the next section, we introduce the main definitions that will be used in the sequel. Section 3 describes the information extraction problem to be solved. Section 4 provides a brief overview of the previous work. In Section 5, we propose a mathematical model and an efficient index-based algorithm to optimize the expected user satisfaction over an infinite horizon. In Section 6 we formulate and prove the paradoxical relationship between the reliability and efficiency of an optimal information extraction process using an AI chatbot. Numerical examples to support and illustrate the studied paradox are presented in Section 7. A summary of contributions and an outline of future research are provided in Section 8.

2. Preliminaries

In this section we provide the basic definitions that will be used in the sequel.

2.1. The Discrete Search Problems with Imperfect Robot’s Sensors

The common discrete search problem is as follows [5,6,7,8,9,10]. A target is hidden in one of the known locations 1, 2,…, N with a probability distribution p = (p1, p2,…, pN), ∑ i pi =1, and remains in this location during the search. A search device (for example, the search-and-rescue robot) must perform a sequence of inspections at locations 1, 2, …, N to find the target, and continues searching until the target is found.
The robot’s sensor is imperfect, that is, for each location i, it has a non-zero overlook probability ai associated with it, so that if the target is at location i and the robot is exploring that location, there is a chance (probability ai > 0) that the sensor will not detect the target for any i = 1, …, N.
Given the above probabilities, along with the duration of the inspections and the reward for detecting the target at a given location, the goal is to define a probabilistic search policy that finds the optimal sequence of robot movements that maximizes the expected total reward over an infinite time interval. Specific details regarding information search/extraction using AI-powered chatbots are presented in the next subsection.

2.2. The Information Extraction Problem Using AI Chatbots

The studied problem refers to searching and extracting relevant information from a large dataset in response to a user’s query. The goal of an AI chatbot is to provide the most useful and accurate information and avoid irrelevant results.
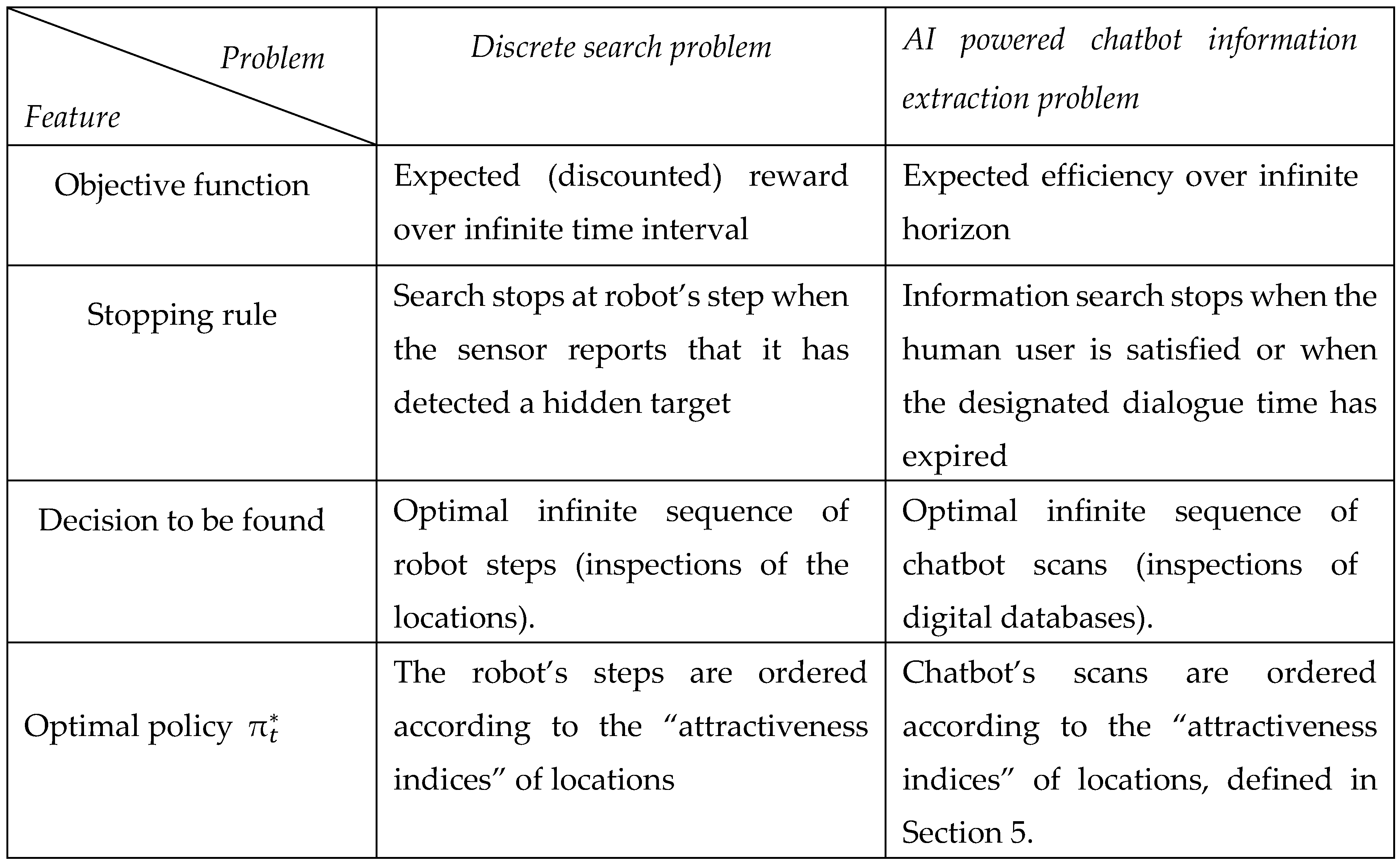
While the task of information extraction using AI chatbots can be considered a special class of the general discrete search problem, these problems differ in their goals, physical environments, and solution methods. Search-and-rescue robots perform searches, typically after disasters, in physical areas seeking to find and rescue survivors, while AI-powered chatbots perform information search and extraction aiming to find, extract, and generate relevant textual and visual answers from digital knowledge bases, documents, and the web. Search-and-rescue robots use discrete pathfinding algorithms such as A*, PRM, and Dijkstra’s algorithm to autonomously navigate physical spaces, while the conversation between a human user and an AI chatbot consists of multiple stages (rounds) during which the user modifies/refines queries while the chatbot improves its responses over time based on user feedback and learning from the user’s interactions with the AI, until the user is satisfied or until a designated dialogue time interval has elapsed.
An AI-powered chatbot searches, discovers and extracts the most relevant information requested through a process called semantic search. This is an advanced information retrieval technology that focuses on understanding the meaning and content of a user’s query, rather than simply searching and matching keywords. The chatbot typically scans hundreds of databases and their clusters depending on the complexity of the query, where thousands of documents can be scanned in milliseconds, making this process efficient. The process consists of the following main steps:
  • query understanding, where the chatbot interprets the human user’s request using natural language processing to extract the meaning and then convert the text into a numerical format,
  • using semantic search, the chatbot compares the query with data stored in databases or multiple database clusters to find the most relevant matches,
  • the chatbot performs ranking/filtering of the query to prioritize the most relevant pieces of information and refine its response, and finally
  • once the relevant information has been found, the robot generates text using natural language and extracts the natural language response.
In the next section we present a mathematical model of the problem.

3. Description of the Efficiency-Maximizing AI-Based Search Problem

The target information is hidden in one of the known database clusters (called locations) 1, 2,…, N with a known probability distribution p = (p1, p2,…, pN), ∑ i pi =1, and remains in this location during the search. The search device (in our case, the AI powered chatbot) must perform a sequence of scans in locations 1, 2, …, N to find the target information, and continues the multi-round search until a human user declares on some round that the target has been found, or until a prespecified search time interval has elapsed; on both cases the search process stops.
The chatbot is imperfect (not completely reliable), i.e., at each stage, for each location i, it has a non-zero overlook probability ai, so that if the requested target information is in location i and the chatbot scans this location, it does not recognize it and does not report the presence of the target information there, i = 1, …, N.
Given the above probabilities p = (p1, p2,…, pN) and a = (a1, a2,…, aN), as well as the duration of all conversation rounds and the user satisfaction levels with the extracted target information in each conversation round, the objective of the information extraction problem under consideration is to determine a stochastic search policy to find the optimal sequence of chatbot location scans that maximizes the expected user satisfaction over an infinite time horizon. In Table 1, we highlight the main differences between the general discrete search and information extraction problems. The essential difference between them is that the present work is motivated by and focused on the practical issue of analyzing the properties of existing AI chatbots.
Consider the mathematical model in more detail. The discrete search area A contains N known database clusters (locations), in one of which a target information is hidden, with a known probability distribution p = (p1, p2,…, pN), ∑ i pi =1. The AI chatbot inspects the area to find and identify a hidden target whose location is unknown in advance; we assume that this smart robot must sequentially perform location scans in each round, one after another. The AI chatbot is imperfect, this means that associated with each location i is a non-zero overlook probability ai, that is, ai is the conditional probability that the robot will not detect the target information in a single scan of location i, given that this location in fact contains the requested information, i∈A = {1, …, N}. Therefore, since ai ≠ 0, for the search to be successful, each location must be searched infinitely often, and, from the mathematical point of view, in general, the sequence of user-chatbot conversational rounds can be infinite.
The duration of the user’s query modifications at each conversation round are assumed to be known in advance. Also, as we indicated above, in this work the search efficiency is measured by the satisfaction level that a human user feels whenever he/she is satisfied by the chatbot response during some stage (round) of the conversation; it is assumed to decrease monotonically in time during the user’s conversation with the chatbot.
The goal of information extraction is to determine the optimal search strategy to find the target information with the maximum expected search efficiency (user’s satisfaction) over an infinite time horizon.
In addition to probabilities pi and ai defined above, we use the following notation:
  • policy π is an infinite sequence of conversation stages (rounds), π = (π1, π2,…); πk is the number of a location (a database cluster) scanned at the kth round of the sequence π, πk∈ A = {1, …, N}, k = 1, 2, …;
  • n is the (unknown) round of the sequence π at which the chatbot successfully extracts the targeted information;
    u i = u π , n is the number of unsuccessful scans (rounds) of location i = πn, before the nth (successful) round of the sequence π; u π , n   ≤ n-1;
  • P π n   is the conditional probability that after u π , n   unsuccessful scans of location πn, the chatbot will successfully detects that location (database cluster) πn contains the target information, given that the latter information is at location πn; P π n = a π n   u ( π , n ) ( 1 − a π n );
  • П π n   = P π n p π n is the unconditional probability that the chatbot will find the requested information at location πn;
  • tk is the known time required for a human user to read, evaluate and refine the chatbot’s response in round k, k =1,2, … ;
  • Tπ,n =   ∑ i = 1 n t π i , the total time spent by a human user in conversation with the chatbot from round 1 to round n in sequence π;
  • r(π) = r π n is the known Likert-scale satisfaction level obtained by the human user when the target information is found at location πn of the sequence π (before discounting). If the search for the target information requires Tπ,n time units, the level of satisfaction is discounted by e − d T π , n for a known discount factor d, d ∈(0,1), i.e., is defined as follows: Rdiscount(π) = r π n e − d T π , n = r π n e − d ∑ i = 1 n t π i .
In the problem under consideration, the satisfaction level is a random variable with value x = r π n e − d ∑ i = 1 n t π i and probability p(x) = P π n p π n = a π n u ( π , n ) ( 1 − a π n )   p π n depending on π. Then the expected discounted satisfaction (search efficiency) corresponds to the expected accumulated information obtained by the human user in the policy π, denoted F(π), and will be defined over an infinite time horizon as follows:
F ( π ) = E ( R d i s c o u n t ( π ) ) =
E ( r π n e − d ∑ i = 1 n t π i ) = ∑ n = 1 ∞ r π n · e − d ∑ i = 1 n t π i · P π n p π n =
∑ n = 1 ∞ r π n · e − d ∑ i = 1 n t π i · a π n u π , n 1 − a π n p π n
The goal is to define a stochastic policy for a search chatbot that determines where it should search at each round, that is, determines an optimal infinite sequence of chatbot actions that maximizes the expected discounted satisfaction of a human user F(π) over an infinite period of time.

4. Previous Work

This section is devoted to two different topics of this study: a review of efficient discrete search algorithms and a brief overview of paradoxical phenomena arising in operations research.

4.1. Index-Based Algorithms for the Discrete Search Problems

The discrete sequential search problem is one of the oldest problems of operations research, first formulated and solved by Bernard Koopman and his team during the World War II, when the military task was to provide effective methods of detecting submarines [11]. An excellent review of search theory and recent bibliography of the discrete search literature can be found in [8,12,13].
Several authors have studied sequential discrete search problems with overlooking probabilities in various settings and developed efficient index-based solution methods (see e.g., [5,6,7,8,9,10]). When a search device, such as a search-and-rescue robot or an unmanned aerial vehicle (drone), is not reliable, the inspection/search of a location is imperfect, and in this case any location may need to be inspected many, even infinite, times. Thus, the discrete search problem is to find an optimal strategy rather than the optimal search sequence. The latter optimal strategy depends on the random moment when the search device finds the target.
A typical stopping rule for a multi-step stochastic search process is: “Stop at a step when the target is found or when the assigned search time has elapses”. Other criteria for terminating the search process, called stopping rules, have been proposed by Ross [5] and Chew [7]. Trummel and Weisinger [14] and Wegener [15] showed that the general discrete search problem is NP-hard.
In a more recent study, Kriheli et al. [16] proposed a fast algorithm for searching for hidden targets by unmanned aerial vehicles under imperfect inspections with non-zero false-positive and false-negative detection probabilities.
Kress et al. [17] analysed several myopic and biology-inspired search strategies that minimize search time and have shown that a local index-based policy is optimal when target detection by an autonomous automated search device is accompanied by reliable verification work performed by a team of humans.
In this paper, we continue and extend the results mentioned in the previous work by focusing on the study of a multi-round search scenario in which imperfect inspections of clustered databases are performed by an AI-powered chatbot accompanied by a human user who verifies the chatbot’s responses and refines his/her queries.

4.2. Paradoxes in Operations Research

In teaching Operations Research and Artificial Intelligence courses, the authors have found that presenting counter-intuitive or paradox-like anomalies can be a great eye-opener for listeners. Studying such anomalies leads to a better understanding of algorithms and a deeper learning of OR and AI techniques. A typical example is the famous Braess paradox that arises in dynamic transportation networks and states that “adding a new wide road to a congested transport network can lead to an increase in overall travel time” [18,19]. Similar counterintuitive effects are known to also occur, for instance, in power transmission systems [20], biological and ecological systems [21], and exploiting generative Artificial Intelligence [22].
A mechanism of this paradox can be explained by changing drivers’ priorities and behaviours after a network’s reconstruction. For example, in response to a capacity addition more drivers begin to use the expanded highway; those previously not traveling at peak times shift to the peak hours, and public transport users shift to driving. From a mathematical perspective, such drivers’ behaviour disrupts the equilibrium and leads to suboptimal traffic flow for everyone. This is because the Nash equilibrium of such a system is not necessarily optimal. The network change induces a new game structure between multiple drivers which leads to a new situation. Unlike a Nash equilibrium, where drivers have no incentive to change their routes, when the system is not in a Nash equilibrium, individual drivers can improve their respective travel times by changing the routes they take. It follows that drivers will continue to switch until they reach a new Nash equilibrium despite the reduction in overall performance.
Another phenomenon, called the Jevons paradox, describes a situation where technological progress increases the efficiency of resource use, reducing the amount required per user and lowering its cost. However, the falling cost of use increases demand. Consequently, while individual resource consumption decreases, total societal resource use by all users increases, regardless of whether this resource is fuel, or a computer, or an electronic device. So, this “paradox” is explained by the substantial societal increase in demand, which outweighs individual gains in resource efficiency, leading to a net increase (rather than decrease) of societal resource consumption [23,24]. These paradoxes warn against making decisions based solely on local or individual optimization without assessing the broader impact on the system.
One more paradox arising in scheduling theory is described by Spieksma and Woeginger [25] and states that “increasing the speed of some machines in a no-wait flow-shop problem can significantly worsen the optimal total time”. There are other, less well known anomalies studied in the literature, for example, so-called “more-for-less paradox” in the classical transportation problem [26] and Graham’s multiprocessor scheduling anomaly [27].
The next sections present another paradoxical “more-for-less” phenomenon, according to which increasing the generative AI’s reliability decreases its efficiency. Note that in all mentioned papers and in this one, the word “paradox” is used to denote a counter-intuitive and surprizing phenomenon, not a classical paradox in the context of formal logic.

5. Finding the Optimal Policy π* for the Problem

In this section, we prove the optimality of the greedy index policy for the information extraction problem. We will use a basic method called the “interchange argument”, which involves exchanging two consecutive search locations. For completeness, we will describe this index policy for solving the problem under study. In what follows, we will use this policy to identify the paradoxical property of the problem. The idea of this method is as follows.
To find the optimal search strategy that maximizes the expected discounted satisfaction presented in (1), it suffices to compare the objective function F(π) for two conjugate infinite sequences π1 and π2, in which exactly two arbitrary neighbouring locations π n 1 and π n + 1   1 are swapped:
π 1 = π 1 1 , π 2 1 , . . . , π n − 1 1 , π n 1 , π n + 1 1 , π n 1 , π n + 2 1 , . . . ;
π 1 = π 1 1 , π 2 1 , . . . , π n − 1 1 , π n 2 , = π n + 1 1 ,   π n + 1 2 = π n 1 ,   π n + 2 2 = π n + 2 1 ,   … .
Having performed elementary arithmetic operations with expression (1), it is easy to obtain that
F π 1 − F π 2 =
[ r π n 1 · e − d T π 1 , n · P π n 1 p π n 1 + r π n + 1 1 · e − d T π 1 , ( n + 1 ) · P π n + 1 1 p π n + 1 1 ] −
[ r π n + 1 1 · e − d ( T π 1 n + 1 − t π n 1 ) · P π n + 1 1 p π n + 1 1 + r π n 1 · e − d T ( π 1 , n + 1 ) · P π n 1 p π n 1 ]
From (2) it follows that F(π1) ≥ F(π2) iff
r π n 1 · e − d t π n 1 · P π n 1 p π n 1 1 − e − d t π n 1   ≥ r π n + 1 1 · e − d t π n + 1 1 · P π n + 1 1 p π n + 1 1 1 − e − d t π n + 1 1 ,
or
r π n 1 · e − d t π n 1 · a π n 1 u ( π 1 , n ) 1 − a π n 1 p π n 1 1 − e − d t π n 1 ≥ r π n + 1 1 · e − d t π n + 1 1 · a π n + 1 1 u π 1 , n + 1 1 − a π n + 1 1 p π n + 1 1 1 − e − d t π n + 1 1 .
Since neighbouring locations are chosen arbitrarily, in order for a sequence π* to have a maximum expected efficiency F(π*), it is sufficient that all its components are chosen sequentially one after another in a non-decreasing order of the coefficients defined in (3). We come to the conclusion that the following two-index parameter Qi,j characterizes the “attractiveness” of location i, given that this location has already been searched unsuccessfully j times, j ≥ :
Q i , j = r i e − d t i · a i j ( 1 − a i ) p i 1 − e − d t i ,   i = 1 , … , N ; j = 1,2 , …
Using relations (2)-(3) and notation (4), we obtain the following result:
Proposition 1. 
If there have already beenj= j(i) unsuccessful scans of each locationi, wherei∈{1, …, N} andj ≥ 1, then choosing for the next scan the location i* that has the maximum value of theparameter Qi,j defined in (4), among all i for a fixedj= j(i), ensures the maximum discounted satisfaction F(π) of the user.
Remark.
The symbol u(π,n) in formula (3) denotes the same term as the symbol j in formula (4), i.e., the number of times a certain location i = π n has already been unsuccessfully scanned by an unreliable chatbot. However, introducing such a double notation in this context is done for convenience, in order to write the formulas in a more readable form. The former notation is convenient when comparing two policies denoted π1 and π2, while the latter will be more convenient below when describing the upcoming multi-round algorithm.

5.1. Iterative Algorithm for Constructing the Optimal Sequence

Proposition 1 formulated above allows us to construct an efficient iterative algorithm for constructing an optimal search policy π*.
The algorithm is defined for an indefinite number of search rounds over an infinite time horizon. It contains an a priori unknown number of rounds and continues until the human user is satisfied with the information obtained or until a predetermined search time has elapses; in both cases, the user stops the search process. In essence, this procedure requires that at each round, for each subsequent search, exactly one known cluster of databases is selected and scanned, namely the cluster having the maximum parameter Qi,j defined in (4) among the values of Qi,j that have not yet been selected.
The results of the calculations at any round k, k = 1,2,… will be represented as a kxN matrix, denoted Mk, in which N columns correspond to predetermined locations for scanning and the number of rows corresponds to the number of search rounds performed before the algorithm stops. The elements mi,j of the matrix Mk represent the parameters Qij from expression (4), computed sequentially round by round. Below we describe round 1 separately, since it differs from all subsequent rounds in that it contains an additional step designated 1.1, in which the first row of the matrix M1 is formed. After that we give a description of the current kth round, the same for all k ≥ 2.
As mentioned, in this procedure, the subscript j denotes how many unsuccessful scans of location i (i=1, …, N) were made by the chatbot before the start of round k (k=1, 2,…). Therefore, this index can be provided with two indicators, namely i and k, and the subscript j will be replaced by the notation jk(i).

5.2. Rounds of the Algorithm

Let us first describe round 1, which consist of the following four steps.
Step 1.1: //Calculate the elements of the first row of the matrix M1.//
In accordance with expression (4), we set j = 1 for all locations, calculate the parameters Qi,1, for all i=1,…N, and write them as the corresponding elements mi,1 of the first row of the matrix M1.
Step 1.2. The chatbot performs the first (preliminary) scan of each location one by one and extracts the relevant information from each location. The chatbot being unreliable, the human user verifies that the target information from the scanned-once locations is not satisfiable yet and hence assign 1 to the number of unsuccessful checks for each location.
Step 1.3. //Determine the location i 1 * and scan it once more //.
Choose location i 1 * such that Q i 1 * , 1 = maxi Qi,1. Scan l o c a t i o n i 1 * = π 1 *   ( f o r t h e s e c o n d t i m e ). If the human user is satisfied with the target information extracted now from location π 1 * =   i 1 * , compute the partial satisfaction level F(π*) obtained so far, where π* = { π 1 * } and terminate the search; highlight Q i 1 * , 1   in cell (1,   i 1 * ) in bold and red (see numerical example in section 7). Otherwise, increase the number of unsuccessful scans for location i 1 * by 1, i.e., set j2( i 1 * ) := j1( i 1 * ) + 1 = 2. Go to the next round 2.
Let us now assume that the rounds 1,…, k (k ≥ 1) are completed and the locations π*1,…, π*k are determined at these rounds, i.e., the optimal subsequence π k * = ( π 1 * ,   π 2 * … , π k * ) is found. At the end of the kth round, all parameters Qi,j, i=1,…, N, j=1,2, …, k+1 are calculated and represented as a known (k+1)xN-matrix M(k+1). Accordingly, the corresponding indices j1(i1*), j2(i2*),…, jk(ik*), and the objective function F(π*) are calculated. Then the next, (k+1)th, round will be as follows.
Round k+1, where k = 1, 2, …, consists of the following three steps.
Step k+1.1. // Determine the location i ( k + 1 ) * to be scanned (k+1)th-in-turn by the iterative algorithm.//
Denote the second index j in the elements of the (k+1)th row of the matrix Mk+1 by jk+1(i) for all i; among all parameters Q i , j k + 1 ( i ) select the location i*k+1 (to be scanned as the next one) which has the maximum Q i , j k + 1 ( i ) as follows: Q i k + 1 * ,   j k + 1 = m a x i = 1 , … , N   Q i , j k + 1 ( i ) . Place Q i k + 1 * ,   j k + 1 in cell (k+1,   i k + 1 * ) of the (k+1)th row of the matrix Mk+1, highlight this item in bold and red.
Step k+1.2.// The human user checks whether the location i k + 1 * contains the required target information; if yes, the search stops; otherwise increase by 1 the number of failed checks for location i k + 1 * .//
Consider a current optimal subsequence π* = π*k+1 which for now is: π b e k + 1 * = ( π 1 * ,   π 2 * … , π k + 1 * ); compute the efficiency F( π k + 1 * ). Increase the number of unsuccessful scans of location π k + 1 * by 1, that is, change the second index for location π k + 1 * as follows: jk+2( π k + 1 * ) := jk+1( π k + 1 * )+1, leaving the second indices for all other locations unchanged: ji,k+2 := ji,k+1, i ≠ i k + 1 * . Go to step k+1.3.
Step (k+1).3. //Determine all elements Qij in the (k+2)th row of matrix Mk+2//.
Define the (k+2)th row of the matrix M(k+2), in which the elements Qij are calculated as follows: (i) place the parameter Q i ( k + 2 ) * ,   j ( k + 2 ) in cell (k+2, jk+2( π k + 1 * )), and (ii) all other elements of the (k+2)th row of M(k+2) must be the same as the corresponding elements in the previous row k+1 in M(k+1), that is, set Q i , j k + 2 ( i ) : =   Q i , j k + 1 ( i ) , for i ≠ i   k + 1 * . Go to the next round. Rows 1, …, k+1 of the matrix Mk+2 are left the same as the rows in the matrix Mk+1; thus, the matrix Mk+2 is built. The rounds are repeated until a human user is satisfied by the target information extracted by the chatbot .
This procedure is illustrated by a numerical example in Section 7. It illustrates the operation of the algorithm and shows that the paradoxical property manifests itself already at the early rounds of the iterative search process under consideration.

6. Comparison of Two Chatbots: The “Paradox”

The goal of this section is to uncover a counterintuitive property of the general AI chatbot information extraction problem when using optimal search policy, an AI based chatbot must find and extract target information in a multi-round iterative process. We suppose that since the search chatbot is unreliable, the human user is never satisfied with the chatbot’s first answer and asks the latter to improve it with a refined query; in other words, a successful round is always preceded by at least one unsuccessful round, i.e., we assume that the parameter u(i) exceeds 1 for any i.
Suppose we have two search chatbots with the same time/efficiency characteristics and the same discount, but with different reliability. Let us denote chatbots 1 and 2, and assume that both are sufficiently reliable in the sense that their overlook probabilities are quite small: 0 < a i s (s) < 0.5, s = 1, 2, in all locations i =1,…, N. For definiteness, let’s assume that the first chatbot is more reliable, that is, 0 < a i ( 1 ) < a i ( 2 ) , i=1,…, N. Both chatbots operate in the same environment, but due to different reliability, their optimal search policies may be different.
Let π*(1) be the optimal policy for chatbot 1, and π*(2) be the optimal policy for chatbot 2. Accordingly, let F1(π*(1)) and F2(π*(2)) denote the satisfaction functions obtained by the first and second chatbot, respectively.
The main theoretical result of this work is as follows:
Proposition 2.
If the chatbbots are sufficiently reliable, that is, 0 < a i ( 1 ) <  a i ( 2 )  π*(1), i=1,…, N, then, when using the optimal search policy, a less reliable chatbot is more efficient, in the sense that its search efficiency is greater than the efficiency of a more reliable chatbot, i.e., F1() < F2(π*(2)).
To prove Proposition 2, we first need to prove the following auxiliary claim:
Proposition 3. 
Let the function f(x) be xk-1(1-x), where k is a positive integer greater than 1. Then f(x) is increasing in x when 0 < x < 0.5.
Proof.
We have: f(x) = xk-1(1-x) = xk-1-xk, k >1.
Then f’(x) = (xk-1- xk)’ = xk-2(k-1-kx). Since x > 0, f’(x) > 0 iff k-1-kx > 0, or, equivalently, f’(x) > 0 iff x < (k-1)/k.
Note that (k-1)/k ≥ 0.5 for any integer k > 1. Then, for k > 1, we have: 0 < x < 0.5 ≤ (k-1)/k.
Therefore, f’(x) > 0, and, hence, f(x) is increasing. □
Now we return to the proof of Proposition 2. Let us denote the optimal expected discounted satisfactions for the chatbots 1 and 2 by F1(π*(1)) = E(Rdisc,1(π*(1))) and F2(π*(2)) = E(Rdisc,2(π*(2))), respectively. Since the reliabilities of the two chatbots are different, the optimal search strategies of these smart robots, denoted π*(1) = ( π 1 * ( 1 ) , π 2 * ( 1 ) , … ,   π m * ( 1 ) , …   ) and π*(2) =( π 1 * ( 2 ) , π 2 * ( 2 ) , … ,   π m * ( 2 ) , … ), respectively, in the general case can be different, despite that all other characteristics of them are pairwise identical. The optimal values of the corresponding expected discounted satisfaction, F1(π*(1)) and F2(π*(2)), can also be different.
According to expression (1), we have:
F 1 ( π * ( 1 ) ) – F 2 ( π * ( 1 ) ) = ∑ m = 1 ∞ r π m * ( 1 )   e − d ∑ k = 1 m t π k * ( 1 )   ( P π m * ( 1 ) p π m * ( 1 ) − P π m * ( 2 ) p π m * ( 1 ) − ) =
∑ m = 1 ∞ r π m * ( 1 ) e − d ∑ k = 1 m t π k * ( 1 ) a π m * 1 u π * 1 , m 1 − a π m * 1 p π m * 1 − a π m * 2 u π * 2 , m 1 − a π m * 2 p π m * 1 .
If 0 < a π m * ( 1 ) < a π m * ( 2 ) < 0.5 for all m, then, according to Proposition 3, we have:
a π m * 1 u π * 1 , m 1 − a π m * 1 p π m * 1 − a π m * 2 u π * 2 , m 1 − a π m * 2 p π m * ( 1 ) ≤ 0 .
Then, from (5) and (6) it follows that, if 0 < a π m * ( 1 ) < a π m * ( 2 ) < 0.5 for all m, then
F 1 π * 1 ≤ F 2 π * 1 .
Next, it is easy to see that
F 2 π * 1 ≤ F 2 π * 2 ,
since π*(2) denotes the optimal policy for the chatbot 2, that is, π*(2) guarantees the maximum expected satisfaction F2(π). From (7) and (8), it follows that a less reliable chatbot is more efficient in the sense that it provides greater expected satisfaction to the human user than a less reliable chatbot. □
Discussion. At this point, two related questions arise: whether the paradoxical situation under consideration occurs: (1) when the chatbot is absolutely reliable, i.e., its probability ai = 0, and (2) when the chatbot is not-perfectly-reliable, that is, such that its overlook probability is arbitrarily small.
Let’s answer the first question first. A simple counterexample clearly shows that the answer is: there is no paradox. For completeness, we provide the proof in the next section.
Let us now answer the second question. At first glance, and here the answer should not be paradoxical, since the objective function defined in expression (1) is continuous in the variable ai and, therefore, one can expect to receive the same answer as in the case when the probability ai = 0. However, this answer is incorrect – in fact, it is only true for the special case where the chatbot is reliable and retrieves the target information during the first round of conversation. In this case, the process is finite and terminates after a single consecutive scan of each locations. But if the chatbot is unreliable and thus does not detect the target in the first round, then, starting from the second round of the multi-round iterative search, the objective function (1) is discontinuous with respect to the discrete variable ui (i.e., the number of unsuccessful scans of location i), and the proof based of the continuity of the objective function is no longer valid. The correct answer to the second question is this: if the AI chatbot does not retrieve a target information in the first round of search, then during the iterative search procedure of Section 5.2, the less reliable chatbot is more efficient - for any positive overlook probability ai, even as small as you wish.
We conducted extensive numerical experiments for various overlook probabilities, including very small ones, which confirmed that the paradoxical phenomenon in question exists in practice and is easily reproducible.

7. Numerical Examples

7.1. The Illustrative Example

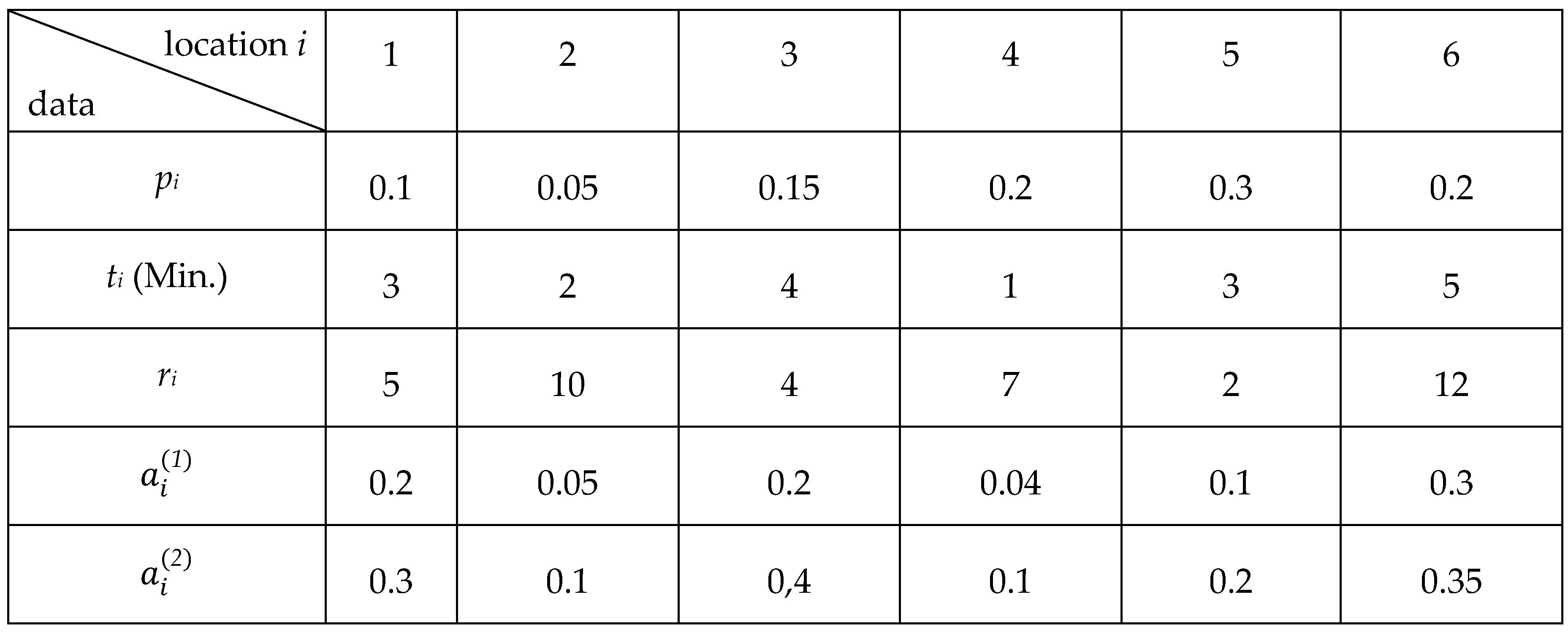
Consider the numerical example with six locations N = 6, two chatbots and input data presented in Table 2. The notation used is explained in Section 3.
Calculations of the algorithm are presented in Table 2 and Table 3 for chatbots 1 and 2, respectively, for 12 consecutive rounds. The table columns correspond to the six locations considered; the rows represent rounds of the search example considered. The elements in the cells are the coefficients Qij, calculated for 12 rounds, row by row.
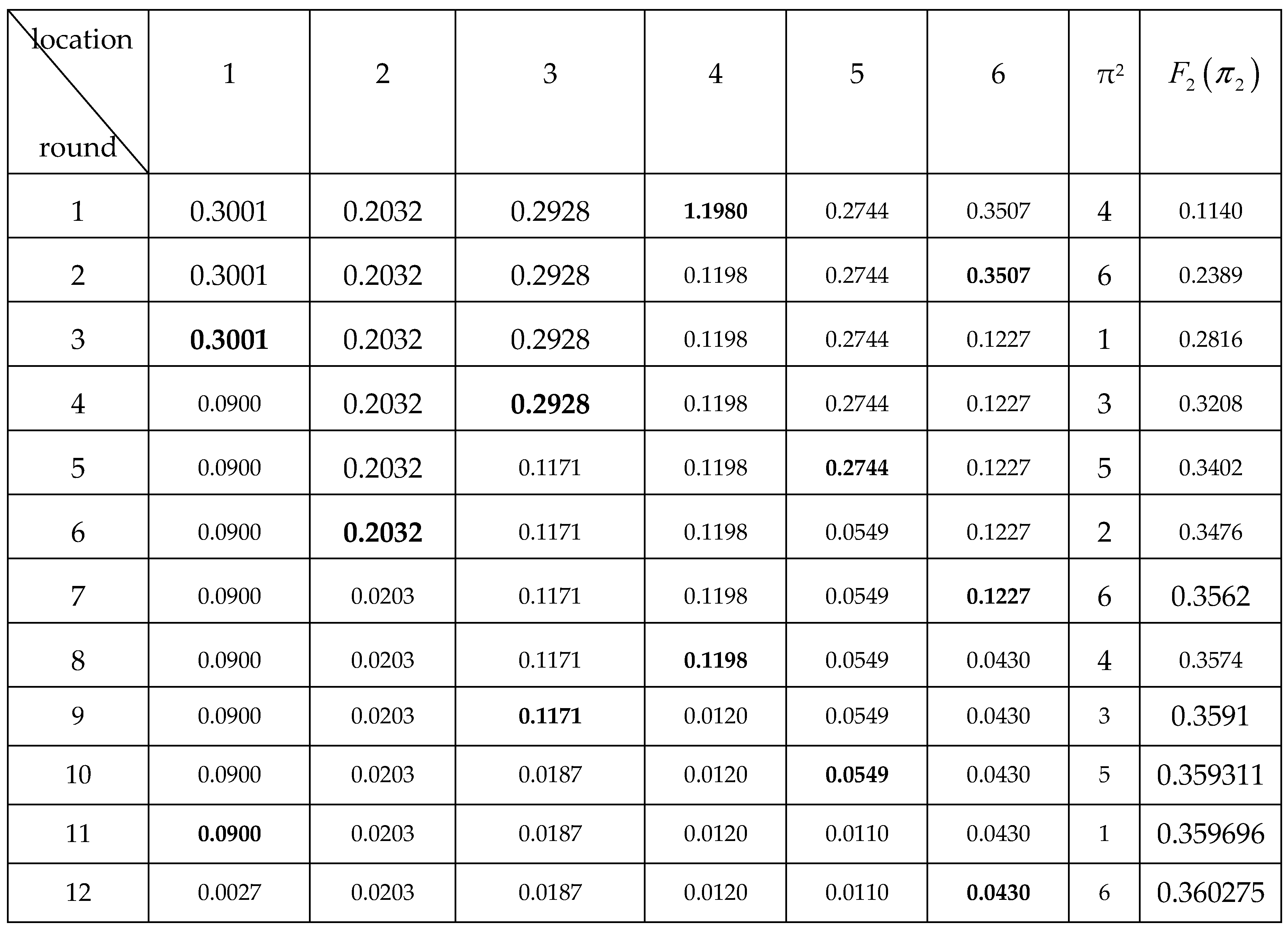
The number in cell (i,j) of these tables represents the parameter Qi,j, calculated by formula (4), where i=1,…, 12; j=1,…, 6, for two chatbots. The tables represent the matrices Mk for two chatbots, introduced in Section 5.2. Let us see the calculations in Table 3 for chatbot 1; similar calculations are performed in Table 4 for chatbot 2.
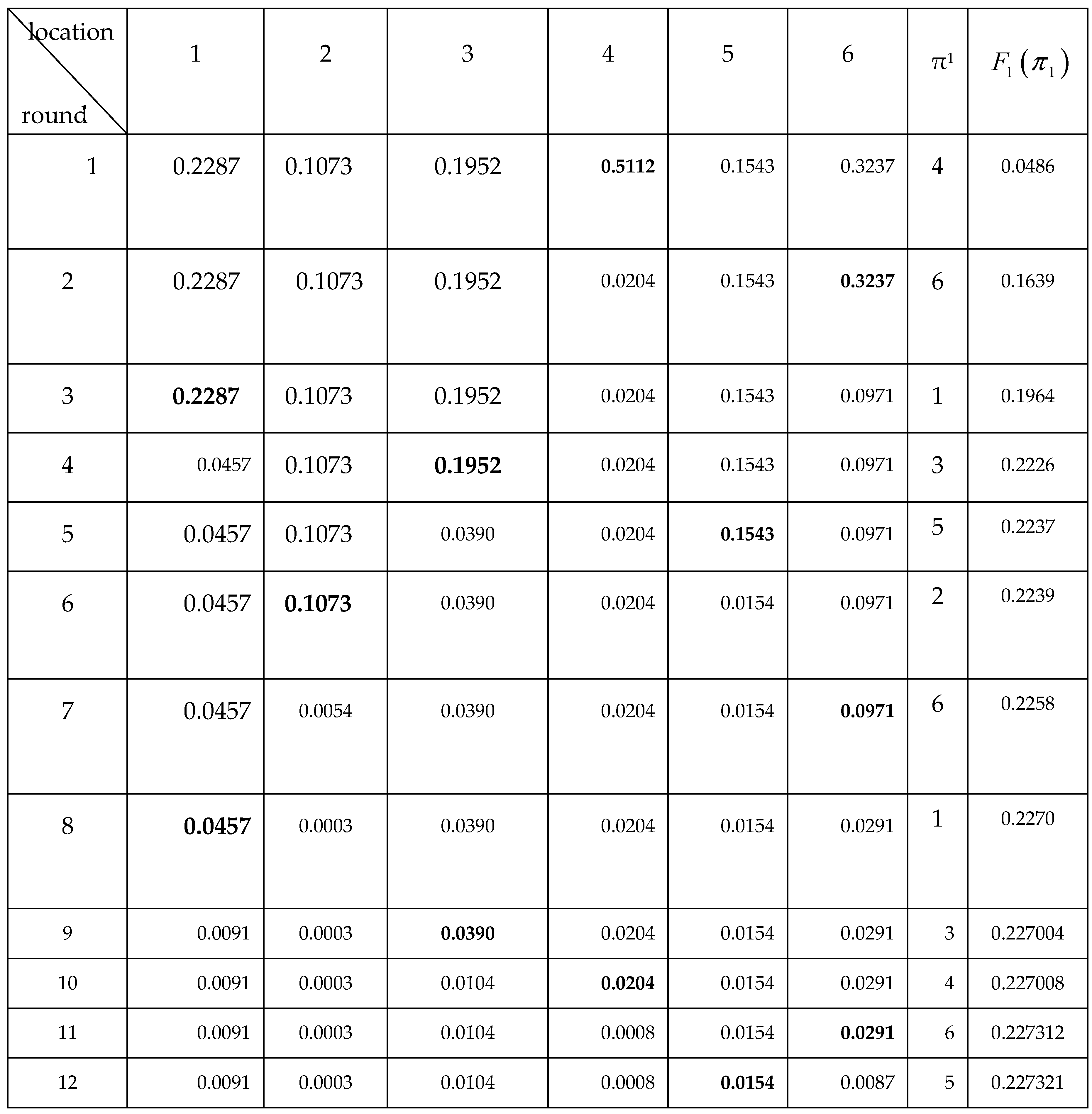
For chatbot 1, in the first round, the first row of matrix M1 (i.e., the first row of Table 3) is filled in with the coefficients Qi,1, i= 1,…, N. Then, all the locations are (unsuccessfully) scanned once, after which the Qi*(1),1 = maxiQi,1 = Q4,1= 0.5112 and the corresponding location i*(1) = 4 are found. Next, during this round, chatbot 1 scans location 4 once more; we assume that in this example it does not discover the relevant target information there. Then the number of unsuccessful scans of this location increases to 2, the corresponding parameter Q4,2 is calculated according to (4), (equals 0.0204) and placed in cell (2,4) of matrix M2. All other elements of the second row of this matrix are left unchanged - the same as in the previous row of M1. The first round of the algorithm is completed, and then the second round starts.
In round 2, the next location to be scanned next is selected by computing Qi*(2),2 = maxiQi,2 = Q6,2= 0.3237, and, hence, the location i*(2) = 6 is chosen. Place Qi*(2),2 in cell (2,   6 ) of the 2nd row of matrix M2, and highlight this item in bold and red.
Next, during this round, chatbot 1 scans location 6 once more; we assume that the human user is not satisfied by the target information extracted there. Then the number of unsuccessful scans of this location increases to 2, the corresponding parameter Q6,3 is calculated according to (4), (and equals 0.0204) and placed in cell (3,6) of the next matrix M3. All other elements of the third row of this matrix are left unchanged - the same as in the previous row of M2. The second round is completed.
During the subsequent rounds, the algorithm filled in sequentially the next rows 3, 4, …, 12 of Table 3, following the instructions of the algorithm as at round 2.
We assume that the human user is satisfied by the target information retrieved in the 12th round. The results obtained for each chatbot over 12 rounds are as follows: (1) The optimal policies for the chatbots 1 and 2 are equal to π*(1) = (4,6,1,3,5,2,6,1,3,4,6,5) and π*(2) = (4,6,1,3,5,2,6,4,3,5,1,6), respectively. (2) The partial efficiency F1(π*(1)) and, accordingly, F2(π*(2)), obtained at each round for two chatbots, is shown in the corresponding cells of the last column of Table 3 and Table 4, respectively. Comparing these results, we can see that in each round of the search process, the optimal expected search efficiency for a less reliable chatbot is noticeably larger than the maximum efficiency of a more reliable chatbot.

7.2. An Absolutely Reliable Chatbot Does Not Have the Paradox in Question

Consider the following example, whose idea was suggested by I.M. Sonin. For the absolutely reliable chatbot numbered 1 set ai1 = 0; for the chatbot 2 set ai2 = 0.1; the known satisfaction levels ri = 1.0 for each chatbot and any location, and the prior probabilities that the target information is hidden at location i are pi=0.5, i=1,2; d = 0.1. Then the absolutely reliable chatbot 1 will inevitably find the target information in a right location either during the first search with a probability of ½, or during the second search (after unsuccessful first search) with a probability of ½, and the search process ends. Assuming d=0.1, the total objective function F1(π *) for the first chatbot will be: pi ·1.0 + pi ·1.0· e − 0.1 , that is, about 0.96.
As for the second, unreliable chatbot, since ai2 > 0, the iterative search in the given two locations can have an infinite number of rounds, and the expected total satisfaction over an infinite horizon will obey expression (1). Elementary arithmetic operations on formula (1) using data for the chatbot 2 and the sum of the infinite geometrical progression show that the expected satisfaction F2(π*) of the second chatbot does not exceed 0.49 points, and in fact it will be even much less for very small ai2 > 0. We see that the efficiency of an absolutely reliable chatbot is greater, which means that there is no paradox for this case.

8. Concluding Remarks and Open Problems

The focus of this work is to study a realistic situation where the overlook probability of a chatbot is non-zero and thus the search process does not end during the first round of human-chatbot conversation. The main contribution of this paper is twofold. First, we derive and study a greedy index-based search policy and prove that it is optimal for the optimal search problem under study. Second, we identify a paradoxical “more-for-less” phenomenon: a less reliable chatbot has a higher efficiency for any positive overlook probability, even if it is very small.
Despite the “paradoxical” wording of the title, the result of this paper is quite logically explainable and completely compatible with common sense. The point is that if a more reliable chatbot has a lower overlook probability, then it is plausible to think that it will find the target information faster, i.e., in fewer search rounds and ultimately in less average search time.
This common sense observation is entirely consistent with the well-known fact from probability theory about the random variable x, which is called the geometric random variable with parameter p, and which represents the random number of independent unsuccessful trials (rounds) before the target is found; this probability is given by p(k) = p(1 − p) k−1, k = 1, 2, ... In this case, it is known that the expected number of trials equals 1/p = 1/(1-ai) [28]. Thus, the higher the overlook probability, the greater the expected number of rounds and the average search time before the target information is found, and therefore the greater the total expected accumulated information and the search efficiency determined by expression (1). So, in essence, there is no contradiction in the obtained result.
It would be interesting to find what paradoxical situations arise for other search/extraction scenarios encountered in AI chatbot search, in particular for multi-target, multi-criteria, and other scenarios. A more general problem is to find and resolve real-world situations for good search policies (ideally, optimal or approximate with efficiency guarantees) based on advanced algorithmic ideas such as optimizing-with-learning [29] and search with reinforcement [30].

Author Contributions

Both authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Boris Kriheli and Eugene Levner. Both authors read and approved the final manuscript.

Acknowledgements

The authors are grateful to I.M. Sonin for helpful discussions.

Statement about Funding

No funds, grants, or other support was received.

Statement about None of Competing Interests

The both authors have no competing interests to declare that are relevant to the content of this article.

References

  1. Nicolescu, L.; Tudorache, M.T. Human-Computer Interaction in Customer Service: The Experience with AI Chatbots—A Systematic Literature Review. Electronics 2022, 11, 1579. [CrossRef]
  2. Izadi, S.; Forouzanfar, M. Error Correction and Adaptation in Conversational AI: A Review of Techniques and Applications in Chatbots. AI 2024, 5, 803–841. [CrossRef]
  3. Akdemir, D.M.; Bulut, Z.A. Business and Customer-Based Chatbot Activities: The Role of Customer Satisfaction in Online Purchase Intention and Intention to Reuse Chatbots. J. Theor. Appl. Electron. Commer. Res. 2024, 19, 2961–2979. [CrossRef]
  4. Alabbas, A.; Alomar, K. A Weighted Composite Metric for Evaluating User Experience in Educational Chatbots: Balancing Usability, Engagement, and Effectiveness. Futur. Internet 2025, 17, 64. [CrossRef]
  5. Ross, S. M., 1969. A problem in optimal search and stop. Operations Research, 17(6), pp.984-992.
  6. Sweat, C.W. Sequential Search with Discounted Income, the Discount a Function of the Cell Searched. Ann. Math. Stat. 1970, 41, 1446–1455. [CrossRef]
  7. Chew M.C. Jr., 1973 Optimal stopping in a discrete search problem. Operations Research 21(3):741–747. 4.
  8. Ross, S. Introduction to Stochastic Dynamic Programming; Elsevier: Amsterdam, NX, Netherlands, 1983; ISBN: .
  9. Levner, E. Infinite-horizon scheduling algorithms for optimal search for hidden objects. Int. Trans. Oper. Res. 1994, 1, 241–250. [CrossRef]
  10. Cheng, T.C.E.; Kriheli, B.; Levner, E.; Ng, C.T. Scheduling an autonomous robot searching for hidden targets. Ann. Oper. Res. 2019, 298, 95–109. [CrossRef]
  11. Koopman, B., 1956. The theory of search, II.Target detection, Operations Research, 4, 324-346.
  12. Mickelsen, R.; Stone, L.D. Theory of Optimal Search.. J. Am. Stat. Assoc. 1976, 71, 1008. [CrossRef]
  13. Stone, L.D.; Royset, J.O.; Washburn, A.R. Optimal Search for Moving Targets; Springer Nature: Dordrecht, GX, Netherlands, 2016; ISBN: .
  14. Trummel, K.E.; Weisinger, J.R. Technical Note—The Complexity of the Optimal Searcher Path Problem. Oper. Res. 1986, 34, 324–327. [CrossRef]
  15. Wegener, I. Optimal search with positive switch cost is NP-hard. Inf. Process. Lett. 1985, 21, 49–52. [CrossRef]
  16. Kriheli, B.; Levner, E.; Spivak, A. Optimal Search for Hidden Targets by Unmanned Aerial Vehicles under Imperfect Inspections. Am. J. Oper. Res. 2016, 06, 153–166. [CrossRef]
  17. Kress, M.; Lin, K.Y.; Szechtman, R. Optimal discrete search with imperfect specificity. Math. Methods Oper. Res. 2008, 68, 539–549. [CrossRef]
  18. Steinberg, R.; Zangwill, W.I. The Prevalence of Braess' Paradox. Transp. Sci. 1983, 17, 301–318. [CrossRef]
  19. Shan, F.; Li, H.; Wang, Z.; Jin, M.; Chen, D. Optimizing Rural Highway Maintenance Scheme with Mathematical Programming. Appl. Sci. 2024, 14, 8253. [CrossRef]
  20. Schäfer, Benjamin, Thiemo Pesch, Debsankha Manik, Julian Gollenstede, Guosong Lin, Hans-Peter Beck, Dirk Witthaut, and Marc Timme, 2022. Understanding Braess’ paradox in power grids. Nature Communications 13, no. 1: 5396.
  21. Gershenson, C.; Helbing, D. When slower is faster. Complexity 2015, 21, 9–15. [CrossRef]
  22. Taitler, Boaz, and Omer Ben-Porat, 2024. Braess’s Paradox of Generative AI. arXiv preprint arXiv:2409.05506.
  23. Sorrell, Steve (2009). Exploring Jevons’ Paradox. Energy Efficiency and Sustainable Consumption: The Rebound Effect. London: Palgrave Macmillan. pp. 136–164.
  24. York, R.; McGee, J.A. Understanding the Jevons paradox. Environ. Sociol. 2015, 2, 77–87. [CrossRef]
  25. Spieksma, F.C.; Woeginger, G.J. The no-wait flow-shop paradox. Oper. Res. Lett. 2005, 33, 603–608. [CrossRef]
  26. Charnes, A. and Klingman, D. 1971. The more-for-less paradox in the distribution model, Cahiers du Centre d’Etudes de Recherche Opérationnelle, 13, pp.11–22.
  27. Graham, R.L. Bounds on Multiprocessing Timing Anomalies. SIAM J. Appl. Math. 1969, 17, 416–429. [CrossRef]
  28. Ross, S.M., 1976. A First Course in Probability, New York: Macmillan.
  29. Powell, W.B. Perspectives of approximate dynamic programming. Ann. Oper. Res. 2012, 241, 319–356. [CrossRef]
  30. Zhang, T.; Mo, H. Reinforcement learning for robot research: A comprehensive review and open issues. Int. J. Adv. Robot. Syst. 2021, 18. [CrossRef]
Table 1. Comparison of two problems.
Table 1. Comparison of two problems.
Preprints 152782 i001
Table 2. Input data for example, d=0.1.
Table 2. Input data for example, d=0.1.
Preprints 152782 i002
Table 3. Calculations of the optimal policy for chatbot 1.
Table 3. Calculations of the optimal policy for chatbot 1.
Preprints 152782 i003
Table 4. Calculations of the optimal policy for chatbot 2.
Table 4. Calculations of the optimal policy for chatbot 2.
Preprints 152782 i004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

55

Views

34

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated