Towards Sustainable Cryptography: A Comprehensive Assessment of Compute Efficiency and Scope 1–3 Emissions for Partially Homomorphic Encryption in the Cloud

1. Introduction

The advent of quantum computing poses a significant threat to existing cryptographic systems, necessitating a transition to post-quantum cryptography (PQC). Recent advancements, such as Google’s Willow quantum chip and Microsoft’s Majorana 1 chip, have demonstrated breakthroughs in quantum error correction, potentially bringing us closer to cryptographically relevant quantum computers (CRQCs). Microsoft’s chip with a quantum processor that uses topological qubits, is designed to be more robust against errors, which could significantly improve the reliability of quantum computations and thus hasten the advent of CRQCs[1]. HPCwire’s 2025 article highlights that these developments could enable CRQCs within the next decade, threatening traditional algorithms like RSA and elliptic curve cryptography (ECC) [2,3]. SecurityWeek’s 2025 report corroborates this, projecting a timeline for CRQCs to emerge, underscoring the urgency for quantum-resistant solutions [4], particularly relevant for cloud-based cryptographic operations, where both security and energy efficiency must be optimized simultaneously. This transition becomes especially critical as AI systems increasingly handle sensitive data processing tasks in cloud environments, where both quantum resistance and energy efficiency are crucial considerations.

As a result of the above innovations, the protection of sensitive information has become more critical than ever. Homomorphic encryption enables calculations on encrypted data without the need to access private keys [5]. This capability allows data such as salaries and pensions to be stored in an encrypted form and securely updated without decryption. This approach has gained significant popularity with the proliferation of cloud computing. Companies increasingly store their data in the cloud rather than on-premise systems, elevating the importance of robust security measures.

In response, the National Institute of Standards and Technology (NIST) finalized the first three PQC standards in 2024, including ML-KEM, ML-DSA, and SPHINCS+, to ensure long-term security against quantum attacks [6]. Furthermore, governmental initiatives are underway to prepare for this transition, with the US government issuing guidelines for PQC adoption, emphasizing the need for a coordinated approach. The United Nations’ designation of 2025 as the International Year of Quantum Science and Technology further underscores the global significance of these developments.

The proliferation of cloud computing and AI applications has significantly increased data center energy consumption, raising environmental concerns. The International Energy Agency (IEA) reports that data centers currently account for approximately 1% of global electricity consumption, with projections indicating a potential doubling by 2026 due to the AI boom [7]. In the United States, Datacenter Dynamics’ 2025 analysis predicts a rise from 17 GW in 2020 to 35 GW by 2030, driven by hyperscale data centers and AI workloads. This escalation not only increases operational costs but also amplifies the environmental footprint, with Scope 1-3 emissions (direct, indirect from purchased electricity, and supply chain impacts) becoming a critical metric [8]. The rapid adoption of large-scale AI models and automated systems has further accelerated this energy consumption trend, making the optimization of underlying cryptographic operations increasingly important for overall data center sustainability.

The Electric Power Research Institute (EPRI) further projects that data centers could consume up to 9% of US electricity by 2030, highlighting the sustainability challenge posed by AI-driven demand [9]. Park Place Technologies’ 2024 study emphasizes the environmental impact, noting that cooling systems and continuous uptime contribute to greenhouse gas emissions, particularly in hyperscale facilities [10]. These findings underscore the need for energy-efficient solutions in data center operations, especially as cryptographic workloads intensify.

Without homomorphic encryption, encrypted data must be decrypted, updated, and then re-encrypted. All updates must be performed on-premises, or the private key must be transmitted to the cloud, which introduces security risks. With homomorphic encryption, sensitive data can be stored and updated directly in the cloud without exposing the private key.

Homomorphic encryption (HE) is a pivotal technology for secure cloud computing, enabling computations on encrypted data without decryption. Fully homomorphic encryption (FHE) supports arbitrary operations, such as addition and multiplication, but is computationally intensive, posing challenges for energy efficiency, particularly in AI and blockchain applications. Venafi’s 2025 analysis highlights FHE’s energy intensity, noting its limitations in large-scale deployments [11]. In contrast, partially homomorphic encryption (PHE), which restricts operations to either addition or multiplication, offers a more energy-efficient alternative, suitable for specific use cases where full homomorphicity is not required[12,13,14]. With the growing deployment of AI-driven applications in cloud environments, the energy efficiency of cryptographic operations becomes a critical factor in managing the overall environmental impact of these systems.

Fully homomorphic encryption (FHE) allows for both addition and multiplication on ciphertexts [15]. Conversely, partially homomorphic encryption (PHE) is more limited, supporting either addition or multiplication, but not both [16]. PHE algorithms can also multiply a ciphertext by a known constant and support regenerating ciphertexts, meaning the same plaintext can have different ciphertext representations. PHE schemes find applications in various contexts such as e-voting and Private Information Retrieval [17]. However, these applications have been limited in scope due to constraints on the types of homomorphic evaluation operations they support. Essentially, PHE schemes are only applicable to specific scenarios where the algorithms involve either addition or multiplication operations exclusively.

Although FHE has become more accessible, PHE is often a more efficient and practical choice for many tasks. PHE is faster, requires fewer computational resources, generates smaller ciphertexts, and uses smaller keys. It is well-suited for environments with limited memory and strikes a good balance for practical applications.

In this paper, LightPHE, a lightweight and hybrid partially homomorphic encryption framework for Python, is used. It is open-sourced at https://github.com/serengil/lightphe and licensed under MIT. While several FHE options are available, such as SEAL [18], TenSEAL [19], Pyfhel [20], or PyFHE [21], there is a notable lack of PHE frameworks. LightPHE aims to address this gap by providing a library that encapsulates various PHE algorithms, including RSA [22], ElGamal [23], Exponential ElGamal, Elliptic Curve ElGamal [24], Paillier [25], Damgard-Jurik [26], Okamoto–Uchiyama [27], Benaloh [28], Naccache–Stern [29], and Goldwasser–Micali [30]. The design of the framework adheres to best practices in software engineering.

Recent research has focused on optimizing HE for energy efficiency. An arXiv paper from 2024 explores Computing-in-Memory (CiM) architectures, demonstrating reduced latency and energy consumption for HE operations [31]. Similarly, IEEE Spectrum’s 2023 article discusses hardware accelerators, such as RISE, enhancing HE’s feasibility on edge devices, though further developments are needed for data center scalability [32]. These advancements suggest a pathway to mitigate the energy demands of HE, aligning with sustainability goals.

In this broader context, organizations aiming to address sustainability must also consider their Scope 1 (direct), Scope 2 (indirect from purchased electricity), and Scope 3 (all other indirect) emissions. Advanced cryptographic methods, including both PHE and FHE, can introduce additional computational overhead, potentially elevating data center power usage [7,8]. Even a slight increase in the required processing power can translate to higher cooling demands and greater greenhouse gas emissions, emphasizing the need for energy-optimized cryptographic solutions. As data centers scale to meet AI-driven workloads, striking a balance between robust encryption and minimal environmental impact becomes ever more critical.

Moreover, the rapid deployment of large-scale AI models amplifies this challenge, as extensive training and inference cycles demand substantial computing resources [9,10]. Cryptographic operations, particularly those running continuously in cloud environments, can compound the energy requirements if not carefully optimized. Evaluating the full life cycle of cryptographic hardware, from raw material extraction (contributing to Scope 3) to disposal, is essential for a holistic view of environmental impact. By adopting encryption methods that reduce computational overhead while preserving security guarantees, organizations can mitigate their overall carbon footprint across all scopes and support a more sustainable trajectory for cloud and AI ecosystems.

1.1. Organization of the Paper

In Section 3, the various algorithms supported by LightPHE are explored. Each algorithm’s capabilities and the theoretical underpinnings of their homomorphic features are explained. A range of algorithms, including RSA, ElGamal, Paillier, and others, are covered. The application of these algorithms to encrypted data, ensuring the security of sensitive information without the need for decryption, is demonstrated.

Moving on to Section 4.1, a detailed examination of the design and structure of LightPHE is provided. The different components of the framework are broken down and their integration is explained. Using diagrams and clear explanations, the management of tasks such as encryption, computation, and decryption by LightPHE is illustrated. This section aims to enhance readers’ understanding of the framework’s functionality and reliability.

In Section 5, the practical use of LightPHE is detailed. Examples and code snippets are provided to guide users through integrating LightPHE into their Python projects. By breaking down the implementation details and offering practical advice, the section aims to facilitate researchers and developers in maximizing the utilization of LightPHE’s features.

In addition to proposing LightPHE, extensive experiments were conducted to evaluate its performance across various cloud environments, including Colab Normal, Colab A100 GPU, Colab L4 GPU, Colab T4 High RAM, Colab TPU2, and Azure Spark. These experiments focused on several critical parameters, including time consumption for key generation, encryption, decryption, and homomorphic operations such as addition or multiplication for different key sizes.

Recent advancements in cloud computing and homomorphic encryption have significantly influenced the design and deployment of secure and efficient cryptographic systems. By leveraging the unique capabilities of these cloud environments, detailed benchmarks were established to provide a comprehensive performance analysis of LightPHE. This analysis not only highlights the practical differences between various cloud setups but also serves as a valuable benchmark for practitioners and researchers in selecting the appropriate environment for their specific needs.

Radar maps were created to visualize and compare the performance metrics across these diverse cloud environments. These visual tools offer insights into the strengths and weaknesses of each setup, aiding in the decision-making process for deploying homomorphic encryption in production systems. The comparative analysis emphasizes factors such as computational efficiency, scalability, and resource utilization, which are crucial for determining the suitability of a particular cloud environment for real-world applications.

Furthermore, the benchmarks provide guidance on selecting the optimal cloud environment based on specific use cases and performance requirements. For instance, environments like Colab A100 GPU and TPU2 are evaluated for their superior computational power, making them suitable for tasks requiring high performance and scalability. Conversely, setups like Colab Normal and Azure Spark are assessed for their cost-effectiveness and accessibility, offering viable options for projects with limited resources.

Following these sections, we introduce a dedicated 2, section (not shown here) to define Scope 1, 2, and 3 emissions and discuss their significance in data center operations. We then expand our that approach to detailing the energy consumption measurement design, including data-collection methods, approximations for hardware power usage, and the calculation of carbon emissions based on typical grid intensities. In this expanded methodological framework, we also address quantum-era security concerns—particularly the impact of larger key sizes on both performance and potential carbon footprint.

Finally, result section is reorganized to include energy and emission metrics, where we correlate the computational performance of different algorithms and key sizes with estimated energy consumption and associated carbon emissions. This holistic view helps stakeholders balance strong cryptographic security with environmental considerations, guiding them toward sustainable implementations of homomorphic encryption technologies.

The insights gained from these experiments are intended to assist organizations in making informed decisions about the deployment of homomorphic encryption technologies in their production systems. By understanding the performance characteristics of different cloud environments—alongside their respective energy usage and emission impacts—stakeholders can better align their infrastructure choices with both operational and sustainability goals, ensuring a robust, efficient, and environmentally responsible implementation of LightPHE.

2. Data Center Emissions

Data centers are experiencing a significant increase in energy consumption due to the proliferation of cloud computing and artificial intelligence (AI) applications, which has profound implications for their environmental footprint, particularly in terms of greenhouse gas emissions. This section provides a detailed analysis of the emissions associated with data centers, categorized under Scope 1, Scope 2, and Scope 3, as defined by the Greenhouse Gas Protocol, and examines how rising energy demands exacerbate these emissions.

As mentioned in the introduction; according to the International Energy Agency (IEA), global data center electricity consumption currently accounts for approximately 1% of global electricity use, estimated at around 240 TWh in 2022. The IEA projects that this could double to 480 TWh by 2026, driven by the rapid expansion of AI and cloud services [7]. In the United States, a 2022 analysis by the Lawrence Berkeley National Laboratory estimates that data center energy consumption was approximately 17 GW in 2020, translating to about 149 TWh per year [33]. Under a high-growth scenario, this is projected to increase to between 26 GW and 35 GW by 2030, indicating a potential rise of 53% to 106% [33]. This escalation is largely attributed to the energy-intensive nature of AI workloads and the construction of hyperscale data centers.

2.0.1. Emissions Categorization and Impact

The environmental impact of data centers is quantified through three scopes of emissions, each contributing differently to the overall carbon footprint:

Scope 1 Emissions: These are direct greenhouse gas emissions from sources owned or controlled by the data center, such as backup generators (e.g., diesel generators) and refrigerant leaks from cooling systems. Scope 1 emissions are typically minimal compared to Scope 2 and 3, with estimates suggesting they constitute only 0.2% to 0.5% of the total carbon footprint [34]. However, in scenarios where backup generators are used more frequently due to power outages, these emissions can increase, though they remain relatively small in the context of total emissions.

Scope 2 Emissions: These are indirect emissions associated with the generation of electricity purchased and consumed by the data center. Given the high electricity demand of data centers, Scope 2 emissions are a major component of their environmental impact. For instance, in 2020, US data centers consumed approximately 149 TWh, and assuming an average carbon intensity of 380 g CO2/kWh for the US grid, the Scope 2 emissions were approximately 56.6 million tons of CO2 [35]. This represents about 1.1% of total US CO2 emissions in 2020, highlighting their significant contribution. As energy consumption rises, particularly with the projected doubling by 2026 globally, Scope 2 emissions are expected to increase proportionally, especially in regions with carbon-intensive electricity grids.

Scope 3 Emissions: These encompass all other indirect emissions occurring in the data center’s value chain, including the production and transportation of hardware (servers, storage devices, etc.), construction of facilities, employee travel, and waste management. Scope 3 emissions are often the largest category, with recent studies indicating they can account for 38% to 69% of the total carbon footprint of data centers [35]. For example, the production of semiconductor chips and other hardware components involves significant embedded carbon, while the construction of new data centers adds to emissions through concrete production and long-distance transportation. Schneider Electric’s 2023 report notes that capital goods, such as hardware, are a primary driver of Scope 3 emissions, with potential for optimization through supply chain strategies [36].

The projected increase in energy consumption will amplify emissions across all scopes, with Scope 2 emissions being directly affected due to higher electricity purchases. If grid decarbonization does not keep pace, the carbon intensity of electricity will continue to drive up Scope 2 emissions. For instance, if global data center consumption reaches 480 TWh by 2026 with an average carbon intensity of 500 g CO2/kWh, Scope 2 emissions could reach 240 million tons of CO2 annually. This is a significant environmental burden, particularly as AI workloads, which are far more energy-intensive than traditional cloud applications, continue to grow [37].

Scope 3 emissions are indirectly affected by increased energy consumption, as higher demand for computing power necessitates more hardware and potentially new data center constructions, both of which increase emissions from manufacturing and building activities. Compass Datacenters’ 2023 analysis highlights that Scope 3 emissions can be mitigated through supply chain optimization and renewable energy procurement, but the scale of growth in AI and cloud services poses challenges. Scope 1 emissions, while smaller, may also rise if backup generators are used more frequently to meet peak loads, though their contribution remains minimal compared to Scope 2 and 3 [34].

Recent industry analyses provide quantitative insights into the distribution of emissions. Data Center Dynamics’ 2024 article reports that Scope 3 emissions can range from 38% to 69% of the total carbon footprint, with Scope 2 emissions accounting for 31% to 61%, and Scope 1 emissions constituting only 0.2% to 0.5% [34]. These percentages can vary based on the data center’s location and energy mix; for example, data centers in regions with high renewable energy penetration (e.g., Nordic countries) may have lower Scope 2 emissions, while those in fossil fuel-dependent regions (e.g., parts of the US) face higher impacts. The following table summarizes the typical components and impacts:

Table 1 illustrates that while Scope 2 emissions are directly tied to energy consumption, Scope 3 emissions are indirectly affected by the need for additional infrastructure, making them a critical area for sustainability strategies.

3. Algorithms

LightPHE wraps RSA, ElGamal, Exponential ElGamal, Elliptic Curve ElGamal, Paillier, Damgard-Jurik, Okamoto–Uchiyama, Benaloh, Naccache–Stern, and Goldwasser–Micali algorithms. Table 2 shows each algorithms homomorphic fetures. In this section, proofs of their homomorphic features will be covered.

3.1. RSA

RSA invented in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman [22]. It is depending on the difficulty of factoring large integers. The cryptosystem show multiplicatively homomorphic features. RSA encryption requires raising the message to the power of the public key e and then taking the result modulo n as show in Formula 1.

$$\epsilon \left(m\right)={\left(m\right)}^{e}modn$$

(1)

If you encrypt a plaintext pair $m_1$ and $m_2$ with RSA, then their corresponding ciphertexts will be calculated using Equations 2 and 3.

$$\epsilon \left(m_1\right)={\left(m_1\right)}^{e}modn$$

(2)

$$\epsilon \left(m_2\right)={\left(m_2\right)}^{e}modn$$

(3)

The multiplication of encrypted values will be calculated using Equation 4.

$$\epsilon \left(m_1\right)\times \epsilon \left(m_2\right)={\left(m_1\right)}^e{\left(m_2\right)}^{e}modn$$

(4)

Multiplication of ciphertexts can be reorganized as shown in Equation 5.

$$\epsilon \left(m_1\right)\times \epsilon \left(m_2\right)={(m_1\times m_2)}^{e}modn$$

(5)

On the other hand, encryption of the multiplication of plain $m_1$ and $m_2$ will be same as shown in Equation 6.

$$\epsilon (m_1\times m_2)={(m_1\times m_2)}^{e}modn$$

(6)

In summary, RSA is homomorphic with respect to the multiplication as shown in Equation 7.

$$\epsilon (m_1\times m_2)=\epsilon \left(m_1\right)\times \epsilon \left(m_2\right)$$

(7)

3.2. ElGamal

ElGamal algorithm was invented by Taher Elgamal in 1985 [23]. It is depending on the difficulty of computing discrete logarithms over finite fields. The algorithm shows multiplicatively homomorphic features. ElGamal encryption requires to calculate of tuple of a public generator to the power of a random integer and plaintext times public key to the power of same random key as shown in Equation 8.

$$\epsilon (m,r)=\left(g^r,m\times h^r\right)modp$$

(8)

If you encrypt a plaintext pair $m_1$ and $m_2$ with ElGamal, then their corresponding ciphertexts will be calculated using Equations 9 and 10.

$$\epsilon (m_1,r_1)=\left(g^{r_1},m_1\times h^{r_1}\right)modp$$

(9)

$$\epsilon (m_2,r_2)=\left(g^{r_2},m_2\times h^{r_2}\right)modp$$

(10)

The multiplication of encrypted values will be calculated using Equation 11.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{r_1},m_1\times h^{r_1}\right)\times \left(g^{r_2},m_2\times h^{r_2}\right)modp\end{array}$$

(11)

Multiplication of ciphertexts can be reorganized as shown in Equation 12 and 13.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ (g^{r_1}\times g^{r_2},m_1\times m_2\times h^{r_1}\times h^{r_2})modp\end{array}$$

(12)

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{r_1+r_2},m_1\times m_2\times h^{r_1+r_2}\right)modp\end{array}$$

(13)

On the other hand, multiplication of plain $m_1$ and $m_2$ with random key $r_1$+$r_2$ will give same result as shown in Equation 14.

$$\begin{array}{c}\epsilon (m_1\times m_2,r_1+r_2)\\ =\\ \left(g^{r_1+r_2},m_1\times m_2\times h^{r_1+r_2}\right)modp\end{array}$$

(14)

In conclusion, ElGamal is homomorphic with respect to the multiplication as shown in Equation 15.

$$\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)=\epsilon (m_1\times m_2,r_1+r_2)$$

(15)

3.3. Exponential ElGamal

ElGamal encryption requires to calculate a tuple and the second item of the tuple has plaintext m as multiplier. If this item is modified to generator g to the power of plaintext m, then the algorithm will start to show additive homomorphic features but it will lose its multiplicative homomorphic features.

$$\epsilon (m,r)=\left(g^r,g^m\times h^r\right)modp$$

(16)

For instance, encryption of plaintext $m_1$ and $m_2$ couple with random keys $r_1$ and $r_2$ will be calculated using Equations 17 and 18.

$$\epsilon (m_1,r_1)=\left(g^{r_1},g^{m_1}\times h^{r_1}\right)modp$$

(17)

$$\epsilon (m_2,r_2)=\left(g^{r_2},g^{m_2}\times h^{r_2}\right)modp$$

(18)

Thereafter, multiplication of ciphertexts will be calculated using Equation 19.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{r_1},g^{m_1}\times h^{r_1}\right)\times \left(g^{r_2},g^{m_2}\times h^{r_2}\right)modp\end{array}$$

(19)

That multiplication can be reorganized as shown in Equations 20 and 21.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{r_1}\times g^{r_2},g^{m_1}\times g^{m_2}\times h^{r_1}\times h^{r_2}\right)modp\end{array}$$

(20)

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{r_1+r_2},g^{m_1+m_2}\times h^{r_1+r_2}\right)modp\end{array}$$

(21)

On the other hand, encryption of the addition of $m_1$ and $m_2$ with random key $r_1$ + $r_2$ will give same results as shown in Equation 22.

$$\begin{array}{c}\epsilon (m_1+m_2,r_1+r_2)\\ =\\ \left(g^{r_1+r_2},g^{m_1+m_2}\times h^{r_1+r_2}\right)modp\end{array}$$

(22)

In summary, exponential ElGamal is homomorphic with respect to the addition as shown in Equation 23. However, it is not homomorphic with respect to the multiplication similar to standard ElGamal.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)=\epsilon (m_1+m_2,r_1+r_2)\end{array}$$

(23)

However, exponential ElGamal comes with some limitations. Once a ciphertext is decrypted, it will give $g^m$ instead of plaintext m. To restore m from $g^m$, discrete logarithm problem must be resolved which is hard for large integers. This makes exponential ElGamal theoritical algorithm instead of practical one. On the other hand, if the plaintext is millonish value, then current processing powers will be able to find it very fast. So, the algorithm can be adopted according to the size of plaintext.

3.3.1. Ciphertext Regeneration Feature

Exponential ElGamal is additively homomorphic and the neutral element in addition is 0. Encrypting the neutral element and then add it into a ciphertext will not change the corresponding plaintext but ciphertext will have a different representation. In that way, ciphertext can be regenerated as shown in Equations 24 and 25where D denotes decryption.

$$\epsilon (m_1,r_1)\times \epsilon (0,r_2)\ne \epsilon (m_1,r_1)$$

(24)

$$D(\epsilon (m_1,r_1)\times \epsilon (0,r_2))=D\left(\epsilon (m_1,r_1)\right)$$

(25)

3.3.2. Scalar Multiplication Feature

Finding the k-th power of a ciphertext is shown in Equation 26 and 27.

$${\epsilon (m_1,r_1)}^k={\left(g^{r_1},g^{m_1}\times h^{r_1}\right)}^{k}modp$$

(26)

$${\epsilon (m_1,r_1)}^k=\left(g^{r_1\times k},g^{m_1\times k}\times h^{r_1\times k}\right)modp$$

(27)

On the other hand, scalar multiplication of k and $m_1$ with random key k times $r_1$ will give the same result as shown in Equation 28. This proves the scalar multiplication feature of exponential ElGamal.

$$\begin{array}{c}\epsilon (m_1\times k,r_1\times k)\\ =\\ \left(g^{r_1\times k},g^{m_1\times k}\times h^{r_1\times k}\right)modp\end{array}$$

(28)

After decryption, only the first parameter of the encryption function will be restored, representing the plaintext multiplied by a constant value.

3.4. Elliptic Curve ElGamal

Co-usage of elliptic curve cryptography and ElGamal algorithm offers additively homomorphic features [24]. Elliptic curve cryptography comes with much smaller key lengths with same level accuracy when compared to RSA or ElGamal. The most common elliptic curve forms are Weierstrass [38], Koblitz [39] and Edwards [40]. The elliptic curve forms differentiate addition formulas but concept of homomorphy becomes same. LightPHE just covers elliptic curves in Weierstrass form.

Similar to ElGamal algorithm, Elliptic Curve ElGamal creates tuples in the ciphertext, but each item of the tuple is also a tuple of 2-dimensional point with x and y coordinates. A generalized encryption procedure of Elliptic Curve ElGamal is shown in Equation29 where G is the public base point and Q is the public key point calculated by private key times base point G.

$$\epsilon (m,r)=(r\times G,r\times Q+m\times G)$$

(29)

Then, encryption of plaintext pairs m1 and m2 with random keys r1 and r2 will be calculated using Equations 30 and 31.

$$\epsilon (m_1,r_1)=(r_1\times G,r_1\times Q+m_1\times G)$$

(30)

$$\epsilon (m_2,r_2)=(r_2\times G,r_2\times Q+m_2\times G)$$

(31)

Thereafter, addition of ciphertexts will be calculated using Equation 32.

$$\begin{array}{c}\epsilon (m_1,r_1)+\epsilon (m_2,r_2)\\ =\\ (r_1\times G,r_1\times Q+m_1\times G)\\ +(r_2\times G,r_2\times Q+m_2\times G)\end{array}$$

(32)

The addition can be reorganized as shown in Equations 33 and 34.

$$\begin{array}{c}\epsilon (m_1,r_1)+\epsilon (m_2,r_2)\\ =\\ (r_1\times G+r_2\times G,\\ r_1\times Q+m_1\times G+r_2\times Q+m_2\times G)\end{array}$$

(33)

$$\begin{array}{c}\epsilon (m_1,r_1)+\epsilon (m_2,r_2)\\ =\\ ((r_1+r_2)\times G,(r_1+r_2)\times Q+(m_1+m_2)\times G)\end{array}$$

(34)

On the other hand, encryption of addition of plaintexts $m_1$ and $m_2$ with random key $r_1$ + $r_2$ will give same result as shown in Equation 35.

$$\begin{array}{c}\epsilon (m_1+m_2,r_1+r_2)\\ =\\ ((r_1+r_2)\times G,(r_1+r_2)\times Q+(m_1+m_2)\times G)\end{array}$$

(35)

In conclusion, Elliptic Curve ElGamal is homomorphic with respect to the addition as shown in Equation 36.

$$\epsilon (m_1,r_1)+\epsilon (m_2,r_2)=\epsilon (m_1+m_2,r_1+r_2)$$

(36)

In elliptic curve ElGamal, plaintexts are casted to points on the given curve and the ciphertexts are points as well. Decryption of a ciphertext will give the cast point. Restoring plaintext from that cast point requires to solve elliptic curve discrete logarithm problem which is hard. Still, restoration calculation can be done fast if the plaintext is millionish number.

3.4.1. Scalar Multiplication Feature

Finding the k-th multiple of a ciphertext is calculated in Equations 37 and 38.

$$k\times \epsilon (m_1,r_1)=k\times (r_1\times G,r_1\times Q+m_1\times G)$$

(37)

$$k\times \epsilon (m_1,r_1)=(k\times r_1\times G,k\times r_1\times Q+k\times m_1\times G)$$

(38)

On the other hand, encryption of k-th multiple of a plaintext $m_1$ with a random key k-th multiple of $r_1$ will give the same result as shown in Equation 39. This proves the scalar multiplication property of elliptic curve ElGamal.

$$\begin{array}{c}\epsilon (k\times m_1,k\times r_1)\\ =\\ (k\times r_1\times G,k\times r_1\times Q+k\times m_1\times G)\end{array}$$

(39)

After decrypting, only the first argument, which is the plain message, of the encryption function will be recovered and the random key in the second argument will be entirely removed.

3.5. Paillier

Paillier cryptosystem was intented by Pascal Paillier in 1999 [25]. It is depending on the difficulty of computing n-th residue classes. A general encryption procedure of Paillier algorithm is shown in Equation 40 where m is plaintext, r is random key, g is generator and n is RSA modulus.

$$\epsilon (m,r)=\left(g^m\times r^n\right)mod{n}^2$$

(40)

Then, encryption of plaintext pairs $m_1$ and $m_2$ with random keys $r_1$ and $r_2$ will be calculated using Equations 41 and 42.

$$\epsilon (m_1,r_1)=\left(g^{m_1}\times {r_1}^n\right)mod{n}^2$$

(41)

$$\epsilon (m_2,r_2)=\left(g^{m_2}\times {r_2}^n\right)mod{n}^2$$

(42)

Thereafter, multiplication of ciphertexts will be calculated using Equation 43.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{m_1}\times {r_1}^n\right)\times \left(g^{m_2}\times {r_2}^n\right)mod{n}^2\end{array}$$

(43)

The multiplication can be reorganized as shown in Equations 44 and 45.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{m_1}\times g^{m_2}\times {r_1}^n\times {r_2}^n\right)mod{n}^2\end{array}$$

(44)

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ (g^{m_1+m_2}\times {(r_1\times r_2)}^n)mod{n}^2\end{array}$$

(45)

On the other hand, encryption of addition of plaintexts $m_1$ and $m_2$ with random key $r_1$×$r_2$ will give same result as shown in Equation 46.

$$\begin{array}{c}\epsilon (m_1+m_2,r_1\times r_2)\\ =\\ (g^{m_1+m_2}\times {(r_1\times r_2)}^n)mod{n}^2\end{array}$$

(46)

In conclusion, Paillier is homomorphic with respect to the addition as shown in Equation 47.

$$\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)=\epsilon (m_1+m_2,r_1\times r_2)$$

(47)

3.5.1. Ciphertext Regeneration Feature

Neutral element in addition is 0. So, if the neutral element is encrypted and then homomorphic addition applied to a ciphertext encrypted by Paillier, corresponding plaintext should be same whereas ciphertext changes. In other words, a plaintext may have many ciphertexts. This basic feature allows us to regenerate ciphertexts as shown in Equations 48 and 49 where D denotes decryption.

$$\epsilon (m_1,r_1)\times \epsilon (0,r_2)\ne \epsilon (m_1,r_1)$$

(48)

$$D(\epsilon (m_1,r_1)\times \epsilon (0,r_2))=D\left(\epsilon (m_1,r_1)\right)$$

(49)

3.5.2. Scalar Multiplication Feature

Even though Paillier cryptosystem is not homomorphic with respect to the multiplication, it allows to multiply a ciphertext with a known constant aka scalar multiplication. This can be calculated with adding a ciphertext into itself a constant k times but this operation’s complexity is $O\left(k\right)$. On the other hand, calculating a ciphertext to the power of that constant will give same result as calculated in Equations 50 and 51.

$${\epsilon (m_1,r_1)}^k={\left(g^{m_1}\times {r_1}^n\right)}^{k}mod{n}^2$$

(50)

$${\epsilon (m_1,r_1)}^k=\left(g^{m_1\times k}\times {r_1}^{n\times k}\right)mod{n}^2$$

(51)

On the other hand, multiplication of $m_1$ and k with the random key k-th power of $r_1$ will give same result as shown in Equation 52.

$$\epsilon (m_1\times k,r_1^k)=\left(g^{m_1\times k}\times {r_1}^{n\times k}\right)mod{n}^2$$

(52)

After decryption, only the first argument of the encryption function will be recovered which is plaintext times constant value.

3.6. Damgard-Jurik

Damgard-Jurik is a generalized type of Paillier algorithm invented by Ivan Damgard and Mads Jurik in 2001 [26]. Pailier uses computations modulo $n^2$ whereas Damgard-Jurik uses $n^{s+1}$ where n is a RSA modulus. In other words, Paillier is a subset of Damgard-Jurik where s equals to 1. Similar to Paillier, it is depending on the difficulty of computing n-th residue classes. A generalized encryption calculation of the cryptosystem is shown in Equation 53.

$$\epsilon (m,r)=\left(g^m\times r^{n^s}\right)mod{n}^{s+1}$$

(53)

Then, encryption of plaintext pairs $m_1$ and $m_2$ with random keys $r_1$ and $r_2$ will be calculated using Equations 54 and 55.

$$\epsilon (m_1,r_1)=\left(g^{m_1}\times {r_1}^{n^s}\right)mod{n}^{s+1}$$

(54)

$$\epsilon (m_2,r_2)=\left(g^{m_2}\times {r_2}^{n^s}\right)mod{n}^{s+1}$$

(55)

Thereafter, multiplication of ciphertext will be calculated using Equation.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{m_1}\times {r_1}^{n^s}\right)\times \left(g^{m_2}\times {r_2}^{n^s}\right)mod{n}^{s+1}\end{array}$$

(56)

The multiplication can be reorganized as shown in Equations 57 and 58.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{m_1}\times g^{m_2}\times {r_1}^{n^s}\times {r_2}^{n^s}\right)mod{n}^{s+1}\end{array}$$

(57)

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ (g^{m_1+m_2}\times {(r_1\times r_2)}^{n^s})mod{n}^{s+1}\end{array}$$

(58)

On the other hand, encryption of addition of plaintexts $m_1$ and $m_2$ with random key $r_1$×$r_2$ will give same result as shown in Equation 59.

$$\begin{array}{c}\epsilon (m_1+m_2,r_1\times r_2)\\ =\\ (g^{m_1+m_2}\times {(r_1\times r_2)}^{n^s})mod{n}^{s+1}\end{array}$$

(59)

In conclusion, Damgard-Jurik is homomorphic with respect to the addition as shown in Equation 60.

$$\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)=\epsilon (m_1+m_2,r_1\times r_2)$$

(60)

3.6.1. Ciphertext Regeneration Feature

Encrypting the neutral element of addition which is 0 and then adding it to a ciphertext will regenerate ciphertext whereas corresponding plaintext remains same as shown in Equation 61 and 62 where D denotes decryption.

$$\epsilon (m_1,r_1)\times \epsilon (0,r_2)\ne \epsilon (m_1,r_1)$$

(61)

$$D(\epsilon (m_1,r_1)\times \epsilon (0,r_2))=D\left(\epsilon (m_1,r_1)\right)$$

(62)

3.6.2. Scalar Multiplication Feature

Even though Damgard-Jurik cryptosystem is not multiplicatively homomorphic, it has scalar multiplication feature. Finding the k-th power of a ciphertext where k is a constant will be calculated as shown Equations 63 and 64.

$${\epsilon (m_1,r_1)}^k={\left(g^{m_1}\times {r_1}^{(}{n}^s)\right)}^{k}mod{n}^{s+1}$$

(63)

$${\epsilon (m_1,r_1)}^k=\left(g^{m_1\times k}\times {r_1}^{(n^s\times k)}\right)mod{n}^{s+1}$$

(64)

On the other hand, encryption of m1 times k with random key r1 to the power of k will give same calculation as shown in 65.

$$\epsilon (m_1\times k,r_1^k)=\left(g^{m_1\times k}\times {r_1}^{(k\times n^s)}\right)mod{n}^{s+1}$$

(65)

The decryption process will restore just the first argument. The second argument, which contains the random number, will be completely discarded.

3.7. Okamoto-Uchiyama

Okamoto-Uchiyama was invented by Tatsuaki Okamoto and Shigenori Uchiyama in 1998 [27]. General encryption rule of Okamoto-Uchiyama cryptosystem is shown in Equation 66.

$$\epsilon (m,r)=\left(g^m\times h^r\right)modn$$

(66)

Then, encryption of plaintext pairs $m_1$ and $m_2$ with random keys $r_1$ and $r_2$ will be calculated using Equations 67 and 68.

$$\epsilon (m_1,r_1)=\left(g^{m_1}\times h^{r_1}\right)modn$$

(67)

$$\epsilon (m_2,r_2)=\left(g^{m_2}\times h^{r_2}\right)modn$$

(68)

Thereafter, multiplication of ciphertext will be calculated using Equation 69.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ \\ =\left(g^{m_1}\times h^{r_1}\right)\times \left(g^{m_2}\times h^{r_2}\right)modn\end{array}$$

(69)

The multiplication can be reorganized as shown in Equations 70 and 71.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{m_1}\times g^{m_2}\times h^{r_1}\times h^{r_2}\right)modn\end{array}$$

(70)

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(g^{m_1+m_2}\times h^{r_1+r_2}\right)modn\end{array}$$

(71)

On the other hand, encryption of addition of plaintexts $m_1$ and $m_2$ with random key $r_1$+$r_2$ will give same result as shown in Equation 72.

$$\begin{array}{c}\epsilon (m_1+m_2,r_1+r_2)\\ =\\ \left(g^{m_1+m_2}\times h^{r_1+r_2}\right)modn\end{array}$$

(72)

In conclusion, Okamoto-Uchiyama is homomorphic with respect to the addition as shown in Equation 73.

$$\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)=\epsilon (m_1+m_2,r_1+r_2)$$

(73)

3.7.1. Ciphertext Regeneration Feature

Encrypting the neutral element of addition which is 0 and then adding it to a ciphertext will regenerate ciphertext whereas corresponding plaintext remains same as shown in Equations 74 and 75 where D denotes decryption.

$$\epsilon (m_1,r_1)\times \epsilon (0,r_2)\ne \epsilon (m_1,r_1)$$

(74)

$$D(\epsilon (m_1,r_1)\times \epsilon (0,r_2))=D\left(\epsilon (m_1,r_1)\right)$$

(75)

3.7.2. Scalar Multiplication Feature

Okamoto-Uchiyama supports scalar multiplication as shown in Equations 76 and 77.

$${\epsilon (m_1,r_1)}^k={\left(g^{m_1}\times h^{r_1}\right)}^{k}modn$$

(76)

$${\epsilon (m_1,r_1)}^k=\left(g^{m_1\times k}\times h^{r_1\times k}\right)modn$$

(77)

On the other hand, encryption of $m_1$ times k with random key $r_1$ to the power of k will give same calculation as shown in 65.

$$\epsilon (m_1\times k,r_1\times k)=\left(g^{m_1\times k}\times h^{r_1\times k}\right)modn$$

(78)

Once the data is decrypted, the random number in the second argument is ignored.

3.8. Goldwasser-Micali

Goldwasser-Micali was invented by Shafi Goldwasser and Silvio Micali in 1982 [30]. The cryptosystem shows homomorphic features with respect to the exclusive or (XOR). A generalized encryption formula of Goldwasser-Micali is shown in Equation 79 where b is the bit value, r is a random integer and x is a non-residue number. Unsimilar to other cryptosystems, Goldwasser-Micali encrypts bits instead of plaintext numbers.

$$\epsilon (b,r)=\left(r^2\times x^b\right)modn$$

(79)

Then, encryption of plain bit text pairs $b_1$ and $b_2$ with random keys $r_1$ and $r_2$ will be calculated using Equations 80 and 81.

$$\epsilon (b_1,r_1)=\left({r_1}^2\times x^{b_1}\right)modn$$

(80)

$$\epsilon (b_2,r_2)=\left({r_2}^2\times x^{b_2}\right)modn$$

(81)

Thereafter, multiplication of ciphertexts will be calculated using Equation 82.

$$\epsilon (b_1,r_1)\times \epsilon (b_2,r_2)=\left({r_1}^2\times x^{b_1}\right)\times \left({r_2}^2\times x^{b_2}\right)modn$$

(82)

The multiplication can be reorganized as shown in Equations 83 and 84.

$$\begin{array}{c}\epsilon (b_1,r_1)\times \epsilon (b_2,r_2)\\ =\\ \left({r_1}^2\times {r_2}^2\times x^{b_1}\times x^{b_2}\right)modn\end{array}$$

(83)

$$\begin{array}{c}\epsilon (b_1,r_1)\times \epsilon (b_2,r_2)\\ =\\ {(r_1\times r_2)}^2\times x^{b_1+b_2}modn\end{array}$$

(84)

On the other hand, encryption of $b_1$ + $b_2$ with random key $r_1$×$r_2$ will give same result as shown in Equation 85. Herein, addition on bits is equivalent to xor operation.

$$\begin{array}{c}\epsilon (b_1\oplus b_2,r_1\times r_2)\\ =\\ {\left(r_1\times r_2\right)}^2\times x^{b_1+b_2}modn\end{array}$$

(85)

In conclusion, Goldwasser-Micali is homomorphic with respect to the exclusive or (XOR) as shown in Equation 86.

$$\epsilon (b_1,r_1)\times \epsilon (b_2,r_2)=\epsilon (b_1\oplus b_2,r_1\times r_2)$$

(86)

3.9. Benaloh

Benaloh cryptosystem was invented by Josh Benaloh in 1985 [28]. It is an extension of Goldwasser-Micali [30] cryptosystem. Benaloh shows additively homomorphic features whereas Goldwasser-Micali was homomorphic with respect to the exclusive or (XOR). A generalized encryption formula of Benaloh is shown in Equation 87.

$$\epsilon (m,r)=\left(y^m\times u^r\right)modn$$

(87)

Then, encryption of plaintext pairs $m_1$ and $m_2$ with random keys $r_1$ and $r_2$ will be calculated using Equations 88 and 89.

$$\epsilon (m_1,r_1)=\left(y^{m_1}\times u^{r_1}\right)modn$$

(88)

$$\epsilon (m_2,r_2)=\left(y^{m_2}\times u^{r_2}\right)modn$$

(89)

Thereafter, multiplication of ciphertexts will be calculated using Equation 90.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(y^{m_1}\times u^{r_1}\right)\times \left(y^{m_2}\times u^{r_2}\right)modn\end{array}$$

(90)

The multiplication can be reorganized as shown in Equations 91 and 92.

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(y^{m_1}\times y^{m_2}\times u^{r_1}\times u^{r_2}\right)modn\end{array}$$

(91)

$$\begin{array}{c}\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)\\ =\\ \left(y^{m_1+m_2}\times u^{r_1+r_2}\right)modn\end{array}$$

(92)

On the other hand, encryption of addition of plaintexts $m_1$ and $m_2$ with random key $r_1$+$r_2$ will give same result as shown in Equation 93.

$$\begin{array}{c}\epsilon (m_1+m_2,r_1+r_2)\\ =\\ \left(y^{m_1+m_2}\times u^{r_1+r_2}\right)modn\end{array}$$

(93)

In conclusion, Benaloh is homomorphic with respect to the addition as shown in Equation 94.

$$\epsilon (m_1,r_1)\times \epsilon (m_2,r_2)=\epsilon (m_1+m_2,r_1+r_2)$$

(94)

Similar to exponential ElGamal and elliptic curve ElGamal, decryption of Benaloh is difficult problem. It requires to solve discrete logarithm to restore the plaintext.

3.9.1. Ciphertext Regeneration Feature

Encrypting the neutral element of addition which is 0 and then adding it to a ciphertext will regenerate ciphertext whereas corresponding plaintext remains same as shown in Equations 95 and 96 where D denotes decryption.

$$\epsilon (m_1,r_1)\times \epsilon (0,r_2)\ne \epsilon (m_1,r_1)$$

(95)

$$D(\epsilon (m_1,r_1)\times \epsilon (0,r_2))=D\left(\epsilon (m_1,r_1)\right)$$

(96)

3.9.2. Scalar Multiplication Feature

Finding the k-th power of ciphertext will be equal to the scalar multiplication of k and plaintext message as shown in Equations 97 and 98.

$${\epsilon (m_1,r_1)}^k={\left(y^{m_1}\times u^{r_1}\right)}^{k}modn$$

(97)

$${\epsilon (m_1,r_1)}^k=\left(y^{m_1\times k}\times u^{r_1\times k}\right)modn$$

(98)

On the other hand, encryption of k times m1 with random key r1 times k will be same as shown in Equation 99.

$$\epsilon (m_1\times k,r_1\times k)=\left(y^{m_1\times k}\times u^{r_1\times k}\right)modn$$

(99)

Once decryption is done, just the first argument of encryption function will be restored,and the random number in the second argument will be dropped.

3.10. Naccache-Stern

Naccache-Stern was invented by David Naccache and Jacques Stern in 1998 [29]. It is depending on the difficulty of higher residuosity problem. A generalized encryption procedure of the cryptosystem is shown in Equation 100.

$$\epsilon (m,\sigma )=\left(g^m\times r^{\sigma }\right)modn$$

(100)

Then, encryption of plaintext pairs $m_1$ and $m_2$ with random keys $r_1$ and $r_2$ will be calculated using Equations 101 and 102.

$$\epsilon (m_1,{\sigma }_1)=\left(g^{m_1}\times r^{{\sigma }_1}\right)modn$$

(101)

$$\epsilon (m_2,{\sigma }_2)=\left(g^{m_2}\times r^{{\sigma }_2}\right)modn$$

(102)

Thereafter, multiplication of ciphertexts will be calculated using Equation 103.

$$\begin{array}{c}\epsilon (m_1,{\sigma }_1)\times \epsilon (m_2,{\sigma }_2)\\ =\\ \left(g^{m_1}\times r^{{\sigma }_1}\right)\times \left(g^{m_2}\times r^{{\sigma }_2}\right)modn\end{array}$$

(103)

The multiplication can be reorganized as shown in Equation 104.

$$\begin{array}{c}\epsilon (m_1,{\sigma }_1)\times \epsilon (m_2,{\sigma }_2)\\ =\\ \left(g^{m_1+m_2}\times r^{{\sigma }_1+{\sigma }_2}\right)modn\end{array}$$

(104)

On the other hand, encryption of addition of plaintexts $m_1$ and $m_2$ will give same result as shown in Equation 105.

$$\begin{array}{c}\epsilon (m_1+m_2,{\sigma }_1+{\sigma }_2)\\ =\\ \left(g^{m_1+m_2}\times r^{{\sigma }_1+{\sigma }_2}\right)modn\end{array}$$

(105)

In conclusion, Naccache-Stern is homomorphic with respect to the addition as shown in Equation 106.

$$\epsilon (m_1,{\sigma }_1)\times \epsilon (m_2,{\sigma }_2)=\epsilon (m_1+m_2,{\sigma }_1+{\sigma }_2)$$

(106)

Similar to Benaloh, decryption of Naccahe-Stern requires to solve discete logarithm problem.

3.10.1. Ciphertext Regeneration Feature

Encrypting the neutral element of addition which is 0 and then adding it to a ciphertext will regenerate ciphertext whereas corresponding plaintext remains same as shown in Equations 107 and 108 where D denotes decryption.

$$\epsilon (m_1,{\sigma }_1)\times \epsilon (0,{\sigma }_2)\ne \epsilon (m_1,{\sigma }_1)$$

(107)

$$D(\epsilon (m_1,{\sigma }_1)\times \epsilon (0,{\sigma }_2))=D\left(\epsilon (m_1,{\sigma }_1)\right)$$

(108)

3.10.2. Scalar Multiplication Feature

Naccache-Stern cryptosystem shows scalar multiplicationf features. Find the k-th power of a ciphertext will be equal the encryption of k times plaintext as shown in Equations 109, 110 and 111.

$${\epsilon (m_1,\sigma )}^k={\left(g^{m_1}\times r^{\sigma }\right)}^{k}modn$$

(109)

$${\epsilon (m_1,\sigma )}^k=\left(g^{m_1\times k}\times r^{\sigma \times k}\right)modn$$

(110)

$$\epsilon (m_1\times k,\sigma \times k)=\left(g^{m_1\times k}\times r^{\sigma \times k}\right)modn$$

(111)

During decryption, the first argument is retrieved while the second argument is omitted.

4. Materials and Methods

4.1. Design and Architecture

An abstract class in programming is a class that cannot be instantiated on its own and is designed to be subclassed, typically containing one or more abstract methods that must be implemented by its subclasses [41]. The LightPHE framework is designed with a generic abstract class called Homomorphic. This class will include all the necessary methods for homomorphic operations, such as the addition of ciphertexts, multiplication of ciphertexts, xor of ciphertext, scalar multiplication of a ciphertext with a constant, and ciphertext regeneration. In addition to these homomorphic operations, the Homomorphic abstract class will have methods for generating key pairs for the cryptosystem, as well as methods for encryption and decryption.

Besides, each PHE algorithm generates different type of ciphertexts. Basically, this specifies the design of the class. Table 3 shows ciphertext types of these algorithms and also the random key availability in the encryption process.

Each partially homomorphic encryption (PHE) algorithm will have its own class that inherits from the Homomorphic abstract class. Abstract class covers all ciphertext types whereas PHE algorithms’ classes followed the design mentioned in Table 3.

For additively homomorphic algorithms, the framework will throw exceptions in PHE classes for homomorphic multiplication and homomorphic XOR operations, as these are not supported by these algorithms. For multiplicatively homomorphic algorithms, the framework will throw exceptions for homomorphic addition and homomorphic XOR operations. Additionally, exceptions will be thrown for scalar multiplication and ciphertext regeneration because these operations are only supported by additively homomorphic algorithms. For exclusively homomorphic algorithms, the framework will throw exceptions for both homomorphic addition and homomorphic multiplication. Similarly, exceptions will be thrown for scalar multiplication and ciphertext regeneration because these operations are only supported by additively homomorphic algorithms. In that way, each PHE algorithm class will have same methods.

Users will only interact with LightPHE class and they do not have to play with backend cryptosystems’ classes at all. Once a cryptosystem is created, it will have its own encrypt and decrypt methods. Encrypt method will return a Ciphertext class, with the returned values from backend cryptosystems set to the value argument of the Ciphertext class. Addition, multiplication and xor methods are overwritten on this class - in this way, adding or multiplying two Ciphertexts classes will perform homomorphic addition, multiplication or xor. Similarly, right multiplication method is overwritten to perform scalar multiplication when multiplying a Ciphertext object with a constant.

The framework’s design considers both computational efficiency and environmental impact, but it is important to note that the implementation presented in this work serves primarily as a demonstration rather than a precise measurement tool. The code measures cryptographic operations’ runtime and applies simplified assumptions (e.g., fixed CPU utilization patterns, base power of 150 W, constant PUE and grid intensity values) to estimate energy consumption and Scope 1–3 emissions. In a real-world data center, actual power usage can fluctuate based on dynamic factors such as server load, cooling requirements, and time-of-day energy mix. Hence, for accurate energy or emission data, one would need to integrate real-time monitoring tools (e.g., Intel RAPL, IPMI, or cloud provider telemetry) and up-to-date information on hardware efficiency, cooling, and local energy grid composition.

Despite these simplifications, the demonstration-based approach still provides insight into how homomorphic encryption algorithms might scale in terms of both resource usage and environmental footprint. As shown in Table ??, certain algorithms—particularly at larger key sizes—require significantly more computational resources. For instance, RSA with a 7680-bit key size demonstrates notably high time consumption in key generation (370.568 seconds), while Damgard-Jurik with the same key size shows substantial encryption and decryption overhead (8.0903 and 8.1464 seconds respectively). These longer runtimes are mapped to estimated energy consumption and greenhouse gas (GHG) emissions using the framework’s model.

Rather than calculating emissions for every algorithm variant, the analysis focuses on low and mid impact cases such as 80-bit and 128-bit resource-intensive homomorphic operations—where environmental considerations are most critical with Colab L4 GPU. Since the comparison with all cpu and gpu types including all data centers that will lead to another research. This targeted assessment investigates how direct on-site emissions (Scope 1), indirect emissions from purchased electricity (Scope 2), and broader lifecycle factors such as hardware manufacturing and cooling systems (Scope 3) scale with computational demand. It is conducted across multiple data centers with varying hardware efficiency (PUE values) and electricity carbon intensities, thereby highlighting how cryptographic security margins intersect with sustainability goals in different operational contexts.

By emphasizing environments where CPU load is highest, this study elucidates the interplay between cryptographic performance and ecological impact. However, all findings should be interpreted as indicative estimates rather than precise measurements. For rigorous emission tracking in an operational data center, one must combine or replace the demonstration model with real-world metrics, such as actual power draw logs and up-to-date carbon intensity data. Within these limitations, the presented framework offers both robust encryption benchmarking and environmental impact estimations, thus enabling more informed decisions about resource allocation and sustainability in cryptographic deployments. Fully Carbon-Based (DC1–DC3): Primarily powered by fossil fuels, leading to high Scope 2 emissions. Fully Renewable (DC4–DC6): Rely on renewable energy sources, resulting in minimal or zero Scope 1 and Scope 2 emissions, leaving mostly Scope 3 (indirect) emissions. Hybrid (DC7–DC9): Operate on a blend of renewable and non-renewable energy, producing emissions that lie between fully carbon-based and fully renewable centers.

Table 4. Sample Data Center Configurations

Data Center	Type	Grid Intensity (gCO2/kWh)	PUE	Renewable Ratio
DC1_Carbon_1	Fully Carbon	600.0	1.3	0.0
DC2_Carbon_2	Fully Carbon	650.0	1.4	0.0
DC3_Carbon_3	Fully Carbon	700.0	1.5	0.0
DC4_Renewable_1	Fully Renewable	100.0	1.1	1.0
DC5_Renewable_2	Fully Renewable	50.0	1.05	1.0
DC6_Renewable_3	Fully Renewable	120.0	1.2	1.0
DC7_Hybrid_1	Hybrid	300.0	1.3	0.6
DC8_Hybrid_2	Hybrid	280.0	1.2	0.7
DC9_Hybrid_3	Hybrid	250.0	1.2	0.8
DC10_Hybrid_4	Hybrid	200.0	1.1	0.9

Table 4. Sample Data Center Configurations

Data Center	Type	Grid Intensity (gCO2/kWh)	PUE	Renewable Ratio
DC1_Carbon_1	Fully Carbon	600.0	1.3	0.0
DC2_Carbon_2	Fully Carbon	650.0	1.4	0.0
DC3_Carbon_3	Fully Carbon	700.0	1.5	0.0
DC4_Renewable_1	Fully Renewable	100.0	1.1	1.0
DC5_Renewable_2	Fully Renewable	50.0	1.05	1.0
DC6_Renewable_3	Fully Renewable	120.0	1.2	1.0
DC7_Hybrid_1	Hybrid	300.0	1.3	0.6
DC8_Hybrid_2	Hybrid	280.0	1.2	0.7
DC9_Hybrid_3	Hybrid	250.0	1.2	0.8
DC10_Hybrid_4	Hybrid	200.0	1.1	0.9

5. Results and Discussion

To use the LightPHE framework, the library is imported and the LightPHE class is initialized with the desired partially homomorphic encryption (PHE) algorithm. The following code example demonstrates this process.

In the example shown in Algorithm 1, the LightPHE class is imported from the lightphe library. The algorithms list contains the names of all the supported PHE algorithms. Initializing the LightPHE class with first algorithm in the list, which corresponds to RSA in this case, generates a random private-public key pair for the chosen cryptosystem. This procedure is sufficient to build a cryptosystem using the selected PHE algorithm.

Algorithm 1: Building a Cryptosystem

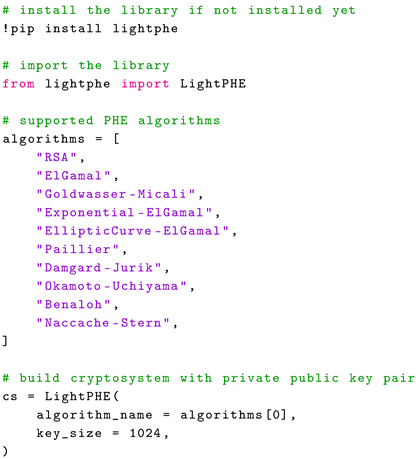Then, the following code demonstrates defining a plaintext value, encrypting it, and then decrypting it to verify correctness.

In the example shown in Algorithm 2, A plaintext value m is defined and set to 17. The encrypt method of the cryptosystem is called with plaintext, producing the ciphertext c. The decrypt method of cryptosystem is then called with ciphertext as the argument to decrypt the ciphertext. An assertion is made to verify that the decrypted value matches the original plaintext m. This ensures that the encryption and decryption processes are functioning correctly within the cryptosystem.

Algorithm 2: Encrypt and Decrypt with Built Cryptosystem

The following code demonstrates homomorphic addition using the Paillier algorithm:

In the example demonstrated in Algorithm 3, the LightPHE class is initialized with the Paillier algorithm. This generates a random private public key pair. Two plaintext values, $m_1$ and $m_2$, are defined and set to 10000, representing the base salary, and 500, representing the wage increase in amount, respectively. The encrypt method of the LightPHE instance cs is called with $m_1$ and $m_2$ as arguments, producing the ciphertexts $c_1$ and $c_2$. Encryption can be done with just public keys, without need of private keys. These are done on premises side and $c_1$, $c_2$ pair and public keys are sent to the cloud environment.

Algorithm 3: On Premises Encryptions

The Algorithm 4 summarizes the operations done in the cloud side. It receives $c_1$, $c_2$ pair and public keys from on premises side. Firsly, cloud cannot decrypt $c_1$, $c_2$ pair because it doesn’t have the private key. Secondly, types of $c_1$ and $c_2$ are casted to Ciphertext and LightPHE overwritten that class’ addition method to perform homomorphic addition as mentioned in Section 4.1. So, homomorphic addition is performed by adding $c_1$ and $c_2$ to produce a new ciphertext $c_3$, which represents the updated encrypted salary. This operation does not require the private key and can be done with public key only. Even though $c_3$ was calculated by the cloud system, cloud itself cannot decrypt it because it doesn’t have the private keys. Finally, cloud stores $c_3$ on its database.

Algorithm 4: Cloud Calculations

Thereafter, The Algorithm 5 summarizes the proof of work. On premises retrieves $c_3$ from cloud. An assertion is made to verify that decrypting $c_3$ returns the sum of the original plaintext values ($m_1$ + $m_2$) on premises side. Decryption can only be done by the data owner who holds private key. This demonstrates the correctness of the homomorphic addition operation.

Algorithm 5: Proof of Work

In the example illustrated in Algorithm 6, a scalar k is defined to represent a 5% wage increase and is set to 1.05. The variable $c_1$ is a type of Ciphertext, representing the encrypted base salary of someone, and the class’s right multiplication method is overridden to perform scalar multiplication. Thus, scalar multiplication is performed by multiplying k with the ciphertext $c_1$ to produce a new ciphertext $c_4$, which represents the encrypted updated salary. This operation does not require the private key and can be done by anyone who has the public keys.

Algorithm 6: Scalar Multiplication

Finally, an assertion is made to verify that decrypting $c_4$ returns the product of the scalar k and the original plaintext $m_1$, demonstrating the correctness of the scalar multiplication operation. This operation can only be done by the data owner who holds private key of the cryptosystem.

The following code in Algorithm 7 demonstrates the limitations of the Paillier algorithm with respect to multiplicative and exclusive homomorphic operations:

Algorithm 7: Unsupported Operations

Since the Paillier algorithm is not multiplicatively homomorphic, attempting to multiply ciphertexts $c_1$ and $c_2$ will raise an error with the message "Paillier is not homomorphic with respect to the multiplication". Similarly, since the Paillier algorithm is not exclusively homomorphic, attempting to perform an exclusive OR operation (XOR) on $c_1$ and $c_2$ will raise another error with the message "Paillier is not homomorphic with respect to the exclusive or". These are thrown by the Paillier class’ homomorphic multiply and homomorphic xor methods. These exceptions demonstrate the algorithm’s limitations concerning these specific homomorphic operations.

5.1. Performance

The provided Table 6, Table 7, Table 8, Table 9 showcase the performance metrics of various cryptographic algorithms with default configurations, specifically focusing on key generation, encryption, decryption, and homomorphic operations such as addition, multiplication or xor with different key sizes. These measurements are crucial in evaluating the practicality and efficiency of these algorithms in real-world applications. Here, the encryption and homomorphic operation times are represented in scientific notation to illustrate the performance differences clearly. The values in cells represent the times in seconds and are the average of five different experiments.

In these experiments, 18-bit plaintexts were used to simulate realistic annual salary values, typically ranging in the hundreds of thousands. This choice reflects a practical application scenario where the encryption of such values is relevant.

The tables also adhere to the National Institute of Standards and Technology (NIST) recommendations for key sizes to achieve specific security levels [42] as detailed in Table 5. For an 80-bit symmetric key security level, NIST suggests using 160-bit keys for elliptic curve cryptography (ECC) and 1024-bit keys for other algorithms. For a 112-bit symmetric key security level, 224-bit ECC keys and 2048-bit keys for other algorithms are recommended. For a 128-bit symmetric key security level, NIST recommends 256-bit ECC keys and 3072-bit keys for other algorithms. These guidelines ensure that the cryptographic strength meets the required security standards.

One notable observation from the tables is the significantly higher decryption times for Elliptic Curve ElGamal and Exponential ElGamal algorithms in particular smaller key sizes. This is attributed to the necessity of solving the Discrete Logarithm Problem (DLP) and Elliptic Curve Discrete Logarithm Problem (ECDLP) during the decryption process. This computational complexity renders these cryptosystems more theoretical than practical, especially given the small plaintext values used in the experiments. As the plaintext size increases, the decryption times are expected to rise even further, exacerbating the impracticality.

Interestingly, larger key sizes do not have a significant impact on the encryption and decryption times of Elliptic Curve ElGamal. This consistency across different key sizes highlights a unique aspect of the algorithm’s performance. However, it is important to note that the decryption time for Elliptic Curve ElGamal is still slow when compared to other cryptosystems, making it less practical with today’s computational power for applications requiring frequent decryption at the 80, 112, and 128-bit symmetric key size equivalents. On the other hand, Elliptic Curve ElGamal becomes advantageous at the 192-bit symmetric key size equivalent, as it becomes faster in key generation, encryption, and decryption when compared to other additively homomorphic encryption algorithms such as Paillier or Damgard-Jurik. Additionally, Elliptic Curve ElGamal has potential in the post-quantum era because its equivalents have a much greater impact on key generation, encryption, and decryption. While the times for these operations increase exponentially with key size for other algorithms, the times for EC ElGamal increase linearly.

Additionally, it is important to mention that the Benaloh and Naccache-Stern cryptosystems were excluded from these experiments. Despite functioning correctly for smaller key sizes, these algorithms encountered significant issues during the key generation step for 1024-bit and 2048-bit keys, effectively hanging and becoming non-operational. This limitation prevented their inclusion in the comparative analysis, highlighting the challenges in scaling certain cryptosystems to higher security levels.

Homomorphic operations and encryptions, as noted in the tables, are very fast. This efficiency is crucial as these operations are typically handled frequently, with encryption being performed on-premise and homomorphic operations executed in the cloud. In cloud environments, where performance is a key concern, the swift execution of these tasks ensures optimal system performance. Although decryption is slower than both homomorphic operations and encryption, its less frequent occurrence mitigates the impact of its slower speed. It’s important to note that key generation occurs only once, and while it may be slightly slower, its infrequent occurrence makes this delay negligible in the overall scheme of cryptographic processes.

Overall, these tables provide valuable insights into the performance and practicality of various cryptographic algorithms under different security settings, emphasizing the balance between theoretical capabilities and real-world applicability.

Finally, all experiments were conducted on a machine with an 11th Gen Intel(R) Core(TM) i7-11370H CPU running at 3.30 GHz with 8 cores. This CPU model belongs to Intel’s Tiger Lake family and is commonly found in high-performance laptops. Therefore, the information provided about the CPU ensures transparency regarding the computational environment in which the experiments were conducted.

Table 6. Time Consumption of Algorithms with 80-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	1024	0.1483	$0.00305\times {10}^{-3}$	0.0038	$1.70708\times {10}^{-5}$
ElGamal	1024	0.0177	$1.31831\times {10}^{-3}$	0.0007	$1.66416\times {10}^{-5}$
Paillier	1024	0.0507	$1.16231\times {10}^{-2}$	0.0120	$1.90258\times {10}^{-5}$
Damgard-Jurik	1024	0.0585	$2.35637\times {10}^{-2}$	0.0245	$3.82900\times {10}^{-5}$
Okamoto-Uchiyama	1024	0.1050	$1.14785\times {10}^{-2}$	0.0037	$1.82629\times {10}^{-5}$
Goldwasser-Micali	1024	0.0400	$2.74090\times {10}^{-4}$	0.0093	$6.70433\times {10}^{-5}$
Exponential-ElGamal	1024	0.0302	$1.09401\times {10}^{-3}$	3.1553	$1.03474\times {10}^{-5}$
EllipticCurve-ElGamal	160	0.0053	$1.01023\times {10}^{-2}$	4.1529	$6.82354\times {10}^{-5}$

Table 6. Time Consumption of Algorithms with 80-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	1024	0.1483	$0.00305\times {10}^{-3}$	0.0038	$1.70708\times {10}^{-5}$
ElGamal	1024	0.0177	$1.31831\times {10}^{-3}$	0.0007	$1.66416\times {10}^{-5}$
Paillier	1024	0.0507	$1.16231\times {10}^{-2}$	0.0120	$1.90258\times {10}^{-5}$
Damgard-Jurik	1024	0.0585	$2.35637\times {10}^{-2}$	0.0245	$3.82900\times {10}^{-5}$
Okamoto-Uchiyama	1024	0.1050	$1.14785\times {10}^{-2}$	0.0037	$1.82629\times {10}^{-5}$
Goldwasser-Micali	1024	0.0400	$2.74090\times {10}^{-4}$	0.0093	$6.70433\times {10}^{-5}$
Exponential-ElGamal	1024	0.0302	$1.09401\times {10}^{-3}$	3.1553	$1.03474\times {10}^{-5}$
EllipticCurve-ElGamal	160	0.0053	$1.01023\times {10}^{-2}$	4.1529	$6.82354\times {10}^{-5}$

Table 7. Time Consumption of Algorithms with 112-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	2048	1.4959	$2.14737\times {10}^{-2}$	0.0235	$5.04017\times {10}^{-5}$
ElGamal	2048	0.6238	$7.15775\times {10}^{-3}$	0.0037	$1.92165\times {10}^{-5}$
Paillier	2048	0.7613	$8.51427\times {10}^{-2}$	0.0847	$5.97000\times {10}^{-5}$
Damgard-Jurik	2048	0.6388	$1.72729\times {10}^{-1}$	0.1997	$1.04141\times {10}^{-4}$
Okamoto-Uchiyama	2048	0.7543	$7.80529\times {10}^{-2}$	0.0239	$3.19004\times {10}^{-5}$
Goldwasser-Micali	2048	0.6725	$6.73010\times {10}^{-4}$	0.0536	$1.94454\times {10}^{-4}$
Exponential-ElGamal	2048	0.3957	$6.95195\times {10}^{-3}$	10.572	$1.69277\times {10}^{-5}$
EllipticCurve-ElGamal	224	0.0060	$8.61859\times {10}^{-3}$	3.6356	$5.64575\times {10}^{-5}$

Table 7. Time Consumption of Algorithms with 112-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	2048	1.4959	$2.14737\times {10}^{-2}$	0.0235	$5.04017\times {10}^{-5}$
ElGamal	2048	0.6238	$7.15775\times {10}^{-3}$	0.0037	$1.92165\times {10}^{-5}$
Paillier	2048	0.7613	$8.51427\times {10}^{-2}$	0.0847	$5.97000\times {10}^{-5}$
Damgard-Jurik	2048	0.6388	$1.72729\times {10}^{-1}$	0.1997	$1.04141\times {10}^{-4}$
Okamoto-Uchiyama	2048	0.7543	$7.80529\times {10}^{-2}$	0.0239	$3.19004\times {10}^{-5}$
Goldwasser-Micali	2048	0.6725	$6.73010\times {10}^{-4}$	0.0536	$1.94454\times {10}^{-4}$
Exponential-ElGamal	2048	0.3957	$6.95195\times {10}^{-3}$	10.572	$1.69277\times {10}^{-5}$
EllipticCurve-ElGamal	224	0.0060	$8.61859\times {10}^{-3}$	3.6356	$5.64575\times {10}^{-5}$

Table 8. Time Consumption of Algorithms with 128-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	3072	5.8871	$0.0886\times {10}^{-2}$	0.1201	$4.106\times {10}^{-5}$
ElGamal	3072	1.5976	$0.0253\times {10}^{-2}$	0.0120	$3.009\times {10}^{-5}$
Paillier	3072	2.5762	$0.3211\times {10}^{-1}$	0.3188	$1.361\times {10}^{-4}$
Damgard-Jurik	3072	3.0325	$0.6973\times {10}^{-1}$	0.6809	$2.054\times {10}^{-4}$
Okamoto-Uchiyama	3072	2.7635	$0.2815\times {10}^{-1}$	0.0881	$6.485\times {10}^{-5}$
Goldwasser-Micali	3072	3.6569	$0.0011\times {10}^{-2}$	0.4216	$3.805\times {10}^{-4}$
Exponential-ElGamal	3072	1.6232	$0.0214\times {10}^{-2}$	23.171	$2.503\times {10}^{-5}$
EllipticCurve-ElGamal	256	0.0086	$0.0119\times {10}^{-2}$	4.3759	$7.157\times {10}^{-5}$

Table 8. Time Consumption of Algorithms with 128-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	3072	5.8871	$0.0886\times {10}^{-2}$	0.1201	$4.106\times {10}^{-5}$
ElGamal	3072	1.5976	$0.0253\times {10}^{-2}$	0.0120	$3.009\times {10}^{-5}$
Paillier	3072	2.5762	$0.3211\times {10}^{-1}$	0.3188	$1.361\times {10}^{-4}$
Damgard-Jurik	3072	3.0325	$0.6973\times {10}^{-1}$	0.6809	$2.054\times {10}^{-4}$
Okamoto-Uchiyama	3072	2.7635	$0.2815\times {10}^{-1}$	0.0881	$6.485\times {10}^{-5}$
Goldwasser-Micali	3072	3.6569	$0.0011\times {10}^{-2}$	0.4216	$3.805\times {10}^{-4}$
Exponential-ElGamal	3072	1.6232	$0.0214\times {10}^{-2}$	23.171	$2.503\times {10}^{-5}$
EllipticCurve-ElGamal	256	0.0086	$0.0119\times {10}^{-2}$	4.3759	$7.157\times {10}^{-5}$

Table 9. Time Consumption of Algorithms with 192-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	7680	370.568	$0.8109\times {10}^0$	0.9861	$1.1673\times {10}^{-4}$
ElGamal	7680	22.1267	$0.2702\times {10}^0$	0.1383	$7.1764\times {10}^{-5}$
Paillier	7680	71.0874	$3.9756\times {10}^0$	4.0049	$5.4407\times {10}^{-4}$
Damgard-Jurik	7680	110.567	$8.0903\times {10}^0$	8.1464	$1.0164\times {10}^{-3}$
Okamoto-Uchiyama	7680	84.0547	$3.8247\times {10}^0$	1.1667	$2.6650\times {10}^{-4}$
Goldwasser-Micali	7680	78.9467	$5.8275\times {10}^{-3}$	4.1952	$2.1928\times {10}^{-3}$
Exponential-ElGamal	7680	49.9941	$0.2669\times {10}^0$	117.68	$7.1144\times {10}^{-5}$
EllipticCurve-ElGamal	384	0.01000	$7.1723\times {10}^{-3}$	3.5553	$5.3978\times {10}^{-5}$

Table 9. Time Consumption of Algorithms with 192-bit Symmetric Key Size Equivalent in Seconds

Algorithm	Key Size	Key Generation	Encrypt	Decrypt	Homomorphic Operation
RSA	7680	370.568	$0.8109\times {10}^0$	0.9861	$1.1673\times {10}^{-4}$
ElGamal	7680	22.1267	$0.2702\times {10}^0$	0.1383	$7.1764\times {10}^{-5}$
Paillier	7680	71.0874	$3.9756\times {10}^0$	4.0049	$5.4407\times {10}^{-4}$
Damgard-Jurik	7680	110.567	$8.0903\times {10}^0$	8.1464	$1.0164\times {10}^{-3}$
Okamoto-Uchiyama	7680	84.0547	$3.8247\times {10}^0$	1.1667	$2.6650\times {10}^{-4}$
Goldwasser-Micali	7680	78.9467	$5.8275\times {10}^{-3}$	4.1952	$2.1928\times {10}^{-3}$
Exponential-ElGamal	7680	49.9941	$0.2669\times {10}^0$	117.68	$7.1144\times {10}^{-5}$
EllipticCurve-ElGamal	384	0.01000	$7.1723\times {10}^{-3}$	3.5553	$5.3978\times {10}^{-5}$

5.2. Cloud Performances

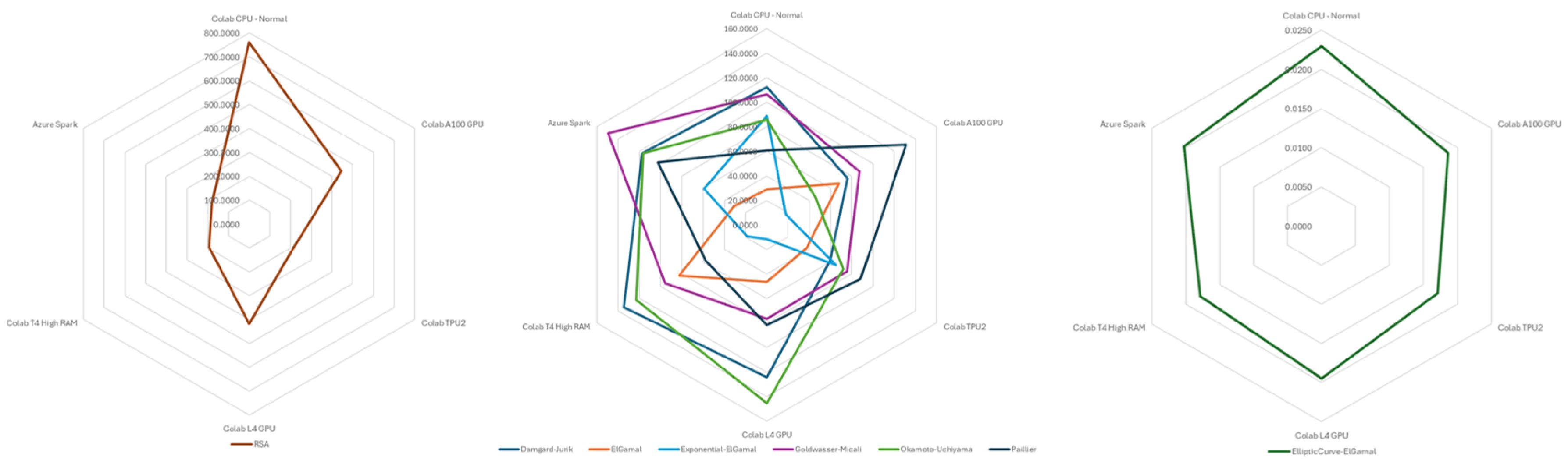
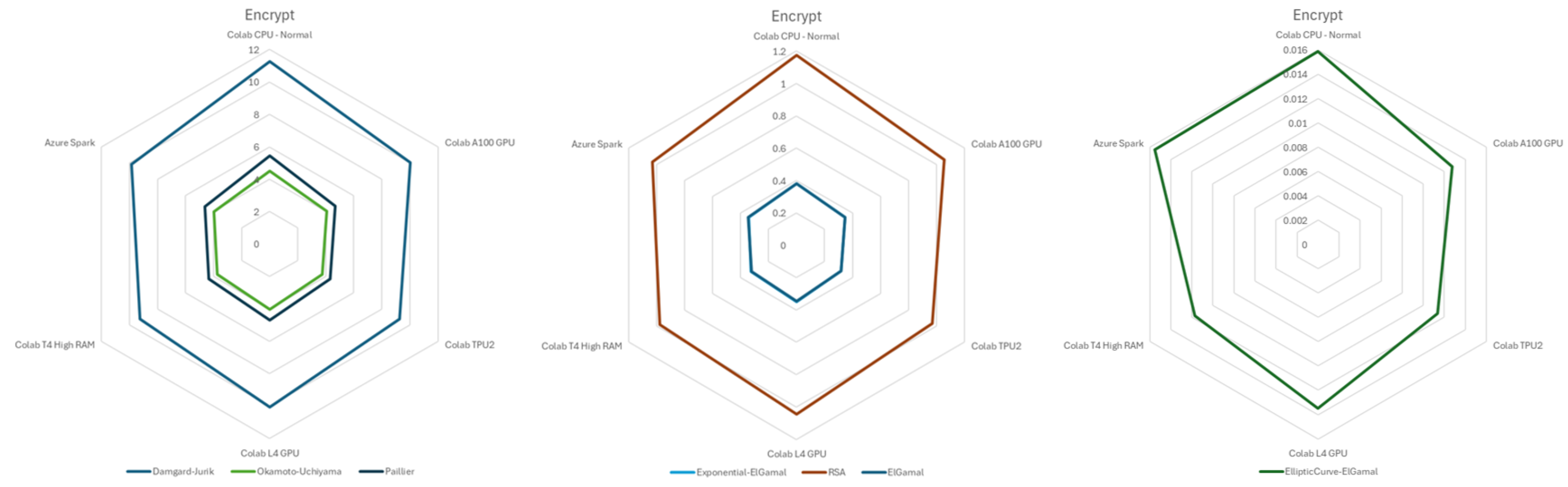
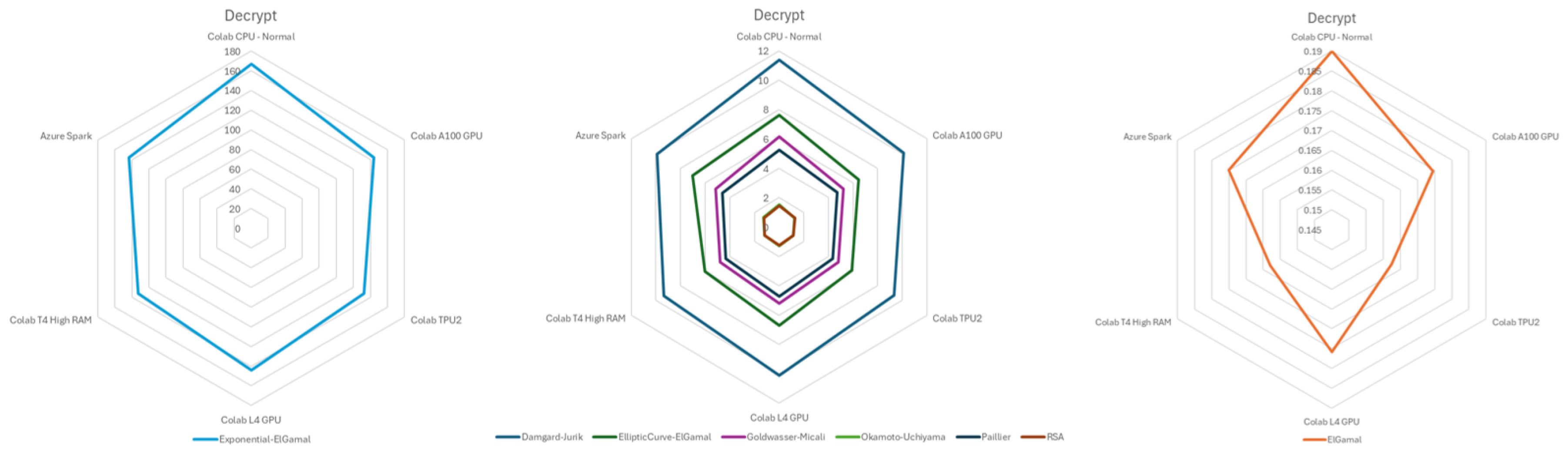
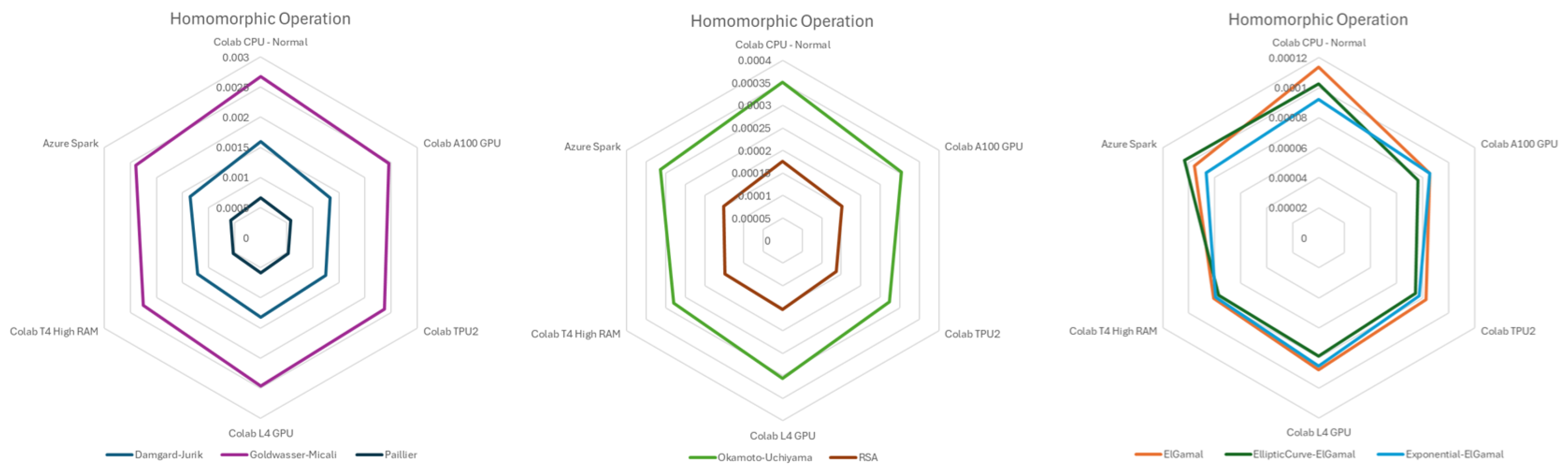
We conducted experiments on key generation, encryption, decryption, and homomorphic operations using various algorithms with an equivalent 192-bit symmetric key size. These experiments were performed across several cloud environments, including Colab Normal, Colab A100 GPU, Colab L4 GPU, Colab T4 High RAM, Colab TPU2, and Azure Spark, running five experiments for each task and averaging the consumption times to ensure accuracy.

We utilize radar map charts to present the performance of various algorithms across diverse cloud environments. Multiple radar maps are shown because consolidating them into a single radar map would render it illegible. Additionally, the radar maps are arranged from left to right to illustrate slower to faster speeds.

Figure 1 illustrates a radar map depicting key generation times in seconds for different algorithms across various cloud environments. Among these algorithms, RSA emerges as the slowest in key generation, with Elliptic Curve ElGamal demonstrating the fastest performance. Following Elliptic Curve ElGamal, ElGamal and Exponential ElGamal exhibit slightly slower key generation times than Elliptic Curve ElGamal. The remaining algorithms exhibit relatively similar performance to each other. Notably, the key generation process exhibits significant instability compared to encryption, decryption, or homomorphic operations. This instability arises from the inherent requirement of generating random values until a specific condition is met, contributing to fluctuating performance levels.

Figure 2 shows the performance comparisons of various algorithms in seconds for encryption tasks across different cloud environments, with values depicted in seconds. Damgard-Jurik, Paillier, and Okamoto-Uchiyama were the slowest performers. ElGamal and Exponential ElGamal charts are overlaid, showcasing moderate performance, with RSA slightly trailing behind in this category. Meanwhile, Elliptic Curve ElGamal emerged as the fastest option.

The decryption performance comparison in seconds, shown in Figure 3, revealed Exponential ElGamal as the slowest, ElGamal as the fastest, and other algorithms displaying moderate performance across different cloud environments.

Figure 4 highlights the performance of various algorithms in seconds for homomorphic operations across different cloud environments, with values depicted in seconds. Damgard-Jurik, Goldwasser-Micali, and Paillier were the slowest, while ElGamal, Exponential ElGamal, and Elliptic Curve ElGamal exhibited the fastest performance. Okamoto-Uchiyama and RSA demonstrated moderate performance in homomorphic operations. In practice, just homomorphic opetaion will be performed on the cloud environment and just this operation will be done often.

In evaluating the performance of various tasks across different cloud environments, it becomes evident that the Colab Normal environment emerges as the slowest, contrasting sharply with the remarkable speed demonstrated by Colab TPU2 and Colab TPU High RAM, irrespective of the algorithm employed. The performances of various tasks across different cloud environments are summarized in Table 10.

5.3. Cloud Emission Calculations

For the calculations each cryptographic operation (key generation, encryption, decryption, and homomorphic operation) is timed, and a simplified model is used to estimate its energy consumption and carbon footprint. First, the duration of the operation ($\mathit{duration}$) is combined with a fixed CPU utilization factor ($\mathit{cpu}\text{\_}\mathit{utilization}$) that is set for each type of operation (e.g., 95%, 85%, etc.). Next, the server’s base power consumption ($\mathit{BASE}\text{\_}\mathit{POWER}$) is used to compute the approximate energy consumption ($\mathit{energy}\text{\_}\mathit{kwh}$) in kWh, as follows:

$$\mathrm{energy}\text{\_}\mathrm{kwh}={\displaystyle \frac{\mathrm{BASE}\text{\_}\mathrm{POWER}\times \mathrm{cpu}\text{\_}\mathrm{utilization}\times \mathrm{duration}\left(\mathrm{s}\right)}{3600}}.$$

This quantity is then multiplied by the data center’s Power Usage Effectiveness (PUE) to account for additional overheads, such as cooling and power distribution. Hence,

$$\mathrm{total}\text{\_}\mathrm{energy}=\mathrm{energy}\text{\_}\mathrm{kwh}\times \mathrm{PUE}.$$

Because a fraction of the power may be from renewable sources, the model uses $\mathit{renewable}\text{\_}\mathit{percentage}$ to distinguish between renewable and non-renewable energy consumption. The non-renewable portion ($\mathit{non}\text{\_}\mathit{renewable}\text{\_}\mathit{energy}$) is assigned a CO₂ intensity ($\mathit{grid}\text{\_}\mathit{intensity}$, in gCO₂/kWh) to estimate Scope 2 (purchased electricity) emissions. A small fraction of these non-renewable emissions is assumed to come from backup generators ($\times 0.05$), which constitutes Scope 1. Finally, the model adds Scope 3 emissions by multiplying the total energy by 0.35, representing life-cycle impacts of hardware, cooling systems, and other indirect factors:

$$\mathrm{scope}1=\mathrm{non}\text{\_}\mathrm{renewable}\text{\_}\mathrm{energy}\times \mathrm{grid}\text{\_}\mathrm{intensity}\times 0.05,$$

$$\mathrm{scope}2=\mathrm{non}\text{\_}\mathrm{renewable}\text{\_}\mathrm{energy}\times \mathrm{grid}\text{\_}\mathrm{intensity},$$

$$\mathrm{scope}3=\mathrm{total}\text{\_}\mathrm{energy}\times \mathrm{grid}\text{\_}\mathrm{intensity}\times 0.35.$$

Summing these yields $\mathrm{total}\text{\_}\mathrm{gCO2}$. Such a model serves as a demonstration rather than an accurate reflection of real-world data-center measurements, since all parameters (PUE, grid intensity, CPU usage patterns) are fixed and not derived from live monitoring. Nevertheless, it provides a comparative view of how varying cryptographic operations and key sizes might drive differences in energy consumption and resulting emissions. As mentioned 80-bit and 128-bit calculations made with Colab L4 GPU, otherwise results will be too complex to visualize and represent with those dimensions. The data encompasses multiple data centers categorized as fully carbon-based (DC1-DC3), fully renewable (DC4-DC6), and hybrid (DC7-DC9), executing operations such as key generation (KG), encryption (E), decryption (D), and homomorphic operations (H) for algorithms including RSA, ElGamal, Paillier, Damgard-Jurik, Okamoto-Uchiyama, Goldwasser-Micali, Exponential-ElGamal, and EllipticCurve-ElGamal. Key sizes analyzed are 1024-bit and 160-bit for the 80-bit security level, and 3072-bit and 256-bit for the 128-bit security level, reflecting equivalent security strengths based on computational complexity.

The obtained results underscore the significant influence of data center energy sources on the carbon footprint of cryptographic operations. Fully renewable data centers (DC4–DC6) exhibit markedly lower carbon emissions due to effectively zero Scope 1 and Scope 2 emissions, leaving only Scope 3 (indirect) emissions—primarily from hardware manufacturing and supply chains.For example, RSA key generation at 1024-bit in DC4 produced only 0.15 gCO2, a reduction of approximately 98% when compared to 9.83 gCO2 in the fossil fuel-powered DC1. Fully carbon-based data centers (DC1–DC3), on the other hand, recorded the highest emissions, predominantly driven by Scope 2. This is best illustrated by RSA 3072-bit key generation in DC1, which emitted 400.29 gCO2 in total, 285.92 gCO2 of which can be attributed to electricity sourced from fossil fuels. Hybrid data centers (DC7–DC9) demonstrated emission levels that fell between these extremes. Specifically, RSA 1024-bit key generation in DC7 emitted 2.55 gCO2, significantly below DC1 but considerably above DC4.

In comparing the energy intensity of different cryptographic tasks, key generation emerged as the most resource-intensive for most algorithms, such as RSA, ElGamal, and Paillier. For instance, RSA 1024-bit key generation in DC1 required 0.0117 kWh (9.83 gCO2), whereas encryption and decryption consumed only 0.000186 kWh (0.16 gCO2) and 0.000209 kWh (0.18 gCO2), respectively. Notable exceptions included Exponential-ElGamal and EllipticCurve-ElGamal, where decryption proved more energy-intensive due to the complexity of homomorphic properties and discrete logarithm-based computations. A prime example is Exponential-ElGamal at 1024-bit, for which the decryption phase in DC1 consumed 0.21183 kWh (177.94 gCO2)—over 260 times that of its own key generation.

Regarding algorithmic efficiency, elliptic curve-based methods stood out for their reduced energy consumption during key generation and encryption. For instance, EllipticCurve-ElGamal at 160-bit in DC1 consumed only 0.000388 kWh (0.33 gCO2) for key generation, noticeably lower than RSA 1024-bit’s 0.0117 kWh. However, decryption costs remained high for these elliptic curve algorithms at larger key sizes: EllipticCurve-ElGamal at 256-bit required 0.271057 kWh (227.69 gCO2) in DC1, contrasting sharply with 0.004277 kWh (3.59 gCO2) for RSA 3072-bit decryption. Additionally, scaling security levels from 80-bit to 128-bit produced substantial jumps in both energy usage and emissions. RSA key generation, for instance, increased from 0.0117 kWh (9.83 gCO2) at 1024-bit in DC1 to 0.47653 kWh (400.29 gCO2) at 3072-bit—approximately a 40-fold rise. Similarly, Exponential-ElGamal decryption escalated sixfold, reaching 1.28965 kWh (1083.31 gCO2) at 3072-bit.

Finally, even among data centers sharing the same primary energy source, operational and hardware variations influenced efficiency. An example is RSA 1024-bit key generation in DC2 (carbon-based), which was more efficient at 0.007571 kWh (6.89 gCO2) than the 0.0117 kWh (9.83 gCO2) measured in DC1. These findings collectively highlight the critical role of energy sourcing, algorithm selection, and hardware optimizations in determining the overall carbon footprint and energy consumption of cryptographic processes.

Table 11. Cloud Emission Calculations 80-bit

Data Center Name	Algorithm	Key Size	Operation	Duration (s)	Energy(kWh)	Scope 1 (gCO2)	Scope 2 (gCO2)	Scope 3 (gCO2)	Total (gCO2)
DC1	RSA	1024	KG	0.2274	0.0117	0.35	7.02	2.46	9.83
DC1	RSA	1024	E	0.004	0.000186	0.01	0.11	0.04	0.16
DC1	RSA	1024	D	0.0045	0.000209	0.01	0.13	0.04	0.18
DC1	RSA	1024	H	0	0	0	0	0	0
DC1	ElGamal	1024	KG	0.0275	0.001417	0.04	0.85	0.3	1.19
DC1	ElGamal	1024	E	0.0015	0.000071	0	0.04	0.01	0.06
DC1	ElGamal	1024	D	0.0009	0.00004	0	0.02	0.01	0.03
DC1	ElGamal	1024	H	0	0	0	0	0	0
DC1	Paillier	1024	KG	0.0439	0.002259	0.07	1.36	0.47	1.9
DC1	Paillier	1024	E	0.0149	0.000686	0.02	0.41	0.14	0.58
DC1	Paillier	1024	D	0.0151	0.000695	0.02	0.42	0.15	0.58
DC1	Paillier	1024	H	0	0.000001	0	0	0	0
DC1	Damgard-Jurik	1024	KG	0.0654	0.003365	0.1	2.02	0.71	2.83
DC1	Damgard-Jurik	1024	E	0.0314	0.001445	0.04	0.87	0.3	1.21
DC1	Damgard-Jurik	1024	D	0.0315	0.001452	0.04	0.87	0.3	1.22
DC1	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC1	Okamoto-Uchiyama	1024	KG	0.076	0.003909	0.12	2.35	0.82	3.28
DC1	Okamoto-Uchiyama	1024	E	0.0139	0.000641	0.02	0.38	0.13	0.54
DC1	Okamoto-Uchiyama	1024	D	0.0047	0.000218	0.01	0.13	0.05	0.18
DC1	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC1	Goldwasser-Micali	1024	KG	0.1013	0.005211	0.16	3.13	1.09	4.38
DC1	Goldwasser-Micali	1024	E	0.0004	0.00002	0	0.01	0	0.02
DC1	Goldwasser-Micali	1024	D	0.0228	0.001052	0.03	0.63	0.22	0.88
DC1	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC1	Exponential-ElGamal	1024	KG	0.0158	0.000811	0.02	0.49	0.17	0.68
DC1	Exponential-ElGamal	1024	E	0.0016	0.000074	0	0.04	0.02	0.06
DC1	Exponential-ElGamal	1024	D	4.6008	0.21183	6.35	127.1	44.48	177.94
DC1	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC1	EllipticCurve-ElGamal	160	KG	0.0075	0.000388	0.01	0.23	0.08	0.33
DC1	EllipticCurve-ElGamal	160	E	0.0132	0.000609	0.02	0.37	0.13	0.51
DC1	EllipticCurve-ElGamal	160	D	6.0519	0.27864	8.36	167.18	58.51	234.06
DC1	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC2	RSA	1024	KG	0.1366	0.007571	0.25	4.92	1.72	6.89
DC2	RSA	1024	E	0.004	0.000199	0.01	0.13	0.05	0.18
DC2	RSA	1024	D	0.0045	0.000224	0.01	0.15	0.05	0.2
DC2	RSA	1024	H	0	0	0	0	0	0
DC2	ElGamal	1024	KG	0.0322	0.001783	0.06	1.16	0.41	1.62
DC2	ElGamal	1024	E	0.0015	0.000076	0	0.05	0.02	0.07
DC2	ElGamal	1024	D	0.0009	0.000043	0	0.03	0.01	0.04
DC2	ElGamal	1024	H	0	0	0	0	0	0
DC2	Paillier	1024	KG	0.0798	0.004423	0.14	2.88	1.01	4.03
DC2	Paillier	1024	E	0.0153	0.000758	0.02	0.49	0.17	0.69
DC2	Paillier	1024	D	0.0153	0.000759	0.02	0.49	0.17	0.69
DC2	Paillier	1024	H	0	0.000001	0	0	0	0
DC2	Damgard-Jurik	1024	KG	0.054	0.002993	0.1	1.95	0.68	2.72
DC2	Damgard-Jurik	1024	E	0.0313	0.00155	0.05	1.01	0.35	1.41
DC2	Damgard-Jurik	1024	D	0.0315	0.001562	0.05	1.02	0.36	1.42
DC2	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC2	Okamoto-Uchiyama	1024	KG	0.0765	0.004239	0.14	2.76	0.96	3.86
DC2	Okamoto-Uchiyama	1024	E	0.0137	0.000678	0.02	0.44	0.15	0.62
DC2	Okamoto-Uchiyama	1024	D	0.0046	0.000229	0.01	0.15	0.05	0.21
DC2	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC2	Goldwasser-Micali	1024	KG	0.1009	0.005594	0.18	3.64	1.27	5.09
DC2	Goldwasser-Micali	1024	E	0.0004	0.00002	0	0.01	0	0.02
DC2	Goldwasser-Micali	1024	D	0.0236	0.00117	0.04	0.76	0.27	1.06
DC2	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC2	Exponential-ElGamal	1024	KG	0.0323	0.001792	0.06	1.16	0.41	1.63
DC2	Exponential-ElGamal	1024	E	0.0016	0.000079	0	0.05	0.02	0.07
DC2	Exponential-ElGamal	1024	D	4.5871	0.227444	7.39	147.84	51.74	206.97
DC2	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC2	EllipticCurve-ElGamal	160	KG	0.0071	0.000395	0.01	0.26	0.09	0.36
DC2	EllipticCurve-ElGamal	160	E	0.0118	0.000585	0.02	0.38	0.13	0.53
DC2	EllipticCurve-ElGamal	160	D	6.0367	0.299318	9.73	194.56	68.09	272.38
DC2	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC3	RSA	1024	KG	0.1787	0.010608	0.37	7.43	2.6	10.4
DC3	RSA	1024	E	0.004	0.000213	0.01	0.15	0.05	0.21
DC3	RSA	1024	D	0.0045	0.000241	0.01	0.17	0.06	0.24
DC3	RSA	1024	H	0	0	0	0	0	0
DC3	ElGamal	1024	KG	0.0177	0.001049	0.04	0.73	0.26	1.03
DC3	ElGamal	1024	E	0.0015	0.000081	0	0.06	0.02	0.08
DC3	ElGamal	1024	D	0.0009	0.000047	0	0.03	0.01	0.05
DC3	ElGamal	1024	H	0	0	0	0	0	0
DC3	Paillier	1024	KG	0.0313	0.00186	0.07	1.3	0.46	1.82
DC3	Paillier	1024	E	0.0152	0.000808	0.03	0.57	0.2	0.79
DC3	Paillier	1024	D	0.0152	0.000806	0.03	0.56	0.2	0.79
DC3	Paillier	1024	H	0	0.000001	0	0	0	0
DC3	Damgard-Jurik	1024	KG	0.055	0.003268	0.11	2.29	0.8	3.2
DC3	Damgard-Jurik	1024	E	0.0316	0.001679	0.06	1.18	0.41	1.65
DC3	Damgard-Jurik	1024	D	0.0317	0.001686	0.06	1.18	0.41	1.65
DC3	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC3	Okamoto-Uchiyama	1024	KG	0.0985	0.005846	0.2	4.09	1.43	5.73
DC3	Okamoto-Uchiyama	1024	E	0.0137	0.000727	0.03	0.51	0.18	0.71
DC3	Okamoto-Uchiyama	1024	D	0.0046	0.000245	0.01	0.17	0.06	0.24
DC3	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC3	Goldwasser-Micali	1024	KG	0.0679	0.00403	0.14	2.82	0.99	3.95
DC3	Goldwasser-Micali	1024	E	0.0005	0.000028	0	0.02	0.01	0.03
DC3	Goldwasser-Micali	1024	D	0.0233	0.001239	0.04	0.87	0.3	1.21
DC3	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC3	Exponential-ElGamal	1024	KG	0.0347	0.002061	0.07	1.44	0.51	2.02
DC3	Exponential-ElGamal	1024	E	0.0016	0.000086	0	0.06	0.02	0.08
DC3	Exponential-ElGamal	1024	D	4.6527	0.247173	8.65	173.02	60.56	242.23
DC3	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC3	EllipticCurve-ElGamal	160	KG	0.007	0.000417	0.01	0.29	0.1	0.41
DC3	EllipticCurve-ElGamal	160	E	0.0117	0.000624	0.02	0.44	0.15	0.61
DC3	EllipticCurve-ElGamal	160	D	5.9809	0.317737	11.12	222.42	77.85	311.38
DC3	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC4	RSA	1024	KG	0.0996	0.004336	0	0	0.15	0.15
DC4	RSA	1024	E	0.0041	0.000159	0	0	0.01	0.01
DC4	RSA	1024	D	0.0046	0.000178	0	0	0.01	0.01
DC4	RSA	1024	H	0	0	0	0	0	0
DC4	ElGamal	1024	KG	0.0464	0.002021	0	0	0.07	0.07
DC4	ElGamal	1024	E	0.0016	0.000062	0	0	0	0
DC4	ElGamal	1024	D	0.0009	0.000034	0	0	0	0
DC4	ElGamal	1024	H	0	0	0	0	0	0
DC4	Paillier	1024	KG	0.0755	0.003289	0	0	0.12	0.12
DC4	Paillier	1024	E	0.0151	0.000588	0	0	0.02	0.02
DC4	Paillier	1024	D	0.0152	0.000592	0	0	0.02	0.02
DC4	Paillier	1024	H	0	0.000001	0	0	0	0
DC4	Damgard-Jurik	1024	KG	0.0629	0.002738	0	0	0.1	0.1
DC4	Damgard-Jurik	1024	E	0.0317	0.001234	0	0	0.04	0.04
DC4	Damgard-Jurik	1024	D	0.0317	0.001237	0	0	0.04	0.04
DC4	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC4	Okamoto-Uchiyama	1024	KG	0.0762	0.00332	0	0	0.12	0.12
DC4	Okamoto-Uchiyama	1024	E	0.0139	0.000541	0	0	0.02	0.02
DC4	Okamoto-Uchiyama	1024	D	0.0046	0.00018	0	0	0.01	0.01
DC4	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC4	Goldwasser-Micali	1024	KG	0.086	0.003746	0	0	0.13	0.13
DC4	Goldwasser-Micali	1024	E	0.0004	0.000017	0	0	0	0
DC4	Goldwasser-Micali	1024	D	0.024	0.000937	0	0	0.03	0.03
DC4	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC4	Exponential-ElGamal	1024	KG	0.0267	0.001162	0	0	0.04	0.04
DC4	Exponential-ElGamal	1024	E	0.0017	0.000065	0	0	0	0
DC4	Exponential-ElGamal	1024	D	4.6526	0.181258	0	0	6.34	6.34
DC4	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC4	EllipticCurve-ElGamal	160	KG	0.0071	0.000309	0	0	0.01	0.01
DC4	EllipticCurve-ElGamal	160	E	0.0122	0.000476	0	0	0.02	0.02
DC4	EllipticCurve-ElGamal	160	D	5.9941	0.233522	0	0	8.17	8.17
DC4	EllipticCurve-ElGamal	160	H	0.0001	0.000002	0	0	0	0
DC5	RSA	1024	KG	0.1244	0.00517	0	0	0.09	0.09
DC5	RSA	1024	E	0.004	0.000149	0	0	0	0
DC5	RSA	1024	D	0.0045	0.000169	0	0	0	0
DC5	RSA	1024	H	0	0	0	0	0	0
DC5	ElGamal	1024	KG	0.0266	0.001107	0	0	0.02	0.02
DC5	ElGamal	1024	E	0.0016	0.000058	0	0	0	0
DC5	ElGamal	1024	D	0.0009	0.000033	0	0	0	0
DC5	ElGamal	1024	H	0	0	0	0	0	0
DC5	Paillier	1024	KG	0.061	0.002535	0	0	0.04	0.04
DC5	Paillier	1024	E	0.0153	0.000571	0	0	0.01	0.01
DC5	Paillier	1024	D	0.0154	0.000573	0	0	0.01	0.01
DC5	Paillier	1024	H	0	0.000001	0	0	0	0
DC5	Damgard-Jurik	1024	KG	0.0601	0.002498	0	0	0.04	0.04
DC5	Damgard-Jurik	1024	E	0.0315	0.001171	0	0	0.02	0.02
DC5	Damgard-Jurik	1024	D	0.0316	0.001174	0	0	0.02	0.02
DC5	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC5	Okamoto-Uchiyama	1024	KG	0.0841	0.003495	0	0	0.06	0.06
DC5	Okamoto-Uchiyama	1024	E	0.0136	0.000507	0	0	0.01	0.01
DC5	Okamoto-Uchiyama	1024	D	0.0047	0.000173	0	0	0	0
DC5	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC5	Goldwasser-Micali	1024	KG	0.0559	0.002322	0	0	0.04	0.04
DC5	Goldwasser-Micali	1024	E	0.0004	0.000016	0	0	0	0
DC5	Goldwasser-Micali	1024	D	0.0233	0.000868	0	0	0.02	0.02
DC5	Goldwasser-Micali	1024	H	0.0001	0.000002	0	0	0	0
DC5	Exponential-ElGamal	1024	KG	0.0451	0.001874	0	0	0.03	0.03
DC5	Exponential-ElGamal	1024	E	0.0016	0.000058	0	0	0	0
DC5	Exponential-ElGamal	1024	D	4.5495	0.169185	0	0	2.96	2.96
DC5	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC5	EllipticCurve-ElGamal	160	KG	0.0075	0.000311	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	160	E	0.0117	0.000435	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	160	D	5.9192	0.220121	0	0	3.85	3.85
DC5	EllipticCurve-ElGamal	160	H	0.0001	0.000002	0	0	0	0
DC6	RSA	1024	KG	0.1165	0.005535	0	0	0.23	0.23
DC6	RSA	1024	E	0.0041	0.000173	0	0	0.01	0.01
DC6	RSA	1024	D	0.0046	0.000194	0	0	0.01	0.01
DC6	RSA	1024	H	0	0	0	0	0	0
DC6	ElGamal	1024	KG	0.0459	0.002178	0	0	0.09	0.09
DC6	ElGamal	1024	E	0.0015	0.000065	0	0	0	0
DC6	ElGamal	1024	D	0.0008	0.000036	0	0	0	0
DC6	ElGamal	1024	H	0	0	0	0	0	0
DC6	Paillier	1024	KG	0.0728	0.003459	0	0	0.15	0.15
DC6	Paillier	1024	E	0.015	0.000639	0	0	0.03	0.03
DC6	Paillier	1024	D	0.0151	0.000642	0	0	0.03	0.03
DC6	Paillier	1024	H	0	0.000001	0	0	0	0
DC6	Damgard-Jurik	1024	KG	0.0891	0.004231	0	0	0.18	0.18
DC6	Damgard-Jurik	1024	E	0.0317	0.001349	0	0	0.06	0.06
DC6	Damgard-Jurik	1024	D	0.0316	0.001342	0	0	0.06	0.06
DC6	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC6	Okamoto-Uchiyama	1024	KG	0.1032	0.004902	0	0	0.21	0.21
DC6	Okamoto-Uchiyama	1024	E	0.0139	0.00059	0	0	0.02	0.02
DC6	Okamoto-Uchiyama	1024	D	0.0047	0.000201	0	0	0.01	0.01
DC6	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC6	Goldwasser-Micali	1024	KG	0.089	0.004226	0	0	0.18	0.18
DC6	Goldwasser-Micali	1024	E	0.0004	0.000018	0	0	0	0
DC6	Goldwasser-Micali	1024	D	0.0229	0.000972	0	0	0.04	0.04
DC6	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC6	Exponential-ElGamal	1024	KG	0.044	0.002091	0	0	0.09	0.09
DC6	Exponential-ElGamal	1024	E	0.0015	0.000063	0	0	0	0
DC6	Exponential-ElGamal	1024	D	4.4484	0.189058	0	0	7.94	7.94
DC6	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC6	EllipticCurve-ElGamal	160	KG	0.0074	0.000351	0	0	0.01	0.01
DC6	EllipticCurve-ElGamal	160	E	0.0119	0.000504	0	0	0.02	0.02
DC6	EllipticCurve-ElGamal	160	D	5.8188	0.247301	0	0	10.39	10.39
DC6	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC7	RSA	1024	KG	0.2148	0.011051	0.07	1.33	1.16	2.55
DC7	RSA	1024	E	0.004	0.000186	0	0.02	0.02	0.04
DC7	RSA	1024	D	0.0046	0.00021	0	0.03	0.02	0.05
DC7	RSA	1024	H	0	0	0	0	0	0
DC7	ElGamal	1024	KG	0.0535	0.002751	0.02	0.33	0.29	0.64
DC7	ElGamal	1024	E	0.0015	0.000071	0	0.01	0.01	0.02
DC7	ElGamal	1024	D	0.0008	0.000039	0	0	0	0.01
DC7	ElGamal	1024	H	0	0	0	0	0	0
DC7	Paillier	1024	KG	0.0936	0.004818	0.03	0.58	0.51	1.11
DC7	Paillier	1024	E	0.0152	0.000698	0	0.08	0.07	0.16
DC7	Paillier	1024	D	0.0152	0.000702	0	0.08	0.07	0.16
DC7	Paillier	1024	H	0	0.000001	0	0	0	0
DC7	Damgard-Jurik	1024	KG	0.0598	0.003079	0.02	0.37	0.32	0.71
DC7	Damgard-Jurik	1024	E	0.0312	0.001437	0.01	0.17	0.15	0.33
DC7	Damgard-Jurik	1024	D	0.0314	0.001446	0.01	0.17	0.15	0.33
DC7	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC7	Okamoto-Uchiyama	1024	KG	0.112	0.005763	0.03	0.69	0.61	1.33
DC7	Okamoto-Uchiyama	1024	E	0.0139	0.00064	0	0.08	0.07	0.15
DC7	Okamoto-Uchiyama	1024	D	0.0047	0.000215	0	0.03	0.02	0.05
DC7	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC7	Goldwasser-Micali	1024	KG	0.0985	0.00507	0.03	0.61	0.53	1.17
DC7	Goldwasser-Micali	1024	E	0.0004	0.000019	0	0	0	0
DC7	Goldwasser-Micali	1024	D	0.0234	0.001079	0.01	0.13	0.11	0.25
DC7	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC7	Exponential-ElGamal	1024	KG	0.0726	0.003735	0.02	0.45	0.39	0.86
DC7	Exponential-ElGamal	1024	E	0.0016	0.000073	0	0.01	0.01	0.02
DC7	Exponential-ElGamal	1024	D	4.5853	0.211113	1.27	25.33	22.17	48.77
DC7	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC7	EllipticCurve-ElGamal	160	KG	0.0072	0.000372	0	0.04	0.04	0.09
DC7	EllipticCurve-ElGamal	160	E	0.0119	0.000547	0	0.07	0.06	0.13
DC7	EllipticCurve-ElGamal	160	D	5.893	0.271324	1.63	32.56	28.49	62.68
DC7	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC8	RSA	1024	KG	0.3302	0.015684	0.07	1.32	1.54	2.92
DC8	RSA	1024	E	0.0041	0.000175	0	0.01	0.02	0.03
DC8	RSA	1024	D	0.0046	0.000196	0	0.02	0.02	0.04
DC8	RSA	1024	H	0	0	0	0	0	0
DC8	ElGamal	1024	KG	0.0425	0.002021	0.01	0.17	0.2	0.38
DC8	ElGamal	1024	E	0.0016	0.000066	0	0.01	0.01	0.01
DC8	ElGamal	1024	D	0.0009	0.000037	0	0	0	0.01
DC8	ElGamal	1024	H	0	0	0	0	0	0
DC8	Paillier	1024	KG	0.0767	0.003641	0.02	0.31	0.36	0.68
DC8	Paillier	1024	E	0.0151	0.000642	0	0.05	0.06	0.12
DC8	Paillier	1024	D	0.0152	0.000647	0	0.05	0.06	0.12
DC8	Paillier	1024	H	0	0.000001	0	0	0	0
DC8	Damgard-Jurik	1024	KG	0.0915	0.004345	0.02	0.37	0.43	0.81
DC8	Damgard-Jurik	1024	E	0.0311	0.001324	0.01	0.11	0.13	0.25
DC8	Damgard-Jurik	1024	D	0.0313	0.001329	0.01	0.11	0.13	0.25
DC8	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC8	Okamoto-Uchiyama	1024	KG	0.1088	0.005169	0.02	0.43	0.51	0.96
DC8	Okamoto-Uchiyama	1024	E	0.0138	0.000586	0	0.05	0.06	0.11
DC8	Okamoto-Uchiyama	1024	D	0.0047	0.0002	0	0.02	0.02	0.04
DC8	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC8	Goldwasser-Micali	1024	KG	0.0693	0.003291	0.01	0.28	0.32	0.61
DC8	Goldwasser-Micali	1024	E	0.0004	0.000018	0	0	0	0
DC8	Goldwasser-Micali	1024	D	0.0234	0.000994	0	0.08	0.1	0.19
DC8	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC8	Exponential-ElGamal	1024	KG	0.0319	0.001513	0.01	0.13	0.15	0.28
DC8	Exponential-ElGamal	1024	E	0.0015	0.000066	0	0.01	0.01	0.01
DC8	Exponential-ElGamal	1024	D	4.5124	0.191777	0.81	16.11	18.79	35.71
DC8	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC8	EllipticCurve-ElGamal	160	KG	0.0072	0.000344	0	0.03	0.03	0.06
DC8	EllipticCurve-ElGamal	160	E	0.0124	0.000529	0	0.04	0.05	0.1
DC8	EllipticCurve-ElGamal	160	D	6.0368	0.256565	1.08	21.55	25.14	47.77
DC8	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC9	RSA	1024	KG	0.117	0.005556	0.01	0.28	0.49	0.78
DC9	RSA	1024	E	0.004	0.000169	0	0.01	0.01	0.02
DC9	RSA	1024	D	0.0045	0.000191	0	0.01	0.02	0.03
DC9	RSA	1024	H	0	0	0	0	0	0
DC9	ElGamal	1024	KG	0.0338	0.001607	0	0.08	0.14	0.23
DC9	ElGamal	1024	E	0.0016	0.000067	0	0	0.01	0.01
DC9	ElGamal	1024	D	0.0009	0.000037	0	0	0	0.01
DC9	ElGamal	1024	H	0	0	0	0	0	0
DC9	Paillier	1024	KG	0.0625	0.00297	0.01	0.15	0.26	0.42
DC9	Paillier	1024	E	0.0152	0.000646	0	0.03	0.06	0.09
DC9	Paillier	1024	D	0.0153	0.000649	0	0.03	0.06	0.09
DC9	Paillier	1024	H	0	0.000001	0	0	0	0
DC9	Damgard-Jurik	1024	KG	0.0823	0.00391	0.01	0.2	0.34	0.55
DC9	Damgard-Jurik	1024	E	0.0317	0.001345	0	0.07	0.12	0.19
DC9	Damgard-Jurik	1024	D	0.0319	0.001357	0	0.07	0.12	0.19
DC9	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC9	Okamoto-Uchiyama	1024	KG	0.1079	0.005126	0.01	0.26	0.45	0.72
DC9	Okamoto-Uchiyama	1024	E	0.0136	0.000576	0	0.03	0.05	0.08
DC9	Okamoto-Uchiyama	1024	D	0.0047	0.0002	0	0.01	0.02	0.03
DC9	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC9	Goldwasser-Micali	1024	KG	0.089	0.004229	0.01	0.21	0.37	0.59
DC9	Goldwasser-Micali	1024	E	0.0004	0.000017	0	0	0	0
DC9	Goldwasser-Micali	1024	D	0.023	0.000976	0	0.05	0.09	0.14
DC9	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC9	Exponential-ElGamal	1024	KG	0.0276	0.001313	0	0.07	0.11	0.18
DC9	Exponential-ElGamal	1024	E	0.0016	0.000068	0	0	0.01	0.01
DC9	Exponential-ElGamal	1024	D	4.5931	0.195208	0.49	9.76	17.08	27.33
DC9	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC9	EllipticCurve-ElGamal	160	KG	0.0072	0.000343	0	0.02	0.03	0.05
DC9	EllipticCurve-ElGamal	160	E	0.0119	0.000508	0	0.03	0.04	0.07
DC9	EllipticCurve-ElGamal	160	D	5.9812	0.254203	0.64	12.71	22.24	35.59
DC9	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC10	RSA	1024	KG	0.1144	0.004982	0	0.1	0.35	0.45
DC10	RSA	1024	E	0.0041	0.00016	0	0	0.01	0.01
DC10	RSA	1024	D	0.0047	0.000182	0	0	0.01	0.02
DC10	RSA	1024	H	0	0	0	0	0	0
DC10	ElGamal	1024	KG	0.0425	0.001852	0	0.04	0.13	0.17
DC10	ElGamal	1024	E	0.0016	0.000061	0	0	0	0.01
DC10	ElGamal	1024	D	0.0008	0.000033	0	0	0	0
DC10	ElGamal	1024	H	0	0	0	0	0	0
DC10	Paillier	1024	KG	0.0593	0.002584	0	0.05	0.18	0.24
DC10	Paillier	1024	E	0.0153	0.000597	0	0.01	0.04	0.05
DC10	Paillier	1024	D	0.0155	0.000604	0	0.01	0.04	0.05
DC10	Paillier	1024	H	0	0.000001	0	0	0	0
DC10	Damgard-Jurik	1024	KG	0.0984	0.004283	0	0.09	0.3	0.39
DC10	Damgard-Jurik	1024	E	0.0312	0.001217	0	0.02	0.09	0.11
DC10	Damgard-Jurik	1024	D	0.0315	0.001228	0	0.02	0.09	0.11
DC10	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC10	Okamoto-Uchiyama	1024	KG	0.0809	0.003524	0	0.07	0.25	0.32
DC10	Okamoto-Uchiyama	1024	E	0.0138	0.000538	0	0.01	0.04	0.05
DC10	Okamoto-Uchiyama	1024	D	0.0048	0.000189	0	0	0.01	0.02
DC10	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC10	Goldwasser-Micali	1024	KG	0.067	0.002919	0	0.06	0.2	0.27
DC10	Goldwasser-Micali	1024	E	0.0004	0.000016	0	0	0	0
DC10	Goldwasser-Micali	1024	D	0.0233	0.000906	0	0.02	0.06	0.08
DC10	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC10	Exponential-ElGamal	1024	KG	0.0258	0.001123	0	0.02	0.08	0.1
DC10	Exponential-ElGamal	1024	E	0.0016	0.000064	0	0	0	0.01
DC10	Exponential-ElGamal	1024	D	4.5842	0.178594	0.18	3.57	12.5	16.25
DC10	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC10	EllipticCurve-ElGamal	160	KG	0.0071	0.00031	0	0.01	0.02	0.03
DC10	EllipticCurve-ElGamal	160	E	0.0117	0.000455	0	0.01	0.03	0.04
DC10	EllipticCurve-ElGamal	160	D	5.8008	0.22599	0.23	4.52	15.82	20.57
DC10	EllipticCurve-ElGamal	160	H	0.0001	0.000002	0	0	0	0

Table 11. Cloud Emission Calculations 80-bit

Data Center Name	Algorithm	Key Size	Operation	Duration (s)	Energy(kWh)	Scope 1 (gCO2)	Scope 2 (gCO2)	Scope 3 (gCO2)	Total (gCO2)
DC1	RSA	1024	KG	0.2274	0.0117	0.35	7.02	2.46	9.83
DC1	RSA	1024	E	0.004	0.000186	0.01	0.11	0.04	0.16
DC1	RSA	1024	D	0.0045	0.000209	0.01	0.13	0.04	0.18
DC1	RSA	1024	H	0	0	0	0	0	0
DC1	ElGamal	1024	KG	0.0275	0.001417	0.04	0.85	0.3	1.19
DC1	ElGamal	1024	E	0.0015	0.000071	0	0.04	0.01	0.06
DC1	ElGamal	1024	D	0.0009	0.00004	0	0.02	0.01	0.03
DC1	ElGamal	1024	H	0	0	0	0	0	0
DC1	Paillier	1024	KG	0.0439	0.002259	0.07	1.36	0.47	1.9
DC1	Paillier	1024	E	0.0149	0.000686	0.02	0.41	0.14	0.58
DC1	Paillier	1024	D	0.0151	0.000695	0.02	0.42	0.15	0.58
DC1	Paillier	1024	H	0	0.000001	0	0	0	0
DC1	Damgard-Jurik	1024	KG	0.0654	0.003365	0.1	2.02	0.71	2.83
DC1	Damgard-Jurik	1024	E	0.0314	0.001445	0.04	0.87	0.3	1.21
DC1	Damgard-Jurik	1024	D	0.0315	0.001452	0.04	0.87	0.3	1.22
DC1	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC1	Okamoto-Uchiyama	1024	KG	0.076	0.003909	0.12	2.35	0.82	3.28
DC1	Okamoto-Uchiyama	1024	E	0.0139	0.000641	0.02	0.38	0.13	0.54
DC1	Okamoto-Uchiyama	1024	D	0.0047	0.000218	0.01	0.13	0.05	0.18
DC1	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC1	Goldwasser-Micali	1024	KG	0.1013	0.005211	0.16	3.13	1.09	4.38
DC1	Goldwasser-Micali	1024	E	0.0004	0.00002	0	0.01	0	0.02
DC1	Goldwasser-Micali	1024	D	0.0228	0.001052	0.03	0.63	0.22	0.88
DC1	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC1	Exponential-ElGamal	1024	KG	0.0158	0.000811	0.02	0.49	0.17	0.68
DC1	Exponential-ElGamal	1024	E	0.0016	0.000074	0	0.04	0.02	0.06
DC1	Exponential-ElGamal	1024	D	4.6008	0.21183	6.35	127.1	44.48	177.94
DC1	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC1	EllipticCurve-ElGamal	160	KG	0.0075	0.000388	0.01	0.23	0.08	0.33
DC1	EllipticCurve-ElGamal	160	E	0.0132	0.000609	0.02	0.37	0.13	0.51
DC1	EllipticCurve-ElGamal	160	D	6.0519	0.27864	8.36	167.18	58.51	234.06
DC1	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC2	RSA	1024	KG	0.1366	0.007571	0.25	4.92	1.72	6.89
DC2	RSA	1024	E	0.004	0.000199	0.01	0.13	0.05	0.18
DC2	RSA	1024	D	0.0045	0.000224	0.01	0.15	0.05	0.2
DC2	RSA	1024	H	0	0	0	0	0	0
DC2	ElGamal	1024	KG	0.0322	0.001783	0.06	1.16	0.41	1.62
DC2	ElGamal	1024	E	0.0015	0.000076	0	0.05	0.02	0.07
DC2	ElGamal	1024	D	0.0009	0.000043	0	0.03	0.01	0.04
DC2	ElGamal	1024	H	0	0	0	0	0	0
DC2	Paillier	1024	KG	0.0798	0.004423	0.14	2.88	1.01	4.03
DC2	Paillier	1024	E	0.0153	0.000758	0.02	0.49	0.17	0.69
DC2	Paillier	1024	D	0.0153	0.000759	0.02	0.49	0.17	0.69
DC2	Paillier	1024	H	0	0.000001	0	0	0	0
DC2	Damgard-Jurik	1024	KG	0.054	0.002993	0.1	1.95	0.68	2.72
DC2	Damgard-Jurik	1024	E	0.0313	0.00155	0.05	1.01	0.35	1.41
DC2	Damgard-Jurik	1024	D	0.0315	0.001562	0.05	1.02	0.36	1.42
DC2	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC2	Okamoto-Uchiyama	1024	KG	0.0765	0.004239	0.14	2.76	0.96	3.86
DC2	Okamoto-Uchiyama	1024	E	0.0137	0.000678	0.02	0.44	0.15	0.62
DC2	Okamoto-Uchiyama	1024	D	0.0046	0.000229	0.01	0.15	0.05	0.21
DC2	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC2	Goldwasser-Micali	1024	KG	0.1009	0.005594	0.18	3.64	1.27	5.09
DC2	Goldwasser-Micali	1024	E	0.0004	0.00002	0	0.01	0	0.02
DC2	Goldwasser-Micali	1024	D	0.0236	0.00117	0.04	0.76	0.27	1.06
DC2	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC2	Exponential-ElGamal	1024	KG	0.0323	0.001792	0.06	1.16	0.41	1.63
DC2	Exponential-ElGamal	1024	E	0.0016	0.000079	0	0.05	0.02	0.07
DC2	Exponential-ElGamal	1024	D	4.5871	0.227444	7.39	147.84	51.74	206.97
DC2	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC2	EllipticCurve-ElGamal	160	KG	0.0071	0.000395	0.01	0.26	0.09	0.36
DC2	EllipticCurve-ElGamal	160	E	0.0118	0.000585	0.02	0.38	0.13	0.53
DC2	EllipticCurve-ElGamal	160	D	6.0367	0.299318	9.73	194.56	68.09	272.38
DC2	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC3	RSA	1024	KG	0.1787	0.010608	0.37	7.43	2.6	10.4
DC3	RSA	1024	E	0.004	0.000213	0.01	0.15	0.05	0.21
DC3	RSA	1024	D	0.0045	0.000241	0.01	0.17	0.06	0.24
DC3	RSA	1024	H	0	0	0	0	0	0
DC3	ElGamal	1024	KG	0.0177	0.001049	0.04	0.73	0.26	1.03
DC3	ElGamal	1024	E	0.0015	0.000081	0	0.06	0.02	0.08
DC3	ElGamal	1024	D	0.0009	0.000047	0	0.03	0.01	0.05
DC3	ElGamal	1024	H	0	0	0	0	0	0
DC3	Paillier	1024	KG	0.0313	0.00186	0.07	1.3	0.46	1.82
DC3	Paillier	1024	E	0.0152	0.000808	0.03	0.57	0.2	0.79
DC3	Paillier	1024	D	0.0152	0.000806	0.03	0.56	0.2	0.79
DC3	Paillier	1024	H	0	0.000001	0	0	0	0
DC3	Damgard-Jurik	1024	KG	0.055	0.003268	0.11	2.29	0.8	3.2
DC3	Damgard-Jurik	1024	E	0.0316	0.001679	0.06	1.18	0.41	1.65
DC3	Damgard-Jurik	1024	D	0.0317	0.001686	0.06	1.18	0.41	1.65
DC3	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC3	Okamoto-Uchiyama	1024	KG	0.0985	0.005846	0.2	4.09	1.43	5.73
DC3	Okamoto-Uchiyama	1024	E	0.0137	0.000727	0.03	0.51	0.18	0.71
DC3	Okamoto-Uchiyama	1024	D	0.0046	0.000245	0.01	0.17	0.06	0.24
DC3	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC3	Goldwasser-Micali	1024	KG	0.0679	0.00403	0.14	2.82	0.99	3.95
DC3	Goldwasser-Micali	1024	E	0.0005	0.000028	0	0.02	0.01	0.03
DC3	Goldwasser-Micali	1024	D	0.0233	0.001239	0.04	0.87	0.3	1.21
DC3	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC3	Exponential-ElGamal	1024	KG	0.0347	0.002061	0.07	1.44	0.51	2.02
DC3	Exponential-ElGamal	1024	E	0.0016	0.000086	0	0.06	0.02	0.08
DC3	Exponential-ElGamal	1024	D	4.6527	0.247173	8.65	173.02	60.56	242.23
DC3	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC3	EllipticCurve-ElGamal	160	KG	0.007	0.000417	0.01	0.29	0.1	0.41
DC3	EllipticCurve-ElGamal	160	E	0.0117	0.000624	0.02	0.44	0.15	0.61
DC3	EllipticCurve-ElGamal	160	D	5.9809	0.317737	11.12	222.42	77.85	311.38
DC3	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC4	RSA	1024	KG	0.0996	0.004336	0	0	0.15	0.15
DC4	RSA	1024	E	0.0041	0.000159	0	0	0.01	0.01
DC4	RSA	1024	D	0.0046	0.000178	0	0	0.01	0.01
DC4	RSA	1024	H	0	0	0	0	0	0
DC4	ElGamal	1024	KG	0.0464	0.002021	0	0	0.07	0.07
DC4	ElGamal	1024	E	0.0016	0.000062	0	0	0	0
DC4	ElGamal	1024	D	0.0009	0.000034	0	0	0	0
DC4	ElGamal	1024	H	0	0	0	0	0	0
DC4	Paillier	1024	KG	0.0755	0.003289	0	0	0.12	0.12
DC4	Paillier	1024	E	0.0151	0.000588	0	0	0.02	0.02
DC4	Paillier	1024	D	0.0152	0.000592	0	0	0.02	0.02
DC4	Paillier	1024	H	0	0.000001	0	0	0	0
DC4	Damgard-Jurik	1024	KG	0.0629	0.002738	0	0	0.1	0.1
DC4	Damgard-Jurik	1024	E	0.0317	0.001234	0	0	0.04	0.04
DC4	Damgard-Jurik	1024	D	0.0317	0.001237	0	0	0.04	0.04
DC4	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC4	Okamoto-Uchiyama	1024	KG	0.0762	0.00332	0	0	0.12	0.12
DC4	Okamoto-Uchiyama	1024	E	0.0139	0.000541	0	0	0.02	0.02
DC4	Okamoto-Uchiyama	1024	D	0.0046	0.00018	0	0	0.01	0.01
DC4	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC4	Goldwasser-Micali	1024	KG	0.086	0.003746	0	0	0.13	0.13
DC4	Goldwasser-Micali	1024	E	0.0004	0.000017	0	0	0	0
DC4	Goldwasser-Micali	1024	D	0.024	0.000937	0	0	0.03	0.03
DC4	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC4	Exponential-ElGamal	1024	KG	0.0267	0.001162	0	0	0.04	0.04
DC4	Exponential-ElGamal	1024	E	0.0017	0.000065	0	0	0	0
DC4	Exponential-ElGamal	1024	D	4.6526	0.181258	0	0	6.34	6.34
DC4	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC4	EllipticCurve-ElGamal	160	KG	0.0071	0.000309	0	0	0.01	0.01
DC4	EllipticCurve-ElGamal	160	E	0.0122	0.000476	0	0	0.02	0.02
DC4	EllipticCurve-ElGamal	160	D	5.9941	0.233522	0	0	8.17	8.17
DC4	EllipticCurve-ElGamal	160	H	0.0001	0.000002	0	0	0	0
DC5	RSA	1024	KG	0.1244	0.00517	0	0	0.09	0.09
DC5	RSA	1024	E	0.004	0.000149	0	0	0	0
DC5	RSA	1024	D	0.0045	0.000169	0	0	0	0
DC5	RSA	1024	H	0	0	0	0	0	0
DC5	ElGamal	1024	KG	0.0266	0.001107	0	0	0.02	0.02
DC5	ElGamal	1024	E	0.0016	0.000058	0	0	0	0
DC5	ElGamal	1024	D	0.0009	0.000033	0	0	0	0
DC5	ElGamal	1024	H	0	0	0	0	0	0
DC5	Paillier	1024	KG	0.061	0.002535	0	0	0.04	0.04
DC5	Paillier	1024	E	0.0153	0.000571	0	0	0.01	0.01
DC5	Paillier	1024	D	0.0154	0.000573	0	0	0.01	0.01
DC5	Paillier	1024	H	0	0.000001	0	0	0	0
DC5	Damgard-Jurik	1024	KG	0.0601	0.002498	0	0	0.04	0.04
DC5	Damgard-Jurik	1024	E	0.0315	0.001171	0	0	0.02	0.02
DC5	Damgard-Jurik	1024	D	0.0316	0.001174	0	0	0.02	0.02
DC5	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC5	Okamoto-Uchiyama	1024	KG	0.0841	0.003495	0	0	0.06	0.06
DC5	Okamoto-Uchiyama	1024	E	0.0136	0.000507	0	0	0.01	0.01
DC5	Okamoto-Uchiyama	1024	D	0.0047	0.000173	0	0	0	0
DC5	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC5	Goldwasser-Micali	1024	KG	0.0559	0.002322	0	0	0.04	0.04
DC5	Goldwasser-Micali	1024	E	0.0004	0.000016	0	0	0	0
DC5	Goldwasser-Micali	1024	D	0.0233	0.000868	0	0	0.02	0.02
DC5	Goldwasser-Micali	1024	H	0.0001	0.000002	0	0	0	0
DC5	Exponential-ElGamal	1024	KG	0.0451	0.001874	0	0	0.03	0.03
DC5	Exponential-ElGamal	1024	E	0.0016	0.000058	0	0	0	0
DC5	Exponential-ElGamal	1024	D	4.5495	0.169185	0	0	2.96	2.96
DC5	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC5	EllipticCurve-ElGamal	160	KG	0.0075	0.000311	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	160	E	0.0117	0.000435	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	160	D	5.9192	0.220121	0	0	3.85	3.85
DC5	EllipticCurve-ElGamal	160	H	0.0001	0.000002	0	0	0	0
DC6	RSA	1024	KG	0.1165	0.005535	0	0	0.23	0.23
DC6	RSA	1024	E	0.0041	0.000173	0	0	0.01	0.01
DC6	RSA	1024	D	0.0046	0.000194	0	0	0.01	0.01
DC6	RSA	1024	H	0	0	0	0	0	0
DC6	ElGamal	1024	KG	0.0459	0.002178	0	0	0.09	0.09
DC6	ElGamal	1024	E	0.0015	0.000065	0	0	0	0
DC6	ElGamal	1024	D	0.0008	0.000036	0	0	0	0
DC6	ElGamal	1024	H	0	0	0	0	0	0
DC6	Paillier	1024	KG	0.0728	0.003459	0	0	0.15	0.15
DC6	Paillier	1024	E	0.015	0.000639	0	0	0.03	0.03
DC6	Paillier	1024	D	0.0151	0.000642	0	0	0.03	0.03
DC6	Paillier	1024	H	0	0.000001	0	0	0	0
DC6	Damgard-Jurik	1024	KG	0.0891	0.004231	0	0	0.18	0.18
DC6	Damgard-Jurik	1024	E	0.0317	0.001349	0	0	0.06	0.06
DC6	Damgard-Jurik	1024	D	0.0316	0.001342	0	0	0.06	0.06
DC6	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC6	Okamoto-Uchiyama	1024	KG	0.1032	0.004902	0	0	0.21	0.21
DC6	Okamoto-Uchiyama	1024	E	0.0139	0.00059	0	0	0.02	0.02
DC6	Okamoto-Uchiyama	1024	D	0.0047	0.000201	0	0	0.01	0.01
DC6	Okamoto-Uchiyama	1024	H	0	0.000001	0	0	0	0
DC6	Goldwasser-Micali	1024	KG	0.089	0.004226	0	0	0.18	0.18
DC6	Goldwasser-Micali	1024	E	0.0004	0.000018	0	0	0	0
DC6	Goldwasser-Micali	1024	D	0.0229	0.000972	0	0	0.04	0.04
DC6	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC6	Exponential-ElGamal	1024	KG	0.044	0.002091	0	0	0.09	0.09
DC6	Exponential-ElGamal	1024	E	0.0015	0.000063	0	0	0	0
DC6	Exponential-ElGamal	1024	D	4.4484	0.189058	0	0	7.94	7.94
DC6	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC6	EllipticCurve-ElGamal	160	KG	0.0074	0.000351	0	0	0.01	0.01
DC6	EllipticCurve-ElGamal	160	E	0.0119	0.000504	0	0	0.02	0.02
DC6	EllipticCurve-ElGamal	160	D	5.8188	0.247301	0	0	10.39	10.39
DC6	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC7	RSA	1024	KG	0.2148	0.011051	0.07	1.33	1.16	2.55
DC7	RSA	1024	E	0.004	0.000186	0	0.02	0.02	0.04
DC7	RSA	1024	D	0.0046	0.00021	0	0.03	0.02	0.05
DC7	RSA	1024	H	0	0	0	0	0	0
DC7	ElGamal	1024	KG	0.0535	0.002751	0.02	0.33	0.29	0.64
DC7	ElGamal	1024	E	0.0015	0.000071	0	0.01	0.01	0.02
DC7	ElGamal	1024	D	0.0008	0.000039	0	0	0	0.01
DC7	ElGamal	1024	H	0	0	0	0	0	0
DC7	Paillier	1024	KG	0.0936	0.004818	0.03	0.58	0.51	1.11
DC7	Paillier	1024	E	0.0152	0.000698	0	0.08	0.07	0.16
DC7	Paillier	1024	D	0.0152	0.000702	0	0.08	0.07	0.16
DC7	Paillier	1024	H	0	0.000001	0	0	0	0
DC7	Damgard-Jurik	1024	KG	0.0598	0.003079	0.02	0.37	0.32	0.71
DC7	Damgard-Jurik	1024	E	0.0312	0.001437	0.01	0.17	0.15	0.33
DC7	Damgard-Jurik	1024	D	0.0314	0.001446	0.01	0.17	0.15	0.33
DC7	Damgard-Jurik	1024	H	0	0.000002	0	0	0	0
DC7	Okamoto-Uchiyama	1024	KG	0.112	0.005763	0.03	0.69	0.61	1.33
DC7	Okamoto-Uchiyama	1024	E	0.0139	0.00064	0	0.08	0.07	0.15
DC7	Okamoto-Uchiyama	1024	D	0.0047	0.000215	0	0.03	0.02	0.05
DC7	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC7	Goldwasser-Micali	1024	KG	0.0985	0.00507	0.03	0.61	0.53	1.17
DC7	Goldwasser-Micali	1024	E	0.0004	0.000019	0	0	0	0
DC7	Goldwasser-Micali	1024	D	0.0234	0.001079	0.01	0.13	0.11	0.25
DC7	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC7	Exponential-ElGamal	1024	KG	0.0726	0.003735	0.02	0.45	0.39	0.86
DC7	Exponential-ElGamal	1024	E	0.0016	0.000073	0	0.01	0.01	0.02
DC7	Exponential-ElGamal	1024	D	4.5853	0.211113	1.27	25.33	22.17	48.77
DC7	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC7	EllipticCurve-ElGamal	160	KG	0.0072	0.000372	0	0.04	0.04	0.09
DC7	EllipticCurve-ElGamal	160	E	0.0119	0.000547	0	0.07	0.06	0.13
DC7	EllipticCurve-ElGamal	160	D	5.893	0.271324	1.63	32.56	28.49	62.68
DC7	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC8	RSA	1024	KG	0.3302	0.015684	0.07	1.32	1.54	2.92
DC8	RSA	1024	E	0.0041	0.000175	0	0.01	0.02	0.03
DC8	RSA	1024	D	0.0046	0.000196	0	0.02	0.02	0.04
DC8	RSA	1024	H	0	0	0	0	0	0
DC8	ElGamal	1024	KG	0.0425	0.002021	0.01	0.17	0.2	0.38
DC8	ElGamal	1024	E	0.0016	0.000066	0	0.01	0.01	0.01
DC8	ElGamal	1024	D	0.0009	0.000037	0	0	0	0.01
DC8	ElGamal	1024	H	0	0	0	0	0	0
DC8	Paillier	1024	KG	0.0767	0.003641	0.02	0.31	0.36	0.68
DC8	Paillier	1024	E	0.0151	0.000642	0	0.05	0.06	0.12
DC8	Paillier	1024	D	0.0152	0.000647	0	0.05	0.06	0.12
DC8	Paillier	1024	H	0	0.000001	0	0	0	0
DC8	Damgard-Jurik	1024	KG	0.0915	0.004345	0.02	0.37	0.43	0.81
DC8	Damgard-Jurik	1024	E	0.0311	0.001324	0.01	0.11	0.13	0.25
DC8	Damgard-Jurik	1024	D	0.0313	0.001329	0.01	0.11	0.13	0.25
DC8	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC8	Okamoto-Uchiyama	1024	KG	0.1088	0.005169	0.02	0.43	0.51	0.96
DC8	Okamoto-Uchiyama	1024	E	0.0138	0.000586	0	0.05	0.06	0.11
DC8	Okamoto-Uchiyama	1024	D	0.0047	0.0002	0	0.02	0.02	0.04
DC8	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC8	Goldwasser-Micali	1024	KG	0.0693	0.003291	0.01	0.28	0.32	0.61
DC8	Goldwasser-Micali	1024	E	0.0004	0.000018	0	0	0	0
DC8	Goldwasser-Micali	1024	D	0.0234	0.000994	0	0.08	0.1	0.19
DC8	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC8	Exponential-ElGamal	1024	KG	0.0319	0.001513	0.01	0.13	0.15	0.28
DC8	Exponential-ElGamal	1024	E	0.0015	0.000066	0	0.01	0.01	0.01
DC8	Exponential-ElGamal	1024	D	4.5124	0.191777	0.81	16.11	18.79	35.71
DC8	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC8	EllipticCurve-ElGamal	160	KG	0.0072	0.000344	0	0.03	0.03	0.06
DC8	EllipticCurve-ElGamal	160	E	0.0124	0.000529	0	0.04	0.05	0.1
DC8	EllipticCurve-ElGamal	160	D	6.0368	0.256565	1.08	21.55	25.14	47.77
DC8	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC9	RSA	1024	KG	0.117	0.005556	0.01	0.28	0.49	0.78
DC9	RSA	1024	E	0.004	0.000169	0	0.01	0.01	0.02
DC9	RSA	1024	D	0.0045	0.000191	0	0.01	0.02	0.03
DC9	RSA	1024	H	0	0	0	0	0	0
DC9	ElGamal	1024	KG	0.0338	0.001607	0	0.08	0.14	0.23
DC9	ElGamal	1024	E	0.0016	0.000067	0	0	0.01	0.01
DC9	ElGamal	1024	D	0.0009	0.000037	0	0	0	0.01
DC9	ElGamal	1024	H	0	0	0	0	0	0
DC9	Paillier	1024	KG	0.0625	0.00297	0.01	0.15	0.26	0.42
DC9	Paillier	1024	E	0.0152	0.000646	0	0.03	0.06	0.09
DC9	Paillier	1024	D	0.0153	0.000649	0	0.03	0.06	0.09
DC9	Paillier	1024	H	0	0.000001	0	0	0	0
DC9	Damgard-Jurik	1024	KG	0.0823	0.00391	0.01	0.2	0.34	0.55
DC9	Damgard-Jurik	1024	E	0.0317	0.001345	0	0.07	0.12	0.19
DC9	Damgard-Jurik	1024	D	0.0319	0.001357	0	0.07	0.12	0.19
DC9	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC9	Okamoto-Uchiyama	1024	KG	0.1079	0.005126	0.01	0.26	0.45	0.72
DC9	Okamoto-Uchiyama	1024	E	0.0136	0.000576	0	0.03	0.05	0.08
DC9	Okamoto-Uchiyama	1024	D	0.0047	0.0002	0	0.01	0.02	0.03
DC9	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC9	Goldwasser-Micali	1024	KG	0.089	0.004229	0.01	0.21	0.37	0.59
DC9	Goldwasser-Micali	1024	E	0.0004	0.000017	0	0	0	0
DC9	Goldwasser-Micali	1024	D	0.023	0.000976	0	0.05	0.09	0.14
DC9	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC9	Exponential-ElGamal	1024	KG	0.0276	0.001313	0	0.07	0.11	0.18
DC9	Exponential-ElGamal	1024	E	0.0016	0.000068	0	0	0.01	0.01
DC9	Exponential-ElGamal	1024	D	4.5931	0.195208	0.49	9.76	17.08	27.33
DC9	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC9	EllipticCurve-ElGamal	160	KG	0.0072	0.000343	0	0.02	0.03	0.05
DC9	EllipticCurve-ElGamal	160	E	0.0119	0.000508	0	0.03	0.04	0.07
DC9	EllipticCurve-ElGamal	160	D	5.9812	0.254203	0.64	12.71	22.24	35.59
DC9	EllipticCurve-ElGamal	160	H	0.0001	0.000003	0	0	0	0
DC10	RSA	1024	KG	0.1144	0.004982	0	0.1	0.35	0.45
DC10	RSA	1024	E	0.0041	0.00016	0	0	0.01	0.01
DC10	RSA	1024	D	0.0047	0.000182	0	0	0.01	0.02
DC10	RSA	1024	H	0	0	0	0	0	0
DC10	ElGamal	1024	KG	0.0425	0.001852	0	0.04	0.13	0.17
DC10	ElGamal	1024	E	0.0016	0.000061	0	0	0	0.01
DC10	ElGamal	1024	D	0.0008	0.000033	0	0	0	0
DC10	ElGamal	1024	H	0	0	0	0	0	0
DC10	Paillier	1024	KG	0.0593	0.002584	0	0.05	0.18	0.24
DC10	Paillier	1024	E	0.0153	0.000597	0	0.01	0.04	0.05
DC10	Paillier	1024	D	0.0155	0.000604	0	0.01	0.04	0.05
DC10	Paillier	1024	H	0	0.000001	0	0	0	0
DC10	Damgard-Jurik	1024	KG	0.0984	0.004283	0	0.09	0.3	0.39
DC10	Damgard-Jurik	1024	E	0.0312	0.001217	0	0.02	0.09	0.11
DC10	Damgard-Jurik	1024	D	0.0315	0.001228	0	0.02	0.09	0.11
DC10	Damgard-Jurik	1024	H	0	0.000001	0	0	0	0
DC10	Okamoto-Uchiyama	1024	KG	0.0809	0.003524	0	0.07	0.25	0.32
DC10	Okamoto-Uchiyama	1024	E	0.0138	0.000538	0	0.01	0.04	0.05
DC10	Okamoto-Uchiyama	1024	D	0.0048	0.000189	0	0	0.01	0.02
DC10	Okamoto-Uchiyama	1024	H	0	0	0	0	0	0
DC10	Goldwasser-Micali	1024	KG	0.067	0.002919	0	0.06	0.2	0.27
DC10	Goldwasser-Micali	1024	E	0.0004	0.000016	0	0	0	0
DC10	Goldwasser-Micali	1024	D	0.0233	0.000906	0	0.02	0.06	0.08
DC10	Goldwasser-Micali	1024	H	0.0001	0.000003	0	0	0	0
DC10	Exponential-ElGamal	1024	KG	0.0258	0.001123	0	0.02	0.08	0.1
DC10	Exponential-ElGamal	1024	E	0.0016	0.000064	0	0	0	0.01
DC10	Exponential-ElGamal	1024	D	4.5842	0.178594	0.18	3.57	12.5	16.25
DC10	Exponential-ElGamal	1024	H	0	0	0	0	0	0
DC10	EllipticCurve-ElGamal	160	KG	0.0071	0.00031	0	0.01	0.02	0.03
DC10	EllipticCurve-ElGamal	160	E	0.0117	0.000455	0	0.01	0.03	0.04
DC10	EllipticCurve-ElGamal	160	D	5.8008	0.22599	0.23	4.52	15.82	20.57
DC10	EllipticCurve-ElGamal	160	H	0.0001	0.000002	0	0	0	0

Table 12. Cloud Emission Calculations 128-bit

Data Center Name	Algorithm	Key Size	Operation	Duration (s)	Energy(kWh)	Scope 1 (gCO2)	Scope 2 (gCO2)	Scope 3 (gCO2)	Total (gCO2)
DC1	RSA	3072	KG	9.2605	0.47653	14.3	285.92	100.07	400.29
DC1	RSA	3072	E	0.08	0.003684	0.11	2.21	0.77	3.09
DC1	RSA	3072	D	0.0929	0.004277	0.13	2.57	0.9	3.59
DC1	RSA	3072	H	0	0.000001	0	0	0	0
DC1	ElGamal	3072	KG	0.7856	0.040426	1.21	24.26	8.49	33.96
DC1	ElGamal	3072	E	0.0271	0.001247	0.04	0.75	0.26	1.05
DC1	ElGamal	3072	D	0.0139	0.00064	0.02	0.38	0.13	0.54
DC1	ElGamal	3072	H	0	0.000001	0	0	0	0
DC1	Paillier	3072	KG	3.4871	0.17944	5.38	107.66	37.68	150.73
DC1	Paillier	3072	E	0.3333	0.015346	0.46	9.21	3.22	12.89
DC1	Paillier	3072	D	0.336	0.01547	0.46	9.28	3.25	12.99
DC1	Paillier	3072	H	0.0001	0.000005	0	0	0	0
DC1	Damgard-Jurik	3072	KG	2.0441	0.105186	3.16	63.11	22.09	88.36
DC1	Damgard-Jurik	3072	E	0.7094	0.032662	0.98	19.6	6.86	27.44
DC1	Damgard-Jurik	3072	D	0.7171	0.033016	0.99	19.81	6.93	27.73
DC1	Damgard-Jurik	3072	H	0.0003	0.00001	0	0.01	0	0.01
DC1	Okamoto-Uchiyama	3072	KG	1.6661	0.085735	2.57	51.44	18	72.02
DC1	Okamoto-Uchiyama	3072	E	0.295	0.013581	0.41	8.15	2.85	11.41
DC1	Okamoto-Uchiyama	3072	D	0.095	0.004374	0.13	2.62	0.92	3.67
DC1	Okamoto-Uchiyama	3072	H	0.0001	0.000003	0	0	0	0
DC1	Goldwasser-Micali	3072	KG	8.5208	0.438466	13.15	263.08	92.08	368.31
DC1	Goldwasser-Micali	3072	E	0.0017	0.000078	0	0.05	0.02	0.07
DC1	Goldwasser-Micali	3072	D	0.4077	0.018771	0.56	11.26	3.94	15.77
DC1	Goldwasser-Micali	3072	H	0.0005	0.00002	0	0.01	0	0.02
DC1	Exponential-ElGamal	3072	KG	1.6957	0.087258	2.62	52.35	18.32	73.3
DC1	Exponential-ElGamal	3072	E	0.0267	0.001231	0.04	0.74	0.26	1.03
DC1	Exponential-ElGamal	3072	D	28.0105	1.28965	38.69	773.79	270.83	1083.31
DC1	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC1	EllipticCurve-ElGamal	256	KG	0.0122	0.000628	0.02	0.38	0.13	0.53
DC1	EllipticCurve-ElGamal	256	E	0.0122	0.00056	0.02	0.34	0.12	0.47
DC1	EllipticCurve-ElGamal	256	D	5.8872	0.271057	8.13	162.63	56.92	227.69
DC1	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC2	RSA	3072	KG	6.5568	0.363356	11.81	236.18	82.66	330.65
DC2	RSA	3072	E	0.0805	0.003993	0.13	2.6	0.91	3.63
DC2	RSA	3072	D	0.0935	0.004636	0.15	3.01	1.05	4.22
DC2	RSA	3072	H	0	0.000002	0	0	0	0
DC2	ElGamal	3072	KG	2.9021	0.160825	5.23	104.54	36.59	146.35
DC2	ElGamal	3072	E	0.0275	0.001364	0.04	0.89	0.31	1.24
DC2	ElGamal	3072	D	0.014	0.000694	0.02	0.45	0.16	0.63
DC2	ElGamal	3072	H	0	0.000001	0	0	0	0
DC2	Paillier	3072	KG	1.4236	0.078891	2.56	51.28	17.95	71.79
DC2	Paillier	3072	E	0.3343	0.016576	0.54	10.77	3.77	15.08
DC2	Paillier	3072	D	0.3352	0.01662	0.54	10.8	3.78	15.12
DC2	Paillier	3072	H	0.0001	0.000005	0	0	0	0
DC2	Damgard-Jurik	3072	KG	1.8657	0.103391	3.36	67.2	23.52	94.09
DC2	Damgard-Jurik	3072	E	0.7041	0.034914	1.13	22.69	7.94	31.77
DC2	Damgard-Jurik	3072	D	0.7075	0.03508	1.14	22.8	7.98	31.92
DC2	Damgard-Jurik	3072	H	0.0003	0.000011	0	0.01	0	0.01
DC2	Okamoto-Uchiyama	3072	KG	4.121	0.228372	7.42	148.44	51.95	207.82
DC2	Okamoto-Uchiyama	3072	E	0.2949	0.01462	0.48	9.5	3.33	13.3
DC2	Okamoto-Uchiyama	3072	D	0.0951	0.004715	0.15	3.06	1.07	4.29
DC2	Okamoto-Uchiyama	3072	H	0.0001	0.000003	0	0	0	0
DC2	Goldwasser-Micali	3072	KG	2.319	0.128511	4.18	83.53	29.24	116.95
DC2	Goldwasser-Micali	3072	E	0.0017	0.000085	0	0.06	0.02	0.08
DC2	Goldwasser-Micali	3072	D	0.4148	0.020567	0.67	13.37	4.68	18.72
DC2	Goldwasser-Micali	3072	H	0.0005	0.000022	0	0.01	0	0.02
DC2	Exponential-ElGamal	3072	KG	0.5733	0.03177	1.03	20.65	7.23	28.91
DC2	Exponential-ElGamal	3072	E	0.0272	0.00135	0.04	0.88	0.31	1.23
DC2	Exponential-ElGamal	3072	D	28.5494	1.415574	46.01	920.12	322.04	1288.17
DC2	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC2	EllipticCurve-ElGamal	256	KG	0.0119	0.000659	0.02	0.43	0.15	0.6
DC2	EllipticCurve-ElGamal	256	E	0.012	0.000596	0.02	0.39	0.14	0.54
DC2	EllipticCurve-ElGamal	256	D	5.8941	0.292249	9.5	189.96	66.49	265.95
DC2	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC3	RSA	3072	KG	19.4154	1.152789	40.35	806.95	282.43	1129.73
DC3	RSA	3072	E	0.0802	0.004262	0.15	2.98	1.04	4.18
DC3	RSA	3072	D	0.0926	0.004919	0.17	3.44	1.21	4.82
DC3	RSA	3072	H	0	0.000002	0	0	0	0
DC3	ElGamal	3072	KG	0.1175	0.006977	0.24	4.88	1.71	6.84
DC3	ElGamal	3072	E	0.0266	0.001414	0.05	0.99	0.35	1.39
DC3	ElGamal	3072	D	0.0137	0.000728	0.03	0.51	0.18	0.71
DC3	ElGamal	3072	H	0	0.000001	0	0	0	0
DC3	Paillier	3072	KG	4.7648	0.28291	9.9	198.04	69.31	277.25
DC3	Paillier	3072	E	0.3295	0.017505	0.61	12.25	4.29	17.16
DC3	Paillier	3072	D	0.333	0.017691	0.62	12.38	4.33	17.34
DC3	Paillier	3072	H	0.0001	0.000006	0	0	0	0.01
DC3	Damgard-Jurik	3072	KG	3.2622	0.193693	6.78	135.59	47.45	189.82
DC3	Damgard-Jurik	3072	E	0.6978	0.037073	1.3	25.95	9.08	36.33
DC3	Damgard-Jurik	3072	D	0.7014	0.037262	1.3	26.08	9.13	36.52
DC3	Damgard-Jurik	3072	H	0.0003	0.000012	0	0.01	0	0.01
DC3	Okamoto-Uchiyama	3072	KG	7.7549	0.460447	16.12	322.31	112.81	451.24
DC3	Okamoto-Uchiyama	3072	E	0.2946	0.015652	0.55	10.96	3.83	15.34
DC3	Okamoto-Uchiyama	3072	D	0.0957	0.005084	0.18	3.56	1.25	4.98
DC3	Okamoto-Uchiyama	3072	H	0.0001	0.000003	0	0	0	0
DC3	Goldwasser-Micali	3072	KG	3.7835	0.224645	7.86	157.25	55.04	220.15
DC3	Goldwasser-Micali	3072	E	0.0016	0.000088	0	0.06	0.02	0.09
DC3	Goldwasser-Micali	3072	D	0.4163	0.022116	0.77	15.48	5.42	21.67
DC3	Goldwasser-Micali	3072	H	0.0005	0.000022	0	0.02	0.01	0.02
DC3	Exponential-ElGamal	3072	KG	0.1746	0.010367	0.36	7.26	2.54	10.16
DC3	Exponential-ElGamal	3072	E	0.0267	0.001417	0.05	0.99	0.35	1.39
DC3	Exponential-ElGamal	3072	D	28.1083	1.493253	52.26	1045.28	365.85	1463.39
DC3	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC3	EllipticCurve-ElGamal	256	KG	0.0115	0.000683	0.02	0.48	0.17	0.67
DC3	EllipticCurve-ElGamal	256	E	0.0112	0.000597	0.02	0.42	0.15	0.59
DC3	EllipticCurve-ElGamal	256	D	5.8273	0.309575	10.84	216.7	75.85	303.38
DC3	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC4	RSA	3072	KG	3.8942	0.16956	0	0	5.93	5.93
DC4	RSA	3072	E	0.0808	0.003149	0	0	0.11	0.11
DC4	RSA	3072	D	0.0934	0.003639	0	0	0.13	0.13
DC4	RSA	3072	H	0	0.000001	0	0	0	0
DC4	ElGamal	3072	KG	0.1506	0.006557	0	0	0.23	0.23
DC4	ElGamal	3072	E	0.0268	0.001042	0	0	0.04	0.04
DC4	ElGamal	3072	D	0.0137	0.000534	0	0	0.02	0.02
DC4	ElGamal	3072	H	0	0.000001	0	0	0	0
DC4	Paillier	3072	KG	1.3062	0.056874	0	0	1.99	1.99
DC4	Paillier	3072	E	0.3308	0.012889	0	0	0.45	0.45
DC4	Paillier	3072	D	0.3319	0.01293	0	0	0.45	0.45
DC4	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC4	Damgard-Jurik	3072	KG	4.0465	0.176191	0	0	6.17	6.17
DC4	Damgard-Jurik	3072	E	0.7067	0.027533	0	0	0.96	0.96
DC4	Damgard-Jurik	3072	D	0.7098	0.027653	0	0	0.97	0.97
DC4	Damgard-Jurik	3072	H	0.0003	0.000009	0	0	0	0
DC4	Okamoto-Uchiyama	3072	KG	1.8452	0.080343	0	0	2.81	2.81
DC4	Okamoto-Uchiyama	3072	E	0.2959	0.011529	0	0	0.4	0.4
DC4	Okamoto-Uchiyama	3072	D	0.0951	0.003705	0	0	0.13	0.13
DC4	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC4	Goldwasser-Micali	3072	KG	3.9703	0.172873	0	0	6.05	6.05
DC4	Goldwasser-Micali	3072	E	0.0017	0.000065	0	0	0	0
DC4	Goldwasser-Micali	3072	D	0.4082	0.015903	0	0	0.56	0.56
DC4	Goldwasser-Micali	3072	H	0.0005	0.000017	0	0	0	0
DC4	Exponential-ElGamal	3072	KG	0.6002	0.026134	0	0	0.91	0.91
DC4	Exponential-ElGamal	3072	E	0.0268	0.001045	0	0	0.04	0.04
DC4	Exponential-ElGamal	3072	D	27.782	1.08234	0	0	37.88	37.88
DC4	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC4	EllipticCurve-ElGamal	256	KG	0.0117	0.000509	0	0	0.02	0.02
DC4	EllipticCurve-ElGamal	256	E	0.012	0.000469	0	0	0.02	0.02
DC4	EllipticCurve-ElGamal	256	D	5.6162	0.218798	0	0	7.66	7.66
DC4	EllipticCurve-ElGamal	256	H	0.0001	0.000002	0	0	0	0
DC5	RSA	3072	KG	18.1789	0.755561	0	0	13.22	13.22
DC5	RSA	3072	E	0.08	0.002977	0	0	0.05	0.05
DC5	RSA	3072	D	0.0929	0.003455	0	0	0.06	0.06
DC5	RSA	3072	H	0	0.000001	0	0	0	0
DC5	ElGamal	3072	KG	0.9141	0.037992	0	0	0.66	0.66
DC5	ElGamal	3072	E	0.0264	0.000983	0	0	0.02	0.02
DC5	ElGamal	3072	D	0.0139	0.000517	0	0	0.01	0.01
DC5	ElGamal	3072	H	0	0.000001	0	0	0	0
DC5	Paillier	3072	KG	2.2975	0.09549	0	0	1.67	1.67
DC5	Paillier	3072	E	0.3322	0.012354	0	0	0.22	0.22
DC5	Paillier	3072	D	0.3337	0.012409	0	0	0.22	0.22
DC5	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC5	Damgard-Jurik	3072	KG	2.645	0.109933	0	0	1.92	1.92
DC5	Damgard-Jurik	3072	E	0.7093	0.026376	0	0	0.46	0.46
DC5	Damgard-Jurik	3072	D	0.7136	0.026537	0	0	0.46	0.46
DC5	Damgard-Jurik	3072	H	0.0003	0.000009	0	0	0	0
DC5	Okamoto-Uchiyama	3072	KG	1.5536	0.064572	0	0	1.13	1.13
DC5	Okamoto-Uchiyama	3072	E	0.2925	0.010878	0	0	0.19	0.19
DC5	Okamoto-Uchiyama	3072	D	0.095	0.003533	0	0	0.06	0.06
DC5	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC5	Goldwasser-Micali	3072	KG	6.0297	0.250609	0	0	4.39	4.39
DC5	Goldwasser-Micali	3072	E	0.0017	0.000062	0	0	0	0
DC5	Goldwasser-Micali	3072	D	0.4028	0.014979	0	0	0.26	0.26
DC5	Goldwasser-Micali	3072	H	0.0005	0.000015	0	0	0	0
DC5	Exponential-ElGamal	3072	KG	0.3619	0.015041	0	0	0.26	0.26
DC5	Exponential-ElGamal	3072	E	0.0276	0.001025	0	0	0.02	0.02
DC5	Exponential-ElGamal	3072	D	28.2721	1.051369	0	0	18.4	18.4
DC5	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC5	EllipticCurve-ElGamal	256	KG	0.0113	0.00047	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	256	E	0.0111	0.000414	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	256	D	5.7932	0.215435	0	0	3.77	3.77
DC5	EllipticCurve-ElGamal	256	H	0.0001	0.000002	0	0	0	0
DC6	RSA	3072	KG	9.3505	0.444149	0	0	18.65	18.65
DC6	RSA	3072	E	0.081	0.003443	0	0	0.14	0.14
DC6	RSA	3072	D	0.0936	0.003978	0	0	0.17	0.17
DC6	RSA	3072	H	0	0.000001	0	0	0	0
DC6	ElGamal	3072	KG	4.8318	0.229511	0	0	9.64	9.64
DC6	ElGamal	3072	E	0.0267	0.001135	0	0	0.05	0.05
DC6	ElGamal	3072	D	0.0136	0.000578	0	0	0.02	0.02
DC6	ElGamal	3072	H	0	0.000001	0	0	0	0
DC6	Paillier	3072	KG	3.0141	0.14317	0	0	6.01	6.01
DC6	Paillier	3072	E	0.3355	0.01426	0	0	0.6	0.6
DC6	Paillier	3072	D	0.337	0.014323	0	0	0.6	0.6
DC6	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC6	Damgard-Jurik	3072	KG	1.0948	0.052003	0	0	2.18	2.18
DC6	Damgard-Jurik	3072	E	0.7117	0.030247	0	0	1.27	1.27
DC6	Damgard-Jurik	3072	D	0.7153	0.0304	0	0	1.28	1.28
DC6	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC6	Okamoto-Uchiyama	3072	KG	2.5016	0.118826	0	0	4.99	4.99
DC6	Okamoto-Uchiyama	3072	E	0.2924	0.012426	0	0	0.52	0.52
DC6	Okamoto-Uchiyama	3072	D	0.0951	0.004042	0	0	0.17	0.17
DC6	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC6	Goldwasser-Micali	3072	KG	3.2757	0.155596	0	0	6.54	6.54
DC6	Goldwasser-Micali	3072	E	0.0017	0.000072	0	0	0	0
DC6	Goldwasser-Micali	3072	D	0.4174	0.017739	0	0	0.75	0.75
DC6	Goldwasser-Micali	3072	H	0.0005	0.000018	0	0	0	0
DC6	Exponential-ElGamal	3072	KG	0.6004	0.028519	0	0	1.2	1.2
DC6	Exponential-ElGamal	3072	E	0.0271	0.001151	0	0	0.05	0.05
DC6	Exponential-ElGamal	3072	D	28.6196	1.216333	0	0	51.09	51.09
DC6	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC6	EllipticCurve-ElGamal	256	KG	0.0112	0.000532	0	0	0.02	0.02
DC6	EllipticCurve-ElGamal	256	E	0.0125	0.000531	0	0	0.02	0.02
DC6	EllipticCurve-ElGamal	256	D	5.7001	0.242254	0	0	10.17	10.17
DC6	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC7	RSA	3072	KG	14.6075	0.751678	4.51	90.2	78.93	173.64
DC7	RSA	3072	E	0.0802	0.003693	0.02	0.44	0.39	0.85
DC7	RSA	3072	D	0.0934	0.0043	0.03	0.52	0.45	0.99
DC7	RSA	3072	H	0	0.000001	0	0	0	0
DC7	ElGamal	3072	KG	0.9031	0.046472	0.28	5.58	4.88	10.74
DC7	ElGamal	3072	E	0.028	0.001289	0.01	0.15	0.14	0.3
DC7	ElGamal	3072	D	0.0142	0.000654	0	0.08	0.07	0.15
DC7	ElGamal	3072	H	0	0.000001	0	0	0	0
DC7	Paillier	3072	KG	3.0224	0.155528	0.93	18.66	16.33	35.93
DC7	Paillier	3072	E	0.3288	0.015137	0.09	1.82	1.59	3.5
DC7	Paillier	3072	D	0.3311	0.015244	0.09	1.83	1.6	3.52
DC7	Paillier	3072	H	0.0001	0.000005	0	0	0	0
DC7	Damgard-Jurik	3072	KG	4.9993	0.257256	1.54	30.87	27.01	59.43
DC7	Damgard-Jurik	3072	E	0.7044	0.032433	0.19	3.89	3.41	7.49
DC7	Damgard-Jurik	3072	D	0.7052	0.032469	0.19	3.9	3.41	7.5
DC7	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC7	Okamoto-Uchiyama	3072	KG	4.7143	0.24259	1.46	29.11	25.47	56.04
DC7	Okamoto-Uchiyama	3072	E	0.2963	0.013641	0.08	1.64	1.43	3.15
DC7	Okamoto-Uchiyama	3072	D	0.0957	0.004406	0.03	0.53	0.46	1.02
DC7	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC7	Goldwasser-Micali	3072	KG	2.6347	0.135577	0.81	16.27	14.24	31.32
DC7	Goldwasser-Micali	3072	E	0.0017	0.000078	0	0.01	0.01	0.02
DC7	Goldwasser-Micali	3072	D	0.4171	0.019204	0.12	2.3	2.02	4.44
DC7	Goldwasser-Micali	3072	H	0.0005	0.00002	0	0	0	0
DC7	Exponential-ElGamal	3072	KG	3.5652	0.183459	1.1	22.02	19.26	42.38
DC7	Exponential-ElGamal	3072	E	0.0271	0.001247	0.01	0.15	0.13	0.29
DC7	Exponential-ElGamal	3072	D	28.0696	1.292371	7.75	155.08	135.7	298.54
DC7	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC7	EllipticCurve-ElGamal	256	KG	0.012	0.000617	0	0.07	0.06	0.14
DC7	EllipticCurve-ElGamal	256	E	0.0117	0.00054	0	0.06	0.06	0.12
DC7	EllipticCurve-ElGamal	256	D	5.674	0.26124	1.57	31.35	27.43	60.35
DC7	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC8	RSA	3072	KG	9.72	0.4617	1.94	38.78	45.25	85.97
DC8	RSA	3072	E	0.0816	0.003469	0.01	0.29	0.34	0.65
DC8	RSA	3072	D	0.0947	0.004025	0.02	0.34	0.39	0.75
DC8	RSA	3072	H	0	0.000001	0	0	0	0
DC8	ElGamal	3072	KG	1.2338	0.058605	0.25	4.92	5.74	10.91
DC8	ElGamal	3072	E	0.0273	0.001161	0	0.1	0.11	0.22
DC8	ElGamal	3072	D	0.0141	0.000599	0	0.05	0.06	0.11
DC8	ElGamal	3072	H	0	0.000001	0	0	0	0
DC8	Paillier	3072	KG	8.5052	0.403997	1.7	33.94	39.59	75.22
DC8	Paillier	3072	E	0.3314	0.014084	0.06	1.18	1.38	2.62
DC8	Paillier	3072	D	0.3326	0.014135	0.06	1.19	1.39	2.63
DC8	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC8	Damgard-Jurik	3072	KG	1.9743	0.093779	0.39	7.88	9.19	17.46
DC8	Damgard-Jurik	3072	E	0.7086	0.030113	0.13	2.53	2.95	5.61
DC8	Damgard-Jurik	3072	D	0.7105	0.030196	0.13	2.54	2.96	5.62
DC8	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC8	Okamoto-Uchiyama	3072	KG	4.0001	0.190005	0.8	15.96	18.62	35.38
DC8	Okamoto-Uchiyama	3072	E	0.2907	0.012357	0.05	1.04	1.21	2.3
DC8	Okamoto-Uchiyama	3072	D	0.094	0.003995	0.02	0.34	0.39	0.74
DC8	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC8	Goldwasser-Micali	3072	KG	2.1896	0.104006	0.44	8.74	10.19	19.37
DC8	Goldwasser-Micali	3072	E	0.0017	0.000071	0	0.01	0.01	0.01
DC8	Goldwasser-Micali	3072	D	0.412	0.01751	0.07	1.47	1.72	3.26
DC8	Goldwasser-Micali	3072	H	0.0005	0.000018	0	0	0	0
DC8	Exponential-ElGamal	3072	KG	3.8172	0.181317	0.76	15.23	17.77	33.76
DC8	Exponential-ElGamal	3072	E	0.0282	0.001198	0.01	0.1	0.12	0.22
DC8	Exponential-ElGamal	3072	D	28.5349	1.212733	5.09	101.87	118.85	225.81
DC8	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC8	EllipticCurve-ElGamal	256	KG	0.0112	0.000532	0	0.04	0.05	0.1
DC8	EllipticCurve-ElGamal	256	E	0.0111	0.00047	0	0.04	0.05	0.09
DC8	EllipticCurve-ElGamal	256	D	5.7602	0.244808	1.03	20.56	23.99	45.58
DC8	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC9	RSA	3072	KG	28.6789	1.362248	3.41	68.11	119.2	190.71
DC9	RSA	3072	E	0.0809	0.003439	0.01	0.17	0.3	0.48
DC9	RSA	3072	D	0.0937	0.003982	0.01	0.2	0.35	0.56
DC9	RSA	3072	H	0	0.000001	0	0	0	0
DC9	ElGamal	3072	KG	5.2391	0.248857	0.62	12.44	21.78	34.84
DC9	ElGamal	3072	E	0.0278	0.001181	0	0.06	0.1	0.17
DC9	ElGamal	3072	D	0.0142	0.000603	0	0.03	0.05	0.08
DC9	ElGamal	3072	H	0	0.000001	0	0	0	0
DC9	Paillier	3072	KG	5.6158	0.266751	0.67	13.34	23.34	37.35
DC9	Paillier	3072	E	0.3359	0.014274	0.04	0.71	1.25	2
DC9	Paillier	3072	D	0.3364	0.014297	0.04	0.71	1.25	2
DC9	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC9	Damgard-Jurik	3072	KG	2.653	0.126018	0.32	6.3	11.03	17.64
DC9	Damgard-Jurik	3072	E	0.7135	0.030323	0.08	1.52	2.65	4.25
DC9	Damgard-Jurik	3072	D	0.7173	0.030485	0.08	1.52	2.67	4.27
DC9	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC9	Okamoto-Uchiyama	3072	KG	2.5479	0.121025	0.3	6.05	10.59	16.94
DC9	Okamoto-Uchiyama	3072	E	0.295	0.012536	0.03	0.63	1.1	1.76
DC9	Okamoto-Uchiyama	3072	D	0.0957	0.004067	0.01	0.2	0.36	0.57
DC9	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC9	Goldwasser-Micali	3072	KG	3.3484	0.159049	0.4	7.95	13.92	22.27
DC9	Goldwasser-Micali	3072	E	0.0017	0.000074	0	0	0.01	0.01
DC9	Goldwasser-Micali	3072	D	0.4144	0.017612	0.04	0.88	1.54	2.47
DC9	Goldwasser-Micali	3072	H	0.0005	0.000018	0	0	0	0
DC9	Exponential-ElGamal	3072	KG	0.8565	0.040684	0.1	2.03	3.56	5.7
DC9	Exponential-ElGamal	3072	E	0.0271	0.001154	0	0.06	0.1	0.16
DC9	Exponential-ElGamal	3072	D	27.9974	1.189889	2.97	59.49	104.12	166.58
DC9	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC9	EllipticCurve-ElGamal	256	KG	0.0113	0.000537	0	0.03	0.05	0.08
DC9	EllipticCurve-ElGamal	256	E	0.0115	0.000489	0	0.02	0.04	0.07
DC9	EllipticCurve-ElGamal	256	D	5.7603	0.244813	0.61	12.24	21.42	34.27
DC9	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC10	RSA	3072	KG	14.6362	0.637285	0.64	12.75	44.61	57.99
DC11	RSA	3072	E	0.0811	0.00316	0	0.06	0.22	0.29
DC12	RSA	3072	D	0.0943	0.003674	0	0.07	0.26	0.33
DC13	RSA	3072	H	0	0.000001	0	0	0	0
DC14	ElGamal	3072	KG	1.8475	0.080443	0.08	1.61	5.63	7.32
DC15	ElGamal	3072	E	0.0274	0.001067	0	0.02	0.07	0.1
DC16	ElGamal	3072	D	0.0142	0.000553	0	0.01	0.04	0.05
DC17	ElGamal	3072	H	0	0.000001	0	0	0	0
DC18	Paillier	3072	KG	2.4511	0.106725	0.11	2.13	7.47	9.71
DC19	Paillier	3072	E	0.3291	0.012821	0.01	0.26	0.9	1.17
DC20	Paillier	3072	D	0.332	0.012934	0.01	0.26	0.91	1.18
DC21	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC22	Damgard-Jurik	3072	KG	4.1464	0.180541	0.18	3.61	12.64	16.43
DC23	Damgard-Jurik	3072	E	0.704	0.027429	0.03	0.55	1.92	2.5
DC24	Damgard-Jurik	3072	D	0.7107	0.027688	0.03	0.55	1.94	2.52
DC25	Damgard-Jurik	3072	H	0.0003	0.000009	0	0	0	0
DC26	Okamoto-Uchiyama	3072	KG	6.2837	0.273603	0.27	5.47	19.15	24.9
DC27	Okamoto-Uchiyama	3072	E	0.2934	0.011429	0.01	0.23	0.8	1.04
DC28	Okamoto-Uchiyama	3072	D	0.0946	0.003685	0	0.07	0.26	0.34
DC29	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC30	Goldwasser-Micali	3072	KG	1.9582	0.085263	0.09	1.71	5.97	7.76
DC31	Goldwasser-Micali	3072	E	0.0017	0.000065	0	0	0	0.01
DC32	Goldwasser-Micali	3072	D	0.4019	0.015657	0.02	0.31	1.1	1.42
DC33	Goldwasser-Micali	3072	H	0.0005	0.000016	0	0	0	0
DC34	Exponential-ElGamal	3072	KG	7.7826	0.338867	0.34	6.78	23.72	30.84
DC35	Exponential-ElGamal	3072	E	0.0273	0.001062	0	0.02	0.07	0.1
DC36	Exponential-ElGamal	3072	D	28.5325	1.111579	1.11	22.23	77.81	101.15
DC37	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC38	EllipticCurve-ElGamal	256	KG	0.0113	0.000492	0	0.01	0.03	0.04
DC39	EllipticCurve-ElGamal	256	E	0.0111	0.000432	0	0.01	0.03	0.04
DC40	EllipticCurve-ElGamal	256	D	5.785	0.225374	0.23	4.51	15.78	20.51
DC41	EllipticCurve-ElGamal	256	H	0.0001	0.000002	0	0	0	0

Table 12. Cloud Emission Calculations 128-bit

Data Center Name	Algorithm	Key Size	Operation	Duration (s)	Energy(kWh)	Scope 1 (gCO2)	Scope 2 (gCO2)	Scope 3 (gCO2)	Total (gCO2)
DC1	RSA	3072	KG	9.2605	0.47653	14.3	285.92	100.07	400.29
DC1	RSA	3072	E	0.08	0.003684	0.11	2.21	0.77	3.09
DC1	RSA	3072	D	0.0929	0.004277	0.13	2.57	0.9	3.59
DC1	RSA	3072	H	0	0.000001	0	0	0	0
DC1	ElGamal	3072	KG	0.7856	0.040426	1.21	24.26	8.49	33.96
DC1	ElGamal	3072	E	0.0271	0.001247	0.04	0.75	0.26	1.05
DC1	ElGamal	3072	D	0.0139	0.00064	0.02	0.38	0.13	0.54
DC1	ElGamal	3072	H	0	0.000001	0	0	0	0
DC1	Paillier	3072	KG	3.4871	0.17944	5.38	107.66	37.68	150.73
DC1	Paillier	3072	E	0.3333	0.015346	0.46	9.21	3.22	12.89
DC1	Paillier	3072	D	0.336	0.01547	0.46	9.28	3.25	12.99
DC1	Paillier	3072	H	0.0001	0.000005	0	0	0	0
DC1	Damgard-Jurik	3072	KG	2.0441	0.105186	3.16	63.11	22.09	88.36
DC1	Damgard-Jurik	3072	E	0.7094	0.032662	0.98	19.6	6.86	27.44
DC1	Damgard-Jurik	3072	D	0.7171	0.033016	0.99	19.81	6.93	27.73
DC1	Damgard-Jurik	3072	H	0.0003	0.00001	0	0.01	0	0.01
DC1	Okamoto-Uchiyama	3072	KG	1.6661	0.085735	2.57	51.44	18	72.02
DC1	Okamoto-Uchiyama	3072	E	0.295	0.013581	0.41	8.15	2.85	11.41
DC1	Okamoto-Uchiyama	3072	D	0.095	0.004374	0.13	2.62	0.92	3.67
DC1	Okamoto-Uchiyama	3072	H	0.0001	0.000003	0	0	0	0
DC1	Goldwasser-Micali	3072	KG	8.5208	0.438466	13.15	263.08	92.08	368.31
DC1	Goldwasser-Micali	3072	E	0.0017	0.000078	0	0.05	0.02	0.07
DC1	Goldwasser-Micali	3072	D	0.4077	0.018771	0.56	11.26	3.94	15.77
DC1	Goldwasser-Micali	3072	H	0.0005	0.00002	0	0.01	0	0.02
DC1	Exponential-ElGamal	3072	KG	1.6957	0.087258	2.62	52.35	18.32	73.3
DC1	Exponential-ElGamal	3072	E	0.0267	0.001231	0.04	0.74	0.26	1.03
DC1	Exponential-ElGamal	3072	D	28.0105	1.28965	38.69	773.79	270.83	1083.31
DC1	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC1	EllipticCurve-ElGamal	256	KG	0.0122	0.000628	0.02	0.38	0.13	0.53
DC1	EllipticCurve-ElGamal	256	E	0.0122	0.00056	0.02	0.34	0.12	0.47
DC1	EllipticCurve-ElGamal	256	D	5.8872	0.271057	8.13	162.63	56.92	227.69
DC1	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC2	RSA	3072	KG	6.5568	0.363356	11.81	236.18	82.66	330.65
DC2	RSA	3072	E	0.0805	0.003993	0.13	2.6	0.91	3.63
DC2	RSA	3072	D	0.0935	0.004636	0.15	3.01	1.05	4.22
DC2	RSA	3072	H	0	0.000002	0	0	0	0
DC2	ElGamal	3072	KG	2.9021	0.160825	5.23	104.54	36.59	146.35
DC2	ElGamal	3072	E	0.0275	0.001364	0.04	0.89	0.31	1.24
DC2	ElGamal	3072	D	0.014	0.000694	0.02	0.45	0.16	0.63
DC2	ElGamal	3072	H	0	0.000001	0	0	0	0
DC2	Paillier	3072	KG	1.4236	0.078891	2.56	51.28	17.95	71.79
DC2	Paillier	3072	E	0.3343	0.016576	0.54	10.77	3.77	15.08
DC2	Paillier	3072	D	0.3352	0.01662	0.54	10.8	3.78	15.12
DC2	Paillier	3072	H	0.0001	0.000005	0	0	0	0
DC2	Damgard-Jurik	3072	KG	1.8657	0.103391	3.36	67.2	23.52	94.09
DC2	Damgard-Jurik	3072	E	0.7041	0.034914	1.13	22.69	7.94	31.77
DC2	Damgard-Jurik	3072	D	0.7075	0.03508	1.14	22.8	7.98	31.92
DC2	Damgard-Jurik	3072	H	0.0003	0.000011	0	0.01	0	0.01
DC2	Okamoto-Uchiyama	3072	KG	4.121	0.228372	7.42	148.44	51.95	207.82
DC2	Okamoto-Uchiyama	3072	E	0.2949	0.01462	0.48	9.5	3.33	13.3
DC2	Okamoto-Uchiyama	3072	D	0.0951	0.004715	0.15	3.06	1.07	4.29
DC2	Okamoto-Uchiyama	3072	H	0.0001	0.000003	0	0	0	0
DC2	Goldwasser-Micali	3072	KG	2.319	0.128511	4.18	83.53	29.24	116.95
DC2	Goldwasser-Micali	3072	E	0.0017	0.000085	0	0.06	0.02	0.08
DC2	Goldwasser-Micali	3072	D	0.4148	0.020567	0.67	13.37	4.68	18.72
DC2	Goldwasser-Micali	3072	H	0.0005	0.000022	0	0.01	0	0.02
DC2	Exponential-ElGamal	3072	KG	0.5733	0.03177	1.03	20.65	7.23	28.91
DC2	Exponential-ElGamal	3072	E	0.0272	0.00135	0.04	0.88	0.31	1.23
DC2	Exponential-ElGamal	3072	D	28.5494	1.415574	46.01	920.12	322.04	1288.17
DC2	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC2	EllipticCurve-ElGamal	256	KG	0.0119	0.000659	0.02	0.43	0.15	0.6
DC2	EllipticCurve-ElGamal	256	E	0.012	0.000596	0.02	0.39	0.14	0.54
DC2	EllipticCurve-ElGamal	256	D	5.8941	0.292249	9.5	189.96	66.49	265.95
DC2	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC3	RSA	3072	KG	19.4154	1.152789	40.35	806.95	282.43	1129.73
DC3	RSA	3072	E	0.0802	0.004262	0.15	2.98	1.04	4.18
DC3	RSA	3072	D	0.0926	0.004919	0.17	3.44	1.21	4.82
DC3	RSA	3072	H	0	0.000002	0	0	0	0
DC3	ElGamal	3072	KG	0.1175	0.006977	0.24	4.88	1.71	6.84
DC3	ElGamal	3072	E	0.0266	0.001414	0.05	0.99	0.35	1.39
DC3	ElGamal	3072	D	0.0137	0.000728	0.03	0.51	0.18	0.71
DC3	ElGamal	3072	H	0	0.000001	0	0	0	0
DC3	Paillier	3072	KG	4.7648	0.28291	9.9	198.04	69.31	277.25
DC3	Paillier	3072	E	0.3295	0.017505	0.61	12.25	4.29	17.16
DC3	Paillier	3072	D	0.333	0.017691	0.62	12.38	4.33	17.34
DC3	Paillier	3072	H	0.0001	0.000006	0	0	0	0.01
DC3	Damgard-Jurik	3072	KG	3.2622	0.193693	6.78	135.59	47.45	189.82
DC3	Damgard-Jurik	3072	E	0.6978	0.037073	1.3	25.95	9.08	36.33
DC3	Damgard-Jurik	3072	D	0.7014	0.037262	1.3	26.08	9.13	36.52
DC3	Damgard-Jurik	3072	H	0.0003	0.000012	0	0.01	0	0.01
DC3	Okamoto-Uchiyama	3072	KG	7.7549	0.460447	16.12	322.31	112.81	451.24
DC3	Okamoto-Uchiyama	3072	E	0.2946	0.015652	0.55	10.96	3.83	15.34
DC3	Okamoto-Uchiyama	3072	D	0.0957	0.005084	0.18	3.56	1.25	4.98
DC3	Okamoto-Uchiyama	3072	H	0.0001	0.000003	0	0	0	0
DC3	Goldwasser-Micali	3072	KG	3.7835	0.224645	7.86	157.25	55.04	220.15
DC3	Goldwasser-Micali	3072	E	0.0016	0.000088	0	0.06	0.02	0.09
DC3	Goldwasser-Micali	3072	D	0.4163	0.022116	0.77	15.48	5.42	21.67
DC3	Goldwasser-Micali	3072	H	0.0005	0.000022	0	0.02	0.01	0.02
DC3	Exponential-ElGamal	3072	KG	0.1746	0.010367	0.36	7.26	2.54	10.16
DC3	Exponential-ElGamal	3072	E	0.0267	0.001417	0.05	0.99	0.35	1.39
DC3	Exponential-ElGamal	3072	D	28.1083	1.493253	52.26	1045.28	365.85	1463.39
DC3	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC3	EllipticCurve-ElGamal	256	KG	0.0115	0.000683	0.02	0.48	0.17	0.67
DC3	EllipticCurve-ElGamal	256	E	0.0112	0.000597	0.02	0.42	0.15	0.59
DC3	EllipticCurve-ElGamal	256	D	5.8273	0.309575	10.84	216.7	75.85	303.38
DC3	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC4	RSA	3072	KG	3.8942	0.16956	0	0	5.93	5.93
DC4	RSA	3072	E	0.0808	0.003149	0	0	0.11	0.11
DC4	RSA	3072	D	0.0934	0.003639	0	0	0.13	0.13
DC4	RSA	3072	H	0	0.000001	0	0	0	0
DC4	ElGamal	3072	KG	0.1506	0.006557	0	0	0.23	0.23
DC4	ElGamal	3072	E	0.0268	0.001042	0	0	0.04	0.04
DC4	ElGamal	3072	D	0.0137	0.000534	0	0	0.02	0.02
DC4	ElGamal	3072	H	0	0.000001	0	0	0	0
DC4	Paillier	3072	KG	1.3062	0.056874	0	0	1.99	1.99
DC4	Paillier	3072	E	0.3308	0.012889	0	0	0.45	0.45
DC4	Paillier	3072	D	0.3319	0.01293	0	0	0.45	0.45
DC4	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC4	Damgard-Jurik	3072	KG	4.0465	0.176191	0	0	6.17	6.17
DC4	Damgard-Jurik	3072	E	0.7067	0.027533	0	0	0.96	0.96
DC4	Damgard-Jurik	3072	D	0.7098	0.027653	0	0	0.97	0.97
DC4	Damgard-Jurik	3072	H	0.0003	0.000009	0	0	0	0
DC4	Okamoto-Uchiyama	3072	KG	1.8452	0.080343	0	0	2.81	2.81
DC4	Okamoto-Uchiyama	3072	E	0.2959	0.011529	0	0	0.4	0.4
DC4	Okamoto-Uchiyama	3072	D	0.0951	0.003705	0	0	0.13	0.13
DC4	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC4	Goldwasser-Micali	3072	KG	3.9703	0.172873	0	0	6.05	6.05
DC4	Goldwasser-Micali	3072	E	0.0017	0.000065	0	0	0	0
DC4	Goldwasser-Micali	3072	D	0.4082	0.015903	0	0	0.56	0.56
DC4	Goldwasser-Micali	3072	H	0.0005	0.000017	0	0	0	0
DC4	Exponential-ElGamal	3072	KG	0.6002	0.026134	0	0	0.91	0.91
DC4	Exponential-ElGamal	3072	E	0.0268	0.001045	0	0	0.04	0.04
DC4	Exponential-ElGamal	3072	D	27.782	1.08234	0	0	37.88	37.88
DC4	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC4	EllipticCurve-ElGamal	256	KG	0.0117	0.000509	0	0	0.02	0.02
DC4	EllipticCurve-ElGamal	256	E	0.012	0.000469	0	0	0.02	0.02
DC4	EllipticCurve-ElGamal	256	D	5.6162	0.218798	0	0	7.66	7.66
DC4	EllipticCurve-ElGamal	256	H	0.0001	0.000002	0	0	0	0
DC5	RSA	3072	KG	18.1789	0.755561	0	0	13.22	13.22
DC5	RSA	3072	E	0.08	0.002977	0	0	0.05	0.05
DC5	RSA	3072	D	0.0929	0.003455	0	0	0.06	0.06
DC5	RSA	3072	H	0	0.000001	0	0	0	0
DC5	ElGamal	3072	KG	0.9141	0.037992	0	0	0.66	0.66
DC5	ElGamal	3072	E	0.0264	0.000983	0	0	0.02	0.02
DC5	ElGamal	3072	D	0.0139	0.000517	0	0	0.01	0.01
DC5	ElGamal	3072	H	0	0.000001	0	0	0	0
DC5	Paillier	3072	KG	2.2975	0.09549	0	0	1.67	1.67
DC5	Paillier	3072	E	0.3322	0.012354	0	0	0.22	0.22
DC5	Paillier	3072	D	0.3337	0.012409	0	0	0.22	0.22
DC5	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC5	Damgard-Jurik	3072	KG	2.645	0.109933	0	0	1.92	1.92
DC5	Damgard-Jurik	3072	E	0.7093	0.026376	0	0	0.46	0.46
DC5	Damgard-Jurik	3072	D	0.7136	0.026537	0	0	0.46	0.46
DC5	Damgard-Jurik	3072	H	0.0003	0.000009	0	0	0	0
DC5	Okamoto-Uchiyama	3072	KG	1.5536	0.064572	0	0	1.13	1.13
DC5	Okamoto-Uchiyama	3072	E	0.2925	0.010878	0	0	0.19	0.19
DC5	Okamoto-Uchiyama	3072	D	0.095	0.003533	0	0	0.06	0.06
DC5	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC5	Goldwasser-Micali	3072	KG	6.0297	0.250609	0	0	4.39	4.39
DC5	Goldwasser-Micali	3072	E	0.0017	0.000062	0	0	0	0
DC5	Goldwasser-Micali	3072	D	0.4028	0.014979	0	0	0.26	0.26
DC5	Goldwasser-Micali	3072	H	0.0005	0.000015	0	0	0	0
DC5	Exponential-ElGamal	3072	KG	0.3619	0.015041	0	0	0.26	0.26
DC5	Exponential-ElGamal	3072	E	0.0276	0.001025	0	0	0.02	0.02
DC5	Exponential-ElGamal	3072	D	28.2721	1.051369	0	0	18.4	18.4
DC5	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC5	EllipticCurve-ElGamal	256	KG	0.0113	0.00047	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	256	E	0.0111	0.000414	0	0	0.01	0.01
DC5	EllipticCurve-ElGamal	256	D	5.7932	0.215435	0	0	3.77	3.77
DC5	EllipticCurve-ElGamal	256	H	0.0001	0.000002	0	0	0	0
DC6	RSA	3072	KG	9.3505	0.444149	0	0	18.65	18.65
DC6	RSA	3072	E	0.081	0.003443	0	0	0.14	0.14
DC6	RSA	3072	D	0.0936	0.003978	0	0	0.17	0.17
DC6	RSA	3072	H	0	0.000001	0	0	0	0
DC6	ElGamal	3072	KG	4.8318	0.229511	0	0	9.64	9.64
DC6	ElGamal	3072	E	0.0267	0.001135	0	0	0.05	0.05
DC6	ElGamal	3072	D	0.0136	0.000578	0	0	0.02	0.02
DC6	ElGamal	3072	H	0	0.000001	0	0	0	0
DC6	Paillier	3072	KG	3.0141	0.14317	0	0	6.01	6.01
DC6	Paillier	3072	E	0.3355	0.01426	0	0	0.6	0.6
DC6	Paillier	3072	D	0.337	0.014323	0	0	0.6	0.6
DC6	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC6	Damgard-Jurik	3072	KG	1.0948	0.052003	0	0	2.18	2.18
DC6	Damgard-Jurik	3072	E	0.7117	0.030247	0	0	1.27	1.27
DC6	Damgard-Jurik	3072	D	0.7153	0.0304	0	0	1.28	1.28
DC6	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC6	Okamoto-Uchiyama	3072	KG	2.5016	0.118826	0	0	4.99	4.99
DC6	Okamoto-Uchiyama	3072	E	0.2924	0.012426	0	0	0.52	0.52
DC6	Okamoto-Uchiyama	3072	D	0.0951	0.004042	0	0	0.17	0.17
DC6	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC6	Goldwasser-Micali	3072	KG	3.2757	0.155596	0	0	6.54	6.54
DC6	Goldwasser-Micali	3072	E	0.0017	0.000072	0	0	0	0
DC6	Goldwasser-Micali	3072	D	0.4174	0.017739	0	0	0.75	0.75
DC6	Goldwasser-Micali	3072	H	0.0005	0.000018	0	0	0	0
DC6	Exponential-ElGamal	3072	KG	0.6004	0.028519	0	0	1.2	1.2
DC6	Exponential-ElGamal	3072	E	0.0271	0.001151	0	0	0.05	0.05
DC6	Exponential-ElGamal	3072	D	28.6196	1.216333	0	0	51.09	51.09
DC6	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC6	EllipticCurve-ElGamal	256	KG	0.0112	0.000532	0	0	0.02	0.02
DC6	EllipticCurve-ElGamal	256	E	0.0125	0.000531	0	0	0.02	0.02
DC6	EllipticCurve-ElGamal	256	D	5.7001	0.242254	0	0	10.17	10.17
DC6	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC7	RSA	3072	KG	14.6075	0.751678	4.51	90.2	78.93	173.64
DC7	RSA	3072	E	0.0802	0.003693	0.02	0.44	0.39	0.85
DC7	RSA	3072	D	0.0934	0.0043	0.03	0.52	0.45	0.99
DC7	RSA	3072	H	0	0.000001	0	0	0	0
DC7	ElGamal	3072	KG	0.9031	0.046472	0.28	5.58	4.88	10.74
DC7	ElGamal	3072	E	0.028	0.001289	0.01	0.15	0.14	0.3
DC7	ElGamal	3072	D	0.0142	0.000654	0	0.08	0.07	0.15
DC7	ElGamal	3072	H	0	0.000001	0	0	0	0
DC7	Paillier	3072	KG	3.0224	0.155528	0.93	18.66	16.33	35.93
DC7	Paillier	3072	E	0.3288	0.015137	0.09	1.82	1.59	3.5
DC7	Paillier	3072	D	0.3311	0.015244	0.09	1.83	1.6	3.52
DC7	Paillier	3072	H	0.0001	0.000005	0	0	0	0
DC7	Damgard-Jurik	3072	KG	4.9993	0.257256	1.54	30.87	27.01	59.43
DC7	Damgard-Jurik	3072	E	0.7044	0.032433	0.19	3.89	3.41	7.49
DC7	Damgard-Jurik	3072	D	0.7052	0.032469	0.19	3.9	3.41	7.5
DC7	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC7	Okamoto-Uchiyama	3072	KG	4.7143	0.24259	1.46	29.11	25.47	56.04
DC7	Okamoto-Uchiyama	3072	E	0.2963	0.013641	0.08	1.64	1.43	3.15
DC7	Okamoto-Uchiyama	3072	D	0.0957	0.004406	0.03	0.53	0.46	1.02
DC7	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC7	Goldwasser-Micali	3072	KG	2.6347	0.135577	0.81	16.27	14.24	31.32
DC7	Goldwasser-Micali	3072	E	0.0017	0.000078	0	0.01	0.01	0.02
DC7	Goldwasser-Micali	3072	D	0.4171	0.019204	0.12	2.3	2.02	4.44
DC7	Goldwasser-Micali	3072	H	0.0005	0.00002	0	0	0	0
DC7	Exponential-ElGamal	3072	KG	3.5652	0.183459	1.1	22.02	19.26	42.38
DC7	Exponential-ElGamal	3072	E	0.0271	0.001247	0.01	0.15	0.13	0.29
DC7	Exponential-ElGamal	3072	D	28.0696	1.292371	7.75	155.08	135.7	298.54
DC7	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC7	EllipticCurve-ElGamal	256	KG	0.012	0.000617	0	0.07	0.06	0.14
DC7	EllipticCurve-ElGamal	256	E	0.0117	0.00054	0	0.06	0.06	0.12
DC7	EllipticCurve-ElGamal	256	D	5.674	0.26124	1.57	31.35	27.43	60.35
DC7	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC8	RSA	3072	KG	9.72	0.4617	1.94	38.78	45.25	85.97
DC8	RSA	3072	E	0.0816	0.003469	0.01	0.29	0.34	0.65
DC8	RSA	3072	D	0.0947	0.004025	0.02	0.34	0.39	0.75
DC8	RSA	3072	H	0	0.000001	0	0	0	0
DC8	ElGamal	3072	KG	1.2338	0.058605	0.25	4.92	5.74	10.91
DC8	ElGamal	3072	E	0.0273	0.001161	0	0.1	0.11	0.22
DC8	ElGamal	3072	D	0.0141	0.000599	0	0.05	0.06	0.11
DC8	ElGamal	3072	H	0	0.000001	0	0	0	0
DC8	Paillier	3072	KG	8.5052	0.403997	1.7	33.94	39.59	75.22
DC8	Paillier	3072	E	0.3314	0.014084	0.06	1.18	1.38	2.62
DC8	Paillier	3072	D	0.3326	0.014135	0.06	1.19	1.39	2.63
DC8	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC8	Damgard-Jurik	3072	KG	1.9743	0.093779	0.39	7.88	9.19	17.46
DC8	Damgard-Jurik	3072	E	0.7086	0.030113	0.13	2.53	2.95	5.61
DC8	Damgard-Jurik	3072	D	0.7105	0.030196	0.13	2.54	2.96	5.62
DC8	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC8	Okamoto-Uchiyama	3072	KG	4.0001	0.190005	0.8	15.96	18.62	35.38
DC8	Okamoto-Uchiyama	3072	E	0.2907	0.012357	0.05	1.04	1.21	2.3
DC8	Okamoto-Uchiyama	3072	D	0.094	0.003995	0.02	0.34	0.39	0.74
DC8	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC8	Goldwasser-Micali	3072	KG	2.1896	0.104006	0.44	8.74	10.19	19.37
DC8	Goldwasser-Micali	3072	E	0.0017	0.000071	0	0.01	0.01	0.01
DC8	Goldwasser-Micali	3072	D	0.412	0.01751	0.07	1.47	1.72	3.26
DC8	Goldwasser-Micali	3072	H	0.0005	0.000018	0	0	0	0
DC8	Exponential-ElGamal	3072	KG	3.8172	0.181317	0.76	15.23	17.77	33.76
DC8	Exponential-ElGamal	3072	E	0.0282	0.001198	0.01	0.1	0.12	0.22
DC8	Exponential-ElGamal	3072	D	28.5349	1.212733	5.09	101.87	118.85	225.81
DC8	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC8	EllipticCurve-ElGamal	256	KG	0.0112	0.000532	0	0.04	0.05	0.1
DC8	EllipticCurve-ElGamal	256	E	0.0111	0.00047	0	0.04	0.05	0.09
DC8	EllipticCurve-ElGamal	256	D	5.7602	0.244808	1.03	20.56	23.99	45.58
DC8	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC9	RSA	3072	KG	28.6789	1.362248	3.41	68.11	119.2	190.71
DC9	RSA	3072	E	0.0809	0.003439	0.01	0.17	0.3	0.48
DC9	RSA	3072	D	0.0937	0.003982	0.01	0.2	0.35	0.56
DC9	RSA	3072	H	0	0.000001	0	0	0	0
DC9	ElGamal	3072	KG	5.2391	0.248857	0.62	12.44	21.78	34.84
DC9	ElGamal	3072	E	0.0278	0.001181	0	0.06	0.1	0.17
DC9	ElGamal	3072	D	0.0142	0.000603	0	0.03	0.05	0.08
DC9	ElGamal	3072	H	0	0.000001	0	0	0	0
DC9	Paillier	3072	KG	5.6158	0.266751	0.67	13.34	23.34	37.35
DC9	Paillier	3072	E	0.3359	0.014274	0.04	0.71	1.25	2
DC9	Paillier	3072	D	0.3364	0.014297	0.04	0.71	1.25	2
DC9	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC9	Damgard-Jurik	3072	KG	2.653	0.126018	0.32	6.3	11.03	17.64
DC9	Damgard-Jurik	3072	E	0.7135	0.030323	0.08	1.52	2.65	4.25
DC9	Damgard-Jurik	3072	D	0.7173	0.030485	0.08	1.52	2.67	4.27
DC9	Damgard-Jurik	3072	H	0.0003	0.00001	0	0	0	0
DC9	Okamoto-Uchiyama	3072	KG	2.5479	0.121025	0.3	6.05	10.59	16.94
DC9	Okamoto-Uchiyama	3072	E	0.295	0.012536	0.03	0.63	1.1	1.76
DC9	Okamoto-Uchiyama	3072	D	0.0957	0.004067	0.01	0.2	0.36	0.57
DC9	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC9	Goldwasser-Micali	3072	KG	3.3484	0.159049	0.4	7.95	13.92	22.27
DC9	Goldwasser-Micali	3072	E	0.0017	0.000074	0	0	0.01	0.01
DC9	Goldwasser-Micali	3072	D	0.4144	0.017612	0.04	0.88	1.54	2.47
DC9	Goldwasser-Micali	3072	H	0.0005	0.000018	0	0	0	0
DC9	Exponential-ElGamal	3072	KG	0.8565	0.040684	0.1	2.03	3.56	5.7
DC9	Exponential-ElGamal	3072	E	0.0271	0.001154	0	0.06	0.1	0.16
DC9	Exponential-ElGamal	3072	D	27.9974	1.189889	2.97	59.49	104.12	166.58
DC9	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC9	EllipticCurve-ElGamal	256	KG	0.0113	0.000537	0	0.03	0.05	0.08
DC9	EllipticCurve-ElGamal	256	E	0.0115	0.000489	0	0.02	0.04	0.07
DC9	EllipticCurve-ElGamal	256	D	5.7603	0.244813	0.61	12.24	21.42	34.27
DC9	EllipticCurve-ElGamal	256	H	0.0001	0.000003	0	0	0	0
DC10	RSA	3072	KG	14.6362	0.637285	0.64	12.75	44.61	57.99
DC11	RSA	3072	E	0.0811	0.00316	0	0.06	0.22	0.29
DC12	RSA	3072	D	0.0943	0.003674	0	0.07	0.26	0.33
DC13	RSA	3072	H	0	0.000001	0	0	0	0
DC14	ElGamal	3072	KG	1.8475	0.080443	0.08	1.61	5.63	7.32
DC15	ElGamal	3072	E	0.0274	0.001067	0	0.02	0.07	0.1
DC16	ElGamal	3072	D	0.0142	0.000553	0	0.01	0.04	0.05
DC17	ElGamal	3072	H	0	0.000001	0	0	0	0
DC18	Paillier	3072	KG	2.4511	0.106725	0.11	2.13	7.47	9.71
DC19	Paillier	3072	E	0.3291	0.012821	0.01	0.26	0.9	1.17
DC20	Paillier	3072	D	0.332	0.012934	0.01	0.26	0.91	1.18
DC21	Paillier	3072	H	0.0001	0.000004	0	0	0	0
DC22	Damgard-Jurik	3072	KG	4.1464	0.180541	0.18	3.61	12.64	16.43
DC23	Damgard-Jurik	3072	E	0.704	0.027429	0.03	0.55	1.92	2.5
DC24	Damgard-Jurik	3072	D	0.7107	0.027688	0.03	0.55	1.94	2.52
DC25	Damgard-Jurik	3072	H	0.0003	0.000009	0	0	0	0
DC26	Okamoto-Uchiyama	3072	KG	6.2837	0.273603	0.27	5.47	19.15	24.9
DC27	Okamoto-Uchiyama	3072	E	0.2934	0.011429	0.01	0.23	0.8	1.04
DC28	Okamoto-Uchiyama	3072	D	0.0946	0.003685	0	0.07	0.26	0.34
DC29	Okamoto-Uchiyama	3072	H	0.0001	0.000002	0	0	0	0
DC30	Goldwasser-Micali	3072	KG	1.9582	0.085263	0.09	1.71	5.97	7.76
DC31	Goldwasser-Micali	3072	E	0.0017	0.000065	0	0	0	0.01
DC32	Goldwasser-Micali	3072	D	0.4019	0.015657	0.02	0.31	1.1	1.42
DC33	Goldwasser-Micali	3072	H	0.0005	0.000016	0	0	0	0
DC34	Exponential-ElGamal	3072	KG	7.7826	0.338867	0.34	6.78	23.72	30.84
DC35	Exponential-ElGamal	3072	E	0.0273	0.001062	0	0.02	0.07	0.1
DC36	Exponential-ElGamal	3072	D	28.5325	1.111579	1.11	22.23	77.81	101.15
DC37	Exponential-ElGamal	3072	H	0	0.000001	0	0	0	0
DC38	EllipticCurve-ElGamal	256	KG	0.0113	0.000492	0	0.01	0.03	0.04
DC39	EllipticCurve-ElGamal	256	E	0.0111	0.000432	0	0.01	0.03	0.04
DC40	EllipticCurve-ElGamal	256	D	5.785	0.225374	0.23	4.51	15.78	20.51
DC41	EllipticCurve-ElGamal	256	H	0.0001	0.000002	0	0	0	0

6. Conclusion

In recent years, the field of encryption technologies has witnessed remarkable progress, culminating in the development of LightPHE—a groundbreaking framework tailored for partially homomorphic encryption (PHE). This innovative tool introduces a unified interface that seamlessly integrates multiple PHE algorithms, empowering developers with a practical and efficient means to safeguard sensitive data while retaining the ability to perform meaningful computations. This paper has meticulously examined the mathematical underpinnings of various PHE algorithms, elucidating their homomorphic properties and establishing a robust foundation for understanding how LightPHE enables secure operations on encrypted datasets.

The architectural design of LightPHE stands out for its modularity and reliance on an abstract class hierarchy. This structure not only facilitates the incorporation of new PHE algorithms but also ensures a consistent and intuitive user experience. Such design choices enhance code reusability and extensibility, enabling developers to rapidly prototype and deploy secure applications. Through practical code examples, we have demonstrated LightPHE’s real-world applicability, showcasing its capacity to execute homomorphic operations—such as addition and multiplication—efficiently. By abstracting the inherent complexities of PHE algorithms, LightPHE allows practitioners to concentrate on application development rather than grappling with cryptographic intricacies.

To assess its performance, LightPHE was subjected to comprehensive evaluations across a spectrum of key sizes and cloud-based environments, including Colab Normal, Colab A100 GPU, Colab T4 High RAM, Colab TPU2, and Azure Spark. These benchmarks reveal the framework’s scalability and adaptability, with high-performance platforms like Colab A100 GPU and TPU2 excelling due to their advanced parallel processing capabilities. More accessible environments, such as Colab Normal and Azure Spark, also proved effective, offering viable solutions for projects with limited computational resources.

Furthermore, this study extends beyond technical performance to address an increasingly critical concern: environmental sustainability. By analyzing Scope 1, 2, and 3 carbon emissions tied to homomorphic encryption workloads in cloud data centers, we highlight the environmental implications of deploying LightPHE. Our findings, which account for variations in infrastructure configurations and regional electricity grids, emphasize the necessity of aligning robust security measures with eco-conscious practices. This dual focus ensures that the advantages of homomorphic encryption are not achieved at the expense of unsustainable resource consumption.

In essence, LightPHE marks a pivotal advancement in the realm of partially homomorphic encryption, delivering a versatile, user-friendly framework that bridges theoretical rigor with practical utility. By lowering the barriers to implementing secure computation, LightPHE sets the stage for its widespread adoption across diverse sectors, including healthcare, finance, and beyond. Looking ahead, future research could prioritize enhancing the framework’s computational efficiency and minimizing its environmental footprint, thereby unlocking new horizons for secure, privacy-preserving, and sustainable computing in an increasingly digital world.