Fully Conjugated Heteroatomic Non- and Quasi-Alternant Polyradicals

1. Introduction

Organic Polyradicals with more than two unpaired electrons comprise interesting classes of compounds that have applications in molecular and quantum technologies [1,2,3,4,5,6,7,8,9]. In our recent works, we showed how to make a leap from diradicals to tetraradicals by the topological control of $\pi$-conjugation [10], we described a planar and fully $\pi$-conjugated tetraradical(oid) [11], and we formulated the theory of rational design of fully $\pi$-conjugated organic polyradicals with any number of unpaired electrons and any ground-state multiplicity. Our method allows the algorithmic design of polyradicals from the fragments of $\gamma$-graphyne, polycyclic aromatic hydrocarbons (PAHs) and any admixture of fully $\pi$-conjugated compounds [12]. In biological systems, heteroatomic aromatic compounds and heteroatomic conjugated systems are common and it is interesting to explore how to create polyradicals from the similar building blocks. Such chemical classes of compounds are also quite underexplored in the context of magnetic properties. Thus, we designed fully $\pi$-conjugated thiophene-based quasi-alternant and non-alternant diradical(oid)s and tetraradical(oid)s with different open-shell characters and low-energy spectrum as a consequence of a topological control of $\pi$-conjugation and following the rules of rational design of polyradicals formulated in our recent publications. Our chemical model requires that designed polyradicals possess a fully conjugated $\pi$-system (including unpaired electrons), ensuring stabilization through delocalization and aromaticity. Also, each pair of directly $\pi$-conjugated unpaired electrons should be bridged by a system possessing aromatic resonance energy equivalent to at least two benzene-like rings, which may be shared among different such pairs. The topological principles by which we analyze the modes of conjugation in the $\pi$-systems allowed the rational design apply not only to alternant hydrocarbons for which it is simple to predict the ground state by Ovchinnikov’s rule [13], but also to the non-alternant systems which have multiple paths of direct $\pi$-conjugation possibly leading to the conflicting spin configurations upon following the Coulson-Rushbrooke pairing theorem, also known as the “mirror theorem” [14,15]. Nonetheless, upon application of the topological principles that had allowed to design polyradicals of any open-shell properties, we can also predict the ground state by analyzing valence bond forms (VBFs) of the presented compounds and paths of direct $\pi$-conjugations between unpaired electrons that can lead to on-bond pairing /allow closing the shell. The presented polyradicals contain five-membered rings such as non-alternant cyclopentadineyl and quasi-alternant thiophene rings, latter of which has aromatic configuration that can be used to stabilize open-shell structure of the designed compound. By employing the topological and resonance factors, we designed the heteroatomic polyradicals, which exemplifies how our theory of polyradical opens possibilities to design heteroatomic polyradicals, which can have important applications in organic magnetic materials and devices.

2. Results and Discussion

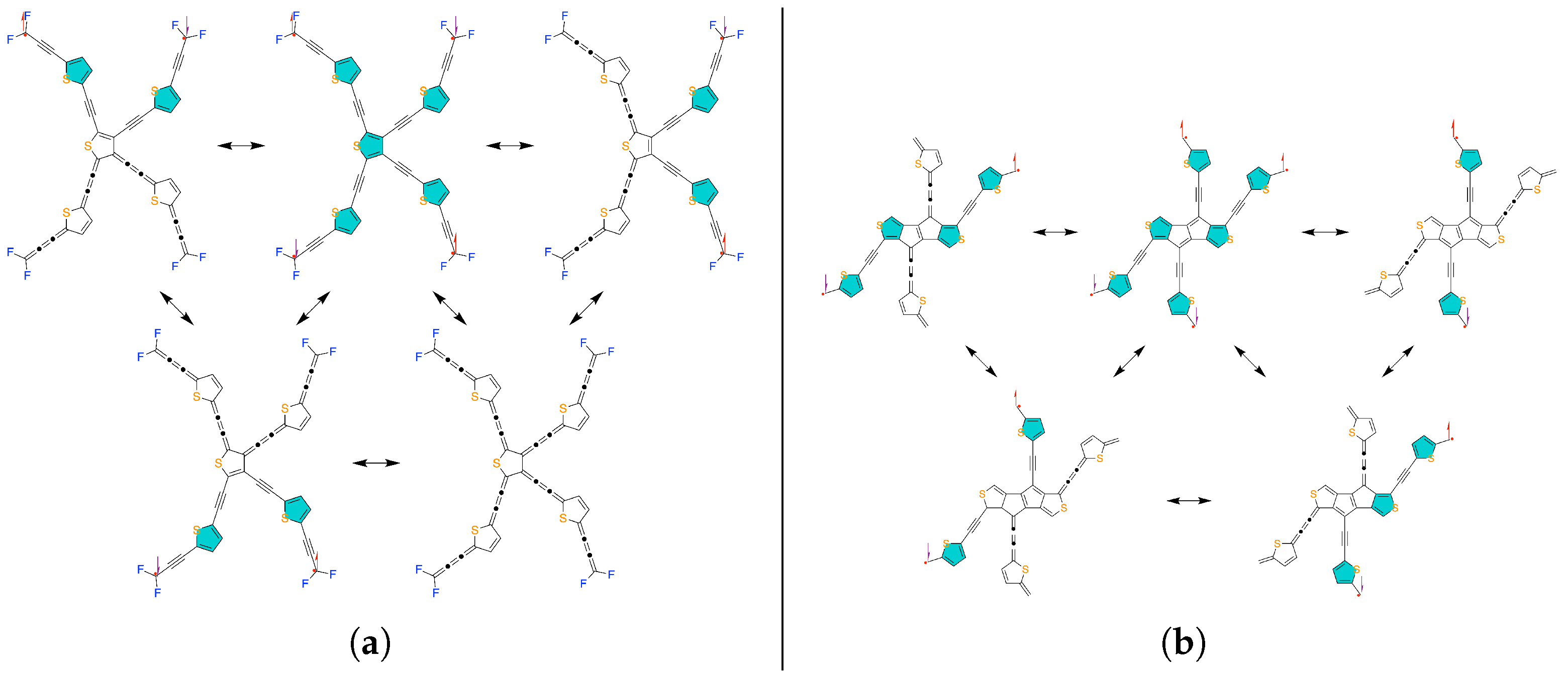
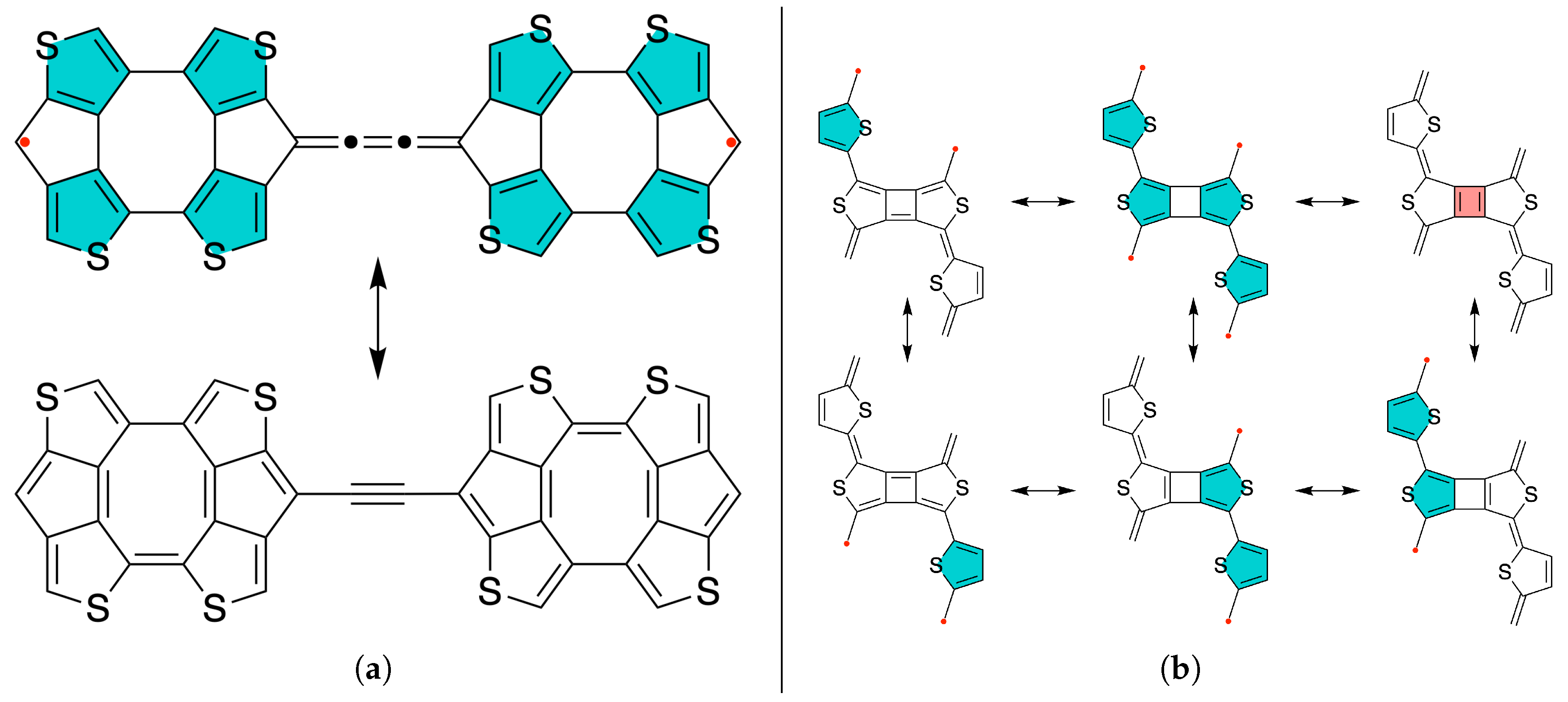
By application of the theory of rational design of polyradicals, we designed parallel- and cross-conjugated tetraradical(oid)s, which contain five-membered cyclopentadienyl and thiophene rings. The aromatic stabilization of thiophene and the topology of the $\pi$-systems leads to high open-shell characters in the designed compounds as results show. The resonance structures of parallel-conjugated thiophenic tetraradical(oid) PT_0,4 is given in Figure 1a and those of cross-conjugated thiophenic tetraradical(oid) CT_2,4 is given in Figure 1b.

Upon analysis of the valence bond forms of PT_0,4 in Figure 1a, we can note that there is no lower-bond restriction for this compound to have open shells, in diradical structure compared to closed-shell structure, two more thiophene rings assume aromatic configuration with 6 $\pi$ electrons. In the tetraradical valence bond form, three more thiophene rings assume aromatic configuration compared to diradical VBFs (Figure 1a). Our theory of polyradical design says that we need the aromatic resonance energy from at least two-three benzene rings to offset the energy of the broken $\pi$ bond upon opening the shell, and the aromatic resonance energy of benzene is about 151 $kj/mol$ while the thiophene’s is about 121 $kj/mol$ [16]. Thus, about 2.5–3.75 thiophene rings are needed to bridge directly $\pi$-conjugated unpaired electrons to maintain the high open shell character. Moreover, as apparent from the resonance structures of PT_0,4 in Figure 1a, each unpaired electron is directly $\pi$-conjugated to two other unpaired electrons, so that in some valence bond forms, each such electron could be paired with any of the other directly $\pi$-conjugated electron and close the corresponding shell. In total, if every unpaired electron becomes paired, the aromatic configuration of all five thiophene rings is lost. This co-dependence between aromaticity and open-shell character leads to high diradical and tetraradical characters of the PT_0,4. We computed the electronic structure of PT_0,4 with complete active space self-consistent field (CASSCF) [17,18,19,20,21,22,23,24] calculations with Dunning’s correlation consistent double-$\zeta$ basis set [25], which showed that the low-energy spectrum of PT_0,4 has narrow spectral range of 72 cm⁻¹, singlet ground state (GS) with a quintet highest-energy spin state (HS), and singlet-triplet gap of 29 cm⁻¹, as shown in taba2 (see computational details thoroughly in section S2 of the Supporting Information). 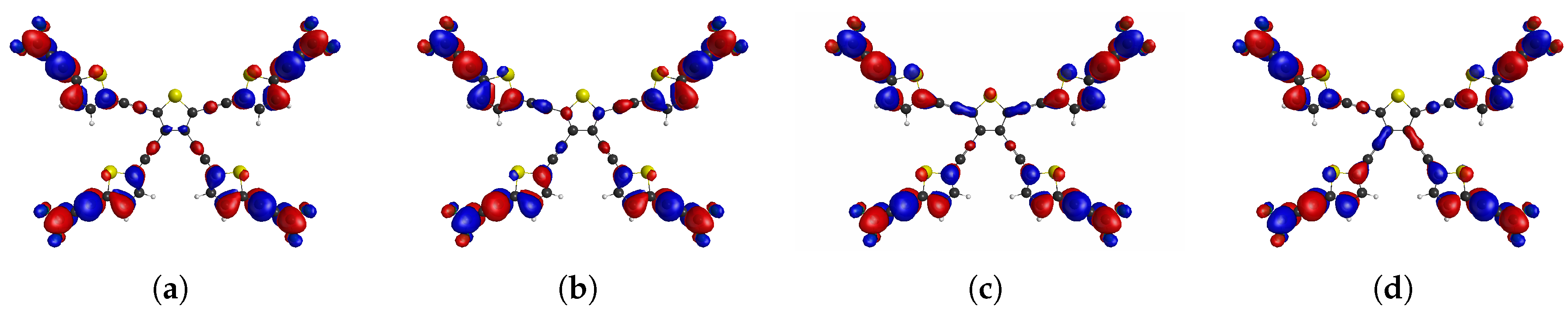The natural orbitals (NOs) are eigenvectors of the first-order density matrix and their occupation numbers are corresponding eigenvalues [26]. Each of these orbitals shows the electron density distribution of the average number of electrons occupying it. Frontier NOs of PT_0,4 with symbolic assignations are given in fig3. These NOs describe the electron density distribution in the spin states of the low-energy spectrum given taba2. As evident from the frontier NO occupation numbers of PT_0,4, even in the singlet ground state, four of $n_{NO}$ values are very close to 1, which means there are almost four unpaired electrons. Diradical and tetraradical $y_0$ and $y_1$ as special cases of polyradical character $y_n$ vary from $y_n=0$ (fully closed shell) to $y_n=1$ (fully open shell) and we are calculating them based on frontier NO occupation number according to the method of Yamaguchi [27]. For PT_0,4, the diradical character $y_0=0.92$ and tetraradical character $y_1=0.90$, implying almost fully open-shell electronic structure with four unpaired electrons. Even though there is no topological restriction for this compound to have an open-shell electronic structure, the electrons remain unpaired because the collective aromatic resonance energy of thiophene rings offsets the energy that would have been gained by $\pi$ bonding if these electrons paired.

Figure 2. The frontier CASSCF NOs of tetraradical(oid) PT_0,4 describing the density distribution of unpaired electrons indicated by NO occupation numbers: (a)$C_0$, (b)$C_1$, (c)$C_1^{\prime }$, (d)$C_2$,

Figure 2. The frontier CASSCF NOs of tetraradical(oid) PT_0,4 describing the density distribution of unpaired electrons indicated by NO occupation numbers: (a)$C_0$, (b)$C_1$, (c)$C_1^{\prime }$, (d)$C_2$,

Table 1. CASSCF(12,12)/cc-pVDZ states of PT_0,4 using quintet UKS/DFT-optimized geometry.

State	Symmetry	HONO – 1		HONO		LUNO		LUNO + 1		$\Delta E$ from G. S. (cm−1)
$S_0$	A	$C_1^{\prime }$	1.050	$C_2$	1.043	$C_0$	0.958	$C_1$	0.948	0.00
$T_0$	A	$L_{+}$	1.037	$R_{-}$	1.012	$R_{+}$	0.989	$L_{-}$	0.962	29.34
$T_1$	A	$C_2$	1.024	$C_1^{\prime }$	1.017	$C_0$	0.983	$C_1$	0.975	44.18
$S_1$	A	$L_{+}$	1.018	$R_{-}$	1.010	$R_{+}$	0.993	$L_{-}$	0.979	58.31
$T_2$	A	$R_{-}$	1.011	$L_{+}$	1.008	$L_{-}$	0.991	$R_{+}$	0.990	64.25
$Q_0$	A	$D_1^{\prime }$	1.000	$D_2$	1.000	$D_0$	1.000	$D_1$	0.999	72.21

Table 1. CASSCF(12,12)/cc-pVDZ states of PT_0,4 using quintet UKS/DFT-optimized geometry.

State	Symmetry	HONO – 1		HONO		LUNO		LUNO + 1		$\Delta E$ from G. S. (cm−1)
$S_0$	A	$C_1^{\prime }$	1.050	$C_2$	1.043	$C_0$	0.958	$C_1$	0.948	0.00
$T_0$	A	$L_{+}$	1.037	$R_{-}$	1.012	$R_{+}$	0.989	$L_{-}$	0.962	29.34
$T_1$	A	$C_2$	1.024	$C_1^{\prime }$	1.017	$C_0$	0.983	$C_1$	0.975	44.18
$S_1$	A	$L_{+}$	1.018	$R_{-}$	1.010	$R_{+}$	0.993	$L_{-}$	0.979	58.31
$T_2$	A	$R_{-}$	1.011	$L_{+}$	1.008	$L_{-}$	0.991	$R_{+}$	0.990	64.25
$Q_0$	A	$D_1^{\prime }$	1.000	$D_2$	1.000	$D_0$	1.000	$D_1$	0.999	72.21

Having characterized the parallel-conjugated tetraradical(oid), let us now focus on the cross-conjugated thiophenic tetraradical(oid) CT_2,4 which includes not only thiophene rings but also fused cyclopentadienyl rings so that it has five-membered rings only based on the carbon atom. It is important to emphasize that we cannot create the true cross-conjugation with only five-membered heterocyclic aromatic rings (furan, pyrrole, thiophene, etc.) as shown in Figure 1a. This is because paths of direct $\pi$-conjugation can diverge in such geometries. However, if we have the five-membered rings with each atom able to form single or double bonds within and outside the ring, we can create such geometries when connected terminal sites can have converging paths of direct $\pi$-conjugation, which can be used to create the topological restriction on the lower-bound number of unpaired electrons. This property was employed in designing CT_2,4 for which resonance structures are shown in Figure 1b. Notably, from these structures it is evident that closing the shell between unpaired electrons on the opposite sides of the pentaleno[1,2-c:4,5-c’]dithiophene subsystem only destroys the aromatic configuration of two thiophene rings, while any other on-bond pairing destroys at least three. Moreover, among diradical VBFs of the CT_2,4, which have equal number of $\pi$ bonds, one of them has highest amount (four) of thiophene rings with aromatic configuration. Thus, according to Clar’s rule [28], it should the most important contributor between diradical VBFs should. In contrast, there are no such differences between diradical valence bond forms of PT_0,4. Hence, CT_2,4 might have a preferred open shell subsystem in some of the states, as evident from $S_0$ and $T_0$ states described by tabab2. This concept allows us to control the tendency of modulation between open-shell characters (diradical, tetraradical, etc.) and energy gaps between lower-energy states and relatively higher-energy states within the spin spectrum of polyradicals.

Table 2. CASSCF(12,12)/cc-pVDZ states of CT_2,4 using triplet UKS/DFT-optimized geometry.

State	Symmetry	HONO – 1		HONO		LUNO		LUNO + 1		$\Delta \mathit{E}$ from G. S. (cm−1)
$S_0$	$A_g$	N	1.848	$L_{+}$*	1.012	$L_{-}$*	0.990	N	0.160	0.00
$T_0$	$B_u$	N	1.852	$L_{+}$*	1.001	$L_{-}$*	1.001	N	0.157	18.84
$T_1$	$A_g$	$C_0$	1.097	$C_1$	1.075	$C_2$	0.934	$C_1^{\prime }$	0.898	5197.44
$T_2$	$B_u$	$C_0$	1.017	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.985	5197.44
$Q_0$	$A_g$	$C_0$	1.017	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.985	5197.44
$S_1$	$A_g$	$C_0$	1.025	$C_1$	1.012	$C_2$	1.011	$C_1^{\prime }$	0.954	5517.36

*These orbital symbols mean the unpaired electrons are in the long (L) chain corresponding to the first resonance structure (top left) in Figure 1b.

Table 2. CASSCF(12,12)/cc-pVDZ states of CT_2,4 using triplet UKS/DFT-optimized geometry.

State	Symmetry	HONO – 1		HONO		LUNO		LUNO + 1		$\Delta \mathit{E}$ from G. S. (cm−1)
$S_0$	$A_g$	N	1.848	$L_{+}$*	1.012	$L_{-}$*	0.990	N	0.160	0.00
$T_0$	$B_u$	N	1.852	$L_{+}$*	1.001	$L_{-}$*	1.001	N	0.157	18.84
$T_1$	$A_g$	$C_0$	1.097	$C_1$	1.075	$C_2$	0.934	$C_1^{\prime }$	0.898	5197.44
$T_2$	$B_u$	$C_0$	1.017	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.985	5197.44
$Q_0$	$A_g$	$C_0$	1.017	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.985	5197.44
$S_1$	$A_g$	$C_0$	1.025	$C_1$	1.012	$C_2$	1.011	$C_1^{\prime }$	0.954	5517.36

*These orbital symbols mean the unpaired electrons are in the long (L) chain corresponding to the first resonance structure (top left) in Figure 1b.

Table 3. CASSCF(12,12/cc-pVDZ states of CT_2,4 using quintet UKS/DFT-optimized geometry.

State	Symmetry	HONO – 1		HONO		LUNO		LUNO + 1		$\Delta E$ from G. S. (cm−1)
$S_0$	$A_g$	$C_0$	1.202	$C_2$	1.002	$C_1$	0.999	$C_1^{\prime }$	0.799	0.00
$T_0$	$B_u$	$C_0$	1.129	$C_2$	1.000	$C_1$	1.000	$C_1^{\prime }$	0.872	254.64
$T_1$	$B_u$	$C_0$	1.006	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.995	671.30
$Q_0$	$A_g$	$C_0$	1.006	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.995	671.33
$T_2$	$A_g$	N/A*
$S_1$	$A_g$	$C_0$	1.025	$C_1$	1.012	$C_2$	1.011	$C_1^{\prime }$	0.954	817.11

*This CASSCF state did not converge for the quintet UKS/DFT-optimized geometry, but is available in CASSCF(12,12) results using triplet UKS/DFT-optimized geometry given in tabab2.

Table 3. CASSCF(12,12/cc-pVDZ states of CT_2,4 using quintet UKS/DFT-optimized geometry.

State	Symmetry	HONO – 1		HONO		LUNO		LUNO + 1		$\Delta E$ from G. S. (cm−1)
$S_0$	$A_g$	$C_0$	1.202	$C_2$	1.002	$C_1$	0.999	$C_1^{\prime }$	0.799	0.00
$T_0$	$B_u$	$C_0$	1.129	$C_2$	1.000	$C_1$	1.000	$C_1^{\prime }$	0.872	254.64
$T_1$	$B_u$	$C_0$	1.006	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.995	671.30
$Q_0$	$A_g$	$C_0$	1.006	$C_1$	1.000	$C_2$	1.000	$C_1^{\prime }$	0.995	671.33
$T_2$	$A_g$	N/A*
$S_1$	$A_g$	$C_0$	1.025	$C_1$	1.012	$C_2$	1.011	$C_1^{\prime }$	0.954	817.11

*This CASSCF state did not converge for the quintet UKS/DFT-optimized geometry, but is available in CASSCF(12,12) results using triplet UKS/DFT-optimized geometry given in tabab2.

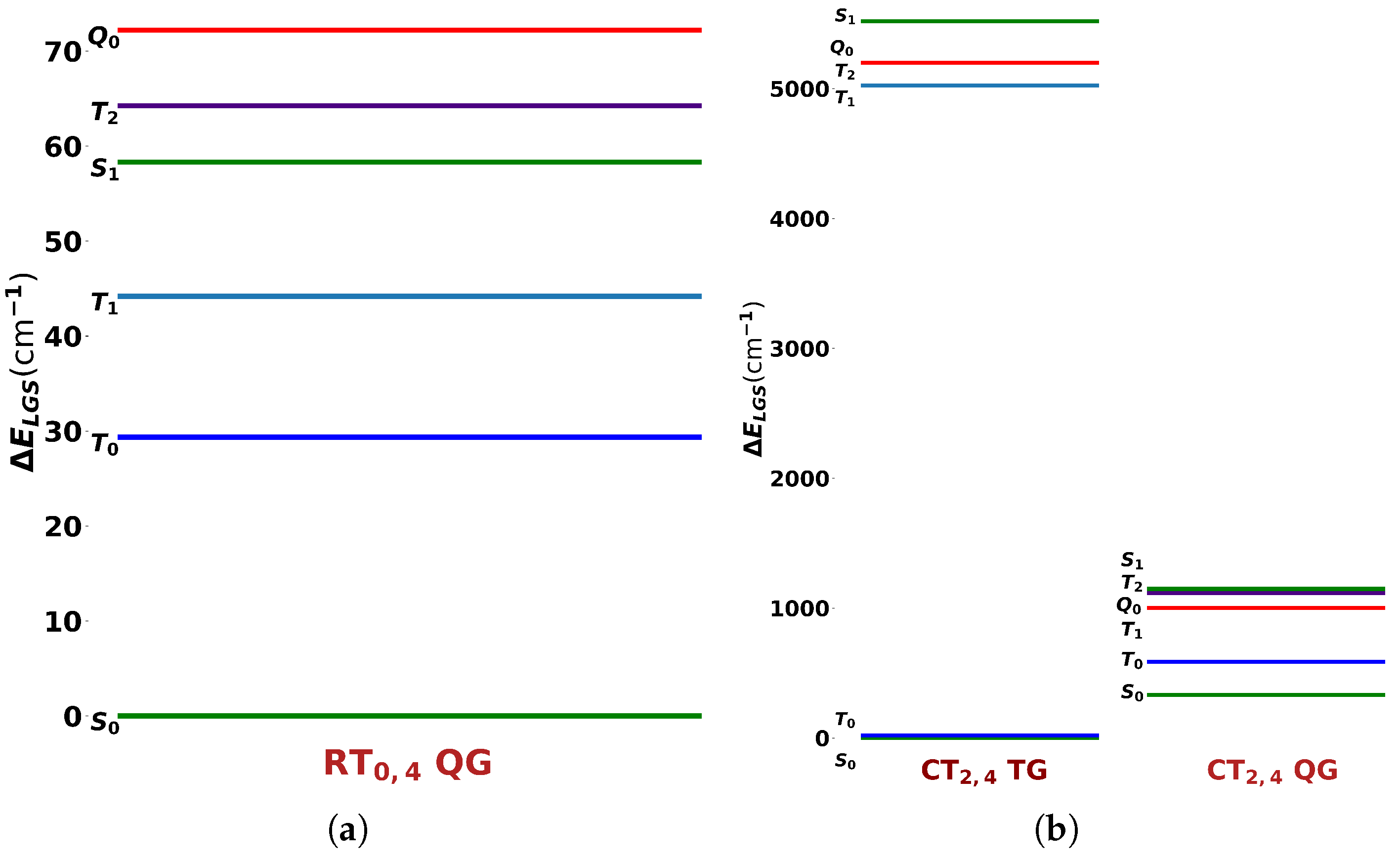
The CASSCF results for different spin states and their characteristics based on frontier NOs and occupation numbers are given in Table 1 and Table 2, and CASSCF frontier NOs with symbolic assignations are given in fig4. The spin state spectrum for triplet UKS/DFT and quintet UKS/DFT-optimized geometries (TG and QG, respectively) is given in Figure 4b. Results show that in the CASSCF(12,12) singlet ground state obtained for triplet UKS/DFT-optimized geometry has two unpaired electrons and the two unpaired electrons are found in the specific parts of the molecule, as shown by the first resonance structure (top left) in Figure 1b. This is because such a resonance structure has the most amount of thiophene rings in the aromatic configuration among the diradical VBFs and for the triplet UKS/DFT-optimized geometry favors this configuration. However, with sufficiently close energies (almost the degenerate region of PES), when the quintet UKS/DFT-optimized geometry is used for CASSCF(12,12) calculations, the singlet ground state has almost four unpaired electrons according to NO occupation numbers of $S_0$ state. The diradical character is $y_0=0.98-1.00$ and tetraradical character is $y_1=0.61$ (for QG). The comparison of these results shows that since CT_2,4 is topologically restricted to be a diradical, its diradical character is higher than that of PT_0,4, which does not have such restrictions. However, since tetraradical valence bond form of PT_0,4 has three more thiophene rings in aromatic configuration compared to diradical valence bond forms, while tetraradical VBF of CT_2,4 has only two more thiophene rings in aromatic configuration compared to one of the diradical VBFs, the tetraradical character of PT_0,4 is higher. The comparison of the structure of the low-energy spectra of these tetraradical(oid)s is given in fig5. The detailed CASSCF results for these compounds are given in section S3 of the Supporting Information. This is an example how to control the tendency of modulation of open-shell characters for two, four and higher number of unpaired electrons. The topological control of $\pi$-conjugation used in conjunction with the control of aromatic stabilization per each pair of directly $\pi$-conjugated unpaired electrons allows the precise control over the open-shell properties of the unsaturated organic compounds.

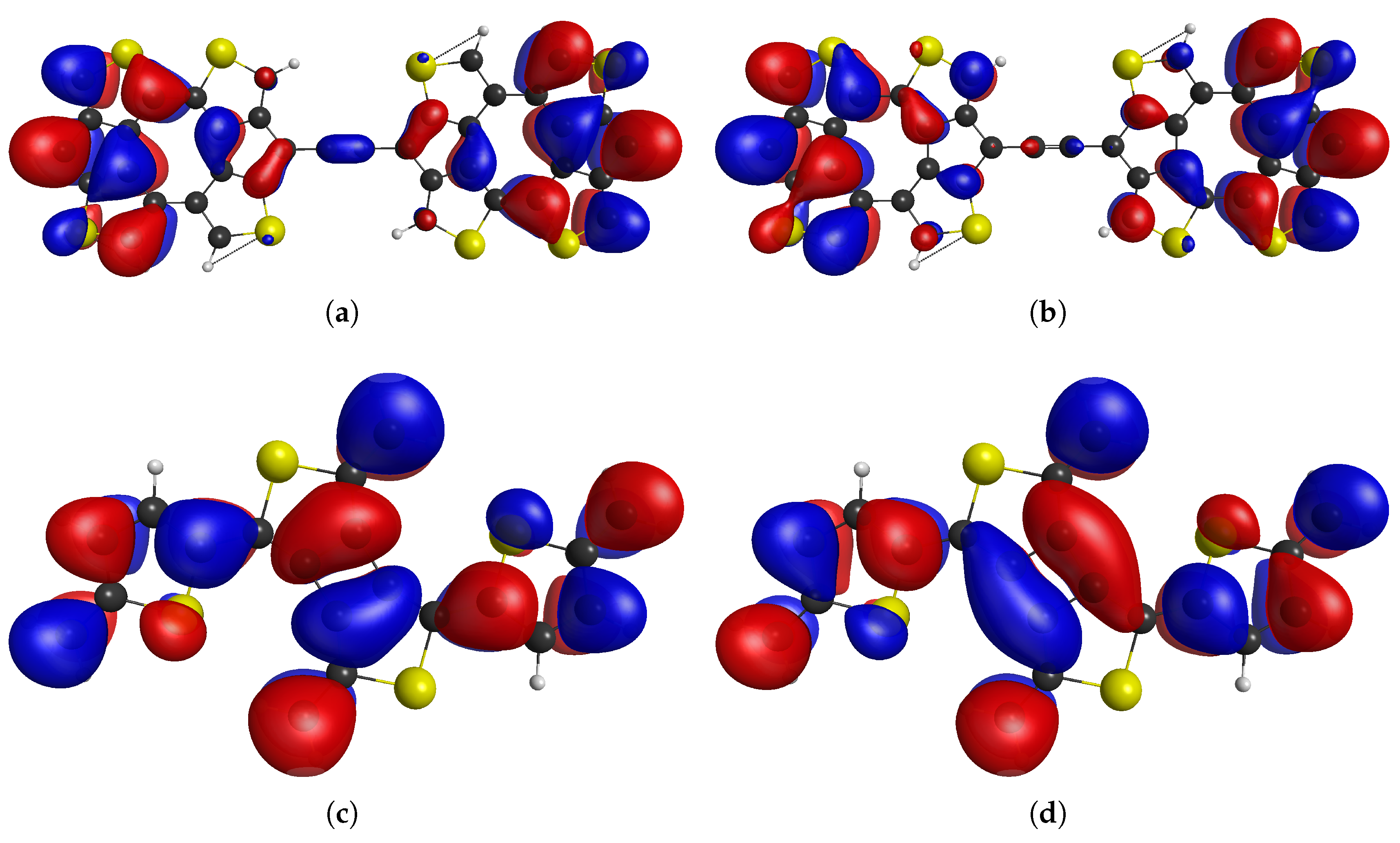
Figure 3. The frontier CASSCF NOs of tetraradical(oid) CT_2,4 describing the density distribution of unpaired electrons indicated by NO occupation numbers: (a)$C_0$, (b)$C_1$, (c)$C_1^{\prime }$, (d)$C_2$,

Figure 3. The frontier CASSCF NOs of tetraradical(oid) CT_2,4 describing the density distribution of unpaired electrons indicated by NO occupation numbers: (a)$C_0$, (b)$C_1$, (c)$C_1^{\prime }$, (d)$C_2$,

Figure 4. The CASSCF spectra of (a) PT_0,4 with quintet-optimized geometry (QG) and (b)CT_2,4 with triplet-optimized geometry (TG) and QG.

Figure 4. The CASSCF spectra of (a) PT_0,4 with quintet-optimized geometry (QG) and (b)CT_2,4 with triplet-optimized geometry (TG) and QG.

We also designed the diradical system which contains only five-membered rings and no terminal methylene groups as shown in Figure 5a, in which the cumulative aromaticity of the thiophene rings results in high open-shell character, as verified by CASSCF(14,14)/cc-pVDZ calculations. Specifically, diradical character $y_0=0.95-0.97$, with a singlet-triplet gap of $\Delta E_{S-T}=5-12$ cm⁻¹. This system is non-alternant, but due to the symmetry between paths of direct $\pi$-conjugation and antiferromagnetic coupling for both paths, it can be predicted that the ground state has a multiplicity of singlet.

In addition to taking advantage of aromaticity and topological restrictions to design compounds with high open-shell characters, we can also take partial or full advantage of anti-aromaticity. In principle, any effect in the compound which stabilizes or destabilizes particular configurations can be used to control some of the properties of compounds. If we are using aromaticity to stabilize open-shell configurations of the compounds, we can use the analogical strategy and use anti-aromaticity to destabilize the closed-shell configurations and in this manner, design compounds with high open-shell character. To exemplify this concept, we designed tetraradical(oid) ${\mathrm{TR}}_{0^{\prime },4}$, which is expected to have significantly higher diradical character than tetraradical character, because two thiophene aromatic rings are not always sufficient to promote very high ($\ge 0.7$) open-shell character, but the additional effect of anti-aromaticity in closed-shell VBF compared to diradical VBF with two thiophene rings in the aromatic configuration is greater difference than diradical VBF compared to tetraradical VBF with four thiophene rings in aromatic configuration. Hence, the additional difference made by anti-aromaticity of the cyclobutadiene creates higher diradical character than tetraradical character, even though each open shell is stabilized by two thiophene rings in aromatic configuration according to the resonance structures in Figure 5b. As a consequence, the diradical character of this compound is $y_0=0.34-0.49$ and tetraradical character is $y_1=0.013-0.058$ according to CASSCF NO occupation numbers of singlet ground state ($S_0$) determined by CASSCF(12,12)/cc-pVDZ calculations for triplet and quintet UKS/DFT-optimized geometries. The detailed CASSCF results for TD_0,2 and ${\mathrm{TR}}_{0^{\prime },4}$ are given in section S3 of the Supporting Information.

The CASSCF frontier NOs of these compounds are shown in fig6 and they clearly show the presence of unpaired electrons. The higher diradical character of TD_0,2 compared to ${\mathrm{TR}}_{0^{\prime },4}$ can simply be explained by greater difference in TD_0,2 in the number of thiophenic rings in aromatic configuration in diradical VBF compared to closed-shell VBF to offset the energy of the broken $\pi$ bond that leads to the unpaired electrons.

Since we established the rules to control the open-shell characters as well as structure of the spin spectrum of the compounds and now we can create polyradicals with heteroatomic aromatic rings, we can envisage multifunctional molecular materials showing cross-dependent effects between magnetic response (diamagnetism versus ordered magnetism) and external oriented electric field or mechanical stress.

Figure 6. The CASSCF NOs of TD_0,2 ((a) and (b)) and ${\mathrm{TR}}_{0^{\prime },4}$ ((c) and (d)).

Figure 6. The CASSCF NOs of TD_0,2 ((a) and (b)) and ${\mathrm{TR}}_{0^{\prime },4}$ ((c) and (d)).

3. Conclusions

In this work, we designed diradical(oid)s and tetraradical(oid)s with different geometries and topologies of $\pi$-systems and by taking advantage of cross-conjugation, aromaticity and anti-aromaticity, we were able to create compounds with moderate to high diradical and tetraradical characters. This study is the extension of our theory of rational design of polyradicals and applies the rules of the theory in the context of quasi-alternant and non-alternant systems. We can thus conclude that the design rules from our theory are able to create polyradicals from the presented class of compounds. The idea is that any $\pi$-(sub)system, which can assume different configurations, can be used for bridging directly $\pi$-conjugated unpaired electrons. If there is sufficient difference in energies of these configurations (i.e. if resonance energy is sufficient), we can expect that the electronic structure outside of this $\pi$-(sub)system will assume the configuration which is compatible with the more stable configuration of the $\pi$-(sub)system. This notion with other rules of our theory can serve as a guidebook for rationally designing polyradicals with any number of unpaired electrons and any ground state multiplicity from different classes of organic compounds, which can lead to multifunctional organic materials.