Accuracy Score for Evaluation of Classification on Imbalanced Data

2.1. AC-Score Characteristics

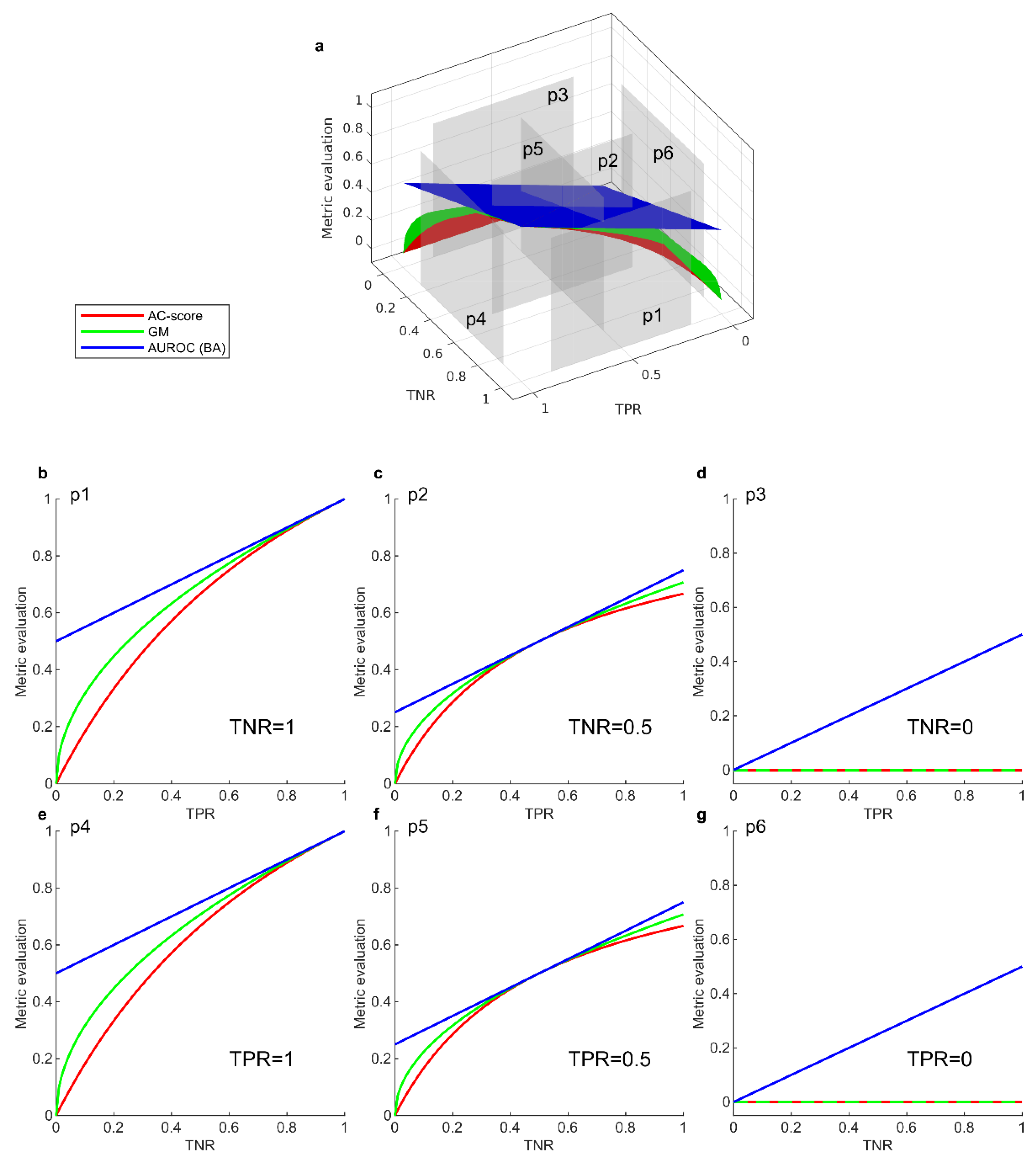
We compared evaluation profiles between AC-score and other null-biased metrics GM, AUROC (and BA as its equivalence, see 3.1) by plotting their evaluation against all parameter values. Figure 1a shows the overall profile of these metrics, and AC-score is shown to have the lowest evaluation everywhere in the plot, indicating AC-score has more pessimistic evaluations than GM, AUROC and BA. This constitutes an advantage since underestimating a model is safer than overestimation.

The sectional curves for these metrics are obtained by fixing one of the two parameters at constant (Figure1b-d by fixing TNR and Figure1e-g by fixing TPR). According to the surface profile, BA and AUROC do not create nonlinear evaluation when the difference between TPR and TNR varies. Compared to GM, AC-score penalizes more strongly when the difference between TPR and TNR gets larger. When TPR or TNR gets zero, AC-score converges to GM, but these are the scenarios of less interests. This characteristic indicates that AC-score has a harsher penalty to the TPR-TNR discrepancy, offering a fair evaluation and thus better fitting of classifiers on imbalanced data.

2.2. AC-Score Evaluates Fairly and Stably Performance of Classifiers on Imbalanced Dataset

To compare evaluations using different metrics for fitted models trained and make predictions on imbalanced data, tests were performed on one binary-pair of the SVHN dataset using LDA and NMC (see 3.3). Three different conditions of data imbalance were tested with negative to positive ratio N:P=1:3, 1:1 and 3:1 in test set respectively. Training set had the same N:P ratio as the test set and was 3:1 in size to test set.

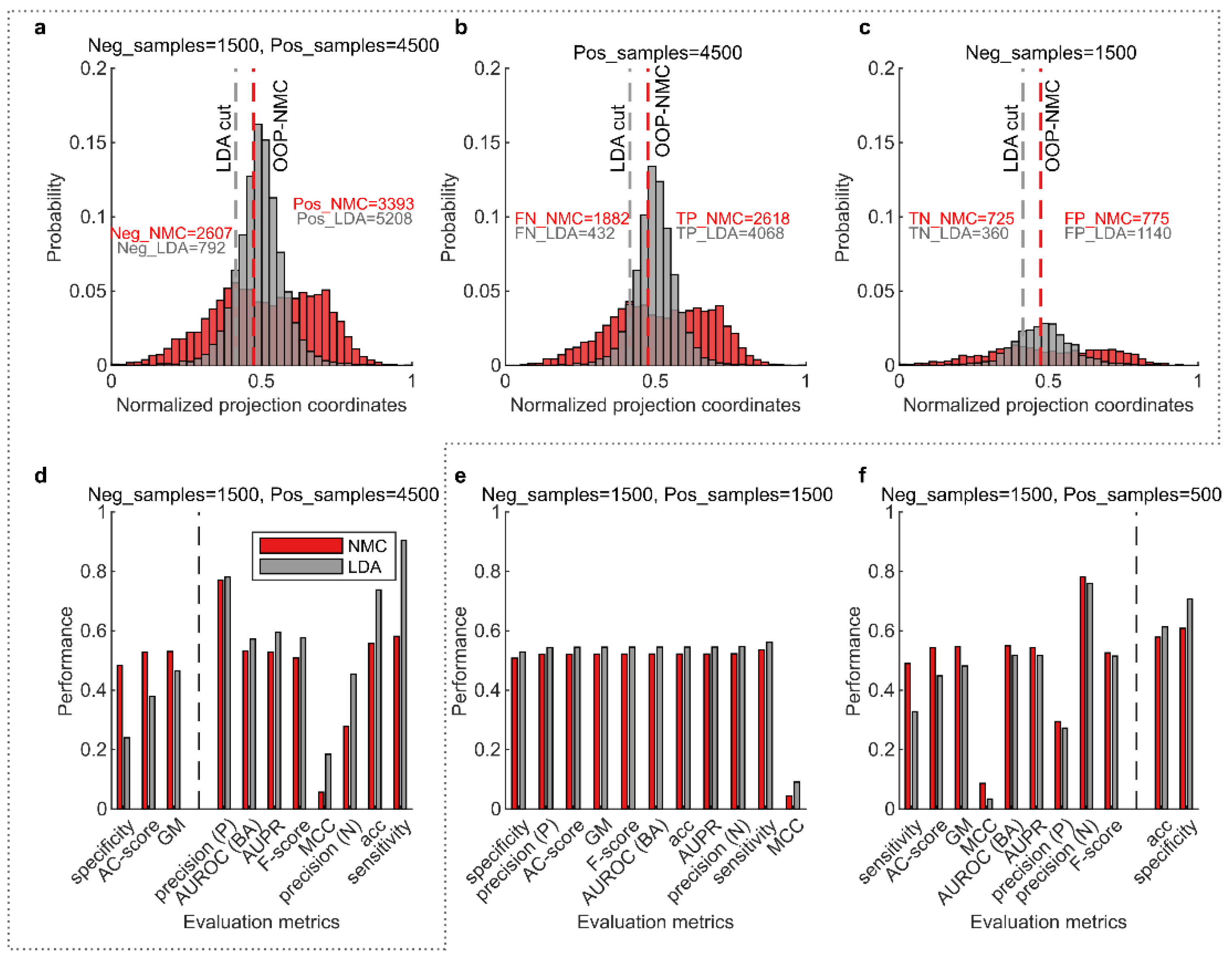
In the case where N:P=1:3 (Figure 2a-c), the NMC classifier equipped with optimal operating point (OOP) search along its discriminant had a more uniform data projection and the OOP was fitted near the middle of the projection. In contrast, due to the lack of the OOP search mechanism, LDA was fitted toward one side of the distribution (Figure 2a). To analyze, the training of NMC is guided by a score incorporating AC-score (see 3.3), while LDA was totally trained with its principle to maximize projection variance ratio. If dividedly by true labels (Figure 2b-c), NMC separated around the middle of each distribution, while LDA separated with an inclination for positive class, sacrificing the negative class which contributes less to its training due to less samples in this class.

In real applications, if the data are randomly sampled, it is reasonable to assume subsequent sampling follows the same distribution of the data in each class that has been already sampled. Hence, if we supplement negative samples in Figure 2c to as many as positive samples in Figure 2b, the sacrifice that was minor before will be magnified. In this situation, it can be indicated that LDA does not give a proper separation, under the conditions that two classes are as same important. However, Figure 2d shows that for all the metrics (ranked on x-axis according to performance difference between NMC and LDA) to the right of the gray dashed line, LDA performs better than AC-score, which are an evaluation of less incredibility. However, AC-score, GM and sensitivity are shown to be able to reflect fairly performance of classifiers.

Further tests were performed with class imbalance N:P=1:1 and 3:1 (Figure 2e-f). By comparing different conditions of class imbalance (Figure 2d-f), only AC-score and GM are stable metrics, while other metrics changed their position on x-axis ranked by performance difference between NMC and LDA. However, AC-score made more significant differentiation between LDA and NMC, especially in the presence of class imbalance (Figure 2 d and f), which is in align with the surface profile in the last section that it can creates harsher penalties for imbalance data evaluation.

3.1. Evaluation Metrics

Performance evaluation metrics are defined using confusion matrix components, including true positive (TP), true negative (TN), false positive (FP) and false negative (FN), from which TPR and TNR can be calculated:

$$TPR(\mathrm{o}\mathrm{r}sensitivity/recall)=TP/(TP+FN)$$

$$TNR(\mathrm{o}\mathrm{r}specificity)=TN/(TN+FP)$$

AC-score is defined by $ACscore=2(TPR\times TNR)/(TPR+TNR)$. The name originates from that it uses the same variable as balanced accuracy. Since TPR and TNR are both null-biased metrics, AC-score as their combination is also a null-biased metric. Other metrics using the combination of TPR and TNR are GM and AUROC, which are therefore also null-biased metrics. Their formulae are given by:

$$GM=\sqrt{TPR\times TNR}$$

$$AUROC={\int }_{x=0}^{1}TPR({FPR}^{-1}(x))dx={\int }_{x=0}^{1}TPR(1-{TNR}^{-1}(x))dx$$

Additionally, BA is proved to be equal to the single test point AUROC for discrete classifiers⁶, i.e. it has only one test point aside from (0,0) and (1,1) on the curve.

Other evaluation metrics used in this study are given below:

$$precisio{n}_{\mathrm{P}}=TP/(TP+FP)$$

$$precisio{n}_{\mathrm{N}}=TN/(TN+FN)$$

$$\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}=(TP+TN)/(TP+FP+TN+FN)$$

$$Fscore=2{\displaystyle \frac{precision\cdot recall}{precision+recall}}$$

Matthews correlation coefficient[10] (MCC): $MCC={\displaystyle \frac{TP\times TN-FP\times FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}}$

Area under the precision-recall curve (AUPR): $AUPR={\int }_{x=0}^{1}precision({recall}^{-1}(x))dx$

3.2. Simulation on the Imbalanced SVHN Dataset

In section 2.2 we compared all the metrics on SVHN dataset. The binary classification was performed on the pair of number “1” and “6”. Three conditions of data imbalance were tested with proportion of negative to positive samples N:P being 1:3, 1:1 and 3:1 respectively, and the proportion of training data to test data was made to 3:1. For these conditions, 18,000, 9,000 and 6,000 training samples are used respectively, and 6,000, 3,000 and 2,000 test samples are used respectively.

3.3. Linear Classifiers

We made two modifications to the original NMC to augment its performance. First, the original NMC uses mean as centroid, but better performance may be achieved when the median is employed as centroid. Therefore, we implemented an adaptive version of NMC that select the best type of centroid according to the score for selecting OOP. Second, the original NMC uses the middle point as the cut, here the NMC is equipped with an OOP search mechanism enabling the training guided by a score that enhances performance.

The training of the classifier NMC is divided into two steps. In the first step the NMC discriminant was obtained by taking the unit vector pointing from centroid of negative class to the one of positive class. In the second step, the data points were projected onto the discriminant and an OOP search was performed from N-1 candidates, which are the middle points of any two consecutive points on the projection axis. The criterion for the best OOP is the score $({Fscore}_{\mathrm{P}}+{Fscore}_{\mathrm{N}}+ACscore)/3$, where F-score was evaluated twice each time for one class because it is not a symmetric measure.

LDA discriminant was obtained using Matlab statistics and machine learning toolbox function fitcdiscr. The cut on the LDA discriminant is determined by its algorithm. A 5-fold cross-validation repeated for 10 times was performed to train the two classifiers. For NMC this was performed for the OOP search instead of the discriminant. For LDA this was performed for both the discriminant and the bias.

Metrics were evaluated in a balanced manner considering equal importance for both classes. Therefore, metrics that is not symmetric with both classes (except for metrics designed for evaluating one class such as sensitivity), which includes AUPR and Fscore, were evaluated for positive class and negative class individually, of which the average was taken as final evaluation.

3.4. Hardware and Software Specifications

The simulations were performed on Lenovo P620 workstation, equipped with AMD Ryzen Threadripper PRO 3995WX 2.7GHz CPU that has 64 cores and 128 threads. Ubuntu 20.04, MATLAB 2021b were used as the environments to run the algorithms.