On Topologies on Simple Graphs. Applications in Radar Chart Methods

1. Introduction

Two important branches of mathematics, general topology [1] and graph theory [2], are closely related. One of the relationships between graph theory and general topology is constructing topologies on the vertices set and the edges set of a graph. Several studies constructed some topologies via directed graphs and undirected graphs. Most of these constructions were in the theory of simple undirected graphs, in particular on the vertices sets of such graphs. In 2018, the authors of the paper [3], introduced new constructions of topologies, incidence topology on the set of vertices for simple graphs $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ without isolated vertices, which has a subbasis $S_{IG}$, where $S_{IG}$ is the family of end-sets that contain only end points of each edge. Kiliciman and Abdu [4], used the graphs $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ to introduce two constructions of topologies on the set $\mathcal{E}\left(\mathcal{G}\right)$, called compatible edge topology and incompatible edge topology. Amiri et al. [5] constructed the graphic topological space of a graph $\mathcal{G}$ as a pair $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{A}\mathcal{V}})$, where $T_{\mathcal{A}\mathcal{V}}$ is an Alexandroff topology on $\mathcal{V}\left(\mathcal{G}\right)$ induced by a subbasis $\mathcal{A}\mathcal{V}$ which is the family of open neighbourhoods $N\left(x\right)$ of vertices in $\mathcal{G}$. Nada et al., [6], introduced a relation on graphs to generate new types of topological structures. In 2019, Nianga and Canoy [7], constructed a topology on simple graphs by using unary and binary operations, and in [8], they introduced some topologies on the vertices set in the theory of simple graphs by using the hop neighborhoods of the graphs (see also [9,10]). In 2020, for the simple graphs without isolated vertices $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$, Sari and Kopuzlu [11], generated topology on the vertices set induced by the same basis which is introduced by Amiri et al. [5] and studied the continuity of functions. The minimal neighborhood system of vertices and the discrete property of topologies for special graphs, such as complete graphs $K_n$, cycle graphs $C_n$ and complete bipartite graphs $K_{n,m}$, are also studied,. In 2021, Zomam et al. [12] studied some conditions for a locally finite property of graphs to get an Alexandroff property for the graphic topological spaces which are introduced by Amiri et al. [5]. In the theory of directed graphs, pathless topological spaces on the vertices set $\mathcal{V}\left(\mathcal{G}\right)$ were introduced by Othman et al. In [13] in 2022, the relation between the pathless topological spaces with the relative topologies and E-generated subgraphs has been presented and the role of pathless topology in the blood circulation of the heart of human body was studied (see also [14]). By using C-sets, Othman et al. [15], have constructed a topology on $\mathcal{V}\left(\mathcal{G}\right)$, called $L_2-$topology. In 2023, [16], Abu-Gdairi et al. explained the role of the topological visualization in the medical field by giving graph analysis and rough sets by using neighbourhood systems. For an approximation neighborhood system, Yao [17] introduced the concepts of lower approximation and upper approximation of any nonempty set as a generalized rough sets by using a binary relation; for similar investigation see [18]. Atik et al. [19] introduced a new type of rough approximation model via graphs and by using j-neighborhood systems. By using an ideal collection, Guler [20] generated different approximations and compared these approximations.

In this paper we use an upper approximation neighbourhood system of simple graphs $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ (which was defined in [19]) to construct a new topology on the vertices set $\mathcal{V}\left(\mathcal{G}\right)$, called an upper approximated G-topology. In Section 3 we give the concept of upper approximated G-topological space and show the discrete property of complete graphs $C_n$, cycle graphs $C_n$ and complete bipartite graphs $K_{n,m}$. Next. we define the minimal operator of vertices in upper approximated G-topological spaces and give some results about the closure operator. Section 4 introduces relations between continuous mappings in upper approximated G-topological spaces and isomorphism mappings in simple graphs. We study the isomorphic fundamental topological properties such as compactness and connectedness. Further, we define a new class of connected graphs, called upper connectedness, and a new class of discrete topologies, called upper discreteness. In Section 5 we prove that if the number of categories for a radar chart is large enough, then the upper approximated G-topological space for the corresponding graph of this radar chart is disconnected and discrete. Upper connectedness and upper discrete properties for corresponding graphs of radar charts are also studied.

2. Preliminaries

In this section we recall some notions in graph theory which we need throughout the paper, mainly following the book [2].

Let X be a nonempty set and $G\subseteq X$. Recall [17] that for any binary relation ∼ on X, the lower approximation $\underline{\sim }\left(G\right)$ and upper approximation $\overline{\sim }\left(G\right)$ of G are given by

$$\underline{\sim }\left(G\right)=\{x\in X:{\sim }_x\subseteq G\}\mathrm{and}\overline{\sim }\left(G\right)=\{x\in X:{\sim }_x\cap G\ne \varnothing \},$$

respectively, where ${\sim }_x=\{y\in X:x\sim y\}$. Throughout this paper, all graphs will be assumed undirected. By a graph $\mathcal{G}$ we mean a pair $\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ of a nonempty vertices set $\mathcal{V}\left(\mathcal{G}\right)$ and edges set $\mathcal{E}\left(\mathcal{G}\right)$. If $\epsilon \in \mathcal{E}\left(\mathcal{G}\right)$ is an edge in $\mathcal{E}\left(\mathcal{G}\right)$ joins x and y in $\mathcal{V}\left(\mathcal{G}\right)$, then we write $\mathcal{V}\left(\epsilon \right)=\{x,y\}$. For $x\in \mathcal{V}\left(\mathcal{G}\right)$, by ${\mathbb{D}}_x$ we mean the number of vertices that adjacent with x which is called the degree of x. For $x\in \mathcal{V}\left(\mathcal{G}\right)$, an edge $\gamma$ with $\mathcal{V}\left(\gamma \right)=\left\{x\right\}$ is called a loop. The two edges $\epsilon$ and ${\epsilon }^{\prime }$ in $\mathcal{E}\left(\mathcal{G}\right)$ are called multiple edges if $\mathcal{V}\left(\epsilon \right)=\mathcal{V}\left({\epsilon }^{\prime }\right)$. A graph $\mathcal{G}$ is called a simple graph if it is without loops and multiple edges. In any simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$, if there is edge between x and y, then it is denoted by ${\mathcal{G}}_{xy}$, where $x,y\in \mathcal{V}\left(\mathcal{G}\right)$. A graph $\mathcal{G}$ is called finite if $\mathcal{V}\left(\mathcal{G}\right)$ and $\mathcal{E}\left(\mathcal{G}\right)$ are both finite sets, and is called locally finite if ${\mathbb{D}}_x$ is finite number for all $x\in \mathcal{V}\left(\mathcal{G}\right)$. In this paper, a path P is defined as an alternating sequence of distinct edges and distinct vertices. The path which starts and ends at the same vertex is called a closed path. A graph $\mathcal{G}$ is called connected if for any two distinct vertices there is a path between them, that is, we can move along the edges from any vertex into any other vertex in $\mathcal{V}\left(\mathcal{G}\right)$. The cycle graph $C_n$ with $n>2$ is a simple graph with n vertices and n edges such that ${\mathbb{D}}_x=2$ for all $x\in \mathcal{V}\left(C_n\right)$. A complete bipartite graph $K_{n,m}$ with $n,m>0$ is a simple graph whose vertices can be partitioned into two subsets $V_n$ with n vertices and $V_m$ with m vertices such that no edge has both endpoints in the same subset, and every possible edge that could connect vertices in different subsets is a part of the graph. A complete graph $K_n$ with $n>0$ is a simple graph with n vertices such that ${\mathbb{D}}_x=n$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$. Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph and ∼ be any binary relation on $\mathcal{V}\left(\mathcal{G}\right)$. Let $\mathcal{H}$ be any subgraph of $\mathcal{G}$. Recall [19] that the lower approximations $\underline{N_j}\left(\mathcal{V}\left(\mathcal{H}\right)\right)$ and upper approximations $\overline{N_j}\left(\mathcal{V}\left(\mathcal{H}\right)\right)$ of $\mathcal{H}$ are given by

$$\underline{N_j}\left(\mathcal{V}\left(\mathcal{H}\right)\right)=\{x\in \mathcal{V}\left(\mathcal{G}\right):N_j\left(x\right)\subseteq \mathcal{V}\left(\mathcal{H}\right)\}$$

and

$$\overline{N_j}\left(\mathcal{V}\left(\mathcal{H}\right)\right)=\mathcal{V}\left(\mathcal{H}\right)\cup \{x\in \mathcal{V}\left(\mathcal{G}\right):N_j\left(x\right)\cap \mathcal{V}\left(\mathcal{H}\right)\ne \varnothing \},$$

respectively, where $j\in \{r,l,r^{\prime },l^{\prime },u,i,u^{\prime },i^{\prime }\}$, $N_r\left(x\right)=\{y\in \mathcal{V}\left(\mathcal{G}\right):x\sim y\}$, $N_l\left(x\right)=\{y\in \mathcal{V}\left(\mathcal{G}\right):y\sim x\}$, $N_{r^{\prime }}\left(x\right)={\bigcap }_{x\in N_r\left(y\right)}{N}_r\left(y\right)$, $N_{l^{\prime }}\left(x\right)={\bigcap }_{x\in N_l\left(y\right)}{N}_l\left(y\right)$, $N_u\left(x\right)=N_r\left(x\right)\cup N_l\left(x\right)$, $N_i\left(x\right)=N_r\left(x\right)\cap N_l\left(x\right)$, $N_{u^{\prime }}\left(x\right)=N_{r^{\prime }}\left(x\right)\cup N_{l^{\prime }}\left(x\right)$ and $N_{i^{\prime }}\left(x\right)=N_{r^{\prime }}\left(x\right)\cap N_{l^{\prime }}\left(x\right)$. In this paper, for any simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$, we will use the relation ∼ on the set $\mathcal{V}\left(\mathcal{G}\right)$ as an adjacent relation, that is, $x\sim y$ if x and y are adjacent. Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph. For the vertex $x\in \mathcal{V}\left(\mathcal{G}\right)$, the open neighbourhood $\mathbb{N}\left(x\right)$ of x is the set of all vertices $y\in \mathcal{V}\left(\mathcal{G}\right)$ such that there is $\epsilon \in \mathcal{E}\left(\mathcal{G}\right)$ joining x and y, that is, $\mathbb{N}\left(x\right)=\{y\in \mathcal{V}(\mathcal{G}):x\sim y\}$. For the vertex $x\in \mathcal{V}\left(\mathcal{G}\right)$, the closed neighbourhood $\mathbb{N}\left[x\right]$ of x is given by $\mathbb{N}\left[x\right]=\mathbb{N}\left(x\right)\cup \left\{x\right\}$.

3. The Upper Approximated G-Topologies

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be a simple graph. We firstly structure the neighborhood system for elements of $\mathcal{V}\left(\mathcal{G}\right).$ By using the notions of rough approximation j-neighborhood systems (which are introduced in [19]), for any vertex $x\in \mathcal{V}\left(\mathcal{G}\right)$, define the upper approximation neighbourhood $\overline{x}$ and lower approximation neighbourhood $\underline{x}$ of x as

$$\overline{x}=\mathbb{N}\left(x\right)\cup {\varnothing }_x\mathrm{and}\underline{x}=\{y\in \mathcal{V}\left(\mathcal{G}\right):\mathbb{N}\left(y\right)\subseteq \mathbb{N}\left(x\right)\},$$

respectively, where ${\varnothing }_x=\{y\in \mathcal{V}\left(\mathcal{G}\right):\mathbb{N}\left(x\right)\cap \mathbb{N}\left(y\right)\ne \varnothing \}$. By $\mathcal{V}\left(\overline{\mathcal{G}}\right)$ we mean the upper approximation neighbourhood system of a graph $\mathcal{G}$, and similarly, by $\mathcal{V}\left(\underline{\mathcal{G}}\right)$ we mean the lower approximation neighbourhood system of a graph $\mathcal{G}$, that is, $\mathcal{V}\left(\overline{\mathcal{G}}\right)=\{\overline{x}:x\in \mathcal{V}\left(\mathcal{G}\right)\}$ and $\mathcal{V}\left(\underline{\mathcal{G}}\right)=\{\underline{x}:x\in \mathcal{V}\left(\mathcal{G}\right)\}$, respectively.

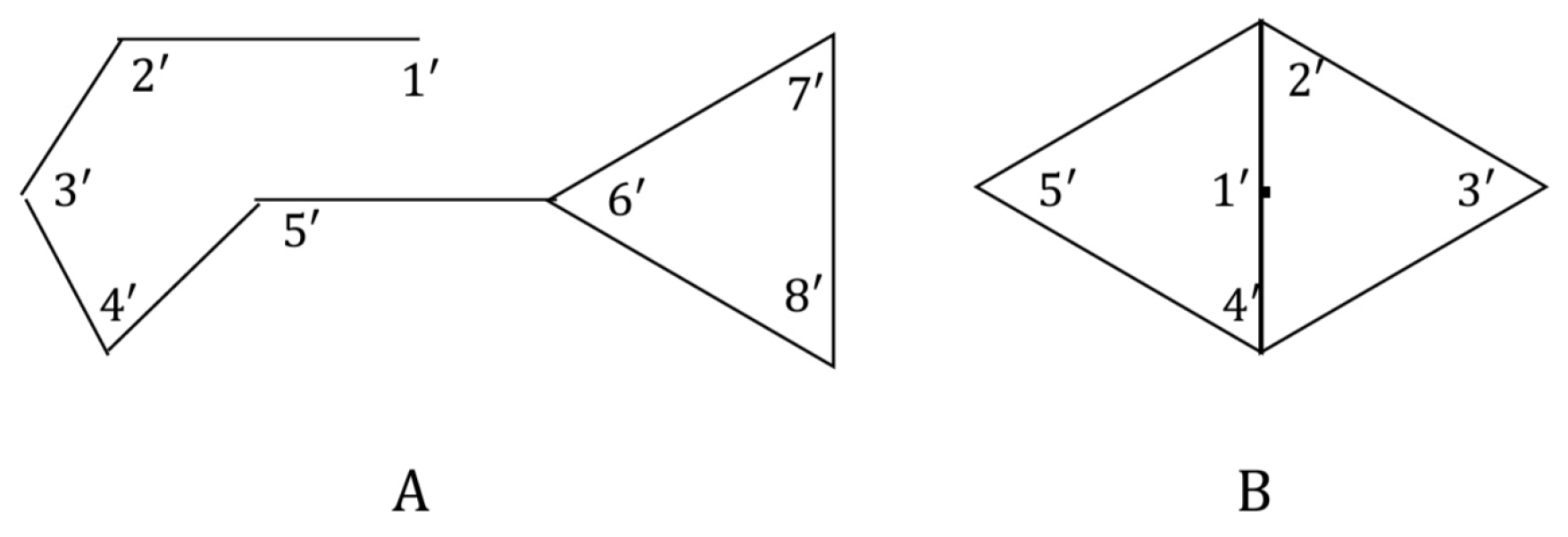
Example 1.

Note that the graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ in Figure 1-A has upper approximation neighbourhood system given by

$$\overline{1^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime }\},\overline{2^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime }\},\overline{3^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\},\overline{4^{\prime }}=\{2^{\prime },3^{\prime },4^{\prime },5^{\prime },6^{\prime }\},$$

$$\overline{5^{\prime }}=\{3^{\prime },4^{\prime },5^{\prime },6^{\prime },7^{\prime },8^{\prime }\},\overline{6^{\prime }}=\{4^{\prime },5^{\prime },6^{\prime },7^{\prime },8^{\prime }\},\overline{7^{\prime }}=\overline{8^{\prime }}=\{5^{\prime },6^{\prime },7^{\prime },8^{\prime }\}.$$

The lower approximation neighbourhood system of $\mathcal{G}$ is given by $\underline{3^{\prime }}=\{1^{\prime },3^{\prime }\}$ and $\underline{k}=\left\{k\right\}$ for all $k=1^{\prime },2^{\prime },4^{\prime },5^{\prime },6^{\prime },7^{\prime },8^{\prime }$.

In Figure 1-B, the graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ has upper approximation neighbourhood system given by

$$\overline{1^{\prime }}=\overline{3^{\prime }}=\overline{5^{\prime }}=\mathcal{V}\left(\mathcal{G}\right)\mathrm{and}\overline{2^{\prime }}=\overline{4^{\prime }}=\mathcal{V}(\mathcal{G}\setminus \left\{1^{\prime }\right\}).$$

The lower approximation neighbourhood system of $\mathcal{G}$ is given by

$$\underline{1^{\prime }}=\underline{3^{\prime }}=\underline{5^{\prime }}=\{1^{\prime },3^{\prime },5^{\prime }\}\mathrm{and}\underline{2^{\prime }}=\underline{4^{\prime }}=\{2^{\prime },4^{\prime }\}.$$

Figure 1. Representation of upper and lower approximation neighbourhood system

Figure 1. Representation of upper and lower approximation neighbourhood system

Theorem 1.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph. The family ${\overline{\mathcal{U}}}_{\mathcal{G}}=\{{\overline{u}}_x:x\in \mathcal{V}\left(\mathcal{G}\right)\}$ forms a basis of a topology on $\mathcal{V}\left(\mathcal{G}\right)$, where ${\overline{u}}_x$ is the intersection set of all upper approximation neighbourhoods containing x in $\mathcal{V}\left(\mathcal{G}\right)$.

Proof. 

It is clear that ${\overline{u}}_x\subseteq \mathcal{V}\left(\mathcal{G}\right)$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$. That is, ${\bigcup }_{x\in \mathcal{V}\left(\mathcal{G}\right)}{\overline{u}}_x\subseteq \mathcal{V}\left(\mathcal{G}\right)$. On the other hand, since $x\in \overline{x}$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$, then $\mathcal{V}\left(\mathcal{G}\right)\subseteq {\bigcup }_{x\in \mathcal{V}\left(\mathcal{G}\right)}{\overline{u}}_x$, i.e., $\mathcal{V}\left(\mathcal{G}\right)={\bigcup }_{x\in \mathcal{V}\left(\mathcal{G}\right)}{\overline{u}}_x$. Now we will prove that for every two elements ${\overline{u}}_x,{\overline{u}}_y\in {\overline{\mathcal{U}}}_{\mathcal{G}}$, there is $C\subseteq \mathcal{V}\left(\mathcal{G}\right)$ such that ${\overline{u}}_x\cap {\overline{u}}_y={\bigcup }_{z\in C}{\overline{u}}_z$. Let ${\overline{u}}_x$ and ${\overline{u}}_y$ be any two elements in ${\overline{\mathcal{U}}}_{\mathcal{G}}$. If ${\overline{u}}_x\cap {\overline{u}}_y=\varnothing$, then take $C=\varnothing$ to get the desired. Let ${\overline{u}}_x\cap {\overline{u}}_y\ne \varnothing$. Then there is at least one $z\in {\overline{u}}_x$ and $z\in {\overline{u}}_y$. Since $z\in {\overline{u}}_x$ then $z\in \overline{\alpha }$ for all $\alpha \in \mathcal{V}\left(\mathcal{G}\right)$ with $x\in \overline{\alpha }$. Similarly, since $z\in {\overline{u}}_y$ then $z\in \overline{\beta }$ for all $\beta \in \mathcal{V}\left(\mathcal{G}\right)$ with $x\in \overline{\beta }$. In all cases we get that $z\in {\bigcup }_{z\in \overline{\alpha }\cap \overline{\beta }}{\overline{u}}_z$. Take $C=\overline{\alpha }\cap \overline{\beta }\subseteq \mathcal{V}\left(\mathcal{G}\right)$. That is, ${\overline{u}}_x\cap {\overline{u}}_y\subseteq {\bigcup }_{z\in C}{\overline{u}}_z$.

On the other hand, let $\zeta \in {\bigcup }_{z\in C}{\overline{u}}_z$, that is, $\zeta \in {\bigcup }_{z\in \overline{\alpha }\cap \overline{\beta }}{\overline{u}}_z$. Hence $\zeta \in {\overline{u}}_z$ for some $\zeta \in \overline{\alpha }\cap \overline{\beta }$. Then $\zeta \in {\bigcap }_{z\in \overline{v}}\overline{v}$ and this implies $\zeta \in \overline{v}$ for all $z\in \overline{v}$. So we have $\zeta \in \overline{\alpha }\cap \overline{\beta }$. Hence $\zeta \in {\bigcap }_{x\in \overline{\alpha }}\overline{\alpha }$ and $\zeta \in {\bigcap }_{y\in \overline{\beta }}\overline{\beta }$, that is, $\zeta \in {\overline{u}}_x$ and $\zeta \in {\overline{u}}_y$. Hence ${\bigcup }_{z\in C}{\overline{u}}_z\subseteq {\overline{u}}_x\cap {\overline{u}}_y$.

From the two cases we get ${\overline{u}}_x\cap {\overline{u}}_y={\bigcup }_{z\in C}{\overline{u}}_z$. Therefore, ${\overline{\mathcal{U}}}_{\mathcal{G}}$ forms a basis of a topology on $\mathcal{V}\left(\mathcal{G}\right)$. □

For any simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$, the topology in the above theorem which is induced by the basis ${\overline{\mathcal{U}}}_{\mathcal{G}}$ will be called an upper approximated G-topology of a graph $\mathcal{G}$ and will be denoted by $T_{\mathcal{G}\left(u\right)}$. From the definitions of the basis ${\overline{\mathcal{U}}}_{\mathcal{G}}$ and an upper approximation neighbourhood system $\mathcal{V}\left(\overline{\mathcal{G}}\right)$, we get that the family $\mathcal{V}\left(\overline{\mathcal{G}}\right)$ forms a subbasis for an upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$.

The simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ of Figure 1-A in Example 1 has an upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ with a basis ${\overline{\mathcal{U}}}_{\mathcal{G}}=\{{\overline{u}}_k:k=1^{\prime },2^{\prime },\cdots 8^{\prime }\}$, where

$${\overline{u}}_{1^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime }\},{\overline{u}}_{2^{\prime }}=\{2^{\prime },3^{\prime }\},{\overline{u}}_{3^{\prime }}=\left\{3^{\prime }\right\},{\overline{u}}_{4^{\prime }}=\left\{4^{\prime }\right\},$$

$${\overline{u}}_{5^{\prime }}=\left\{5^{\prime }\right\},{\overline{u}}_{6^{\prime }}=\{5^{\prime },6^{\prime }\},{\overline{u}}_{7^{\prime }}={\overline{u}}_{8^{\prime }}=\{5^{\prime },6^{\prime },7^{\prime },8^{\prime }\}.$$

In Figure 1-B, the graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ has the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ with a basis ${\overline{\mathcal{U}}}_{\mathcal{G}}=\{{\overline{u}}_k:k=1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}$, where

$${\overline{u}}_{1^{\prime }}={\overline{u}}_{3^{\prime }}={\overline{u}}_{5^{\prime }}=\mathcal{V}\left(\mathcal{G}\right)\mathrm{and}{\overline{u}}_{2^{\prime }}={\overline{u}}_{4^{\prime }}=\mathcal{V}(\mathcal{G}\setminus \left\{1^{\prime }\right\}).$$

Example 2.

The graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ in Figure 2-A has the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ with a basis ${\overline{\mathcal{U}}}_{\mathcal{G}}=\{{\overline{u}}_k:k=1^{\prime },2^{\prime },\cdots ,9^{\prime }\}$ where

$${\overline{u}}_{1^{\prime }}={\overline{u}}_{8^{\prime }}={\overline{u}}_{9^{\prime }}=\{1^{\prime },8^{\prime },9^{\prime }\},{\overline{u}}_{2^{\prime }}={\overline{u}}_{4^{\prime }}={\overline{u}}_{5^{\prime }}=\{1^{\prime },2^{\prime },4^{\prime },5^{\prime },8^{\prime },9^{\prime }\},$$

$${\overline{u}}_{3^{\prime }}={\overline{u}}_{6^{\prime }}={\overline{u}}_{7^{\prime }}=\{1^{\prime },3^{\prime },6^{\prime },7^{\prime },8^{\prime },9^{\prime }\},{\overline{u}}_{2^{\prime }}={\overline{u}}_{4^{\prime }}={\overline{u}}_{5^{\prime }}=\{1^{\prime },2^{\prime },4^{\prime },5^{\prime },8^{\prime },9^{\prime }\}.$$

The graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ in Figure 2-B has the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ with a basis ${\overline{\mathcal{U}}}_{\mathcal{G}}=\{{\overline{u}}_k:k=1^{\prime },2^{\prime },\cdots ,{12}^{\prime }\}$, where

$${\overline{u}}_{1^{\prime }}={\overline{u}}_{5^{\prime }}=\{1^{\prime },5^{\prime },9^{\prime }\},{\overline{u}}_{2^{\prime }}={\overline{u}}_{7^{\prime }}=\{2^{\prime },7^{\prime },{11}^{\prime }\},{\overline{u}}_{3^{\prime }}={\overline{u}}_{6^{\prime }}=\{3^{\prime },6^{\prime },{10}^{\prime }\},$$

$${\overline{u}}_{4^{\prime }}={\overline{u}}_{8^{\prime }}=\{4^{\prime },8^{\prime },{12}^{\prime }\},{\overline{u}}_k=\left\{k\right\},$$

for all $k=9^{\prime },{10}^{\prime },{11}^{\prime },{12}^{\prime }$.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph. If $x\in \mathcal{V}\left(\mathcal{G}\right)$ is an isolated vertex, then it is clear that the set $\left\{x\right\}$ is an open set in the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ and also if ${\mathcal{G}}_{xy}\in \mathcal{E}\left(\mathcal{G}\right)$ is an isolated edge, then the set $\{x,y\}$ is an open set. Furthermore, if we have an isolated path P in $\mathcal{G}$ of length two of the form $P=\{{\mathcal{G}}_{1^{\prime }{2}^{\prime }},{\mathcal{G}}_{2^{\prime }{3}^{\prime }}\}$, then the set $\{1^{\prime },2^{\prime },3^{\prime }\}$ is an open set. If we have an isolated path P in $\mathcal{G}$ of length 3 of the form $P=\{{\mathcal{G}}_{1^{\prime }{2}^{\prime }},{\mathcal{G}}_{2^{\prime }{3}^{\prime }},{\mathcal{G}}_{3^{\prime }{4}^{\prime }}\}$, that is, $\mathcal{V}\left(P\right)=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}$, then it is easy to see that the upper approximated G-topological space $(\mathcal{V}\left(P\right),T_{P\left(u\right)})$ has a basis ${\overline{\mathcal{U}}}_{\mathcal{G}}$ which is given by ${\overline{\mathcal{U}}}_P=\{1^{\prime },2^{\prime },3^{\prime }\},\{2^{\prime },3^{\prime }\},\{2^{\prime },3^{\prime },4^{\prime }\}\}$.

Theorem 2.

Let P be a path of the form

$$P=\{P_{1^{\prime }{2}^{\prime }},P_{2^{\prime }{3}^{\prime }},\cdots ,P_{{(n-2)}^{\prime }{(n-1)}^{\prime }},P_{{(n-1)}^{\prime }{n}^{\prime }}\},$$

where $n>4$. Then the basis of $(\mathcal{V}\left(P\right),T_{P\left(u\right)})$ is given by

$${\overline{\mathcal{U}}}_P=\{\{1^{\prime },2^{\prime },3^{\prime }\},\{2^{\prime },3^{\prime }\},\left\{k^{\prime }\right\},\{{(n-2)}^{\prime },{(n-1)}^{\prime }\},\{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\}$$

for all $k=3,4,....,n-2$.

Proof. 

Note that

$${\overline{u}}_{1^{\prime }}=\overline{1^{\prime }}\cap \overline{2^{\prime }}\cap \overline{3^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}=\{1^{\prime },2^{\prime },3^{\prime }\}\in {\overline{\mathcal{U}}}_P,$$

$${\overline{u}}_{2^{\prime }}=\overline{1^{\prime }}\cap \overline{2^{\prime }}\cap \overline{3^{\prime }}\cap \overline{4^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}\cap \{2^{\prime },3^{\prime },4^{\prime },5^{\prime },6^{\prime }\}$$

$$=\{2^{\prime },3^{\prime }\}\in {\overline{\mathcal{U}}}_P,$$

$${\overline{u}}_{{(n-1)}^{\prime }}=\overline{{(n-3)}^{\prime }}\cap \overline{{(n-2)}^{\prime }}\cap \overline{{(n-1)}^{\prime }}\cap \overline{n^{\prime }}=\{{(n-5)}^{\prime },{(n-4)}^{\prime },{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime }\}$$

$$\cap \{{(n-4)}^{\prime },{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\cap \{{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\cap \{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}$$

$$=\{{(n-2)}^{\prime },{(n-1)}^{\prime }\}\in {\overline{\mathcal{U}}}_P,$$

$${\overline{u}}_{n^{\prime }}=\overline{{(n-2)}^{\prime }}\cap \overline{{(n-1)}^{\prime }}\cap \overline{n^{\prime }}=\{{(n-4)}^{\prime },{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}$$

$$\cap \{{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\cap \{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}$$

$$=\{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\in {\overline{\mathcal{U}}}_P,$$

$${\overline{u}}_{3^{\prime }}=\overline{1^{\prime }}\cap \overline{2^{\prime }}\cap \overline{3^{\prime }}\cap \overline{4^{\prime }}\cap \overline{5^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}$$

$$\cap \{2^{\prime },3^{\prime },4^{\prime },5^{\prime },6^{\prime }\}\cap \{3^{\prime },4^{\prime },5^{\prime },6^{\prime },7^{\prime }\}=\left\{3^{\prime }\right\}\in {\overline{\mathcal{U}}}_P$$

and similarly, ${\overline{u}}_{4^{\prime }}=\overline{2^{\prime }}\cap \overline{3^{\prime }}\cap \overline{4^{\prime }}\cap \overline{5^{\prime }}\cap \overline{6^{\prime }}=\left\{4^{\prime }\right\}\in {\overline{\mathcal{U}}}_P$. For all $k=5,6,\cdots ,n-2$, we have

$${\overline{u}}_{k^{\prime }}=\overline{{(k-2)}^{\prime }}\cap \overline{{(k-1)}^{\prime }}\cap \overline{k^{\prime }}\cap \overline{{(k+1)}^{\prime }}\cap \overline{{(k+2)}^{\prime }}=\{{(k-4)}^{\prime },{(k-3)}^{\prime },{(k-2)}^{\prime },{(k-1)}^{\prime },k^{\prime }\}$$

$$\cap \{{(k-3)}^{\prime },{(k-2)}^{\prime },{(k-1)}^{\prime },k^{\prime },{(k+1)}^{\prime }\}\cap \{{(k-2)}^{\prime },{(k-1)}^{\prime },k^{\prime },{(k+1)}^{\prime },{(k+2)}^{\prime }\}$$

$$\cap \{{(k-1)}^{\prime },k^{\prime },{(k+1)}^{\prime },{(k+2)}^{\prime },{(k+3)}^{\prime }\}\cap \{k^{\prime },{(k+1)}^{\prime },{(k+2)}^{\prime },{(k+3)}^{\prime },{(k+4)}^{\prime }\}$$

$$=\left\{k^{\prime }\right\}\in {\overline{\mathcal{U}}}_P.$$

Hence,

$${\overline{\mathcal{U}}}_P=\{\{1^{\prime },2^{\prime },3^{\prime }\},\{2^{\prime },3^{\prime }\},\left\{k^{\prime }\right\},\{{(n-2)}^{\prime },{(n-1)}^{\prime }\},\{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\}$$

for all $k=3,4,....,n-2$. □

Theorem 3.

The upper approximated G-topological space $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ of a complete graph $K_n$ is an indiscrete space for all $n>0$.

Proof. 

In case $n=1$, $\mathcal{V}\left(K_n\right)=\left\{x\right\}$, then it is clear that ${\overline{u}}_x=\left\{x\right\}$. That is, $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ is an indiscrete space. If $n>2$, and $x\in \mathcal{V}\left(K_n\right)$ is any vertex, then ${\mathbb{D}}_x=n$, that is, $\mathbb{N}\left(x\right)=\mathcal{V}\left(K_n\right)\setminus \left\{x\right\}$. Hence, $\overline{x}=\mathcal{V}\left(K_n\right)$ for all $x\in \mathcal{V}\left(K_n\right)$, that is, ${\overline{u}}_x=\mathcal{V}\left(K_n\right)$ for all $x\in \mathcal{V}\left(K_n\right)$. Hence, $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ is an indiscrete space for all $n>0$. □

Theorem 4.

The upper approximated G-topological space $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$ of a complete bipartite graph $K_{n,m}$ is an indiscrete space for all $n,m>0$.

Proof. 

In case $n=m=1$, $\mathcal{V}\left(K_{n,m}\right)=\{x,y\}$, then it is clear that $\mathbb{N}\left(x\right)=\left\{y\right\}$ and $\mathbb{N}\left(y\right)=\left\{x\right\}$. That is, ${\overline{u}}_x=\{x,y\}$ and ${\overline{u}}_x=\{x,y\}$. Hence, $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$ is an indiscrete space. Let $n,m>1$ and $\mathcal{V}\left(K_{n,m}\right)={\mathcal{V}}_n\cup {\mathcal{V}}_m$. Let $x\in \mathcal{V}\left(K_{n,m}\right)$ be any vertex. Since ${\mathcal{V}}_n\cap {\mathcal{V}}_m=\varnothing$, then $x\in {\mathcal{V}}_n$ or $x\in {\mathcal{V}}_m$. Let $x\in {\mathcal{V}}_n$. By definition of the complete bipartite graph $K_{n,m}$, $\mathbb{N}\left(x\right)={\mathcal{V}}_m$. Now we will show that ${\mathcal{V}}_n\subseteq {\varnothing }_x$. Let $y\in {\mathcal{V}}_n$ be any vertex. Then $\mathbb{N}\left(y\right)={\mathcal{V}}_m$. So we have $\mathbb{N}\left(x\right)\cap \mathbb{N}\left(y\right)={\mathcal{V}}_m\ne \varnothing$, that is, $y\in {\varnothing }_x$. Hence, ${\mathcal{V}}_n\subseteq {\varnothing }_x$. Then we have $\overline{x}=\mathbb{N}\left[x\right]\cup {\varnothing }_x={\mathcal{V}}_m\cup {\mathcal{V}}_n=\mathcal{V}\left(K_{n,m}\right)$ and hence ${\overline{u}}_x=\mathcal{V}\left(K_{n,m}\right)$. Similarly, if $x\in {\mathcal{V}}_m$, we get that ${\overline{u}}_x=\mathcal{V}\left(K_{n,m}\right)$. Since x was an arbitrary vertex, then $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$ is an indiscrete space for all $n,m>0$. □

For a cycle graph $C_n$ with $n=3$, say $C_n:1^{\prime }\to 2^{\prime }\to 3^{\prime }\to 1^{\prime }$, we note that ${\overline{u}}_{k^{\prime }}=\mathcal{V}\left(C_n\right)$ for all $k=1,2,3$. That is, the upper approximated G-topological space $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ of $C_n$ is an indiscrete space. Similarly, if $n=4$ or $n=5$, then we get that ${\overline{u}}_{k^{\prime }}=\mathcal{V}\left(C_n\right)$ for all $k=1,2,3,4$ or for all $k=1,2,3,4,5$, respectively. That is, the upper approximated G-topological space $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ of $C_n$ is an indiscrete space for $n=4,5$. The following theorem shows that the upper approximated G-topological space $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ of $C_n$ is a discrete space for all $n>5$.

Theorem 5.

The upper approximated G-topological space $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ of a cycle graph $C_n$ is a discrete space for all $n>5$.

Proof. 

Consider the cycle graph $C_n$,

$$C_n=1^{\prime }\to 2^{\prime }\to 3^{\prime }\to \cdots \to {(n-2)}^{\prime }\to {(n-1)}^{\prime }\to n^{\prime }\to 1^{\prime },$$

where $n>5$. By definition of $C_n$ and since ${\mathbb{D}}_x=2$ for all $x\in \mathcal{V}\left(C_n\right)$, we have

$${\overline{u}}_{1^{\prime }}=\overline{{(n-1)}^{\prime }}\cap \overline{n^{\prime }}\cap \overline{1^{\prime }}\cap \overline{2^{\prime }}\cap \overline{3^{\prime }}=\{{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime }\}\cap \{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime }\}$$

$$\cap \{{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime },3^{\prime }\}\cap \{n^{\prime },1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}=\left\{1^{\prime }\right\}\in {\overline{\mathcal{U}}}_{C_n},$$

$${\overline{u}}_{2^{\prime }}=\overline{n^{\prime }}\cap \overline{1^{\prime }}\cap \overline{2^{\prime }}\cap \overline{3^{\prime }}\cap \overline{4^{\prime }}=\{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime }\}\cap \{{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime },3^{\prime }\}$$

$$\cap \{n^{\prime },1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}\cap \{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime }\}\cap \{2^{\prime },3^{\prime },4^{\prime },5^{\prime },6^{\prime }\}=\left\{2^{\prime }\right\}\in {\overline{\mathcal{U}}}_{C_n},$$

$${\overline{u}}_{n^{\prime }}=\overline{{(n-2)}^{\prime }}\cap \overline{{(n-1)}^{\prime }}\cap \overline{n^{\prime }}\cap \overline{1^{\prime }}\cap \overline{2^{\prime }}=\{{(n-4)}^{\prime },{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}$$

$$\cap \{{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime }\}\cap \{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime }\}$$

$$\cap \{{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime },3^{\prime }\}\cap \{n^{\prime },1^{\prime },2^{\prime },3^{\prime },4^{\prime }\}=\left\{n^{\prime }\right\}\in {\overline{\mathcal{U}}}_{C_n}$$

and

$${\overline{u}}_{{(n-1)}^{\prime }}=\overline{{(n-3)}^{\prime }}\cap \overline{{(n-2)}^{\prime }}\cap \overline{{(n-1)}^{\prime }}\cap \overline{n^{\prime }}\cap \overline{1^{\prime }}=\{{(n-5)}^{\prime },{(n-4)}^{\prime },{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime }\}$$

$$\cap \{{(n-4)}^{\prime },{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime }\}\cap \{{(n-3)}^{\prime },{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime }\}$$

$$\cap \{{(n-2)}^{\prime },{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime }\}\cap \{{(n-1)}^{\prime },n^{\prime },1^{\prime },2^{\prime },3^{\prime }\}=\left\{{(n-)}^{\prime }\right\}\in {\overline{\mathcal{U}}}_{C_n}.$$

Now for all $k=3,4,\cdots ,n-2$, since the cycle graph $C_n$ is a closed path then from the proof of Theorem 2 we have

$${\overline{u}}_{k^{\prime }}=\overline{{(k-2)}^{\prime }}\cap \overline{{(k-1)}^{\prime }}\cap \overline{k^{\prime }}\cap \overline{{(k+1)}^{\prime }}\cap \overline{{(k+2)}^{\prime }}=\left\{k^{\prime }\right\}\in {\overline{\mathcal{U}}}_{C_n}.$$

Hence, ${\overline{\mathcal{U}}}_{C_n}=\{\left\{k^{\prime }\right\}:k=1,2,\cdots ,n$. This meams $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ is a discrete space for all $n>5$. □

The following theorem shows that the Alexandroff topological property will be satisfied for the upper approximated G-topological spaces of locally finite simple graphs, i.e., the arbitrary intersection of open sets is an open set.

In our next work, any simple graph will be locally finite.

Theorem 6.

The upper approximated G-topological space of any simple graph is an Alexandroff space.

Proof. 

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph. Let Z be any nonempty subset of $\mathcal{V}\left(\mathcal{G}\right)$. Let $\mathcal{F}$ be the collection of all the upper approximated neighbourhoods of elements of Z. We will prove that ${\bigcap }_{x\in Z}\overline{x}$ is an open set in $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$. Let $y\in {\bigcap }_{x\in Z}\overline{x}$. Then $y\in \overline{x}$ for all $x\in Z$. Hence $x\in \overline{y}$ for all $x\in Z$. So, $Z\subseteq \overline{y}$. Since $\mathcal{G}$ is locally finite, then $\overline{y}$ is finite and so Z is finite. Hence, ${\bigcap }_{x\in Z}\overline{x}$ is an open set. This proves that the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is an Alexandroff space. □

In the class of locally finite simple graphs $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$, by using the Alexandroff topological property of the upper approximated G-topological spaces $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$, we can define an operator $O_u$ from the vertices set $\mathcal{V}\left(\mathcal{G}\right)$ into the upper approximated G-topology $T_{\mathcal{G}\left(u\right)}$ by $O_u\left(x\right)$ is the smallest open set containing x, $x\in \mathcal{V}\left(\mathcal{G}\right)$. It is clear that $O_u\left(x\right)=\left\{x\right\}$ for an isolated point $x\in \mathcal{V}\left(\mathcal{G}\right)$ in any graph G, and if ${\mathcal{G}}_{xy}\in \mathcal{E}\left(\mathcal{G}\right)$ is an isolated edge, then $O_u\left(x\right)=O_u\left(y\right)=\{x,y\}$. Furthermore, if we have an isolated path P in $\mathcal{G}$ of length two of the form $P=\{{\mathcal{G}}_{1^{\prime }{2}^{\prime }},{\mathcal{G}}_{2^{\prime }{3}^{\prime }}\}$, then $O_u\left(1^{\prime }\right)=O_u\left(2^{\prime }\right)=O_u\left(3^{\prime }\right)=\{1^{\prime },2^{\prime },3^{\prime }\}$.

Theorem 7.

For any simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$, $O_u\left(x\right)={\overline{u}}_x$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$.

Proof. 

By the definition of the family $\mathcal{V}\left(\overline{\mathcal{G}}\right)$ and Theorem 1, $\overline{x}$ is an open set in the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$. By Theorem 1, ${\overline{u}}_x$ is an open set containing x. Since $O_u\left(x\right)$ is the smallest open set containing x, then $O_u\left(x\right)\subseteq {\overline{u}}_x.$

On the other hand, since $O_u\left(x\right)$ is the intersection of all open sets containing x, then let $O_u\left(x\right)={\bigcap }_{y\in Q}\overline{y}$ for some subset Q of $\mathcal{V}\left(\mathcal{G}\right)$. Then $x\in \overline{y}$ for all $y\in Q$, and this implies $y\in \overline{x}$ for all $y\in Q$. Ome concludes $Q\subseteq \overline{x}$. Hence, ${\overline{u}}_x\subseteq {\bigcap }_{y\in Q}\overline{y}=O_u\left(x\right).$ So, $O_u\left(x\right)={\overline{u}}_x.$ □

Theorem 8.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be a simple graph. For any two vertices $x,y\in \mathcal{V}\left(\mathcal{G}\right)$, $\overline{y}\subseteq \overline{x}$ if and only if $x\in O_u\left(y\right)$.

Proof. 

Let $x,y\in \mathcal{V}\left(\mathcal{G}\right)$ be any two vertices and $\overline{y}\subseteq \overline{x}$. By Theorem 7, $x\in {\bigcap }_{z\in \overline{x}}\overline{z}$. Since $\overline{y}\subseteq \overline{x}$, then ${\bigcap }_{z\in \overline{x}}\overline{z}\subseteq {\bigcap }_{z\in \overline{y}}\overline{z}$. Hence $x\in {\bigcap }_{z\in \overline{y}}\overline{z}=O_u\left(y\right)$.

Conversely, let $x\in O_u\left(y\right)$. By using Theorem 7 again, we can get that $\overline{y}={\bigcap }_{z\in \overline{y}}\overline{z}$. Then $x\in {\bigcap }_{z\in \overline{y}}\overline{z}$. It mens $x\in \overline{z}$ for all $z\in \overline{y}$. This implies $z\in \overline{x}$ for all $z\in \overline{y}$. Hence, $\overline{y}\subseteq \overline{x}$. □

Theorem 9.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be a simple graph. Then for all $x,y\in \mathcal{V}\left(\mathcal{G}\right)$, $\overline{y}⊈\overline{x}$ and $\overline{x}⊈\overline{y}$ if and only if $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is discrete.

Proof. 

Let x be any vertex in $\mathcal{V}\left(\mathcal{G}\right)$. It is clear that $x\in \overline{x}$. Suppose that $y\in \mathcal{V}\left(\mathcal{G}\right)$ is any vertex. If $y\in \overline{x}$, then by Theorem 8, $\overline{x}\subseteq \overline{y}$ and this is in contradiction with the hypothesis. Hence, $O_u\left(x\right)=\left\{x\right\}$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$, i.e., $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is discrete.

The reverse implication is clear since $\overline{x}=\left\{x\right\}$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$. □

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph and $X\subseteq \mathcal{V}\left(\mathcal{G}\right)$. The closure of X, denoted by $\mathrm{Cl}\left(X\right)$, is defined as the intersection of all closed sets containing X in the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$. Note that $x\in \mathrm{Cl}\left(X\right)$ if and only if for every open set G containing x, $X\cap G\ne \varnothing$ (see, [1]).

Theorem 10.

For any simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ and for all $x\in \mathcal{V}\left(\mathcal{G}\right)$, $\mathrm{Cl}\left(\overline{x}\right)\subseteq \mathrm{Cl}\left(\overline{y}\right)$ for all $y\in \overline{x}$.

Proof. 

Let $\zeta \in \mathrm{Cl}\left(\overline{x}\right)$. Then for each open set G containing $\zeta$, $G\cap \overline{x}\ne \varnothing$. Since $\overline{x}\subseteq \overline{y}$ for all $y\in \overline{x}$, then $G\cap \overline{y}\ne \varnothing$ for all $y\in \overline{x}$, i.e., $\zeta \in \mathrm{Cl}\left(\overline{y}\right)$ for all $y\in \overline{x}$. Hence, $\mathrm{Cl}\left(\overline{x}\right)\subseteq \mathrm{Cl}\left(\overline{y}\right)$ for all $y\in \overline{x}$. □

From Theorem 10, for any vertex $x\in \mathcal{V}\left(\mathcal{G}\right)$, $\mathrm{Cl}\left(\left\{x\right\}\right)\subseteq \left[\mathrm{Cl}\right]\left(\overline{\mathrm{y}}\right)$ for all $y\in \overline{x}$.

Corollary 1.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph and $x,y\in \mathcal{V}\left(\mathcal{G}\right)$. Then $x\in Cl\left(\right\{y\left\}\right)$ if and only if $\overline{x}\subseteq \overline{y}$.

4. On Isomorphic Properties

In this section we first study the relationship between isomorphic relations for simple graphs and homeomorphic relations of their upper approximated G-topological spaces. Next, we give some results about some isomorphic properties.

Let ${\mathcal{G}}_1=(\mathcal{V}\left({\mathcal{G}}_1\right),\mathcal{E}\left({\mathcal{G}}_1\right))$ and ${\mathcal{G}}_2=(\mathcal{V}\left({\mathcal{G}}_2\right),\mathcal{E}\left({\mathcal{G}}_2\right))$ be two simple graphs without isolated vertices. The graphs ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ are called isomorphic, denoted ${\mathcal{G}}_1\cong {\mathcal{G}}_2$, if there is a bijective mapping $\gamma :\mathcal{V}\left({\mathcal{G}}_1\right)\to \mathcal{V}\left({\mathcal{G}}_2\right)$ such that ${\left({\mathcal{G}}_1\right)}_{xy}\in \mathcal{E}\left({\mathcal{G}}_1\right)$ if and only if ${\left({\mathcal{G}}_2\right)}_{\gamma \left(x\right)\gamma \left(y\right)}\in \mathcal{E}\left({\mathcal{G}}_2\right)$ for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$. A mapping $g:(M_1,{\tau }_1)\to (M_2,{\tau }_2)$ of a topological space $(M_1,{\tau }_1)$ into a topological space $(M_2,{\tau }_2)$ is continuous if $g\left(\mathrm{Cl}\right(G\left)\right)\subseteq \mathrm{Cl}\left(g\right(G\left)\right)$ for all $G\subseteq M_1$. A mapping $g:(M_1,{\tau }_1)\to (M_2,{\tau }_2)$ is called closed if $g\left(G\right)$ is closed set in $M_2$ for all closed set $G\subseteq M_1$. Recall [1] that if a mapping $g:(M_1,{\tau }_1)\to (M_2,{\tau }_2)$ is bijective, closed nd continuous, then it is called a homeomorphism.

Theorem 11.

Let ${\mathcal{G}}_1=(\mathcal{V}\left({\mathcal{G}}_1\right),\mathcal{E}\left({\mathcal{G}}_1\right))$ and ${\mathcal{G}}_2=(\mathcal{V}\left({\mathcal{G}}_2\right),\mathcal{E}\left({\mathcal{G}}_2\right))$ be two simple graphs and $\gamma :\mathcal{V}\left({\mathcal{G}}_1\right)\to \mathcal{V}\left({\mathcal{G}}_2\right)$ be any mapping of the upper approximated G-topological spaces $(\mathcal{V}\left({\mathcal{G}}_1\right),T_{\mathcal{NP}\left({\mathcal{G}}_1\right)})$ into $(\mathcal{V}\left({\mathcal{G}}_2\right),T_{\mathcal{NP}\left({\mathcal{G}}_2\right)})$. Then $\gamma$ is a continuous mapping if and only if for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$, $\overline{x}\subseteq \overline{y}$ implies $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$.

Proof. 

Let $\overline{x}\subseteq \overline{y}$ implies $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$ for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$. Let O be any subset of $\mathcal{V}\left({\mathcal{G}}_1\right)$ and $x\in O$. If $x\in \mathrm{Cl}\left(O\right)$ then $x\in \mathrm{Cl}\left(\right\{y\left\}\right)$ for some $y\in O$. Hence $\overline{x}\subseteq \overline{y}$. By the hypothesis we get $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$. Then $\gamma \left(x\right)\in \mathrm{Cl}\left(\right\{\gamma \left(y\right)\left\}\right)\subseteq \mathrm{Cl}\left(\gamma \right(O\left)\right).$ Hence, $\gamma$ is continuous.

Conversely, let $\gamma$ be continuous and $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$ be any two vertices such that $\overline{x}\subseteq \overline{y}$. By Corollary(1) we get $x\in Cl\left(\right\{y\left\}\right)$, and by continuity of $\gamma$, $\gamma \left(x\right)\in \gamma \left(\mathrm{Cl}\right(\left\{y\right\}\left)\right)\subseteq \mathrm{Cl}\left(\right\{\gamma \left(y\right)\left\}\right)$. Thus, by Corollary(1), we get $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$. □

Theorem 12.

Let ${\mathcal{G}}_1=(\mathcal{V}\left({\mathcal{G}}_1\right),\mathcal{E}\left({\mathcal{G}}_1\right))$ and ${\mathcal{G}}_2=(\mathcal{V}\left({\mathcal{G}}_2\right),\mathcal{E}\left({\mathcal{G}}_2\right))$ be two simple graphs. Then a mapping $\gamma :\mathcal{V}\left({\mathcal{G}}_1\right)\to \mathcal{V}\left({\mathcal{G}}_2\right)$ is closed if $\gamma$ is onto and for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$, $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$ implies $\overline{x}\subseteq \overline{y}$.

Proof. 

Let O be any closed set in $\mathcal{V}\left({\mathcal{G}}_1\right)$. Since $\gamma$ is onto, then there is a mapping $\psi :\mathcal{V}\left({\mathcal{G}}_2\right)\to \mathcal{V}\left({\mathcal{G}}_1\right)$ such that $\gamma \circ \psi =i{d}_{\mathcal{V}\left({\mathcal{G}}_2\right)}$. Now we prove that $\psi$ is continuous. Let $x,y\in \mathcal{V}\left({\mathcal{G}}_2\right)$ be arbitrary vertices such that $\overline{x}\subseteq \overline{y}$. Hence $\overline{\gamma \left(\psi \right(x\left)\right)}\subseteq \overline{\gamma \left(\psi \right(y\left)\right)}$. By the hypothesis we get $\overline{\psi \left(x\right)}\subseteq \overline{\psi \left(y\right)}$. By Theorem 11 $\psi$ is continuous. Hence $\gamma \left(O\right)={\psi }^{\leftarrow }\left(O\right)$ is closed set and so $\gamma$ is a closed mapping. □

Theorem 13.

Let ${\mathcal{G}}_1=(\mathcal{V}\left({\mathcal{G}}_1\right),\mathcal{E}\left({\mathcal{G}}_1\right))$ and ${\mathcal{G}}_2=(\mathcal{V}\left({\mathcal{G}}_2\right),\mathcal{E}\left({\mathcal{G}}_2\right))$ be two simple graphs. If a mapping $\gamma :\mathcal{V}\left({\mathcal{G}}_1\right)\to \mathcal{V}\left({\mathcal{G}}_2\right)$ is closed and one-to-one, then for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$, $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$ implies $\overline{x}\subseteq \overline{y}$.

Proof. 

Let $x,y\in \mathcal{V}\left({\mathcal{G}}_2\right)$ be any two vertices such that $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$. Since $\gamma$ is one-to-one, then there is a function $\psi :\mathcal{V}\left({\mathcal{G}}_2\right)\to \mathcal{V}\left({\mathcal{G}}_1\right)$ such that $\psi \circ \gamma =i{d}_{\mathcal{V}\left({\mathcal{G}}_1\right)}$. Since $\gamma$ is one-to-one and closed, it is easy to see that $\psi$ is continuous. This implies that $\overline{\psi \left(\gamma \right(x\left)\right)}\subseteq \overline{\psi \left(\gamma \right(y\left)\right)}$, that is, $\overline{x}\subseteq \overline{y}$. □

Theorem 14.

A bijective mapping $\gamma :\mathcal{V}\left({\mathcal{G}}_1\right)\to \mathcal{V}\left({\mathcal{G}}_2\right)$ of two simple graphs ${\mathcal{G}}_1=(\mathcal{V}\left({\mathcal{G}}_1\right),\mathcal{E}\left({\mathcal{G}}_1\right))$ and ${\mathcal{G}}_2=(\mathcal{V}\left({\mathcal{G}}_2\right),\mathcal{E}\left({\mathcal{G}}_2\right))$ is a homeomorphism if and only if for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$, $\overline{x}\subseteq \overline{y}$ if and only if $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$.

The following theorem shows that the isomorphic relation of simple graphs without isolated vertices gives us the homeomorphic relation of their upper approximated G-topological spaces.

Theorem 15.

Let ${\mathcal{G}}_1=(\mathcal{V}\left({\mathcal{G}}_1\right),\mathcal{E}\left({\mathcal{G}}_1\right))$ and ${\mathcal{G}}_2=(\mathcal{V}\left({\mathcal{G}}_2\right),\mathcal{E}\left({\mathcal{G}}_2\right))$ be two simple graphs without isolated vertices. If ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$ are isomorphic, then there is a homeomorphism between upper approximated G-topological spaces $(\mathcal{V}\left({\mathcal{G}}_1\right),T_{\mathcal{NP}\left({\mathcal{G}}_1\right)})$ and $(\mathcal{V}\left({\mathcal{G}}_1\right),T_{\mathcal{NP}\left({\mathcal{G}}_1\right)})$.

Proof. 

Let $\gamma :\mathcal{V}\left({\mathcal{G}}_1\right)\to \mathcal{V}\left({\mathcal{G}}_2\right)$ be a bijective function such that ${\left({\mathcal{G}}_1\right)}_{xy}\in \mathcal{E}\left({\mathcal{G}}_1\right)$ if and only if ${\left({\mathcal{G}}_2\right)}_{\gamma \left(x\right)\gamma \left(y\right)}\in \mathcal{E}\left({\mathcal{G}}_2\right)$ for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$. Let $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$ be any two vertices with $y\in \overline{x}$. Then we have $y\in \mathbb{N}\left(x\right)$ or $\mathbb{N}\left(x\right)\cap \mathbb{N}\left(y\right)\ne \varnothing$. Let $y\in \mathbb{N}\left(x\right)$. Then there is an edge ${\left({\mathcal{G}}_1\right)}_{xy}\in \mathcal{E}\left({\mathcal{G}}_1\right)$ which joins x and y in ${\mathcal{G}}_1$. By the isomorphism of ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$, we get that the edge ${\left({\mathcal{G}}_2\right)}_{\gamma \left(x\right)\gamma \left(y\right)}$ joins $\gamma \left(x\right)$ and $\gamma \left(y\right)$ in ${\mathcal{G}}_2$, that is, $\gamma \left(y\right)\in \mathbb{N}\left(\gamma \right(x\left)\right)$. So, in this case, $\gamma \left(y\right)\in \overline{\gamma \left(x\right)}$. Now, in the other case, if $\mathbb{N}\left(x\right)\cap \mathbb{N}\left(y\right)\ne \varnothing$, then there is some $z\in \mathbb{N}\left(x\right)$ and $z\in \mathbb{N}\left(y\right)$. Then, similarly to the first case, we get $\gamma \left(z\right)\in \mathbb{N}\left(\gamma \right(x\left)\right)$ and $\gamma \left(z\right)\in \mathbb{N}\left(\gamma \right(y\left)\right)$, that is, $\mathbb{N}\left(\gamma \right(x\left)\right)\cap \mathbb{N}\left(\gamma \right(y\left)\right)\ne \varnothing$. Hence, $\gamma \left(y\right)\in \overline{\gamma \left(x\right)}$. Hence for all $x,y\in \mathcal{V}\left({\mathcal{G}}_1\right)$, $\overline{x}\subseteq \overline{y}$ if and only if $\overline{\gamma \left(x\right)}\subseteq \overline{\gamma \left(y\right)}$. Then by Theorem 14, $\gamma$ is a homeomorphism of upper approximated G-topological spaces $(\mathcal{V}\left({\mathcal{G}}_1\right),T_{\mathcal{NP}\left({\mathcal{G}}_1\right)})$ into $(\mathcal{V}\left({\mathcal{G}}_2\right),T_{\mathcal{NP}\left({\mathcal{G}}_2\right)})$. □

Note that if a homeomorphic relation of upper approximated G-topological spaces, then the isomorphic relation of induced simple graphs need not be satisfied. For example, by Theorem 4, the complete bipartite graph $K_{n,m}$ with $\mathcal{V}\left(K_{n,m}\right)={\mathcal{V}}_n\cup {\mathcal{V}}_m$ has an indiscrete upper approximated G-topological space $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$, and by Theorem 3, $K_{n+m}$ has an indiscrete upper approximated G-topological space $(\mathcal{V}\left(K_{n+m}\right),T_{K_{n+m}\left(u\right)})$. So $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$ and $(\mathcal{V}\left(K_{n+m}\right),T_{K_{n+m}\left(u\right)})$ are homeomorphic, while the graphs $K_{n,m}$ and $K_{n+m}$ are not isomorphic, since if $x\in {\mathcal{V}}_n$ and $y\in {\mathcal{V}}_m$, then x and y are joined in $K_{n+m}$ but not in $K_{n,m}$.

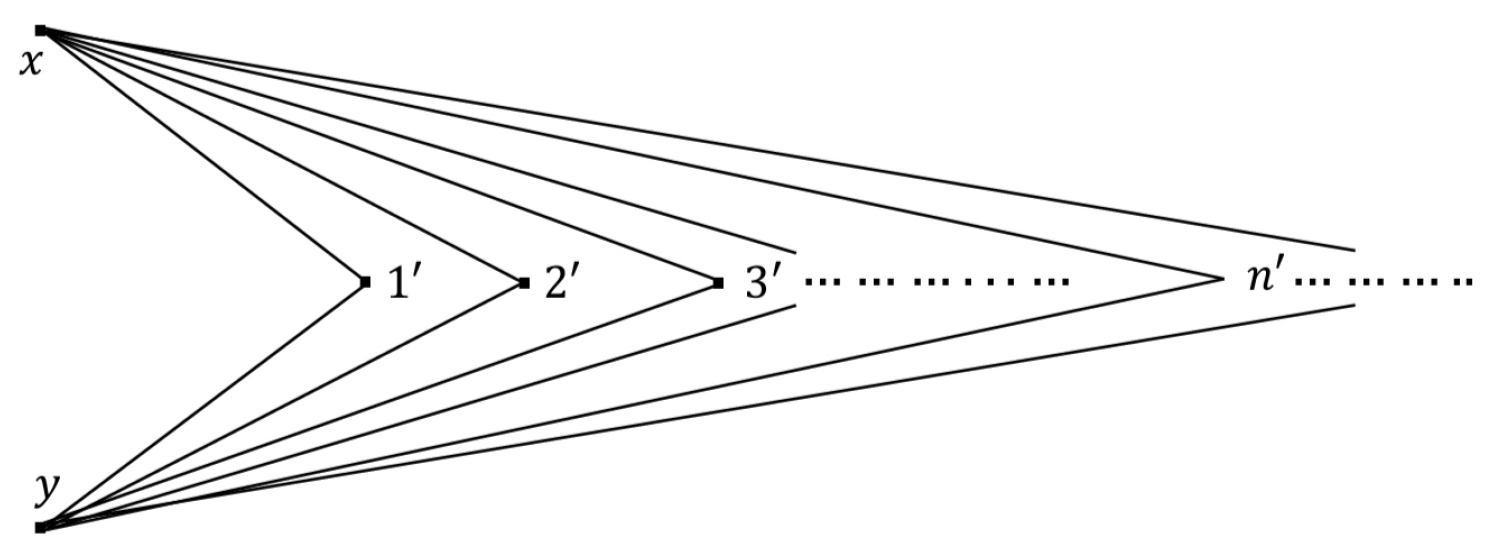
Recall [1] that the compactness is a topological property. So, by Theorem 15, the compactness is an isomorphic property in the theory of simple graphs. It is clear that the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ of any simple graph $\mathcal{G}$ is a compact space if $\mathcal{V}\left(\mathcal{G}\right)$ is finite. The upper approximated G-topological spaces induced by infinite graphs need not be compact. For example, in Figure 3, the simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ with an infinite vertices set $\mathcal{V}\left(\mathcal{G}\right)=\{x,y,1^{\prime },2^{\prime },3^{\prime },\cdots \}$ has the subbasis $\mathcal{V}\left(\overline{\mathcal{G}}\right)$ given by $\mathcal{V}\left(\overline{\mathcal{G}}\right)=\{\overline{\alpha }=\mathcal{V}\left(\mathcal{G}\right):\alpha \in \mathcal{V}\left(\mathcal{G}\right)\}$. The upper approximated G-topology of the graph $\mathcal{G}$ is an indiscrete spaces and so it is a compact space.

Also we have that from Theorem 3, the upper approximated G-topology $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ of a complete graph $K_n$ is a discrete space, and if $\mathcal{V}\left(K_n\right)$ is infinite, then $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ is not a compact space.

The following theorem shows a relationship between connectedness property of upper approximated G-topological spaces and connectedness property of simple graphs.

Theorem 16.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph without isolated vertices. If the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is a connected space, then $\mathcal{G}$ is a connected graph.

Proof. 

Suppose that $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ is a disconnected simple graph. Consider $\mathcal{Q}:=\{{\mathcal{G}}_m:m\in M\}$, the family of all components in $\mathcal{G}$, where ${\mathcal{G}}_m=(\mathcal{V}\left({\mathcal{G}}_m\right),\mathcal{E}\left({\mathcal{G}}_m\right))$ for all $m\in M$. Now for all $m\in M$, $\mathcal{V}\left({\mathcal{G}}_m\right)={\bigcup }_{x\in \mathcal{V}\left({\mathcal{G}}_m\right)}\overline{x}$. Then $M:=\mathcal{V}\left({\mathcal{G}}_{m_o}\right)$ is a nonempty proper open subset of $\mathcal{V}\left(\mathcal{G}\right)$, where $m_o\in M$. Then ${\left[\mathcal{V}\left({\mathcal{G}}_m\right)\right]}^c={\bigcup }_{m\in M\setminus \left\{m_o\right\}}\mathcal{V}\left({\mathcal{G}}_m\right)$ is also a nonempty proper open subset of $\mathcal{V}\left(\mathcal{G}\right)$. This means that $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is a disconnected space which contradicts connectedness of $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$. Hence, $\mathcal{G}$ is a connected graph. □

Connected simple graphs need not induce connected upper approximated G-topological spaces. For example, by Theorem 5, the cycle graph $C_n$ is a connected graph, and has disconnected upper approximated G-topological space $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$, since it is discrete.

By Theorem 3, the complete graph $K_n$ is connected and has connected the upper approximated G-topological space $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$, since it is indiscrete. Also by Theorem 4, the connected graph $K_{n,m}$ has connected the upper approximated G-topological space $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be any simple graph. Define ${\mathbb{U}}_3\left(\mathcal{G}\right)$ as the subset of $\mathcal{V}\left(\mathcal{G}\right)$ containing all vertices x with $|{\overline{u}}_x| \le 3$, where $|{\overline{u}}_x|$ denotes the number of elements in ${\overline{u}}_x$. A simple graph $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ is called an upper connected graph if the subgraph ${\mathcal{G}}^{{\mathbb{U}}_3}$ of $\mathcal{G}$, induced by ${\mathbb{U}}_3\left(\mathcal{G}\right)$, is connected. If the relative topology $T_{\mathcal{G}\left(u\right)}{|}_{{\mathbb{U}}_3\left(\mathcal{G}\right)}$ is discrete on the set ${\mathbb{U}}_3\left(\mathcal{G}\right)$, then the upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ will be called upper discrete. For any simple graph $\mathcal{G}$, if ${\mathbb{U}}_3\left(\mathcal{G}\right)=\varnothing$, then we assume $\mathcal{G}$ is upper connected and $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is upper discrete. For the cycle graph $C_n$, if $n=3$, then ${\mathbb{U}}_3\left(C_n\right)=\mathcal{V}\left(C_n\right)$ and so $C_n$ is upper connected with $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ not upper discrete. If $n=4,5$, then ${\mathbb{U}}_3\left(C_n\right)=\varnothing$ and so $C_n$ is an upper connected graph with $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ which is an upper discrete space. From Theorem 5, for all $n>5$, ${\mathbb{U}}_3\left(C_n\right)=\mathcal{V}\left(C_n\right)$ and hence $C_n$ is an upper connected graph, and $(\mathcal{V}\left(C_n\right),T_{C_n\left(u\right)})$ is an upper discrete space. For the complete graph $K_n$, $n\le 3$, ${\mathbb{U}}_3\left(K_n\right)=\mathcal{V}\left(K_n\right)$ and hence $K_n$ is upper connected and $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ is not upper discrete. If $n>3$, then by Theorem 3, ${\mathbb{U}}_3\left(K_n\right)=\varnothing$ and hence $K_n$ is an upper connected graph having the space $(\mathcal{V}\left(K_n\right),T_{K_n\left(u\right)})$ which is an upper discrete space.

For the complete bipartite graph $K_{n,m}$, if $\left|\mathcal{V}\right(K_{n,m}\left)\right|\le 3$, then ${\mathbb{U}}_3\left(K_{n,m}\right)=\mathcal{V}\left(K_{n,m}\right)$ and hence $K_{n,m}$ is upper connected with $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$ that is not upper discrete. If $\left|\mathcal{V}\right(K_{n,m}\left)\right|>3$, then by Theorem 4, ${\mathbb{U}}_3\left(K_{n,m}\right)=\varnothing$ and hence $K_{n,m}$ is an upper connected graph with upper discrete space $(\mathcal{V}\left(K_{n,m}\right),T_{K_{n,m}\left(u\right)})$,

Note that in Figure 2-A of Example 2, ${\mathbb{U}}_3\left(\mathcal{G}\right)=\left\{1^{\prime }\right\}$. So we get that $\mathcal{G}$ is an upper connected graph for which the space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is upper discrete.

In Figure 2-B of Example 2, ${\mathbb{U}}_3\left(\mathcal{G}\right)=\mathcal{V}\left(\mathcal{G}\right)$. So we get that $\mathcal{G}$ is an upper connected graph, and the space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is not upper discrete.

Sari and Kopuzlu, [11] introduced the graphic topological spaces $(\mathcal{V}\left(\mathcal{G}\right),{\tau }_{\mathcal{G}})$ in the theory of undirected graphs induced by a subbasis $S_{\mathcal{G}}$ which is the family of open neighbourhoods $N\left(x\right)$ of vertices in $\mathcal{G}$ and proved that the graphic topological space $(\mathcal{V}\left(\mathcal{G}\right),{\tau }_{\mathcal{G}})$ of any locally finite graph $\mathcal{G}$ is an Alexandroff space. By this property for $(\mathcal{V}\left(\mathcal{G}\right),{\tau }_{\mathcal{G}})$, we can define the minimal operator in $(\mathcal{V}\left(\mathcal{G}\right),{\tau }_{\mathcal{G}})$ as a function $\mathbb{R}$ from $\mathcal{V}\left(\mathcal{G}\right)$ into ${\tau }_{\mathcal{G}}$ which is given by: for all $x\in \mathcal{V}\left(\mathcal{G}\right)$, ${\mathbb{R}}_x$ is the smallest open set in $(\mathcal{V}\left(\mathcal{G}\right),{\tau }_{\mathcal{G}})$ containing x. Since $N\left(x\right)\subseteq \overline{x}$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$ and by the two definitions of graphic topological space $(\mathcal{V}\left(\mathcal{G}\right),{\tau }_{\mathcal{G}})$ and an upper approximated G-topological space $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$, we get ${\mathbb{R}}_x\subseteq O_x$ for all $x\in \mathcal{V}\left(\mathcal{G}\right)$.

Recall [1] that in a topological space $(M,\tau )$, a subset G is called dense in M if $\mathrm{Cl}\left(G\right)=M$, that is, if $M\cap O\ne \varnothing$ for all open sets O.

Theorem 17.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be an upper connected graph. Then $\mathcal{P}$ is dense in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$, where $\mathcal{P}$ is the set of all vertices in ${\mathbb{U}}_3\left(\mathcal{G}\right)$ with degrees greater than one.

Proof. 

Let $x\in {\mathbb{U}}_3\left(\mathcal{G}\right)$. Since ${\mathbb{R}}_x$ is the smallest open set containing x, then to show that $\mathcal{P}\cap O\ne \varnothing$ for all open sets O in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$, we will prove that $\mathcal{P}\cap {\mathbb{R}}_x\ne \varnothing$ for all $x\in {\mathbb{U}}_3\left(\mathcal{G}\right)\setminus \mathcal{P}$. Let $x\in {\mathbb{U}}_3\left(\mathcal{G}\right)\setminus \mathcal{P}$. Since x is not isolated, then there is $y\in {\mathbb{U}}_3\left(\mathcal{G}\right)$ such that $O_u\left(x\right)=\left\{y\right\}$. Hence ${\mathbb{R}}_x=O_u\left(y\right)$. Hence, ${\mathbb{D}}_y>1$. So, there exists some $z\in \mathcal{P}$ such that $z\in O_u\left(y\right)$. Then $z\in \mathcal{P}\cap O_u\left(y\right)=\mathcal{P}\cap {\mathbb{R}}_x$, that is, $\mathcal{P}\cap {\mathbb{R}}_x\ne \varnothing$ for all $x\in {\mathbb{U}}_3\left(\mathcal{G}\right)\setminus \mathcal{P}$. Therefore, $\mathcal{P}$ is dense in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$. □

Theorem 18.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be an upper connected graph, $\zeta$ be the family of smallest open sets of all vertices in ${\mathbb{U}}_3\left(\mathcal{G}\right)$ and ${\beta }_{\zeta }$ be the family of all minimal sets in $\zeta$. If $\mathcal{P}\subseteq {\mathbb{U}}_3\left(\mathcal{G}\right)$ is a minimal dense set in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$ then there is an onto mapping $\eta :{\beta }_{\zeta }\to \mathcal{P}$ such that $\eta \left({\mathbb{R}}_x\right)\in {\mathbb{R}}_x$ for all ${\mathbb{R}}_x\in {\beta }_{\zeta }$.

Proof. 

By the form of ${\beta }_{\zeta }$, the intersection of every pair of distinct elements of ${\beta }_{\zeta }$ is empty set. Since $\mathrm{Cl}\left(G\right)={\mathbb{U}}_3\left(\mathcal{G}\right)$ in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$, there is some $x\in G\cap \mathcal{P}$ for all $G\in {\beta }_{\zeta }$. Since $x\in G$ and $G\in {\beta }_{\zeta }$, then $G\subseteq {\mathbb{R}}_x$ and it is clear that ${\mathbb{R}}_x\subseteq G$, that is, ${\mathbb{R}}_x=G$. If $y\in G\cap (\mathcal{P}\setminus \{x\left\}\right)$, then similarly we get that ${\mathbb{R}}_x={\mathbb{R}}_y=G$. Hence $\mathrm{Cl}\left(\right\{x\left\}\right)=\mathrm{Cl}\left(\right\{y\left\}\right)$. Then $\mathrm{Cl}(\mathcal{P}\setminus \left\{y\right\})={\mathbb{U}}_3\left(\mathcal{G}\right)$ and we have a contradiction. So, $G\cap \mathcal{P}=\left\{x\right\}$.

Define the mapping $\eta :{\beta }_{\zeta }\to \mathcal{P}$ of ${\beta }_{\zeta }$ into $\mathcal{P}$ sending $G\in {\beta }_{\zeta }$ into the single element of $G\cap (\mathcal{P}\setminus \{x\left\}\right)$. Now we will prove that $\eta$ is onto. Let $g\in \mathcal{P}$. We prove that ${\mathbb{R}}_g\in {\beta }_{\zeta }$ such that $\eta \left({\mathbb{R}}_g\right)=g$. If ${\mathbb{R}}_g\notin {\beta }_{\zeta }$, then there is $x\in {\mathbb{U}}_3\left(\mathcal{G}\right)$ such that ${\mathbb{R}}_x\subset {\mathbb{R}}_g$ is a proper subset of ${\mathbb{R}}_g$. Then $\mathrm{Cl}\left({\mathbb{R}}_g\right)=\mathrm{Cl}\left({\mathbb{R}}_x\right)$. In this case we get that $\mathrm{Cl}(\mathcal{P}\setminus \left\{g\right\})={\mathbb{U}}_3\left(\mathcal{G}\right)$, a contradiction. Hence, ${\mathbb{R}}_g\in {\beta }_{\zeta }$ such that $\eta \left({\mathbb{R}}_g\right)=g$. □

Theorem 19.

Let $\mathcal{G}=\left(\mathcal{V}\right(\mathcal{G}),\mathcal{E}(\mathcal{G}\left)\right)$ be an upper connected graph, $\zeta$ be the family of smallest open sets of all vertices in ${\mathbb{U}}_3\left(\mathcal{G}\right)$ and ${\beta }_{\zeta }$ be the family of all minimal sets in $\zeta$. If $\eta :{\beta }_{\zeta }\to \mathcal{V}\left(\mathcal{G}\right)$ is a mapping such that $\eta \left({\mathbb{R}}_x\right)\in {\mathbb{R}}_x$ for all ${\mathbb{R}}_x\in {\beta }_{\zeta }$, then $\eta \left({\beta }_{\zeta }\right)$ is a minimal dense set in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)}$.

Proof. 

It is easy to see that for all $x\in {\mathbb{U}}_3\left(\mathcal{G}\right)$ there is $y\in {\mathbb{U}}_3\left(\mathcal{G}\right)$ such that ${\mathbb{R}}_y\in {\beta }_{\zeta }$ and ${\mathbb{R}}_y\subseteq {\mathbb{R}}_x$. Hence we get $\eta \left({\mathbb{R}}_y\right)\in {\mathbb{R}}_x\cap \eta \left({\beta }_{\zeta }\right)$, that is, $\eta \left({\beta }_{\zeta }\right)$ is dense in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$.

To prove that $\eta \left({\beta }_{\zeta }\right)$ is minimal dense set in $({\mathbb{U}}_3\left(\mathcal{G}\right),{\tau }_{{\mathbb{U}}_3\left(\mathcal{G}\right)})$, let $Cl\left(\mathcal{P}\right)={\mathbb{U}}_3\left(\mathcal{G}\right)$ and $\mathcal{P}\subseteq \eta \left({\beta }_{\zeta }\right)$. Suppose that ${\mathbb{R}}_x\in {\beta }_{\zeta }$ such that $\eta \left({\mathbb{R}}_x\right)\notin \mathcal{P}$. Then there is $y\in {\mathbb{U}}_3\left(\mathcal{G}\right)$ such that ${\mathbb{R}}_y\in {\beta }_{\zeta }$ and $\eta \left({\mathbb{R}}_y\right)\in {\mathbb{R}}_x\cap \mathcal{P}$. Since $\eta \left({\mathbb{R}}_y\right)\in {\mathbb{R}}_x\cap {\mathbb{R}}_y$ and $\eta \left({\mathbb{R}}_x\right)\notin \mathcal{P}$, that is, $\eta \left({\mathbb{R}}_x\right)\in {\mathbb{R}}_x\setminus \mathcal{P}$, then ${\mathbb{R}}_x={\mathbb{R}}_y$ and so $\eta \left({\mathbb{R}}_x\right)=\eta \left({\mathbb{R}}_y\right)\in \mathcal{P}$. This is a contradiction. □

5. Some Applications On Radar Charts

The radar chart or web chart is a graphical method in statistics which consists of a sequence of equiangular radii such that each radii represents one of variables (categories) as in Figure 4. The data length of a radii is proportional to the size of data variable relative to the maximum size of the variable across all data points (groups) [21]. In this section we will prove that if the number of categories for a radar chart is large enough, then the upper approximated G-topological space for the corresponding graph of this radar chart is disconnected and discrete. Furthermore, we will show the upper connectedness and upper discreteness for corresponding graphs of radar charts.

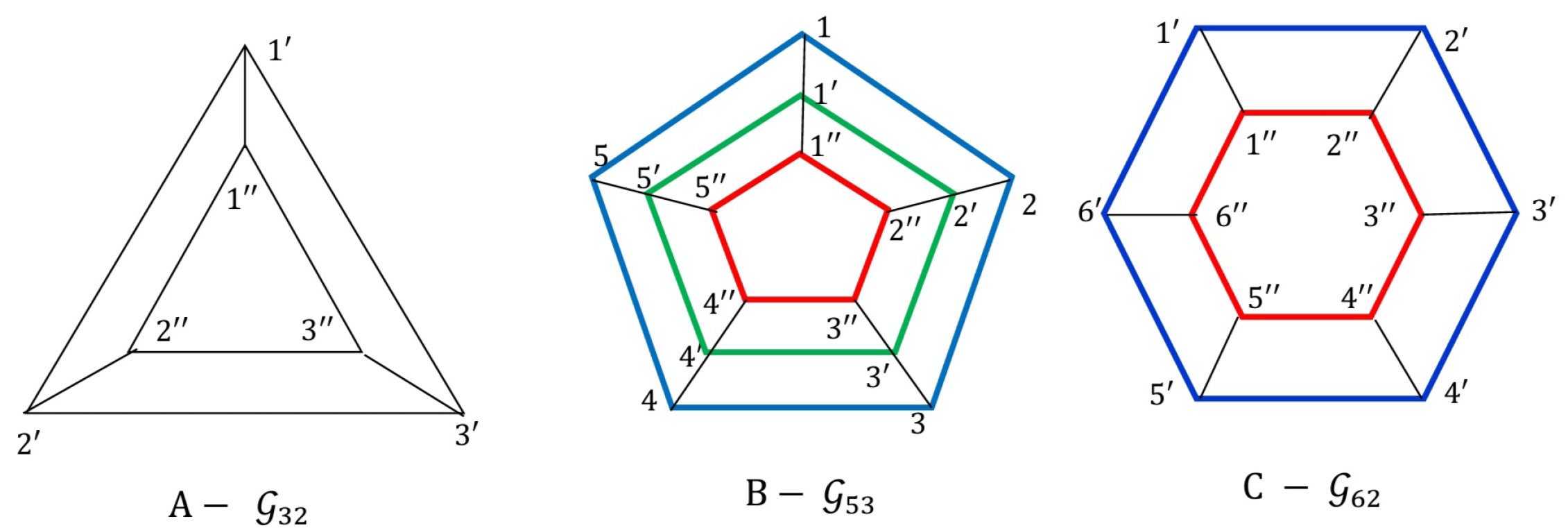
In a radar chart, m denotes the number of categories and n denotes the number of groups. The graph ${\mathcal{G}}_{mn}$ denotes the corresponding graph of a radar chart with m categories and n groups. If $n=1$ and $m>2$, then the corresponding graph of the radar chart will be a cycle graph $C_m$. So, by Theorem 5, the upper approximated G-topological space $(\mathcal{V}\left(C_m\right),T_{C_m\left(u\right)})$ is discrete and so disconnected if $m>5$. Since ${\mathbb{U}}_3\left(C_m\right)=\mathcal{V}\left(C_m\right)$, then then space $(\mathcal{V}\left(C_m\right),T_{C_m\left(u\right)})$ is also upper discrete.

In Figure 6-A, the radar chart has $m=3$ categories and $n=2$ groups. The graph ${\mathcal{G}}_{32}=(\mathcal{V}\left({\mathcal{G}}_{32}\right),\mathcal{E}\left({\mathcal{G}}_{32}\right))$ has vertices set $\mathcal{V}\left({\mathcal{G}}_{32}\right)=\{1,2,3,1^{\prime },2^{\prime },3^{\prime }\}$, and the upper approximated G-topological space $(\mathcal{V}\left({\mathcal{G}}_{32}\right),T_{{\mathcal{G}}_{32}\left(u\right)})$ has a subbasis $\mathcal{V}\left(\overline{{\mathcal{G}}_{32}}\right)=\{\overline{k}=\mathcal{V}\left(\overline{{\mathcal{G}}_{32}}\right):k=1,2,3,1^{\prime },2^{\prime },3^{\prime }\}$. So we get that $(\mathcal{V}\left({\mathcal{G}}_{32}\right),T_{{\mathcal{G}}_{32}\left(u\right)})$ is indiscrete and so connected. Since ${\mathbb{U}}_3\left({\mathcal{G}}_{32}\right)=\varnothing$, then $(\mathcal{V}\left({\mathcal{G}}_{32}\right),T_{{\mathcal{G}}_{32}\left(u\right)})$ is upper discrete.

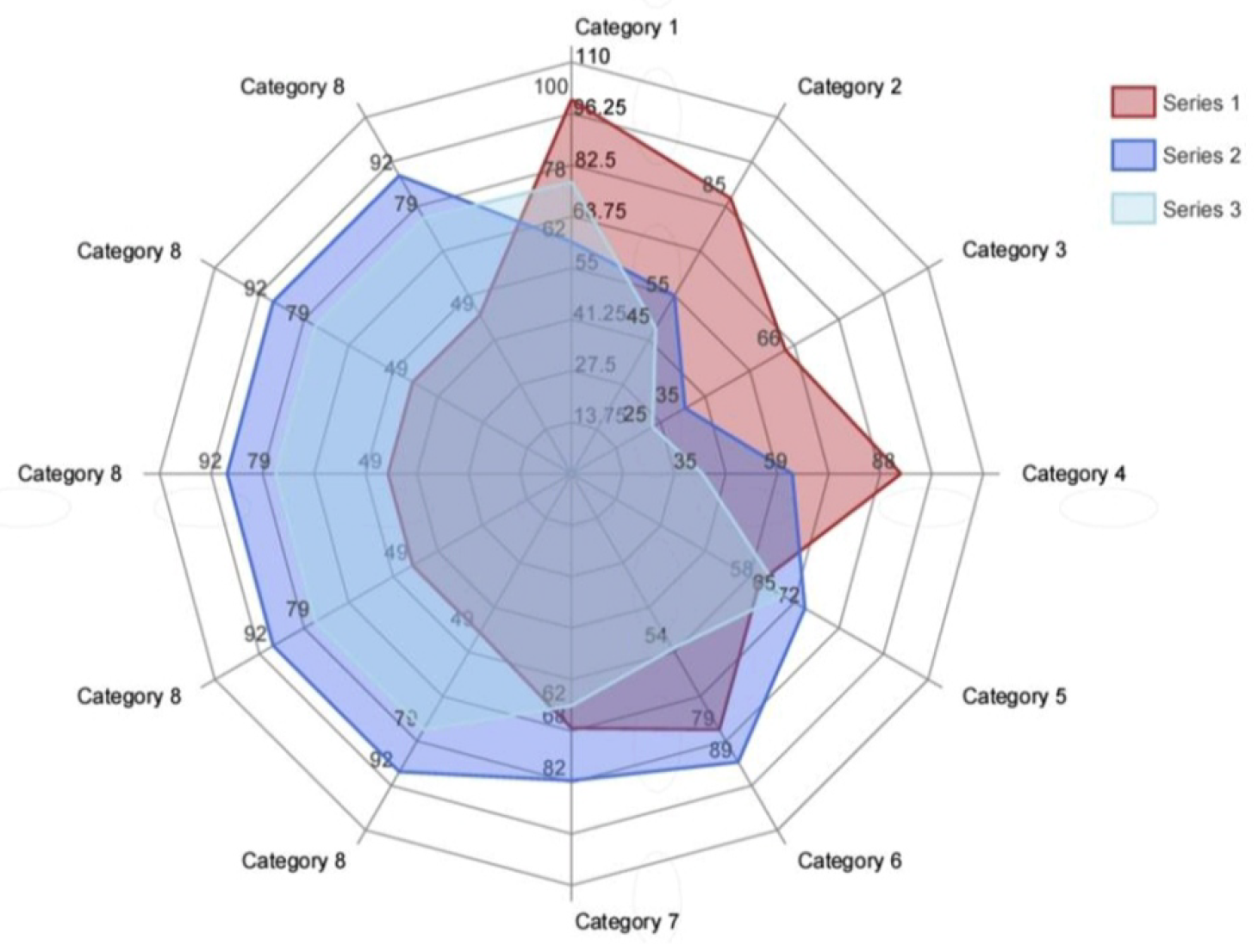
In Figure 5-A, the radar chart has $m=5$ categories and $n=3$ groups. The corresponding graph ${\mathcal{G}}_{53}=(\mathcal{V}\left({\mathcal{G}}_{53}\right),\mathcal{E}\left({\mathcal{G}}_{53}\right))$ in Figure 6-B has vertices set ${\mathcal{G}}_{53}=(\mathcal{V}\left({\mathcal{G}}_{53}\right)=\{k,k^{\prime },k^{″}:k=1,2,3,4,5\}$, and the upper approximated G-topological space $(\mathcal{V}\left({\mathcal{G}}_{53}\right),T_{{\mathcal{G}}_{53}\left(u\right)})$ has a subbasis $\mathcal{V}\left(\overline{{\mathcal{G}}_{53}}\right)$ given by

$$\overline{1}=\{1,2,3,4,5,5^{\prime },1^{\prime },2^{\prime },1^{″}\},\overline{2}=\{1,2,3,4,5,1^{\prime },2^{\prime },3^{\prime },2^{″}\},$$

$$\overline{3}=\{1,2,3,4,5,2^{\prime },3^{\prime },4^{\prime },3^{″}\},\overline{4}=\{1,2,3,4,5,3^{\prime },4^{\prime },4^{\prime },4^{″}\},$$

$$\overline{5}=\{1,2,3,4,5,4^{\prime },5^{\prime },1^{\prime },5^{″}\},\overline{1^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },5,1,2,5^{″},1^{″},2^{″}\},$$

$$\overline{2^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },1,2,3,1^{″},2^{″},3^{″}\},\overline{3^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },2,3,4,2^{″},3^{″},4^{″}\},$$

$$\overline{4^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },3,4,5,3^{″},4^{″},5^{″}\},\overline{5^{\prime }}=\{1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },4,5,1,4^{″},5^{″},1^{″}\},$$

$$\overline{1^{″}}=\{1^{″},2^{″},3^{″},4^{″},5^{″},5^{\prime },1^{\prime },2^{\prime },1\},\overline{2^{″}}=\{1^{″},2^{″},3^{″},4^{″},5^{″},1^{\prime },2^{\prime },3^{\prime },2\},$$

$$\overline{3^{″}}=\{1^{″},2^{″},3^{″},4^{″},5^{″},2^{\prime },3^{\prime },4^{\prime },3\},\overline{4^{″}}=\{1^{″},2^{″},3^{″},4^{″},5^{″},3^{\prime },4^{\prime },5^{\prime },4\}$$

and $\overline{5^{″}}=\{1^{″},2^{″},3^{″},4^{″},5^{″},4^{\prime },5^{\prime },1^{\prime },5\}.$ So we get that $(\mathcal{V}\left({\mathcal{G}}_{53}\right),T_{{\mathcal{G}}_{53}\left(u\right)})$ is discrete and so disconnected. Since ${\mathbb{U}}_3\left({\mathcal{G}}_{53}\right)=\mathcal{V}\left({\mathcal{G}}_{53}\right)$, then $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is upper discrete, and ${\mathcal{G}}_{53}$ is upper connected.

Figure 5. Radar chart with $m=5$, $n=3$ and $m=6$, $n=2$

Figure 5. Radar chart with $m=5$, $n=3$ and $m=6$, $n=2$

Figure 6. Representation of radar chart with ($m=3$, $n=2$), ($m=5$, $n=3$) and ($m=6$, $n=2$)

Figure 6. Representation of radar chart with ($m=3$, $n=2$), ($m=5$, $n=3$) and ($m=6$, $n=2$)

In Figure 5-B, the radar chart has $m=6$ categories and $n=2$ groups. The corresponding graph ${\mathcal{G}}_{62}=(\mathcal{V}\left({\mathcal{G}}_{62}\right),\mathcal{E}\left({\mathcal{G}}_{62}\right))$ in Figure 6-C has vertices set ${\mathcal{G}}_{62}=(\mathcal{V}\left({\mathcal{G}}_{62}\right)=\{k,k^{\prime }:k=1,2,3,4,5,6\}$, and the upper approximated G-topological space $(\mathcal{V}\left({\mathcal{G}}_{62}\right),T_{{\mathcal{G}}_{62}\left(u\right)})$ has a subbasis $\mathcal{V}\left(\overline{{\mathcal{G}}_{62}}\right)$ similar for then graph above. We get that ${\overline{U}}_k=\left\{k\right\}$ for all $k\in \mathcal{V}\left({\mathcal{G}}_{62}\right)$. Therefore, we get that $(\mathcal{V}\left({\mathcal{G}}_{62}\right),T_{{\mathcal{G}}_{62}\left(u\right)})$ is discrete and so disconnected. Since ${\mathbb{U}}_3\left({\mathcal{G}}_{62}\right)=\mathcal{V}\left({\mathcal{G}}_{62}\right)$, then $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is upper discrete, and ${\mathcal{G}}_{62}$ is upper connected.

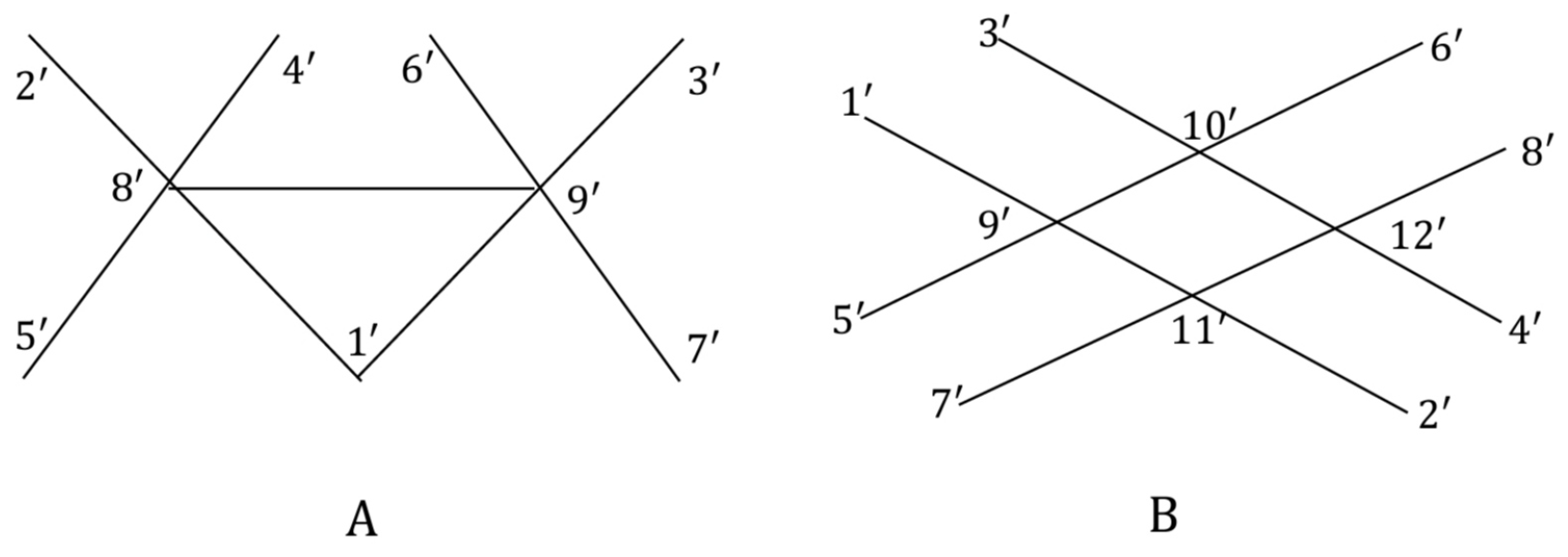
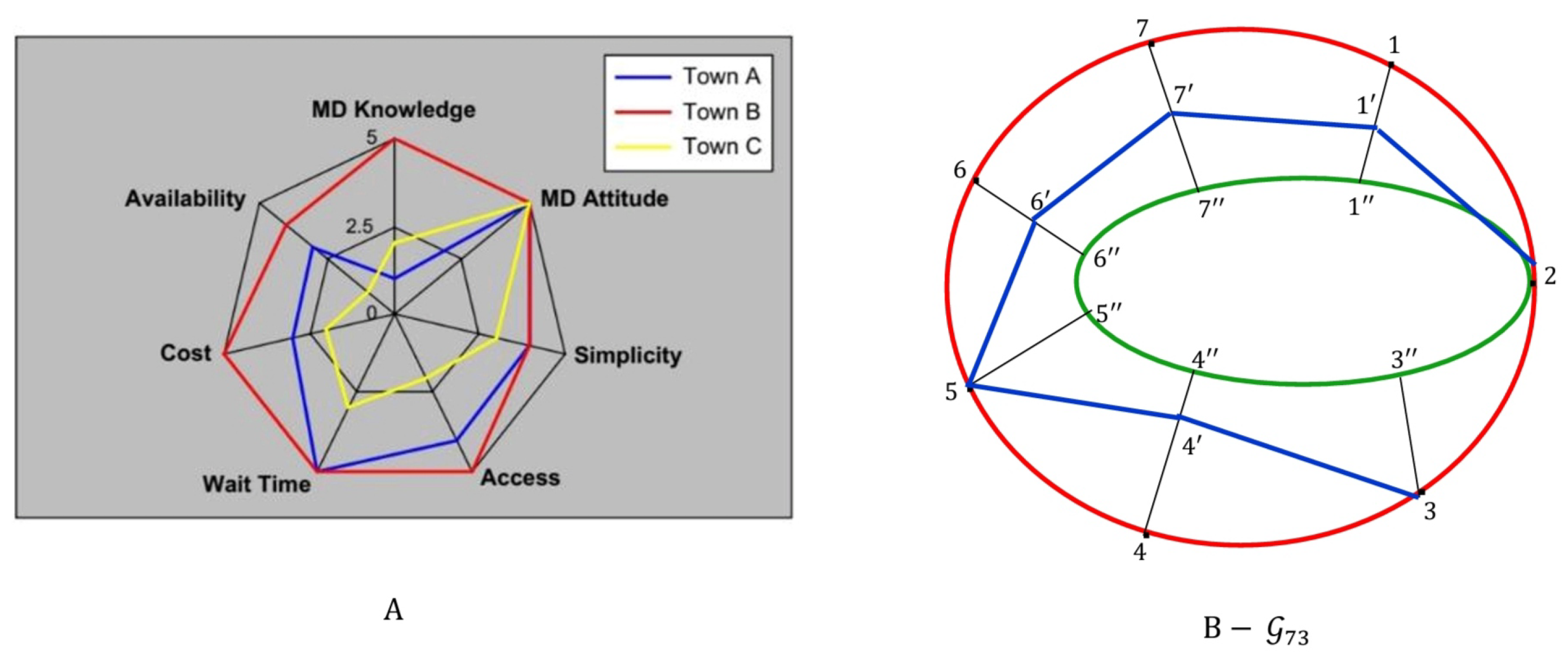
The discrete and upper discrete properties are also satisfied if there is intersection between group charts such as in the radar chart in Figure 7-A (see [22]). The radar chart has $m=7$ categories and $n=3$ groups with intersection points between groups. The corresponding graph ${\mathcal{G}}_{73}=(\mathcal{V}\left({\mathcal{G}}_{73}\right),\mathcal{E}\left({\mathcal{G}}_{73}\right))$ in Figure 7-B has vertices set

$$\mathcal{V}\left({\mathcal{G}}_{73}\right)=\{1,2,3,4,5,6,7,1^{\prime },4^{\prime },6^{\prime },7^{\prime },1^{″},3^{″},4^{″},5^{″},6^{″},7^{″}\}$$

with intersection vertices 2, 3 and 5. The upper approximated G-topological space $(\mathcal{V}\left({\mathcal{G}}_{73}\right),T_{{\mathcal{G}}_{73}\left(u\right)})$ has a subbasis $\mathcal{V}\left(\overline{{\mathcal{G}}_{73}}\right)$ given in Table 1. So, by the details in Table 1, we get that $(\mathcal{V}\left({\mathcal{G}}_{73}\right),T_{{\mathcal{G}}_{73}\left(u\right)})$ is discrete and so disconnected. Since ${\mathbb{U}}_3\left({\mathcal{G}}_{73}\right)=\mathcal{V}\left({\mathcal{G}}_{73}\right)$, then $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is upper discrete.

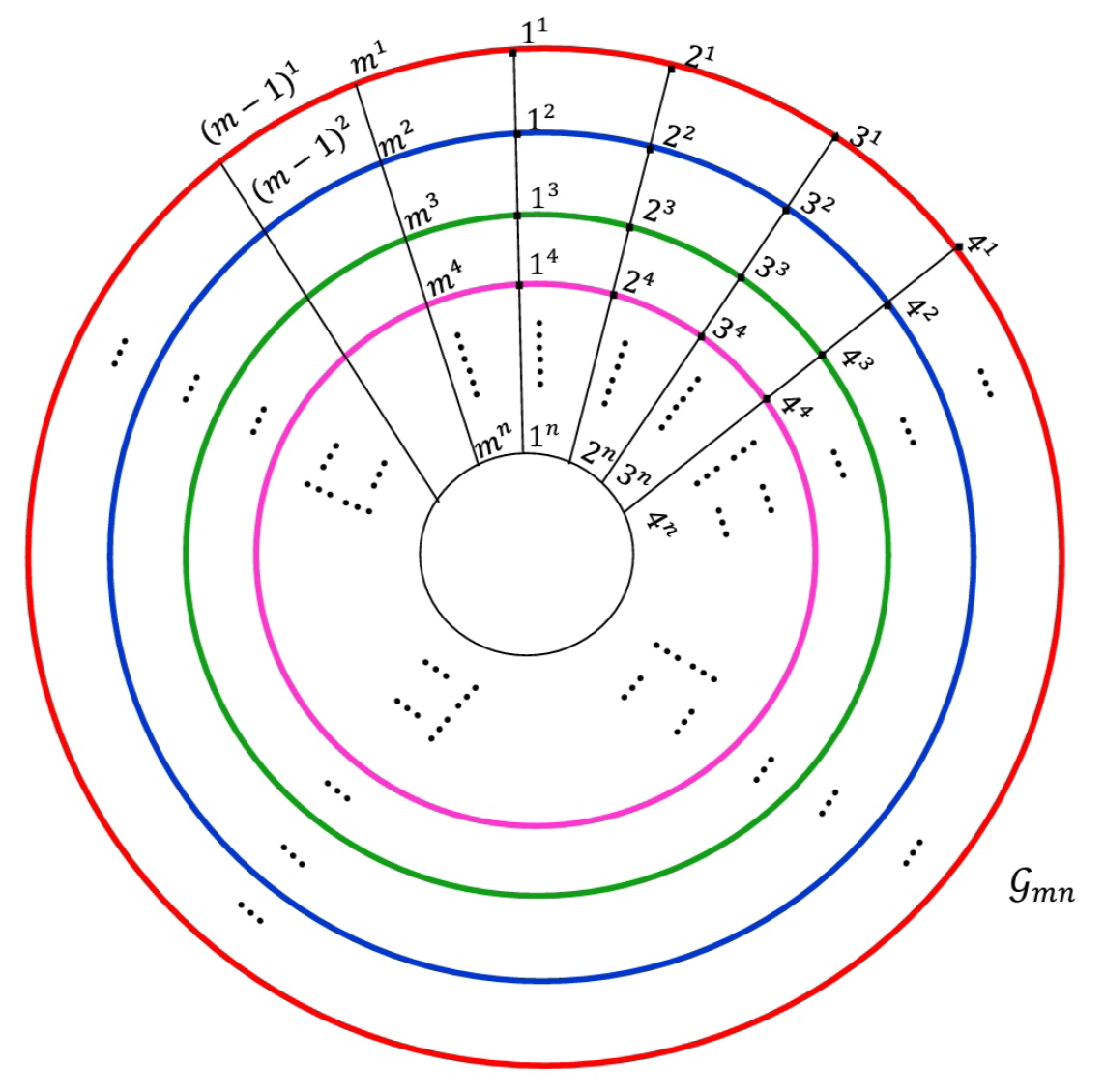
Now, in general we study the connectedness and discreteness for the corresponding graphs of the radar charts with $m>5$ categories and $n>5$ groups. The corresponding graph ${\mathcal{G}}_{mn}=(\mathcal{V}\left({\mathcal{G}}_{mn}\right),\mathcal{E}\left({\mathcal{G}}_{mn}\right))$ in Figure 8 has vertices set $\mathcal{V}\left({\mathcal{G}}_{mn}\right)=\{j^k:k=1,2,\cdots ,n\mathrm{and}j=1,2,\cdots ,m\}$. For the upper approximated G-topological space $(\mathcal{V}\left({\mathcal{G}}_{mn}\right),T_{{\mathcal{G}}_{mn}\left(u\right)})$, some upper approximation neighbourhoods are given in Table 2. Similarly, for all vertices x that lie on the groups 1,2, $n-1$ and n, we have ${\overline{u}}_x=\left\{x\right\}$.

For all $k=3,4,\cdots ,n-2$ and $j=3,4,\cdots ,m-2$, we have

$$\overline{j^k}{=\{(j-2)}^k,{(j-1)}^{k-1},{(j-1)}^k,{(j-1)}^{k+1},j^{k-2},j^{k-1},j^k,j^{k+1},j^{k+2},$$

$${(j+1)}^{k-1},{(j+1)}^k,{(j+1)}^{k+1},{(j+2)}^k\}.$$

Hence

$${\overline{u}}_{j^k}=\overline{{(j-2)}^k}\cap \overline{{(j-1)}^{k-1}}\cap \overline{{(j-1)}^k}\cap \overline{{(j-1)}^{k+1}}\cap \overline{j^{k-2}}\cap \overline{j^{k-1}}\cap \overline{j^k}\cap \overline{j^{k+1}}\cap \overline{j^{k+2}}$$

$$\cap \overline{{(j+1)}^{k-1}}\cap \overline{{(j+1)}^k}\cap \overline{{(j+1)}^{k+1}}\cap \overline{{(j+2)}^k}=\left\{j^k\right\}.$$

So, we conclude that the upper approximated G-topological space $(\mathcal{V}\left({\mathcal{G}}_{mn}\right),T_{{\mathcal{G}}_{mn}\left(u\right)})$ is discrete and so disconnected. Since ${\mathbb{U}}_3\left({\mathcal{G}}_{mn}\right)=\mathcal{V}\left({\mathcal{G}}_{mn}\right)$, then $(\mathcal{V}\left(\mathcal{G}\right),T_{\mathcal{G}\left(u\right)})$ is upper discrete.

6. Conclusions

We have defined a new topology, called the upper approximated G-topology, on the vertices set $\mathcal{V}\left(\mathcal{G}\right)$ of a simple graph $\mathcal{G}$ and investigated several topological properties (discreteness, compactness, connectedness) related to this topology. The topology is define by using upper approximation neighbourhood systems of graphs. In particular, the study includes some well known graphs, as complete graphs $K_n$, cycle graphs $C_n$ and complete bipartite graphs $K_{n,m}$. Some applications to radar charts are given. We expect that our study can be applied to other classes of graphs and other topological properties.