Submitted:
26 January 2025
Posted:
28 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
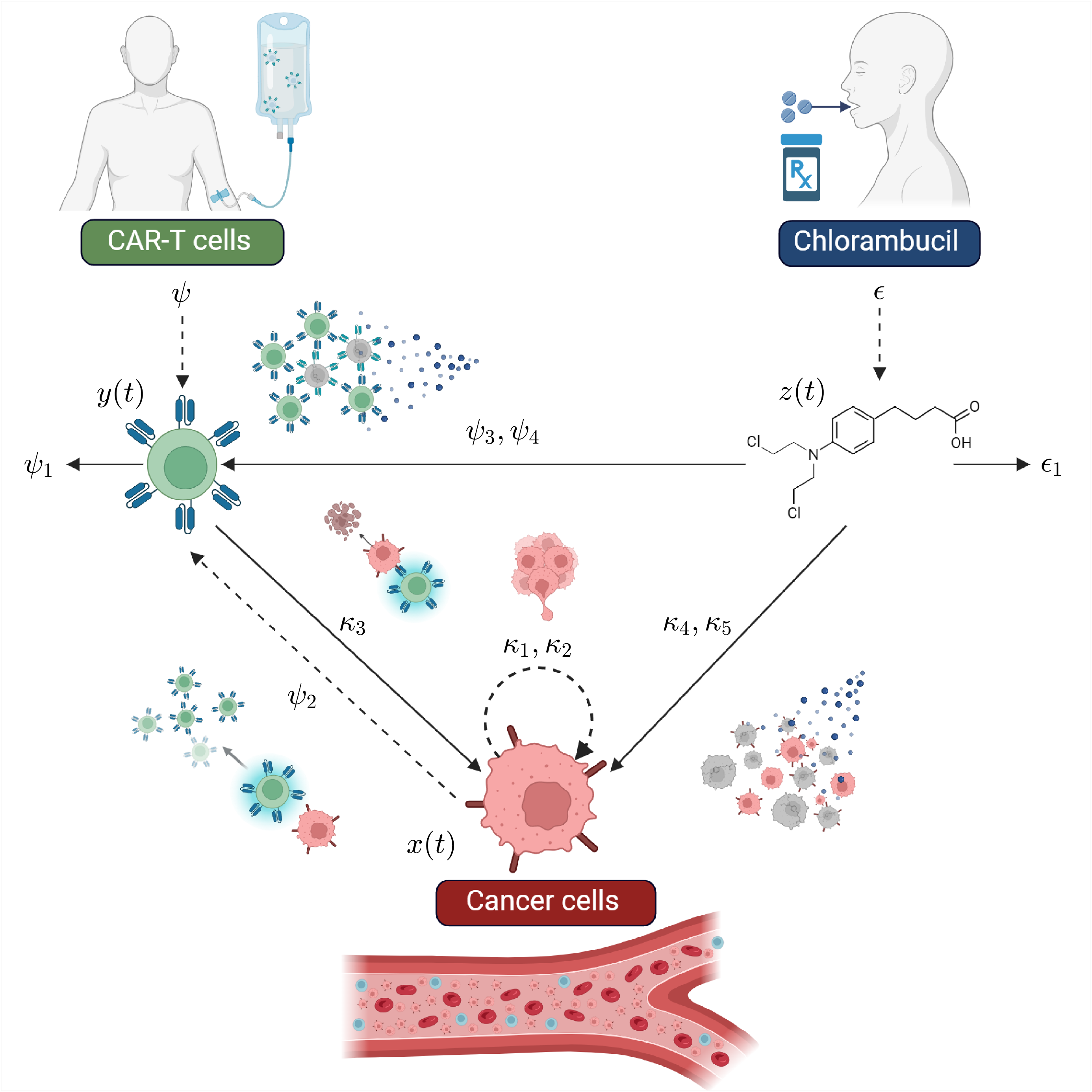
2. Materials and Methods
2.1. The CLL Mathematical Model
2.2. Parameter Estimation
3. Results: Nonlinear Dynamical Properties of the System
3.1. Localizing Domain
| Chemotherapy off | Chemotherapy on |
| where |
| Immunotherapy | Chemotherapy | Chemoimmunotherapy |
- Case 1:.
- In this case chemotherapy is not considered at the beginning of the treatment, therefore:
- Case 2:.
- In this case, bounds are given as follows:
- Case 3: .
- In this case, bounds are defined as follows:
- Case 4: .
- In this case, the initial condition is given by the chemotherapy dose. Thus, when considering parameter values, bounds are given by:
- Case 1: Immunotherapy.
- The Iterative Theorem of the LCIS method is applied as follows:and by substituting the corresponding value of Case 1 for the CAR-T cells lower bound one can get the next result:
- Case 2: Chemotherapy.
- When only the chlorambucil drug is being considered, the Iterative Theorem is applied as shown below:and the lower bound is defined as follows
- Case 3: Chemoimmunotherapy.
- Now, let us explore the case when the combined therapy is applied, thus, the Iterative Theorem yields the next result:then, when substituting the corresponding value of Case 2 for the CAR-T cells lower bound the next result can be establish:
3.2. Eradication Conditions
- Case 1: Immunotherapy.
- When only the CAR-T cells are applied for cancer treatment the time-derivative can be bounded from above as follows:where , and the next constraint can be formulated on the immunotherapy concentration:
- Case 2: Chemotherapy.
- When only the chlorambucil drug is being considered from the beginning of the treatment the time-derivative is bounded from above as indicated below:where as , and the next constraint is formulated on the chemotherapy concentrationhowever, it is evident from the denominator that the next condition relating the rates of CLL cells growth and cytotoxicity of the drug should be fulfilled:or else, condition (12) will not have a biologically feasible solution.
- Case 3: Chemoimmunotherapy.
- When the combined therapy is applied the time-derivative is bounded as follows:where . In order to properly solve this condition, we set the CAR-T cells as the control therapy and come to the following result:in this case it is important to consider two paths. If condition (13) is satisfied, chemotherapy alone could eradicate the leukemia cells population described by the CLL mechanistic model (1)–(3). However, both therapies may be combined in varying proportions to design a successful protocol that ultimately achieves cancer eradication. Conversely, if condition (13) is not fulfilled, then a biologically feasible solution can be computed to estimate the concentration of CAR-T cells required to ensure the complete eradication of cancer cells in the corresponding scenarios.
3.3. Persistence Conditions
- Case 1: Equilibrium
-
The Jacobian matrix has the following form:Hence, it is evident that this equilibrium is unstable, as one of the eigenvalues is positive,This outcome is to be expected, as once cancer cells evade the immune response, either by suppressing the immune system or by remaining undetected by effector cells, they will grow to their maximum carrying capacity or to the extent that the subject can endure. This scenario also indicates that treatment strategies were either unsuccessful or not administered.
- Case 2: Equilibrium
-
The Jacobian matrix evaluated at this equilibrium point is given by:with the next eigenvalues:It is evident that the radicands in and will be positive and real if the persistence condition (4) from Remark III holds, i.e., ,which allows us to conclude that equilibrium (16) is locally asymptotically stable. Conversely, if condition (4) is not satisfied, equilibrium (16) becomes unstable and biologically infeasible, as . In this case, if therapies are unsuccessful, cancer cells will grow to their maximum carrying capacity , making (17) the only locally asymptotically stable equilibrium point of the system as it is shown in the next case.
- Case 3: Equilibrium
-
The Jacobian matrix is upper triangular, as shown below:Therefore, the eigenvalues correspond to the diagonal elements of the matrix:From these results, two scenarios are identified. First, equilibrium point (17) is locally asymptotically stable ifThis indicates that the persistence condition (4) from Remark III is not satisfied. In this case, long-term persistence of CAR-T cells cannot be expected, as equilibrium (16) does not exist within the positive and biologically feasible domain of the system. Nonetheless, if the persistence condition (4) is satisfied, equilibrium (17) becomes unstable, and the only locally asymptotically stable equilibrium point is (16). This implies that both cell populations described by the CLL mechanistic model (1)–(3) coexist. However, the in silico experimentation will reveal whether this sustained immune response by the CAR-T cells is sufficient to reduce the tumor burden to a level that is manageable for the subject’s health. Results from these three cases allows us to conclude that if the chemoimmunotherapy treatment strategy is not successful, leukemia cells will always persist.
3.4. Existence and Uniqueness
4. Discussion: In Silico Experimentation
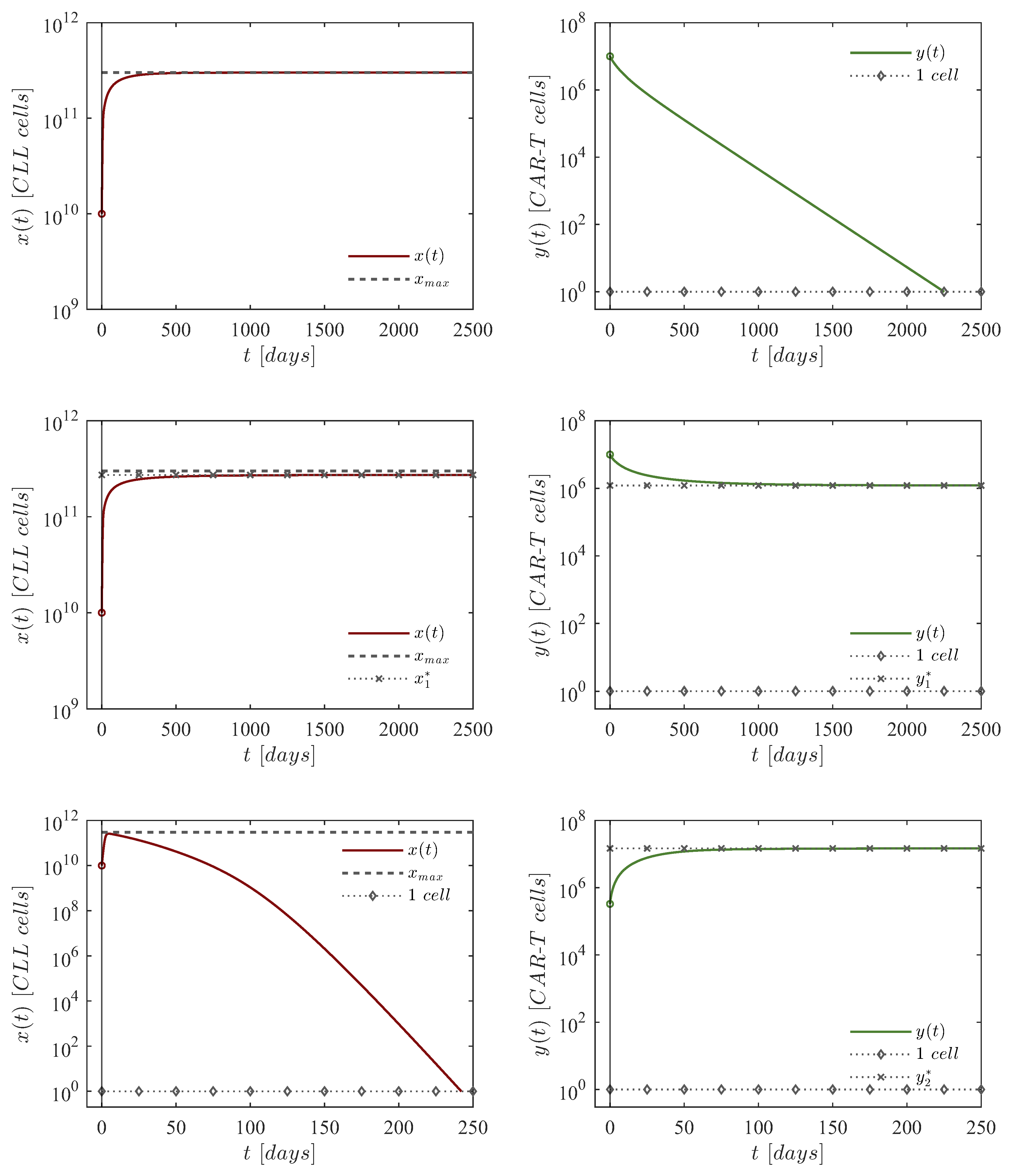
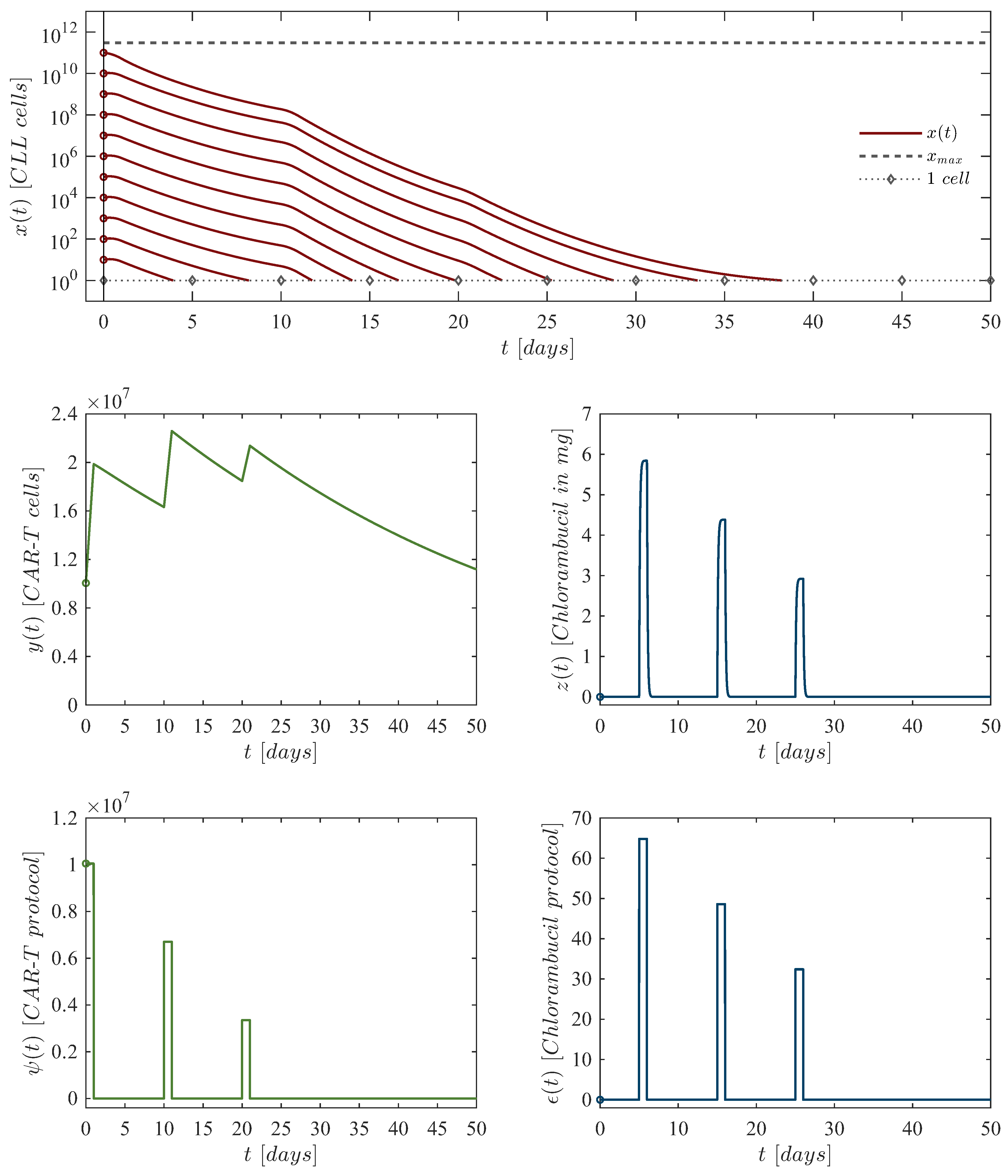
- Case 1: Depletion of CAR-T cells.
- Depletion of CAR-T cells in the short-term happens when condition (4) is not satisfied. As expected, the concentration of CLL cells grows to their maximum carrying capacity, while CAR-T cells eventually fall below the threshold of clinically significant biological behavior, defined as fewer than 1 cell. Hence, solutions go to the equilibrium point (17), i.e, . For the sake of numerical simulations, dynamics are simulated following a single application of the therapy under the next set of initial conditions: CLL cells, CAR-T cells (unique dose), and mg of chlorambucil. Parameter values are as follows: , , , , . Other parameters are set as zero, as chemotherapy is not considered in this scenario. Results for this in silico experimentation are shown in the top panels of Figure 2.
- Case 2: Persistence of CAR-T cells.
- Long-term persistence of CAR-T cells is observed when condition (4) is fulfilled. In this case, cells concentrations stabilize at a steady-state defined by the equilibrium point (16) . However, this outcome does not represent a viable treatment strategy for real-world clinical scenarios, because the tumor burden remains near the maximum carrying capacity. For the sake of numerical simulations, dynamics are simulated following a single application of the therapy under the next set of initial conditions: CLL cells, CAR-T cells (unique dose), and mg of chlorambucil. Parameter values are as follows: , , , , . Other parameters are set as zero, as chemotherapy is not considered in this scenario. Results for this in silico experimentation are shown in the middle panels of Figure 2.
- Case 3: Eradication of CLL cells.
- Within the scope of system (1)–(3), eradication of CLL cells is ensured when the concentration of CAR-T cells meets condition (11). Hence, the immunotherapy control parameter is set with a constant value of which equals to cells. Dynamics are simulated following a constant application of the therapy under the next set of initial conditions: CLL cells, CAR-T cells (constant dose), and mg of chlorambucil. Parameter values are as follows: , , , , . Other parameters are set as zero, as chemotherapy is not considered in this scenario. Results for this in silico experimentation are shown in the bottom panels of Figure 2.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Notations and Mathematical Foundations
Appendix A.1. Positiveness of Solutions
Appendix A.2. Localization of Compact Invariant Sets Method
Appendix A.3. Stability in the Sense of Lyapunov
- Positive definiteness: and for all .
- Radial unboundedness: as .
- The origin is asymptotically stable if all eigenvalues of A satisfy .
- The origin is unstable if one or more eigenvalues of Asatisfy .
Appendix A.4. Lipschitz Condition
References
- Yao, Y.; Lin, X.; Li, F.; Jin, J.; Wang, H. The global burden and attributable risk factors of chronic lymphocytic leukemia in 204 countries and territories from 1990 to 2019: analysis based on the global burden of disease study 2019. BioMedical Engineering OnLine 2022, 21. [Google Scholar] [CrossRef] [PubMed]
- Ghia, P.; Ferreri, A.J.; Caligaris-Cappio, F. Chronic lymphocytic leukemia. Critical Reviews in Oncology/Hematology 2007, 64, 234–246. [Google Scholar] [CrossRef] [PubMed]
- Burger, J.A.; O’Brien, S. Evolution of CLL treatment — from chemoimmunotherapy to targeted and individualized therapy. Nature Reviews Clinical Oncology 2018, 15, 510–527. [Google Scholar] [CrossRef]
- Sun, D.; Shi, X.; Li, S.; Wang, X.; Yang, X.; Wan, M. CAR-T cell therapy: A breakthrough in traditional cancer treatment strategies (Review). Molecular Medicine Reports 2024, 29. [Google Scholar] [CrossRef] [PubMed]
- Borogovac, A.; Siddiqi, T. Advancing CAR T-cell therapy for chronic lymphocytic leukemia: exploring resistance mechanisms and the innovative strategies to overcome them. Cancer Drug Resistance 2024. [Google Scholar] [CrossRef]
- Hallek, M. Chronic lymphocytic leukemia: 2020 update on diagnosis, risk stratification and treatment. American Journal of Hematology 2019, 94, 1266–1287. [Google Scholar] [CrossRef]
- Brady, R.; Enderling, H. Mathematical Models of Cancer: When to Predict Novel Therapies, and When Not to. Bulletin of Mathematical Biology 2019, 81, 3722–3731. [Google Scholar] [CrossRef]
- Malinzi, J.; Basita, K.B.; Padidar, S.; Adeola, H.A. Prospect for application of mathematical models in combination cancer treatments. Informatics in Medicine Unlocked 2021, 23, 100534. [Google Scholar] [CrossRef]
- Joslyn, L.R.; Huang, W.; Miles, D.; Hosseini, I.; Ramanujan, S. Digital twins elucidate critical role of Tscm in clinical persistence of TCR-engineered cell therapy. npj Systems Biology and Applications 2024, 10. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zhang, J.; Yan, L.; Zhao, H.; Ding, L.; Bhatara, S.; Yang, X.; Yoshimura, S.; Yang, W.; et al. Single-cell systems pharmacology identifies development-driven drug response and combination therapy in B cell acute lymphoblastic leukemia. Cancer Cell 2024, 42, 552–567.e6. [Google Scholar] [CrossRef]
- Love, S.B.; Brown, S.; Weir, C.J.; Harbron, C.; Yap, C.; Gaschler-Markefski, B.; Matcham, J.; Caffrey, L.; McKevitt, C.; Clive, S.; et al. Embracing model-based designs for dose-finding trials. British journal of cancer 2017, 117, 332–339. [Google Scholar] [CrossRef] [PubMed]
- Belov, A.; Schultz, K.; Forshee, R.; Tegenge, M.A. Opportunities and challenges for applying model-informed drug development approaches to gene therapies. CPT: Pharmacometrics & Systems Pharmacology 2021, 10, 286–290. [Google Scholar] [CrossRef]
- Chelliah, V.; Lazarou, G.; Bhatnagar, S.; Gibbs, J.P.; Nijsen, M.; Ray, A.; Stoll, B.; Thompson, R.A.; Gulati, A.; Soukharev, S.; et al. Quantitative systems pharmacology approaches for immuno-oncology: adding virtual patients to the development paradigm. Clinical Pharmacology & Therapeutics 2021, 109, 605–618. [Google Scholar] [CrossRef]
- Milo, R.; Phillips, R. Cell biology by the numbers; Garland Science: New York, New York, USA, 2015. [Google Scholar]
- Dominik, W.; Natalia, K. Dynamics of cancer: mathematical foundations of oncology; World Scientific: Hackensack, New Jersey, USA, 2014. [Google Scholar]
- Britton, N.F. Essential mathematical biology; Springer Science & Business Media: New York, New York, USA, 2012. [Google Scholar] [CrossRef]
- Holford, N. Pharmacodynamic principles and the time course of immediate drug effects. Translational and clinical pharmacology 2017, 25, 157–161. [Google Scholar] [CrossRef]
- Norton, L. Cancer log-kill revisited. American Society of Clinical Oncology Educational Book 2014, 34, 3–7. [Google Scholar] [CrossRef]
- de Pillis, L.; Fister, K.R.; Gu, W.; Collins, C.; Daub, M.; Gross, D.; Moore, J.; Preskill, B. Mathematical model creation for cancer chemo-immunotherapy. Computational and Mathematical Methods in Medicine 2009, 10, 165–184. [Google Scholar] [CrossRef]
- Byers, J.P.; Sarver, J.G. Pharmacokinetic modeling. In Pharmacology; Elsevier: New York, New York, USA, 2009; pp. 201–277. [Google Scholar] [CrossRef]
- De Leenheer, P.; Aeyels, D. Stability properties of equilibria of classes of cooperative systems. IEEE Transactions on Automatic Control 2001, 46, 1996–2001. [Google Scholar] [CrossRef]
- Valle, P.A.; Coria, L.N.; Plata, C.; Salazar, Y. CAR-T Cell Therapy for the Treatment of ALL: Eradication Conditions and In Silico Experimentation. Hemato 2021, 2, 441–462. [Google Scholar] [CrossRef]
- Guzev, E.; Luboshits, G.; Bunimovich-Mendrazitsky, S.; Firer, M.A. Experimental Validation of a Mathematical Model to Describe the Drug Cytotoxicity of Leukemic Cells. Symmetry 2021, 13, 1760. [Google Scholar] [CrossRef]
- Guzev, E.; Jadhav, S.S.; Hezkiy, E.E.; Sherman, M.Y.; Firer, M.A.; Bunimovich-Mendrazitsky, S. Validation of a Mathematical Model Describing the Dynamics of Chemotherapy for Chronic Lymphocytic Leukemia In Vivo. Cells 2022, 11, 2325. [Google Scholar] [CrossRef]
- Donnou, S.; Galand, C.; Touitou, V.; Sautès-Fridman, C.; Fabry, Z.; Fisson, S. Murine models of B-cell lymphomas: promising tools for designing cancer therapies. Advances in hematology 2012, 2012, 701704. [Google Scholar] [CrossRef] [PubMed]
- Mashima, K.; Azuma, M.; Fujiwara, K.; Inagaki, T.; Oh, I.; Ikeda, T.; Umino, K.; Nakano, H.; Morita, K.; Sato, K.; et al. Differential localization and invasion of tumor cells in mouse models of human and murine leukemias. Acta Histochemica et Cytochemica 2020, 53, 43–53. [Google Scholar] [CrossRef]
- Sender, R.; Weiss, Y.; Navon, Y.; Milo, I.; Azulay, N.; Keren, L.; Fuchs, S.; Ben-Zvi, D.; Noor, E.; Milo, R. The total mass, number, and distribution of immune cells in the human body. Proceedings of the National Academy of Sciences 2023, 120, e2308511120. [Google Scholar] [CrossRef] [PubMed]
- Hatton, I.A.; Galbraith, E.D.; Merleau, N.S.; Miettinen, T.P.; Smith, B.M.; Shander, J.A. The human cell count and size distribution. Proceedings of the National Academy of Sciences 2023, 120, e2303077120. [Google Scholar] [CrossRef] [PubMed]
- Porter, D.L.; Levine, B.L.; Kalos, M.; Bagg, A.; June, C.H. Chimeric antigen receptor–modified T cells in chronic lymphoid leukemia. New England Journal of Medicine 2011, 365, 725–733. [Google Scholar] [CrossRef]
- National Center for Biotechnology Information (2022). PubChem Compound Summary for CID 2708, Chlorambucil. https://pubchem.ncbi.nlm.nih.gov/compound/Chlorambucil, 2024. Updated: September/14/2024.
- Valle, P.A.; Garrido, R.; Salazar, Y.; Coria, L.N.; Plata, C. Chemoimmunotherapy Administration Protocol Design for the Treatment of Leukemia through Mathematical Modeling and In Silico Experimentation. Pharmaceutics 2022, 14, 1396. [Google Scholar] [CrossRef]
- Eichhorst, B.F.; Busch, R.; Stilgenbauer, S.; Stauch, M.; Bergmann, M.A.; Ritgen, M.; Kranzhöfer, N.; Rohrberg, R.; Söling, U.; Burkhard, O.; et al. First-line therapy with fludarabine compared with chlorambucil does not result in a major benefit for elderly patients with advanced chronic lymphocytic leukemia. Blood, The Journal of the American Society of Hematology 2009, 114, 3382–3391. [Google Scholar] [CrossRef]
- Access Pharmacy. Drug Monogrpahs: Chlorambucil. https://accesspharmacy.mhmedical.com/, 2024. Accessed: 01/October/2024.
- de Pillis, L.G.; Gu, W.; Radunskaya, A.E. Mixed immunotherapy and chemotherapy of tumors: modeling, applications and biological interpretations. Journal of theoretical biology 2006, 238, 841–862. [Google Scholar] [CrossRef]
- Silber, R.; Degar, B.; Costin, D.; Newcomb, E.W.; Mani, M.; Rosenberg, C.R.; Morse, L.; Drygas, J.C.; Canellakis, Z.N.; Potmesil, M. Chemosensitivity of lymphocytes from patients with B-cell chronic lymphocytic leukemia to chlorambucil, fludarabine, and camptothecin analogs. Blood 1994, 84, 3440–46. [Google Scholar] [CrossRef]
- Drugbank Online. Chlorambucil. https://go.drugbank.com/drugs/DB00291, 2024. Updated: August/02/2024.
- Lee, D.W.; Kochenderfer, J.N.; Stetler-Stevenson, M.; Cui, Y.K.; Delbrook, C.; Feldman, S.A.; Fry, T.J.; Orentas, R.; Sabatino, M.; Shah, N.N.; et al. T cells expressing CD19 chimeric antigen receptors for acute lymphoblastic leukaemia in children and young adults: a phase 1 dose-escalation trial. Lancet 2015, 385, 517–528. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Z.; Yang, Z.; Wang, M.; Li, S.; Li, Y.; Zhang, R.; Xiong, Z.; Wei, Z.; Shen, J.; et al. Phase I escalating-dose trial of CAR-T therapy targeting CEA+ metastatic colorectal cancers. Molecular Therapy 2017, 25, 1248–1258. [Google Scholar] [CrossRef] [PubMed]
- George, P.; Dasyam, N.; Giunti, G.; Mester, B.; Bauer, E.; Andrews, B.; Perera, T.; Ostapowicz, T.; Frampton, C.; Li, P.; et al. Third-generation anti-CD19 chimeric antigen receptor T-cells incorporating a TLR2 domain for relapsed or refractory B-cell lymphoma: a phase I clinical trial protocol (ENABLE). BMJ open 2020, 10, e034629. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhao, H.; Luo, J.; Liao, Y.; Dan, X.; Hu, G.; Gu, W. A phase I dose-escalation study of neoantigen-activated haploidentical T cell therapy for the treatment of relapsed or refractory peripheral T-cell lymphoma. Frontiers in Oncology 2022, 12, 944511. [Google Scholar] [CrossRef]
- Bulsara, S.; Wu, M.; Wang, T. Phase I CAR-T Clinical Trials Review. Anticancer research 2022, 42, 5673–5684. [Google Scholar] [CrossRef]
- Williams, A.M.; Baran, A.M.; Schaffer, M.; Bushart, J.; Rich, L.; Moore, J.; Barr, P.M.; Zent, C.S. Significant weight gain in CLL patients treated with ibrutinib: a potentially deleterious consequence of therapy. American journal of hematology 2019, 95, E16. [Google Scholar] [CrossRef]
- Sitlinger, A.; Deal, M.A.; Garcia, E.; Thompson, D.K.; Stewart, T.; MacDonald, G.A.; Devos, N.; Corcoran, D.; Staats, J.S.; Enzor, J.; et al. Physiological fitness and the pathophysiology of chronic lymphocytic leukemia (CLL). Cells 2021, 10, 1165. [Google Scholar] [CrossRef]
- Liu, C.; Yang, M.; Zhang, D.; Chen, M.; Zhu, D. Clinical cancer immunotherapy: Current progress and prospects. Frontiers in immunology 2022, 13, 961805. [Google Scholar] [CrossRef]
- Ling, S.P.; Ming, L.C.; Dhaliwal, J.S.; Gupta, M.; Ardianto, C.; Goh, K.W.; Hussain, Z.; Shafqat, N. Role of Immunotherapy in the treatment of cancer: A systematic review. Cancers 2022, 14, 5205. [Google Scholar] [CrossRef]
- Hallek, M.; Cheson, B.D.; Catovsky, D.; Caligaris-Cappio, F.; Dighiero, G.; Döhner, H.; Hillmen, P.; Keating, M.; Montserrat, E.; Chiorazzi, N.; et al. iwCLL guidelines for diagnosis, indications for treatment, response assessment, and supportive management of CLL. Blood, The Journal of the American Society of Hematology 2018, 131, 2745–2760. [Google Scholar] [CrossRef]
- Krishchenko, A.P. Localization of invariant compact sets of dynamical systems. Differ Equ 2005, 41, 1669–1676. [Google Scholar] [CrossRef]
- Krishchenko, A.P.; Starkov, K.E. Localization of compact invariant sets of the Lorenz system. Phys Lett A 2006, 353, 383–388. [Google Scholar] [CrossRef]
- Krishchenko, A.P.; Starkov, K.E. Localization of compact invariant sets of nonlinear time-varying systems. International Journal of Bifurcation and Chaos 2008, 18, 1599–1604. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear systems, 3 ed.; Prentice-Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Hahn, W.; Hosenthien, H.H.; Lehnigk, S.H. Theory and application of Liapunov’s direct method; Dover Publications, Inc.: Mineola, NY, USA, 2019. [Google Scholar]
| Parameter | Description | Units |
|---|---|---|
| CLL cancer cells growth rate | ||
| Maximum leukemia cells carrying capacity | ||
| Eradication rate of CLL cancer cells by CAR-T cells | ||
| Chlorambucil cytotoxicity rate on CLL cancer cells | ||
| Chlorambucil concentration producing of the | ||
| maximum cytotoxicity on CLL cancer cells | ||
| Death rate of CAR-T cells | ||
| Activation rate of CAR-T cells due to encounters | ||
| with CLL cancer cells | ||
| Chlorambucil cytotoxicity rate on CAR-T cells | ||
| Chlorambucil concentration producing of the | ||
| maximum cytotoxicity on CAR-T cells | ||
| Decay rate of the chlorambucil drug | ||
| External CAR-T cell therapy administration | ||
| External chlorambucil drug administration |
| Parameter | Value | Units |
|---|---|---|
| Dimensionless | ||
| Dimensionless |
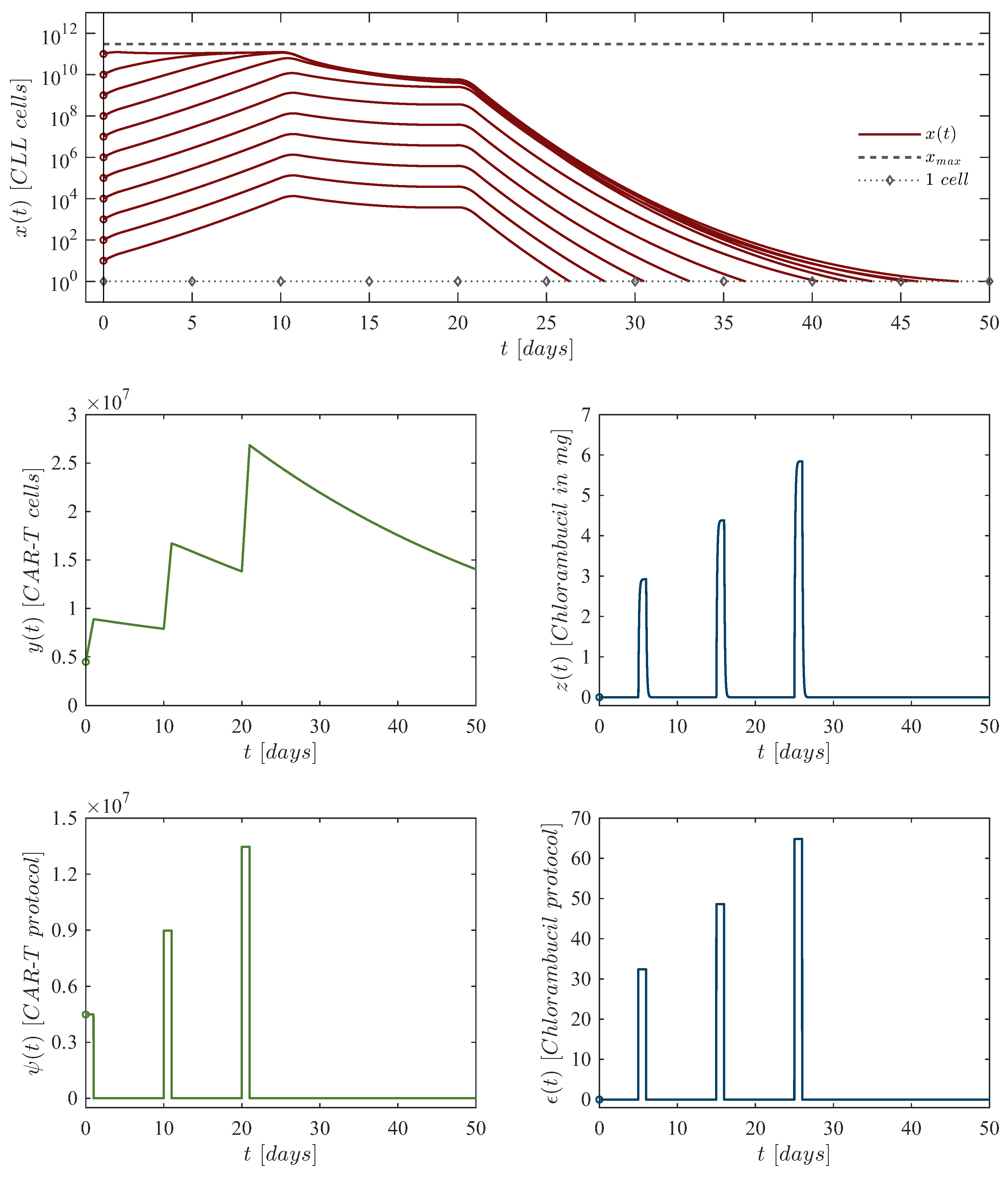
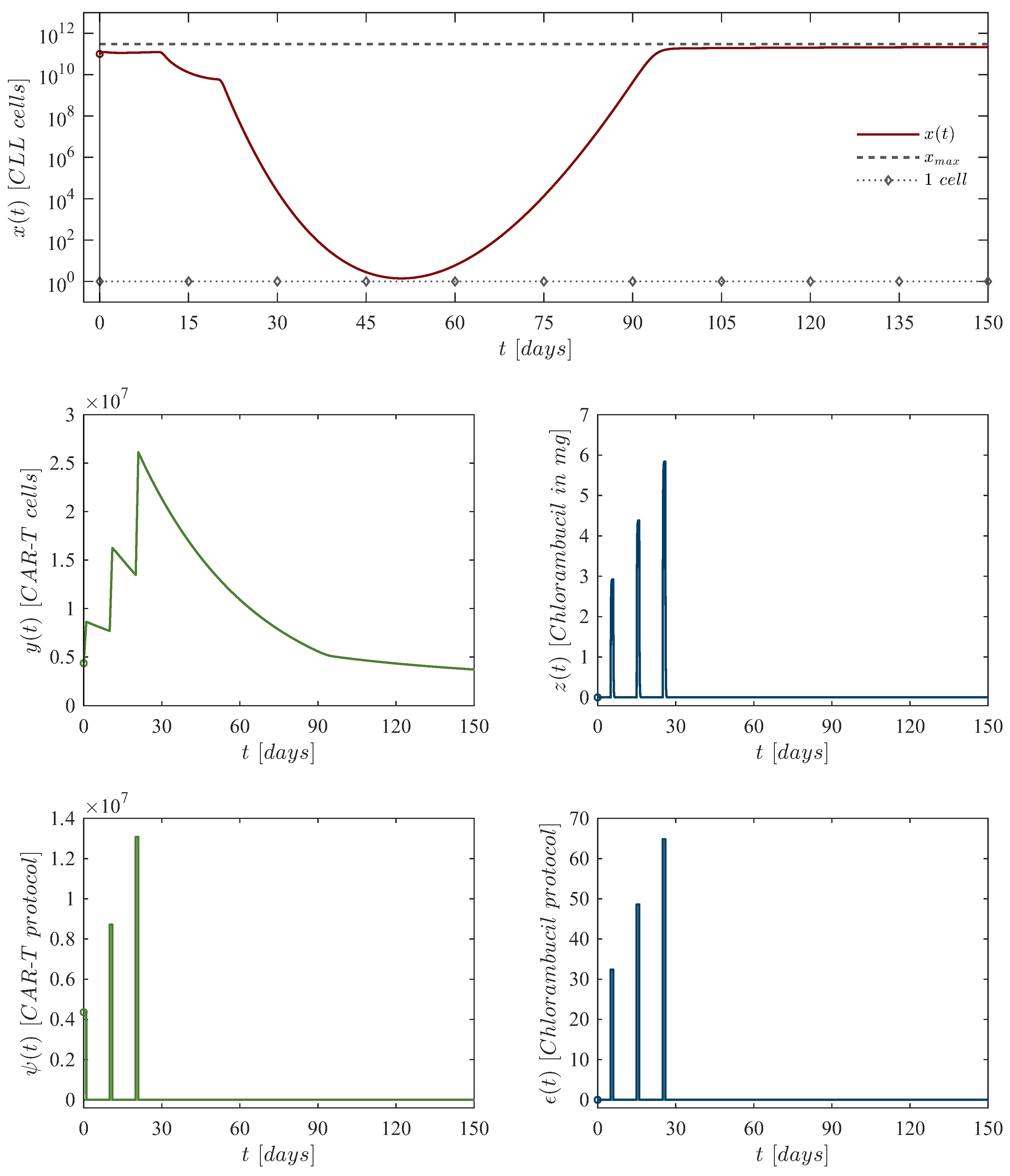
| First dose: |
CAR-T cells at day zero, of chlorambucil at day 5. |
| Second dose: |
CAR-T cells at day 10, of chlorambucil at day 15. |
| Third dose: |
CAR-T cells at day 20, of chlorambucil at day 25. |
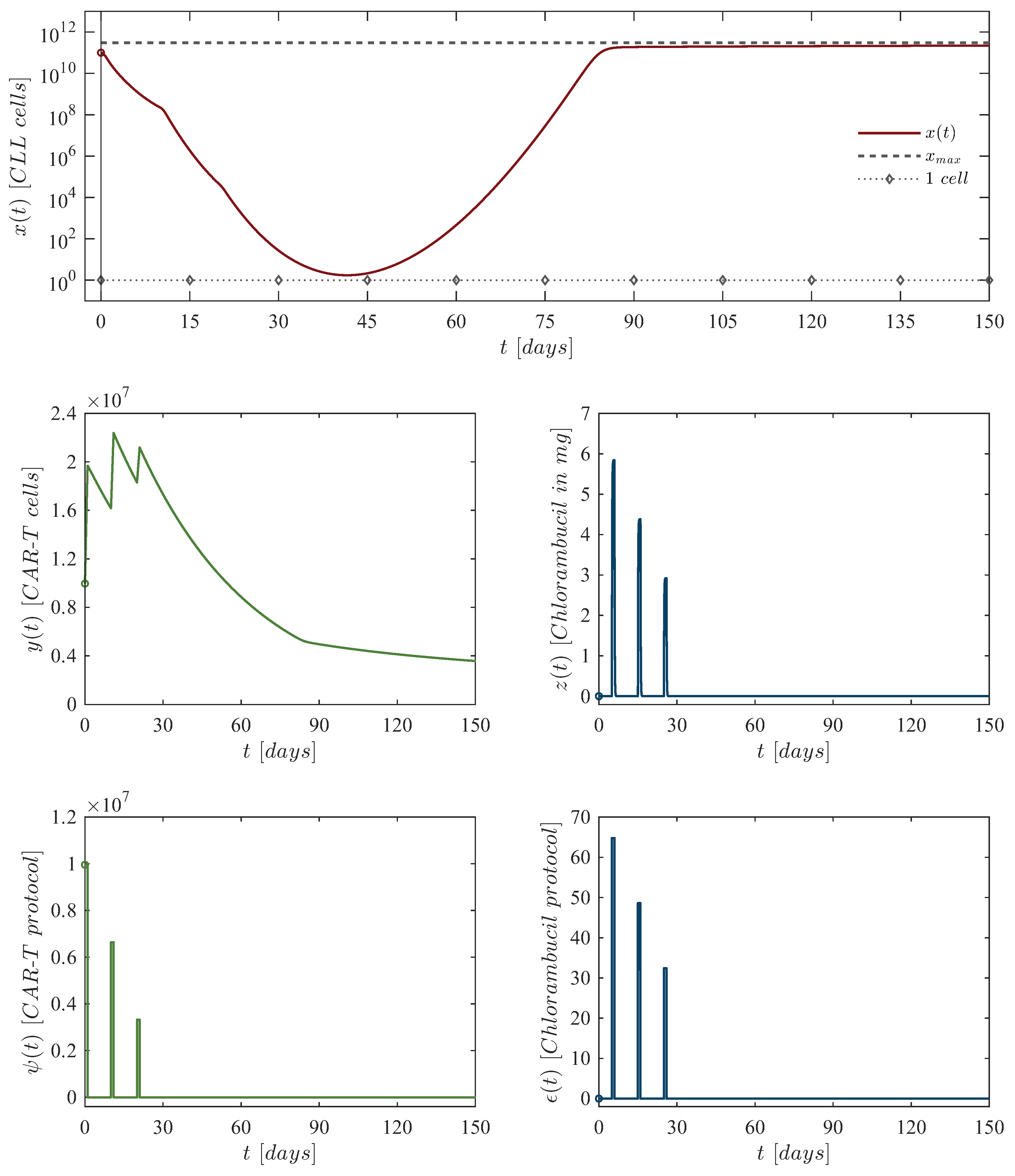
| Chlorambucil dosing | |||
|---|---|---|---|
| First dose: |
CAR-T cells at day zero, of chlorambucil at day 5. |
| Second dose: |
CAR-T cells at day 10, of chlorambucil at day 15. |
| Third dose: |
CAR-T cells at day 20, of chlorambucil at day 25. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





