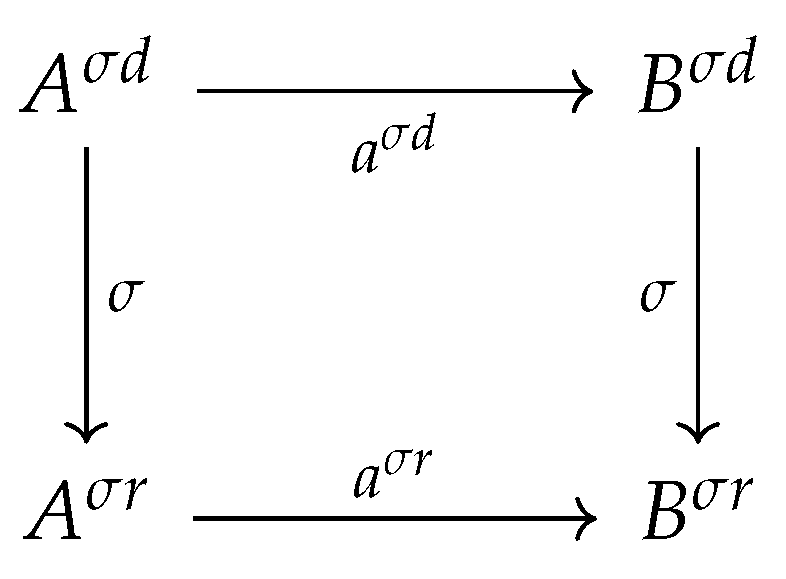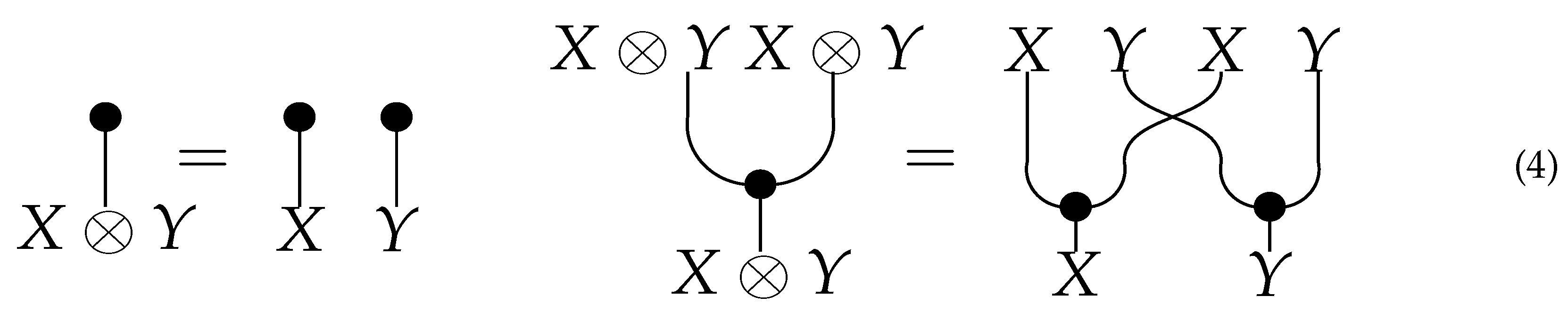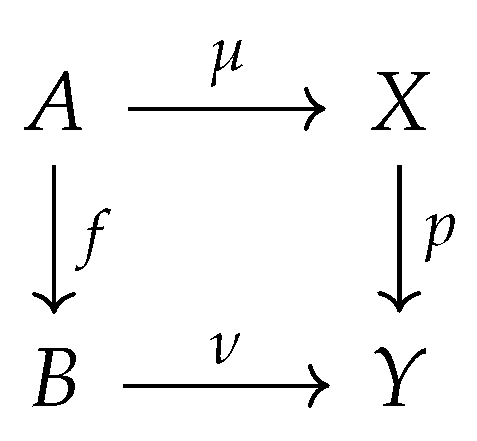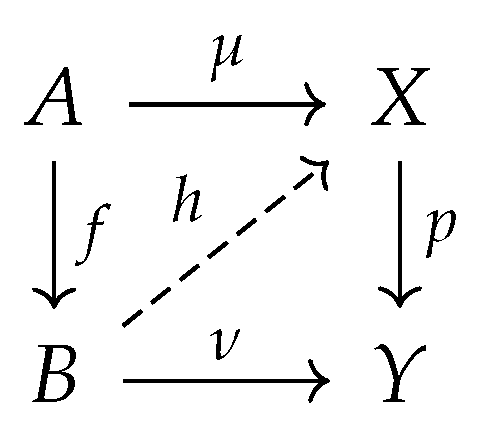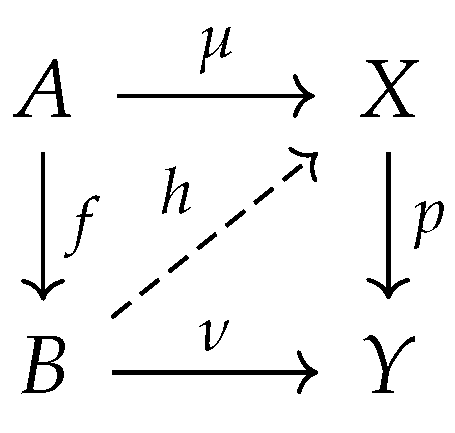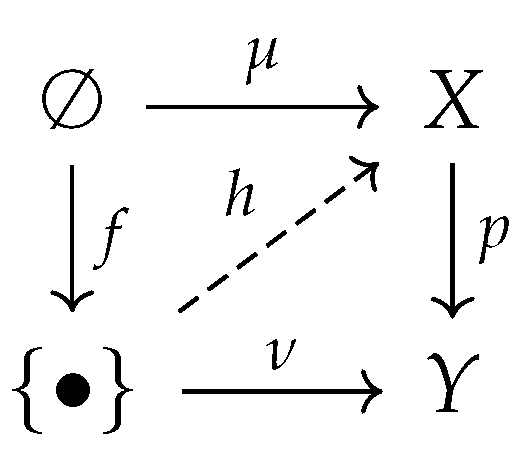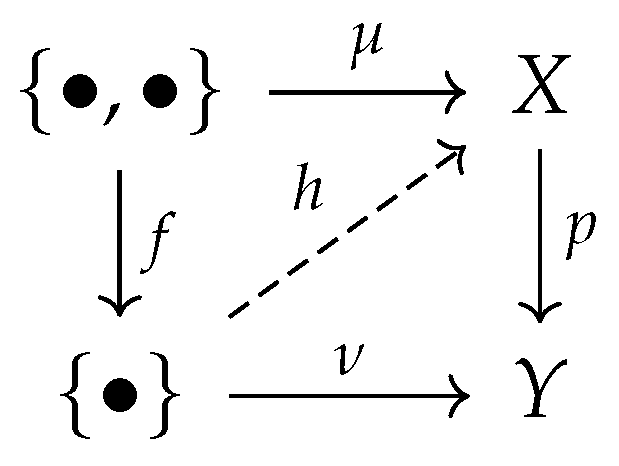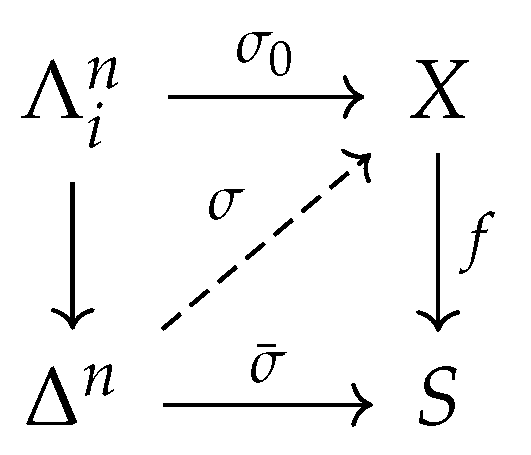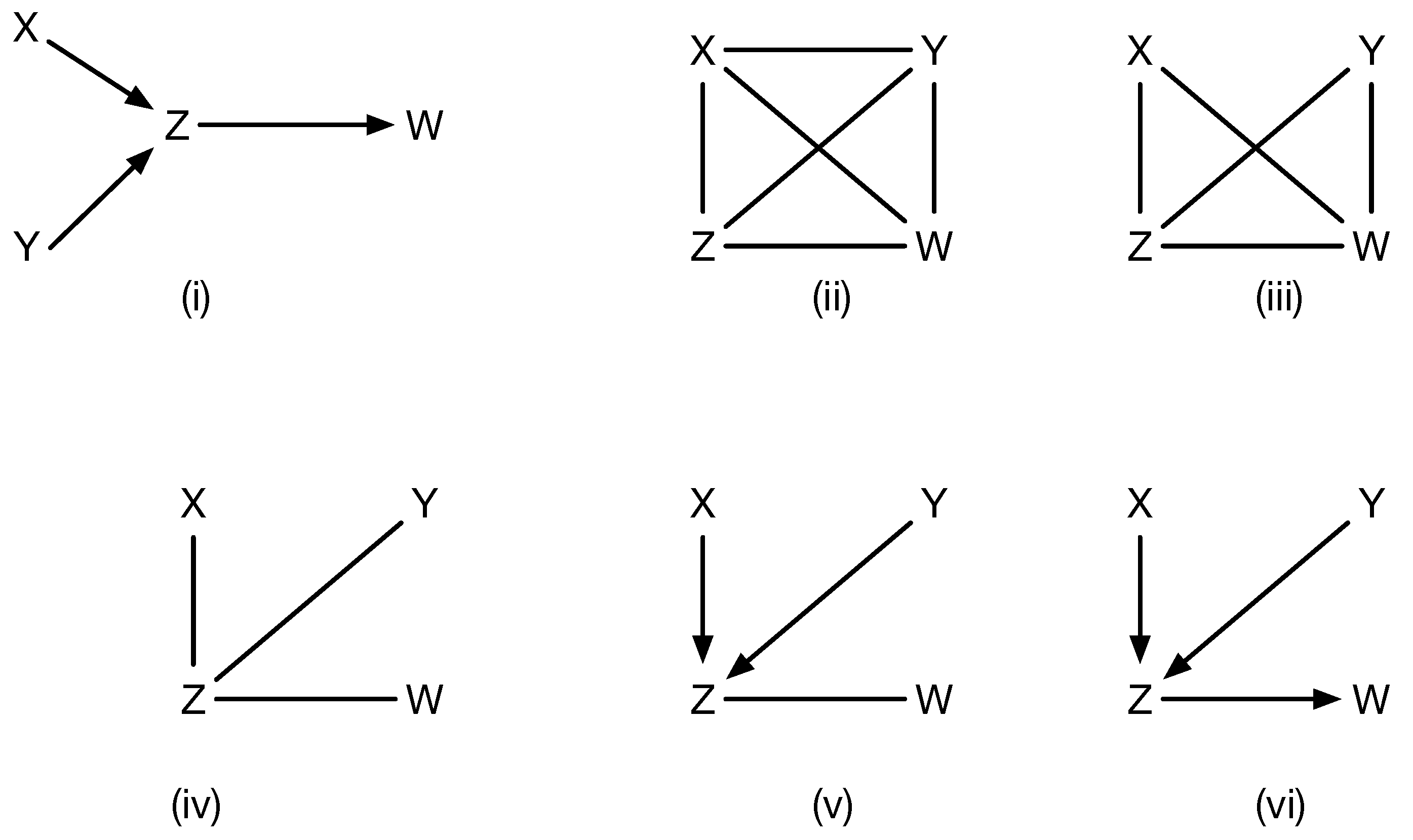A Higher Algebraic K-Theory of Causality

1. Introduction

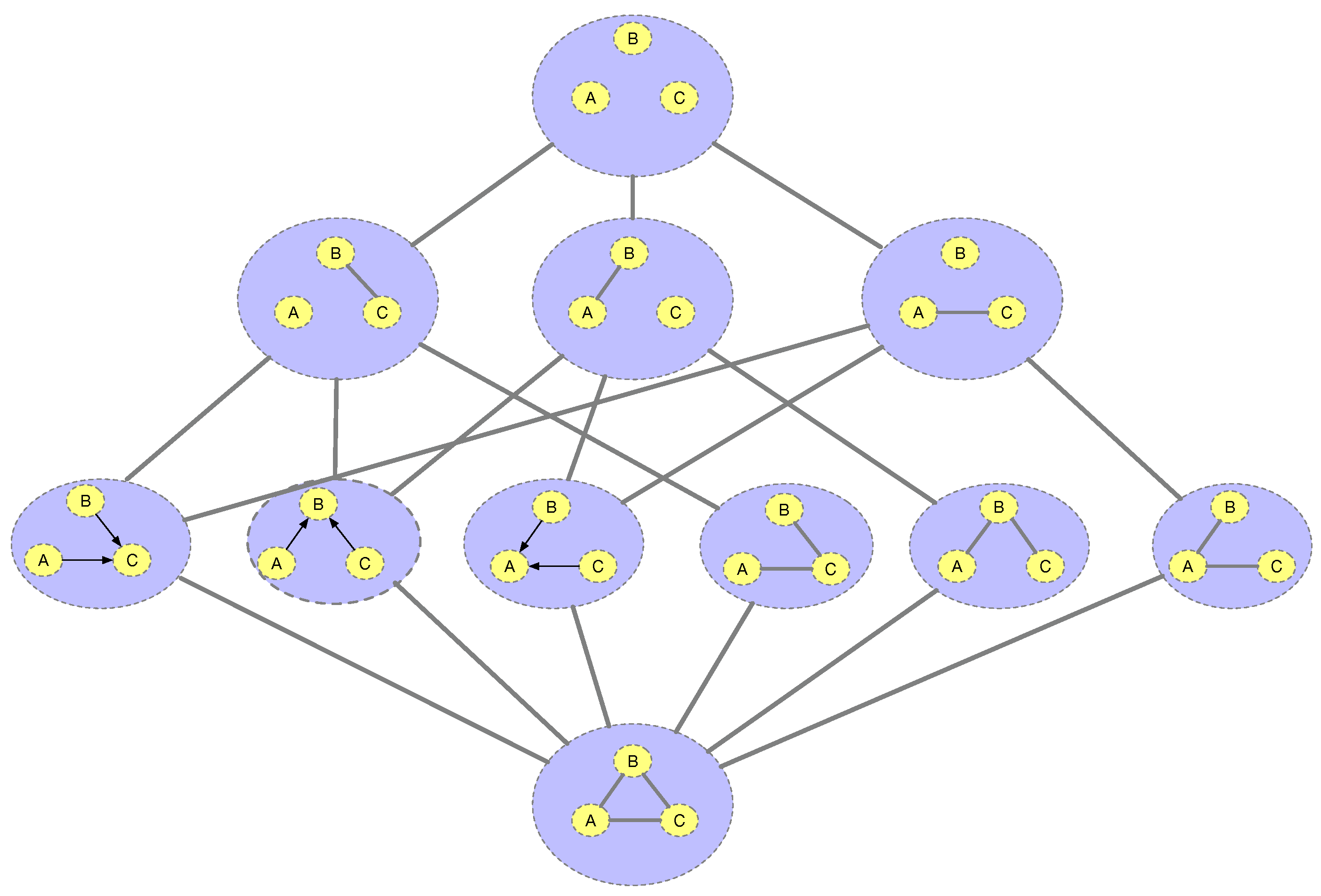
Causal discovery using methods such as FCI [11] or IC [12], as well as the many variants and extensions of these classic methods developed over the past several decades [2,3,13,14,15], involves searching super-exponential spaces as the number of causal DAGs grows extremely large in the number of variables. For $n=3$ variables, there are 11 equivalence classes of DAG models (see Figure 1). There are approximately ${10}^{18}$ DAG models on just 11 labeled variables.1 To make matters worse, DAG models capture only a tiny portion of the space because for $n=4$, there are $18,300$ conditional independence structures, but DAG models capture only roughly 1% of this space! More powerful models like integer-valued multisets (imsets) [16] that model conditional independences by mapping the powerset of all variables into integers grow even larger still (of the order of $2^{2^n}$). Representing this space efficiently with categorical representations like affine CDU categories [8] or Markov categories [17] will require defining equivalence classes over string diagrams to combat this curse of dimensionality. This challenge motivates the need for a deeper categorical understanding of the equivalence classes of observationally indistinguishable models [1]. While allowing for arbitrary interventions on causal models enables accurate identification [14,15], such interventions are rarely practical in the real world. Insights such as the Meek-Chickering theorem [2,18,19] allow a deeper understanding of connected paths among equivalent causal DAG models, which we propose to study using a homotopy framework in this paper.

Causal discovery poses some unique challenges for categorical modeling. Figure 1 illustrates the structure of causal equivalence classes on causal DAGs with 3 variables represented as essential graphs [20] or `patterns" [11] or PDAGs [2], which combine undirected edges that could be oriented in either direction with directed edges. As Verma and Pearl [1] noted several decades ago, two DAGs are equivalent if their underlying skeletons (undirected graph structure ignoring edge directions) and V-structures $X\to Z\leftarrow Y$ are the same. The DAG at the bottom satisfies no conditional independences, and the DAG on the top satisfies all conditional independences. Our goal here is to build on the ideas in [2] on connected paths between observationally equivalent models, in particular the Meek-Chickering theorem, which we want to generalize to the categorical setting. As Chickering [2] notes, this theorem, which was originally a conjecture by Meek, implies that there exists a sparse search space, where each candidate model is connected to a small fraction of the total space, given a generative distribution that has a perfect map in a DAG defined over the observables. This property leads to the development of a greedy search algorithm that in the limit of training data can identify the correct model.

In practice, existing causal discovery algorithms, such as PC [11] or IC [21] or their many extensions and variants combine both directional and non-directional encoding of causal models. Specifically, a common assumption, such as in PC, is that given an unknown true causal model (shown in Figure 2 by panel (i)), the initial causal model (shown as (ii) in Figure 2) is an undirected graph connecting all variables to each other, which satisfies no conditional independences, and is progressively refined (panels (ii)-(vi) in Figure 2) based on conditional independence data and using edge orientation and propagation rules, such as the Meek rules [18]. For example, the initial stage is to simply check all marginal independences, and given that $X\perp -10mu\perp Y$, that eliminates the undirected edge between X and Y. However, each undirected edge between two vertices, say A and B, that needs to eliminated due to conditional independence must be checked for increasingly large subsets $\left(A\perp -10mu\perp B\right|C)$, and while methods like FCI and later enhancements [14,15] incorporate rather sophisticated methods to prune the space, this process remains computationally expensive, and its practicality remains in question as in the real world, interventions on arbitrary separating sets [14] may be infeasible. While remarkable progress has been made over the past few decades (see [15] for a state of the art method), it still can be prohibitive, and does not always end up with the right model. Edges that remain undirected are interpreted to indicate latent confounders.

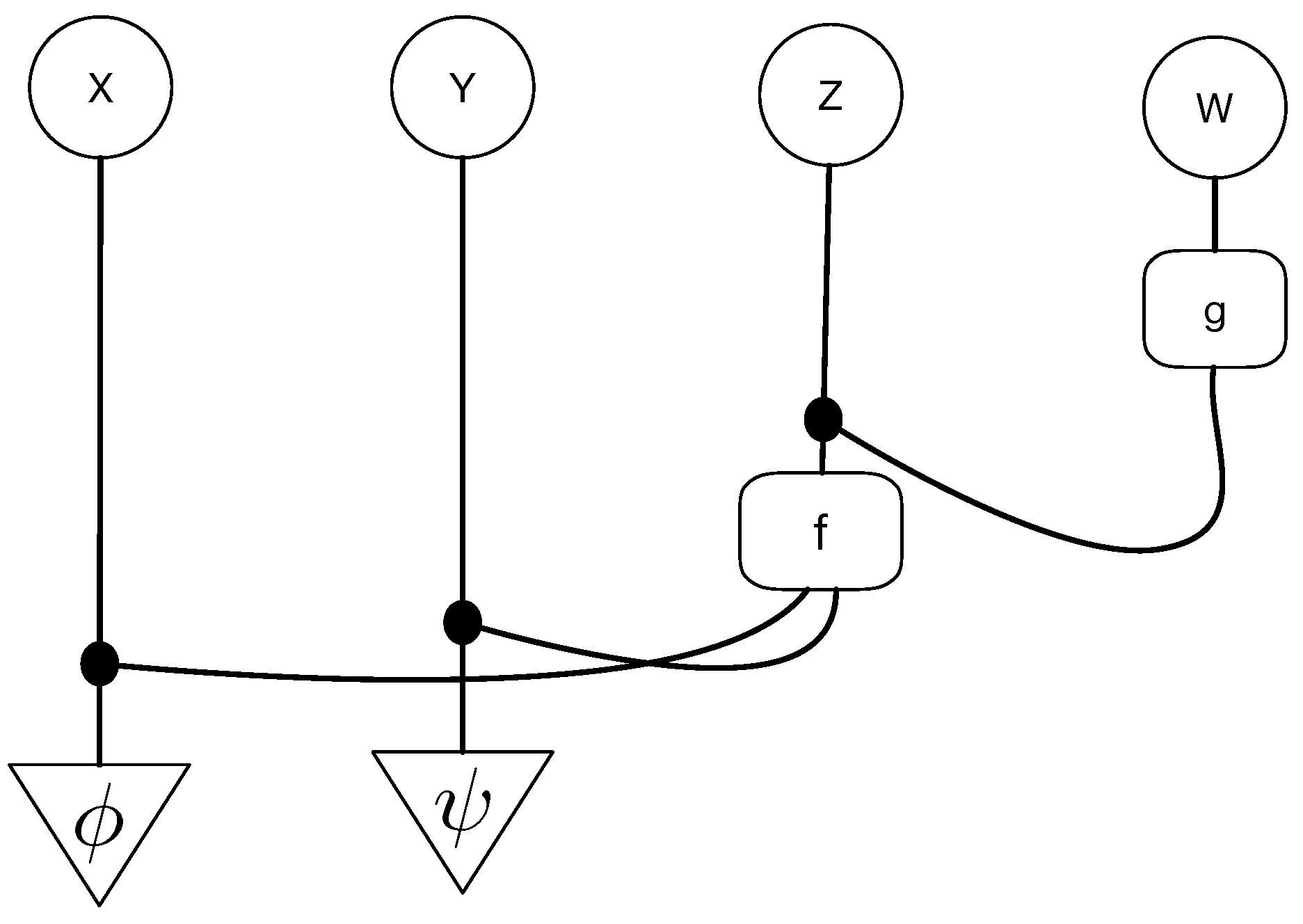
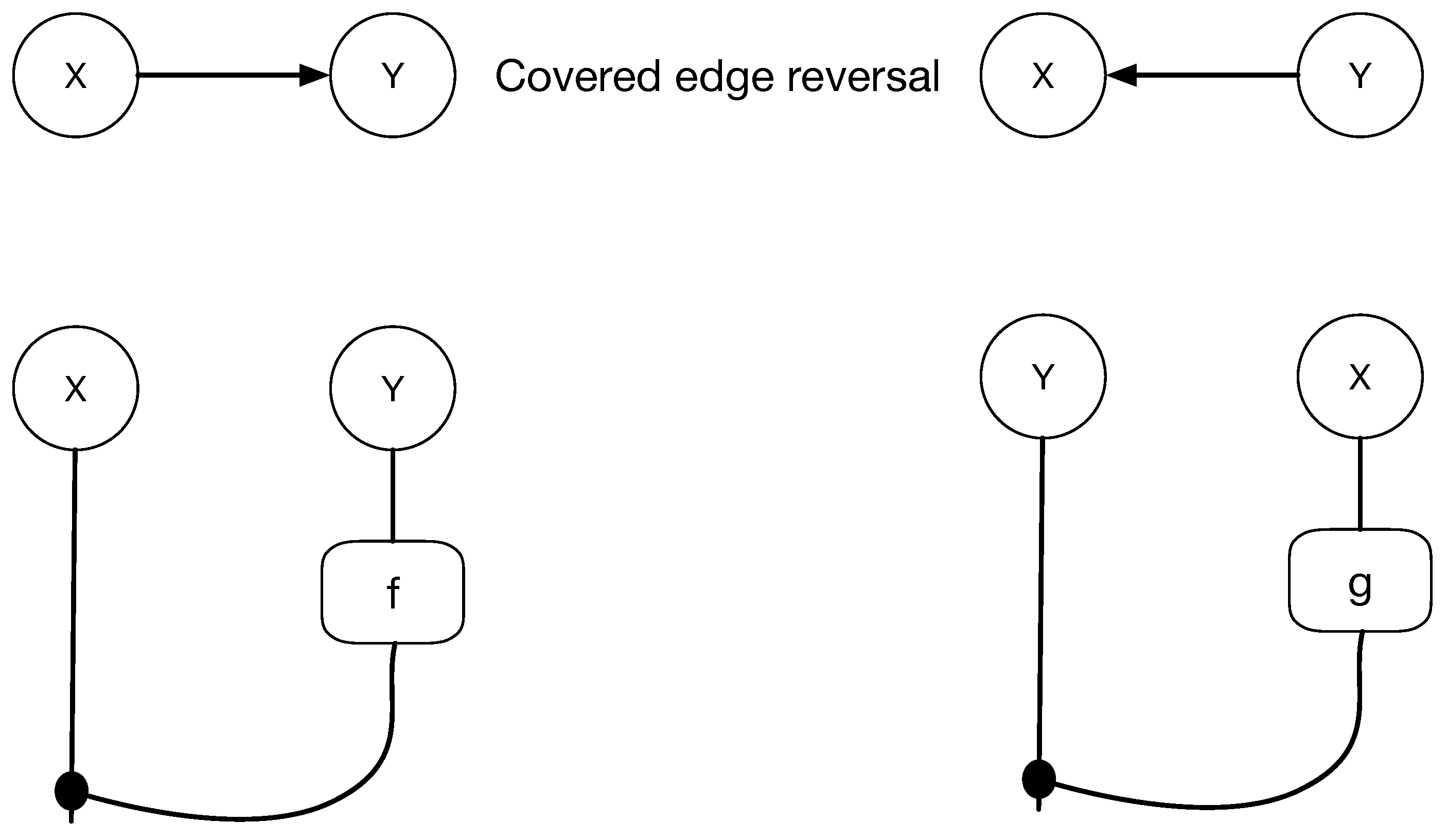
To generalize the Meek-Chickering theorem to the categorical setting, some challenges need to be addressed. Figure 3 shows a string diagram representation of the causal model in Figure 2. Such string diagrams are used in affine CD [8] and Markov categories [17]. However, as Figure 4 shows, Meek-Chickering equivalence implies that covered edges can be reversed while maintaining DAG equivalence, which imposes an equivalence structure on string diagrams as shown. As the number of causal models grows exponentially, so does the number of string diagrams, and to develop deeper insight into the underlying topological structure of causal equivalences, we introduce a coalgebraic theory of causal inference based on a categorical structure we call cPROP, defined as a functor category from a PROP [22] to a symmetric monoidal category [23]. We build on the work of Fox [4] who studied functor categories mapping PROPs to symmetric monoidal categories in his PhD dissertation in 1976. Crucially, Fox [4] studied a particular functor category from a coalgebraic PROP to symmetric monoidal categories that defined a right adjoint from the category MON of all symmetric monoidal categories to CART, the category of all Cartesian categories.2. In this sense, cPROPs are formally an algebraic theory in the sense of Lawvere [5].

Objects in a cPROP are functors mapping a PROP P – a symmetric monoidal category over natural numbers – to a symmetric monoidal category $\mathcal{C}$. The structure PROP (for Products and Permutations) was originally introduced by Maclane [22], and it has seen widespread use in many areas such as modeling connectivity in networks [25,26]. A trivial example of a PROP is the free monoidal category $\Gamma$ over the category 1, whose objects can be interpreted as the natural numbers, the unit object is 0, and the tensor product is addition. More generally, a PROP P is a small monoidal category with a strict monoidal functor $\Gamma \to P$ that is a bijection on objects. A cPROP is a functor category ${\mathrm{C}}^P$, where C is a symmetric monoidal category, where in addition there is usually some constraints placed on the specific PROP P.

As a simple example, we consider cPROPs where the PROP P is generated by a coalgebraic structure defined by the maps $\delta :1\to 2$ and $ϵ:1\to 0$ satisfying a set of commutative diagrams. Such cPROPs are closely related to symmetric monoidal category structures used in previous work on categorical models of causality, probability and statistics [7,17,27,28,29]. 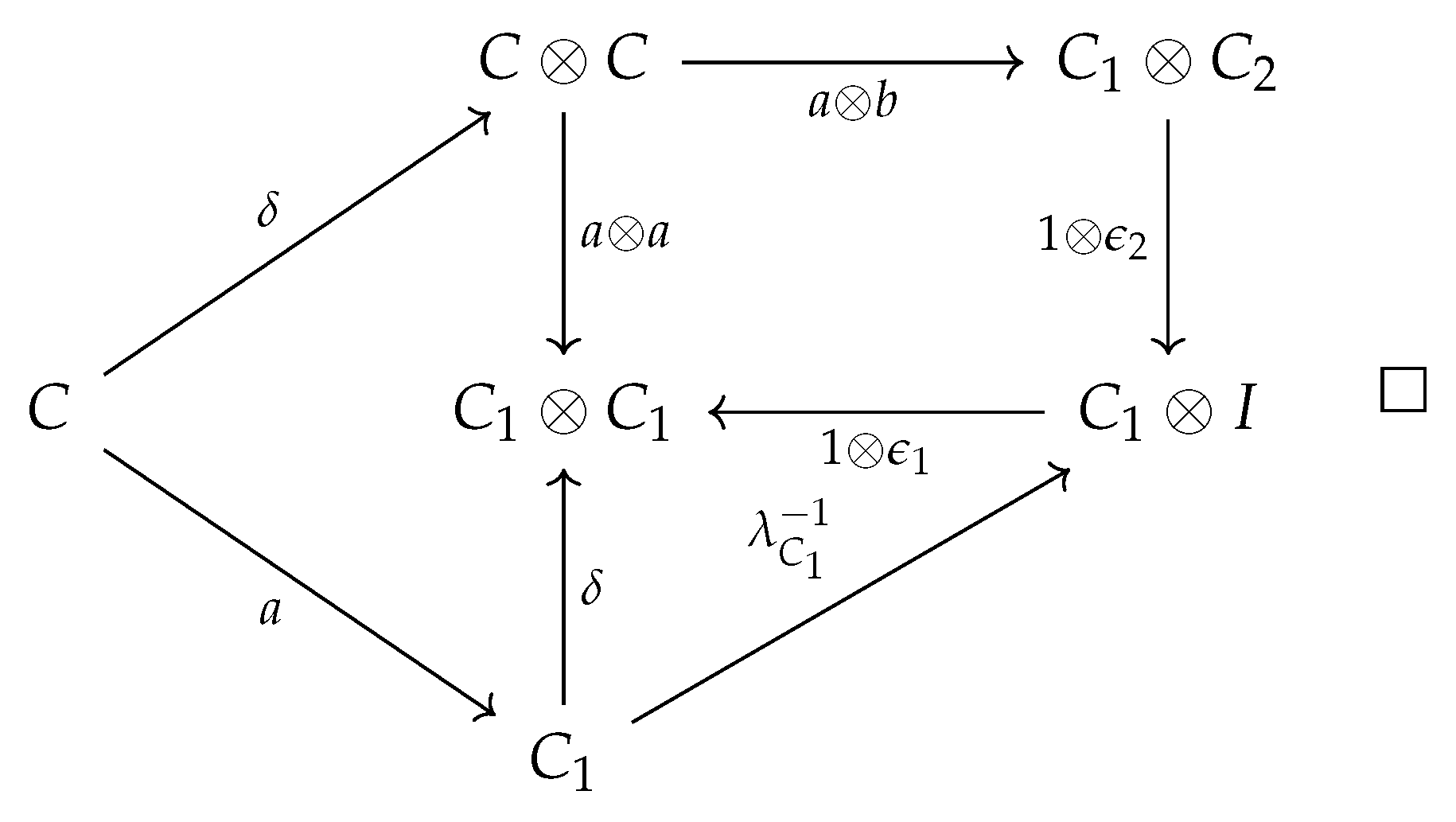In particular, Markov categories [6,17] and affine CDU (“copy-delete-uniform") categories used to model causal inference include a comonoidal “copy delete" structure correspond to such a cPROP, which we note is distinctive in that “delete" has a uniform structure, but “copy" does not, leading to a semi-Cartesian category.

In our previous work on universal causality [29], we proposed the use of simplicial sets, which both provide a way to encode directional and non-directional edges, as well as forms the basis for topological realization for cPROPs and plays a central role in higher-order ∞-categories [30,31]. We study the classifying spaces [9] of cPROPs in this paper, showing that they provide deeper insight into the connections between different cPROP categories that correspond to Markov categories, such as FinStoch [6].

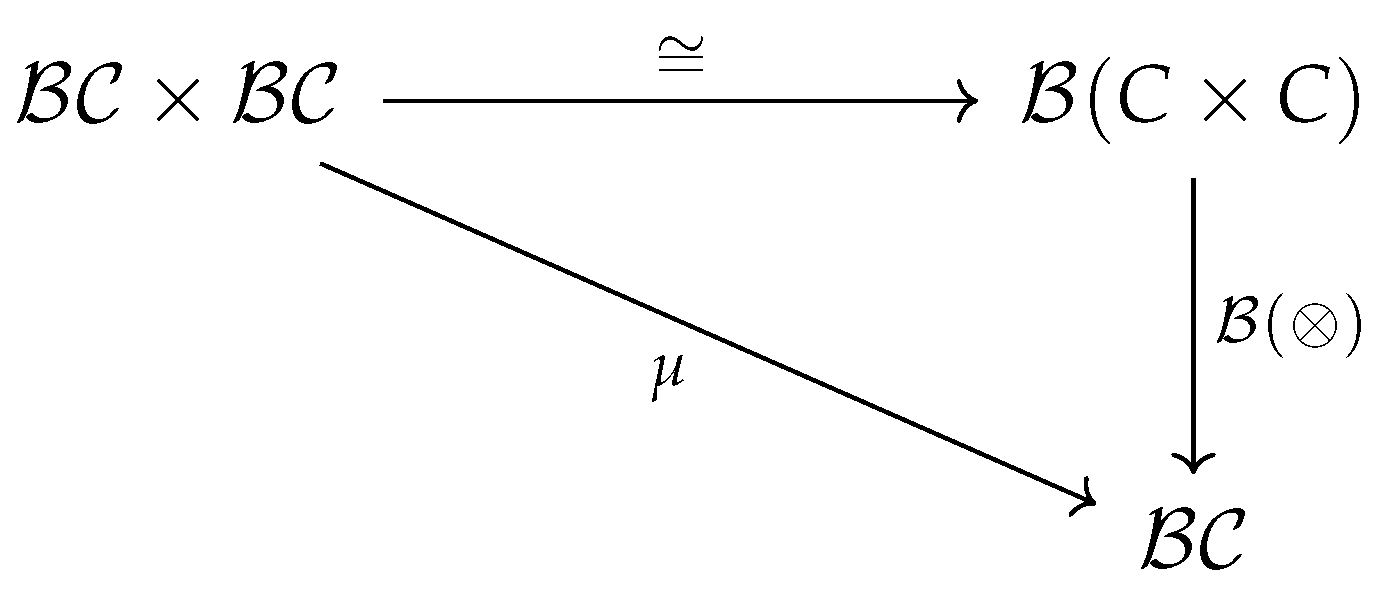
In particular, we build on longstanding ideas in abstract homotopy theory on modeling equivalence classes of objects in a category [32] by mapping a category into a topological space, where (weak) equivalences can be modeled in terms of topological structures, such as homotopies. To make this more concrete, Jacobs et al. [8] modeled a Bayesian network as a CDU functor $\mathcal{F}:\mathcal{C}\to \mathbf{FinStoch}$ between two affine CDU or Markov categories, one specifying the graph structure of the model, and the other modeling its semantics as an object in the category of finite stochastic processes FinStoch. A CDU functor is a special type of cPROP functor. Two Bayesian networks modeled as such cPROP functors that are observationally equivalent – such as $A\to B\to C$ and $A\to B\leftarrow C$ since the edge $B\leftarrow C$ is a covered edge that can be reversed – induce a natural transformation $\tau :{\mathcal{F}}_1\Rightarrow {\mathcal{F}}_2$. Using the associated classifying spaces $\mathcal{B}\mathcal{C}$ and $\mathcal{B}\mathbf{FinStoch}$, the natural transformation induces a homotopy between ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$.

The idea of associating a topological space with a category goes back to Grothendieck, but was popularized by Segal [9]: map a category $\mathcal{C}$ to a sequence of sets (or objects) $X_0,X_1,\dots$, where the k-simplex $X_k$ represents composable morphisms of length k. A standard topological realization proposed by Milnor [33] constructs a topological CW-complex out of simplicial sets. Segal called such a construction the classifying space $\mathcal{BC}$ of category $\mathcal{C}$. Our paper can be seen as an initial step in building a higher algebraic K-theory [10] for causal inference, using as a concrete example the study of classifying spaces of cPROPs. A 0-simplex in a simplicial cPROP would be defined by its objects $X,Y,X\otimes Y,\dots$, which map to 0-cells in its classifying space. An example 2-simplex in a cPROP, such as $I\to X\otimes Y\to X$ maps to a 2 cell or simplicial triangle.

We build on the insight underlying Fox’s dissertation on universal coalgebras [4], which shows that the subcategory of coalgebraic objects in a monoidal category forms its Cartesian closure. The adjoint functor theorems show that cofree algebras – right adjoints to forgetful functors – exist in such cases. In particular, Fox’s theorem implies that cPROPs that come with a type of “uniform copy-delete" structure [34] are Cartesian symmetric monoidal categories, where the tensor product $X\otimes Y$ becomes a Cartesian product operation through natural transformations, rather than the standard universal property. We note that Markov categories are semi-Cartesian because the comonoidal ${copy}_X$ structure is not uniform, but only ${\mathsf{del}}_X$ is. however, they contain a subcategory of deterministic morphisms that induce a Cartesian category using the uniform copy delete structure. It is worth noting here that Pearl [12] has long advocated causality as being being intrinsically deterministic in his structural causal models (SCMs), where the role of probabilities is reflected in the uncertainty associated with exogenous variables that cannot be causally manipulated.

Here is a roadmap to the rest of the paper. We begin in Section 2 with a concrete procedure for causal discovery called Greedy Equivalent Search (GES) [2,18], which illustrates the definition of causal equivalence we wish to study in its topological and homotopic sense, and which is also illustrative of a broad class of similar algorithms. Numerous refinements are possible, including the ability to intervene on arbitrary subsets [14,15], which we overlook in the interests of simplicity. Section 3 begins with an introduction to algebraic theories of the type proposed by Lawvere [5], a brief review of symmetric monoidal categories and an introduction to PROPs and cPROPs. We define functor categories mapping a PROP to a symmetric monoidal category. We review the central result of Fox showing that the inclusion of all Cartesian categories CART in the larger category of all symmetric monoidal categories MON has a right adjoint, which is defined by a coalgebraic PROP functor category. This coalgebraic structure relates to the “uniform copy-delete" structure studied by [34]. In Section 4, we explore the relationships between cPROPs with uniform copy and delete natural transformations and previous work on affine CDU categories [7] and Markov categories [6]. In Section 5, we give a brief overview of Cartesian symmetric monoidal structure in topological spaces, which motivates our use of simplicial set topological realizations of cPROPs. In Section 6, we define simplicial objects in cPROP categories. Section 7 defines the abstract homotopy of cPROPs at a high level. Section 8 drills down into showing the homotopic structure of cPROP functors that represent Bayesian networks, which closely relates to the work on CDU functors [8]. We characterize natural transformations in the functor category of Bayesian networks modeled as cPROPs using Yoneda’s coend calculus [23], and define an equivalence relationship among functors. In particular, we present categorical generalizations of the definitions of equivalent causal models in [2,18], and state a homotopic generalization of the well-known Meek-Chickering theorem for cPROPs. We associate with each edge reversal of a covered edge corresponds to natural transformation between corresponding cPROP functor. We formally characterize the classifying spaces of cPROPs in terms of associative and commutative H-spaces [32]. Finally, we combine the results of the previous section in Section 10, stating the main result that the Grayson-Quillen procedure applied to cPROP yields a category ${\mathcal{C}}^{-1}\mathcal{C}$ that represents a Grothendieck group completion of cPROP category $\mathcal{C}$ and whose connected components that define the 0^th order homology (loop) space is isomorphic to the Meek-Chickering equivalence classes. We summarize the paper and outline a few directions for further work in Section 11.

2. Greedy Equivalence Search

To motivate the theoretical development in subsequent sections, we focus our attention in this section to a specific causal discovery algorithm, Greedy Equivalence Search (GES), originally proposed by Meek [18], whose correctness and asymptotic optimality was subsequently shown by Chickering [2] constituting an a algorithmic proof of the Meek-Chickering theorem. We do not present this framework as a state of the art causal discovery algorithm (e.g., Zanga and Stella [3] provide a detailed survey of many causal discovery methods), but rather as an exemplar of the idea of searching in a space of equivalence classes of DAG models. Our ultimate goal is to provide a topological and abstract homotopic characterization of the search space in causal discovery, both for DAG and non-DAG models. It would help concretize the following theoretical abstractions to ground out the ideas in a specific algorithm.

For the sake of space, our discussion will be brief, and we relegate all missing details to the original paper [2]. Broadly, the idea underlying GES is to search over equivalence classes of DAGs, by moving at each step to a neighbor – meaning a model outside the current equivalence class by edge addition or deletion – that has the highest Bayesian score on a given IID dataset, if it improves the score. Bayesian approaches to learning models from data use a scoring function, such as Bayesian Information Criterion (BIC), denoted as $S(\mathcal{G},\mathbf{D})$ where D is an IID (independent and identically distributed) dataset sampled from the original (unknown) model. It is commonly assumed that such as a score is locally decomposable, meaning that

$$S(\mathcal{G},\mathbf{D})=\sum _{i=1}^{n}s(X_i,{\mathbf{Pa}}_i^{\mathcal{G}})$$

meaning that the overall score of a candidate DAG G is the sum of local scores for each node $X_i$ that is purely a function of the projected data D onto the node and its parents ${\mathbf{Pa}}_i^{\mathcal{G}}$. Given a dag G and a probability distribution $p(.)$, G is a perfect map of p if (i) every independence constraint in p is implied by the structure of G and (ii) every independence constraint implied by the structure of G holds in p. If there exists a DAG G that is a perfect map of distribution $p(.)$, p is called DAG-perfect. Under the assumption that the dataset D is an IID sample from some DAG-perfect distribution $p(.)$, the GES algorithm consists of two phases that is guaranteed to find the correct DAG G optimally in the limit of large datasets. The precise statement is as follows:

Theorem 1.([2]) Let ${\mathcal{E}}^{*}$ denote the equivalence class that is a perfect map of the generative distribution $p(.)$ and let m be the number of samples in a datasetD. Then in the limit of large m, $S_B({\mathcal{E}}^{*},\mathbf{D})>S_B(\mathcal{E},\mathbf{D})$ for any equivalence class $\mathcal{E}\ne {\mathcal{E}}^{*}$.

Here, $S_B$ is a Bayesian scoring method, like BIC, and it is assumed to score all DAGs in an equivalence class the same. The notion of equivalence classes is obviously fundamental to GES, and the formal statement of this characterization comes from the following transformational characterization of Bayesian networks. As previously noted, a covered edge in a DAG G is an edge $X\to Y$ with the property that the parents of Y are the same as the parents of X along with X itself.

Theorem 2. 

(Meek-Chickering Theorem[2,18]) Let $\mathcal{G}$ and $\mathcal{H}$ be any pair of DAGs such that $\mathcal{G}\le \mathcal{H}$, meaning that $\mathcal{H}$ is an independence map of $\mathcal{G}$, that is, every independence property in $\mathcal{H}$ holds in $\mathcal{G}$. Intuitively, $\mathcal{G}\le \mathcal{H}$ implies $\mathcal{H}$ contains more edges than $\mathcal{G}$. Let r be the number of edges in $\mathcal{H}$ that have opposite orientations in $\mathcal{G}$ and let m be the number of edges in $\mathcal{H}$ that do not exist in either orientation in G. Then, there is a sequence of $r+2m$ edge reversals and additions in $\mathcal{G}$ with the following properties:

• Each edge reversed is a covered edge.
• After each reversal and addition, $\mathcal{G}$ is a DAG and $\mathcal{G}\le \mathcal{H}$.
• After all reversals and additions, $\mathcal{G}=\mathcal{H}$.

To relate this result and the ensuing GES algorithm to the original PC algorithm illustrated in Figure 2, unlike PC, GES begins at the opposite end of the lattice of DAG models shown in Figure 1, the empty DAG (which can be viewed as the $\mathcal{G}$ DAG in Theorem 2, and then progressively adds edges in the first phase, and then deletes edges in the second phase. In Section 8, we will generalize this theorem to construct a topological and abstract homotopical equivalence across functors between cPROP categories. These functors are equivalent to the CDU functors proposed by Jacobs et al. [8] to model Bayesian networks previously. Edge reversals or additions will correspond to natural transformations.

A further characterization of causal equivalence classes emerges from our application of higher algebraic K-theory [9,10]. Informally, we can define the notion of connectedness of a category in terms of the equivalence class of the relation defined over morphisms (two objects are in the same equivalence class if they are connected by a (perhaps zig-zag) morphism). We can treat each equivalence class as a topologically locally connected space and then the homotopy groups ${\pi }_n\left(\mathcal{B}\mathcal{C}\right)$ of the classifying space BC of cPROP category $\mathcal{C}$ gives us an algebraic invariant of causal equivalence classes.

3. CPROPs as Algebraic Theories

In this section, we introduce cPROPs, building on the work of Fox [4] who studied functor categories mapping PROPs to symmetric monoidal categories in his PhD dissertation in 1976. A cPROP is a functor category, whose objects are functors mapping a PROP P – a symmetric monoidal category over natural numbers – to a symmetric monoidal category $\mathcal{C}$. In the next Section 4, we consider cPROPs where the PROP P is generated by a coalgebraic structure defined by the maps $\delta :1\to 2$ and $ϵ:1\to 0$ satisfying a set of commutative diagrams. Such cPROPs are related to symmetric monoidal category structures used in previous work on categorical models of causality, probability and statistics [7,17,27,28,29].

3.1. Algebraic Theories

In an influential paper, Lawvere [5] defined an algebraic theory as a small category A, whose objects are the natural numbers $0,1,\dots$, in which each object n is the categorical product (i.e., addition) of the unit object 1 with itself n times. Morphisms in A are defined as maps $n\to m$. Lawvere [5] showed that many common algebraic structures, such as groups, monoids, and rings, which are defined using finitary operations determines an algebraic theory. Homomorphisms between algebraic structures, such as groups or rings, in turn can be used to define a category.

Definition 1. 

[5] Every map of algebraic theories $f:\mathcal{A}\to \mathcal{B}$ determines a contravariant set-valued functor ${\mathbf{Sets}}^f:{\mathbf{Sets}}^B\to {\mathbf{Sets}}^A$, where ${\mathbf{Set}}^f$ is defined as analgebraic functor, and ${\mathbf{Sets}}^A$ is defined as analgebraic category .

Example 1. 

The category of rings (with a unit element) and that of monoids are algebraic categories, and the functor that assigns to a ring the monoid consisting of the same objects under multiplication only is an algebraic functor.

A fundamental theorem shown by Lawvere [5] states that:

Theorem 3. 

[5] Every algebraic functor has an adjoint.

In terms of Example 1, the adjoint of the algebraic functor mapping rings to monoids is the free ring constructed from the elements of the monoid.

We show below that cPROPs are exactly (co)algebraic theories in the sense of Lawvere [5], as they are defined as the right adjoint of the inclusion functor from the category CART of all Cartesian categories into MON, the category of all symmetric monoidal categories. We review these notions first before introducing cPROPs more formally.

3.2. Symmetric Monoidal Categories

We assume the reader understands the basics of symmetric monoidal categories, which we briefly review below (see Figure 5). Good introductions are available in a number of textbooks [23,32]. A brief introduction to some basic category theory suitable for causal inference is in my previous paper [29]. Detailed overviews of symmetric monoidal categories appear in many books, and our definitions are based on [32].

Definition 2. 

Amonoidal categoryis a category C together with a functor $\otimes :\mathcal{C}\times \mathcal{C}\to \mathcal{C}$, an identity object e of C and natural isomorphisms $\alpha ,\lambda ,\rho$ defined as:

$$\begin{array}{ccc}\hfill {\alpha }_{C_1,C_2,C_3}:C_1\otimes (C_2\otimes C_3)& \cong & (C_1\otimes C_2)\otimes C_2,forallobjects{C}_1,C_2,C_3\hfill \\ \hfill {\lambda }_C:e\otimes C& \cong & C,forallobjectsC\hfill \\ \hfill \rho :C\otimes e& \cong & C,forallobjectsC\hfill \end{array}$$

The natural isomorphisms must satisfy coherence conditions called the “pentagon" and “triangle" diagrams [23]. An important result shown in [23] is that these coherence conditions guarantee that all well-formed diagrams must commute.

There are many natural examples of monoidal categories, the simplest one being the category of finite sets, termed FinSet in [6], where each object C is a set, and the tensor product ⊗ is the Cartesian product of sets, with functions acting as arrows. Deterministic causal models can be formulated in the category FinSet. Other examples include the category of sets with relations as morphisms, and the category of Hilbert spaces [34]. The category FinSet has other properties, principally that the ⊗ is actually a product (in that it satisfies the universal property of products in categories, and is formally a limit). Not all monoidal categories satisfy this property. Sets are also Cartesian closed categories, meaning that there is a right adjoint to the tensor product, which represents exponential objects, and is often referred to as the “internal hom" object. Markov categories to be defined in Section 4 are monoidal categories, where the identity element e is also a terminal object, meaning there is a unique “delete" morphism $d_e:X\to e$ associated with each object X. This property can be used to show that projections of tensor products $X\otimes Y$ exist, but they do not satisfy the universal property. We will return to this question below in Section 4.1. Markov categories do not satisfy uniform copying.

Definition 3. 

Asymmetric monoidal categoryis a monoidal category $(\mathcal{C},\otimes ,e,\alpha ,\lambda ,\rho )$ together with a natural isomorphism

$$\begin{array}{c}\hfill {\tau }_{C_1,C_2}:C_1\otimes C_2\cong C_2\otimes C_1,forallobjects{C}_1,C_2\end{array}$$

where τ satisfies the additional conditions: for all objects $C_1,C_2$${\tau }_{C_2,C_1}\circ {\tau }_{C_1,C_2}\cong 1_{C_1\otimes C_2}$, and for all objects C, ${\rho }_C={\lambda }_C\circ {\tau }_{C,e}:C\otimes e\cong C$.

An additional hexagon axiom is required to ensure that the $\tau$ natural isomorphism is compatible with $\alpha$. The $\tau$ operator is called a “swap" in Markov categories [6]. These isomorphisms are easier to visualize as string diagrams, as will be illustrated below in Section 4.

3.3. PROPs

The structure PROP (for Products and Permutations) was originally introduced by Maclane [22], and it has seen widespread use in many areas such as modeling connectivity in networks [25,26]. A trivial example of a PROP is the free monoidal category $\Gamma$ over the category 1, whose objects can be interpreted as the natural numbers, the unit object is 0, and the tensor product is addition. More generally, a PROP P is a small monoidal category with a strict monoidal functor $\Gamma \to P$ that is a bijection on objects. A cPROP is a functor category ${\mathrm{C}}^P$, where C is a symmetric monoidal category, where in addition there is usually some constraints placed on the specific PROP P.

Definition 4. 

[4] APROP$\underline{P}$ is a small symmetric monoidal category with a strict monoidal functor $\Gamma \to \underline{P}$, which is a bijection on objects. A PROP $\underline{P}$ isalgebraic(respectivelycoalgebraic) if its set of maps is generated by a set of maps having codomain 1 (respectively, domain 1).

Given a map $\sigma$ in $\underline{P}$, let $\sigma d$ and $\sigma r$ define its domain and range respectively (both are natural numbers). Fox [4] defines a propable category ${\mathcal{C}}^P$ as one that satisfies the following commutative diagram:

For example, given the PROP map $ϵ:1\to 0$, the commutative diagram states that there is a natural transformation ${ϵ}_X:X\to I$ for each object X in C (where $X^0=I$, the unit element). In Section 4, we will see that this structure defines the ${del}_X$ “delete" structure in Markov and affine CDU categories.

3.4. cPROPs

We now define a cPROP as a functor category whose objects are functors from a PROP $\underline{P}$ to a symmetric monoidal category $\mathcal{C}$.

Definition 5. 

AcPROPis a functor category from a PROP $\underline{P}$ to a symmetric monoidal category C, which comes with the usual forgetful functor mapping a functor in cPROP to a symmetric monoidal category C.

We are usually interested in cPROPs with a special structure on $\underline{P}$, which captures some of the typical structures used in applications, such as causal inference [11,12]. In such cases, we would like to be able to represent probability distributions, do causal interventions on graphs representing distributions, and marginalize over distributions to compute answers using rules like those of do-calculus [12]. We identify one simple example of such a regularity, which will turn out to be important in terms of its relationship to previous work on categorical causal models discussed in Section 4.

Definition 6. 

Let $c\underline{P}$ denote a cPROP as a functor category from a coalgebraic PROP $\underline{P}$ generated by the maps $\delta :1\to 2$ and $ϵ:1\to 0$, satisfying the following commutative diagrams (where τ is a “twist" morphism also commonly referred to as a braiding [23]).

Note that the $\delta$ coalgebraic map in Markov and affine CDU categories defines the ${copy}_X$ map, which we discuss in more detail in Section 4. Fox [4] shows that the cPROP category $c\underline{P}$ of coalgebraic structures defines by the above commutative diagrams is Cartesian. This result also is shown by Heunen and Vicary [34], whose work we discuss in Section 4. It’s worth emphasizing that in Markov categories, ${del}_X$ is assumed to obey its commutative diagram above, but ${copy}_X$ does not. We can easily model a Markov category as a cPROP where the commutative diagram for $copy$ is not imposed uniformly over the category C as it is for $del$.

Theorem 4. 

[4] The cPROP category $c\underline{P}$ is Cartesian.

Proof: The category $c\underline{P}$ consists of comonoidal objects $(C_i,{\delta }_i,{ϵ}_i)$ over which a tensor product structure can be defined as follows. If $(C_1,{ϵ}_1,{\delta }_1)$ and $(C_2,{\delta }_2,{ϵ}_2)$ are two objects in $c\underline{P}$, their tensor product in $c\underline{P}$ is defined to be object

$$(C_1\otimes C_2,(1\otimes \tau \otimes 1)\circ ({\delta }_1\otimes {\delta }_2),{ϵ}_1\otimes {ϵ}_2)$$

It may be easier to visualize this as a string diagram (see Equation (4) for the specific example from Markov categories). To show that this particular tensor product is actually the categorical product in $c\underline{P}$, let $(C,\delta ,ϵ)$ be any object in $c\underline{P}$, and let the “projection" arrows in $c\underline{P}$ be defined as $a:C\to C_1$ and $b:C\to C_2$. A diagram chase using the below commutative diagram shows that $1\otimes {ϵ}_2:C_1\otimes C_2\to C_1$ is indeed the product projection.

Fox [4] additionally proves the following result showing that the coalgebraic category $c\underline{P}$ forms a Cartesian closure of the category of symmetric monoidal categories MON.

Theorem 5. 

[4] DefineCARTto be the category of all Cartesian categories with strictly product preserving functors, andMONbe the category of symmetric monoidal categories with strict monoidal functors as arrows. Then the functor F that maps a category inMONtoCARTvia its coalgebraic PROP structure is right adjoint to the inclusion functor fromCARTtoMON .

Proof: Define a functor F that maps a category in MON to the CPROP category $c\underline{P}$ using the PROP maps $\delta :1\to 2$ and $ϵ:1\to 0$. Let $\mathcal{D}$ be any Cartesian category, and let $F:\mathcal{D}\to \mathcal{C}$ be an arrow in MON, i.e. a strictly monoidal functor. For any object X in D, let $\Delta :X\to X\times X$ be its diagonal map (which exists because D is Cartesian), and define the composed morphism ${ϵ}_X:X\stackrel{\cong }{\to }X\otimes I\stackrel{\pi }{\to }I$ (where the projection $\pi$ exists because I is terminal). Define the functor F that maps from MON to CART by mapping an object X to the comonoidal object $c\underline{P}$ as $\left(F\right(X),F(\Delta ),F(ϵ\left)\right)$. F preserves products by the diagram chase shown above. Then F has a left adjoint defined by the forgetful functor U from the cPROP category $c\underline{P}$ to MON. □

3.5. Closed Locally Presentable cPROPs

We turn now to discuss the property of closedness and accessibility in cPROP categories. These will be useful in forming exponential objects, as well as in being able to apply the special adjoint functor theorem (SAFT) [23] (Theorem 2, Section V.8).

Definition 7. 

A cPROP category C isclosed Cartesianif it has all finite products and if the symmetric monoidal structure $(\mathcal{C},\times ,e)$ is closed. In other words, for all objects C, the functor $(-)\otimes C$ possess a right adjoint (which is referred to as an “exponential" object or an “internal hom" object).

$$\mathcal{C}(X\otimes Y,Z)\cong \mathcal{C}(X,Z^Y)$$

We define subobjects of objects in cPROP categories.

Definition 8. 

For any cPROP category C, given two monomorphisms $f:X\to Y$ and $g:Z\to Y$ that share a common co-domain, let $f\le g$ when f factors through g, namely $f=g\circ f^{\prime }$ for some arrow $f^{\prime }$ (which must also be a monomorphism). If both $f\le g$ and $g\le f$, the induced equivalence classes of monomorphisms $f\equiv g$ with codomain Y define thesubobjectsof Y.

To construct accessible cPROP categories, they need to be locally presentable through a cogenerating set $\mathcal{M}$ of objects.

Definition 9. 

Acogeneratingset of objects M for a cPROP category C exists if for every parallel pair of arrows $h\ne h^{\prime }:X\to Y$, there is an object Q in M and an arrow $g:Y\to Q$ such that $g\circ h\ne g\circ h^{\prime }$.

This property lets us construct initial objects for cPROP categories.

Theorem 6. 

[23] (Special Initial-Object Theorem: If a cPROP category C is small-complete (implying that it has finite products and a terminal object), and a small cogenerating set M, then C has an initial object assuming every set of subobjects of X in C has a finite intersection.

The proof is simple and involves constructing the product $X_0$ of all objects in the cogenerating set M and then taking the intersection of all the subobjects of $X_0$. Since the set of subobjects is a partial ordering under the relation ≤ in Definition 8, and Cartesianness of the cPROP category gives us pullbacks, we can use this universal construction to find the meet or intersection of any set of subobjects. An important result that depends on this property is the Special Adjoint Functor Theorem [23].

Theorem 7. Special Adjoint Functor Theorem (SAFT):Given a small-complete cPROP category M, with small hom-sets, and a small cogenerating set M, where every set of subobjects of objects in C has a pullback, then any functor $G:\mathcal{C}\to \mathcal{D}$ has a left adjoint if and only if G preserves all small limits and all pullbacks of families of monomorphisms.

Fox [4] shows that the cPROP category $c\underline{P}$ has a small cogenerating set of objects, and that the functor F from $c\underline{P}$ to MON creates colimits. This is used to show that $c\underline{P}$ is locally presentable, and by the SAFT, there exists a right adjoint to the forgetful functor $U:c\underline{P}\to \mathbf{MON}$.

In Section 5, we will discuss the importance of Cartesian structure in topological spaces that will act as the realizations of cPROPs. The topological realization of cPROPs will be done using the nerve functor that maps a cPROP into a simplicial set, which will be discussed in Section 6.

4. Affine CDU and Markov Categories as cPROPs

In this section, we relate cPROPs to previous work on affine CDU categories [7] and Markov categories [6]. Markov categories have been studied extensively as a unifying categorical model for causal inference, probability and statistics. They are symmetric monoidal categories, which we reviewed in Section 3.2, combined with a comonoidal structure on each object. Importantly, Markov categories are semi-Cartesian because they do not use uniform copying, but contain a Cartesian subcategory defined by deterministic morphisms. We give a brief review of Markov categories, and significant additional details that are omitted can be found in [6,7,17]. For the sake of clarity, we follow the definitions in [6], although we will explore some of the subtleties in these definitions in Section 4.1 relating to the Cartesian structure of a Markov category.

Definition 10. 

AMarkov category$\mathcal{C}$[6] is a symmetric monoidal category in which every object $X\in \mathcal{C}$ is equipped with a commutative comonoid structure given by a comultiplication ${\mathsf{copy}}_X:X\to X\otimes X$ and a counit ${\mathsf{del}}_X:X\to I$, depicted in string diagrams as

and satisfying the commutative comonoid equations,

as well as compatibility with the monoidal structure,

and naturality of $\mathsf{del}$, which means that

for every morphism f.

Note that to adequately represent discovery algorithms like PC, and their many extensions and variants like greedy equivalent search [2], it is necessary to modify string diagrams to represent equivalence class of causal models. The challenge we have to face is that causal discovery requires searching through a super-exponentially large space of such string diagrams. Note that string diagrams defined over Markov categories are essentially induced by the PROP maps that define its (co)algebraic structure. In Section 6 and Section 7, we show how such string diagrams can be converted into continuous maps over “nice" topological spaces, in particular CW-complexes using the nerve functor that maps a (symmetric monoidal) category into a simplicial set [9]. Thus, the tensor product bifunctor $\otimes :\mathcal{C}\times \mathcal{C}\to \mathcal{C}$ leads to an H-space, or a topological space with a chosen basepoint (which can be defined as the topological 0-cell associated with the terminal object I in a Markov category), and a continuous map $\mathcal{BC}\times \mathcal{BC}\to \mathcal{BC}$. The comonoid comultiplication ${\mathsf{copy}}_X:X\to X\otimes X$ induces a diagonal map $\mathcal{BC}\to \mathcal{BC}\times \mathcal{BC}$. Since I is a terminal object in a Markov category, its classifying spaces $\mathcal{BC}$ are contractible.

4.1. Cartesian Structure in Markov Categories

We now discuss a subcategory of Cartesian categories within Markov that involves uniform ${copy}_X$ and ${del}_X$ morphisms. One fundamental property of Markov categories is that they are semi-Cartesian, as the unit object is also a terminal object. But, a subtlety arises in how these copy and delete operators are modeled, as we discuss below.

Definition 11. 

A symmetric monoidal category $\mathcal{C}$ isCartesianif the tensor product ⊗ is the categorical product.

If $\mathcal{C}$ and $\mathcal{D}$ are symmetric monoidal categories, then a functor $F:\mathcal{C}\to \mathcal{D}$ is monoidal if the tensor product is preserved up to coherent natural isomorphisms. F is strictly monoidal if all the monoidal structures are preserved exactly, including ⊗, unit object I, symmetry, associative and unit natural isomorphisms. Denote the category of symmetric monoidal categories with strict functors as arrows as MON. Let us review the basic definitions given by Heunen and Vicary [34], which will give some further clarity on the Cartesian structure in affine CDU and Markov categories.

Definition 12. 

The subcategory of comonoidscoMONin the ambient categoryMONof all symmetric monoidal categories is defined for any specific category C as a collection of “coalgebraic" objects $(X,{copy}_X,{del}_X)$, where X is in C, and arrows defined as comonoid homomorphisms from $(X,{copy}_X,{del}_X)$ to $(Y,{copy}_Y,{del}_Y)$ that act uniformly, in the sense that if $f:X\to Y$ is any morphism in C, then:

$$\begin{array}{c}\hfill (f\otimes f)\circ {copy}_X={copy}_Y\circ f\\ \hfill {del}_Y\circ f={del}_X\end{array}$$

Heunen and Vicary [34] define the process of “uniform copying and deleting" in the category coMON, which we now relate to Markov categories. A subtle difference worth emphasizing with Definition 10 is that in Markov categories, only ${del}_X$ is “uniform", but not ${copy}_X$ in the sense defined by Heunen and Vicary [34]. This distinction can be modeled in a cPROP category that is semi-Cartesian like Markov categories by suitably modifying the definition of the associated PROP map for copying.

Definition 13. 

[34] A symmetric monoidal category C admitsuniform deletingif there is a natural transformation $e_X:X\stackrel{e_X}{\to }I$ for all objects in the subcategory ${\mathcal{C}}_{\mathbf{coMON}}$ of comonoidal objects, where $e_I={id}_I$, as shown in Equation (5).

This condition was referred to by Cho and Jacobs [7] as a causality condition on the arrow $e_X$. Essentially, it states that if you process some object and then discard it, it’s equivalent to discarding it without processing.

Theorem 8. 

[34] A symmetric monoidal category C has uniform deleting if and only if I is terminal.

This property holds for Markov categories, as noted in [6], and a simple diagram chasing proof is given in [34].

Definition 14. 

[34] A symmetric monoidal category C hasuniform copyingif there is a natural transformation ${copy}_X:X\to X\otimes X$ such that ${del}_I={\rho }_I^{-1}$ satisfying Equation (2) and Equation (3).

We can now state an important result proved in [34] (Theorem 4.28), which relates to the more general results shown earlier by Fox [4].

Theorem 9. 

[4,34] The following conditions are equivalent for a symmetric monoidal category C.

• The category C isCartesianwith tensor products ⊗ given by the categorical product and the tensor unit is given by the terminal object.
• The symmetric monoidal category C hasuniform copying and deleting, and Equation (2) holds.

As noted by Fritz [6], not all Markov categories are Cartesian, because their copy_X is not uniform, but only del_X is. For example, consider the category FinStoch, where a joint distribution is specified by the morphism $\psi :I\to X\otimes Y$. In this case, the marginal distributions can be formed as the composite morphisms

$$\begin{array}{c}\hfill I\stackrel{\psi }{\to }X\otimes Y\stackrel{{del}_Y}{\to }X\\ \hfill I\stackrel{\psi }{\to }X\otimes Y\stackrel{{del}_X}{\to }Y\end{array}$$

But to require that in this case ⊗ is the categorical product implies that the marginal distributions defined as the above composites must be in bijection with the joint distribution.

To summarize this section, we reviewed affine CD categories [7] and Markov categories [6] and showed that they are closely related to cPROPs. Markov categories are semi-Cartesian as the unit element I is terminal, but not Cartesian as they do not allow uniform copying. They do contain a subcategory defined by their comonoidal objects that is Cartesian. In the remainder of this paper, we construct simplicial objects over cPROP categories, and then in Section 7, define the basic concepts of homotopies in cPROP categories.

5. Cartesian Topological Spaces

In this section, we discuss “nice" categories of topological spaces, showing that the obvious categorization leads to a symmetric monoidal structure where the tensor product ⊗ is defined as a product of topological spaces, but it is not a Cartesian category. Restricting to the subcategory of CW complexes (or compactly generated weak Hausdorff spaces [35]) allows defining a suitable Cartesian structure. This review will motivate the construction of topological structures from cPROPs through the use of simplicial sets, which is the topic of the next section.

5.1. Cartesian Structure in Topological Spaces

Our goal in this paper is to construct topological representations of equivalence classes of observationally indistinguishable causal (DAG) models. To this end, we need to understand some basics about categories of topological spaces [36] and why the simplicial set construction in Section 6 leads to a nice topological structure.

Definition 15. 

The categoryTopdefines the category of all topological spaces, where objects are topological spaces, and arrows are continuous functions from one space into another.

The category Top has a natural symmetric monoidal structure, as defined in the following results (see Borceux [36], Chapter 7).

Theorem 10. 

The categoryTophas a natural closed symmetric monoidal structure imposed on it where

• The set underlying the tensor product $X\otimes Y$ of two spaces X and Y must necessarily be the Cartesian product $X\times Y$ of the underlying sets.
• The set underlying the internal “hom object" function space $[X,Y]$ is necessarily the set $\mathbf{Top}(X,Y)$ of continuous mappings from X to Y.

However, this natural monoidal structure does not have the right topological properties, because of the following result:

Theorem 11. 

The categoryTopis not Cartesian closed.

As before, we require that a Cartesian structure must require the ability to construct exponential objects.

Definition 16. 

A topological space X isexponentiableif the product functor $-\times X:\mathbf{Top}\to \mathbf{Top}$ has a right adjoint.

Fortunately, it is possible to construct such a subcategory of topological spaces.

Definition 17. 

A topological space X is locally compact when every neighborhood of a point contains a compact neighborhood of this point.

This restriction leads to a satisfactory outcome for constructing exponentiable objects.

Theorem 12. 

A locally compact space is exponentiable. The right adjoint to the functor $-\times X$ is given by the functor mapping Y to the set $\mathbf{Top}(X,Y)$ of continuous functions, topologized with the compact open topology.

The compact open topology on $\mathbf{Top}(X,Y)$ is defined as

$$\langle K,U\rangle =\{f\in \mathbf{Top}(X,Y\left)\right|f\left(K\right)\subseteq U$$

where K is over the compact subsets of X and U is over the open subsets of Y.

An ideal Cartesian structure on topological spaces is given by the category of compact Hausdorff spaces with compact open mappings.

Theorem 13. 

The categoryCGHausof compact Hausdorff spaces and compactly continuous mappings is Cartesian closed.

Finally, we note that the simplicial set construction to be defined in the next Section 6 yields CW complexes (compactly generated weak Hausdorff), which is defined as the following:

Definition 18. 

A space X isweak Hausdorffif the image of any continuous map with compact Hausdorff domain is closed in X.

These properties will be useful in understanding the topological structure of classifying spaces of cPROP categories, in particular they lead to associative and multiplicative spaces called H-spaces

6. Simplicial Objects in cPROPs

We now turn to the embedding of cPROPs in the category of simplicial sets, which will be a prelude to constructing “nice" topological realizations and the study of their classifying spaces. To help guide intuition, a general principle in category theory is to replace objects X by their resolution$\widehat{X}$ that are “weakly equivalent" to it in some way, and that satisfy properties that the original objects do not (like limits and pullbacks, or colimits and pushouts). In Quillen’s model category framework for doing abstract homotopy in a category [10], a (co)fibrant object play this role of having useful properties that the original objects do not, but are weakly equivalent to them. For example, in a cPROP (or Markov category), where I is a terminal object, an object X is considered a fibrant object if the unique morphism $X\to I$ to the terminal object is a fibration. We discuss below these notions using the framework of lifting diagrams. In this paper, we will not get into the details of model category structure for cPROPs (or Markov categories), but it will suffice to introduce ideas that will allow us to define the necessary homotopy structures in Section 7.

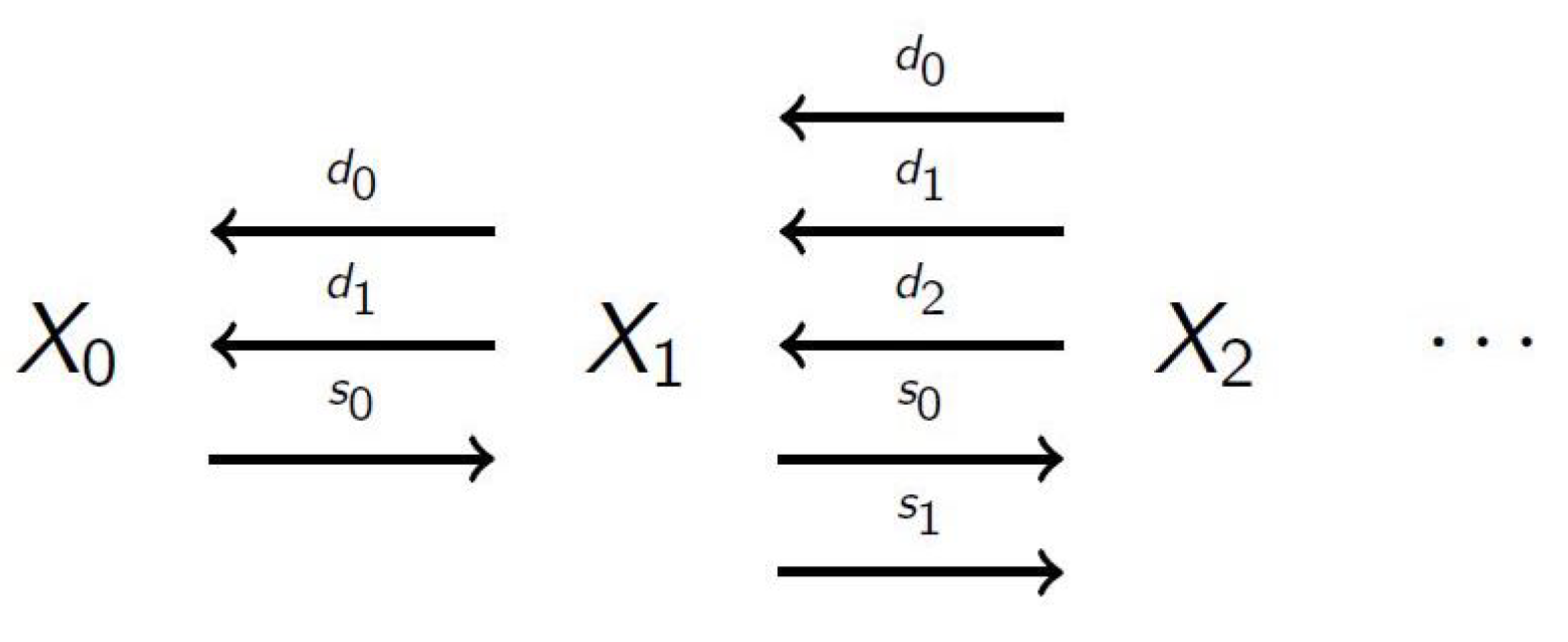
Figure 6 gives the high level intuition. A simplicial set X is defined as a collection of sets $X_0,X_1,\dots$, combined with degeneracy maps (indicated as $d_i$ in the figure) and face maps (indicated as $s_j$ in the figure). As a simple guide to help build intuition, any directed graph can be viewed as a simplicial set, where $X_0$ is the set V of vertices, $X_1$ is the E of edges, and the two face maps $d_0$ and $d_1$ from $X_1$ to $X_0$ yield the initial and final vertex of the edge. The single degeneracy map $s_0$ between $X_0$ and $X_1$ adds a self loop to each vertex. Simplicial sets generalize graphs when we consider higher-order simplices. For example, between $X_1$ and $X_2$, there are three face maps, mapping a simplicial triangle (a $2-simplex$) $\Delta$ to each of its 1-simplicial components, namely its edges.

We give a brief review of simplicial sets, summarizing some points we made in our previous paper on simplicial set representations in causal inference [29]. A more detailed review can be found in many references [32,37]. Simplicial sets are higher-dimensional generalizations of directed graphs, partially ordered sets, as well as regular categories themselves. Importantly, simplicial sets and simplicial objects form a foundation for higher-order category theory [30,31]. Using simplicial sets and objects enables a powerful machinery to reason about both directional and non-directional paths in causal models, and to model equivalence classes of causal models.

Simplicial objects have long been a foundation for algebraic topology [37,38], and more recently in higher-order category theory [30,31,39]. The category $\Delta$ has non-empty ordinals $\left[n\right]=\{0,1,\dots ,n]$ as objects, and order-preserving maps $\left[m\right]\to \left[n\right]$ as arrows. An important property in $\Delta$ is that any many-to-many mapping is decomposable as a composition of an injective and a surjective mapping, each of which is decomposable into a sequence of elementary injections ${\delta }_i:\left[n\right]\to [n+1]$, called coface mappings, which omits $i\in \left[n\right]$, and a sequence of elementary surjections ${\sigma }_i:\left[n\right]\to [n-1]$, called co-degeneracy mappings, which repeats $i\in \left[n\right]$. The fundamental simplex $\Delta \left(\right[n\left]\right)$ is the presheaf of all morphisms into $\left[n\right]$, that is, the representable functor $\Delta (-,[n\left]\right)$. The Yoneda Lemma [23] assures us that an n-simplex $x\in X_n$ can be identified with the corresponding map $\Delta \left[n\right]\to X$. Every morphism $f:\left[n\right]\to \left[m\right]$ in $\Delta$ is functorially mapped to the map $\Delta \left[m\right]\to \Delta \left[n\right]$ in $\mathcal{S}$.

Any morphism in the category $\Delta$ can be defined as a sequence of co-degeneracy and co-face operators, where the co-face operator ${\delta }_i:[n-1]\to \left[n\right],0\le i\le n$ is defined as:

$${\delta }_i\left(j\right)=\left\{\begin{array}{cc}j,\hfill & for0\le j\le i-1\hfill \\ j+1\hfill & fori\le j\le n-1\hfill \end{array}\right.$$

Analogously, the co-degeneracy operator ${\sigma }_j:[n+1]\to \left[n\right]$ is defined as

$${\sigma }_j\left(k\right)=\left\{\begin{array}{cc}j,\hfill & for0\le k\le j\hfill \\ k-1\hfill & forj<k\le n+1\hfill \end{array}\right.$$

Note that under the contravariant mappings, co-face mappings turn into face mappings, and co-degeneracy mappings turn into degeneracy mappings. That is, for any simplicial object (or set) $X_n$, we have $X\left({\delta }_i\right)d_i:X_n\to X_{n-1}$, and likewise, $X\left({\sigma }_j\right)s_j:X_{n-1}\to X_n$.

The compositions of these arrows define certain well-known properties [32,37]:

$$\begin{array}{ccc}\hfill {\delta }_j\circ {\delta }_i& =& {\delta }_i\circ {\delta }_{j-1},i<j\hfill \\ \hfill {\sigma }_j\circ {\sigma }_i& =& {\sigma }_i\circ {\sigma }_{j+1},i\le j\hfill \\ \hfill {\sigma }_j\circ {\delta }_i\left(j\right)& =& \left\{\begin{array}{cc}{\sigma }_i\circ {\sigma }_{j+1},\hfill & fori<j\hfill \\ 1_{\left[n\right]}\hfill & fori=j,j+1\hfill \\ {\sigma }_{i-1}\circ {\sigma }_j,fori>j+1\hfill \end{array}\right.\hfill \end{array}$$

Example 2. 

The “vertices” of a simplicial object X in a cPROP category $\mathcal{C}$ are the objects $X_0$ in $\mathcal{C}$, and the “edges” $X_1$ are its arrows $f:C_i\to C_j$, where $C_i$ and $C_j$ are objects in $\mathcal{C}$. Note that $X_0$ is a contravariant functor $X:\left[0\right]\to \mathcal{C}$, and since $\left[0\right]$ has only one object, the effect of this functor is to pick out objects in $\mathcal{C}$. The simplicial object $X_1:\left[1\right]\to \mathcal{C}$. Given any such arrow, the face operators $d_{0}f=C_j$ and $d_{1}f=C_i$ recover the source and target of each arrow. Also, given an object X of category $\mathcal{C}$, we can regard the degeneracy operator $s_{0}X$ as its identity morphism ${\mathbf{1}}_X:X\to X$.

Example 3. 

Given a cPROP category $\mathcal{C}$, we can identify an n-simplex $X_n$ of a simplicial object in a cPROP category $s{\mathcal{C}}_n$ with the sequence:

$$X_n=C_o\stackrel{f_1}{\to }{C}_1\stackrel{f_2}{\to }\dots \stackrel{f_n}{\to }{C}_n$$

the face operator $d_0$ applied to $X_n$ yields the sequence

$$d_0{X}_n=C_1\stackrel{f_2}{\to }{C}_2\stackrel{f_3}{\to }\dots \stackrel{f_n}{\to }{C}_n$$

where the object $C_0$ is “deleted” along with the morphism $f_0$ leaving it.

Example 4. 

Given a cPROP category $\mathcal{C}$, and an n-simplex $X_n$ of the simplicial object in a cPROP category $X_n$, the face operator $d_n$ applied to $X_n$ yields the sequence

$$d_n{X}_n=C_0\stackrel{f_1}{\to }{C}_1\stackrel{f_2}{\to }\dots \stackrel{f_{n-1}}{\to }{C}_{n-1}$$

where the object $C_n$ is “deleted” along with the morphism $f_n$ entering it.

Example 5. 

Given a cPROP category $\mathcal{C}$, and an n-simplex $X_n$ of the simplicial object, the face operator $d_i,0<i<n$ applied to $X_n$ yields the sequence

$$d_i{X}_n=C_0\stackrel{f_1}{\to }{C}_1\stackrel{f_2}{\to }\dots C_{i-1}\stackrel{f_{i+1}\circ f_i}{\to }{C}_{i+1}\dots \stackrel{f_n}{\to }{C}_n$$

where the object $C_i$ is “deleted” and the morphisms $f_i$ is composed with morphism $f_{i+1}$.

Example 6. 

Given a cPROP category $\mathcal{C}$, and an n-simplex $X_n$ of the simplicial object defined over the cPROP category, the degeneracy operator $s_i,0\le i\le n$ applied to $X_n$ yields the sequence

$$s_i{X}_n=C_0\stackrel{f_1}{\to }{C}_1\stackrel{f_2}{\to }\dots C_i\stackrel{{\mathbf{1}}_{C_i}}{\to }{C}_i\stackrel{f_{i+1}}{\to }{C}_{i+1}\dots \stackrel{f_n}{\to }{C}_n$$

where the object $C_i$ is “repeated” by inserting its identity morphism ${\mathbf{1}}_{C_i}$.

Definition 19. 

Given a cPROP category $\mathcal{C}$, and an n-simplex $X_n$ of the simplicial object associated with the category, $X_n$ is adegeneratesimplex if some $f_i$ in $X_n$ is an identity morphism, in which case $C_i$ and $C_{i+1}$ are equal.

6.1. Simplicial Subsets and Horns of cPROP Categories

One significant strength of the simplicial object construction outlined above is that the resulting structures lead to topologically “nice" representations, in particular CW-complexes [33]. One crucial property is that any $n-1$ simplex $X_{n-}$ can be formed as a retract of an n-simplex $X_n$ by applying one of the face operators described earlier. Such nice structures are called Kan complexes. To define this property, we describe simplicial subsets and horns. These structures will play a key role in defining suitable lifting problems that are needed to explain Kan complexes.

Definition 20. 

Thestandard simplex${\Delta }^n$ is the simplicial set defined by the construction

$$(\left[m\right]\in \Delta )\mapsto {\mathbf{Hom}}_{\Delta }(\left[m\right],\left[n\right])$$

By convention, ${\Delta }^{-1}\varnothing$. The standard 0-simplex ${\Delta }^0$ maps each $\left[n\right]\in {\Delta }^{op}$ to the single element set $\{•\}$.

Definition 21. 

Let S denote a simplicial object, where $S_n$ is its $n^{th}$ simplex. If for every integer $n\ge 0$, we are given a subset $T_n\subseteq S_n$, such that the face and degeneracy maps

$$d_i:S_n\to S_{n-1}{s}_i:S_n\to S_{n+1}$$

applied to $T_n$ result in

$$d_i:T_n\to T_{n-1}{s}_i:T_n\to T_{n+1}$$

then the collection ${\left\{T_n\right\}}_{n\ge 0}$ defines asimplicial subset$T_{•}\subseteq S_{•}$

Definition 22. 

Theboundaryis a simplicial set $(\partial {\Delta }^n):{\Delta }^{op}\to$Setdefined as

$$(\partial {\Delta }^n)\left(\left[m\right]\right)=\{\alpha \in {\mathbf{Hom}}_{\Delta }(\left[m\right],\left[n\right]):\alpha isnotsurjective\}$$

Note that the boundary $\partial {\Delta }^n$ is a simplicial subset of the standard n-simplex ${\Delta }^n$.

Definition 23. 

TheHorn${\Lambda }_i^n:{\Delta }^{op}\to$Setis defined as

$$\left({\Lambda }_i^n\right)\left(\left[m\right]\right)=\{\alpha \in {\mathbf{Hom}}_{\Delta }(\left[m\right],\left[n\right]):\left[n\right]\neg \subseteq \alpha \left(\left[m\right]\right)\cup \left\{i\right\}\}$$

Intuitively, the Horn ${\Lambda }_i^n$ can be viewed as the simplicial subset that results from removing the interior of the n-simplex ${\Delta }^n$ together with the face opposite its ith vertex.

6.2. Lifting Problems in cPROP Categories

Lifting problems provide elegant ways to define basic notions in a wide variety of areas in mathematics [40]. For example, the notion of injective and surjective functions, the notion of separation in topology, and many other basic constructs can be formulated as solutions to lifting problems. Database queries in relational databases can be defined using lifting problems [41]. Lifting problems define ways of decomposing structures into simpler pieces, and putting them back together again. Our goal here is to illustrate that simplicial objects in Markov categories can solve certain types of lifting problems corresponding to inner horns. A fuller discussion of these issues can be found in [31].

Definition 24. 

Let $\mathcal{C}$ be a cPROP category. Alifting problemin $\mathcal{C}$ is a commutative diagram σ in $\mathcal{C}$.

Definition 25. 

Let $\mathcal{C}$ be a cPROP category. Asolution to a lifting problemin $\mathcal{C}$ is a morphism $h:B\to X$ in $\mathcal{C}$ satisfying $p\circ h=\nu$ and $h\circ f=\mu$ as indicated in the diagram below.

Definition 26. 

Let $\mathcal{C}$ be a cPROP category. If we are given two morphisms $f:A\to B$ and $p:X\to Y$ in $\mathcal{C}$, we say that f has theleft lifting propertywith respect to p, or that p has theright lifting propertywith respect to f if for every pair of morphisms $\mu :A\to X$ and $\nu :B\to Y$ satisfying the equations $p\circ \mu =\nu \circ f$, the associated lifting problem indicated in the diagram below.

admits a solution given by the map $h:B\to X$ satisfying $p\circ h=\nu$ and $h\circ f=\mu$.

Example 7. 

Given the paradigmatic non-surjective morphism $f:\varnothing \to \{•\}$, any morphism p that has the right lifting property with respect to f is asurjective mapping. .

Example 8. 

Given the paradigmatic non-injective morphism $f:\{•,•\}\to \{•\}$, any morphism p that has the right lifting property with respect to f is aninjective mapping. .

6.3. Filling Inner vs. Outer Horns in Markov Categories

Consider the problem of composing 1-dimensional simplices to form a 2-dimensional simplicial object in a Markov category $\mathcal{C}$. Each simplicial subset of an n-simplex induces a a horn${\Lambda }_k^n$, where $0\le k\le n$. Intuitively, a horn is a subset of a simplicial object that results from removing the interior of the n-simplex and the face opposite the ith vertex. Consider the three horns defined below. The dashed arrow ⤏ indicates edges of the 2-simplex ${\Delta }^2$ not contained in the horns.

The inner horn ${\Lambda }_1^2$ is the middle diagram above, and admits an easy solution to the “horn filling” problem of composing the simplicial subsets. The two outer horns on either end pose a more difficult challenge. For example, filling the outer horn ${\Lambda }_0^2$ when the morphism between $\left\{0\right\}$ and $\left\{1\right\}$ is f and that between $\left\{0\right\}$ and $\left\{2\right\}$ is tantamount to finding the left inverse of f up to homotopy. Dually, in this case, filling the outer horn ${\Lambda }_2^2$ is tantamount to finding the right inverse of f up to homotopy. A considerable elaboration of the theoretical machinery in category theory is required to describe the various solutions proposed, which led to different ways of defining higher-order category theory [30,31,39].

6.4. Kan complexes in cPROP Categories

To show that the nerve functor applied to cPROP categories produces only certain types of lifts, we need to introduce the notion of fibrations.

Definition 27. 

Let $f:X\to S$ be a morphism of simplicial objects in a cPROP category $\mathcal{C}$. We say f is aKan fibrationif, for each $n>0$, and each $0\le i\le n$, every lifting problem.

admits a solution. More precisely, for every map of simplicial sets ${\sigma }_0:{\Lambda }_i^n\to X$ and every n-simplex $\overline{\sigma }:{\Delta }^n\to S$ extending $f\circ {\sigma }_0$, we can extend ${\sigma }_0$ to an n-simplex $\sigma :{\Delta }^n\to X$ satisfying $f\circ \sigma =\overline{\sigma }$.

Example 9. 

Given a simplicial object X in a cPROP category $\mathcal{C}$, a projection map $X\to {\Delta }^0$ that is a Kan fibration is called aKan complex .

Example 10. 

Any isomorphism between simplicial objects in a cPROP category $\mathcal{C}$ is a Kan fibration.

Example 11. 

The collection of Kan fibrations in cPROP categories is closed under retracts.

Definition 28. 

[31] A simplicial object X in a cPROP category $\mathcal{C}$ satisfies the following condition:

• For $0<i<n$, every map of simplicial objects ${\sigma }_0:{\Lambda }_i^n\to SX$ can be extended to a map $\sigma :{\Delta }^n\to X_i$.

Simplicial objects in cPROP categories can solve inner horn extension problems, but not the outer horn problems that are more challenging. are thus Kan complexes, which is obvious from the construction of the nerve functor. Simplicial objects that satisfy property C above can be identified with the nerve of a category, which yields a full and faithful embedding of a category in the category of sets. Definition 28 generalizes both of these definitions, and was called a quasicategory in [30] and weak Kan complexes in [39] when $\mathcal{C}$ is a category. We will use the nerve of a category below in defining homotopy colimits as a way of characterizing a causal model.

6.5. Topological Embedding of Simplicial Objects in cPROP Categories

Simplicial objects in cPROP categories can be embedded in a topological space using a construction originally proposed by Milnor [33].

Definition 29. 

Thegeometric realization$\left|X\right|$ of a simplicial object X in cPROP category $\mathcal{C}$ defined as the topological space

$$\left|X\right|=\underset{n\ge 0}{⨆}{X}_n\times {\Delta }^n/\sim$$

where the n-simplex $X_n$ is assumed to have adiscretetopology (i.e., all subsets of $X_n$ are open sets), and ${\Delta }^n$ denotes thetopologicaln-simplex

$${\Delta }^n=\{(p_0,\dots ,p_n)\in {\mathbb{R}}^{n+1}|0\le p_i\le 1,\sum _i{p}_i=1$$

The spaces ${\Delta }^n,n\ge 0$ can be viewed ascosimplicialtopological spaces with the following degeneracy and face maps:

$${\delta }_i(t_0,\dots ,t_n)=(t_0,\dots ,t_{i-1},0,t_i,\dots ,t_n)for0\le i\le n$$

$${\sigma }_j(t_0,\dots ,t_n)=(t_0,\dots ,t_j+t_{j+1},\dots ,t_n)for0\le i\le n$$

Note that ${\delta }_i:{\mathbb{R}}^n\to {\mathbb{R}}^{n+1}$, whereas ${\sigma }_j:{\mathbb{R}}^n\to {\mathbb{R}}^{n-1}$.

The equivalence relation ∼ above that defines the quotient space is given as:

$$(d_i\left(x\right),(t_0,\dots ,t_n))\sim (x,{\delta }_i(t_0,\dots ,t_n))$$

$$(s_j\left(x\right),(t_0,\dots ,t_n))\sim (x,{\sigma }_j(t_0,\dots ,t_n))$$

Topological Embeddings as Coends

We now bring in the perspective that topological embeddings of simplicial objects in cPROP categories can be interpreted as a coend [23] as well. Consider the functor

$$F:{\Delta }^o\times \Delta \to Top$$

where

$$F(\left[n\right],\left[m\right])=X_n\times {\Delta }^m$$

where F acts contravariantly as a functor from $\Delta$ to $\mathbf{Sets}$ mapping $\left[n\right]\mapsto X_n$, and covariantly mapping $\left[m\right]\mapsto {\Delta }^m$ as a functor from $\Delta$ to the category $Top$ of topological spaces.

The coend defines a topological embedding of a simplicial object X in a cPROP category, where $X_n$ represents composable morphisms of length n. Given this simplicial object, we can now construct a topological realization of it as a coend object

$${\int }^n\left(X_n\right)·\Delta n$$

where $X:{\Delta }^{op}\to \mathcal{C}$ is the simplicial object defined by the contravariant functor from the simplicial category $\Delta$ into the category of simplicial objects in cPROP categories, and $\Delta :|\Delta |\to \mathbf{Top}$ is a functor from the topological n-simplex realization of the simplicial category $\Delta$ into topological spaces $\mathbf{Top}$. As MacLane [23] explains it picturesquely, the “coend formula describes the geometric realization in one gulp". The formula says essentially to take the disjoint union of affine n-simplices, one for each $n\in X_n$, and glue them together using the face and degeneracy operations defined as arrows of the simplicial category $\Delta$.

7. Homotopy in cPROP Categories

We define homotopy in cPROP categories somewhat abstractly in this section, but we will illustrate these definitions more concretely for Bayesian networks defined as functors between cPROP categories, analogous to CDU functors [8] later in Section 8.

To motivate the need for considering homotopy in categorical models of causal inference, and in particular for cPROP categories, note that causal models can only be determined up to some equivalence class from data, and while many causal discovery algorithms assume arbitrary interventions can be carried out, for example on separating sets [14] and other types of subsets [15], to discover the unique structure, such interventions are generally impossible to do in practical applications. The concept of essential graph [20] and chain graph [42] are attempts to formulate the notion of a “quotient space” of graphs, but similar issues arise more generally for non-graph based models as well. Thus, it is useful to understand how to formulate the notion of equivalent classes of causal models in an arbitrary category. For example, given the conditional independence structure $A\perp -10mu\perp B|C$, there are at least three different symmetric monoidal categorical representations that all satisfy this conditional independence [8,17,27], and we need to define the quotient space over all such equivalent categories.

7.1. Homotopy in cPROP Categories

We will discuss homotopy in cPROP categories more generally now. This abstract notion of homotopy generalizes the notion of homotopy in topology, which defines why an object like a coffee cup is topologically homotopic to a doughnut (they have the same number of “holes”).

Definition 30. 

Let C and $C^{\prime }$ be a pair of objects in a cPROP category $\mathcal{C}$. We say C isa retractof $C^{\prime }$ if there exists maps $i:C\to C^{\prime }$ and $r:C^{\prime }\to C$ such that $r\circ i={id}_{\mathcal{C}}$.

Definition 31. 

Let $\mathcal{C}$ be a cPROP category. We say a morphism $f:C\to D$ is aretract of another morphism$f^{\prime }:C\to D$ if it is a retract of $f^{\prime }$ when viewed as an object of the functor categoryHom$\left(\right[1],\mathcal{C})$. A collection of morphisms T of $\mathcal{C}$ isclosed under retractsif for every pair of morphisms $f,f^{\prime }$ of $\mathcal{C}$, if f is a retract of $f^{\prime }$, and $f^{\prime }$ is in T, then f is also in T.

Definition 32. 

Let X and Y be simplicial cPROP categories represented as simplicial sets, and suppose we are given a pair of morphisms $f_0,f_1:X\to Y$. Ahomotopyfrom $f_0$ to $f_1$ is a morphism $h:{\Delta }^1\times X\to Y$ satisfying $f_0{=h|}_{0\times X}$ and $f_1=h_{1\times X}$.

7.2. Classifying Spaces of cPROP Categories

We now introduce a formal way to define causal effects in our cPROP framework, which relies on the construction of a topological space associated with the nerve of a cPROP category. As shown in [9], the nerve of a category is a full and faithful embedding of a category as a simplicial object.

Definition 33. 

Theclassifying space$\mathcal{BC}$ of a cPROP category $\mathcal{C}$ is the topological space associated with the nerve of the category $\mathcal{C}$.

To understand the classifying space $\mathcal{BC}$ of a cPROP category $\mathcal{C}$, let us go over some simple examples to gain some insight.

Example 12. 

Consider a discrete cPROP category ${\mathcal{C}}_X$ as a subcategory overFinSetdefined as discrete finite sets X with no non-trivial morphisms, the classifying space $B{\mathcal{C}}_X$ is just the discrete topology over X (where the open sets are all possible subsets of X).

Example 13. 

Consider a cPROP category $\mathcal{C}$ defined as a partially ordered set $\left[n\right]$, with its usual order-preserving morphisms, then the nerve of $\left[n\right]$ is isomorphic to the representable functor $\Delta (-,[n\left]\right)$, as shown by the Yoneda Lemma, and in that case, the classifying space is just the topological space associated with ${\Delta }_n$ (the topological n-simplex).

7.3. Singular Homology of a cPROP Category

Our goal is to define an abstract notion of a causal model in terms of its underlying classifying space as a cPROP category, and show how it can be useful in defining causal homotopy. We will also clarify how it relates to determining equivalences among causal models, namely homotopical invariance, and also how it sheds light on causal identification. First, we need to define more concretely the topological n-simplex that provides a concrete way to attach a topology to a simplicial object. Our definitions below build on those given in [31]. For each integer n, define the topological space $\mathcal{B}{\Delta }_n$ realized by the object ${\Delta }_n$ as

$$\mathcal{B}{\Delta }_n=\{t_0,t_1,\dots ,t_n\in {\mathbb{R}}^{n+1}:t_0+t_1+\dots +t_n=1\}$$

This is the familiar n-dimensional simplex over n variables. For any causal model, its classifying space $\mathcal{BC}$ defines a topological space. We can now define the singularn-simplex as a continuous mapping $\sigma :\mathcal{B}{\Delta }_N\to \mathcal{BC}$. Every singular n-simplex $\sigma$ induces a collection of $n-1$-dimensional simplices called faces, denoted as

$$d_i\sigma (t_0,\dots ,t_{n-1})=(t_0,t_1,\dots ,t_{i-1},0,t_i,\dots ,t_{n-1})$$

Note that as discussed above, a causal intervention on a variable in a DAG can be modeled as applying one of these degeneracy operators $d_i$. The above definition shows that every such intervention has an effect on the topology associated with the causal model. Define the set of all morphisms ${Sing}_n\left(X\right)={\mathbf{Hom}}_{\mathbf{Top}}({\Delta }_n,\mathcal{BC})$ as the set of singular n-simplices of $\mathcal{BC}$.

Definition 34. 

For any topological space $\mathcal{BC}$ defined by a cPROP category $\mathcal{C}$, thesingular homology groups$H_{*}(\mathcal{BC};\mathbf{Z})$ are defined as the homology groups of a chain complex

$$\dots \stackrel{\partial }{\to }\mathbf{Z}\left({Sing}_2\left(\mathcal{BC}\right)\right)\stackrel{\partial }{\to }\mathbf{Z}\left({Sing}_1\left(\mathcal{BC}\right)\right)\stackrel{\partial }{\to }\mathbf{Z}\left({Sing}_0\left(\mathcal{BC}\right)\right)$$

where $\mathbf{Z}\left({Sing}_n\left(\mathcal{BC}\right)\right)$ denotes the free Abelian group generated by the set ${Sing}_n\left(\mathcal{BC}\right)$ and the differential ∂ is defined on the generators by the formula

$$\partial \left(\sigma \right)=\sum _{i=0}^n{(-1)}^i{d}_i\sigma$$

Intuitively, a chain complex builds a sequence of vector spaces that can be used to construct an algebraic invariant of a causal model from its classifying space by choosing the left k module $\mathbf{Z}$ to be a vector space. Each differential ∂ then becomes a linear transformation whose representation is constructed by modeling its effect on the basis elements in each $\mathbf{Z}\left({Sing}_n\left(X\right)\right)$.

Example 14. 

Let us illustrate the singular homology groups defined by an integer-valued multiset [16] used to model conditional independence. Imsets over a DAG of three variables $N=\{a,b,c\}$ can be viewed as a finite discrete topological space. For this topological space X, the singular homology groups $H_{*}(X;\mathbf{Z})$ are defined as the homology groups of a chain complex

$$\mathbf{Z}\left({Sing}_3\left(X\right)\right)\stackrel{\partial }{\to }\mathbf{Z}\left({Sing}_2\left(X\right)\right)\stackrel{\partial }{\to }\mathbf{Z}\left({Sing}_1\left(X\right)\right)\stackrel{\partial }{\to }\mathbf{Z}\left({Sing}_0\left(X\right)\right)$$

where $\mathbf{Z}\left({Sing}_i\left(X\right)\right)$ denotes the free Abelian group generated by the set ${Sing}_i\left(X\right)$ and the differential ∂ is defined on the generators by the formula

$$\partial \left(\sigma \right)=\sum _{i=0}^4{(-1)}^i{d}_i\sigma$$

The set ${Sing}_n\left(X\right)$ is the set of all morphisms ${\mathbf{Hom}}_{Top}(\mathcal{B}{\Delta }_n,X)$. For an imset over the three variables $N=\{a,b,c\}$, we can define the singular n-simplex σ as:

$$\sigma :\mathcal{B}{\Delta }^4\to Xwhere\mathcal{B}{\Delta }^n=\{t_0,t_1,t_2,t_3\in {[0,1]}^4:t_0+t_1+t_2+t_3=1\}$$

The n-simplex σ has a collection of faces denoted as $d_0\sigma ,d_1\sigma ,d_2\sigma$ and $d_3\sigma$. If we pick the k-left module $\mathbf{Z}$ as the vector space over real numbers $\mathbb{R}$, then the above chain complex represents a sequence of vector spaces that can be used to construct an algebraic invariant of a topological space defined by the integer-valued multiset. Each differential ∂ then becomes a linear transformation whose representation is constructed by modeling its effect on the basis elements in each $\mathbf{Z}\left({Sing}_n\left(X\right)\right)$.

7.4. Homotopy Colimits of cPROP Categories

Definition 35. 

Thehomotopy colimitof a cPROP category model is defined as nerve of the category of elements associated with the set-valued functor $\delta :\mathcal{C}\to$Setmapping the cPROP category $\mathcal{C}$ to a dataset, namely $B\left(\int \delta \right)$.

In general, we may want to evaluate the homotopy colimit of a cPROP category not only with respect to the data used in a causal experiment, but also with respect to some underlying topological space or some measurable space. We can extend the above definition straightforwardly to these cases using an appropriate functor $\mathcal{T}$: Set→Top, or alternatively $\mathcal{M}$: Set→ Meas. These augmented constructions can then be defined with respect to a more general notion called the homotopy colimit [32] of a causal model.

Definition 36. 

Thetopological homotopy colimit${hocolim}_{\mathcal{T}\circ \delta }$ of a cPROP category $\mathcal{C}$, along with its associated category of elements associated with a set-valued functor $\delta :\mathcal{C}\to$Set, and a topological functor $\mathcal{T}$:Set→Topis isomorphic to topological space associated with the nerve of the category of elements, that is ${hocolim}_{\mathcal{T}\circ \delta }\simeq \mathcal{B}\left(\int \delta \right)$.

Example 15. 

The classifying space ${\mathcal{B}\mathcal{C}}_{CDU}$ associated with CDU symmetric monoidal category encoding of a causal Bayesian DAG [8] is defined using the monoidal category (C, ⊗, I), where each object A has a copy map $C_A:A\to A\otimes A$, and discarding map $D_A:A\to I$, and a uniform state map $U_A:I\to A$, is defined as the topological realization of its nerve. As before, the nerve $B\left(\mathcal{C}\right)$ of the CDU (or Markov) category is defined as the set of sequences of composable morphisms of length n.

$$\{C_o\stackrel{f_1}{\to }{C}_1\stackrel{f_2}{\to }\dots \stackrel{f_n}{\to }{C}_n|C_{i}isanobjectin\mathcal{C},f_{i}isamorphismin\mathcal{C}\}$$

Note that the CDU category was associated with a CDU functor $F:$Syn_G→Stochto the category of stochastic matrices. We can now define the homotopy colimit ${hocolim}_{\mathcal{F}}$ of the CDU causal model associated with the CDU category $\mathcal{C}$, along with its associated category of elements associated with a set-valued functor $\delta :\mathcal{C}\to$Set, and a topological functor $\mathcal{F}$:Set→Stochis isomorphic to topological space associated with the nerve of the category of elements over the composed functor, that is ${hocolim}_{\mathcal{F}\circ \delta }$.

7.5. Defining Causal Effect in cPROP categories using Homotopy

Finally, we turn to defining causal effect using the notion of classifying space and homotopy colimits, as defined above. Space does not permit a complete discussion of this topic, but the basic idea is that once a causal model is defined as a topological space, there are a large number of ways of comparing two topological spaces from analyzing their chain complexes, or using a topological data analysis method such as UMAP [43].

Definition 37. 

Let the classifying space under “treatment” be defined as the topological space $B{\mathcal{C}}_1|$ associated with the nerve of a cPROP category ${\mathcal{C}}_1$ under some intervention, which may result in a topological deformation of the model (e.g., deletion of an edge). Similarly, the classifying space under “no treatment” be defined as the $B{\mathcal{C}}_0$ under a no-treatment setting, with no intervention. Acausally non-isomorphic effectexists between cPROP categories ${\mathcal{C}}_1$ and ${\mathcal{C}}_0$, or ${\mathcal{C}}_1\neg \cong {\mathcal{C}}_0$ if and only if there is no invertible morphism $f:{\mathcal{B}\mathcal{C}}_1\to {\mathcal{B}\mathcal{C}}_0$ between the “treatment” and “no-treatment” topological spaces, namely f must be bothleft invertibleandright invertible.

There is an equivalent notion of causal effect using the homotopy colimit definition proposed above, which defines the nerve functor using the category of elements. This version is particularly useful in the context of evaluating a causal model over a dataset.

Definition 38. 

Let the homotopy colimit ${hocolim}_1=\mathcal{B}\int {\delta }_1$ be the topological space associated with a cPROP category ${\mathcal{C}}_1$ under the “treatment’ condition be defined with respect to an associated category of elements defined by a set-valued functor ${\delta }_1:\mathcal{C}\to$Setover a dataset of “treated” variables, and corresponding “no-treatment” ${hocolim}_0=\mathcal{B}\int {\delta }_0$ be the topological space of a causal model associated with a cPROP category ${\mathcal{C}}_0$ be defined over an associated category of elements defined by a set-valued functor ${\delta }_0:\mathcal{C}\to$Setover a dataset of “placebo” variables. Acausally non-isomorphic effectexists between cPROP categories ${\mathcal{C}}_1$ and ${\mathcal{C}}_0$, or ${\mathcal{C}}_1\neg \cong {\mathcal{C}}_0$ if and only if there is no invertible morphism $f:\mathcal{B}\int {\delta }_1\to \mathcal{B}{\delta }_0$ between the “treatment” and “no-treatment” homotopy colimit topological spaces, namely f must be bothleft invertibleandright invertible.

8. Classifying Spaces of Functors on cPROP Categories

In this section, we drill down from the abstractions above to prove a set of more concrete results regarding the classifying spaces of cPROP functors that correspond to Bayesian networks [44], and can be seen as analogous to CDU functors in affine CD categories [8]. In this section, we restrict our attention to the cPROP category $c\underline{P}$ defined by the coalgebraic PROP $\underline{P}$ defined by the PROP maps $\delta :1\to 2$ and $ϵ:1\to 0$, as discussed earlier in Section 3. We also build on the results of the previous sections to state a categorical generalization of the Meek-Chickering (MC) theorem for cPROP categories [2,18]. This theorem, originally stated as a conjecture in Meek’s dissertation [18] was formally proved by Chickering [2]. The MC theorem states that given any two causal DAG models $\mathcal{G}$ and $\mathcal{H}$, where $\mathcal{H}$ is an independence map of $\mathcal{G}$, that is any conditional independence implied by the structure of $\mathcal{H}$ is also implied by the structure of $\mathcal{G}$. Furthermore, there exists a finite sequence of edge additions and covered edge reversals such that after each edge change, $\mathcal{G}$ remains a DAG, and $\mathcal{H}$ remains an independence map of $\mathcal{G}$, and finally $\mathcal{G}=\mathcal{H}$ after the sequence is completed.

To begin with, we build on the characterization of a causal DAGs $\mathcal{G}$, or Bayesian networks [12,44], as functors from the cPROP (or equivalently CDU) category ${\mathbf{Syn}}_G$ to FinStoch (see [8] for more details). We assume the reader is familiar with the terminology of DAG models in this section, and we refer the reader to [2] for additional details that we omit in the interests of space. We give a brief overview of the Markov category FinStoch (which was called Stoch in [8]), whose objects are finite sets and morphisms $f:A\to B$. States are stochastic matrices from a trivial input $I:=\{*\}$, are essentially column vectors representing marginal distributions. The counit is a stochastic matrix with a row vector consisting only of 1’s. The composition of morphisms is defined by matrix multiplication. The monoidal product ⊗ in FinStoch is the Cartesian product on objects, and Kronecker product of matrices: ${(f\otimes g)}_{(i,j)}^{(k,l)}:=f_i^k{g}_j^l$. The Kronecker product corresponds to taking product distributions. FinStoch realizes the “swap" operation defined by the string diagram in Definition 10 as $\sigma :A\otimes B\to B\otimes A$ given by ${\sigma }_{ij}^{kl}:={\delta }_i^l{\delta }_j^k$, making it into a symmetric monoidal category.

Theorem 14.(Proposition 3.1, [8]) There is a 1-1 correspondence between Bayesian networks based on a DAG $\mathcal{G}$ and cPROP functors of the type $F:$${\mathbf{Syn}}_{\mathcal{G}}\to$FinStoch

This theorem is essentially the same as that in [8], since functors between CDU categories ${\mathbf{Syn}}_{\mathcal{G}}$ and FinStoch are special types of functors between cPROP categories. We can model the category of all Bayesian networks as a functor category ${\mathbf{FinStoch}}^{{Syn}_{\mathcal{G}}}$ on cPROP categories. In this section, we explore the homotopic structure of this functor category, whose objects are Bayesian networks represented as functors, and whose arrows are natural transformations.

Let us now build on the homotopic structures defined earlier in Section 7 in terms of viewing each cPROP category $\mathcal{C}$ in terms of its classifying space $\mathcal{BC}$. The following theorem is straightforward to prove.

Theorem 15. 

Each Bayesian network encoded as a cPROP functor $F:$${\mathbf{Syn}}_G\to$FinStochinduces a continuous and cellular map of CW complexes (i.e., compactly generated spaces with a weak Hausdorff topology [35]).

$$\mathcal{BF}:\mathcal{B}{\mathbf{Syn}}_G\to \mathcal{B}\mathbf{FinStoch}$$

Proof. 

Recall that B is a functor from the category Cat to the category Top of topological spaces defined as the classifying space of a category, constructed by forming the simplicial set using the nerve of the category (where each n-simplex represents composable morphisms in a category of length n), and using its topological realization as defined by Milnor [33].    □

We can define an equivalence structure on cPROP functors representing DAG models, generalizing the classical definitions in Pearl [12], and using Theorem 14 above.

Theorem 16. 

Two cPROP functors $F_1:$${\mathbf{Syn}}_{{\mathcal{G}}_1}\to$FinStochand $F_2:$${\mathbf{Syn}}_{{\mathcal{G}}_2}\to$FinStochareequivalent, denoted as $F_1\approx F_2$ where we use the same symbol ≈ used in [2] for DAG equivalence, if they are constructed from DAG models ${\mathcal{G}}_1$ and ${\mathcal{G}}_2$, respectively, that have the same skeletons and the same v-structures.

Proof. 

Two DAGs are known to be equivalent, meaning they are distributionally equivalent and independence equivalent, if their skeletons, namely the underlying undirected graph ignoring edge orientations, are isomorphic, and have the same v-structures, meaning an ordered triple of nodes $(X,Y,Z)$ where $\mathcal{G}$ contains the edges $X\to Y$ and $Z\to Y$ and X and Z are not adjacent in $\mathcal{G}$. Given that Theorem 14 gives us a 1-1 correspondence between DAG models and cPROP functors, the theorem follows straightforwardly.    □

We can characterize the interaction between two Bayesian networks represented as cPROP functors through Yoneda’s (co)end calculus, where for simplicity we use the same cPROP category ${\mathbf{Syn}}_{\mathcal{G}}$ to denote that these DAGs have the same skeleton and v-structures.

Theorem 17. 

Given two cPROP functors $F_1:$${\mathbf{Syn}}_G\to$FinStochand $F_2:$${\mathbf{Syn}}_G\to$FinStochrepresenting two DAG models, the set of natural transformations between them can be defined as an end

$${\mathbf{FinStoch}}^{{Syn}_G}(F_1,F_2)={\int }_c\mathbf{FinStoch}(F_1\left(c\right),F_2\left(c\right))$$

Proof. 

The proof of this result follows readily from the standard result that the set of natural transformations between two functors is an end (see page 223 in [23]).    □

We can this use this result to construct a homotopic structure on the topological space of all continuous and cellular maps of CW complexes defined in Theorem 15 above.

Theorem 18. 

The topological space of all continuous and cellular maps of CW complexes, where each map is defined as

$$\mathcal{BF}:\mathcal{B}{\mathbf{Syn}}_{\mathcal{G}}\to \mathcal{B}\mathbf{FinStoch}$$

is decomposed into equivalence classes by the equivalence relation ≈ defined in Theorem 16.

Proof. 

The equivalence relation ≈ on cPROP functors is reflexive, symmetric and transitive, because as Theorem 14 showed, there is a 1-1 correspondence between causal DAG models and cPROP functors. Each equivalence class of DAG models maps precisely into an equivalence class of cPROP functors.    □

Theorem 19. 

We can now bring to bear some properties of the classifying space developed by Segal [9] to construct a homotopy on cPROP categories and functors.

• For any two cPROP functors $F_1:$${\mathbf{Syn}}_{\mathcal{G}}\to$FinStochand $F_2:$${\mathbf{Syn}}_{\mathcal{G}}\to$FinStoch, a natural transformation $\tau :F_1\Rightarrow F_2$ induces a homotopy between $\mathcal{B}{F}_1$ and $\mathcal{B}{F}_2$.
• If $F:{\mathbf{Syn}}_{\mathcal{G}}\to {\mathbf{FinStoch}}_{\mathcal{G}}$ and $G:{\mathbf{FinStoch}}_{\mathcal{G}}\to {\mathbf{Syn}}_{\mathcal{G}}$ is an adjoint pair of functors, then $\mathcal{B}{\mathbf{FinStoch}}_G$ is homotopy equivalent to $\mathcal{B}{\mathbf{Syn}}_G$ (here, ${\mathbf{FinStoch}}_{\mathcal{G}}$ is a subcategory of $\mathbf{FinStoch}$ that is defined by the mapping of each object and morphism in ${\mathbf{Syn}}_{\mathcal{G}}$).

Proof. 

• We can think of the natural transformation $\tau$ as a functor $T_{\mathcal{G}}$ from ${\mathbf{Syn}}_{\mathcal{G}}\times \left[1\right]$ to ${\mathbf{FinStoch}}_{\mathcal{G}}$. We define the action of $T_{\mathcal{G}}$ on objects as $T_{\mathcal{G}}(C,0)=F_1\left(C\right)$ and $T_{\mathcal{G}}(C,1)=F_2\left(C\right)$. On morphisms $f\in {\mathbf{Syn}}_{\mathcal{G}}(C_1,C_2)$, we can set $T_{\mathcal{G}}(f,1_0)=F_1\left(f\right)$ and $T_{\mathcal{G}(}f,1_1)=F_2\left(f\right)$. For the only non-trivial morphism $0<1$ in $\left[1\right]$, we define $T_{\mathcal{G}}(1_C,0<1)={\tau }_C$. The composite structure

  $$\mathcal{B}{\mathbf{Syn}}_{\mathcal{G}}\times [0,1]\equiv \mathcal{B}({\mathbf{Syn}}_{\mathcal{G}}\times \left[1\right])\stackrel{\mathcal{B}\left(T_{\mathcal{G}}\right)}{\to }\mathcal{B}{\mathbf{Stoch}}_{\mathcal{G}}$$

  yields the desired homotopy.
• Given any adjoint pair of functors $F:{\mathbf{Syn}}_{\mathcal{G}}\to {\mathbf{FinStoch}}_{\mathcal{G}}$ and $G:{\mathbf{FinStoch}}_{\mathcal{G}}\to {\mathbf{Syn}}_{\mathcal{G}}$, we can define the induced natural transformations $\eta :Id\Rightarrow GF$ and $ϵ:FG\Rightarrow Id$. From the just established results on the natural transformation $\tau$, the desired homotopy follows.

   □

8.1. Generalizing the Meek-Chickering Theorem to cPROP Categories

We now turn to discussing a homotopic generalization of the Meek-Chickering theorem for DAG models [2,18] to functors between cPROP categories defined above.

Definition 39. 

Let $F_{\mathcal{G}}$ be a cPROP functor defined from $\mathcal{G}=(V,E)$, any DAG model. An edge $X\to Y\in E$ iscoveredif X and Y have identical parents, with the caveat that X is not a parent of itself. In other words, the parents of Y in $\mathcal{G}$ are the parents of X along with X itself. Then, each covered edge in $\mathcal{G}$ induces a corresponding covered morphism in ${\mathbf{Syn}}_{\mathcal{G}}$ that corresponds to $X\to Y$ in the corresponding cPROP category ${\mathbf{Syn}}_{\mathcal{G}}$.

Since cPROP functors are in 1-1 correspondence with DAG models from Theorem 14, we can associate with any covered edge in a DAG model $\mathcal{G}$, an equivalent covered morphism in the Markov category ${\mathbf{Syn}}_{\mathcal{G}}$ associated with the DAG model $\mathcal{G}$.

Theorem 20. 

Let $\mathcal{G}$ be any DAG model, with associated cPROP functor $F_{\mathcal{G}}$, and let $\mathcal{G}$’ be the result of reversing the edge $X\to Y$, and let $F_{{\mathcal{G}}^{\prime }}:{\mathbf{Syn}}_{{\mathcal{G}}^{\prime }}\to {\mathbf{Stoch}}_{{\mathcal{G}}^{\prime }}$ be the corresponding modified cPROP functor. Then there is an induced natural transformation corresponding to reversing an edge, and $F_{\mathcal{G}}\approx F_{{\mathcal{G}}^{\prime }}$ using the definition of cPROP functor equivalence in Theorem 16 if and only if the edge $X\to Y$ is a covered edge in $\mathcal{G}$.

Proof. 

The proof of this theorem follows readily from Lemma 2 in [2] showing that $\mathcal{G}$’ is a DAG model that is equivalent to $\mathcal{G}$ if and only if the edge that is reversed, namely $X\to Y$, is covered in $\mathcal{G}$.    □

Theorem 21. 

[2] Let $F_{\mathcal{G}}$ and $F_{{\mathcal{G}}^{\prime }}$ be a pair of equivalent cPROP functors corresponding to two equivalent DAG models $\mathcal{G}$ and ${\mathcal{G}}^{\prime }$, for which there δ edges in $\mathcal{G}$ that have the opposite orientation in ${\mathcal{G}}^{\prime }$. Then, there exists a sequence of δ corresponding natural transformations transforming the functor $F_{\mathcal{G}}$ into the functor $F_{{\mathcal{G}}^{\prime }}$, where natural transformation can be implemented by constructing the cPROP functor for each intervening DAG model that is based on reversing a single additional edge, satisfying the following properties:

• Each natural transformation in $F_{\mathcal{G}}$ must correspond to a covered edge in $\mathcal{G}$.
• After each natural transformation, the functors $F_{\mathcal{G}}\approx F_{{\mathcal{G}}^{\prime }}$.
• After all natural transformations are composed, the two functors $F_G\approx F_{G^{\prime }}$.

Proof. 

Once again, the proof follows readily from the equivalent Theorem 3 in [2] exploiting the isomorphism between causal DAG models and cPROP functors from Theorem 14.    □

To state the homotopic generalization of the Meek-Chickering theorem for functors between cPROP categories, we need to define the partial ordering on cPROP functors.

Definition 40. 

Define the partial ordering ${\mathbf{Syn}}_{\mathcal{G}}\le {\mathbf{Syn}}_{\mathcal{H}}$ to indicate that the corresponding causal DAG $\mathcal{H}$ is an independence map of $\mathcal{G}$. Here, ≤ implies that if $\mathcal{G}\le \mathcal{H}$, then by necessity $\mathcal{H}$ contains more edges than $\mathcal{G}$.

Once again, it follows from the 1-1 correspondence between Bayesian networks and cPROP functors that the corresponding cPROP category ${\mathbf{Syn}}_{\mathcal{H}}$ must contain more morphisms than ${\mathbf{Syn}}_{\mathcal{G}}$. We can now state the generalized Meek-Chickering theorem for functors between cPROP categories.

Theorem 22. 

Let${\mathbf{Syn}}_{\mathcal{G}}$ and${\mathbf{Syn}}_{\mathcal{H}}$ be cPROP categories corresponding to any pair of DAGs $\mathcal{G}$ and $\mathcal{H}$ such that $\mathcal{G}\le \mathcal{H}$. Let r be the number of edges in $\mathcal{H}$ that have the opposite orientation in $\mathcal{G}$, and let m be the number of edges in $\mathcal{H}$ that do not exist in either orientation in $\mathcal{G}$. These edges translate correspondingly to the differences in morphisms in${\mathbf{Syn}}_{\mathcal{G}}$ and${\mathbf{Syn}}_{\mathcal{H}}$. Then, there exists a sequence of at most $r+2m$ natural transformations that map the cPROP functor $F_{\mathcal{G}}$ into the cPROP functor $F_{\mathcal{H}}$ satisfying the following properties:

• Each edge reversal and corresponding natural transformation corresponds to a covered edge.
• After each natural transformation corresponding to an edge reversal and edge addition, ${\mathbf{Syn}}_{\mathcal{G}}\le {\mathbf{Syn}}_{\mathcal{H}}$.
• After all $r+2m$ natural transformations are composed, $Sy{n}_{\mathcal{G}}\approx Sy{n}_{\mathcal{H}}$ is a natural isomorphism.

Proof. 

The proof generalizes in a straightforward way from Theorem 4 in [2] since we are exploiting the 1-1 correspondences between causal DAG models and cPROP functors. The proof of this theorem in [2] is constructive since it involves an algorithm, and it would take more space than we have to sketch out the entire process of categorifying it. But, each step in the Algorithm APPLY-EDGE-ORIENTATION in [2] can be equivalently implemented for cPROP categories using the correspondences between causal DAGs and cPROP functors.    □

8.2. The Category of Fractions in a cPROP Category

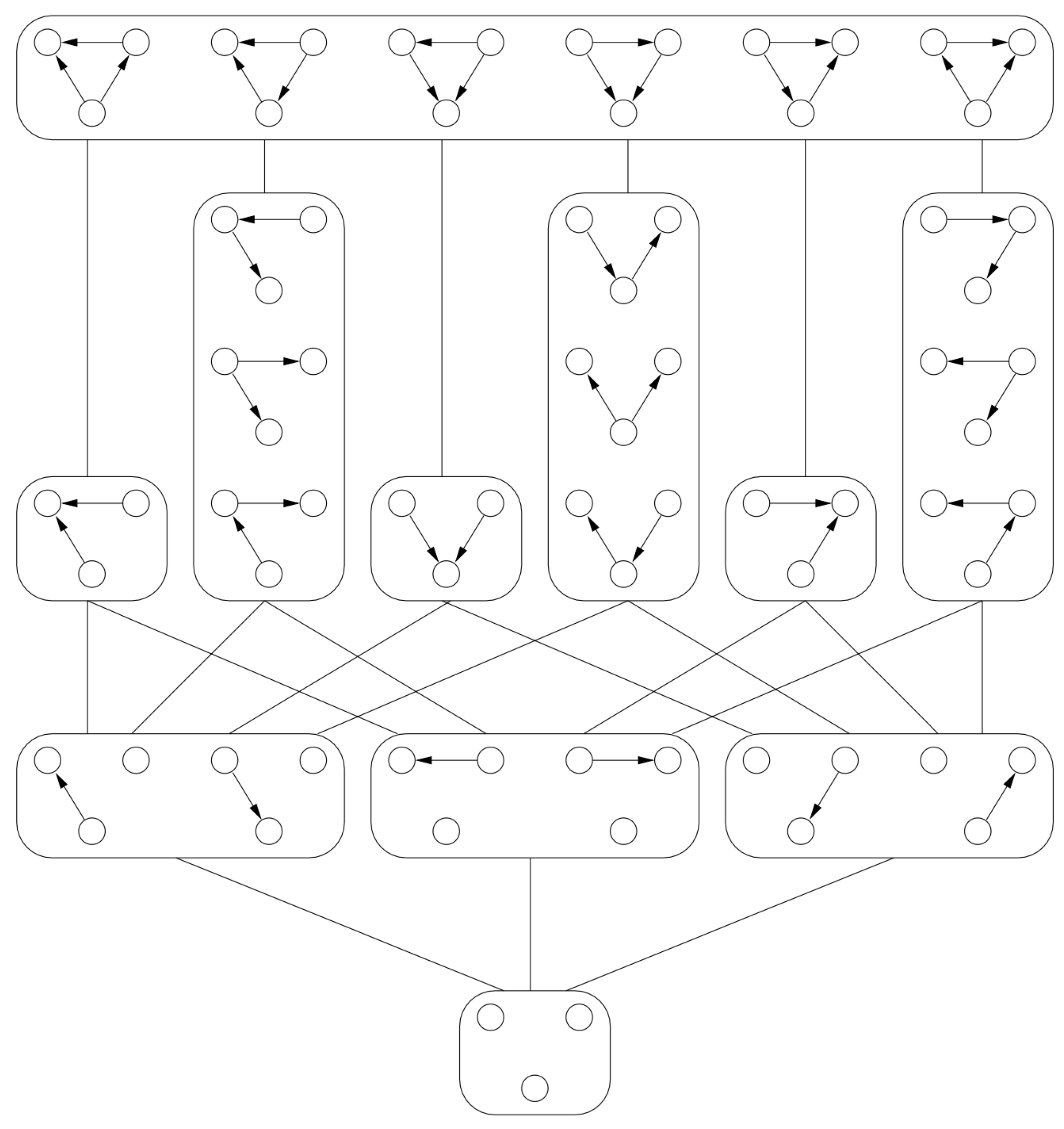
A principal challenge in causal discovery is that models can be inferred from data only up to an equivalence class. Figure 7 illustrates the equivalence classes of causal DAGs over 3 variables (this figure is reproduced from [19], and can be viewed as an expanded version of Figure 1).

We can view the morphisms between equivalent causal models as “invertible” arrows. The problem of defining a category with a given subclass of invertible morphisms, is called the category of fractions [45]. It is also useful in the context of causal inference, as for example, in defining the Markov equivalence class of directed acyclic graphs (DAGs) as a category that is localized by considering all invertible arrows as isomorphisms. Borceux [36] has a detailed discussion of the “calculus of fractions”, namely how to define a category where a subclass of morphisms are to be treated as isomorphisms. The formal definition is as follows:

Definition 41. 

Consider a cPROP category $\mathcal{C}$ and a class Σ of arrows of $\mathcal{C}$. Thecategory of fractions$\mathcal{C}\left({\Sigma }^{-1}\right)$ is said to exist when a category $\mathcal{C}\left({\Sigma }^{-1}\right)$ and a functor $\varphi :\mathcal{C}\to \mathcal{C}\left({\Sigma }^{-1}\right)$ can be found with the following properties:

• $\forall f,\varphi \left(f\right)$ is an isomorphism.
• If $\mathcal{D}$ is a cPROP category, and $F:\mathcal{C}\to \mathcal{D}$ is a functor such that for all morphisms $f\in \Sigma$, $F\left(f\right)$ is an isomorphism, then there exists a unique functor $G:\mathcal{C}\left({\Sigma }^{-1}\right)\to \mathcal{D}$ such that $G\circ \varphi =F$.

A detailed construction of the category of fractions is given in [36], which uses the underlying directed graph skeleton associated with the category. The characterization of the Markov equivalent class of acyclic directed graphs is an example of the abstract concept of category of fractions [20]. Briefly, this condition states that two acyclic directed graphs are Markov equivalent if and only if they have the same skeleton and the same immoralities.

To summarize the results of this section, we showed that we can construct a homotopic equivalence across causal models represented as functors on cPROP categories. We introduced categorical generalizations of the definitions in [2] and stated the categorical generalization of the Meek-Chickering theorem for Markov categories. We note that the results presented above are not the most general that can be shown, but for the purposes of this paper, we chose the simplest ones to present.

8.3. Homotopy Groups of Meek-Chickering Causal Equivalences

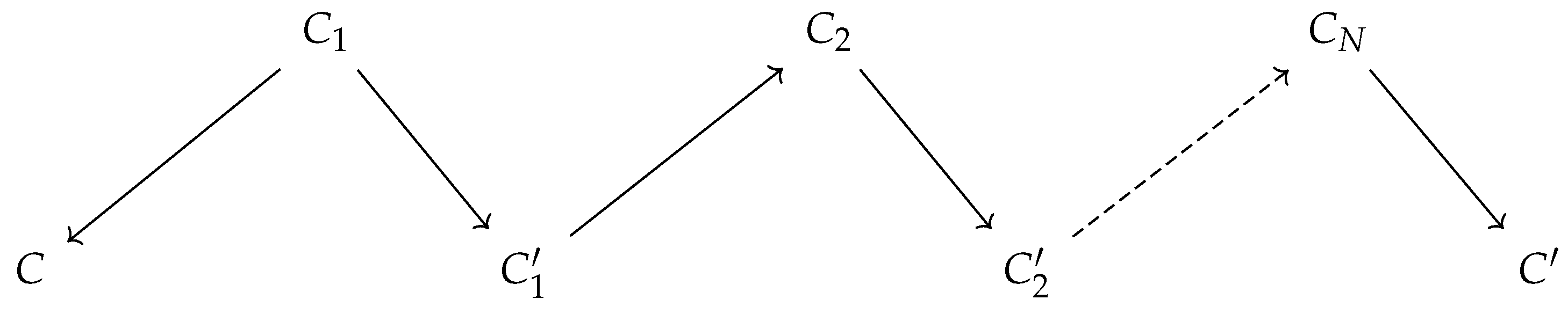
We can now define the equivalence classes under the Meek-Chickering formulation in a more abstract manner using abstract homotopy. First, we define the notion of an equivalence class of objects in any category $\mathcal{C}$ simply as that defined by the connectedness relation defined by the morphisms. Two objects C and $C^{\prime }$ are in the same equivalence class $\mathcal{E}$ in a category $\mathcal{C}$ if the following structure holds true:

Definition 42. 

Define the set ofpath componentsof a category $\mathcal{C}$ as the set of equivalence classes of the morphism relation on the objects by ${\pi }_0\mathcal{C}$.

Theorem 23. 

[32] The set of path components of the topological space $\mathcal{BC}$, namely ${\pi }_0\mathcal{BC}$ is in bijection with the set of path components of $\mathcal{C}$.

This relationship between the original category $\mathcal{C}$ and its topological realization $\mathcal{BC}$ now gives us a homotopic characterization of the GES algorithm described in Section 2. More formally, GES proceeds by moving from one equivalence class of causal models to the next by addition or removal of (non-covered) edges. These steps can be characterized in terms of natural transformations between equivalence classes of cPROP (or CDU [8]) functors that define the causal DAGs. As shown in Figure 7, we treat the equivalence class of DAGs within each connected component as a locally connected topological space. Thus, the set ${\pi }_0\mathcal{C}$ is exactly the number of equivalence classes in Figure 7, which is again the same as the number of connected components in ${\pi }_0\mathcal{BC}$, defining the 0^th homotopy group in the topological realization of the category $\mathcal{C}$.

Theorem 24. 

The GES procedure can be formally characterized topologically as moving from one equivalence class of connected topological spaces in $\mathcal{BC}$ to another, where an equivalence class of connected objects in $\mathcal{BC}$ is defined by the connectedness relation of natural transformations that correspond to reversals of covered edges within an equivalence class.

Proof: The proof of this theorem follows directly from Theorem 23, Theorem 2, and its homotopic version stated as Theorem 22. □

9. Classifying Spaces of cPROP Categories

We return to a more abstract discussion of the classifying spaces $\mathcal{BC}$ of a cPROP category $\mathcal{C}$. As a cPROP category $\mathcal{C}$ is a symmetric monoidal category, there is a wealth of known results that can be brought to bear on its homotopic structure, and a full discussion of this topic is beyond the scope of this introductory paper. We want to give the reader a taste of the many approaches that can be brought to bear on the structure of equivalence classes in causal models. First, we want to discuss the connection between the multiplicative structure of symmetric monoidal categories, like Markov categories, and the commutative H-space structure on $\mathcal{BC}$, its classifying space.

Definition 43. 

[32] An H-space is a topological space X with a chosen base point $x_0$ (which in cPROP categories can be associated with the topological realization of the terminal object), and a continuous map $\mu :X\times X\to X$ such that the maps $\mu (x_0,.)$ and $\mu (.,x_0)$ are homotopic to the identity map on X with respect to homotopies that preserve the basepoint $x_0$. An H-space is associative if μ is associative up to homotopy, and it is commutative if μ is commutative up to homotopy.

Definition 44. 

[32] An H-space X is group-like if there is a continuous map $\chi :X\to X$ such that $\mu \circ (1_{id}\times \chi )\circ \Delta$ is homotopic to the identity, where Δ is the the diagonal map on X.

It is worth mentioning that the comonoidal structure of a cPROP category $\mathcal{C}$ induces a diagonal map $\Delta :\mathcal{BC}\to \mathcal{BC}\times \mathcal{BC}$ on its topological realization through the nerve, through the (uniform) copy map ${copy}_X:X\to X\otimes X$.

Theorem 25. 

Let $\mathcal{C}$ be a cPROP category. Then its classifying space $\mathcal{BC}$ is an associative and commutative H-space.

Proof. 

The proof of this theorem is based on a simple diagram chase, building on the standard result for (small) symmetric monoidal categories.

The complete proof can be seen in [32] (Theorem 13.1.4). □

Theorem 26. 

The classifying space $\mathcal{BC}$ of a small cPROP category $\mathcal{C}$ is contractible.

Proof. 

This result follows from the fact that the tensor unit element I in a cPROP category is a terminal element, implying there is a unique morphism ${del}_X:X\to I$ as discussed previously. Using the result from Theorem 19, we exploit the fact that there is an adjoint pair of functors from $\mathcal{C}$ to $\left[0\right]$, and the topological realization $\mathcal{B}\left[0\right]$ is a point. □

We can define the higher homotopy groups of a cPROP category C as follows.

Definition 45. 

Given a cPROP category $\mathcal{C}$, and an arbitrary object X in $\mathcal{C}$. For $n\ge 0$, the $n^{th}$ homotopy group of $\mathcal{C}$ with respect to the basepoint X is defined as

$${\pi }_n(X,\mathcal{C})={\pi }_n(\mathcal{BC},\left[X\right])$$

where $\left[X\right]$ is the 0-simplex associated to the basepoint X.

10. Towards a Higher Algebraic K-Theory for Causal Inference

Finally, we build on the above results to give a formal higher algebraic K-Theory of causal inference in terms of the causal equivalence classes. To make the construction concrete, we begin with the notion of Grothendieck group completion defined by the Grayson-Quillen construction. Here, the intuition is to begin with an Abelian monoid and make it into a universal group by adding `inverse" elements to each monoid element. The result is a characterization of the K-Theory structure.

10.1. Grayson-Quillen Group Completion

The basic idea for a “K-Theory" arose from the notion of a Grothendieck “K" group that came out from his proof of the Riemann-Roch theorem, which involved the analysis of isomorphism classes of objects of an Abelian category with a tensor product (direct sum). This specific construction was later generalized in the following way. Consider a commutative monoid M for which the most general Abelian group K needs to be constructed by building “inverse" elements to all the elements of M. Such a “group completion" always exists, and is characterized by a universal property

$$i:M\to K,$$

where i is a monoid homomorphism mapping M to the group K that satisfies the universal property that for any other monoid homomorphism

$$f:M\to A,$$

there is a unique group homomorphism

$$g:K\to A$$

such that $f=g\circ i$. To show the relevance of this construction to causal inference, we briefly outline the Grayson-Quillen K-Theory for symmetric monoidal categories Grayson [46] that we can use to associate with any cPROP category $\mathcal{C}$ an augmented category ${\mathcal{C}}^{-1}\mathcal{C}$ using a particular group completion method.

Definition 46. 

Let $(\mathcal{C},\otimes ,e,\tau )$ be a small symmetric monoidal category. Denote by ${\mathcal{C}}^{-1}\mathcal{C}$ the category whose objects are pairs of objects of $\mathcal{C}$. Morphisms in ${\mathcal{C}}^{-1}\mathcal{C}$ from $(C_1,D_1)$ to $(C_2,D_2)$ are equivalence classes of pairs of morphisms

$$(f:C_1\otimes E\to C_2,g:D_1\otimes E\to D_2)$$

where E is an object of C. Such pairs of morphisms are equivalent to

$$(f^{\prime }:C_1^{\prime }\otimes E^{\prime }\to C_2,g^{\prime }:D_1\otimes E^{\prime }\to D_2)$$

if there is an isomorphism $h\in \mathcal{C}(E,E^{\prime })$ such that the following diagram commutes:

The category ${\mathcal{C}}^{-1}\mathcal{C}$ is called theGrayson-Quillenconstruction of C.

Note that this construction depends on the choice of object E. If E is selected to be the unit element I of a cPROP (or Markov category), then every pair of morphisms in $\mathcal{C}$ gives rise to a morphism in ${\mathcal{C}}^{-1}\mathcal{C}$.

Theorem 27.([32], Lemma 13.3.2) The category ${\mathcal{C}}^{-1}\mathcal{C}$ is symmetric monoidal as well, and there is a lax monoidal functor $j:\mathcal{C}\to {\mathcal{C}}^{-1}\mathcal{C}$, and ${\pi }_0\left({\mathcal{B}\mathcal{C}}^{-1}\mathcal{C}\right)$ is an Abelian group.

Definition 47. 

TheK-Theoryspace associated with a cPROP category $\mathcal{C}$ is the classifying space $\mathcal{KC}={\mathcal{B}\mathcal{C}}^{-1}\mathcal{C}$, where the $n^{th}$ K-group of $\mathcal{C}$ is its $n^{th}$ homotopy group ${\pi }_n{\mathcal{B}\mathcal{C}}^{-1}\mathcal{C}$. Specifically, the fundamental group ${\pi }_0\left({\mathcal{B}\mathcal{C}}^{-1}\mathcal{C}\right)$ is the Grothendieck group completion of the Abelian monoid induced by the path components ${\pi }_0\left(\mathcal{C}\right)$.

Let us now connect this procedure with the 0^th homotopy group of the Meek-Chickering equivalence class.

Theorem 28. 

Let the cPROP category $\mathcal{C}$ correspond to causal DAG models, that is each object is a functor representing a Bayesian network and the arrows are natural transformations representing the corresponding covered edge reversals within a class. These connected components represent Meek-Chickering equivalence classes. Then,

$$K_0\left(\mathcal{C}\right)={\pi }_0\left(\mathcal{KC}\right)=\simeq G_0\left({\pi }_0\left(\mathcal{C}\right)\right)$$

Proof. 

This theorem states that the 0^th order homotopy group corresponding to the Meek-Chickering equivalence classes is isomorphic to the Grothendieck group completion of the Abelian monoid ${\pi }_0\left(\mathcal{C}\right)$. The proof follows readily from the more general result that holds in any symmetric monoidal category (see Lema 13.3.4 in [32]). □

10.2. cPROP Groupoids and their Classifying Spaces

A groupoid is a category whose every morphism is invertible. We can characterize the Meek-Chickering causal equivalences in terms of the classifying spaces of their induced groupoids.

Definition 48. 

Define theMoore-Chickeringgroupoid as the cPROP category ${\mathcal{G}}_{MC}$ whose objects are defined as the equivalence classes defined by the Moore-Chickering theorem, and whose invertible morphisms correspond to covered edge reversals that map from an object back to itself.

We can now give a simple characterization of the Moore-Chickering equivalence classes in terms of the classifying space of their induced groupoids.

Theorem 29. 

The classifying space of the Moore-Chickering groupoid category ${\mathcal{B}\mathcal{G}}_{MC}$ is defined as

$${\mathcal{B}\mathcal{G}}_{MC}=\underset{i}{⨆}{\mathcal{B}\mathcal{G}}_{MC}^i$$

where disjoint sum index i ranges over equivalence classes.

To put this result in more concrete terms, the classifying space of the Moore-Chickering groupoid ${\mathcal{G}}_{MC}$ for the example shown in Figure 7 decomposes into a topological disjoint union of 11 smaller classifying spaces.

11. Summary and Future Work

In this paper, we analyzed the homotopic structure of observationally equivalent causal models using a categorical structure called cPROPs, a functor category from a coalgebraic PROP P to a symmetric monoidal category $\mathcal{C}$. Such functor categories define the right adjoint of the inclusion of Cartesian categories in the larger category of all symmetric monoidal categories. cPROPs are an algebraic theory in the sense of Lawvere [5]. cPROPs relate closely to previous categorical models, such as Markov categories [6] and affine CDU categories [7,8], which can be viewed as a special type of cPROP defined by the PROP maps $\delta :1\to 2$ and $ϵ:1\to 0$ that satisfy a set of commutative diagrams. To obtain topological insight into observationally equivalent classes of causal models, we characterized the classifying spaces of cPROPs by constructing their simplicial realization through the nerve functor. As a concrete application to causal inference, we showed that causal DAG equivalence generalizes to induce a homotopic equivalence across observationally equivalent cPROP functors. We presented a homotopic generalization of the Meek-Chickering theorem on causal equivalence in DAG models, where we view covered edge reversals connecting causally equivalent DAGs in terms of natural transformations between homotopically equivalent cPROPs.

These results are a small sampling of the wide range of tools available in abstract homotopy theory, which we briefly describe next.

11.1. Operads and Iterated Loop Spaces

There is a rich set of theoretical results that connect the K-Theory classifying spaces of symmetric monoidal categories, and cPROP and Markov categories, with the geometry of iterated loop spaces and operads [47]. In particular, it is known that all connective spectra are based on some symmetric monoidal category, and that special types of monoidal categories called permutative categories yield Barrat-Eccles operads as their classifying spaces, a type of $E_{\infty }$ operad. A full discussion of these connections is a topic for future papers.

11.2. Model Categories on cPROP Categories

A standard approach to performing abstract homotopy on a category is to define its associated model structure. One way to do that implicit in our work is through its simplicial object structure. The category of simplicial sets is well known to have a rich model structure, which has been extensively studied [48]. This construction requires partitioning the space of morphisms into fibrations, cofibrations and weak equivalences to construct a model category structure for causal inference [49]. We plan to devote a separate paper on this topic.

11.3. Causal Discovery through Homotopy

Causal discovery remains a major challenge as the number of structures to be searched is super-exponential in the number of variables. There has been an incredible variety of causal discovery methods developed in the literature over the past several decades, and Zanga and Stella [3] contains a detailed overview of many methods. While ideas like the Meek-Chickering theorem are useful in optimal structure identification using greedy search [2], the number of possible structures remains intractable. Castelo and Kocka [19] remark that experimental work has shown that the size of equivalence classes using the Meek-Chickering equivalences remains relatively small ($\approx 3$ in an experimental study), suggesting that the reduction is insufficient to tame the curse of dimensionality.

In our past work on the homotopy of causal models represented as finite topological spaces [50], we built on the ideas in algebraic topology of finite spaces [51]. In particular, the main idea is to construct a homotopy core of a finite space (which is essentially a partially ordered set) by removing “beat" points in the Hasse diagram. These are closely related to the notion of covering edge in [2]. What our analysis showed is that there is a significant reduction in the enumeration of simplicial complexes represented as causal DAG models by removing beat points, which achieves a greater reduction in asymptotic size than the Meek-Chickering approach. We plan to combine both approaches in further work.

11.4. Asymptotic Causality

In a previous paper on asymptotic causality [52], we highlighted the work on extremal combinatorics that showed that almost all partial orders are of size 3, meaning that as the number $n\to \infty$, causal DAG models will form a very canonical structure with the variables all grouped in three layers. This convergence to an asymptotic structure implies that algorithms like greedy equivalent search [2] may scale better in higher dimensions, but require adapting their search method towards such canonical structures, rather than only based on the scores computed from data.

11.5. cPROPs for non-graphical causal models

We have restricted our attention in this paper to defining cPROPs for causal directed acyclic graph (DAG) models, as these are the most popular representation studied in previous work on categorical causality [8,17,27,29]. But, the general framework of cPROPs can be easily extended to non-graphical representations, such as integer-valued multisets (or imsets) [16]. For the specific case of a DAG model $\mathcal{G}=(V,E)$, an imset in standard form [16] is defined as

$$u_{\mathcal{G}}={\delta }_V-{\delta }_{\varnothing }+\sum _{i\in V}({\delta }_{{\mathbf{Pa}}_i}-{\delta }_{i\cup {\mathbf{Pa}}_i})$$

where each ${\delta }_V$ term is the characteristic function associated with a set of variables V. Finally, a separoid [53] is an algebraic framework for characterizing conditional independence as an abstract property, defined by a join semi-lattice equipped with a partial ordering ≤, and a ternary property $\perp -10mu\perp$ over triples of elements such that $X\perp -10mu\perp Y|Z$ defines the property that X is conditionally independent of Y given Z. One can define cPROPs for separoids as well.