Physics-Informed Neural Networks for Modal Wave Field Predictions in 3D Room Acoustics

1. Introduction

Today, there are persisting challenges in (room) acoustics simulations, with errors mainly arising from uncertain input parameters of used building material, resulting in high uncertainty of the used boundary conditions [1,2]. In particular, at low-frequent waves, the material parameters are off [3,4], hindering more accurate simulation results. These uncertain simulation input data underscore the importance of using algorithms that allow for the on-the-fly minimization of the model discrepancy with reality. As a selected algorithm, physics-informed neural networks (PINNs) can be used in forward mode (to predict the wave field) and inverse mode to infer material or boundary condition parameters with the use of data [3]. However, the computation of the time-harmonic acoustic wave field in large 3D geometries represents a challenge for current wave-based numerical and machine-learned methods [4,5]. The solutions to the Helmholtz equation in 3D are essential for understanding low-frequent room acoustic scenarios. The Finite Element Methods (FEM) analysis provides accurate results [4], but the extension to inverse parameters estimation is tedious compared to PINNs. PINNs show promising capabilities for that purpose, such that the interest in tailoring these algorithms to the accuracy of FEM became an interesting topic. So far, PINNs were used to solve the Helmholtz equation [6,7,8] only in 1D and 2D for acoustic simulations [3,9,10,11,12,13,14,15], ultra-sound application [16], electromagnetic waveguides [17,18] and aeroacoustics [19].

In extending the feasibility study [5], this paper performs a structured hyperparameter study of PINNs to solve the Helmholtz equation in 3D for a simple room acoustic simulation. We investigated the network size (concerning the results of [20]), the activation functions, and various backends, including PyTorch [21], TensorFlow 1 and 2 [22]. Compared to previous studies performed with well-behaving smooth excitation [9,20], we will analyze a realistic excitation scenario caused by a loudspeaker-like confined source. A first structured hyper-parameter study was conducted in [20], with hardly conclusive results on the network shape for the 3D setup as the outcome of hyper-parameter optimization using Gaussian processes-based Bayesian optimization. Furthermore, the loss metric, a point-wise l2 error measure, is suitable for training. However, it is questionable that a random distribution of evaluation points is computing a reliable error measure for the final neural network testing. In general, the Helmholtz equation is a linear partial differential equation, resulting in oscillatory fields, being a prototype for more complex solutions in fluid mechanics [23]. It was already observed and expected that the training deteriorates with increasing wave number due to the frequency-principle [24,25]. In addition to the standard neural network architectures, the locally adaptive activation functions with slope recovery [26] and the multi-scale Fourier feature network [27] are investigated for potentially improved neural network performance. The accuracy is evaluated by comparing the results on a structured evaluation grid with the FEM results and computing an L2 error norm during the hyperparameter study in 3D.

The article starts with Sec. 3 introducing the numerical examples of 3D room-like geometry with sound-hard boundary conditions, differential equation forcing including adaptive narrowing of the source by a sharpness parameter s, and material parameters. Section 4 presents the theoretical background of PINNs, experimental hyperparameter analysis, the multi-scale Fourier feature network [27], and the locally adaptive activation functions with slope recovery [26] in the context of acoustics. It is followed by the results section that presents the details of the investigations, the comparison to the FEM solution by error analysis, and the conclusions.

2. Room acoustic application

In the first step, we present the application example since it is essential to set up details on the PINN later. Previous studies have shown that the expected solution for the application example may significantly influence the network shape and capabilities used.

2.1. Case study setup

On a simple room-like 3D domain $\Omega ={[0,1]}^3$, the inhomogeneous Helmholtz equation

$$\begin{array}{cc}\hfill (\Delta +k^2)p(\omega ,\mathit{x})& =g(\omega ,\mathit{x})\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill \nabla p\left(\mathit{x}\right)·\mathit{n}& =0,\mathit{x}\in {\Gamma }_N\hfill \end{array}$$

(1b)

with homogeneous Neumann boundary conditions on $\partial \Omega ={\Gamma }_N$ is solved. In this equation, $p\in {\mathbb{C}}^3$ is the time-harmonic acoustic pressure, $k=\omega /c=2\pi /\lambda$ is the wavenumber, $\omega$ the angular frequency, c the speed of sound, g the forcing term, and $\Delta$ is the Laplacian operator. A homogeneous Neumann boundary conditions model the room walls. The forcing consists of

$$g(x,y,z)=2k^{2}cos\left(kx\right)cos\left(ky\right)cos\left(kz\right){\mathrm{e}}^{-{\displaystyle \frac{{(x-0.5)}^2+{(y-0.5)}^2+{(z-0.5)}^2}{2s^2}}},$$

(2)

with a source sharpness parameter s. As a follow-up to the previous 3D room acoustic examples [5], the source is modeled more realistically by a point source in the center of the room modeled for sufficiently small s. Throughout the study and in the hyperparameter study [20], the following physical parameter set

$${\theta }_{\mathrm{phy}}=\{\lambda ,s\}$$

(3)

is varied.

2.2. Analytic solution and spatial frequency content

For $s\to \infty$, the forcing can be simplified to

$$g(x,y,z)=2k^{2}cos\left(kx\right)cos\left(ky\right)cos\left(kz\right).$$

(4)

This leads to an analytic solution of

$$p(x,y,z)=cos\left(kx\right)cos\left(ky\right)cos\left(kz\right)$$

(5)

that satisfies the forcing and the homogeneous Neumann boundary condition $\nabla p(x,y,z)·\mathit{n}=0$. In the current case, the solution is only real-valued $p\in \mathbb{R}$; however, in the general case, the solution is complex $p\in \mathbb{C}$ and may be treated by two independent networks, providing the independent solutions parts $\Re \left(p\right)$ and $\Im \left(p\right)$. The spatial frequency $f_{\mathrm{x}}=1/{\lambda }_{\mathrm{x}}$ of the solution is directly connected to the excited source by the linearity of the equation and is provided by the value of ${\lambda }_{\mathrm{x}}=\lambda$. For cases with $s>\lambda$, the solution wavenumber is primarily determined by $\lambda$. However, in the case of $s<\lambda$, the wave number content of the Gaussian envelope becomes important, which is determined by the Fourier transform of it

$$\mathcal{F}\left[{\mathrm{e}}^{-{(x/s)}^2}\right]\left(f_{\mathrm{x}}\right)=\sqrt{2\pi }s{\mathrm{e}}^{-2{\left(\pi s{f}_{\mathrm{x}}\right)}^2}.$$

(6)

The frequency content governed by the Gaussian $f_{\mathrm{x}}$ is sufficiently low for values of $f_{\mathrm{x}}$ being smaller than two standard deviations. In our case, this condition reads $f_{\mathrm{x}}<1/\left(\pi s\right)$ or more specifically $\lambda >\pi s$.

2.3. FEM reference simulation

A reference solution is computed using the FEM on the same setup with openCFS [28]. A fine mesh is used with approximately 40 degrees of freedom per wavelength $\lambda$ satisfying the conditions of [29], resulting in 512000 elements of the computational domain. The mesh will deliver accurate results for $\lambda >0.25$ and $s\approx 0.25/\pi$. For quadratic FEM basis functions, the mesh will provide accurate results for $\lambda >0.06125$ and $s\approx 0.06125/\pi$ [30].

3. Physics-informed neural networks for wave-based room acoustics

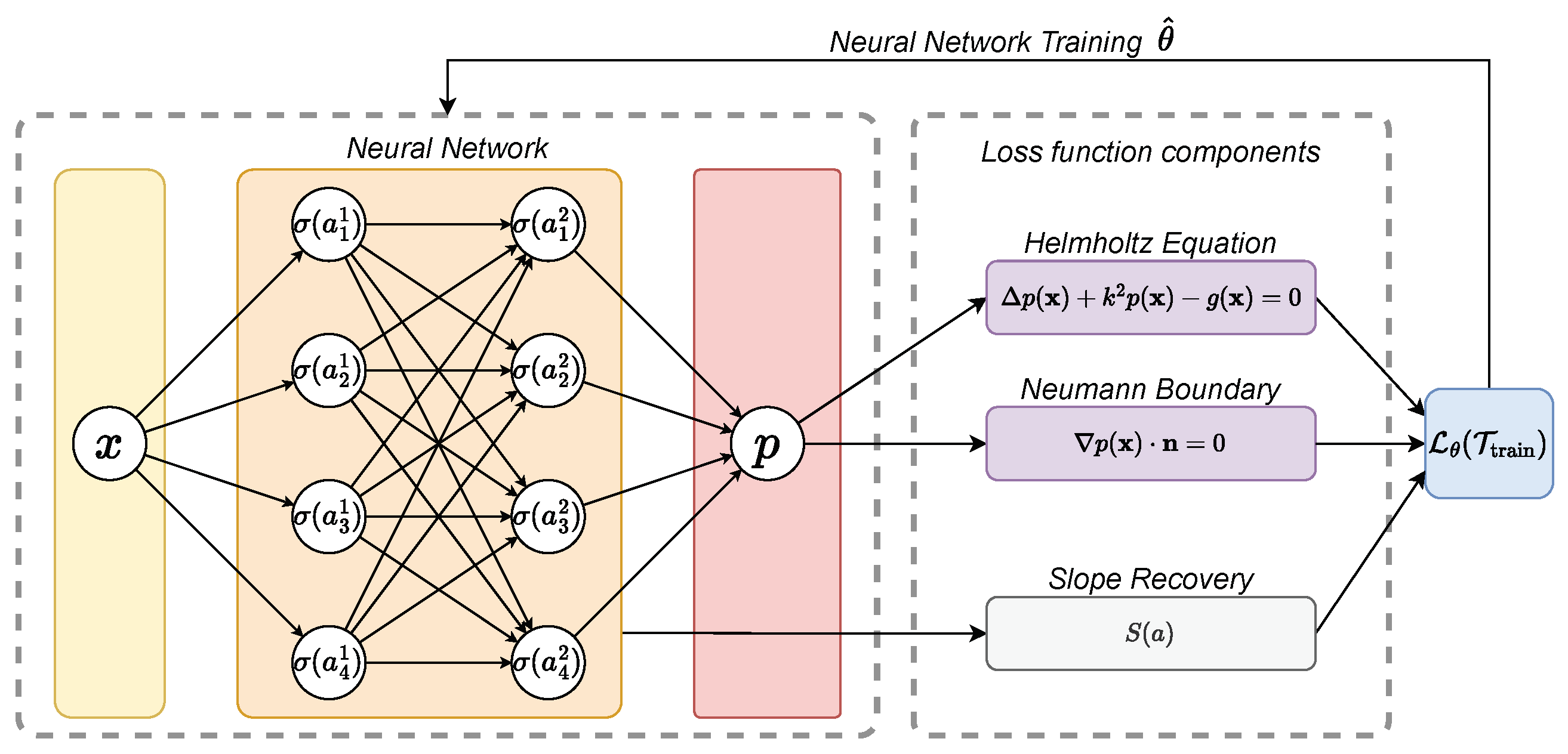
PINNs are fusing neural networks and complex partial differential equations (PDEs) for simulating physical systems using automated differentiation [31]. Figure 1 shows a multi-layer perceptron [32,33] network that can solve the Helmholtz Equation (1b) with appropriate boundary conditions.

Let ${\mathcal{N}}^L\left(\mathit{x}\right):{\mathbb{R}}^{d_{\mathrm{in}}}\to {\mathbb{R}}^{d_{\mathrm{out}}}$ be a L-layer-feed-forward neural network (FNN) (with $(L-1)$-hidden neural network layers) to predict $\widehat{p}(\omega ,\mathit{x})$, with $N_{\ell }$ neurons in the ℓ-th layer $\left(N_0=d_{\mathrm{in}},N_L=d_{\mathrm{out}}\right)$. The output at a layer of a feed-forward neural network is calculated by repeated nonlinear activation-function $\sigma$ weighted tensor products of (i) inputs and (ii) bias vector and weight matrix (e.g. in the ℓ-th layer by ${\mathit{W}}^{\ell }\in {\mathbb{R}}^{N_{\ell }\times N_{\ell -1}}$ and ${\mathit{b}}^{\ell }\in {\mathbb{R}}^{N_{\ell }}$, respectively), such that the FNN is recursively defined by

$$\begin{array}{cc}\hfill \mathrm{input}\mathrm{layer}\text{:}& {\mathcal{N}}^0\left(\mathit{x}\right)=\mathit{x}\in {\mathbb{R}}^{d_{\mathrm{in}}}\hfill \\ \hfill \mathrm{hidden}\mathrm{layers}\text{:}& \sigma \left({\mathcal{N}}^{\ell }\left(\mathit{x}\right)\right)=\sigma \left({\mathit{W}}^{\ell }{\mathcal{N}}^{\ell -1}\left(\mathit{x}\right)+{\mathit{b}}^{\ell }\right)\in {\mathbb{R}}^{N_{\ell }},\mathrm{for}1\le \ell \le L-1,\hfill \\ \hfill \mathrm{output}\mathrm{layer}\text{:}& {\mathcal{N}}^L\left(\mathit{x}\right)={\mathit{W}}^L{\mathcal{N}}^{L-1}\left(\mathit{x}\right)+{\mathit{b}}^L\in {\mathbb{R}}^{d_{\mathrm{out}}};\hfill \end{array}$$

(7)

In the 3D case, the coordinates of one point $\mathit{x}=(x,y,z)$ are provided at the input layer. Defined by the neural network, the output prediction at the output layer L is calculated by

$$\begin{array}{cc}\hfill \widehat{p}=& {\mathit{W}}^L\sigma \left({\mathcal{N}}^{L-1}\left(\mathbf{x}\right)\right)+{\mathit{b}}^L={\mathit{W}}^L\sigma \left({\mathit{W}}^{L-1}\sigma \left({\mathcal{N}}^{L-2}\left(\mathbf{x}\right)\right)+{\mathit{b}}^{L-1}\right)+{\mathit{b}}^L=\cdots \hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill =& {\mathcal{N}}^L\circ \sigma \circ {\mathcal{N}}^{L-1}\circ \sigma \circ \cdots \circ \sigma \circ {\mathcal{N}}^1\circ \mathit{x}=\mathcal{N}(\mathsf{\theta },\mathit{x}),\hfill \end{array}$$

(9)

being a series of transformation functions. The network transformative operations can be summarized by a nonlinear operation $\mathcal{N}(\mathsf{\theta },\mathit{x})$ depending on the trainable parameters, $\mathsf{\theta }$ collecting all weights and biases $\mathsf{\theta }={\{{\mathit{W}}^l,{\mathit{b}}^l\}}_{1\le l\le L}$, and the network input $\mathit{x}$.

During training, $\mathsf{\theta }$ will be learned by unlabeled training data ${\mathcal{T}}_{\mathrm{train}}={\left\{{\mathit{x}}_i\right\}}_{i=1}^{|{\mathcal{T}}_{\mathrm{train}}|}$, to approximate a continuous function mapping $h\left(\mathit{x}\right)=p$. The neural network operator $\widehat{p}=\mathcal{N}(\mathsf{\theta },\mathit{x})$ approximates $h\left(\mathit{x}\right)=p$, regarding the minimal error described by the loss function $\mathcal{L}(\mathsf{\theta },{\mathcal{T}}_{\mathrm{train}})$. The loss will be minimized by

$$\widehat{\mathsf{\theta }}=\underset{\mathsf{\theta }\in {\mathbb{R}}^{\mid \mathsf{\theta }\mid }}{argmin}\left(\mathcal{L}(\mathsf{\theta },{\mathcal{T}}_{\mathrm{train}})\right),$$

(10)

such that the weights and biases $\mathsf{\theta }$ are adjusted to the converged ones $\widehat{\mathsf{\theta }}$. Within the study, we used the gradient-based optimization algorithm Adam [34] and the quasi-Newton method LBFGS [35]. The weights and biases are adapted iteratively by the gradient of ${\nabla }_{\mathsf{\theta }}\mathcal{L}$ to decrease $\mathcal{L}$, using backpropagation [36] and automatic differentiation [37]. A gradient descent algorithm updates the parameters such that

$${\mathsf{\theta }}_{i+1}={\mathsf{\theta }}_i-{\alpha }_i{\nabla }_{{\mathsf{\theta }}_i}\mathcal{L},$$

(11)

with $\alpha$ representing the learning rate and i the epoch number.

The residual of the Helmholtz equation $r_{\mathrm{PDE}}$

$$\begin{array}{cc}\hfill r_{\mathrm{PDE}}\left(\mathit{x}\right)& =\Delta \widehat{p}\left(\mathit{x}\right)+k^2\widehat{p}\left(\mathit{x}\right)-f\left(\mathit{x}\right)\forall \mathit{x}\in D_{\mathrm{PDE}}\hfill \\ \hfill {\mathcal{L}}_{\mathrm{PDE}}(\mathsf{\theta },{\mathcal{T}}_f)& ={\displaystyle \frac{1}{|{\mathcal{T}}_{\mathrm{train},\Omega }|}}\sum _{i=1}^{|{\mathcal{T}}_{\mathrm{train},\Omega }|}{\Vert r_{\mathrm{PDE}}\left(\mathit{x}\right)\Vert }^2\hfill \end{array}$$

(12)

with $\parallel ·\parallel$ being the $l_2$-norm integrated into the loss function to incorporate the inherent physical knowledge into the neural network training. It is evaluated at randomly sampled collocation points $\mathit{x}$ within the computational domain $\Omega$, forming the dataset ${\mathcal{T}}_{\mathrm{train}}$ comprises two sets, the points in the domain $\Omega$, ${\mathcal{T}}_{\mathrm{train},\Omega }$ of $|{\mathcal{T}}_{\mathrm{train},\Omega }|$ samples for the PDE residual and the points on the boundary $\Gamma$, ${\mathcal{T}}_{\mathrm{train},\Gamma }$ of $|{\mathcal{T}}_{\mathrm{train},\Gamma }|$ samples for the boundary condition residual. The Neumann boundary condition residual $r_{\mathrm{NBC}}$ is

$$\begin{array}{cc}\hfill r_{\mathrm{NBC}}& =\nabla p\left(\mathit{x}\right)·\mathit{n}\forall \mathit{x}\in D_{\mathrm{NBC}}\hfill \\ \hfill {\mathcal{L}}_{\mathrm{NBC}}(\mathsf{\theta },{\mathcal{T}}_{b2})& ={\displaystyle \frac{1}{|{\mathcal{T}}_{\mathrm{train},\Gamma }|}}\sum _{i=1}^{|{\mathcal{T}}_{\mathrm{train},\Gamma }|}{\Vert r_{\mathrm{NBC}}\left(\mathit{x}\right)\Vert }^2,\hfill \end{array}$$

(13)

which is sampled on the Neumann boundary ${\Gamma }_N$ forming the set ${\mathcal{T}}_{\mathrm{train},\Gamma }={\left\{{\mathit{x}}_i\right\}}_{i=1}^{|{\mathcal{T}}_{\mathrm{train},\Gamma }|}$. The total loss function can be described by

$$\mathcal{L}=w_{\mathrm{PDE}}{\mathcal{L}}_{\mathrm{PDE}}+w_{\mathrm{NBC}}{\mathcal{L}}_{\mathrm{NBC}},$$

(14)

where $w_{\mathrm{PDE}}$ and $w_{\mathrm{NBC}}$ are weighting factors for the individual loss terms.

3.1. Initial Setup

The wavelength is selected to be $\lambda =1/2$. The PINN is set up using DeepXDE. Ten random collocation points per wavelength along each direction for training and 30 for validating are defined. A fully connected neural network uses a layer number $L-1=3$ layers and a layer width of $W=180$ neurons. A sinus activation function is used with Glorot uniform bias and weights initialization [38]. The loss term is defined in Equation (14), with $w_{\mathrm{NBC}}=5$, and $w_{\mathrm{PDE}}=1$. 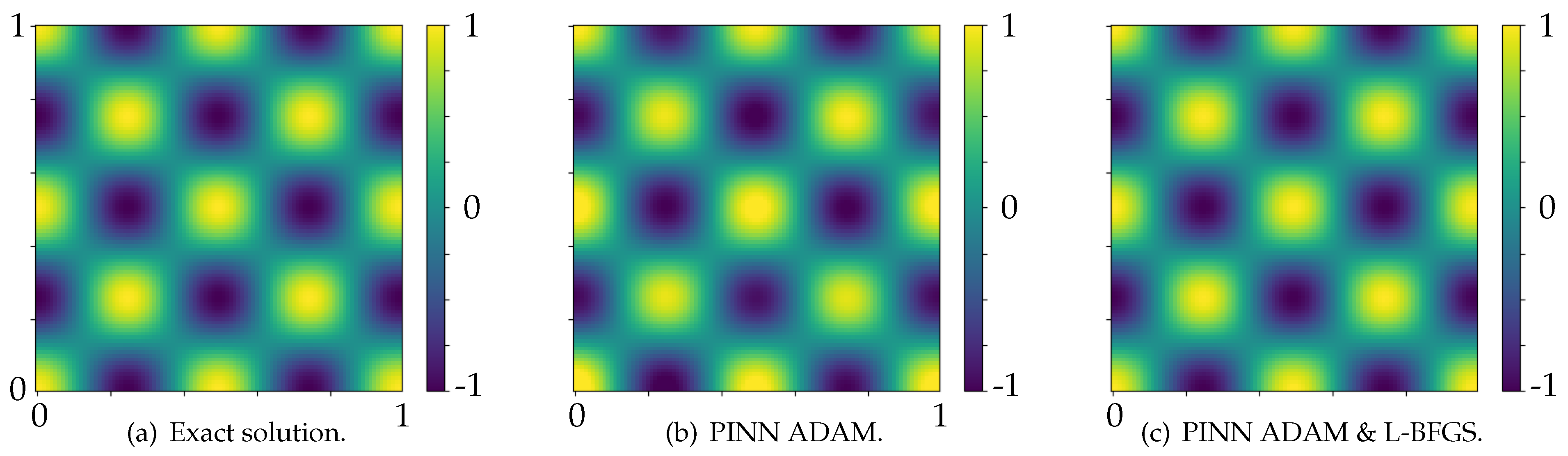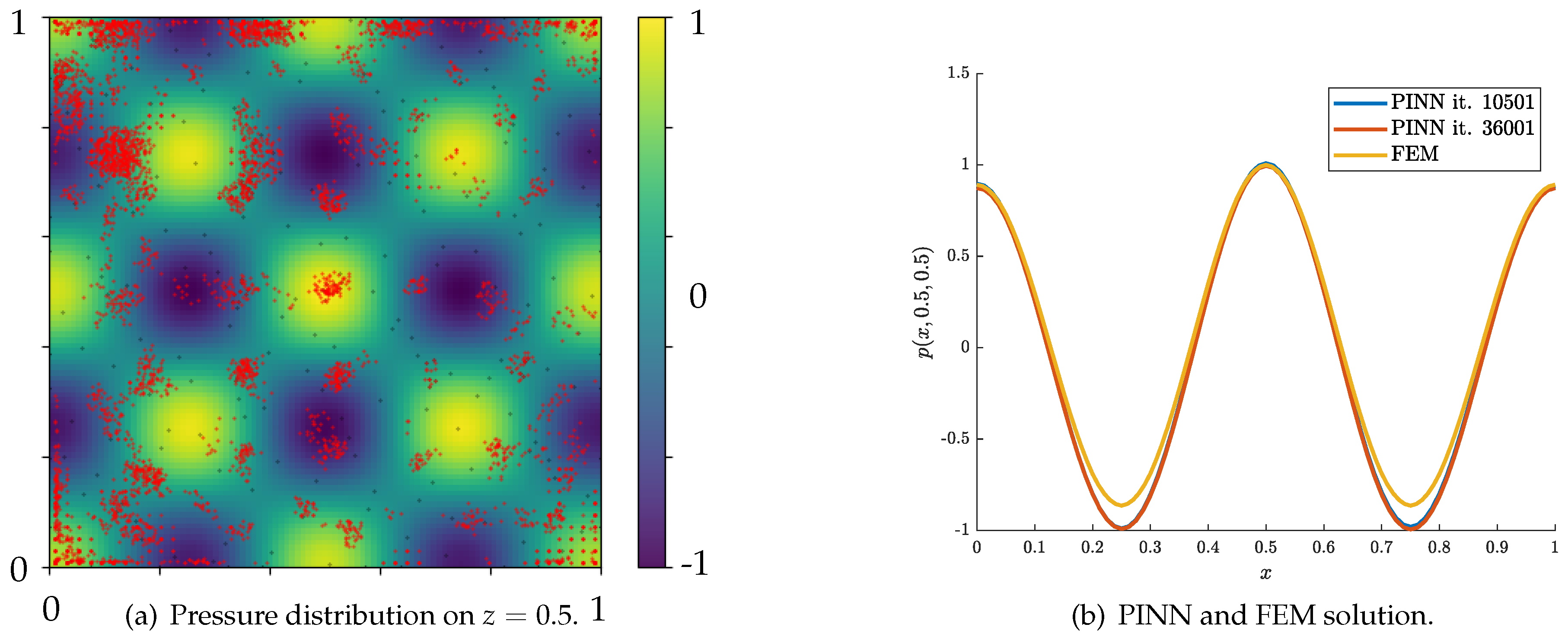Figure 2a shows the exact solution of the acoustic pressure ($s\to \infty )$ in a cut through the whole domain at $z=0.5$. The network is trained over 30000 iterations by the ADAM optimizer with a learning rate of $\eta =0.001$, resulting in a validation loss of 0.1248 (see Figure 2b). After 200 000 iterations by the ADAM optimizer, resulting in a validation loss of 0.0952, the relative error $e_{\mathrm{rel}}$ was 0.36% compared to the analytic solution. When changing the optimizer L-BFGS optimizer for 2000 iterations brings down the test loss to 0.0609 (see Figure 2c) and $e_{\mathrm{rel}}$ to 0.35%.

An explorative hyperparameter study was performed using the following parameter space ${\theta }_{\mathrm{NN}}$

$${\theta }_{\mathrm{NN}}=\{L-1,W,w_{\mathrm{NBC}},\sigma ,\mathcal{B}\},$$

(15)

with $L-1=\{1,2,3,4,5\}$, $W=\{20,40,60,120,180,300\}$, $w_{\mathrm{NBC}}=\{500,50,5,1,1/5,1/50\}$, $\sigma =\{$sin, ELU, GELU, ReLU, SELU, sigmoid, SiLU, swish, tanh}, $\mathcal{B}=\{$ PyTorch(P), TensorFlow 1 (T1), TensorFlow 2 (T2)}.

3.2. Locally adaptive activation functions

The locally adaptive activation function (LAAF) with slope recovery [26] is a method designed to improve the training speed and performance of deep and physics-informed neural networks. It introduces a scalable parameter, so-called activation slope $n{a}_i^{\ell }$ (for layer ℓ and neuron i), to the activation function optimized during training. The locally adaptive activation function neural network (at the neuron level) is defined as

$$\begin{array}{cc}\hfill \mathrm{input}\mathrm{layer}\text{:}& {\mathcal{N}}^0\left(\mathbf{x}\right)=\mathbf{x}\in {\mathbb{R}}^{d_{\mathrm{in}}}\hfill \\ \hfill \mathrm{hidden}\mathrm{layers}\text{:}& \sigma \left(n{a}^{\ell }{\mathcal{N}}^{\ell }\left(\mathbf{x}\right)\right)=\sigma \left(n{a}^{\ell }({\mathit{W}}^{\ell }{\mathcal{N}}^{\ell -1}\left(\mathbf{x}\right)+{\mathit{b}}^{\ell })\right)\in {\mathbb{R}}^{N_{\ell }},\mathrm{for}1\le \ell \le L-1,\hfill \\ \hfill \mathrm{output}\mathrm{layer}\text{:}& {\mathcal{N}}^L\left(\mathbf{x}\right)={\mathit{W}}^L{\mathcal{N}}^{L-1}\left(\mathbf{x}\right)+{\mathit{b}}^L\in {\mathbb{R}}^{d_{\mathrm{out}}};\hfill \end{array}$$

(16)

The output prediction at the output layer L is calculated by

$$\widehat{p}={\mathcal{N}}^L\circ \sigma \circ n{a}^{L-1}{\mathcal{N}}^{L-1}\circ \sigma \circ \cdots \circ \sigma \circ n{a}^1{\mathcal{N}}^1\circ \mathit{x},$$

(17)

being a series of transformation functions. The slope recovery term $S\left(a\right)$

$${\displaystyle \frac{1}{S\left(a\right)}}={\displaystyle \frac{1}{L-1}}\sum _{\ell =1}^{L-1}exp\left({\displaystyle \frac{{\sum }_{i=1}^{N_{\ell }}{a}_i^{\ell }}{N_{\ell }}}\right)$$

(18)

encourages the network to increase the activation slope, leading to faster training. The loss function is extended to include the slope recovery term by

$$\mathcal{L}=w_{\mathrm{PDE}}{\mathcal{L}}_{\mathrm{PDE}}+w_{\mathrm{NBC}}{\mathcal{L}}_{\mathrm{NBC}}+w_{\mathrm{a}}S\left(a\right).$$

(19)

The analysis in [26] shows that LAAFs effectively multiply the gradients by conditioning matrices, accelerating convergence without explicitly calculating these matrices. Experiments demonstrated that LAAF works for deep neural networks in application for standardized datasets MNIST [39], Fashion-MNIST [40] and KMNIST [41], Semeion [42], SVHN [43], CIFAR [44]. Compared to fixed and global adaptive activations, neuron-wise LAAF exhibited faster training speeds when approximating a discontinuous function and, in combination with PINNs, the inverse problem of identifying the material coefficient of Poisson’s equation and Burgers equation in 2D. LAAF contributes to the overall challenge of reducing the number of iterations needed for convergence compared to the fixed activation function. This feature was tested with the backend TensorFlow 1 in DeepXDE and $n=10$ for the reliable hyperparameters with a network depth of $L-1=2$, each layer consisting of 180 neurons, $w_{\mathrm{NBC}}=5$, the n of the DeepXDE implementation of layer-wise (a uniform $a_i^{\ell }=a^{\ell }$ for all neurons in the layer) LAAF is selected to be 2. The parameters selected were a good compromise for the standard PINN.

3.3. Multi-scale Fourier feature networks

The multi-scale Fourier feature architecture was proposed in [27] to address the spectral bias and low convergence rates observed in conventional PINN models [45]. The spectral bias expresses that the target function is first learned along the eigendirections connected to the larger eigenvalues of the neural tangent kernel and gradually the remaining components of smaller eigenvalues. Translated to conventional, fully connected neural networks, the eigenvalues are lowered by the increasing frequency of the corresponding eigenfunctions. As a result, the convergence rate of high-frequency components of $p\left(x\right)$ is low [46,47]. This learning tendency is a significant challenge when dealing with multi-scale problems like localized acoustic sources featuring space-dependent high-frequency solution features. The challenge is addressed by embedding multiple Fourier features into the network to learn features across scales and to mitigate the spectral bias behavior. Firstly, the input coordinates are transformed using multiple Fourier feature mappings. The forward pass of M Fourier features with $m=1,...,M$ is defined by

$$\begin{array}{cc}\hfill \mathrm{input}\mathrm{layer}\text{:}& {\mathcal{N}}^0\left(\mathbf{x}\right)=\mathbf{x}\in {\mathbb{R}}^{d_{\mathrm{in}}}\hfill \\ \hfill \mathrm{Fourier}\mathrm{layer}\text{:}& {\gamma }^{\left(m\right)}\left(\mathbf{x}\right)=\left[\begin{array}{c}cos\left(2\pi B^{\left(m\right)}x\right)\\ sin\left(2\pi B^{\left(m\right)}x\right)\end{array}\right]\in {\mathbb{R}}^{2d_{\mathrm{in}}\times M}\hfill \\ \hfill 1\mathrm{st}\mathrm{hidden}\mathrm{layer}\text{:}& \sigma \left({\mathcal{N}}^{1,\left(m\right)}\left(\mathbf{x}\right)\right)=\sigma \left({\mathit{W}}^1{\gamma }^{\left(m\right)}\left(\mathbf{x}\right)+{\mathit{b}}^1\right)\in {\mathbb{R}}^{N_1},\hfill \\ \hfill \mathrm{hidden}\mathrm{layers}\text{:}& \sigma \left({\mathcal{N}}^{\ell ,\left(m\right)}\left(\mathbf{x}\right)\right)=\sigma \left({\mathit{W}}^{\ell }{\mathcal{N}}^{\ell -1,\left(m\right)}\left(\mathbf{x}\right)+{\mathit{b}}^{\ell }\right)\in {\mathbb{R}}^{N_{\ell }},\mathrm{for}2\le \ell \le L-1,\hfill \\ \hfill \mathrm{output}\mathrm{layer}\text{:}& \widehat{p}\left(\mathbf{x}\right)={\mathit{W}}^L·\left[\sigma \left({\mathcal{N}}^{L,\left(1\right)}\right),\sigma \left({\mathcal{N}}^{L,\left(2\right)}\right),...,\sigma \left({\mathcal{N}}^{L,\left(M\right)}\right)\right]+{\mathit{b}}^L\in {\mathbb{R}}^{d_{\mathrm{out}}};\hfill \end{array}$$

(20)

where $B^{\left(m\right)}$ are preselected matrices with entries randomly sampled from a Gaussian distribution $N(0,{\widehat{s}}_m^2)$. The choice of ${\widehat{s}}_m$ values are additional hyperparameters that may be optimized, and typical values can be 1, 20, 50, 100 [27]. Overall, no new training parameters $\theta$ are introduced by this architecture compared to a standard fully connected neural network.

Figure 4. Schematic representation of a PINN with multi-scale Fourier feature architecture.

Figure 4. Schematic representation of a PINN with multi-scale Fourier feature architecture.

3.4. Validation and testing procedure

The final physical validation (testing) of the PINN simulation was performed in pyCFS-data [48] using the relative $l^2$-error measure on an evenly spaced evaluation sample (being an approximate of the relative $L^2$-error)

$$e_{\mathrm{rel}}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^{N_{\mathrm{pts}}}{\left(p_{i,\mathrm{FEM}}-p_{i,\mathrm{PINN}}\right)}^2}{{\sum }_{i=1}^{N_{\mathrm{pts}}}{\left(p_{i,\mathrm{FEM}}\right)}^2}}},$$

(21)

where $N_{\mathrm{pts}}$ is the number of evaluation points, $p_{i,\mathrm{FEM}}$ is the FEM reference pressure result and $p_{i,\mathrm{PINN}}$ is the pressure result from the PINN. This error measure on a structured evaluation point sample is proportional to the $L^2$ error. The $N_{\mathrm{pts}}$ evenly spaced evaluation points of the FEM simulation have been used to evaluate the PINN prediction.

4. Results

The results are presented for the basic room application examples in 3D. Firstly, recent distinct hyperparameters are studied relying on optimization hypotheses in [20]. In [20], the authors presented a framework for automatically analyzing a set of hyperparameters in a Gaussian processes-based Bayesian optimization. Both a 2D and a 3D scenario were studied with a distributed force $s\to \infty$, with a very detailed description of the 2D case (Dirichlet problem), which in turn is not directly translatable to the 3D case (Neumann problem). The representativeness of the study shows limited training runs for the expensive training runs. The hyperparameter optimization study for the 3D case found an optimal configuration, learning rate ${10}^{-4}$, width of 207, depth of 10, with the sine activation function and a boundary weight term of 1 and the second best had a learning rate close to ${10}^{-3}$, width of 292, depth of 3, with the sine activation function and a boundary weight term of 19.1. The diversity of these two nearly optimal solutions expresses the challenge of training a network for this task. It was reported that for increased wave numbers, the performance of the PINNs was low in the 2D and 3D cases. Furthermore, by uniformly increasing the density of collocation points, the performance of the network prediction capability improved, suggesting that adaptive refinement may lead to further improvements. Upon those results [20], a structured hyperparameter exploration was conducted for the general 3D case with a finite source sharpness parameter s.

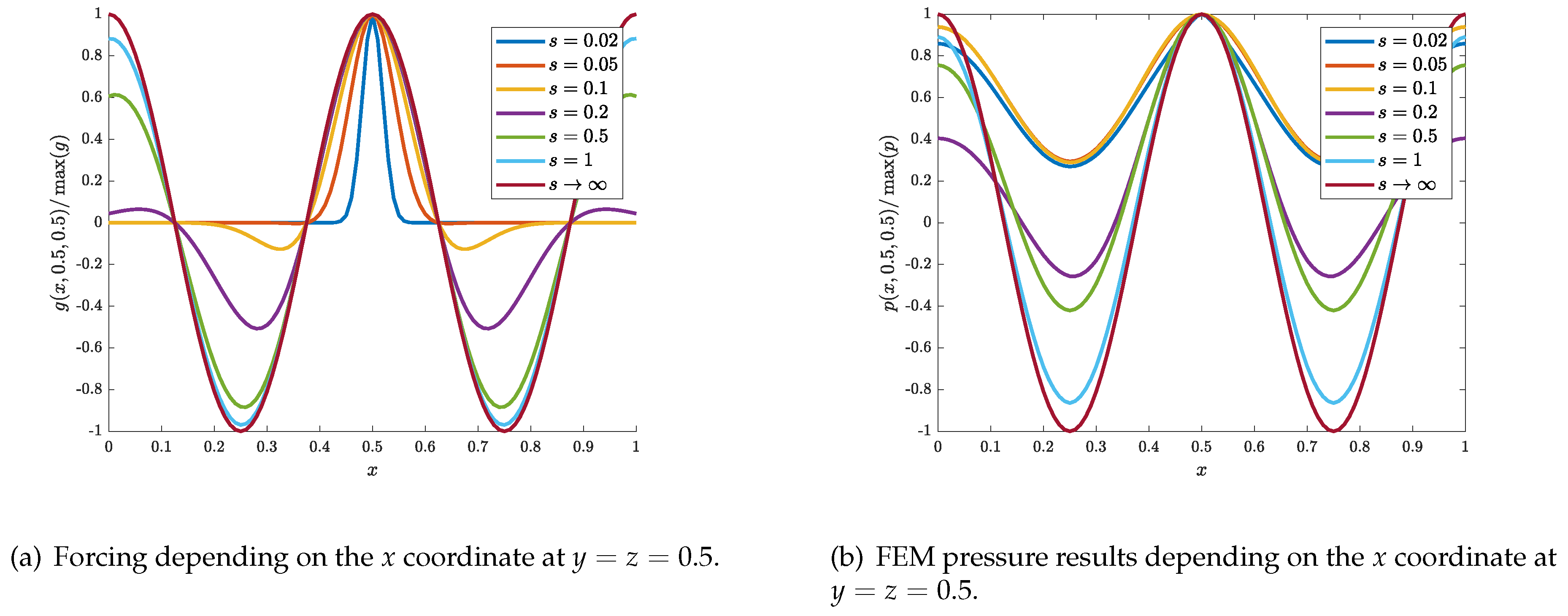
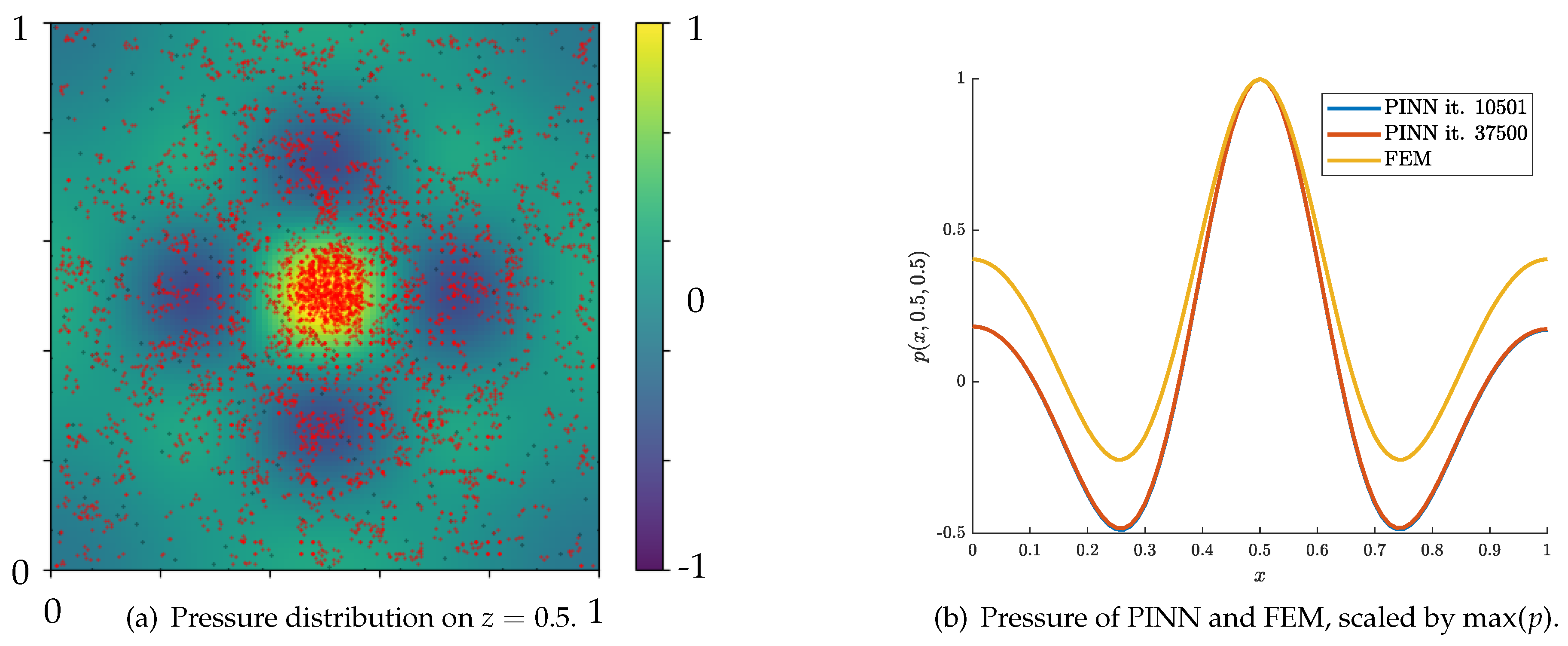
4.1. Sharpening the excitation source localization

In the next test, the source is modeled more by a gradually confined source in the center of the room modeled by (2) and illustrated in Figure 5a. The sharpness of the source can be tuned by the parameter s in the exponential. When sharpening the excitation of the source, additional spatial modes are immediately necessary to be modeled by the neural network and feature a multi-scale problem. As pointed out [27] and indicated by the modal description of a point source [49], it may be difficult for a standard fully-connected neural network to produce accurate results of the acoustic pressure Figure 5b.

The respective $l^2$ deviation

$$d_{\mathrm{rel}}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^{N_{\mathrm{pts}}}{\left(p_{i,\mathrm{ANA}}-p_{i,\mathrm{FEM}}\right)}^2}{{\sum }_{i=1}^{N_{\mathrm{pts}}}{\left(p_{i,\mathrm{ANA}}\right)}^2}}},$$

(22)

from the FEM pressure results to the case $s\to \infty$ (analytical case $p_{i,\mathrm{ANA}}$) is given in the Table 1 for the following s-parameters investigated. The relative deviations are important since any meaningful learned solution to that problem may at least have an error below that level.

The lowest level of $s=0.02$ was chosen to respect the frequency considerations for accurate FEM solutions of the source concerning the FEM mesh. The standard network with hyperparameters ${\theta }_{\mathrm{NN}}=\{L-1=3,W=180,w_{\mathrm{NBC}}=5,sin,$ PyTorch}, a learning rate of ${10}^{-3}$ and after 200 000 iterations motivated by [5,27] resulted in an error of $e_{\mathrm{rel}}=99.99\%$ for $s=0.2$, resulted in an error of $e_{\mathrm{rel}}=85.45\%$ for $s=0.1$, resulted in an error of $e_{\mathrm{rel}}=94.97\%$ for $s=0.05$, and $e_{\mathrm{rel}}=99.93\%$ for $s=0.02$. In conclusion, the standard networks were not able to learn a solution that was close to the FEM solution as soon as the source was sharpened.

4.2. Explorative hyperparameter study for $s=1$

Compared to the previous studies conducted for $s\to \infty$, the study investigates the networks’ capability of calculating the results for a slightly distorted field based on $s=1$. In that case, the amplitudes of the solution are marginally higher due to reflections at the sound-hard walls than for the simple example $s\to \infty$.

A relative error less than the relative deviations $e_{\mathrm{rel}}<d_{\mathrm{rel}}$ from the case $s\to \infty$ indicates that the network has learned a meaningful description of the field. The $L-1=3$ configuration performed best in Table 2 and for the first cohort (separated by rules in the table). This trend was observable for all hyperparameter tests provided in Table 2. In the second and third cohorts, a combination of switching the optimizer during the training was tested, and the effect of this on performance was examined.

Interestingly, when using $w_{\mathrm{NBC}}=50$, the PDE and the BC loss were initially of the same level and caused an excellent prediction when combining it with the LBFGS optimizer to further iterate on the network parameters (orange row in Table 2). In the final two cohorts, the boundary condition weights were tested.

In a subsequent study, the network width was tested, and its influence on the performance (Table 3). As expected, narrow networks performed poorly, and until 60 neurons of layer width, nearly no convergence to the FEM results was obtained. In conclusion, the layer width between 120 and 240 gave acceptable results for this case. The accuracy was in the bounds for all tested backends, with a somewhat superior performance of TensorFlow 1 leading to an error below 2%.

Following up on the layer number and width study (Table 4), the activation functions were tested $\sigma =\{$sin, ELU, GELU, ReLU, SELU, sigmoid, SiLU, swish, tanh}. From the shape of the solution, oscillating around the zero, the functions ELU, GELU, ReLU, SELU, sigmoid, and SiLU potentially performed poor, which was confirmed in the tests; none of the networks using those activation functions reached converged results with error less than 50%. The sinus function performed best; the swish and tanh activation reached similar errors, which were already quite large.

To improve the convergence and accuracy of the results, the layer-wise LAAF is a promising approach with its additional degrees of freedom and more rapid adjustments in learning the function approximation. For the layer-wise LAAF, only a few new parameters were added to the network, the number of hidden layers. Overall, the performance of the $n=2$ LAAF was superior compared to other n parameters tested.

As a conclusion for this experimental hyperparameter study, we found that a layer number of 2 or 3 will be a reasonable choice for this network. The layer width of around 120-240 is preferable, with the sin activation function and switching the training from initial Adams iterations of about 100 000 with a boundary weight of 5 and then switching to L-BFGS using a boundary weight of 50. The LAAF PINN structure did not further enhance the performance and accuracy. Overall, the accuracy compared to the FEM seems limited already for this relatively distributed source at $s=1$. As a next step, we are investigating the potential of adaptive refinement in terms of the network accuracy and if further data is needed for that application example to improve for $s=1$ and the cases of $s=\{0.2,0.1,0.05,0.02\}$.

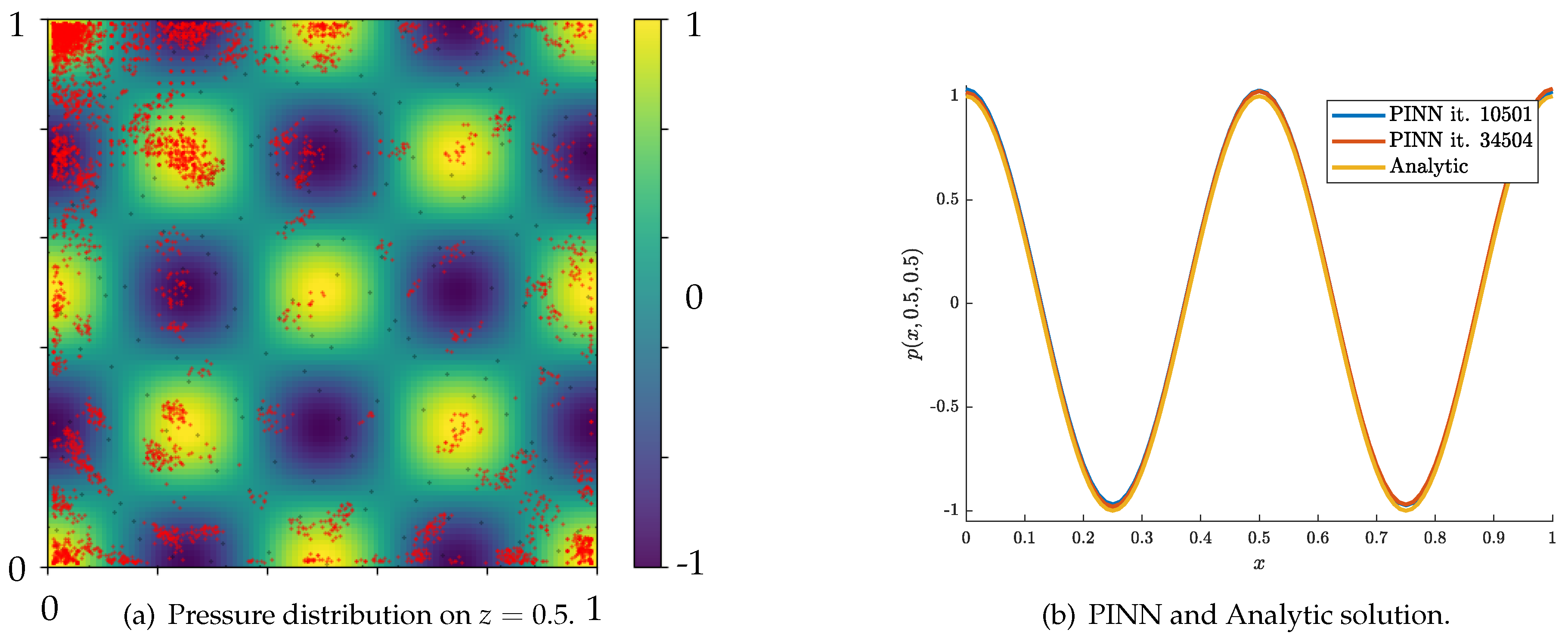
4.3. Adaptive refinement of training set

In a subsequent step, the pre-trained standard network architecture with hyperparameters ${\theta }_{\mathrm{NN}}=\{L-1=3,W=180,w_{\mathrm{NBC}}=5,sin,$ PyTorch}, a learning rate of ${10}^{-3}$ and after 200 000 iterations are used for adaptive fine-tuning of the model. The idea that adaptive refinement may improve the results came up by looking at Figure 6a and the overlaid black dots, which seemed to be distributed nicely but were relatively few points compared to a FEM mesh. The adaptive refinement procedure worked in the following steps; in the first data refinement step, $j=1,...,10$, the domain was sampled uniformly for a new dataset ${\mathcal{T}}_{\mathrm{samp},\Omega ,j}$. At these data points the residual of the loss (14) was evaluated and the arbitrary choice of 150 data points with the most significant residual was added to ${\mathcal{T}}_{\mathrm{train},\Omega ,j}={\mathcal{T}}_{\mathrm{train},\Omega }\cup ({\mathcal{T}}_{\mathrm{samp},\Omega ,j}\mid {max}_{i=1...150}\left(\mathcal{L}\left({\mathit{x}}_{\mathcal{i}}\right)\right)),\forall {\mathit{x}}_i\in {\mathcal{T}}_{\mathrm{samp},\Omega ,n}$. After the uniform refinement step, another 25 data refinement steps $j=11,...,35$ with random data point sampling were added to the training data points. In each refinement cycle, 1000 iterations of the optimizer were carried out, with early stopping activated.

The relative error results (21) for the case $s\to \infty$ present a reduction of the error from 0.35% to 0.33% in the first refinement stage and then another reduction to 0.28% after the whole procedure of adaptive refinement. This reduction of 0.07% points is an improvement of the network’s prediction accuracy by 20%. Figure 6a illustrates the pressure field predicted by the PINN in the evaluation plane ($z=0.5$) with a colormap representing the pressure magnitude. Overlaid black dots highlight the training points close to the evaluation plane. Overlaid red dots highlight the training points the adaptive refinement procedure added and indicate regions where the training error was high before the refinement. Figure 6b shows the pressure field predicted by the PINN compared to the analytic solution in the evaluation line ($y=z=0.5$). Notably, the graphs do coincide qualitatively.

In the case of $s=1$, the relative error results (21) present a reduction of the error from 2.38% to 1.41% in the first refinement stage and then and a relative increase to 1.78% after the whole procedure of adaptive refinement. Overall, the improvement was 25.2% with an improvement of 40.8% after the first refinement stage.

Figure 7 summarizes the adaptive refinement procedure and the added data points to the training set. Notably, more training points were added in central areas of the plot compared to the case of $s\to \infty$. Interestingly, in Figure 7b, the pressure results of the PINN are good at approximating the amplitude reduction close to the boundary for $x=0$ and $x=1$. However, deviations occur in the intermediate range, where $x=0.25$ and $x=0.75$.

Since the relative errors were significant for the cases of $s<1$, we expect some improvements to the results from the adaptive refinement procedure. For example, the case $s=0.2$ is discussed, featuring an error of nearly 100%. In the adaptive refinement step, the error was reduced to about 70%, but still in the range of being unacceptable compared to the FEM results.

Due to the adaptive refinement, the point distribution showed a remarkably uniform behavior, and the loss is significant in a large area (see Figure 8). Furthermore, a strong cluster of points close to the source location at $x=y=z=0.5$ is visible and was expected. Overall, the amplitude of the FEM result of $max\left(p\right)=1.56$ was not captured by the neural network solution. Based on Figure 8, the qualitative behavior of the PINN solution looks fair. With further improvement and studies on the network’s capabilities, the solution to the forward problem in room acoustics is within reach.

4.4. Multi-scale Fourier feature networks

The pre-knowledge of spatial scales in the system is strongly driven by the behavior of the wave and the emissions coinciding with the wavelength $\lambda$. Furthermore, it is expected that based on the sharpening of the force, the spatial frequency content gets more dispersed over the wave number and can lead to approximation difficulties using a modal field [49]. This was formally shown in the Section 2.2. We selected an architecture with hyperparameters ${\theta }_{\mathrm{NN}}=\{L-1=2,W=80,w_{\mathrm{NBC}}=5,sin,$ TensorFlow 1}, a learning rate of ${10}^{-3}$ and after 200 000 the errors were evaluated. The Fourier features were selected from a normal distribution with a standard deviation of ${\widehat{s}}_1=0.5$ and ${\widehat{s}}_1=1.0$, which is in the range of the wavelength based on the selected wave number. In the case of $s\to \infty$, the relative error (21) with 1.5% was in the range of the ordinary feed-forward network with the same number of trainable parameters. This was also observed for the case $s=1$ with an error of 5.4%. We observed no convergence for all the repeated test runs for $s<1$, which was unexpected. In a second test, the activation function of the network neurons was altered to tanh to avoid the possible poor performance of a combination of Fourier feature inputs and sinus activation functions. Similarly, the relative error measure was 1.4%, 5.6%, and no convergence for $s\to \infty$, for $s=1$ and $s=0.2$, respectively.

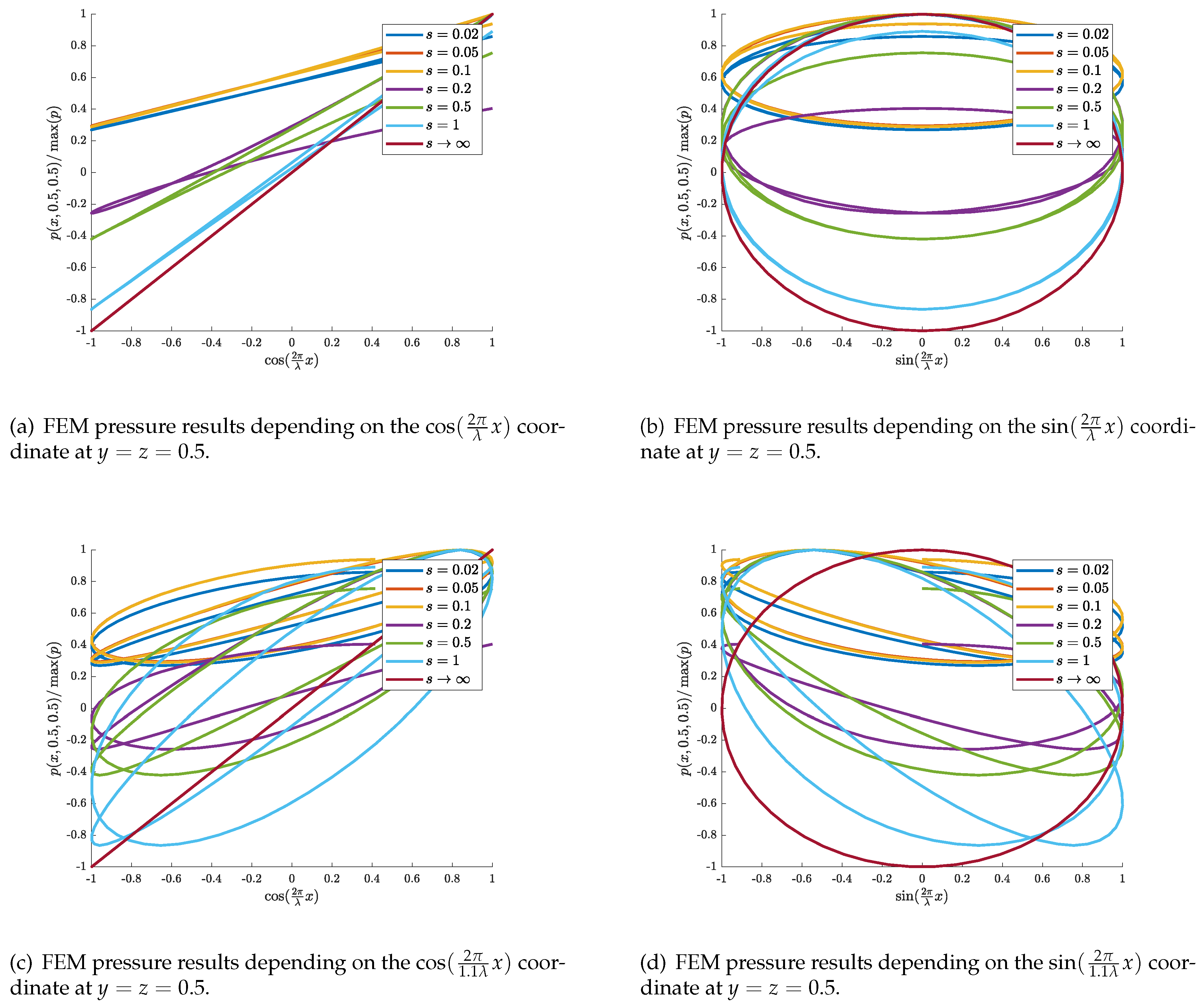
Overall, the multi-scale Fourier feature networks performed similarly to the standard model. A possible explanation is based on the exact linearization of the input-output relation due to the wave’s dispersion relation [50]. In the precise form, the cosine and sine transformation result for the various FEM results in the following linear relations illustrated in Figure 9.

Furthermore, the cosine Figure 9a analytically fulfills the boundary condition of sound hard walls. However, for a slightly shifted wavelength (by 10%), one can identify that the cosine and sine both transform into ellipses, making it comparably hard to solve the wave equation and estimate the solution. As soon as there is a deviation in the wave number, inherently present in the multi-scale network by the random draw of the Fourier features, it is fundamentally hard for the network architecture to find the solution of the wave equation. These facts motivate deterministic feature engineering [51,52] for the spatial coordinates to satisfy the dispersion relation of the wave.

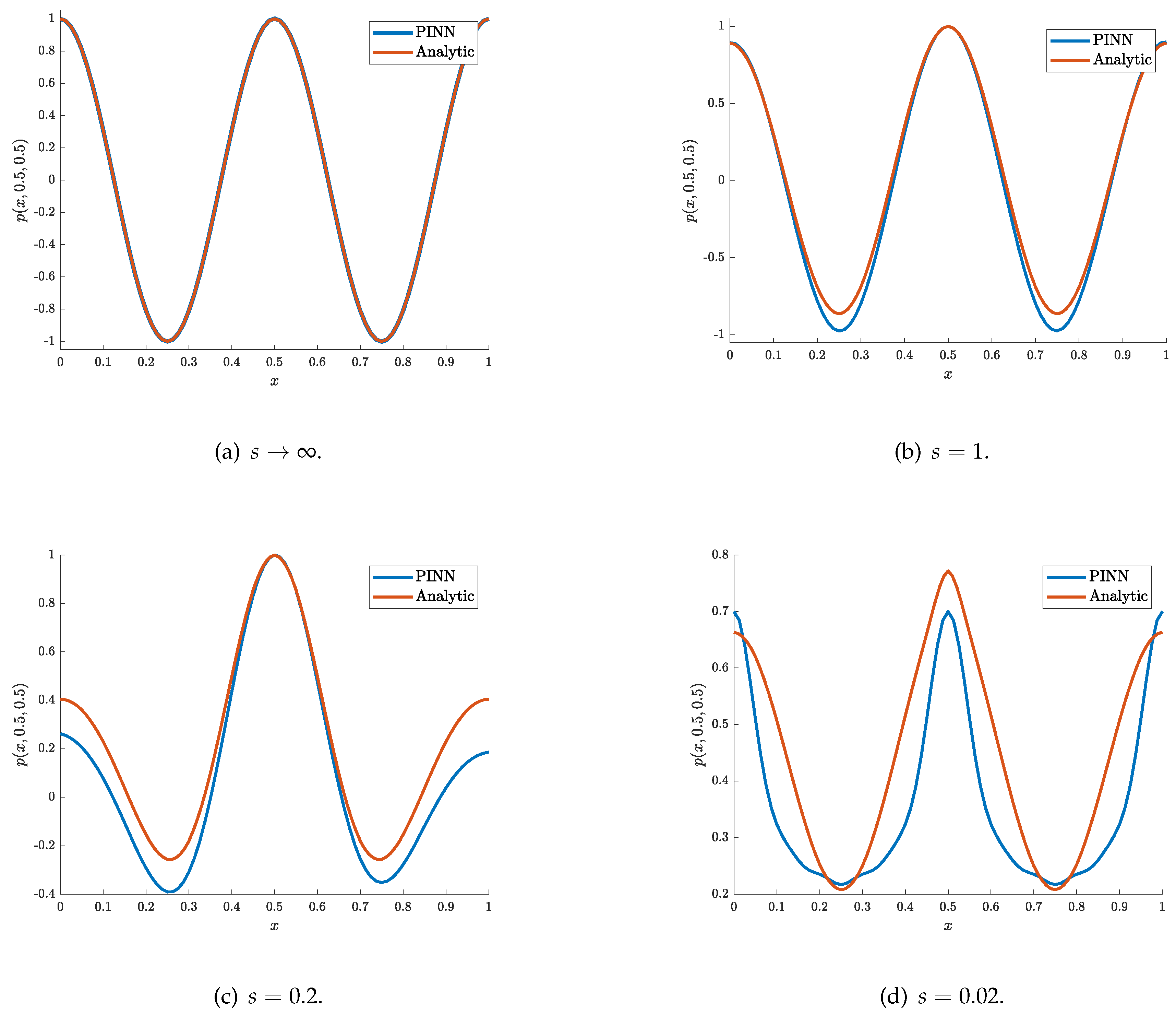
4.5. Input feature generation

The ordinary input $\mathit{x}$ is now transformed before feeding it into the input by ${\Pi }_{i{x}_{\in }x,y,z}cos\left({\displaystyle \frac{2\pi }{\lambda }}{x}_i\right)$, with $\lambda =0.5$m such that the wave number frequency relation is respected. The transform is motivated by Green’s function of the waves in a box modeled by a complete orthonormal solution basis as a product of solutions for each Cartesian coordinate:

$$\begin{array}{c}\hfill {\psi }_j\left(\mathit{r}\right)=\prod _{x_i\in x,y,z}cos\left({\displaystyle \frac{2\pi }{{\lambda }_i}}{x}_i\right).\end{array}$$

(23)

Note that an additive ansatz would fail and not reduce the complexity of the PINN problem. We selected an architecture with hyperparameters ${\theta }_{\mathrm{NN}}=\{L-1=2,W=10,w_{\mathrm{NBC}}=5,sin,$ PyTorch}, a learning rate of ${10}^{-3}$ and after 20 000 iterations the errors were evaluated. In doing so, the following errors were reached $2·{10}^{-4}$%, 1.54%, and 69% $s\to \infty$, $s=1$, and $s=0.2$, respectively. This significantly improves the other network structures by ingraining expert knowledge. For $s\to \infty$, the errors are in the range of the FEM method, and training took a few seconds, which is even faster than the FEM solution. We obtained no convergence of the amplitudes in the case of $s=0.2$ and $s=0.02$. In Figure 10, the pressure prediction of the PINN compared to the analytic or FEM results is illustrated.

5. Conclusion

This study demonstrates the feasibility of using PINNs (DeepXDE) to model 3D sound fields governed by the Helmholtz equation in a confined room. The prediction accuracy was assessed by a reference FEM simulation in openCFS. Three different network architectures and feature engineering were used to improve the pressure field prediction. The most significant improvement was reached by ingraining the characteristics of the Green’s function based on modal expansion via feature into the PINN. Before reaching this model, a detailed hyperparameter study highlights the importance of optimizing network shape and activation functions to improve the prediction capability for a simple, fully connected neural network architecture. The variation of the deep learning backend showed slight improvements in the prediction accuracy. Due to the high computational demand and focus on the prediction accuracy in terms of a relative L² error, no comparison of network architectures concerning the computational speed was carried out by intention. The fully connected layer-based PINN approach successfully converges to accurate solutions, as validated by FEM results, with relative errors as low as 0.28% for distributed sources. Adaptive refinement improved the prediction accuracy. It was shown that with the use of random Fourier features, no significant improvement was gained. Also, the network structure of layer-wise locally adaptive activation functions with slope recovery did not show improvements in prediction capability. However, the neuron-wise algorithm, introducing more additional degrees of freedom, might be a promising alternative for future evaluations. By incorporating Green’s function features equivalent to embedding the wave’s dispersion relation, a significantly reduced number of trainable parameters reached 5%, while improving accuracy by three orders of magnitude. This work underscores the potential of PINNs as a memory-efficient alternative to traditional methods for low-frequency room acoustic simulations, addressing challenges related to material absorption properties and complex excitation scenarios. As a result, future work could address the challenges of modeling confined source regions.