Fuzzy Uniform Topology on a PUP-Algebra

1. Introduction

The concept of a uniform space was first introduced by Weil in 1938 in [6] aWeil introduced the concept of a uniform space as a tool distinct from metrics, allowing the study of topological spaces without relying on countability assumptions. A uniform space can be viewed either as an axiomatization of certain geometric ideas, which are closely related to but independent of the concept of a topological space, or as a useful framework for examining topological structures. The theory of uniform spaces shows notable similarities to the theory of metric spaces, though its applicability extends much further. For instance, every topological group possesses three natural uniformities that are particularly useful in applications involving topological groups.

In daily life, a variety of models and traditional methods are used to manage uncertainty and imprecision. Fields such as medicine, social sciences, and physical sciences rely extensively on these tools to handle data-related imprecision and uncertainty. To address these challenges, new theories and approaches are continuously being developed. One significant contribution is by Zadeh [5], who introduced the concept of fuzzy sets, which is applicable in many contexts. In 2023 Mechderso et al. [1,2] applied fuzzy concepts to the PUP ideal and congruence relation of PUP algebra.

Motivated by this previous research, we aim to answer the following question: How can a fuzzified version of the uniform topology for PUP-algebra be developed using ideal theory? We define the family of extreme fuzzy PUP ideals ℵ, on the larger class of PUP-algebra, denoted by X, to construct a fuzzy uniform structure $(X,K)$. The component K induces a fuzzy uniform topology ${\tau }_{\aleph }$ in X. We prove that the pair $(X,{\tau }_{\aleph })$ forms a fuzzy topological PUP algebra and investigate some properties of $(X,{\tau }_{\aleph })$. Finally, we provide characterizations of the fuzzy topological properties of $(X,{\tau }_{\aleph })$.

2. Preliminaries

In this section, we review key concepts and definitions that are fundamental to this paper.

Lemma 1. 

[10] In a PUP-algebra X the following holds, for each $x\in X$,

1)

$a·0=0\mathrm{and}a★0=0$,

2)

$0·a=a\mathrm{and}0★a=a$, and

3)

$a·a=0\mathrm{and}a★a=0$.

Definition 1. 

[1] A fuzzy relation ψ on a set X is termed a fuzzy congruence relation on a PUP-algebra of X if it meets the following axioms for any $a,b,c\in X$.

1)

$\psi (a,a)=1$,

2)

$\psi (a,b)={\psi }^{-1}(b,a)$,

3)

$\psi (a,c)\ge {sup}_{b\in X}\left\{min\{\psi (a,b),\psi (b,c)\}\right\}$,

4)

$\psi (a·c,b·c)\ge \psi (a,b)$ and $\psi (a★c,b★c)\ge \psi (a,b)$, and

5)

$\psi (c·a,c·b)\ge \psi (a,b)$ and $\psi (c★a,c★b)\ge \psi (a,b).$

Theorem 2.1. 

[1] A fuzzy equivalence relation ψ of X is a fuzzy congruence relation PUP-algebra of X if and only if $\psi (a·u,b·v)\ge min\left\{\psi \right(a,b),\psi (u,v\left)\right\}$ and $\psi (a★u,b★v)\ge min\left\{\psi \right(a,b),\psi (u,v\left)\right\}$.

Theorem 2.2. 

[1] Let μ be a PUP ideal of X, and define a fuzzy relation ${\psi }_{\mu }(x,y)=min\{\mu (x·y),\mu (x★y),\mu (y·x),\mu (y★x)\}$. This is a fuzzy congruence relation on X.

Theorem 2.3. 

[2] Let $f:X\to Y$ be a homomorphism of a PUP algebra. If ψ be a fuzzy PUP ideal of Y. Then $f^{-1}\left(\psi \right)$ is a fuzzy PUP ideal of X

Theorem 2.4. 

[2] Let $(X,·,★,0)$ and $(Y,·,★,0)$ be a PUP-algebra. $f:X\to Y$ is surjective and ψ is a fuzzy PUP ideals of X. Then $f\left(\psi \right)$ is a fuzzy PUP ideals of Y, provided that the sup property holds.

3. Fuzzy Uniform Structure on a PUP-Algebra

In this section, we construct the fuzzy uniform structures by the special family of extreme fuzzy PUP ideal, and then induce fuzzy uniform topologies. Moreover, we show that PUP algebras with fuzzy uniform topologies are fuzzy topological PUP-algebra, and also some properties are investigated.

Notation: Let X be a non empty PUP-algebra, $\psi$ and $\varphi$ be fuzzy relations on $X\times X$. Then we define the following:

1.

$1_X\left(x\right)=1$ and $0_X\left(x\right)=0$, for all $x\in X,$

2.

${\psi }^{-1}(x,y)=\psi (y,x),$ for all $(x,y)\in X\times X,$

3.

${\psi }^{\left[x\right]}\left(y\right)=\psi (x,y),$ for all $(x,y)\in X\times X,$

4.

$(\psi \circ \varphi )(x,y)={sup}_{z\in X}\{min\{\psi (x,z),\varphi (z,y)\},\mathrm{for}\mathrm{all}(x,y)\in X\times X\}.$

Definition 2. 

A fuzzy PUP ideal μ of a PUP algebra X is called an extreme fuzzy PUP ideal of X if $\mu \left(0\right)=1.$ The family of an extreme fuzzy PUP ideals of X is denoted by ℵ.

Interestingly, any fuzzy PUP ideal of a PUP-algebra can be extended into an extreme fuzzy PUP ideal within the PUP-algebraX.

Theorem 3.1. 

Let ν be a fuzzy PUP ideal of X. Then there exists an extreme fuzzy PUP ideal μ of X such that $\nu \subseteq \mu .$

Proof. 

Let $\nu$ be a fuzzy PUP ideal of X and we define an extreme fuzzy PUP ideal $\mu$ by

$$\mu \left(x\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}x=0\hfill \\ \nu \left(x\right),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Clearly, $\nu \subseteq \mu$. □

In general, the extension of a fuzzy PUP ideal into extreme fuzzy PUP ideal is not unique.

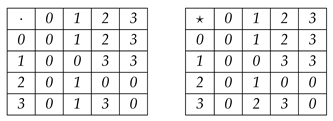
Example 3.2. 

Let $X=\{0,1,2,3\}$ be a set with a binary operation $"·"$ and $"★"$ defined by the following cayley table:

See [3], $(X,·,★,0)$ is a PUP-algebra. We define a fuzzy set $\nu :X\to [0,1]$ as follows, $\nu \left(0\right)=0.8,\nu \left(1\right)=0.6,\nu \left(2\right)=0.4,\nu \left(3\right)=0.3$. It is easily checked that $\nu$ is a fuzzy PUP ideal of X. We define a fuzzy set $\mu :X\to [0,1]$ as follows, $\mu \left(0\right)=1,\mu \left(1\right)=0.6,\mu \left(2\right)=0.4,\mu \left(3\right)=0.3,$ and $\lambda \left(0\right)=1,\lambda \left(1\right)=0.7,\lambda \left(2\right)=0.4,\lambda \left(3\right)=0.3$. Through standard calculation, $\mu$ and $\lambda$ can be expressed as extensions of $\nu$, but $\mu \ne \lambda$.

Definition 3. 

Suppose that ℵ is an arbitrary family of an extreme fuzzy PUP ideals of a PUP-algebra X. A fuzzy relation $\psi \in I^{X\times X}$, then we define the following:

1.

${\psi }_{\mu }(x,y)=min\{\mu (x·y),\mu (x★y),\mu (y·x),\mu (y★x)\}$, for all $(x,y)\in X\times X,$

2.

${\psi }_{\mu }^{\left[x\right]}\left(y\right)={\psi }_{\mu }(x,y),\mathrm{for}y\in X$, and ${\psi }_{\mu }^{\left[\lambda \right]}\left(x\right)={sup}_{y\in X}\left\{min\{\lambda \left(y\right),{\psi }_{\mu }(x,y)\}\right\},\mathrm{for}\lambda \in I^X,$

3.

$K^{★}=\{{\psi }_{\mu }:\mu \in \aleph \},$

4.

$\mathbb{K}=\{\psi :{\psi }_{\mu }\subseteq \psi ,forsome{\psi }_{\mu }\in K^{★}\}.$

Definition 4. 

A fuzzy uniformity K on a set X is a collection of fuzzy relations on $X\times X$, ($i.e$ each element of K is a fuzzy relation such that function from $X\times X\to I$), which fulfills the following properties:

$U_1$.

$\psi \in K$, $\psi (x,x)=1$ for all $x\in X,$

$U_2$.

$\psi \in K\Rightarrow {\psi }^{-1}\in K,$

$U_3$.

$\psi \in K$, there exist a fuzzy relation $\varphi \in K$ such that $\varphi \circ \varphi \subseteq \psi ,$

$U_4$.

$\psi ,\varphi \in K$, then $\psi \cap \varphi \in K,$

$U_5$.

$\psi \in K$ and $\psi \subseteq \varphi$, then $\varphi \in K.$

Then the pair $(X,K)$ is a fuzzy uniform space.

Theorem 3.3. 

Let ℵ be family of an extreme fuzzy PUP ideals of a PUP-algebra X, then $K^{★}$ meets the criteria $\left(U_1\right)$ through $\left(U_4\right)$.

Proof. 

Suppose $\mu \in \aleph$ and $\psi$ is a fuzzy relation.

$U_1$. Let ${\psi }_{\mu }\in K^{★}$. Then ${\psi }_{\mu }(x,x)=min\{\mu (x·x),\mu (x★x),\mu (x·x),\mu (x★x)\}$$=min\left\{\mu \right(0),\mu (0),\mu (0),\mu (0\left)\right\}=1.$ Thus ${\psi }_{\mu }(x,x)=1.$

$U_2.$ Let ${\psi }_{\mu }\in K^{★}$, then we have

$${\psi }_{\mu }^{-1}(x,y)={\psi }_{\mu }(y,x)=min\{\mu (y·x),\mu (y★x),\mu (x·y),\mu (x★y)\}=min\{\mu (x·y),\mu (x★y),\mu (y·x),\mu (y★x)\}={\psi }_{\mu }(x,y).$$

Hence, ${\psi }_{\mu }^{-1}\in K^{★}$.

$U_3.$ Let ${\psi }_{\mu }\in K^{★}$ and $({\psi }_{\mu }\circ {\psi }_{\mu })(x,z)$, then there exist $y\in X$ such that

${\psi }_{\mu }\circ {\psi }_{\mu }(x,z)={sup}_{y\in X}\left\{min\{{\psi }_{\mu }(x,y),{\psi }_{\mu }(y,z)\}\right\}\le {\psi }_{\mu }(x,z)$, by Theorem 2.2${\psi }_{\mu }$ is a fuzzy congruence relation on $X.$ Thus ${\psi }_{\mu }\circ {\psi }_{\mu }\subseteq {\psi }_{\mu }.$

$U_4.$ Let $\mu ,\lambda \in \aleph$ and ${\psi }_{\mu },{\psi }_{\lambda }\in K^{★}$. We need to show that ${\psi }_{\mu }\cap {\psi }_{\lambda }\in K^{★}.$

$$\begin{array}{ccc}\hfill ({\psi }_{\mu }\cap {\psi }_{\lambda })(x,y)& =min\{{\psi }_{\mu }(x,y),{\psi }_{\lambda }(x,y)\}\hfill & \\ \hfill & =min\left\{min\right\{\mu (x·y),\mu (x★y),\mu (y·x),\mu (y★x)\},min\{\lambda (x·y),\lambda (x★y)\lambda (y·x),\lambda (y★x)\left\}\right\}\hfill & \\ \hfill & =min\left\{min\right\{\mu (x·y),\mu (x★y),\lambda (x·y),\lambda (x★y)\},min\{\mu (y·x),\mu (y★x)\lambda (y·x),\lambda (y★x)\left\}\right\}\hfill & \\ \hfill & =min\left\{\right(\mu \cap \lambda \left)\right(x·y),(\mu \cap \lambda \left)\right(x★y),(\mu \cap \lambda \left)\right(y·x),(\mu \cap \lambda \left)\right(y★x\left)\right\}\}\hfill & \\ \hfill & ={\psi }_{\mu \cap \lambda }(x,y).\hfill \end{array}$$

Therefore, ${\psi }_{\mu }\cap {\psi }_{\lambda }={\psi }_{\mu \cap \lambda }$, then we have ${\psi }_{\mu }\cap {\psi }_{\lambda }\in K^{★}$, since ${\psi }_{\mu \cap \lambda }\in K^{★}.$

Hence, $K^{★}$ satisfies the conditions $\left(U_1\right)$ through $\left(U_4\right).$ □

Remark 3.4. 

$K^{★}$ is not a fuzzy uniform structure on X.

Example 3.5. 

Let$X=\{0,a,b,c\}$and two binary operation$"·"$and$"★"$defined by the following cayley table:

[b]0.33

See [3] $(X,·,★)$ is a PUP-algebra. We define a fuzzy set μ as follows:

$\mu \left(0\right)=1,\mu \left(a\right)=0.5=\mu \left(b\right)=\mu \left(c\right)$. Then μ is an extreme fuzzy PUP ideal of a pseudo-UP algebra. And ${\psi }_{\mu }(0,0)={\psi }_{\mu }(a,a)={\psi }_{\mu }(b,b)={\psi }_{\mu }(c,c)=1$, ${\psi }_{\mu }(0,a)={\psi }_{\mu }(a,0)={\psi }_{\mu }(a,b)={\psi }_{\mu }(b,a)={\psi }_{\mu }(c,a)=(b,c)={\psi }_{\mu }(c,b)={\psi }_{\mu }(a,c)=0.5$. Again we define a fuzzy set λ as follows $\lambda \left(0\right)=1$, $\lambda \left(a\right)=0.7=\lambda \left(b\right)$ and $\lambda \left(c\right)=0.9$ and then we have, ${\psi }_{\lambda }(0,0)={\psi }_{\lambda }(a,a)={\psi }_{\lambda }(b,b)={\psi }_{\lambda }(c,c)=1,{\psi }_{\lambda }(a,b)={\psi }_{\lambda }(a,0)={\psi }_{\lambda }(0,b)={\psi }_{\lambda }(a,c)={\psi }_{\lambda }(b,c)=0.7$ and ${\psi }_{\lambda }(c,0)={\psi }_{\lambda }(0,c)=0.9$. It follows that ${\psi }_{\mu }\subseteq {\psi }_{\lambda }$. However, λ does not qualify as a fuzzy PUP ideal of X, which means

$$\begin{array}{ccc}\hfill \Rightarrow \lambda (b·a)& \ge min\left\{\lambda \right(b·(c★a),\lambda \left(c\right)\left)\right\}\hfill & \\ \hfill \Rightarrow \lambda \left(a\right)& \ge min\left\{\lambda \right(b·b),\lambda (c\left)\right\}\hfill & \\ \hfill \Rightarrow \lambda \left(a\right)& \ge min\left\{\lambda \right(0),\lambda (c\left)\right\}\hfill & \\ \hfill \Rightarrow 0.7& \ge min\{1,0.9\}.\hfill \end{array}$$

This is inconsistent with the definition of a fuzzy PUP ideal. Which implies that ${\psi }_{\lambda }\notin K^{★}.$ Hence, $K^{★}$ does not satisfy condition $U_5$ from Definition 4.

Corollary 3.6. 

Let X be a PUP-algebra, and define $\mathbb{K}=\{\psi :\exists {\psi }_{\mu }\in K^{★}\mathrm{such}\mathrm{that}{\psi }_{\mu }\subseteq \psi \}$. Then $\mathbb{K}$ is a fuzzy uniform structure on X.

Proof. 

From the above Theorm 3.3, we find that $\mathbb{K}$ satisfies conditions $\left(U_1\right)$ through $\left(U_4\right)$. It is sufficient to demonstrate that $\mathbb{K}$ satisfies $\left(U_5\right)$. Let $\psi \in \mathbb{K}$ and $\psi \subseteq \varphi$, then there exist ${\psi }_{\mu }\subseteq \psi \subseteq \varphi$ implies that ${\psi }_{\mu }\subseteq \varphi$, which means that $\varphi \in \mathbb{K}$. Hence, the pair $(X,\mathbb{K})$ forms a fuzzy uniform structure on the PUP algebra X. □

Definition 5. 

Let $(X,K)$ be a fuzzy uniform space. A subfamily of fuzzy relation Φ of K is called a base for K if $\psi \in K$ there exist $\beta \in \Phi$ such that $\beta \subseteq \psi$.

Theorem 3.7. 

A non-void family of fuzzy relations Φ is a base for some fuzzy uniformity on X if and only if the following conditions holds:

1.

$\forall \beta \in \Phi ,\beta (x,x)=1,$

2.

$\forall \beta \in \Phi$ implies ${\beta }^{-1}$ contanis some elements of $\Phi ,$

3.

$\forall \beta ,{\beta }^{\prime }\in \Phi$ implies $\beta \cap {\beta }^{\prime }$ contians some elements of $\Phi .$

4.

$\forall \beta \in \Phi$ there exist ${\beta }^{★}\in \Phi$ such that ${\beta }^{★}\circ {\beta }^{★}\subseteq \beta ,$

Proof. 

Let X be a non empty PUP-algebra, and define $K=\{\psi :\beta \subseteq \psi ,\mathrm{for}\mathrm{some}\beta \in \Phi \}$, where $\Phi$ is a non-void family of fuzzy relation. Suppose $\Phi$ is a base for a fuzzy uniformity K. We need to show that conditions (1) through (4) are satisfied.

1. Let $\beta \in \Phi$, then $\beta \in K,$ since $\Phi$ is a base for fuzzy uniformity K. Which implies that $\beta (x,x)=1$, by Definition 4$\left(U_1\right)$. Therefore, for all $\beta \in K$, $\beta (x,x)=1.$

2. Let $\beta \in \Phi$, then $\beta \in K$, since $\Phi$ is a base for a fuzzy uniformity.

$$\begin{array}{ccc}\hfill & \Rightarrow \exists {\beta }^{‵}\in \Phi \mathrm{such}\mathrm{that}{\beta }^{‵}(x,y)\le \beta (x,y),(\mathrm{by}\mathrm{the}\mathrm{definition}\mathrm{of}\mathrm{base})\hfill & \\ \hfill & \Rightarrow {\beta }^{{‵}^{-1}}(y,x)={\beta }^{‵}(x,y)\le \beta (x,y)={\beta }^{-1}(y,x)\hfill & \\ \hfill & \Rightarrow {\beta }^{{‵}^{-1}}(y,x)\le {\beta }^{-1}(y,x)\hfill & \\ \hfill & \Rightarrow {\beta }^{{‵}^{-1}}\subseteq {\beta }^{-1}\hfill & \\ \hfill & \Rightarrow {\beta }^{{‵}^{-1}}\in K.\hfill \end{array}$$

Which implies that there exist ${\beta }^{★}\in \Phi$ such that ${\beta }^{★}(y,x)\le {\beta }^{{‵}^{-1}}(y,x)\le {\beta }^{-1}(y,x)$ implies ${\beta }^{-1}$ contains some elements of $\Phi$ such that ${\beta }^{★}\subseteq {\beta }^{-1}$.

3. Let $\beta ,{\beta }^{‵}\in \Phi$, then $\beta ,{\beta }^{‵}\in K$. Which implies $\beta \cap {\beta }^{‵}\in K$, then there exist ${\beta }^{★}\in \Phi$ such that ${\beta }^{★}(x,y)\le min\{\beta (x,y),{\beta }^{‵}(x,y)\}\Rightarrow {\beta }^{★}\subseteq \beta \cap {\beta }^{‵}.$ Therefore, $\beta \cap {\beta }^{‵}$ contains some memebers of $\Phi$.

4. Let $\beta \in \Phi$, then $\beta \in K$. And there exist ${\beta }^{‵}\in \Phi$ such that ${\beta }^{‵}(x,y)\le \beta (x,y)\Rightarrow {\beta }^{‵}\subseteq \beta$, then ${\beta }^{‵}\in K$. Now, by Definition 4$\left(U_3\right)$, we have ${\beta }^{‵}\circ {\beta }^{‵}\subseteq \beta$

$\Rightarrow {\beta }^{‵}\circ {\beta }^{‵}(x,y)\le \beta (x,y)$

$\Rightarrow {sup}_{z\in X}\left\{min\{{\beta }^{‵}(x,z),{\beta }^{‵}(z,y)\}\right\}\le \beta (x,y).$

Then there exist ${\beta }^{★}\in \Phi$ such that ${\beta }^{★}(x,y)\le {\beta }^{‵}(x,y)\Rightarrow {\beta }^{★}\subseteq {\beta }^{‵}$. Which implies that ${\beta }^{★}\circ {\beta }^{★}(x,y)={sup}_{z\in X}\left\{min\{{\beta }^{★}(x,z),{\beta }^{★}(z,y)\}\right\}\le {sup}_{z\in X}\left\{min\{{\beta }^{‵}(x,z),{\beta }^{‵}(z,y)\}\right\}\le \beta (x,y)\Rightarrow {\beta }^{★}\circ {\beta }^{★}\subseteq \beta .$

Hence, for $\beta \in \Phi$ there exist ${\beta }^{★}\in \Phi$ such that ${\beta }^{★}\circ {\beta }^{★}\subseteq \beta .$

Conversely, suppose $\Phi$ is a base for some fuzzy uniformity that satisfies conditions (1) through (4), and define $K=\{\psi :\beta \subseteq \psi ,\mathrm{for}\mathrm{some}\beta \in \Phi \}$. Then we need to show that K is a fuzzy uniformity on X.

$U_1.$ Let $\psi \in K$, then there exist $\beta \in \Phi$ such that $\beta (x,y)\le \psi (x,y)$. From condition $\left(1\right)$, we have $1=\beta (x,x)\le \psi (x,x)\Rightarrow \psi (x,x)=1.$

$U_2.$ Let $\psi \in K$, then there exist $\beta \in \Phi$ such that $\beta (x,y)\le \psi (x,y)$

$$\begin{array}{ccc}\hfill & \Rightarrow {\beta }^{-1}(y,x)=\beta (x,y)\le \psi (x,y)={\psi }^{-1}(y,x)\hfill & \\ \hfill & \Rightarrow {\beta }^{-1}(y,x)\le {\psi }^{-1}(y,x)\hfill & \\ \hfill & \Rightarrow {\beta }^{-1}\subseteq {\psi }^{-1}.\hfill \end{array}$$

From condition $\left(2\right)$, there exist ${\beta }^{★}\in \Phi$ such that ${\beta }^{★}(y,x)\le {\beta }^{-1}(y,x)$ implies ${\beta }^{★}(y,x)\le {\beta }^{-1}(y,x)\le {\psi }^{-1}(y,x)\Rightarrow {\beta }^{★}\subseteq {\psi }^{-1}\Rightarrow {\psi }^{-1}\in K.$

$U_3.$ Let $\psi ,\varphi \in K$, then there exist ${\beta }_1,{\beta }_2\in \Phi$ such that ${\beta }_1(x,y)\le \psi (x,y)$ and ${\beta }_2(x,y)\le \varphi (x,y).$

$\Rightarrow min\{{\beta }_1(x,y),{\beta }_2(x,y)\}\le min\{\psi (x,y),\varphi (x,y)\}\Rightarrow {\beta }_1\cap {\beta }_2\subseteq \psi \cap \varphi .$

From condition $\left(4\right)$, there exist $\beta \in \Phi$ such that

$$\begin{array}{ccc}\hfill \beta (x,y)& \le min\{{\beta }_1(x,y),{\beta }_2(x,y)\}\hfill & \\ \hfill & \le min\left\{\psi \right(x,y),\varphi (x,y\left)\right\}\hfill & \\ \hfill \Rightarrow \beta (x,y)& \le min\left\{\psi \right(x,y),\varphi (x,y\left)\right\}\hfill & \\ \hfill \Rightarrow \beta & \subseteq \psi \cap \varphi \hfill & \\ \hfill \Rightarrow \psi \cap \varphi & \in K.\hfill \end{array}$$

$U_4.$ Let $\psi \in K$, then there exist $\beta \in \Phi$ such that $\beta (x,y)\le \psi (x,y)$. From condition $\left(3\right)$, there exist ${\beta }^{‵}\in \Phi$ such that ${\beta }^{‵}\circ {\beta }^{‵}(x,y)={sup}_{z\in X}\left\{min\{{\beta }^{‵}(x,z),{\beta }^{‵}(z,y)\}\right\}\le \beta (x,y)\le \psi (x,y)\Rightarrow {\beta }^{‵}\circ {\beta }^{‵}(x,y)\le \psi (x,y)\Rightarrow {\beta }^{‵}\circ {\beta }^{‵}\subseteq \psi$, such that there exist ${\beta }^{‵}\in \Phi \Rightarrow {\beta }^{‵}\in K$. Therefore, $\psi \in K$, there exist ${\beta }^{‵}\in K$ such that ${\beta }^{‵}\circ {\beta }^{‵}\subseteq \psi .$

$U_5.$ Let $\psi \in K$ and $\psi \subseteq \varphi$. There exist $\beta \in \Phi$ such that $\beta \subseteq \psi \subseteq \varphi \Rightarrow \beta \subseteq \varphi \Rightarrow \varphi \in K.$ By definition of fuzzy uniformity, $K=\{\psi :\beta \subseteq \psi ,\mathrm{for}\mathrm{some}\beta \in \Phi \}$ is a fuzzy uniform space on X. □

Definition 3.8. 

Let $(X,K)$ be a fuzzy uniform space. A sub family of fuzzy relation $\mathfrak{S}$ of K is called a subbase for K if all finite intersection member of $\mathfrak{S}$ forms a base for a fuzzy uniformity K.

Proposition 3.9. 

Let X be a non-empty PUP algebra. Then a non-empty class fuzzy relation $\mathfrak{S}$ on $X\times X$ is a subbase for some fuzzy uniformity on X if the following conditions hold:

1.

For all $S\in \mathfrak{S},S(x,x)=1,\mathrm{for}\mathrm{all}x\in X$

2.

For all $S\in \mathfrak{S}\Rightarrow S^{-1}$ contains some elements of $\mathfrak{S},$

3.

For all $S\in \mathfrak{S}$, there exist $S^{★}\in \mathfrak{S}$ such that $S^{★}\circ S^{★}\subseteq S.$

Proof. 

Let $(X,K)$ be a fuzzy uniform space. Let $\mathfrak{S}$ be a non-empty class of fuzzy relation on $X\times X$ that satisfies conditions (1)through (3).

Define: $\Phi =inf\{S_i,S_i\in \mathfrak{S},\mathrm{for}\mathrm{each}\mathrm{i}=1,2,3,...,\mathrm{n}\}$. Now $\mathfrak{S}$ to be a subbase for fuzzy uniformity, $\Phi$ must be a base for a fuzzy uniformity. Now we need to prove that $\Phi$ is a base for a fuzzy uniform space $(X,K)$.

1. Let $\psi \in \Phi$. Define $\psi (x,y)=inf\{S_i(x,y)$, where $S_i\in \mathfrak{S}$ and for each $i=1,2,3,...,n\}$. From condition (1), we have $S_i(x,x)=1$ which implies that $inf\left\{S_i(x,x)\right\}=1$$\Rightarrow \psi (x,x)=1$. Thus $\psi \in \Phi ,\psi (x,x)=1$.

2. Let $\psi \in \Phi$. Define $\psi (x,y)=inf\{S_i(x,y)$ where $S_i\in \mathfrak{S}$, for each $i=1,2,3,...,n\}$. From condtion (2), we have $S_i\in \mathfrak{S}$ implies that $S_i^{-1}$ contains some elements of $\mathfrak{S}$. Then there exist ${\lambda }_i\in \mathfrak{S}$ such that ${\lambda }_i\subseteq S_i^{-1}$, for each $i=1,2,3,...,n.$. It is clear that $inf\left\{{\lambda }_i(x,y)\right\}\le inf\left\{S_i^{-1}(x,y)\right\}.$ Now we need to show that ${\psi }^{-1}(x,y)=inf\left\{S_i^{-1}(x,y)\right\}$, for each i. Now

$$\begin{array}{ccc}\hfill {\psi }^{-1}(x,y)& =\left\{\psi \right(y,x):(x,y)\in X\times X\}\hfill & \\ \hfill & =\{inf\left\{S_i(y,x)\right\}:(x,y)\in X\times X,\mathrm{for}\mathrm{each}i\}\hfill & \\ \hfill & =\{inf\left\{S_i^{-1}(x,y)\right\}:(x,y)\in X\times X\}\hfill & \\ \hfill \Rightarrow {\psi }^{-1}(x,y)& =inf\left\{S_i^{-1}(x,y)\right\}.\hfill \end{array}$$

Let ${\psi }^{★}\in \Phi$ and let $inf\left\{{\lambda }_i(x,y)\right\}={\psi }^{★}(x,y)$ such that ${\psi }^{★}(x,y)=inf\left\{{\lambda }_i(x,y)\right\}\le inf\left\{S_i^{-1}(x,y)\right\}={\psi }^{-1}(x,y)$. Which implies that ${\psi }^{★}\subseteq {\psi }^{-1}$.

Hence, ${\psi }^{-1}$ contains some elements of $\Phi$.

3. Let $\psi \in \Phi$. Define $\psi (x,y)=inf\{S_i(x,y),S_i\in \mathfrak{S}\}$, for some i, from condition (3), then there exist ${\lambda }_i\in \mathfrak{S}$ such that ${\lambda }_i\circ {\lambda }_i\subseteq S_i$, for each $i=1,2,3,...,n$ implies that $inf\left\{({\lambda }_i\circ {\lambda }_i)(x,y)\right\}\le inf\left\{{\lambda }_i(x,y)\right\}\circ inf\left\{{\lambda }_i(x,y)\right\}\le inf\left\{S_i(x,y)\right\},$ for some i. Let ${\psi }^{★}\in \Phi$ and let $inf\left\{{\lambda }_i(x,y)\right\}={\psi }^{★}(x,y)$. Hence, ${\psi }^{★}\circ {\psi }^{★}\subseteq \psi$. For all $\psi \in \Phi$, there exist ${\psi }^{★}$ such that ${\psi }^{★}\circ {\psi }^{★}\subseteq \psi .$

4. Let $\psi ,{\psi }^{*}\in \Phi$. Define $\psi (x,y)=inf\{S_i(x,y)$, for each $i=1,2,3,...,n\}$ and ${\psi }^{*}(x,y)=inf\{S_i(x,y),$ for each $i=1,2,3,...,k\}$. Now, $min\{\psi (x,y),{\psi }^{*}(x,y)\}=min\{inf\left\{S_i(x,y)\right\},inf\left\{S_i(x,y)\right\}\}=inf\{S_i(x,y)$, for each $i=1,2,3,...,t\}$, where $t=min\{k,n\}$. Which implies that $\psi \cap {\psi }^{*}$ contains it self where $\psi \cap {\psi }^{*}\in \Phi .$ Thus by Theorem 3.7$\Phi$ is a base for a fuzzy uniform space $(X,K)$. Therefore, $\mathfrak{S}$ is a subbase for a fuzzy uniform space. □

Theorem 3.10. 

Let $\omega =\{{\beta }_{\mu }:\mu \in \aleph \}$, then ω is a subbase for a fuzzy uniformity.

Proof. 

$\omega$ satisfies all conditoins of Proposition 3.9 becuase ${\psi }_{\mu }$ is a fuzzy equvalance relation and by Theorem 3.3. So it is easy to show $\omega$ is a subabse for a fuzzy uniformity. □

Lemma 3.11. 

Let ψ and ϕ be fuzzy relations. If $\psi \subseteq \varphi$, then ${\psi }^{\left[x\right]}\subseteq {\varphi }^{\left[x\right]}$, for $x\in X$.

Proof. 

Suppose that $\psi$, $\varphi$ are fuzzy relations, and $\psi \subseteq \varphi$. We claim that ${\psi }^{\left[x\right]}\subseteq {\varphi }^{\left[x\right]}$. Now, there exist $b\in X$ such that ${\psi }^{\left[x\right]}\left(b\right)=\psi (x,b)\le \varphi (x,b)\Rightarrow {\psi }^{\left[x\right]}\left(b\right)\le {\varphi }^{\left[x\right]}\left(b\right)$. Which implies that ${\psi }^{\left[x\right]}\subseteq {\varphi }^{\left[x\right]}$. □

Lemma 3.12. 

Let $\mu ,\lambda \in \aleph$. If $\lambda \subseteq \mu$, then ${\psi }_{\lambda }\subseteq {\psi }_{\mu }.$

Proof. 

Suppose $\lambda \subseteq \mu$ that is $\lambda \left(x\right)\le \mu \left(x\right)$.

Now, ${\psi }_{\lambda }(x,y)=min\{\lambda (x·y),\lambda (y·x),\lambda (x★y),\lambda (y★x)\}\le min\{\mu (x·y),\mu (y·x),\mu (x★y),\mu (y★x)\}={\psi }_{\mu }(x,y)$. Hence, ${\psi }_{\lambda }\subseteq {\psi }_{\mu }.$ □

Theorem 3.13. 

Let $(X,K)$ be a fuzzy uniform structure, then $\tau =\{G\subseteq I^X:G\left(x\right)=1,\mathrm{there}\mathrm{exist}\psi \in K,{\psi }^{\left[x\right]}\subseteq G\}$ is a fuzzy topology on a PUP algebra X.

Proof. 

Define $\tau =\{G\subseteq I^X:G\left(x\right)=1,\mathrm{there}\mathrm{exist}\psi \in K,{\psi }^{\left[x\right]}\subseteq G\}$. We need to show that $\tau$ is a fuzzy topology on X. Let $(X,K)$ be a fuzzy uniform stucture, there exist $\psi \in K,1_X\left(x\right)=1$, forall $x\in X$ then ${\psi }^{\left[x\right]}\subseteq 1_X$. Thus $1_X\in \tau$.

Suppose $0\in K$ and we define $0^{\left[x\right]}\left(y\right)=0(x,y)=\left\{\begin{array}{cc}1,\hfill & ifx=y\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$

A fuzzy subset in X is empty iff its membership function is identically zero on X and it is denoted by $0_X$. And we define the fuzzy sets $0_X\left(x\right)=\left\{\begin{array}{cc}0,\hfill & ifx\in X\hfill \\ 1,\hfill & ifx\notin X.\hfill \end{array}\right.$. Then which implies that $0^{\left[x\right]}\subseteq 0_X$ for all $x\notin X.$ Thus, $0_X\in \tau$.

Let $\left\{G_{i,i\in I}\right\}\subseteq \tau .$ We need to show that ${\cup }_{i\in I}{G}_i\in \tau .$ By the definition of $\tau$, for each $G_i\in \tau$, there exist ${\psi }_i\in K$ such that ${\psi }_i^{\left[x\right]}\subseteq G_i$. This implies that ${\psi }_i^{\left[x\right]}\subseteq {\cup }_{i\in I}{G}_i.$ Hence, ${\cup }_{i\in I}{G}_i\in \tau .$

Let $G_1,G_2\in \tau$. By definition there exist ${\psi }_1,{\psi }_2\in K$ such that ${\psi }_1^{\left[x\right]}\subseteq G_1$ and ${\psi }_2^{\left[x\right]}\subseteq G_2$, for all $x\in X$. Consider $G=G_1\cap G_2$, then $G\left(x\right)=min\{G_1\left(x\right),G_2\left(x\right)\}$. We need to show that there exist $\psi \in K$ such that ${\psi }^{\left[x\right]}\subseteq G$. Since K is a fuzzy uniformity, it is closed under finite intersections. Therefore, $\psi ={\psi }_1\cap {\psi }_2$. For each $x\in X,{\psi }^{\left[x\right]}\subseteq {\psi }_1^{\left[x\right]}\cap {\psi }_2^{\left[x\right]}\subseteq G_1\cap G_2=G\Rightarrow G\in \tau .$ Therefore, $\tau$ is closed under finite intersection. Hence, $\tau$ is a fuzzy topology on X. □

Theorem 3.14. 

Let Φ be a base for the fuzzy uniformity K and $x\in X$. Then $\{{\varphi }^{\left[x\right]}:\varphi \in \Phi \}$ is a base for the fuzzy topology τ.

Proof. 

Let $(X,K)$ be a fuzzy uniform space. Let $\tau =\{G\subseteq I^X:G\left(x\right)=1,\mathrm{there}\mathrm{exist}\psi \in K,{\psi }^{\left[x\right]}\subseteq G\}$ be a fuzzy topology on X. Let $\Phi$ be a base for fuzzy uniformity K.

Consider $G_B=\{{\varphi }^{\left[x\right]}:\varphi \in \Phi \}.$ We need to show that $G_B$ is a base for a fuzzy topological space. By Theorem 3.13$G\left(x\right)=1$, then there exist $\psi \in K$ such that ${\psi }^{\left[x\right]}\subseteq G$. Since $\Phi$ is a base for fuzzy uniform space, then there exist $\varphi \in \Phi$ such that $\varphi \subseteq \psi$. By Lemma 3.11, we have, ${\varphi }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}\Rightarrow {\varphi }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}\subseteq G$. Which implies that ${\varphi }^{\left[x\right]}\subseteq G$. For all $G\in \tau$, there exist ${\varphi }^{\left[x\right]}\in G_B$ such that ${\varphi }^{\left[x\right]}\subseteq G$. By Definition 5, $G_B$ is a base for a fuzzy topology $\tau$ on X. □

4. Fuzzy Uniform Topological Space

Note that from Theorem 3.13 the family ℵ of extreme fuzzy PUP ideals of the PUP-algebra X is closed under intersection. This allows us to induce a fuzzy uniform topology ${\tau }_{\aleph }$ on X. In this section, we explore the fuzzy topological properties on $(X,{\tau }_{\aleph })$. Let X be a PUP-algebra and suppose ${\psi }_{\mu }^{\left[x\right]}$, ${\psi }_{\lambda }^{\left[y\right]}$ are belongs to ${\tau }_{\aleph }$, then we define

$$({\psi }_{\mu }^{\left[x\right]}·{\psi }_{\lambda }^{\left[y\right]})\left(r\right)=\underset{r=a·b}{sup}\left\{min\{{\psi }_{\mu }(x,a),{\psi }_{\lambda }(y,b)\}\right\}\mathrm{and}({\psi }_{\mu }^{\left[x\right]}★{\psi }_{\lambda }^{\left[y\right]})\left(t\right)=\underset{t=a★b}{sup}\left\{min\{{\psi }_{\mu }(x,a),{\psi }_{\lambda }(y,b)\}\right\}.$$

Definition 4.1. 

A pseudo-UP algebra X equipped with a fuzzy topology τ is called a fuzzy topological PUP algebra if for each an open fuzzy set G neighborhood of $x·y$, and open fuzzy set H neighborhood of $x★y$, then there exist two open fuzzy sets $U,V$ neighborhoods of x and y, respectively such that $U·V\subseteq G,U★V\subseteq H$.

Definition 4.2. 

If $(X,K)$ is a fuzzy uniform space, then the fuzzy topology τ is called fuzzy uniform topology on X induced by K.

Theorem 4.3. 

Let $(X,{\tau }_{\aleph })$ be a fuzzy uniform topological space. Then ${\mathfrak{B}}_{\aleph }=\{{\psi }_{\mu }^{\left[x\right]}:x\in X\}$ is a base for ${\tau }_{\aleph }.$

Proof. 

Let $(X,{\tau }_{\aleph })$ be a fuzzy uniform topological space. For $\psi \in K$, and for all $x\in X$, we get ${\psi }_{\mu }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}.$ Then ${\tau }_{\aleph }=\{G\subseteq I^X:G\left(x\right)=1\exists \mu \in \aleph \mathrm{such}\mathrm{that}{\psi }_{\mu }^{\left[x\right]}\subseteq G\}.$ Then it is easy show that ${\mathfrak{B}}_{\aleph }$ is a base for ${\tau }_{\aleph }$. That is, for all $G\in {\tau }_{\aleph }$, there exist ${\psi }_{\mu }^{\left[x\right]}\in {\mathfrak{B}}_{\aleph }$ such that ${\psi }_{\mu }^{\left[x\right]}\subseteq G$. By Definition 5, ${\mathfrak{B}}_{\aleph }$ is a base for a fuzzy uniform topology on X. □

Theorem 4.4. 

In a pseudo-UP algebra X, let ${\tau }_{\aleph }$ be a fuzzy uniform topology induced by K. Then $(X,{\tau }_{\aleph })$ is a fuzzy topological PUP algebra.

Proof. 

Define $K=\{\psi :{\psi }_{\mu }\subseteq \psi ,\mathrm{for}\mathrm{some}{\psi }_{\mu }\in K^{★}\}$. For all $\psi \in K,\mu \in \aleph$, and for all $x\in X$ we get ${\psi }_{\mu }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}$ for some ${\psi }_{\mu }\in K^{★}$. Then ${\tau }_{\aleph }=\{G\subseteq I^X:G\left(x\right)=1,\exists \mu \in \aleph \mathrm{such}\mathrm{that}{\psi }_{\mu }^{\left[x\right]}\subseteq G\}$ be a fuzzy uniform topology on X, and G and H are fuzzy open set of ${\tau }_{\aleph }$ such that $G(x·y)=1$ and $H(x★y)=1$. Which implies that there exist $\psi \in K$ such that ${\psi }^{[x·y]}\subseteq G$ and ${\psi }^{[x★y]}\subseteq H$. Since $\mu$ is an extreme fuzzy PUP ideal such that ${\psi }_{\mu }\subseteq \psi .$

We claim that ${\psi }_{\mu }^{\left[x\right]}·{\psi }_{\mu }^{\left[y\right]}\subseteq G$ and ${\psi }_{\mu }^{\left[x\right]}★{\psi }_{\mu }^{\left[y\right]}\subseteq H.$ Now

$$\begin{array}{ccc}\hfill ({\psi }_{\mu }^{\left[x\right]}·{\psi }_{\mu }^{\left[y\right]})\left(r\right)& =\underset{r=a·b}{sup}\{min\{{\psi }_{\mu }^{\left[x\right]}\left(a\right),{\psi }_{\mu }^{\left[y\right]}\left(b\right)\}\}\hfill & \\ \hfill & =\underset{r=a·b}{sup}\left\{min\{{\psi }_{\mu }(x,a),{\psi }_{\mu }(y,b)\}\right\}\hfill & \\ \hfill & \le \underset{r=a·b}{sup}\left\{min\{\psi (x,a),\psi (y,b)\}\right\},\sin \mathrm{ce}{\psi }_{\mu }\subseteq \psi \hfill & \\ \hfill & \le \underset{r=a·b}{sup}\left\{\psi (x·y,a·b)\right\},\mathrm{by}\mathrm{Theorem}\hfill & \\ \hfill & =\underset{r=a·b}{sup}\left\{{\psi }^{[x·y]}(a·b)\right\}\hfill & \\ \hfill \Rightarrow \underset{r=a·b}{sup}\left\{{\psi }^{[x·y]}(a·b)\right\}& \le G(a·b).\hfill \end{array}$$

Thus, ${\psi }_{\mu }^{\left[x\right]}·{\psi }_{\mu }^{\left[y\right]}\subseteq G.$

$$\begin{array}{ccc}\hfill ({\psi }_{\mu }^{\left[x\right]}★{\psi }_{\mu }^{\left[y\right]})\left(t\right)& =\underset{t=a★b}{sup}\{min\{{\psi }_{\mu }^{\left[x\right]}\left(a\right),{\psi }_{\mu }^{\left[y\right]}\left(b\right)\}\}\hfill & \\ \hfill & =\underset{t=a★b}{sup}\left\{min\{{\psi }_{\mu }(x,a),{\psi }_{\mu }(y,b)\}\right\}\hfill & \\ \hfill & \le \underset{t=a★b}{sup}\{min\left\{{\psi }_{\mu }(x★y,a★b)\right\}\},\sin \mathrm{ce}{\psi }_{\mu }\subseteq \psi \hfill & \\ \hfill & \le \underset{t=a★b}{sup}\left\{\psi (x★y,a★b)\right\},\mathrm{by}\mathrm{Theorem}\hfill & \\ \hfill & =\underset{t=a★b}{sup}\left\{{\psi }^{[x★y]}(a★b)\right\}\hfill & \\ \hfill \Rightarrow \underset{t=a★b}{sup}\left\{{\psi }^{[x★y]}(a★b)\right\}& \le H(a★b).\hfill \end{array}$$

Thus, ${\psi }_{\mu }^{\left[x\right]}★{\psi }_{\mu }^{\left[y\right]}\subseteq H.$

Hence, $(X,{\tau }_{\aleph })$ is a fuzzy topological PUP-algebra. □

Theorem 4.5. 

Let $\mu ,\lambda \in \aleph$. If $\lambda \subseteq \mu$, then ${\tau }_{\mu }\subseteq {\tau }_{\lambda }.$

Proof. 

Suppose $\aleph =\left\{\mu \right\}$, $K^{★}=\left\{{\psi }_{\mu }\right\}$ and $K=\{\psi :{\psi }_{\mu }\subseteq \psi ,\mathrm{for}\mathrm{some}{\psi }_{\mu }\in K^{★}\}.$ Let $O\in {\tau }_{\mu }$. Then for all $x\in X$ such that $O\left(x\right)=1,$ there exist $\psi \in K$ such that ${\psi }^{\left[x\right]}\subseteq O$ and so ${\psi }_{\mu }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}\subseteq O.$ By Lemma 3.12${\psi }_{\lambda }\subseteq {\psi }_{\mu }.$ It follows that ${\psi }_{\lambda }^{\left[x\right]}\subseteq {\psi }_{\mu }^{\left[x\right]}\subseteq O\Rightarrow O\in {\tau }_{\lambda }$. Hence, ${\tau }_{\mu }\subseteq {\tau }_{\lambda }.$ □

Theorem 4.6. 

Let ℵ be a family of extreme fuzzy PUP ideals of a PUP-algebra X which is closed under intersection. If $\lambda =\cap \{\mu :\mu \in \aleph \}$, then ${\tau }_{\aleph }={\tau }_{\lambda }$.

Proof. 

Let K and $K^{★}$ defined as in Definition 3. Now consider ${\aleph }_1=\left\{\lambda \right\}$ and define $K_1=\{\psi :{\psi }_{\lambda }\subseteq \psi \}$ and $K_1^{★}=\left\{{\psi }_{\lambda }\right\}.$ Suppose that $O\in {\tau }_{\aleph }.$ Then $O\left(x\right)=1$ there exist a fuzzy relation $\psi \in K$ such that ${\psi }^{\left[x\right]}\subseteq O$. Since $\psi \in K$ there exist $\mu \in \aleph$ such that ${\psi }_{\mu }^{\left[x\right]}\subseteq \psi$. Since $\lambda \subseteq \mu$ by Lemma 3.12${\psi }_{\lambda }\subseteq {\psi }_{\mu }.$ Hence, ${\psi }_{\lambda }^{\left[x\right]}\subseteq {\psi }_{\mu }^{\left[x\right]}\subseteq O$, which implies that $O\in {\tau }_{\lambda }$. Therefore, ${\tau }_{\aleph }\subseteq {\tau }_{\lambda }.$

Conversely, let $O\in {\tau }_{\lambda }$. Then for all $x\in X$ such that $O\left(x\right)=1$, there exist $\psi \in K_1$ such that ${\psi }^{\left[x\right]}\subseteq O$. So, ${\psi }_{\lambda }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}$. Since ℵ is closed under intersection, then $\lambda \in \aleph$. Then we obtain ${\psi }_{\lambda }\in K$ and $O\in {\tau }_{\aleph }\Rightarrow {\tau }_{\lambda }\subseteq {\tau }_{\aleph }$. Hence, ${\tau }_{\lambda }={\tau }_{\aleph }.$ □

Definition 4.7. 

Let $(X,K)$ be a fuzzy uniform structure is called fuzzy compact set if every fuzzy open cover has a finite fuzzy sub cover.

Theorem 4.8. 

Let μ be an extreme fuzzy PUP ideal of X, then μ is fuzzy compact in $(X,{\tau }_{\mu })$.

Proof. 

For $\psi \in K,\mu \in \aleph$, for all $x\in X$ such that ${\psi }_{\mu }^{\left[x\right]}\subseteq {\psi }^{\left[x\right]}$, then we get ${\tau }_{\mu }=\{O:O\left(x\right)=1,{\psi }_{\mu }^{\left[x\right]}\subseteq O\}$. Suppose that ${\psi }_{\mu }^{\left[x\right]}\subseteq {\cup }_{i\in \Lambda }{O}_i$, where $O_i$ is fuzzy open set in ${\tau }_{\mu }$, for each $i\in \Lambda$. Since $\mu \left(0\right)=1$ and there exist $i\in \Lambda$ such that $O_i\left(0\right)=1$. Then an extreme fuzzy PUP ideal $\mu \left(0\right)={\psi }_{\mu }^{\left[0\right]}\left(0\right)$. Which implies that $\mu ={\psi }_{\mu }^{\left[0\right]}\subseteq O_i$. Since $\mu$ is entirely contained in one of the fuzzy open set $O_i$. Hence, $\mu$ is a fuzzy compact of $(X,{\tau }_{\mu }).$ □

Theorem 4.9. 

Let ℵ be a family of extreme fuzzy PUP ideals of a PUP algebra X which is closed under intersection. If $\lambda =\cap \{\mu :\mu \in \aleph \}$ then for all $x\in X$, ${\psi }_{\lambda }^{\left[x\right]}$ is fuzzy compact in $(X,{\tau }_{\aleph }).$

Proof. 

Suppose $\lambda =\cap \{\mu :\mu \in \aleph \}$. Let ${\psi }_{\lambda }^{\left[x\right]}\subseteq {\cup }_{i\in \Lambda }{O}_i$, where $O_i$ is a fuzzy open set of ${\tau }_{\aleph }$ and $\Lambda$ is any index set. For $x\in X$ such that $O_i\left(x\right)=1$. Then ${\psi }_{\lambda }^{\left[x\right]}\subseteq O_i$. Hence, ${\psi }_{\lambda }^{\left[x\right]}$ is a fuzzy compact in $(X,{\tau }_{\aleph })$. □

Definition 4.10. 

Let $(X,{\tau }_{\aleph })$ be a fuzzy topological space where ℵ is a family of an extreme fuzzy PUP ideals of X and $\mu \in \aleph$. Then for any fuzzy subset λ of X, $cl\left(\lambda \right)\left(x\right)=inf\{{\psi }_{\mu }^{\left[\lambda \right]}\left(x\right):{\psi }_{\mu }\in K^{★}\}.$

Theorem 4.11. 

Let $f:X\to Y$ be a PUP homomorphism between two PUP algebras of X and Y and let μ be an extreme fuzzy PUP ideal of Y, then for $x_1,x_2$

$${\psi }_{f^{-1}\left(\mu \right)}(x_1,x_2)={\psi }_{\mu }(f\left(x_1\right),f\left(x_2\right)).$$

Proof. 

For all $x_1,x_2\in X,$ we have

$$\begin{array}{ccc}\hfill {\psi }_{f^{-1}\left(\mu \right)}(x_1,x_2)& =min\{f^{-1}\left(\mu \right)(x_1·x_2),f^{-1}\left(\mu \right)(x_2·x_1),f^{-1}\left(\mu \right)(x_1★x_2),f^{-1}\left(\mu \right)(x_2★x_1)\}\hfill & \\ \hfill & =min\{\mu \left(f(x_1·x_2)\right),\mu \left(f(x_2·x_1)\right),\mu \left(f(x_1★x_2)\right),\mu \left(f(x_2★x_1)\right)\}\hfill & \\ \hfill & =min\{\mu (f\left(x_1\right)·f\left(x_2\right)),\mu (f\left(x_2\right)·f\left(x_1\right)),\mu (f\left(x_1\right)★f\left(x_2\right)),\mu (f\left(x_2\right)★f\left(x_1\right))\}\hfill & \\ \hfill & ={\psi }_{\mu }(f\left(x_1\right),f\left(x_2\right)).\hfill \end{array}$$

Hence, ${\psi }_{f^{-1}\left(\mu \right)}(x_1,x_2)={\psi }_{\mu }(f\left(x_1\right),f\left(x_2\right)).$ □

Theorem 4.12. 

Let $f:X\to Y$ be a PUP isomorphism between two PUP-algebras $X,Y$ and let μ be an extreme fuzzy PUP ideal in Y. Then the following statements hold, for all $x\in Y$ and $y\in Y$.

1)

$f\left({\psi }_{f^{-1}\left(\mu \right)}^{\left[x\right]}\right)\ge {\psi }_{\mu }^{\left[f\right(x\left)\right]}.$

2)

$f^{-1}\left({\psi }_{\mu }^{\left[y\right]}\right)={\psi }_{f^{-1}\left(\mu \right)}^{\left[f^{-1}\left(y\right)\right]}.$

Proof. 

1) Let $y\in Y$, then there exist $x_1\in X$ such that $f\left(x_1\right)=y.$ Now

$$\begin{array}{ccc}\hfill f\left({\psi }_{f^{-1}\left(\mu \right)}^{\left[x\right]}\right)\left(y\right)& =\underset{x_1\in f\left(y\right)}{sup}\{{\psi }_{f^{-1}\left(\mu \right)}^{\left[x\right]}\left(x_1\right),f^{-1}\left(y\right)\ne \varnothing \}\hfill & \\ \hfill & =\underset{x_1\in f^{-1}\left(y\right)}{sup}\left\{{\psi }_{f^{-1}\left(\mu \right)}(x,x_1)\right\}\hfill & \\ \hfill & =\underset{x_1\in f^{-1}\left(y\right)}{sup}\left\{min\{f^{-1}\left(\mu \right)(x·x_1),f^{-1}\left(\mu \right)(x★x_1),f^{-1}\left(\mu \right)(x_1·x),f^{-1}\left(\mu \right)(x_1★x)\}\right\}\hfill & \\ \hfill & =\underset{x_1\in f^{-1}\left(y\right)}{sup}\left\{min\{\mu \left(f(x·x_1)\right),\mu \left(f(x★x_1)\right),\mu \left(f(x_1·x)\right),\mu \left(f(x_1★x)\right)\}\right\}\hfill & \\ \hfill & =\underset{x_1\in f^{-1}\left(y\right)}{sup}\left\{min\{\mu (f\left(x\right)·f\left(x_1\right)),\mu (f\left(x\right)★f\left(x_1\right)),\mu (f\left(x_1\right)·f\left(x\right)),\mu (f\left(x_1\right)★f\left(x\right))\}\right\}\hfill & \\ \hfill & =\underset{x_1\in f^{-1}\left(y\right)}{sup}\left\{min\{\mu (f\left(x\right)·y),\mu (f\left(x\right)★y),\mu (y·f\left(x\right)),\mu (y★f\left(x\right))\}\right\}\hfill & \\ \hfill & =sup\left\{{\psi }_{\mu }^{\left[f\right(x\left)\right]}\left(y\right)\right\}\hfill & \\ \hfill & \ge {\psi }_{\mu }^{\left[f\right(x\left)\right]}\left(y\right).\hfill & \\ \hfill \Rightarrow f\left({\psi }_{f^{-1}\left(\mu \right)}^{\left[x\right]}\right)\left(y\right)& \ge {\psi }_{\mu }^{\left[f\right(x\left)\right]}\left(y\right)\hfill \end{array}$$

$\Rightarrow {\psi }_{\mu }^{\left[f\right(x\left)\right]}\subseteq f\left({\psi }_{f^{-1}\left(\mu \right)}^{\left[x\right]}\right)$.2) We need to show that $f^{-1}\left({\psi }_{\mu }^{\left[y\right]}\right)={\psi }_{f^{-1}\left(\mu \right)}^{\left[f^{-1}\left(y\right)\right]}.$

$$\begin{array}{ccc}\hfill f^{-1}{\left({\psi }_{\mu }\right)}^{\left[y\right]}\left(x\right)& ={\psi }_{\mu }^{\left[y\right]}\left(f\left(x\right)\right)\hfill & \\ \hfill & ={\psi }_{\mu }(f\left(x\right),y)\hfill & \\ \hfill & ={\psi }_{f^{-1}\left(\mu \right)}\left(f^{-1}(f\left(x\right),f^{-1}\left(y\right))\right),\mathrm{by}\mathrm{Theorem}\hfill & \\ \hfill & ={\psi }_{f^{-1}\left(\mu \right)}(x,f^{-1}\left(y\right))\hfill & \\ \hfill & ={\psi }_{f^{-1}\left(\mu \right)}^{\left[f^{-1\left(y\right)}\right]}\left(x\right).\hfill \end{array}$$

Therefore, $f^{-1}\left({\psi }_{\mu }^{\left[y\right]}\right)={\psi }_{f^{-1}\left(\mu \right)}^{\left[f^{-1}\left(y\right)\right]}.$ □