Techniques for Outlier Detection: A Comprehensive View

1. Introduction

1.1. Outlier Detection

Outlier detection is a critical aspect of data analysis, machine learning, and various scientific fields. Outliers, or anomalies, refer to data points that deviate significantly from the general pattern in a dataset. Their identification is vital for a variety of reasons: they can represent noise or errors in the data, but in some cases, outliers may signal valuable information such as identifying rare but important events, fraudulent activities, or even new discoveries in research (Aggarwal, 2017). Consequently, detecting and managing outliers effectively is crucial to ensuring the accuracy and reliability of data-driven models.

1.2. The Importance of Outlier Detection

Outliers can arise for several reasons, including measurement errors, data entry mistakes, or genuine anomalies. For example, in the financial sector, outliers may indicate suspicious transactions that could signal fraud (Bolton & Hand, 2002). In manufacturing, they might point to malfunctioning equipment. Effective detection of these outliers is critical for several reasons:

1. 

Model Integrity: Outliers can skew results in machine learning models, leading to inaccurate predictions or biased estimations (Aggarwal, 2017). For instance, outliers may cause overfitting, where the model becomes too attuned to anomalies rather than representing the overall data structure accurately (Hodge & Austin, 2004).

2. 

Data Cleaning: In many cases, outliers are due to data errors, such as sensor malfunctions or incorrect data entries. Identifying and removing these outliers is crucial to improving the quality of the dataset, which in turn enhances the performance of machine learning algorithms (García et al., 2016).

3. 

Anomaly Detection: Sometimes, outliers represent meaningful anomalies rather than noise. Detecting these can lead to crucial insights, such as identifying network intrusions in cybersecurity or detecting disease outbreaks in healthcare data (Chandola, Banerjee, & Kumar, 2009). These examples illustrate the value of outlier detection in real-world applications, where finding anomalies can drive business decisions or public health interventions.

1.3. Types of Outlier Detection Techniques

Several techniques exist for detecting outliers, which can be classified into three major categories: statistical methods, machine learning-based approaches, and proximity-based methods. Each has its advantages and is suitable for specific types of data and applications.

1.3.1. Statistical Methods for Outlier Detection

Statistical methods are among the oldest and most widely applied techniques for outlier detection. These methods typically rely on the assumption that the data follows a specific distribution, such as a normal distribution, to identify points that deviate from the expected behavior.

A) 

Z-Score Method

The Z-Score method measures the number of standard deviations a data point lies from the mean. It’s a popular technique for detecting outliers in normally distributed data, with data points typically considered outliers if they have a Z-score greater than 3 or less than -3 (Madsen, 2007). This method is efficient for datasets that follow a normal distribution but becomes less effective with non-normal data, where the presence of outliers may distort the mean and standard deviation.

B) 

Boxplot and Interquartile Range (IQR)

A Boxplot visualizes data distribution using quartiles and identifies outliers based on the Interquartile Range (IQR). Outliers are data points that lie beyond 1.5 times the IQR above the third quartile or below the first quartile (Tukey, 1977). The IQR method is robust and works well even with non-normal distributions (Vandervieren & Hubert, 2004). However, it may not perform optimally when applied to datasets with high dimensionality or when multiple variables interact non-linearly.

C) 

Machine Learning-Based Approaches

With the growing complexity of data, machine learning-based methods have become increasingly popular for detecting outliers. These techniques are highly flexible, capable of identifying complex patterns in data without making strong assumptions about the distribution.

D) 

Isolation Forest

The Isolation Forest is an unsupervised machine learning algorithm designed for anomaly detection. It isolates data points by constructing random decision trees and identifies anomalies as points that are isolated more quickly (Liu, Ting, & Zhou, 2008). Isolation Forest is scalable and efficient for large datasets, making it suitable for modern big data environments. However, it can be sensitive to hyperparameter settings, such as the number of trees and sample size (Hariri, Kind, & Brunner, 2019).

E) 

Support Vector Machines (SVM) for One-Class Classification

The One-Class SVM is a variation of the traditional SVM that focuses on learning the boundary for normal data points, classifying those outside this boundary as anomalies (Schölkopf et al., 2001). This method is highly effective in high-dimensional spaces and can handle non-linear relationships between variables by using kernel functions. However, SVMs require careful parameter tuning and are computationally intensive for large datasets (Tax & Duin, 2004).

F) 

Autoencoders

Autoencoders are neural networks used in unsupervised learning tasks like anomaly detection. The network learns to compress data into a lower-dimensional space (encoding) and reconstructs it back to its original form (decoding). Outliers are identified by their high reconstruction error, as the autoencoder struggles to reconstruct these anomalous points (Chalapathy & Chawla, 2019). Autoencoders are particularly useful in high-dimensional data, such as time series or images, but they require substantial amounts of training data and are computationally expensive to train and deploy.

1.3.2 Proximity-Based Methods

Proximity-based methods detect outliers by comparing the distance of a data point from its neighbors. The assumption is that normal data points are close to each other, while outliers are more isolated.

A) 

K-Nearest Neighbors (KNN)

The K-Nearest Neighbors (KNN) algorithm identifies outliers by calculating the average distance of each point to its nearest neighbors. A point is considered an outlier if this distance is significantly greater than the average distance of its neighbors (Breunig et al., 2000). KNN is simple to implement but becomes computationally expensive as the dataset size grows. Additionally, its performance is sensitive to the choice of kkk, the number of neighbors, which must be carefully selected based on the dataset (Eskin, 2000).

B) 

Local Outlier Factor (LOF)

The Local Outlier Factor (LOF) improves upon KNN by incorporating local density into its calculations. It measures the local density of a point relative to its neighbors, identifying outliers as points with significantly lower density than their surrounding points (Breunig et al., 2000). LOF is effective in datasets where anomalies occur in regions with varying densities, such as fraud detection in financial data or network intrusion detection (Campos et al., 2016). However, it is sensitive to hyperparameters and may not scale well to extremely large datasets.

1.4 Challenges in Outlier Detection

Despite the variety of techniques available, outlier detection presents several challenges:

A)

High Dimensionality: As the number of features increases, the difficulty of detecting outliers grows. In high-dimensional spaces, traditional methods like Z-Score and IQR may fail to capture complex relationships between variables. Machine learning-based methods like Autoencoders and One-Class SVMs are more suitable in such cases, but they come with increased computational costs (Aggarwal, 2015).

B)

Scalability: Many proximity-based techniques, like KNN and LOF, suffer from scalability issues in large datasets because they require calculating distances between all points. Techniques such as Isolation Forest are better suited for large-scale applications due to their efficiency in handling vast amounts of data (Liu et al., 2008).

C)

Imbalanced Data: In many cases, outliers constitute a small portion of the dataset. This imbalance can affect the performance of certain algorithms, which may be biased toward detecting the majority class. Approaches like resampling, ensemble learning, or cost-sensitive learning can help address this issue (He & Garcia, 2009).

Outlier detection is essential for improving data quality, ensuring model integrity, and identifying critical anomalies in various domains. While simple statistical methods like Z-Score and IQR are effective for smaller, normally distributed datasets, more sophisticated techniques, such as Isolation Forest and Autoencoders, are better suited for large, high-dimensional data. The appropriate choice of method depends on the nature of the dataset, the complexity of the data structure, and the specific application at hand.

The challenges of high-dimensional data, scalability, and imbalanced datasets continue to push the boundaries of outlier detection research. Future advances are likely to focus on developing more scalable and flexible techniques capable of adapting to the growing complexity of modern datasets.

2. Methodology

2.1. Machine Learning Approaches for Outlier Detection

Machine learning methods for outlier detection are powerful because they can identify complex patterns and relationships within data without relying on strong assumptions about data distributions. In this section, we focus on several prominent machine learning techniques for outlier detection: Isolation Forest, Support Vector Machines (SVM) for one-class classification, and Autoencoders. Each method is discussed with a mathematical framework, including relevant equations for a formal understanding.

2.1.1 Isolation Forest

The Isolation Forest is an ensemble method designed for anomaly detection by isolating data points using random decision trees. The core idea behind the method is that outliers are easier to isolate compared to normal data points due to their sparse nature. Let's formalize this.

A) 

Random Partitioning and Isolation

Isolation Forest works by recursively partitioning the data until each data point is isolated. A random feature $X_j$ is selected, and then a random split is made between the minimum and maximum values of that feature in the current subset of the data. For a data point $x_i$, the path length $h\left(x_i\right)$, representing the number of splits required to isolate $x_i$, forms the basis of the anomaly score.

The anomaly score $s\left(x_i\right)$  for a given point $x_i$  is computed as follows:

$$s\left(x_i\right)=2^{-{\displaystyle \frac{\left.Eh\left(x_i\right)\right]}{c(n)}}}$$

where $E\left[h\left(x_i\right)\right]$ is the expected path length of $x_i$, and $c(n)$ is the average path length of a binary search tree, given by:

$$c(n)=2H(n-1)-{\displaystyle \frac{2(n-1)}{n}}$$

where $H(i)$ is the harmonic number:

$$H(i)=\sum _{k=1}^i {\displaystyle \frac{1}{k}}$$

Anomaly score $s\left(x_i\right)$ ranges between 0 and 1, where points closer to 1 are more likely to be anomalies.

• Threshold for Anomalies

After computing the anomaly scores for all data points, a threshold can be set to label points as outliers. Typically, a score of 0.5 is considered the cutoff, with points scoring above 0.5 being classified as outliers, though this threshold can be adjusted based on domain-specific requirements.

2.2. Support Vector Machines (SVM) for One-Class Classification

One-class Support Vector Machines (SVM) are a popular method for outlier detection, particularly when dealing with high-dimensional data. The method works by finding a hyperplane that separates the data points from the origin (assuming they are mapped to a feature space through a kernel function). The algorithm attempts to find the maximal margin hyperplane that encloses the majority of the data points, considering those that fall outside as outliers.

2.2.1 Mathematical Formulation

Given a training set $\left\{x_1,x_2,\dots ,x_n\right\}$, where $x_i\in {\mathbb{R}}^d$, the goal is to find a decision function $f(x)$ such that:

$$f(x)=w^T\varphi (x)-\rho$$

where $\varphi (x)$ is a mapping of the input data into a higher-dimensional space, $w$ is a weight vector, and $\rho$ is the bias term. The optimization problem for one-class SVM is defined as:

$$\underset{w,{\xi }_i,\rho }{\mathrm{m}\mathrm{i}\mathrm{n}} {\displaystyle \frac{1}{2}}\Vert w{\Vert }^2+{\displaystyle \frac{1}{\nu n}}\sum _{i=1}^n {\xi }_i-\rho$$

subject to the constraints:

$$w^T\varphi \left(x_i\right)\ge \rho -{\xi }_i,\mathrm{}{\xi }_i\ge 0,\mathrm{}i=1,\dots ,n$$

Here, ${\xi }_i$ represents the slack variable, which allows for some points to fall outside the decision boundary, and $\nu \in (\mathrm{0,1}]$ is a hyperparameter that controls the trade-off between maximizing the margin and the amount of training error allowed.

Anomaly Detection

After solving the optimization problem, the decision function $f(x)$ is used to classify new data points. If $f(x)<0$, the point is classified as an anomaly. The kernel trick can be used to apply this method in non-linear feature spaces, such as the radial basis function (RBF) kernel:

$$K\left(x_i,x_j\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\gamma {‖x_i-x_j‖}^2\right)$$

where $\gamma$ is the kernel parameter that controls the influence of each training point on the decision boundary.

3. Autoencoders for Outlier Detection

Autoencoders are a type of neural network designed to learn a compressed representation of the input data. They are composed of two main parts: an encoder that maps the input to a lower dimensional latent space, and a decoder that attempts to reconstruct the input from the latent representation. The idea is that normal data points will be well-reconstructed, while outliers will have high reconstruction errors.

2.3.1 Neural Network Structure

Given an input $x\in {\mathbb{R}}^d$, the encoder $f_{\theta }(x)$ maps it to a latent space $z\in {\mathbb{R}}^k$, with $k<d$, as follows:

$$z=f_{\theta }(x)=\sigma \left(W_{e}x+b_e\right)$$

where $W_e$ and $b_e$ are the weight matrix and bias vector of the encoder, respectively, and $\sigma (\cdot )$ is a non-linear activation function such as ReLU or Sigmoid. The decoder $g_{\theta }(z)$ then maps $z$ back to the input space:

$$\hat{x}=g_{\theta }(z)=\sigma \left(W_{d}z+b_d\right)$$

where $W_d$ and $b_d$ are the weight matrix and bias vector of the decoder, respectively.

• Reconstruction Error

The reconstruction error for each data point is calculated as the difference between the original input $x$ and its reconstruction $\hat{x}$ :

$$L(x,\hat{x})=\Vert x-\hat{x}{\Vert }^2$$

If the reconstruction error exceeds a pre-defined threshold, the data point is classified as an outlier. The threshold is usually determined empirically by analyzing the distribution of reconstruction errors across the dataset.

2.4. Hyperparameter Selection

In all machine learning methods for outlier detection, hyperparameter tuning is crucial to optimize performance. For Isolation Forest, the number of trees and sub-sample size are important hyperparameters that control the effectiveness of anomaly detection (Liu, Ting, & Zhou, 2008). In the case of one-class SVMs, the choice of kernel and the value of $\nu$ significantly affect the decision boundary's shape and the model's sensitivity to outliers. For autoencoders, the architecture (number of layers, neurons per layer), the activation function, and the threshold for reconstruction error must be carefully selected.Overall, machine learning approaches for outlier detection provide powerful tools for identifying anomalies in complex, high-dimensional datasets. Isolation Forest isolates data points using random partitioning, while one-class SVMs construct a boundary around normal data points in a highdimensional space. Autoencoders learn a compressed representation of the data and detect anomalies based on reconstruction errors. Each method offers advantages depending on the nature of the dataset, with the mathematical formulations providing a rigorous foundation for their operation.

4. Results

4.1. Outlier Detection Using Machine Learning Methods

In this section, we discuss the graphical outputs generated by each machine learning method for outlier detection: Isolation Forest, One-Class SVM, and Autoencoder. Each method was applied to a synthetic dataset containing both normal data points and artificially generated outliers. The results highlight the strengths and weaknesses of each approach.

4.1.1. Isolation Forest

In the graph generated by the Isolation Forest method (Graph 1), we can observe that the algorithm has effectively separated normal data points (blue) from outliers (red). The blue points are clustered tightly around the center of the plot, while the red points are more spread out and located on the edges. This aligns with the Isolation Forest's mechanism of recursively partitioning the feature space to isolate outliers.

Graph 1. Isolation Forest Outlier Detection with normal data and outliers properly depicted. Source: Author.

Graph 1. Isolation Forest Outlier Detection with normal data and outliers properly depicted. Source: Author.

Since outliers are typically more isolated in the dataset, they are easier to "cut off" by the random partitions. In this case, the model identified the extreme values outside the clusters as outliers, which is expected, given the random distribution of the outliers in the synthetic data.

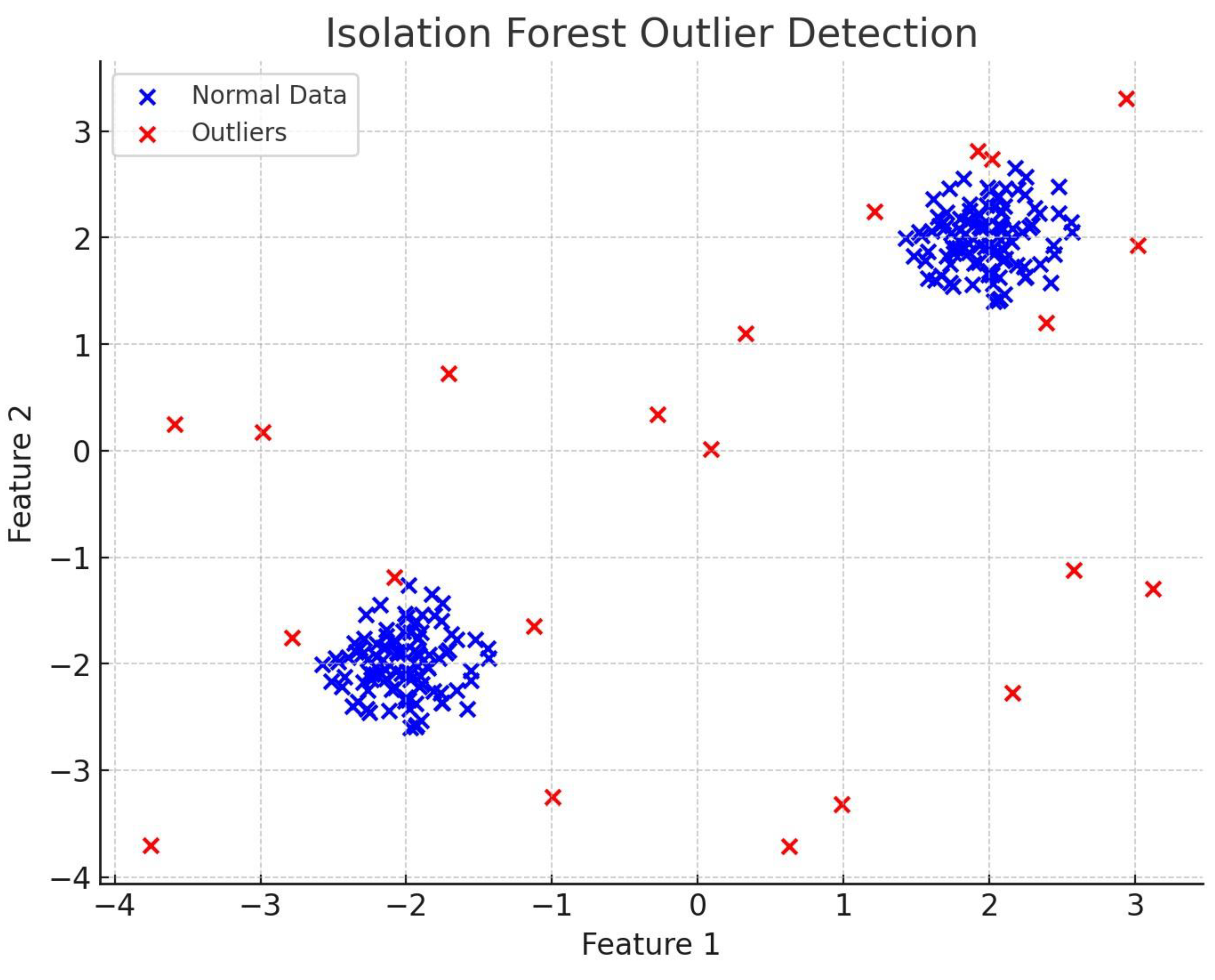
• Observations:

• Effectiveness: Isolation Forest performed well, detecting most of the outliers that were scattered around the edge of the feature space.
• Limitations: The performance is highly dependent on the contamination parameter, which determines the proportion of outliers. If this is not chosen carefully, the algorithm may misclassify normal data points as outliers.

4.1.2. One-Class SVM

The graph produced by the One-Class SVM algorithm (Graph 2) shows similar results to the Isolation Forest. Normal data points (blue) are located in dense regions near the center, while outliers (red) are scattered farther away. One-Class SVM effectively creates a boundary around the majority of the data points, treating points outside this boundary as anomalies.

Graph 2. One Class SVM Outlier Detection with normal data and outliers. Source: Author.

Graph 2. One Class SVM Outlier Detection with normal data and outliers. Source: Author.

Graph 3. Autoencoder Outlier Detection: a neural network that learns to compress and reconstruct data. Source: Author

Graph 3. Autoencoder Outlier Detection: a neural network that learns to compress and reconstruct data. Source: Author

This boundary-based approach is particularly useful in high-dimensional datasets or non-linearly separable data, as it constructs a non-linear boundary (thanks to the RBF kernel used) that encloses most of the normal data. The decision boundary separates normal data from outliers based on the distance from this hyperplane.

Observations:

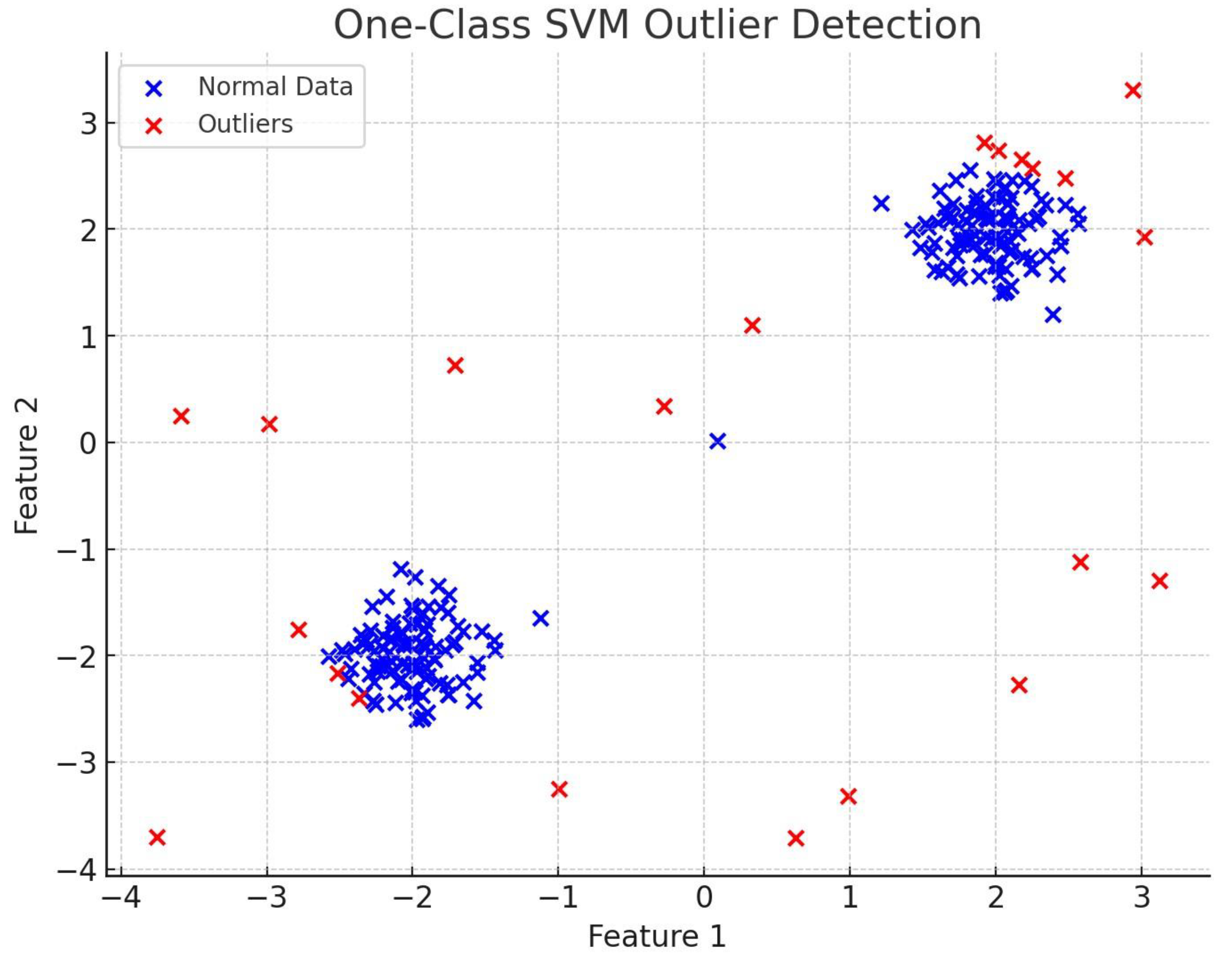
• Effectiveness: One-Class SVM performed well in detecting the outliers scattered around the dense clusters. The use of the RBF kernel helps capture the non-linearity in the dataset, improving accuracy.
• Limitations: One-Class SVM is sensitive to hyperparameters like the kernel parameter γ\gammaγ and ν\nuν, which controls the fraction of outliers. Adjusting these parameters is crucial for obtaining good results. Additionally, the computational complexity increases significantly for larger datasets.

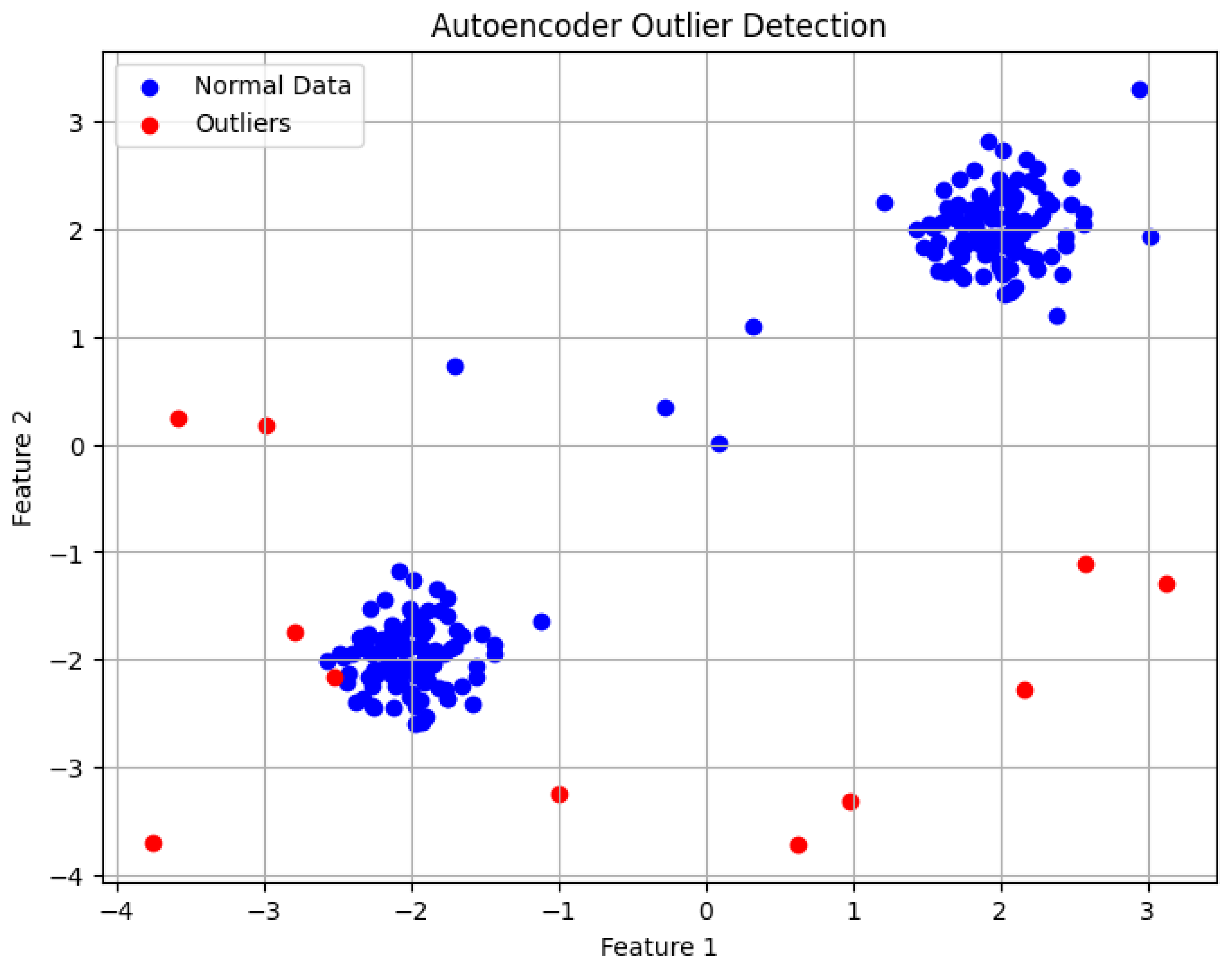
4.1.3. Autoencoder

The Autoencoder method also produced a graph showing the detected normal data points (blue) and outliers (red). The Autoencoder is a neural network that learns to compress and reconstruct the data. In this case, the normal data points were reconstructed with minimal error, while outliers had higher reconstruction errors, which is why they were classified as anomalies.

In the plot, we see that most of the points near the central clusters were classified as normal data, while the points scattered outside these clusters were classified as outliers. The threshold for reconstruction error (95th percentile) ensured that only the most extreme reconstruction errors were flagged as outliers.

• Observations:

• Effectiveness: The Autoencoder captured complex patterns in the data and accurately reconstructed normal data points. The model effectively identified outliers that differed significantly from the majority of the data.
• Limitations: Autoencoders require substantial amounts of data for training and are computationally expensive, particularly when dealing with high-dimensional data. Additionally, setting the threshold for reconstruction error is an empirical process that can vary depending on the dataset. Choosing a poor threshold can lead to false positives or missed outliers.

4.2. Summary of Results

The graphical outputs from each method highlight the differences in their approach to detecting outliers:

• Isolation Forest: Random partitioning allows Isolation Forest to efficiently isolate outliers, making it suitable for large datasets with complex relationships.
• One-Class SVM: The ability to create a flexible boundary around normal data points makes One-Class SVM effective in high-dimensional or non-linearly separable data. However, it is computationally intensive and requires careful parameter tuning.
• Autoencoder: Autoencoders are powerful in identifying outliers by measuring reconstruction error, making them suitable for high-dimensional datasets. However, they are resource-intensive and require substantial training data.
• Each method has its strengths and is suitable for different use cases. Isolation Forest is ideal for large-scale applications, while One-Class SVM and Autoencoders offer advantages in high-dimensional datasets. The choice of method depends on the specific characteristics of the dataset and the application context.

5.Discussion

5.1. Comparative Analysis of Machine Learning Methods for Outlier Detection

Outlier detection is an essential task in data analysis, with applications spanning across diverse fields, including finance, healthcare, and cybersecurity. In this discussion, we will evaluate the performance of the machine learning methods used—Isolation Forest, One-Class SVM, and Autoencoders—based on their effectiveness, computational efficiency, scalability, and suitability for various datasets. We will also explore their practical applications, the challenges encountered, and the potential areas for improvement.

5.2. Machine Learning Methods for Outlier Detection: Strengths and Weaknesses

The three machine learning methods explored each have distinctive approaches to identifying outliers in a dataset. While they share a common goal, their underlying mechanisms and applications differ substantially.

5.2.1. Isolation Forest

Isolation Forest is a tree-based ensemble method explicitly designed for anomaly detection. The method’s core idea—isolating outliers faster than normal data points due to their sparse nature—makes it intuitive and computationally efficient. It excels in scenarios where the dataset is large and high-dimensional.

Strengths

Scalability and Efficiency

Isolation Forest is particularly well-suited for large datasets, as its computational complexity is logarithmic with respect to the number of samples. The ensemble approach, where multiple random trees are constructed, allows the algorithm to efficiently handle high-dimensional data and complex relationships between features (Liu, Ting, & Zhou, 2008). Its ability to isolate points based on random splits means that the method does not rely on distance-based metrics or kernel transformations, which can be computationally expensive in large datasets.

Versatility in Data Distributions:

Another advantage of Isolation Forest is its independence from any assumptions regarding the distribution of the data. Unlike statistical methods that require the data to follow a specific distribution (e.g., Gaussian), Isolation Forest operates effectively in datasets with various distributions. This versatility makes it a popular choice in fields where data is often messy, noisy, and highly variable, such as fraud detection in finance (Hariri, Kind, & Brunner, 2019).

Weaknesses

Dependence on Hyperparameter:

A notable limitation of Isolation Forest is its sensitivity to the choice of hyperparameters, particularly the contamination parameter, which determines the proportion of data points classified as outliers. If this parameter is not tuned carefully, it can lead to high false positives or false negatives, especially in datasets with imbalanced classes (Aggarwal, 2017). In practice, this requires domain expertise to ensure the chosen contamination level aligns with the expected ratio of anomalies in the dataset.

Inability to Capture Contextual Outliers

While Isolation Forest is adept at identifying global outliers—points that deviate significantly from the majority of the data—it may struggle with contextual outliers. Contextual outliers are points that are anomalous only within a specific context (Campos et al., 2016). For example, a transaction amount might be normal in one region but anomalous in another. Isolation Forest’s reliance on random splits makes it less effective in capturing these nuanced relationships between features.

5.2.2. One-Class Support Vector Machine (SVM)

The One-Class SVM is a variation of the traditional SVM algorithm, which focuses on learning a boundary around normal data points in a high-dimensional space. By creating this boundary, it identifies points that lie outside it as outliers. The method is particularly powerful in scenarios involving non-linearly separable data, where the use of kernel functions allows the model to capture complex relationships between features.

Strengths

Effectiveness in High-Dimensional Data:

One-Class SVM excels in scenarios where the dataset is high-dimensional and non-linearly separable. The use of the RBF kernel (or other kernel functions) enables the algorithm to capture intricate relationships between features and model complex boundaries (Schölkopf et al., 2001). This makes it particularly suitable for applications like network intrusion detection and image recognition, where data often exhibits non-linear patterns.

Robustness to Complex Data Distributions

By mapping the input data into a higher-dimensional feature space, One-Class SVM can effectively handle datasets that do not adhere to any specific distribution. This flexibility allows it to be applied in diverse domains, such as fraud detection, medical diagnosis, and environmental monitoring (Tax & Duin, 2004).

Weaknesses

Computational Complexity

One of the primary drawbacks of One-Class SVM is its computational expense. The algorithm requires the computation of pairwise distances between data points, which scales poorly with large datasets. The complexity of One-Class SVM increases quadratically with the number of data points, making it unsuitable for applications involving millions of records unless the dataset is carefully pre-processed (Eskin, 2000).

Sensitivity to Hyperparameters:

Similar to Isolation Forest, One-Class SVM is highly sensitive to hyperparameters, particularly the nu (ν) parameter and the gamma (γ) parameter in the RBF kernel (Schölkopf et al., 2001). The nu parameter controls the fraction of outliers that the model allows, while gamma influences the smoothness of the decision boundary. Improper tuning of these parameters can significantly degrade the model’s performance, leading to false positives or missed anomalies.

Imbalanced Data Challenges

In highly imbalanced datasets, where the number of outliers is small compared to normal data points, One-Class SVM may suffer from overfitting to the majority class. This can result in a decision boundary that fails to generalize well to new data, particularly when the anomalies are subtle or sparse (Manevitz & Yousef, 2001). Strategies like oversampling, undersampling, or adjusting the class weights can partially mitigate this issue, but they often introduce new challenges in model training.

5.2.3. Autoencoders

Autoencoders are neural networks designed to learn a compact representation of the data (the encoding) and subsequently reconstruct the original input from this reduced representation (the decoding). Outliers are identified based on their reconstruction error—the difference between the original input and the autoencoder’s reconstruction.

Strengths

Effective in High-Dimensional Spaces

Autoencoders are particularly well-suited for high-dimensional datasets, such as image data, time-series data, and sensor data. By compressing the data into a lower-dimensional latent space, the autoencoder can capture the most important features, while ignoring noise and irrelevant details (Chalapathy & Chawla, 2019). This makes them powerful tools for tasks like image anomaly detection, where detecting small deviations from the normal pattern is critical.

Flexibility in Network Design

Autoencoders provide flexibility in designing the network architecture, allowing users to tailor the number of layers, neurons per layer, and activation functions to suit the specific dataset. This flexibility is a significant advantage when dealing with complex, high-dimensional data that requires sophisticated feature extraction. For example, autoencoders can be adapted for time-series anomaly detection, where the temporal aspect of the data adds an additional layer of complexity (Malhotra et al., 2016).

Weaknesses

Computational and Data Requirements

Despite their power, autoencoders have several limitations. Training a deep autoencoder requires a substantial amount of computational resources and data, particularly if the model has multiple layers. Large datasets are necessary to ensure the autoencoder learns a meaningful latent representation, and training deep neural networks is time-consuming (Chalapathy & Chawla, 2019). In scenarios where data is scarce or computational resources are limited, autoencoders may not be the best choice.

Choosing the Right Threshold for Reconstruction Error

An additional challenge with autoencoders is determining the right threshold for classifying a data point as an outlier based on its reconstruction error. This threshold is often chosen empirically, based on the distribution of reconstruction errors across the dataset. However, choosing an inappropriate threshold can result in false positives (classifying normal data as outliers) or false negatives (failing to detect genuine outliers). Techniques like using percentile-based thresholds or cross-validation can help mitigate this issue, but they require additional computation (Aggarwal, 2015).

Lack of Explainability

Finally, autoencoders, like most neural networks, suffer from a lack of interpretability. While the model may be able to detect outliers effectively, it provides little insight into why a particular point is classified as an outlier. This is particularly problematic in domains like healthcare or finance, where explainability is critical for decision-making (Rudin, 2019). Although there are ongoing research efforts to improve the interpretability of neural networks, such as attention mechanisms and layer-wise relevance propagation, these techniques are not yet widely adopted in anomaly detection.

5.3 Practical Applications and Domain-Specific Considerations

Each of the machine learning methods discussed has unique strengths that make them more suitable for specific types of datasets and applications. Below, we outline a few domain-specific applications and discuss which methods are best suited for each.

5.3.1. Financial Fraud Detection

In the financial sector, detecting fraud in transactions is a critical application of outlier detection. Isolation Forest has been widely used in this domain due to its scalability and effectiveness in identifying fraudulent transactions, which are typically sparse and spread across a large feature space. Additionally, the algorithm’s ability to handle large-scale data and its relatively low computational cost make it ideal for real-time fraud detection (Bolton & Hand, 2002).

For more complex fraud patterns that involve intricate relationships between features, One-Class SVM may offer superior performance due to its ability to capture non-linear relationships. However, the computational overhead associated with SVM may make it less suitable for real-time applications.

6. Conclusions

In this article, we explored three machine learning techniques for outlier detection—Isolation Forest, One-Class Support Vector Machines (SVM), and Autoencoders—each providing unique methods for identifying anomalies within datasets. These methods are vital in various fields, such as finance, healthcare, cybersecurity, and manufacturing, where detecting outliers can significantly enhance decision-making and prevent adverse outcomes.

6.1. Summary of Findings

• Isolation Forest offers an efficient and scalable solution for large datasets, particularly when no assumptions about the data distribution can be made. Its strength lies in its ability to isolate anomalies based on recursive partitioning, making it an excellent choice for high-dimensional datasets. However, its performance is heavily dependent on the careful tuning of hyperparameters, such as the contamination ratio.
• One-Class SVM shines in situations involving high-dimensional and non-linearly separable data. The ability to leverage kernel methods allows One-Class SVM to construct complex boundaries that effectively separate normal data from outliers. However, its computational complexity and sensitivity to hyperparameters like ν\nuν and γ\gammaγ can limit its applicability in large-scale real-time environments.
• Autoencoders are highly effective in detecting anomalies in high-dimensional data, such as images and time-series datasets. By compressing data into a latent space and reconstructing it, autoencoders flag anomalies based on reconstruction error. While autoencoders are powerful tools, they require large datasets for training, considerable computational resources, and careful threshold selection for classification, which may pose challenges in certain practical applications.

6.2. Practical Implications

The choice of outlier detection method should be guided by the specific characteristics of the dataset and the problem domain. Isolation Forest is ideal for large-scale, complex datasets where efficiency is a priority. One-Class SVM is suited to high-dimensional and intricate datasets, particularly when complex relationships between features exist. Autoencoders, while resource-intensive, provide excellent performance in identifying outliers in high-dimensional data, such as images or time series, where other methods may struggle.

Challenges and Future Directions

Each method also presents certain limitations. Future research and development should focus on improving the explainability of machine learning models like autoencoders, where the lack of transparency is a significant challenge, particularly in critical fields like healthcare. Furthermore, improving the scalability of computationally intensive methods like One-Class SVM while maintaining accuracy is another area that warrants exploration. Developing hybrid approaches that combine the strengths of multiple algorithms may also provide a path forward, allowing for more robust and flexible outlier detection across varied datasets.

In conclusion, outlier detection remains a crucial area of research and application, and as data complexity and volume continue to grow, the development of more efficient, scalable, and interpretable techniques will be essential for addressing the challenges of the future.

• The Author claims no conflicts of interest.