Part-Prototypes Models in Medical Imaging: Applications and Current Challenges

1. Introduction

Machine and Deep Learning (ML and DL) models are collecting interesting performances in supporting Medical Imaging (MI) analysis, but their black-box nature poses technical, ethical and legal controversy in this high-stakes domain. In this scenario, Explainable Artificial Intelligence (XAI) offers many opportunities to foster the development of responsible and trustworthy AI systems for healthcare applications [1,2,3,4,5].

The last decades of ML explainability research were mainly focused on developing methods for explaining complex black-box models (post-hoc interpretability), which typically include saliency-based visual methods [2,3,4]. Saliency approaches exploit the spatial information, preserved through the convolutional layers of DL models, to analyse which parts of an image lead to a resulting decision. However, these methods are often criticized for providing incorrect and incomplete representations of the black-box models’ behaviour, and explanations not fully interpretable for a human user [5,6,7,8].

To overcome the limits reported by post-hoc XAI, a most recent trend started proposing models intentionally designed to be self-explanatory (ante-hoc interpretability, or interpretability-by-design). This includes low-level complexity ML models e.g., decision tree, but also black-box methods augmented with explainability methods [1,4].

Authors started developing DL architectures known as Part-Prototype (PP) neural networks (also known as self-explaining neural networks) that perform image classification based on the identification of class-representative prototypical parts in the input image, a reasoning process based on the recognition-by-components theory [8,9]. PP networks are self-explaining models which reproduce the human case-based reasoning process, and their explanations are faithful representations of the computations performed by the model to make its decisions [6,8,10].

A PP neural network is generally constituted by a deep neural network backbone trained to learn prototypical parts. This feature extractor is trained only using image-level labels (no additional image sub-annotations are required). Once trained, the PP model classifies an input image by detecting the image patches more similar to the learned prototypical parts. The model’s interpretability is provided thanks to the transparent reasoning process implemented in the form of “this looks like that", and the direct relation between the prototypes and the classification prevents unfaithful explanation [8,10,11,12]. A representative example of the PP Net reasoning process is reported in Figure 1.

Following the XAI taxonomy [5], a PP Net can provide both global (overall model’s behaviour) and local (relative to a certain prediction) explanations by respectively showing all the learned prototypes and the detected prototypes for the given prediction as shown in Figure 2.

In addition to designing explainable models, also properly evaluating XAI is crucial to promote their application in real-world scenarios [5]. The evaluation process of XAI methods is currently an open challenge, and several works started proposing systematic evaluation frameworks to objectively assess the system developed [1,13,14]. Aspects such as the XAI multidisciplinarity and the absence of a gold standard “good explanation" make the interpretability assessment a non-trivial task, and is still not clear how XAI methods -including PP-Nets- should be evaluated [5].

This narrative review provides a summary of existing PP networks, their application in MI analysis and their current open challenges.

2. Baseline Prototypical-Part Models

There are different PP model variants proposed to date in literature [8,15], including ProtoPNet [10], XProtoNet [16], ProtoTree [17], ProtoPShare [18], ProtoPool [19], and PIPNet [8]. This section aims to summarize the main theoretical characteristics of the existing PP-nets. For each network, we will describe the architecture, training process, and visualization of the prototypical parts as patches of the input images.

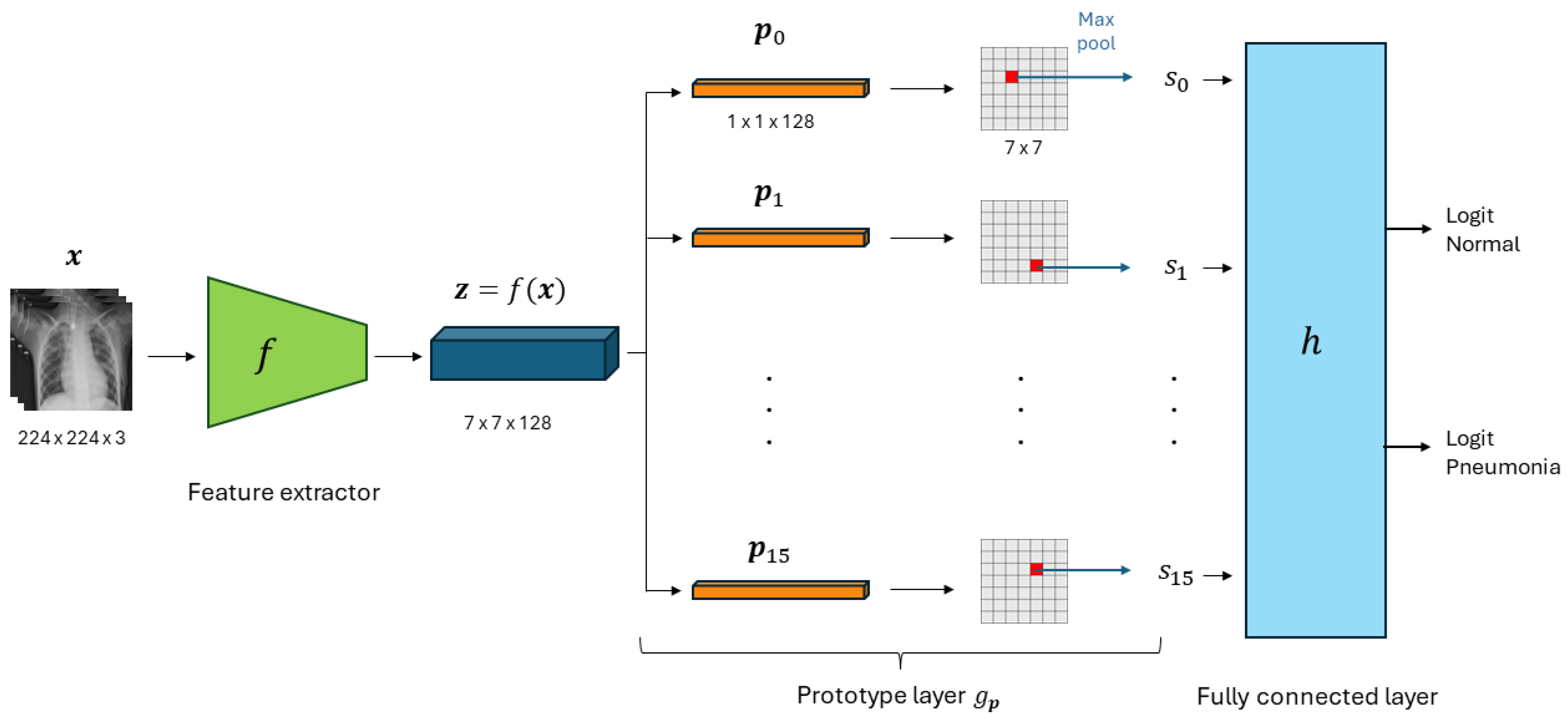
2.1. Prototypical Part Network (ProtoPNet)

2.1.1. Architecture

ProtoPNet [10] was the first PP network proposed in the CV domain. ProtoPNet architecture is composed by a (1) CNN backbone f with parameters $w_f$; a (2) prototype layer$g_p$ of M prototypes $\mathbf{P}=\left\{{\mathbf{p}}_{j=1}^M\right\}$; and a final (3) fully connected layer h with weight $w_h$.

We reported the ProtoPNet architecture in Figure 3.

The CNN backbone takes an input image $\mathbf{x}$ and returns as output the extracted features $\mathbf{z}=f\left(\mathbf{x}\right|w_f)$ with dimension $H\times W\times D$. This could be any available CNN’s feature extractor, such as pre-trained architectures like VGG-16, VGG-19, ResNet-34, ResNet-152, DenseNet-121, or DenseNet-161.

The network learns M prototypes $\mathbf{P}=\left\{{\mathbf{p}}_{j=1}^M\right\}$ of shape $H_1\times W_1\times D$, where $H_1\le H$, $W_1\le W$. Every prototype ${\mathbf{p}}_j$ represents an activation pattern of the convolutional output, corresponding to a certain prototypical image patch in the original pixel space. In this way, a prototype ${\mathbf{p}}_j$ is the latent representation of a certain image prototypical part. The prototype layer $g_{\mathbf{p}}$ performs the computation reported in eq. (1). It evaluates the squared $L^2$ distances between the $j-$th prototype ${\mathbf{p}}_j$ and patches of z with the same shape as ${\mathbf{p}}_j$. These distances are inverted to produce an activation map of similarity score, which indicates how strong a prototypical part is present in the image. Finally, a global max pooling of every prototype’s activation map returns a similarity score which indicates how strongly a prototypical part is present in some patch of the input image (eq. 1). The model requires the allocation of a pre-determined number of prototypes $M_k$ for each class $k\in \{1,...,K\}$, and the subset of prototypes associated with class k${\mathbf{P}}_k\subseteq \mathbf{P}$ should capture the most relevant parts for identifying images of that class.

$$g_{{\mathbf{p}}_j}\left(\mathbf{z}\right)=ma{x}_{\overline{\mathbf{z}}\in patches\left(\mathbf{z}\right)}log\left({\displaystyle \frac{\left|\right|\overline{\mathbf{z}}-{\mathbf{p}}_j{\left|\right|}_2^2+1}{\left|\right|\overline{\mathbf{z}}-{\mathbf{p}}_j{\left|\right|}_2^2+ϵ}}\right)$$

(1)

The last fully connected layer h multiplies the m similarity scores by the weight matrix $w_h$ to produce the output logits, which are finally normalized with a softmax function to obtain the class probabilities. The weight $w_h^{(j,k)}$ corresponds to the connection between the output of a class prototype unit $g_{{\mathbf{p}}_j}$ and the logit of class k. Here, a positive (and respectively a negative) connection between prototype j and class k means that the similarity to a class prototype j increases (decreases) the probability that the image belongs to class k.

2.1.2. Training

The ProtoPNet training process requires three main steps: (1) Optimization of the convolutional and prototype layers; (2) Prototypes’ projection; (3) Convex optimization of the fully connected layer.

The backbone and prototype layers’ optimization (1) aims to learn a meaningful latent space, where the most important patches for classifying images are clustered (in L2-distance) around semantically similar prototypes of the images’ true classes; and the clusters of different classes are well-separated. The weights of CNN backbone $w_f$ and the prototypes layer $\mathbf{P}=\left\{{\mathbf{p}}_{j=1}^M\right\}$ are jointly optimized using stochastic gradient descent (SGD), while the weights of fully connected layer $w_h$ are fixed and set to:

$$w_h^{(j,k)}=\left\{\begin{array}{cc}1\hfill & \forall j\mathrm{if}{\mathbf{p}}_j\in {\mathbf{P}}_k\hfill \\ -0.5\hfill & \forall j\mathrm{if}{\mathbf{p}}_j\notin {\mathbf{P}}_k\hfill \end{array}\right.$$

(2)

In this way, the similarity to a prototype (not) of class k (decreases) increases the predicted probability that the image belongs to class k. SDG optimizes the following loss function:

$$mi{n}_{\mathbf{P},{\mathbf{w}}_{\mathbf{f}}}{\displaystyle \frac{1}{n}}\sum _{i=1}^{n}CrsEnt(h\circ g_{\mathbf{p}}\circ f\left({\mathbf{x}}_{\mathbf{i}}\right),y_i)+{\lambda }_{1}Clst+{\lambda }_{2}Sep$$

(3)

Where:

• $CrsEnt(.):$ Cross entropy loss, penalizes misclassification on the training data.
• $Clst:$ Cluster cost, promotes every training image to have some latent patch that is close to at least one prototype of its own class.

  $$Clst={\displaystyle \frac{1}{n}}\sum _{i=1}^{n}mi{n}_{j:{\mathbf{p}}_j\in {\mathbf{P}}_{y_i}}mi{n}_{\mathbf{z}\in patches\left(f\left({\mathbf{x}}_i\right)\right)}\left|\right|\mathbf{z}-{\mathbf{p}}_j{\left|\right|}_2^2$$

  (4)
• $Sep:$ Separation cost, promotes every latent patch of a training image to stay away from the prototypes not of its class.

  $$Sep=-{\displaystyle \frac{1}{n}}\sum _{i=1}^{n}mi{n}_{j:{\mathbf{p}}_j\notin {\mathbf{P}}_{y_i}}mi{n}_{\mathbf{z}\in patches\left(f\left({\mathbf{x}}_i\right)\right)}\left|\right|\mathbf{z}-{\mathbf{p}}_j{\left|\right|}_2^2$$

  (5)

With the prototypes’ projection (2) every prototype ${\mathbf{p}}_j$ is projected onto the nearest latent training patch of a training image of the same class. After projection, a prototype ${\mathbf{p}}_j$ corresponds to some patch of the latent representation $f\left(\mathbf{x}\right)$, of an image in the training set $\mathbf{x}$.

$$\forall {\mathbf{p}}_j\leftarrow argmi{n}_{\mathbf{z}\in Z_j}\left|\right|\mathbf{z}-{\mathbf{p}}_j{\left|\right|}_2$$

(6)

where $Z_j=\{\overline{\mathbf{z}}:\overline{\mathbf{z}}\in patches\left(f\left({\mathbf{x}}_i\right)\right)\forall i\mathrm{s}.\mathrm{t}.y_i=k\}$.

The fully connected layer optimization (3) adjusts connections from similarity score and the logit of class to enhance sparsity:

$$mi{n}_{w_h}{\displaystyle \frac{1}{n}}\sum _{i=1}^{n}CrsEnt(h\circ g_{\mathbf{p}}\circ f\left({\mathbf{x}}_{\mathbf{i}}\right),y_i)+\lambda \sum _{k=1}^K\sum _{j:{\mathbf{p}}_j\notin {\mathbf{P}}_k}\left|w_h^{(k,j)}\right|$$

(7)

that is for k and j with ${\mathbf{p}}_j\notin {\mathbf{P}}_k$ we have $w_h^{(j,k)}\approx 0$. In doing so, we foster the model in implementing a positive reasoning process (use prototypes which add evidence for a class, not the ones whose presence decreases the evidence for the class), and further improve accuracy without changing the learned latent space or prototypes.

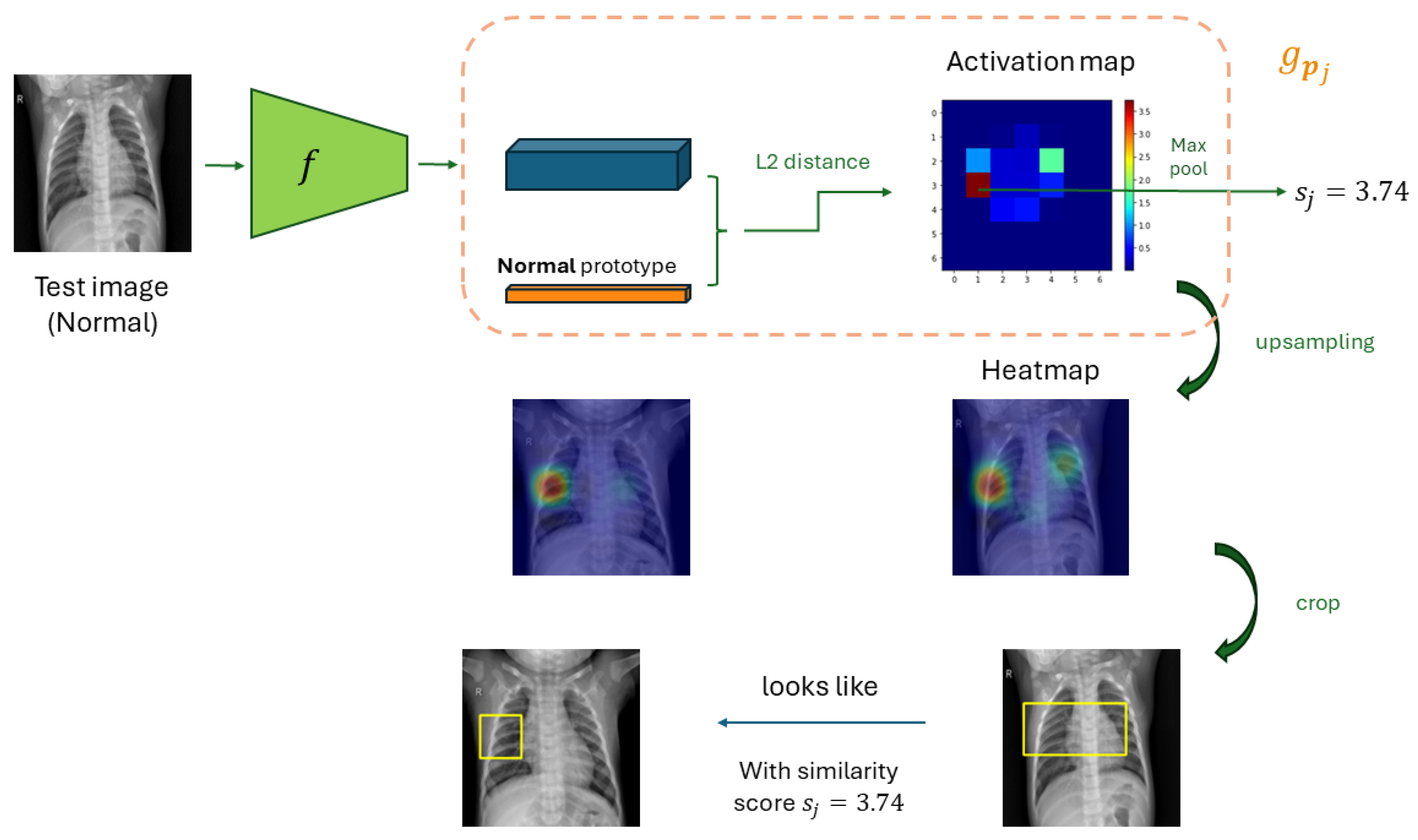
2.1.3. Prototypes’ visualization

Once the ProtoPNet is trained, we can visualize every prototype ${\mathbf{p}}_j$ as a patch of an image $\mathbf{x}$ in the training set. This visualization process involves the following steps:

• Forwarding $\mathbf{x}$ through a ProtoPNet to produce the activation map associated with the prototypes ${\mathbf{p}}_j$
• Upsampling the activation map to the dimension of the input image
• Localizing the smallest rectangular patch whose corresponding activation is at least as large as the 95th-percentile of all activation values in that same map

We schematically reported the visualization process in Figure 4.

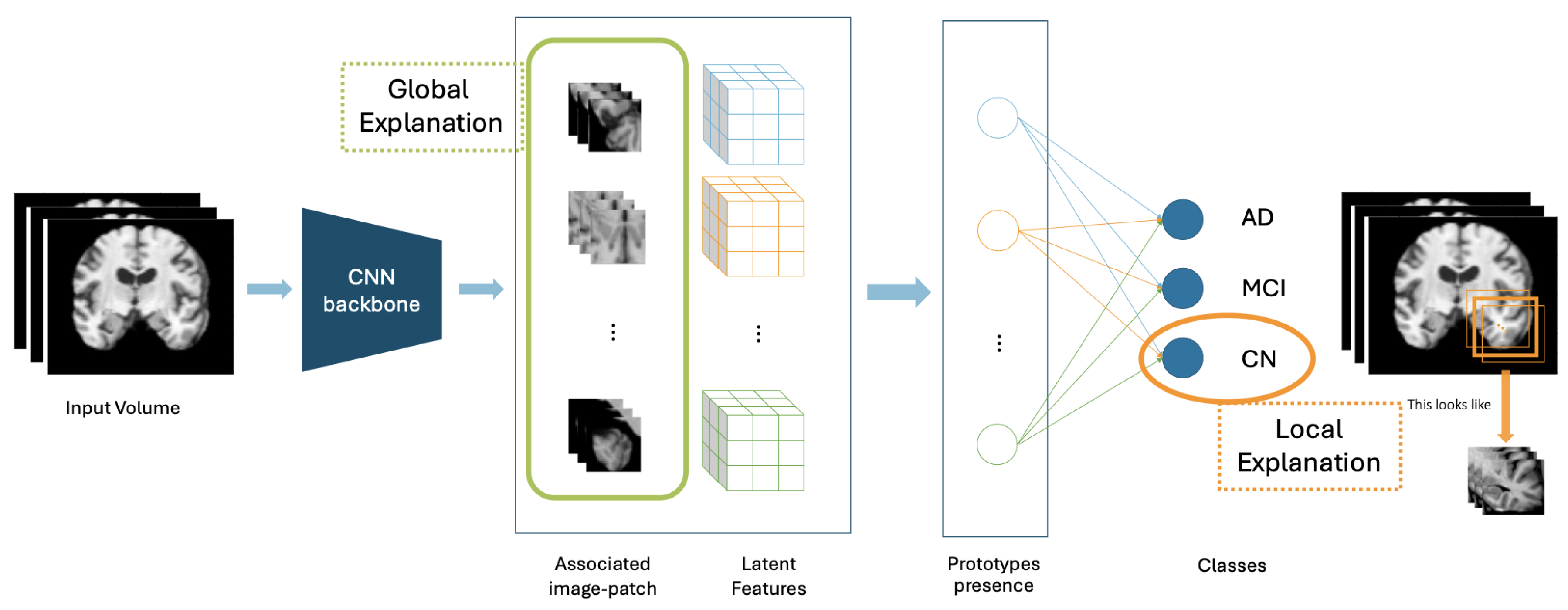
2.2. XProtoNet

XProtoNet differs from ProtoPNet due to the ability to learn representative features within a dynamic area.

2.2.1. Architecture

XProtoNet is composed by a (1) Feature extractor with two main modules: a (1.a) Feature module F and a (1.b) Occurrence module $M_{{\mathbf{p}}_k^c}$; a (2) Similarity score measurement; and a final (3) Fully connected layer.

XProtoNet takes an input image $\mathbf{x}$ and extracts the feature vector ${\mathbf{f}}_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}$ for each one of the learned prototypes per class $k,{\mathbf{P}}_k={\left\{{\mathbf{p}}_j\right\}}_{j=1}^{M_k}$ with $k=\{1,...,K\}$.

$${\mathbf{f}}_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}=\sum _u{M}_{{\mathbf{p}}_k^c\left(\mathbf{x}\right),u}{F}_u\left(\mathbf{x}\right)$$

(8)

Where $u\in [H\times W)$ denotes the spatial location of $F\left(\mathbf{x}\right)$ and $M_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}$. The feature module extracts the image latent representation $F\left(\mathbf{x}\right)\in {\mathbb{R}}^{H\times W\times D}$ while the occurrence module predicts an occurrence map for each prototype $M_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}\in {\mathbb{R}}^{H\times W}$, which indicates where every prototype is likely to appear. The feature vector ${\mathbf{f}}_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}$ then represents a certain feature in the highly activated area of the occurrence map.

Then, XProtNet uses the cosine similarity to compute a similarity score between the feature of the input image to every prototype:

$$s(\mathbf{x},{\mathbf{p}}_k^c)={\displaystyle \frac{f_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}·{\mathbf{p}}_k^c\left(\mathbf{x}\right)}{\left|\right|f_{{\mathbf{p}}_k^c\left(\mathbf{x}\right)}\left|\right|\left|\right|{\mathbf{p}}_k^c\left(\mathbf{x}\right)\left|\right|}}$$

(9)

Finally, every prototype $p_k^c$ contributes to the prediction score of the related class with an importance determined by the weights of the linear layer $w_{p_k^c}$.

$$p\left(y^c\right|\mathbf{x})=\sigma \left(\sum _{{\mathbf{p}}_k^c\in {\mathcal{P}}^c}{w}_{p_k^c}s(\mathbf{x},{\mathbf{p}}_k^c)\right)$$

(10)

Where $\sigma$ is a sigmoid activation function.

2.2.2. Training

XProtoNet follows the ProtoPNet training scheme (backbone and prototypes optimization; prototypes projection; fully connected layer optimization). Its cost function is composed by three different terms:

$${\mathcal{L}}_{total}={\mathcal{L}}_{cls}+{\lambda }_{clst}{\mathcal{L}}_{clst}+{\lambda }_{sep}{\mathcal{L}}_{sep}+{\lambda }_{occur}{\mathcal{L}}_{occur}$$

(11)

Where:

• Classification weighted loss, ${\mathcal{L}}_{cls}^c$ to address the imbalance in the dataset:

  $${\mathcal{L}}_{cls}^c=-\sum _i{\displaystyle \frac{1}{|N_{pos}^c|}}{(1-p_i^c)}^{\gamma }{y}_i^{c}log\left(p_i^c\right)-\sum _i{\displaystyle \frac{1}{|N_{neg}^c|}}{\left(p_i^c\right)}^{\gamma }(1-y_i^c)log(1-p_i^c)$$

  (12)
  Where $p_i^c=p\left(y^c\right|{\mathbf{x}}_i)$ is the prediction score of the $i-$th sample ${\mathbf{x}}_i$, $\gamma$ is a parameter for class balance, $|N_{neg}^c|$ and $|N_{pos}^c|$ the number of negative and positive labels on disease c, and $y_i^c\in \{0,1\}$ the target label of ${\mathbf{x}}_i$ on disease c.
• Regularization for Interpretability which, similarly to [10], includes two different terms ${\mathcal{L}}_{clst}^c$ and ${\mathcal{L}}_{sep}^c$ to respectively maximize similarity between x and ${\mathbf{p}}_k^c$ for positive samples and minimize it for negative samples:

  $${\mathcal{L}}_{clst}^c=-y^{c}ma{x}_{{\mathbf{p}}_k^c\in {\mathcal{P}}^c}s(\mathbf{x},{\mathbf{p}}_k^c)$$

  (13)

  $${\mathcal{L}}_{sep}^c=(1-y^c)ma{x}_{{\mathbf{p}}_k^c\in {\mathcal{P}}^c}s(\mathbf{x},{\mathbf{p}}_k^c)$$

  (14)
• Regularization for the occurrence map:

  $${\mathcal{L}}_{occur}^c={\mathcal{L}}_{trans}^c+\sum _{{\mathbf{p}}_k^c\in {\mathcal{P}}^c}\left|\right|M_{{\mathbf{p}}_k^c}\left(\mathbf{x}\right){\left|\right|}_1$$

  (15)
  Where:

  –

  The term ${\mathcal{L}}_{trans}^c$ considers that an affine transformation $A(.)$ of an image does not change the relative location, so it shouldn’t affect the occurrence map, either

  $${\mathcal{L}}_{trans}^c=\sum _{{\mathbf{p}}_k^c\in {\mathcal{P}}^c}\left|\right|A\left(M_{{\mathbf{p}}_k^c}\left(\mathbf{x}\right)\right)-M_{{\mathbf{p}}_k^c}\left(A\left(\mathbf{x}\right)\right){\left|\right|}_1$$

  (16)

  –

  The term ${\sum }_{{\mathbf{p}}_k^c\in {\mathcal{P}}^c}\left|\right|M_{{\mathbf{p}}_k^c}\left(\mathbf{x}\right){\left|\right|}_1$ regularize to have an occurrence area as small as possible to not include unnecessary regions

Once the model is trained, the prototype ${\mathbf{p}}_k^c$ is replaced with the most similar feature vector ${\mathbf{f}}_{{\mathbf{p}}_k^c}$ from the training images.

2.2.3. Protypes’ Visualization

The learned prototypes are visualized by:

• Upsampling the occurrence maps to the input image size
• Normalizing with the maximum value of the upsampled mask
• Marking with contour the occurrence values are greater than a factor of 0.3 of the maximum intensity

2.3. Neural Prototype Tree (ProtoTree)

Nauta et al. [17] developed Neural Protype Tree (ProtoTree), which integrates the prototype learning approach into a hierarchical decision tree structure. The model includes a CNN followed by a binary tree structure, where each node corresponds to a prototypical part. The prototypical parts are tensors that can be visualized as a patch of a training sample learned with backpropagation during the training process, without requiring additional annotations. Similarly to PP network, the ProtoTree architecture itself explains the global reasoning process implemented (here, as a hierarchical sequence of steps), and the local explanations are constituted by the route through the tree for every single prediction.

2.3.1. Architecture

ProtoTree consists of a (1) CNN backbone f with parameters $w_f$; a (2) binary soft decision tree constituted of $\mathcal{N}$ nodes, $\mathcal{L}$ leaves, and $\mathcal{E}$ edges, which takes the image latent representation and returns the class probability distribution over the K classes.

The CNN backbone takes the input image $\mathbf{x}$ and extract the latent features $\mathbf{z}=f(\mathbf{x};w_f)$ consisting of D 2-dim $(H\times W)$ feature maps, $(H\times W\times D)$.

The binary soft decision tree takes as input the image latent representation $\mathbf{z}$ and returns the class probability distribution over the K classes $\widehat{\mathbf{y}}$. Each internal node $n\in N$ has two children $n.right$ and $n.left$ connected respectively with $e(n,n.right)\in \mathcal{E}$$e(n,n.left)\in \mathcal{E}$ and corresponds to a prototype ${\mathbf{p}}_n\in \mathbf{P}$. Here, a prototype is a trainable tensor of shape $H_1\times W_1\times D$, with the same depth as the convolutional output $\mathbf{z}$ and $H_1\le H,W_1\le W$. The prototype ${\mathbf{p}}_n$ acts as a kernel which slides over $\mathbf{z}$, computes the Euclidean distance between ${\mathbf{p}}_n$ and its receptive field $\tilde{z}$ and applies a minimum pooling to select the patch $H_1\times W_1\times D$ closest to ${\mathbf{p}}_n$:

$${\tilde{\mathbf{z}}}^{*}=argmi{n}_{\tilde{\mathbf{z}}}\left|\right|\tilde{\mathbf{z}}-{\mathbf{p}}_n\left|\right|$$

(17)

The selected closest patch is then routed through both edges (soft routing) of child nodes with:

$$p_{e(n,n.right)}\left(\mathbf{z}\right)=exp(-||{\tilde{\mathbf{z}}}^{*}-{\mathbf{p}}_n\left|\right|)$$

(18)

$$p_{e(n,n.left)}=1-p_{e(n,n.right)}$$

(19)

So, the similarity between ${\mathbf{p}}_n$ and ${\tilde{\mathbf{z}}}^{*}$ determines to which extent $\mathbf{z}$ is routed to the right node child $n.right$. Each leaf node $l\in \mathcal{L}$ receives the convolutional output $\mathbf{z}$ with a probability given by the product of the edges probabilities $p_e$ in the path ${\mathcal{P}}_l$ followed by $\mathbf{z}$ from the root node to leaf l:

$${\pi }_l\left(\mathbf{z}\right)=\prod _{e\in {\mathcal{P}}_l}{p}_e\left(\mathbf{z}\right)$$

(20)

Each leaf has a trainable parameter ${\mathbf{c}}_l$ which denotes the class probability distribution over the K classes and computes the class probability distribution of leaf l applying the softmax normalization $\sigma \left({\mathbf{c}}_l\right)$. The class probability distribution over the K classes $\widehat{\mathbf{y}}$ is given by the weighted contribution of all the leaves.

$$\widehat{\mathbf{y}}\left(\mathbf{x}\right)=\sum _{l\in \mathcal{L}}\sigma \left({\mathbf{c}}_l\right)·{\pi }_l\left(f(\mathbf{x};\mathbf{w})\right)$$

(21)

2.3.2. Training

The ProtoTree’s architecture is initialized by selecting a pre-trained CNN backbone $f(\mathbf{x};\mathbf{w})$ and defining the maximum height h of the binary tree, which determines the number of prototypes $\left|P\right|=2^h-1$. Then, the training process is constituted by the (1) Optimization of the convolutional and prototype layers; (2) Convex optimization of the decision tree’s leaves; and (3) Prototypes’ projection.

The CNN backbone ${\mathbf{w}}_{\mathbf{f}}$ and prototype layers’ $\mathbf{P}$ are optimized (1) with backpropagation gradient descent by minimizing the cross-entropy loss between the predicted class probability distribution $\widehat{\mathbf{y}}$ and ground-truth $\mathbf{y}$.

The convex optimization of $\mathbf{c}$ (2) learns the leaves’ distribution using a derivative-free approach

$${\mathbf{c}}_l^{(t+1)}=-{\displaystyle \frac{1}{B}}·{\mathbf{c}}_l^{\left(t\right)}+\sum _{\mathbf{x},\mathbf{y}\in \mathcal{T}}(\sigma \left({\mathbf{c}}_l^{\left(t\right)}\right)\odot \mathbf{y}\odot {\pi }_l)\oslash \widehat{\mathbf{y}}$$

(22)

Where t indexes a training epoch.

Finally, with the prototypes’ projection (3) ${\mathbf{p}}_n\leftarrow {\tilde{\mathbf{z}}}_n^{*}$ every prototype ${\mathbf{p}}_n\in \mathbf{P}$ is replaced with its nearest latent patch present in the training data ${\mathbf{z}}_n^{*}$:

$${\mathbf{z}}_n^{*}=argmi{n}_{\mathbf{z}\in \left\{f\right(\mathbf{x}\left)\right\},\forall \mathbf{x}\in \mathcal{T}}\left|\right|{\mathbf{z}}^{*}-{\mathbf{p}}_n\left|\right|$$

(23)

Once trained, ProtoTree has a pruning step to prone ineffective prototypes reducing the explanation’s sizes, which brings benefit to the model’s interpretability. This consists of removing leaves with nearly uniform distributions, signs of little discriminative power between classes, by defining a threshold $\tau$ slightly greater than ${\displaystyle \frac{1}{K}}$ and pruning the ones where $max\left(\sigma \left({\mathbf{c}}_l\right)\right)\le \tau$.

2.3.3. Prototypes’ Visualization:

Considering ${\mathbf{x}}_n^{*}$ as the training image corresponding to the latent patch ${\tilde{\mathbf{z}}}^{*}$, the prototype ${\mathbf{p}}_n$ is visualized as a patch of ${\mathbf{x}}_n^{*}$ by:

• Forwarding ${\mathbf{x}}_n^{*}$ through $f:z=f\left({\mathbf{x}}_n^{*}\right)$
• Create a 2-dim similarity map:

  $$S_n^{(i,j)}=exp(-|\left|\right|{\tilde{\mathbf{z}}}^{(i,j)}-{\mathbf{p}}_n\left|\right|)$$

  (24)
  Where $(i,j)$ denotes the location of patch $\tilde{\mathbf{z}}$ in patches of z
• Upsampling $S_n$ with bicubic interpolation to the shape of ${\mathbf{x}}_n^{*}$
• Visualize ${\mathbf{p}}_n$ as a rectangular patch at the same location nearest to the latent patch ${\tilde{\mathbf{z}}}_n^{*}$

2.4. Protypical Part Shared Network (ProtoPShare)

Rymarczyk et al. [18] developed ProtoPShare, a part-prototype network which extended ProtoPNet addressing two of its limitations: the (1) Ability to share prototypes between the classes; the (2) Ability to identify semantically similar prototypes, even with a distant representation in the latent space. The authors achieved this by implementing a data-dependent pruning algorithm based on the feature maps. This results in a model with a reduced explanation size, fostering its interpretability.

2.4.1. Architecture

ProtoPShare shared the same architecture as ProtoPNet constituted of a CNN backbone f extracting the latent representation of the image $\mathbf{z}=f\left(\mathbf{x}\right)$; a prototype layer g of $m_k$ prototypes per classes ${\mathbf{P}}_{\mathbf{k}}=\left\{{\mathbf{p}}_{\mathbf{j}}{j=1}^{m_k}\right\}$; and a fully connected layer of weight $w_h$ which predicts the output class.

2.4.2. Training

ProtoPShared adopted the ProtoPNet training scheme followed by a data-dependent merge-pruning to obtain a network with a smaller number of shared prototypes. The pruning process consists of the following steps:

• Computing the data-dependent similarity for pair of prototypes $(\mathbf{p},\tilde{\mathbf{p}})\in {\mathbf{P}}^2$, given by the compliance on the similarity scores for all the training input image $\mathbf{x}\in \mathbf{X}$. This considers two prototypes similar if they activate alike on the training images, even if far in the latent space:

  $$d_{DD}(\mathbf{p},\tilde{\mathbf{p}})={\displaystyle \frac{1}{{\sum }_{\mathbf{x}\in \mathbf{X}}{(g_{{\mathbf{p}}_i}\left(\mathbf{z}\right)-g_{{\tilde{\mathbf{p}}}_i}\left(\mathbf{z}\right))}^2}}$$

  (25)
• Select a percentage $\zeta$ of the most similar pairs of prototypes to merge per step $(\mathbf{p},\tilde{\mathbf{p}})$
• For each pair, remove prototype $\mathbf{p}$ and its weights $w_h\left(\mathbf{p}\right)$ and reuses prototype $\tilde{\mathbf{p}}$ aggregating weights $w_h\left(\tilde{\mathbf{p}}\right)$ and $w_h\left(\mathbf{p}\right)$

Results obtained compared to other self-explained prototypical parts models suggested an increase in interpretability and a novel ability to discover semantic similarity discovery while maintaining high accuracy.

2.4.3. Prototypes’ Visualization

As ProtoPNet [10], the visualization process of the prototypes ${\mathbf{p}}_j$ is based on the localization of the smallest and most activated rectangular patch in the upsampled image activation map.

2.5. ProtoPool

Rymarczyk et al. [19] developed ProtoPool integrating into PP-network (1) the concept of prototypes soft assignment, which optimizes for model’s compactness without requiring a pruning stage into the training process; and (2) the definition of focal similarity function to focus the model on salient features. As ProtoPShare [18], the prototypes can be shared between classes.

2.5.1. Architecture

ProtoPool shared the same architecture as ProtoPNet constituted of a CNN backbone f; a prototype layer g of m prototypes $\mathbf{P}=\{{\mathbf{p}}_{j=1}^M\in {\mathbf{R}}^D\}$; and a fully connected layer of weight $w_h$ which predicts the output class.

The image latent representation $\mathbf{z}=f\left(\mathbf{x}\right)$ with dimension $H\times W\times D$ is considered as a set of $H\dot{W}$ vectors each one corresponding to a location in the image and with dimension D: $Z_x=\{z_i\in f\left(x\right):z_i\in {\mathbf{R}}^D,i=1,...,H\dot{W}\}$.

The prototype layer contains K slots for each class, and each slot is implemented as a distribution of the prototypes in the pool $q_k\in {\mathbf{R}}^M$ where $q_k$ is the probability of assigning successive prototypes to the slot. The layer computes on each k slot the aggregated similarity between $Z_x$ and all prototypes considering their slot distribution $q_k$:

$$g_k=\sum _{i=1}^M{q}_k^i{g}_{p_i}$$

(26)

Here, ProtoPool computes the activation of prototype p w.r.t. image x$g_p$ using the novel-introduced focal similarity function:

$$g_p=ma{x}_{z\in Z_x}{g}_p\left(z\right)-mea{n}_{z\in Z_x}{g}_p\left(z\right)$$

(27)

Where:

$$g_p\left(z\right)=log\left(1+{\displaystyle \frac{1}{\left|\right|z-{p\left|\right|}^2}}\right)$$

(28)

The focal similarity has the advantage of preventing: high activation due to all the elements in $Z_x$ are similar to a prototype, which might result in obtaining prototypes focused on the background regions, and the gradient is passed only through the most active part of the image. ProtoPool also uses the concept of soft assignment on prototype distributions, applying the Gumbel-softmax estimator to avoid many prototypes being assigned to one slot (which might decrease interpretability):

$$\mathrm{Gumbel}\text{-}\mathrm{softmax}(q,\tau )=(y^1,...,y^M)\in {\mathbf{R}}^M$$

(29)

Where:

$$y^i={\displaystyle \frac{exp(q^i+{\eta }_i)/\tau }{{\sum }_{m=1}^{M}exp((q^m+{\eta }_m)/\tau )}}$$

(30)

Where $et{a}_m$ for $m\in 1,...,M$ are sampled from the standard Gumbel distribution.

2.5.2. Training

ProtoPool adopted the ProtoPNet training scheme (backbone and prototype training; prototypes projection; backbone, prototypes and fully connected layer fine-tuning) by extending the loss function to avoid that the same prototype will be assigned to many slots of one class:

$${\mathcal{L}}_{orth}=\sum _{i<j}^K{\displaystyle \frac{\langle q_i,q_j\rangle }{\left|\right|q_i{\left|\right|}_2·\left|\right|q_j{\left|\right|}_2}}$$

(31)

As in ProtoPNet, the prototypes are projected to replace every learned abstract prototype with the representation of the nearest training patch:

$$\mathbf{p}\leftarrow argmi{n}_{\mathbf{z}\in Z_C}\left|\right|\mathbf{z}-{\mathbf{p}\left|\right|}_2$$

(32)

Where $Z_C=\{z:z\in Z_x\forall (x,y):y\in C\}$; here, differently from ProtoPNet, C is the set of all the classes assigned to prototype p.

2.5.3. Prototypes’ Visualization

Even for ProtoPool, the visualization process of the prototypes is based on the upsampling of the activation maps as in ProtoPNet [10].

2.6. Patch-based Intuitive Prototypes Network (PIPNet)

Nauta et al. [8] developed a Part-Prototype architecture which presents different advantages compared to the existing models: (1) Absence of semantic gap between the learned prototypes and human vision; (2) Compactness; and (3) Ability to handle Out-of-Distribution (OoD) data.

The lack of semantic gap means that the prototypes learned correlate with human concepts, ground-truth object parts and human visual perception. This was covered by implementing an extra regularization of the prototypes using Self-supervised Representation Learning. PIPNet overcomes the assumption that part of the images from the same class have the same prototypes (regularization of interpretability at the class level).

The model’s compactness was promoted by regularizing for sparsity during training of the weights in the fully connected layer between prototypes and classes. PIP-Net only needs an upper bound on the number of prototypes selecting as few prototypes as possible for good classification accuracy and allowing class-sharable prototypes This regularization was performed by introducing a novel function that optimizes classification performances and compactness simultaneously, which is also able to handle OoD data.

Finally, PIP-Net manages OoD data by abstain from decisions when no relevant prototypes are present in the image. This was implemented enabling the assignment of near-zero scores for all classes using a normalization (necessary for scale-invariance issues) in logits where a score of zero stays zero and allows the prototype presence score to behave independently of each other.

2.6.1. Architecture

PIP-Net consists of a (1) CNN backbone f with parameters $w_f$ followed by a softmax activation; a (2) Global Max-pooling operation extracting the prototype layer $\mathbf{p}$; and a final positive sparse (3) fully connected layer ${\mathbf{w}}_{\mathbf{c}}$ which acts as a scoring sheet system to predict the output classes. PIP-Net classifies images based on the presence of prototypical parts in the input image. The relevantly present prototypical parts add up scores (evidence) to the model’s classes with a proportional contribution determined by the linear weights and the model can abstain from decisions when there isn’t enough evidence for any classes.

The CNN backbone takes the input image $\mathbf{x}$ and extract the latent features $\mathbf{z}=f(\mathbf{x};w_f)$ consisting of D 2-dim $(H\times W)$ feature maps, $(H\times W\times D)$. The softmax activation normalizes so that $z={\sum }_{d=1}^D{z}_{h,w,d}=1$. Here $z_{h,w,d}$ represents the probability that a patch in position $h,w\in H\times W$ corresponds to the prototype d, that is, the one-hot encoding of patch $h,w$ to the prototype d.

The global max-pooling 2D operation extracts D prototypes and calculates the prototypes presence scores $\mathbf{p}$ where $p\in {[0.,1.]}^D$, where $p_j$ measures the presence of the prototype d in the input image.

Finally, a linear sparse classification layer with positive weights ${\mathbf{w}}_{\mathbf{c}}\in {\mathbf{R}}_{\ge 0}^{D\times K}$ connects the prototypes to the classes acting as a scoring sheet systems: $\mathbf{o}=\mathbf{p}·{\mathbf{w}}_{\mathbf{c}}$ with $\mathbf{o}$ is $1\times K$ and $o_k={\sum }_{d=1}^D{p}_d{w}_c^{d,k}$, where $w_c^{d,k}$ represents the contribution of prototype d for class k.

2.6.2. Training

The PIPNet training process is composed of two main steps: the (1) Self-Supervised Pre-Training of Prototypes; and the (2) PIP-Net training.

The prototypes’ pre-training aims to learn an image encoding p with semantic similarity independently from the classification task (the last linear layer is kept frozen). Authors optimize for patch alignment under a contrastive learning approach by training PIP-Net to assign the same prototypes to two views of an augmented image patch. This involves a positive pair creation $x^{\prime },x^{\prime \prime }$ step by applying data augmentation transformation to input image x selected so that humans consider the two views similar. The Adam optimizer optimizes the following loss function:

$${\lambda }_A{\mathcal{L}}_A+{\lambda }_T{\mathcal{L}}_T$$

(33)

Where:

• Alignment Loss, ${\mathcal{L}}_A$ optimizes for near-binary encodings where an image patch corresponds to exactly one prototype

  $${\mathcal{L}}_A=-{\displaystyle \frac{1}{HW}}\sum _{(h,w)\in H\times W}log(z_{h,w,:}^{\prime }·z_{h,w,:}^{\prime \prime })$$

  (34)
  Where the dot product $z_{h,w,:}^{\prime }·z_{h,w,:}^{\prime \prime }$ assess the similarity between the latent patches of two views of an image patch, if $z_{h,w,:}^{\prime }=z_{h,w,:}^{\prime \prime }\Rightarrow {\mathcal{L}}_A=0$
• Tanh-Loss, ${\mathcal{L}}_T$ prevents the trivial solution that one prototype node is activated on all image patches in each image in the dataset forcing that every prototype should be at least once present in a mini-batch

  $${\mathcal{L}}_T\left(p\right)=-{\displaystyle \frac{1}{D}}\sum _{d=1}^{D}log(\left(tanh\left(\sum _{b=1}^B\right)p_b\right)+ϵ)$$

  (35)

The PIPNet training optimizes classification performances and fine-tunes the prototypes for the downstream classification task.

$${\lambda }_A{\mathcal{L}}_A+{\lambda }_T{\mathcal{L}}_T+{\lambda }_C{\mathcal{L}}_C$$

(36)

Where the Classification Loss, ${\mathcal{L}}_C$, is the Log-likelihood loss between the ground-truth labels and the predictions During training, the output scores are computed as $\mathbf{o}=log({\left(\mathbf{p}{\mathbf{w}}_c\right)}^2+1)$, acting as regularization for sparsity.

2.6.3. Prototypes’ Visualization

The visualization process of the prototypes ${\mathbf{p}}_j$ is based on the upsampling of the latent output based on the single most activated latent patch.

3. Application and Advances in Medical Imaging

There is an increasing interest in applying PP model in medical imaging. We searched in major databases (Google Scholar, Scopus, Web of Science) articles including original research papers and preprints on PP networks applied in medical image classification published from 2019 to August 2024. We summarized collected works in Table 1.

Singh et al. proposed three ProtoPNet variants for classifying chest images into Covid-19, Pneumonia and Normal: Negative-Positive ProtoPNet (NP-ProtoPNet) [20], Generalized ProtoPNet (Gen-ProtoPNet) [21], and Pseudo-ProtoPNet (Ps-ProtoPNet) [22]. In NP-ProtoPNet [20] authors modified the original fully connected layer by connecting similarity scores to correct/incorrect classes’ logits with weights fixed respectively to 1 or -1. This allows the network to reason both in a “positive” way (“this looks like that”) and in a “negative” way (“this does not look like those”), i.e., by exclusion. In Gen-ProtoPNet [21] authors introduced a generalized distance function to select prototypes of varying dimensions. They achieved accuracies of 88.99% in the first work and of 87.27% in the second. They also trained black-box CNNs for the same task, showing that their explainable models’ performances are comparable with state-of-the-art (SOTA) black-box models. For both works, they used a combination of two datasets, one containing frontal chest radiographs of healthy people and pneumonia patients (Chest X-ray [23]), and the COVID-19 Image Data Collection [24], from which they took radiographs of COVID patients. The Ps-ProtoPNet [22] integrates NP-ProtoPNet and Gen-ProtoPNet. For this implementation, they used CT images from COVIDx CT-2 Dataset available on Kaggle, achieving an accuracy of 99.24%

• Kim et al. [16] implemented X-ProtoPNet, which introduces the prediction of occurrence maps, which indicate the area where a sign of the disease (i.e., a prototype) is likely to appear, so compares the features in the predicted area with the prototypes. This novelty can help to identify whether the model is focusing on the correct parts of the image or if it is being misled by irrelevant features. They used the NIH chest X-ray dataset [25] for a multilabel classification task (Atelectasis, Cardiomegaly, Effusion, Infiltration, Mass, Nodule, Pneumonia, Pneumathorax Consolidation, Edema, Emphysema, Fibrosis, Pleural Thickening, and Hernia), achieving a mean area under the receiver operating characteristic (AUROC) of 0.822.
• Mohammadjafari et al. [26] applied ProtoPNet to brain MRI scans to detect Alzheimer’s disease, achieving an accuracy of 87.17% in the OASIS dataset [27] and of 91.02% in the ADNI dataset. They used different CNN architectures as feature extractors, and ProtoPNet’s performances were demonstrated to be comparable to or slightly less than their black-box counterparts.
• Barnett et al. [28] designed a novel PP net modifying the training process of ProtoPNet with a loss function including fine-grade expert image annotation and using a top-k average pooling instead max-pooling. They trained their model on an internal dataset of digital mammograms for mass-margin classification and mass-margin malignancy prediction and reported equal or higher accuracy compared to PrototPNet and a black-box model.
• Carloni et al. [29] used ProtoPNet to classify benign/malignant breast masses from mammogram images from a publicly available dataset (CBIS-DDSM [30]), achieving an accuracy of 68.5%. While this performance may not yet be ideal for clinical practice, the authors suggest three tasks for a qualitative evaluation of the explanations by a radiologist.
• Amorim et al. [31] implemented ProtoPNet to classify histologic patches from the PatchCamelyon dataset [32] into benign and malignant using a top-k average pooling instead a max-pooling to extract similarity scores from the activation maps. The authors achieved an accuracy of 98.14% by using Densenet-121 as a feature extractor. This performance was comparable with the one obtained with the black-box CNN.
• Flores-Araiza et al. [33] used ProtoPNet to identify the type of kidney stones (Whewellite, Weddellite, Uric Acid anhydrous, Struvite, Brushite and Cystine) using a simulated in-vivo dataset of endoscopic images. They achieved an accuracy of 88.21% and further evaluated the explanations by perturbing global visual characteristics of images (hue, texture, contrast, shape, brightness, and saturation) to describe their relevance to the prototypes and the sensitivity of the model.
• Kong et al. [34] designed a dual-path PP network, DP-ProtoNet, to increase the generalization performances of single networks. They applied their model to the public ISIC - HAM10000 skin disease dermatoscopic dataset [35]. Compared to ProtoPNet, DP-ProtoNet achieved higher performances while maintaining the model’s interpretability.
• Santiago et al. [36] integrated ProtoPNet with content-based image-retrieval to provide explanations in terms of image-level prototypes and patch-level prototypes. They applied their approach to the skin lesions diagnosis in the public ISIC dermoscopic images [35], outperforming both black-box models and SOTA explainable approaches.
• Cui et al. [37] proposed MBC-ProtoTree, an interpretable fine-grained image classification network based on ProtoTree. They improved ProtoTree by designing a multi-grained feature extraction network, a new background-prototypes removing mechanism, and a novel loss function. The improved model achieved higher classification accuracy on the Chest X-ray dataset.
• Nauta et al. [11] applied their PIP-Net to two open benchmark datasets, respectively for skin cancer diagnosis (ISIC), bone X-ray abnormality detection (MURA), and two real-world datasets respectively for hip and ankle fracture detection. From this study, authors obtained prototypes generally in line with medical knowledge and demonstrated the possibility of correcting the undesired model’s reasoning process with a human-in-the-loop configuration.
• Santos et al. [38] integrated ProtoPNet into a Deep Active Learning framework to predict diabetic retinopathy on the Messidor dataset [39]. The framework allows to train the ProtoPNet on a training set of instances selected using a search strategy, and this may offer benefits in scenarios where the datasets are expensive to be labelled. Performances reported demonstrated the success of applying interpretable models with reduced training data.
• Wang et al. [40] proposed InterNRL integrating ProtoPNet into a student-teacher framework, together with an accurate global image classifier. They applied their model for breast cancer and retinal disease diagnosis and obtained SOTA performances demonstrating the success of the reciprocal learning training paradigm in the medical imaging domain.
• Xu et al. [41] proposed a prototype-based vision transformer applied to COVID-19 classification. They replaced the last two layers of a transformer encoder with a prototype block similar to ProtoPNet and obtained good performances on three different public datasets.
• Sinhamahapatra et al. [42] proposed ProtoVerse, a PP model with a novel objective function applied to the vertebral compression fractures classification. The model interpretability was evaluated by expert radiologists, and predictive performances outperformed ProtoPNet and other SOTA PP architectures.
• Pathak et al. [15] further applied PIP-Net to three different public datasets for breast cancer classification obtaining competitive performances w.r.t. other SOTA black-box and prototype-based models and assessed the coherence of the model with quantitative metrics.
• Gallée et al. [43] applied the Proto-Caps PP-net, in lung chest CT nodules malignancy prediction and performed a human evaluation of the model with a user study.

Most of the existing PP-Nets were originally designed for general CV purposes, so they typically work by taking RGB-images as input. However, medical imaging diagnosis is often performed using the entire volumetric human anatomy, so being able to efficiently process 3D data volumes might be particularly relevant in this context. Wei et al. [44] proposed MProtoNet as the first medical prototype network extending PP models to 3D brain tumour classification from multiparametric MRI (mpMRI). This is based on an implementation of the XProtoNet with a 3D ResNet backbone and the novelty proposed soft masking and online-CAM loss function to enhance the localization of attention regions. Authors further proposed novel metrics to assess the correctness and localization coherence of prototypes (following the Co-12 taxonomy [45]). The MProtoNet obtained classification accuracy in line with the baseline CNN counterpart and ProtoPNet (re-implementated for 3D images).

Vaseli et al. [46] proposed ProtoASNet, a PP model which extracts spatio-temporal feature vectors to detect aortic stenosis from B-mode echocardiography videos. They both assessed their model on a private and on the public TMED-2 dataset [47] outperforming the baseline ProtoPNet and XProtoNet. De Santi et al. [48] extended PIP-Net to classify 3D MRI for Alzheimer’s disease. They tested the model using different CNN backbones and obtained the best result with the ResNet-18 3D, and comparable results with the corresponding black-box counterpart. They further proposed two novel quantitative metrics of explainability: the prototype brain entropy to assess the covariate complexity and localization consistency to assess the consistency in prototype localization (under the Co-12 properties). They also evaluated prototypes with domain experts with a survey and assessed the coherency of prototypes in terms of localization, pattern and classification.

Clinicians often use multiple data sources in their decision-making process [43,49], so developing explainable multimodal models (models which use multiple data sources to predict outcomes) might help in creating models which implement a decision-making process closer to a real-life application scenario. In the context of multimodality-based prototype learning, we can distinguish two main approaches in producing the prototype representation according to the way of introducing different modalities: (1) deterministic prototypes and (2) shifted prototypes [50]. The first approach typically trains different encoders for all the different modalities, then a connection layer (cross-modal encoder) concatenates the output feature vector extracted generating an unimodal vector into a joint space, used by the PP-Net to perform similarity calculation. Alternatively, some studies have introduced multimodal feature vectors to shift the prototype representations without prior fusion. Here, existing approaches leverage auxiliary modalities to enrich the embedding representation of a main modality. The shifted prototype can be explicitly modelled or their influence can be indirectly added to the objective function used to train an embedded network [50]. Most of the multimodal PP networks proposed in general CV applications integrate visual information with text data [50]. Despite being still considered a relatively unexplored field, we can also find some applications in medical imaging.

Table 1. Part Prototype Network applied in medical imaging. Here, we reported predictive Accuracy (Acc), Balanced Accuracy (Bal Acc), and Area Under the Curve (AUC) according to the provided predictive performances.

Paper	Modality	Dataset	Classes	Results
2D image models
Singh et al. [20]	X-ray	Chest X-ray, COVID-19 Image	Normal, Pneumonia, Covid-19	Acc = 88.99%
Singh et al. [21]	X-ray	Chest X-ray, COVID-19 Image	Normal, Pneumonia, Covid-19	Acc = 87.27%
Singh et al. [22]	CT	COVIDx CT-2	Normal, Pneumonia, Covid-19	Acc = 99.24%
Kim et al. [16]	X-ray	NIH chest x-ray	Atelectasis, Cardiomegaly, Effusion, Infiltration, Mass, Nodule, Pneumonia, Pneumathorax, Consolidation, Edema, Emphysema, Fibrosis, Pleural Thickening, Hernia	Mean AUC = 0.822
Mohammadjafari et al. [26]	MRI	OASIS, ADNI	Normal vs. Alzheimer’s disease	Acc: 87.17% (OASIS), 91.02% (ADNI)
Barnett et al. [28]	Mammography	Internal dataset	Mass-margin classification Malignancy prediction	AUC: 0.951 (Mass-margin) 0.84 (Malignancy)
Carloni et al. [29]	Mammography	CBIS-DDSM	Benign, malignant	Acc = 68.5%
Amorim et al. [31]	Histology	PatchCamelyon	Benign, malignant	Acc = 98.14%
Flores-Araiza et al. [33]	Endoscopy	Simulated in-vivo dataset	Whewellite, Weddellite, Uric Acid anhydrous, Struvite, Brushite, Cystine	Acc = 88.21%
Kong et al. [34]	Dermatoscopic images	ISIC - HAM10000	Actinic keratosis intraepithelial carcinoma, Nevi, Basal cell carcinoma, Benign Keratosis-like Lesions, Dermatofibroma, Melanoma, Vascular lesions	F1 = 74.6
Santiago et al. [36]	Dermatoscopic images	ISIC - HAM10000	Actinic keratosis intraepithelial carcinoma, Nevi, Basal cell carcinoma, Benign Keratosis-like Lesions, Dermatofibroma, Melanoma, Vascular lesions	Bal Acc = 75.0% (Highest, achieved with DenseNet)
Cui et al. [37]	X-ray	Chest X-ray	Normal, Pneumonia	Acc = 91.4%
Nauta et al. [11]	Dermoscopic images, X-Ray	ISIC, MURA, Hip and ankle fraction internal dataset	Benignant, malignant, Normal, abnormal, Fracture, no fracture	Acc: 94.1% (ISIC) 82.1% (MURA) 94.0% (Hip) 77.3% (Ankle)
Santos et al. [38]	Retinograph	Messidor	Healthy vs. Diseased retinopathy	AUC = 0.79
Wang et al. [40]	Mammography, Retinal OCT	Mammography internal dataset, CMMD, NEH OCT	Cancer vs. Non-cancer Benignant vs. Malignant Normal, Drusen, and Choroidal neovascularization	AUC = 91.49 (Internal) AUC = 89.02 (CMMD) Acc = 91.9 (NEH OCT)
Xu et al. [41]	X-ray Lung CT	COVIDx CXR-3 COVID-QU-Ex Lung CT scan	COVID-10 Normal Pneumonia	F1: 99.2 96.8 98.5
Sinhamahapatra et al. [42]	CT	VerSe’19 dataset	Fracture vs. Healthy	F1 = 75.97
Pathak et al. [15]	Mammography	CBIS, VinDir, CMMD	Benignant vs. Malignant	F1 (PIP-Net model): 63±3% (CBIS) 63±3% (VinDir) 70±1% (CMMD)
Gallée et al. [43]	Thorax CT	LIDC-IDRI	Benignant vs. Malignant	Acc = 93.0%
3D image models
Wei et al. [44]	3D mpMRI: T1, T1CE, T2, FLAIR	BraTS 2020	High-grade vs. Low-grade glioma	Bal Acc = 85.8%
Vaseli et al. [46]	Echocardiography	Private dataset TMED-2	Normal vs. Mild vs. Severe Aortic Stenosis	Acc: 80.0% (Private) 79.7 (TMED-2)%
De Santi et al. [48]	3D MRI	ADNI	Normal vs. Alzheimer’s disease	Bal Acc = 82.02%
Multimodal models
Wolf et al. [51]	3D 18F-FDG PET and Tabular data	ADNI	Normal vs. Alzheimer’s disease	Bal Acc = 60.7%
Wang et al. [52]	Chest X-ray and reports	MIMIC-CXR	Atelectasis, Cardiomegaly, Consolidation, Edema, Enlarged Cardiomediastinum, Fracture, Lung Lesion, Lung Opacity, Pleural Effusion, Pleural Other, Pneumonia, Pneumothorax, Support Device	Mean AUC = 0.828
De Santi et al. [53]	3D MRI and Ages	ADNI	Normal vs. Alzheimer’s disease	Bal Acc = 83.04%

Table 1. Part Prototype Network applied in medical imaging. Here, we reported predictive Accuracy (Acc), Balanced Accuracy (Bal Acc), and Area Under the Curve (AUC) according to the provided predictive performances.

Paper	Modality	Dataset	Classes	Results
2D image models
Singh et al. [20]	X-ray	Chest X-ray, COVID-19 Image	Normal, Pneumonia, Covid-19	Acc = 88.99%
Singh et al. [21]	X-ray	Chest X-ray, COVID-19 Image	Normal, Pneumonia, Covid-19	Acc = 87.27%
Singh et al. [22]	CT	COVIDx CT-2	Normal, Pneumonia, Covid-19	Acc = 99.24%
Kim et al. [16]	X-ray	NIH chest x-ray	Atelectasis, Cardiomegaly, Effusion, Infiltration, Mass, Nodule, Pneumonia, Pneumathorax, Consolidation, Edema, Emphysema, Fibrosis, Pleural Thickening, Hernia	Mean AUC = 0.822
Mohammadjafari et al. [26]	MRI	OASIS, ADNI	Normal vs. Alzheimer’s disease	Acc: 87.17% (OASIS), 91.02% (ADNI)
Barnett et al. [28]	Mammography	Internal dataset	Mass-margin classification Malignancy prediction	AUC: 0.951 (Mass-margin) 0.84 (Malignancy)
Carloni et al. [29]	Mammography	CBIS-DDSM	Benign, malignant	Acc = 68.5%
Amorim et al. [31]	Histology	PatchCamelyon	Benign, malignant	Acc = 98.14%
Flores-Araiza et al. [33]	Endoscopy	Simulated in-vivo dataset	Whewellite, Weddellite, Uric Acid anhydrous, Struvite, Brushite, Cystine	Acc = 88.21%
Kong et al. [34]	Dermatoscopic images	ISIC - HAM10000	Actinic keratosis intraepithelial carcinoma, Nevi, Basal cell carcinoma, Benign Keratosis-like Lesions, Dermatofibroma, Melanoma, Vascular lesions	F1 = 74.6
Santiago et al. [36]	Dermatoscopic images	ISIC - HAM10000	Actinic keratosis intraepithelial carcinoma, Nevi, Basal cell carcinoma, Benign Keratosis-like Lesions, Dermatofibroma, Melanoma, Vascular lesions	Bal Acc = 75.0% (Highest, achieved with DenseNet)
Cui et al. [37]	X-ray	Chest X-ray	Normal, Pneumonia	Acc = 91.4%
Nauta et al. [11]	Dermoscopic images, X-Ray	ISIC, MURA, Hip and ankle fraction internal dataset	Benignant, malignant, Normal, abnormal, Fracture, no fracture	Acc: 94.1% (ISIC) 82.1% (MURA) 94.0% (Hip) 77.3% (Ankle)
Santos et al. [38]	Retinograph	Messidor	Healthy vs. Diseased retinopathy	AUC = 0.79
Wang et al. [40]	Mammography, Retinal OCT	Mammography internal dataset, CMMD, NEH OCT	Cancer vs. Non-cancer Benignant vs. Malignant Normal, Drusen, and Choroidal neovascularization	AUC = 91.49 (Internal) AUC = 89.02 (CMMD) Acc = 91.9 (NEH OCT)
Xu et al. [41]	X-ray Lung CT	COVIDx CXR-3 COVID-QU-Ex Lung CT scan	COVID-10 Normal Pneumonia	F1: 99.2 96.8 98.5
Sinhamahapatra et al. [42]	CT	VerSe’19 dataset	Fracture vs. Healthy	F1 = 75.97
Pathak et al. [15]	Mammography	CBIS, VinDir, CMMD	Benignant vs. Malignant	F1 (PIP-Net model): 63±3% (CBIS) 63±3% (VinDir) 70±1% (CMMD)
Gallée et al. [43]	Thorax CT	LIDC-IDRI	Benignant vs. Malignant	Acc = 93.0%
3D image models
Wei et al. [44]	3D mpMRI: T1, T1CE, T2, FLAIR	BraTS 2020	High-grade vs. Low-grade glioma	Bal Acc = 85.8%
Vaseli et al. [46]	Echocardiography	Private dataset TMED-2	Normal vs. Mild vs. Severe Aortic Stenosis	Acc: 80.0% (Private) 79.7 (TMED-2)%
De Santi et al. [48]	3D MRI	ADNI	Normal vs. Alzheimer’s disease	Bal Acc = 82.02%
Multimodal models
Wolf et al. [51]	3D 18F-FDG PET and Tabular data	ADNI	Normal vs. Alzheimer’s disease	Bal Acc = 60.7%
Wang et al. [52]	Chest X-ray and reports	MIMIC-CXR	Atelectasis, Cardiomegaly, Consolidation, Edema, Enlarged Cardiomediastinum, Fracture, Lung Lesion, Lung Opacity, Pleural Effusion, Pleural Other, Pneumonia, Pneumothorax, Support Device	Mean AUC = 0.828
De Santi et al. [53]	3D MRI and Ages	ADNI	Normal vs. Alzheimer’s disease	Bal Acc = 83.04%

Wolf et. al [51] developed PANIC, a Prototypical Additive Neural Network for Interpretable Classification of Alzheimer’s Disease, which performs the classification Alzheimer’s Disease vs. Healthy from 3D 18F-FDG PET images integrated with tabular data. PANIC integrated the image prototypes extracted by a 3D ProtoPNet with N tabular features using an interpretable Generative Additive Model. PANIC obtained a higher balanced accuracy compared to the performances obtained with a black-box model for heterogeneous data. Wang et al. [52] proposed MProtoNet, an interpretable multimodal network which performs diagnosis using images and textual information from medical reports. The architecture combines a position embedding and a multimodal attention module applied to the chest MIMIC-CXR dataset [54], and reported improvements in predictive performances with respect to ProtoPNet without sacrificing the interpretable nature. De Santi et al. [53] proposed Patch-based Intuitive Multimodal Prototypes Network (PIMPNet), a multimodal prototype classifier which learns 3D image part-prototypes and prototypical values from structured data, to predict patient’s cognitive level in AD from sMRI and age values. They introduce the concept of age-prototypical layer to directly learn relevant age values. PIMPNet performed the classification concatenating the image prototypes extracted by a 3D PIPNet with the age prototypes using an intepretable scoring-sheet system; however, the age prototypes do not improve the predictive performance of the model trained with images only.

4. Evaluation of Prototypes

Evaluating XAI method is crucial to verify that the explanations produced are robust, sensitive to the model and data, and consistent, but this is still considered an open and developing field [5,55].

Assessing XAI outputs is considered challenging: there is still no agreement on what interpretability and explainability really are, and a general ground truth to compare explanations is missing. Researchers have proposed different evaluation frameworks to assess XAI methods, and despite there not being a a unique solution yet, most approaches agree concerning the need of considering the multidisciplinary and multidomain nature of the explanation [1]. In this scenario, including quantitative metrics to assess the technical appropriateness and reliability of explanations is crucial. To effectively capture the whole impact of XAI on supporting decision systems in real-world scenarios, is also fundamental to include the human aspect of explanation in the evaluation process [14,56]. The human evaluation should assess how explanations are perceived, their relationship with any expert-domain background knowledge, and how they affect the classification performances, and how all those aspects vary according to the presentation format of explanations.

However, while the effectiveness of post-hoc explainability methods has been investigated extensively, research lines on quantitative analysis of self-explainable approaches are still in their early stage [57]. Particularly relevant for PP-network is the general evaluation framework proposed by Nauta et al. [45]. Here, the “explainability" is considered as a non-binary characteristic, and authors developed a categorization scheme by identifying 12 conceptual properties, the so-called “Co-12 properties”. Nauta et al. [12] further applied their Co-12 evaluation strategy to PP models, providing a recipe to systematically evaluate this family of interpretable models. This overview might be particularly relevant such as most of XAI evaluation methods were designed for posthoc XAI [12,57]. We summarized the evaluation framework grouped with properties grouped by their most prominent dimension in Table 2.

Wei et al. [44] proposed two novel interpretability metrics to assess correctness and localization coherence of prototypes (following the Co-12 taxonomy [45]). The correctness was evaluated proposing the incremental deletion score (IDS) and is based on an incremental deletion process. The localization coherence was evaluated with activation precision (AP) metrics, which and assessed the intersection between the activation map and human-annotated label.

Pathak et al. [15] further developed a general framework for Coherence (one of the Co-12 properties), the so-called PEF-Coh, to quantitatively measure the quality of prototypes w.r.t. domain knowledge for breast cancer prediction from mammography. The PEF-Coh presents six metrics, whose assessment requires a dataset annotated with regions of interest: Relevance; Specialization; Uniqueness; Coverage; Class-specific; and Localization.

Gallée et al. [43] evaluated the Proto-Caps PP-net, which predicts malignancy scores in lung chest CT nodules, and provides explanations in terms of predefined image features attributes and image prototypes. They evaluated their model by performing a user study with 6 radiologists based on a survey to test how explanations affect the (1) user’s performance; (2) trust in the model and if they are (3) helpful or not. They structured a questionnaire differentiating by radiologists’ experience; assessing for the malignancy; their confidence in the prediction and the model’s output. Here, test cases were provided to the users with different levels of explainability. Finally, the questioner asked for an overall assessment of the explanations’ helpfulness. Results confirmed existing literature in observing that: (1) explanations improve performances when the model is correct, but might also convince the user of incorrect predictions; (2) the trust in the model is both influenced by the model’s accuracy and the extent of model’s reasoning; and (3) explanations are generally perceived as useful for the user.

Recent work aims to evaluate explanations using synthetic datasets. In particular, the FunnyBirds framework introduces a synthetically generated dataset of birds with concepts-parts annotation, and a set of metrics to evaluate explanations following the e Co-12 taxonomy. Opłatek et al. [58] applied the FunnyBirds framework to evaluate prototypes produced by ProtoPNet. Their results suggested that explanations provided in the form of similarity maps instead of bounding boxes provide a more faithful representation of the model, resulting in higher-quality explanations. This study further highlights the importance of considering proper visualization techniques in PP models.

The prototype evaluation process has also recently highlighted some concerns about the correctness of the spatial localization of the prototypes [57]. The visualization process of the prototypical part extracted by PP models is generally based on the upsampling of the extracted similarity maps. Despite being PP-Nets claimed to implement an inherently self-explainable case-based reasoning process, recent work reports concerns about the faithfulness of the model-agnostic upsampling process for the part-prototype visualization [57,59]. Guatam et al. [57] proposed Prototype Relevance Propagation (PRP) as a model-aware visualization strategy of prototypical part to address the main drawbacks of the PP-Net upsampling visualization: the low resolution activation maps and spatially imprecise prototype explanations. Xu et al. observed that the upsampling process may incorrectly locate parts of the images, suggesting to use of what they reported as more faithful saliency methods like SmoothGrads or PRP [59].

5. Discussion

Part-prototype networks are self-explainable methods which combine the computational power of DL into an interpretable-by-design decision-making process. PP-nets constitute a prominent solution in medical imaging analysis, where explainability is crucial to ensure the trustworthiness of the AI system, but post-hoc explainable methods reported several drawbacks in terms of reliability and completeness [5,15].

ProtoPNet is the first part-prototype network proposed to perform an interpretable imaging classification, then, other architectural variants follow it [10]. These still implement a classification using a case-based reasoning process, but differ from the first one for how combining prototypical parts to base decisions [17], for introducing the concept of class-shared prototypes [18], and addressing some of reported ProtoPNet limitations, likes the semantic gap between latent and image prototypes representations [8].

Most of PP-Net were originally designed in general CV applications and then shifted to the medical imaging domain. Integrating a deep features extractor into a PP-network often reported competitive performances compared to the fully black-box model counterparts [21,26,31], with the further potential of being able of correcting undesired reasoning process by performing a prototype suppression [11]. Medical images have already reported benefits from the general CV PP-Net; however, this domain might also require peculiar adaptation such as the ability to process 3D image scans and multimodal data domain [44,51,53].

Evaluating XAI methods, including PP-Nets, with standard quantitative frameworks is still considered an open challenge, but crucial to developing reliable and trustworthy systems. Authors generally agree that the evaluation process should be multidisciplinary and multidomain, to be able to capture the multiple aspects that characterize explanations, such as the evaluation recipee proposed by Nauta et al. [12]. Most MI applications of PP-Net performed an evaluation process including domain expert user studies and quantitative metrics. Despite the training of PP-Net does not require further annotation to the class-level labels, most of the prototype evaluation metrics proposed are based on the usage of further image-level annotations such as the segmentation of regions of interest in the images. So, the availability of sub-annotated image dataset might be also beneficial or the development of PP models. Finally, despite the general belief in considering PP-nets as reliable XAI methods due to their self-explainable nature; recent works highlighted drawbacks in the prototypes visualization based on a model-agnostic upsampling process, and proposed alternative solution to produce more spatially-accurate prototypes [57,59].