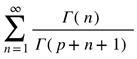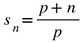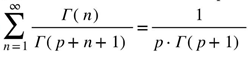Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Symmetry between Series if Entangled by Sums

Submitted:

28 August 2024

Posted:

29 August 2024

You are already at the latest version

Abstract
In analogy with entanglement in physics, the concept of entanglement has been developed in mathematics as a symmetry to build upon as a tool to study 'proximity' relations between different number sequences and series in a unifying way. Examples of entanglement are shown. A general algorithm for detecting entangled sequences/series is given in the appendix. The novelty of this paper is to propose the concept of entanglement as a tool to study different sequences and se-ries-series phenomena. To enable useful treatment suggested by Poincaré.
Keywords: 
entanglement
;  
Gosper
;  
Kummer
;  
sequences
;  
series
;  
closed form sum
Subject: 
Computer Science and Mathematics  -   Computational Mathematics

1. Introducing Entanglement of Series

Student in a mathematics class: “In physics class we learn about entanglement. Why doesn’t entanglement exist in mathematics?” The student apparently was unaware of H. W. Lenstra’s introduction of entangled radicals in algebra [1], followed-up by [2,3,4,5,6]. By analogy we also find annihilation in biology [7], after discovery of the surprising abundance of naturally entangled protein structures. Misfolded entangled subpopulations might become thermosensitive or escape the homeostasis network and deteriorate the brain. Entanglement in engineering is in coating aircraft against meteorites where fibred layers have to be designed in precisely ‘entangled’ layers of composite [8]. Physicists describe entanglement in a way that cannot be explained in this way (because physical entanglement disappears after observation [9,10]). Its mathematical properties are studied in [11].
We introduce entanglement using the method of gradual comprehension, as explained by Codes et. al. [12]. Therefore we start with Levrie’s seed of two series. The idea of entanglement between two series is visualized Table 1 of Levrie [13]. The Fibonacci seed, is not without general interest. The abundance in nature of the Fibonacci series arises from modeling spatial growth patterns, even human skin. The surgeon S. P. Paul [14] operated experimentally on skin to confirm Fibonacci growth changes that occur in tissue when it is stretched. Castellano studied Fibonacci series [15,16] and noted that Levrie’s summed columns are correct to a hundred decimals, if generated by
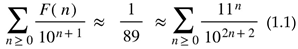
Preprints 116593 i001
The paired columns below show a different speed of convergence towards the sum 1/89. Loosely speaking we say that the two different series (1.1) are ‘entangled’.
A first question that comes to mind is “Do similar pairs exist?” The answer is Yes. For instance about the number π is known from the Indian mathematician Madhava (1350-1425CE) https://www.famousmathematicians.net/madhava/ that
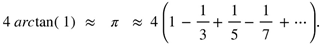
Preprints 116593 i002
The latter series is rediscovered in Europe by Gregory in about 1670 and since than bears his name. The concept of entanglement is beautifully illustrated by Borwein and Bailey’s treatment (in [17], Ch. 2.2) via Joseph Roy North’s 1988 observation of an anomaly in the summation of the first 5 million terms of the Gregory series. This says: the Madhava-Gregory approximation is almost faithful to π but very slow in computational approximation. Different approximations give different computational speeds. Two series of approximations to same sum are said to be in entanglement.
To grasp the idea geometrically by a display from Alexander Farrugia [18], in Figure 2, we see four entangled polygons, each covering in red π/4 square units of surface. The polygons differ, but the surface is equal, in this example exactly equal.
Preprints 116593 g001
Figure 1. from Farrugia [18] in the pubic domain. The red areas above are all equal to π/4 square units. And it would still be π/4 square units if the polygon has more sides!
Figure 1. from Farrugia [18] in the pubic domain. The red areas above are all equal to π/4 square units. And it would still be π/4 square units if the polygon has more sides!
Preprints 116593 g001
Before we define this exactly we give a few examples.
Example 1. 
of an entangled pair approximating π, by Maze and Minder [19], is
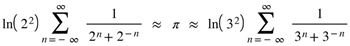
Preprints 116593 i003
Entangled sums obtained via different accelerations are not necessarily integer. Integer sums are rare, for instance, when is a Fibonacci number Fn = n? The first examples are F0 = 0, F1 = 1, F5 = 5. Seemingly exact sums may go astray, as Lenstra [20] reports: over two hundred decimals similarity and a sudden disparity. 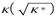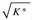Note that Lenstra’s entanglement [20] ameliorates ambiguity between each element of Preprints 116593 i016 to be written as a sum of finitely many elements of Preprints 116593 i017.
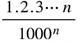Poincaré puts convergence of series in a broader context than just acceleration. This explains why we will not pay in this paper particular attention to convergence and divergence, quoting Poincaré (Ch. 8, p. 317 in [21]) “. . . consider two series that have the following general term Preprints 116593 i018 and Preprints 116593 i019. Pure mathematicians would say that the first series converges and even that it converges rapidly since the millionth term is much smaller than the 999999th; however, they will consider the second series to be divergent since the general term is able to grow beyond all bounds. Conversely, astronomers will consider the first series to be divergent since the first thousand terms increase; they will call the second series convergent since the first thousand terms decrease and since this decrease is rapid at first.”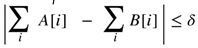
We supersede convergence in such way that practical applications can be supported via boundaries epsilon and delta as Poincaré implicitly suggested.
Entangled numbers solve the entanglement Diophantine equation
f (x) + f (y) = n = f (z) + f (t)
where f (x) is a power of x or a binomial coefficient for fixed n.
Other examples also satisfy the Diophantine equation (1.2). For instance the sum 1729, nowadays known as the ‘taxicab number’ (after a famous anecdote of the British mathematician G. H. Hardy [22]), is the smallest number expressible as the sum of two cubes in two different ways 13 + 123 = 1729 = 93 + 103. Leech [23] reports 27 numbers n < 100 satisfying (1.2). Other sums of two cubes in two or more ways from [24], are 1729, 4104, 13832, 20683, 32832, 39312, 40033, 46683, 64232, ... A classification of such entangled cases in classes is in [25].
Example 2. 
The Münchhausen number 3435 in base ten [25,26,27] is entangled <<< correct Engels? by its sum of digits raised to own powers (the Münchhausen effect)
3 103 + 4 102 + 3 101 + 5 = 3435 = 33 + 44 + 33 + 55.
Example 3. 
Factorions ([25,27] p. 204). The numbers 1, 2, 145 and 40585 are factorions 4 104 +5 102 + 8 101 + 5 = 40585 = 4! + 0! + 5! + 8! + 5!
Example 4. 
Gelderman numbers [27] p. 230 are numbers 142, 8833, …, as shown 102 + 4 101 + 2 = 142 = 141 + 27
8 103 + 8 102 + 3 101 + 3 = 8833 = 882 + 332
Example 5. 
Energetic numbers, [28] are those numbers raised to the power of its base, such as 2 102 + 5 101 + 4 = 254 = 27 + 53 + 40 . Here is δ = 0 and ε = 150 by our Definition 1.
To fix thoughts, the definition of summative mathematical entanglement, provoked by the student’s question, is:
Definition. 
Entanglement between two number sequences A and B, not necessarily of equal length, with (almost) equal sum. The shorter sequence is padded with zeros, to equal length of A and B. We say that sequences A and B are entangled if and only if there exist positive constants epsilon and delta such that the sum of the terms in A is (almost) equal to the sum of the terms in B, ifPreprints 116593 i020
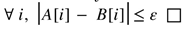
For every term in , there exists a corresponding term in B that is within ɛ of it, i.e., Preprints 116593 i021

2. Creating Series Entanglement by Speed-Up of Convergence

The main idea of this chapter is to maintain the sum of a series by accelerating its convergence, this automatically keeps the series entangled according to the given definition. Acceleration was firstly studied by Euler [29,30] via regrouping of the Gregory series such that its convergence becomes faster. The practical problem of too slow convergence is explained in Euler’s transform is to regroup terms of a convergent series by weight ½. Usually the terms are taken alternating, see section 3.6.27 in [31] and telescoping examples in [32]. The speed-up of convergence can be mandatory. For example, after summing the first three million terms of the Gregory’s infinite series this still does not give us even the first correct digit after the decimal [33].
To understand the generality of Euler’s method we follow Gosper [34,35] with a non-alternating series
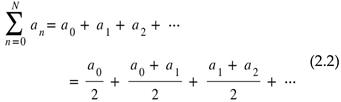
Preprints 116593 i004
Generalizing into possibly unequal weights per term and pairwise regrouping, gives
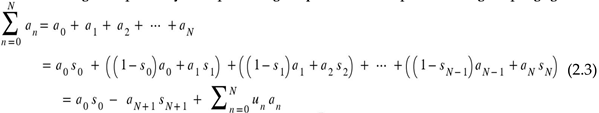
Preprints 116593 i005
Preprints 116593 i006
Before Gosper endeavored in series summation it was A .A. Markoff who followed up on Euler’s work. An historical rectification of Markoff’s role in summation of series is in [36]. Gosper says to start where Stirling [37] left off, as is exemplified by Levrie in [38].
We first give three examples of Gosper’s closed forms, or maximal speed-up of summation by annihilation, un = 0, recall ‘closed forms’.
Example 6. 
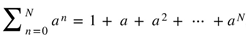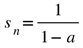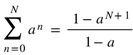The simplest geometric seriesPreprints 116593 i022, m < N, withPreprints 116593 i023in (2.3) satisfies un = 0 for all n (2.4). Then (2.3) results inPreprints 116593 i024.
Example 7. 
(Knopp [39] p. 241; Short [40], Weisstein [41]) The infinite series sumPreprints 116593 i025has term ratioPreprints 116593 i026. Its secret function isPreprints 116593 i027satisfies un = 0 in (2.4), hence the sum of the series according (2.3) isPreprints 116593 i028
Example 8. 
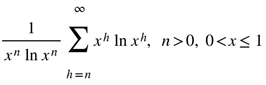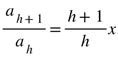(Sum of Shannon Entropy) The sum of the infinite seriesPreprints 116593 i029has term ratioPreprints 116593 i030.
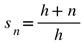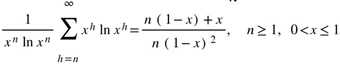Its secret function Preprints 116593 i031 satisfies un = 0 in (2.4), and results in the closed form Preprints 116593 i032.
Example 9. 
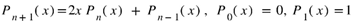Pell polynomials [42] arePreprints 116593 i033, while Pell-Lucas polynomials share this recurrence, but start with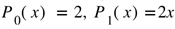Preprints 116593 i034. For these types of polynomials we obtain the closed form
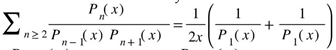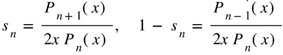Preprints 116593 i035with help of Gosper’s secret functionPreprints 116593 i036.
Remark 1. 
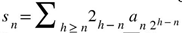Van Wijngaarden [43,44] transforms a positive series into alternating one plus rest. The rest is an accelerated sum of the original. For instance, with Preprints 116593 i037 Van Wijngaarden’s general transform in Gosper’s format is 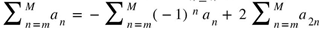Preprints 116593 i038. Gosper’s snan from (3.4) makes up for 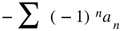Preprints 116593 i039. The rest series converges faster than the original series.
Remark 2 
. An interesting alternative to series transformation by Euler’s method of regrouping is via Abel’s Continuity Theorem [45]. Another method for hypergeometric functions introduced by Forrey [46], is to simplify by Abel’s difference germ functions, which is also the germ of telescopy for sums.
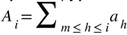A weighted form of telescopy is also from Abel. The weight is Preprints 116593 i040, in the telescoped sum 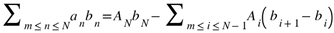Preprints 116593 i041. Abel’s difference is also applicable to non-trivial series as [47].
Remark 3. 
Abel’s method in previous Remark is basic to Gosper’s celebrated algorithmin 1978 [48]. Gosper considers a sum of the form (2.2) where the smmand is a hypergeometric term, hence the ratio of successive terms is a rational function of n [49].In indefinite integration we search for a function which has the integrand as its derivative; for a given hypergeometric term there exists another hypergeometric term, say S(n), such that its difference is the original summand, expressed in the form S(n) – S(n-1).
Finding an ‘antidifference’ a discrete analogue of symbolic integration. is called indefinite summation, and Gosper’s algorithm finds those S(n) such that S(n)/S(n-1) is a rational function of n. Definite summation then follows by Abels’ telescoping. Recall that many summation methods exist [35,40,50,51,52], Gosper’s method is just one of them. The mathematical concept of sequence transformation in general is treated by Delahaye [53].

2.1. Gosper’s Approach from Kummer’s Convergence Criterion

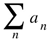Given a convergent series Preprints 116593 i042 we want to construct a better converging series. Testing convergence has many disguises [54], Kummer’s test is most general, because it asks for a companion series 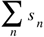Preprints 116593 i043 with elements sn ≤ an for all n is also convergent. From sn ≤ an follows the decreased radius of convergence
Preprints 116593 i007
The reverse is not true, i.e., from (3.1) does not follow sn ≤ an. To speed up convergence of the a-series Gosper [34] deduces from (3.1) Kummer’s functional requirement ([39], section 145)
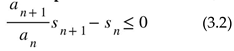
Preprints 116593 i008
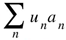To construct a series s with faster convergence than a is (3.2) sufficient. The term wise construction operator guarantees to yield a better converging series Preprints 116593 i044 because from the requirement sn ≤ an it follows un < 1 for all n. So, we obtain Gosper’s result (2.4)
Preprints 116593 i009
Gosper focuses on solving this single functional equation, while Krattenthaler, Zeilberger, Petkovics focus on finding such recurrencies. Gosper’s transformed series then has split off a first term amsm of the infinite series.
Preprints 116593 i010
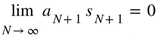For convergent infinite series Preprints 116593 i045 then Preprints 116593 i046. Telescoping occurs if the functional equation (3.3) has a solution sn such that un = 0. In these cases Gosper [34] names solutions s his ‘secret functions’. Search for solving un = 0 is the implicit purpose in (3.3) of his renown algorithm [48], as currently built in Maple and Mathematica and other computer algebra packages. The implemented version of Gosper’s algorithm assumes a rational coercion for s and a in hypergeometric format.
Remark 4.Two solutions of the functional equation (3.3) are
Preprints 116593 i011
Preprints 116593 i012
The two general methods in numerical mathematics for acceleration of series summation [44] are reflected in (3.5) resp. (3.6), note Glaister’s two ‘derived’ series (3) and (4) in [55]. The first general method is by modifying the summand of the series and the second general method is by estimation of the rest of the series [56], i < n analogous to (3.6). From the format of (3.5) and (3.6) can directly be seen why Gosper’s algorithms search for rational simplification of s, otherwise the sum is not dissolved in the final result.
Note the use of our Definition of Entanglement: both sums in (3.5) and (3.6) satisfy the Definition of .

2.2. Criteria for Gosper’s Transformation

Gosper’s term-wise multiplier un (3.3) maintains entanglement if
  • un = 1, i.e., the identity transform does not alter the series, i.e., δ = 0
  • un = 0, yields a closed form (Examples 5 – 7 above), i.e., δ = ε = 0
  • un < 1, gives a different series: entangled and faster converging
  • un > 1, gives a different series: entangled and diverging.
The commonly chosen heuristic to find such homogenous solutions is by assuming that rn is hypergeometric [34,49,57].
A linear scheme with generalized hypergeometric (Meijer’s G) functions for rational approximations is by Fields in two papers [58]. Of course is software available for prior detection of the type of series at hand [59,60].
Example 9. 
Karr’s [61] extended summation in [62] yield results such asPreprints 116593 i047.
Proof. 
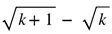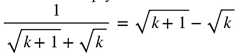multiply numerator and denominator byPreprints 116593 i048. Then telescopy occurs withPreprints 116593 i049.
Example 10. 
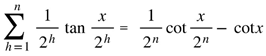The sum of tangentsPreprints 116593 i050.
Telescopy occurs with Preprints 116593 i051. This example is one of many Abelian differences. A result on finding such Abelian differences for Jacobi theta functions is in Lemma 1.2 of [47].

2.3. Knopp’s Transformation Invokes Wilf and Zeilberger’s WZ Pairs

While Gosper’s algorithm deals with a summand in one summation variable, Zeilberger algorithm considers a sum of the form F(n,k), where the summation index k runs through all the integers if not explicitly specified, and F(n,k) is double hypergeometric with finite support with respect to k, so that the sum) is finite. Zeilberger’s method first produces a discrete function G(n,k) which satisfies a recurrence relation between two differences. This recurrence is the recurrence derived by Knopp in his ‘big reordering theorem’, as will be treated below.
Zeilberger’s algorithm does not necessarily fail if a hypergeometric term is not proper, see [60].
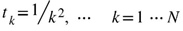
The big transformation of series by Knopp introduces a transformation count to keep track of current status. An example by Knopp is the speed-up of computation of Riemann’s zeta function, by term wise development of Preprints 116593 i052
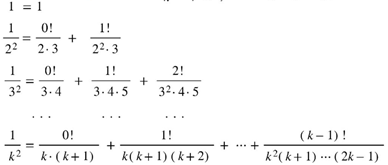
Preprints 116593 i013
Knopp’s method of reordering from expanding rows to adding columns add columns. The columns s are counted by n = 1, 2, 3, …, amounting to the sum of column
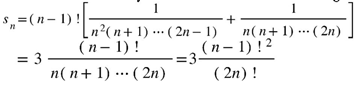
Preprints 116593 i014
The result for Riemann’s zeta is
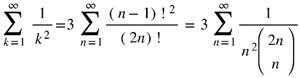
Preprints 116593 i015
What happened is the duality of counting the original column via n and the transformed rows via k. This ‘Umordnung’ (reordering) is the technique by Markoff and subsequently Wilf and Zeilberger: the creative telescopy cerificates shift from summing over n to summing over the transformed series summing over k.
Kondratieva [36] and Andrews [63] both studied the WZ technique. Andrews compared it to Pfaff’s summation method, with the conclusion that Pfaff’s method cannot replace the WZ method. Kondratieva criticised its historic origin and concluded that the WZ method originates with Markoff’s method. A conclusion we just sustained.

3. Discussion

We demonstrated series entanglement by examples of convergence speed-up of geometric series by Gosper’s algorithm, viewed from his ‘secret function’ approach, i.e., without assuming a hypergeometric series format. His strange results triggered early checks by Gessel and Stanton [64]. Acceleration of series summation is of industrial and physical interest [46] if computational processes would otherwise take too long, for instance in the domain of anytime computing i.e., in time-critical industrial or transportation machines (e.g., cars, aeroplanes). The obtained speed-up can be illustrative, see remarkable examples in [65].
We demonstrated sequences entanglement. Discovery of sequence entanglement is harder than of series entanglement. A first attempt to generalize collected cases from [27] into classes is in [25].
The somewhat similar concept of Van der Corput’s discrepancy [66] is older and different from our definition of entanglement. His discrepancy is a measure of how well a sequence of numbers approximates a uniform distribution. A sequence with low discrepancy is considered to be more “random” than a sequence with high discrepancy. In other words, it is a measure of how uniformly a given sequence is spread over a given interval.
The entanglement definition given above, is a formalization of the idea that two sequences are entangled if their terms are closely related. This is a more general concept than Van der Corput’s discrepancy, as it neglects whether they are attempting to approximate a uniform distribution, see Table 2.

Author Contributions

Conceptualization, H.K.; methodology, H.K.; software, H.K.; validation, P.N., M.L.; writing—original draft preparation, H.K.; writing—review and editing, P.N. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The first author is indebted to two brilliant friends: his dear friend and long time [67,68] collaborator Gijs Segers (who is swamped in psychometric data: https://www.visualperformance.nl/en/homepage/ entangled in the sensorimotor system) and to his (former) student and (nowadays) dear friend Ir. Thijs van den Berg, for discussions and his question(s). Thijs won twice the Dutch National Physics TV Context.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

The algorithm below takes two number sequences A and B as input and returns True if A and B are entangled, and False otherwise. The algorithm uses the epsilon-delta definition of entanglement and the concept of delta-closeness in Python code:
def is_entangled(seqs1, seqs2, epsilon, delta):
  total1 = sum(seqs1)
  total2 = sum(seqs2)
  if abs(total1 - total2) ≤ delta:
    for i in range(len(seqs1)):
      if abs(seqs1[i] - seqs2[i]) > epsilon:
      return False
    return True
  return False
end
Import two sequences of random data:
  seqs1 = [random.randint(0, 10) for _ in range(10)]
  seqs2 = [random.randint(0, 10) for _ in range(10)]
  epsilon = 0.01
  delta = 0.01
  is_entangled = is_entangled(seqs1, seqs2, epsilon, delta)
  print("Is entangled:", is_entangled)
end
If the output of the above program is: “Is entangled: False” this means that the two sequences of random inputs are not entangled.

References

  1. Lenstra, H.W. Entangled Radicals. Ann. Math. 2010, 103, 593–610. [Google Scholar]
  2. Lenstra, H.W., Jr.; Stevenhagen, P.; Moree, P. Character sums for primitive root densities. Math. Proc. Cambridge Philos. Soc. 2014, 157, 489–511. [Google Scholar] [CrossRef]
  3. Perucca, A.; Sgobba, P.; Tronto, S. Kummer theory for number fields via entanglement groups. Manuscripta Math. 2022, 169, 251–270. [Google Scholar] [CrossRef]
  4. Campagna, F.; Pengo, R. Entanglement in the family of division fields of elliptic curves with complex multiplication. Pacific J. Math. 2020, 317, 21–66. [Google Scholar] [CrossRef]
  5. Daniels, H.B.; Morrow, J.S. A group theoretic perspective on entanglements of division fields. Trans. Am. Math. Soc. Ser. B 2022, 9, 827–858. [Google Scholar] [CrossRef]
  6. Mercier, H.; Augier, M.; Lenstra, A.K. STEP-archival: Storage Integrity and Anti-Tampering using Data Entanglement. In Proceedings of the IEEE Int. Symp. on Information Theory (ISIT); 2015; pp. 1590–1594. [Google Scholar]
  7. Salicari, L.; Baiesi, M.; Orlandini, E.; Trovato, A. Folding kinetics of an entangled protein. PLoS Comput. Biol. 2023, 19, 1–30. [Google Scholar] [CrossRef] [PubMed]
  8. Netten, B.; Vingerhoeds, R.; Koppelaar, H. Expert assisted conceptual design: An application to fibre reinforced composite panels. Des. Res. Netherlands 1995, 37, 125–139. [Google Scholar]
  9. Bub, J. Bananaworld; Oxford University Press (OUP): Oxford, 2016; ISBN 978-0-19-881784-0. [Google Scholar]
  10. Chamgordani, M.A.; Naderi, N.; Koppelaar, H.; Bordbar, M. The entanglement dynamics of superposition of fermionic coherent states in Heisenberg spin chains. Int. J. Mod. Phys. B 2019, 33, 1950180–1. [Google Scholar] [CrossRef]
  11. Plenio, M.B.; Virmani, S. An introduction to entanglement measures. Quant. Inf. Comput. 2007, 7, 1–51. [Google Scholar] [CrossRef]
  12. Codes, M.; González Astudillo, M.T.; Delgado Martín, M.L.; Monterrubio Pérez, M.C. Growth in the understanding of infinite numerical series: a glance through the Pirie and Kieren theory. Int. J. Math. Educ. Sci. Technol. 2013, 44, 652–662. [Google Scholar] [CrossRef]
  13. Levrie, P. 1/89 Interessant getal. Pythagoras 2023, 62, 29. [Google Scholar]
  14. Paul, S.P. Golden Spirals and Scalp Whorls: Nature’s Own Design for Rapid Expansion. PLoS One 2016, 11, e0162026–1. [Google Scholar] [CrossRef]
  15. Castellanos, D. Rapidly converging expansions with Fibonacci coefficients. Fibonacci Q. 1986, 24, 70–82. [Google Scholar]
  16. Castellanos, D. A Generalization of Binet’s Formula and some of its consequences. Fibonacci Q. 1989, 27, 424–438. [Google Scholar]
  17. Borwein, J.M.; Bailey, D.H. Mathematics by Experiment; A. K. Peters, Natick, MA: Natick, Massachusetts, 2004; ISBN 1-56881-211-6. [Google Scholar]
  18. Farrugia, A. What are some awesome coincidences in geometry? Available online:. Available online: https://www.quora.com/What-are-some-awesome-coincidences-in-geometry/answer/Alexander-Farrugia (accessed on Aug 28, 2024).
  19. Maze, G.; Minder, L. A new family of almost identities. Elem. der Math. 2007, 62, 89–97. [Google Scholar] [CrossRef]
  20. Lenstra, H. Profinite Fibonacci numbers. Nieuw Arch. Voor Wiskd. 2005, 5/6, 297–300. [Google Scholar]
  21. Poincaré New methods of celestial mechanics; Goroff, D.L., Ed.; Vol. 1,2,3.; American Institute of Physics, 1993.
  22. Hardy, G.H. A mathematician’s apology; Cambridge University Press, 1940. [Google Scholar]
  23. Leech, J. Some solutions of diophantine equations. Math. Proc. Cambridge Philos. Soc. 1957, 53, 778–780. [Google Scholar] [CrossRef]
  24. Sloane, N.J.A. Taxicab numbers Available online:. Available online: https://oeis.org/A001235 (accessed on Feb 9, 2024).
  25. Koppelaar, H.; Nasehpour, P. On Hardy’s Apology Numbers. J. Algorithms Comput. 2020, 52, 67–83. [Google Scholar]
  26. van Berkel, D. On a curious property of 3435 Available online:. Available online: http://arxiv.org/abs/0911.3038 (accessed on Feb 25, 2024).
  27. Looijen, M. Talking about Numbers; 4th ed.; van Haren Publishing, 2021; ISBN 9789401806015.
  28. Wilson, D.W. Energetic numbers Available online:. Available online: https://oeis.org/A072096 (accessed on Feb 4, 2024).
  29. Euler, L. Introductio in Analysin Infinitorum, volume 1, (1748); Euler Arch.; University of the Pacific, 2018.
  30. Euler, L. Introductio in Analysin Infinitorum, volume 2, (1748); Euler Arch.; University of the Pacific, 2018.
  31. Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; 10th ed.; Dover: New York, 1972.
  32. Chen, H. On the telescoping sum. Int. J. Math. Educ. Sci. Technol. 2004, 35, 270–281. [Google Scholar] [CrossRef]
  33. Campbell, J.M.; Chu, W. Lemniscate-like constants and infinite series. Math. Slovaca 2021, 71, 845–858. [Google Scholar] [CrossRef]
  34. Gosper, R.W. Calculus of Series Rearrangements. In Algorithms and Complexity; Traub, J.E., Ed.; Academic Press: New York, 1976; pp. 121–151. [Google Scholar]
  35. Smith, C.J.; Tefera, A.; Zeleke, A. Computerized proof techniques for undergraduates. Int. J. Math. Educ. Sci. Technol. 2012, 43, 1067–1077. [Google Scholar] [CrossRef]
  36. Kondratieva, M.; Sadov, S. Markov’s transformation of series and the WZ method. Adv. Appl. Math. 2005, 34, 393–407. [Google Scholar] [CrossRef]
  37. Tweddle, I. James Stirling’s Methodus Differentialis; Springer Berlin Heidelberg New York, 2003.
  38. Levrie, P.; Nimbran, A.S. Recycling Stirling’s series acceleration technique. Math. Gaz. 2017, 101, 69–82. [Google Scholar] [CrossRef]
  39. Knopp, K. Theorie und Anwendung der Unendlichen Reihen; Springer Verlag, Berlin, 1964; ISBN 3-540-03138-3.
  40. Short, L. Summation of series. Int. J. Math. Educ. Sci. Technol. 1991, 22, 985–996. [Google Scholar] [CrossRef]
  41. Weisstein, E. Convergence Improvement Available online: https://mathworld.wolfram.com/ConvergenceImprovement.html.
  42. Horadam, A.F. Abstract Lambda Lucas polynomials and their convolutions. Notes Number Theory Discret. Math. 2003, 9, 13–27. [Google Scholar]
  43. Van Wijngaarden, A. A Transformation of Formal Series. I. Indag. Math. 1953, 56, 522–533. [Google Scholar] [CrossRef]
  44. Jentschura, U.D.; Aksenov, S. V.; Mohr, P.J.; Savageau, M.A.; Soff, G. Convergence Acceleration Techniques. arXiv: math.NA 2002, 1–6.
  45. Chen, Z.; Wei, S.; Xiao, X. Finding sums for an infinite class of alternating series. Int. J. Math. Educ. Sci. Technol. 2012, 43, 694–702. [Google Scholar] [CrossRef]
  46. Forrey, R.C. Computing the Hypergeometric Function. J. Comput. Phys. 1997, 137, 79–100. [Google Scholar] [CrossRef]
  47. Xu, J.; Ma, X. General q-series transformations based on Abel’s lemma on summation by parts and their applications. J. Differ. Equations Appl. 2024, 30, 553–576. [Google Scholar] [CrossRef]
  48. Gosper, R.W. Decision procedure for indefinite hypergeometric summation (algorithm/binomial coefficient identities/closed form/symbolic computation/linear recurrences). Proc. Nat. Acad. Sci. USA 1978, 75, 40–42. [Google Scholar] [CrossRef]
  49. Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics; Addison-Wesley: Boston, 1989; ISBN 0-201-5802-5. [Google Scholar]
  50. Wright, C.; Osler, T.J. Four derivations of an interesting bilateral series generalizing the series for zeta of 2. Int. J. Math. Educ. Sci. Technol. 2013, 44, 456–461. [Google Scholar] [CrossRef]
  51. Lee, T.Y.; Lim, Y.C.; Wu, S.A. Finding sums for an infinite class of convergent series. Int. J. Math. Educ. Sci. Technol. 2016, 47, 649–651. [Google Scholar] [CrossRef]
  52. Abramov, S.A.; Carette, J.J.; Geddes, K.O.; Le, H.Q. Telescoping in the context of symbolic summation in Maple. J. Symb. Comput. 2004, 38, 1303–1326. [Google Scholar] [CrossRef]
  53. Delahaye, J.-P. Sequence Transformations; Springer Verlag: Berlin, 1988. [Google Scholar]
  54. Bourchtein, L.; Bourchtein, A. Comparison of some tests for convergence of positive series. Int. J. Math. Educ. Sci. Technol. 2016, 47, 474–489. [Google Scholar] [CrossRef]
  55. Glaister, P. Generating sums of series using simple differential operators. Int. J. Math. Educ. Sci. Technol. 2006, 37, 341–349. [Google Scholar] [CrossRef]
  56. Gal-Ezer, J.; Zwas, G. Corrected summation of alternating series. Int. J. Math. Educ. Sci. Technol. 1993, 24, 171–176. [Google Scholar] [CrossRef]
  57. Long, L. Hypergeometric evaluation identities and supercongruences. Pacific J. Math. 2011, 249, 405–418. [Google Scholar] [CrossRef]
  58. Fields, J.L. A linear scheme for rational approximations I, II. J. Approx. Theory 1972, 6, 161–175. [Google Scholar] [CrossRef]
  59. Fessler, T.; Ford, W.; Smith, D.A. Algorithm 602: HURRY: An Acceleration Algorithm for Scalar Sequences and Series. ACM Trans. Math. Softw. 2002, 9, 355–357. [Google Scholar] [CrossRef]
  60. Abramov, S.A.; Le, H.Q. A criterion for the applicability of Zeilberger’s algorithm to rational functions. Discrete Math. 2002, 259, 1–17. [Google Scholar] [CrossRef]
  61. Karr, M. Summation in finite terms. J. ACM 1981, 28, 305–350. [Google Scholar] [CrossRef]
  62. Kauers, M.; Schneider, C. Symbolic Summation with Radical Expressions. Proc. Int. Symp. Symb. Algebr. Comput. 2007, 219–226. [Google Scholar]
  63. Andrews, G.E. Pfaff’s Method (III): Comparison with the WZ Method. Electron. J. Comb. 1996, 3, 1–16. [Google Scholar] [CrossRef]
  64. Gessel, I.; Stanton, D. Strange Evaluations of Hypergeometric Series. SIAM J. Math. Anal. 1982, 13, 295–308. [Google Scholar] [CrossRef]
  65. Levrie, P.; Campbell, J. Series acceleration formulas obtained from experimentally discovered hypergeometric recursions. Discret. Math. Theor. Comput. Sci. 2022, 24, 1–19. [Google Scholar] [CrossRef]
  66. Chazelle, B. The Discrepancy Method; Cambridge University Press; ISBN 0521003571.
  67. Koppelaar, H.; Kordestani-Moghadan, P.; Khan, K.; Kouhkani, S.; Segers, G.; Warmerdam, M. van Reaction Time Improvements by Neural Bistability. Behav. Sci. (Basel). 2019, 9, 1–14. [Google Scholar]
  68. Koppelaar, H.; Kordestani-Moghadam, P.; Kouhkani, S.; Irandoust, F.; Segers, G.; Haas, L. de; Bantje, T.; Warmerdam, M. van Proof of Concept of Novel Visuo-Spatial-Motor Fall Prevention Training for Old People. Geriatrics 2021, 6, 1–27. [Google Scholar] [CrossRef]
  69. Frontczak, R.; Prasad, K. Balancing Polynomials, Fibonacci Numbers and Some New Series for π. Mediterr. J. Math. 2023, 20, 1–16. [Google Scholar] [CrossRef]
Table 1.
Fibonacci sequence1 Powers of 11
0, 1, 1, 2, 3, 5, 8, 13, … 110 , 111 , 112 , 113 , 114 , …

0,01
0,01
0,001 0,0011
0,0002 0,000121
0,00003 0,00001331
0,000005 0,0000014641
0,0000008 0,000000161051
0,00000013 0,00000001771561
0,000000021 0,0000000019487171
0,0000000034 0,000000000214358881
0,00000000055 0,00000000002357947691
0,000000000089 0,0000000000025937424601
0,0000000000144 0,000000000000285311670611
0,00000000000233 0,00000000000003138428376721
0,000000000000377 0,0000000000000034522712143931
+----------------------------------------- +-------------------------------------------
0,01123595505? 0,01123595505?...................................
1 The two sums in Levrie [13].
Table 2. summarizing the key differences between the two concepts is:.
Table 2. summarizing the key differences between the two concepts is:.
Feature Van der Corput’s discrepancy Our Entanglement definition
Application Measuring the randomness of a sequence Formalizing the idea that two sequences are entangled
Specificity Focuses on sequences that approximate a uniform distribution More general and can be applied to any two sequences
Focus Uniformity of distribution Pairwise Difference between terms
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated