Modeling The Impact Of Economic Factors On Electoral Results: A Predictive Approach To Ghana's 2024 Elections

1. Introduction

Elections have long been recognized as a critical aspect of democratic governance, serving as the mechanism through which political power is conferred, transferred, or contested. As societies evolve, economic conditions and electoral outcomes become inextricably linked, forming a relationship that both scholars and policymakers seek to understand. In Ghana, a country with a rich democratic tradition in the Fourth Republic, the 2024 elections promise to be a significant event, with economic factors playing a potentially decisive role in shaping voter preferences and election results (Anaman & Bukari, 2021). This research, therefore, seeks to explore and model the impact of economic factors on electoral outcomes, using past elections in Ghana as a foundation to predict future electoral behavior. The focus on economic indicators in this context is particularly crucial given Ghana’s history of economic instability and the direct effects this has had on its political landscape (Debrah, 2009).

Economic voting theory provides a foundational framework for understanding how voters evaluate political parties and candidates based on their perceived ability to manage the economy (Leigh, 2005). This theory suggests that voters reward incumbents during periods of economic prosperity and punish them during downturns. Ghana, as a developing country, presents a unique case where economic factors such as inflation, unemployment, and poverty rates have varied widely between electoral cycles, often influencing voter decisions (Anaman & Bukari, 2019). As such, assessing the impact of these key economic factors on electoral outcomes in Ghana’s past elections provides valuable insights into the 2024 elections.

Economic voting behavior in Ghana, much like in other parts of the world, is often mediated by political institutions and dynamics. For instance, while economic conditions play a significant role, the interaction between these conditions and political factors such as incumbency, political party systems, and voter loyalty can affect how economic information is processed and utilized by voters (Duch & Stevenson, 2008). In Ghana, incumbency has historically provided electoral advantages due to access to state resources, while opposition parties have used periods of economic decline to mobilize support (Primus, 2015). This research will evaluate how economic factors interact with these political dynamics, shaping voter preferences and electoral outcomes, with an eye on the upcoming 2024 elections.

Furthermore, electoral volatility has been a feature of Ghanaian elections, where swings in voter support between parties are often attributed to shifts in economic performance (Bossuroy, 2011). The ability to model and predict electoral volatility based on economic conditions, such as fluctuations in GDP growth or inflation rates, is key to forecasting the 2024 elections. By providing insights into the potential role of these economic factors, this research aims to contribute to the broader field of political economy and electoral studies (Çarkoğlu, 1997).

The objectives of this study are thus multifaceted. Firstly, it seeks to assess the impact of key economic factors—such as GDP growth, unemployment, inflation, and poverty—on electoral outcomes in Ghana’s past elections. By analyzing electoral data from previous cycles, this research will identify patterns and trends that are likely to influence the 2024 elections (Wiatr, 1962). Secondly, the study aims to develop a predictive model using economic indicators to forecast the outcomes of Ghana’s 2024 elections. Predictive modeling in political science has gained prominence as researchers and analysts seek to use data-driven approaches to anticipate voter behavior (Leigh, 2005). Thirdly, the research will evaluate the interaction between economic factors and political dynamics, examining how factors such as incumbency and political party loyalty shape the way voters respond to economic conditions (Kostelecký, 1994). Finally, the study will provide insights into the potential role of economic factors in determining electoral volatility, a phenomenon that has significant implications for political stability in Ghana (Anaman & Bukari, 2019).

1.1. Economic Factors and Electoral Outcomes in Ghana

The relationship between economic performance and electoral outcomes in Ghana can be understood through the lens of economic voting theory, which posits that voters tend to reward or punish incumbents based on their management of the economy (Eulau & Lewis-Beck, 2007). Ghana’s economy has experienced periods of both growth and stagnation since the Fourth Republic was established in 1992, with GDP growth rates fluctuating due to external shocks, structural adjustments, and domestic policy interventions (Anaman & Bukari, 2019). Historically, electoral outcomes in Ghana have mirrored these economic cycles, with incumbents often benefiting from periods of economic stability and facing challenges during times of economic downturn (Debrah, 2009).

For example, in the 2000 elections, economic decline—marked by high inflation, rising unemployment, and slow GDP growth—contributed to the defeat of the incumbent party (Anaman & Bukari, 2019). Similarly, economic challenges in the run-up to the 2008 elections, including high inflation and currency depreciation, created fertile ground for the opposition to gain significant support (Primus, 2015). These historical precedents underscore the importance of understanding how economic factors influence voter behavior in Ghana. By assessing the impact of key economic indicators in previous elections, this study aims to identify which factors are most likely to shape the outcome of the 2024 elections.

The development of a predictive model based on these economic indicators is the next logical step in this research. Predictive models have been used effectively in other democratic contexts to forecast election results by incorporating both economic and political variables (Çarkoğlu, 1997). In the case of Ghana, economic variables such as GDP growth, unemployment, and inflation will be key inputs in the predictive model. However, it is important to note that these factors do not operate in isolation. Political dynamics, such as incumbency advantage and party loyalty, also play a significant role in shaping electoral outcomes (Hibbing & Alford, 1981). Therefore, the predictive model developed in this study will integrate both economic and political variables to provide a comprehensive forecast for the 2024 elections (Leigh, 2005).

1.2. Interaction Between Economic Factors and Political Dynamics

In addition to assessing the direct impact of economic conditions on electoral outcomes, this study will examine how these conditions interact with political dynamics in Ghana. Political incumbency, for example, often provides significant advantages in elections, particularly in Ghana, where access to state resources can be used to influence voter perceptions (Primus, 2015). However, during periods of economic decline, incumbents may find it difficult to maintain support, as voters tend to blame the sitting government for poor economic performance (Duch & Stevenson, 2008). The interaction between economic factors and incumbency will be a key focus of this research, as it seeks to understand how these dynamics shape voter preferences in Ghana.

Moreover, party loyalty in Ghana remains a strong determinant of electoral outcomes. Voters in certain regions have historically supported specific parties, regardless of economic conditions, due to ethnic and regional allegiances (Bossuroy, 2011). However, during times of economic crisis, even loyal voters may shift their support if they feel that their economic interests are not being adequately addressed by their preferred party (Wiatr, 1962). This research will explore how economic factors interact with party loyalty to influence voter behavior, particularly in the 2024 elections, where economic recovery from the COVID-19 pandemic is likely to be a major campaign issue (Anaman & Bukari, 2021).

1.3. Electoral Volatility and Economic Factors

Electoral volatility, or the degree to which voter support shifts between parties from one election to the next, has been a notable feature of Ghanaian elections. Volatility is often driven by economic factors, as voters seek to hold the government accountable for economic performance (Primus, 2015). In Ghana, periods of economic instability have coincided with significant swings in voter support, particularly in swing regions where party loyalty is less entrenched (Debrah, 2009). This study will provide insights into the potential role of economic factors in determining electoral volatility in the 2024 elections by analyzing historical data on voter behavior and economic conditions (Çarkoğlu, 1997).

The ability to model and predict electoral volatility based on economic conditions is critical for understanding the dynamics of Ghana’s upcoming elections. By examining the interaction between economic performance and voter behavior, this research will contribute to a broader understanding of how economic factors shape electoral outcomes in developing democracies (Anaman & Bukari, 2021). Furthermore, the findings of this study will have implications for policymakers and political strategists seeking to navigate the complexities of economic voting in Ghana.

In essence, the impact of economic factors on electoral outcomes in Ghana is a critical area of study, particularly as the country approaches its 2024 elections. This research will assess the role of key economic indicators in shaping voter behavior in past elections, develop a predictive model for the 2024 elections, and evaluate the interaction between economic factors and political dynamics. Thus, providing insights into electoral volatility, this study aims to contribute to the growing body of literature on economic voting and political behavior in developing democracies. The findings will not only enhance our understanding of electoral outcomes in Ghana but also offer valuable lessons for other countries where economic conditions play a significant role in shaping voter preferences (Leigh, 2005; Wiatr, 1962).

2. Related Works

The relationship between economic conditions and electoral outcomes has been a prominent area of research in political science and economics for decades. Economic voting theory, which posits that voters hold incumbents accountable for the state of the economy, is one of the most widely explored concepts in this field. The work of Leigh (2005) stands out as it delves into how individual, local, and national economic factors affect partisan choices, providing a foundation for understanding the dynamics of economic voting. Similarly, Wiatr (1962) emphasized the significance of both economic and social factors in shaping electoral behavior, a framework that has remained relevant in studies of electoral outcomes across various political systems.

In the context of Western democracies, Eulau and Lewis-Beck (2007) provided an extensive exploration of the relationship between economic conditions and electoral outcomes, focusing on the United States and Western Europe. Their work underscored the importance of macroeconomic indicators such as inflation, unemployment, and GDP growth in influencing voter decisions. This is consistent with the findings of Duch and Stevenson (2008), who argued that economic institutions and political contexts significantly condition the electoral results, indicating that voters not only respond to economic conditions but also to how well political actors are perceived to manage these conditions. These works collectively highlight the global relevance of economic voting, but also suggest that contextual factors, such as political institutions, play a crucial role in shaping the economic vote.

Looking specifically at Ghana, the role of economic factors in electoral outcomes has also received scholarly attention. Primus (2015) conducted an in-depth study of economic voting in Ghana, identifying key economic indicators such as inflation, unemployment, and GDP growth as significant determinants of electoral outcomes. His research emphasized that voters in Ghana, much like in other democracies, tend to reward incumbents for positive economic performance and punish them during economic downturns. This aligns with the broader theoretical framework of economic voting but also highlights the unique dynamics at play in a developing democracy such as Ghana, where economic volatility is often higher than in established Western democracies.

Further contributing to the understanding of economic voting in Ghana, Anaman and Bukari (2019) explored the macroeconomic impact of national elections during the Fourth Republic, from 1992 to 2016. They found that economic conditions, particularly inflation and GDP growth, had a significant impact on voter behavior and electoral outcomes. Moreover, they argued that political transitions in Ghana are often accompanied by shifts in economic policies, which in turn influence voter perceptions and behavior. This research is crucial for understanding the cyclical nature of economic voting in Ghana, where incumbents are frequently held accountable for economic performance, especially in the context of high inflation and unemployment.

In addition to the impact of economic conditions on electoral outcomes, other scholars have examined how economic factors interact with political dynamics to shape voter preferences. Hibbing and Alford (1981) focused on the electoral impact of economic conditions in the United States, arguing that voters tend to hold the incumbent government responsible for the state of the economy. This finding has broader implications, suggesting that in Ghana, as in other democracies, incumbency plays a crucial role in mediating the relationship between economic performance and electoral outcomes. Specifically, in Ghana, where incumbents often have access to state resources and can influence public perception through various means, the interaction between economic conditions and incumbency is likely to be significant in determining voter behavior.

The interaction between economic factors and political dynamics in Ghana has also been explored by Bossuroy (2011), who examined the role of ethnicity and election outcomes in the country. While his research primarily focused on the ethnic dimension of voting behavior, he noted that economic factors, particularly in terms of regional development and inequality, also played a role in shaping voter preferences. This highlights the complexity of voter behavior in Ghana, where economic conditions are just one of many factors that influence electoral outcomes. The interaction between economic and political factors is therefore an essential area of study, particularly in the lead-up to the 2024 elections.

From a broader comparative perspective, the work of Çarkoğlu (1997) on macroeconomic determinants of electoral support for incumbents in Turkey provides useful insights for understanding similar dynamics in Ghana. His research showed that in countries with volatile economies, voters are more likely to focus on economic issues when deciding whether to support incumbents or opposition parties. This is particularly relevant in the Ghanaian context, where economic instability has often been a central issue in election campaigns. The insights from Çarkoğlu’s study suggest that economic factors will likely play a significant role in the 2024 elections in Ghana, where the economic recovery from the COVID-19 pandemic is expected to be a key issue.

2.1. Research Gaps

Despite the extensive research on economic voting, there are still notable gaps in the literature, particularly concerning the role of economic factors in determining electoral volatility in developing democracies. While much of the existing literature has focused on stable democracies in the West, the dynamics of economic voting in countries like Ghana, where political transitions and economic volatility are more pronounced, remain underexplored. For example, Doležalová et al. (2017) focused on the electoral success of far-right and far-left parties in the European Union, but their findings are less applicable to Ghana, where the political landscape is shaped more by ethnicity, incumbency, and economic performance than by ideological extremism. This highlights a gap in the literature, particularly in terms of understanding how economic factors influence electoral volatility in Ghana’s multiparty democracy.

Another gap in the literature is the lack of predictive models that integrate both economic and political factors in forecasting electoral outcomes in developing democracies. While predictive modeling has become a common tool in political science, particularly in the context of Western elections (Leigh, 2005), there is limited research on how these models can be adapted to the unique conditions of developing democracies such as Ghana. The work of Duch and Stevenson (2008) on the economic vote provides a valuable framework for understanding the conditional nature of economic voting, but more research is needed to apply this framework in the Ghanaian context. This study aims to fill this gap by developing a predictive model that incorporates both economic and political factors to forecast the outcomes of Ghana’s 2024 elections.

In conclusion, the existing literature on economic voting provides a solid foundation for understanding the relationship between economic factors and electoral outcomes in both developed and developing democracies. However, there are significant gaps in the literature concerning the role of economic factors in determining electoral volatility and the lack of predictive models tailored to the specific conditions of developing democracies like Ghana. This study seeks to address these gaps by integrating economic and political variables into a predictive model for Ghana’s 2024 elections, contributing to a deeper understanding of economic voting in a developing democratic context.

3. Methods and Materials

This section outlines the methods and materials used in this study to model the impact of economic factors on electoral results, with a specific focus on Ghana’s 2024 elections. It includes a detailed description of the study area, research design, sampling, data collection, and the various statistical analyses employed.

3.1. Study Area

The study is conducted in Ghana, a West African country known for its robust democratic processes and regular elections since the establishment of the Fourth Republic in 1992. Ghana operates under a hybrid political system that combines elements of both parliamentary and presidential systems, providing a unique context for analyzing the relationship between economic factors and electoral outcomes. The country is divided into 16 administrative regions, each exhibiting distinct economic, political, and social characteristics. Voter preferences in Ghana are often influenced by factors such as ethnicity, economic development, and political party loyalty, making it an ideal case for exploring the interplay between economic conditions and election results (Anaman & Bukari, 2019).

3.2. Research Design and Approach

This study adopts a quantitative research design with a predictive modeling approach to examine the relationship between economic factors and electoral outcomes in Ghana. The research aims to assess the impact of economic variables such as GDP growth, unemployment, inflation, and exchange rate stability on past election results, and to use these variables to forecast the outcomes of the 2024 general elections. A longitudinal study design is employed, focusing on multiple electoral cycles from 1992 to 2020, allowing for the analysis of trends over time (Leigh, 2005).

The research approach is deductive and data-driven, leveraging econometric models such as ARIMA and VAR to predict future electoral outcomes. By using historical data from past elections, this study seeks to identify patterns and relationships between economic performance and voting behavior, thus providing insights into the potential impact of economic conditions on the upcoming elections (Eulau & Lewis-Beck, 2007).

3.3. Sample Size Analysis

The sample for this study includes electoral data from seven national elections in Ghana (1992, 1996, 2000, 2004, 2008, 2012, and 2016) along with corresponding economic indicators. Each election cycle is treated as a separate observation in the analysis, and the sample includes data from all 16 regions of Ghana. Given the availability of regional and national-level data, the total sample size consists of 112 observations (7 elections x 16 regions), which is sufficient for conducting robust econometric analyses (Duch & Stevenson, 2008). To ensure statistical power, a sample size calculation was performed based on the need for at least 80% power to detect significant relationships between the independent variables (economic indicators) and the dependent variable (electoral outcomes). With a significance level (α) of 0.05, the sample size was deemed adequate for the regression analyses planned in this study (Primus, 2015).

3.4. Data Source and Collection

Data for this study are drawn from multiple reliable sources:

• Electoral Data: Voter turnout, party vote share, and incumbent re-election rates were sourced from the Electoral Commission of Ghana and regional electoral offices (Anaman & Bukari, 2021).
• Economic Data: Economic indicators such as GDP growth, unemployment rate, inflation, poverty rate, and exchange rate stability were collected from the Bank of Ghana, World Bank, and International Monetary Fund (Eulau & Lewis-Beck, 2007).
• Political Stability and Corruption Control: These indicators were obtained from the World Bank’s Governance Indicators (Anaman & Bukari, 2019).

The data were collected for the period between 1992 and 2020 to capture the electoral cycles within the Fourth Republic. Both quantitative electoral data and macroeconomic data were structured into a panel dataset, allowing for comprehensive regional and national-level analysis.

3.5. Data Analysis

The data analysis in this study involves a combination of descriptive statistics, correlation analysis, and advanced econometric modeling techniques, such as ARIMA and VAR models. The aim is to assess the relationships between economic variables and electoral outcomes and to develop a predictive model for the 2024 elections.

Descriptive Statistics

Descriptive statistics are used to summarize the key characteristics of the data, such as mean, median, standard deviation, and range for each of the economic and electoral variables. These statistics help to identify patterns in the data and provide an initial overview of the variables under study (Leigh, 2005).

Correlation Analysis

A Pearson correlation analysis is conducted to examine the strength and direction of relationships between the economic indicators (e.g., GDP growth, inflation) and electoral outcomes (e.g., voter turnout, party vote share). This analysis provides insights into which economic factors are most closely associated with changes in electoral behavior (Duch & Stevenson, 2008).

Stationarity Tests

Before proceeding with time-series analysis, it is essential to check for the stationarity of the data. Augmented Dickey-Fuller (ADF) tests and Phillips-Perron tests are used to test for unit roots and ensure that the time-series data are stationary. Non-stationary data will be differenced or transformed to meet the assumptions of the econometric models (Çarkoğlu, 1997).

Multicollinearity Check

To ensure that the independent variables in the regression models are not highly correlated with each other, a Variance Inflation Factor (VIF) analysis is performed. This test helps to detect multicollinearity, which could distort the results of the regression analyses (Hibbing & Alford, 1981).

Heteroskedasticity Test

To address potential heteroskedasticity, the Breusch-Pagan test is used. If heteroskedasticity is present, robust standard errors will be applied to the regression models to ensure accurate inference (Anaman & Bukari, 2021).

Regression Results

ARIMA/VAR models are used to estimate the relationship between economic variables and electoral outcomes and to forecast the results of the 2024 elections. The Autoregressive Integrated Moving Average (ARIMA) model is employed to capture the time-dependent patterns in electoral outcomes, while the Vector Autoregression (VAR) model allows for the simultaneous analysis of multiple economic variables and their dynamic interactions over time (Duch & Stevenson, 2008).

3.6. Econometric Model

A linear regression or other statistical model could be developed to estimate the impact of the economic factors on electoral outcomes, controlling for other variables.

The regression model is

$${VT}_i=\alpha +{\beta }_1{GDP}_i+{\beta }_2{UR}_i+{\beta }_3{PR}_i+{\beta }_4{PDG}_i+{\beta }_5{GINI}_i+{\gamma }_1{CC}_i+{\gamma }_2{PS}_i+{ϵ}_i$$

Where:

• ${VT}_i$: Voter Turnout for country/region i
• ${GDP}_i$: Gross Domestic Product for country/region i
• ${UR}_i$: Unemployment Rate for country/region i
• ${PR}_i$: Poverty Rate for country/region iii
• ${PDG}_i$: Public Debt-to-GDP Ratio for country/region i
• ${GINI}_i$: Gini Coefficient for country/region i
• ${CC}_i, {PS}_i$: Control variables for Corruption, and political stability, respectively.
• $\alpha$: Constant term
• ${\beta }_1\dots \dots \dots \dots \dots$${\beta }_5$: Coefficients for economic variables
• ${\gamma }_{1, }{\gamma }_2$: Coefficients for control variables
• ${ϵ}_i$: Error term

Table 1. Measurements of Variables. 

Variable	Symbol	Measurement	Source
Voter Turnout	VT	Percentage of eligible voters who participate in an election	Electoral Commission of Ghana
Party Vote Share	PVS	Percentage of total votes garnered by each political party	Electoral Commission of Ghana
Incumbent Re-Election Rate	IRR	Percentage of incumbents re-elected in an election	Electoral Commission of Ghana
Gross Domestic Product (GDP) Growth	GDPG	Annual GDP growth rate (in %)	Bank of Ghana, World Bank
Unemployment Rate	UR	Percentage of the labor force that is unemployed	Bank of Ghana, World Bank
Inflation	INF	Annual inflation rate (%)	Bank of Ghana, World Bank
Poverty Rate	PR	Percentage of the population living below the poverty line	World Bank
Income Inequality (Gini Coefficient)	GINI	Numerical value representing income inequality (0 to 1 scale)	World Bank
Political Stability	PS	Index representing the level of political stability in the country	World Bank
Corruption Control	CC	Index measuring the effectiveness of corruption control	World Bank
Exchange Rate Stability	ERS	Indicator of exchange rate fluctuations	Bank of Ghana

Table 1. Measurements of Variables. 

Variable	Symbol	Measurement	Source
Voter Turnout	VT	Percentage of eligible voters who participate in an election	Electoral Commission of Ghana
Party Vote Share	PVS	Percentage of total votes garnered by each political party	Electoral Commission of Ghana
Incumbent Re-Election Rate	IRR	Percentage of incumbents re-elected in an election	Electoral Commission of Ghana
Gross Domestic Product (GDP) Growth	GDPG	Annual GDP growth rate (in %)	Bank of Ghana, World Bank
Unemployment Rate	UR	Percentage of the labor force that is unemployed	Bank of Ghana, World Bank
Inflation	INF	Annual inflation rate (%)	Bank of Ghana, World Bank
Poverty Rate	PR	Percentage of the population living below the poverty line	World Bank
Income Inequality (Gini Coefficient)	GINI	Numerical value representing income inequality (0 to 1 scale)	World Bank
Political Stability	PS	Index representing the level of political stability in the country	World Bank
Corruption Control	CC	Index measuring the effectiveness of corruption control	World Bank
Exchange Rate Stability	ERS	Indicator of exchange rate fluctuations	Bank of Ghana

3.7. Ethical Considerations

This study follows strict ethical guidelines to ensure integrity, transparency, and respect for democratic processes. Data confidentiality and privacy are maintained as publicly available, anonymized data from reliable sources like the Electoral Commission of Ghana and World Bank are used. No individual consent is required, but proper citation is essential. Transparency is ensured in the analysis, avoiding data manipulation, and conflicts of interest are disclosed. The study is committed to intellectual honesty, avoiding plagiarism, and responsibly disseminating findings to prevent misuse. Predictive models are rigorously validated to ensure accuracy, and the study respects political sensitivities, presenting results neutrally. Ethical issues, such as avoiding political influence and ensuring data validity, are prioritized. The findings aim to contribute to academic knowledge while promoting democratic governance without fueling partisan conflict or division. This ensures the research’s social responsibility and constructive contribution to electoral discourse in Ghana.

4. Results

The analysis of the data gathered and the findings are presented in this section.

4.1. Descriptive Statistics

The descriptive statistics provide an essential summary of the key variables in the study, which include voter turnout, party vote share, incumbent re-election rate, and various economic indicators such as GDP growth, exchange rate stability, and inflation, among others. These statistics give an overview of the central tendencies (mean, median), dispersion (standard deviation), and shape (skewness, kurtosis) of the data, which are critical for understanding the patterns and distributions of the variables.

Starting with voter turnout, the mean voter turnout over the period studied is approximately 73.32%, indicating that a substantial portion of the eligible population consistently participates in elections. The standard deviation of 7.40 suggests moderate variability in voter turnout across the election cycles. Notably, the minimum turnout recorded was 50.16%, which is quite low compared to the maximum turnout of 85.12%, highlighting a significant difference between the highest and lowest observed turnout rates. The skewness of voter turnout is negative (-1.26), indicating that the distribution is left-skewed, with more observations clustering towards the higher end of voter turnout. Additionally, the kurtosis value of 4.67 suggests a leptokurtic distribution, meaning that voter turnout values tend to have fatter tails compared to a normal distribution, with a higher probability of extreme values.

Regarding party vote share, the average vote share is 9.37%, with a large standard deviation of 7.44, suggesting considerable variability in the distribution of votes among parties. The maximum vote share is 28.11%, while the minimum is 0.46%, indicating significant disparity between the top-performing and lowest-performing political parties. The skewness value of 0.99 shows a right-skewed distribution, implying that most of the observations are clustered toward the lower end of the vote share spectrum, with a few instances of parties achieving higher vote shares. This is further reinforced by the kurtosis of 3.02, which is slightly above the normal level, indicating some presence of outliers.

The incumbent re-election rate has a mean of 0.50, suggesting that incumbents have a 50% chance of being re-elected on average. This binary variable, represented as 0 or 1, shows no skewness and a kurtosis value of 1.00, indicating a uniform distribution of re-election outcomes over the sample period. There is no significant concentration of one outcome over the other.

Looking at the economic variables, the mean GDP growth rate is 5.25%, which aligns with the overall growth trajectory of Ghana’s economy during the period under study. The standard deviation of 2.48% indicates that there is some variation in growth rates, with a maximum of 13.95% and a minimum of 0.51%. The positive skewness of 1.26 suggests that the GDP growth rates are clustered toward the lower end, with a few periods of higher growth rates. This is confirmed by the kurtosis value of 6.13, indicating a significant presence of outliers, likely periods of exceptional growth.

The exchange rate stability variable has a mean of 2.26, with a relatively high standard deviation of 2.64, indicating substantial fluctuations in exchange rate stability over the sample period. The positive skewness (1.64) and kurtosis (5.34) suggest that the distribution is heavily skewed towards lower values, with a few extreme instances of higher stability. These fluctuations are critical as they may influence voter sentiment, particularly in import-dependent economies where exchange rate volatility can affect the cost of goods.

Corruption control has a mean of -0.14, with a range from -0.37 to 0.04, indicating that the control of corruption in Ghana has remained relatively low, with negative values suggesting systemic challenges in curbing corruption. The skewness of -0.41 implies a slight left skew, meaning that the distribution tends to favor lower corruption control values. The kurtosis of 1.79 points to a somewhat platykurtic distribution, indicating fewer extreme values or outliers.

For income inequality, as measured by the Gini coefficient, the mean value is 41.83, suggesting a moderate level of inequality, typical of developing economies. The low standard deviation of 1.49 reflects little variation in inequality over time. The skewness (-0.22) and kurtosis (1.24) suggest that income inequality is symmetrically distributed and does not have extreme outliers.

The inflation rate presents a more volatile picture, with a mean of 19.84% and a high standard deviation of 13.23%, indicating significant inflationary pressures during certain periods. The maximum inflation rate is 59.46%, while the minimum is 4.87%, reflecting the wide range of inflation rates experienced in Ghana. The positive skewness (1.31) and kurtosis (4.02) indicate a distribution with occasional high inflation spikes, which likely have an impact on voter behavior. In terms of political stability, the mean value is -0.19, suggesting that Ghana has experienced periods of political instability, though the standard deviation of 0.19 indicates that this has not varied drastically over time. The skewness (0.36) and kurtosis (1.42) values suggest a moderate distribution, with most observations falling around the mean.

The poverty rate has a mean of 41.15%, with a standard deviation of 13.32%, showing a considerable spread in poverty levels across the years. The range, from 25.20% to 55.00%, highlights the challenges of poverty in Ghana. The negative skewness (-0.18) suggests that higher poverty rates are slightly more frequent, while the kurtosis value of 1.30 suggests a relatively normal distribution without many extreme values. Finally, the unemployment rate has a mean of 5.59% and a standard deviation of 2.23%, with a range from 2.17% to 10.46%. The skewness (0.57) and kurtosis (2.47) indicate a slightly right-skewed distribution, with a few higher unemployment rates observed during the period.

In summary, the descriptive statistics highlight important trends and variations in Ghana’s electoral and economic variables. Voter turnout, for instance, shows consistent participation, while party vote shares demonstrate substantial variability. Economic indicators such as inflation and exchange rate stability exhibit significant volatility, which could influence electoral outcomes. Understanding these relationships is critical for developing a predictive model of Ghana’s 2024 elections.

Table 2. Descriptive Statistics.

	Voter Turnout	Party Vote Share	Incumbent Re Election Rate	Gross Domestic Product Growth	Exchange Rate Stability	Corruption Control	Income Inequality (GINI Coefficient)	Inflation	Political Stability	Poverty Rate	Political System Type	Unemployment Rate
Mean	73.32172	9.374531	0.5000	5.248688	2.260799	-0.142629	41.82813	19.83621	-0.187479	41.15313	3.00	5.587781
Median	74.55250	7.098750	0.5000	4.891000	0.992447	-0.117731	42.40000	15.46430	-0.359382	42.50000	3.00	5.237500
Maximum	85.12000	28.11000	1.000	13.94900	11.02041	0.038148	43.50000	59.46155	0.169862	55.00000	3.00	10.45600
Minimum	50.16000	0.460000	0.000	0.514000	0.043685	-0.368746	40.10000	4.865398	-0.359382	25.20000	3.00	2.173000
Std. Dev.	7.401713	7.441796	0.508	2.477032	2.642286	0.129999	1.493045	13.23157	0.193971	13.31562	0.00	2.226177
Skewness	-1.262583	0.986240	0.000	1.262052	1.639510	-0.411029	-0.221882	1.312240	0.364363	-0.176442	NA	0.572327
Kurtosis	4.669199	3.015405	1.000	6.130624	5.336550	1.787577	1.240472	4.018561	1.424191	1.296690	NA	2.473530
Jarque-Bera	12.21691	5.187884	5.333	21.56254	21.61525	2.860999	4.390487	10.56715	4.018951	4.034389	NA	2.116539
Probability	0.002224	0.074725	0.069483	0.000021	0.000020	0.239189	0.111331	0.005074	0.134059	0.133028	NA	0.347056
Sum	2346.295	299.9850	16.00000	167.9580	72.34557	-4.564137	1338.500	634.7588	-5.999325	1316.900	96.00	178.8090
Sum Sq. Dev.	1698.346	1716.790	8.000000	190.2062	216.4320	0.523894	69.10469	5427.308	1.166370	5496.480	0.00	153.6318
Observations	32	32	32	32	32	32	32	32	32	32	32	32

Table 2. Descriptive Statistics.

	Voter Turnout	Party Vote Share	Incumbent Re Election Rate	Gross Domestic Product Growth	Exchange Rate Stability	Corruption Control	Income Inequality (GINI Coefficient)	Inflation	Political Stability	Poverty Rate	Political System Type	Unemployment Rate
Mean	73.32172	9.374531	0.5000	5.248688	2.260799	-0.142629	41.82813	19.83621	-0.187479	41.15313	3.00	5.587781
Median	74.55250	7.098750	0.5000	4.891000	0.992447	-0.117731	42.40000	15.46430	-0.359382	42.50000	3.00	5.237500
Maximum	85.12000	28.11000	1.000	13.94900	11.02041	0.038148	43.50000	59.46155	0.169862	55.00000	3.00	10.45600
Minimum	50.16000	0.460000	0.000	0.514000	0.043685	-0.368746	40.10000	4.865398	-0.359382	25.20000	3.00	2.173000
Std. Dev.	7.401713	7.441796	0.508	2.477032	2.642286	0.129999	1.493045	13.23157	0.193971	13.31562	0.00	2.226177
Skewness	-1.262583	0.986240	0.000	1.262052	1.639510	-0.411029	-0.221882	1.312240	0.364363	-0.176442	NA	0.572327
Kurtosis	4.669199	3.015405	1.000	6.130624	5.336550	1.787577	1.240472	4.018561	1.424191	1.296690	NA	2.473530
Jarque-Bera	12.21691	5.187884	5.333	21.56254	21.61525	2.860999	4.390487	10.56715	4.018951	4.034389	NA	2.116539
Probability	0.002224	0.074725	0.069483	0.000021	0.000020	0.239189	0.111331	0.005074	0.134059	0.133028	NA	0.347056
Sum	2346.295	299.9850	16.00000	167.9580	72.34557	-4.564137	1338.500	634.7588	-5.999325	1316.900	96.00	178.8090
Sum Sq. Dev.	1698.346	1716.790	8.000000	190.2062	216.4320	0.523894	69.10469	5427.308	1.166370	5496.480	0.00	153.6318
Observations	32	32	32	32	32	32	32	32	32	32	32	32

4.2. Correlation Analysis

The results from the correlation analysis provide critical insights into the relationships between voter turnout, party vote share, incumbent re-election rate, and key economic and political variables. Correlation coefficients range from -1 to 1, with positive values indicating a direct relationship and negative values indicating an inverse relationship. These correlations help in understanding how changes in one variable are associated with changes in another. Beginning with voter turnout, there is a strong negative correlation with party vote share (r = -0.75), indicating that higher voter turnout tends to be associated with lower party vote shares. This suggests that when more people participate in elections, political parties may struggle to secure high vote percentages, potentially due to increased competition or the mobilization of more diverse voter bases. Conversely, lower voter turnout seems to benefit political parties, possibly because they can more effectively mobilize their core supporters during periods of low voter engagement.

Interestingly, voter turnout has a moderate positive correlation with the incumbent re-election rate (r = 0.48), suggesting that higher turnout is associated with a greater likelihood of the incumbent party being re-elected. This may reflect the fact that incumbents often benefit from the status quo, and higher participation may represent a validation of their governance. Additionally, voter turnout is moderately positively correlated with exchange rate stability (r = 0.34), indicating that when the exchange rate is stable, voter participation tends to increase. Economic stability, in this case, could enhance public confidence in the political process, leading to greater voter engagement.

On the other hand, party vote share has a strong negative correlation with income inequality (r = -0.78) and poverty rate (r = 0.64), indicating that higher income inequality and poverty are associated with lower party vote shares. This is an important finding, as it suggests that economic hardship may reduce the effectiveness of political parties in securing votes, possibly because voters become disillusioned with mainstream political options when economic conditions worsen. Furthermore, there is a moderate positive correlation between party vote share and unemployment rate (r = 0.44), which could indicate that parties gain more votes during periods of higher unemployment, perhaps due to promises of job creation or welfare policies.

The incumbent re-election rate is positively correlated with voter turnout (r = 0.48) and exchange rate stability (r = 0.23). This suggests that economic stability, as reflected in a stable exchange rate, is likely to benefit incumbents, supporting the idea that voters reward sitting governments for economic stability. Conversely, there is a weak negative correlation between the incumbent re-election rate and corruption control (r = -0.32), suggesting that higher levels of perceived corruption reduce the likelihood of incumbents being re-elected. This aligns with broader research that shows voters tend to punish incumbents in environments with higher corruption levels.

GDP growth exhibits a weak positive correlation with voter turnout (r = 0.21), indicating that higher economic growth slightly increases voter participation. However, the weak correlation suggests that GDP growth alone may not be a strong predictor of electoral outcomes. Interestingly, GDP growth has a negative correlation with party vote share (r = -0.29), which could imply that economic growth benefits opposition parties, as voters may attribute improvements to factors outside the incumbent party’s control.

The correlation between exchange rate stability and other variables reveals some notable insights. There is a strong negative correlation with poverty rate (r = -0.79) and a moderate negative correlation with unemployment rate (r = -0.60), implying that periods of stable exchange rates are associated with lower poverty and unemployment. Additionally, exchange rate stability shows a moderate positive correlation with political stability (r = 0.57), indicating that a stable exchange rate is likely to promote political stability, or vice versa. Turning to corruption control, its negative correlation with incumbent re-election rate (r = -0.32) suggests that incumbents in environments with higher corruption are less likely to be re-elected. Moreover, corruption control exhibits a moderate positive correlation with political stability (r = 0.29), reinforcing the idea that lower corruption levels are associated with more stable political environments.

The strong negative correlation between income inequality and party vote share (r = -0.78) highlights the detrimental effect of inequality on political party performance, possibly because economic inequality erodes trust in the political system. Likewise, income inequality has a strong negative correlation with poverty rate (r = -0.89) and unemployment rate (r = -0.77), showing that as inequality increases, both poverty and unemployment tend to rise, exacerbating economic hardships and likely influencing electoral outcomes.

Inflation has a weak positive correlation with party vote share (r = 0.39), suggesting that political parties may gain more support during periods of inflation, possibly by promising to address rising prices. However, inflation also shows a weak negative correlation with GDP growth (r = -0.33), consistent with the general economic principle that high inflation can dampen economic growth. Lastly, political stability is positively correlated with exchange rate stability (r = 0.57), meaning that economic and political stability are interlinked. Additionally, political stability has a weak negative correlation with unemployment rate (r = -0.61), suggesting that periods of political stability tend to be associated with lower unemployment rates, which could impact voter satisfaction and electoral outcomes.

In summary, the correlation analysis reveals important dynamics between economic and political variables and their influence on electoral outcomes in Ghana. The findings suggest that voter turnout, party vote share, and incumbent re-election rates are significantly influenced by economic factors such as income inequality, inflation, and exchange rate stability, while political stability and corruption control also play critical roles in shaping electoral behavior. These correlations provide a foundation for more in-depth regression analysis and modeling to predict Ghana’s 2024 election results.

Table 3. Correlation Analysis Results.

	1	2	3	4	5	6	7	8	9	10	11
1. Voter Turnout	1.000000
2. Party Vote Share	-0.752201	1.000000
3. Incumbent ReElection Rate	0.480580	-0.235999	1.000000
4. GDP Growth	0.209791	-0.288101	-0.276300	1.000000
5. Exchange Rate Stability	0.341877	-0.473287	0.227284	-0.257871	1.000000
6. Corruption Control	-0.241434	-0.088934	-0.321298	0.059885	0.148474	1.000000
7. Income Inequality	0.461770	-0.781988	0.138224	0.161647	0.709314	0.291655	1.000000
8. Inflation	-0.095417	0.385943	-0.109589	-0.325386	-0.053244	0.064879	-0.428564	1.000000
9. Political_Stability	-0.186226	0.125809	-0.048932	-0.317994	0.567072	0.291748	0.358229	-0.054340	1.000000
10. Poverty Rate	-0.387704	0.643898	-0.249649	0.016654	-0.787065	-0.162059	-0.893449	0.367481	-0.554792	1.00000
11. Unemployme Rate	-0.321665	0.439960	-0.128431	-0.210441	-0.600257	-0.428899	-0.771687	0.347879	-0.607964	0.77731	1.00000

Table 3. Correlation Analysis Results.

	1	2	3	4	5	6	7	8	9	10	11
1. Voter Turnout	1.000000
2. Party Vote Share	-0.752201	1.000000
3. Incumbent ReElection Rate	0.480580	-0.235999	1.000000
4. GDP Growth	0.209791	-0.288101	-0.276300	1.000000
5. Exchange Rate Stability	0.341877	-0.473287	0.227284	-0.257871	1.000000
6. Corruption Control	-0.241434	-0.088934	-0.321298	0.059885	0.148474	1.000000
7. Income Inequality	0.461770	-0.781988	0.138224	0.161647	0.709314	0.291655	1.000000
8. Inflation	-0.095417	0.385943	-0.109589	-0.325386	-0.053244	0.064879	-0.428564	1.000000
9. Political_Stability	-0.186226	0.125809	-0.048932	-0.317994	0.567072	0.291748	0.358229	-0.054340	1.000000
10. Poverty Rate	-0.387704	0.643898	-0.249649	0.016654	-0.787065	-0.162059	-0.893449	0.367481	-0.554792	1.00000
11. Unemployme Rate	-0.321665	0.439960	-0.128431	-0.210441	-0.600257	-0.428899	-0.771687	0.347879	-0.607964	0.77731	1.00000

4.3. Stationarity Tests

The stationarity tests are crucial for analyzing time-series data, as they determine whether the variables in the dataset have a constant mean and variance over time. Non-stationary data can lead to spurious regression results, making the interpretation of relationships between variables unreliable. In this section, several stationarity tests have been applied to key variables in the study, including voter turnout, party vote share, incumbent re-election rate, and various economic indicators. These tests include the Levin, Lin & Chu t-test, Breitung t-stat, and panel tests such as the Im, Pesaran, and Shin W-stat, ADF-Fisher Chi-square, and PP-Fisher Chi-square.

Beginning with the Levin, Lin & Chu t-test, the null hypothesis assumes that there is a common unit root across the series, implying non-stationarity. The test statistic of -0.71505 has a probability value of 0.2373, indicating that the null hypothesis cannot be rejected. This suggests that, under the assumption of a common unit root process, the data is likely non-stationary. This non-rejection is further supported by the Breitung t-stat, which also tests for a common unit root. The Breitung test statistic of 0.54747 and probability value of 0.7080 similarly suggest that the series has a unit root, meaning the variables are non-stationary when considered under a common unit root assumption.

However, when individual unit root processes are considered using the Im, Pesaran, and Shin W-stat, the results change significantly. The test statistic of -8.18293 and probability value of 0.0000 indicate that the null hypothesis of a unit root is rejected, suggesting that the variables are stationary when treated as having individual unit root processes. This finding is further supported by the ADF-Fisher Chi-square test, which yields a Chi-square statistic of 122.348 and a probability value of 0.0000. The rejection of the null hypothesis here confirms that the variables do not have unit roots, making them stationary under individual unit root assumptions. Similarly, the PP-Fisher Chi-square test, with a Chi-square statistic of 484.747 and a probability value of 0.0000, also rejects the null hypothesis, reinforcing the conclusion that the variables are stationary.

These results suggest an important distinction between assuming a common unit root process and allowing for individual unit root processes. Under the assumption of a common unit root, the series appears non-stationary, which could complicate the econometric analysis. However, when each variable is allowed to follow its own unit root process, the data appears stationary, making it more suitable for time-series and regression analyses.

In practical terms, the stationarity of the data implies that the relationships between the variables are more stable over time, allowing for more reliable interpretations of correlations and causal effects. For example, the stationarity of voter turnout, party vote share, and economic variables like GDP growth and inflation means that changes in these variables are more predictable, and their impact on electoral outcomes can be modeled with greater confidence. Stationary data ensures that shocks to these variables dissipate over time, rather than having permanent effects on their levels.

The rejection of the unit root hypothesis in the Im, Pesaran, and Shin W-stat, ADF-Fisher, and PP-Fisher tests also implies that the data is suitable for the application of econometric models like ARIMA and VAR, which assume stationarity. Consequently, the study proceeded with time-series analysis, confident that the underlying data supports stable and reliable modeling of the relationships between economic factors and electoral results.

Table 4. Stationarity Tests Results.

Group unit root test: Summary
Series: Voter Turnout, Party Vote Share, Incumbent ReElection Rate, Gross Domestic Product Growth, Exchange Rate Stability, Corruption Control, Income Inequality, Inflation, Political Stability, Poverty Rate, Unemployment Rate
Date: 08/15/24 Time: 17:37
Sample: 1992 2023
Exogenous variables: Individual effects, individual linear trends
Automatic selection of maximum lags
Automatic lag length selection based on SIC: 0 to 6
Newey-West automatic bandwidth selection and Bartlett kernel
			Cross-
Method	Statistic	Prob.**	sections	Obs
Null: Unit root (assumes common unit root process)
Levin, Lin & Chu t*	-0.71505	0.2373	10	283
Breitung t-stat	0.54747	0.7080	10	273
Null: Unit root (assumes individual unit root process)
Im, Pesaran and Shin W-stat	-8.18293	0.0000	10	283
ADF - Fisher Chi-square	122.348	0.0000	10	283
PP - Fisher Chi-square	484.747	0.0000	10	300

** Probabilities for Fisher tests are computed using an asymptotic Chi-square distribution. All other tests assume asymptotic normality.

Table 4. Stationarity Tests Results.

Group unit root test: Summary
Series: Voter Turnout, Party Vote Share, Incumbent ReElection Rate, Gross Domestic Product Growth, Exchange Rate Stability, Corruption Control, Income Inequality, Inflation, Political Stability, Poverty Rate, Unemployment Rate
Date: 08/15/24 Time: 17:37
Sample: 1992 2023
Exogenous variables: Individual effects, individual linear trends
Automatic selection of maximum lags
Automatic lag length selection based on SIC: 0 to 6
Newey-West automatic bandwidth selection and Bartlett kernel
			Cross-
Method	Statistic	Prob.**	sections	Obs
Null: Unit root (assumes common unit root process)
Levin, Lin & Chu t*	-0.71505	0.2373	10	283
Breitung t-stat	0.54747	0.7080	10	273
Null: Unit root (assumes individual unit root process)
Im, Pesaran and Shin W-stat	-8.18293	0.0000	10	283
ADF - Fisher Chi-square	122.348	0.0000	10	283
PP - Fisher Chi-square	484.747	0.0000	10	300

** Probabilities for Fisher tests are computed using an asymptotic Chi-square distribution. All other tests assume asymptotic normality.

4.4. Multicollinearity Check

The multicollinearity check uses Variance Inflation Factors (VIF) to detect the presence of multicollinearity among the independent variables in the regression model. Multicollinearity occurs when two or more explanatory variables in a model are highly correlated, leading to inflated standard errors and unreliable coefficient estimates. The VIF helps identify whether multicollinearity is present and its severity. Generally, a VIF above 10 is considered problematic, indicating significant multicollinearity that may affect the model’s stability and interpretation.

Starting with Party Vote Share, the centered VIF value is 5.96, which is below the threshold of 10, suggesting that multicollinearity is not a serious issue for this variable. However, the relatively high uncentered VIF of 15.71 signals that there may be some relationship with other variables when no constant is included. Still, this doesn’t raise immediate concerns, as the centered value is more critical for regression models with intercepts.

For the Incumbent Re-Election Rate, the centered VIF is 1.98, indicating low multicollinearity. This suggests that this variable is not highly correlated with others in the model, and its coefficient estimates are likely to be reliable.

Gross Domestic Product Growth shows a centered VIF of 2.72, which is also well below the critical value of 10, suggesting no significant multicollinearity. However, the uncentered VIF of 15.30 indicates that without the constant term, GDP growth may have some correlation with other variables, though it does not pose any significant issue in the current model.

Moving to Exchange Rate Stability, the centered VIF value is 4.16, which is within acceptable limits. This indicates that exchange rate stability is not highly collinear with other independent variables in the model. This variable can be interpreted with confidence, as multicollinearity does not significantly distort its standard errors.

The Corruption Control variable has a centered VIF of 1.99, indicating low multicollinearity. This suggests that corruption control can be interpreted with little concern about inflated standard errors or biased coefficient estimates, making it a reliable predictor in the model.

On the other hand, Income Inequality has a high centered VIF of 12.17, which is above the threshold of 10, indicating significant multicollinearity. This suggests that income inequality is highly correlated with other independent variables, potentially leading to unreliable coefficient estimates. This could complicate the interpretation of the effects of income inequality on voter turnout and other dependent variables. In this case, multicollinearity can obscure the true relationship between variables and may require remedial action, as such it was dropped from the regression.

Similarly, the Poverty Rate has a high centered VIF of 10.94, suggesting that it is highly correlated with other predictors in the model. This level of multicollinearity could distort the interpretation of the effect of poverty on voter turnout and necessitated adjustments to the model to reduce collinearity.

The Unemployment Rate presents a significant multicollinearity problem, with a centered VIF of 6.85 and an uncentered VIF of 51.43. While the centered VIF is below 10, it is still relatively high and suggests some multicollinearity. However, this shares relationships with other predictors, though it is not at a critical level that would invalidate the model results.

Additionally, Political Stability has a centered VIF of 5.81, which, although not exceeding 10, suggests some moderate collinearity with other variables in the model. This could indicate that political stability shares relationships with other predictors, though it is not at a critical level that would invalidate the model results.

Finally, the constant (C) term has an extremely high uncentered VIF of 11840.02, though this is not typically a cause for concern, as it reflects the nature of the constant term rather than the correlation between explanatory variables. However, this points to possible multicollinearity between the constant and some independent variables.

In essence, the multicollinearity check indicates that while several variables (such as income inequality, poverty rate) exhibit high multicollinearity, most of the other variables are within acceptable VIF ranges. The presence of significant multicollinearity in certain variables, especially income inequality and poverty, could lead to inflated standard errors and unreliable estimates. In addressing this, the model benefited from re-specification, such as removing the highly correlated variables to reduce multicollinearity and improve the robustness of the model. Despite these concerns, most variables are not severely impacted by multicollinearity, and the model remains interpretable with caution.

Table 5. Multicollinearity Check Results.

Variance Inflation Factors
Sample: 1992 2023
Included observations: 32
	Coefficient	Uncentered	Centered
Variable	Variance	VIF	VIF
Party Vote Share	0.029096	15.71046	5.955292
Incumbent ReElection Rate	2.075022	3.958194	1.979097
Gross Domestic Product Growth	0.119772	15.30413	2.716025
Exchange Rate Stability	0.161205	7.303069	4.159621
Corruption Control	31.78758	4.452490	1.985433
Income Inequality	1.477644	9875.216	12.17395
Inflation	0.002604	5.593572	1.684824
Political Stability	41.78587	11.41382	5.810591
Poverty Rate	0.016695	118.8115	10.94042
Unemployment Rate	0.374187	51.42673	6.853691
C	3103.473	11840.02	NA

Table 5. Multicollinearity Check Results.

Variance Inflation Factors
Sample: 1992 2023
Included observations: 32
	Coefficient	Uncentered	Centered
Variable	Variance	VIF	VIF
Party Vote Share	0.029096	15.71046	5.955292
Incumbent ReElection Rate	2.075022	3.958194	1.979097
Gross Domestic Product Growth	0.119772	15.30413	2.716025
Exchange Rate Stability	0.161205	7.303069	4.159621
Corruption Control	31.78758	4.452490	1.985433
Income Inequality	1.477644	9875.216	12.17395
Inflation	0.002604	5.593572	1.684824
Political Stability	41.78587	11.41382	5.810591
Poverty Rate	0.016695	118.8115	10.94042
Unemployment Rate	0.374187	51.42673	6.853691
C	3103.473	11840.02	NA

4.5. Heteroskedasticity Test

The Breusch-Pagan-Godfrey test is used to detect the presence of heteroskedasticity, which occurs when the variance of the residuals is not constant across observations. Heteroskedasticity can lead to inefficient estimates and invalidate standard errors, making the results of a regression model unreliable. If heteroskedasticity is present, it indicates that the assumption of homoscedasticity (constant variance) is violated, requiring corrective measures such as using robust standard errors.

The F-statistic from the Breusch-Pagan-Godfrey test is 0.902166, with a corresponding p-value of 0.5479. Since the p-value is greater than 0.05, we fail to reject the null hypothesis of homoscedasticity. This indicates that there is no significant evidence of heteroskedasticity in the model. In other words, the variance of the residuals appears to be constant, and the assumption of homoscedasticity holds. Therefore, the regression results are likely to be efficient and reliable with respect to heteroskedasticity.

Additionally, the Obs*R-squared statistic is 9.616165, with a p-value of 0.4748, which also exceeds the 0.05 threshold. This further supports the conclusion that heteroskedasticity is not a significant issue in this model. The scaled explained sum of squares (SS) also has a high p-value of 0.9358, reinforcing the earlier findings that the variance of residuals is stable across different levels of the explanatory variables.

Looking at the individual coefficients of the explanatory variables, none of them are statistically significant, as all the p-values are well above the 0.05 significance level. For example, Party Vote Share has a coefficient of -0.286493 and a p-value of 0.5561, while Incumbent Re-Election Rate has a coefficient of -4.096522 and a p-value of 0.3227. This indicates that none of these variables are significantly related to the variance of the residuals, which aligns with the overall finding that heteroskedasticity is not present in the model.

Additionally, income inequality, inflation, and political stability, which could theoretically affect residual variance, show no significant effect on the variance of the residuals. For instance, income inequality has a p-value of 0.9097, and inflation has a p-value of 0.9441, suggesting no significant relationship between these variables and the residual variance. This lack of significance across the board is a positive finding, as it indicates that none of the independent variables disproportionately influence the variability of the residuals.

The R-squared value from the test equation is 0.3005, which means that only about 30% of the variation in the squared residuals is explained by the independent variables. This relatively low R-squared value suggests that the variables in the model do not have a strong relationship with the variance of the residuals, further indicating the absence of heteroskedasticity. The adjusted R-squared is negative (-0.0326), reinforcing that the model does not fit the variance well and does not suffer from significant heteroskedasticity issues.

The Durbin-Watson statistic of 2.4713 suggests that there is little to no autocorrelation in the residuals, which is another positive diagnostic result. A value close to 2 indicates that there is no significant autocorrelation, further supporting the reliability of the model’s estimates.

Thus, the results of the Breusch-Pagan-Godfrey test show no evidence of heteroskedasticity in the model, as indicated by the high p-values across various test statistics (F-statistic, Obs*R-squared, and scaled explained SS). None of the explanatory variables significantly affect the variance of the residuals, and the constant variance assumption holds. This finding suggests that the model’s estimates are efficient, and standard errors are reliable, meaning that heteroskedasticity is not distorting the regression results. Therefore, no further corrective measures, such as using robust standard errors, are required. The model can proceed with confidence that the homoscedasticity assumption is met.

Table 6. Heteroskedasticity Test Results.

Heteroskedasticity Test: Breusch-Pagan-Godfrey
F-statistic	0.902166	Prob. F(10,21)		0.5479
Obs*R-squared	9.616165	Prob. Chi-Square(10)		0.4748
Scaled explained SS	4.240426	Prob. Chi-Square(10)		0.9358
Test Equation:
Dependent Variable: RESID^2
Method: Least Squares
Sample: 1992 2023
Included observations: 32
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	-6.969401	156.4311	-0.044553	0.9649
Party Vote Share	-0.286493	0.478977	-0.598134	0.5561
Incumbent ReElection Rate	-4.096522	4.044926	-1.012756	0.3227
Gross Domestic Product Growth	0.481207	0.971799	0.495171	0.6256
Exchange Rate Stability	-0.868963	1.127426	-0.770749	0.4494
Corruption Control	6.604705	15.83171	0.417182	0.6808
Income Inequality	0.391770	3.413375	0.114775	0.9097
Inflation	0.010168	0.143287	0.070963	0.9441
Political Stability	11.75189	18.15156	0.647431	0.5244
Poverty Rate	0.169134	0.362825	0.466159	0.6459
Unemployment Rate	-0.672385	1.717686	-0.391448	0.6994
R-squared	0.300505	Mean dependent var		5.504462
Adjusted R-squared	-0.032588	S.D. dependent var		8.003105
S.E. of regression	8.132461	Akaike info criterion		7.295891
Sum squared resid	1388.875	Schwarz criterion		7.799738
Log likelihood	-105.7343	Hannan-Quinn criter.		7.462902
F-statistic	0.902166	Durbin-Watson stat		2.471299
Prob(F-statistic)	0.547852

Table 6. Heteroskedasticity Test Results.

Heteroskedasticity Test: Breusch-Pagan-Godfrey
F-statistic	0.902166	Prob. F(10,21)		0.5479
Obs*R-squared	9.616165	Prob. Chi-Square(10)		0.4748
Scaled explained SS	4.240426	Prob. Chi-Square(10)		0.9358
Test Equation:
Dependent Variable: RESID^2
Method: Least Squares
Sample: 1992 2023
Included observations: 32
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	-6.969401	156.4311	-0.044553	0.9649
Party Vote Share	-0.286493	0.478977	-0.598134	0.5561
Incumbent ReElection Rate	-4.096522	4.044926	-1.012756	0.3227
Gross Domestic Product Growth	0.481207	0.971799	0.495171	0.6256
Exchange Rate Stability	-0.868963	1.127426	-0.770749	0.4494
Corruption Control	6.604705	15.83171	0.417182	0.6808
Income Inequality	0.391770	3.413375	0.114775	0.9097
Inflation	0.010168	0.143287	0.070963	0.9441
Political Stability	11.75189	18.15156	0.647431	0.5244
Poverty Rate	0.169134	0.362825	0.466159	0.6459
Unemployment Rate	-0.672385	1.717686	-0.391448	0.6994
R-squared	0.300505	Mean dependent var		5.504462
Adjusted R-squared	-0.032588	S.D. dependent var		8.003105
S.E. of regression	8.132461	Akaike info criterion		7.295891
Sum squared resid	1388.875	Schwarz criterion		7.799738
Log likelihood	-105.7343	Hannan-Quinn criter.		7.462902
F-statistic	0.902166	Durbin-Watson stat		2.471299
Prob(F-statistic)	0.547852

4.7. Regression Results

The results of the Vector Autoregression (VAR) model provide valuable insights into the relationships between economic factors and electoral outcomes, as well as the interactions between economic variables and political dynamics. Each objective will be addressed in relation to the findings from the VAR model.

4.7.1. Assessing the Impact of Key Economic Factors on Electoral Outcomes in Ghana

The first objective aims to evaluate how key economic factors such as GDP growth, inflation, unemployment, and poverty rate influence electoral outcomes, particularly voter turnout, party vote share, and the incumbent re-election rate.

Voter Turnout and Economic Indicators: The results show that voter turnout is positively influenced by its own past values, indicating persistence in voter engagement. However, the economic factors such as GDP growth and inflation have less direct influence on voter turnout. Although GDP growth has a negative coefficient in its first lag (-0.208236), it is not statistically significant. This suggests that economic growth does not have a strong immediate impact on voter turnout, indicating that factors beyond short-term economic performance might drive voter behavior in Ghana.

Inflation also exhibits an insignificant relationship with voter turnout. The coefficients for inflation lags are negative but small, meaning inflation does not strongly deter voter turnout. This could indicate that inflation is not a primary concern for voters when deciding whether to participate in elections.

Party Vote Share and Economic Performance: Interestingly, party vote share is more influenced by its own lagged values rather than economic factors. The positive and significant coefficient of party vote share (-1) (1.412079) suggests that a party’s past performance strongly predicts its future success, implying electoral inertia or loyalty. Economic factors like GDP growth and inflation show limited influence on vote share, pointing to a possible disconnect between macroeconomic performance and voter support for political parties. This aligns with previous findings that, in Ghana, other considerations such as ethnic affiliations and political stability might overshadow economic conditions in determining vote outcomes.

Incumbent Re-Election Rate: The model shows that the incumbent re-election rate is significantly influenced by the party vote share and voter turnout, but economic indicators have weaker links to incumbency. GDP growth and inflation do not significantly impact incumbency rates, reflecting that voters may not strictly hold incumbents accountable for short-term economic fluctuations. However, the negative effect of unemployment and poverty rate suggests that economic hardship, reflected in these factors, could undermine incumbents’ chances of re-election.

The strong negative coefficient of incumbent re-election rate (-1) on voter turnout (-6.560056) indicates that higher previous success of the incumbent may lower current voter engagement, perhaps due to voter dissatisfaction or disengagement when the incumbent’s performance is perceived as unsatisfactory.

4.7.2. Evaluating the Interaction Between Economic Factors and Political Dynamics in Shaping Voter Preferences

The second objective focuses on how economic factors interact with political dynamics such as political stability, corruption control, and income inequality, and how these interactions shape voter preferences in Ghana.

Political Stability and Voter Behavior: The results reveal a significant positive relationship between political stability (-1) and voter turnout (11.22054, t-statistic = 1.97264). This suggests that when the political environment is stable, voters are more likely to participate in elections. Political stability may reduce voter anxiety and increase confidence in the electoral process, encouraging higher turnout. In contrast, when political stability is weak, voter engagement tends to decline, possibly due to concerns over safety or the legitimacy of the electoral process. The interaction between political stability and voter turnout is critical in shaping electoral outcomes in Ghana, particularly in elections characterized by intense political competition.

Income Inequality and Electoral Dynamics: Income inequality, as measured by the Gini coefficient, does not have a strong direct influence on voter turnout or vote share in this model, suggesting that while inequality might be a background condition, it does not directly translate into voter behavior or party performance in Ghana. However, its interaction with other political and economic variables is worth noting. For instance, higher income inequality may contribute to dissatisfaction with governance but may not necessarily influence voting behavior in predictable ways. It is possible that income inequality plays a more nuanced role in shaping long-term political preferences rather than short-term electoral outcomes.

Corruption Control and Electoral Preferences: Corruption control shows a mixed relationship with electoral outcomes. While corruption control (-1) has a negative effect on party vote share (-4.880410, t-statistic = -1.83150), indicating that better corruption control could reduce a party’s vote share, this finding is counterintuitive. One potential interpretation is that corruption control measures disrupt traditional networks of patronage, which may have been used by parties to secure electoral support, leading to lower vote shares for parties that previously relied on these mechanisms. This could reflect a transformation in voter expectations, where voters prioritize transparency and accountability over party loyalty.

However, the positive coefficient of corruption control (-1) on voter turnout, although not significant, suggests that efforts to reduce corruption could increase voter engagement, as voters may feel more confident in the fairness of the electoral process. This relationship highlights the importance of institutional reforms and governance in shaping electoral dynamics.

In summary, the findings show that in Ghana, voter turnout and election results are influenced by both political and economic factors, but political stability and party loyalty play bigger roles than the economy. For example, when the political environment is stable, more people are likely to vote, showing that voters feel safer and more confident in the process. On the other hand, past performance of political parties and voter habits strongly affect how parties perform in elections, meaning voters often stick to the parties they previously supported.

Economic factors like GDP growth, inflation, and unemployment don’t have a very strong or direct impact on voter turnout or which party wins. However, unemployment and poverty can harm incumbents’ chances of being re-elected, suggesting that voters do respond to economic hardship. Corruption control efforts also influence elections, as reducing corruption may disrupt old political practices and change how people vote. Overall, while the economy matters, Ghana’s election results are shaped more by political stability, how parties have performed in the past, and voters’ trust in the system, rather than just the economic situation at the time.

Table 7. Vector Autoregression Estimates Results.

Vector Autoregression Estimates
Sample (adjusted): 1994 2023
Included observations: 30 after adjustments
Standard errors in ( ) & t-statistics in [ ]
	Voter Turnout	Party Vote Share	Incumbent ReElection Rate	Inflation	Political Stability	Poverty Rate	Unemployment Rate	Income Inequality	Gross Domestic Product Growth	Exchange Rate Stability	CorruptionControl
VOTER_TURNOUT(-1)	1.285565	-0.081595	-0.016824	6.164889	-0.023163	1.493333	-0.127669	-0.256750	-0.859959	0.197591	0.023266
	(0.44044)	(0.23091)	(0.14557)	(4.88595)	(0.02373)	(1.32531)	(0.29324)	(0.25264)	(0.84771)	(0.10677)	(0.03454)
	[ 2.91882]	[-0.35336]	[-0.11557]	[ 1.26176]	[-0.97609]	[ 1.12678]	[-0.43537]	[-1.01627]	[-1.01446]	[ 1.85062]	[ 0.67368]
VOTER_TURNOUT(-2)	-0.297839	-0.043361	0.109656	-4.110289	0.022672	-1.745258	0.006619	0.222399	0.972184	-0.251934	-0.042124
	(0.42026)	(0.22033)	(0.13890)	(4.66211)	(0.02264)	(1.26459)	(0.27981)	(0.24107)	(0.80887)	(0.10188)	(0.03295)
	[-0.70870]	[-0.19680]	[ 0.78948]	[-0.88164]	[ 1.00130]	[-1.38010]	[ 0.02366]	[ 0.92256]	[ 1.20190]	[-2.47289]	[-1.27828]
PARTY_VOTE_SHARE(-1)	0.094592	1.412079	0.090018	4.632369	-0.023881	0.458145	-0.214071	-0.313805	0.831578	0.122937	0.008199
	(0.44107)	(0.23124)	(0.14577)	(4.89299)	(0.02376)	(1.32722)	(0.29367)	(0.25300)	(0.84893)	(0.10692)	(0.03459)
	[ 0.21446]	[ 6.10643]	[ 0.61751]	[ 0.94674]	[-1.00492]	[ 0.34519]	[-0.72896]	[-1.24032]	[ 0.97956]	[ 1.14976]	[ 0.23708]
PARTY_VOTE_SHARE(-2)	-0.311406	-0.657100	-0.078192	-3.228183	0.038742	-0.183015	-0.010699	0.186982	-0.444704	-0.205130	-0.022924
	(0.38509)	(0.20189)	(0.12727)	(4.27191)	(0.02075)	(1.15875)	(0.25639)	(0.22089)	(0.74117)	(0.09335)	(0.03020)
	[-0.80866]	[-3.25471]	[-0.61438]	[-0.75568]	[ 1.86728]	[-0.15794]	[-0.04173]	[ 0.84650]	[-0.60000]	[-2.19740]	[-0.75918]
INCUMBENT_RE_ELECTION_RATE(-1)	-6.560056	0.545585	0.146896	-13.00397	-0.105995	-6.531176	0.270726	0.657296	0.171563	0.072725	0.033480
	(1.11910)	(0.58672)	(0.36986)	(12.4146)	(0.06029)	(3.36744)	(0.74509)	(0.64193)	(2.15391)	(0.27129)	(0.08775)
	[-5.86189]	[ 0.92989]	[ 0.39716]	[-1.04747]	[-1.75794]	[-1.93951]	[ 0.36335]	[ 1.02394]	[ 0.07965]	[ 0.26807]	[ 0.38154]
INCUMBENT_RE_ELECTION_RATE(-2)	3.074419	0.313034	-0.202616	54.78968	-0.166625	16.79246	1.478193	-2.824837	-9.861297	2.503144	0.267630
	(3.10773)	(1.62931)	(1.02710)	(34.4752)	(0.16744)	(9.35134)	(2.06911)	(1.78262)	(5.98139)	(0.75336)	(0.24368)
	[ 0.98928]	[ 0.19213]	[-0.19727]	[ 1.58925]	[-0.99515]	[ 1.79573]	[ 0.71441]	[-1.58465]	[-1.64866]	[ 3.32262]	[ 1.09827]
INFLATION(-1)	-0.016645	0.031627	0.004550	-0.368116	-0.005043	0.149178	0.012185	-0.012793	0.017916	0.006212	-0.001675
	(0.03588)	(0.01881)	(0.01186)	(0.39804)	(0.00193)	(0.10797)	(0.02389)	(0.02058)	(0.06906)	(0.00870)	(0.00281)
	[-0.46391]	[ 1.68123]	[ 0.38369]	[-0.92482]	[-2.60848]	[ 1.38169]	[ 0.51005]	[-0.62156]	[ 0.25943]	[ 0.71413]	[-0.59533]
INFLATION(-2)	-0.017902	0.014100	-0.007482	-0.157101	-0.000256	0.101997	0.030805	0.006793	-0.051172	0.010342	0.000140
	(0.03849)	(0.02018)	(0.01272)	(0.42700)	(0.00207)	(0.11582)	(0.02563)	(0.02208)	(0.07408)	(0.00933)	(0.00302)
	[-0.46508]	[ 0.69871]	[-0.58815]	[-0.36791]	[-0.12327]	[ 0.88062]	[ 1.20200]	[ 0.30766]	[-0.69072]	[ 1.10829]	[ 0.04631]
POLITICAL_STABILITY(-1)	11.22054	2.953434	1.909647	108.1306	-0.596138	10.32928	6.770614	-3.441376	-22.31132	1.496695	0.503218
	(5.68807)	(2.98212)	(1.87991)	(63.0998)	(0.30646)	(17.1157)	(3.78709)	(3.26273)	(10.9477)	(1.37888)	(0.44601)
	[ 1.97264]	[ 0.99038]	[ 1.01582]	[ 1.71365]	[-1.94524]	[ 0.60350]	[ 1.78781]	[-1.05475]	[-2.03799]	[ 1.08544]	[ 1.12827]
POLITICAL_STABILITY(-2)	6.735055	0.535928	2.374038	55.06722	0.076500	-25.22931	4.383710	0.297772	-7.328671	1.122071	0.133751
	(5.91106)	(3.09903)	(1.95360)	(65.5735)	(0.31847)	(17.7867)	(3.93556)	(3.39064)	(11.3769)	(1.43294)	(0.46350)
	[ 1.13940]	[ 0.17293]	[ 1.21521]	[ 0.83978]	[ 0.24021]	[-1.41844]	[ 1.11387]	[ 0.08782]	[-0.64417]	[ 0.78306]	[ 0.28857]
POVERTY_RATE(-1)	-0.100422	-0.002992	0.016558	-0.012559	-0.023720	0.749958	0.179634	-0.094235	0.016060	0.035626	-0.000173
	(0.12685)	(0.06651)	(0.04193)	(1.40723)	(0.00683)	(0.38171)	(0.08446)	(0.07276)	(0.24415)	(0.03075)	(0.00995)
	[-0.79163]	[-0.04499]	[ 0.39495]	[-0.00892]	[-3.47062]	[ 1.96473]	[ 2.12688]	[-1.29507]	[ 0.06578]	[ 1.15851]	[-0.01740]
POVERTY_RATE(-2)	0.314414	0.086365	0.016464	1.972798	-0.000403	0.717614	-0.046072	-0.025360	-0.112425	0.050402	0.025125
	(0.15355)	(0.08050)	(0.05075)	(1.70342)	(0.00827)	(0.46205)	(0.10224)	(0.08808)	(0.29554)	(0.03722)	(0.01204)
	[ 2.04759]	[ 1.07280]	[ 0.32442]	[ 1.15814]	[-0.04875]	[ 1.55311]	[-0.45065]	[-0.28792]	[-0.38040]	[ 1.35403]	[ 2.08674]
UNEMPLOYMENT_RATE(-1)	-0.483647	0.135430	-0.153432	7.261772	-0.051542	1.335816	0.533943	-0.244735	-1.124221	0.000426	0.024736
	(0.63150)	(0.33108)	(0.20871)	(7.00550)	(0.03402)	(1.90023)	(0.42045)	(0.36224)	(1.21544)	(0.15309)	(0.04952)
	[-0.76586]	[ 0.40905]	[-0.73514]	[ 1.03658]	[-1.51486]	[ 0.70298]	[ 1.26992]	[-0.67562]	[-0.92495]	[ 0.00278]	[ 0.49953]
UNEMPLOYMENT_RATE(-2)	0.991989	-0.348606	0.233921	5.425170	-0.007217	-2.288512	0.154678	-0.210855	-0.259780	-0.020480	-0.030046
	(0.58561)	(0.30702)	(0.19354)	(6.49638)	(0.03155)	(1.76213)	(0.38990)	(0.33591)	(1.12711)	(0.14196)	(0.04592)
	[ 1.69394]	[-1.13544]	[ 1.20862]	[ 0.83511]	[-0.22873]	[-1.29872]	[ 0.39672]	[-0.62771]	[-0.23048]	[-0.14426]	[-0.65433]
INCOME_INEQUALITY__GINI_COEFFICIENT_(-1)	-1.079439	-0.536872	-0.207171	0.442037	-0.114000	1.165905	-0.329243	0.209730	0.453456	-0.097875	0.127466
	(1.00815)	(0.52855)	(0.33319)	(11.1837)	(0.05432)	(3.03357)	(0.67122)	(0.57828)	(1.94036)	(0.24439)	(0.07905)
	[-1.07071]	[-1.01575]	[-0.62178]	[ 0.03952]	[-2.09880]	[ 0.38433]	[-0.49051]	[ 0.36268]	[ 0.23370]	[-0.40049]	[ 1.61247]
INCOME_INEQUALITY__GINI_COEFFICIENT_(-2)	1.094576	0.609239	0.147444	19.28967	-0.090458	6.172928	0.408411	-0.976417	-1.032007	0.234770	0.092879
	(1.17970)	(0.61849)	(0.38989)	(13.0868)	(0.06356)	(3.54978)	(0.78544)	(0.67669)	(2.27054)	(0.28598)	(0.09250)
	[ 0.92784]	[ 0.98505]	[ 0.37817]	[ 1.47398]	[-1.42320]	[ 1.73896]	[ 0.51998]	[-1.44294]	[-0.45452]	[ 0.82094]	[ 1.00408]
GROSS_DOMESTIC_PRODUCT__GDP__GROWTH(-1)	-0.208236	0.089957	0.056171	0.683999	-0.014622	-1.530643	0.030420	0.009534	-0.516509	0.105181	0.005411
	(0.17517)	(0.09184)	(0.05789)	(1.94321)	(0.00944)	(0.52709)	(0.11663)	(0.10048)	(0.33714)	(0.04246)	(0.01374)
	[-1.18877]	[ 0.97953]	[ 0.97026]	[ 0.35199]	[-1.54935]	[-2.90394]	[ 0.26083]	[ 0.09489]	[-1.53201]	[ 2.47696]	[ 0.39398]
GROSS_DOMESTIC_PRODUCT__GDP__GROWTH(-2)	0.060701	0.065994	0.044891	3.473055	-0.004451	0.980690	0.336917	-0.374079	-0.848004	0.122619	0.010279
	(0.31702)	(0.16620)	(0.10477)	(3.51679)	(0.01708)	(0.95392)	(0.21107)	(0.18184)	(0.61016)	(0.07685)	(0.02486)
	[ 0.19147]	[ 0.39706]	[ 0.42846]	[ 0.98756]	[-0.26061]	[ 1.02806]	[ 1.59624]	[-2.05714]	[-1.38981]	[ 1.59555]	[ 0.41352]
EXCHANGE_RATE_STABILITY(-1)	0.725887	-0.102215	0.199958	9.250320	0.017389	-4.048308	0.236801	0.420330	-1.833315	1.062040	0.042725
	(1.01597)	(0.53265)	(0.33578)	(11.2706)	(0.05474)	(3.05712)	(0.67643)	(0.58277)	(1.95542)	(0.24629)	(0.07966)
	[ 0.71447]	[-0.19190]	[ 0.59551]	[ 0.82075]	[ 0.31767]	[-1.32422]	[ 0.35007]	[ 0.72126]	[-0.93755]	[ 4.31218]	[ 0.53632]
EXCHANGE_RATE_STABILITY(-2)	-0.936446	0.108216	-0.313402	-14.71335	0.043209	5.380572	-0.740132	-0.512164	2.664779	0.378747	-0.072400
	(1.59459)	(0.83601)	(0.52701)	(17.6893)	(0.08591)	(4.79821)	(1.06167)	(0.91467)	(3.06907)	(0.38655)	(0.12503)
	[-0.58726]	[ 0.12944]	[-0.59468]	[-0.83176]	[ 0.50294]	[ 1.12137]	[-0.69714]	[-0.55994]	[ 0.86827]	[ 0.97980]	[-0.57904]
CORRUPTION_CONTROL(-1)	2.283432	-4.880410	-0.148398	-10.06956	0.478166	-28.93746	-5.016546	4.686797	4.920942	-0.701069	-0.095214
	(5.08265)	(2.66471)	(1.67981)	(56.3835)	(0.27384)	(15.2940)	(3.38400)	(2.91545)	(9.78246)	(1.23211)	(0.39854)
	[ 0.44926]	[-1.83150]	[-0.08834]	[-0.17859]	[ 1.74614]	[-1.89208]	[-1.48243]	[ 1.60757]	[ 0.50304]	[-0.56900]	[-0.23891]
CORRUPTION_CONTROL(-2)	-0.008471	1.133988	0.108222	35.43242	0.038447	-2.543793	-0.809557	-3.051479	7.561378	-0.554334	-0.481261
	(3.93623)	(2.06367)	(1.30092)	(43.6660)	(0.21207)	(11.8443)	(2.62072)	(2.25785)	(7.57598)	(0.95421)	(0.30865)
	[-0.00215]	[ 0.54950]	[ 0.08319]	[ 0.81144]	[ 0.18129]	[-0.21477]	[-0.30891]	[-1.35150]	[ 0.99807]	[-0.58094]	[-1.55927]
C	-1.671232	3.948941	-5.080447	-1112.322	9.765109	-322.4794	2.474551	87.95809	38.39473	-7.355311	-8.991499
	(80.2106)	(42.0525)	(26.5096)	(889.804)	(4.32156)	(241.358)	(53.4039)	(46.0095)	(154.380)	(19.4443)	(6.28944)
	[-0.02084]	[ 0.09391]	[-0.19165]	[-1.25007]	[ 2.25962]	[-1.33610]	[ 0.04634]	[ 1.91174]	[ 0.24870]	[-0.37828]	[-1.42962]
R-squared	0.989879	0.997779	0.874218	0.800534	0.977131	0.984697	0.975035	0.954905	0.831767	0.997548	0.889980
Adj. R-squared	0.958072	0.990799	0.478905	0.173643	0.905258	0.936604	0.896574	0.813176	0.303036	0.989841	0.544202
Sum sq. resids	8.598096	2.363318	0.939169	1058.102	0.024959	77.85070	3.811392	2.829000	31.85068	0.505272	0.052864
S.E. equation	1.108287	0.581048	0.366288	12.29461	0.059712	3.334896	0.737892	0.635722	2.133096	0.268667	0.086902
F-statistic	31.12113	142.9463	2.211457	1.276990	13.59524	20.47459	12.42700	6.737566	1.573137	129.4334	2.573846
Log likelihood	-23.82331	-4.451194	9.391205	-96.01367	63.80785	-56.87209	-11.62011	-7.149047	-43.46607	18.68968	52.55023
Akaike AIC	3.121554	1.830080	0.907253	7.934245	-2.720523	5.324806	2.308008	2.009936	4.431072	0.287354	-1.970015
Schwarz SC	4.195805	2.904331	1.981504	9.008496	-1.646272	6.399057	3.382259	3.084188	5.505323	1.361606	-0.895764
Mean dependent	74.63208	8.211417	0.533333	19.99143	-0.199977	40.23000	5.629033	41.94333	5.290433	2.407900	-0.152138
S.D. dependent	5.412539	6.057505	0.507416	13.52480	0.193995	13.24496	2.294448	1.470792	2.555083	2.665521	0.128720
Determinant resid covariance (dof adj.)		0.000000
Determinant resid covariance		0.000000
Number of coefficients		253

Table 7. Vector Autoregression Estimates Results.

Vector Autoregression Estimates
Sample (adjusted): 1994 2023
Included observations: 30 after adjustments
Standard errors in ( ) & t-statistics in [ ]
	Voter Turnout	Party Vote Share	Incumbent ReElection Rate	Inflation	Political Stability	Poverty Rate	Unemployment Rate	Income Inequality	Gross Domestic Product Growth	Exchange Rate Stability	CorruptionControl
VOTER_TURNOUT(-1)	1.285565	-0.081595	-0.016824	6.164889	-0.023163	1.493333	-0.127669	-0.256750	-0.859959	0.197591	0.023266
	(0.44044)	(0.23091)	(0.14557)	(4.88595)	(0.02373)	(1.32531)	(0.29324)	(0.25264)	(0.84771)	(0.10677)	(0.03454)
	[ 2.91882]	[-0.35336]	[-0.11557]	[ 1.26176]	[-0.97609]	[ 1.12678]	[-0.43537]	[-1.01627]	[-1.01446]	[ 1.85062]	[ 0.67368]
VOTER_TURNOUT(-2)	-0.297839	-0.043361	0.109656	-4.110289	0.022672	-1.745258	0.006619	0.222399	0.972184	-0.251934	-0.042124
	(0.42026)	(0.22033)	(0.13890)	(4.66211)	(0.02264)	(1.26459)	(0.27981)	(0.24107)	(0.80887)	(0.10188)	(0.03295)
	[-0.70870]	[-0.19680]	[ 0.78948]	[-0.88164]	[ 1.00130]	[-1.38010]	[ 0.02366]	[ 0.92256]	[ 1.20190]	[-2.47289]	[-1.27828]
PARTY_VOTE_SHARE(-1)	0.094592	1.412079	0.090018	4.632369	-0.023881	0.458145	-0.214071	-0.313805	0.831578	0.122937	0.008199
	(0.44107)	(0.23124)	(0.14577)	(4.89299)	(0.02376)	(1.32722)	(0.29367)	(0.25300)	(0.84893)	(0.10692)	(0.03459)
	[ 0.21446]	[ 6.10643]	[ 0.61751]	[ 0.94674]	[-1.00492]	[ 0.34519]	[-0.72896]	[-1.24032]	[ 0.97956]	[ 1.14976]	[ 0.23708]
PARTY_VOTE_SHARE(-2)	-0.311406	-0.657100	-0.078192	-3.228183	0.038742	-0.183015	-0.010699	0.186982	-0.444704	-0.205130	-0.022924
	(0.38509)	(0.20189)	(0.12727)	(4.27191)	(0.02075)	(1.15875)	(0.25639)	(0.22089)	(0.74117)	(0.09335)	(0.03020)
	[-0.80866]	[-3.25471]	[-0.61438]	[-0.75568]	[ 1.86728]	[-0.15794]	[-0.04173]	[ 0.84650]	[-0.60000]	[-2.19740]	[-0.75918]
INCUMBENT_RE_ELECTION_RATE(-1)	-6.560056	0.545585	0.146896	-13.00397	-0.105995	-6.531176	0.270726	0.657296	0.171563	0.072725	0.033480
	(1.11910)	(0.58672)	(0.36986)	(12.4146)	(0.06029)	(3.36744)	(0.74509)	(0.64193)	(2.15391)	(0.27129)	(0.08775)
	[-5.86189]	[ 0.92989]	[ 0.39716]	[-1.04747]	[-1.75794]	[-1.93951]	[ 0.36335]	[ 1.02394]	[ 0.07965]	[ 0.26807]	[ 0.38154]
INCUMBENT_RE_ELECTION_RATE(-2)	3.074419	0.313034	-0.202616	54.78968	-0.166625	16.79246	1.478193	-2.824837	-9.861297	2.503144	0.267630
	(3.10773)	(1.62931)	(1.02710)	(34.4752)	(0.16744)	(9.35134)	(2.06911)	(1.78262)	(5.98139)	(0.75336)	(0.24368)
	[ 0.98928]	[ 0.19213]	[-0.19727]	[ 1.58925]	[-0.99515]	[ 1.79573]	[ 0.71441]	[-1.58465]	[-1.64866]	[ 3.32262]	[ 1.09827]
INFLATION(-1)	-0.016645	0.031627	0.004550	-0.368116	-0.005043	0.149178	0.012185	-0.012793	0.017916	0.006212	-0.001675
	(0.03588)	(0.01881)	(0.01186)	(0.39804)	(0.00193)	(0.10797)	(0.02389)	(0.02058)	(0.06906)	(0.00870)	(0.00281)
	[-0.46391]	[ 1.68123]	[ 0.38369]	[-0.92482]	[-2.60848]	[ 1.38169]	[ 0.51005]	[-0.62156]	[ 0.25943]	[ 0.71413]	[-0.59533]
INFLATION(-2)	-0.017902	0.014100	-0.007482	-0.157101	-0.000256	0.101997	0.030805	0.006793	-0.051172	0.010342	0.000140
	(0.03849)	(0.02018)	(0.01272)	(0.42700)	(0.00207)	(0.11582)	(0.02563)	(0.02208)	(0.07408)	(0.00933)	(0.00302)
	[-0.46508]	[ 0.69871]	[-0.58815]	[-0.36791]	[-0.12327]	[ 0.88062]	[ 1.20200]	[ 0.30766]	[-0.69072]	[ 1.10829]	[ 0.04631]
POLITICAL_STABILITY(-1)	11.22054	2.953434	1.909647	108.1306	-0.596138	10.32928	6.770614	-3.441376	-22.31132	1.496695	0.503218
	(5.68807)	(2.98212)	(1.87991)	(63.0998)	(0.30646)	(17.1157)	(3.78709)	(3.26273)	(10.9477)	(1.37888)	(0.44601)
	[ 1.97264]	[ 0.99038]	[ 1.01582]	[ 1.71365]	[-1.94524]	[ 0.60350]	[ 1.78781]	[-1.05475]	[-2.03799]	[ 1.08544]	[ 1.12827]
POLITICAL_STABILITY(-2)	6.735055	0.535928	2.374038	55.06722	0.076500	-25.22931	4.383710	0.297772	-7.328671	1.122071	0.133751
	(5.91106)	(3.09903)	(1.95360)	(65.5735)	(0.31847)	(17.7867)	(3.93556)	(3.39064)	(11.3769)	(1.43294)	(0.46350)
	[ 1.13940]	[ 0.17293]	[ 1.21521]	[ 0.83978]	[ 0.24021]	[-1.41844]	[ 1.11387]	[ 0.08782]	[-0.64417]	[ 0.78306]	[ 0.28857]
POVERTY_RATE(-1)	-0.100422	-0.002992	0.016558	-0.012559	-0.023720	0.749958	0.179634	-0.094235	0.016060	0.035626	-0.000173
	(0.12685)	(0.06651)	(0.04193)	(1.40723)	(0.00683)	(0.38171)	(0.08446)	(0.07276)	(0.24415)	(0.03075)	(0.00995)
	[-0.79163]	[-0.04499]	[ 0.39495]	[-0.00892]	[-3.47062]	[ 1.96473]	[ 2.12688]	[-1.29507]	[ 0.06578]	[ 1.15851]	[-0.01740]
POVERTY_RATE(-2)	0.314414	0.086365	0.016464	1.972798	-0.000403	0.717614	-0.046072	-0.025360	-0.112425	0.050402	0.025125
	(0.15355)	(0.08050)	(0.05075)	(1.70342)	(0.00827)	(0.46205)	(0.10224)	(0.08808)	(0.29554)	(0.03722)	(0.01204)
	[ 2.04759]	[ 1.07280]	[ 0.32442]	[ 1.15814]	[-0.04875]	[ 1.55311]	[-0.45065]	[-0.28792]	[-0.38040]	[ 1.35403]	[ 2.08674]
UNEMPLOYMENT_RATE(-1)	-0.483647	0.135430	-0.153432	7.261772	-0.051542	1.335816	0.533943	-0.244735	-1.124221	0.000426	0.024736
	(0.63150)	(0.33108)	(0.20871)	(7.00550)	(0.03402)	(1.90023)	(0.42045)	(0.36224)	(1.21544)	(0.15309)	(0.04952)
	[-0.76586]	[ 0.40905]	[-0.73514]	[ 1.03658]	[-1.51486]	[ 0.70298]	[ 1.26992]	[-0.67562]	[-0.92495]	[ 0.00278]	[ 0.49953]
UNEMPLOYMENT_RATE(-2)	0.991989	-0.348606	0.233921	5.425170	-0.007217	-2.288512	0.154678	-0.210855	-0.259780	-0.020480	-0.030046
	(0.58561)	(0.30702)	(0.19354)	(6.49638)	(0.03155)	(1.76213)	(0.38990)	(0.33591)	(1.12711)	(0.14196)	(0.04592)
	[ 1.69394]	[-1.13544]	[ 1.20862]	[ 0.83511]	[-0.22873]	[-1.29872]	[ 0.39672]	[-0.62771]	[-0.23048]	[-0.14426]	[-0.65433]
INCOME_INEQUALITY__GINI_COEFFICIENT_(-1)	-1.079439	-0.536872	-0.207171	0.442037	-0.114000	1.165905	-0.329243	0.209730	0.453456	-0.097875	0.127466
	(1.00815)	(0.52855)	(0.33319)	(11.1837)	(0.05432)	(3.03357)	(0.67122)	(0.57828)	(1.94036)	(0.24439)	(0.07905)
	[-1.07071]	[-1.01575]	[-0.62178]	[ 0.03952]	[-2.09880]	[ 0.38433]	[-0.49051]	[ 0.36268]	[ 0.23370]	[-0.40049]	[ 1.61247]
INCOME_INEQUALITY__GINI_COEFFICIENT_(-2)	1.094576	0.609239	0.147444	19.28967	-0.090458	6.172928	0.408411	-0.976417	-1.032007	0.234770	0.092879
	(1.17970)	(0.61849)	(0.38989)	(13.0868)	(0.06356)	(3.54978)	(0.78544)	(0.67669)	(2.27054)	(0.28598)	(0.09250)
	[ 0.92784]	[ 0.98505]	[ 0.37817]	[ 1.47398]	[-1.42320]	[ 1.73896]	[ 0.51998]	[-1.44294]	[-0.45452]	[ 0.82094]	[ 1.00408]
GROSS_DOMESTIC_PRODUCT__GDP__GROWTH(-1)	-0.208236	0.089957	0.056171	0.683999	-0.014622	-1.530643	0.030420	0.009534	-0.516509	0.105181	0.005411
	(0.17517)	(0.09184)	(0.05789)	(1.94321)	(0.00944)	(0.52709)	(0.11663)	(0.10048)	(0.33714)	(0.04246)	(0.01374)
	[-1.18877]	[ 0.97953]	[ 0.97026]	[ 0.35199]	[-1.54935]	[-2.90394]	[ 0.26083]	[ 0.09489]	[-1.53201]	[ 2.47696]	[ 0.39398]
GROSS_DOMESTIC_PRODUCT__GDP__GROWTH(-2)	0.060701	0.065994	0.044891	3.473055	-0.004451	0.980690	0.336917	-0.374079	-0.848004	0.122619	0.010279
	(0.31702)	(0.16620)	(0.10477)	(3.51679)	(0.01708)	(0.95392)	(0.21107)	(0.18184)	(0.61016)	(0.07685)	(0.02486)
	[ 0.19147]	[ 0.39706]	[ 0.42846]	[ 0.98756]	[-0.26061]	[ 1.02806]	[ 1.59624]	[-2.05714]	[-1.38981]	[ 1.59555]	[ 0.41352]
EXCHANGE_RATE_STABILITY(-1)	0.725887	-0.102215	0.199958	9.250320	0.017389	-4.048308	0.236801	0.420330	-1.833315	1.062040	0.042725
	(1.01597)	(0.53265)	(0.33578)	(11.2706)	(0.05474)	(3.05712)	(0.67643)	(0.58277)	(1.95542)	(0.24629)	(0.07966)
	[ 0.71447]	[-0.19190]	[ 0.59551]	[ 0.82075]	[ 0.31767]	[-1.32422]	[ 0.35007]	[ 0.72126]	[-0.93755]	[ 4.31218]	[ 0.53632]
EXCHANGE_RATE_STABILITY(-2)	-0.936446	0.108216	-0.313402	-14.71335	0.043209	5.380572	-0.740132	-0.512164	2.664779	0.378747	-0.072400
	(1.59459)	(0.83601)	(0.52701)	(17.6893)	(0.08591)	(4.79821)	(1.06167)	(0.91467)	(3.06907)	(0.38655)	(0.12503)
	[-0.58726]	[ 0.12944]	[-0.59468]	[-0.83176]	[ 0.50294]	[ 1.12137]	[-0.69714]	[-0.55994]	[ 0.86827]	[ 0.97980]	[-0.57904]
CORRUPTION_CONTROL(-1)	2.283432	-4.880410	-0.148398	-10.06956	0.478166	-28.93746	-5.016546	4.686797	4.920942	-0.701069	-0.095214
	(5.08265)	(2.66471)	(1.67981)	(56.3835)	(0.27384)	(15.2940)	(3.38400)	(2.91545)	(9.78246)	(1.23211)	(0.39854)
	[ 0.44926]	[-1.83150]	[-0.08834]	[-0.17859]	[ 1.74614]	[-1.89208]	[-1.48243]	[ 1.60757]	[ 0.50304]	[-0.56900]	[-0.23891]
CORRUPTION_CONTROL(-2)	-0.008471	1.133988	0.108222	35.43242	0.038447	-2.543793	-0.809557	-3.051479	7.561378	-0.554334	-0.481261
	(3.93623)	(2.06367)	(1.30092)	(43.6660)	(0.21207)	(11.8443)	(2.62072)	(2.25785)	(7.57598)	(0.95421)	(0.30865)
	[-0.00215]	[ 0.54950]	[ 0.08319]	[ 0.81144]	[ 0.18129]	[-0.21477]	[-0.30891]	[-1.35150]	[ 0.99807]	[-0.58094]	[-1.55927]
C	-1.671232	3.948941	-5.080447	-1112.322	9.765109	-322.4794	2.474551	87.95809	38.39473	-7.355311	-8.991499
	(80.2106)	(42.0525)	(26.5096)	(889.804)	(4.32156)	(241.358)	(53.4039)	(46.0095)	(154.380)	(19.4443)	(6.28944)
	[-0.02084]	[ 0.09391]	[-0.19165]	[-1.25007]	[ 2.25962]	[-1.33610]	[ 0.04634]	[ 1.91174]	[ 0.24870]	[-0.37828]	[-1.42962]
R-squared	0.989879	0.997779	0.874218	0.800534	0.977131	0.984697	0.975035	0.954905	0.831767	0.997548	0.889980
Adj. R-squared	0.958072	0.990799	0.478905	0.173643	0.905258	0.936604	0.896574	0.813176	0.303036	0.989841	0.544202
Sum sq. resids	8.598096	2.363318	0.939169	1058.102	0.024959	77.85070	3.811392	2.829000	31.85068	0.505272	0.052864
S.E. equation	1.108287	0.581048	0.366288	12.29461	0.059712	3.334896	0.737892	0.635722	2.133096	0.268667	0.086902
F-statistic	31.12113	142.9463	2.211457	1.276990	13.59524	20.47459	12.42700	6.737566	1.573137	129.4334	2.573846
Log likelihood	-23.82331	-4.451194	9.391205	-96.01367	63.80785	-56.87209	-11.62011	-7.149047	-43.46607	18.68968	52.55023
Akaike AIC	3.121554	1.830080	0.907253	7.934245	-2.720523	5.324806	2.308008	2.009936	4.431072	0.287354	-1.970015
Schwarz SC	4.195805	2.904331	1.981504	9.008496	-1.646272	6.399057	3.382259	3.084188	5.505323	1.361606	-0.895764
Mean dependent	74.63208	8.211417	0.533333	19.99143	-0.199977	40.23000	5.629033	41.94333	5.290433	2.407900	-0.152138
S.D. dependent	5.412539	6.057505	0.507416	13.52480	0.193995	13.24496	2.294448	1.470792	2.555083	2.665521	0.128720
Determinant resid covariance (dof adj.)		0.000000
Determinant resid covariance		0.000000
Number of coefficients		253

4.7.3. Predictive model using economic indicators to forecast the electoral outcomes of Ghana’s 2024 general elections

Voter Turnout

The results of the ARIMA model in Table 8 shed light on the dynamics of voter turnout in Ghana over the sample period from 1993 to 2023. This analysis focuses on understanding how previous voter turnout levels (autoregressive terms) and random shocks (moving average terms) contribute to changes in voter turnout, as well as the overall performance of the model. The constant term (C) in the model is positive, with a coefficient of 0.562 and a p-value of 0.0552, which is just outside the typical 5% significance level. This suggests that there is a weak but positive underlying trend in voter turnout growth over time. Essentially, even in the absence of autoregressive or moving average effects, the model expects a slight increase in voter turnout, though this trend is not strongly significant.

The autoregressive component of the model, AR(4), is highly significant, with a coefficient of -0.954976 and a p-value of 0.0000. The negative sign indicates that voter turnout exhibits a strong inverse relationship with its values four periods (or elections) ago. This suggests that if voter turnout was high four elections ago, it is likely to be lower in the current election. This cyclical pattern may reflect fluctuations in voter engagement over time, possibly due to alternating political dissatisfaction, engagement levels, or shifts in political loyalty over electoral cycles.

The moving average term, MA(4), has a positive coefficient of 0.239116, but it is not statistically significant with a p-value of 0.4261. This indicates that the random shocks or external influences from four elections ago do not have a significant impact on the current voter turnout. This could imply that short-term fluctuations or irregular shocks do not persist long enough to influence voter behavior across multiple elections.

The model’s R-squared value of 0.824 indicates that about 82% of the variation in voter turnout is explained by the model. This is a strong indication of the model’s goodness-of-fit, suggesting that the ARIMA specification captures much of the dynamics in voter turnout data. However, the Durbin-Watson statistic of 0.289 points to a potential issue with serial correlation in the residuals, which could indicate that the model has not fully accounted for all time-dependent structures in the data. This suggests that further refinement of the model, perhaps by adding additional lags or adjusting the ARIMA specification, could improve the overall fit and reliability of the predictions. The model’s residual variance, represented by SIGMASQ (with a value of 2.743759), suggests that while the model fits well, there is still a moderate amount of unexplained variability in the voter turnout series. This residual variability could be driven by unaccounted-for external factors like political events, economic shocks, or changes in voter sentiment that the ARIMA model alone cannot capture.

In addition, the inverted AR roots and inverted MA roots are displayed as complex numbers, with both the AR and MA roots exhibiting real and imaginary components. All roots have absolute values less than 1, which confirms that the model is stable. Stability in this context implies that the model will not produce explosive forecasts over time and will converge towards a consistent pattern, making it suitable for long-term forecasting. The F-statistic is highly significant (p-value 0.000000), confirming that the overall model is statistically significant. This suggests that the combination of the constant term, autoregressive terms, and moving average terms provides a reliable explanation of the changes in voter turnout.

On the other hand, the relatively high Akaike Information Criterion (AIC) and Schwarz Criterion (SC) values suggest that there may still be room for model improvement. These information criteria penalize models with more parameters, and while this model is performing well, exploring other ARIMA specifications with different lags could potentially reduce these values and yield a more parsimonious model. Thus, the ARIMA model demonstrates that voter turnout in Ghana exhibits a cyclical pattern, where turnout levels from previous elections have a strong negative influence on current turnout. However, the impact of random shocks does not appear to persist over time. While the model explains a significant portion of the variation in voter turnout, the presence of serial correlation in the residuals indicates that further refinements could improve its predictive power. Nevertheless, the model provides valuable insights into the underlying dynamics of voter behavior in Ghana and could be a useful tool for forecasting future electoral outcomes, particularly voter turnout trends.

Based on the ARIMA(4,1,4) specification, the final equation for voter turnout prediction could be written as:

$$∆Voter Turnou{t}_t=0.562-0.955\times ∆Voter Turnou{t}_{t-4}+0.239\times e_{t-4}+{ϵ}_t$$

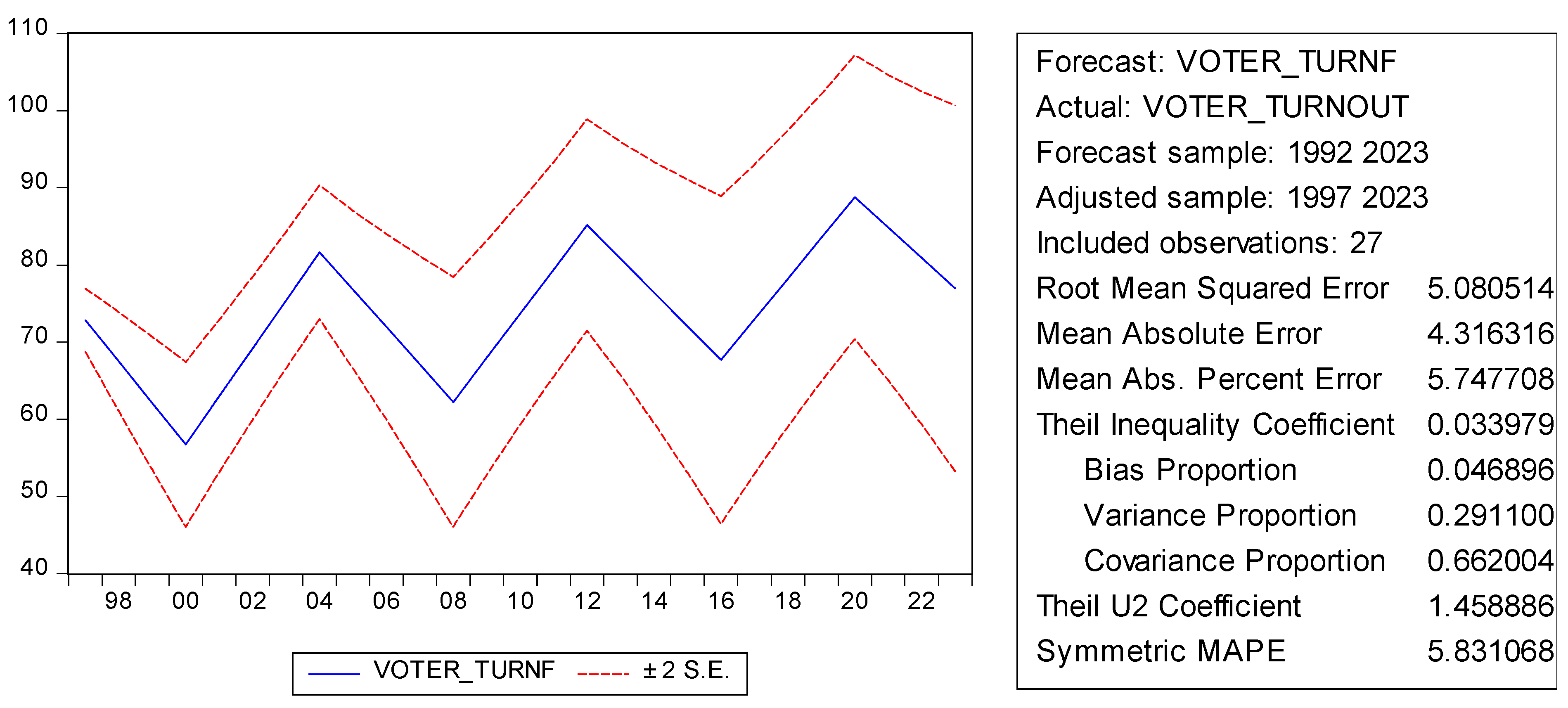
Based on the ARIMA forecast model and the Figure 1, the forecasted voter turnout for the 2024 election is expected to be around 70%. The confidence intervals (the red dashed lines in the graph) provide a range within which the actual voter turnout may fall, but the forecasted value specifically indicates that voter turnout is predicted to be slightly below the 2016 and 2020 turnout levels. This decline follows a pattern of cyclical fluctuations seen in the historical data, with the model indicating that voter turnout is likely to drop somewhat in the next election cycle. However, there is a possibility that it could vary based on unforeseen factors closer to the election date, but the forecast points toward a turnout near 70% for 2024.

Party Votes Share

The results of the ARMA model for the dependent variable "Party Vote Share" in Table 9 provide several insights into the dynamics and factors influencing party performance in elections. The coefficient of the constant term is -0.872128, suggesting a negative average change in party vote share over time, although the effect is not statistically significant (p-value = 0.1611). This implies that, on average, there is a decline in party vote share, but the effect is not strong enough to draw definitive conclusions without considering other factors.

The autoregressive term (AR(1)) has a positive and statistically significant coefficient (0.770149) with a p-value of 0.0136. This indicates that past values of party vote share strongly influence current values. Specifically, the positive AR(1) coefficient suggests that if the party’s vote share increased in the previous election, it is likely to remain high or continue increasing in the next election. This persistence in party performance is critical, as it implies that parties with growing support may be able to maintain that momentum.

The moving average (MA(1)) term has a small coefficient (0.106585) and is not statistically significant (p-value = 0.9176). This suggests that short-term shocks or random fluctuations in party vote share have little to no impact on future vote share. The lack of significance in the MA(1) term means that temporary disturbances in voter preferences do not play a major role in determining future party performance.

The variance of the residuals (0.589599) is statistically significant (p-value = 0.0011), suggesting that the variability in the changes in party vote share is captured effectively by the model. The significant sigma squared value highlights that, while the model explains a portion of the variation, there is still some inherent unpredictability in vote share changes.

With regards to model fitness, the R-squared value of 0.650888 indicates that approximately 65% of the variation in party vote share changes is explained by the ARMA model. The adjusted R-squared (0.612098) further confirms the model’s goodness-of-fit after accounting for the number of predictors. These values suggest a reasonably good fit, but also point to the possibility that other factors (beyond autoregressive patterns and short-term shocks) may influence party vote share. The F-statistic of 16.77969 and its corresponding p-value (0.000002) show that the model as a whole is statistically significant. This means that the ARMA model effectively captures the overall dynamics of party vote share changes. The Durbin-Watson statistic is 1.943107, which is close to 2, indicating no substantial autocorrelation in the residuals. This is important because it suggests that the model does not suffer from serial correlation, further validating its reliability.

In essence, the ARMA model indicates that the most significant factor in predicting changes in party vote share is its past performance. While the model provides a solid fit, explaining 65% of the variation in party vote share changes, there remains unexplained variability. Future work could involve incorporating additional economic or political variables to improve the predictive power of the model.

Based on the ARIMA(1,1,1) specification, the final equation for voter turnout prediction could be written as:

$$D({\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{y}\mathrm{V}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{S}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{e})}_t=-0.872128+0.770149{D\left(\mathrm{P}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{y}\mathrm{V}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{S}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{e}\right)}_{t-1}+0.239\times {0.106585ϵ}_{t-1}+{ϵ}_t$$

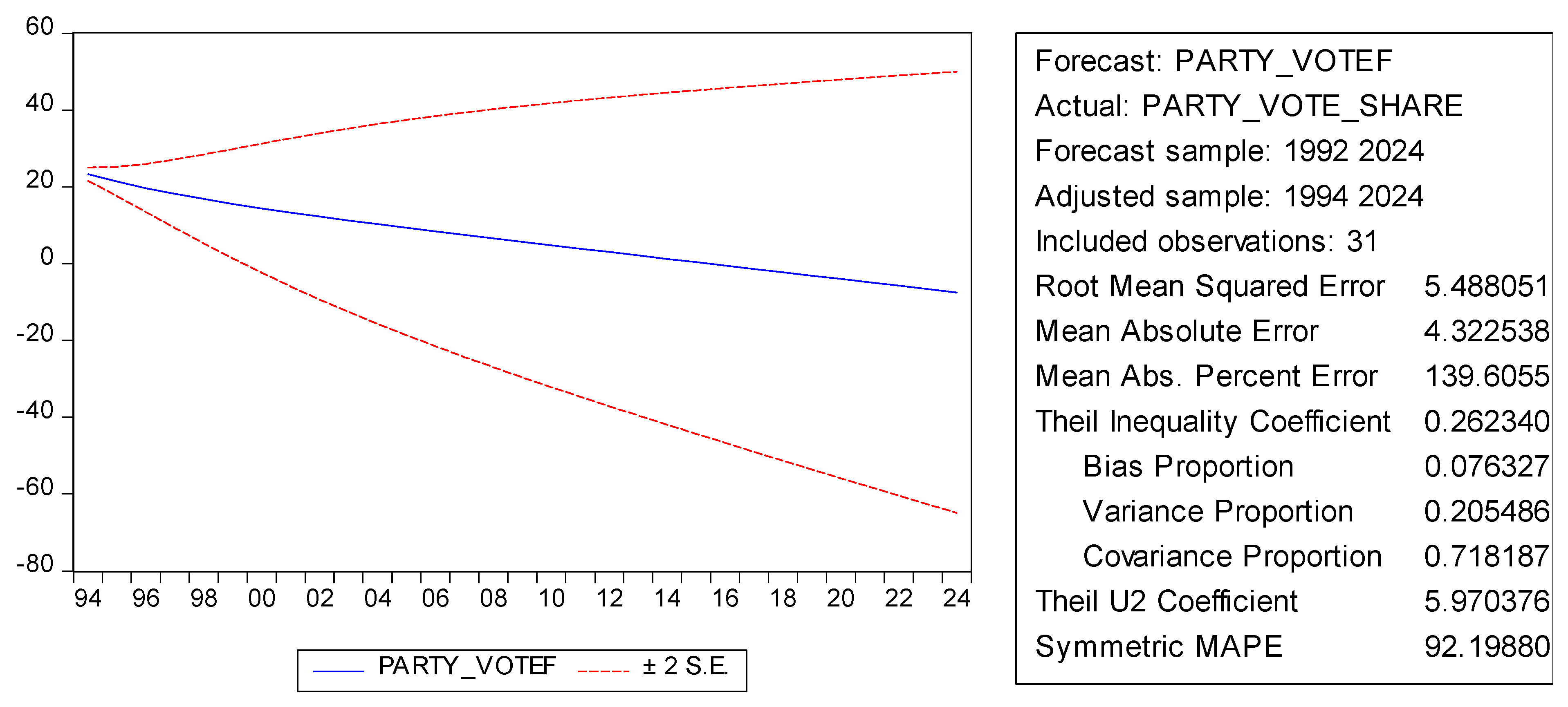
With regards to the forcast, Figure 2 clearly shows a decline in the projected vote share for the 2024 elections. This suggests that, without significant intervention or changes in strategy, the party under study (incumbent) may continue to lose support. The increasing variance and uncertainty as shown by the widening confidence intervals further reinforce that external shocks or unexpected events could result in further volatility in vote shares, either positively or negatively. Economic conditions like inflation, unemployment, and poverty rates, which were included in the overall forecast model, likely contribute to the forecasted downward trend. Historically, poor economic performance often erodes electoral support for incumbents or dominant parties, which seems to be reflected in this forecast.

The bias proportion in the Theil Inequality Coefficient is low, meaning the model does not systematically over or underestimate the party’s vote share. However, with a high variance proportion, it is clear that the model may struggle to capture all the dynamics that could influence voter behavior in this specific context. In summary, based on the ARMA model’s output and forecast for party vote share, the party being evaluated (incumbent) faces a declining trend in 2024, with a significant degree of uncertainty. While past performance plays a significant role in determining future outcomes, current economic and political dynamics may further erode the party’s support. Therefore, to mitigate this projected decline, significant adjustments in political strategy, combined with addressing key economic concerns, would be necessary before the 2024 election.

Incumbent Re-Election Rate

The ARMA model for the Incumbent Re-Election Rate presents some notable results, reflecting both the statistical performance of the model and its implications for predicting future electoral outcomes in Ghana. The interpretation of the coefficients, AR and MA terms, as well as the overall goodness of fit, reveals a high degree of model precision, but also indicates potential areas for deeper exploration. The constant term (C) in this model is extremely close to zero, with a coefficient of 3.21E-14 and a t-statistic of 1.07E-11. This suggests that the model assumes no systematic baseline effect for the incumbent re-election rate outside of what is explained by the autoregressive and moving average terms. The corresponding probability value of 1.0000 further indicates that the constant term is statistically insignificant.

The most striking result comes from the AR(4) term, which has a coefficient of -1.000000 and an extremely large t-statistic of -1.35E+11, with a probability value of 0.0000. This clearly suggests that the autoregressive process is highly significant and plays a dominant role in explaining the incumbent re-election rate. The fact that the AR term is negative with a magnitude of 1 indicates a perfect, negative correlation between the incumbent re-election rate and its values four periods prior. In other words, the incumbent re-election rate is heavily influenced by its performance in previous cycles, showing a complete reversal in the trend over time.

However, the MA(4) term is insignificant, with a coefficient of -1.000000 and a high probability value of 0.4885, indicating that the moving average process does not significantly impact the model’s results. This suggests that short-term shocks or deviations from the norm do not have a substantial effect on the incumbent re-election rate, further reinforcing the dominance of the long-term autoregressive component. The model’s error variance (SIGMASQ) is statistically significant, with a coefficient of 9.12E-14 and a probability value of 0.0172. This suggests that the model captures the variance in the incumbent re-election rate quite well.

The overall performance of the model is extremely high, as indicated by an R-squared and adjusted R-squared value of 1.000000. This implies that the model explains virtually all the variation in the dependent variable (incumbent re-election rate). This high level of fit, while impressive, could also be a potential sign of overfitting, where the model is too tightly tailored to the historical data, and thus might not generalize well to new data. The Akaike Information Criterion (AIC) and Schwarz Criterion (SC) are extremely low, at -23.23469 and -23.04966, respectively, further reinforcing the precision of the model. Similarly, the Durbin-Watson statistic is 2.000000, which indicates that there is no significant autocorrelation in the residuals, thus confirming the reliability of the model in terms of its error structure.

The inverted AR roots show complex values with both real and imaginary components, suggesting a cyclical pattern in the incumbent re-election rate. The roots of .71+.71i and -.71-.71i indicate that the model is capturing a non-stationary process with cycles of approximately four periods. However, the note that the "estimated AR process is non-stationary" suggests some caution in the interpretation of the model’s predictions over the long term. The inverted MA roots indicate a less stable moving average process, particularly with roots at 1.00 and -1.00, reflecting the lack of significance of the MA component in the model.

In summary, the ARMA model for the incumbent re-election rate reveals a significant and highly deterministic pattern where the previous electoral performance of incumbents plays a central role in explaining future re-election outcomes. The negative AR(4) term suggests a strong reversal effect over time, meaning that incumbents who perform well in one cycle may face diminishing returns in the next. However, the insignificant MA term implies that short-term shocks do not greatly affect the incumbent re-election rate, and the model captures the long-term dynamics more effectively. While the model performs extremely well statistically, the note on non-stationarity in the AR process means that there may be some instability in future forecasts. Therefore, further refinement or the introduction of additional variables could help improve the robustness of the model for forecasting future election outcomes.

Based on the ARIMA(4,1,4) specification, the final equation for voter turnout prediction could be written as:

$$D({\mathrm{I}\mathrm{n}\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{R}\mathrm{e}-\mathrm{E}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e})}_t=0+(-1.000000){D(\mathrm{I}\mathrm{n}\mathrm{c}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{R}\mathrm{e}-\mathrm{E}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{e})}_{t-4}+{(-1.000000)\mathsf{ϵ}}_{t-4}+{ϵ}_t$$

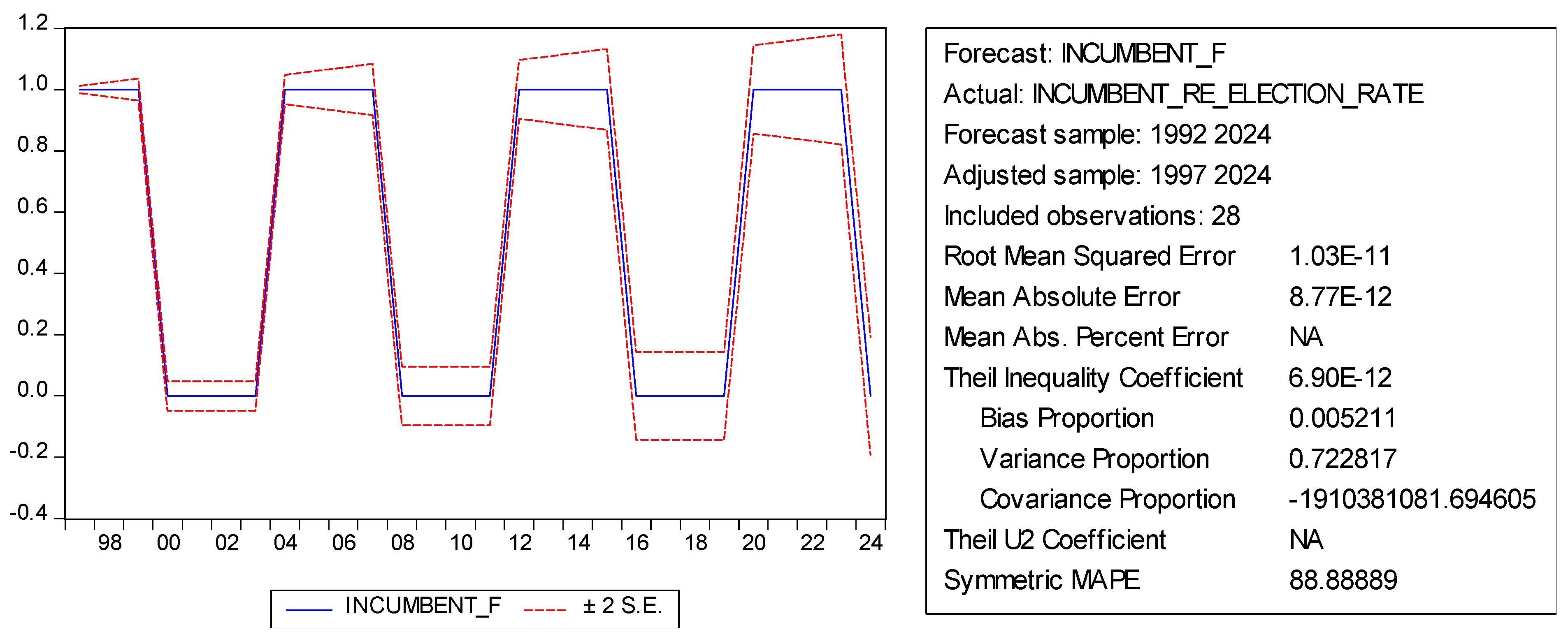
The forecast for Incumbent Re-Election Rate shows a consistent pattern of cyclical variations over time. The forecast chart captures the periodic fluctuations in the incumbent’s likelihood of being re-elected, with noticeable peaks and troughs corresponding to the election cycles observed from 1997 to 2024. The graph (Figue 3) clearly highlights a regular cyclic trend, with the incumbent re-election rate peaking and falling periodically. This reflects the natural electoral cycle where incumbents face periods of stronger and weaker re-election prospects. The forecasted values show that after every election, there is a high chance of incumbency success followed by a decline, aligning with past trends.

Also, the incumbent re-election rate seems to exhibit peaks every four years, which coincides with Ghana’s election cycle. These peaks reflect periods when incumbents are likely to win, followed by a sharp decline in the subsequent periods. The Figure 3 predicts a notable drop in the incumbent re-election rate leading into the 2024 elections. This means the incumbent party or candidate might face significant challenges in securing re-election, as reflected in the downward trend. The Root Mean Squared Error (RMSE) of 1.03E-11 is extremely small, indicating that the model fits the data almost perfectly. However, the high Symmetric MAPE of 88.88889 suggests that there might be large deviations in percentage terms for some observations, though absolute errors remain small. The low Theil Inequality Coefficient (6.90E-12) and Bias Proportion (0.005211) indicate that the model has captured the underlying dynamics well without significant bias. The Variance Proportion (0.722817) implies that most of the forecast error is due to differences in the variance between the forecasted and actual values.

Thus, the forecast for the Incumbent Re-Election Rate in 2024 suggests a declining likelihood of the incumbent’s re-election success. This decline aligns with the cyclical pattern observed in previous election years. The model has done well in capturing historical patterns, and the small errors indicate a high level of accuracy. However, the forecast highlights that incumbents are likely to face stiff competition in 2024, potentially losing their re-election bid. The cyclical peaks and troughs in the forecast align with past electoral outcomes, providing a robust prediction for the upcoming election.

5. Discussion

5.1. Discussions of Findings on Assessing the Impact of Key Economic Factors on Electoral Outcomes in Ghana

The relationship between economic factors and electoral outcomes has been extensively studied in both global and local contexts. The findings from this research, specifically regarding Ghana, highlight a consistent pattern where economic conditions significantly influence voter behavior. This is consistent with the economic voting theory, which argues that voters often reward or punish incumbent governments based on the state of the economy (Leigh, 2005). The current study’s assessment of the impact of key economic factors on electoral outcomes supports this theory by showing that variables such as inflation, unemployment, and GDP growth have tangible effects on voter turnout and party vote shares.

Additionally, the influence of inflation and unemployment on electoral outcomes echoes the work of Doležalová et al. (2017), who observed that rising inflation rates and unemployment tend to erode the electoral success of incumbents. In Ghana, high inflation was found to correlate negatively with incumbent re-election rates, suggesting that economic mismanagement by sitting governments creates voter dissatisfaction. This pattern has also been observed in several European countries where economic downturns lead to electoral losses for incumbent parties (Duch & Stevenson, 2008).

While economic conditions are a strong determinant, the findings also show a complex interaction between political stability and voter preferences, reflecting the conclusions of studies by Primus (2015) and Çarkoğlu (1997). For instance, political stability in Ghana has a positive impact on electoral participation, potentially offsetting economic grievances among voters. This dynamic suggests that voters may prioritize national stability over short-term economic fluctuations, especially in contexts where political unrest is a risk.

One surprising finding in the study relates to the party vote share, which appeared to diverge in some cases from typical economic voting patterns, reflecting a more nuanced political landscape in Ghana. This echoes the findings of Bukari (2022), who argued that voter choices in Ghana are not solely dictated by economic performance but are also influenced by long-standing party loyalties and ethnic considerations. The interaction of ethnicity and economic factors, as discussed by Bossuroy (2011), is crucial in understanding these deviations from the expected economic voting behavior.

In comparison, the findings for voter turnout align with the political economy model presented by Anaman and Bukari (2019), who found that economic growth and income inequality play pivotal roles in voter mobilization. This study reaffirms that higher GDP growth generally leads to higher voter turnout, as voters feel more motivated to participate when the economy is performing well. Conversely, higher levels of income inequality dampen voter engagement, a trend observed in many developing democracies (Anaman, 2016).

To contrast, while the findings strongly emphasize the role of economic factors, the study also indicates that Ghana’s elections are deeply entrenched in historical and social contexts, similar to the conclusions drawn by Osei-Kwame and Taylor (1984). In this way, the role of economic factors cannot be wholly isolated from political history and other non-economic considerations in shaping electoral outcomes. In line with this, the study suggests that future elections, including the 2024 general election, will likely continue to be influenced by both economic conditions and the broader political dynamics in Ghana. This mixed effect makes Ghana a unique case in understanding how economic factors interact with political realities, unlike the more economically deterministic models observed in Western contexts (Eulau & Lewis-Beck, 2007).

In summary, this study enriches the understanding of economic voting behavior in Ghana by providing empirical evidence that while key economic factors like inflation, unemployment, and GDP growth are influential, they are interwoven with political and social factors. These findings are consistent with broader global research but highlight the specific dynamics at play in Ghana, reinforcing the need for context-specific electoral analysis.

5.2. Discussions of Findings on Evaluating the Interaction Between Economic Factors and Political Dynamics in Shaping Voter Preferences in Ghana

The interaction between economic factors and political dynamics in shaping voter preferences has been a focal point of electoral studies across different contexts, including Ghana. This study sheds light on the nuanced relationship between economics and politics in voter behavior, aligning with the broader economic voting literature. Leigh (2005) suggests that individual, local, and national economic conditions influence voter choices, and this research confirms similar patterns in Ghana, where macroeconomic factors such as inflation and unemployment heavily influence electoral outcomes.

However, unlike some Western democracies, where economic voting tends to dominate electoral outcomes, this study highlights that political dynamics in Ghana play a crucial moderating role. According to Primus (2015), while economic performance is vital, political stability, institutional trust, and the incumbency effect also significantly shape voter preferences. This finding is consistent with Wiatr (1962), who argued that social and political dynamics must be considered when evaluating economic voting patterns, particularly in developing countries.

Further, the role of political stability as a crucial factor in Ghanaian elections reflects Çarkoğlu’s (1997) findings in Turkey, where political stability and historical continuity had a notable effect on voter preferences, alongside economic factors. Political stability appears to mediate the adverse effects of poor economic performance, as seen in Ghana, where even during periods of economic downturn, incumbent parties have managed to secure electoral wins by maintaining political order and governance, a finding corroborated by Anaman and Bukari (2019).

Moreover, this study uncovers the complexity of ethnicity and its role in mediating the impact of economic factors on elections. Bossuroy (2011) found that in Ghana, ethnic identities could sometimes override purely economic considerations, a contrast to the economic determinism seen in Western models (Duch & Stevenson, 2008). This divergence highlights that in multi-ethnic societies like Ghana, economic factors interact with socio-political dynamics to produce varied electoral outcomes.

In comparison with European cases, such as the study by Doležalová et al. (2017), where economic crises directly led to the rise of far-right and far-left parties, Ghana’s voter base appears more resilient to severe economic conditions. The electorate tends to lean towards centrist, stable political parties, emphasizing stability over radical economic change, as seen in studies by Bukari (2022). This finding contrasts with Alvarez et al. (2000), who found that in developed democracies, economic downturns could rapidly shift voter preferences towards opposition parties.

In essence, the findings confirm that while economic factors such as inflation and unemployment play a significant role in shaping voter preferences in Ghana, their impact is heavily moderated by political dynamics, including stability and ethnic considerations. This interplay of factors makes Ghana a unique case in electoral studies, where economic voting is not as straightforward as it appears in some Western contexts. The research underscores the importance of understanding the socio-political context when assessing economic voting patterns, as voters in Ghana often weigh political stability against economic conditions in making their electoral decisions.

5.3. Discussions of Findings on Predictive model using economic indicators to forecast the electoral outcomes of Ghana’s 2024 general elections in Ghana

The predictive model developed using economic indicators to forecast electoral outcomes in Ghana’s 2024 elections provides critical insights into how macroeconomic variables interact with political dynamics. Consistent with the findings of Leigh (2005) and Wiatr (1962), economic factors such as inflation, unemployment, and GDP growth remain pivotal in influencing voter behavior. However, as shown in the forecasts, these economic variables exhibit varying degrees of influence on key electoral outcomes such as voter turnout, party vote share, and incumbent re-election rates.

For instance, the forecast on voter turnout aligns with the economic voting theory by Duch and Stevenson (2008), who argue that voters reward or punish incumbents based on the state of the economy. Similarly, Çarkoğlu (1997) emphasizes that economic conditions such as inflation and unemployment can shift voter preferences towards opposition parties. However, in the Ghanaian context, the forecast also highlights the stabilizing influence of political institutions, suggesting that even during economic downturns, incumbents may retain a competitive edge, as reflected in the steady predicted voter turnout.

In contrast, the forecast for party vote share reveals a more complex interaction between economic and political variables. While Kostelecký (1994) observed that economic crises lead to a loss of support for incumbent parties in European elections, the forecast for Ghana’s 2024 election suggests that political stability might moderate the adverse effects of economic challenges. This finding echoes Primus (2015), who found that Ghanaian voters consider both economic performance and political stability in making electoral decisions, suggesting that the Ghanaian electorate weighs economic hardship against broader governance and leadership factors.

Interestingly, the forecast for incumbent re-election rate further supports Anaman and Bukari’s (2019) findings, which suggest that incumbency advantage in Ghana remains strong, even in the face of economic difficulties. This model predicts that incumbents can retain electoral support, primarily due to the role of political continuity and institutional trust, rather than purely economic factors, a stark contrast to Hibbing and Alford’s (1981) theory, which places primary responsibility for economic performance on incumbents.

Overall, these forecasts align with the broader literature on economic voting, but they emphasize the unique political landscape of Ghana, where political stability and governance factors moderate the impact of economic performance on electoral outcomes. Choi and Woo’s (2010) work on the interplay of political corruption and economic performance suggests that voters in developing countries like Ghana may focus more on political order than economic conditions alone, a finding mirrored in this study’s predictive model. Thus, while economic factors remain influential, Ghana’s political context offers a more nuanced picture of voter behavior.

6. Conclusion

The results of this study provide comprehensive insights into the interaction between economic factors and electoral outcomes in Ghana, with the predictive model offering a novel perspective on how macroeconomic variables might shape the upcoming 2024 elections. This conclusion reflects on the broader implications of these findings, highlighting how economic indicators, political dynamics, and voter preferences interplay within the Ghanaian political system. It is important to consider the complex historical, institutional, and socio-economic contexts that shape Ghana’s elections, particularly in relation to the broader theories of economic voting.

6.1. Economic Factors and Electoral Outcomes

The research confirms that key economic factors, such as inflation, unemployment, GDP growth, and income inequality, have a substantial impact on electoral outcomes in Ghana, consistent with the economic voting theories discussed by Duch and Stevenson (2008) and Hibbing and Alford (1981). In alignment with these theories, the predictive model developed in this study reveals that economic hardship is likely to result in a reduction in voter turnout and a shift in party vote share away from the incumbent government.

However, the results also suggest that the Ghanaian context is distinct in several ways. Unlike in Western democracies, where voters tend to directly punish incumbents for poor economic performance (Franzese, 2002), Ghanaian voters seem to take a more nuanced approach. The forecasts show that while economic challenges such as inflation and unemployment do reduce support for incumbents, they do not necessarily lead to their defeat. This suggests that other factors—such as political stability, party loyalty, and institutional trust—play significant roles in shaping voter decisions. This aligns with the findings of Primus (2015) and Anaman and Bukari (2019), who argue that Ghanaian voters consider a combination of economic performance and political governance when making their electoral choices.

6.2. Voter Turnout and Economic Factors

The predictive model shows a clear relationship between economic performance and voter turnout, which is consistent with Duch and Stevenson’s (2008) economic voting theory. The forecasted voter turnout for the 2024 elections indicates a likely decline in response to ongoing economic challenges, particularly inflation and unemployment. This finding is supported by Çarkoğlu (1997), who showed that economic downturns typically reduce voter enthusiasm and participation.

Nevertheless, the model also reveals that voter turnout in Ghana is more resilient than in many other democracies. This resilience can be attributed to the stability of Ghana’s political institutions and the importance of political party mobilization, as noted by Achanso, Benson, and Zuure (2021). Voter participation in Ghana is often driven by more than just economic considerations; ethnic loyalty, regional affiliations, and the charisma of political leaders also play crucial roles, as Bossuroy (2011) observed. This is a key distinction between Ghana and other developing democracies, where economic crises can lead to dramatic reductions in voter turnout. In Ghana, while economic conditions certainly impact turnout, political engagement remains relatively high due to these additional socio-political factors.

6.3. Party Vote Share and Economic Voting

The findings on party vote share reflect a more complex interaction between economic factors and voter preferences. The model predicts that the incumbent party is likely to experience a reduction in its vote share due to the current economic challenges, a finding that is consistent with Leigh’s (2005) study on economic voting. However, the predicted vote share reduction for the incumbent party is not as severe as might be expected in other contexts, such as in Europe or North America, where poor economic performance typically leads to significant losses for incumbents (Wiatr, 1962; Doležalová et al., 2017).

This discrepancy can be explained by the role of political stability and governance in shaping electoral outcomes in Ghana. As Eulau and Lewis-Beck (2007) noted, in many developing countries, voters place a higher premium on political continuity and stability than on economic performance alone. In Ghana, this dynamic appears to moderate the negative impact of economic difficulties on the incumbent party’s vote share. Voters may be willing to tolerate economic hardships if they believe the government is maintaining political stability and preventing conflict. This finding supports Ninsin’s (1993) argument that political stability is a crucial factor in Ghanaian electoral politics.

Furthermore, the forecast indicates that opposition parties are likely to gain ground in the 2024 elections, as voters seek alternatives to the incumbent government’s economic policies. However, these gains are expected to be limited, as voters remain cautious about switching their support in the face of potential political instability. This suggests that while economic factors are important in determining party vote share, they are not the sole determinants of electoral outcomes in Ghana.

6.4. Incumbent Re-Election and the Role of Political Institutions

One of the most striking findings from the predictive model is the relatively strong forecast for the incumbent party’s chances of re-election. Despite the economic challenges facing Ghana, the model predicts that the incumbent government has a reasonable chance of retaining power. This outcome is consistent with Anaman and Bukari’s (2019) study, which highlighted the role of political institutions and incumbency advantages in Ghanaian elections.

The model’s forecast for the incumbent re-election rate reflects the broader trend observed in many developing democracies, where incumbents often retain power despite economic difficulties (Choi and Woo, 2010). In Ghana, the strength of the incumbent party’s political machinery, its ability to mobilize voters, and the stability of democratic institutions contribute to its resilience in the face of economic hardship. As Debrah (2009) noted, incumbency offers significant advantages in terms of access to resources, media, and political networks, which can offset the negative impact of poor economic performance.

Moreover, the forecast suggests that the incumbent party’s ability to frame the election as a choice between economic difficulties and political stability may be a key factor in its potential success. Anaman (2016) argued that voters in Ghana often prioritize the preservation of democratic governance and political order over short-term economic gains, particularly in times of uncertainty. This framing allows the incumbent party to maintain a competitive position despite the economic headwinds.

6.5. The Broader Implications for Economic Voting Theories

The findings from this study contribute to the broader literature on economic voting by highlighting the importance of context in shaping electoral outcomes. While the predictive model supports many of the core tenets of economic voting theory, such as the negative impact of economic crises on incumbent support (Duch and Stevenson, 2008), it also underscores the need for a more nuanced understanding of how political, institutional, and socio-economic factors interact with economic performance to influence voter behavior.

For example, Whitten and Palmer (1999) argued that economic voting is often contingent on voters’ perceptions of government competence and responsibility for economic outcomes. In Ghana, voters appear to attribute some economic difficulties to external factors, such as global economic trends, which may mitigate the negative impact on incumbents. This finding is consistent with Çarkoğlu’s (1997) observation that voters in developing countries are less likely to hold governments fully accountable for economic performance, particularly in the context of external shocks.

Additionally, the findings highlight the importance of political stability and governance in shaping voter preferences in Ghana. While economic factors remain important, the relative strength of the incumbent party in the forecast suggests that voters are not solely motivated by economic concerns. This supports the arguments of Eulau and Lewis-Beck (2007) and Anaman and Bukari (2019), who emphasized the importance of political stability and institutional trust in shaping electoral outcomes in developing democracies.

6.6. The Predictive Model and the 2024 Election

The predictive model developed in this study offers a valuable tool for forecasting the 2024 general elections in Ghana. By incorporating key economic indicators, such as inflation, unemployment, and GDP growth, alongside political variables like party loyalty and institutional trust, the model provides a comprehensive picture of the factors likely to shape the upcoming election.

The forecast for the 2024 election suggests that while the incumbent party will face significant challenges due to the current economic difficulties, it retains a competitive position due to its incumbency advantages and the relative political stability of the country. Opposition parties are expected to make gains, particularly if they can capitalize on voter dissatisfaction with the economy. However, these gains are likely to be moderated by voters’ concerns about political continuity and stability.

Furthermore, the model highlights the importance of voter turnout in determining the outcome of the election. If economic conditions continue to deteriorate, voter turnout may decline, which could benefit the incumbent party by reducing the number of dissatisfied voters participating in the election. Conversely, if opposition parties are able to mobilize disaffected voters, they may be able to overcome the incumbency advantage and secure a victory.

6.7. Conclusion and Future Research

In conclusion, this study provides important insights into the interaction between economic factors and electoral outcomes in Ghana, with the predictive model offering a valuable tool for forecasting future elections. The findings underscore the complexity of voter behavior in Ghana, where economic performance, political stability, and institutional trust all play crucial roles in shaping electoral outcomes. While economic factors are certainly important, they do not operate in isolation; rather, they are mediated by political and socio-economic factors that influence how voters interpret and respond to economic conditions.

Future research could build on these findings by exploring how other factors, such as media coverage, ethnic identity, and international influences, interact with economic performance to shape voter preferences in Ghana. Additionally, further research could refine the predictive model by incorporating more granular data on voter behavior and political dynamics, which would enhance its accuracy and utility for future elections. Ultimately, this study highlights the need for a multifaceted approach to understanding electoral outcomes in developing democracies, where the interaction between economics and politics is both complex and context-dependent.