Revisiting Maxwell's Equations for Observers: Direct Derivation of Doppler and Sagnac Effect

1. Introduction

Maxwell’s equations [1] provide a comprehensive description of EM wave propagation. What is missing from the picture is how an EM wave will be perceived by different observers. Different observers will measure the same EM wave differently, for example, Doppler effect [2,3] shows that the same EM wave will be measured at different frequencies. While the frequency of the original EM wave doesn’t change after emission, the frequency “as measured” varies for different observers. Hence, Maxwell’s equations in current form only describe the EM wave “as propagated” but not “as measured”. This paper mathematically derives a general form of Maxwell’s equations which also describe the EM wave “as measured” by the observer. 

The key to understand the difference between “as propagated” and “as measured” is the concept of “time scaling factor”, which explains the phenomenon: when an observer moving away from a clock, the clock appears ticking slower and when the velocity approaches $c$, he will see the clock coming to a stall. If he compares the observed clock with his own clock, he will see a “time scaling factor”, which is due to the asymmetry between the light emission time $t_s$ at the light source and the observed time $t_o$ by the observer, and mathematically represented as $d{t}_o/d{t}_s$. A formula for $d{t}_o/d{t}_s$ is mathematically derived in Asymmetry Theory [5]. The well-established principle of the constancy of the velocity of light [4] can be mathematically represented as $\mathit{O}\left(t_o\right)-\mathit{S}\left(t_s\right)=\mathit{c}\left(t_o-t_s\right)$. Based solely on this equation without any other assumption, a comprehensive set of results was derived through pure mathematics, named Asymmetry Theory [5,6,7].

The time $t$ in original Maxwell’s equations represents the clock for propagation. If we substitute it with the observer’s clock, i.e. $t_o$, a generalized form of Maxwell’s equations for moving observer is mathematically derived in [5]. The transformed Maxwell’s equations are shown covariant for different observer reference frames in [5] and the original form of Maxwell’s equations is just a special case when $t=$$t_o$.

In this paper, we further extend the case to also include the motion of the EM emitter. A general form of Maxwell’s equations is mathematically derived, and the original form is just a special case when the observer and emitter are static. Its solution demonstrated that the light velocity to observers is independent of the motion of the emitter, which demonstrates the principle of constancy of light velocity. The Doppler effect and Sagnac effect [10] are mathematically derived from the solution. A summary of the solutions of general equations in special cases is shown to be in harmony with all established experiments.

This paper is organized as follows:

Section II introduces the notations and background of the time-scaling factor.

Section III introduces how to mathematically transform the original Maxwell’s equations by substituting the time $t$ with $t_o$.

Section IV presents the mathematical transformation of a general form of Maxwell’s equations for observers and the derivation of Doppler effect and Sagnac effect.

2. Notations and Background

2.1. Notations

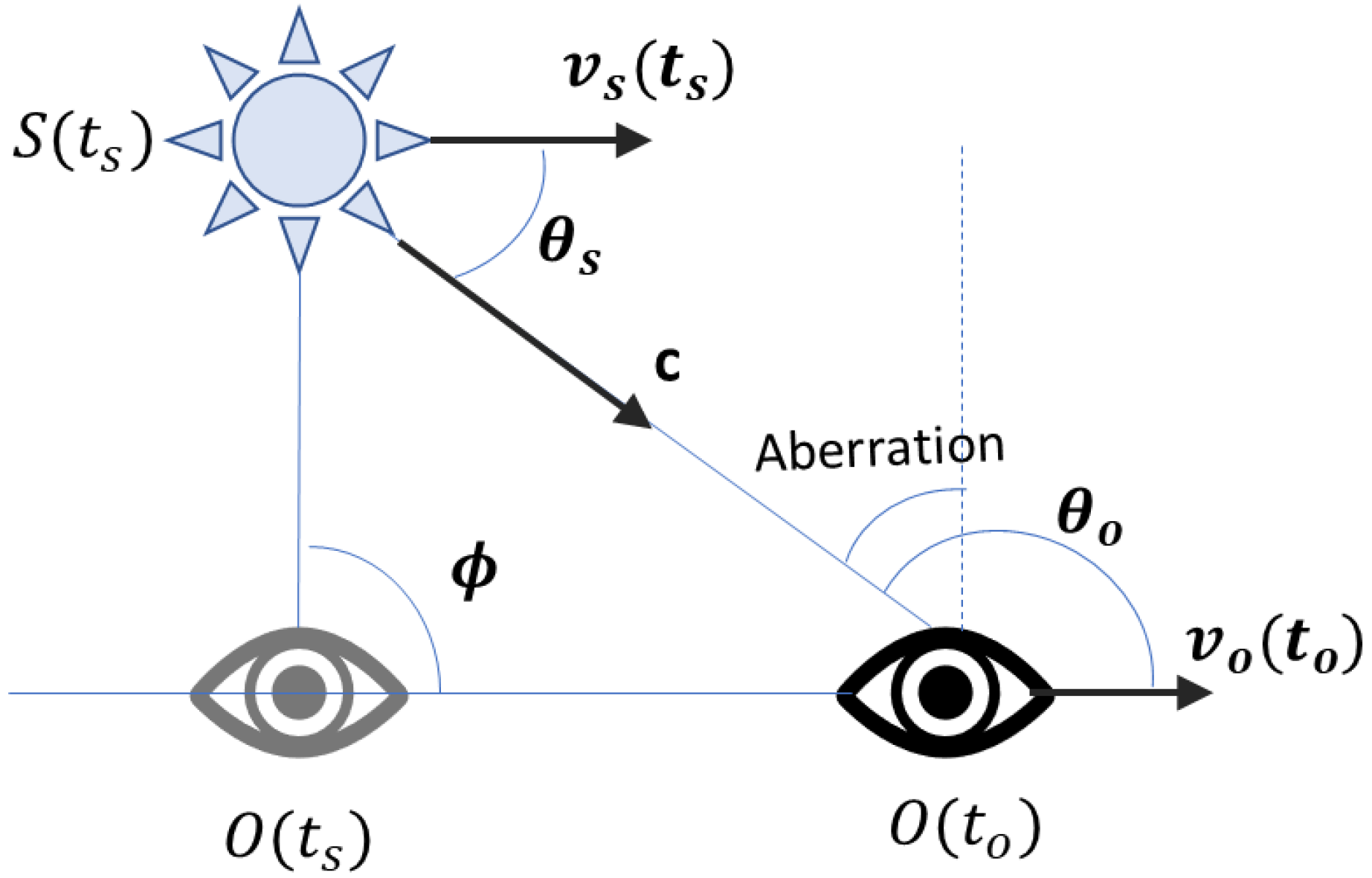
Define $t_s$ as the emission time of a light; $S\left(t_s\right)$ as the origin of the light when emitted at $t_s$; $t_o$ as the time an observer $O$ observed the light from $S\left(t_s\right)$; $O\left(t_o\right)$ as the position of $O$ at $t_o$. Define $v_o\left(t_o\right)$ as the velocity of the observer $O$ relative to $S\left(t_s\right)$ at $t_o$ and $v_s\left(t_s\right)$ as the velocity of the emitter relative $S\left(t_s\right)$ at $t_s$. Figure 1 also shows key angles for the velocity of light, ${\theta }_s,{\theta }_o,\varphi$.

2.2. Principle of Constancy of the Velocity of Light

Principle 1: In empty space, the light always propagates with a velocity $c$. independent of the state of motion of the emitting body [4].

Principle 1 can be mathematically represented as:

$$\mathit{O}\left(t_o\right)-\mathit{S}\left(t_s\right)=\mathit{c}\left(t_o-t_s\right)$$

(1)

This paper is solely based on the mathematical derivation from equation (1) without any other assumptions.

2.3. The Formula of $d{t}_o/d{t}_s$

Perform an inner product of both sides of (3), we have:

$$\left(\mathit{O}\left(t_o\right)-\mathit{S}\left(t_s\right)\right)•\left(\mathit{O}\left(t_o\right)-\mathit{S}\left(t_s\right)\right)=c^2{\left(t_o-t_s\right)}^2$$

Differentiate both sides as to $t_s$ and reorganize:

$${\displaystyle \frac{\left(\mathit{O}\left(t_o\right)-\mathit{S}\left(t_s\right)\right)}{c\left(t_o-t_s\right)}}•\left({\mathit{v}}_{\mathit{o}}\left(t_o\right){\displaystyle \frac{d{t}_o}{d{t}_s}}-{\mathit{v}}_{\mathit{s}}\left(t_s\right)\right)=c\left({\displaystyle \frac{d{t}_o}{d{t}_s}}-1\right)$$

Let ${\mathit{i}}_{os}$ denote the unit vector in $\overrightarrow{\mathit{S}\left(t_s\right)\mathit{O}\left(t_s\right)}$, we have:

$${\mathit{i}}_{os}•{\mathit{v}}_o\left(t_o\right){\displaystyle \frac{d{t}_o}{d{t}_s}}-{\mathit{i}}_{os}•{\mathit{v}}_{\mathit{s}}\left(t_s\right)=c\left({\displaystyle \frac{d{t}_o}{d{t}_s}}-1\right)$$

Finally, the formula of time scaling factor [5] is:

$${\displaystyle \frac{d{t}_o}{d{t}_s}}={\displaystyle \frac{c-v_s\left(t_s\right)\cos \left({\theta }_s\right)}{c+v_o\left(t_o\right)\cos \left({\theta }_o\right)}}$$

(2)

When $v_o\left(t\right), v_s\left(t\right)$ are constant $v_o, v_s$ and ${\theta }_s=0,{ \mathsf{\theta }}_o=\pi$, (2) reduces to:

$${\displaystyle \frac{d{t}_o}{d{t}_s}}={\displaystyle \frac{c-v_s}{c-v_o}}$$

(3)

3. Maxwell Wave Equations for Observers

In this section, we introduce how to mathematically transform and solve the Maxwell wave equations for observers in [5].

3.1. Maxwell Wave Equations for Observers

Maxwell’s standard wave equations [1] in a vacuum and charge-free space are:

$${\nabla }^{2}E\left(\mathit{r}, \mathrm{t}\right)-{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^2}{\partial t^2}}E\left(\mathit{r}, \mathrm{t}\right)=0$$

(4)

$${\nabla }^{2}B\left(\mathit{r}, \mathrm{t}\right)-{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^2}{\partial t^2}}B\left(\mathit{r}, \mathrm{t}\right)=0$$

(5)

Let’s consider a reference frame that the wave emitter is static to the wave origin, i.e. $v_s=0$. The clock of the wave propagation, i.e. t, is in the same scale as the clock of the light emitter, i.e. $t_s$. (4) can be written as:

$${\nabla }^{2}E\left(\mathit{r},{ \mathrm{t}}_s\right)-{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^2}{\partial t_s^2}}E\left(\mathit{r},{ \mathrm{t}}_s\right)=0$$

(6)

By solving this equation (6), the wave propagation velocity is constant $c$, consistent with Principle 1.

From the perspective of an observer, only the time it detects the light, i.e. $t_o$, can be used to measure the wave propagation. Assume an observer with a velocity $v_o$ along the direction of the wave propagation. From equation (3), since $v_s=0$, we have

$${\displaystyle \frac{d{t}_o}{d{t}_s}}={\displaystyle \frac{c}{c-v_o}}$$

(7)

Substitute $t_s$ with $t_o$ in (6), we have:

$${\nabla }^{2}E\left(\mathit{r},{ \mathrm{t}}_o\right)-{\displaystyle \frac{1}{{\left(c-v_o\right)}^2}}{\displaystyle \frac{{\partial }^2}{\partial t_o^2}}E\left(\mathit{r},{ \mathrm{t}}_o\right)=0$$

(8)

Similarly,

$${\nabla }^{2}B\left(\mathit{r},t_o\right)-{\displaystyle \frac{1}{{\left(c-v_o\right)}^2}}{\displaystyle \frac{{\partial }^2}{\partial t_o^2}}B\left(\mathit{r},{ \mathrm{t}}_o\right)=0$$

(9)

(8), (9) are the Maxwell wave equations as to an observer, which are mathematically equivalent to the original equations, simply in another form using $t_o$ for the observer’s perspective. They are shown covariant for different observer reference frames in [5]. When $v_o=0$, they reduce to the original Maxwell’s equations.

3.2. Solution and Derivation of Classical Doppler Effect

The Doppler effect [2] is the change in frequency of the light to an observer who is moving relative to the light source, which is mathematically derived in [5] from solving Maxwell’s equations for observers (8), (9). The general solution to (8) is a linear superposition of waves of the form. Let

$$E\left(\mathit{r},t_o\right)=g\left(2\pi f_o{t}_o-k•\mathit{r}\right)$$

where $f_o$ is the frequency observed by the observer, $k$ is the wave vector and $k=\left|k\right|$ is the wavenumber. From (8), $f_o,k$ shall satisfy:

$$k^2-{\displaystyle \frac{1}{{\left(c-v_o\right)}^2}}{\left(2\pi f_o\right)}^2=0$$

Hence, the wave propagation speed $c_{so}$ is:

$$c_{so}={\displaystyle \frac{2\pi f_o}{k}}=c-v_o$$

(10)

The observed wave frequency $f_o$ is:

$$f_o=\left(c-v_o\right)*k/2\pi$$

Since the emission wave frequency is $f_s=c\ast k/2\pi$, we have:

$${\displaystyle \frac{f_o}{f_s}}={\displaystyle \frac{c-v_o}{c}}$$

(11)

which is the same formula as the classical Doppler effect.

In summary, the formula of Doppler effect can be mathematically derived from the Maxwell wave equations for observers, which validates its physical correctness.

4. General Maxwell’s Equations for Observers

Now let’s consider the general case that both EM wave emitter and observer are moving. As Doppler effect shows the motion of the emitter also impacts how an observer measures the EM wave. This section will mathematically derive a general Maxwell’s equations for observers, which describe how the motions of emitter and observer impact the measurement of the EM wave.

4.1. General Maxwell’s Equations for Observers

First, let $\left(\mathit{r},t_s\right)$ be the frame in which the EM wave emitter always stays in the center. Assuming ${\mathit{v}}_{\mathit{o}}\left(t\right),{\mathit{v}}_{\mathit{s}}\left(t\right)$ are constant ${\mathit{v}}_{\mathit{o}},{\mathit{v}}_{\mathit{s}}$, we define:

$${\mathit{r}}^{\prime }=\mathit{r}-{\mathit{v}}_{\mathit{s}}{t}_s,t^{\prime }=t_s,$$

(12)

and transfer to a new frame $\left({\mathit{r}}^{\prime },t^{\prime }\right)$, in which the light origin is static. Hence, in this frame, the original Maxwell’s equations apply:

$${\nabla }^2\mathrm{E}\left({\mathbf{r}}^{\prime },{\mathrm{t}}^{\prime }\right)-{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^2}{\partial {{\mathrm{t}}^{\prime }}^2}}\mathrm{E}\left({\mathbf{r}}^{\prime },{\mathrm{t}}^{\prime }\right)=0$$

(13)

It follows:

$${\nabla }^2\mathrm{E}\left(\mathit{r}-{\mathit{v}}_{\mathit{s}}{\mathrm{t}}_s,{ \mathrm{t}}_{\mathrm{s}}\right)-{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^2}{\partial t_s^2}}\mathrm{E}\left(\mathit{r}-{\mathit{v}}_{\mathit{s}}{\mathrm{t}}_s,{ \mathrm{t}}_{\mathrm{s}}\right)=0$$

(14)

We have:

$${\nabla }^2\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{s}}\right)-{\displaystyle \frac{1}{c^2}}\left({\displaystyle \frac{{\partial }^2}{\partial t_s^2}}\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{s}}\right)-2\left({\mathit{v}}_{\mathit{s}}·\nabla \right){\displaystyle \frac{\partial }{\partial t_s}}\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{s}}\right)+\left(v_s·\nabla \right)\left(v_s·\nabla \right)\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{s}}\right)\right)=0$$

(15)

Substitute $t_s$ with $t_o$ using $\left(2\right)$,we have:

$$\left(c^2{\nabla }^2-\left({\mathit{v}}_{\mathit{s}}·\nabla \right)\left(v_s·\nabla \right)\right)\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{o}}\right)+2{\displaystyle \frac{c-v_s\cos {\theta }_s}{c+v_o\cos {\theta }_o}}\left({\mathit{v}}_{\mathit{s}}·\nabla \right){\displaystyle \frac{\partial }{\partial t_o}}\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{o}}\right)-{\displaystyle \frac{{\left(c-v_s\cos {\theta }_s\right)}^2}{{\left(c+v_o\cos {\theta }_o\right)}^2}}{\displaystyle \frac{{\partial }^2}{\partial t_o^2}}\mathrm{E}\left(\mathit{r},{ \mathrm{t}}_{\mathrm{o}}\right)=0$$

(16)

(16) is the general form of Maxwell’s equations for observers. Similarly, we can get the same wave equation for the magnetic field $B\left(\mathit{r}, \mathrm{t}\right)$.

4.2. Principle of Constancy of the Velocity of Light

Consider the simpler case where a polarized uniform plane wave propagates along the x direction, and ${\theta }_s=0,{ \theta }_o=\pi .$ (16) becomes:

$${\displaystyle \frac{c+v_s}{c-v_s}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}\mathrm{E}\left(x,{\mathrm{t}}_{\mathrm{o}}\right)+{\displaystyle \frac{2v_s}{\left(c-v_s\right)\left(c-v_o\right)}}{\displaystyle \frac{{\partial }^2}{\partial x\partial {\mathrm{t}}_o}}\mathrm{E}\left(x,{\mathrm{t}}_{\mathrm{o}}\right)-{\displaystyle \frac{1}{{\left(c-v_o\right)}^2}}{\displaystyle \frac{{\partial }^2}{\partial t_o^2}}\mathrm{E}\left(x,{\mathrm{t}}_{\mathrm{o}}\right)=0$$

(17)

The general solution to (16) is a linear superposition of waves. Let the solution be:

$$E\left(x,t_o\right)=g\left(2\pi f_o{t}_o-kx\right)$$

From (16), $f_o,k$ shall satisfy:

$$\left({\displaystyle \frac{c+v_s}{c-v_s}}k+{\displaystyle \frac{2\pi f_o}{c-v_o}}\right)\left(k-{\displaystyle \frac{2\pi f_o}{c-v_o}}\right)=0$$

We have:

$$c_{so}={\displaystyle \frac{2\pi f_o}{k}}=c-v_o$$

(18)

It is important to note that (17) shows the EM wave speed to any observer is independent of the motion of emitter $v_s$, which clearly demonstrates the principle of constancy of the velocity of light [4].

Further note that $c_{so}$ in (17) is for one-way, which currently is considered un-measurable. The round way light speed can be calculated as:

$$c_{so}={\displaystyle \frac{2}{\frac{1}{c-v_o}+\frac{1}{c+v_o}}}=c\ast \left(1-{\displaystyle \frac{v_o^2}{c^2}}\right)$$

Hence, the round-trip light speed always approximates $c$ if $v_o\ll c$, which is consistent with experiments.

4.3. Derivation of Doppler Effect

From (17), we have the observed wave frequency $f_o$ as:

$$f_o=\left(c-v_o\right)\ast k/2\pi$$

(19)

To get the emission wave frequency $f_s$, we need to use the equation (15) with emission timing $t_s$, which can be written as:

$$\left(c^2-v_s^2\right){\displaystyle \frac{{\partial }^2}{\partial x^2}}\mathrm{E}\left(x,{\mathrm{t}}_{\mathrm{s}}\right)+2v_s{\displaystyle \frac{{\partial }^2}{\partial x\partial {\mathrm{t}}_s}}\mathrm{E}\left(x,{\mathrm{t}}_s\right)-{\displaystyle \frac{{\partial }^2}{\partial t_s^2}}\mathrm{E}\left(x,{\mathrm{t}}_s\right)=0$$

(20)

Solving (20) similarly, we have:

$$\left(\left(c+v_s\right)k+2\pi f_s\right)\left(\left(c-v_s\right)k-2\pi f_s\right)=0$$

Hence,

$$f_s=\left(c-v_s\right)\ast k/2\pi$$

(21)

Finally, combine (19) and (21) and we have:

$${\displaystyle \frac{f_o}{f_s}}={\displaystyle \frac{c-v_o}{c-v_s}}$$

(22)

So, we mathematically derived the same formula of traditional Doppler effect from the solution of the general form of Maxwell’s equations.

4.4. Reduced Forms and Solutions in Special Cases

The general Maxwell’s equations for observers (17) are mathematically transformed from the original equations. So, they are mathematically equivalent, and the general form reduces to the original form when $v_s$=$v_o$=0. Table 1 lists the reduced form and solution of Maxwell’s equations in some exemplary special cases.

In scenario 2, $v_s\ne$0 $v_o$=0, the solution shows that the EM wave speed is constant $c$ independent of the motion of the emitter, i.e. $v_s$, which is consistent with the principle of constancy of the velocity of light.

In scenario 3, $v_s$= $v_o\ne$0, i.e. the emitter and observer are relatively static, the solution shows there is no Doppler effect, which is consistent with experiment.

Currently, many formulas are required to describe Doppler effect in different scenarios, for example, the scenario of moving emitter requires a different formula than the scenario of moving observer. But this general Maxwell’s equations provide a unified solution that is consistent with experiments in all scenarios.

4.5. Derivation of Sagnac Effect

The Sagnac effect [10] shows that two light beams, sent clockwise and counterclockwise around a closed path on a rotating disk, take different time intervals to travel the path, which contradicted the assumption that the light velocity is independent of the motion of the observer. Special Relativity attributed this contradiction to the rotating/accelerating frame [4,16]. Sagnac effect can be extended to a FOG [11] with

$$\Delta t\approx 2vL/c^2$$

(23)

where $v$ is the detector speed, $L$ is the path length.

The phase variation $\phi$ of a light wave over the propagation path is given by:

$$\phi =k\ast L$$

(24)

where $k$ is the wave number. Use + and – distinguish the two light beams, we have the phase difference in the interferometer as:

$$\Delta \phi =\left(k^{+}-k^{-}\right)\ast L$$

(25)

From (19), it follows that:

$$\Delta \phi =\left({\displaystyle \frac{2\pi f_o^{+}}{c-v_o^{+}}}-{\displaystyle \frac{2\pi f_o^{-}}{c-v_o^{-}}}\right)\ast L$$

(26)

Since this is the scenario3 in Table 1,

$$f_o^{+}=f_o^{-}=f_s$$

We have:

$$\Delta \phi =2\pi f_s{\displaystyle \frac{\left(v_o^{+}-v_o^{-}\right)L}{\left(c-v_o^{+}\right)\left(c-v_o^{-}\right)}}$$

(27)

Since $v_o^{+}-v_o^{-}=2v$, hence

$$\Delta \phi =2\pi f_s{\displaystyle \frac{2vL}{\left(c-v_o^{+}\right)\left(c-v_o^{-}\right)}}\approx 2\pi f_s{\displaystyle \frac{2vL}{c^2}}$$

(28)

Since $\Delta t=\Delta \phi /2\pi f_s$, finally we have:

$$\Delta t\approx {\displaystyle \frac{2vL}{c^2}}$$

(29)

which is the same formula of Sagnac effect as (23). So, we mathematically derived the same formula of Sagnac effect from the solution of Maxwell’s equations.

5. Conclusion

Maxwell’s equations in traditional form describe EM wave from the propagation perspective, where the time $\mathrm{t}$ represents the propagation clock. Through mathematical transformation, a general form of Maxwell’s equations is derived to describe the EM wave from observer’s perspective by incorporating the time-scaling factor, i.e. using each observer’s own clock ${\mathrm{t}}_o$. The traditional form is just a special case when static. The solution of this general form of Maxwell’s equations is consistent with all established experiments. The formulas of classical and transverse Doppler effect and Sagnac effect can be directly derived from the solution, further confirming its physical validity. This result offers a comprehensive perspective of EM phenomena for both propagation and observers. One application is to predict the measurement of EM waves by a moving observer, say radar, and leverage it to improve design and performance.