Theoretical WIMP-Nucleus Scattering Rates For Isomeric Nuclei

John Demetrios Vergados; Dennis Bonatsos

doi:10.20944/preprints202408.0035.v1

Preprint

Article

Theoretical WIMP-Nucleus Scattering Rates For Isomeric Nuclei

This version is not peer-reviewed.

John Demetrios Vergados^*,

Dennis Bonatsos

John Demetrios Vergados^*,

Dennis Bonatsos

This version is not peer-reviewed.

Downloads

Views

Comments

Submitted:

30 July 2024

Posted:

01 August 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

The direct detection of dark matter constituents, in particular the weakly interacting massive particles (WIMPs), is central to particle physics and cosmology. In this paper we develop the formalism for WIMP-Nucleus induced transitions from isomeric nuclear states. We specialize it in the case of the experimentally interesting target 180 Ta

Keywords:

Dark matter

;

Isomeric Nuclei

;

Nuclear structure models and methods

;

Shell model

;

Collective models

;

Nilsson Model

Subject:

Physical Sciences - Nuclear and High Energy Physics

1. Introduction

At present there exists plenty of evidence of the existence of dark matter i) from cosmological observations, DASI [1], COBE/DMR Cosmic Microwave Background (CMB) observations [2] as well as the recent WMAP [3] and Planck [4] data. It is, however, essential to directly detect such matter in order to unravel the nature of its constituents.

At present there exist many such candidates, called Weakly Interacting Massive Particles (WIMPs).

WIMP direct searches have been performed by exploiting WIMP-Nucleus elastic scattering, see, e.g., the collaborations PandaX-II [5], XENONIT [6,7] and CDMSLite [8]. No WIMPs have been directly detected, but quite stringent exclusion limits have been extracted for the WIMP-Nucleon scattering cross section vs dark matter mass, see, e.g., the recent review [9].

Spin dependent WIMP-nucleon interactions can lead to inelastic WIMP-nucleus scattering with a non negligible probability, provided that the energy of the excited state is sufficiently low. So, for sufficiently heavy WIMPs, the available energy via the high velocity tail of the M-B distribution maybe adequate to allow scattering to low lying excited states of of certain targets, e.g. of

57.7

keV for the

7 / 2^{+}

excited state of

^{127}

I, the 39.6 keV for the first excited

3 / 2^{+}

^{129}

Xe, the 35.48 keV for the first excited

3 / 2^{+}

state of

^{125}

Te and the 9.4 keV for the first excited

7 / 2^{+}

state of

^{83}

Kr . In fact calculations of the event rates for the inelastic WIMP-nucleus transitions involving the above systems have been performed [10].

The interest in the inelastic WIMP-nucleus scattering has recently been revived by a new proposal of searching for the collisional de-excitation of metastable nuclear isomers [11]. The longevity of these isomers is related to a strong suppression of

γ

and

β

-transitions, typically inhibited by a large difference in the angular momentum for the nuclear transition. The collisional de-excitation by dark matter is possible since heavy dark matter particles can have a momentum exchange with the nucleus comparable to the inverse nuclear size. In fact the transition can lead to the ground sate or a lower excited state. In the latter case one may detect the

γ

ray following the de-excitation of the final state, thus providing an extra signature against background.

2. Expressions for the Cross Section

The evaluation of the differential rate for a WIMP induced transition

A_{i s o}^{i} (E_{x})

for an isomeric nuclear state at excitation energy

E_{x}

to another one

A_{i s o}^{f} (E_{x}^{'})

(or to the ground state) proceeds in a fashion similar to that of the standard inelastic WIMP induced transition, except that the kinematics is different. We will make a judicious choice of th final nuclear state that it can decay in a standard way to the ground state or to another lower excited state:

A_{i s o}^{i} (E_{x}) + χ \to A_{i s o}^{f} (E_{x}^{'}) + χ

(1)

with

χ

the dark matter particle (WIMP. )Assuming that all particles involved are non relativistic we get:

\frac{p_{χ}^{2}}{2 m_{χ}} + E_{x} = \frac{p_{χ}^{' 2}}{2 m_{χ}} + E_{x}^{'} + \frac{q^{2}}{2 m_{A}}

(2)

where

q

is the momentum transfer to the nucleus

q = p_{χ} - p_{χ}^{'}

. So the above equation becomes

\frac{- q^{2}}{2 μ_{r}} + υ ξ q - Δ = 0, Δ = E_{x} - E^{'} x \Leftrightarrow - \frac{m_{A}}{μ_{r}} E_{R} + υ ξ \sqrt{2 m_{A} E_{R}} + Δ = 0, Δ > 0

(3)

Where

ξ

is the cosine of the angle between the incident WIMP and the recoiling nucleus,

υ

the oncoming WIMP velocity,

E_{R}

the nuclear recoil energy and

μ_{r}

the reduced mass of the WIMP-nucleus system , i.e.

\frac{1}{μ_{r}} = \frac{1}{m_{χ}} + \frac{1}{m_{A}} .

(4)

The differential cross section is given by

d σ = \frac{1}{υ} \frac{1}{{(2 π)}^{2}} d^{3} q δ (\frac{q^{2}}{2 μ_{r}} - q υ ξ - Δ) {(\frac{G_{F}}{\sqrt{2}})}^{2} {| M E (q^{2}) |}^{2}

(5)

where

{| M E (q) |}^{2}

is the nuclear matrix element of the WIMP-nucleus interaction in dimensionless units and

G_{F}

the standard weak interaction strength.

We find it convenient to express it in terms of the nucleon cross section so that our results are independent of the scale parameters

f_{V}

and

f_{A}

. The total WIMP-nucleon cross section can easily be obtained (see the Appendix I of ref. [12]). Thus Equation (5) can be cast in the form:

d σ = Λ \frac{σ_{N}}{m_{N}^{2}} \frac{1}{υ} \frac{1}{{(2 π)}^{2}} d^{3} q δ (\frac{q^{2}}{2 μ_{r}} - q υ ξ - Δ) \frac{| M E (q^{2}) |^{2} |}{f_{V}^{2} + 3 f_{A}^{2}}, Λ = \frac{2 π}{4}

(6)

Folding Equation (6) with the velocity distribution we find1

\begin{matrix} \frac{1}{υ_{0}} \frac{1}{σ_{N}} 〈 υ \frac{d σ}{d E_{R}} 〉 = & Λ \frac{m_{A}}{m_{N}^{2}} \frac{1}{υ_{0}} \frac{1}{2 π} \frac{| M E (q^{2}) |^{2}}{f_{V}^{2} + 3 f_{A}^{2}} \\ [(Θ (Δ - \frac{M_{A} E_{R}}{μ_{r}})) \int_{υ_{1}}^{υ_{e s c}} K (υ) d υ + (Θ (- Δ + \frac{M_{A} E_{R}}{μ_{r}})) \int_{υ_{2}}^{υ_{e s c}} K (υ) d υ] \end{matrix}

(7)

where

E_{R}

is the nuclear recoil energy,

Θ

is the step function and

K (υ)

given by the velocity distribution

K (υ) = \int d Ω (\hat{υ}) υ f_{d i s t r} (v)

(8)

Furthermore

υ_{1} = \frac{1}{q} (Δ - \frac{q^{2}}{2 μ_{r}}), υ_{2} = \frac{1}{q} (\frac{q^{2}}{2 μ_{r}} - Δ)

(9)

Note the dependence of the cross section on the recoil energy comes in two ways: i) From the nuclear form factor and ii) from the minimum required velocities

υ_{1}

and

υ_{2}

in the folding with the velocity distribution.

We will specialize our results in the commonly used Maxwell- Boltzmann (MB) distribution in the local frame [12]. The integrals involved can by computed analytically

\begin{matrix} \frac{1}{υ_{0}} \frac{1}{σ_{N}} 〈 υ \frac{d σ}{d E_{R}} 〉 = & Λ \frac{m_{A}}{m_{N}^{2}} \frac{1}{υ_{0}^{2}} \frac{1}{2 π} \frac{| M E (q^{2}) |^{2} |}{f_{V}^{2} + 3 f_{A}^{2}} \\ [(Θ (Δ - \frac{M_{A} E_{R}}{μ_{r}})) ψ_{1} (y_{1}, y_{e s c}) + (Θ (- Δ + \frac{M_{A} E_{R}}{μ_{r}})) ψ_{2} (y_{2}, y_{e s c})] \end{matrix}

(10)

where

\begin{matrix} ψ_{1} (y_{1}, y_{e s c}) = & \frac{1}{4} \sqrt{π} (\erf (1 - y_{1}) + \erf (y_{1} + 1)) - \frac{1}{4} \sqrt{π} (\erf (1 - y_{e s c}) + \erf (y_{e s c} + 1)), \\ ψ_{2} (y_{2}, y_{e s c}) = & \frac{1}{4} \sqrt{π} (\erf (1 - y_{2}) + \erf (y_{2} + 1)) - \frac{1}{4} \sqrt{π} (\erf (1 - y_{e s c}) + \erf (y_{e s c} + 1)) \end{matrix}

(11)

where

e r f (z) = \frac{2}{\sqrt{π}} \int_{0}^{z} E^{- t^{2}} d t (error function)

The functions

ψ_{i} (y_{i}, y_{e s c})

depend on the momentum transfer. This depends on the specific nuclear target and will be discussed below.

3. Nuclear Structure

The isomeric nuclei are deformed and have complicated structure. So the usual technics employed in obtaining the structure of atomic nuclei terms of the spherical shell model do not apply. We find it simple and appropriate to use the Nilsson model in which a cylindrical harmonic oscillator is used instead of a spherical one, characterized by a deformation

ϵ

, reflecting the departure of the cylindrical shape from sphericity. The single particle orbitals in the Nilsson model are labeled by

Ω [N n_{z} Λ]

, where N is the total number of the oscillator quanta,

n_{z}

is the number of quanta along the z-axis of cylindrical symmetry, while

Λ

(

Ω

) is the projection of the orbital (total) angular momentum on the z-axis.

In what follows it will be of interest to consider the expansions of the Nilsson orbitals in the spherical shell model basis

| N l j Ω 〉

, where N is the principal quantum number, l (j) is the orbital (total) angular momentum, and

Ω

is the projection of the total angular momentum on the z-axis. The necessary expansions have been obtained as described in Ref. [13] and are found found in the Append IV of ref. [12] for three different values of the deformation

ϵ

4. The Nucleus $^{180}$ Ta

This nucleus is preferred for experimental reasons. The even-even core of

_{73}^{180}

_{107}

_{72}^{178}

_{106}

, for which the experimental value of the collective deformation variable

β

is 0.2779 [14], thus the Nilsson deformation

ϵ = 0.95 β

[15] is 0.2640 .

Several different theoretical calculations, including covariant density functional theory using the DDME2 functional [16,17], Skyrmre-Hartree-Fock-BCS2 [18], as well as a two quasiparticle plus rotor model in the mean field represented by a deformed Woods-Saxon potential [19] agree that the first neutron orbital lying above the Fermi surface of the core nucleus

_{72}^{178}

_{106}

is the 9/2[624] orbital, while the first proton orbital lying above the Fermi surface of the core nucleus

_{72}^{178}

_{106}

is the 9/2[514] orbital. Therefore it is safe to assume that these two orbitals will play a major role in the formation of the

9^{-}

isomer state of

_{73}^{180}

Ta.

It is instructive to consider the formation of the above mentioned states under the light of the expansions of the Nilsson orbitals in terms of spherical shell model orbitals, found in the Append IV of ref. [12].

The orbitals participating in the formation of the

9^{-}

isomer, proton 9/2[514] and neutron 9/2[624], are both intruder orbitals, thus the main contribution comes from the

| 5 5 11 / 2 9 / 2 〉

component of the former and the

| 6 6 13 / 2 9 / 2 〉

component of the latter.

The orbitals participating in the formation of the

2^{+}

excited state are the proton 9/2[514] (intruder) and neutron 5/2[512] (normal parity) orbitals, from which the leading contribution will come from the

| 5 5 11 / 2 9 / 2 〉

and

| 5 3 7 / 2 5 / 2 〉

vectors respectively.

5. Some Features Regarding the Target $^{180}$ Ta

We begin by considering the transition of the isomeric

9^{-}

state to the

2^{+}

state. The momentum dependence of the cross section arising from the velocity distribution for a transition energy is

Δ = 37

keV is given in Figure 1.

To proceed further we need to determine the structure of the target

^{180}

Ta. As explained in Section 4 in the context of the Nilsson model we can consider the proton orbital

\frac{9}{2}

[514] both in the initial state

9^{-}

and the final

2^{+}

. Furthermore for the neutrons we use

\frac{9}{2}

[624] for the

9^{-}

and the

\frac{5}{2}

[512] for the

2^{+}

. To proceed further we use the expansion of the Nilsson orbitals into shell model states found in Appendix IV of [12] for a deformation parameter 0.30. Note that in this case only the neutrons can undergo transitions, while the protons are just spectators.

5.1. Shell Model Form Factors

The vector and axial vector reduced nuclear matrix elements can be obtained using the standard technics as described in the Appendix II and Appendix III of [12] with the quantities with subscript 1 indicate neutrons and those with 2 are associated with protons. Thus we find:

\begin{matrix} R M E_{V} = & \frac{f_{V}}{f_{A}} (0.0644445 F (4, 3, 7, u) + 1.01419 F (4, 5, 7, u) + 1.01419 F (4, 5, 9, u) + 1.52946 F (6, 3, 7, u) \\ + 1.52946 F (6, 3, 9, u) + 1.52946 F (6, 5, 7, u) + 1.79799 F (6, 5, 9, u) + 2.19718 F (6, 5, 11, u) \end{matrix}

\begin{matrix} R M E_{A} = & 0.321503 F (4, 3, 7, u) + 2.05117 F (4, 5, 7, u) + 2.16715 F (4, 5, 9, u) + 2.04512 F (6, 3, 7, u) \\ + 3.3217 F (6, 3, 9, u) + 2.04512 F (6, 5, 7, u) + 2.31181 F (6, 5, 9, u) + 3.58938 F (6, 5, 11, u) \end{matrix}

In the above expressions

F (ℓ, ℓ^{'}, λ)

are the single particle form factors. The first two integers indicate orbital angular momentum quantum numbers

ℓ, ℓ^{'}

, while the last integer

λ

gives the multipolarity of the transition. The quantity u corresponds to

b_{N} q

, where

b_{N}

is the harmonic oscillator length parameter. The relevant form factors are exhibited in Figure 2(a).

The relevant nuclear ME is given by:

R_{M E}^{2} (q^{2}) = \frac{1}{19} (R M E_{V}^{2} + R M E_{A}^{2})

(12)

Its momentum dependence is exhibited in Figure 3(a). We should note that the large value of the matrix element in the case of large

f_{V}

is due to the normalization adopted to make the matrix element independent of the scale. Recall that a combination factor appear in the cross section. In the present work we will adopt

f_{V} = f_{A}

5.2. Phenomenological Form Factors

It is generally believed that the shell model single particle factors lead to large suppression. So some phenomenological form factors. One example is the the Helm like single particle form factors:

F_{λ} (q) = (2 λ + 1) e^{- \frac{1}{2} a^{2} q^{2}} \frac{j_{λ} (q R)}{q R}

(13)

Our treatment means that the radial integrals are independent of the angular momentum quantum numbers

ℓ, ℓ^{'}

. The obtained results are exhibited in Figure 2(b) (odd (parity changing) transitions are relevant). The reduced matrix elements for the vector and the axial vector are:

\begin{matrix} R M E H_{A} = & 3.58938 F_{11} (a, q, R) + 6.46292 F_{7} + 7.80066 F_{9} (a, q, R) \\ R M E H_{V} = & \frac{f_{V}}{f_{A}} (2.19718 F_{11} (a, q, R) + 4.13756 F_{7} (a, q, R) + 4.34165 F_{9} (a, q, R)) \end{matrix}

(14)

where

F_{λ}

are the Helm single particle form factors. The nuclear matrix element is:

R_{M E H}^{2} (q^{2}) = \frac{1}{19} (R M E H_{V}^{2} + R M E H_{A}^{2})

(15)

The momentum dependence of this ME is exhibited in Figure 3(b) .

5.3. Some Results for $^{180}$ Ta

The numerical value of

Λ \frac{m_{A}}{m_{N}^{2}} \frac{1}{υ_{0}^{2}} \frac{1}{2 π}

in Equation (7) for

f_{A} / f_{V} = 1

, is 0.068 for A=180, expressed in units of keV

^{- 1}

. The plot of for

\frac{1}{υ_{0}} \frac{1}{σ_{N}} 〈 υ \frac{d σ >}{d E_{R}} 〉

vs the previous one multiplied with 0.063. We prefer to express it as a function of

E_{R}

in units of keV, i.e Figure 4(a). It can be shown that a similar expression holds for the rate

\frac{1}{R_{N}} \frac{d R}{d E_{R}}

, see Figure 4(b).

The expressions for

σ

and R for

^{180}

Ta can be obtained using the relevant values for the nucleon (see the Appendix I of ref. [12]):

σ_{N} = 8.8 \times 10^{- 40} {cm}^{2} (f_{V}^{2} + 3 f_{A}^{2})

f_{R} = 2.1 \times 10^{38}

^{- 2}

^{- 1} \frac{m_{N}}{m_{χ}}

(kinematics factor), yielding . This leads to the total rate:

R_{N} = f_{R} σ_{N} = 0.72

^{- 1} (f_{V}^{2} + 3 f_{A}^{2})

For orientation purposes we employ here

f_{V} = f_{A} = 1

One can integrate the differential cross section over the recoil energy

E_{R}

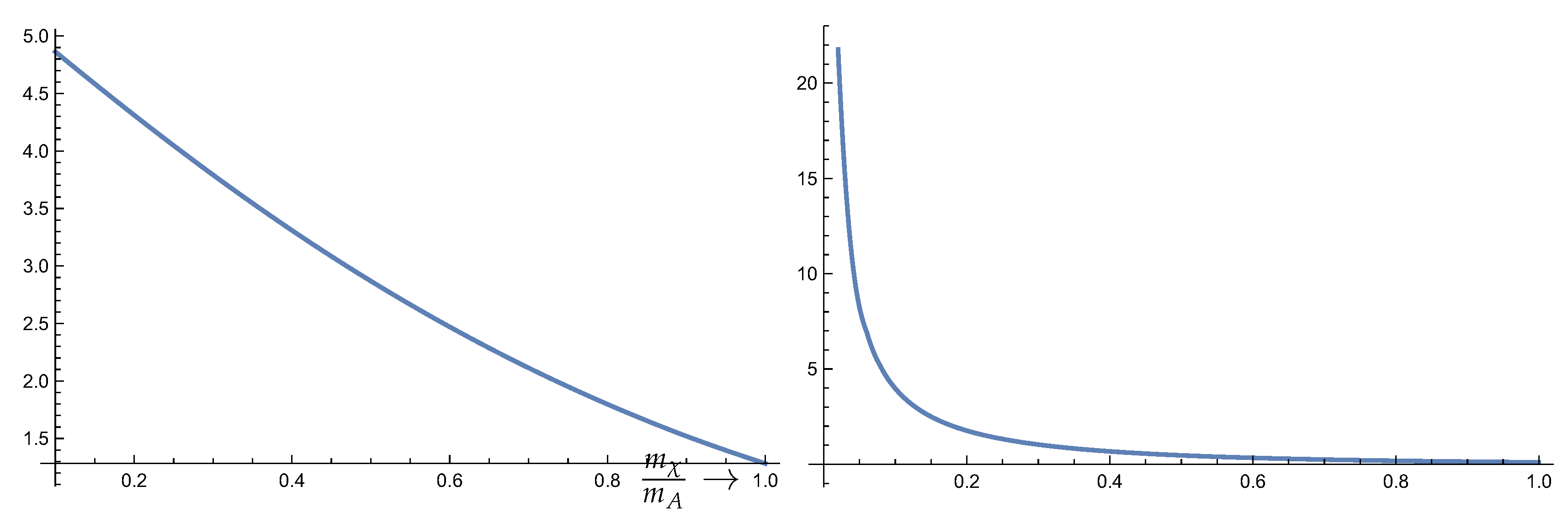
and multiply with the total nucleon to obtain the WIMP-Nucleus cross section as a function of the wimp mass

m_{χ}

this is exhibited in Figure 5(a)

In the same fashion one can obtain differential rate

\frac{1}{R_{N} (m_{χ})} \frac{d R}{d E_{R}}

since the WIMP density used in obtaining the densities is the same. The situation is, however, changed if one is comparing the obtained differential rate relative to the total rate for the nucleon at some fixed value of the WIMP mass. We note that the overall momentum dependence comes by combining the effect of the velocity distribution, see Figure 1, and the momentum dependence of the nuclear matrix element as given by Figure 3(b). The exhibited differential rate contains, of course, the WIMP mass dependence arising from the WIMP density in our galaxy. The thus obtained differential rate in units total rate of the nucleon for

m_{N} / m_{χ} = 1

is exhibited in Figure 4(b).

One can integrate the differential rate over the recoil energy

E_{R}

and multiply with the total nucleon rate to obtain the the total WIMP-Nucleus rate section as a function of the wimp mass

m_{χ}

this is exhibited in Figure 5(b).

6. Discussion

We have seen that, not unexpectedly, the nuclear ME encountered in the inelastic WIMP-nucleus scattering involving isomeric nuclei is much smaller than that involved in the elastic process considered in the standard WIMP searches. This occurs for two reasons: a) the form factor in the elastic being favorable and b) in the elastic case the cross section is proportional to the mass number

A^{2}

. In the present case the nuclear matrix element for

^{180}

Ta, as indicated by the coefficients appearing in Equation (14), is not unusually small compared to other typical inelastic processes. The Nilsson model is expected to work well in the case of

^{180}

Ta, but he obtained event rate is quite small. It seems that the mechanism of suppression encountered in the standard decay of the isomeric state, may somewhat persist in the WIMP-nucleus cross section as well.

The expected events in this work have been obtained with with an unrealistic target mass

10^{24}

particles, compared to more realistic

10^{19}

[12]. On the other hand an estimated half-life time limit is

4.5 \times 10^{16}

years (90% 350 C.L.) [20]. Further improvement can be achieved using in the experiments larger mass of the isomer combined with a better detection efficiency. Furthermore the experiments can exploit the signal provided by the subsequent standard decay of the

2^{+}

state to the ground state. This is an advantage not available in the conventional WIMP searches.

Funding

I would like to thank the organising committee of the Athens "Physics Beyond the Standard Model in Leptonic

Acknowledgments

The author J. D. V is indebted to Rick Casten for useful comments and suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Halverson, N.W.; et al. Degree angular scale interferometer first results: a measurement of the cosmic microwave background angular power spectrum. Astrophys. J. 2002, 568, 38. [Google Scholar] [CrossRef]
Smoot, G.F.; et al. (COBE Collaboration). Structure in the COBE differential microwave radiometer first-year maps. Astrophys. J. 1992, 396, L1–L5. [Google Scholar] [CrossRef]
Spergel, D.N.; et al. Three-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: implications for cosmology. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
Ade, A.P.R.; et al. The Planck Collaboration. arXiv:1303.5076 [astro-ph.CO].
Cui, X.; et al. Dark matter results from 54-ton-day exposure of PandaX-II experiment. Phys. Rev. Lett 2017, 119, 181302. [Google Scholar] [CrossRef] [PubMed]
Aprile, E.; et al. Light dark matter search with ionization signals in XENON1T. Phys. Rev. Lett 2019, 123.25, 251801. [Google Scholar] [CrossRef] [PubMed]
Aprile, E.; et al. Search for light dark matter interactions enhanced by the Migdal effect or Bremsstrahlung in XENON1T. Phys. Rev. Lett 2019, 123, 241803. [Google Scholar] [CrossRef] [PubMed]
Agnese, R.; et al. Search for low-mass dark matter with CDMSlite using a profile likelihood fit. Phys. Rev. D. 2019, 99, 062001. [Google Scholar] [CrossRef]
Arbey, A.; Mahmoudi, F. Dark matter and the early Universe: a review. Progress in Particle and Nuclear Physics CERN-TH-2021-066 2021, 119, 103865. [Google Scholar] [CrossRef]
Vergados, J.D.; et al. Theoretical direct WIMP detection rates for transitions to the first excited state in Kr 83. Phys. Rev. D 2015, 92, 015015. [Google Scholar] [CrossRef]
Pospelov, M.; Rajendran, S.; Ramani, H. Metastable nuclear isomers as dark matter accelerators. Phys. Rev. D 2020, 101, 055001. [Google Scholar] [CrossRef]
Smirnov, M.; Yang, G.; Novikov, Y.; Vergados, J.; Bonatsos, D. Nuc. Phys. B, 1005, 116594 (2024), arXiv:2401.14917.
Bonatsos, D.; Sobhani, H.; Hassanabadi, H. Shell model structure of proxy-SU (3) pairs of orbitals. Eur. Phys. J. 2020, 135, 710. [Google Scholar] [CrossRef]
Pritychenko, B.; Birch, M.; Singh, B.; Horoi, M. At. Data Nucl. Data Tables 109, 1 (2016), erratum: At. Data Nucl. Data Tables 114 - 371 (2017).
Nilsson, S.G.; Ragnarsson, I. Shapes and Shells in Nuclear Structure; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
Bonatsos, D.; Karakatsanis, K.; Martinou, A.; Mertzimekis, T.; Minkov, N. Microscopic origin of shape coexistence in the N=90, Z=64 region. Phys. Lett. B 2022, 829, 137009. [Google Scholar] [CrossRef]
Bonatsos, D.; et al. Islands of shape coexistence from single-particle spectra in covariant density functional theory. Phys. Rev. C 2022, 106.4, 044323, K. E. Karakatsasnis - Private communication.
Minkov, N.; et al. K-isomeric states in well-deformed heavy even-even nuclei. Phys. Rev. C 2022, 105.4, 044329, N. Minkov - Private communication.
Patial, M.; et al. Nonadiabatic quasiparticle approach for deformed odd-odd nuclei and the proton emitter 130 Eu. Phys. Rev. C 2013, 88, 054302. [Google Scholar] [CrossRef]
Lehnert, B.; Hult, M.; Lutter, G.; Zuber, K. Physical Review C 95, 04436 (2017), iSSN 2469-9993, URL http://dx.doi.org/ 526.

1	The factor $\frac{1}{υ_{0}}$ , with dimension of inverse velocity, was introduced for convenience. A compensating factor $υ_{0}$ will be used in multiplying the particle density obtaining the flux. Thus we get the traditional formulas, flux=particle density × velocity and rate= flux × cross section.
2	see also N. Minkov, private communication.

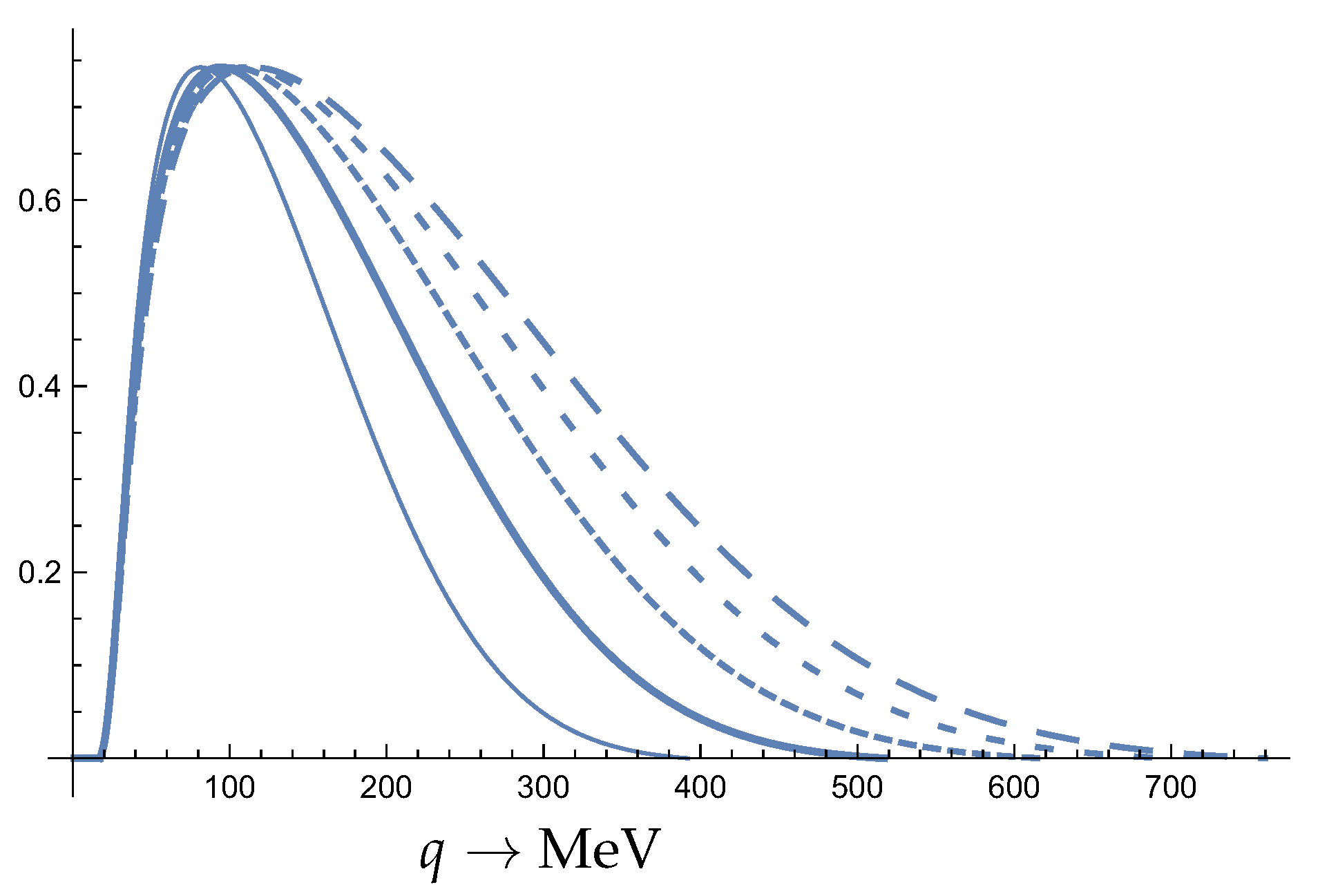
Figure 1. The allowed momentum distribution arising the maximum allowed velocity (escape velocity) of the distribution, in the case of

^{180}

Ta. The fine solid line, the thick solid line, short dash, short long dash, and long dash correspond to the WIMP masses

m_{χ} = (0.1, 0.5, 1, 2, 5) m_{A}

. The transition energy is

Δ = 37

keV.

Figure 1. The allowed momentum distribution arising the maximum allowed velocity (escape velocity) of the distribution, in the case of

^{180}

Ta. The fine solid line, the thick solid line, short dash, short long dash, and long dash correspond to the WIMP masses

m_{χ} = (0.1, 0.5, 1, 2, 5) m_{A}

. The transition energy is

Δ = 37

keV.

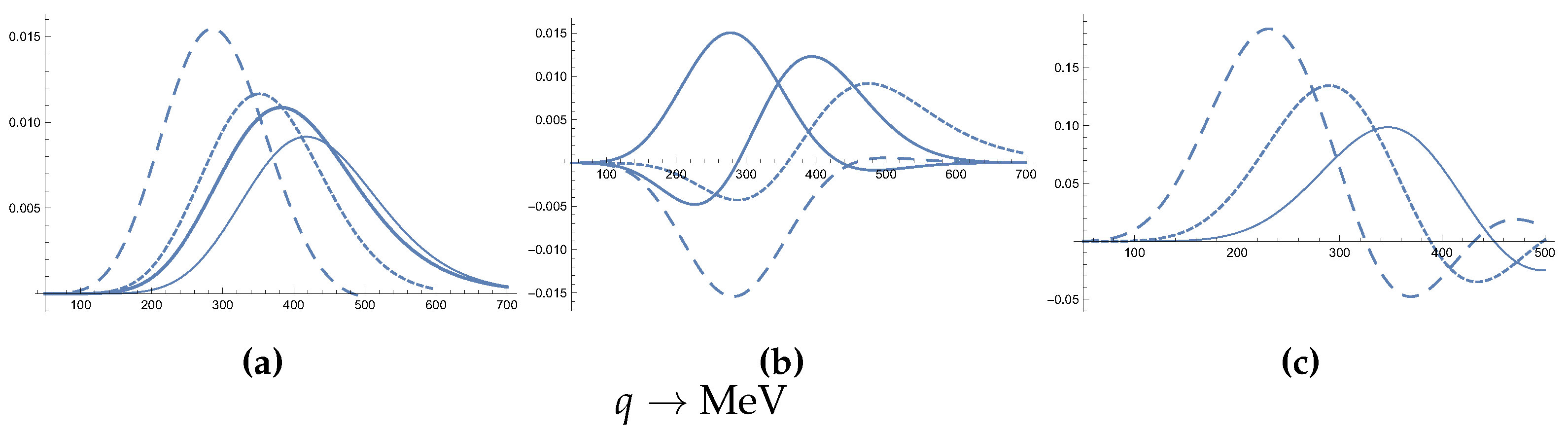
Figure 2. The shell model form factors (a) for F(6,5,7,u), F(6,5,9,u), F(6,5,11,u) and F(6,3,9,u) are exhibited with long dashed, short dashed, fine solid and thick solid lines respectively (b) The form factors F(6,3,7,u), F(4,5,7,u), F(4,5,9,u) and F(4,3,7,u) correspond to long dashed, short dashed, fine solid and thick solid curves respectively. (c) The Helm type form factors, relevant for the target

^{180}

Ta, for

λ = 7

λ = 9

and

λ = 11

for short dashed, long dashed and continuous curves respectively. These are relevant for the target

^{180}

Ta.

^{180}

Ta, for

λ = 7

λ = 9

and

λ = 11

for short dashed, long dashed and continuous curves respectively. These are relevant for the target

^{180}

Ta.

Figure 3. The momentum dependence of the expression

R_{M E}^{2} (q^{2})

for the target

^{180}

Ta is exhibited. The case

f_{V} = f_{A}

corresponds to a solid line, while

f_{V} = 0

and

f_{V} = \sqrt{3} f_{A}

correspond to to a short dashed and a long dashed line respectively (a) obtained with shell model form factors and (b) using the Helm type form factors. It is clear that the last form factors lead to a much larger contribution.

Figure 3. The momentum dependence of the expression

R_{M E}^{2} (q^{2})

for the target

^{180}

Ta is exhibited. The case

f_{V} = f_{A}

corresponds to a solid line, while

f_{V} = 0

and

f_{V} = \sqrt{3} f_{A}

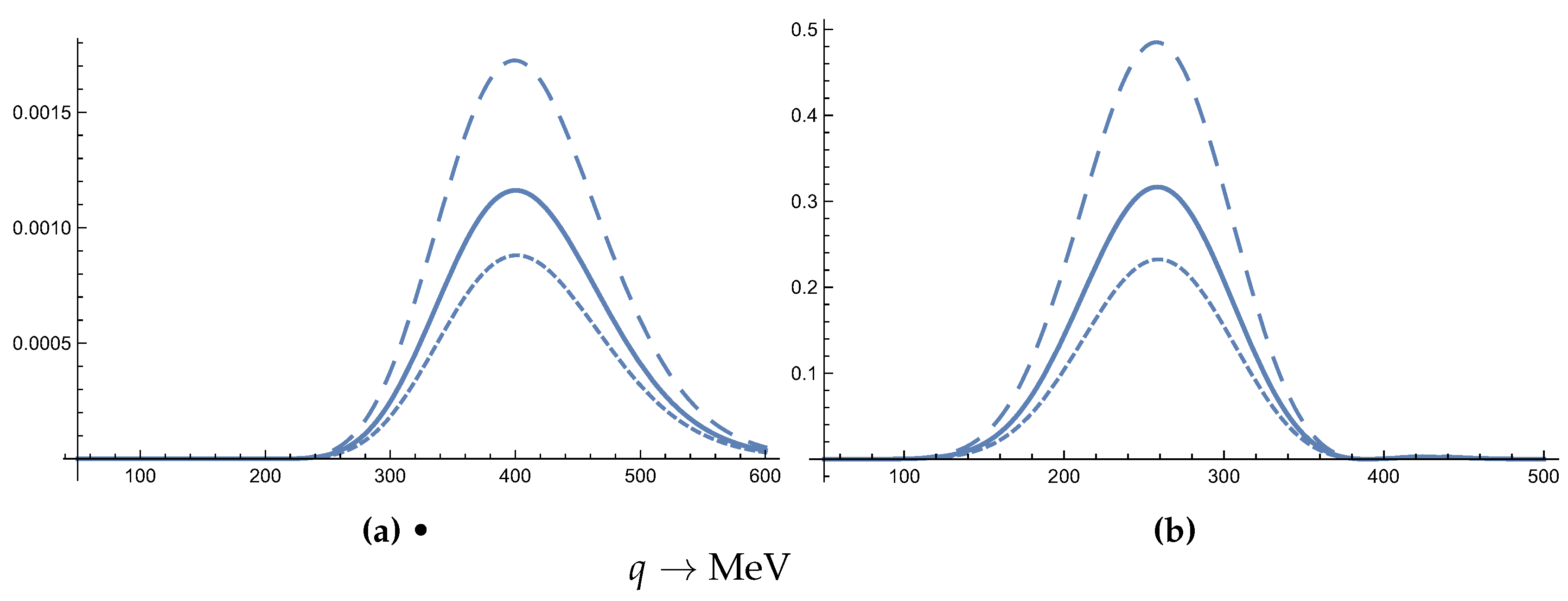
Figure 4. (a)The function

\frac{1}{υ_{0}} \frac{1}{σ_{N}} 〈 υ \frac{d σ >}{d E_{R}} 〉

in units of keV

^{- 1}

in the case of the target

^{180}

Ta. (b) The differential rate relative to the total nucleon rate (for

m_{χ} = m_{N}

\frac{1}{R_{N} (m_{χ} = m_{N})} \frac{d R}{d E_{R}}

, in units of keV

^{- 1}

for the Ta target. The long dashed curve in the drawing has been reduced by a factor of 5, so the related rate must be multiplied by 5. The labeling of the curves is the same as in Figure 1. The Helm type form factor has been employed.

Figure 4. (a)The function

\frac{1}{υ_{0}} \frac{1}{σ_{N}} 〈 υ \frac{d σ >}{d E_{R}} 〉

in units of keV

^{- 1}

in the case of the target

^{180}

Ta. (b) The differential rate relative to the total nucleon rate (for

m_{χ} = m_{N}

\frac{1}{R_{N} (m_{χ} = m_{N})} \frac{d R}{d E_{R}}

, in units of keV

^{- 1}

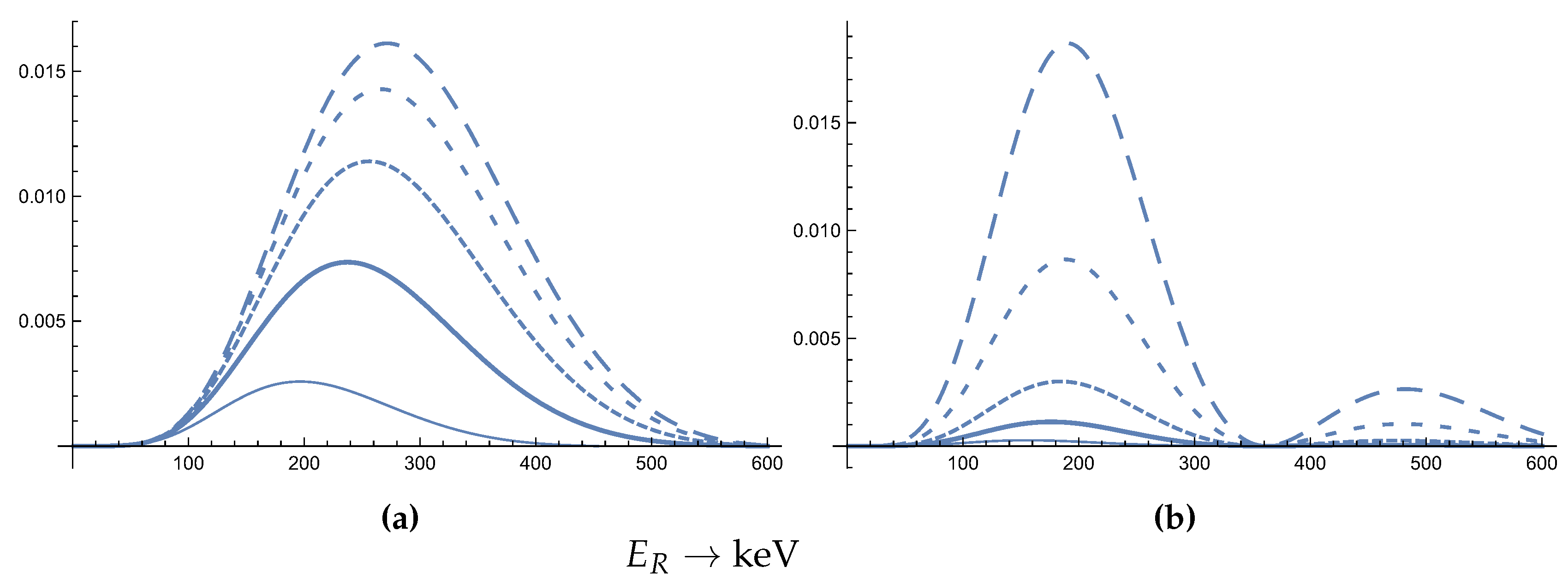
Figure 5. (a)The total WIMP-Nucleus cross section in units of

10^{- 40}

^{2}

in the case of the Ta target as a function of the WIMP mass. (b)The total WIMP-Nucleus event rate in units of y

^{- 1}

in the case of the Ta target as a function of the WIMP mass in units of the nuclear mass

m_{A}

. In evaluating the rate we assumed

10^{24}

nuclei of Ta in the target.

Figure 5. (a)The total WIMP-Nucleus cross section in units of

10^{- 40}

^{2}

in the case of the Ta target as a function of the WIMP mass. (b)The total WIMP-Nucleus event rate in units of y

^{- 1}

in the case of the Ta target as a function of the WIMP mass in units of the nuclear mass

m_{A}

. In evaluating the rate we assumed

10^{24}

nuclei of Ta in the target.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Theoretical WIMP-Nucleus Scattering Rates For Isomeric Nuclei

Abstract

Keywords:

Subject:

1. Introduction

2. Expressions for the Cross Section

3. Nuclear Structure

4. The Nucleus 180 Ta

5. Some Features Regarding the Target 180 Ta

5.1. Shell Model Form Factors

5.2. Phenomenological Form Factors

5.3. Some Results for 180 Ta

6. Discussion

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4. The Nucleus $^{180}$ Ta

5. Some Features Regarding the Target $^{180}$ Ta

5.3. Some Results for $^{180}$ Ta