Prerpints.org logo
Preprint
Review

Significance of Internal Variability for Numerical Experimentation and Analysis

Altmetrics

Downloads

100

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 July 2024

Posted:

29 July 2024

You are already at the latest version

Alerts
Abstract
When limited area models of the hydrodynamics of the atmosphere and of the ocean are 1 run over an extended time, variability unrelated to external "drivers" emerge - this variability is 2 colloquially named "hydrodynamical noise" or just "noise". This article summarises what we have 3 learned in the past few years about the properties of such noise, and the implications for numerical 4 experimentation and analysis. The presence of this noise can be identified easily in ensembles of 5 numerical simulations, and it turns out that the intensity of the noise is closely linked to the scale- 6 dependent "memory". At the system level, this "memory" term as given by Hasselmann’s Stochastic 7 Climate model plays a key role. In the case of marginal seas, the process of baroclinic instability 8 modulated by tides and the formation of seasonal thermoclines are significant aspects. Some more 9 general aspects are discussed, such as the applicability of the Stochastic Climate model to systems 10 outside of atmospheric and oceanic dynamics, the irreversibility of tipping points and the challenges 11 of detecting changes beyond a noise level and of the attribution of causes of change.
Keywords: 
Subject: Environmental and Earth Sciences  -   Oceanography

1. Motivation

Ocean variability arises from the external forcing (for example, solar radiation) and internal processes associated with the nonlinearity and multi-scale integrations within the system ([1]). Such variability caused by internal processes is called internal variability, which is intrinsic, unprovoked, and chaotic, and cannot be linked directly to external forcing or the details of the initial state ([2]).To study internal, unprovoked variability in observational data of the atmosphere and ocean weather is difficult; there are baroclinic disturbances in the atmosphere, which are a manifestation of such variability, but that they are really forming spontaneously became clear only when atmospheric models became available in the 1970 for extended simulations allowing the analysis of unprovoked variability; the challenge of how to determine the "noise level" and how to perform statistical tests was introduced by [3,4]. Thus, the recognition of internal variability dates some 50 years back. A nice illustration of the formation of such unprovoked variability is provided by Fischer’s experiment [5] running an aqua-planet experiment initiated at a state of rest, i.e., with zero wind everywhere (see Figure 1). During the first, say, 10 days, the atmosphere remains at a state of rest, but then the general circulation begins to emerge, in particular the baroclinic storms at Northern and Southern Hemisphere mid-latitudes.
Such a recognition for limited area models of the atmospheric dynamics took much longer, because of a tacit understanding that any such possible variability would quickly be wiped out by the continuously updated lateral boundary conditions. However, when eventually ensembles of simulations in the regional model were integrated [6,7], it became quickly clear that relevant intra-ensemble variability would form [8]. The tendency to build internal variability depends on the size of the integration area: in small areas the noise level becomes very small (e.g. [9]); in large areas substantial noise forms, see e.g. [10].
In the ocean, the recognition of internal variability had to wait much longer, until the availability of satellites, which showed this ubiquity of meso-scale eddies and other meso-scale features (Figure 2). Since the early 2000s studies evaluating ensembles of ocean simulations began to be published, and with it the recognition of internal variability formed in the ocean, and not just inherited from the atmosphere: Leading examples were Jochum and Murtugudde [11,12], Arbic [13] or Sèrazin [14]; a first systematic analysis of the formation and of characteristics of internally generated variability in the global ocean was done by Penduff et al. [15].
The question of internal variability in marginal seas was taken up even later, even if the observation of divergent trajectories of tracers was long known (Figure 3). Pioneers were Büchmann and Söderkvist [16], Waldman et al. [17], Tang et al. [18,19], Lin et al. [20,21] and Benincasa et al. [22] using the ensemble framework (see Section 3). Tang demonstrated for the South China Sea that increasing the horizontal spatial resolution leads to the formation of more intrinsic variability and that the external forcing is dominant for large scales, while most of the small scale is internally generated. Lin et al.[21], on the other hand found the tendency to generate internal variability to be dependent on the presence of tides and of a seasonal thermocline - and demonstrated the significance of baroclinic instability in forming noise [23], consistent with the results of Waldman et al. [24]. More on this in Section 3.1.
The concept that climate is not static but rather undergoes variations across all time scales has been recognized for a considerable period, as evidenced by works such as those of Brūckner [26] in 1890 and Mitchell [27] in 1976 (cf. Figure 4). The debate surrounding whether these variations stem from anthropogenic sources, particularly deforestation, or are intrinsic to Earth’s internal processes (referred to as "cosmic" processes), has been ongoing since at least the mid-19th century, if not earlier, extending beyond academic circles to encompass political discourse.
In 1976, Klaus Hasselmann [1] introduced an alternative mechanism, proposing the integration of short-term small-scale weather fluctuations (such as atmospheric storms and oceanic eddies) in systems with significant "memory." This proposition, articulated in his "Stochastic Climate model," among other achievements, ultimately earned him the Nobel Prize in Physics in 2021.
The challenge to "detect" and characterize such "unprovoked variability" and to "attribute" plausible causes and processes for its emergence has persisted to some extent. In the realm of global atmospheric dynamics, detection became straightforward once global general circulation models of the atmosphere could be integrated over extended periods or in ensembles of simulations. Similarly, attribution was relatively uncomplicated, given the recognition of baroclinic instability since the time of Vilhelm Bjerknes [28], .
In contrast, the detection and attribution process for the global ocean occurred much later, coinciding with the availability of eddy-permitting models and high-resolution satellite imagery of the ocean surface. Similar delays were observed in the case of regional atmospheric and oceanic systems, where detection efforts were initially limited. However, pioneers in ocean noise research like Penduff [15] shed light on macro-scale internal variability. Waldman [17] and Lin [23] determined a dominant role of baroclinicity in amplifying small-scale variations to large-scale variability. Nonetheless, other processes may also contribute to the formation of macro-scale noise.
The emergence of macro-scale noise carries three significant implications. The motivation of this article is to illustrate these challenges in Section 4:
  • Firstly, this noise is expected to arise in systems influenced by short-term weather variations, which lack strong damping but possess a robust memory. Such systems are foremost all atmospheric and oceanic hydrodynamical systems with short-term variations related to eddies, internal tides, fronts, and other phenomena. A very different case of such systems encompasses regional morphodynamics, as highlighted by a CNN report1 following a US submarine incident in the South China Sea, which emphasized the ongoing, albeit gradual, changes in the environment and seafloor. This underscores the necessity for continuous bottom contour mapping in the region. Additionally, ecosystem dynamics may also be affected by such noise.
  • Another aspect pertains to the realm of numerical experimentation, where alterations in factors such as parametrizations, boundary conditions, and atmospheric composition are introduced in simulations. In such experiments, appropriately designed ensembles are crucial for estimating the extent of inherent variability, determining whether changes between ensembles can be attributed solely to internal variability, or if external factors play a role (an issue akin to detection) (e.g., [29,30]).
  • The third one is the conventional “detection and attribution” challenge [31] if observed variations may be understood in the framework of internal variability, or if an external factor needs to be determined for explaining the observed change, which brings us back to the initial observations of the need to separate forced and unforced climate variations mentioned in the beginning.

2. The Stochastic Climate Model

The "Stochastic Climate Model" was originally introduced by Klaus Hasselmann [1] in [1], and its applicability was demonstrated by [32,33,34]. Originally, it was quite a challenge to understand the concept, but as people got more used to it, it became really simple. When considering stationary solutions of the dynamics x of a not too non-linear system
d y d t = F ( y )
it may be approximated by a linear stochastic system
d x d t = α × x + ϵ
or
x t + 1 = α × x t + 1 + ϵ t + 1
with a "memory-term" α and a stochastic "forcing" component ϵ t + 1 . This formulation is based on the assumption that the slow part of y, named x, is exposed to the action of the fast components of y which may be summarized as white noise ϵ .
More complex approximations than (2) are of course possible, but (3) named "Ornstein-Uhlenbeck" or "autogressive process of 1st order" (AR-1) have turned out quite successful. For further details, refer to Hasselmann [1] or the textbook [35].
The key parameter in (3) is the memory term α , which controls the time within which a random excursion, excited by ϵ , is decaying. A useful approximation is the lag-1 auto-correlation of x. A larger α goes with a slower decay of the auto-correlation function and with more variance at slow frequencies of the auto-spectrum [35]. For two values of α , namely 0.3 and 0.9, the auto-correlation function as well as the auto-spectra are displayed in Figure 5.
The main message of the Stochastic Climate model is, first, that short-term variability matters for the overall variability, which turns out to be a mixture of more or less sharp spectral peaks related to specific periodic forcing, such as the daily or annual cycles, and the smooth spectrum of random forced variations (as depicted in Mitchell’s sketch, cf. Figure 4), and, second, given the same noise-seeding, a system with a larger memory generates more energetic long-term variability.

3. Noise in Marginal Seas

The work on unprovoked variability in marginal seas is based on work by Chinese students, supervised by Hans von Storch [36] at the Helmholtz-Zentrum HZG in Geesthacht (now hereon).

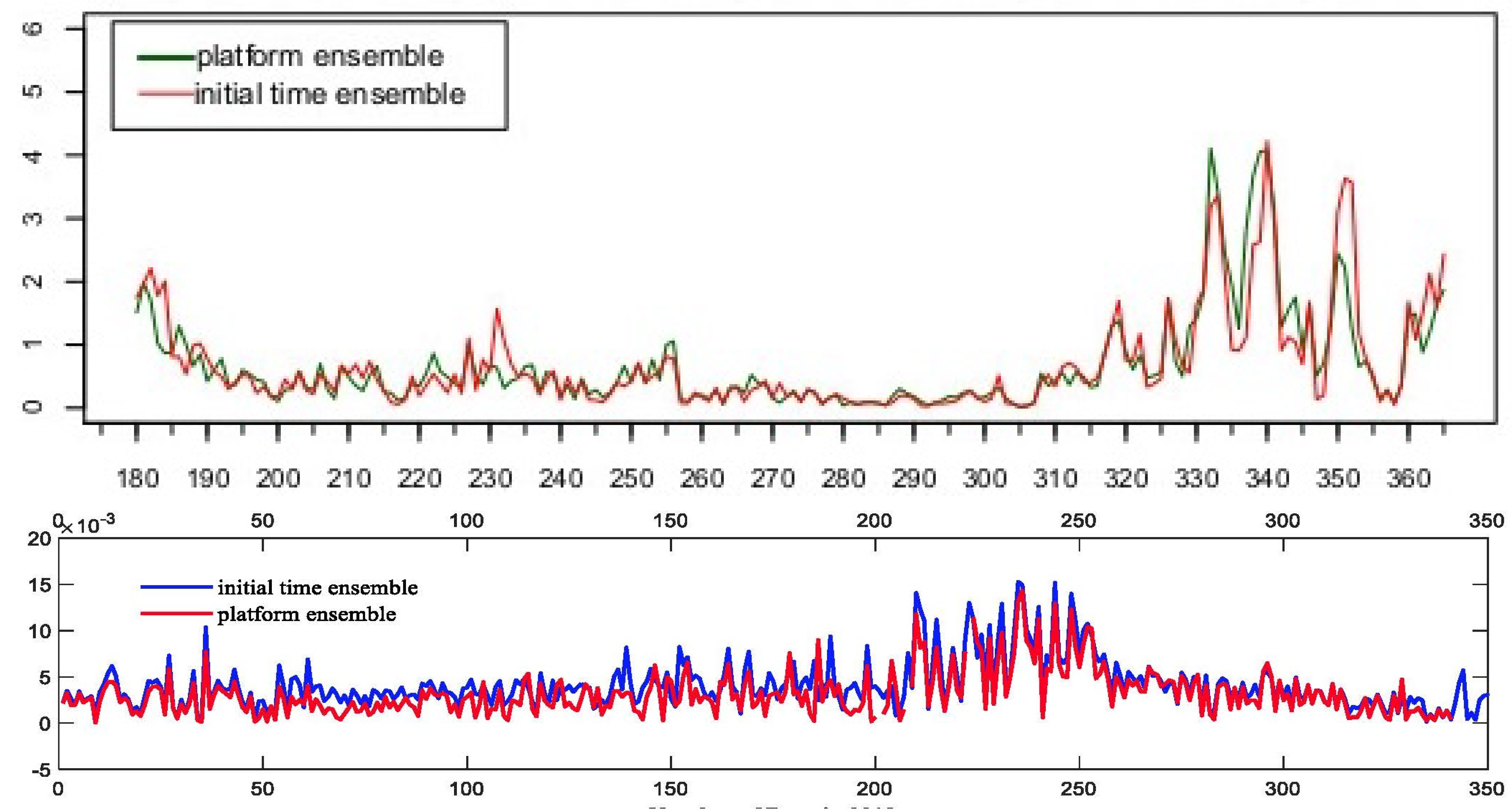
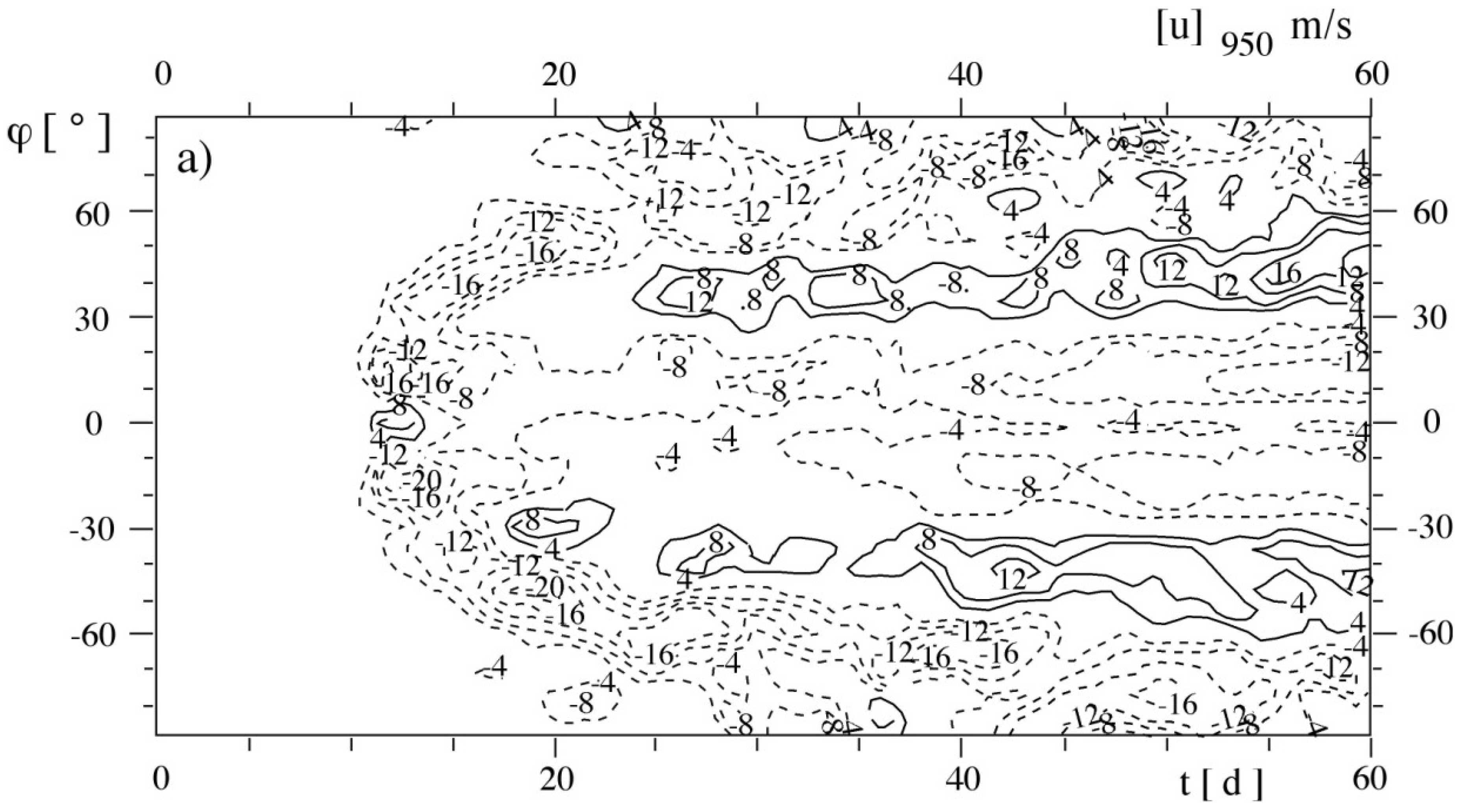
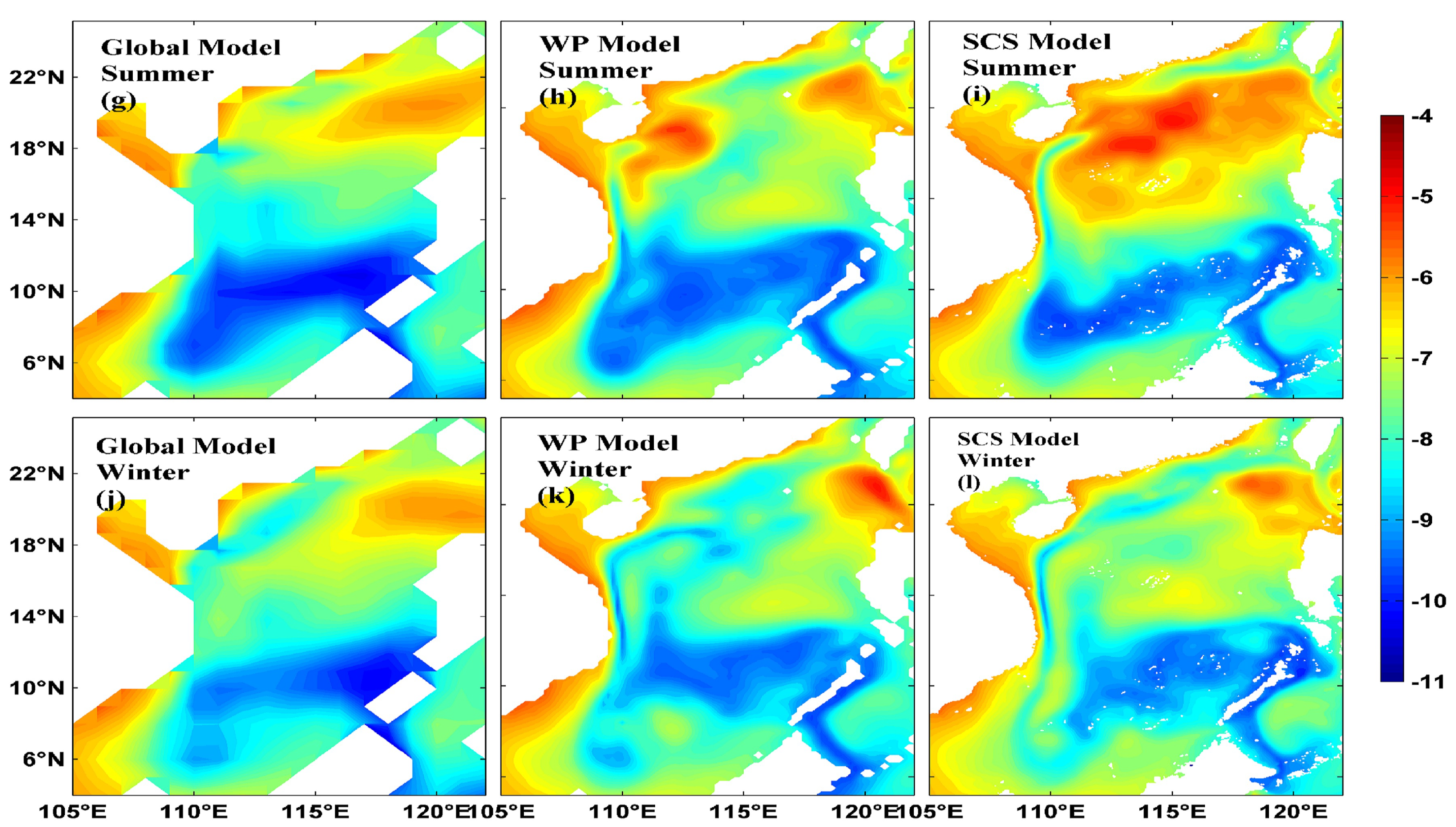
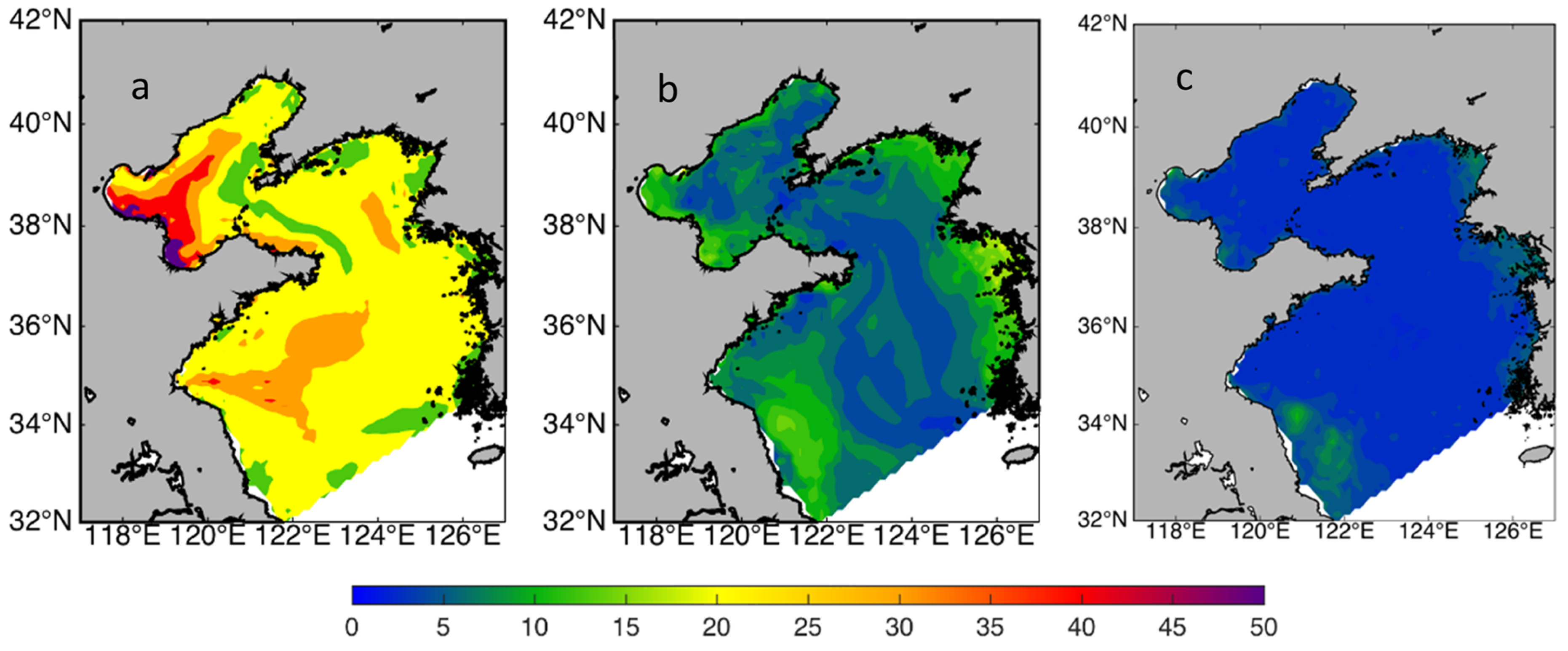
3.1. Emerging Noise in Marginal Seas

It began with the analysis of hydrodynamic variability in the South China Sea. First was Meng Zhang [37], who was tasked with conditioning ocean eddy statistics by the large-scale state of the South China Sea. Analyzing a multi-decadal simulation of a eddy-permitting ocean model of the South China Sea, good statistics of these eddies could be derived, but efforts to condition their statistics failed - the eddy activity turned out mostly a manifestation of internal processes.
Based on this result, then Shengquan Tang [18,19] focused on the internal variability in extended simulation of the hydrodynamics of the South China Sea, its dependency on scales and on the model grid resolution. For doing so, he used a hydrodynamical model of the near global ocean south of 54∘ N and north of 30∘ S with a grid resolution of 1 ∘ , an embedded West Pacific model with a grid resolution of 0.2 ∘ , and an embedded model of the South China Sea with a grid resolution of 0.04 ∘ (see Figure 1 in [18]). For forcing atmospheric fluxes of momentum and of heat were calculated for each calendar month, and averaged across many years. In this way, a climatological forcing was constructed, without weather variation, but with an annual cycle.
Figure 6 demonstrates, first, that there is variability on times scales (of days) without a corresponding forcing, thus internally generated variability. Second the "noise"-level, i.e., the intensity of the unprovoked variability increases with enhanced grid resolution, and third, that at least for the high-resolution model, the noise is larger in summer than in winter, which has been hypothesized as being an effect of the presence of stronger seasonal thermocline [22,38].
The next step in Tang et al.’s analysis [19] was to introduce a method to split the horizontal fields into a series of components associated with spatial scales. To do so, he calculated EOFs from all members of his ensembles of identical simulations, and determined the spatial auto-correlation function of each normalized EOF pattern. The spatial scale was then that length when the auto-correlation calculated jointly of all grid points fell below a certain threshold. It turned out that the lower the EOF index, i.e. the more variance it would represent, the larger the spatial scales (Figure 5 in [19]).
Tang et al. [19] ran ensembles of 4 simulations for the year 2018, with time varying atmospheric surface fluxes. The members of the ensembles were identical apart of the time of initialization and the length of the integration time, which covered the full year 2008 (see Section 3). The EOFs 1-10 were identified as "large", with a spatial scale of 220 km and more, the EOFs 11-50 as "mid-scale" with a middle scale of on-average scale of110 km, and the remaining EOFs with scales of about 30 km as small-scale.
For each of the EOFs, daily times series of principal components are available for the four ensemble members: the daily means across the ensemble, are considered deterministic, while the deviations at each day as noise. The "noise level" is determined as the 2008 time mean of the daily noise, and the "signal" as the standard deviation of the daily means. The signal-to-noise level became smaller and smaller for growing EOF numbers - the internal variability dominates for small scales, while the signal is large only for large scales (see Figure 8 in [19]). Figure 7 shows this for the case of the Bo Hai and Yellow Sea.
The South China Sea is mostly a deep marginal sea; Lin et al. [20] began her work by demonstrating that the results of Tang et al. [18,19] would also apply to the rather shallow Bo Hai and Yellow Sea. We hypothesized that the emergence of internal variability would be strongly damped if tides are active - thus she built ensembles with tides turned on and turned off - and, indeed the noise level was strongly decreased for large- and mid-scale disturbances when the tides are active, while the signal was found to be mostly unchanged.
Already in this first paper by Lin et al. [20] the hypothesis was voiced that this sensitivity of the noise generation may be explained in the framework of the Stochastic climate model (Section 2).
The issue of detecting the emergence of hydrodynamical noise was taken up by Benincasa et al [22] for the case of the Mediterranean Sea. The numerical experiment was in principle the same but it was a different model. The ensemble was much larger. A potentially more significant difference was that the previous model simulations were forced with given fluxes, while Benincasa used fluxes as derived through bulk-formula. It turned out that previously found results were found to be valid also for the Mediterranean Sea. Namely, "Intrinsic variability displayed a distinct seasonal cycle in the surface layers, with a prominent maximum at around 30 m depth during the summer probably connected to the summer thermocline formation processes." [22].

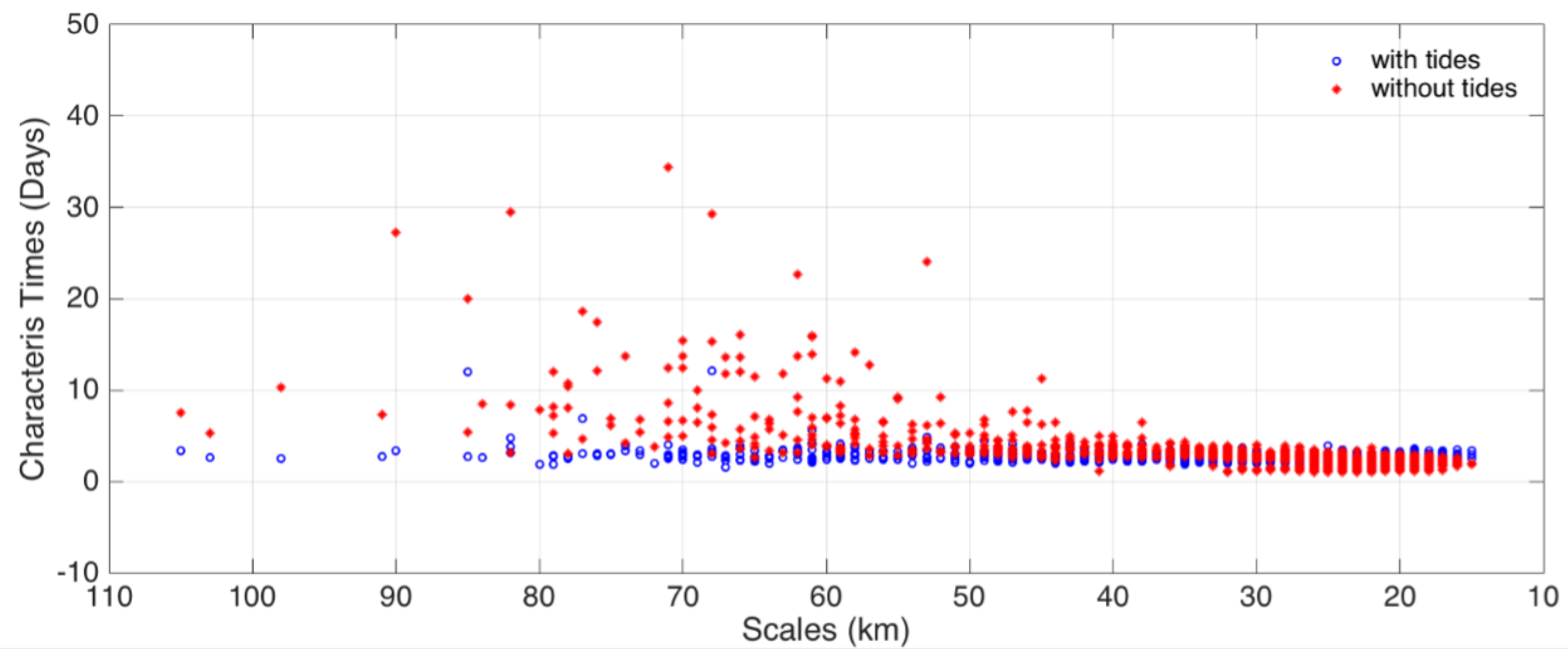
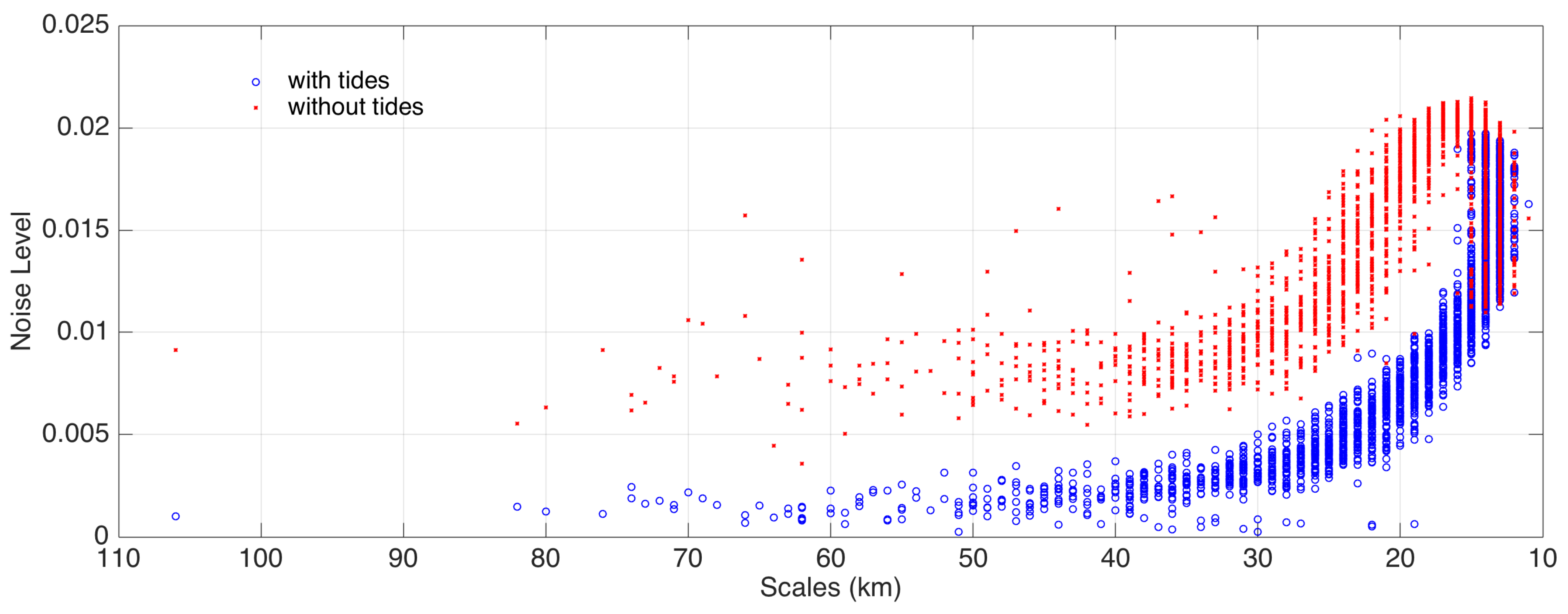
3.2. Sensitivity to Tides and Changing Seasonal Conditions

Lin’s another paper [21] focused on the applicability of the Stochastic Climate Model for understanding the seasonality of the formation of noise, and the sensitivity to the presence of tides. To do so, she derived the memory α (see Section 2) and compared these with the slopes of the auto spectra of noise-variability for each principal component time series.
This study yielded two primary outcomes. Firstly, indications were found of an underlying low-dimensional dynamical core with relatively sluggish fluctuations, which facilitates the transfer of short-term internal variability to longer timescales, in the Bohai and Yellow Sea. This aligns with Hasselmann’s concepts of both the Stochastic Climate model (SCM) and PIPS-and-POPs [39]. Second, as predicted by the SCM, a modification of the memory is associated with a corresponding adjustment in the long-term variance, particularly on a large-scale basis.
Active tides limit the generation of large-scale internal variability (Figure 8; the large scales are associated with long-term variability.) Also, the memory is strongly reduced when tides are active (Figure 8), or in other words - tides block the accumulation of unprovoked variability on spatial scales of 30 and more kms, and reduce the characteristic times (memory); the auto-spectra of the leading principal components get considerably flatter, their slopes get smaller - all as predicted by the Stochastic Climate Model (3). The understanding is that the tides dissipate random disturbances so that they can not develop for a longer time, and not build persistent large-scale anomalies.
When comparing the situation in winter with that in summer, similar results are found - in winter, when there is hardly a thermocline, the generation of internal variability is strong, but in summer, when a clear thermocline is present much less so. (see Lin et al. [21], but also Figure 9).
This is an analysis on the system level, but the question remains which processes are responsible? Using the hypothesis of modified baroclinicity, Lin et al [23] calculated the intensity of internal variability and the Eady estimate of theoretical diffusivity for the pairs of ensembles "with/without tides" and ensembles "winter/summer", and found the expected changes (namely internal variability increase with baroclinic instability increase), consistent with Waldman’s [17] and Benincasa’s [22] results.
Preprints 113425 g009
Figure 9. Memory vs. spatial scales in the numerical experiments, with and without tides, in the South China Sea. Note that, deviating from Figure 8, the large scales are on the left. From [21].
Figure 9. Memory vs. spatial scales in the numerical experiments, with and without tides, in the South China Sea. Note that, deviating from Figure 8, the large scales are on the left. From [21].
Preprints 113425 g009
Preprints 113425 g010
Figure 10. Time series of standard deviations of the time series anomalies (i.e., deviations from the daily means of each ensemble) of atmospheric temperature (top; [40]) and of oceanic depth-averaged velocity (top; [38]) at a grid point.
Figure 10. Time series of standard deviations of the time series anomalies (i.e., deviations from the daily means of each ensemble) of atmospheric temperature (top; [40]) and of oceanic depth-averaged velocity (top; [38]) at a grid point.
Preprints 113425 g010

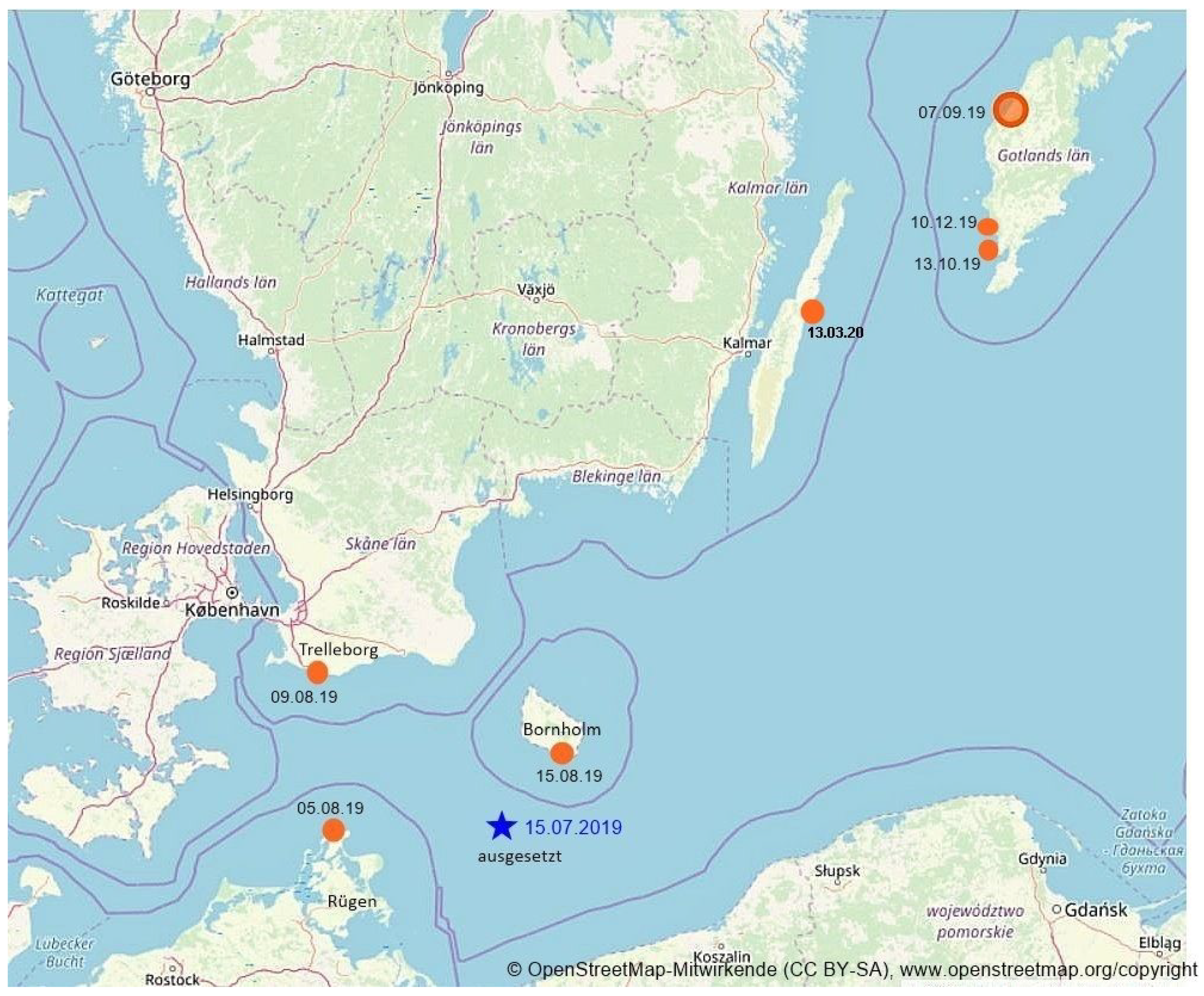
4. Seeding Noise

Ensembles of extended simulations using regional atmospheric and oceanic models were initially conducted by varying the initialization time. This allowed the models to have different lengths of spin-up periods before the period of interest. During the spin-up period, which lasted a few months, the same oceanic forcing (sea surface temperature and lateral atmospheric forcing) or atmospheric forcing (vertical fluxes at the surface and lateral oceanic forcing) was applied. Consequently, the entire simulation period, including both the spin-up and experimental phases, remained consistent and identical across the different ensemble members during overlapping times[8,19].
By coincidence, identical simulations using the same limited area model code, initial conditions, and forcing conditions but performed on different computer platforms became available, first in atmospheric sciences and later in oceanography. The intensity and timing of deviations across different ensemble members were statistically identical [38,40]. In atmospheric models, the periods of divergence were shorter and appeared to be influenced by the strength of the flow at the lateral boundaries, whereas in ocean models, it was very likely affected by the seasonal strength of the thermocline.
For each day, when all members of both ensembles, those generated by using different times of initialization and by using different computing platforms, are available, daily mean values across each ensemble, as well as the standard deviations of the deviations from these means, were calculated. Figure 9 shows these time series for the atmospheric case of a Northern European limited area model (top) and the oceanic case of a limited area model of the Bo Hai and Yellow Sea (bottom).
Minuscule changes, whether in the initial state or caused by different compilers, can trigger significant and persistent deviations. The way these small changes are introduced is irrelevant. This phenomenon, where unavoidable small disturbances grow to substantial spatial scales and intensities, aligns with the Stochastic Climate model theory. Such sensitivity to minor disturbances is not necessarily indicative of chaotic processes and can even occur in linear systems. A memory term α , which may vary over time, is required. These variations can be due to factors like the strength of the constraining boundary values [40] or seasonal variations in baroclinic stability [23].

5. Challenges Arising from the Presence of Noise

In the "motivation"-Section 1, some implications of the presence of hydrodynamic noise have already been touched. Here, we deepen this discussion further.

5.1. Stochastic Climate Model: Not just atmosphere and ocean

A main conclusion in Section 3 was that the Stochastic Climate model-concept (Section 2) applies not only to the classical oceanographic and atmospheric cases documented in the literature, but also to the hydrodynamics of marginal seas: whenever a system is not too nonlinear with a limited damping then significant internal variably should emerge. Thus observation led to the hypothesis that such variability should occur in other areas as well, such as in morphodynamics.
To do so, a simple model of the morphodynamics of a small bay, with a narrow entry to the open sea is considered [41]. The ocean influences the bay through a mono-frequency tide. Initially, the morphology is uniform, but in the course of time, a variety of channels forms. Without any noise seeding, the distribution of the channels is symmetric, as no Coriolis force is active in this setup.
Hydrodynamical noise is excited by adding small disturbances to the tidal variation for the first 20 tidal cycles, i.e. during the first 10 days. The figure shows how these small initial disturbances diverge within 240 years. While the general pattern is the same with mostly two major channels through the entry of the bay, the details are all different. Small initial disturbances lead to an ensemble with significant variations of all channels, not only but also the large ones. Thus, we find the hypothesis that the development of internal variability also in the morphodynamic is consistent with the Stochastic Climate model, namely that short-term random disturbances are leading to red noise slow variations.
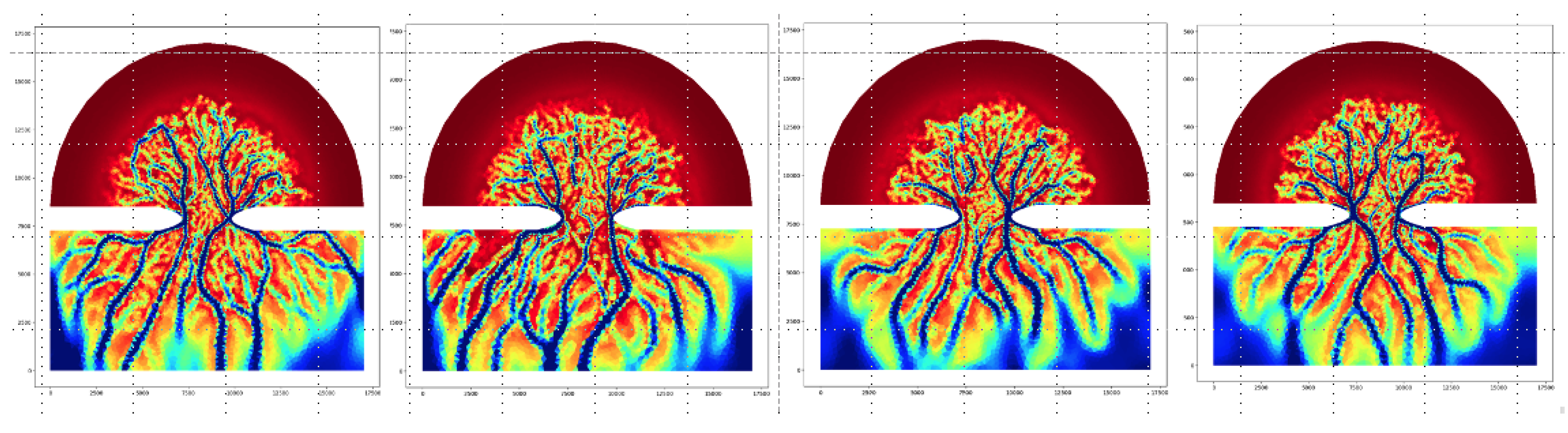
Preprints 113425 g011
Figure 11. Morphology in a small bay after 240 years of integration, initialized at rest and exposed to slightly disturbed tides during the fist 10 days [41]) a grid point.
Figure 11. Morphology in a small bay after 240 years of integration, initialized at rest and exposed to slightly disturbed tides during the fist 10 days [41]) a grid point.
Preprints 113425 g011

5.2. Assessing the Outcome of Numerical Experiments

An aspect relates to numerical experimentation, where changes in factors such as parameterizations, boundary conditions, and atmospheric composition are introduced in simulations [3]. In these experiments, appropriately designed ensembles are crucial for estimating the extent of inherent variability. This helps to determine whether changes between ensembles can be attributed solely to internal variability or if external factors play a role.
If “something” is expected to produce a certain effect, whether in the real world represented by observational data or in numerical simulations, it is simplistic to assume that the difference between the state when the "something" is active and the state when it is not active would accurately represent this effect, or the "signal.”
Recognizing the presence of variations unprovoked by the “something” using the technique of statistical hypothesis testing with the null hypothesis H0: <“something” has no effect> is appropriate. If this null-hypothesis is rejected with a sufficiently small risk, then a valid conclusion is that an external factor is active. In the case of a numerical experiment with an active and a passive “something,” the external factor is indeed the “something.” However, in the case of observational data, there may be a variety of factors changing the observational record.
The determination if a “something” is active is called “detection” – the presence of a “signal is detected”, but it is not necessarily clear which factor is causing this signal. If a variety of candidates for the change exists, then the process of determining the most plausible mix of factors is determined – a process called “attribution”.
The term “(statistical) significance” in science refers to a statistical assessment of the probability that a given event is drawn from a certain population (even if "significance" is also used as in ordinary English, also in this article). If this probability is small, then the null-hypothesis “event is consistent with standard conditions” is rejected, and the alternative “event is evidence for the presence of non-standard conditions” is accepted. If it is “not small”, then the null-hypothesis is “not rejected” and the alternative hypothesis is also not accepted. The choice of “small” is subjective; in our field, it is usually 5%.
Obviously, the "local" tests need to be done at grid points but could be done in any other representation of the fields, say EOFs, and then only with components of interest, such as large scales. Hasselmann [31,42] suggested different strategies (see also [43]).
A problem arises when such a test is done at many grid points. This is well-known among global atmospheric modellers, but possibly less so among regional modellers. If the null hypothesis is valid at all of these grid points, then one would expect, on average, at 5% of them the null hypothesis to be rejected falsely. The number of false rejections is itself a random variable, and the percentage of rejections may be much larger, say 20%, or so. If, however, the rate is larger than, say 20%, then it is unlikely that all rejections are false, but some are valid. For further details on this aspect, refer to the textbook [35]
An example of such testing is that of a numerical experiment on the formation of the seasonal cold water pool off Qingdao [30]. Here, the effect of tides as well as of variable winds is examined - and three ensembles were built with both, tides and realistic wind variability, one without tides, and one with zero wind. Those points, where the null hypothesis is rejected are marked by crosses, which are 51% and 90% of all vgrid pæoints, indicating global significance (i.e., not the effect of doing multiple local tests). Obviously, the null hypothesis that the tides and wind forcing have no effect is untenable.
Preprints 113425 g012
Figure 12. Sensitivity of the formation of the spring cold water circulation in the western Yellow Sea to the presence of tides (left) and the presence of seasonal variations of wind stress (right). Three ensembles of simulations with full forcing (tides and wind), with disregarding tidal forcing (top) and with disregarding the annual march of wind stress. Those points, at which a local t-test indicates the presence of a signal, are marked with a cross. The diagram is taken from [30]
Figure 12. Sensitivity of the formation of the spring cold water circulation in the western Yellow Sea to the presence of tides (left) and the presence of seasonal variations of wind stress (right). Three ensembles of simulations with full forcing (tides and wind), with disregarding tidal forcing (top) and with disregarding the annual march of wind stress. Those points, at which a local t-test indicates the presence of a signal, are marked with a cross. The diagram is taken from [30]
Preprints 113425 g012
For regional oceanographers, it seems that it is uncommon to examine their numerical sensitivity experiments.

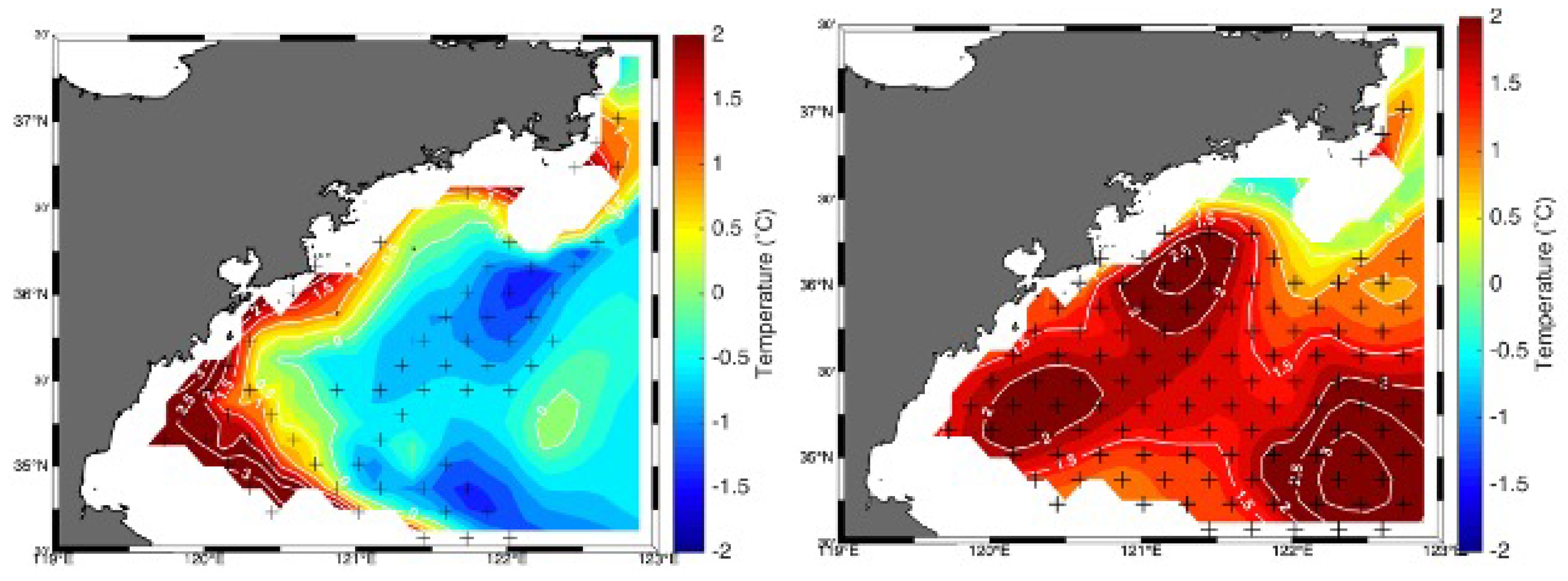
5.3. Detection and Attribution

Another challenge is the "detection and attribution" problem in climate change studies, which involves determining whether observed variations can be explained by internal variability alone or if an external factor is needed to explain the observed change. This underscores the importance of distinguishing between forced and unforced climate variations, as mentioned earlier.
In this case, it is just one case, which needs to be evaluated, and the estimation of the noise must be done separately by considering the output of model "control" runs without changing atmospheric conditions. After detecting that the thus estimated internal variability alone cannot explain the ongoing change (“detection”; see above), then the attribution step compares the ongoing change with suggestions of climate models as a response to given changes. Then that combination of drivers, which explains the ongoing change best, is chosen as the plausible cause of the change. Thus, attribution is a plausibility argument.[31,44].
This procedure is nowadays a standard approach in the toolbox of climate change scientists. The analysis of the effect of baroclinic instability on the level of internal variability (Section 3.1), may be considered as an example [17,23]

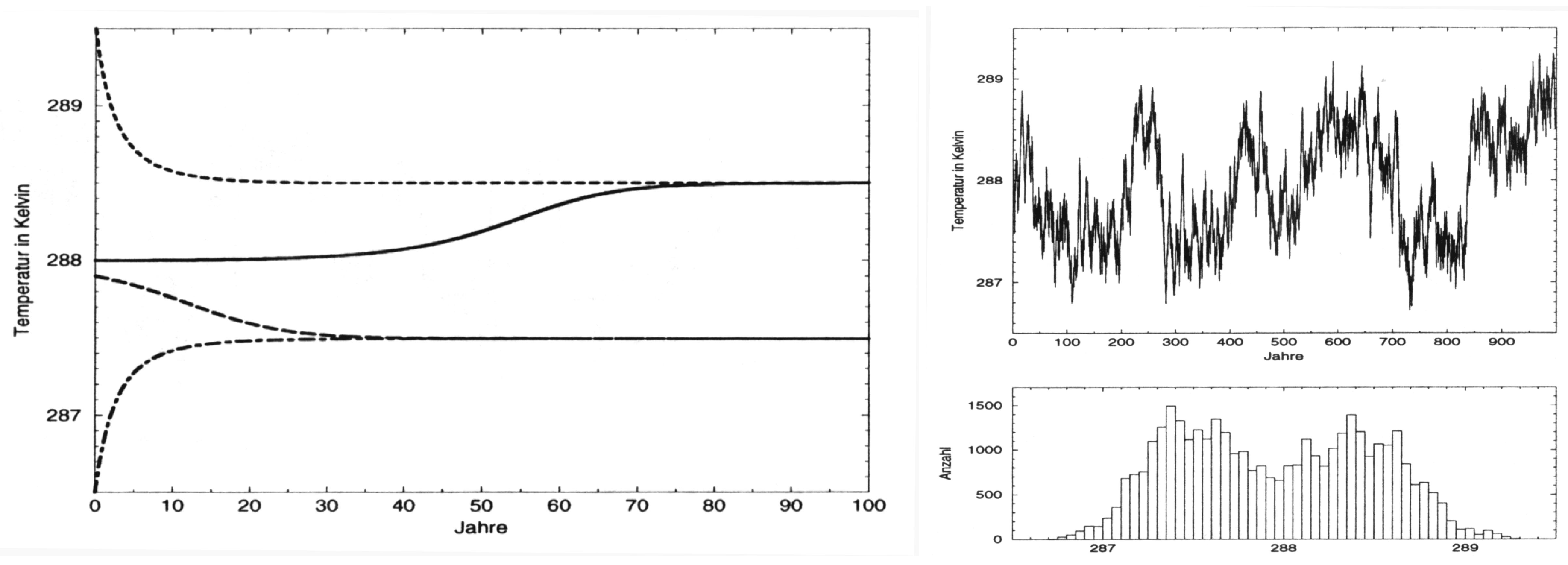
5.4. Multiple Equillibria

Another issue, which may be significantly affected by the presence of hydrodynamical noise is tipping points. Low-dimensional systems such as those proposed by [45] and [46] point to the possibility that the earth system may have two, or more, stable states, and which state the system is eventually ending depends on the initial state.
However, when noise is added, for instance by describing cloudiness as partly random, then the system varies considerably, and travels between the two preferred states, as displayed in Figure 13. While this system questions the concept of irreversibility of tipping points, it illustrates the need to consider the presence of noise, when examining such irreversibility.

6. Conclusions

"Noise" is a ubiquitous phenomenon in systems with memory and moderate nonlinearity, such as atmospheric and oceanic dynamics, morphodynamics, and sometimes ecodynamics [48,49,50].
  • This noise can be understood within the framework of the Hasselmann Stochastic Climate Model [1].
  • Internal variability, which refers to variations that cannot be attributed to specific external drivers, is an intrinsic part of the system’s dynamics rather than just a nuisance.
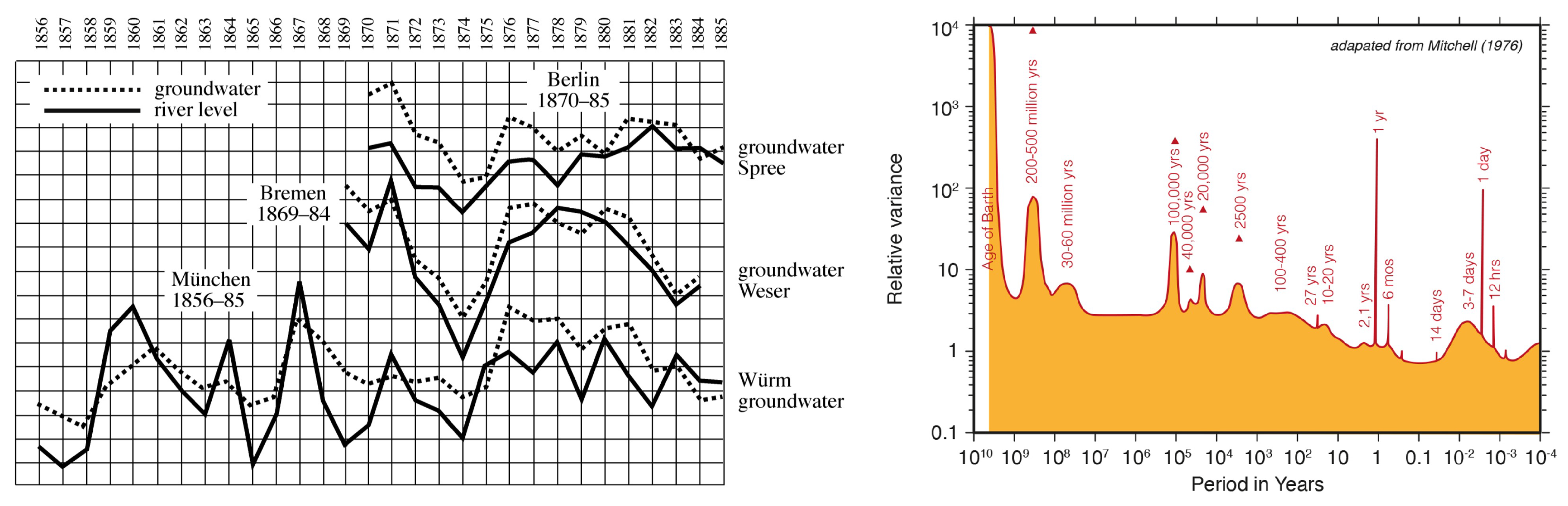
  • In the absence of external drivers, the system exhibits variability across all spatial and temporal scales.
  • In simulations, identifying this noise is relatively straightforward. It can be achieved by constructing ensembles of simulations with minor, insignificant variations introduced by shifting the initial time or using different computer platforms.
  • To determine the impact of external factors, statistical testing is required, using "no effect" as the null hypothesis. This can be done through numerical experiments with ensembles of simulations Attributing causal mechanisms, especially when multiple causes are possible, can be approached with a plausibility argument.

Author Contributions

Conceptualization, HvS and LL.; writing—original draft preparation, HvS; writing—review and editing, LL; Both authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

Significant parts of knowledge summarized here are due to Ulrich Callies, Shengquan Tang, Zhang Wenyan and Meng Zhang. The unwavering and ongoing inspiration by Klaus Hasselmann is gratefully acknowledged.

References

  1. Hasselmann, K. Stochastic climate models. Part I. Theory. Tellus 1976, 28, 473–485. [Google Scholar]
  2. von Storch, H.; von Storch, J.S.; Müller, P. Noise in the Climate System - Ubiquitous, Constitutive and Concealing. In Mathematics Unlimited - 2001 and Beyond. Part II; Engquist, B.; Schmid, W., Eds.; Springer-Verlag, 2001; pp. 1179–1194.
  3. Chervin, R.; Gates, W.; Schneider, S. The effect of the time averaging on the noise level of climatological statistics generated by atmospheric general circulation models. J. Atmos. Sci. 1974, 31, 2216–2219. [Google Scholar] [CrossRef]
  4. Chervin, R.M.; Schneider, S.H. On Determining the Statistical Significance of Climate Experiments with General Circulation Models. Journal of Atmospheric Sciences 1976, 33, 405–412. [Google Scholar] [CrossRef]
  5. Fischer, G.; Kirk, E.; Podzun, R. Physikalische Diagnose eines numerischen Experiments zur Entwicklung der grossräumigen atmosphärischen Zirkulation auf einem Aquaplaneten. Meteor. Rdsch 1991, 43, 33–42. [Google Scholar]
  6. Ji, Y.; Vernekar, A.D. Simulation of the Asian summer monsoons of 1987 and 1988 with a regional model nested in a global GCM. Journal of Climate 1997, 10, 1965–1979. [Google Scholar] [CrossRef]
  7. Rinke, A.; Dethloff, K. On the sensitivity of a regional arctic climate model to initial and boundary conditions. Climate Research 2000, 14, 101–113. [Google Scholar] [CrossRef]
  8. Feser, F.; von Storch, H. A Dynamical Downscaling Case Study for Typhoons in Southeast Asia Using a Regional Climate Model. Monthly Weather Review 2008, 136, 1806–1815. [Google Scholar] [CrossRef]
  9. Schaaf, B.; von Storch, H.; Feser, F. Does Spectral Nudging Have an Effect on Dynamical Downscaling Applied in Small Regional Model Domains? Monthly Weather Review 2017, 145, 4303–4311. [Google Scholar] [CrossRef]
  10. Rockel, B.; Castro, C.L.; Pielke Sr., R. A.; von Storch, H.; Leoncini, G. Dynamical downscaling: Assessment of model system dependent retained and added variability for two different regional climate models. Journal of Geophysical Research: Atmospheres 2008, 113. [Google Scholar] [CrossRef]
  11. Jochum, M.; Murtugudde, R. Internal variability of the tropical Pacific ocean. Geophysical Research Letters 2004, 31. [Google Scholar] [CrossRef]
  12. Jochum, M.; Murtugudde, R. Internal Variability of Indian Ocean SST. Journal of Climate 2005, 18, 3726–3738. [Google Scholar] [CrossRef]
  13. Arbic, B.K.; Müller, M.; Richman, J.G.; Shriver, J.F.; Morten, A.J.; Scott, R.B.; Sérazin, G.; Penduff, T. Geostrophic Turbulence in the Frequency–Wavenumber Domain: Eddy-Driven Low-Frequency Variability. Journal of Physical Oceanography 2014, 44, 2050–2069. [Google Scholar] [CrossRef]
  14. Sérazin, G.; Penduff, T.; Grégorio, S.; Barnier, B.; Molines, J.M.; Terray, L. Intrinsic Variability of Sea Level from Global Ocean Simulations: Spatiotemporal Scales. Journal of Climate 2015, 28, 4279–4292. [Google Scholar] [CrossRef]
  15. Penduff, T.; Close, S.; Molines, J.M.; Barnier, B.; Bessières, L.; Maze, G. Chaotic Variability of Ocean Heat Content: Climate-Relevant Features and Observational Implications. Oceanography 2018, 31. [Google Scholar] [CrossRef]
  16. Büchmann, B.; Söderkvist, J. Internal variability of a 3-D ocean model. Tellus A: Dynamic Meteorology and Oceanography 2016, 68, 30417. [Google Scholar] [CrossRef]
  17. Waldman, R.; Somot, S.; Herrmann, M.; Sevault, F.; Isachsen, P.E. On the Chaotic Variability of Deep Convection in the Mediterranean Sea. Geophysical Research Letters 2018, 45, 2433–2443. [Google Scholar] [CrossRef]
  18. Tang, S.; von Storch, H.; Chen, X.; Zhang, M. “Noise” in climatologically driven ocean models with different grid resolution. Oceanologia 2019, 61, 300–307. [Google Scholar] [CrossRef]
  19. Tang, S.; von Storch, H.; Chen, X. Atmospherically forced regional ocean simulations of the South China Sea: Scale-dependency of the signal-to-noise ratio. J. Phys. Oceano. 2020, 50, 133–144. [Google Scholar] [CrossRef]
  20. Lin, L.; von Storch, H.; Guo, D.; Tang, S.; Zheng, P.; Chen, X. The effect of tides on internal variability in the Bohai and Yellow Sea. Dynamics of Atmospheres and Oceans 2022, 98, 101301. [Google Scholar] [CrossRef]
  21. Lin, L.; von Storch, H.; X. .; Chen. The Stochastic Climate Model helps reveal the role of memory in internal variability in the Bohai and Yellow Sea. Communications Earth & Environment 2023, 4, 347. [Google Scholar] [CrossRef]
  22. Benincasa, R.; Liguori, G.; Pinardi, N.; von Storch, H. Internal and forced ocean variability in the Mediterranean Sea. EGUsphere 2024, 2024, 1–15. [Google Scholar] [CrossRef]
  23. Lin, L.; von Storch, H.; Chen, X.; Jiang, W.; Tang, S. Link between the internal variability and the baroclinic instability in the Bohai and Yellow Sea. Ocean Dynamics 2023, 73, 793–806. [Google Scholar] [CrossRef]
  24. Waldman, R.; Somot, S.; Herrmann, M.; Bosse, A.; Caniaux, G.; Estournel, C.; Houpert, L.; Prieur, L.; Sevault, F.; Testor, P. Modeling the intense 2012–2013 dense water formation event in the northwestern Mediterranean Sea: Evaluation with an ensemble simulation approach. Journal of Geophysical Research: Oceans 2017, 122, 1297–1324. [Google Scholar] [CrossRef]
  25. Callies, U. ; H. von Storch. Extreme separations of bottle posts in the southern Baltic Sea - tentative interpretation of an experiment-of-opportunity. Oceanologia, 2022. [Google Scholar] [CrossRef]
  26. Brückner, E. Klimaschwankungen seit 1700 nebst Bemerkungen über die Klimaschwankungen der Diluvialzeit; Geographische Abhandlungen, E.D. Hölzel: Wien and Olmütz, 1890. [Google Scholar]
  27. Mitchell, J.M. An overview of climatic variability and its causal mechanisms. Quaternary Research 1976, 6, 481–493. [Google Scholar] [CrossRef]
  28. Friedman, R.M. Appropriating the Weather; Cornell University Press, 1989.
  29. Chervin, R.M.; Gates, W.L.; Schneider, S.H. The Effect of Time Averaging on the Noise Level of Climatological Statistics Generated by Atmospheric General Circulation Models. Journal of Atmospheric Sciences 1974, 31, 2216–2219. [Google Scholar] [CrossRef]
  30. Lin, L.; von Storch, H.; Ding, Y. The anti-cyclonic gyre around the Qingdao cold water mass in the China marginal sea. EGUsphere 2024, 2024, 1–26. [Google Scholar] [CrossRef]
  31. Hasselmann, K. Optimal Fingerprints for the Detection of Time-dependent Climate Change. Journal of Climate 1993, 6, 1957–1971. [Google Scholar] [CrossRef]
  32. Lemke, P. Stochastic climate models, part 3. Application to zonally averaged energy models. Tellus 1977, 29, 385–392. [Google Scholar] [CrossRef]
  33. Frankignoul, C.; Hasselmann, K. Stochastic climate models, Part II Application to sea-surface temperature anomalies and thermocline variability. Tellus 1977, 29, 289–305. [Google Scholar] [CrossRef]
  34. Lemke, P.; Trinkl, E.W.; Hasselmann, K. Stochastic Dynamic Analysis of Polar Sea Ice Variability. Journal of Physical Oceanography 1980, 10, 2100–2120. [Google Scholar] [CrossRef]
  35. von Storch, H.; Zwiers, F.W. Statistical analysis in climate research; Cambridge University Press, 1999.
  36. von Storch, H.; Li, D. Statistics and Modelling of Regional Climate Variability in China; WORLD SCIENTIFIC (EUROPE), 2024. [CrossRef]
  37. Zhang, M.; von Storch, H.; Chen, X.; Wang, D.; Li, D. Temporal and spatial statistics of travelling eddy variability in the South China Sea. Ocean Dynamics 2019, 69, 879–898. [Google Scholar] [CrossRef]
  38. Lin, L.; von Storch, H.; Chen, X. Seeding Noise in Ensembles of Marginal Sea Simulations - The Case of Bohai and Yellow Sea. Advances in Computer and Communication 2023, 4, 70–73. [Google Scholar] [CrossRef]
  39. Hasselmann, K. PIPs and POPs: The reduction of complex dynamical systems using principal interaction and oscillation patterns. Journal of Geophysical Research: Atmospheres 1988, 93, 11015–11021. [Google Scholar] [CrossRef]
  40. Geyer, B.; Ludwig, T.; von Storch, H. Reproducibility and regional climate models - seeding noise by changing computers and initial conditions. Communications Earth & Environment 2021, 2, 17. [Google Scholar] [CrossRef]
  41. Lin, L.; Zhang, W.; P. Arlinghaus.; von Storch, H. Internal variability in an idealized morphodynamic model. in preparation 2024. [Google Scholar]
  42. Hasselmann, K. On the signal-to-noise problem in atmospheric response studies. In Meteorology over the tropical oceans; B.D.Shaw., *!!! REPLACE !!!*, Ed.; Royal Met. Soc.: Bracknell, Berkshire, England, 1979; pp. 251–259. [Google Scholar]
  43. Hannoschöck, G.; Frankignoul, C. Multivariate Statistical Analysis of a Sea Surface Temperature Anomaly Experiment with the GISS General Circulation Model I. Journal of Atmospheric Sciences 1985, 42, 1430–1450. [Google Scholar] [CrossRef]
  44. Barnett, T.; Zwiers, F.; Hengerl, G.; Allen, M.; Crowly, T.; Gillett, N.; Hasselmann, K.; Jones, P.; Santer, B.; Schnur, R.; Scott, P.; Taylor, K.; Tett, S. Detecting and Attributing External Influences on the Climate System: A Review of Recent Advances. Journal of Climate 2005, 18, 1291–1314. [Google Scholar] [CrossRef]
  45. Budyko, M.I. The effect of solar radiation variations on the climate of the Earth. tellus 1969, 21, 611–619. [Google Scholar] [CrossRef]
  46. Sellers, W.D. A global climatic model based on the energy balance of the earth-atmosphere system. Journal of Applied Meteorology and Climatology 1969, 8, 392–400. [Google Scholar] [CrossRef]
  47. von Storch, H.; Güss, S.; Heimann, M. Das Klimasystem und seine Modellierung. Eine Einführung; Springer Verlag: Berlin - Heidelberg - New York, 1999; p. 255. [Google Scholar]
  48. Gehlen, M.; Berthet, S.; Séférian, R.; Ethé, C.; Penduff, T. Quantification of Chaotic Intrinsic Variability of Sea-Air CO 2 Fluxes at Interannual Timescales. Geophysical Research Letters 2020, 47, e2020GL088304. [Google Scholar] [CrossRef]
  49. Mayersohn, B.; Smith, K.S.; Mangolte, I.; Lévy, M. Intrinsic timescales of variability in a marine plankton model. Ecological Modelling 2021, 443, 109446. [Google Scholar] [CrossRef]
  50. Mayersohn, B.; Lévy, M.; Mangolte, I.; Smith, K.S. Emergence of Broadband Variability in a Marine Plankton Model Under External Forcing. Journal of Geophysical Research: Biogeosciences 2022, 127, e2022JG007011. [Google Scholar] [CrossRef]
1
see "Damaged US Navy sub was operating in one of world’s most difficult undersea environments, analysts say", CNN, October 8, 2021
Preprints 113425 g001
Figure 1. Fischer’s numerical experiment [5] running an atmospheric general circulation model of an aqua-planet Earth with an initial atmospheric state at rest. The shown variable is zonally averaged zonal wind at 950hPa.
Figure 1. Fischer’s numerical experiment [5] running an atmospheric general circulation model of an aqua-planet Earth with an initial atmospheric state at rest. The shown variable is zonally averaged zonal wind at 950hPa.
Preprints 113425 g001
Preprints 113425 g002
Figure 2. Satellite image of small-scale features in the Baltic Sea.
Figure 2. Satellite image of small-scale features in the Baltic Sea.
Preprints 113425 g002
Preprints 113425 g003
Figure 3. Locations where bottles, released into the Baltic Sea at the same place (see star off Bornholm) and at the same time, were eventually found after drifting through the Southern Baltic Sea [25]. Note that the bottles were not only moved by the currents but also by the wind.
Figure 3. Locations where bottles, released into the Baltic Sea at the same place (see star off Bornholm) and at the same time, were eventually found after drifting through the Southern Baltic Sea [25]. Note that the bottles were not only moved by the currents but also by the wind.
Preprints 113425 g003
Preprints 113425 g004
Figure 4. Left: Analysis of river levels and groundwater levels in the 19th century as prepared by Eduard Brückner [26] Right: proposition of the temporal spectrum of climate variability, as sketched by J. Murray Mitchell [27].
Figure 4. Left: Analysis of river levels and groundwater levels in the 19th century as prepared by Eduard Brückner [26] Right: proposition of the temporal spectrum of climate variability, as sketched by J. Murray Mitchell [27].
Preprints 113425 g004
Preprints 113425 g005
Figure 5. Auto-correlation function (left) and auto-spectrum(right) of an AR(1) process with α = 0.3 and α = 0.5 . In the diagram with the spectra, also that of white noise is added as horizontal line. From [35]
Figure 5. Auto-correlation function (left) and auto-spectrum(right) of an AR(1) process with α = 0.3 and α = 0.5 . In the diagram with the spectra, also that of white noise is added as horizontal line. From [35]
Preprints 113425 g005
Preprints 113425 g006
Figure 6. Logarithm of daily variances of sea surface height in the SCS simulated for summer (top: g+h+i) and winter (bottom: j+k+l) by the low-resolution near-global model (left;g+j), the mid-resolution West Pacific model (middle; h+k) and the high-resolution South China Sea model (right: i+l). From [18]
Figure 6. Logarithm of daily variances of sea surface height in the SCS simulated for summer (top: g+h+i) and winter (bottom: j+k+l) by the low-resolution near-global model (left;g+j), the mid-resolution West Pacific model (middle; h+k) and the high-resolution South China Sea model (right: i+l). From [18]
Preprints 113425 g006
Preprints 113425 g007
Figure 7. S/N ratios of zonal and meridional surface currents for the Bo Hai and Yellow Sea for (a) the large-scale EOFs, (b) the mid-size EOFs, and (c) the small-scale EOFs. From [20].
Figure 7. S/N ratios of zonal and meridional surface currents for the Bo Hai and Yellow Sea for (a) the large-scale EOFs, (b) the mid-size EOFs, and (c) the small-scale EOFs. From [20].
Preprints 113425 g007
Preprints 113425 g008
Figure 8. Noise levels vs. spatial scales in the numerical experiments, with and without tides, in the South China Sea. Note that the small scales are on the right. From [21]
Figure 8. Noise levels vs. spatial scales in the numerical experiments, with and without tides, in the South China Sea. Note that the small scales are on the right. From [21]
Preprints 113425 g008
Preprints 113425 g013
Figure 13. Integration of en energy-balance model with nonlinear albedo (cold temperatures go with a high albedo, low temperature with high albedo). Left, development from different initial states, ending up in one of the two stable states. Right: Integration, when also the transmissivity (for instance by random variations in cloudiness) is considered random. Then the system meanders between the two preferred states, and the frequency distribution becomes bimodal. The diagram is taken from [47]
Figure 13. Integration of en energy-balance model with nonlinear albedo (cold temperatures go with a high albedo, low temperature with high albedo). Left, development from different initial states, ending up in one of the two stable states. Right: Integration, when also the transmissivity (for instance by random variations in cloudiness) is considered random. Then the system meanders between the two preferred states, and the frequency distribution becomes bimodal. The diagram is taken from [47]
Preprints 113425 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated