Explicit Solutions for Coupled Parallel Queues

1. Introduction

This paper fits into a greater scientific effort which aims at finding explicit analytic solutions for the joint probability distribution (or probability generating function) of the numbers of customers in a system of two coupled discrete-time queues. Various instances of such systems have been studied before, both differing in the cause of the coupling between the two queues or in the scientific perspective taken in the study.

With no claim on completeness, we mention a number of possible causes for the presence of coupling between queues. A first cause may be that the arrival streams into the queues are mutually interdependent or state-dependent, i.e., dependent on the system contents, i.e., the numbers of customers present in the queues. Mutual dependence between arrivals occurs, for instance, in the context of communications networks, where the nodes of the network contain switching systems which have to forward digital packets from many different origins to many different destinations. In such switches, each destination has (at least, conceptually) its own dedicated buffer to temporarily store arriving packets, and, since packets destined to one destination do not enter the output buffer associated to another destination, the arrivals within such output buffers are mutually correlated. Buffered slotted switches were studied, e.g., in [1,2,3,4,5,6]. State-dependence of arrivals occurs, for instance, in join-the-shortest-queue systems, where arriving customers adapt their behavior at the entrance of the system to the system contents upon arrival; see, e.g., [7,8,9]. More conceptual studies of queues with interdependent arrivals include [5,6,10,11].

Another (major) cause of coupling may be that the queues of the system have to share the same service facilities. This situation occurs, for instance, in polling systems, where one server periodically visits multiple customer queues to serve a number of customers and then go to the next queue; various variants of polling systems have been studied quite intensively in the past (see, e.g., [12,13,14,15,16,17,18,19]). Sharing of servers also occurs in so-called alternating service systems, where one server is allocated for alternating random durations of time to either of the two queues, regardless of the states of these queues, (see, e.g., [11,20,21,22,23,24,25,26,27,28]), or in priority queues, where one common service facility gives preferential service to one class of customers over the other class(es) of customers; a large body of research results is available on various types of priority queueing systems (see, e.g., [29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46]). Similar ideas are also implemented in so-called (generalized) processor sharing (GPS) systems, whereby the service facility is randomly allocated to multiple queues according to preset weights; as opposed to randomly alternating service systems, however, GPS-systems usually allow the server to deliver service to customers of a queue to which it is not allocated when the queue to which it is allocated is empty, thus making the system work-conserving. In fact, GPS-systems can also be viewed as systems with alternating priorities; some papers dealing with GPS-systems are [25,47,48,49,50,51]. We should also mention serve-the-longest-queue systems, where, upon a service completion, a server can autonomously decide to give preference to the queue that contains the largest number of customers; see, e.g, [52,53]. Recently, some authors have examined the combined join-the-shortest-queue and serve-the-longest-queue scenario; see [54,55].

A third possible cause of coupling in two-queue systems can be that (part of) the output stream of one queue constitutes (part of) the input stream into the other queue, such as in the context of tandem queues (see, e.g., [45,56,57]), or, more generally, in a network environment.

As far as the scientific perspective taken by various authors in the literature is concerned, we see a main difference between considering the involved (two-queue) queueing system as the basic concept of the study, where the determination of the joint (or, total) system-content distribution of both queues, the overflow probabilities, the customer delays, etc. is the main objective, versus a more fundamental, mathematically-oriented point of view, whereby the underlying random walks that model the system contents of both queues are the basic concepts of the study (see, e.g., [58,59,60,61,62]). Usually, the aim of such papers is to shed more light on the structural properties of these random walks required to admit elegant solutions. Moreover, the involved random walks are often of nearest-neighbor type, which is rather restrictive in a queueing context, and the structure of their transition probabilities may be quite arbitrary and not necessarily reflect the behavior of a queueing system.

The present paper does not take the mathematical study of the random walk that models the two-queue system explicitly as a major point of interest, but rather concentrates on the explicit determination of the joint pgf of the two system contents in the two queues of the system. Specifically, we consider a conceptually very simple system of two coupled parallel discrete-time queues. The queues are named queue 1 and queue 2, both have their own dedicated server and infinite storage capacity. Customers arriving to queue 1 and to queue 2 are referred to as type-1 and type-2 customers, respectively. The service times of the customers are deterministically equal to one time slot, regardless of the customer type. New customer arrivals of both types occur independently from slot to slot, but are possibly type-interdependent within a slot. This is the only source of coupling in this model. Earlier studies of various instances of this type of two-queue system include [1,2,3,4,5,6,10,11,63].

It is well-known that, in general, determining the steady-state joint pgf $U(z_1,z_2)$ of the system contents in a system of two coupled queues is a formidable task, because it requires the solution of a possibly complicated, nonlinear functional equation for $U(z_1,z_2)$, which contains the unknown boundary functions $U(z_1,0)$ and/or $U(0,z_2)$. In many previous papers, the analysis consists of first determining these boundary functions through various complex-analysis techniques, upon which $U(z_1,z_2)$ can be computed from the functional equation by subsequent substitution of the expressions found for $U(z_1,0)$ and/or $U(0,z_2)$. In this paper, we use a different, purely algebraic, technique, which can be best described as a two-step process: first, we make an educated guess of the solution for $U(z_1,z_2)$, and, next, we prove that the proposed $U(z_1,z_2)$ indeed satisfies the functional equation. Of course, in this approach, making an educated guess of the solution is crucial. In fact, this step is essentially a process of trial and error, based on the intuition gained from the preliminary study of a large number of simple special cases in earlier papers.

For the specific coupled-queues system considered in this paper, explicit results have been obtained thus far only in a number of isolated cases, for very specific choices of the arrival pgf $A(z_1,z_2)$ (see, e.g., [5]). Furthermore, these special cases are of a rather simple nature: either the arrivals of both types should be mutually independent, or the two queues should receive identical numbers of arrivals in each slot, or one of both queues should receive no more than one single arrival per slot, implying that in this queue no accumulation of customers occurs. Some initial indications to extend the class of “solvable” arrival pgfs $A(z_1,z_2)$ were also given in [5], but the extensions are limited.

In this paper, we introduce a multi-parameter, generic class of arrival pgfs $A(z_1,z_2)$, for which we succeed to explicitly determine the joint pgf $U(z_1,z_2)$, using the algebraic approach described above. By making specific choices for the many parameters of the model, we also define three interesting subclasses of arrival pgfs which lead to even more explicit solutions. We find that for arrival pgfs of the classes considered in this paper, the bivariate joint system-content pgf $U(z_1,z_2)$ has a denominator which is a product, say $r_1\left(z_1\right)r_2\left(z_2\right)$ of two univariate functions. This property allows a straightforward inversion of the pgf $U(z_1,z_2)$ by means of an inversion technique we developed in a previous paper [11], resulting in a pmf $u(m,n)$ which can be expressed as a finite linear combination of bivariate geometric terms. We observe that our generic model encompasses most of the previously known results as special cases. In fact, it was by studying these special cases that we developed the intuition needed to be able to identify the class of arrival pgfs introduced in this paper.

The rest of this paper is organized as follows. In Section 2 we introduce the detailed mathematical model of the system under study and establish a functional equation for the joint pgf $U(z_1,z_2)$. The solution of this functional equation is, in fact, the main purpose of the paper. Section 3 defines the generic class of arrival pgfs $A(z_1,z_2)$ that will be studied in this paper. In Section 4, we present and prove the main result of the paper in the form of Theorem 1 which gives an explicit expression for the joint system-content pgf $U(z_1,z_2)$ associated to the joint arrival pgf $A(z_1,z_2)$ defined in Section 3. Section 5 defines three interesting subclasses, named A, B and C, of the generic class of arrival pgfs $A(z_1,z_2)$ defined in Section 3, and establishes even more explicit formulas for the associated system-content pgfs $U(z_1,z_2)$ in these cases, in the form of three corrolaries, also named A, B and C, of Theorem 1. In Section 6, we consider several instances of subclasses A, B and C, whereby specific choices are made for the various parameters and functions appearing in the formulations of Corrolaries A, B and C. Section 7 discusses a fundamental method to invert the system-content pgf $U(z_1,z_2)$, i.e., to determine the pmf $u(m,n)$ from the pgf $U(z_1,z_2)$, and illustrates this techniques by means of specific examples within subclasses A, B and C. Finally, we state some concluding remarks in Section 8.

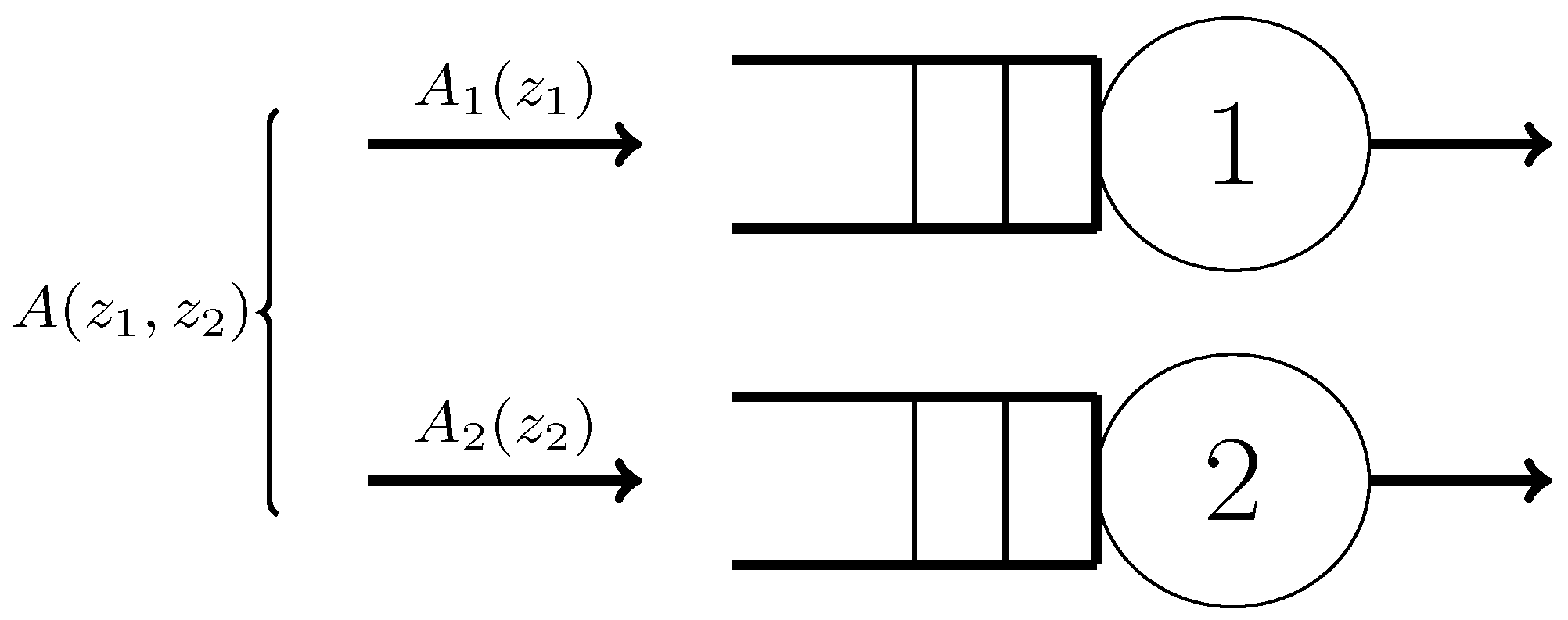
2. Mathematical Model and Queueing Analysis

We define the random variables $a_{1,k}$ and $a_{2,k}$ as the numbers of type-1 and type-2 arrivals, respectively, during slot k. Their joint probability mass function (pmf) $a(i,j)$ and probability generating function (pgf)$A(z_1,z_2)$ are indicated as

$$a(i,j)\triangleq \mathrm{Prob}\left[a_{1,k}=i\mathrm{and}{a}_{2,k}=j\right],i,j\ge 0,$$

$$A(z_1,z_2)\triangleq E\left[z_1^{a_{1,k}}{z}_2^{a_{2,k}}\right]\triangleq \sum _{i=0}^{\infty }\sum _{j=0}^{\infty }a(i,j)z_1^i{z}_2^j,$$

(1)

which are independent of k. The (marginal) pgfs of $a_{1,k}$ and $a_{2,k}$ are given by

$$A_1\left(z_1\right)\triangleq E\left[z_1^{a_{1,k}}\right]=A(z_1,1),A_2\left(z_2\right)\triangleq E\left[z_2^{a_{2,k}}\right]=A(1,z_2),$$

(2)

respectively. The mean number of arrivals of type i per slot is denoted as ${\lambda }_i\triangleq A_i^{\prime }\left(1\right)$. A graphical representation of the system under study is shown in Figure 1.

Let $u_{1,k}$ and $u_{2,k}$ indicate the system contents, i.e., the total numbers of customers present, in queue 1 and queue 2, respectively, including the customer(s) in service, if any, at the beginning of slot k. We indicate their joint pgf as

$$U_k(z_1,z_2)\triangleq E\left[z_1^{u_{1,k}}{z}_2^{u_{2,k}}\right].$$

(3)

Furthermore, let $q_{1,k}$ and $q_{2,k}$ indicate the queue contents, i.e., the numbers of waiting customers, in queue 1 and queue 2, respectively, excluding the customer(s) in service, if any, at the beginning of slot k. We indicate their joint pgf as

$$Q_k(z_1,z_2)\triangleq E\left[z_1^{q_{1,k}}{z}_2^{q_{2,k}}\right].$$

(4)

It is not difficult to see that the following relationships exist between the system contents and the queue contents:

$$q_{1,k}={(u_{1,k}-1)}^{+},q_{2,k}={(u_{2,k}-1)}^{+},$$

(5)

where we have introduced the notation ${\left(x\right)}^{+}$ to indicate the quantity $max(0,x)$.

The main purpose of the paper is to analyze the steady-state behavior of the queueing system under study, i.e., we are interested in determining the steady-state joint pgfs of the two system contents and/or queue contents, provided that such a steady state exists. Specifically, we wish to study the following limit functions:

$$U(z_1,z_2)\triangleq \underset{k\to \infty }{lim}{U}_k(z_1,z_2),Q(z_1,z_2)\triangleq \underset{k\to \infty }{lim}{Q}_k(z_1,z_2),$$

(6)

if they exist. A steady state exists if and only if both queues are stable, i.e., receive, on average, less customers per slot than they can serve, i.e., if and only if the following stability conditions are fulfilled:

$${\lambda }_1<1,{\lambda }_2<1.$$

(7)

As mentioned in e.g., [5,6], the evolution of the system contents is described by the following system equations:

$$u_{1,k+1}=a_{1,k}+{(u_{1,k}-1)}^{+},u_{2,k+1}=a_{2,k}+{(u_{2,k}-1)}^{+}.$$

(8)

Using standard z-tranform techniques, the equations (8) can be translated into one corresponding transform equation between the joint pgfs $U_k(z_1,z_2)$ and $U_{k+1}(z_1,z_2)$, by using definition (3). Assuming the system reaches a steady state, i.e., assuming the stability conditions (7) are met, letting the time parameter k go to infinity, and using the definitions (3) and (6), the latter transform equation translates into the following functional equation for the steady-state system-content pgf $U(z_1,z_2)$:

$$K(z_1,z_2)U(z_1,z_2)=A(z_1,z_2)L(z_1,z_2),$$

(9)

where the unknown function $L(z_1,z_2)$ is defined as

$$L(z_1,z_2)\triangleq (z_2-1)U(z_1,0)+(z_1-1)U(0,z_2)+(z_1-1)(z_2-1)U(0,0)$$

(10)

and the kernel $K(z_1,z_2)$ is given by

$$K(z_1,z_2)\triangleq z_1{z}_2-A(z_1,z_2).$$

(11)

Although, in general, the functional Equation (9) is hard to solve for $U(z_1,z_2)$, it is fairly easy to derive explicit expressions for the marginal pgfs $U(z_1,1)$ and $U(1,z_2)$ of the individual system contents in queues 1 and 2, by choosing either $z_2=1$ or $z_1=1$ in (9), because such choices greatly simplify the L-function. As a result, we then obtain

$$U(z_1,1)=\frac{U(0,1)(z_1-1)A_1\left(z_1\right)}{z_1-A_1\left(z_1\right)},U(1,z_2)=\frac{U(1,0)(z_2-1)A_2\left(z_2\right)}{z_2-A_2\left(z_2\right)}.$$

(12)

Invoking the normalization condition $U(1,1)=1$ yields $U(0,1)=1-{\lambda }_1$ and $U(1,0)=1-{\lambda }_2$. The expressions in (12) are very well-known in the context of discrete-time queueing theory; see, for instance [64]; they will be very useful further in this paper.

We now turn our attention to the queue contents. Using (5) in (8), we readily get

$$u_{1,k+1}=a_{1,k}+q_{1,k},u_{2,k+1}=a_{2,k}+q_{2,k}.$$

Transforming these relationships to pgfs, we obtain, on account of the definitions (3) and (4),

$$U_{k+1}(z_1,z_2)=A(z_1,z_2)Q_k(z_1,z_2).$$

In view of (6), this implies that

$$U(z_1,z_2)=A(z_1,z_2)Q(z_1,z_2),Q(z_1,z_2)=\frac{U(z_1,z_2)}{A(z_1,z_2)}.$$

(13)

Equation (13) makes clear that $Q(z_1,z_2)$ is known as soon as $U(z_1,z_2)$ is known, and vice versa. In the remainder of this paper, we mainly concentrate on the determination of $U(z_1,z_2)$.

3. Defining a Class of Arrival pgfs $A(z_1,z_2)$

Let $f_1\left(z_1\right)$, $f_2\left(z_2\right)$, $g_1\left(z_1\right)$, $g_2\left(z_2\right)$, $h_1\left(z_1\right)$, $h_2\left(z_2\right)$ denote one-dimensional probability generating functions. Furthermore, let $n_{11}$, $n_{12}$, $n_{21}$, $n_{22}$ denote a set of normalized probabilities, i.e.,

$$n_{11},n_{12},n_{21},n_{22}\ge 0,n_{11}+n_{12}+n_{21}+n_{22}=1,$$

and $d_1$ and $d_2$ two nonnegative real parameters. We then use all the above quantities to define a whole class of bivariate functions $A(z_1,z_2)$ as follows:

$$A(z_1,z_2)=\frac{n_{11}{z}_1{z}_2+n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)+n_{22}{h}_1\left(z_1\right)h_2\left(z_2\right)}{1+d_1+d_2-d_1{g}_1\left(z_1\right)-d_2{g}_2\left(z_2\right)}.$$

(14)

We now show that the above function is a genuine joint pgf, i.e., it can be developed as a two-dimensional power series in $z_1$ and $z_2$ with nonnegative coefficients which add up to 1.

Let us denote the numerator and the denominator of (14) as $n(z_1,z_2)$ and $d(z_1,z_2)$, respectively, i.e.,

$$A(z_1,z_2)=\frac{n(z_1,z_2)}{d(z_1,z_2)}=n(z_1,z_2)\left(\frac{1}{d(z_1,z_2)}\right),$$

(15)

with

$$\begin{array}{cc}\hfill n(z_1,z_2)& \triangleq n_{11}{z}_1{z}_2+n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)+n_{22}{h}_1\left(z_1\right)h_2\left(z_2\right),\hfill \\ \hfill d(z_1,z_2)& \triangleq 1+d_1+d_2-d_1{g}_1\left(z_1\right)-d_2{g}_2\left(z_2\right).\hfill \end{array}$$

(16)

It is clear that both $n(z_1,z_2)$ and $d(z_1,z_2)$ are normalized, i.e., $n(1,1)=1$ and $d(1,1)=1$, which implies that $A(z_1,z_2)$ is also normalized, i.e., $A(1,1)=1$. The numerator $n(z_1,z_2)$ is a probabilistic mixture of four valid pgfs, and, therefore, is a valid pgf too. The function $1/d(z_1,z_2)$ is also a genuine pgf since it can be developed as a two-dimensional power series in $z_1$ and $z_2$ with nonnegative coefficients as follows:

$$\begin{array}{cc}\hfill \frac{1}{d(z_1,z_2)}& =\frac{1}{(1+d_1+d_2)-d_1{g}_1\left(z_1\right)-d_2{g}_2\left(z_2\right)}\hfill \\ & =\frac{1}{(1+d_1+d_2)\left(1-{\pi }_1{g}_1\left(z_1\right)-{\pi }_2{g}_2\left(z_2\right)\right)}\hfill \\ & =\left(\frac{1}{1+d_1+d_2}\right)\sum _{i=0}^{\infty }{\left({\pi }_1{g}_1\left(z_1\right)+{\pi }_2{g}_2\left(z_2\right)\right)}^i,\hfill \end{array}$$

where the probabilies ${\pi }_1$ and ${\pi }_2$ have been defined as

$${\pi }_1=\frac{d_1}{1+d_1+d_2},{\pi }_2=\frac{d_2}{1+d_1+d_2}.$$

Equation (15) thus shows that $A(z_1,z_2)$ can be expressed as the product of two valid joint pgfs, and, therefore, is a valid joint pgf too.

In this paper, we will examine a parallel-queues system with joint arrival pgf $A(z_1,z_2)$ defined in (14). The corresponding marginal arrival pgfs $A_1\left(z_1\right)$ and $A_2\left(z_2\right)$ are

$$\begin{array}{cc}\hfill A_1\left(z_1\right)& =A(z_1,1)=\frac{n(z_1,1)}{d(z_1,1)}=\frac{(n_{11}+n_{12})z_1+n_{21}{f}_1\left(z_1\right)+n_{22}{h}_1\left(z_1\right)}{1+d_1-d_1{g}_1\left(z_1\right)},\hfill \\ \hfill A_2\left(z_2\right)& =A(1,z_2)=\frac{n(1,z_2)}{d(1,z_2)}=\frac{(n_{11}+n_{21})z_2+n_{12}{f}_2\left(z_2\right)+n_{22}{h}_2\left(z_2\right)}{1+d_2-d_2{g}_2\left(z_2\right)}.\hfill \end{array}$$

(17)

The mean arrival rates ${\lambda }_1$ and ${\lambda }_2$ are

$$\begin{array}{cc}\hfill {\lambda }_1& \triangleq A_1^{\prime }\left(1\right)=n_{11}+n_{12}+n_{21}{f}_1^{\prime }\left(1\right)+n_{22}{h}_1^{\prime }\left(1\right)+d_1{g}_1^{\prime }\left(1\right)\hfill \\ \hfill {\lambda }_2& \triangleq A_2^{\prime }\left(1\right)=n_{11}+n_{21}+n_{12}{f}_2^{\prime }\left(1\right)+n_{22}{h}_2^{\prime }\left(1\right)+d_2{g}_2^{\prime }\left(1\right).\hfill \end{array}$$

(18)

We assume that ${\lambda }_1<1,{\lambda }_2<1$.

4. The Main Result

According to (12), the marginal system-content pgfs are given by

$$\begin{array}{cc}\hfill U(z_1,1)& =\frac{U(0,1)(z_1-1)A_1\left(z_1\right)}{z_1-A_1\left(z_1\right)}=\frac{U(0,1)(z_1-1)n(z_1,1)}{k_1\left(z_1\right)},\hfill \\ \hfill U(1,z_2)& =\frac{U(1,0)(z_2-1)A_2\left(z_2\right)}{z_2-A_2\left(z_2\right)}=\frac{U(1,0)(z_2-1)n(1,z_2)}{k_2\left(z_2\right)},\hfill \end{array}$$

(19)

where

$$k_1\left(z_1\right)\triangleq z_{1}d(z_1,1)-n(z_1,1),k_2\left(z_2\right)\triangleq z_{2}d(1,z_2)-n(1,z_2).$$

(20)

We are now ready to formulate the main result of this paper.

Theorem 1:

In the stable parallel-queues system with joint arrival pgf

$$A(z_1,z_2)=\frac{n(z_1,z_2)}{d(z_1,z_2)}=\frac{n_{11}{z}_1{z}_2+n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)+n_{22}{h}_1\left(z_1\right)h_2\left(z_2\right)}{1+d_1+d_2-d_1{g}_1\left(z_1\right)-d_2{g}_2\left(z_2\right)},$$

(21)

where $f_1\left(z_1\right)$, $f_2\left(z_2\right)$, $g_1\left(z_1\right)$ and $g_2\left(z_2\right)$ are arbitrary one-dimensional pgfs, and

$$n_{11},n_{12},n_{21},n_{22}\ge 0,n_{11}+n_{12}+n_{21}+n_{22}=1,$$

(22)

the steady-state joint system-content pgf $U(z_1,z_2)$ is given by

$$U(z_1,z_2)=\frac{n(z_1,z_2)U(z_1,1)U(1,z_2)}{n(z_1,1)n(1,z2)}=\frac{U(0,1)U(1,0)(z_1-1)(z_2-1)n(z_1,z_2)}{k_1\left(z_1\right)k_2\left(z_2\right)},$$

(23)

provided that the functions $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ are genuine one-dimensional pgfs, given by

$$\begin{array}{cc}\hfill h_1\left(z_1\right)& ={\alpha }_1{z}_1+{\beta }_1{f}_1\left(z_1\right)+{\gamma }_1{z}_1{g}_1\left(z_1\right),\hfill \\ \hfill h_2\left(z_2\right)& ={\alpha }_2{z}_2+{\beta }_2{f}_2\left(z_2\right)+{\gamma }_2{z}_2{g}_2\left(z_2\right),\hfill \end{array}$$

(24)

where $\{{\alpha }_1,{\beta }_1,{\gamma }_1\}$ and $\{{\alpha }_2,{\beta }_2,{\gamma }_2\}$ are two sets of “normalized constants”, i.e.,

$${\alpha }_1+{\beta }_1+{\gamma }_1=1,{\alpha }_2+{\beta }_2+{\gamma }_2=1,$$

(25)

satisfying the restrictions

$${\beta }_1>0,,{\beta }_2>0,{\gamma }_1=\frac{d_1{\beta }_1}{n_{21}}\ge 0,{\gamma }_2=\frac{d_2{\beta }_2}{n_{12}}\ge 0.$$

(26)

4.1. Some Remarks on the Terms of Theorem 1

According to equations (24), Theorem 1 requires that $h_1\left(z_1\right)$ be a linear combination of $z_1$, $f_1\left(z_1\right)$ and $z_1{g}_1\left(z_1\right)$, and, similarly that $h_2\left(z_2\right)$ a linear combination of $z_2$, $f_2\left(z_2\right)$ and $z_2{g}_2\left(z_2\right)$, with coefficients that add up to 1. It is easily seen that, as required, this implies that $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ are normalized, i.e., $h_1\left(1\right)=h_2\left(1\right)=1$. However, for arbitrary choices of the parameters ${\beta }_1$, ${\beta }_2$, $d_1$, $d_2$, $n_{12}$ and $n_{21}$, the functions $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$, as given in (24), could, in general, contain linear terms in $z_1$ or $z_2$ with a negative coefficient, which would prevent them from being genuine pgfs. Indeed, whereas the coefficients ${\beta }_1$, ${\gamma }_1$, ${\beta }_2$ and ${\gamma }_2$ are certainly nonnegative, this not necessarily the case for the coefficients of the linear terms in (24). It is clear that sufficient conditions to guarantee that $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ are valid pgfs are

$${\alpha }_1\ge 0,{\alpha }_2\ge 0,$$

(27)

but these conditions are not necessary. In order to determine the linear terms in (24) completely, it is useful to decompose the functions $f_1\left(z_1\right)$, $f_2\left(z_2\right)$, $g_1\left(z_1\right)$ and $g_2\left(z_2\right)$ as follows:

$$f_1\left(z_1\right)=f_{10}+f_{11}{z}_1+z_1^2{v}_1\left(z_1\right),f_2\left(z_2\right)=f_{20}+f_{21}{z}_2+z_2^2{v}_2\left(z_2\right),$$

(28)

and

$$g_1\left(z_1\right)=g_{10}+z_1{w}_1\left(z_1\right),g_2\left(z_2\right)=g_{20}+z_2{w}_2\left(z_2\right).$$

(29)

Substitution of (28) and (29) in (24) yields

$$\begin{array}{cc}\hfill h_1\left(z_1\right)& ={\beta }_1{f}_{10}+\left({\alpha }_1+{\beta }_1{f}_{11}+{\gamma }_1{g}_{10}\right)z_1+\left({\beta }_1{v}_1\left(z_1\right)+{\gamma }_1{w}_1\left(z_1\right)\right)z_1^2\hfill \\ \hfill h_2\left(z_2\right)& ={\beta }_2{f}_{20}+\left({\alpha }_2+{\beta }_2{f}_{21}+{\gamma }_2{g}_{20}\right)z_2+\left({\beta }_2{v}_2\left(z_2\right)+{\gamma }_2{w}_2\left(z_2\right)\right)z_2^2.\hfill \end{array}$$

(30)

The above expressions make clear that $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ are genuine pgs if and only if

$${\alpha }_1+{\beta }_1{f}_{11}+{\gamma }_1{g}_{10}\ge 0,{\alpha }_2+{\beta }_2{f}_{21}+{\gamma }_2{g}_{20}\ge 0,$$

(31)

which are milder conditions than (27).

4.2. Proving Theorem 1

In order to prove Theorem 1, we first establish a technical lemma. Let us define the bivariate function $e(z_1,z_2)$ as

$$\begin{array}{cc}\hfill e(z_1,z_2)\triangleq n(0,1)n(1,0)& n(z_1,z_2)+n(0,1)n(z_1,0)k_2\left(z_2\right)+n(1,0)n(0,z_2)k_1\left(z_1\right)\hfill \\ & +n(0,0)k_1\left(z_1\right)k_2\left(z_2\right).\hfill \end{array}$$

(32)

Lemma 1:The function $e(z_1,z_2)$ can be expressed as

$$e(z_1,z_2)=n(0,1)n(1,0)z_1{z}_{2}d(z_1,z_2).$$

Proof. 

Combining (24), (25) and (26), and due to the fact that ${\beta }_1$ and ${\beta }_2$ are assumed to be strictly positive, we can compute the functions $n_{21}{f}_1\left(z_1\right)$ and $n_{12}{f}_2\left(z_2\right)$ in terms of $g_1\left(z_1\right)$, $g_2\left(z_2\right)$, $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$, as follows:

$$\begin{array}{cc}\hfill n_{21}{f}_1\left(z_1\right)& =\frac{{\beta }_1{z}_1\left(n_{21}+d_1(1-g_1\left(z_1\right))\right)+n_{21}\left(z_1-h_1\left(z_1\right)\right)}{{\beta }_1},\hfill \\ \hfill n_{12}{f}_2\left(z_2\right)& =\frac{{\beta }_2{z}_2\left(n_{12}+d_2(1-g_2\left(z_2\right))\right)+n_{12}\left(z_2-h_2\left(z_2\right)\right)}{{\beta }_2}.\hfill \end{array}$$

(33)

Inserting (33) in (16), we then get

$$n(z_1,z_2)=n_{22}\left(h_1\left(z_1\right)h_2\left(z_2\right)-z_1{z}_2\right)+z_1{z}_{2}d(z_1,z_2)-\frac{n_{21}{z}_2\left(z_1-h_1\left(z_1\right)\right)}{{\beta }_1}-\frac{n_{12}{z}_1\left(z_2-h_2\left(z_2\right)\right)}{{\beta }_2},\left[0.3cm\right]$$

(34)

where we have also used the definition (16) of $d(z_1,z_2)$.

Choosing either $z_1=0$ or $z_2=0$ in (34) yields

$$n(z_1,0)=f_2\left(0\right)\left(n_{12}{z}_1+{\beta }_2{n}_{22}{h}_1\left(z_1\right)\right),n(0,z_2)=f_1\left(0\right)\left(n_{21}{z}_2+{\beta }_1{n}_{22}{h}_2\left(z_2\right)\right),$$

(35)

and, from this,

$$n(0,0)=f_1\left(0\right)f_2\left(0\right)n_{22}{\beta }_1{\beta }_2.$$

(36)

On the other hand, choosing either $z_1=1$ or $z_2=1$ in (34) leads to

$$\begin{array}{cc}\hfill n(z_1,1)& =n_{22}{h}_1\left(z_1\right)+z_1\left(d(z_1,1)-n_{22}\right)-\frac{n_{21}\left(z_1-h_1\left(z_1\right)\right)}{{\beta }_1},\hfill \\ \hfill n(1,z_2)& =n_{22}{h}_2\left(z_2\right)+z_2\left(d(1,z_2)-n_{22}\right)-\frac{n_{12}\left(z_2-h_2\left(z_2\right)\right)}{{\beta }_2},\hfill \end{array}$$

(37)

and, from this,

$$n(0,1)=f_1\left(0\right)\left({\beta }_1{n}_{22}+n_{21}\right),n(0,1)=f_2\left(0\right)\left({\beta }_2{n}_{22}+n_{12}\right).$$

(38)

Using (37) and (38) in (20), we can express $k_1\left(z_1\right)$ and $k_2\left(z_2\right)$ as

$$\begin{array}{cc}\hfill k_1\left(z_1\right)& \triangleq z_{1}d(z_1,1)-n(z_1,1)=\frac{{\beta }_1{n}_{22}+n_{21}}{{\beta }_1}\left(z_1-h_1\left(z_1\right)\right)=\frac{n(0,1)}{{\beta }_1{f}_1\left(0\right)}\left(z_1-h_1\left(z_1\right)\right),\hfill \\ \hfill k_2\left(z_2\right)& \triangleq z_{2}d(1,z_2)-n(1,z_2)=\frac{{\beta }_2{n}_{22}+n_{12}}{{\beta }_2}\left(z_2-h_2\left(z_2\right)\right)=\frac{n(1,0)}{{\beta }_2{f}_2\left(0\right)}\left(z_2-h_2\left(z_2\right)\right).\hfill \end{array}$$

(39)

Substitution of (34), (35), (36) and (39) in (32) then leads to

$$\begin{array}{cc}\hfill e(z_1& ,z_2)=n(0,1)n(1,0)(n_{22}\left(h_1\left(z_1\right)h_2\left(z_2\right)-z_1{z}_2\right)+z_1{z}_{2}d(z_1,z_2)-\frac{n_{21}{z}_2\left(z_1-h_1\left(z_1\right)\right)}{{\beta }_1}\hfill \\ & -\frac{n_{12}{z}_1\left(z_2-h_2\left(z_2\right)\right)}{{\beta }_2})+n(0,1)f_2\left(0\right)\left(n_{12}{z}_1+{\beta }_2{n}_{22}{h}_1\left(z_1\right)\right)\frac{n(1,0)}{{\beta }_2{f}_2\left(0\right)}\left(z_2-h_2\left(z_2\right)\right)\hfill \\ & +n(1,0)f_1\left(0\right)\left(n_{21}{z}_2+{\beta }_1{n}_{22}{h}_2\left(z_2\right)\right)\frac{n(0,1)}{{\beta }_1{f}_1\left(0\right)}\left(z_1-h_1\left(z_1\right)\right)\hfill \\ & +f_1\left(0\right)f_2\left(0\right)n_{22}{\beta }_1{\beta }_2\frac{n(0,1)}{{\beta }_1{f}_1\left(0\right)}\left(z_1-h_1\left(z_1\right)\right)\frac{n(1,0)}{{\beta }_2{f}_2\left(0\right)}\left(z_2-h_2\left(z_2\right)\right).\hfill \end{array}$$

(40)

It is then a matter of straightforward algebra to prove that all the terms in the above equation containing $h_1\left(z_1\right)$ and/or $h_2\left(z_2\right)$ compensate each other. The final result is

$$e(z_1,z_2)=n(0,1)n(1,0)z_1{z}_{2}d(z_1,z_2).$$

This concludes the proof of Lemma 1. □

Proof of Theorem 1

The proof of Theorem 1 consists of two steps. In a first step, we show that the function $U(z_1,z_2)$, defined in (23), is a genuine joint pgf. In the second step, we prove that, under the conditions of Theorem 1, $U(z_1,z_2)$ satisfies the functional Equation (9) of the system.

Step 1: $U(z_1,z_2)$ is a genuine joint pgf

Proof. 

In view of the relationship (13) between $U(z_1,z_2)$ and $Q(z_1,z_2)$ (and the corresponding marginal pgfs), Equation (23) can be rewritten as

$$U(z_1,z_2)=\frac{n(z_1,z_2)U(z_1,1)U(1,z_2)}{n(z_1,1)n(1,z_2)}=\frac{n(z_1,z_2)A(z_1,1)Q(z_1,1)A(1,z_2)Q(1,z_2)}{n(z_1,1)n(1,z_2)}.$$

Using (17), we then easily obtain

$$U(z_1,z_2)=\frac{n(z_1,z_2)Q(z_1,1)Q(1,z_2)}{d(z_1,1)d(1,z_2)}=n(z_1,z_2)Q(z_1,1)Q(1,z_2)\left(\frac{1}{d(z_1,1)}\right)\left(\frac{1}{d(1,z_2)}\right),$$

where the right-hand side is a product of five valid pgfs. Hence, $U(z_1,z_2)$ is a valid pgf as well. □

Step 2: $U(z_1,z_2)$ satisfies the functional equation

Proof. 

Combining (9) and (11), we can express the functional equation as

$$\left(z_1{z}_2-A(z_1,z_2)\right)U(z_1,z_2)=A(z_1,z_2)L(z_1,z_2),$$

and, from this,

$$A(z_1,z_2)\left(L(z_1,z_2)+U(z_1,z_2)\right)=z_1{z}_{2}U(z_1,z_2).$$

Inserting the expression (15) for $A(z_1,z_2)$ then leads to

$$L(z_1,z_2)+U(z_1,z_2)=\frac{z_1{z}_{2}d(z_1,z_2)U(z_1,z_2)}{n(z_1,z_2)}.$$

(41)

The function $L(z_1,z_2)$ can be computed from (10) as

$$L(z_1,z_2)\triangleq (z_2-1)U(z_1,0)+(z_1-1)U(0,z_2)+(z_1-1)(z_2-1)U(0,0),$$

(42)

where $U(z_1,0)$ and $U(0,z_2)$ can be derived from (23) as

$$U(z_1,0)=\frac{U(0,1)U(1,0)(z_1-1)n(z_1,0)}{n(1,0)\left(k_1\left(z_1\right)\right)},U(0,z_2)=\frac{U(0,1)U(1,0)(z_2-1)n(0,z_2)}{n(0,1)(k_2\left(z_2\right)},$$

(43)

which also implies

$$U(0,0)=\frac{U(0,1)U(1,0)n(0,0)}{n(0,1)n(1,0)}.$$

(44)

Substitution of (43) and (44) in (42) then leads to

$$L(z_1,z_2)=\ell (z_1,z_2)b(z_1,z_2),$$

(45)

where we have defined $\ell (z_1,z_2)$ and $b(z_1,z_2)$ as short-hand notations for

$$\begin{array}{cc}\hfill \ell (z_1,z_2)& \triangleq n(0,1)n(z_1,0)k_2\left(z_2\right)+n(1,0)n(0,z_2)k_1\left(z_1\right)+n(0,0)k_1\left(z_1\right)k_2\left(z_2\right),\hfill \\ \hfill b(z_1,z_2)& \triangleq \frac{U(0,1)U(1,0)(z_1-1)(z_2-1)}{n(0,1)n(1,0)k_1\left(z_1\right)k_2\left(z_2\right)}.\hfill \end{array}$$

On the other hand, in view of (23), $U(z_1,z_2)$ can be expressed as

$$U(z_1,z_2)=n(0,1)n(1,0)n(z_1,z_2)b(z_1,z_2).$$

(46)

Inserting (42) and (46) in (41), we then get

$$\left(\ell (z_1,z_2)+n(0,1)n(1,0)n(z_1,z_2)\right)b(z_1,z_2)=\left(n(0,1)n(1,0)z_1{z}_{2}d(z_1,z_2)\right)b(z_1,z_2).$$

(47)

It thus suffices to show that the expressions between the large parentheses in the left-hand side and the right-hand side of (47) are equal. The expression in the left-hand side is exactly the function $e(z_1,z_2)$, defined in (32). Lemma 1 thus proves that (47) is fulfilled. This concludes the proof of Theorem 1. □

5. Subclasses A, B and C

Theorem 1 provides an explicit solution for the steady-state joint system-contents pgf $U(z_1,z_2)$, for any joint arrival pgf $A(z_1,z_2)$ that satisfies the shape specified in equations (21), (24), (25) and (26), whereby $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ are valid pgfs. We now define some interesting subclasses of arrival pgfs that correspond to specific choices of the (many) parameters that the model contains.

5.1. Subclass A: $d_1=0,d_2=0$

In this special case, $d(z_1,z_2)=1$ and the arrival pgf $A(z_1,z_2)$, defined in (14), simplifies to

$$A(z_1,z_2)=n(z_1,z_2)=n_{11}{z}_1{z}_2+n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)+n_{22}{h}_1\left(z_1\right)h_2\left(z_2\right).$$

(48)

We define the subclass A of arrival pgfs $A(z_1,z_2)$ by the condition $d_1=0,d_2=0$. We notice that, within subclass A, the pgfs $g_1\left(z_1\right)$ and $g_2\left(z_2\right)$ play no role anymore in $A(z_1,z_2)$. We also observe that, since $A(z_1,z_2)=n(z_1,z_2)$, the joint queue-content pgf $Q(z_1,z_2)$, given in (13), reduces to

$$Q(z_1,z_2)=\frac{U(z_1,z_2)}{n(z_1,z_2)},$$

and, hence, our main result (23) in Theorem 1 is equivalent to

$$Q(z_1,z_2)=Q(z_1,1)Q(1,z_2),$$

(49)

i.e., for arrival pgfs within subclass A, the queue contents of both queues are mutually independent.

The parameters ${\gamma }_1$ and ${\gamma }_2$, defined in (26), are both equal to zero, and, hence, the functions $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$, defined in (24), are given by

$$\begin{array}{c}\hfill h_1\left(z_1\right)=(1-{\beta }_1)z_1+{\beta }_1{f}_1\left(z_1\right),h_2\left(z_2\right)=(1-{\beta }_2)z_2+{\beta }_2{f}_2\left(z_2\right).\end{array}$$

(50)

Substitution of (50) in (48) then leads to

$$\begin{array}{cc}\hfill A(z_1,z_2)=n(z_1,z_2)=n_{11}{z}_1{z}_2& +n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)\hfill \\ & +n_{22}\left((1-{\beta }_1)z_1+{\beta }_1{f}_1\left(z_1\right)\right)\left((1-{\beta }_2)z_2+{\beta }_2{f}_2\left(z_2\right)\right),\hfill \end{array}$$

(51)

which can be rewritten as

$$A(z_1,z_2)=n(z_1,z_2)=m_{11}{z}_1{z}_2+m_{12}{z}_1{f}_2\left(z_2\right)+m_{21}{z}_2{f}_1\left(z_1\right)+m_{22}{f}_1\left(z_1\right)f_2\left(z_2\right),$$

if we define the new parameters $m_{11}$, $m_{12}$, $m_{21}$ and $m_{22}$ as

$$\begin{array}{cc}& m_{11}\triangleq (1-{\beta }_1)(1-{\beta }_2)n_{22},m_{12}\triangleq n_{12}+(1-{\beta }_1){\beta }_2{n}_{22},\hfill \\ & m_{21}\triangleq n_{21}+{\beta }_1(1-{\beta }_2)n_{22},m_{22}\triangleq {\beta }_1{\beta }_2{n}_{22}.\hfill \end{array}$$

It is easily seen that, if we choose ${\beta }_1\le 1$ and ${\beta }_2\le 1$, the sufficient conditions (27) are fulfilled, and the parameters $m_{11}$, $m_{12}$, $m_{21}$ and $m_{22}$ also represent a normalized set of probabilities, just as the original parameters $n_{11}$, $n_{12}$, $n_{21}$ and $n_{22}$, i.e.,

$$m_{11},m_{12},m_{21},m_{22}\ge 0,m_{11}+m_{12}+m_{21}+m_{22}=1,$$

(52)

The marginal arrival pgfs $A_1\left(z_1\right)$ and $A_2\left(z_2\right)$, given in (17), reduce to

$$A_1\left(z_1\right)=(m_{11}+m_{12})z_1+(m_{21}+m_{22})f_1\left(z_1\right),A_2\left(z_2\right)=(m_{11}+m_{21})z_2+(m_{12}+m_{22})f_2\left(z_2\right),$$

(53)

whereas the marginal mean arrival rates, given in (18), simplify to

$${\lambda }_1=1-(m_{21}+m_{22})\left(1-f_1^{\prime }\left(1\right)\right],{\lambda }_2=1-(m_{12}+m_{22})\left(1-f_2^{\prime }\left(1\right)\right].$$

(54)

Hence, the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with

$$f_1^{\prime }\left(1\right)<1,f_2^{\prime }\left(1\right)<1.$$

The functions $k_1\left(z_1\right)$ and $k_2\left(z_2\right)$, defined in (20), reduce to

$$k_1\left(z_1\right)=(m_{21}+m_{22})\left(z_1-f_1\left(z_1\right)\right),k_2\left(z_2\right)=(m_{12}+m_{22})\left(z_2-f_2\left(z_2\right)\right),$$

and, hence, the joint pgf $U(z_1,z_2)$ can be derived from (23) as

$$U(z_1,z_2)=\frac{M(z_1-1)(z_2-1)n(z_1,z_2)}{\left(z_1-f_1\left(z_1\right)\right)\left(z_2-f_2\left(z_2\right)\right)},$$

(55)

where the constant M is defined as

$$M\triangleq \frac{U(0,1)U(1,0)}{(m_{21}+m_{22})(m_{12}+m_{22})}.$$

The only remaining unknown M in Equation (55) can be computed from the normalization condition $U(1,1)=1$, which results in

$$M=\left(1-f_1^{\prime }\left(1\right)\right)\left(1-f_2^{\prime }\left(1\right)\right).$$

(56)

A fully explicit expression for $U(z_1,z_2)$ then follows from (55) and (56).

In summary, we have thus proven the following corrolary of Theorem 1:

Corrolary A

In the stable parallel-queues system with joint arrival pgf

$$A(z_1,z_2)=m_{11}{z}_1{z}_2+m_{12}{z}_1{f}_2\left(z_2\right)+m_{21}{z}_2{f}_1\left(z_1\right)+m_{22}{f}_1\left(z_1\right)f_2\left(z_2\right),$$

(57)

where $f_1\left(z_1\right)$ and $f_2\left(z_2\right)$ are arbitrary one-dimensional pgfs, and

$$m_{11},m_{12},m_{21},m_{22}\ge 0,m_{11}+m_{12}+m_{21}+m_{22}=1,$$

(58)

the steady-state queue contents of both queues are mutually independent, and the steady-state joint system-content pgf $U(z_1,z_2)$ is given by

$$U(z_1,z_2)=\frac{\left(1-f_1^{\prime }\left(1\right)\right)\left(1-f_2^{\prime }\left(1\right)\right)(z_1-1)(z_2-1)A(z_1,z_2)}{\left(z_1-f_1\left(z_1\right)\right)\left(z_2-f_2\left(z_2\right)\right)}.$$

(59)

Remark

If we define the discriminant D of $A(z_1,z_2)$ as $D\triangleq m_{12}{m}_{21}-m_{11}{m}_{22}$, then it is easily seen that if $D=0$, the pgf $A(z_1,z_2)$ has a product form, i.e.,

$$A(z_1,z_2)=\frac{\left(m_{11}{z}_1+m_{21}{f}_1\left(z_1\right)\right)\left(m_{11}{z}_2+m_{12}{f}_2\left(z_2\right)\right)}{m_{11}},$$

and the arrivals of both customer types are mutually independent. It is clear from (59) that, in this case, the pgf $U(z_1,z_2)$ reduces to a product form too, i.e., the two steady-state system contents are also mutually independent.

5.2. Subclass B: ${\alpha }_1=0,{\alpha }_2=0$

The requirements (27) represent sufficient conditions to guarantee that the functions $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ are valid pgfs. A trivial way to satisfy (27) is to choose

$${\alpha }_1=0,{\alpha }_2=0.$$

(60)

We define the subclass B of arrival pgfs $A(z_1,z_2)$ by the condition (60). From (25) and (26), it follows that (60) is equivalent with

$${\gamma }_1=\frac{d_1}{d_1+n_{21}},{\gamma }_2=\frac{d_2}{d_2+n_{12}}.$$

(61)

Substitution of (60) in (24) then yields

$$h_1\left(z_1\right)=(1-{\gamma }_1)f_1\left(z_1\right)+{\gamma }_1{z}_1{g}_1\left(z_1\right),h_2\left(z_2\right)=(1-{\gamma }_2)f_2\left(z_2\right)+{\gamma }_2{z}_2{g}_2\left(z_2\right).$$

(62)

Equation (62) implies that

$$h_1^{\prime }\left(1\right)=(1-{\gamma }_1)f_1^{\prime }\left(1\right)+{\gamma }_1[1+g_1^{\prime }\left(1\right)],h_2^{\prime }\left(1\right)=(1-{\gamma }_2)f_2^{\prime }\left(1\right)+{\gamma }_2[1+g_2^{\prime }\left(1\right)],$$

so that the mean arrival rates, given in (18), can be expressed as

$$\begin{array}{cc}\hfill {\lambda }_1& =(n_{11}+n_{12}+{\gamma }_1{n}_{22})+(n_{21}+(1-{\gamma }_1)n_{22})f_1^{\prime }\left(1\right)+(d_1+{\gamma }_1{n}_{22})g_1^{\prime }\left(1\right),\hfill \\ \hfill {\lambda }_2& =(n_{11}+n_{21}+{\gamma }_2{n}_{22})+(n_{12}+(1-{\gamma }_2)n_{22})f_2^{\prime }\left(1\right)+(d_2+{\gamma }_2{n}_{22})g_2^{\prime }\left(1\right).\hfill \end{array}$$

(63)

The functions $k_1\left(z_1\right)$ and $k_2\left(z_2\right)$, defined in (20), are given by

$$\begin{array}{cc}\hfill k_1\left(z_1\right)& =\frac{n_{21}+(1-{\gamma }_1)n_{22}}{1-{\gamma }_1}\left([1-{\gamma }_1{g}_1\left(z_1\right)]z_1-(1-{\gamma }_1)f_1\left(z_1\right)\right),\hfill \\ \hfill k_2\left(z_2\right)& =\frac{n_{12}+(1-{\gamma }_2)n_{22}}{1-{\gamma }_2}\left([1-{\gamma }_2{g}_2\left(z_2\right)]z_2-(1-{\gamma }_2)f_2\left(z_2\right)\right).\hfill \end{array}$$

(64)

The joint pgf $U(z_1,z_2)$ can be derived from (23) and (64) as

$$U(z_1,z_2)=\frac{M(z_1-1)(z_2-1)n(z_1,z_2)}{\left([1-{\gamma }_1{g}_1\left(z_1\right)]z_1-(1-{\gamma }_1)f_1\left(z_1\right)\right)\left([1-{\gamma }_2{g}_2\left(z_2\right)]z_2-(1-{\gamma }_2)f_2\left(z_2\right)\right)},$$

(65)

where the constant M has been defined as

$$M\triangleq \frac{U(0,1)U(1,0)(1-{\gamma }_1)(1-{\gamma }_2)}{\left(n_{21}+(1-{\gamma }_1)n_{22}\right)\left(n_{12}+(1-{\gamma }_2)n_{22}\right)}.$$

The only remaining unknown M in Equation (88) can be computed from the normalization condition $U(1,1)=1$, which results in

$$M=\left((1-{\gamma }_1)[1-f_1^{\prime }\left(1\right)]-{\gamma }_1{g}_1^{\prime }\left(1\right)\right)\left((1-{\gamma }_2)[1-f_2^{\prime }\left(1\right)]-{\gamma }_2{g}_2^{\prime }\left(1\right)\right).$$

(66)

A fully explicit expression for $U(z_1,z_2)$ then follows from (65) and (66).

Summarizing again, we have thus proven the following corrolary of Theorem 1:

Corrolary B

In the stable parallel-queues system with joint arrival pgf

$$A(z_1,z_2)=\frac{n(z_1,z_2)}{1+d_1+d_2-d_1{g}_1\left(z_1\right)-d_2{g}_2\left(z_2\right)},$$

(67)

where $n(z_1,z_2)$ is defined as

$$\begin{array}{cc}\hfill n(z_1,z_2)\triangleq n_{11}& z_1{z}_2+n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)\hfill \\ & +n_{22}\left((1-{\gamma }_1)f_1\left(z_1\right)+{\gamma }_1{z}_1{g}_1\left(z_1\right)\right)\left((1-{\gamma }_2)f_2\left(z_2\right)+{\gamma }_2{z}_2{g}_2\left(z_2\right)\right),\hfill \end{array}$$

(68)

with $f_1\left(z_1\right)$, $f_2\left(z_2\right)$, $g_1\left(z_1\right)$, $g_2\left(z_2\right)$ arbitrary one-dimensional pgfs, and

$$n_{11},n_{12},n_{21},n_{22}\ge 0,n_{11}+n_{12}+n_{21}+n_{22}=1,{\gamma }_1\triangleq \frac{d_1}{d_1+n_{21}},{\gamma }_2\triangleq \frac{d_2}{d_2+n_{12}},$$

the steady-state joint system-content pgf $U(z_1,z_2)$ is given by

$$U(z_1,z_2)=\frac{M(z_1-1)(z_2-1)n(z_1,z_2)}{\left([1-{\gamma }_1{g}_1\left(z_1\right)]z_1-(1-{\gamma }_1)f_1\left(z_1\right)\right)\left([1-{\gamma }_2{g}_2\left(z_2\right)]z_2-(1-{\gamma }_2)f_2\left(z_2\right)\right)},$$

(69)

with

$$M\triangleq \left((1-{\gamma }_1)[1-f_1^{\prime }\left(1\right)]-{\gamma }_1{g}_1^{\prime }\left(1\right)\right)\left((1-{\gamma }_2)[1-f_2^{\prime }\left(1\right)]-{\gamma }_2{g}_2^{\prime }\left(1\right)\right).$$

(70)

5.3. Subclass C: No Linear Terms in $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$

The requirements (31) are necessary and sufficient conditions in order for $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ to represent genuine pgfs. In this subsection, we examine the extreme case whereby the inequalities in (31) are replaced by equalities, i.e., where

$${\alpha }_1+{\beta }_1{f}_{11}+{\gamma }_1{g}_{10}=0,{\alpha }_2+{\beta }_2{f}_{21}+{\gamma }_2{g}_{20}=0.$$

(71)

In view of (25) and (26), (71) can be rewritten as

$$(1-{\alpha }_1)(n_{21}{f}_{11}+d_1{g}_{10})+{\alpha }_1(n_{21}+d_1)=0,(1-{\alpha }_2)(n_{12}{f}_{21}+d_2{g}_{20})+{\alpha }_2(n_{12}+d_2)=0.$$

(72)

Solving (72) for ${\alpha }_1$ and ${\alpha }_2$, we find

$${\alpha }_1=-\frac{n_{21}{f}_{11}+d_1{g}_{10}}{n_{21}(1-f_{11})+d_1(1-g_{10})},{\alpha }_2=-\frac{n_{12}{f}_{21}+d_2{g}_{20}}{n_{12}(1-f_{21})+d_2(1-g_{20})}.$$

(73)

In these circumstances, due to (30), the functions $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ can be expressed as

$$\begin{array}{cc}\hfill h_1\left(z_1\right)& =\frac{n_{21}{f}_{10}+z_1^2\left(n_{21}{v}_1\left(z_1\right)+d_1{w}_1\left(z_1\right)\right)}{n_{21}(1-f_{11})+d_1(1-g_{10})},\hfill \\ \hfill h_2\left(z_2\right)& =\frac{n_{12}{f}_{20}+z_2^2\left(n_{12}{v}_2\left(z_2\right)+d_2{w}_2\left(z_2\right)\right)}{n_{12}(1-f_{21})+d_2(1-g_{20})},\hfill \end{array}$$

(74)

and, hence, contain no linear terms in $z_1$ and $z_2$, respectively.

In order to further simplify the expressions, let us consider the (further) special case where

$$v_1\left(z_1\right)=w_1\left(z_1\right),v_2\left(z_2\right)=w_2\left(z_2\right).$$

(75)

Of course, we then also have $v_1\left(1\right)=w_1\left(1\right),v_2\left(1\right)=w_2\left(1\right)$. From (28) and (29), we readily obtain

$$v_1\left(1\right)=1-\left(f_{10}+f_{11}\right),v_2\left(1\right)=1-\left(f_{20}+f_{21}\right),w_1\left(1\right)=1-g_{10},w_2\left(1\right)=1-g_{20},$$

and, hence, $v_1\left(1\right)=w_1\left(1\right),v_2\left(1\right)=w_2\left(1\right)$ implies

$$f_{11}=g_{10}-f_{10},f_{21}=g_{20}-f_{20}.$$

We now choose to additionally simplify the model by assuming

$$g_{10}=f_{10}\triangleq 1-{\omega }_1,g_{20}=f_{20}\triangleq 1-{\omega }_2\iff f_{11}=0,f_{20}=0,$$

(76)

where we have introduced the new parameters ${\omega }_1$ and ${\omega }_2$, which are valid probabilities.

By definition, we refer to arrival pgfs $A(z_1,z_2)$ (of the form considered in Theorem 1) as pgfs of subclass C if and only if they comply with the conditions (71), (75) and (76).

Using (75) and (76), we obtain the following expressions for $h_1\left(z_1\right)$ and $h_2\left(z_2\right)$ from (74):

$$h_1\left(z_1\right)=\frac{n_{21}(1-{\omega }_1)+(n_{21}+d_1)z_1^2{v}_1\left(z_1\right)}{n_{21}+d_1{\omega }_1},h_2\left(z_2\right)=\frac{n_{12}(1-{\omega }_2)+(n_{12}+d_2)z_2^2{v}_2\left(z_2\right)}{n_{12}+d_2{\omega }_2},$$

(77)

From their definitions in (28) and (29), it follows that the functions $v_1\left(z_1\right)$ and $v_2\left(z_2\right)$ only contain powers of $z_1$ and $z_2$ with nonnegative coefficients, but are not necessarily normalized. It is useful to replace them by new functions, say $c_1\left(z_1\right)$ and $c_2\left(z_2\right)$, that do satisfy a normalization condition, and, hence, are genuine pgfs, as follows:

$$c_1\left(z_1\right)\triangleq \frac{v_1\left(z_1\right)}{v_1\left(1\right)}=\frac{v_1\left(z_1\right)}{{\omega }_1},c_2\left(z_2\right)\triangleq \frac{v_2\left(z_2\right)}{v_2\left(1\right)}=\frac{v_2\left(z_2\right)}{{\omega }_2}.$$

(78)

All the defining functions of our model can then be expressed in terms of the pgfs $c_1\left(z_1\right)$ and $c_2\left(z_2\right)$ as follows:

$$f_1\left(z_1\right)=1-{\omega }_1+{\omega }_1{z}_1^2{c}_1\left(z_1\right),f_2\left(z_2\right)=1-{\omega }_2+{\omega }_2{z}_2^2{c}_2\left(z_2\right),[0.3cm]$$

(79)

$$g_1\left(z_1\right)=1-{\omega }_1+{\omega }_1{z}_1{c}_1\left(z_1\right),g_2\left(z_2\right)=1-{\omega }_2+{\omega }_2{z}_2{c}_2\left(z_2\right),\left[0.3cm\right]$$

(80)

$$h_1\left(z_1\right)=1-{\theta }_1+{\theta }_1{z}_1^2{c}_1\left(z_1\right),h_2\left(z_2\right)=1-{\theta }_2+{\theta }_2{z}_2^2{c}_2\left(z_2\right),\left[0.3cm\right]$$

(81)

where we have defined the probabilities ${\theta }_1$ and ${\theta }_2$ as

$${\theta }_1\triangleq \frac{(n_{21}+d_1){\omega }_1}{n_{21}+d_1{\omega }_1},{\theta }_2\triangleq \frac{(n_{12}+d_2){\omega }_2}{n_{12}+d_2{\omega }_2}.$$

(82)

The arrival pgf $A(z_1,z_2)$ can be determined by substitution of (79), (80) and (81) in (21):

$$A(z_1,z_2)=\frac{n(z_1,z_2)}{1+d_1{\omega }_1\left(1-z_1{c}_1\left(z_1\right)\right)+d_2{\omega }_2\left(1-z_2{c}_2\left(z_2\right)\right)},$$

(83)

where

$$\begin{array}{cc}\hfill n(z_1,z_2)\triangleq n_{11}{z}_1{z}_2& +n_{12}{z}_1\left(1-{\omega }_2+{\omega }_2{z}_2^2{c}_2\left(z_2\right)\right)+n_{21}{z}_2\left(1-{\omega }_1+{\omega }_1{z}_1^2{c}_1\left(z_1\right)\right)\hfill \\ & +n_{22}\left(1-{\theta }_1+{\theta }_1{z}_1^2{c}_1\left(z_1\right)\right)\left(1-{\theta }_2+{\theta }_2{z}_2^2{c}_2\left(z_2\right)\right).\hfill \end{array}$$

(84)

The marginal mean arrival rates can be computed from (18), which results in

$$\begin{array}{cc}\hfill {\lambda }_1& =1-\frac{n_{21}+n_{22}+{\omega }_1{d}_1}{n_{21}+{\omega }_1{d}_1}\left(n_{21}+{\omega }_1{d}_1-{\omega }_1(n_{21}+d_1)\left(2+c_1^{\prime }\left(1\right)\right)\right)\hfill \\ \hfill {\lambda }_2& =1-\frac{n_{12}+n_{22}+{\omega }_2{d}_2}{n_{12}+{\omega }_2{d}_2}\left(n_{12}+{\omega }_2{d}_2-{\omega }_2(n_{12}+d_2)\left(2+c_2^{\prime }\left(1\right)\right)\right).\hfill \end{array}$$

(85)

Consequently, the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with

$$c_1^{\prime }\left(1\right)<\frac{n_{21}-{\omega }_1(2n_{21}+d_1)}{{\omega }_1(n_{21}+d_1)},c_2^{\prime }\left(1\right)<\frac{n_{12}-{\omega }_2(2n_{12}+d_2)}{{\omega }_2(n_{12}+d_2)}.$$

The functions $k_1\left(z_1\right)$ and $k_2\left(z_2\right)$ that constitute the denominator of $U(z_1,z_2)$ can be derived from (39):

$$\begin{array}{cc}\hfill k_1\left(z_1\right)& =\frac{n_{21}+n_{22}+{\omega }_1{d}_1}{n_{21}+{\omega }_1{d}_1}\left(n_{21}(z_1-1)+{\omega }_1(n_{21}+d_1{z}_1)-{\omega }_1(n_{21}+d_1)z_1^2{c}_1\left(z_1\right)\right),\hfill \\ \hfill k_2\left(z_2\right)& =\frac{n_{12}+n_{22}+{\omega }_2{d}_2}{n_{12}+{\omega }_2{d}_2}\left(n_{12}(z_2-1)+{\omega }_2(n_{12}+d_2{z}_2)-{\omega }_2(n_{12}+d_2)z_2^2{c}_2\left(z_2\right)\right),\hfill \end{array}$$

(86)

where we have also used (82). Introducing the notations $V_1\left(z_1\right)$ and $V_2\left(z_2\right)$ as

$$\begin{array}{cc}\hfill V_1\left(z_1\right)& \triangleq \frac{z_1-1}{n_{21}(z_1-1)+{\omega }_1(n_{21}+d_1{z}_1)-{\omega }_1(n_{21}+d_1)z_1^2{c}_1\left(z_1\right)},\hfill \\ \hfill V_2\left(z_2\right)& \triangleq \frac{z_2-1}{n_{12}(z_2-1)+{\omega }_2(n_{12}+d_2{z}_2)-{\omega }_2(n_{12}+d_2)z_2^2{c}_2\left(z_2\right)},\hfill \end{array}$$

(87)

we can compute the joint pgf $U(z_1,z_2)$ from (23) and (86) as

$$U(z_1,z_2)=M{V}_1\left(z_1\right)V_2\left(z_2\right)n(z_1,z_2),$$

(88)

where the constant M has been defined as

$$M\triangleq \frac{U(0,1)U(1,0)(n_{21}+{\omega }_1{d}_1)(n_{12}+{\omega }_2{d}_2)}{(n_{21}+n_{22}+{\omega }_1{d}_1)(n_{12}+n_{22}+{\omega }_2{d}_2)}.$$

As before, the remaining unknown M can be determined by invoking the normalization condition $U(1,1)=1$, which results in

$$M=\left(n_{21}+{\omega }_1{d}_1-{\omega }_1(n_{21}+d_1)\left(2+c_1^{\prime }\left(1\right)\right)\right)\left(n_{12}+{\omega }_2{d}_2-{\omega }_2(n_{12}+d_2)\left(2+c_2^{\prime }\left(1\right)\right)\right).$$

(89)

A fully explicit expression for $U(z_1,z_2)$ then follows from (88), (87) and (89).

Summarizing again, we have thus proven the following corrolary of Theorem 1:

Corrolary C

In the stable parallel-queues system with joint arrival pgf

$$A(z_1,z_2)=\frac{n(z_1,z_2)}{1+d_1{\omega }_1\left(1-z_1{c}_1\left(z_1\right)\right)+d_2{\omega }_2\left(1-z_2{c}_2\left(z_2\right)\right)},$$

(90)

where

$$\begin{array}{cc}\hfill n(z_1,z_2)\triangleq n_{11}{z}_1{z}_2& +n_{12}{z}_1\left(1-{\omega }_2+{\omega }_2{z}_2^2{c}_2\left(z_2\right)\right)+n_{21}{z}_2\left(1-{\omega }_1+{\omega }_1{z}_1^2{c}_1\left(z_1\right)\right)\hfill \\ & +n_{22}\left(1-{\theta }_1+{\theta }_1{z}_1^2{c}_1\left(z_1\right)\right)\left(1-{\theta }_2+{\theta }_2{z}_2^2{c}_2\left(z_2\right)\right),\hfill \end{array}$$

(91)

with $c_1\left(z_1\right)$ and $c_2\left(z_2\right)$ arbitrary one-dimensional pgfs, and

$$\begin{array}{c}\hfill n_{11},n_{12},n_{21},n_{22}\ge 0,n_{11}+n_{12}+n_{21}+n_{22}=1,\\ \hfill 0\le {\omega }_1& ,{\omega }_2\le 1,{\theta }_1\triangleq \frac{(n_{21}+d_1){\omega }_1}{n_{21}+d_1{\omega }_1},{\theta }_2\triangleq \frac{(n_{12}+d_2){\omega }_2}{n_{12}+d_2{\omega }_2},\hfill \end{array}$$

the steady-state joint system-content pgf $U(z_1,z_2)$ is given by

$$U(z_1,z_2)=M{V}_1\left(z_1\right)V_2\left(z_2\right)n(z_1,z_2),$$

(92)

where

$$\begin{array}{cc}\hfill V_1\left(z_1\right)& \triangleq \frac{z_1-1}{n_{21}(z_1-1)+{\omega }_1(n_{21}+d_1{z}_1)-{\omega }_1(n_{21}+d_1)z_1^2{c}_1\left(z_1\right)},\hfill \\ \hfill V_2\left(z_2\right)& \triangleq \frac{z_2-1}{n_{12}(z_2-1)+{\omega }_2(n_{12}+d_2{z}_2)-{\omega }_2(n_{12}+d_2)z_2^2{c}_2\left(z_2\right)},\hfill \end{array}$$

(93)

and

$$M\triangleq \left(n_{21}+{\omega }_1{d}_1-{\omega }_1(n_{21}+d_1)\left(2+c_1^{\prime }\left(1\right)\right)\right)\left(n_{12}+{\omega }_2{d}_2-{\omega }_2(n_{12}+d_2)\left(2+c_2^{\prime }\left(1\right)\right)\right).$$

(94)

6. Special Cases within Subclasses A, B and C

In this section we consider several instances of subclasses A, B and C, whereby specific choices are made for the various parameters and functions appearing in the formulations of Corrolaries A, B and C.

6.1. Special Cases within Subclass A

6.1.1. At Most One Arrival per Slot in Queue 1

Here we choose

$$f_1\left(z_1\right)=1-{\sigma }_1+{\sigma }_1{z}_1,f_1^{\prime }\left(1\right)={\sigma }_1,$$

(95)

which implies that the pgf $A(z_1,z_2)$, given in (57), reduces to

$$A(z_1,z_2)=\left((m_{21}{\sigma }_1+m_{11})z_2)+(m_{22}{\sigma }_1+m_{12})f_2\left(z_2\right)\right)z_1+(1-{\sigma }_1)(m_{21}{z}_2+m_{22}{f}_2\left(z_2\right),$$

which is clearly linear in $z_1$, meaning that queue 1 receives at most one arrival per slot. The marginal arrival pgf $A_2\left(z_2\right)$ and the mean arrival rate ${\lambda }_2$ follow from (53) and (54) as

$$A_2\left(z_2\right)=(m_{11}+m_{21})z_2+(m_{12}+m_{22})f_2\left(z_2\right),{\lambda }_2=1-(m_{12}+m_{22})[1-f_2^{\prime }\left(1\right)],$$

from which we can deduce that

$$f_2\left(z_2\right)=\frac{A_2\left(z_2\right)-(m_{11}+m_{21})z_2}{m_{12}+m_{22}},1-f_2^{\prime }\left(1\right)=\frac{1-{\lambda }_2}{m_{12}+m_{22}}.$$

(96)

According to Corrolary A, the pgf $U(z_1,z_2)$ can be obtained from (59) by substitution of (95), i.e.,

$$U(z_1,z_2)=\frac{(1-{\sigma }_1)\left(1-f_2^{\prime }\left(1\right)\right)(z_1-1)(z_2-1)A(z_1,z_2)}{\left(z_1-(1-{\sigma }_1+{\sigma }_1{z}_1)\right)\left(z_2-f_2\left(z_2\right)\right)}=\frac{\left(1-f_2^{\prime }\left(1\right)\right)(z_2-1)A(z_1,z_2)}{z_2-f_2\left(z_2\right)}.$$

Owing to (96) and (52), this can be rewritten as

$$U(z_1,z_2)=\frac{\left(1-{\lambda }_2\right)(z_2-1)A(z_1,z_2)}{z_2-A_2\left(z_2\right)}.$$

This particular result is well-known. We first established it through an alternative, more direct, approach in our earlier short paper [5]. It is interesting that we retrieve it here as a very simple special case of our more general results.

6.1.2. The Case $m_{12}=m_{21}=0$

Again in our earlier paper [5], we stated (without proof) the following theorem. Later, we also provided a formal proof in [11].

Theorem 2:If $V(z_1,z_2)$ denotes the joint system-content pgf in a parallel-queues system with joint arrival pgf $E(z_1,z_2)$, and a new arrival pgf $A(z_1,z_2)$ is defined as

$$A(z_1,z_2)\triangleq (1-\nu )z_1{z}_2+\nu E(z_1,z_2),\mathrm{where}0<\nu \le 1,$$

(97)

then the joint system-content pgf $U(z_1,z_2)$ corresponding with arrival pgf $A(z_1,z_2)$ is given by

$$U(z_1,z_2)=\frac{V(z_1,z_2)A(z_1,z_2)}{E(z_1,z_2)}.$$

Specifically, if the arrivals of both types are mutually independent in the original system, i.e., if $E(z_1,z_2)$ has a product form, $E(z_1,z_2)=E_1\left(z_1\right)E_2\left(z_2\right)$, then $V(z_1,z_2)$ has a product form too, i.e., $V(z_1,z_2)=V(z_1,1)V(1,z_2)$, with, similar to (12),

$$V(z_1,1)=\frac{\left(1-E_1^{\prime }\left(1\right)\right)(z_1-1)E_1\left(z_1\right)}{z_1-E_1\left(z_1\right)},V(1,z_2)=\frac{\left(1-E_2^{\prime }\left(1\right)\right)(z_2-1)E_2\left(z_2\right)}{z_2-E_2\left(z_2\right)},$$

(98)

and (99) reduces to

$$U(z_1,z_2)=\frac{V(z_1,1)V(1,z_2)A(z_1,z_2)}{E_1\left(z_1\right)E_2\left(z_2\right)}=\frac{\left(1-E_1^{\prime }\left(1\right)\right)\left(1-E_2^{\prime }\left(1\right)\right)(z_1-1)(z_2-1)A(z_1,z_2)}{\left(z_1-E_1\left(z_1\right)\right)\left(z_2-E_2\left(z_2\right)\right)}.$$

(99)

It is remarkable that we can easily retrieve this property as a simple instance of our subclass-A results, if we choose

$$m_{11}=1-\nu ,m_{12}=m_{21}=0,m_{22}=\nu ,f_1\left(z_1\right)=E_1\left(z_1\right),f_2\left(z_2\right)=E_2\left(z_2\right).$$

Indeed, equations (57) and (59) from the formulation of Corrolary A are then equivalent with equations (97) and (99) from the formulation of Theorem 2. We do emphasize that Theorem 2 was proven to be valid also if $E(z_1,z_2)$ does not have a product form.

6.1.3. Geometric f-Distributions

Here, we choose geometric distributions with respective mean values ${\sigma }_1$ and ${\sigma }_2$ for the pgfs $f_1\left(z_1\right)$ and $f_2\left(z_2\right)$:

$$f_1\left(z_1\right)=\frac{1}{1+{\sigma }_1-{\sigma }_1{z}_1},f_2\left(z_2\right)=\frac{1}{1+{\sigma }_2-{\sigma }_2{z}_2},f_1^{\prime }\left(1\right)={\sigma }_1,f_2^{\prime }\left(1\right)={\sigma }_2.$$

(100)

The arrival pgf $A(z_1,z_2)$ then follows from (57) as

$$A(z_1,z_2)=\frac{F(z_1,z_2)}{(1+{\sigma }_1-{\sigma }_1{z}_1)(1+{\sigma }_2-{\sigma }_2{z}_2)},$$

where $F(z_1,z_2)$ is a quadratic polynomial in both $z_1$ and $z_2$, defined as

$$\begin{array}{cc}\hfill F(z_1,z_2)\triangleq m_{22}+m_{12}{z}_1(1+{\sigma }_1& -{\sigma }_1{z}_1)+m_{21}{z}_2(1+{\sigma }_2-{\sigma }_2{z}_2)\hfill \\ & +m_{11}{z}_1{z}_2(1+{\sigma }_1-{\sigma }_1{z}_1)(1+{\sigma }_2-{\sigma }_2{z}_2).\hfill \end{array}$$

The marginal mean arrival rates follow from (54):

$${\lambda }_1=1-(m_{21}+m_{22})(1-{\sigma }_1),{\lambda }_2=1-(m_{12}+m_{22})(1-{\sigma }_2).$$

(101)

The stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are therefore equivalent with ${\sigma }_1<1,{\sigma }_2<1$.

The system-content pgf $U(z_1,z_2)$ can be obtained by using (100) in (59):

$$U(z_1,z_2)=\frac{(1-{\sigma }_1)(1-{\sigma }_2)F(z_1,z_2)}{(1-{\sigma }_1{z}_1)(1-{\sigma }_2{z}_2)},$$

(102)

a remarkably simple expression. The zeroes of the denominator are

$$z_1=\frac{1}{{\sigma }_1}>1,z_2=\frac{1}{{\sigma }_2}>1.$$

We return to this special case further in the paper.

6.1.4. Binomial f-Distributions

Here, we choose binomial distributions of order 2, again with respective mean values ${\sigma }_1$ and ${\sigma }_2$, for the pgfs $f_1\left(z_1\right)$ and $f_2\left(z_2\right)$:

$$f_1\left(z_1\right)={\left(1-\frac{{\sigma }_1}{2}-\frac{{\sigma }_1}{2}{z}_1\right)}^2,f_2\left(z_2\right)={\left(1-\frac{{\sigma }_2}{2}-\frac{{\sigma }_2}{2}{z}_2\right)}^2,f_1^{\prime }\left(1\right)={\sigma }_1,f_2^{\prime }\left(1\right)={\sigma }_2.$$

(103)

The arrival pgf $A(z_1,z_2)$ follows from (57) as

$$\begin{array}{cc}\hfill A(z_1,z_2)=m_{11}{z}_1{z}_2+m_{12}{z}_1(1& -\frac{{\sigma }_2}{2}-\frac{{\sigma }_2}{2}{z}_2{)}^2+m_{21}{z}_2{\left(1-\frac{{\sigma }_1}{2}-\frac{{\sigma }_1}{2}{z}_1\right)}^2\hfill \\ & +m_{22}{\left(1-\frac{{\sigma }_1}{2}-\frac{{\sigma }_1}{2}{z}_1\right)}^2{\left(1-\frac{{\sigma }_2}{2}-\frac{{\sigma }_2}{2}{z}_2\right)}^2,\hfill \end{array}$$

and is a quadratic polynomial in both $z_1$ and $z_2$. Again, the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with ${\sigma }_1<1,{\sigma }_2<1$.

The system-content pgf $U(z_1,z_2)$ can be obtained by using (103) in (59):

$$U(z_1,z_2)=\frac{16(1-{\sigma }_1)(1-{\sigma }_2)A(z_1,z_2)}{\left({(2-{\sigma }_1)}^2-{\sigma }_1^2{z}_1\right)\left({(2-{\sigma }_2)}^2-{\sigma }_2^2{z}_2\right)},$$

again a rather simple expression. The zeroes of the denominator are

$$z_1={\left(\frac{2-{\sigma }_1}{{\sigma }_1}\right)}^2>1,z_2={\left(\frac{2-{\sigma }_2}{{\sigma }_2}\right)}^2>1.$$

6.1.5. Batch-2-Geometric f-Distributions

Here, we choose batch-2-geometric distributions with respective mean values ${\sigma }_1$ and ${\sigma }_2$ for the pgfs $f_1\left(z_1\right)$ and $f_2\left(z_2\right)$:

$$f_1\left(z_1\right)=\frac{2}{2+{\sigma }_1-{\sigma }_1{z}_1^2},f_2\left(z_2\right)=\frac{2}{2+{\sigma }_2-{\sigma }_2{z}_2^2},f_1^{\prime }\left(1\right)={\sigma }_1,f_2^{\prime }\left(1\right)={\sigma }_2.$$

(104)

The terminology batch-2-geometric reflects the fact that a random variable with this distribution can only take values equal to geometrically distributed multiples of the batch-size 2. The arrival pgf $A(z_1,z_2)$ follows from (57) as

$$A(z_1,z_2)=\frac{F(z_1,z_2)}{\left(2+{\sigma }_1-{\sigma }_1{z}_1^2\right)\left(2+{\sigma }_2-{\sigma }_2{z}_2^2\right)},$$

where $F(z_1,z_2)$ is a cubic polynomial in both $z_1$ and $z_2$, defined as

$$\begin{array}{cc}\hfill F(z_1,z_2)\triangleq 4m_{22}+2m_{12}{z}_1(2+{\sigma }_1& -{\sigma }_1{z}_1^2)+2m_{21}{z}_2(2+{\sigma }_2-{\sigma }_2{z}_2^2)\hfill \\ & +m_{11}{z}_1{z}_2(2+{\sigma }_1-{\sigma }_1{z}_1^2)(2+{\sigma }_2-{\sigma }_2{z}_2^2).\hfill \end{array}$$

Once again, the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with ${\sigma }_1<1,{\sigma }_2<1$.

The system-content pgf $U(z_1,z_2)$ can be obtained by using (104) in (59):

$$U(z_1,z_2)=\frac{(1-{\sigma }_1)(1-{\sigma }_2)F(z_1,z_2)}{\left(2-{\sigma }_1{z}_1(1+z_1)\right)\left(2-{\sigma }_2{z}_2(1+z_2)\right)},$$

a remarkably simple expression. The zeroes of the denominator lie outside the unit disks $\{z_1:|z_1|\le 1\}$ and $\{z_2:|z_2|\le 1\}$ in the complex $z_1$-plane and $z_2$-plane, respectively, and are given by

$$\begin{array}{cc}\hfill z_1& =\frac{\sqrt{{\sigma }_1({\sigma }_1+8)}-{\sigma }_1}{2{\sigma }_1}>1\mathrm{and}{z}_1=-\frac{\sqrt{{\sigma }_1({\sigma }_1+8)}+{\sigma }_1}{2{\sigma }_1}<-1\hfill \\ \hfill z_{2a}& =\frac{\sqrt{{\sigma }_2({\sigma }_2+8)}-{\sigma }_2}{2{\sigma }_2}>1\mathrm{and}{z}_2=-\frac{\sqrt{{\sigma }_2({\sigma }_2+8)}+{\sigma }_2}{2{\sigma }_2}<-1.\hfill \end{array}$$

6.2. Special Cases within Subclass B

In subclass A, the bivariate arrival pgf $A(z_1,z_2)$ is completely determined by the univariate pgfs $f_1\left(z_1\right)$ and $f_2\left(z_2\right)$, and the pgfs $g_1\left(z_1\right)$ and $g_2\left(z_2\right)$ play no role. In subclass B, however, all the defining one-dimensional pgfs contribute to $A(z_1,z_2)$. In order to specifically examine the effect of $g_1\left(z_1\right)$ and $g_2\left(z_2\right)$, we consider two examples where $f_1\left(z_1\right)=f_2\left(z_2\right)=1$, combined with different choices for $g_1\left(z_1\right)$ and $g_2\left(z_2\right)$.

6.2.1. The Case $f_1\left(z_1\right)=f_2\left(z_2\right)=1,g_1\left(z_1\right)=z_1,g_2\left(z_2\right)=z_2$

Here, we choose

$$f_1\left(z_1\right)=f_2\left(z_2\right)=1,g_1\left(z_1\right)=z_1,g_2\left(z_2\right)=z_2,f_1^{\prime }\left(1\right)=f_2^{\prime }\left(1\right)=0,g_1^{\prime }\left(1\right)=1,g_2^{\prime }\left(1\right)=1.$$

(105)

The arrival pgf $A(z_1,z_2)$ follows from (67) and (68) as

$$A(z_1,z_2)=\frac{n_{11}{z}_1{z}_2+n_{12}{z}_1+n_{21}{z}_2+n_{22}(1-{\gamma }_1+{\gamma }_1{z}_1^2)(1-{\gamma }_2+{\gamma }_2{z}_2^2)}{1+d_1+d_2-d_1{z}_1-d_2{z}_2}.$$

(106)

In view of (63), the marginal mean arrival rates are

$${\lambda }_1=1-\frac{1-2{\gamma }_1}{1-{\gamma }_1}\left(n_{21}+(1-{\gamma }_1)n_{22}\right),{\lambda }_2=1-\frac{1-2{\gamma }_2}{1-{\gamma }_2}\left(n_{12}+(1-{\gamma }_2)n_{22}\right),$$

and, hence, the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with ${\gamma }_1<1/2,{\gamma }_2<1/2$.

The joint system-content pgf $U(z_1,z_2)$ can be obtained by using (105) in (68), (65) and (66), which results in

$$U(z_1,z_2)=\frac{(1-2{\gamma }_1)(1-2{\gamma }_2)\left(n_{11}{z}_1{z}_2+n_{12}{z}_1+n_{21}{z}_2+n_{22}[1-{\gamma }_1+{\gamma }_1{z}_1^2][1-{\gamma }_2+{\gamma }_2{z}_2^2]\right)}{(1-{\gamma }_1-{\gamma }_1{z}_1)(1-{\gamma }_2-{\gamma }_2{z}_2)}.$$

(107)

The zeroes of the denominator are given by

$$z_1=\frac{1-{\gamma }_1}{{\gamma }_1}>1,z_2=\frac{1-{\gamma }_2}{{\gamma }_2}>1.$$

Remark

It is worth mentioning that a special instance of this case was treated in our recent paper [6]. There, we considered a parallel-queues system, whereby the total number of arrivals per slot (of both customer types together) has a shifted geometric distribution with pgf $C\left(z\right)$ and mean value $q\ge 1$, i.e., $C\left(z\right)=z/[q-(q-1\left)z\right]$, and new arrivals are routed independently and probabilistically to queue 1 or 2 with probabilities p and $1-p$ respectively, implying that the joint arrival pgf $A(z_1,z_2)$ is given by

$$A(z_1,z_2)=C(p{z}_1+(1-p)z_2)=\frac{p{z}_1+(1-p)z_2}{q-(q-1)p{z}_1-(q-1)(1-p)z_2}.$$

(108)

In appendix A of [6], we formally proved that the joint system-content pgf $U(z_1,z_2)$ for this system is

$$U(z_1,z_2)=\frac{({\kappa }_1-1)({\tau }_1-1)\left(p{z}_1+(1-p)z_2\right)}{({\kappa }_1-z_1)({\tau }_1-z_2)},\mathrm{with}{\kappa }_1\triangleq \frac{1-p}{p(q-1)},{\tau }_1\triangleq \frac{p}{(1-p)(q-1)}.$$

(109)

The proof in [6] was a (rather complicated) constructive proof, whereby we explicitly solved the functional Equation (9),

$$K(z_1,z_2)U(z_1,z_2)=A(z_1,z_2)L(z_1,z_2),$$

by expressing that the unknown function $L(z_1,z_2)$ should vanish for all $(z_1,z_2)$ in the area of convergence of $U(z_1,z_2)$ for which the kernel $K(z_1,z_2)$ vanishes. This allowed us to determine the boundary functions $U(z_1,0)$ and $U(0,z_2)$, and, from this, the function $L(z_1,z_2)$, and, eventually, the pgf $U(z_1,z_2)$, as given in (109).

The function $A(z_1,z_2)$ in (108) is clearly of the form (106) considered in the current subsection, provided we choose

$$n_{11}=0,n_{12}=p,n_{21}=1-p,n_{22}=0,d_1=p(q-1),d_2=(1-p)(q-1).$$

(110)

We now show that the solution (109) can be easily retrieved from the results in the current subsection.

Proof. 

Using (110) in the definitions (61) of our current parameters ${\gamma }_1$ and ${\gamma }_2$ leads to

$${\gamma }_1\triangleq \frac{d_1}{d_1+n_{21}}=\frac{p(q-1)}{p(q-1)+1-p},{\gamma }_2\triangleq \frac{d_2}{d_2+n_{12}}=\frac{(1-p)(q-1)}{(1-p)(q-1)+p},$$

and, from this,

$$\frac{1-{\gamma }_1}{{\gamma }_1}=\frac{1-p}{p(q-1)}={\kappa }_1,\frac{1-{\gamma }_2}{{\gamma }_2}=\frac{p}{(1-p)(q-1)}={\tau }_1,$$

(111)

and

$$\frac{1-2{\gamma }_1}{{\gamma }_1}=\frac{1-p}{p(q-1)}={\kappa }_1-1,\frac{1-2{\gamma }_2}{{\gamma }_2}=\frac{p}{(1-p)(q-1)}={\tau }_1-1.$$

(112)

Inserting (110) in (107) yields

$$U(z_1,z_2)=\frac{(1-2{\gamma }_1)(1-2{\gamma }_2)\left(p{z}_1+(1-p)z_2\right)}{(1-{\gamma }_1-{\gamma }_1{z}_1)(1-{\gamma }_2-{\gamma }_2{z}_2)}.$$

(113)

Division of both the numerator and the denominator of the above expression by ${\gamma }_1{\gamma }_2$ and substitution of (111) and (112) then clearly shows that (113) is identical to (109). □

We have thus been able, once again, to recover a specific existing result as a particular case of the results of the current paper.

6.2.2. The Case $f_1\left(z_1\right)=f_2\left(z_2\right)=1,g_1\left(z_1\right)=z_1^2,g_2\left(z_2\right)=z_2^2$

Here, we choose

$$f_1\left(z_1\right)=f_2\left(z_2\right)=1,g_1\left(z_1\right)=z_1^2,g_2\left(z_2\right)=z_2^2,f_1^{\prime }\left(1\right)=f_2^{\prime }\left(1\right)=0,g_1^{\prime }\left(1\right)=2,g_2^{\prime }\left(1\right)=2.$$

(114)

The arrival pgf $A(z_1,z_2)$ follows from (67) and (68) as

$$A(z_1,z_2)=\frac{n_{11}{z}_1{z}_2+n_{12}{z}_1+n_{21}{z}_2+n_{22}(1-{\gamma }_1+{\gamma }_1{z}_1^3)(1-{\gamma }_2+{\gamma }_2{z}_2^3)}{1+d_1+d_2-d_1{z}_1^2-d_2{z}_2^2}.$$

The marginal mean arrival rates can be deduced from (63):

$${\lambda }_1=1-\frac{1-3{\gamma }_1}{1-{\gamma }_1}\left(n_{21}+(1-{\gamma }_1)n_{22}\right),{\lambda }_2=1-\frac{1-3{\gamma }_2}{1-{\gamma }_2}\left(n_{12}+(1-{\gamma }_2)n_{22}\right),$$

and, hence, the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with ${\gamma }_1<1/3,{\gamma }_2<1/3$.

The joint system-content pgf $U(z_1,z_2)$ can be obtained by using (114) in (68), (65) and (66), which results in

$$U(z_1,z_2)=\frac{(1-3{\gamma }_1)(1-3{\gamma }_2)\left(n_{11}{z}_1{z}_2+n_{12}{z}_1+n_{21}{z}_2+n_{22}[1-{\gamma }_1+{\gamma }_1{z}_1^3][1-{\gamma }_2+{\gamma }_2{z}_2^3]\right)}{\left(1-{\gamma }_1-{\gamma }_1{z}_1(1+z_1)\right)\left(1-{\gamma }_2-{\gamma }_2{z}_2(1+z_2)\right)}.$$

(115)

Again, it is easy to show that the zeroes of the denominator lie outside the unit disks $\{z_1:|z_1|\le 1\}$ and $\{z_2:|z_2|\le 1\}$ in the complex $z_1$-plane and $z_2$-plane, respectively. We return to this special case in more detail further in the paper.

6.3. Special Cases within Subclass C

In order to simplify the expressions in this subsection, we first make the following assumptions:

$$n_{11}=0,n_{12}=n_{21}=d_1=d_2=d,n_{22}=1-2d,{\omega }_1={\omega }_2=\frac{1}{4}.$$

(116)

According to (90) and (91), the arrival pgf is given by

$$A(z_1,z_2)=\frac{n(z_1,z_2)}{1+\frac{d}{4}\left(2-z_1{c}_1\left(z_1\right)-z_2{c}_2\left(z_2\right)\right)},$$

where

$$n(z_1,z_2)=\frac{d}{4}\left(z_1\left(3+z_2^2{c}_2\left(z_2\right)\right)+z_2\left(3+z_1^2{c}_1\left(z_1\right)\right)\right)+\frac{1-2d}{25}\left(3+z_2^2{c}_2\left(z_2\right)\right)\left(3+z_1^2{c}_1\left(z_1\right)\right).$$

(117)

The marginal mean arrival rates are

$${\lambda }_1=1-\frac{4-3d}{20}\left(1-2c_1^{\prime }\left(1\right)\right),{\lambda }_2=1-\frac{4-3d}{20}\left(1-2c_2^{\prime }\left(1\right)\right),$$

which implies that the stability conditions ${\lambda }_1<1,{\lambda }_2<1$ are equivalent with $c_1^{\prime }\left(1\right)<1/2,c_2^{\prime }\left(1\right)<1/2$. From (93) and (94), we get

$$V_1\left(z_1\right)=\frac{4(z_1-1)}{d\left(5z_1-2z_1^2{c}_1\left(z_1\right)-3\right)},V_2\left(z_2\right)=\frac{4(z_2-1)}{d\left(5z_2-2z_2^2{c}_2\left(z_2\right)-3\right)},$$

and

$$M=\frac{d^2}{16}\left(1-2c_1^{\prime }\left(1\right)\right)\left(1-2c_2^{\prime }\left(1\right)\right).$$

It then follows from (92) that the system-content pgf is given by

$$U(z_1,z_2)=\frac{\left(1-2c_1^{\prime }\left(1\right)\right)\left(1-2c_2^{\prime }\left(1\right)\right)(z_1-1)(z_2-1)n(z_1,z_2)}{\left(3-5z_1+2z_1^2{c}_1\left(z_1\right)\right)\left(3-5z_2+2z_2^2{c}_2\left(z_2\right)\right)},$$

We now make a number of different choices for the pgfs $c_1\left(z_1\right)$ and $c_2\left(z_2\right)$.

6.3.1. Bernoulli c-Distributions

Here, we choose Bernoulli distributions with parameters ${\sigma }_1$ and ${\sigma }_2$ for the pgfs $c_1\left(z_1\right)$ and $c_2\left(z2\right)$:

$$c_1\left(z_1\right)=1-{\sigma }_1+{\sigma }_1{z}_1,c_2\left(z_2\right)=1-{\sigma }_2+{\sigma }_2{z}_2,c_1^{\prime }\left(1\right)={\sigma }_1,c_2^{\prime }\left(1\right)={\sigma }_2.$$

The pgf $U(z_1,z_2)$ then reduces to

$$U(z_1,z_2)=\frac{(1-2{\sigma }_1)(1-2{\sigma }_2)n(z_1,z_2)}{(3-2z_1-2{\sigma }_1{z}_1^2)(3-2z_2-2{\sigma }_2{z}_2^2)}.$$

(118)

We come back to this special case further in this paper.

6.3.2. Geometric c-Distributions

Here, we choose geometric distributions with respective mean values ${\sigma }_1$ and ${\sigma }_2$ for the pgfs $c_1\left(z_1\right)$ and $c_2\left(z2\right)$:

$$c_1\left(z_1\right)=\frac{1}{1+{\sigma }_1-{\sigma }_1{z}_1},c_2\left(z_2\right)=\frac{1}{1+{\sigma }_2-{\sigma }_2{z}_2},c_1^{\prime }\left(1\right)={\sigma }_1,c_2^{\prime }\left(1\right)={\sigma }_2.$$

(119)

The pgf $U(z_1,z_2)$ then reduces to

$$U(z_1,z_2)=\frac{(1-2{\sigma }_1)(1-2{\sigma }_2)(1+{\sigma }_1-{\sigma }_1{z}_1)(1+{\sigma }_2-{\sigma }_2{z}_2)n(z_1,z_2)}{\left(3(1+{\sigma }_1)-(2+5{\sigma }_1)z_1\right)\left(3(1+{\sigma }_2)-(2+5{\sigma }_2)z_2\right)}.$$

The zeroes of the denominator are given by

$$z_1=\frac{3(1+{\sigma }_1)}{2+5{\sigma }_1}>1,z_2=\frac{3(1+{\sigma }_2)}{2+5{\sigma }_2}>1.$$

6.3.3. Negative Binomial c-Distributions

Here, we choose negative binomial distributions of order two for the pgfs $c_1\left(z_1\right)$ and $c_2\left(z_2\right)$:

$$c_1\left(z_1\right)=\frac{4}{{(2+{\sigma }_1-{\sigma }_1{z}_1)}^2},c_2\left(z_2\right)=\frac{4}{{(2+{\sigma }_2-{\sigma }_2{z}_2)}^2},c_1^{\prime }\left(1\right)={\sigma }_1,c_2^{\prime }\left(1\right)={\sigma }_2.$$

(120)

In this case, the pgf $U(z_1,z_2)$ is given by

$$U(z_1,z_2)=W_1\left(z_1\right)W_2\left(z_2\right)n(z_1,z_2),$$

where

$$\begin{array}{cc}\hfill W_1\left(z_1\right)& \triangleq \frac{(1-2{\sigma }_1){(2+{\sigma }_1-{\sigma }_1{z}_1)}^2}{\left(3{(2+{\sigma }_1)}^2-4(2+{\sigma }_1)(1+2{\sigma }_1)z_1+5{\sigma }_1^2{z}_1^2\right)},\hfill \\ \hfill W_2\left(z_2\right)& \triangleq \frac{(1-2{\sigma }_2){(2+{\sigma }_2-{\sigma }_2{z}_2)}^2}{\left(3{(2+{\sigma }_2)}^2-4(2+{\sigma }_2)(1+2{\sigma }_2)z_2+5{\sigma }_2^2{z}_2^2\right)}.\hfill \end{array}$$

Again, the zeroes of the denominator are the solutions of quadratic equations and can be computed explicitly; also, it is not difficult to show that they lie outside the unit disks in the $z_1$-plane and the $z_2$-plane; their exact expressions are omitted, as they are of no particular importance at this stage.

7. Inverting the Joint pgf $U(z_1,z_2)$

In this section, we focus on the derivation of the steady-state joint probability mass function (pmf) $u(m,n)$ of the system contents in queues 1 and 2, which is defined as

$$u(m,n)\triangleq \underset{k\to \infty }{lim}\mathrm{Prob}\left[u_{1,k}=m,u_{2,k}=n\right],$$

and is related to the joint pgf $U(z_1,z_2)$ by the equation

$$U(z_1,z_2)=\sum _{m=0}^{\infty }\sum _{n=0}^{\infty }u(m,n)z_1^m{z}_2^n.$$

In an earlier paper [11], we proved (with slightly different notations) the following useful theorem to determine $u(m,n)$ from $U(z_1,z_2)$ for “interior states” $(m,n)$ in the state space.

Theorem 3

If the joint pgf $U(z_1,z_2)$ is arationalfunction of $z_1$ and $z_2$ of the form

$$U(z_1,z_2)=\frac{B(z_1,z_2)}{r_1\left(z_1\right)r_2\left(z_2\right)}=\frac{B(z_1,z_2)}{{\prod }_{i=1}^{L_1}(z_1-{\kappa }_i){\prod }_{j=1}^{L_2}(z_2-{\tau }_j)},$$

(121)

where the numerator $B(z_1,z_2)$ is a bivariate polynomial of degree $K_1$ in $z_1$ and $K_2$ in $z_2$, and the denominator is a product of two univariate functions $r_1\left(z_1\right)$ and $r_2\left(z_2\right)$, having only zeroes of multiplicity 1, and the numerator and the denominator are mutually prime, then threshold values $m_0$ and $n_0$ can be defined as $m_0\triangleq max(0,K_1-L_1+1),n_0\triangleq max(0,K_2-L_2+1)$, such that for $m\ge m_0,n\ge n_0$, the pmf $u(m,n)$ is given by a finite linear combination of bivariate geometric terms, i.e.,

$$u(m,n)=\sum _{i=1}^{L_1}\sum _{j=1}^{L_2}{\mu }_{i,j}{\left(\frac{1}{{\kappa }_i}\right)}^m{\left(\frac{1}{{\tau }_j}\right)}^n,m\ge m_0,n\ge n_0,$$

(122)

where

$${\mu }_{i,j}\triangleq \frac{B({\kappa }_i,{\tau }_j)}{{\kappa }_i{\tau }_j{r}_1^{\prime }\left({\kappa }_i\right)r_2^{\prime }\left({\tau }_j\right)}.$$

(123)

7.1. Some Comments

In all the examples that we have considered in this paper, we have chosen rational functions for the constituting one-dimensional pgfs $f_1\left(z_1\right)$, $f_2\left(z_2\right)$, $g_1\left(z_1\right)$, $g_2\left(z_2\right)$, $h_1\left(z_1\right)$, $h_2\left(z_2\right)$ of the joint arrival pgf $A(z_1,z_2)$, defined in (21). This implies that the pgf $U(z_1,z_2)$, given in (23) by

$$U(z_1,z_2)=\frac{U(0,1)U(1,0)(z_1-1)(z_2-1)n(z_1,z_2)}{k_1\left(z_1\right)k_2\left(z_2\right)},$$

(124)

is a rational bivariate function whose denominator is a product of two univariate functions, and can therefore be expressed in the form required to apply Theorem 3.

By definition, the quantities ${\kappa }_i$ and ${\tau }_j$, occurring in (122), are the zeroes of $r_1\left(z_1\right)$ (or $k_1\left(z_1\right)$) and $r_2\left(z_2\right)$ (or $k_2\left(z_2\right)$). According to (122), the geometric decay rates of the system-content distribution are the inverse values of these zeroes, i.e., the ith decay rate for queue 1 is equal to $1/{\kappa }_i$, and the jth decay rate for queue 2 is given by $1/{\tau }_j$. Each bivariate geometric term in $u(m,n)$ thus corresponds to a couple $({\kappa }_i,{\tau }_j)$ of zeroes of $r_1\left(z_1\right)$ and $r_2\left(z_2\right)$, but the opposite is not necessarily true, since, for some i and j, it may happen that the coefficient ${\mu }_{i,j}$ in Equation (122) is zero. According to (123), this situation occurs if $B({\kappa }_i,{\tau }_j)=0$. If this is the case for one or more couples $({\kappa }_i,{\tau }_j)$, the number of nonzero bivariate geometric terms in $u(m,n)$ is lower than the product $L1\times L2$.

7.2. Specific Examples

In this subsection, we apply Theorem 3 in a number of examples of arrival pgfs $A(z_1,z_2)$ belonging to subclasses A, B and C, as defined before.

7.2.1. An Example within Subclass A

In this example, we revisit the model of subSection 6.1.3. The system-content pgf $U(z_1,z_2)$ is given in (102). The parameters and functions, appearing in the formulation of Theorem 3 are $K_1=K_2=2,L_1=L_2=1$, and

$$B(z_1,z_2)=(1-{\sigma }_1)(1-{\sigma }_2)F(z_1,z_2),r_1\left(z_1\right)=1-{\sigma }_1{z}_1,r_2\left(z_2\right)=1-{\sigma }_2{z}_2,$$

with

$$\begin{array}{cc}\hfill F(z_1,z_2)\triangleq m_{22}+m_{12}{z}_1(1+{\sigma }_1& -{\sigma }_1{z}_1)+m_{21}{z}_2(1+{\sigma }_2-{\sigma }_2{z}_2)\hfill \\ & +m_{11}{z}_1{z}_2(1+{\sigma }_1-{\sigma }_1{z}_1)(1+{\sigma }_2-{\sigma }_2{z}_2).\hfill \end{array}$$

The zeroes of $r_1\left(z_1\right)$ and $r_2\left(z_2\right)$ are

$${\kappa }_1=\frac{1}{{\sigma }_1}>1,{\tau }_1=\frac{1}{{\sigma }_2}>1.$$

The coefficient ${\mu }_{1,1}$ can be computed from (123) as

$${\mu }_{1,1}=(1-{\sigma }_1)(1-{\sigma }_2).$$

Finally, the pmf $u(m,n)$ for interior states $(m,n)$ follows from (122) as

$$u(m,n)=(1-{\sigma }_1)(1-{\sigma }_2){\left(\frac{1}{{\sigma }_1}\right)}^m{\left(\frac{1}{{\sigma }_2}\right)}^n,m\ge 2,n\ge 2.$$

7.2.2. An Example within Subclass B

Here, we consider a symmetric instance of the model of subSection 6.2.2, with the following specific parameter choices:

$$n_{12}=n_{21}=n_0,d_1=d_2=d,{\gamma }_1={\gamma }_2=\gamma .$$

The joint system-content pgf $U(z_1,z_2)$ can be obtained from (115):

$$U(z_1,z_2)=\frac{{(1-3\gamma )}^2\left(n_{11}{z}_1{z}_2+n_0{z}_1+n_0{z}_2+n_{22}[1-\gamma +\gamma z_1^3][1-\gamma +\gamma z_2^3]\right)}{\left(1-\gamma -\gamma z_1(1+z_1)\right)\left(1-\gamma -\gamma z_2(1+z_2)\right)}.$$

We can apply Theorem 3 with $K_1=K_2=3,L_1=L_2=2$,

$$B(z_1,z_2)\triangleq {(1-3\gamma )}^2\left(n_{11}{z}_1{z}_2+n_0{z}_1+n_0{z}_2+n_{22}[1-\gamma +\gamma z_1^3][1-\gamma +\gamma z_2^3]\right),$$

and

$$r_1\left(z_1\right)\triangleq 1-\gamma -\gamma z_1(1+z_1),r_2\left(z_2\right)\triangleq 1-\gamma -\gamma z_2(1+z_2).$$

The zeroes of $r_1\left(z_1\right)$ and $r_2\left(z_2\right)$ lie outside the unit disks $\{z_1:|z_1|\le 1\}$ and $\{z_2:|z_2|\le 1\}$ in the complex $z_1$-plane and $z_2$-plane, respectively, and are given by

$${\kappa }_1={\tau }_1=\frac{\sqrt{\gamma (4-3\gamma )}-\gamma }{2\gamma }>1,{\kappa }_2={\tau }_2=-\frac{\sqrt{\gamma (4-3\gamma )}+\gamma }{2\gamma }<-1.$$

The coefficients ${\mu }_{i,j}$ can be computed from (123):

$$\begin{array}{cc}\hfill {\mu }_{1,1}& =\mu \frac{1-\gamma +(1-4n_0)(1+\sqrt{\gamma (4-3\gamma )})}{2-\gamma -\sqrt{\gamma (4-3\gamma )}},{\mu }_{2,2}=\mu \frac{1-\gamma +(1-4n_0)(1-\sqrt{\gamma (4-3\gamma )})}{2-\gamma +\sqrt{\gamma (4-3\gamma )}}\hfill \\ \hfill {\mu }_{1,2}& ={\mu }_{2,1}=\mu \frac{1-\gamma -n_0(2-3\gamma )}{1-\gamma },\mathrm{where}\mu \triangleq \frac{{(1-3\gamma )}^2}{\gamma (4-3\gamma )}.\hfill \end{array}$$

(125)

In general, all these coefficients are nonzero, and the linear combination in (122) contains four terms:

$$u(m,n)={\mu }_{1,1}{\left(\frac{1}{{\kappa }_1}\right)}^{m+n}+{\mu }_{12}\left({\left(\frac{1}{{\kappa }_1}\right)}^m{\left(\frac{1}{{\kappa }_2}\right)}^n+{\left(\frac{1}{{\kappa }_2}\right)}^m{\left(\frac{1}{{\kappa }_1}\right)}^n\right)+{\mu }_{2,2}{\left(\frac{1}{{\kappa }_2}\right)}^{m+n},m\ge 2,n\ge 2.$$

Careful study shows that it is impossible to choose the parameter $n_0$, appearing in (125), in such a way that the coefficients ${\mu }_{1,1}$, ${\mu }_{1,2}$ or ${\mu }_{2,1}$ are zero, but there does exist a value of $n_0$ such that ${\mu }_{2,2}$ vanishes; the required $n_0$-value is

$$n_0=\frac{2-\gamma +\sqrt{\gamma (4-3\gamma )}}{4\left(1+\sqrt{\gamma (4-3\gamma )}\right)}>0.$$

(126)

This is an acceptable value since it implies that

$$n_{11}+n_{22}=1-n_{12}-n_{21}=1-2n_0=\frac{\gamma +\sqrt{\gamma (4-3\gamma )}}{2\left(1+\sqrt{\gamma (4-3\gamma )}\right)}>0$$

So, in case $n_0$ is chosen in accordance with (126), the linear combination in (122) contains only three bivariate geometric terms:

$$u(m,n)={\mu }_{1,1}{\left(\frac{1}{{\kappa }_1}\right)}^{m+n}+{\mu }_{12}\left({\left(\frac{1}{{\kappa }_1}\right)}^m{\left(\frac{1}{{\kappa }_2}\right)}^n+{\left(\frac{1}{{\kappa }_2}\right)}^m{\left(\frac{1}{{\kappa }_1}\right)}^n\right),m\ge 2,n\ge 2,$$

and does not contain a term with two negative decay rates.

7.2.3. An Example within Subclass C

We now go back to the model in subSection 6.3.1. Here, the system-content pgf $U(z_1,z_2)$ is given by (118). We can apply Theorem 3 provided we choose $K_1=K_2=3,L_1=L_2=2$,

$$B(z_1,z_2)=(1-2{\sigma }_1)(1-2{\sigma }_2)n(z_1,z_2),r_1\left(z_1\right)=(3-2z_1-2{\sigma }_1{z}_1^2),r_2\left(z_2\right)=(3-2z_2-2{\sigma }_1{z}_2^2),$$

where, owing to (117), $n(z_1,z_2)$ is given by

$$\begin{array}{cc}\hfill n(z_1,z_2)=\frac{d}{4}(& z_1\left(3+z_2^2(1-{\sigma }_2+{\sigma }_2{z}_2)\right)+z_2\left(3+z_1^2(1-{\sigma }_1+{\sigma }_1{z}_1)\right))\hfill \\ & +\frac{1-2d}{25}\left(3+z_1^2(1-{\sigma }_1+{\sigma }_1{z}_1)\right)\left(3+z_2^2(1-{\sigma }_2+{\sigma }_2{z}_2)\right).\hfill \end{array}$$

(127)

The zeroes of $r_1\left(z_1\right)$ and $r_2\left(z_2\right)$ lie outside the unit disks $\{z_1:|z_1|\le 1\}$ and $\{z_2:|z_2|\le 1\}$ in the complex $z_1$-plane and $z_2$-plane, respectively, and are given by

$$\begin{array}{cc}\hfill {\kappa }_1& =\frac{\sqrt{1+6{\sigma }_1}-1}{2{\sigma }_1}>1,{\kappa }_2=-\frac{\sqrt{1+6{\sigma }_1}+1}{2{\sigma }_1}<-1\hfill \\ \hfill {\tau }_1& =\frac{\sqrt{1+6{\sigma }_2}-1}{2{\sigma }_2}>1,{\tau }_2=-\frac{\sqrt{1+6{\sigma }_2}+1}{2{\sigma }_2}<-1.\hfill \end{array}$$

The coefficients ${\mu }_{i,j}$ can be computed from (123):

$$\begin{array}{cc}\hfill {\mu }_{1,1}& =\mu \frac{4+d({\sigma }_1{\kappa }_1+{\sigma }_2{\tau }_1-1)}{(1+2{\sigma }_1{\kappa }_1)(1+2{\sigma }_2{\tau }_1)},{\mu }_{1,2}=\mu \frac{4+d({\sigma }_1{\kappa }_1+{\sigma }_2{\tau }_2-1)}{(1+2{\sigma }_1{\kappa }_1)(1+2{\sigma }_2{\tau }_2)},\hfill \\ \hfill {\mu }_{2,1}& =\mu \frac{4+d({\sigma }_1{\kappa }_2+{\sigma }_2{\tau }_1-1)}{(1+2{\sigma }_1{\kappa }_2)(1+2{\sigma }_2{\tau }_1)},{\mu }_{2,2}=\mu \frac{4+d({\sigma }_1{\kappa }_2+{\sigma }_2{\tau }_2-1)}{(1+2{\sigma }_1{\kappa }_2)(1+2{\sigma }_2{\tau }_2)},\hfill \end{array}$$

where we have defined $\mu$ as

$$\mu \triangleq \frac{(1-2{\sigma }_1)(1-2{\sigma }_2)}{16}.$$

Again, in general, all these coefficients are nonzero, and the linear combination in (122) contains four terms:

$$u(m,n)={\mu }_{1,1}{\left(\frac{1}{{\kappa }_1}\right)}^m{\left(\frac{1}{{\tau }_1}\right)}^n+{\mu }_{12}{\left(\frac{1}{{\kappa }_1}\right)}^m{\left(\frac{1}{{\tau }_2}\right)}^n+{\left(\frac{1}{{\kappa }_2}\right)}^m{\left(\frac{1}{{\tau }_1}\right)}^n+{\mu }_{2,2}{\left(\frac{1}{{\kappa }_2}\right)}^m{\left(\frac{1}{{\tau }_2}\right)}^n,m\ge 2,n\ge 2.$$

(128)

Let $d_{ij}$ denote the value of d that makes ${\mu }_{i,j}$ zero, then we can easily compute the following values:

$$\begin{array}{cc}\hfill d_{11}& =\frac{8}{4-\sqrt{1+6{\sigma }_1}-\sqrt{1+6{\sigma }_2}},d_{12}=\frac{8}{4-\sqrt{1+6{\sigma }_1}+\sqrt{1+6{\sigma }_2}},\hfill \\ \hfill d_{21}& =\frac{8}{4+\sqrt{1+6{\sigma }_1}-\sqrt{1+6{\sigma }_2}},d_{22}=\frac{8}{4+\sqrt{1+6{\sigma }_1}+\sqrt{1+6{\sigma }_2}}.\hfill \end{array}$$

Taking into account the stability conditions ${\sigma }_1<1/2,{\sigma }_2<1/2$, as we have shown in subSection 6.3.1, it is readily seen that all these d-values are positive, as required, but none of them is lower than $1/2$, which is also necessary, because in this model, according to (116), $n_{22}=1-2d$ and needs to be positive. We conclude that, in this particular case, the pmf $u(m,n)$ always contains exactly four bivariate geometric terms, as shown in (128).

8. Concluding REMARKS

This paper has considered the steady-state queueing analysis of a system of two parallel discrete-time single-server queues with mutually interdependent arrivals, characterized by the joint arrival pgf $A(z_1,z_2)$. We have identified a very broad, multi-parameter, generic, class of arrival pgfs $A(z_1,z_2)$ for which we were able to determine explicit analytic solutions for the joint system-content pgf $U(z_1,z_2)$. We think this is the main virtue of the paper. It is also interesting to observe that our results encompass most of the previously known results for this kind of system, which is known to be hard to analyze.

Although the class of arrival pgfs $A(z_1,z_2)$ examined in this paper is very broad, it still has its limitations, which are mainly due to the shape of the arrival pgf, i.e., Equation (14),

$$A(z_1,z_2)=\frac{n_{11}{z}_1{z}_2+n_{12}{z}_1{f}_2\left(z_2\right)+n_{21}{z}_2{f}_1\left(z_1\right)+n_{22}{h}_1\left(z_1\right)h_2\left(z_2\right)}{1+d_1+d_2-d_1{g}_1\left(z_1\right)-d_2{g}_2\left(z_2\right)},$$

and the requirement that the pgfs appearing in the above expression should be related as stated in equations (24) or (33), which can be rewritten as

$$\begin{array}{c}\hfill {\beta }_1{n}_{21}\left(z_1-f_1\left(z_1\right)\right)+{\beta }_1{d}_1{z}_1\left(1-g_1\left(z_1\right)\right)+n_{21}\left(z_1-h_1\left(z_1\right)\right)=0,\\ \hfill {\beta }_2{n}_{12}\left(z_2-f_2\left(z_2\right)\right)+{\beta }_2{d}_2{z}_2\left(1-g_2\left(z_2\right)\right)+n_{12}\left(z_2-h_2\left(z_2\right)\right)=0.\end{array}$$

Since the parameters ${\beta }_1$ and ${\beta }_2$ need to be strictly positive – we need this in the proof of Lemma 1 – we can thus not have a constant numerator for $A(z_1,z_2)$ without the requirement that the denominator be also constant. Hence, a seemingly simple arrival pgf like

$$A(z_1,z_2)=\frac{1}{1+d_1+d_2-d_1{z}_1-d_2{z}_2}$$

(129)

is not a special case of our model. So far, we have never seen a solution for the “global geometric” arrival pgf in (129), and the current paper also does not provide one.

Future work could go in several directions. We may try to further extend the class of arrival pgfs which lead to explicit solutions for the parallel-queues system, dealt with in this paper, but we may also consider other types of coupled queues, such as the (other) ones mentioned in the introduction section of this paper.