Electric Capacitors Based on Silicone Oil and Iron Oxide Microfibres: Effects of the Magnetic Field on the Electrical Susceptance and Conductance

1. Introduction

Advancements in capacitor technology are pivotal for the development of modern electronic devices and systems [1,2,3,4,5]. Electrical capacitors are essential components in a wide range of applications, from energy storage systems [6,7,8] to advanced sensors [9,10,11] and transducers [12,13,14]. The performance and functionality of capacitors are significantly influenced by the properties of the dielectric materials used, which has led to ongoing research and innovation in this field [15,16]. They form components of an electrical circuit that consist of two or more electrodes with a dielectric material placed between them.

Various types of electrical capacitors are known, each defined by the dielectric material used. For instance, some capacitors utilize dielectric materials such as oil-impregnated paper [17], mineral oil [18], or nonlinear dielectric materials [19,20]. Another category includes electrolytic capacitors, where both the electrodes and the dielectric material are produced using nanotechnology processes [21,22]. These capacitors are specifically designed for storing electrical energy [23]. Additionally, there are capacitors based on silicon oil (SO) and magnetizable nano-microparticles. In these capacitors, the equivalent electrical components can be adjusted magnetically [24,25,26,27,28].

Andrei et al. [24], manufactured capacitors using suspensions based on SO, iron microparticles, and stearic acid with varying mass ratios. These capacitors are characterized by an increase in electrical conductance with the increase in the ratio of stearic acid to the magnetizable phase in a magnetic field. Conversely, the duration for establishing electrical conduction decreases slightly with the increasing intensity of the applied magnetic field. The capacitors detailed in Refs. [25,26] are based on commercially available cotton fabrics impregnated with liquid suspensions that include carbonyl iron microparticles and varying ratios of honey and turmeric powder. When studied in an alternating electric field with frequencies ranging from 25 Hz to 1 MHz, superimposed on a static magnetic field, the equivalent electrical capacitance and resistance of the capacitors are measured. These properties are coarsely adjusted by the ratios of honey to turmeric powder and the values of magnetic flux density, while fine adjustments are achieved through the frequency of the alternating electric field. The capacitors described by Bica et al. [27] are constructed from medical-grade cotton gauze impregnated with liquid composites containing multifloral honey, carbonyl iron microparticles, and varying amounts of turmeric powder. In these capacitors, electrical conductance is coarsely adjusted by the ratio of honey to turmeric quantities and finely tuned by the intensity of the electric field. Iacobescu et al. [28] produced capacitors using cotton fabric impregnated with a magnetic liquid based on mineral oil and magnetite nanoparticles. By maintaining a constant quantity of magnetic liquid, it was observed that the electrical conductance of the composite can be coarsely adjusted by applying compressive stress and finely tuned by the values of the magnetic flux density.

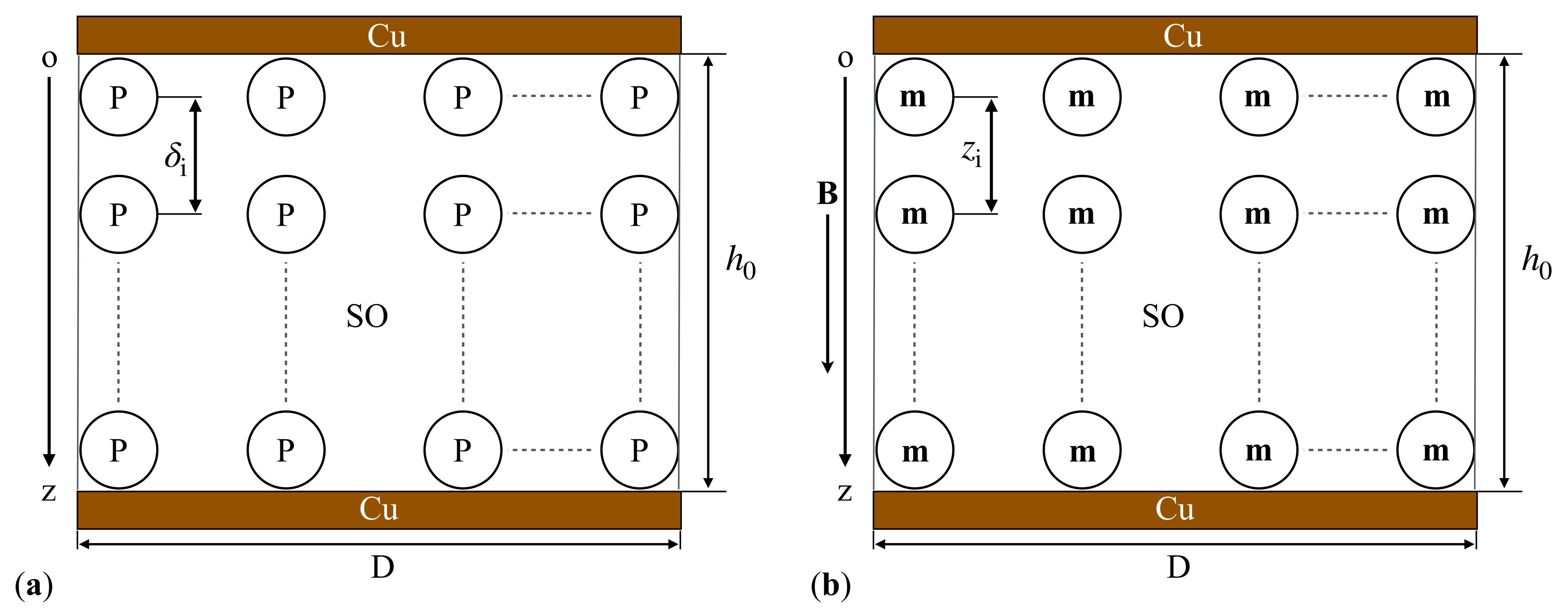
Following this research direction, the present study describes the manufacturing method of capacitors based on SO and microfibers containing $\alpha$-Fe${}_2$O${}_3$, $\gamma$-Fe${}_2$O${}_3$, and Fe${}_3$O${}_4$. The study investigates the electrical behavior of these capacitors under the influence of an external magnetic field superimposed on an alternating electric field, across four distinct volume concentrations of microfibers. Electrical capacitance and resistance measurements are conducted every second over a 60-second interval, revealing significant dependencies on both the quantity of magnetizable phase and the applied magnetic flux density. The obtained data are analyzed to demonstrate that in a medium-frequency electric field, both electrical conductance and susceptance can be coarsely adjusted by varying the ratio of SO to microfibers and finely tuned by the magnetic flux density. Compared to the capacitors produced in [24,25,26,27,28], this study shows that the presence of semiconductor iron oxides in the microfibers alters the behaviour of electrical conductance when a magnetic field is applied. A theoretical model based on dipolar approximations is proposed to explain the underlying physical mechanisms governing the electrical properties of the capacitors.

By providing valuable insights into the design and optimization of magnetodielectric-based capacitors, our findings can influence the development of advanced microelectronic devices and sensor technologies. Improved capacitors with adjustable electrical properties have the potential to enhance the performance and efficiency of energy storage systems, leading to more reliable and scalable renewable energy solutions. Additionally, the ability to fine-tune the electrical characteristics of capacitors through magnetic fields can lead to innovations in electronic circuits, allowing for more adaptable and multifunctional electronic components. This research contributes to the advancement of composites based on iron microfibers and SO, paving the way for new applications and improvements in existing technologies.

This paper is structured as follows: Section 2 provides a detailed description of the materials and methods used in the study, including the preparation of magnetodielectric materials and the manufacturing process of electrical capacitors. Section 3 presents the results of the experimental investigations, analyzing the dependencies of electrical capacitance, resistance, conductance, and susceptance on the volume concentration of microfibers and the applied magnetic flux density. Section 4 discusses the implications of the findings, comparing them with previous studies and theoretical models. Finally, Section 5 concludes the paper by summarizing the key outcomes and suggesting potential directions for future research. The appendices provide additional technical details and supporting data for the experimental and theoretical analyses conducted in the study.

2. Materials and Methods

2.1. Preparation of Magnetodielectric Materials

The materials used for preparation of the magnetodielectric materials are the following:

• SO, from Silicone Comerciale SpA (Italia), with a mass density of ${\rho }_{\mathrm{SO}}=0.97$ g/cm${}^3$ and dynamic viscosity ${\eta }_{\mathrm{SO}}=97$ mPa·s at $T=295$ K.
• The iron oxide microfibers (mFe) are obtained in microwave microplasma, following a procedure described in Ref. [29]. They contain oxides of the type $\alpha -{\mathrm{Fe}}_2{\mathrm{O}}_3$ (12 % by mass), $\gamma -{\mathrm{Fe}}_2{\mathrm{O}}_3$ (62 % by mass), and ${\mathrm{Fe}}_3{\mathrm{O}}_4$ (26 % by mass). The mass density of the microfibers is ${\rho }_{\mathrm{mFe}}=2.875{\mathrm{g}/\mathrm{cm}}^3$ at $T=295\mathrm{K}$ and they exhibit a specific saturation magnetization, ${\sigma }_{\mathrm{mFe}}=22.7$ A·m${}^2$/kg, at a magnetic field intensity, $H=477\mathrm{kA}/\mathrm{m}$. A structural analysis of these microfibers based on SEM, is presented in Appendix A. The average diameter of the nano-microparticles in the microfibers is $d_{\mathrm{m}}=0.94\mu \mathrm{m}\pm 0.01\mu \mathrm{m}$ (see Figure A1).

The magnetodielectric materials consist of mixtures of mFe and SO at four different concentrations, in the form of composite liquids (CL), as listed in Table 1. Each mixture $C{L}_i$ ($i=1,2,3,4$) is mechanically homogenized for a duration of about 300 s at a temperature $T\approx 410$ K. The homogenization of the samples continues until the mixtures are brought to ambient temperature ($T\approx 300$ K).

In the study of the magnetic properties of composite materials, the relationship used to determine the specific saturation magnetization ${\sigma }_{{\mathrm{s}}_{\mathrm{CL}}}$ is ${\mu }_0{\sigma }_{{\mathrm{s}}_{\mathrm{CL}}}={\mu }_0{\Phi }_{\mathrm{mFe}}{\sigma }_{\mathrm{mFe}}$ [30], where ${\mu }_0$ is the vacuum magnetic permeability, ${\Phi }_{mFe}$ is the volume fraction of the mFe microfibers, and ${\sigma }_{\mathrm{mFe}}$ is the specific saturation magnetization. For ${\sigma }_{\mathrm{mFe}}=22.7$ A·m${}^2$/kg and the ${\Phi }_{\mathrm{mFe}}$ values from Table 1, when introduced into the specified relationship above, the ${\sigma }_{{\mathrm{s}}_{\mathrm{CL}}}$ values (see Table 1) of the specific saturation magnetization of the liquids CL are obtained. It is observed from Table 1 that increasing the amount of mFe microfibers results in increased values of ${\sigma }_{{\mathrm{s}}_{\mathrm{CL}}}$.

2.2. Manufacturing Cylindrical Electrical Capacitors

The materials used for manufacturing the cylindrical electrical capacitors (CECs) are the liquids CL${}_i$ ($i=1,2,3,4$) and a textolite plate, single-sided with copper foil. The printed circuit board (PCB), type LMM 100x210E1, is purchased from Electroniclight. The actual board is made from FR4 type epoxy resin, reinforced with fiberglass. On one side of the actual board, an electrolytic copper foil, with a thickness of 35 $\mu$m, is deposited (Figure 1a, pos. 1).

Two PCB boards are used to manufacture the CEC. On the copper foil (pos. 1 in Figure 1b), an insulating material ring (pos. 2 in Figure 1b) is fixed with an adhesive. At the end of this procedure, a cylinder with dimensions 28 mm $\times 1.4$ mm is formed. In the cylinder from Figure 1(b), the liquids CL${}_i$ ($i=1,2,\dots ,4$) are introduced one by one. On top of the cylinder, filled with CL (Figure 2a), the copper-faced side of the second PCB board is fixed by sliding. At the end of this step, the CEE is obtained as shown in Figure 2(b). This assembly is then consolidated with a medical adhesive tape (Figure 2c).

2.3. Experimental Setup and Measurement Protocol

The experimental setup designed for studying the susceptance and electrical conductance of CECs has the overall configuration shown in Figure 3. The setup includes a handmade electromagnet (EM) with a coil connected to a direct current source (DCS), type RXN3020D (made in China). Between the N and S poles of the electromagnet, the CECs and the Hall probe (h) of the gaussmeter (GS), type DX-102 (made in China), are fixed by turn. The CEC is connected to the RLC bridge, type CHY 41R (made in Taiwan). The CHY 41R bridge, set at a frequency of 1 kHz, is used to measure the equivalent electrical capacitance and the equivalent electrical resistance of CECs, which are connected in parallel. The measured values, taken at intervals of $\Delta t=1$ s, are transmitted and recorded by the computing unit (CU) via the RS232 interface.

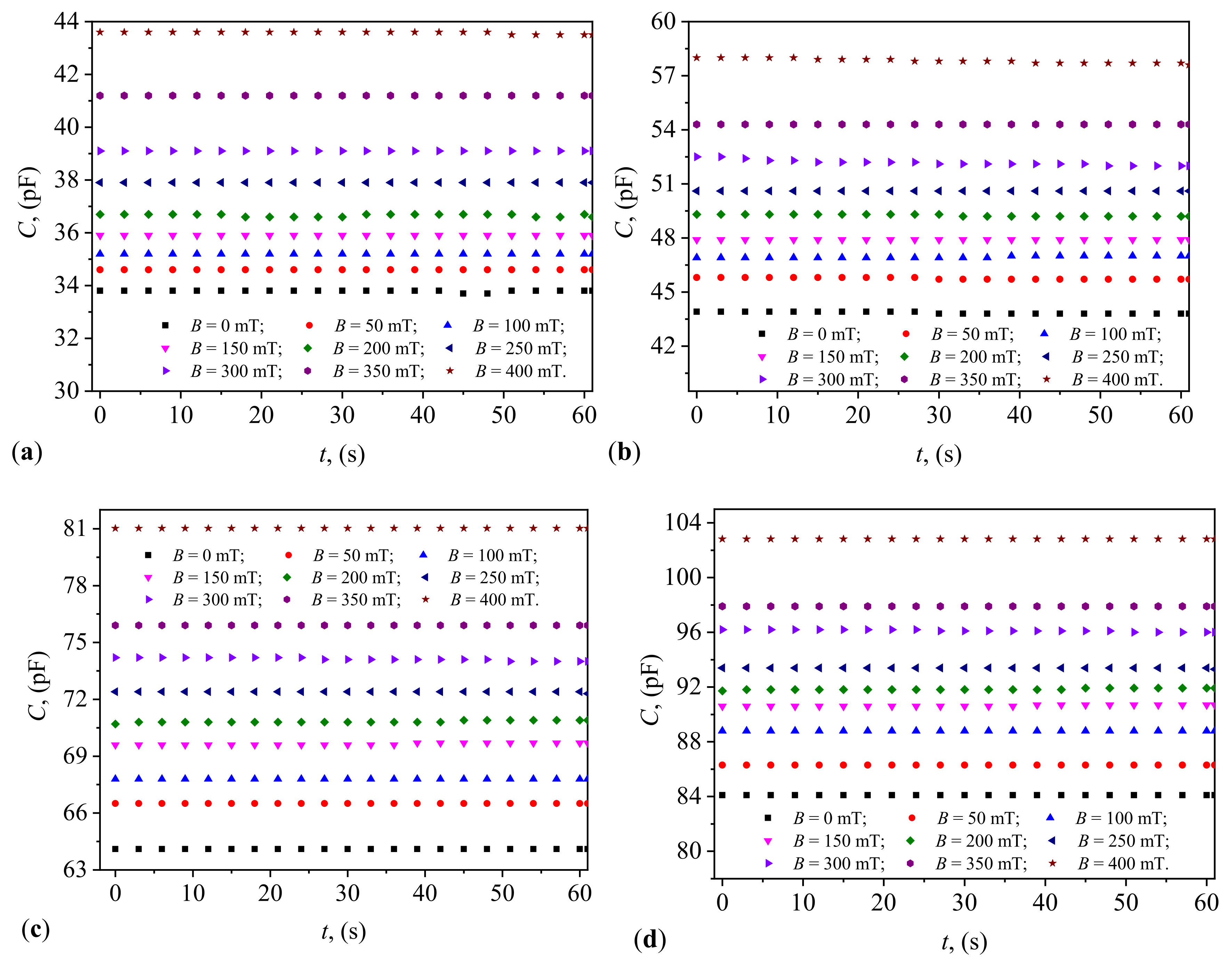
3. Results

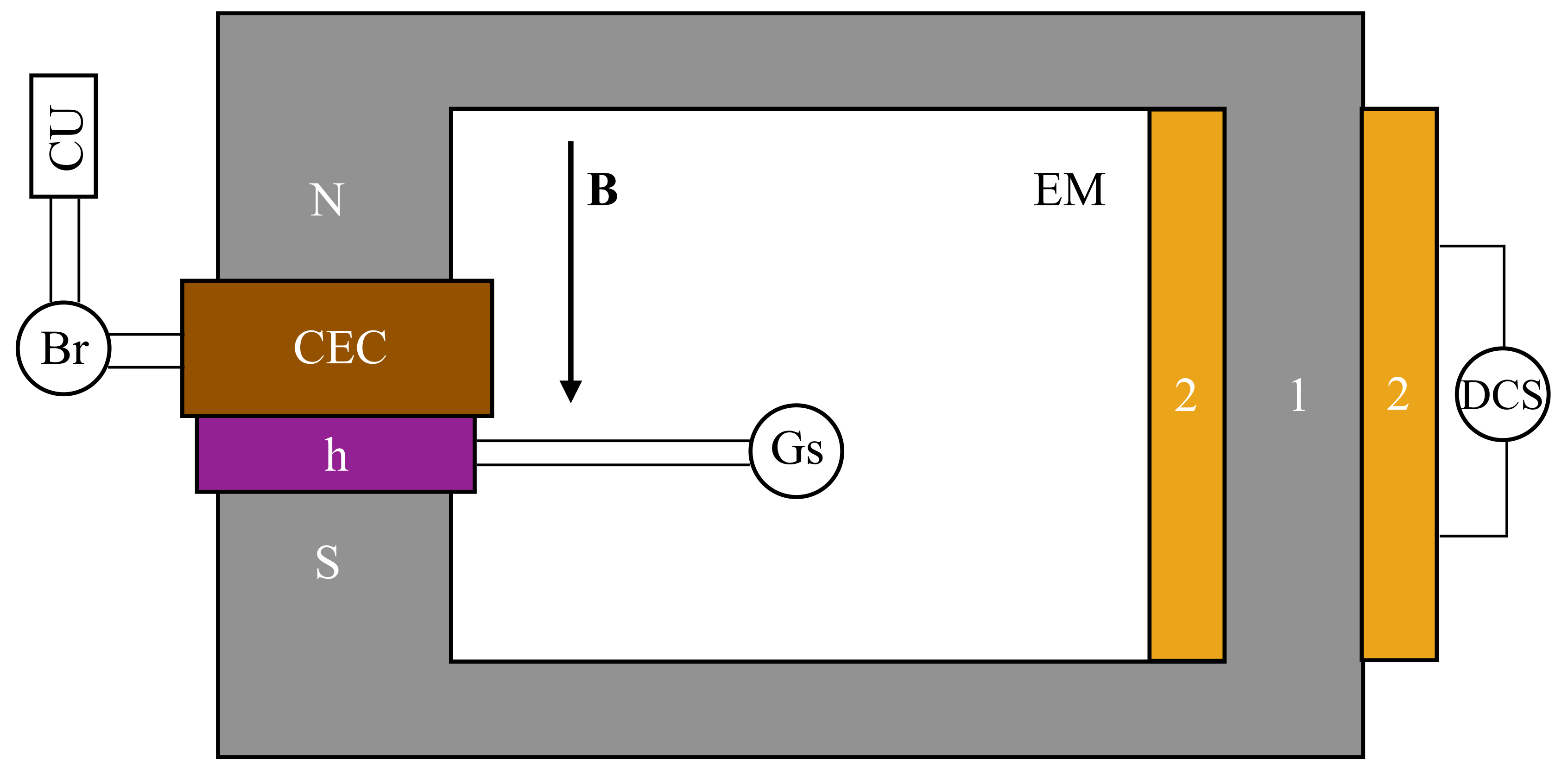
The CEC is placed between the N and S poles of the electromagnet shown in Figure 3. Using measurements from the h connected to the DX-102 gaussmeter, the magnetic flux densities are adjusted to values $B\le 0.2$ mT. The terminals of the CEC are connected to the input of the CHY 41R bridge, set at a frequency of $f=1$ kHz. The equivalent electrical capacitance C and the equivalent electrical resistance R are measured and recorded, considering the electrical representation of the CECs as an electric dipole consisting of an ideal capacitor connected in parallel with an ideal resistor. Measurements are recorded at time intervals $\Delta t=1$ s over a period of 60 s, for magnetic flux density values B adjusted in steps of $\Delta B=50$ mT up to a maximum of 400 mT. After recording the values of C and R, the magnetic flux density B is adjusted to a new value, without reverting to the initial value, and measurements of C and R continue at one-second intervals until the 60-second period is exhausted. This procedure is then repeated.

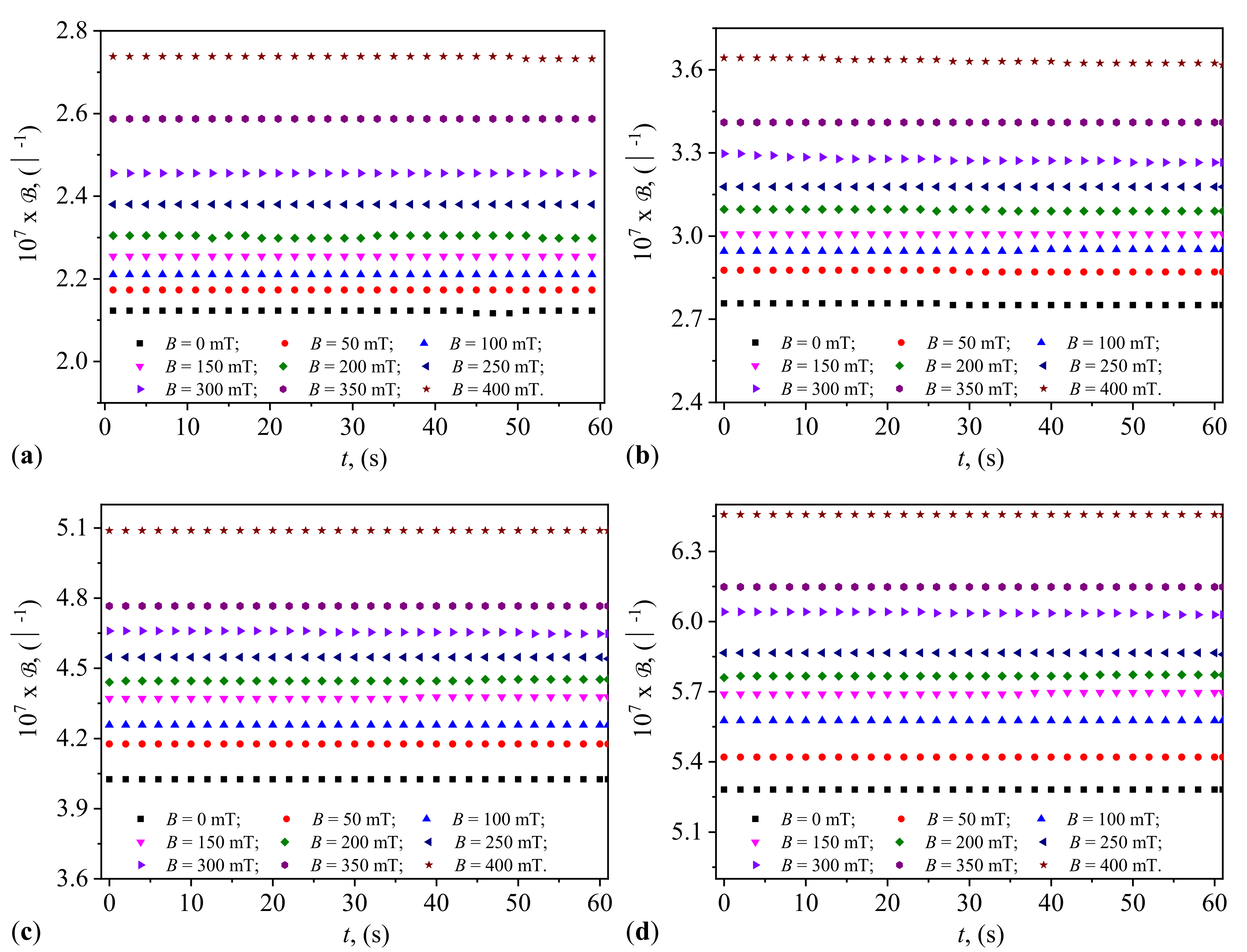
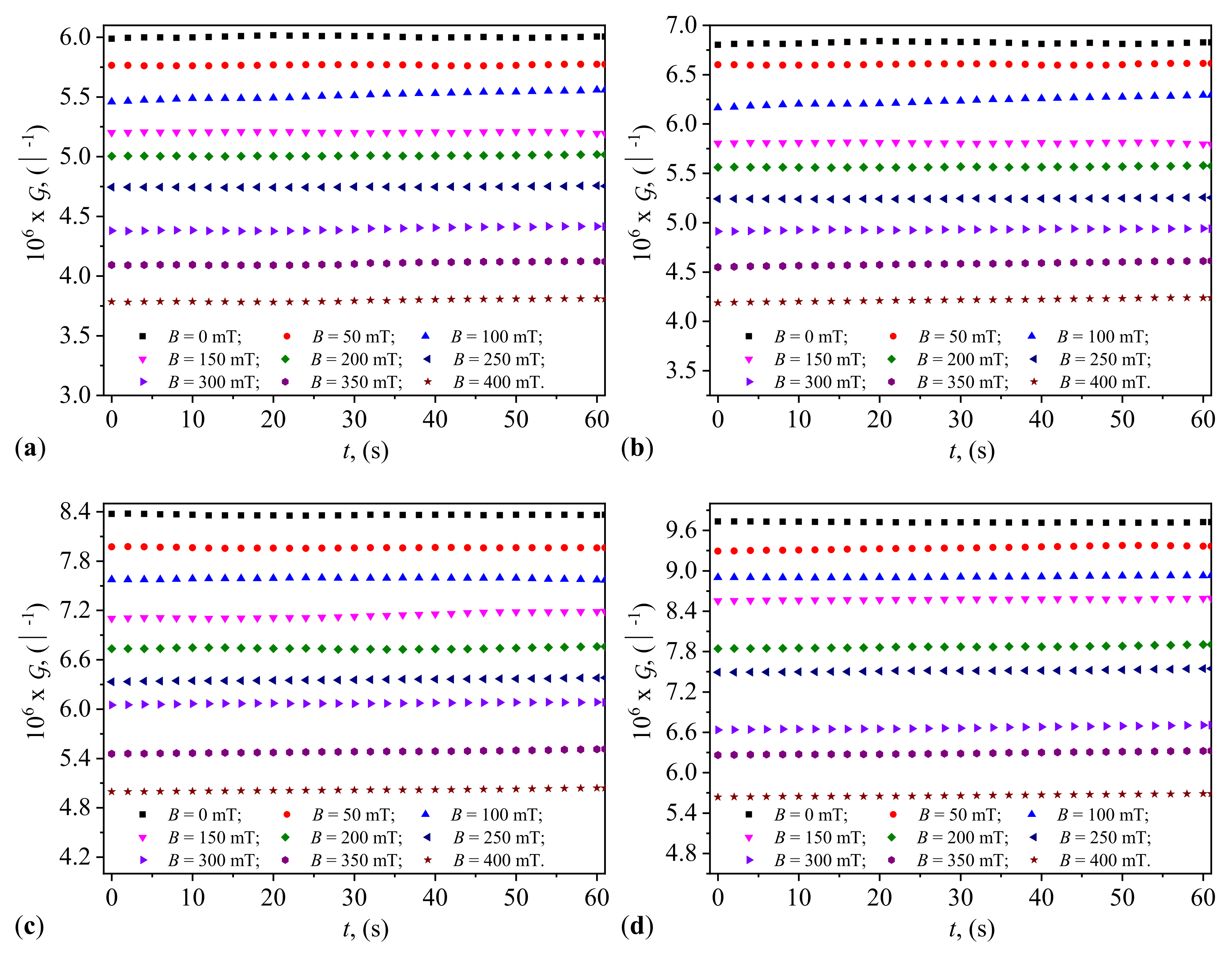
Using this method, for the four capacitors, we obtain the functions $C=C{\left(t\right)}_{\mathrm{B}}$ and $R=R{\left(t\right)}_{\mathrm{B}}$ graphically represented in Appendix B (Figure A2 and Figure A3). Knowing that the electrical susceptance and conductance of the CECs are defined by the relationships $\mathcal{B}=2\pi fC$ and respectively $\mathcal{G}=1/R$, we then obtain the functions $\mathcal{B}=\mathcal{B}{\left(t\right)}_{\mathrm{B}}$ and $\mathcal{G}=\mathcal{G}{\left(t\right)}_{\mathrm{B}}$, graphically represented in Figure 4 and Figure 5.

It can be observed from Figure 4 and Figure 5 that the quantities $\mathcal{B}$ and $\mathcal{G}$ are stable over time. This stability is related to the fact that during the preparation of the CLs, nano-microparticles of hematite, maghemite, and magnetite detach from the mFe microfibers. The hematite nano-microparticles instantly polarize magnetically and form stable aggregates in the absence of the magnetic field [31,32]. These aggregates, based on reports in [31], exhibit high friction when moving in the SO, thus eliminating or at least reducing the sedimentation of the solid phase. This effect is observed by noting that the values $\mathcal{B}$ and the $\mathcal{G}$ are stable over time. Figure 4 and Figure 5 also show that the quantities $\mathcal{B}$ and $\mathcal{G}$ increase with the increasing values of $\Phi$ in the CLs of CECs (see Appendix C).

On the other hand, while the functions $\mathcal{B}={\mathcal{B}}_{\mathrm{B}}$ increase with the increasing values B of the magnetic flux density in accordance with relation (A21) in Appendix F, the functions $\mathcal{G}=\mathcal{G}{\left(t\right)}_{\mathrm{B}}$ show values that decrease with the increasing values of the same magnetic flux density, contrary to relation (A23) in Appendix F. This discrepancy is due to the semiconductor properties of the hematite nano-microparticles [33]. As the values of the magnetic flux density increase, the thickness of the layer formed by the hematite nano-microparticles increases in the vicinity of the magnetite and maghemite microparticles. The effect is the reduction of electrical conductivity and the increase in the relative dielectric permittivity of the liquids due to the concentration of electric charges in the volume of the CLs. The observed effects are the increase in the value of $\mathcal{B}$ and the decrease in the values of $\mathcal{G}$ with the increasing magnetic flux density.

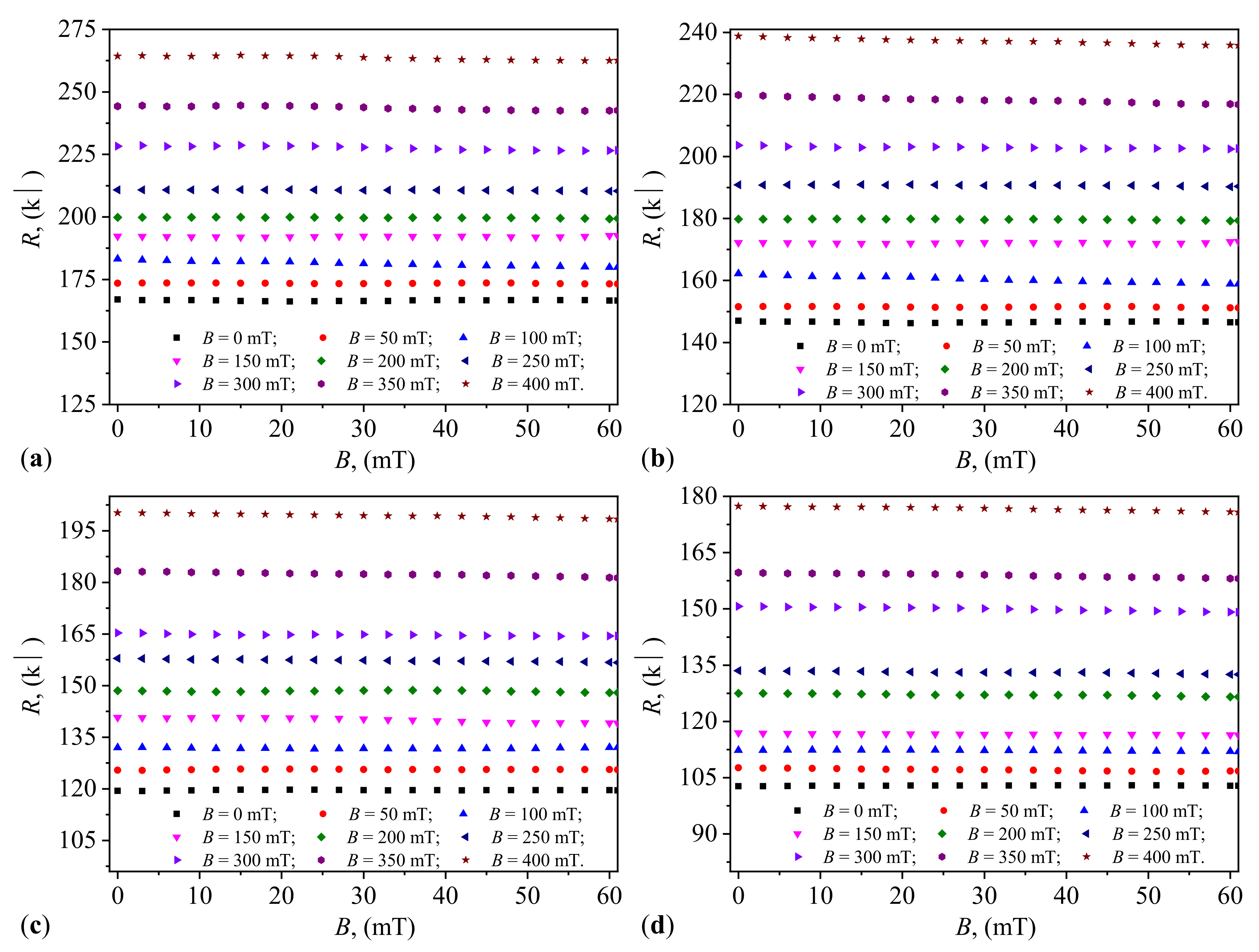
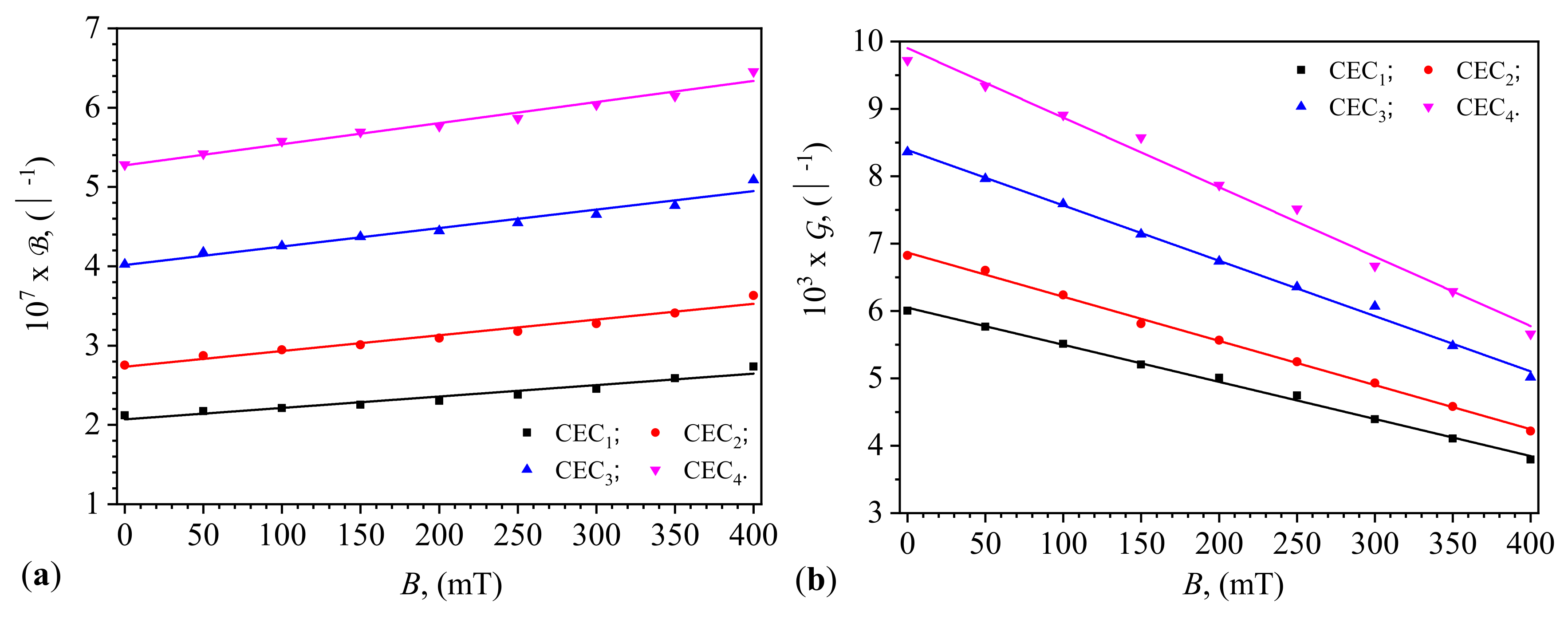
Using the functions $\mathcal{B}=\mathcal{B}{\left(t\right)}_{\mathrm{B}}$ from Figure 4 for $0\le t\left(\mathrm{s}\right)\le 60$, the average values ${\mathcal{B}}_{\mathrm{m}}$ are calculated as a function of the values B of the magnetic flux density. The functions ${\mathcal{B}}_{\mathrm{m}}={\mathcal{B}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$, for $i=1,2,3,4$, are obtained and shown in Figure 6(a). Proceeding identically, but using the functions $\mathcal{G}=\mathcal{G}{\left(t\right)}_{\mathrm{B}}$ from Figure 5, the functions ${\mathcal{G}}_{\mathrm{m}}={\mathcal{G}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ are obtained and shown in Figure 6(b).

It is observed from Figure 6(a) that the functions ${\mathcal{B}}_{\mathrm{m}}={\mathcal{B}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ have the form:

$${\mathcal{B}}_m={\mathcal{B}}_0+{\alpha }_{\mathcal{B}}·B,$$

(1)

where ${\mathcal{B}}_0$ is the initial electric susceptibility and ${\alpha }_{\mathcal{B}}$ is the slope. By fitting data in Figure 6(a) with Equation 1, one obtains the values of the parameters ${\mathcal{B}}_0$ and ${\alpha }_{\mathcal{B}}$, as listed in Table 2.

From Figure 6(b), we observe that the functions ${\mathcal{G}}_{\mathrm{m}}={\mathcal{G}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ have the form:

$${\mathcal{G}}_m={\mathcal{G}}_0-{\alpha }_{\mathcal{G}}·B,$$

(2)

where ${\mathcal{G}}_0$ is the initial electric conductance and ${\alpha }_{\mathcal{G}}$ is the slope. By fitting data in Figure 6(b) with Equation 2, one obtains the values of the parameters ${\mathcal{G}}_0$ and ${\alpha }_{\mathrm{G}}$, as listed in Table 2.

It can be observed from Figure 6 that the dependence of the quantities ${\mathcal{B}}_{\mathrm{m}}$ and $G_{\mathrm{m}}$ on the values B of the magnetic flux density is linear, in accordance with Equation (A21) from Appendix F. This result is due to hematite nano-microparticles which form aggregates that cannot be broken down by thermal energy [31,32,33]. On the other hand, the viscosity ${\eta }_i$ of the liquids CL${}_i$ ($i=1,2,3,4$) increases with the increasing values of B of the magnetic flux density, accompanied by the formation of new aggregate structures [31,32]. From Figure 6, we observe that the values of the quantities ${\mathcal{B}}_{\mathrm{m}}$ and $G_{\mathrm{m}}$ of the capacitors CEC${}_i$ are coarsely adjusted by the choice of liquids CL${}_i$ and finely by the values of B of the magnetic flux density.

The dynamic viscosity ${\eta }_i$ of the liquids CL${}_i$ ($i=1,2,3,4$) in the absence of a magnetic field can be approximated using the relation [34,35]:

$${\eta }_i={\eta }_{SO}(1+2.5{\Phi }_i+6.4{\Phi }_i^2),$$

(3)

where ${\eta }_{SO}=0.97\mathrm{Pa}·\mathrm{s}$ is the dynamic viscosity of SO at a temperature of ${24}^{\circ }\mathrm{C}$. For the volume fractions ${\Phi }_i$ given in Table 1, the dynamic viscosity of the liquids CL${}_i$ in the absence of a magnetic field has the following values:

$$\eta (\mathrm{Pa}\times \mathrm{s})=\left\{\begin{array}{cc}1.70332,\hfill & \mathrm{for}{\Phi }_1=20\mathrm{vol}\%\hfill \\ 2.93328,\hfill & \mathrm{for}{\Phi }_2=40\mathrm{vol}\%\hfill \\ 4.65988,\hfill & \mathrm{for}{\Phi }_3=60\mathrm{vol}\%\hfill \\ 6.88312,\hfill & \mathrm{for}{\Phi }_4=80\mathrm{vol}\%\hfill \end{array}\right.$$

(4)

From the set of values in Equation 3, it can be observed that the dynamic viscosity increases with the increase in the volume fractions of microfibers.

It is well-known that in a magnetic field, the solid phase, in the form of ferri-ferromagnetic nano-microparticles, forms aggregates within the liquid matrix [24,27,28]. This effect transforms the liquid from Newtonian to non-Newtonian [36,37]. To determine the viscosity of the liquids in a magnetic field, we use Equation (A21) from Appendix F, from which we obtain:

$${\eta }_{B_i}=\frac{{\Phi }_i^{1/3}{B}^{2}t}{16{\mu }_0\left(1-\frac{{\mathcal{B}}_{0_i}}{{\mathcal{B}}_{{\mathrm{m}}_i}}\right)},i=1,2,3,4,$$

(5)

where ${\mathcal{B}}_{0_i}$ and ${\mathcal{B}}_{{\mathrm{m}}_i}$ are the average values of the susceptance of the capacitors CEC${}_i$ at the initial moment and at time t, respectively. The latter one is the average duration of maintaining the capacitors CEC${}_i$ in the magnetic field (see above).

For $t=30\mathrm{s}$, ${\mu }_0=4\pi \times {10}^{-7}\mathrm{H}/\mathrm{m}$, and the values of ${\Phi }_i$ ($i=1,2,\dots ,4$) from Table 1, when substituted in Equation (5), we obtain the following expressions for the viscosity of the liquids CL${}_i$ in a magnetic field:

$${\eta }_{B_i}=\left\{\begin{array}{cc}\frac{0.873B^2\left(\mathrm{mT}\right)}{1-\frac{{\mathcal{B}}_{0_1}}{{\mathcal{B}}_{{\mathrm{m}}_1}}},\hfill & \mathrm{for}{\Phi }_1=20\mathrm{vol}\%\hfill \\ \frac{1.010B^2\left(\mathrm{mT}\right)}{1-\frac{{\mathcal{B}}_{0_2}}{{\mathcal{B}}_{{\mathrm{m}}_2}}},\hfill & \mathrm{for}{\Phi }_2=40\mathrm{vol}\%\hfill \\ \frac{1.259B^2\left(\mathrm{mT}\right)}{1-\frac{{\mathcal{B}}_{0_3}}{{\mathcal{B}}_{{\mathrm{m}}_3}}},\hfill & \mathrm{for}{\Phi }_3=60\mathrm{vol}\%\hfill \\ \frac{1.386B^2\left(\mathrm{mT}\right)}{1-\frac{{\mathcal{B}}_{0_4}}{{\mathcal{B}}_{{\mathrm{m}}_4}}},\hfill & \mathrm{for}{\Phi }_4=80\mathrm{vol}\%\hfill \end{array}\right.$$

(6)

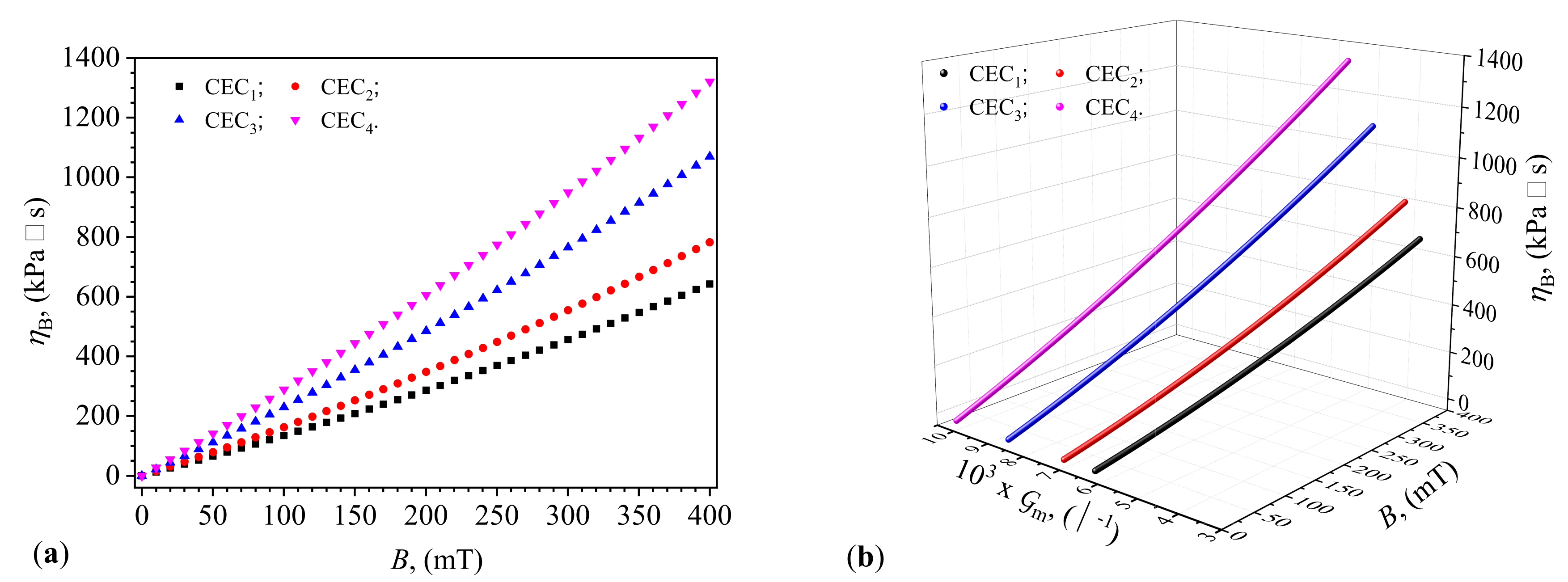
In these expressions, we substitute the functions ${\mathcal{B}}_{\mathrm{m}}={\mathcal{B}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ ($i=1,2,\dots ,4$) from Figure 6(a), and obtain the functions ${\eta }_{B_i}={\eta }_{B_i}{\left(B\right)}_{{\mathrm{CEC}}_i}$ as shown in Figure 7(a). It can be observed from this figure and the group of values in Equation (3) that the viscosity ${\eta }_B$ increases by up to three orders of magnitude in a magnetic field and remains stable over time, as the liquids CL${}_i$ do not sediment. From the same Figure 7(a), it is observed that the viscosity ${\eta }_B$ of the liquids depends on the amount of magnetizable phase used and is significantly influenced by the values of B of the magnetic flux density. The obtained results are due to the formation of aggregates in the SO, an effect also demonstrated in Refs. [36,37]. In Ref. [36], a composite liquid consisting of SO with carbonyl iron microparticles stabilized with silicon nanoparticles is used. The dynamic viscosities of these composites, as with those in the present work, depend on the volume fractions of the magnetizable phase and stabilizing additives, and are significantly influenced by the magnetic field. The values obtained for the dynamic viscosity with these composite liquids are comparable to those in Figure 7(a). Ref. [37] reports an extensive study on the stability of magnetizable composite liquids. This study discusses preparation methods based on carbonyl iron microparticles, SO, and additives. The results regarding the rheological properties of the composite liquids are remarkable and comparable to those in Figure 7(a), but obtained through a multi-phase technological process.

The quantities ${\eta }_B$ and ${\mathcal{G}}_{\mathrm{m}}$ share the same feature, namely they describe CL${}_i$ in the capacitors CEC${}_i$ ($i=1,2,3,4$) subjected to a magnetic field. Hence, the natural relationship between ${\eta }_B$, ${\mathcal{G}}_{\mathrm{m}}$, and the values B of the magnetic flux density is depicted in Figure 7(b). This shows that from the conductance measurements corresponding to the values B of the magnetic flux density, the values of ${\eta }_B$ for the magnetically active CL${}_i$ can be determined. The functions ${\mathcal{G}}_{\mathrm{m}}={\mathcal{G}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ and ${\mathcal{B}}_{\mathrm{m}}={\mathcal{B}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$, describe physical mechanisms occurring on the same basis, namely the liquids CL${}_i$. Thus, there are correlations between these functions, as shown in Figure 8(a). These results demonstrate that by choosing the composition of the liquids CL${}_i$ the operating points (${\mathcal{B}}_{\mathrm{m}},{\mathcal{G}}_{\mathrm{m}}$) of the capacitors CEC${}_i$ can be coarsely adjusted. In contrast, by selecting the values of B of the magnetic flux density, the values of ${\mathcal{B}}_{\mathrm{m}}$ and ${\mathcal{G}}_{\mathrm{m}}$ can be finely tuned. Therefore, by adjusting the values of B of the magnetic flux density, the capacitors CEC${}_i$ can be transformed into ideal capacitors, where ${\mathcal{G}}_{\mathrm{m}}$ is zero, or into ideal resistors, where ${\mathcal{B}}_{\mathrm{m}}$ has zero values. This property of the capacitors CEC${}_i$ makes them useful for creating passive circuit elements and/or energy storage elements, where the internal consumption of electrical energy is negligible.

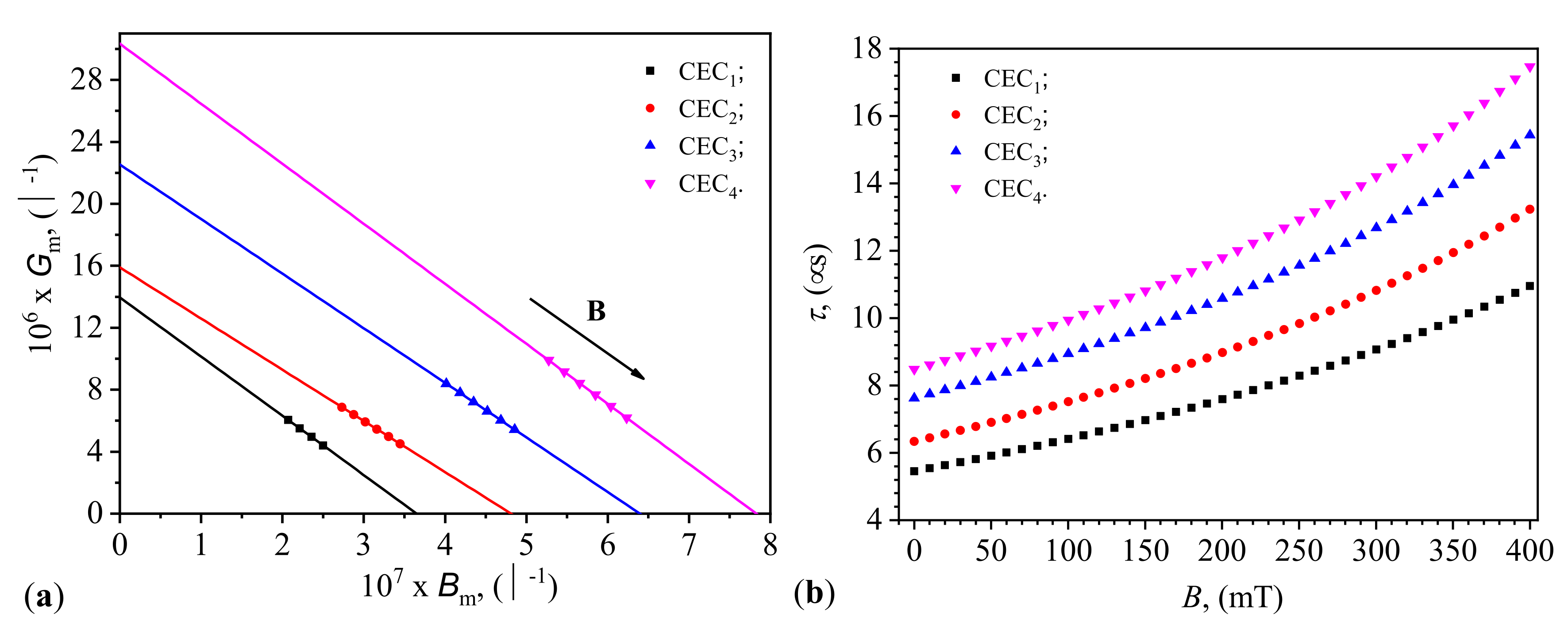
Given the functions ${\mathcal{B}}_{\mathrm{m}}={\mathcal{B}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ from Figure 6(a) and ${\mathcal{G}}_{\mathrm{m}}={\mathcal{G}}_{\mathrm{m}}{\left(B\right)}_{{\mathrm{CEC}}_i}$ from Figure 8(b), we define the time constant $\tau$ of the capacitors CEC${}_i$ ($i=1,2,\dots ,4$) using the expression:

$$\tau =\frac{{\mathcal{B}}_{\mathrm{m}}}{2\pi f{\mathcal{G}}_{\mathrm{m}}},$$

(7)

where f is the frequency of the alternating electric field. By substituting the functions from Figure 6(a,b) in Equation 7 and setting $f=1\mathrm{kHz}$, we obtain the functions $\tau =\tau {\left(B\right)}_{{\mathrm{CEC}}_i}$ shown in Figure 8(b). It can be observed from this figure that the values of $\tau$ can be coarsely adjusted by selecting the ratio of mFe microfibers to SO, and finely tuned by the values of B of the magnetic flux density. This result leads us to conclude that the capacitors CEC${}_i$ are useful for creating magnetically controlled time relays and, in a medium-frequency electric field, useful for automating technological processes.

4. Discussions

The investigation into the electrical behavior of cylindrical capacitors utilizing magnetodielectric materials composed of magnetizable microfibers dispersed within a SO matrix has yielded several significant findings. These results have important implications for the design and optimization of capacitors for applications in microelectronics and sensor technologies.

Figure 4 and Figure 5 illustrate the variation of electrical susceptance and conductance with time under different magnetic flux densities for the four different volume concentrations of microfibers in the capacitors. The susceptance increased over time, indicating the capacitors’ ability to dynamically adjust their electrical properties in response to external magnetic fields, consistent with trends reported in studies involving magnetodielectric composites (Andrei et al. [24]). Conversely, conductance decreased with increasing magnetic flux density, highlighting the magnetic field’s influence in controlling conductive pathways within the dielectric medium, as observed by Iacobescu et al. [28]. The temporal stability of both conductance and susceptance suggests that the capacitors maintain consistent performance under continuous exposure to the magnetic field, essential for reliable operation in practical applications.

Figure 6 demonstrates the variation of susceptance and conductance with magnetic flux density, where susceptance showed a linear increase, affirming the magnetic field’s effectiveness in enhancing the dielectric properties of the capacitors, consistent with the dipolar approximation model by Bica et al. [38]. Conversely, conductance exhibited a linear decrease with increasing magnetic flux density, attributed to the formation of chain-like structures of microfibers under the magnetic field, which increases the dielectric constant while reducing overall conductivity due to decreased mobility of charge carriers. These effects have potential applications in designing tunable electronic components, such as adaptive filters and sensors, which can benefit from dynamically adjustable electrical properties.

The variation of viscosity with magnetic flux density, as shown in Figure 7, provides further insights into the internal dynamics of the magnetodielectric materials. The increase in viscosity with magnetic flux density is consistent with the aggregation of iron oxide microfibers, forming stable structures that resist shear flow. This transformation from a Newtonian to a non-Newtonian fluid under the influence of a magnetic field has significant implications for the mechanical stability and performance of the capacitors. This behavior is well-documented in the rheological studies of magnetic fluids by Wu et al. [39], where the magnetic field induces the formation of chain-like structures, increasing the fluid’s viscosity. Additionally, the correlation between viscosity, magnetic flux density, and conductance underscores the complex interplay between mechanical and electrical properties in these composite materials, thereby enhancing their application potential in adaptive systems.

The linear relationship observed between the average conductance and average susceptance with magnetic flux density in Figure 8, confirms the predictable nature of the capacitors’ performance under varying magnetic fields. This predictability is crucial for the practical application of these capacitors in real-world systems, as highlighted by Zhang et al. [40], who demonstrated the importance of stable and predictable electrical properties in the development of smart electronic components. The time constant, which can be adjusted by changing the ratio of microfibers to SO and the magnetic flux density, highlights the potential for fine-tuning the response time of these capacitors for specific applications. This tunability is particularly valuable in various automation technologies, where the magnetic control of electrical properties can be used to develop advanced systems with enhanced performance characteristics.

5. Conclusions

In this study, we successfully fabricated electrical capacitors using cost-effective materials, specifically a composite liquid synthesized from silicone oil (SO) and iron oxide microfibers (hematite, maghemite, and magnetite) at high temperatures. The presence of hematite, a semiconductor iron oxide with spontaneous magnetization, was pivotal in forming stable aggregates with maghemite and magnetite nano-microparticles. These aggregates, characterized by low mass density and high roughness, resisted sedimentation, ensuring long-term stability of the capacitors’ electrical properties.

Our findings revealed that the susceptance and electrical conductance of these capacitors remained stable over extended periods. Unlike traditional capacitors utilizing carbonyl iron microparticles, our capacitors demonstrated a unique behavior where electrical conductance decreased with increasing magnetic flux density. This phenomenon is attributed to the semiconductor properties of hematite, which differs significantly from the behavior of conventional magnetizable composite liquids where conductance typically increases with magnetic field strength.

The dynamic viscosity of the composite liquids also increased notably in the presence of a magnetic field, similar to classical magnetizable composites. The major advantage of our proposed method lies in its single-phase, cost-efficient production process for these composite liquids. The linear dependency of susceptance and conductance values observed in the developed capacitors suggests their potential application in electrical equipment designed for testing rheological properties and in control blocks.

The capacitors’ predictable performance under varying magnetic fields underscores their practical applicability in real-world systems, particularly in automation technologies. The ability to fine-tune the capacitors’ response time by adjusting the microfiber-to-SO ratio and magnetic flux density is especially valuable. These attributes make the capacitors suitable for developing advanced systems with enhanced performance characteristics, such as adaptive sensors and electronic components with dynamically adjustable properties.

Our research contributes significantly to the understanding and advancement of magnetodielectric-based capacitors, offering insights into their design and optimization for various applications in microelectronics and sensor technologies. The theoretical model based on dipolar approximations provided a robust framework to explain the observed phenomena, further validating our experimental results.

In conclusion, the innovative use of iron oxide microfibers in a SO matrix presents a promising avenue for developing high-performance, cost-effective capacitors. Future research should focus on exploring the long-term stability and scalability of these capacitors in various environmental conditions, as well as their integration into more complex electronic systems.