Submitted:
17 June 2024
Posted:
18 June 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
- Model Innovation: we propose a novel hybrid model named GraphResLSTM, which boasts a distinctive architecture that represents a theoretical and methodological breakthrough in the task of OD prediction for ITS;
- Data Processing and Source Innovation: departing from the conventional reliance on road segment traffic volume data, the study adopts road segment average speed data along road segments for OD prediction. This strategy not only simplifies the data acquisition process but also enhances both the accuracy and real-time nature of the predictions;
- Critical Road Section Selection and Data Preprocessing Methodology Innovation: We employ a synthesis of the Entropy Weight Method and the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) to identify 41 most distinctive key road segments within the experimental road network;
2. Data
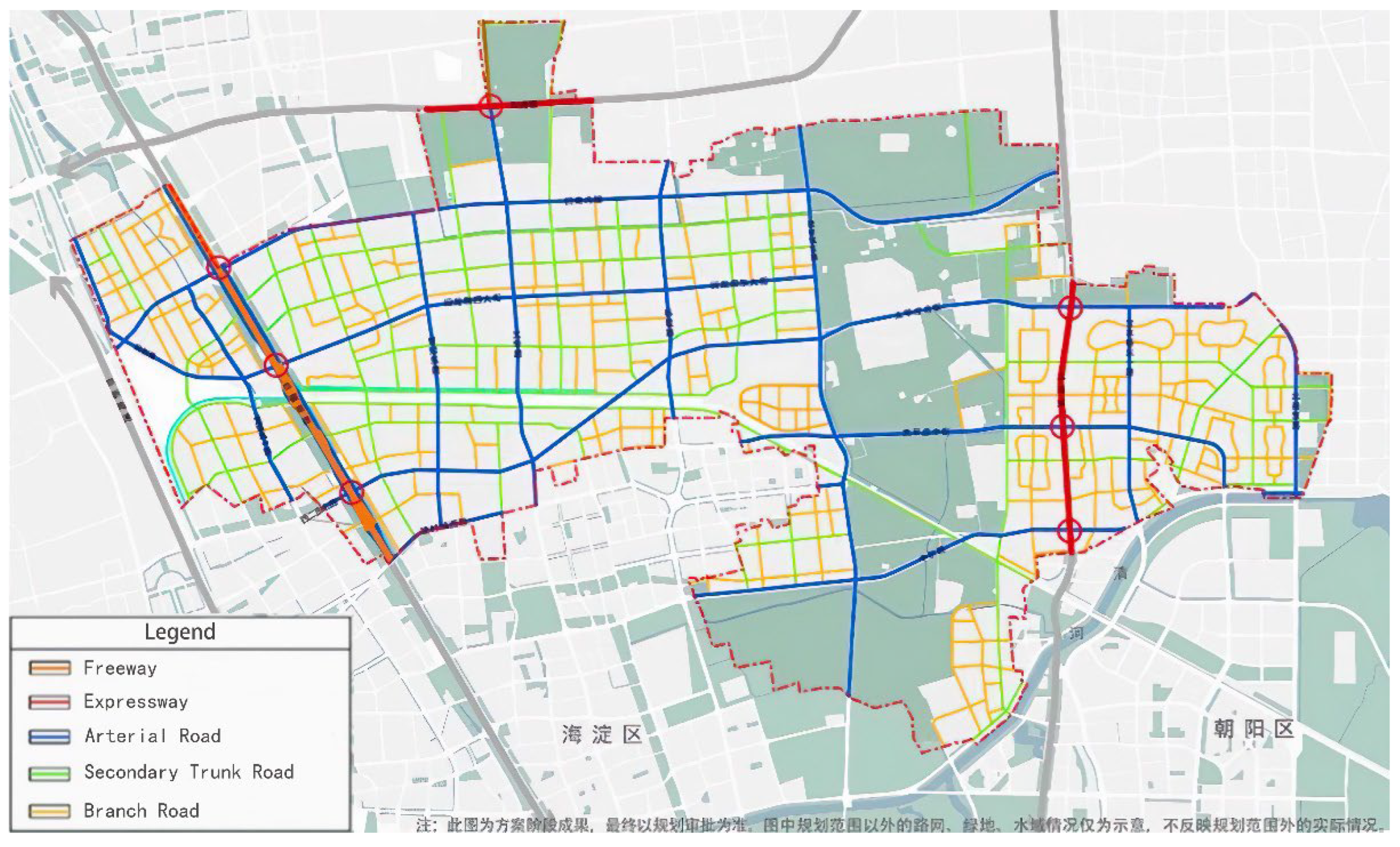
3. Road Selection
3.1. Necessity and advantages of road selection
- Focus on Critical Areas: concentrate on areas that significantly influence overall traffic conditions, thereby gaining deeper insights and explanations of the operational characteristics of the transportation system, enhancing both depth and accuracy of the study;
- Cost-Effective Data Collection: Targeted selection of representative road segments enables us to reduce time and resource costs associated with data collection;
- Optimized Resource Utilization: significantly alleviate the demands on data gathering and processing, ultimately enabling a more effective allocation of finite research resources;
- Enhanced Explainability and Applicability: refines the model's emphasis on key road sections, which not only boosts the model's interpretability but also significantly aids in elucidating the underlying logic behind its predictions.
- Degree: represents the number of other road segments connected to a given road segment. A higher degree indicates stronger connectivity of the road segment within the network;
- Clustering Coefficient: measures the ratio of actual connections among a road segment's neighboring nodes to the maximum possible connections. The higher the clustering coefficient, the closer-knit the connections are among the neighboring road segments;
- Degree Centrality: quantifies the relative importance of a road segment in the entire network. A higher degree centrality signifies a more prominent position for the road segment in the network;
- Betweenness Centrality: reflects the significance of a road segment in connecting other road segments within the network. A higher betweenness centrality implies greater control or influence over the flow of traffic within the network by the road segment;
- Closeness Centrality: gauges how easily a road segment can reach all other road segments in the network. A higher closeness centrality means better accessibility from the road segment to the rest of the network;
- Eigenvector Centrality: assesses the extent to which a road segment is linked with other important road segments in the network. Higher eigenvector centrality indicates a stronger connection between the road segment and other influential nodes in the network.
3.2.1. Entropy of road section
3.2.2. Entropy Weight Method
3.2.3. Weight Distribution
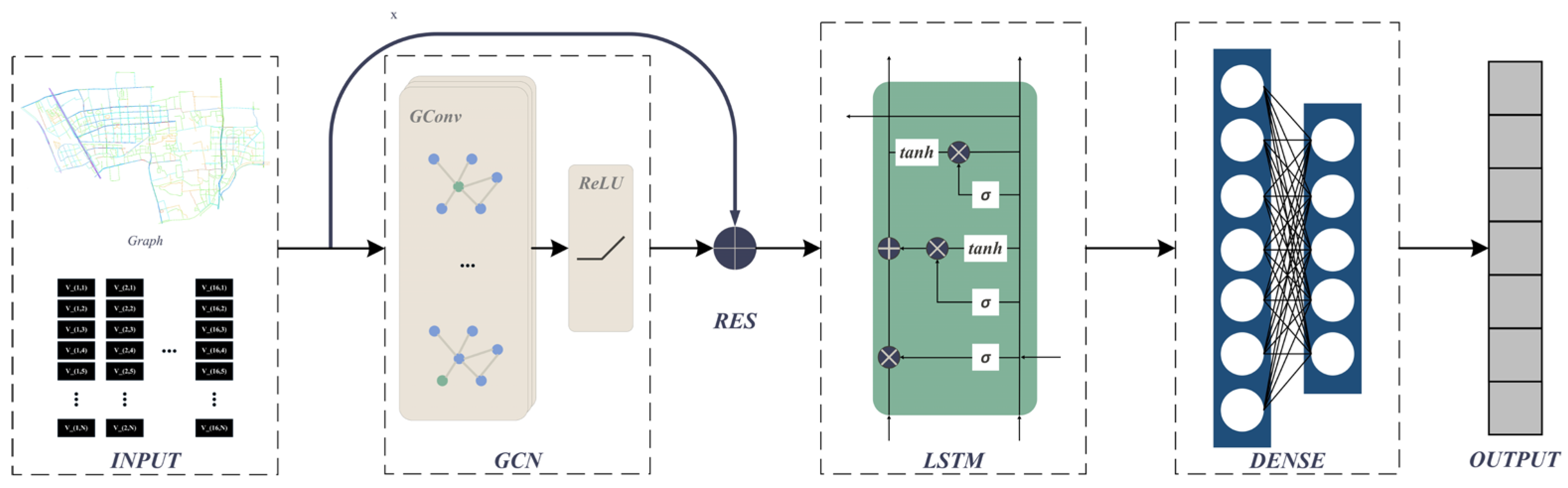
4. Method
4.1. CNN
4.2. GCN
4.3. LSTM
4.4. ResNet
4.5. GraphResLSTM
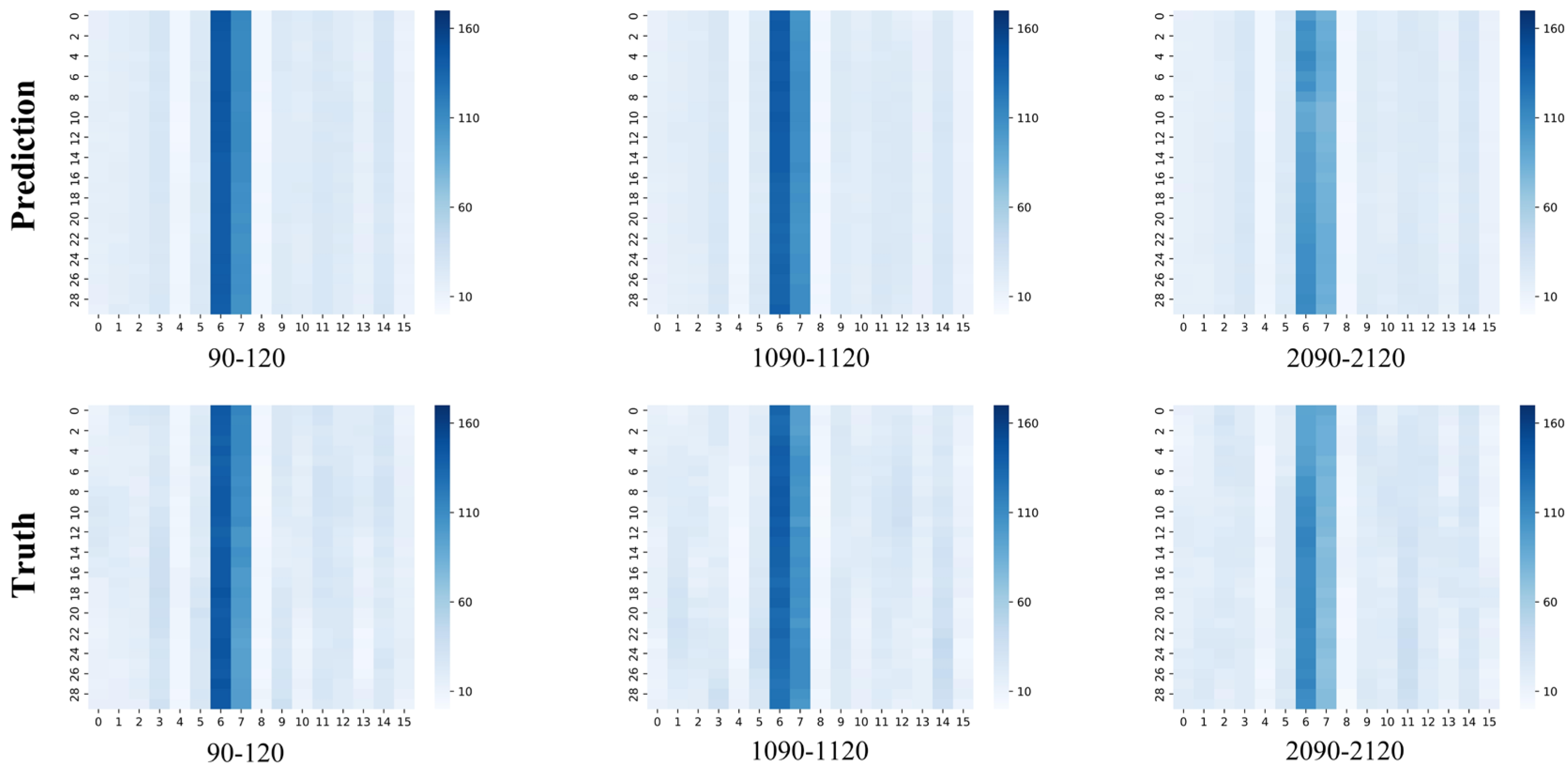
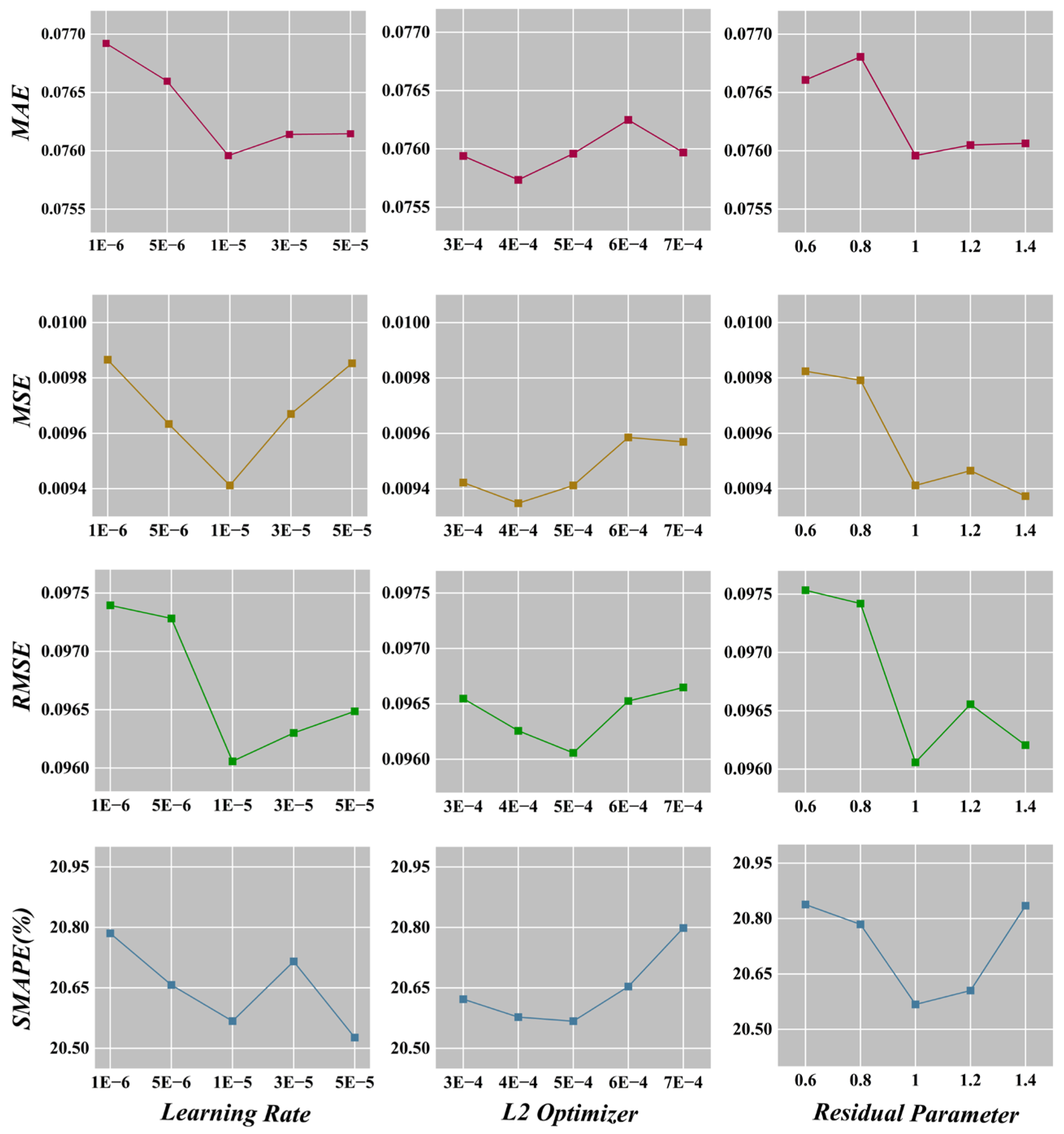
5. Experiment
5.2 Model Evaluate
6. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Munizaga, M.A.; Palma, C. Estimation of a disaggregate multimodal public transport Origin–Destination matrix from passive smartcard data from Santiago, Chile, Transport Res C-Emer, 24, (2012), 9-18. [CrossRef]
- Zhang, B.; Zhong, Z.; Zhou, X. et al., Optimization Model and Solution Algorithm for Rural Customized Bus Route Operation under Multiple Constraints, Sustainability, 15, (2023), 3883.
- Ou, H.; Tang, T.-Q. Impacts of carpooling on trip costs under car-following model, Physica A, 505, (2018), 136-143. [CrossRef]
- Bąk, A.; Nawrocka, E.; Jaremen, D.E. , “Sustainability” as a Motive for Choosing Shared-Mobility Services: The Case of Polish Consumers of Uber Services, Sustainability, 14, (2022), 6352.
- Ding, H.; Li, J.; Zheng, N. Dynamic dispatch of connected taxis for large-scale urban road networks with stochastic demands: An MFD-enabled hierarchical and cooperative approach, Transport Res C-Emer, 142, (2022), 103792. [CrossRef]
- Ji, Y.; Lu, X.; Jiang, H. et al., Layout Optimization for Shared Parking Spaces Considering Shared Parking Walking Time and Parking Fee, Sustainability, 14, (2022), 5635.
- Singh, S.; Singh, J.; Goyal, S.B. et al, A novel framework to avoid traffic congestion and air pollution for sustainable development of smart cities, Sustain Energy Techn, 56, (2023), 103-125. [CrossRef]
- Tsanakas, N.; Gundlegård, D.; Rydergren, C. O–D matrix estimation based on data-driven network assignment, Transportmetrica B, 11, (2023), 376-407. [CrossRef]
- Mei, Y.; Wang, S.; Gong, M. et al., Urban Traffic Dominance: A Dynamic Assessment Using Multi-Source Data in Shanghai, Sustainability, 16, (2024), 4956.
- Bell, M.G.H. The Estimation of an Origin-Destination Matrix from Traffic Counts, Transport Sci, 17, (1983), 198-217. [CrossRef]
- Krishnakumari, P.; van Lint, H.; Djukic, T. et al, A data driven method for OD matrix estimation, IEEE T Intell Transp, 113, (2020), 38-56. [CrossRef]
- Lin, P.-W.; Chang, G.-L. A generalized model and solution algorithm for estimation of the dynamic freeway origin–destination matrix, Transportation Research Part B: Methodological, 41, (2007), 554-572. [CrossRef]
- Zhou, X.; Mahmassani, H.S. A structural state space model for real-time traffic origin–destination demand estimation and prediction in a day-to-day learning framework, Transportation Research Part B: Methodological, 41, (2007), 823-840. [CrossRef]
- Ashok, K.; Ben-Akiva, M.E. Alternative Approaches for Real-Time Estimation and Prediction of Time-Dependent Origin–Destination Flows, Transport Sci, 34, (2000), 21-36. [CrossRef]
- Yang, H.; Iida, Y.; Sasaki, T. An analysis of the reliability of an origin-destination trip matrix estimated from traffic counts, Transportation Research Part B: Methodological, 25, (1991), 351-363. [CrossRef]
- Ashok, K.; Ben-Akiva, M.E. Estimation and Prediction of Time-Dependent Origin-Destination Flows with a Stochastic Mapping to Path Flows and Link Flows, Transport Sci, 36, (2002), 184-198. [CrossRef]
- Hazelton, M.L. Inference for origin–destination matrices: estimation, prediction and reconstruction, Transportation Research Part B: Methodological, 35, (2001), 667-676. [CrossRef]
- Yang, F.; Shuai, C.; Qian, Q. et al, Predictability of short-term passengers’ origin and destination demands in urban rail transit, Transportation, 50, (2023), 2375-2401. [CrossRef]
- Cheng, Z.; Trépanier, M.; Sun, L. Real-Time Forecasting of Metro Origin-Destination Matrices with High-Order Weighted Dynamic Mode Decomposition, Transport Sci, 56, (2022), 904-918. [CrossRef]
- Tang, J.; Zhang, S.; Chen, X. et al, Taxi trips distribution modeling based on Entropy-Maximizing theory: A case study in Harbin city—China, Physica A, 493, (2018), 430-443. [CrossRef]
- Vahidi, M.; Shafahi, Y. Time-dependent estimation of origin–destination matrices using partial path data and link counts, Transportation, (2023). [CrossRef]
- Ye, J.; Zhao, J.; Zheng, F. et al, Completion and augmentation-based spatiotemporal deep learning approach for short-term metro origin-destination matrix prediction under limited observable data, Neural Comput Appl, 35, (2023), 3325-3341. [CrossRef]
- Jiang, W.; Ma, Z.; Koutsopoulos, H.N. Deep learning for short-term origin–destination passenger flow prediction under partial observability in urban railway systems, Neural Comput Appl, 34, (2022), 4813-4830. [CrossRef]
- Chu, K.F.; Lam, A.Y.S.; Li, V.O.K. Deep Multi-Scale Convolutional LSTM Network for Travel Demand and Origin-Destination Predictions, IEEE T Intell Transp, 21, (2020), 3219-3232. [CrossRef]
- Zhang, D.; Xiao, F.; Shen, M. et al, DNEAT: A novel dynamic node-edge attention network for origin-destination demand prediction, Transport Res C-Emer, 122, (2021), 102851. [CrossRef]
- Zhang, D.; Xiao, F. Dynamic Auto-Structuring Graph Neural Network: A Joint Learning Framework for Origin-Destination Demand Prediction, IEEE T Knowl Data En, 35, (2023), 3699-3711. [CrossRef]
- Noursalehi, P.; Koutsopoulos, H.N.; Zhao, J. Dynamic Origin-Destination Prediction in Urban Rail Systems: A Multi-Resolution Spatio-Temporal Deep Learning Approach, IEEE T Intell Transp, 23, (2022), 5106-5115. [CrossRef]
- Pamuła, T.; Żochowska, R. Estimation and prediction of the OD matrix in uncongested urban road network based on traffic flows using deep learning, Eng Appl Artif Intel, 117, (2023), 105550. [CrossRef]
- Zou, X.; Zhang, S.; Zhang, C. et al, Long-Term Origin-Destination Demand Prediction With Graph Deep Learning, IEEE Transactions on Big Data, 8, (2022), 1481-1495. [CrossRef]
- Liu, L.; Zhu, Y.; Li, G. et al, Online Metro Origin-Destination Prediction via Heterogeneous Information Aggregation, IEEE Transactions on Pattern Analysis and Machine Intelligence, 45, (2023), 3574-3589. [CrossRef]
- Shuai, C.; Shan, J.; Bai, J. et al, Relationship analysis of short-term origin–destination prediction performance and spatiotemporal characteristics in urban rail transit, Transport Res A-Pol, 164, (2022), 206-223. [CrossRef]
- Zhang, J.; Che, H.; Chen, F. et al, Short-term origin-destination demand prediction in urban rail transit systems: A channel-wise attentive split-convolutional neural network method, Transport Res C-Emer, 124, (2021), 102928. [CrossRef]
- Wang, Q.; Yuan, Y.; Zhang, Q. et al, Signalized arterial origin-destination flow estimation using flawed vehicle trajectories: A self-supervised learning approach without ground truth, Transport Res C-Emer, 145, (2022), 103917. [CrossRef]
- Jin, M.; Wang, M.; Gong, Y. et al, Spatio-temporally constrained origin–destination inferring using public transit fare card data, Physica A, 603, (2022), 127642. [CrossRef]
- Municipality, C.D.G.O.B. Control detailed plan for CP02-0101~0602 blocks (neighborhood level) of Huiyuan and Tiantongyuan areas, Changping District, Beijing (2020-2035), (2022), http://www.bjchp.gov.cn/cpqzf/xxgk2671/tzgg30/zwgg/cp5509619/index.html.
| Data ID | Time | Road 0 | Road 1 | … | Road 40 |
|---|---|---|---|---|---|
| 0 | 6000 | 15.22 | 3.63 | … | 12.61 |
| 1 | 6060 | 14.08 | 4.87 | … | 11.08 |
| 2 | 6120 | 14.13 | 5.25 | … | 13.25 |
| … | … | … | … | … | … |
| 1439800 | 86394000 | 0.00 | 0.00 | … | 7.00 |
| OD ID | Time | OD 0 | OD 1 | … | Road 15 |
|---|---|---|---|---|---|
| 0 | 6000 | 417 | 216 | … | 290 |
| 1 | 6060 | 322 | 190 | … | 316 |
| 2 | 6120 | 386 | 220 | … | 356 |
| … | … | … | … | … | … |
| 1439800 | 86394000 | 18 | 14 | … | 16 |
| Parameters | Describe | Values |
| out_channels_gcn | number of channels in the output data of GCN | 64 |
| hidden_size_lstm | size of LSTM hidden layer | 64 |
| learning_rate | learning rate | 0.00001 |
| num_epochs | num of epochs | 1000 |
| batch_size_train | batch size | 512 |
| l2_loss | L2 regularization coefficient in the optimizer | 0.0005 |
| res_ratio | the residual ratio in the residual layers | 1 |
| MAE | MSE | RMSE | SMAPE | |
|---|---|---|---|---|
| CNN | 0.082804094 | 0.011285882 | 0.10456171 | 22.37051838 |
| GCN | 0.084134158 | 0.011512537 | 0.106558977 | 22.83664327 |
| LSTM | 0.07940893 | 0.010252437 | 0.101354543 | 22.0205108 |
| CNN LSTM | 0.084023348 | 0.011509673 | 0.10608842 | 22.45860681 |
| GCN LSTM | 0.084090347 | 0.011510888 | 0.099953406 | 20.50259149 |
| GraphResLSTM | 0.075958893 | 0.009412067 | 0.096057905 | 20.64164395 |
| MAE | MSE | RMSE | SMAPE | |
|---|---|---|---|---|
| flow | 0.082804094 | 0.011285882 | 0.10456171 | 22.37051838 |
| waiting | 0.084134158 | 0.011512537 | 0.106558977 | 22.83664327 |
| travel | 0.07940893 | 0.010252437 | 0.101354543 | 22.0205108 |
| halting | 0.084023348 | 0.011509673 | 0.10608842 | 22.45860681 |
| speed | 0.075958893 | 0.009412067 | 0.096057905 | 20.64164395 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





