Prerpints.org logo
Preprint
Article

Predicting Student Performance Using Ensemble Models and Learning Analytics Techniques

Altmetrics

Downloads

102

Views

58

Comments

0

This version is not peer-reviewed

Submitted:

14 June 2024

Posted:

20 June 2024

You are already at the latest version

Alerts
Abstract
This paper explores the utilization of ensemble models and learning analytics techniques to predict student academic performance. With the advent of educational big data, institutions are increasingly leveraging advanced analytics to gain insights into student learning patterns and optimize educational outcomes. Ensemble models, which combine the predictive power of multiple algorithms, offer a robust approach to enhance prediction accuracy. The performance of the ensemble models was analyzed and compared using the Open University Learning Analytics Dataset, which consists of sources such as demographic information, historical performance data, and engagement metrics for 23,344 students. The evaluation of various ensemble models across different classification scenarios revealed that the proposed stacking model consistently emerges as the best-performing model, excelling in both multi-class and binary classification tasks.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

MSC:  60E05; 62H30

1. Introduction

In recent years, predicting student performance has become a pivotal aspect of educational data mining and learning analytics. The ability to accurately forecast student outcomes allows educators and administrators to identify at-risk students, tailor interventions, and enhance overall educational effectiveness [1]. Early identification of students who might struggle academically is crucial, as it enables timely support and resources to be provided, thereby improving retention rates and overall student success [2,3]. Traditional methods of predicting student performance often relied on simple statistical techniques and historical data. However, these methods frequently fell short due to their inability to handle complex, high-dimensional data sets commonly found in educational environments [3].
With the advent of advanced machine learning techniques, ensemble models have emerged as powerful tools for making such predictions, leveraging the strengths of multiple algorithms to improve accuracy and robustness. Ensemble learning, which involves combining multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent models alone, addresses many of the limitations of traditional methods. These models work on the principle that a group of weak learners can come together to form a strong learner, thus improving the model’s overall performance [4,5,6].
Ensemble methods such as Random Forests, Gradient Boosting, and Stacking are particularly well-suited for educational data mining. Random Forests, for instance, can handle large datasets with numerous features, making them ideal for analyzing complex educational data. They work by constructing multiple decision trees during training time and outputting the mode of the classes as the prediction. Gradient Boosting, on the other hand, builds models sequentially, with each new model attempting to correct the errors made by the previous ones. This method is highly effective in improving predictive accuracy and reducing overfitting. Stacking involves training a new model to combine the predictions of several base models, which allows it to leverage the strengths and compensate for the weaknesses of each base model [7,8,9,10,11,12,13].
There have been many studies which demonstrate the success of ensembling methods by utilizing student performance prediction. For example, an ensemble of models have been shown to substantially outperform single-model approaches in both accuracy and reliability when predicting student success and at-risk students. These models are even more predictive when combined with other sources of data, such as demographic information, academic performance and interaction data from the learning management systems. At a basic level, this integration is an essence of learning analytics that has the goal of optimizing learning and the learning environments by understanding and analyzing educational data [14,15,16,17].
The use of these models in an educational context builds from the wider field of learning analytics where data about learners and their context are collected, analysed, and reported in order to understand and optimize learning and the environments in which it occurs. [16] defines learning analytics as “the measurement, collection, analysis and reporting of data about learners and their contexts, for purpose of understanding and optimizing learning and the environments in which it occurs. Big Data is capitalizing on the field to improve educational outcomes by producing information that can drive decision-making processes at institutional levels [18].
Learning analytics combines multiple sources of data (especially academic records, demographic information, and data produced from interactions with learning management systems) to help educators understand the behaviour and performance of students. Academic records for instance contain historical data of performance that can help to predict outcomes [19]. Disaggregation of data by demographic characteristics (e.g., age, gender, socioeconomic status and educational background) can provide some of this context and hence facilitate more nuanced analysis, and focused interventions [20]. Data traces of the interactions of students in a Learning Management System such as how often they logged in, the time that they spent in different modules, how they participated in online discussions or the moment at which they submitted their assignments can be used to produce Student focus models and, in doing so, distinguishing patterns of engagement of students at-risk of failure [1].
Moreover, the inclusion of data form various sources in the creation of these models provides the ability to tackle a variety of educational problems. For example, predictive models can predict that a student is likely to drop out, which allows for timely intervention to retain the student [21]. Analytics can also be applied to create personalized learning experiences, adjusting content and methods of instruction to meet the specific needs of each individual learner [22]. As an example, this is crucial in the case of adaptive learning technologies that improve student engagement by modifying content delivery on the fly based on student performance/engagement via data-driven insights [23].
Learning analytics is designed to produce answers to these questions in the form of actionable intelligence that may be used to improve learning. With the right information about what works towards student success, educators can design curricula more effectively, provide the appropriate help, and cultivate learning environments built around academic accomplishment. It thus follows that the data coming from learning analytics is of a type that is used to bolster the larger picture of a student’s success or failure, which can be further tailored toward larger institutional goals, such as improving retention rates, increasing student satisfaction and certification of academic excellence [24].
Many research works have proved the effectiveness of ensemble models in predicting student performance across multiple educational environments, showing their widespread applicability as well as their robustness. In the studies by [14,15], Random Forests accurately identified students at risk of dropping out based on academic performance and engagement metrics, achieving significant predictive accuracy compared to other models. Similarly, [25] utilized Random Forests to analyze engineering student data, successfully reducing dropout rates by identifying at-risk students early on and enabling timely interventions.
Another powerful ensemble technique known as Gradient Boosting has also been successfully used to predict whether students are likely to fail a course or not. Among such, [26] investigate if Gradient Boosting can help in predetermining any risk of students from online learning environments. Their research showed that Gradient Boosting achieved a higher accuracy than standard classification techniques. In addition to that, [27] also used Gradient Boosting to predict student performance in MOOCs (Massive Open Online Courses) with high accuracy, for more personalized learning experiences.
As educational data mining tasks are often characterized by complex and voluminous data, model efficacy is favoured by their capability to process large datasets with high-dimensional features. As an example, [10] pointed out that Random Forests handles large feature sets effectively, preventing overfitting - an important characteristic for educational datasets which typically include various inputs like demographic information, prior academic records, and real-time interaction data from learning management systems. Additionally, Gradient Boosting with its iterative nature during the model building provides the flexibility to capture complex patterns in student behaviour and performance critical for accurate predictions in dynamic educational scenarios.
Additionally, Stacking, which combines multiple models to leverage their individual strengths, has proven effective in educational contexts. [11] introduced the concept of Stacked Generalization, which has since been applied in various domains, including education. By combining models like Random Forests, Gradient Boosting, and others, Stacking achieves superior predictive performance and provides more reliable insights into student outcomes. This approach has been particularly useful in predicting multifaceted educational phenomena, such as student retention and course completion rates. Moreover, the interpretability and reliability of ensemble models are particularly beneficial in educational contexts, where decisions based on predictive analytics can have significant impacts on students’ academic trajectories. The combination of high predictive accuracy and the capacity to provide actionable insights makes ensemble models a valuable asset in the toolkit of educational institutions.
Therefore, the objective of this paper is to explore the utilization of ensemble models and learning analytics techniques to predict student academic performance. The focus of this study is to harness the predictive power of ensemble models, which combine multiple algorithms to enhance accuracy and robustness. Specifically, the performance of various ensemble models is analyzed and compared using the Open University Learning Analytics Dataset. By evaluating these models across different classification scenarios, this study seeks to identify the most effective method for predicting student performance, with a particular focus on the stacking model.

2. Material and Methods

2.1. Dataset

The dataset used in this study consists of features on student behaviour and performance and crucial elements in the framework for predicting student outcomes in the United Kingdom. It encompasses detailed information from 22 different courses, involving 23,344 students. The dataset includes a variety of data points such as assessment results and extensive logs of student interactions with the Virtual Learning Environment (VLE). The behaviour aspect is captured through daily summaries of student clicks within the VLE, resulting in a substantial 207,242 entries. These logs provide insight into students’ engagement and activity patterns, which are essential for understanding their learning behaviours and predicting their performance. Performance data includes assessment results, which give a direct measure of students’ academic achievements. By integrating both behaviour and performance data, the dataset enables a thorough analysis of how students interact with the learning platform and how these interactions correlate with their academic outcomes. In addition, the dataset is big data with seven dimensions. Of the seven dimensions, only four dimensions were utilized in this study. The dimensions are "assessment", "studentAssessment", "studentInfo" and "studentvle". The full description of the variables in each dimension can be found in [28]. The performance results are represented in categories (Distinction, Pass, Fail, Withdrawn). Figure 1. presents the data schema used to combine the data dimensions.
Figure 1 shows the snowflake schema employed in the study. The assessment dimension table was merged with the student assessment table using " i d a s s e s s m e n t " as the matching variable. In the next step, the resultant table from the previous step was merged with the student information table using " i d s t u d e n t " . 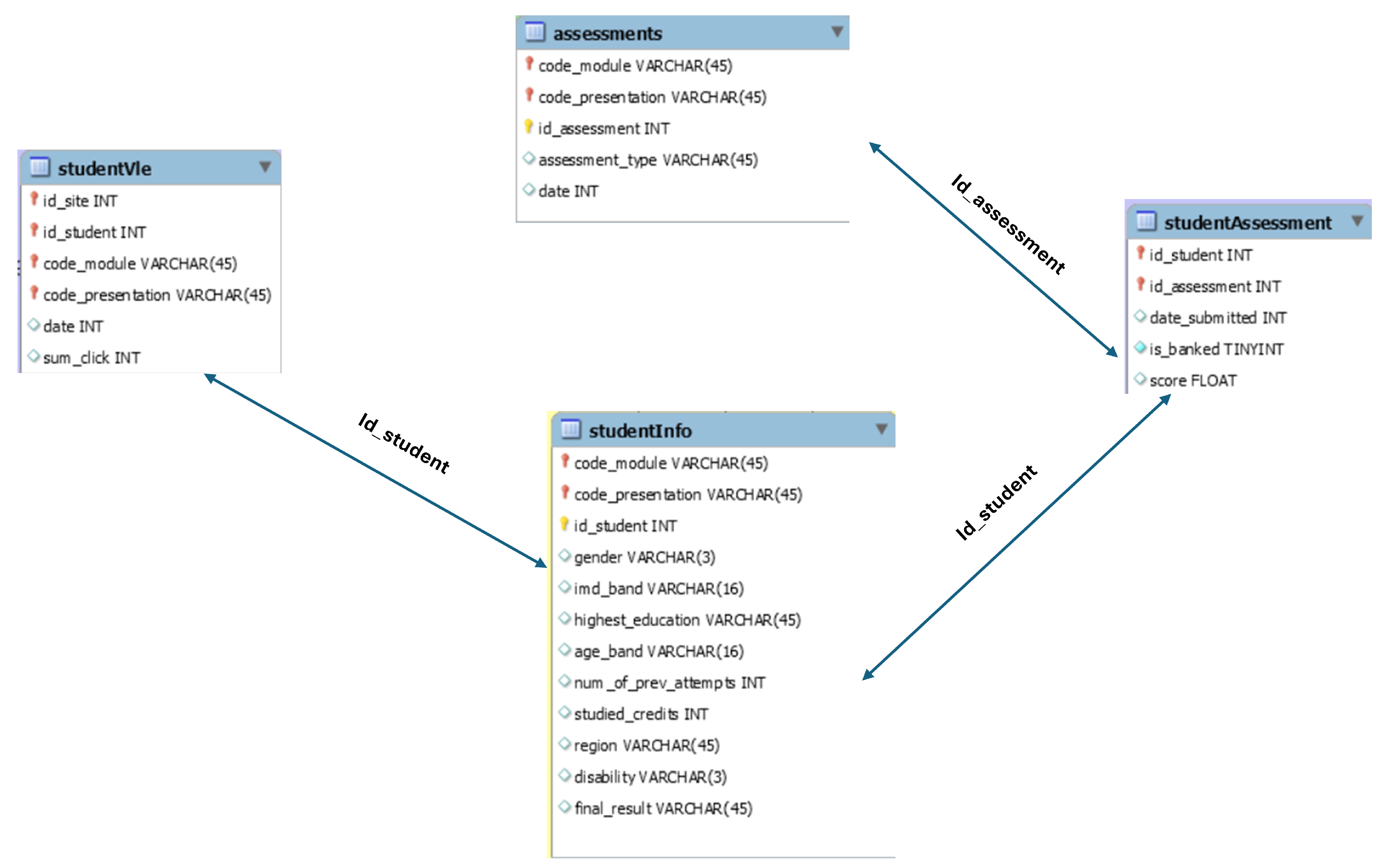The data warehousing process was completed by merging the table in step two with the student virtual learning environment table using " i d s t u d e n t " .

2.2. Data Pre-Processing

2.2.1. Data Partitioning

The next step before machine learning is to partition the dataset into the training and testing dataset. The dataset was partitioned using a ratio of 70% training and 30% testing. The cross-validation scheme employed is the random split where the 70% and 30% instances in the training and testing sets are randomly assigned. To ensure reproducibility, the random state was set to zero for the random splitting [29].

2.2.2. Over-Sampling of the Unbalanced Data

During the exploratory analysis stage, it was observed that student performance was significantly imbalanced, with a higher number of Pass (50.1%) compared to Distinction, Fail and Withdrawn with 12.1%, 22.8% and 15.0% students respectively. To address this imbalance, we applied an over-sampling technique. Over-sampling is a technique used to address class imbalance by increasing the number of instances in the minority class(es) to achieve a balanced class distribution. One common method for over-sampling is random duplication of minority class samples. Random over-sampling involves randomly duplicating instances from the minority class(es) and adding them to the dataset. The algorithm procedure starts with a dataset D with features and class labels. If we denote D m i n : as the number of instances in the minority class in this case (Distinction category). In the over-sampling step, we selected randomly twice the number of instances in the minority class across the categories [30].

2.3. Ensemble Models

Ensemble models are machine learning techniques that combine the predictions of multiple base models to produce a single, more accurate prediction. The rationale behind ensemble methods is that a group of weak learners can form a strong learner, thus improving the model’s overall performance. These models enhance prediction accuracy and robustness by aggregating the strengths of various algorithms while mitigating their individual weaknesses [5].

2.3.1. Random Forest

Random Forest [7] is an ensemble learning method that operates by constructing multiple decision trees during training and outputting the mode of the classes for classification tasks or the mean prediction for regression tasks. It is known for its high accuracy, ability to handle large datasets with many features, and robustness to overfitting. Random Forest can be implemented by following the following steps:
  • Data Preparation: Split the dataset into training and testing sets.
  • Model Training: Train multiple decision trees on different subsets of the data.
  • Aggregation: Aggregate the predictions from all trees to form the final prediction.
Random Forest is especially useful in predicting student performance as this algorithm can deal with many variables, and complex interactions between them, such as demographic data, VLE interactions and assessment results.

2.3.2. Gradient Boosting

Gradient Boosting [9] constructs models progressively - each new model tries to fix the errors of the previous models. This method helps to build a robust model which identifies the complex patterns present in the data Gradient Boosting can be implemented by following the following steps:
  • Initialization: Start with an initial model, typically a simple decision tree.
  • Sequential Training: Train subsequent models to predict the residuals (errors) of the previous models.
  • Combination: Combine the predictions of all models to produce the final output.
Gradient Boosting is suitable for educational data mining because of its ability to handle noisy data and improve prediction accuracy iteratively.

2.3.3. ExtraTrees

ExtraTrees, or Extremely Randomized Trees [31], works in a similar way as a Random Forest, but introduces additional randomness by selecting cut points for each feature at random. This method is used to reduce variance and prevent overfitting. ExtraTreesClassifier by following these procedures.
  • Data Preparation: Split the dataset into training and testing sets.
  • Model Training: Train multiple extremely randomized trees on different subsets of the data.
  • Aggregate the predictions from all trees to form the final prediction.
ExtraTrees is particularly suitable for student performance prediction given its efficiency and good performance when the data dimension is large.

2.3.4. AdaBoost

AdaBoost [32], stands for Adaptive Boosting, works by combining multiple weak classifiers to form a good classifier. It updates the weights of misclassified samples more so that difficult cases get more weight in each next iteration. Below are the steps to implement AdaBoost:
  • Initialization: Assign equal weights to all training instances.
  • Sequential Training: Train a weak learner and adjust weights based on classification errors.
  • Combination: Combine the weak learners’ predictions through weighted voting.
There are many cases where AdaBoost tends to produce more detailed classifiers by refining weights it misclassified, and thus can compensate for features with fewer weights in its refinement process, e.g. in moderately noisy data, which may itself be not too challenging, thus not too noisy, so with regard to the solution generated by the "more powerful learners", such potential "defective" features might be better compensated.

2.3.5. Bagging

Bagging [33], or Bootstrap Aggregating, involves training multiple base models on different subsets of the data created through bootstrapping and then averaging their predictions. Bagging can be implemented by following the following steps:
  • Data Preparation: Create multiple bootstrap samples from the training set.
  • Model Training: Train a base model on each bootstrap sample.
  • Aggregation: Average the predictions of all base models to form the final output.
Bagging is particularly useful for reducing variance and avoiding overfitting, making it suitable for diverse educational datasets.

2.3.6. Proposed Model: Stacking

The proposed ensemble model used in the study is stacking. Stacking [11] involves training multiple base models and then using another model, called a meta-learner, to combine their predictions. This method leverages the strengths of different models to improve overall performance. In this study, we utilize four base models: Random Forest, Gradient Boosting, ExtraTrees, and AdaBoost. Stacking involves training a meta-learner to combine the predictions of the base models. The procedure is as follows:
  • First-Level Training:
    (a)
    Each of the four base models (Random Forest, Gradient Boosting, ExtraTrees, and AdaBoost) is trained on the training dataset.
    (b)
    The trained base models make predictions on the training dataset, and these predictions are used as input features for the meta-learner (Random Forest).
  • Meta-Learner Training:
    (a)
    The meta-learner is typically a simple model, such as logistic regression, which takes the predictions of the base models as input and learns to combine them optimally.
    (b)
    The meta-learner is trained on the predictions made by the base models on the training dataset.
  • Final Predictions:
    (a)
    The trained base models make predictions on the testing dataset.
    (b)
    These predictions are then fed into the trained meta-learner to produce the final predictions.

2.4. Evaluation Criteria

Various metrics are typically used to assess the performance of the ensemble models in predicting student performance. Some of these metrics include accuracy, precision, recall, F-Measure, Area Under the Receiver Operating Characteristic Curve (AUC), etc. Every metric shows a different aspect of the efficiency and accuracy of the model predictions [29,34,35].

2.4.1. Accuracy

Accuracy represents the classifier’s ability to correctly predict outcomes and is a measure of the classifier’s overall capacity to make correct predictions. It is calculated as the ratio of the number of correct predictions (both true positives and true negatives) to the total number of predictions made [29,34]. The formula for accuracy [29,34] is given by:
A c c u r a c y = T P + T N T P + T N + F P + F N
where:
  • True Positives (TP): Cases that are correctly predicted as positive.
  • True Negatives (TN): Cases that are correctly predicted as negative.
  • False Positives (FP): Cases that are incorrectly predicted as positive.
  • False Negatives (FN): Cases that are incorrectly predicted as negative.
Accuracy provides a straightforward measure of how often the model’s predictions are correct. However, it can be misleading in imbalanced datasets where the number of true negatives might outweigh other cases significantly.

2.4.2. Precision

Precision measures the accuracy of the positive predictions made by the classifier. It is defined as the ratio of true positive predictions to the total positive predictions, both correct and incorrect [29,34]. The formula for precision [29,34] is:
P r e c i s i o n = T P T P + F P
Precision is particularly important in contexts where the cost of false positives is high, as it indicates the reliability of positive predictions [29,34].

2.4.3. Recall

Recall, also known as sensitivity, measures the classifier’s ability to correctly identify all positive instances [29,34]. It is calculated as the ratio of true positive predictions to the total actual positives. The formula for the recall [29,34] is:
P r e c i s i o n = T P T P + F N
Recall is crucial when the cost of false negatives is high, as it indicates how well the model captures all positive cases [29,34].

2.4.4. F-Measure

The F-Measure (or F1 score) combines precision and recall into a single metric by taking their harmonic mean [29,34]. It provides a balanced measure when both precision and recall are important. The formula for the F1 score [29,34] is:
F 1 − M e a s u r e = 2 × R e c a l l × P r e c i s i o n R e c a l l + P r e c i s i o n
The F1 score is particularly useful in scenarios where there is an uneven class distribution, and a balance between precision and recall is required [29,34].

2.4.5. Area Under the Curve (AUC)

The Area Under the Receiver Operating Characteristic Curve (AUC) measures the model’s ability to distinguish between classes. It plots the true positive rate (recall) against the false positive rate (1 - specificity) at various threshold settings [29,34]. AUC provides an aggregate measure of performance across all classification thresholds and is particularly valuable for comparing different models. A higher AUC value indicates better overall performance. AUC is a robust metric because it considers all possible classification thresholds, providing a comprehensive view of the model’s performance. The AUC value is the area under the ROC curve. It can be calculated using various numerical methods such as the trapezoidal rule. The formula for the AUC [29,34]:
A U C = ∑ i N − 1 ( x i + 1 − x i ) y i + 1 + y i 2
where
  • x i and x i + 1 are consecutive points on the FP axis.
  • y i and y i + 1 are consecutive points on the TP axis.
The formula essentially calculates the area under the piecewise linear segments that form the ROC curve [29,34].

3. Results and Discussions

The results in Table 1, Table 2, and Table 3 illustrate the performance of various ensemble models in predicting student outcomes across different classification schemes. The evaluation metrics used to measure the performance include Precision, Recall, F1 Score, Accuracy, and AUC (Area Under the Curve). These metrics provide a complete understanding of the models’ effectiveness in different scenarios. For the purpose of comprehensive model building, the performances of the various models were observed across three classification scenarios. Scenario 1 involves the prediction of the four classes of students’ performance (Distinction, Fail, Pass, and Withdrawn). Scenario 2 consists of predicting 3 classes of students’ performance (Distinction & Pass, Fail and Withdrawn). And lastly, scenario 3 consists of predicting 2 classes of students’ performance (Distinction & Pass and Fail & Withdrawn).
Table 1 presents the evaluation metrics for models predicting four classes of student results: Distinction, Fail, Pass, and Withdrawn. The Stacking model exhibits the highest performance across most metrics, with a Precision of 83%, Recall of 81%, F1 Score of 81%, Accuracy of 81%, and an AUC of 96%. This indicates that the Stacking model is the most effective in handling the complexity of four distinct classes. In contrast, the AdaBoost model performs the poorest, with the lowest metrics in all categories, especially an F1 Score of 46% and an Accuracy of 50%. This suggests that AdaBoost struggles with the multi-class classification problem.
Figure 2 and Figure 3 show the confusion matrices and ROC curves of the models for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results. Figure 2 shows that all the models consistently predict the correct performances except Gradient Boosting and AdaBoost which returned poor predictions for students in the failure category. Similar results were observed in the ROC curves for the Fail categories in Figure 3 for Gradient Boosting and AdaBoost.
Table 2 summarizes the performance of the models for three classes: Fail, Pass & Distinction, and Withdrawn. The Stacking model again leads with 88% across all metrics and an AUC of 97%, showing strong predictive capability. Random Forest and ExtraTrees also perform well, each achieving 87% Precision, Recall, F1 Score, and Accuracy, with an AUC of 96%. AdaBoost shows improvement compared to the four-class scenario but remains the weakest, with an F1 Score of 57% and an Accuracy of 63%. This indicates that reducing the number of classes improves the model’s performance, but not uniformly across all models.
Figure 4 and Figure 5 show the confusion matrices and ROC curves of the models for the three classes (Fail, Pass & Distinction, Withdrawn. Figure 4 shows that all the models consistently predict the correct performances except Gradient Boosting and AdaBoost which returned poor predictions for students in the failure category. Similar results were observed in the ROC curves for the Fail categories in Figure 5 for Gradient Boosting and AdaBoost.
Table 3 displays results for the simplest classification, dividing the outcomes into two classes: Pass & Distinction versus Fail & Withdrawn. Here, all models show significant performance improvements. The Stacking and Random Forest models both achieve 96% across all metrics, including an AUC of 99%. This near-perfect performance indicates that the models are highly effective when the classification task is simplified. ExtraTrees and Bagging also perform remarkably well, with metrics around 94-95% and an AUC of 99%. AdaBoost, while still the lowest performer, achieves a relatively high F1 Score of 85% and an Accuracy of 86%, demonstrating considerable improvement in a binary classification context.
The results indicate that model performance varies significantly depending on the complexity of the classification task. In the four-class scenario, the complexity is higher, and only the Stacking model manages to maintain high performance, while others like AdaBoost fall behind. As the number of classes decreases, all models show improvement, with the two-class scenario yielding the highest metrics across the board. This trend suggests that ensemble models handle binary classification tasks more effectively, likely due to reduced complexity and clearer distinctions between the classes.
Stacking emerges as the most robust model across all scenarios, consistently achieving the highest or near-highest scores. This model’s ability to combine the strengths of various base learners likely contributes to its superior performance. Conversely, AdaBoost’s relatively poor performance, especially in multi-class scenarios, indicates a potential limitation in its ability to handle more complex classification tasks.
Figure 6 and Figure 7 show the confusion matrices and ROC curves of the models for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results. Figure 6 shows that all the models consistently predict the correct performances except Gradient Boosting and AdaBoost which returned moderate predictions for students in the failure category. Similar results were observed in the ROC curves for the Fail categories in Figure 7 for Gradient Boosting and AdaBoost.

4. Conclusions

The evaluation of various ensemble models across different classification scenarios reveals several key findings. The proposed stacking model consistently emerges as the best-performing model, excelling in both multi-class and binary classification tasks. Random Forest and ExtraTrees also demonstrate high effectiveness, particularly in binary and reduced class scenarios, where they achieve near-perfect metrics. Bagging performs commendably across all scenarios, though slightly below the top performers. On the other hand, Gradient Boosting and AdaBoost show weaker performance, particularly in multi-class scenarios, though they improve considerably as the classification task is simplified.
Overall, the results indicate that while complex classification tasks present challenges, ensemble models like Stacking, Random Forest, and ExtraTrees can achieve high accuracy and reliability. Simplifying the classification task generally enhances model performance, suggesting a potential strategy for improving predictive accuracy by reducing the complexity of classification schemes. These findings highlight the importance of selecting appropriate ensemble methods and optimizing classification granularity to achieve the best predictive outcomes for student performance analysis.

Author Contributions

Conceptualization, M.R.A; methodology, M.R.A; software, M.R.A; validation, M.R.A; formal analysis, M.R.A; investigation, M.R.A; resources, M.R.A.; data curation, M.R.A; writing—original draft preparation, M.R.A; writing—review and editing, M.R.A; visualization, M.R.A; supervision, M.R.A; project administration, M.R.A All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Romero, C.; Ventura, S. Educational data mining: a review of the state of the art. IEEE Transactions on Systems, Man, and Cybernetics, Part C (applications and reviews) 2010, 40, 601–618. [Google Scholar] [CrossRef]
  2. Baker, R.S.; Yacef, K.; others. The state of educational data mining in 2009: A review and future visions. Journal of educational data mining 2009, 1, 3–17.
  3. Jie, H. Assessing Students’ Digital Reading Performance: An Educational Data Mining Approach; Routledge, 2022.
  4. Dietterich, T.G. Ensemble methods in machine learning. International workshop on multiple classifier systems. Springer, 2000, pp. 1–15.
  5. Zhou, Z.H. Ensemble methods: foundations and algorithms; CRC press, 2012.
  6. Rokach, L. Ensemble-based classifiers. Artificial intelligence review 2010, 33, 1–39. [Google Scholar] [CrossRef]
  7. Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  8. Popoola, J.; Yahya, W.B.; Popoola, O.; Olaniran, O.R. Generalized self-similar first order autoregressive generator (gsfo-arg) for internet traffic. Statistics, Optimization & Information Computing 2020, 8, 810–821. [Google Scholar]
  9. Friedman, J.H. Greedy function approximation: a gradient boosting machine. Annals of statistics, 2001; 1189–1232. [Google Scholar] [CrossRef]
  10. Liaw, A.; Wiener, M.; others. Classification and regression by randomForest. R news 2002, 2, 18–22.
  11. Wolpert, D.H. Stacked generalization. Neural networks 1992, 5, 241–259. [Google Scholar] [CrossRef]
  12. Olaniran, O.R.; Abdullah, M.A.A. Bayesian weighted random forest for classification of high-dimensional genomics data. Kuwait Journal of Science 2023, 50, 477–484. [Google Scholar] [CrossRef]
  13. Olaniran, O.R.; Alzahrani, A.R.R. On the Oracle Properties of Bayesian Random Forest for Sparse High-Dimensional Gaussian Regression. Mathematics 2023, 11, 4957. [Google Scholar] [CrossRef]
  14. Mduma, N. Data balancing techniques for predicting student dropout using machine learning. Data 2023, 8, 49. [Google Scholar] [CrossRef]
  15. Gray, G.; McGuinness, C.; Owende, P.; Hofmann, M. Learning factor models of students at risk of failing in the early stage of tertiary education. Journal of learning analytics 2016, 3, 330–372. [Google Scholar] [CrossRef]
  16. Siemens, G. Learning analytics: The emergence of a discipline. American Behavioral Scientist 2013, 57, 1380–1400. [Google Scholar] [CrossRef]
  17. Chatti, M.A.; Dyckhoff, A.L.; Schroeder, U.; Thüs, H. A reference model for learning analytics. International journal of Technology Enhanced learning 2012, 4, 318–331. [Google Scholar] [CrossRef]
  18. Long, P.; Siemens, G. Penetrating the fog: analytics in learning and education. Italian Journal of Educational Technology 2014, 22, 132–137. [Google Scholar]
  19. Agudo-Peregrina, Á.F.; Iglesias-Pradas, S.; Conde-González, M.Á.; Hernández-García, Á. Can we predict success from log data in VLEs? Classification of interactions for learning analytics and their relation with performance in VLE-supported F2F and online learning. Computers in human behavior 2014, 31, 542–550. [Google Scholar] [CrossRef]
  20. Tempelaar, D.T.; Rienties, B.; Giesbers, B.; Gijselaers, W.H. The pivotal role of effort beliefs in mediating implicit theories of intelligence and achievement goals and academic motivations. Social Psychology of Education 2015, 18, 101–120. [Google Scholar] [CrossRef]
  21. Arnold, K.E.; Pistilli, M.D. Course signals at Purdue: Using learning analytics to increase student success. Proceedings of the 2nd international conference on learning analytics and knowledge, 2012, pp. 267–270.
  22. Ferguson, R. Learning Analytics: drivers, developments and challenges. Italian Journal of Educational Technology 2014, 22, 138–147. [Google Scholar] [CrossRef]
  23. Kizilcec, R.F.; Piech, C.; Schneider, E. Deconstructing disengagement: analyzing learner subpopulations in massive open online courses. Proceedings of the third international conference on learning analytics and knowledge, 2013, pp. 170–179.
  24. Siemens, G.; Long, P. Penetrating the fog: Analytics in learning and education. EDUCAUSE review 2011, 46, 30. [Google Scholar]
  25. Pal, S. Mining educational data to reduce dropout rates of engineering students. International Journal of Information Engineering and Electronic Business 2012, 4, 1. [Google Scholar] [CrossRef]
  26. Gupta, A.; Garg, D.; Kumar, P. An ensembling model for early identification of at-risk students in higher education. Computer Applications in Engineering Education 2022, 30, 589–608. [Google Scholar] [CrossRef]
  27. Hew, K.F.; Hu, X.; Qiao, C.; Tang, Y. What predicts student satisfaction with MOOCs: A gradient boosting trees supervised machine learning and sentiment analysis approach. Computers & Education 2020, 145, 103724. [Google Scholar]
  28. Kuzilek, J.; Hlosta, M.; Zdrahal, Z. Open university learning analytics dataset. Scientific data 2017, 4, 1–8. [Google Scholar] [CrossRef] [PubMed]
  29. Olaniran, O.; Abdullah, M. Subset selection in high-dimensional genomic data using hybrid variational Bayes and bootstrap priors. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1489, p. 012030.
  30. Zheng, Z.; Cai, Y.; Li, Y. Oversampling method for imbalanced classification. Computing and Informatics 2015, 34, 1017–1037. [Google Scholar]
  31. Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Machine learning 2006, 63, 3–42. [Google Scholar] [CrossRef]
  32. Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of computer and system sciences 1997, 55, 119–139. [Google Scholar] [CrossRef]
  33. Breiman, L. Bagging predictors. Machine learning 1996, 24, 123–140. [Google Scholar] [CrossRef]
  34. Powers, D.M. Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv preprint 2020, arXiv:2010.16061. [Google Scholar]
  35. Olaniran, O.R.; Alzahrani, A.R.R.; Alzahrani, M.R. Eigenvalue Distributions in Random Confusion Matrices: Applications to Machine Learning Evaluation. Mathematics 2024, 12, 1425. [Google Scholar] [CrossRef]
Preprints 109341 g001
Figure 1. Open University Learning Analytics Dataset Schema.
Figure 1. Open University Learning Analytics Dataset Schema.
Preprints 109341 g001
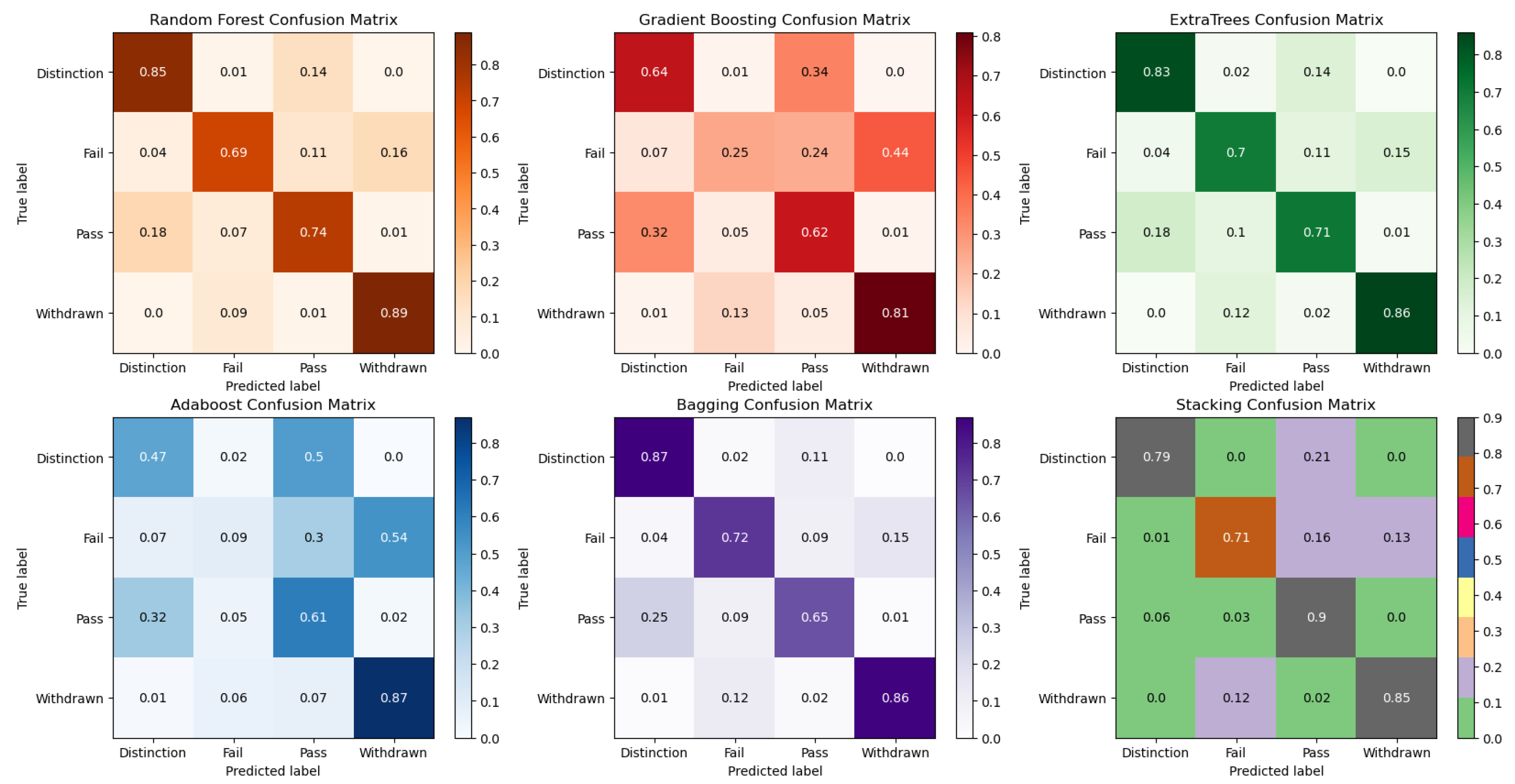
Preprints 109341 g002
Figure 2. Confusion matrices of the various machine learning models for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results.
Figure 2. Confusion matrices of the various machine learning models for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results.
Preprints 109341 g002
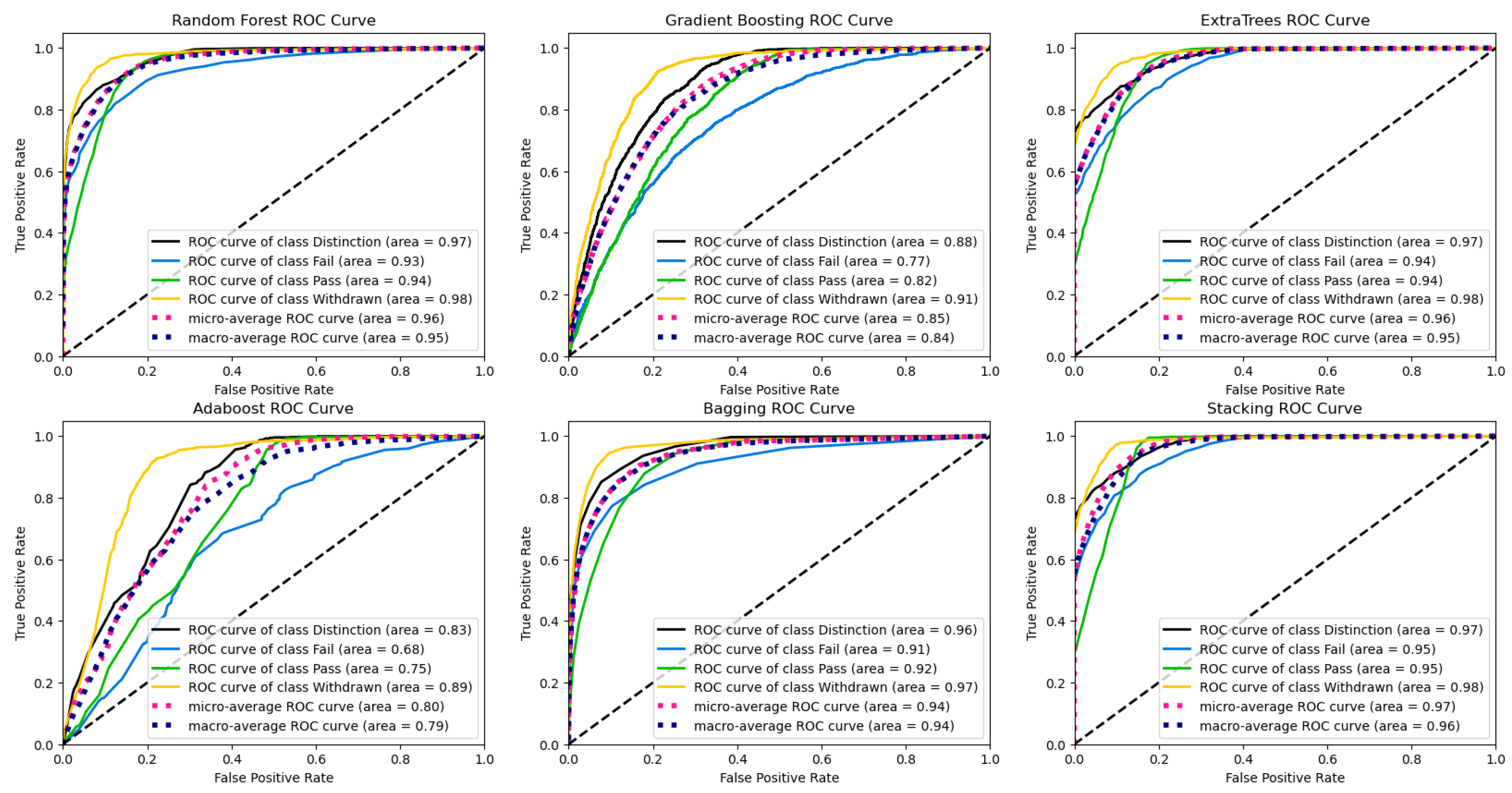
Preprints 109341 g003
Figure 3. Receiver operating characteristics curves (ROC) of the various machine learning models for for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results.
Figure 3. Receiver operating characteristics curves (ROC) of the various machine learning models for for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results.
Preprints 109341 g003
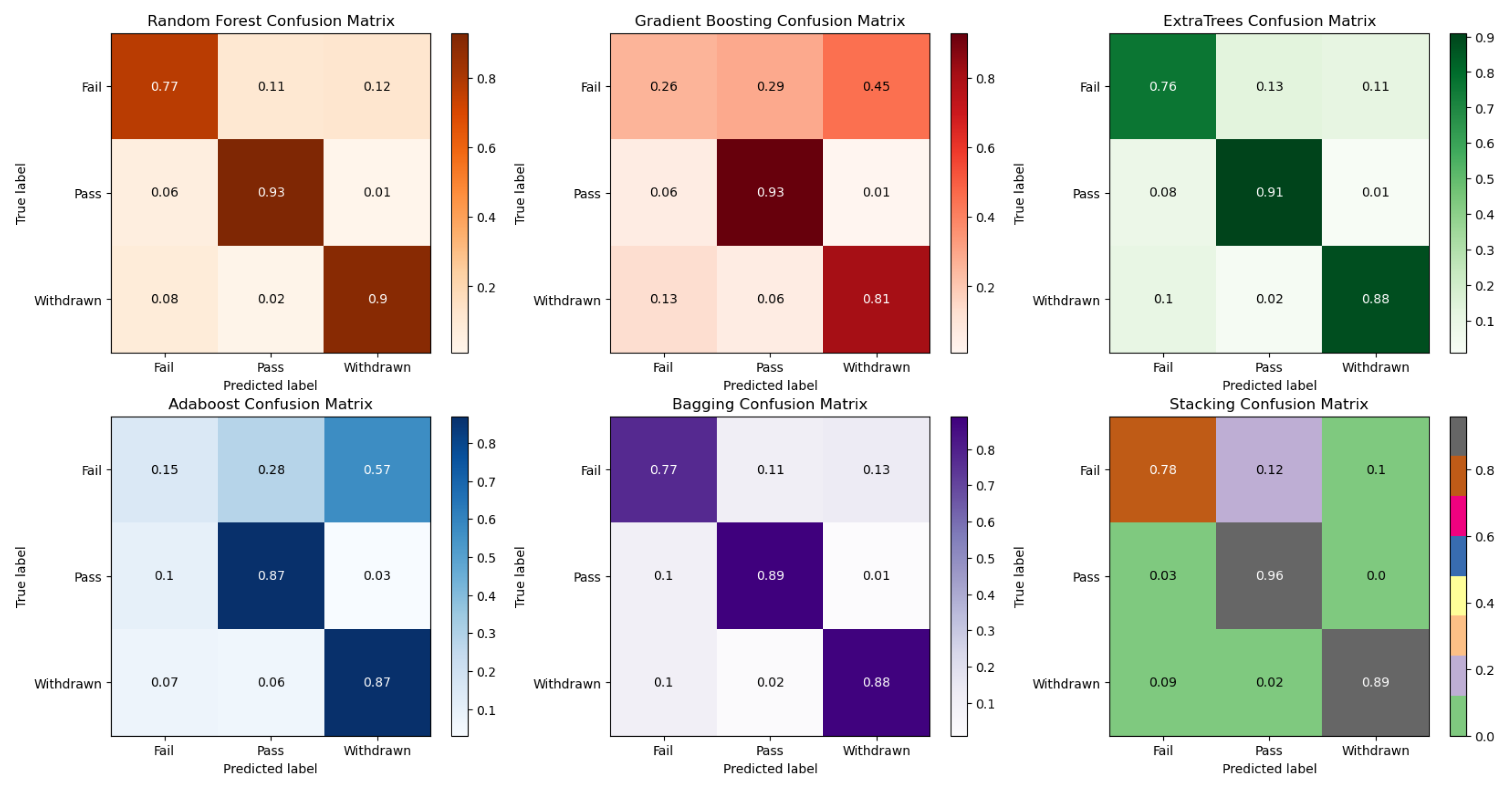
Preprints 109341 g004
Figure 4. Confusion matrices of the various machine learning models for the three classes (Fail, Pass & Distinction, Withdrawn.
Figure 4. Confusion matrices of the various machine learning models for the three classes (Fail, Pass & Distinction, Withdrawn.
Preprints 109341 g004
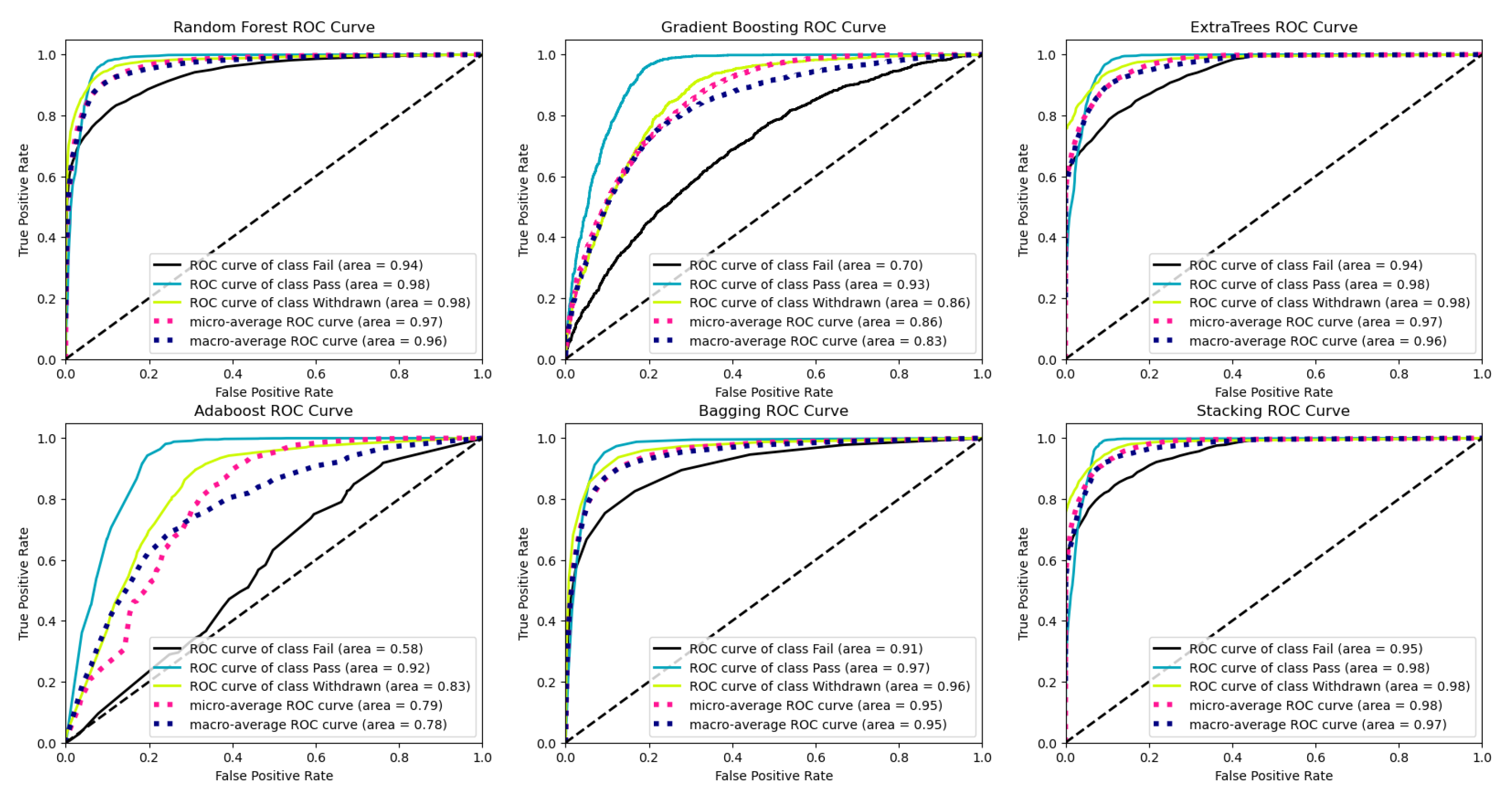
Preprints 109341 g005
Figure 5. Receiver operating characteristics curves (ROC) of the various machine learning models for the three classes (Fail, Pass & Distinction, Withdrawn
Figure 5. Receiver operating characteristics curves (ROC) of the various machine learning models for the three classes (Fail, Pass & Distinction, Withdrawn
Preprints 109341 g005
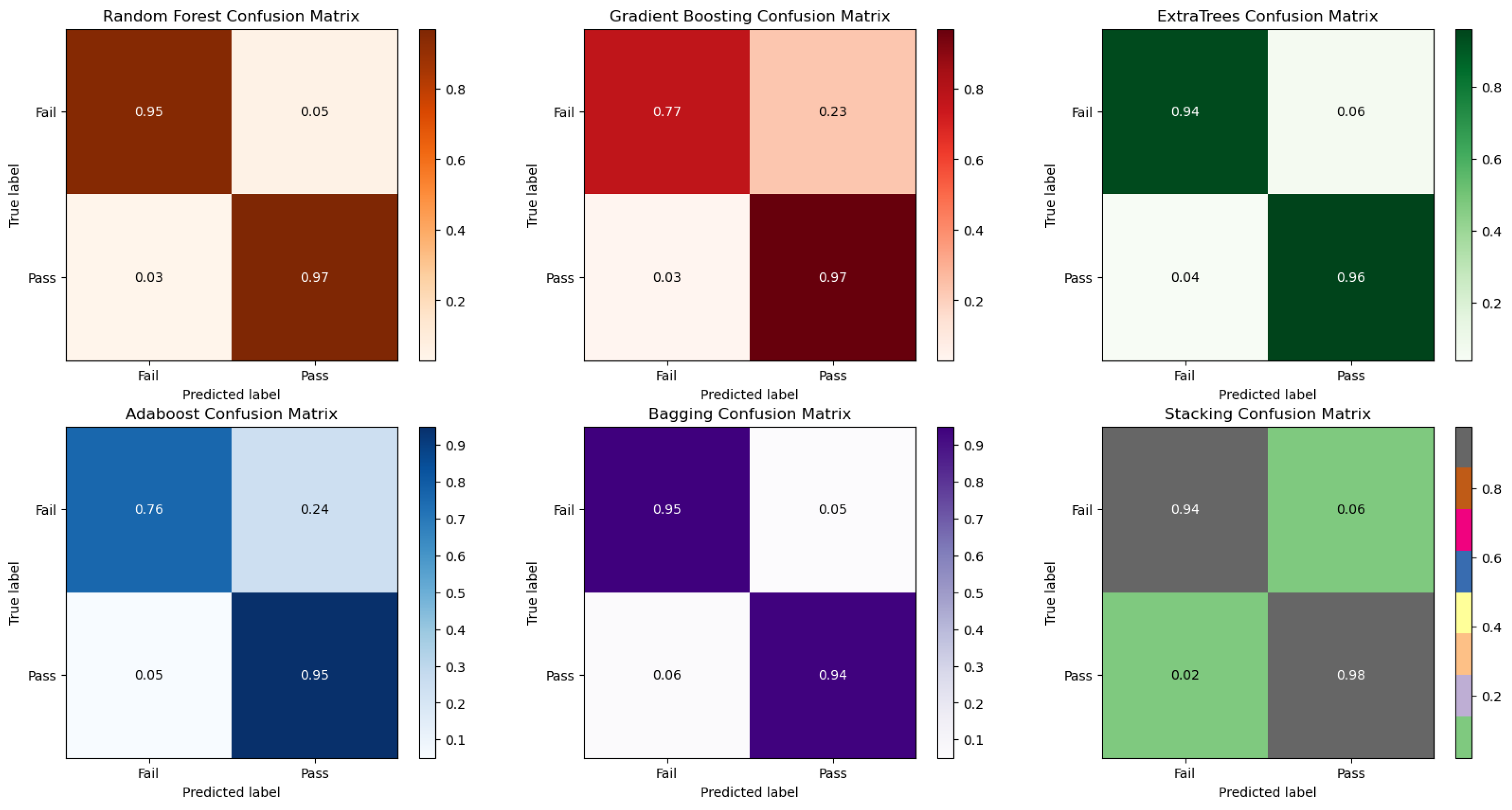
Preprints 109341 g006
Figure 6. Confusion matrices of the various machine learning models for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results
Figure 6. Confusion matrices of the various machine learning models for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results
Preprints 109341 g006
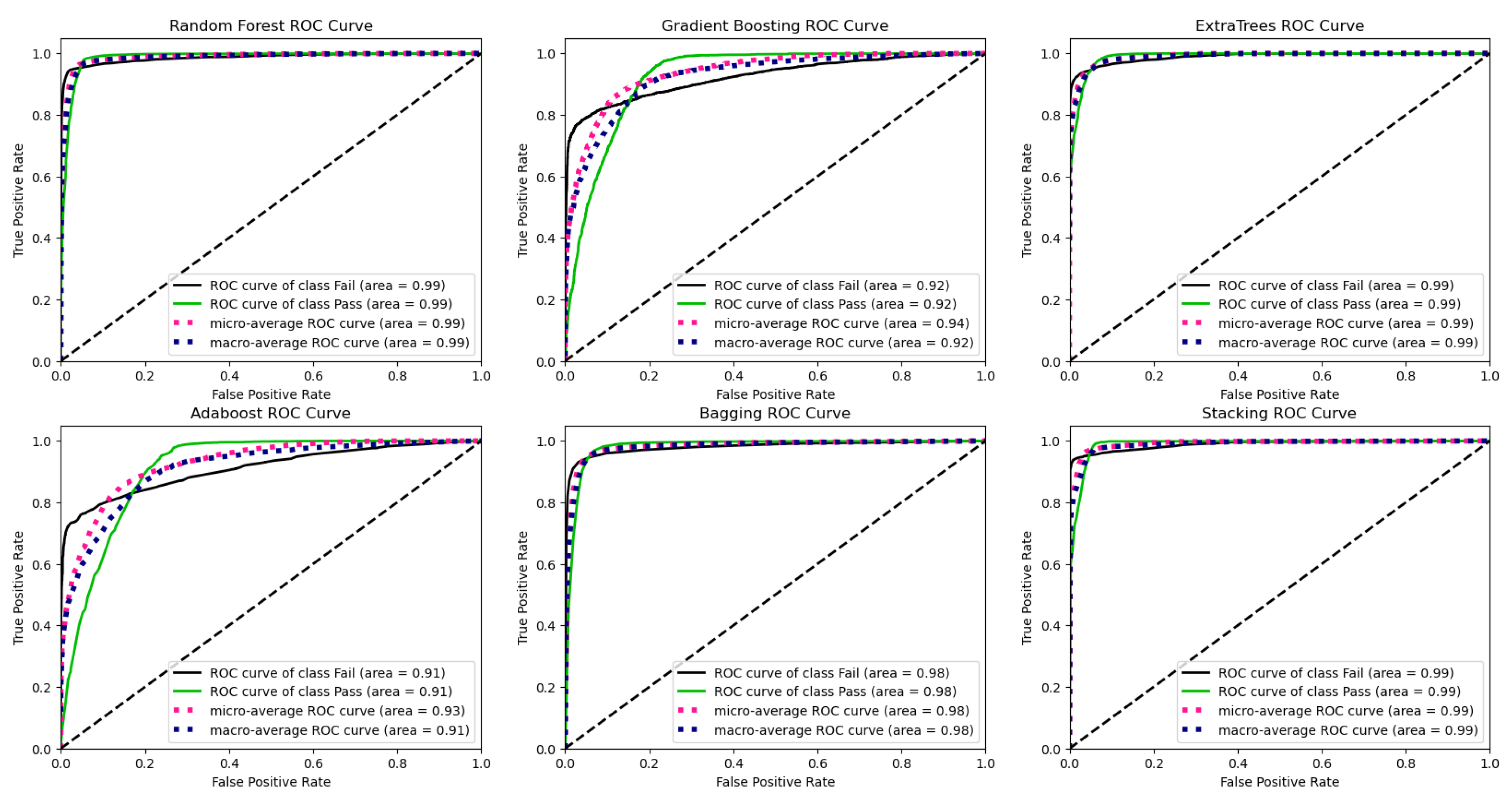
Preprints 109341 g007
Figure 7. Receiver operating characteristics curves (ROC) of the various machine learning models for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results
Figure 7. Receiver operating characteristics curves (ROC) of the various machine learning models for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results
Preprints 109341 g007
Table 1. Evaluation metrics of the various ensemble models predictions for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results.
Table 1. Evaluation metrics of the various ensemble models predictions for the four classes (Distinction, Fail, Pass, Withdrawn) of the students’ final results.
Evaluation Metrics
Models Precision Recall F1 Accuracy AUC
Random Forest 79% 79% 79% 79% 95%
Gradient Boosting 58% 58% 56% 58% 84%
ExtraTrees 78% 78% 78% 78% 95%
AdaBoost 49% 51% 46% 50% 79%
Bagging 77% 77% 77% 77% 94%
Stacking 83% 81% 81% 81% 96%
Table 2. Evaluation metrics of the various ensemble models predictions for the three classes (Fail, Pass & Distinction, Withdrawn) of the students’ final results.
Table 2. Evaluation metrics of the various ensemble models predictions for the three classes (Fail, Pass & Distinction, Withdrawn) of the students’ final results.
Evaluation Metrics
Models Precision Recall F1 Accuracy AUC
Random Forest 87% 87% 87% 87% 96%
Gradient Boosting 65% 67% 63% 66% 83%
ExtraTrees 85% 85% 85% 85% 96%
AdaBoost 59% 63% 57% 63% 78%
Bagging 84% 84% 84% 84% 95%
Stacking 88% 88% 88% 88% 97%
Table 3. Evaluation metrics of the various ensemble models predictions for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results.
Table 3. Evaluation metrics of the various ensemble models predictions for the two classes (Pass & Distinction, Fail & Withdrawn) of the students’ final results.
Evaluation Metrics
Models Precision Recall F1 Accuracy AUC
Random Forest 96% 96% 96% 96% 99%
Gradient Boosting 88% 87% 87% 87% 92%
ExtraTrees 95% 95% 95% 95% 99%
AdaBoost 87% 86% 85% 86% 91%
Bagging 94% 94% 94% 94% 98%
Stacking 96% 96% 96% 96% 99%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated