Crossroads between Stability and Randomness of the Non-stationaryQueue’s Pointwise Stationary Fluid Flow Approximation modelCrossroads between Stability and Randomness of the Non-stationary Queue’s Pointwise Stationary Fluid Flow Approximation

Ismail A Mageed; Amina Becheroul

doi:10.20944/preprints202405.0544.v1

Preprint

Article

Crossroads between Stability and Randomness of the Non-stationaryQueue’s Pointwise Stationary Fluid Flow Approximation modelCrossroads between Stability and Randomness of the Non-stationary Queue’s Pointwise Stationary Fluid Flow Approximation

This version is not peer-reviewed.

This version is not peer-reviewed.

Downloads

Views

Comments

Submitted:

08 May 2024

Posted:

09 May 2024

You are already at the latest version

Abstract

The current work reveals the fine tuning between stability zones and randomness of Pointwise Stationary Fluid Flow Approximation (PSFFA) model of the non-stationary queueing D/M/1 system. More specifically, this clearly provides more insights into developing a contemporary PSFFA theory that unifies non-stationary queueing theory with chaos theory and fields in both theoretical physics and chaotic systems. This opens new grounds for stability analysis of non-stationary queueing systems.

Keywords:

State variable

;

mean arrival rate

;

time

;

time dependent root parameter

;

PSFFA

;

Subject:

Computer Science and Mathematics - Applied Mathematics

1. Introduction

Day to day queues include time varying arrival process of customers, which is interpreted by its variance- based nature on the time of day. This can be caused by factors like failure of network resources or non-stationary input loads. These bursty and non-stationary in character networks’ traffic as communication networks become more complicated with fluctuating data speeds and quality of service needs. Queuing theory deals with analyzing and understanding waiting times in various scenarios, such as waiting for service in banks or supermarkets, waiting for a response from computers, waiting for failures to occur, or waiting for public transport.

Simulation techniques in the context of queueing systems involve tracking the behavior of the system through repeated execution of the simulation and averaging relevant quantities over different runs at specific time points. By collecting data at various time instants, the system’s Behavior can be evaluated over time[1].

In analytical transient investigations, transform techniques are commonly employed to solve differential/difference equation models that arise from an embedded Markov process/chain. These techniques help in analyzing the behaviour of the system over time by transforming the equations into a more manageable form, facilitating the study of transient phenomena in queueing systems.

This paper’s road map is: PSFFA theory is overviewed in section 2. In section 3, the

G I / M / 1

Queueing Model is discussed in more details. In section 4, ρ- threshold of the non-stationary

D / M / 1

queue’s

G I / M / 1

PSFFA model of the is revealed. In section 5, typical numerical experiments to evidence the derived analytic results against the numerical portraits. Closing remarks combined with the next phase of research are highlighted in Section 6.

2. PSFFA

The PSFFA is a simulation technique that uses a single non-linear differential equation to estimate the queue’s average number of users. An equation’s form based on steady-state queueing relationships is obtained by this revolutionary approach to provide advantages in terms of generality, simplicity, and computational efficiency. Moreover, these methods have potential applications in developing dynamic network control mechanisms[1].

Think about a queueing system for a single server that has a non-stationary arrival process.

μ (t)

and

λ (t)

serve as the time-dependent average queue service and arrival rates, respectively.The system’s ensemble average time-dependent state variable is referred to as

x (t),

x^{.} (t) = \frac{d x (t)}{d t}

. Define

f_{i n} (t)

and

f_{o u t} (t)

respectively, to be the system’s time-dependent flow into and out. Notably,

x^{.} (t),

f_{i n} (t)

and

f_{o u t} (t)

are related by:

x^{.} (t) = - f_{o u t} (t) + f_{i n} (t)

(1)

Consequently,

f_{o u t} (t) = μ (t) ρ (t)

(2)

Here

ρ (t)

defines the underlying queue’s server utilization.

For an infinite queue waiting space is infinite,

f_{i n} (t) = λ (t)

(3)

Equation (1)‘s fluid flow model becomes:

x^{.} (t) = - μ (t) ρ (t) + λ (t), 1 > ρ (t) = \frac{λ (t)}{μ (t)} > 0

(4)

Setting

x^{.} (t) =

0, implies

x = G_{1} (ρ)

(5)

Additonally, we assume the numerical invertibility of

G_{1} (ρ)

, namely

ρ = G_{1}^{- 1} (x)

(6)

Equationally, PSFFA rewrites to:

x^{.} (t) = - μ (t) (G_{1}^{- 1} (x (t))) + λ (t)

(7)

Notably, (7) is extremely general in nature, since the closed form represention of

G_{1}

can be computed for many queues. However, we can numerically or by data of an existing system’s fitting curve calculate

G_{1} .

3. The $G I / M / 1$ Queueing Model

This section discusses the

G I / M / 1

queueing model, in which the service time has an exponential distribution, and the inter-arrival process has an identical distribution with successive inter-arrival periods. Let

A (t)

stand for the distribution of inter-arrival times. The

G I / M / 1

queue’s steady state probability for the number of customers a new arrival finds in the system is a geometric distribution:

π_{n} = (1 - σ) σ^{n}

(10)

σ

(

1 > σ > 0)

uniquely solves:

σ = f_{a}^{*} (s) |_{s = μ (1 - σ)}

(11)

where

f_{a}^{*} (s)

is the Laplace-Stieltjes transform of the inter-arrival time distribution

A (t)

, that is:

f_{a}^{*} (s) = L^{*} (A (t)) = \int_{0}^{\infty} e^{- s t} d A (t)

(12)

Notably,

σ = 1

solves (11),

a n d t h e s t a t e v a r i a b l e

x

reads as:

x = \frac{λ}{μ (1 - σ)} = \frac{ρ}{(1 - σ)}

(13)

In determining the PSFFA model, equation (13) re-writes to

ρ (t) = x (t) μ (1 - σ (t))

(14)

We believe that the non-stationary load will exhibit sinusoidal mean behaviour, which will describe the cyclic load pattern over a specified time period (for example, day) in accordance with the prior research on non-stationary analysis of communication networks[2,3,4,5,6], namely

λ (t) = A + B s i n (w t + D),

for more details see[7,8,9].

Thus, the required model reads as:

x^{.} (t) = μ x (t) (1 - σ (t)) + λ (t)

(15)

We can numerically solve (15) to visualize the queue’s time varying behaviour.

Depending on the inter-arrival distribution

A (t),

the precise process for figuring out will vary, although it usually involves a root-finding approach like Laguerre’s method. The time varying

D / M / 1

queue’s

G I / M / 1

PSFFA model reads:

x^{.} (t) = - μ x (t) (1 - σ (t)) + λ (t), σ (t) = e^{\frac{(σ (t) - 1)}{ρ (t)}}

(16)

ρ (t) = t i m e - d e p e n d e n t s e r v e r u t i l i z a t i o n = \frac{λ (t)}{μ}

The

D / M / 1

case in equation (16) corresponds to a deterministic arrival process where the inter-arrival distribution

A (t)

is a delta function (i.e.,

d A (t) = f_{a} (t) d t a n d f_{a} (t) = δ (t - \frac{1}{λ})

)

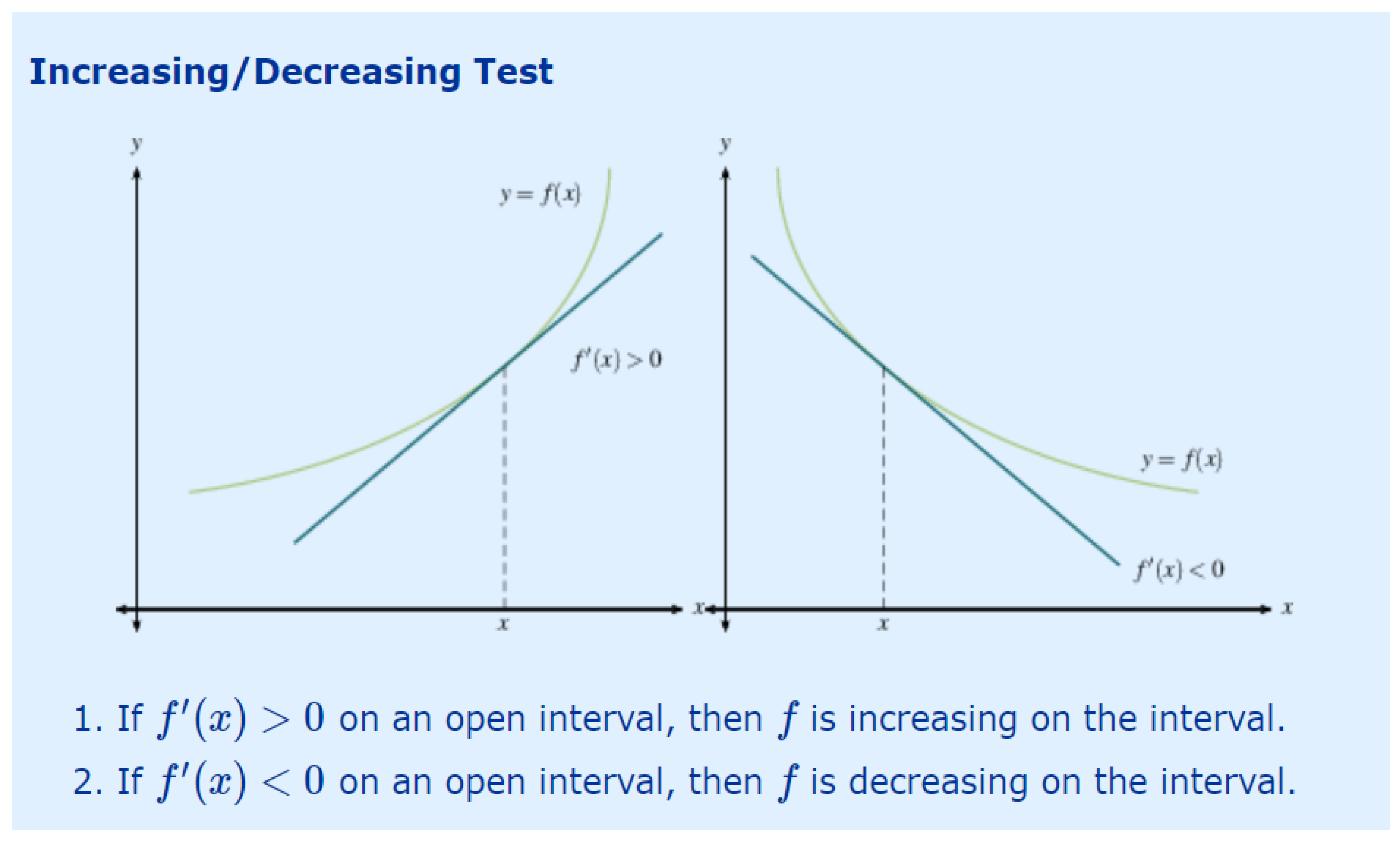
Mastering the increasability(decreasability) for a function,

f (x)

, a shorthand note reads:

f^{'} > 0 ⟺ f ↑

f^{'} < 0 ⟺ f ↓

In a more tangible form, we can visualize Figure 1(c.f., [10]).

4. The $ρ -$ Theshold Theory of $t h e n o n - s t a t i o n a r y t h e D / M / 1$ $q u e u e G I / M / 1$ PSFFA Model

Theorem 1 The time-dependent server utilization,

ρ (t)

(c.f., (16)) is forever increasing in

σ (t) (σ (t) \in (0,1))

Proof

Let the time-dependent root parameter,

σ (t) b e s u c h t h a t 1 > σ (t) > 0

. By (16), it follows that:

ρ (t) = \frac{λ (t)}{μ} = \frac{(σ (t) - 1)}{l n (σ (t))}

(17)

We have

\frac{\partial ρ}{\partial σ} = \frac{l n σ - 1 + \frac{1}{σ}}{{(l n σ)}^{2}}

(18)

Following mathematical analysis(c.f., [11]),

1 - \frac{1}{σ} < l n σ < σ - 1

(19)

Communicating (18), and (19), the result follows.

We can see that:

{{l i m}_{σ (t) \to 1} ρ (t) = l i m}_{σ (t) \to 1} \frac{(σ (t) - 1)}{l n (σ (t))} = {l i m}_{σ (t) \to 1} \frac{1}{\frac{1}{(σ (t))}} 1 (L ’ H o p i t a l ’ s r u l e)

(20)

and

{l i m}_{σ (t) \to \infty} ρ (t) = {l i m}_{σ (t) \to \infty} \frac{(σ (t) - 1)}{l n (σ (t))} = {l i m}_{σ (t) \to \infty} \frac{1}{\frac{1}{(σ (t))}} = \infty (L ’ H o p i t a l ’ s r u l e)

(21)

5. Typical Numerical Experiments

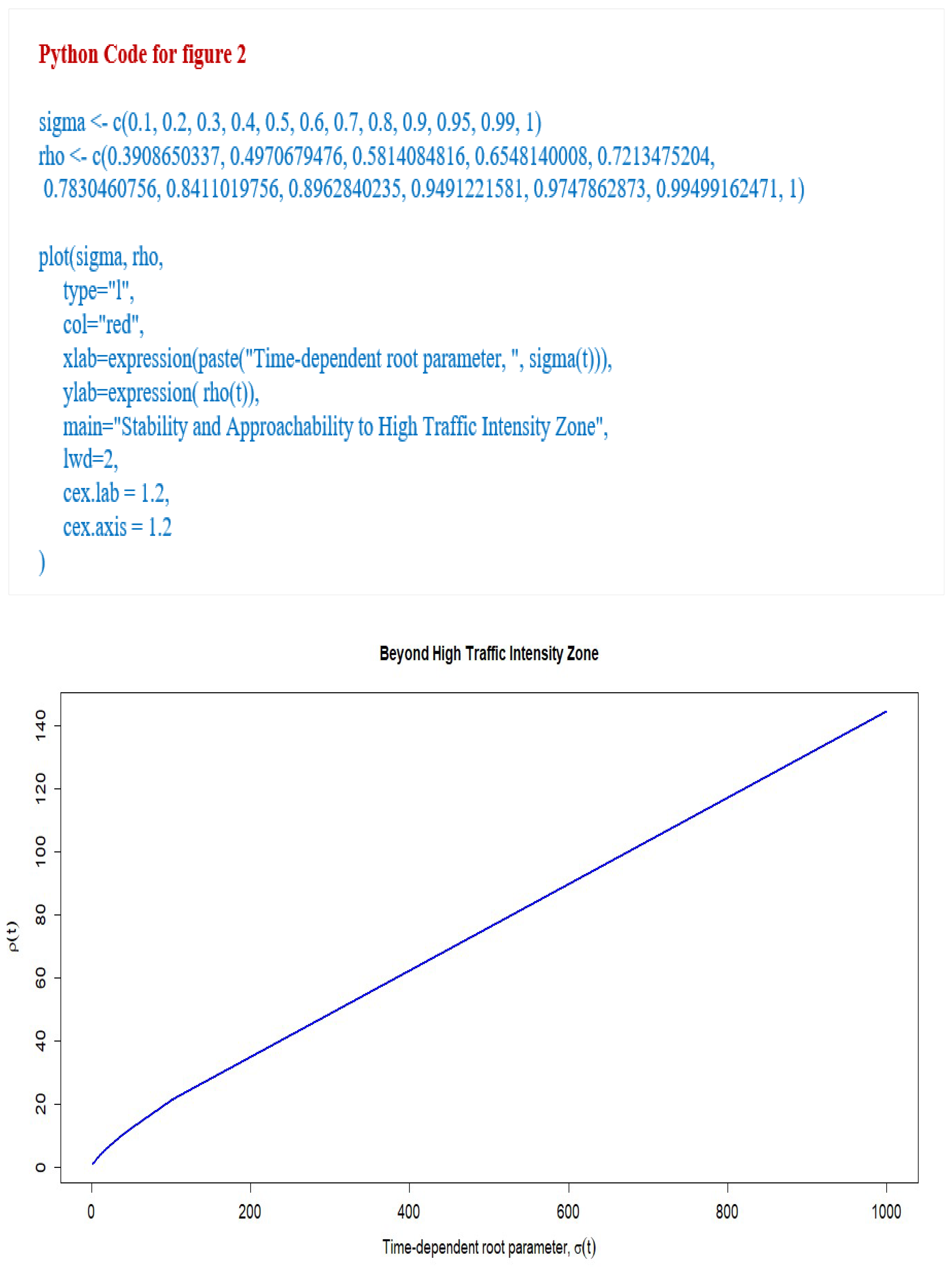
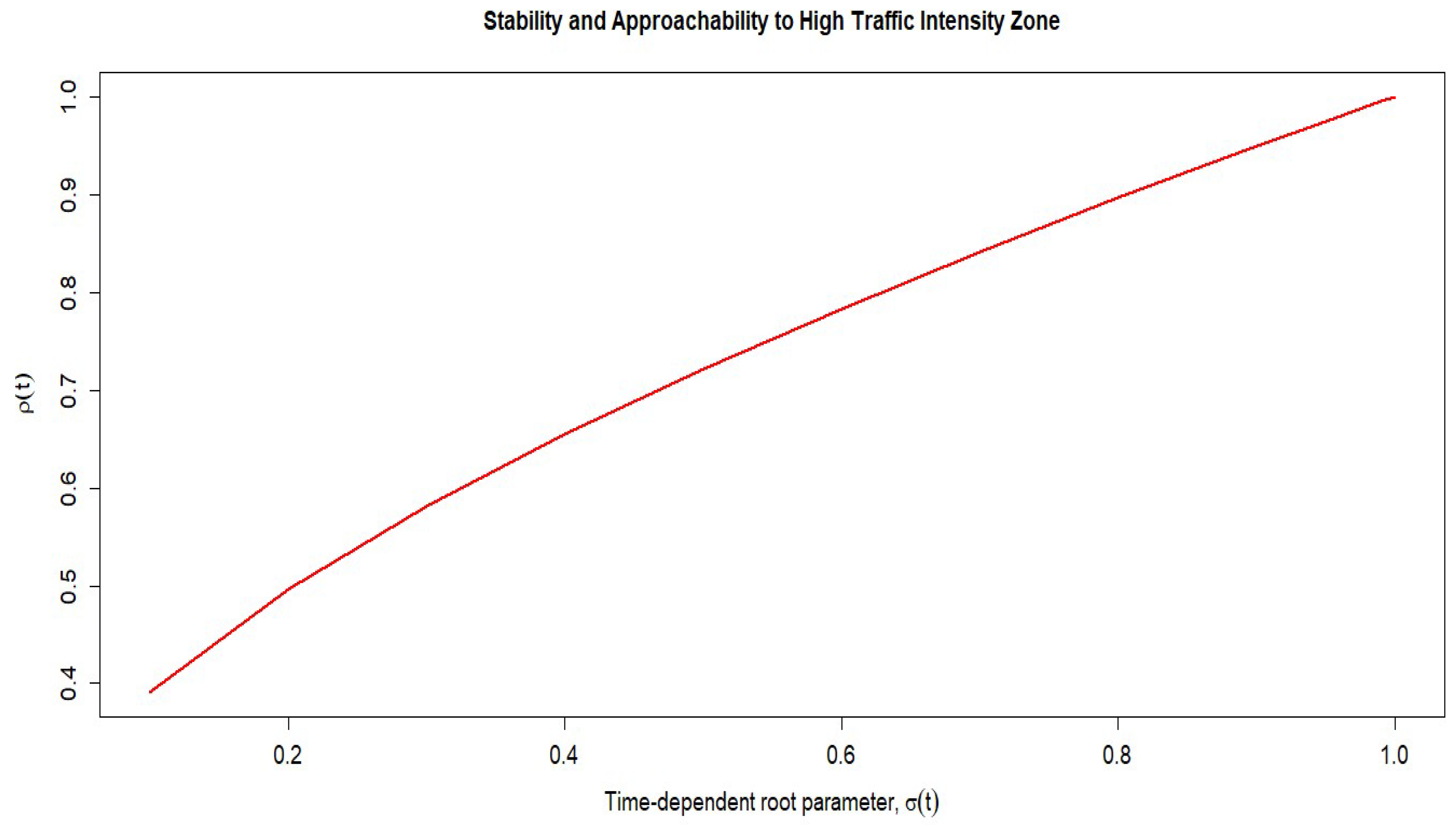
It is observed from Figure 2 and Figure 3, that the time-dependent root parameter,

σ (t)

has a significant impact on the underlying queue’s stability, by directly impacting the time- dependent server utilization,

ρ (t)

. Touching upon stability, it can be seen that

σ (t)

acts as a cutting-edge fine tuning to either approaching a high traffic intensity zone, corresponding to

ρ (t) = 1 .

Moreover, the progressive increase of

σ (t)

, will steer the whole system into a randomness zone, corresponding to

ρ (t) > 1 .

It can be easily verified that the numerical setup is validating the obtained analytic results of Theorem 1.

Figure 3.

6. Conclusions and Future Work

An exposition is undertaken to reveal the threshold theory of the time-dependent server utilization of

D / M / 1

queueing system’s

G I / M / 1

PSFFA closed form expression. Moreover, some numerical experiments are provided to validate the analytic results. Future work involves further investigation of similar threshold theorems of

G / M / 1

PSFFA model of t

h e n o n - s t a t i o n a r y E_{k} / M / 1 a n d I P P / M / 1

queueing systems.

References

Wang, W-P., Tipper, D., and Banerjee, S. 1996: A simple Approximation for Modelling Non-Stationary Queues, IEEE.
Poryazov S, Andonov V, Saranova E. Methods for Modelling of Overall Telecommunication Systems. Research in Computer Science in the Bulgarian Academy of Sciences. 2021:325-61.
Zhu M, Gao S, Tu G, Chen D. Multi-Access Edge Computing (MEC) Based on MIMO: A Survey. Sensors. 2023 Apr 11;23(8):3883. [CrossRef]
Mageed IA, Zhang Q, Modu B. The Linearity Theorem of Rényian and Tsasllisian Maximum Entropy Solutions of The Heavy-Tailed Stable M/G/1 Queueing System entailed with Potential Queueing-Theoretic Applications to Cloud Computing and IoT. electronic Journal of Computer Science and Information Technology. 2023 Apr 23;9(1):15-23.
Grassmann, W.K. 1990: Computational Methods in Probability Theory, Handbook in Operations Research and Management Science, Vol.2, North Holland.
Mageed IA, Zhang,Q. Solving the open problem for GI/M/1 pointwise stationary fluid flow approximation model (PSFFA) of the non-stationary D/M/1 queueing system. electronic Journal of Computer Science and Information Technology. 2023 Apr 23;9(1):1-6.
Chang J, Chan HK, Lin J, Chan W. Non-homogeneous continuous-time Markov chain with covariates: Applications to ambulatory hypertension monitoring. Statistics in Medicine. 2023 May 30;42(12):1965-80. [CrossRef]
GRASSMANN WK. Finding Transient Solutions in Markovian Event Systems Through Numerical Solution of Markov Chains. 2021 Jun 30:357.
A Mageed, D.I. Effect of the root parameter on the stability of the Non-stationary D/M/1 queue’s GI/M/1 model with PSFFA applications to the Internet of Things (IoT). Preprints 2024, 2024011835. [CrossRef]
Mageed, I. A., & Zhang, Q. (2023). Threshold Theorems for the Tsallisian and Rényian (TR) Cumulative Distribution Functions (CDFs) of the Heavy-Tailed Stable M/G/1 Queue with Tsallisian and Rényian Entropic Applications to Satellite Images (SIs). electronic Journal of Computer Science and Information Technology, 9(1), 41-47.
[Kozma, L. 2020: Useful inequalities, online source, available at http://www.Lkozma.net/inequalities_cheat_sheet.

Figure 1.

Figure 2.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Crossroads between Stability and Randomness of the Non-stationaryQueue’s Pointwise Stationary Fluid Flow Approximation modelCrossroads between Stability and Randomness of the Non-stationary Queue’s Pointwise Stationary Fluid Flow Approximation

Abstract

Keywords:

Subject:

1. Introduction

2. PSFFA

3. The G I / M / 1 Queueing Model

4. The ρ − Theshold Theory of t h e n o n − s t a t i o n a r y t h e D / M / 1 q u e u e G I / M / 1 PSFFA Model

5. Typical Numerical Experiments

6. Conclusions and Future Work

References

MDPI Initiatives

Important Links

Subscribe

3. The $G I / M / 1$ Queueing Model

4. The $ρ -$ Theshold Theory of $t h e n o n - s t a t i o n a r y t h e D / M / 1$ $q u e u e G I / M / 1$ PSFFA Model