Prerpints.org logo
Preprint
Article

Effect of Electric Field on Hydrogen Storage in Clathrate Hydrates

This version is not peer-reviewed.

Submitted:

05 May 2024

Posted:

06 May 2024

You are already at the latest version

Abstract
In this exploratory work, we have examined the impact of an external static electric field on the H2 storage capacity of clathrate hydrates. To this end, we have chosen the 512 clathrate hydrate and examined the encapsulation of 1 - 4 H2 molecules within it. Results suggest that with the help of moderate electric fields (±0.10 to ±0.31V/Å), the encapsulation of 1 H2 molecule within the 512 clathrate hydrate becomes thermodynamically more favorable. In the cases of 4H2@512 and 2H2@512, however, the concerned processes become thermodynamically more favorable only when the field is applied along a specific direction. No favorable outcome could be observed in the case of 3H2@512, irrespective of the direction of the applied field. It appears from the results obtained herein that it might be possible to design a suitable external electric field to facilitate the hydrogen storage capacity of clathrate hydrates at ambient conditions, at least in certain cases.
Keywords: 
Hydrogen storage
;  
clathrate hydrates
;  
pentagonal dodecahedron cavity
;  
static electric field
;  
density functional theory
Subject: 
Chemistry and Materials Science  -   Theoretical Chemistry

Introduction

Gas hydrates chemistry has become a matured topic of research. It is well known to the scientific community that clathrate hydrates are inclusion compounds made up of water and small guest molecules. Water molecules associate via hydrogen bonding to form the cage wall. Nonreactive small molecules function as the guest. Such cage-like composites are one among the emerging materials containing potential applications [1]. In the last three decades this water containing materials have drawn significant attention of the scientific community, although there exists a research history of around two centuries. Water cage compounds first came in to existence in the year 1811: Sir H. Davy disclosed to the Royal Society of Chemistry, London, about a new compound comprising chlorine and water bearing higher melting point with respect to ice [2]. Afterwards, Faraday stated that the composition of the compound is Cl2(H2O)10 [3]. Passing a surprising pause of ~ 130 years, Clausen and co-workers reported crystal structures of such type of compounds, namely structure I (sI) and structure II (sII) clathrate hydrates [4,5,6]. Later, in the year 1987, Ripmeester and co-workers reported about a third type of water molecules associated hexagonal cubic form (sH crystal) [7]. Existence of such sH crystal of water and gas mixture was confirmed by Lu and co-workers [8]. Two types of cavities are present in sI crystal, pentagonal dodecahedron (512) and hexagonal truncated trapezohedron (51262). sII crystals are formed by 512 and hexadecahedron (51264) pockets. sH clathrates are composed of 512, dodecahedra (435663), and irregular icosahedron (51268) cavities. Radius of 512 and 51262 cavities in sI are 3.96 and 4.33 Å, respectively. Radius of 512 and 51264 cavities in sII are 3.91 and 4.73 Å, respectively. Radius of 512, 435663, and 51268 cavities in sH are 3.91, 4.06, and 5.71 Å, respectively [1,9,10,11,12].
Day by day, study on gas hydrates is becoming multiple faceted. We have been studying clathrate hydrates to disclose its potential as hydrogen storage material (hydrogen hydrates), possibility of methane storage (methane hydrates), nucleation of gas hydrates, etc. [13,14,15,16,17,18,19,20]. Out of the many branches, research on hydrogen hydrates has extraordinary significance as it encompasses the possibility of achieving one of the best hydrogen storage materials [13,19]. So far, many research groups around the globe have been exploring clathrate hydrates as possible hydrogen storage material. Dyadin et al. and Mao et al. reported about the synthesis of hydrogen gas encapsulated hydrates at high pressure and low temperature [21,22]. Chattaraj et al. disclosed the efficacy of selected hydrate cavities of sI, sII and sH forms in storing molecular hydrogen. Moreover, they reported the structure and stability of hydrogen loaded clathrate hydrates, the hydrogen hydrates [13,19]. In another study, metastable nature of sI hydrogen hydrate slab was disclosed [14]. Later, Koh and Sum et al. synthesized sI hydrogen hydrates and revealed the occupancy of both 512 and 51262 cavities by hydrogen molecules [23]. How HF doping (substitutional) influences the thermodynamics and kinetics of formation of hydrogen hydrates from hydrogen and water molecules were also reported [15]. Recently, Chattaraj and coworkers in a study of sH binary hydrates revealed that the hydrogen storage efficiency of the 51268 cavity increases when host former methane and ethane molecules are present [20].
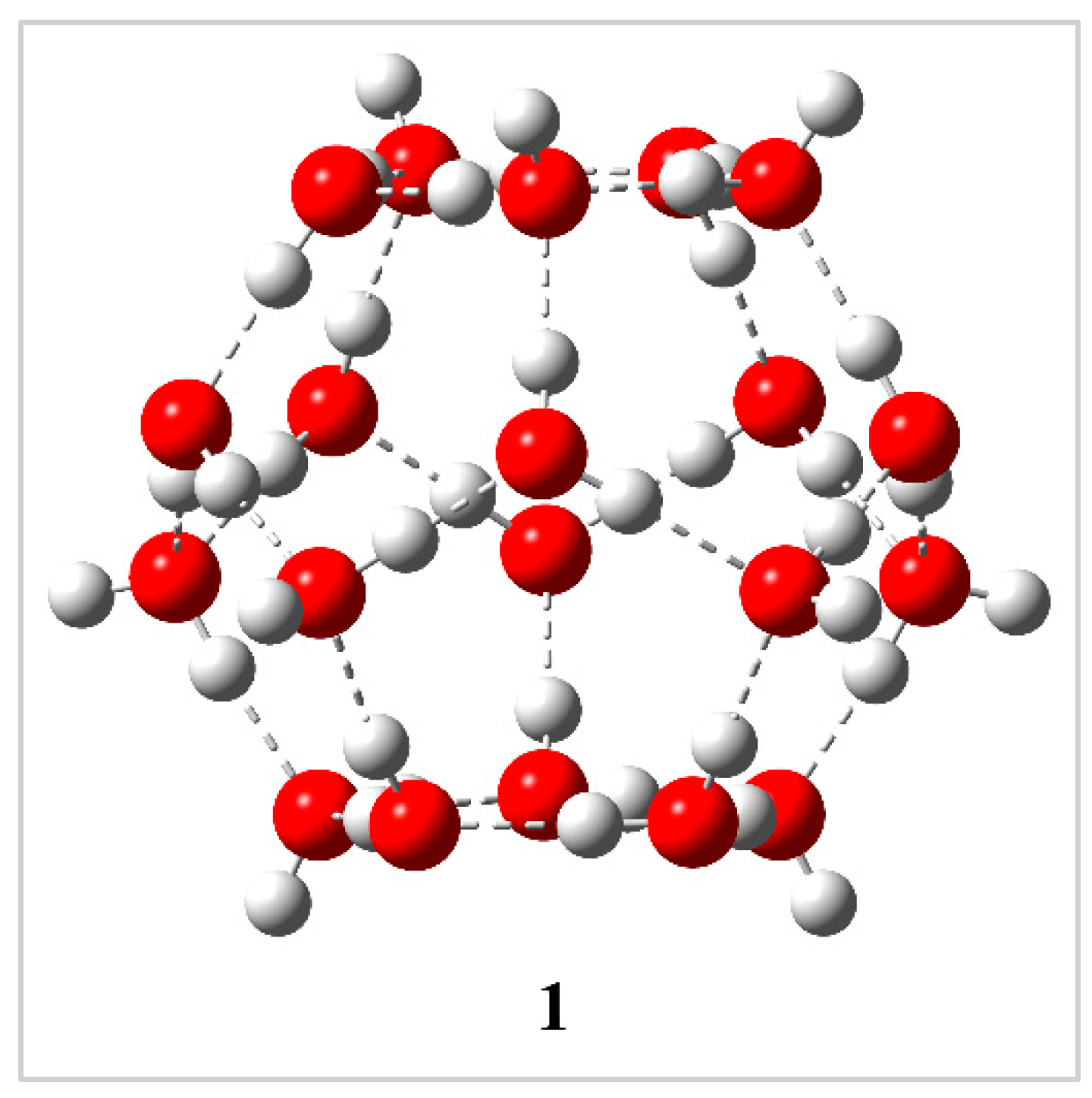
In continuation of our research on clathrate hydrates, we have started to assess the effect of electric field on the structure, stability and reactivity of hydrates and hydrogen hydrates. Significance of electric field on hydrogen storage is already reported by many researchers, particularly, when H2 binds via weak interaction [24,25,26]. It could be noted that the application of electric fields in chemistry has opened a new path to investigate various reactions and catalysis [27,28,29,30,31]. In this regard, we intend to investigate herein whether an external electric field could be utilized to enhance the H2 storage capacity by clathrate hydrates. As a model case study, keeping in mind the computational cost, we have chosen the 512 cavity. Moreover, the pentagonal dodecahedron cage comprises only 20 H2O molecules and it is present in all the three types of clathrate hydrate crystals. Structure of the 512 cavity (1) is provided in Figure 1, hydrogen bonds are indicated by dotted lines.

Computational Details

Initial guess structures were modelled with the help of GaussView 6 software [32]. PBE0 functional in combination with def2-TZVP basis set and Grimme dispersion D3 approximations was used to optimize the modelled structures in Gaussian 16 program [33,34,35]. Harmonic vibrational frequency analysis was carried out to characterize the nature of the stationary points at the respective potential energy surfaces (PES).
In order to study the effect of external electric field on the hydrogen storage capacity of the host clathrate hydrate system, a static electric field was applied (in both parallel as well as anti-parallel directions) using the keyword ‘Field’, as implemented in Gaussian 16 program [35]. Conceptual density functional theory (CDFT) [36,37,38] based global reactivity descriptors such as chemical hardness and polarizability have been calculated in order to understand the reactivity patterns in the studied systems. The following relations have been used in order to compute the chemical hardness ( η ) and polarizability (α):
η = I P − E A 2    ;   I P = I o n i z a t i o n   p o t e n t i a l ,   E A = E l e c t r o n   a f f i n i t y
α = α x x + α y y + α z z 3   ;   α x x / z z / y y     a r e   p o l a r i z a b i l t y   t e n s o r s

Results and Discussion

In this work, we have considered the 512 clathrate hydrate as the representative model for the host system. Herein, 512 denotes a cavity having 12 pentagonal faces formed by water molecules. We have considered moderate external electric fields having strengths ± 0.10   t o   ± 0.31   V / Å in this work. 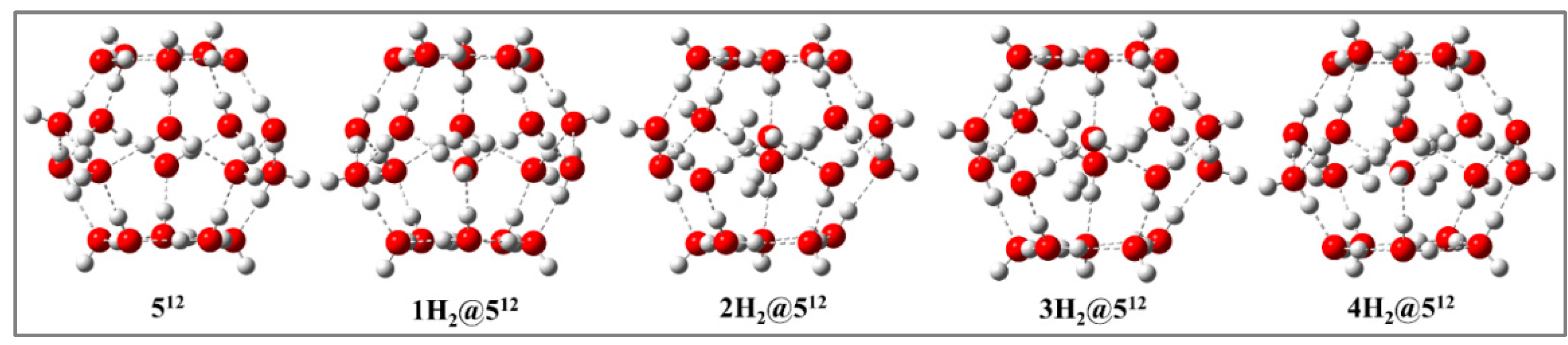Given the fact that the host system comprises (primarily) non-covalent interactions among the constituent H2O molecules, application of very strong external electric fields might distort the structural integrity of the host. We have considered encapsulation of 1 - 4 hydrogen molecules within the host (Figure 2).
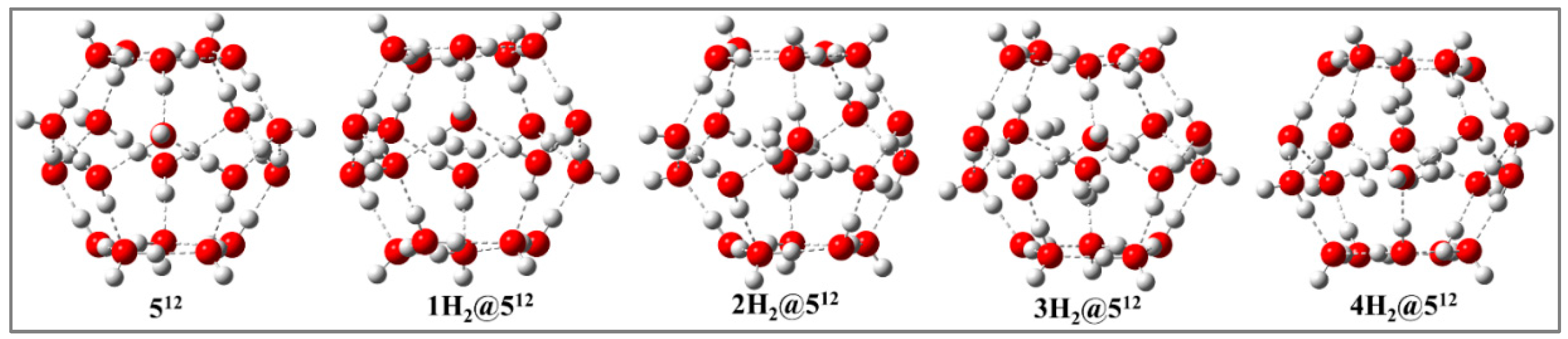
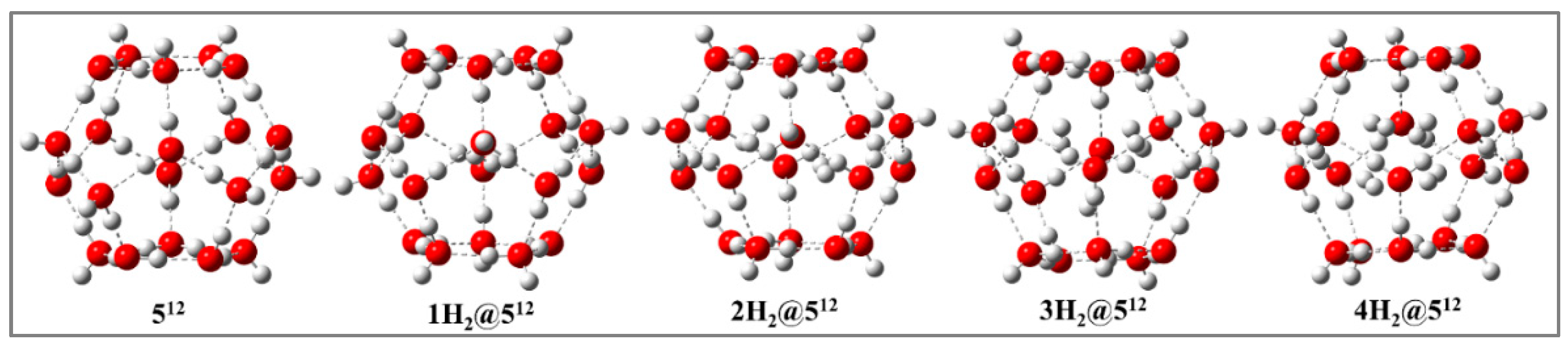
The nH2@512 (n = 1 - 4) systems have been placed under the influence of the external perturbation. Harmonic vibrational frequency analysis suggests that all the reported structures in this work belong to the minima in the PES. Some representative geometries of the concerned systems in the presence of external electric fields have been shown in Figure 3 and Figure 4. Results suggest that under the impact of the considered perturbations, the structural arrangement of the host remains intact, albeit some insignificant minor changes.
We have presented the Gibbs free energy changes ( ∆ G ;   298.15   K ) and zero-point vibrational energy (ZPVE) corrected interaction energies ( ∆ E ) for the concerned systems in Table 1, Table 2, Table 3 and Table 4.
Results indicate that the encapsulation of one H2 molecule within the 512 clathrate hydrate is unfavorable from thermodynamic point of view ( ∆ G ) at 298.15 K. However, in the presence of static external electric fields, this process becomes thermodynamically more favorable irrespective of direction of the applied field. As we increase the strength of the external electric field, the concerned encapsulation process becomes more favorable thermodynamically. Similar trend is observed in the case of the interaction energies among the host and the guest. We note that the 512 clathrate hydrate possesses the following values of chemical hardness ( η ) and polarizability (α) in its free state: 4.19 eV and 162.19 a.u. (PBE0-D3/def2-TZVP level of theory). Upon encapsulation of the H2 molecule, the η value shows only a minor change (4.24 eV) whereas the α value increases to 165.99 a.u. (as compared to the 512 clathrate hydrate in its free state). It appears that due to the encapsulation process, the properties of the frontier molecular orbitals do not change by much whereas the 1H2@512 system becomes more polarizable (and therefore more reactive) as compared to the corresponding guest system in its free state. The concerned values for the systems in the presence of external perturbation are presented in Table 1. As could be seen from the presented values, the η value only shows some minor changes whereas the α values, effectively, remain constant. Therefore, it could be stated that the external perturbation does not alter the properties of the frontier molecular orbitals by much. α values for these systems, on the other hand, are not good indicators for their concerned stability and reactivity patterns. It appears that higher order response properties might be needed to understand the changes in the reactivity/stability of the studied systems. It is not quite surprising as the concerned host-guest system is bound by non-covalent interactions only and does not involve any ‘genuine’ covalent bonds (and therefore significant bonding orbital interactions among the host and the guest).
We now consider the case of 2H2@512. In the cases when the electric field is applied along the x-direction corresponding to the molecular frame, the encapsulation processes become thermodynamically more favorable. This situation changes when direction of the applied field is flipped (-x), but for one case. The interaction energies among the host and the guests becomes more attractive when the field is applied along the x-direction corresponding to the molecular frame as compared to the case when no external perturbation is present. The α values show negligible changes in all the cases whereas the η value tend to decrease by some extent when the strength of the applied field is enhanced.
In the case of 3H2@512, however, the applied electric field makes the guest encapsulation processes thermodynamically unfavorable irrespective of the direction of the applied field.
In the cases of 4H2@512, if the electric field is applied along the -x direction corresponding to the molecular frame, the encapsulation processes become thermodynamically more favorable in conjunction with more attractive interaction energies among the host and the guests.
It appears from the aforementioned discussion that it might be possible to design a suitable external electric field to facilitate the hydrogen storage capacity of clathrate hydrates at ambient conditions. Given the observed trends in the global reactivity descriptors, it could be stated that the driving force for such processes is not controlled by the frontier molecular orbitals for the concerned systems in a major way. Rather, it appears that the electric fields create suitable ‘electrostatic’ environments within the host-guest system thereby facilitating attractive interactions among the host and the guests.

Conclusions

Application of electric fields of moderate strength ( ± 0.10   t o   ± 0.31   V / Å ) can monitor the encapsulation of molecular hydrogen by clathrate hydrates. Particularly, encaging of 1 H2 molecule by 512 hydrate becomes thermodynamically more favorable. On the other hand, for the 4H2@512 and 2H2@512 cases the encapsulation becomes more favorable when the field is applied from the -x direction (in comparison to the cases when electric field was applied from the x-direction). The reference point, of course, in all the cases are the corresponding processes in absence of any external perturbation. Encapsulation of three hydrogen molecules is not favorable. The concerned processes are not controlled by the properties of the frontier molecular orbitals in a major way. It appears that the electric fields create suitable ‘electrostatic’ environments within the host-guest system thereby facilitating attractive interactions among the host and the guests. Whether these properties could be exploited further with the suitable choice of the external fields remains to be examined further.

Acknowledgements

PKC Thanks DST, New Delhi for the J. C. Bose fellowship. SM Thanks University Grants Commission, New Delhi for UGC-BSR Research Start-Up-Grant(No.F.30-458/2019[BSR]). DC thanks SERB, New Delhi (File No. SRG/2022/001280) for the financial assistance. Authors thank the HPC facility of BIT, Mesra and the Department of Education, Assam University for providing the computational facility.

Conflict of Interest

The authors declare no competing interests.

References

  1. E. D. Sloan, C. A. Koh, Clathrate Hydrates of Natural Gases, 3rdEdition. CRC Press—Taylor and Francis Group LLC, Boca Raton, FL 2008.
  2. H. Davy, Philos. Trans. R Soc. London, 1811, 101, 1.
  3. M. Faraday, Philos. Trans. R. Soc. London, 1823, 113, 160.
  4. W. F. Clausen, J. Chem. Phys., 1951, 19, 259.
  5. W. F. Clausen, J. Chem. Phys., 1951, 19, 1425.
  6. H. R. Muller, M. v. Stackelberg, Naturwissenschaften, 1952, 39, 20.
  7. J. A. Ripmeester, J. S. Tse, C. I. Ratcliffe, B. M. Powell, Nature, 1987, 325, 135.
  8. H. Lu, Y. T. Seo, J. W. Lee, I. Moudrakovski, J. A. Ripmeester, N. R. Chapman, R. B. Coffin, G. Gardner, J. Pohlman, Nature, 2007, 445, 303.
  9. E. D. Sloan, Energy Fuels, 1998, 12, 191.
  10. E. D. Sloan, Nature, 2003, 426, 353.
  11. C. A. Koh, Chem. Soc. Rev., 2002, 31, 157.
  12. T. S. Collet, AAPG Bull, 2002, 86, 1971.
  13. P. K. Chattaraj, S. Bandaru, S. Mondal, J. Phys. Chem. A, 2011, 115, 187.
  14. S. Mondal, S. Ghosh, P. K. Chattaraj, J. Mol. Model., 2013, 19, 2785.
  15. S. Mondal, S. Giri, P. K. Chattaraj, J. Phys. Chem. C, 2013, 117, 11625.
  16. S. Mondal, S. Giri, P. K. Chattaraj, Chem. Phys. Lett., 2013, 578, 110.
  17. S. Mondal, P. K. Chattaraj, Phys. Chem. Chem. Phys., 2018, 16, 17943.
  18. S. Mondal, T. Goswami, G. Jana, A. Misra, P. K. Chattaraj, Chem. Phys. Lett., 2018, 691, 415.
  19. D. Chakraborty, S. Mondal, R. Das, and P. K. Chattaraj, 2021, ‘Effect of Confinement on Gas Storage Potential and Catalytic Activity’, In Chemical Reactivity in Confined Systems (eds P.K. Chattaraj and D. Chakraborty).
  20. S. Mondal, G. Jana, H. K. Srivastava, G. N. Sastry, P. K. Chattaraj, J. Comp. Chem., 2023, 44, 1446.
  21. Y. A. Dyadin, E. G. Larionov, E. Y. Aladko, A. Y. Manakov, F. V. Zhurko, T. V. Mikina, V. Y. Komarov, E. V. J. Grachev, Struct. Chem., 1999, 40, 790.
  22. W. L. Mao, H. -K. Mao, A. F. Goncharov, V. V. Struzhkin, Q. Guo, J. Hu, J. Shu, R, J. Hemley, M. Somayazulu, Y. Zhao, Science, 2002, 297, 2247.
  23. R. G. Grim, P. B. Kerkar, M. Shebowich, M. Arias, E. D. Sloan, C. A. Koh, and A. K. Sum, J. Phys. Chem. C, 2012, 116, 18557.
  24. J. Zhou, Q. Wang, Q. Sun, P. Jena and X. S. Chen Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 2801.
  25. X. Sun, J.-Y. Hwang and S. Shi, J. Phys. Chem. C, 2010, 114, 7178.
  26. S. Mondal, K. Srinivasu, Swapan K. Ghosh, and P. K. Chattaraj, RSC Advances, 2013, 3, 6991.
  27. S. Shaik, S. P. de Visser, D. Kumar, J. Am. Chem. Soc., 2004, 126, 11746.
  28. S. Shaik, R. Ramanan, D. Danovich, D. Mandal, Chem. Soc. Rev., 2018, 47, 5125.
  29. A. C. Aragones, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez, M. L. Coote, Nature, 2016, 531, 88–91.
  30. M. Dittner, B. Hartke, J. Chem. Phys., 2020, 152, 11.
  31. M. Arepalli, S. Mondal, D. Chakraborty, P. K. Chattaraj, Molecules, 2023, 28, 6169.
  32. GaussView, Version 6, Dennington, Roy; Keith, Todd A.; Millam, John M. Semichem Inc., Shawnee Mission, KS, 2016.
  33. C. Adamo, V. Barone, J. Chem. Phys., 1999, 110, 6158.
  34. S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys., 2010, 132, 154104.
  35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Jr. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 16, Revision C.01, Gaussian Inc, Wallingford CT 2016.
  36. R. G. Parr and W. T. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701.
  37. P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793.
  38. D. Chakraborty, P. K. Chattaraj, Chem. Sci., 2021, 12, 6264.
Preprints 105661 g001
Figure 1. Structure of the pentagonal dodecahedron cavity [(H2O)20, 512]. The oxygen and hydrogen atoms are indicated by red and off-white color spheres, respectively. Hydrogen bonds are shown by dotted lines.
Figure 1. Structure of the pentagonal dodecahedron cavity [(H2O)20, 512]. The oxygen and hydrogen atoms are indicated by red and off-white color spheres, respectively. Hydrogen bonds are shown by dotted lines.
Preprints 105661 g001
Preprints 105661 g002
Figure 2. Minimum energy structures of nH2@512 (n = 2- 4) at PBE0-D3/def2-TZVP level in the absence of electric field.
Figure 2. Minimum energy structures of nH2@512 (n = 2- 4) at PBE0-D3/def2-TZVP level in the absence of electric field.
Preprints 105661 g002
Preprints 105661 g003
Figure 3. Minimum energy structures of nH2@512 (n = 2- 4) at PBE0-D3/def2-TZVP level in presence of external electric field (0.10 V/Å).
Figure 3. Minimum energy structures of nH2@512 (n = 2- 4) at PBE0-D3/def2-TZVP level in presence of external electric field (0.10 V/Å).
Preprints 105661 g003
Preprints 105661 g004
Figure 4. Minimum energy structures of nH2@512 (n = 2- 4) at PBE0-D3/def2-TZVP level in presence of external electric field ((-0.31 V/Å).
Figure 4. Minimum energy structures of nH2@512 (n = 2- 4) at PBE0-D3/def2-TZVP level in presence of external electric field ((-0.31 V/Å).
Preprints 105661 g004
Table 1. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: H2 + 512 → H2@512; computed η   and α values for the concerned systems (at PBE0-D3/def2-TZVP level of theory).
Table 1. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: H2 + 512 → H2@512; computed η   and α values for the concerned systems (at PBE0-D3/def2-TZVP level of theory).
System Field Strength
(Fx) (V/Å)		 ∆ G (kcal/mol) ∆ E (kcal/mol) η (eV) α (a.u.)
1H2@512 0 1.92 -1.82 4.24 165.99
1H2@512 0.10 1.81 -1.90 4.25 165.99
1H2@512 0.21 1.74 -1.94 4.16 165.99
1H2@512 0.31 1.71 -1.97 4.10 166.00
1H2@512 -0.10 1.84 -1.87 4.25 165.99
1H2@512 -0.21 1.75 -1.91 4.19 165.99
1H2@512 -0.31 1.68 -1.94 4.13 165.99
Table 2. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: 2H2+ 512 → 2H2@512; computed η   and α values for the concerned systems (at PBE0-D3/def2-TZVP level of theory).
Table 2. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: 2H2+ 512 → 2H2@512; computed η   and α values for the concerned systems (at PBE0-D3/def2-TZVP level of theory).
System Field Strength
(Fx) (V/Å)		 ∆ G (kcal/mol) ∆ E (kcal/mol) η (eV) α (a.u.)
2H2@512 0 10.85 3.04 4.30 170.48
2H2@512 0.10 10.59 2.86 4.29 170.49
2H2@512 0.21 10.33 2.67 4.23 170.49
2H2@512 0.31 10.26 2.39 4.15 170.51
2H2@512 -0.10 10.95 3.15 4.27 170.49
2H2@512 -0.21 11.03 3.18 4.21 170.48
2H2@512 -0.31 10.71 3.15 4.14 170.48
Table 3. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: 3H2 + 512 → 3H2@512; computed η   and α values for the concerned systems (PBE0-D3/def2-TZVP level of theory).
Table 3. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: 3H2 + 512 → 3H2@512; computed η   and α values for the concerned systems (PBE0-D3/def2-TZVP level of theory).
System Field Strength
(Fx) (V/Å)		 ∆ G (kcal/mol) ∆ E (kcal/mol) η (eV) α (a.u.)
3H2@512 0 21.95 10.13 4.31 174.73
3H2@512 0.10 22.14 10.22 4.27 174.76
3H2@512 0.21 22.14 10.22 4.20 174.78
3H2@512 0.31 22.15 10.26 4.12 174.79
3H2@512 -0.10 22.09 10.15 4.28 174.73
3H2@512 -0.21 22.07 10.12 4.21 174.73
3H2@512 -0.31 22.01 10.05 4.13 174.72
Table 4. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: 4H2 + 512 → 4H2@512; computed η   and α values for the concerned systems (at PBE0-D3/def2-TZVP level of theory).
Table 4. Gibbs free energy change (ΔG, kcal/mol) at 298 K and 1 atmosphere pressure, ZPVE-corrected interaction energy ( ∆ E , kcal/mol) for the association process: 4H2 + 512 → 4H2@512; computed η   and α values for the concerned systems (at PBE0-D3/def2-TZVP level of theory).
System Field Strength
(Fx) (V/Å)		 ∆ G (kcal/mol) ∆ E (kcal/mol) η (eV) α (a.u.)
4H2@512 0 35.78 20.10 4.32 179.55
4H2@512 0.10 35.96 20.25 4.28 179.57
4H2@512 0.21 36.01 20.34 4.21 179.59
4H2@512 0.31 36.89 21.39 3.96 179.67
4H2@512 -0.10 35.38 19.77 4.31 179.54
4H2@512 -0.21 35.17 19.60 4.25 179.52
4H2@512 -0.31 34.95 19.39 4.17 179.50
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

95

Views

28

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated