Fractal and Complex Patterns Existing in Music: Application to the Composition Diaphonies of Michael Paouris

1. Introduction

Historically and still, music is considered as a strict deterministic, mathematical representation following certain harmony rules which have to be governed by the performers in order to master musical scores and the composers in order to compose music. On the other hand, the mathematical rules seem to loosen when music components are complex related and this, especially, occurs when there is a co-affection of music with human feelings, soul and brain dynamics, all of which are of multifractal nature (see e.g., references in [1,2] as well as several available papers from human-related ECG studies). Although the subject of human feelings, brain dynamics and music connection is intriguing, it is far from being confined or solved. However, there is enough evidence that support the view that music can be considered as a non-linear non-deterministic/chaotic phenomenon. For example, there are studies that have suggested that musical signals are non-stationary and non-linear and they exhibit non-deterministic, chaotic patterns [3,4] and references therein. Fractal analysis of music signals looks to be an acceptable approach in this situation since it can reveal hidden geometry structures existing in the signal, by estimating the self-similarity content of the chaotic system. [5] investigated possible ways through which nature generates structures that may be described by fractals, as e.g., coastlines, mountains and plant structures and stated that fractal theory might be utilised to understand nature’s harmony. Fractals are also found in many natural processes and have been addressed also in music (e.g., [6]). Music components such as noise, pitch, loudness variations, accent, note sequence and melody in musical pieces, exhibit non-deterministic inter-linked structures that lead to the conclusion that music might also have SOC structures [6]. Until now, much research has been conducted to analyse a wide range of music signals utilising the main properties of musical sound, namely pitch, loudness, and timbre [1]. By calculating the power spectrum for slowly moving parameters such as loudness and pitch, [7] explored features in music and speech. Continuing, [8] and [9] used music in which notes were picked at random while their frequency, f, obeyed a known distribution function. They discovered that a number of musical styles, among which, classical music, jazz and blues, have a combination of regularity and spontaneity, the latter being typical of a power-law $1/f^{\beta }$ process. They also reported that the aesthetically attractive music has a power spectrum with power-law $\beta$ exponent within $0.5<\beta <1.5$ tying, hence, the morphology of music to the $1/f^{\beta }$ physical process [8]. Today (2022), these $1/f^b$ processes are considered to be the subject of the science of non-linear phenomena, with the specific attention of the processes of $b=2$, which are thought to belong to the science of stochastic phenomena. From the non-linear point of view, the stochastic processes, not only follow a probability distribution function, with a completely random selection way, but, most importantly, are deterministic, in the sense, that their evolution can be predicted once the initial conditions are given. This is because the probability distribution function governs their progress so, that any deviations are only due to statistical uncertainties. The reader should note in relation, that the Monte Carlo technique utilises this deterministic-statistical property of stochastic phenomena in order to model processes that are difficult to be measured, hence, estimating parameters that would, otherwise, be impossible to evaluate (e.g., [10]). From the non-linear phenomena point of view, the stochastic processes follow the $1/f$ law, which is also known as flicker-noise [11,12]. With f being the frequency content of the sound spectrum, the Fourier Analysis and the FFT are the most often spectrum-analysis deterministic techniques [13]. However, the Fourier Analysis is unable to track all the changes in a musical composition and this is because the square wave approximation that it employs, results in considerable data loss, especially when abrupt changes in music parameters are present. As the music computing technology has progressed, many rigorous techniques have been found, that allow for greater in-depth analysis of music signals. The related research indicates that music signals may exhibit unusual behaviour that remains to be outlined. Recent works as those of [1,6] and [1] and [14] employed multifractal detrended fluctuation analysis (MFDFA) to outline unusual complex patterns in music attempting also to combine music to complex dynamics present in human brain. This view however has a history already from the late eighties, when Bak et al. (1987), employed the concept of the self-organised criticality (SOC) to describe the origins of $1/f^{\beta }$ fluctuations. They suggested that the $1/f^{\beta }$-law is a common feature of critical complex grids as those of the brain. Later [15] expressed such aspects by suggesting that the $1/f$ processes may associate with a potential self-organisation of the brain via complex links with the inner natural physiological processes of the body. The power-law, fractal, SOC and non-deterministic patterns present in time-series (also music series as indicated above) are, theoretically and practically, inter-connected, as shown by several publications (see e.g., [12,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]). Researchers have pointed out recently, that different methodological approaches can be used, to investigate the inter-change phases of a non-linear system, e.g., the time-evolution of Spectral Fractal Analysis, Detrended Fluctuation Analysis (DFA), Rescale-Range (R/S) Analysis, analysis of the Fractal Dimension (FD) with the methods of Higuchi, Katz and Sevcik, entropy dynamics (Boltzmann- Gibbs, Tsallis and Normalised Tsallis Entropy) via information and symbolic dynamics and, most importantly , through the meta-analysis of the combination of two up to thirteen of these techniques [42,43,44,45,46]. Accounting the above findings, in conjunction with the potential relation between music and non-linear procedures, this paper focuses on the analysis of music in an effort to delineate hidden fractal and complex features that may be present. The application case is the work DIAPHONIES of a composer and virtuoso of the Greek traditional instrument called Bouzouki and also one of the best performers in Guitar with plectrum. The work is analysed through spectral fractal analysis versus time which is the most suitable technique to identify hidden power-law properties in a signal. As will be shown, significant fractal parts are found in DIAPHONIES which have important critical properties similar to those found in other research fields (e.g., earthquakes, air-pollution, heart seizures). Several arguments given later in text provide enough evidence to justify that this special critical behaviour makes this work general and significant in the field of music research. The paper is organised as follows. In the Section 3 the reasons for selecting the work DIAPHONIES are given. Thereafter, the spectral fractal analysis (hereafter fractal analysis) versus time is described. Several noteworthy results are presented some of which together with the corresponding music score parts. Fractal and complex parts are given while non-fractal and random parts are also reported. Pure random parts are analysed in the last section of the results that correspond to other music compositions. The simultaneous finding of pure random parts is deemed of extreme importance and for this reason, it is stressed at the end of work. The results are expected to add value to the knowledge to music research and, especially, the non-linear phenomena addressed in music. It is anticipated that it will provide insights to investigations of other disciplines such as those focussing on the effects of music to human brain, hearth and feelings.

2. The Application Case of Fractals: DIAPHONIES, Michael Paouris

Michael Paouris is an extinguishing composer, soloist and performer. To date, he has received 65 first prize international awards for his compositions and performances in the most historical places. The Mozart’s house in Vienna, the Carnegie Hall in New York, the Royal Albert Hall in London, the Mozarteum University in Salzburg are some of them. Michael Paouris is considered to be an extraordinary fast Bouzouki and Guitar player with plectrum. Apart from his acknowledged skills in Jazz, he created the term Contemporary Bouzouki in the framework of which several new demanding classical-type compositions were generated. The work DIAPHONIES is one of his unique creations of two main parts (DIAPHONIES 1 and 2) of three movements each. In this composition, there is not just one soloist and an orchestra, but five soloists who are “musically” inter-relating at a very high performance level.The composition utilises different melodic paths generating a very complex and special sound motif. The term DIAPHONIES means discord, disagreement a fact which reflects the musical fractional movement. The peculiar melodic lines of DIAPHONIES together with the international acknowledgement of Michael Paouris justify the selection of this composition as the example case for identifying fractal features in music; a subversive example for utilising non-trivial computational, mathematical, signal analysis methods, depending on the point of view of fractals uses in engineering.

3. Materials and Methods

3.1. Fractal Analysis

3.1.1. Theoretical Background

As mentioned in Section 1, musical systems may also present scale-invariant features and long-range power-law connections. The related states are associated with complex linkages between space and time that generate characteristic fractal structures [22,25,29] and self-organised critical (SOC) phases of spatio-temporal fractal organisation [41,47]. The above properties of complex (also music) systems can unfold via the power-law fractal analysis ([12,22,23,35,41] and references therein). A very significant parameter in this analysis is the power spectral density (PSD). The PSD provides information concerning the extend of each frequency within the investigated signal according to Equation (1)

$$S\left(f\right)=\underset{T\to \infty }{lim}E\left[\frac{{\left|W\left(f\right)\right|}^2}{T}\right]$$

(1)

where $W_T\left(f\right)$ is an applied transform. Usually $W_T\left(f\right)$ is the continuous Fourier transform or the FFT for digitised signals. The reader should recall that the Fourier transform might not be proper, especially, when the signal changes abruptly and this because in such cases the Fourier transform results in considerable data loss. Due to this, the continuous wavelet transform (CWT) has been used in several publications with the Morlet base function in the PSD because it is very advantageous, especially, when compared to the FFT, since it manages to decompose, excellently, even transient or non-stationary signals (e.g., [17,18,19,22,23,34,40]). The CWT that is used in this paper is given by Equation (2)

$$C(a,b;f\left(t\right),\psi \left(t\right))={\int }_{-\infty }^{\infty }f\left(t\right)\{\frac{1}{a}{\psi }^{*}\frac{(t-ba)}{a})dt\}$$

(2)

where $\psi$ is the wavelet-base function, a is the scale ($a>0$ ), b is a position inside the signal, $C(a,b)$ , are the coefficients of CWT and ⁎ is the complex conjugate. The reader should note that the CWT coefficients are influenced not only by the scale and position values, but also by the wavelet used. The CWT coefficients $C(a,b)$ are produced by continuously altering the values of the scale parameter, a, and the position parameter, b. The Morlet wavelet utilised here is given by Equation (3)

$$\psi \left(t\right)=\frac{1}{\sqrt{\pi B}}{e}^{\frac{-t^2}{B}}{e}^{j2\pi Ct}$$

(3)

where B is the bandwidth and C is the central frequency of the wavelet. Temporal fractals have time series, $A\left(t_i\right)$, with PSD, $S\left(f\right)$, that follows a power-law of the form of Equation (4)

$$S\left(f\right)=a·f^{-b}$$

(4)

where f is the frequency of an applied transform. In all related publications (e.g., [23,35] and references therein), f is taken as the central frequency C of the Morlet wavelet of equation 2. Note that the above power-law PSD f dependence is a straight line in a $log\left(S\left(f\right)\right)-log\left(f\right)$ conversion. The slope of this line is the power-law scaling exponent b and the intercept is the spectral amplification a. The amplification a quantifies the strength of the spectral components f following the power law and the spectral scaling exponent b, is the measure of the strength of the time correlations.

3.1.2. Application of Fractal Analysis

In the consensus of the related research in the field of fractal analysis [17,18,19,21,22,23,28,29,30,31,32,34,35,40,41,47], the following steps are followed in this paper for the fractal analysis of the musical signals under investigation:

1)

The music time-series is divided into segments (windows). In accordance to the previous papers, the segmentation is set to 1024 samples per window.

2)

The PSD of the musical signal is calculated in each discrete window utilising the CWT with the Morlet base wavelet.

3)

The PSD is checked for hidden power-law $S\left(f\right)=\mathrm{a}·f^{-b}$ trends of Equation (4), in each segment, by utilising as frequency (f) the central frequency of the Fourier transform of each Morlet wavelet of Equation (3) at the corresponding scale (C). This is implemented via a least square fit to the linear transformation $log\left(S\left(f\right)\right)log\left(f\right)$ of (4).

4)

Accurate fractal segments are considered those with square of the Spearman’s correlation coefficient, $r^2\ge 0.95$ of the linear fit.

Two different approximations are followed for the implementation of fractal analysis:

(i)

Sliding window technique: According to existing research (e.g., [19,32,34,35,40] and references therein) the window size is 1024 samples and the window step is 1 sample.

(ii)

Lumping technique: For comparison purposes the window size is 1024 sample and the window step is also 1024 samples. Hence this technique generates sequential discrete windows of 1024 samples each (e.g., [36,40,48,49]).

As follows from the above discussion, the most significant parameter of the fractal analysis of musical signals, is the power-law b exponent. The related software produces in each run (i) a time evolution multiplot of the b exponent, the Spearman’s $r^2$ coefficient and the sampled amplitude of the analysed musical signal and (b) an ASCII file containing all values for time t, b and $r^2$. The reader should consider in relation, that time t corresponds to a whole window. As in other publications, t is taken as the time moment of the first sample of each window under investigation (see e.g., [46] and references therein). In case of sliding window technique, finally all times but the actual $t=0s$ are considered. This can be understood if one accounts that the first t moment corresponds to the first 1024 samples altogether, since the window size is 1024. Due to this, the sampled time evolution of amplitude of the signal is almost identical to the waveform of the actual amplitude. In lumping, the first t is as in the sliding window technique, the second t is the one of sample 1025 and so on. Due to this raw analysis the amplitude of the signal is a very rough-average representation of the actual amplitude. For this reason, the software that creates the corresponding multiplot (see (i) above), plots the actual signal instead of the sampled one.

3.1.3. Classifications

According to associated publications ([19,22,23,28,29,30,31,32,34,35,40] and references therein), the following classifications are valid for the scaling exponent b of the power-law behaviour:

1.

Regarding the characterisation of the related physical process:

a)

A value of $b=1$ implies that the variations of the musical procedures do not grow, i.e., the related music is stationary;

b)

Values of b in the range $1<b<2$ means that the associated music is antipersistent;

c)

A value of $b=2$ means that the related music follows random paths that are described by non-memory dynamics, because there is no correlation between the increments of the musical process. The related music is stochastic, deterministic and mathematical;

d)

Values b in the range $2.0<b\le 3.0$ suggest musical signal’s persistency.

2.

Regarding the modelling class of the related process:

a)

Values b between $-1\le b<1$ are related to music that follows the fractional Gaussian noise (fGn);

b)

Values n the range $1<b\le 3$ mean that the time profile of the associated music is a temporal fractal and that it follows the fractional Brownian motion (fBm);

3.

Regarding the classification of the b segments of the musical signal:

(a)

Class I segments: These comprise the music time series segments with accurate fractal description ($r^2\ge 0.95$) that, simultaneously, follow the fBm class ($1<b\le 3$). According to publications these segments can be classified of noteworthy criticality value [17,18,19] and, especially, the segments with clear changes between persistency and great antipersistency, namely changes between $1.7<b<2$ (great antipersistency) and $b>2$ (persistency). Most important, however, are the segments with $b>2$ or, better, with b above or equal 2.3 (great persistent behaviour). According to numerous publications ([19,28,29,30,31,32,34,35,40] and references therein) the latter Class I segments ($b\ge 2.3$) are characterised as footprints of criticality.

(b)

Class II segments: These consist of the music windows that do not follow the fBm class, i.e., $r^2<0.95$ and $1\le b\le 3$, or follow the fGn class. i.e., $-1\le b<1$. These windows are of low criticality value according to previous research [17,18,19,28,29,30,31,32,34,35,40]. Apparently, Class I and Class II segments are complements of each other.

4. Results and Discussion

As with any system explored for possible trends of fractality and complexity with the sliding-window technique, there is always a vital point, concerning the duration of the relative time series for investigation. This is because the generated database can be so big, that the total time needed for the sliding-window analysis could extend up to several days with a usual computer. There have been addressed cases where sliding-window fractal spectrography results could be obtained only via virtual cloud computers. On the other hand, as mentioned in Section 3, the lumping technique produces much less data with the cost of very raw signal representation. The use, hence, of the sliding-window technique in musical signals, is associated strongly with the type and size of music to analyse. Considering that it is the lossless audio format not compressing the analog audio from which it is derived, the WAV type is an appropriate file type and, for this reason, is utilised hereafter. On the other hand, the size of music depends on two parameters; the digitisation frequency and the length of the selected parts for analysis. To provide dense data for the analysis 48,000 samples are digitised in every second, namely the time interval between two consecutive samples is $dt=\frac{1}{48000}s$ or, in other words, the dead time for which no digitised sound exist in music is $dt$. Under this digitisation rate, as many as 240,000 samples are collected from every 5 s of music. This number corresponds to the analysis of a typical 3 day earthquake signal (see e.g., [40]). In this way, the 240,000 samples signal length is a fair compromise between execution time and total size of all output files, concerning the sliding-window technique. For this reason, hereafter, the music analysed with the sliding-window technique is organised in 5 s chunks. Considering these constraints and that the composition DIAPHONIES comprises two main works, DIAPHONIES 1 and DIAPHONIES 2 with three movements each, the composer indicates certain parts whose creation, interpretation and listening appears complex and interesting for investigation. These interesting parts are organised as follows:

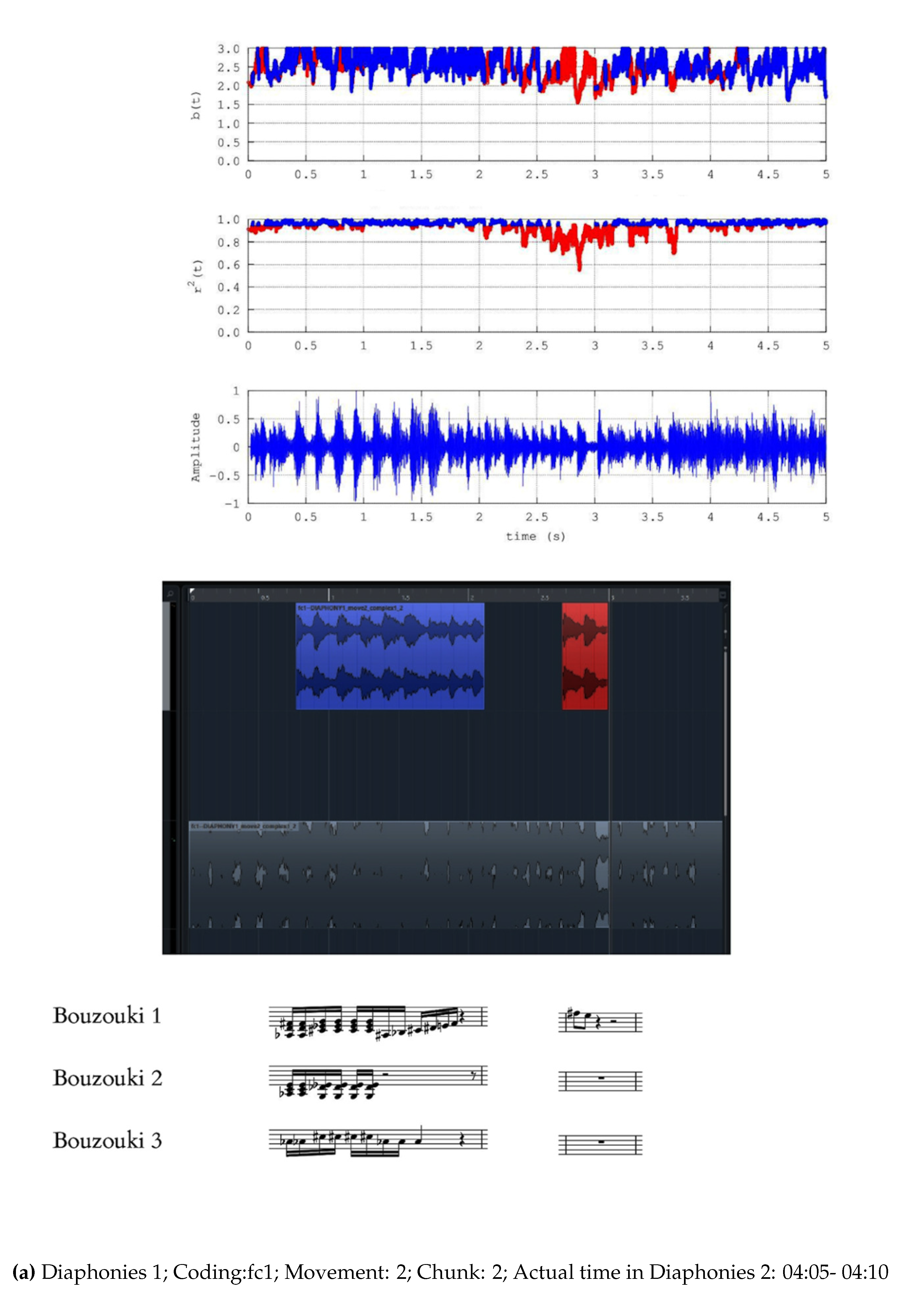
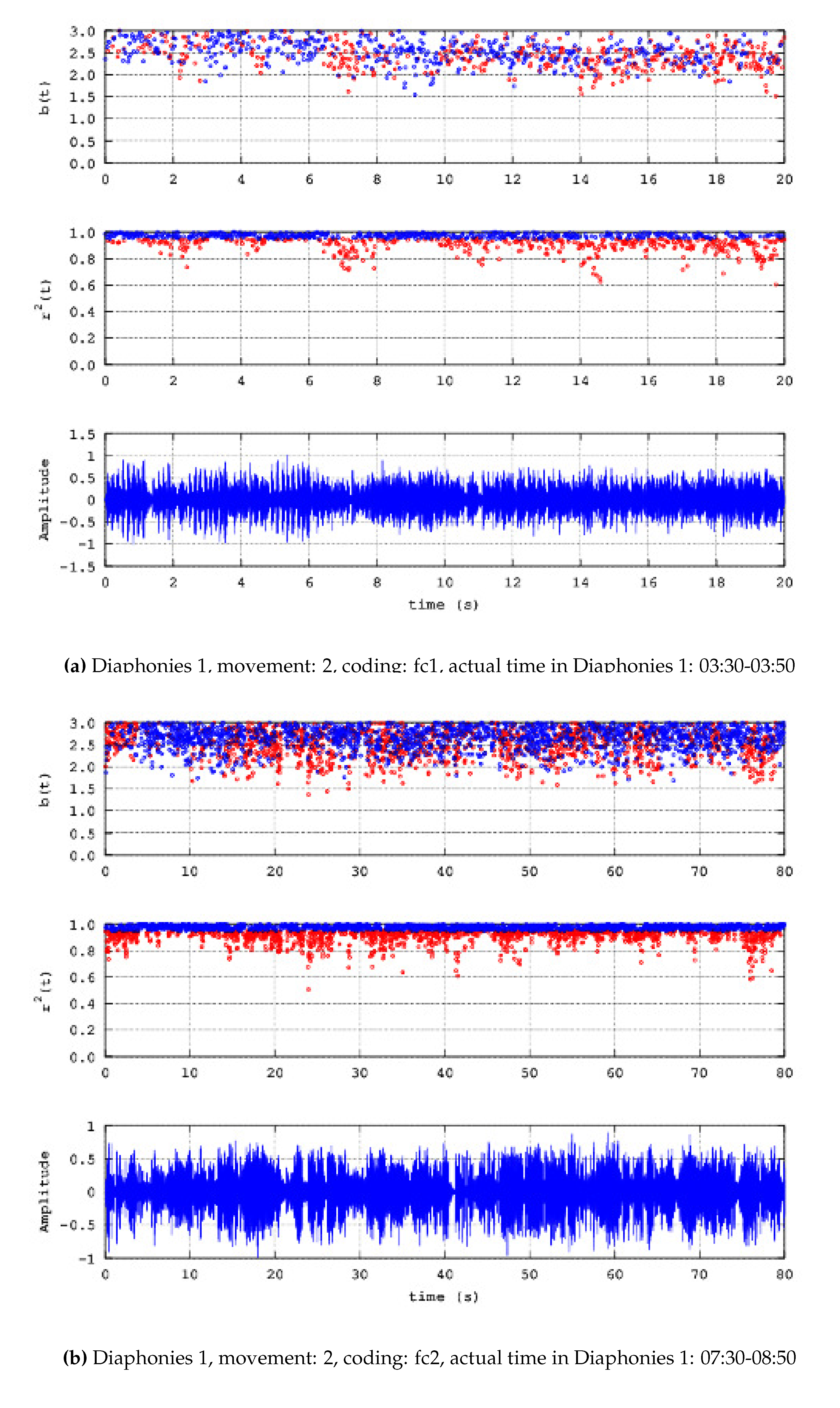
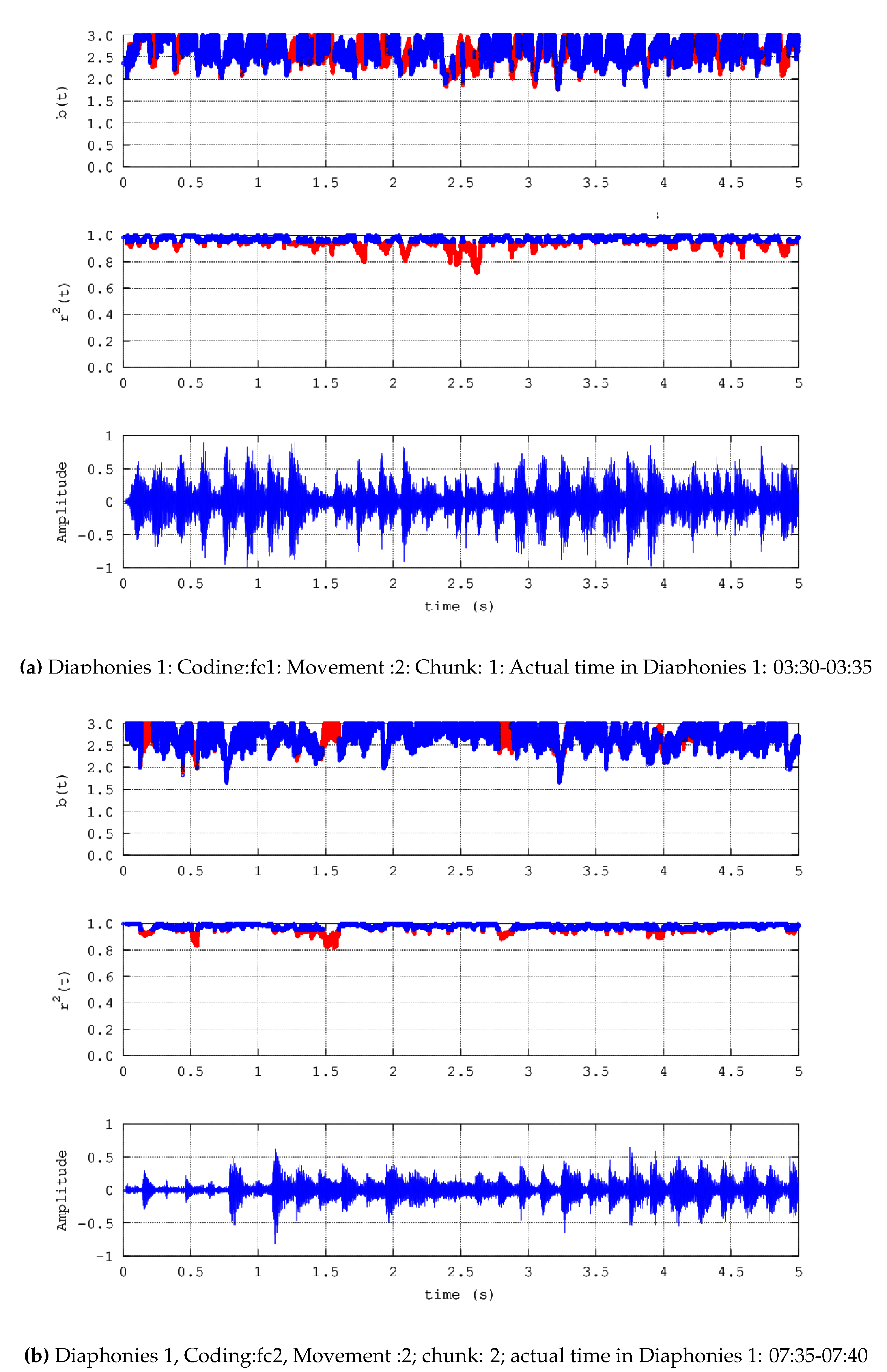
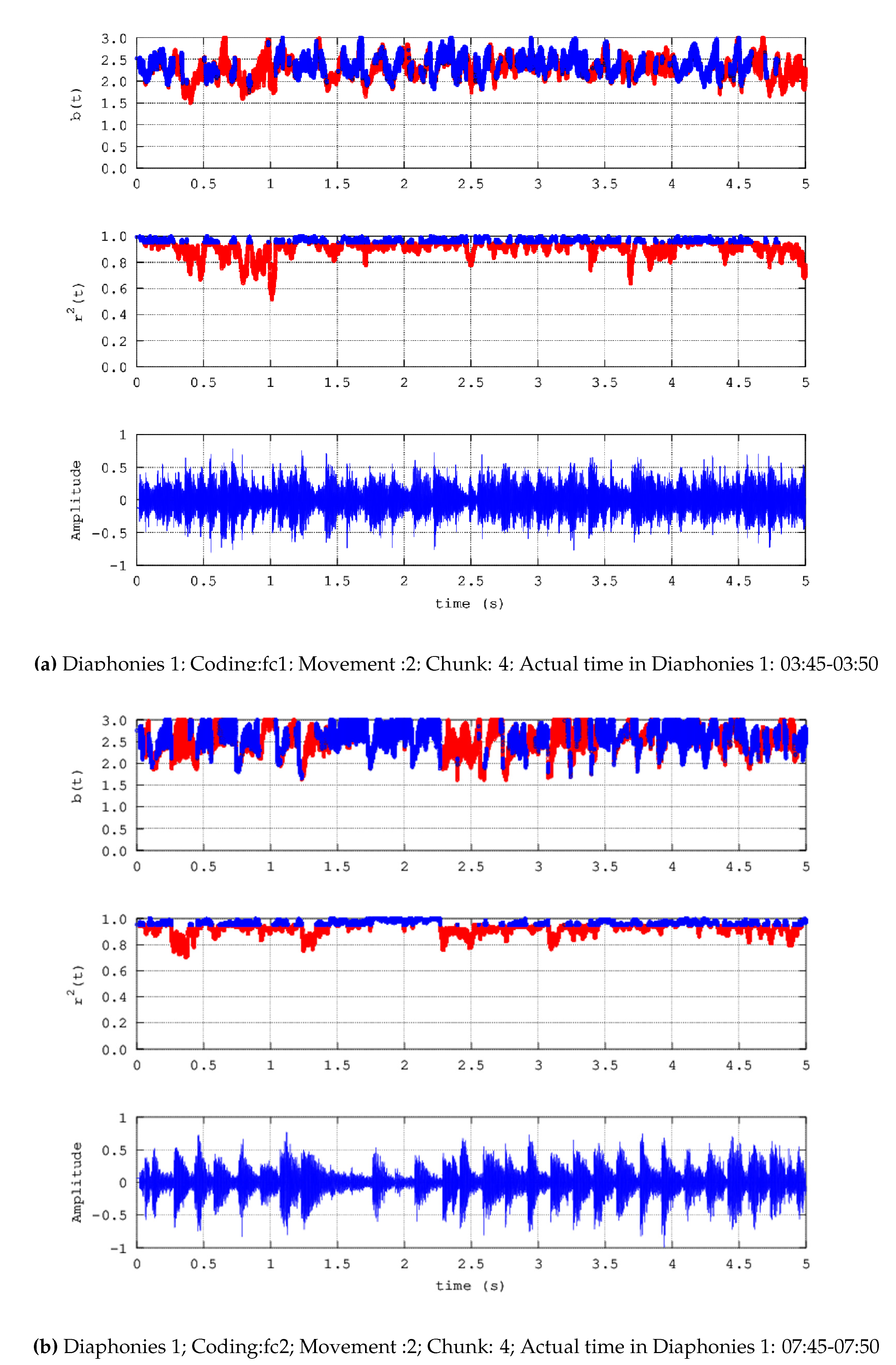
• Diaphonies 1; Coding: fc1; Movement :2; Number of chunks: 4; Actual time in Diaphonies 1: 03:30-03:50
• Diaphonies 1; Coding: fc2; Movement :2; Number of chunks: 16; Actual time in Diaphonies 1: 07:30-08:50
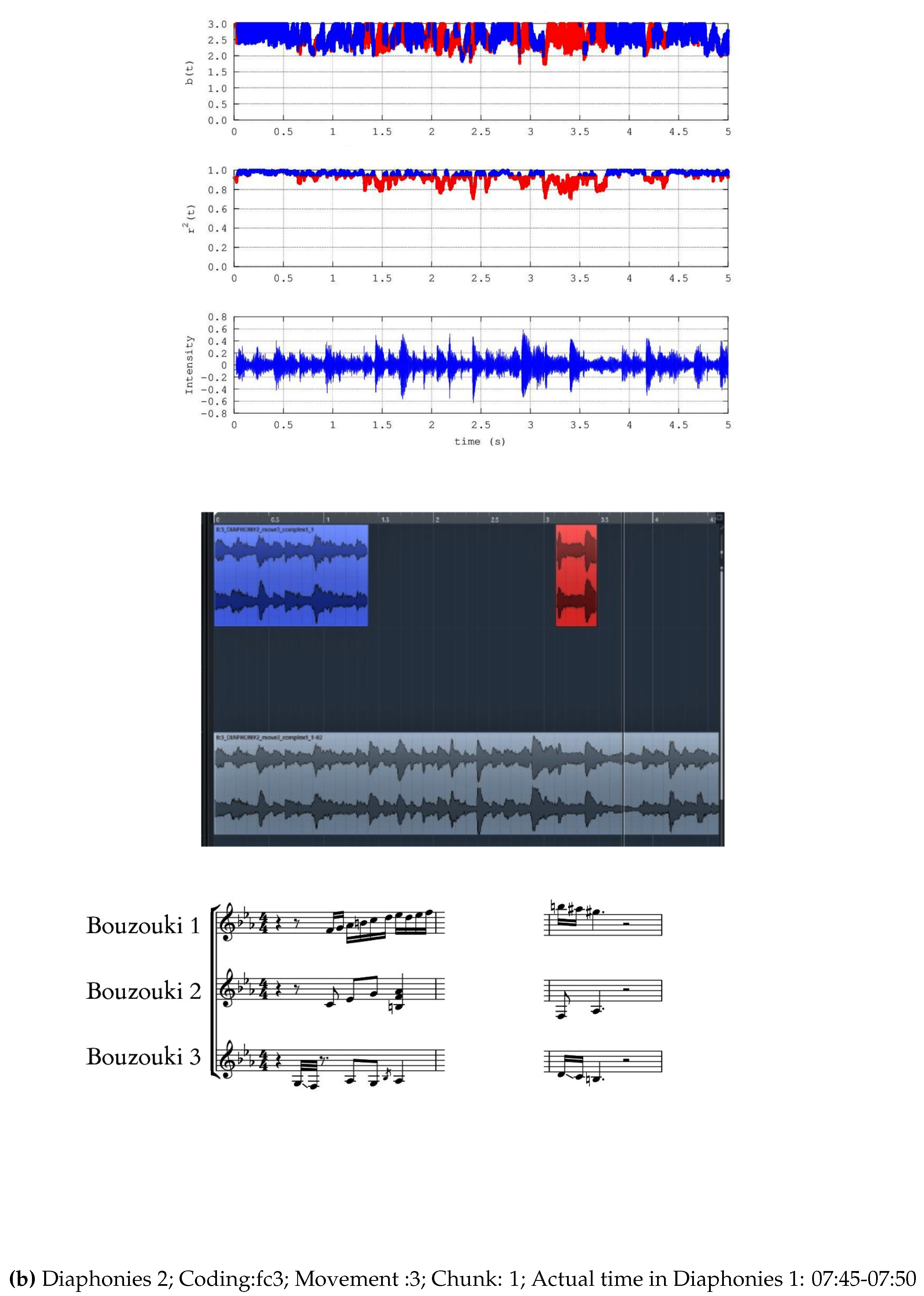
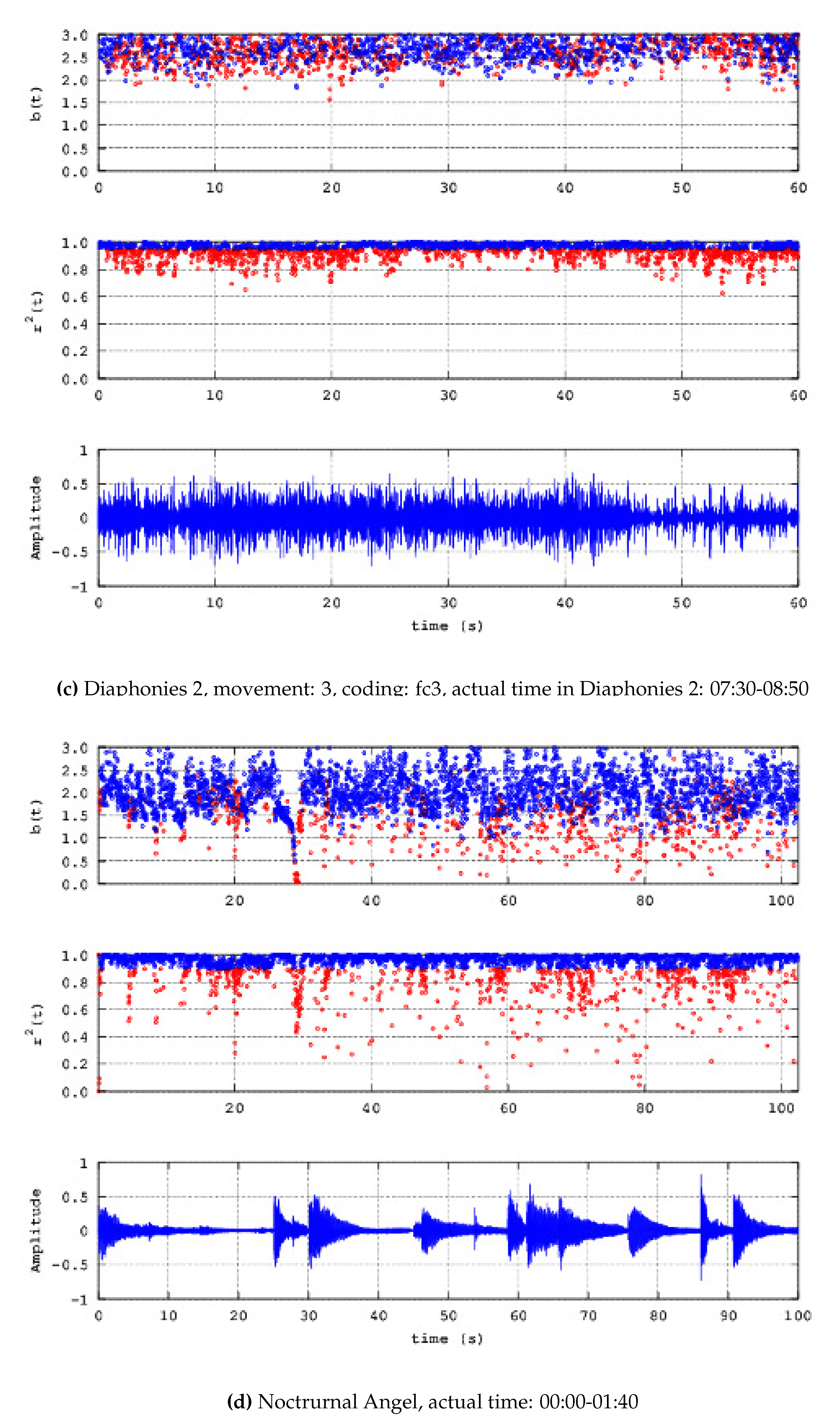
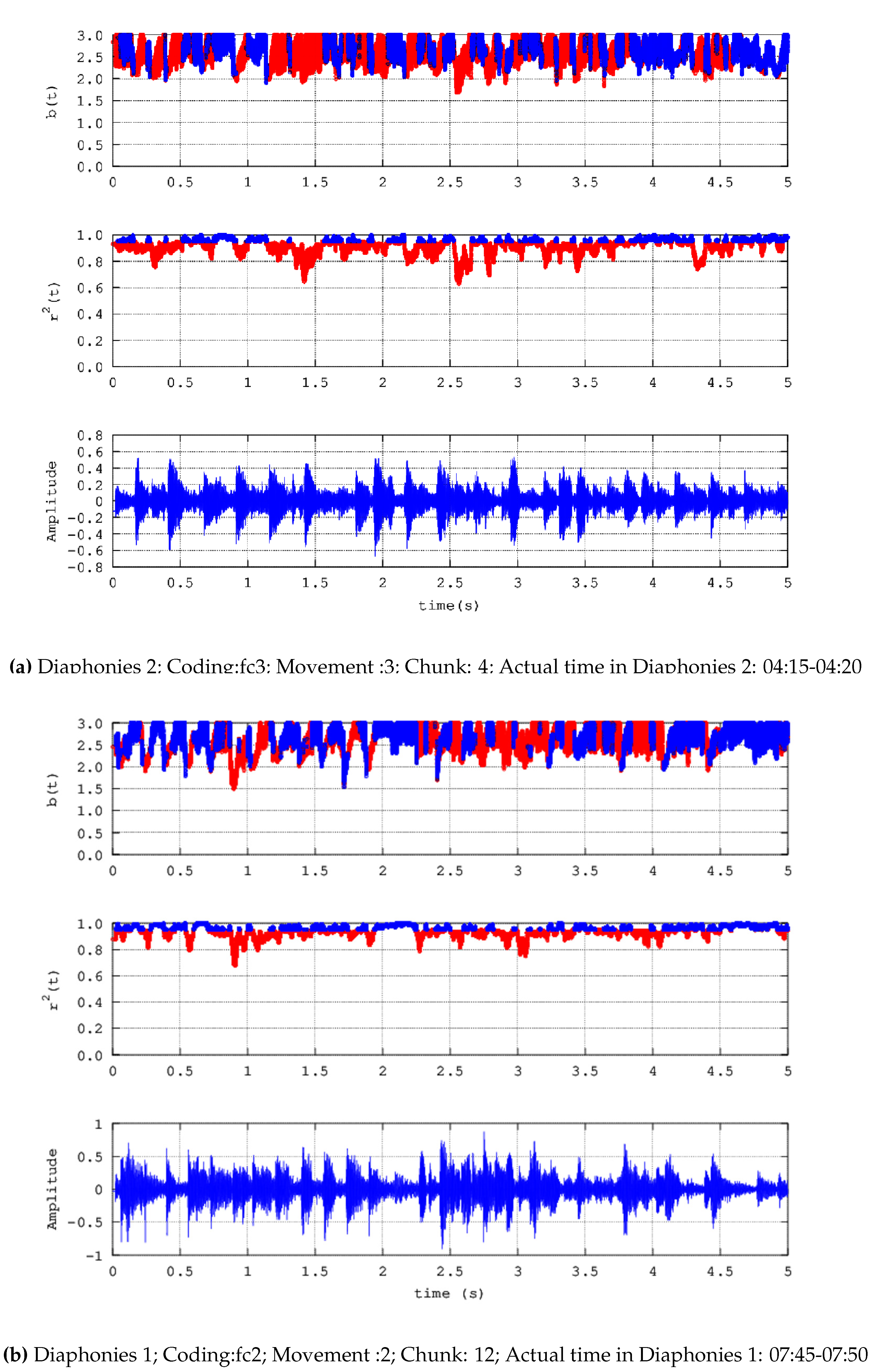
• Diaphonies 2; Coding: fc3; Movement :3; Number of chunks: 12; Actual time in Diaphonies 2: 04:00-05:00

The selection of the above parts of DIAPHONIES and the segmentation of the signals is done via software developed in Octave (GNU commitment) in LINUX computers. The software is developed specially for this purpose. The duration of each chunk is selected by the user and the software produces the partial WAV files, ASCII (dat) files of the waveforms of each of the two channels available in the WAV file and the waveform plots. A database is generated and all these outputs are stored for analysis and future use. The database is generated in a manner that future analysis can also be added. On the other hand, fractal analysis is implemented with the sliding-window technique, by software developed from 2010 in LINUX Octave and that is used for the generation of all the data presented in associated publications (e.g., [17,18,19,28,29,30,31,32,34,35,40]). It can be supported that the related software is well established and tested in practice. This software and the same (also tested) methodology as in the above publications, is used in this paper for the analysis of all thirty two $5s$ chunks of DIAPHONIES described above. The reader may recall that the corresponding steps are described in Section 3.1.2. Each separate run needs approximately 8 hours to complete including the time needed for output files organisation. The total time to implement the fractal analysis with sliding-window of the above chunks is 256 hours, i.e., approximately 15 days to implement. Therefore, the reader should consider that this analysis (a) is not trivial and b) needs a lot of time to implement, not including the working hours to develop and debug the related software. The related analysis and output can be characterised as big-data analysis. Characteristic results from the fractal analysis are presented in Figure 1, Figure 2 and Figure 3.

Inspecting Figure 1, Figure 2 and Figure 3, noteworthy variations are observed in power-law b exponents values. As a first overview, the following general observations can be done:

a)

Noteworthy number of segments (blue areas, middle and upper plots) present successive ($r^2\ge 0.95$) power-law b-values between 1.7 and 2.0;

b)

Significant number of segments (blue areas, middle and upper plots) exhibit successive ($r^2\ge 0.95$) b-values greater than 2.0 and in several cases, greater than 2.3;

c)

There are many segments that do not exhibit fractal behaviour (red areas, middle and upper plots);

d)

There are cases where some non-fractal segments (red areas, middle and upper plots) are dipped within many successive fractal segments;

e)

Periods of significant waveform amplitude variations are not associated de facto with observations (a)-(c).

In order to delineate the figures and interpret the implications of the b variations in terms of science, some significant information about the power-law scaling exponents should be considered in advance. First is what is called persistency. This property refers to all musical parts associated with $b>2$ and, preferably, with $b>2.3$, because the latter implies more pronounced effects. If there is persistency, then a great musical signal’s amplitude value is followed, more likely, by a greater amplitude value and vice versa; a small amplitude value is followed, more likely, by smaller amplitude value. All these tendencies continue in the future in a long-term association. Secondly is the, so called, antipersisteny. Antipersistency, refers to a situation where a great musical signal’s amplitude value is followed, more likely by a smaller value and vice versa; a small amplitude value is, more likely, followed by a bigger value. This tendency also continue in the future as a long-term association. Hence, persistency is associated with the musical signal’s amplitude tendency to continuously increase or decrease, whereas the antipersistency, with the tendency of the signal’s amplitude to inter-change between high and low (relatively referring) values. Both strong persistent and strong antipersistent behaviour, are associated with musical system’s long-memory. In the cases of where $1.7<b<2$ or $b>2.3$ (or even higher), the musical system exhibits long-term interactions and long-range dependencies similar to physical systems in criticality (e.g., [28,29,30,31,32,34,35,40] and references therein). In these cases a very uncommon situation occurs. Each value (amplitude value for music) is associated not only with its past value, but also, with its future value. This interesting finding has been expressed in the various publications of the subject (e.g., [5,12,41,50,51,52,53,54,55] among many other papers). The very peculiar situation with the key periods of musical signal with strong persistency or strong antipersistency-persistency inter-changes, is that during these, the presence of the system is not only determined by its past, but (and this is the interesting part) also determines the future of the system in a fractal long-memory manner. The reader may locate several areas in the example Figure 1, Figure 2 and Figure 3 with strong persistency and strong antipersistency-persistency inter-changes. It is very important to clarify in association, that the system in these numerous cases is non-Markovian and non-deterministic. The reader should recall in relation that the Markovian systems are determined by their past while the deterministic systems are defined once the initial conditions are given. Therefore, for the cases where the investigated musical compositions have long-memory behaviour, the usual musical harmony breaks down and this is because, too many linear procedures (e.g.,harmonics) are involved in such a way, that the musical system gets out of equilibrium and becomes non-linear. Note in association that for physics, musical harmony is just a deterministic procedure of matching certain, mathematically calculated, combinations of Fourier-defined frequencies. In other words, musical harmony is, physically speaking, the Fourier transform of music where notes are attributed to certain Fourier basic frequencies and some of their multiples in a way, that the matching ones follow certain mathematical-deterministic rules. In fact, this is independent from the musical instrument since different instruments are comprehended by the human ear just as a different mix of frequency multiples, depending, of course, on the sensitivity differentiations between the hearing and the frequency discrimination ability of each individual. Importantly, the aspect of harmony breakdown has been expressed in other references as well [1,3,4,6,14,56,57]. This scientific data presented in this paper so-far support this completely different view, at least for the special high-fractality cases. Moreover, the fact that the fractal analysis of this paper utilises the, completely superior to the Fourier, wavelet transform, reinforces the statements even more. Accounting the modelling class of the related musical signals it is observed that only successive fBm modelling class is found and non fGn class. As mentioned many papers (e.g., [18,21,23,45] and references therein) the fBm class has noteworthy predictive power, in terms, that after a critical point and for high b values, the evolution of the musical composition is guided to collapse, in the aspect, that it will yield to a musical outbreak, to a solution that will render the system out of chaos and balance it back to the trivial harmony behaviour. In all previous states, the musical system has so many non-linearities that it is unpredictable, chaotic and, simultaneously fractal. Accounting that fractals are combined with nature [5] and that they resemble harmony hidden in nature, it is not surprising that music may be fractal as well, as this paper indicates as well. Signifying the findings even more, it should be mentioned that the fractal analysis of the musical signals of this paper, achieves to:

• use raw amplitude data, i.e.,data without any mathematical processing;
• identify fBm Class I segments where the musical system has increased possibility to evolve to a chaotic solution out-breaking of which will make the system to return to harmony description;
• recognise persistent and anti-persistent areas with tendencies to increase (decrease) or to inter-change between high and low amplitude values;
• locate fractal versus non-fractal (deterministic-mathematical) areas of each signal under investigation;

The latter point is deemed by the composer as very interesting and important. Figure presents a characteristic example of fractal analysis with a mix of Class I and Class II areas with musical score of selected the analysis parts. It is very significant that the score of the successive fractal part (blue) refers to a diminished harmony, which, from an alternate point of view, may not end and continue to other harmonic parts of it. Completely different is score for the non-fractal parts.

Figure 4. Characteristic examples of fractal analysis with a mix of Class I and Class II areas with musical score of selected the analysis parts. Sliding-windows of size 1024 samples and step 1 sample. In top sub-figure (from bottom to top): sampled signal, square of the Spearman's coefficient, r² and power-law exponent, b. Colours in r² and b plots: Blue, Class I segments, Red, Class II segments. In central subfigure: waveform with blue background refer to successive fractal parts (blue) of upper subfigure and waveform in red background to the non-fractal parts (red) of upper subfigure. I bottom subfigure: Left the score for the successive fractal parts (blue) and right the score for non-fractal parts (red).

Figure 4. Characteristic examples of fractal analysis with a mix of Class I and Class II areas with musical score of selected the analysis parts. Sliding-windows of size 1024 samples and step 1 sample. In top sub-figure (from bottom to top): sampled signal, square of the Spearman's coefficient, r² and power-law exponent, b. Colours in r² and b plots: Blue, Class I segments, Red, Class II segments. In central subfigure: waveform with blue background refer to successive fractal parts (blue) of upper subfigure and waveform in red background to the non-fractal parts (red) of upper subfigure. I bottom subfigure: Left the score for the successive fractal parts (blue) and right the score for non-fractal parts (red).

All these interesting fractal outcomes refer to the analysed parts of DIAPHONIES from Michael Paouris.All these issues are, possibly, linked to the non-linear behaviour of human brain (e.g., [1,2,14,58,59,60,61] among some of the related papers). Possibly the composer of DIAPHONIES generated composite sounds that are, potentially, due to inner non-linear brain procedures during composition of DIAPHONIES. Nevertheless, the important finding is that Michael Paouris DIAPHONIES have fractal areas similar to those identified in other critical non-linear phenomena. Table 1 presents the overall results derived by sliding-window fractal analysis in the thirty two 5s chunks of DIAPHONIES. This table contains some selected counting outputs of the full ASCII database of fractal analysis. It is important to emphasise on the size of this database via sliding window analysis. Each chunk contains 238,976 segments of 4-column data of analysis (t-segment number, b, $r^2$, sampled amplitude). The counting software searches each output file and produces a counting file of 21 line data (here used 9 of these). Accounting the 32 chunks of sliding-window analysis and the above line data, a total of 32x238,976x4= 30 ,588,928 column data is accessed and 32x238,976x21=160,591,872 column data is generated. Table 1 contains 13x36=4,068 of this database. It is evident hence, why it is very difficult to analyse the whole DIAPHONIES composition. This provides also proper justification why the composer selected these parts. The problem is also mentioned; the analysis of music with this well-investigated technique requires significant CPU and storage resources and also significant amount of time to perform. However, very importantly, this analysis is implemented in significant more segments than any analysis in the related references of the subject. For example, [62] report analysis in three windows with the FFT technique. [63] report the fractal analysis of less than 40 segments. [1] report the MFDA analysis of 11 segmented parts. [6] report MFDFA parameters analysis of 24 segments. [64] reports the three power-law exponents of three time series. [57] report 12 fractal dimensions parameters of 12 songs segments. It becomes evident why the analysis of this paper is very important. Going into the details of Table 1, it is easily observed that there is a plethora of persistent (P), antipersistent (A) and PA segments. Therefore, an arbitrary selection of a segment may provide misleading results about its fractal behaviour. Initially the data can be organised in (a) Class I-Class II categories; (b) P, A and AP categories ($0<b<1$, $b=1$ , $1<b<2$, $b=2$, $2<b<=3$) and (c) b-threshold limit categories ($1.7<b<2.3$ versus $2.3<=b<=3$ or $1.7<b<=3$ versus $1.7<b<2$). The reader should emphasise on this categorisation because it is based on arguments expressed in several papers [5,12,21,22,23,28,29,30,31,32,33,34,35,36,37,38,39,40,41,43,44,45,46,55]. As aforementioned, the Class I category is deemed of prognostic value whereas the Class II ones are non-fractal. Importantly, these Class II non-fractal areas refer, most possibly, to typical musical harmony, viz. music following well-accepted rules. This is a very significant fact that should be stressed by the reader, because it clearly shows that, even in musical compositions with noteworthy parts exhibiting fractal and power-law properties, a significant music part still follows harmony rules, as numerous segments are not fractal. Note, that this harmony view is usually pre-assumed in music research.It is significant to mention here that the aspect of harmony music mainstream quenched inside fractal areas (and vice versa) is also stressed in the papers referenced in Section 1 and the analysis presented there. On the other hand, all persistent Class I areas (namely all segments with $2<b<=3$ have been recognised as a footprint of criticality behaviour in papers (e.g., [21,22,23] and all references therein). Moreover, [59] reported similar b-range, importantly, in pre-epileptic seizures. Critical behaviour is also identified in heart rate dynamics and ECG in general (e.g., [65,66] and references therein). This paper, signifies all aspects and for this reason Table 1 contains diverging b-value range. In addition, going on step further, accepts as footprints of rigid criticality the strong persistent areas with $2.3<=b<=3$. It also accepts as indicators of criticality the areas with antipersistency-persistency interchanges ($1.7<b<2.3$). Both aspects have also been supported by other investigators [34,35,43,44,45,46]. For these reasons both strong persistent areas with $2.3<=b<=3$ and in areas of antipersistency-persistency interchanges with $1.7<b<2.3$ are deemed of extreme importance for the criticality of the analysed music and under this view all results are discussed already and hereafter.

The absolute counting values are very important because they provide category discrimination between the various chunks. The Class I-Class II categories seem to be balanced between the various segments. Interesting mild deviating examples are (a) fc2-D1, chunk 3 and fc2-d-D3 chunk 8 with more Class I segments and the contrary (b) fc2-D1 chunks 4, 10 and 12, fc2-D1 chunks 3 and 4 and fc3-D2 chunks 10, 11 and 12. Next, there are no stationary, successive ($r^2\ge 0.95$) fGn ($0<b<1$) or pure random segments. This latter fact contradicts to the findings of [62] that report power-law values of approximately 0.55, however, for music tempo only. Then, there is a noteworthy number of antipersistent segments with $1<b<2$. [62] also report such values. Importantly, these $1<b<2$ are significantly low for fc3-D2 chunks 3, 6, 8 and 11. These low b values are not critical, are of low-fractality and, possibly, may associate with underlying motive (e.g.,tempo) repetitions in a low fractal manner, where a certain underlying motive pattern is a raw self-similar imitation of another, simply at another scale. This is however the case in the so many persistent ($2<b<=3$), strong persistent ($2.3<=b<=3$) segments and the numerous segments with persistency-antipersistency inter-changes ($1.7<b<2.3$). Also many segments are between $1.7<b<=3$ and $1.7<b<2$. There are some segments with noteworthy,relatively, different values of the above category types. Segments with lower strong persistent segments are fc2-D1 chunks 4,5, 6 and 12 and fc3-D2 chunks 3,4, and 11 (the lowest relative value in $2.3<=b<=3$ category). The corresponding $1.7<b<2.3$ category values are also relatively lower. Nevertheless, even for these cases the total number of segments is very big, implying great fractality in the analysed parts of DIAPHONIES composition. As mentioned above, these segments have patterns that are self-similar, i.e., they are smaller or bigger scale imitations of an underlying pattern. This is very important because it implies that the DIAPHONIES music in these segments is a temporal fractal. Such temporal fractals, as already mentioned in several parts of the text, produce a very different acoustical pattern that is closer to the underlying fractal nature of the human brain, making these DIAPHONIES parts to sound interestingly different than a simple harmony or a synthetic music. It is significant however to place emphasis on a very important issues. The above discussed noteworthy fractal nature of DIAPHONIES, might be characteristic both for the composition and the composer, but by far have a more general application. This can be supported by the following, already shown, facts; (a) the critical behaviour is not a signature of music itself, on the contrary, it is addressed in many other disciplines as earthquakes, urban air-pollution, heart-failure and heart-rate dynamic, pre-epileptic seizures and many others; (b) fractal and power-law behaviour have been addressed in music by others as well and significantly, in recent studies; (c) the footprints of criticality identified (for first time in music in this paper) constitute a very significant general finding of systems under collapse or non-Markowian systems for which the present is mixed not only with the past (deterministic manner) but also to it long-term future (certain deterministic chaotic solution-pathway that the system is almost probable to follow in the future);(d) several papers (already mentioned and many others that are given therein) support all these theoretical and practical aspects. Due to the above, this paper manages to provide, on the one hand, advanced analysis and discussion for DIAPHONIES and the composer Michael Paouris and, on the other hand, to outline the applicability of the general framework both in other disciplines and, of course, music.

Figure 5. Fractal an analysis via lumping.The window size is 1024 samples. In each sub-figure (from bottom to top): sampled signal, square of the Spearman's coefficient, r² and power-law exponent, b. Colours in r² and b plots: Blue, Class I segments, Red, Class II segments.

Figure 5. Fractal an analysis via lumping.The window size is 1024 samples. In each sub-figure (from bottom to top): sampled signal, square of the Spearman's coefficient, r² and power-law exponent, b. Colours in r² and b plots: Blue, Class I segments, Red, Class II segments.

The above findings are associated with complexity differentiations. This can be easily understood by the concept of fractal dimension. As indicated in several publications (e.g., [36,37,40] and references therein), the fractal dimension (D) measures complexity since it relates the total length of a curve (L) with the maximum total area (A) that this curve could fill, in the way $L^{\frac{1}{D}}=k·A^{\frac{1}{2}}$ where k is a constant. When the path is a straight line, $D=1$. When the curve tends to fill the space, D would approach 2. The more convoluted the patterns, the higher the fractal dimension. In time-series analysis, D quantifies irregularities and complexities or, in other words, it measures the roughness of a profile. If the Hurst exponent H of a complex system is known, the fractal dimension D of the system can be estimated by $D=2-H$ ([36,37,40] and references therein). Considering that H, for Class-I scaling exponents ($1<b\le 3$, Section 3.1.3) equals $H=0.5(b-1)$ [34], it becomes that:

$$D=2.5-0.5b$$

(5)

For $b=1$, $D=2$ and for $b=3$, $D=1$. Time series with low fractal dimensions are regular and predictable. Similarly, time-series with high fractal dimensions have irregularly spaced changes in direction, apparently at random. Time series with random directional changes are identified in mathematics under the term ’random walk’. Time-series with D values approaching 2 are random walks. Under these aspects, the differentiations in strong persistent segments imply strong alterations in complexity. For example the values $b=2.3$ has a fractal dimension $D=1.35$ and the values b as high as 2.7 have fractal dimensions of $D=1.15$. Therefore ,the $D=1.35$ areas are rougher than the $D=1.15$ segments. The reader may explain all profiles and data of Table 1 in this way. However, as indicated in all related references focusing on fractal dimensions [34,43,45] there are noteworthy differentiations between the techniques for calculating fractal dimensions. This is however out of the scope of this paper. It should be emphasised that all partial data that produce Table 1 do not follow the normal distribution (Shapiro-Wilk and Kolmogorov-Smirnov test in R, with p-values well below 0.05) and therefore, no linear statistics can be employed (e.g average, standard deviation and other moments) This fact is expected since the underlying phenomena are non-linear. However, it is of great significance and should be emphasised, that not only the potential detection of positive fractal-complex areas is needed for a successive analysis, but also, the, equally significant, identification of non-fractal areas and, most importantly, stochastic parts. The importance of finding stochastic parts can be understood by the fact, as also mentioned in the Introduction Section 1, that music is anticipated to be mainly stochastic-deterministic, i.e., is expected to be described mathematically and, hence, studied in terms of mathematical harmony.Towards this, a very simple composition of Michael Paouris called Nocturnal Angel is analysed. To extend the analysis to greater than 5 s chunks, the lumping technique is employed in this analysis. The reader should recall that the lumping technique refers to sequential non-overlapping windows in contrary to the sliding window technique where the windows overlap. As already mentioned, lumping techniques is applied to windows of 1024 samples. In this way a 100 s part of Nocturnal Angel is analysed which is approximately the 20% of the piece. To achieve a full comparison with DIAPHONIES parts, the full sections of DIAPHONIES 1 and 2 (codings:fc1,fc2,fc3) are analysed also with the lumping technique of 1024 window (namely a sliding window with 1024 window size and 1024 window step). It is very important that the fractal analysis output of the 100 s part of Nocturnal Angel via lumping is very different from the corresponding full parts of DIAPHONIES. This latter fact is also very important. This is because it indicates that lumping produces similar fractal analysis outputs as the sliding-window analysis of all the chunks of Table 1, which justifies once more, that the fractal sliding-window technique in 1024 sample window is a powerful tool not depending on the nearby windows. This fact has been acknowledged in all previous publications mentioned in text for the sliding-window technique. One the one hand, it can be supported, also for the cases of the analysed musical signals of DIAPHONIES, that lumping is a useful and quick method for deriving fractal analysis outputs, however on the cost of roughness of the corresponding analysis. The most important finding though is that the composition Nocturnal Angel has associated successive fractal output that follows the normal distribution (Shapiro-Wilk p-values equal 0.12). This means that the average and standard deviation of the mean fractal outputs are meaningful. The most significant finding to the authors of this paper is that the average power-law b exponent is $\overline{b}=1.98$ ($\sigma =0.3$) which is practically 2, namely the corresponding music of Nocturnal Angel is random, stochastic and deterministic. The reader should consider that the identification of a true negative state is very difficult in critical non-linear phenomena. It has not been found in earthquake related signals nor in air-pollution time-series, but is addressed in music. This fact is so important that support all analysis and expressed views, a-priory. The finding of such an important case of randomness, with identical software, methodological approach and similar analysis logic. Most important, this justifies in the most outstanding way, the results of fractal analysis of this paper regarding the excellent and tedious composition of DIAPHONIES from Michel Paouris.

5. Conclusions

This paper analyses demanding music parts of the composition DIAPHONIES by Michael Paouris. The investigation focuses on the fractal segments of these parts via methodologies well documented by several publications on critical non-linear phenomena. Sliding windows of 1024 samples and step 1 provide a fine-tuned segmentation of all signals. Long-range power-law dependence is sought in every window from which the scaling exponent b is calculated. More than $30x{10}^6$ power-law data is accessed and more than $160x{10}^6$ data is generated for 160 s of very complex symphonic music. The results indicate areas of continuous fractality dipped in non-fractal and, possibly deterministic and stochastic music. Diverging cases of more non-fractal areas are addressed, as well as, of mixed fractal and non-fractal areas. Some significant overall b data are tabulated and the implications are discussed. There is a plethora of persistent ($2<b<=3$), antipersistent ($1<b<2$) and persistent-antipersistent segments. No data are found on categories $0<b<1$, $b=1$ (stationary music) and $b=2$ (pure random music). Several segments fall into the b-threshold limit categories $1.7<b<2.3$ (significant strong antipersistent-persistent interchanges) and $2.3<=b<=3$ (strong persistent variations).The latter categories are deemed as of significant criticality, fractality and non-linear behaviour. Fractal data on categories $1.7<b<=3$ and $1.7<b<2$ are reported. The data is organised also in Class I (predictive) and Class-II (non-predictive) categories. Fractal dimensions calculated from b-values, indicate segments with different complexity implying that the DIAPHONIES composition follows paths of different associations between musical amplitude shape and equivalent fractal space that this shape fills. The related approach is very detailed and the novel big-data viewpoint of this analysis is compared to existing papers on the subject of fractals and music. While the power-law value range is within the one of the related references, this paper provides very important findings regarding fractals present in music considering this as a part of fractals in arts in general. The power-law b values reported are within the well-published range of power-law exponents of critical processes. The musical signal in these phases is a scaled imitation of a smaller or bigger part and this is significant since fractal are related to harmony in nature. Finally lumping analysis is reported in the whole DIAPHONIES part and in a simple-harmony composition called Nocturnal Angel. The important finding is that while the DIAPHONIES analysis results are comparable to those of the sliding window technique, those of Nocturnal Angel behave statistically, follow the normal distribution and have average $\overline{b}=1.98$ ($\sigma =0.3$) which implies pure deterministic music. The latter is the most significant justification of the results since with the same technique statistical and deterministic music is found which has completely different fractal profile from the ones of DIAPHONIES.