Feasibility of Using SWIR Transformed Reflectance (STR) in Place of Surface Temperature (Ts) for the Mapping of Irrigated Landcover

1. Introduction

Irrigation is critical for agricultural production, and it plays an important role in food security in many areas of the world [1,2,3]. Irrigation not only increases crop yield by overcoming climatic constraints, but it also modifies local climatic conditions and adds to evapotranspiration [4,5]. In addition, irrigation can have some environmental impacts like increased soil salinity [6], changes in water table [7] and altered hydrological cycles [8]. The stated economic and ecological importance of irrigation warrants that the extent and distribution of irrigation is mapped precisely and monitored regularly.

Soil moisture is a key indicator of surface irrigation and irrigated landcover. The interaction of electromagnetic (EM) radiation with soil moisture and irrigated land has shown significant correlation at various wavelengths. As a result, several methods have been developed to map surface irrigation in different EM regions, namely optical, thermal and microwave. These methods have been summarised in detail in several recent studies [9,10,11,12]. As the microwave sensors are particularly sensitive to the changes in ground moisture, these have been used in mapping irrigated landcovers in many studies [13]. Though microwave sensors have provided promising results for the detection of irrigation in many areas, the coarse spatial resolution and the confounding effects of topography and vegetation created notable uncertainties in some regions [14]. However, the launch of Sentinel-1 satellites constellation (S1-A and S1-B) provided an unprecedented radar data coverage at a high spatial and temporal resolution. This has led to some new approaches of mapping irrigation, based on machine learning and empirical modelling, providing improved results [15,16].

Thermal infrared (TIR) sensors are considered highly relevant for irrigation mapping [17,18]. To distinguish between ‘irrigated’ and ‘non-irrigated’ land, TIR-derived surface temperature (Ts) has been widely used [19,20]. Ts is invariably used in combination with certain vegetation measures to map irrigated agriculture. There are very many vegetation indices which have been developed since the early attempts in 1960s - 1970s [21,22], frequently using a combination of spectral responses between visible and the near- or mid-infrared range [23]. The most used vegetation measure is the normalized difference vegetation index (NDVI), which is based on near-infrared (NIR) and red wavebands. Presently there are many satellites with optical sensors onboard, providing images suitable for vegetation indices at medium to high spatial resolution. However, there is a lack of satellites that provide thermal images with acceptable resolution, except for Landsat series of satellites (presently Landsat-8/9) which continues to provide concurrent thermal and optical observations at a nominal resolution of 30 m.

Though the thermal-based methods are powerful for irrigation mapping since they have physical rationale for their application, most methods depend on local weather conditions such as air temperature (Ta) close to the time of satellite overpass. The relationship between Ts and soil moisture is highly influenced by Ta and other atmospheric conditions [24]. Without the calibration of Ts, the results are likely to vary spatially across different landcovers, confounding the distinction of irrigated landcover. Considering this limitation, efforts have been made to find a robust substitute of Ts in the optical range to adequately account for surface moisture. Several indices that utilize optical observations have been proposed for the quantification of surface moisture or the lack of it, as shown in Table 1. Some of these indices are based on triangular or trapezoidal pixel distributions of optical observations in different spectral frequency range. It is notable that these optical indices (Table 1) are mostly empirical and lack any physical foundation. However, in a recent development, a method which is supported by both theory and experimental data, has been proposed by Sadeghi et al. [25]. This new method which has been designed to measure soil moisture is based on a linear model in shortwave infrared (SWIR) wavelengths, termed as ‘SWIR transformed reflectance’ (STR). We have chosen this measure to use in our study to explore its feasibility as a substitute of TIR-derived surface temperature for the mapping of irrigated land cover in the Central Goulburn Irrigation District (CGID) of Victoria, Australia, during the peak irrigation season (i.e., Summer) of 2020-21.

The objectives of this study are: (1) To assess the feasibility of using STR for mapping irrigated landcover; and (2) To compare TIR-based landcover classification (thermal approach) with STR-based landcover (optical approach).

3.1. Subsection

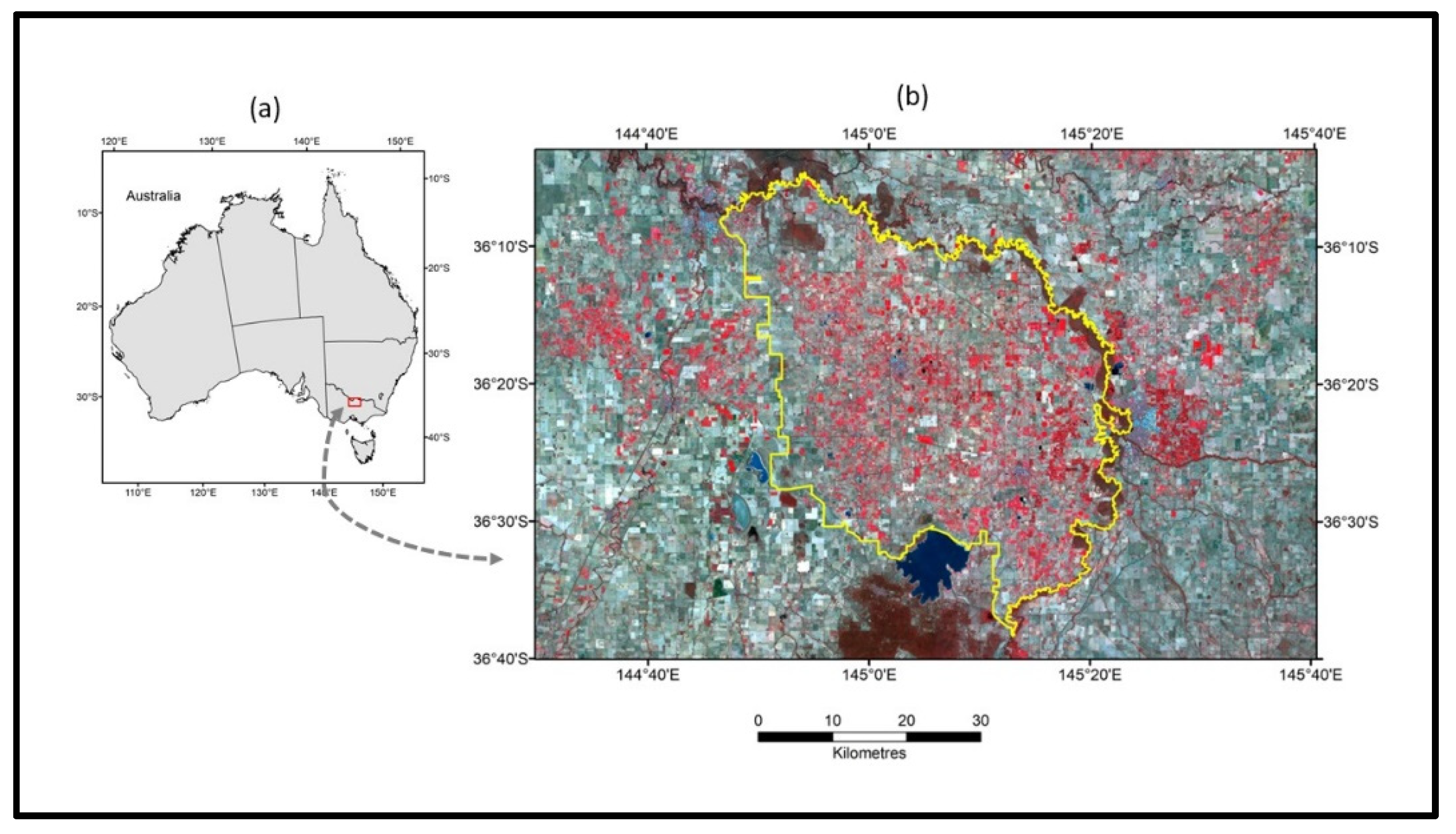
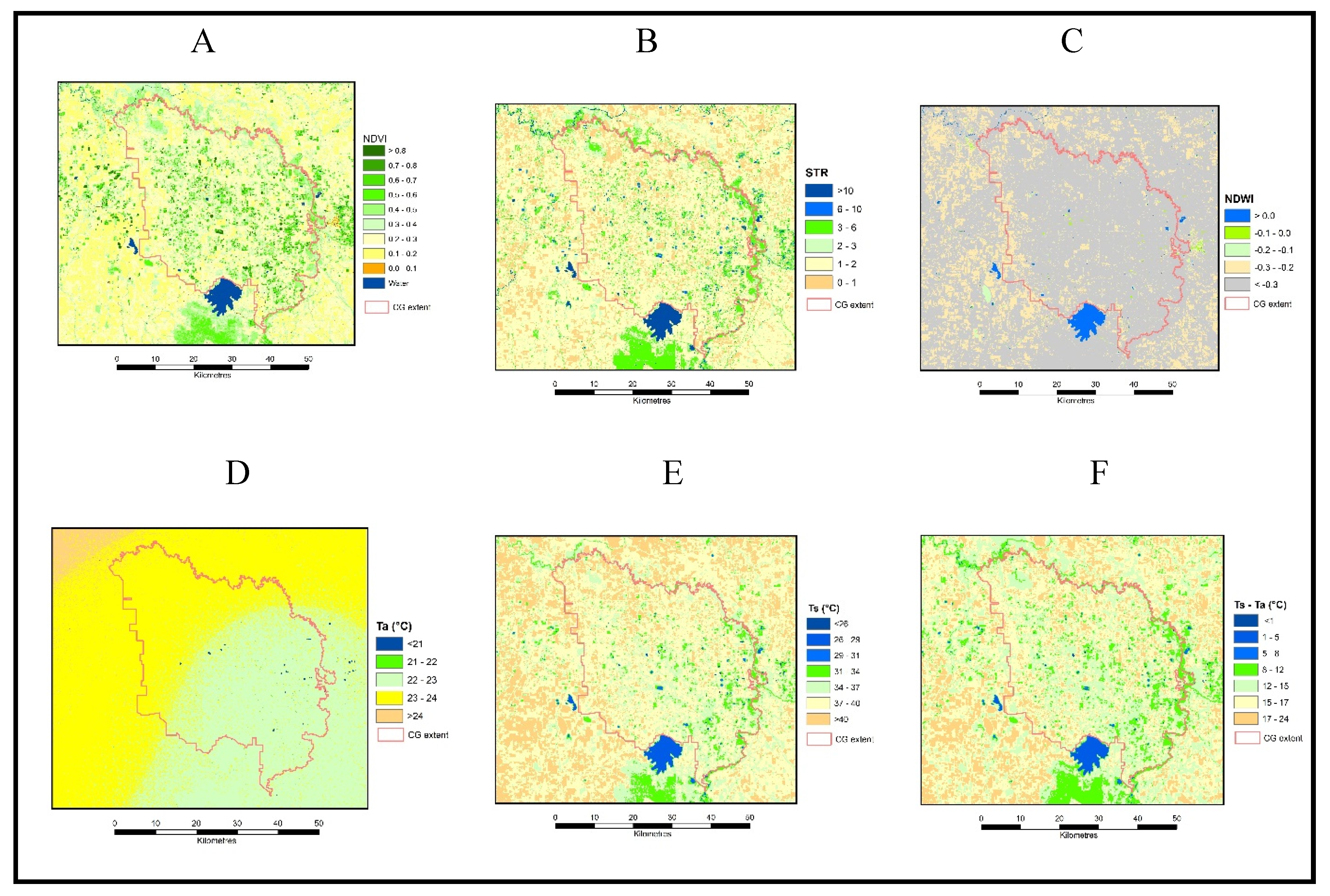
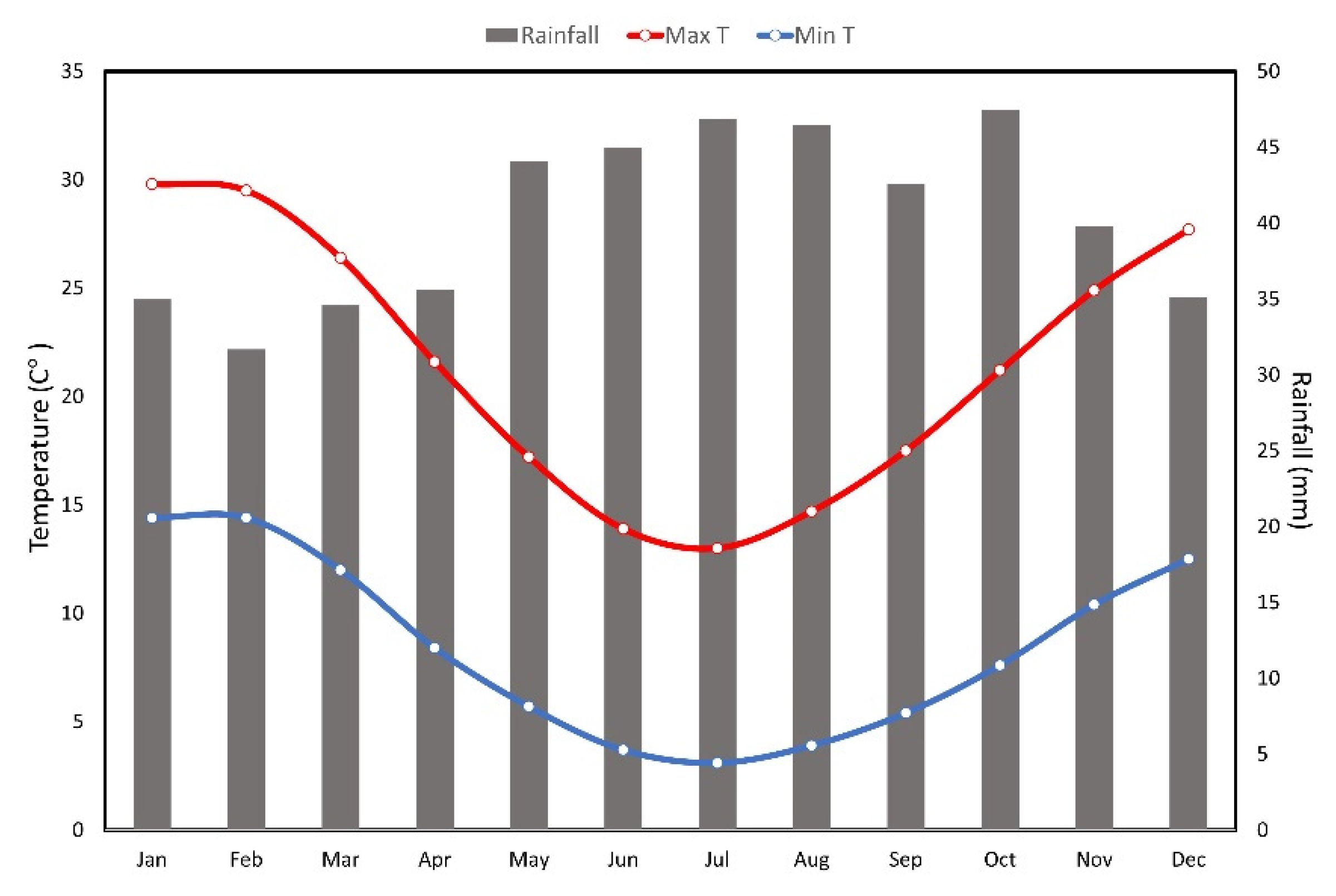
The CGID is located approximately between 36°04′41″S and 36°38′26″S latitudes, and between 144°46′37″E and 145°23′41″E longitudes, in the northern part of Victoria, Australia, (Figure 1). It is spread across the council jurisdiction of the Greater Shepparton City. It covers an area of about 1,900 sq. km., of which a large part is irrigated. The climate is temperate, and the region is relatively dry with average annual rainfall between 200 mm and 400 mm. In general, most of the rainfall is received during winter (June to August). Summers (December to February) are usually dry. The average maximum temperature ranges between 12° to 15°C in winter, increasing to 27° to 30°C in summer (December to February). The average minimum temperature varies from 3° to 6°C in winter to 12° to 15°C in summer (Figure 2). Victoria’s largest river, the Goulburn, flows on the eastern boundary before it joins the Australia’s largest river, the Murray, in the north. The flat terrain is covered by a network of irrigation channels. The irrigation systems used in the region include micro-irrigation, conventional sprinkler, flood, and furrow. The main industries are dairying, horticulture, cropping, and grazing.

2. Materials and Methods

The The study was undertaken in three broad steps. First, the satellite images were processed to generate the relevant measures for a representative date (8 Jan 2021) for the summer season. Second, a thresholding process was adopted to identify relative differences of surface temperature (Ts-Ta), surface moisture (STR) and vegetation status, which were then used to identify irrigated pixels. As a third step, the classified pixels were aggregated at farm scale as to match the irrigation water supply information and to measure the classification accuracy.

2.1. Satellite Data

A Landsat-8 Satellite Scene (Path 93/ Row 85) covered the study area. The image of this scene was taken from Landsat-8 Collection-2 Tier-1, which were calibrated as top-of-atmosphere (TOA) reflectance as follows [35]:

$$\rho \lambda =\frac{\pi \cdot L_{\lambda }\cdot d^2}{{\mathrm{ESUN}}_{\lambda }\cdot \cos {\theta }_{\mathrm{s}}}$$

(1)

Elements of Equation (1) are:

$\rho \lambda$= TOA reflectance [-]

$\pi$= Constant equal to ~3.14159 [-]

L_λ = Spectral radiance [W/ (m² sr μm)]

d = Earth-Sun distance [Astronomical units]

ESUN_λ = Mean solar irradiance [W/ (m² μm)]

θ_s = Solar zenith angle [Degrees]

Pixels with clouds, cloud shadows and cirrus clouds were masked out in the selected image.

2.2. Calculation of Surface Temperature (Ts)

At-sensor brightness temperature (Ts) was calculated using the following formula [35]:

$$\mathrm{T}\mathrm{s}=\frac{K2}{nl\left(\frac{K1}{L_{\lambda }}+1\right)}$$

(2)

Elements of Equation (2) are:

Ts = Effective at-sensor brightness temperature [K]

K2 = Calibration constant 2 [K]

K1 = Calibration constant 1 [W/(m² sr μm)]

L_λ = Spectral radiance at the sensor’s aperture [W/(m² sr μm)]

nl = Natural logarithm

For this study, Band 11 TIR2 (11500 - 12510 nm) was used for L_λ.

2.3. Surface-Air Temperature Difference (Ts−Ta)

Surface temperature has long been used to understand vegetation water status [36]. As plants transpire, water loss reduces leaf temperature due to evaporative cooling. The surface temperature of vegetation often becomes much lower than that of the surrounding air in situations of optimum water supply. Conversely, in water-stressed situations, vegetation transpires less and vegetation surface temperature increases, usually rising above the surrounding air temperature [37]. The difference between the surface and air temperatures (Ts−Ta) is therefore considered a logical variable to assess vegetation water status.

The air temperature data, close to the time of the satellite overpass, was sourced from the Bureau of Meteorology (www.bom.gov.au) and the SILO website (www.longpaddock.qld.gov.au/silo/) for multiple weather stations across and surrounding the study area. The point data of air temperature (Ta) was rasterized, using inverse distance weighted (IDW) method, to match the Ts from satellite.

2.4. Calculation of Shortwave-Infrared Transformed Reflectance (STR)

The concept of STR has been proposed by Sadeghi et al. [25] in relation to soil moisture. The derivation of STR is based on a simple model of Kubelka-Munk theory [38], which describes radiative transfer with absorption (k) and scattering (s) in a soil layer, considering a downward and an upward light propagation flux, perpendicular to the layer. By analytical solution of the equations for absorption and scattering coefficients, reflectance (R) is obtainable as the function of k and s [39]:

$$R=1+\frac{k}{s}\sqrt{\left({\left.\frac{k}{s}\right)}^2+2\frac{k}{s}\right.}$$

(3)

The rearrangement of Equation (3) gives ‘transformed reflectance’ (r) denoted by r = k/s [25]:

$$r=\frac{k}{s}=\frac{{(1-R)}^2}{2R}$$

(4)

Sadeghi et al. [25] tested Equation (4) for soil moisture using multiple spectral frequencies in laboratory conditions, and found that SWIR bands (wavelength between 350 and 2500 nm) are optimal for soil moisture detection. Therefore Equation (4) was qualified as ‘SWIR transformed reflectance’ (STR) [40]:

$$\mathrm{S}\mathrm{T}\mathrm{R}=\frac{{(1-SWIR)}^2}{2\left(SWIR\right)}$$

(5)

In the calculation of STR, commonly used spectral bands include Landsat-8 Band 7, Sentinel-2 Band 12 and MODIS Band 7 [40,41,42,43,44]. For this study, SWIR in Equation (5) refers to Landsat-8 Band 7 (2200 nm). High STR values indicate high soil moisture and vice versa.

2.5. Calculation of Vegetation and Water Indices

Normalised difference vegetation index (NDVI) was calculated as follows [22,45]:

$$\mathrm{N}\mathrm{D}\mathrm{V}\mathrm{I}=\frac{NIR-Red}{NIR+Red}$$

(6)

NIR denotes Band 5 (865 nm) and Red Band 4 (655 nm). NDVI was one of two key variables in land cover classification.

Normalised difference water index (NDWI) was calculated as follows [27]:

$$\mathrm{N}\mathrm{D}\mathrm{W}\mathrm{I}=\frac{Green-NIR}{Green+NIR}$$

(7)

Green denotes Band 3 (560 nm). NDWI was used to detect and mask out surface water to ensure the STR estimates were confined to soil moisture.

2.6. Thresholding Process for Landcover Classification

An operational classification approach based on iterative thresholds has been adopted for this study. This approach, that generates bilevel classes of satellite-derived measures, has been previously used for the landcover classification in the irrigation regions [46,47]. Here we describe the process of both approaches: Optical and thermal.

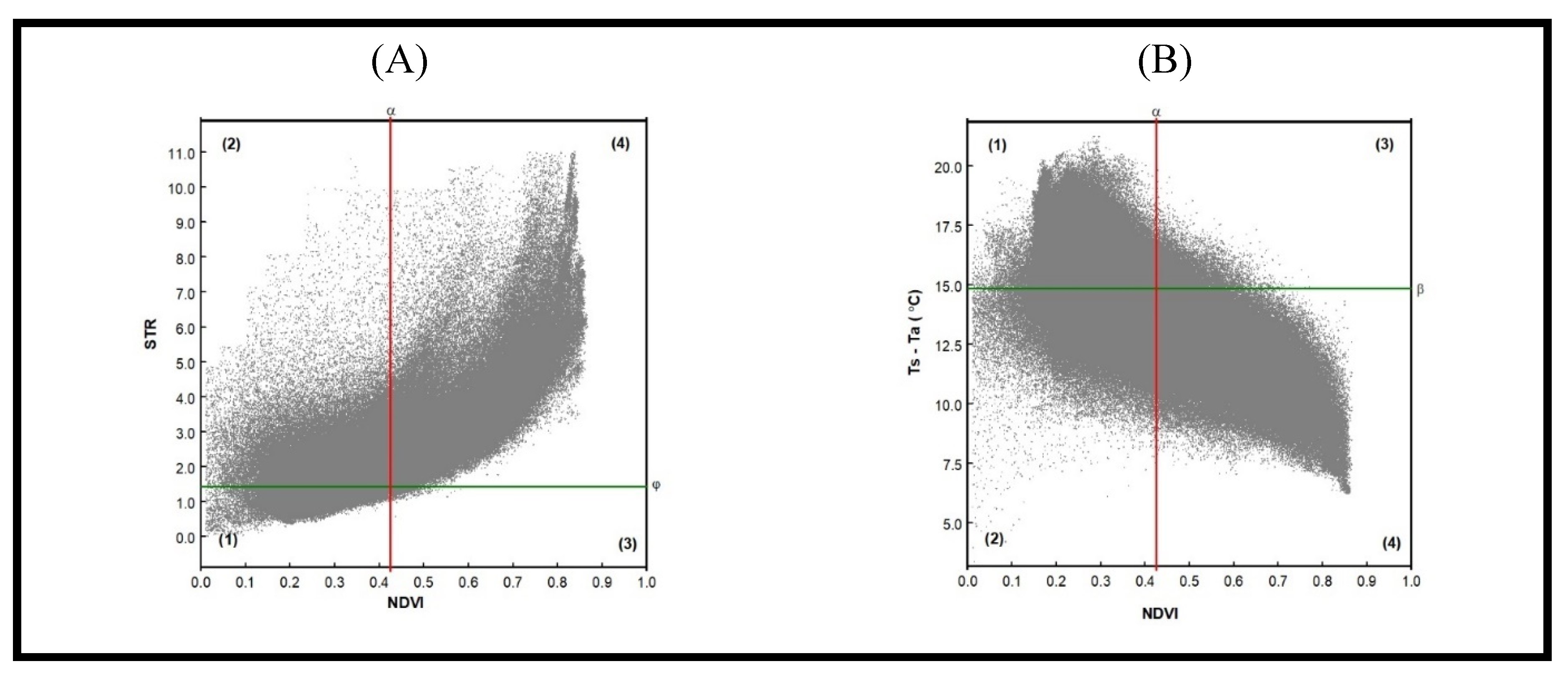
It is widely accepted that an ‘irrigated’ crop has high vegetation and high soil moisture as compared to non-irrigated crops or other dry landcovers. On this basis, STR (soil moisture indicator) and NDVI (vegetation status) were segmented into two classes each. STR classes referred to ‘irrigated’ (relatively high soil moisture) and ‘non-irrigated’ (relatively low soil moisture), and vegetation classes were ‘crop’ (relatively high NDVI) and ‘non-crop’ (relatively low NDVI). An iterative thresholding method was used to achieve the binary classification by minimizing within-class variance, ${\sigma }_{Within}^2$ [48]:

$${\sigma }_{Within}^2\left(T_i\right)={\omega }_0{\sigma }_0^2\left(T_i\right)+{\omega }_1{\sigma }_1^2\left(T_i\right)$$

(8)

Here, $\left(T_i\right)$is the threshold which varies by iteration i, ω₀ and ω₁ are the weights of the two classes; and ${\sigma }_0^2$ and ${\sigma }_1^2$are the variance of the two classes.

For applying the thresholding procedure in operation, the relationship of ${\sigma }_{Within}^2$ with between-class variance (${\sigma }_{Between}^2$) and total variance (${\sigma }_{Total}^2$) was made use of as follows [48]:

$${\sigma }_{Within}^2\left(T_i\right)={\sigma }_{Total}^2\left(T_i\right)-{\sigma }_{Between}^2\left(T_i\right)$$

(9)

Initial NDVI threshold (α) was taken as 0.4. All pixels ≥α were considered as ‘crop’. Initial soil moisture threshold was the median value of STR (φ) or Ts-Ta (β). The iteration interval was set at 0.005 within the limit of ±0.025 of the initial thresholds. Altogether, 11 iterations each for NDVI and STR/Ts-Ta were performed for the image. Thresholds with minimum σ²_Within were used for binary classification.

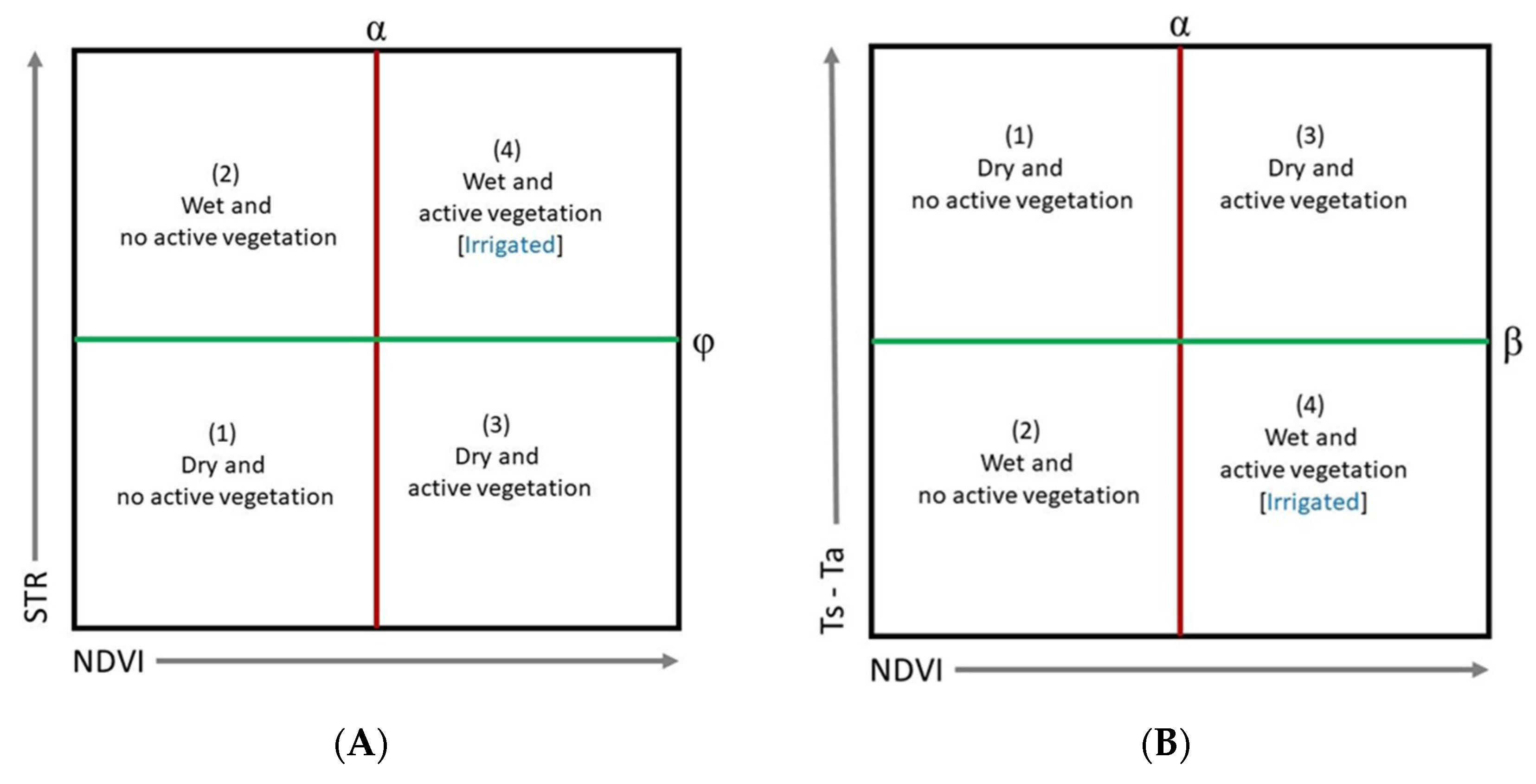
In the context of the ‘optical approach’, each pixel was identified with the defined binary classes of NDVI and STR. This resulted in four combinations as shown in Figure 3A. Pixels in sector (1) denote dry conditions with no or low vegetation. Pixels in sector (2) denote wet conditions with low or no vegetation. Pixels in sector (3) indicate some vegetation, which may be crop or pasture but without irrigation. Sector (4) denotes vegetation with wet condition indicating irrigated crop or pasture.

In the context of the ‘thermal approach’, the thresholding process for both NDVI and Ts-Ta was the same as described earlier. As shown in Figure 3B, the four sectors define the vegetation status and wet/dry conditions. Here as well the pixels in Sector (4) indicate irrigated crop or pasture.

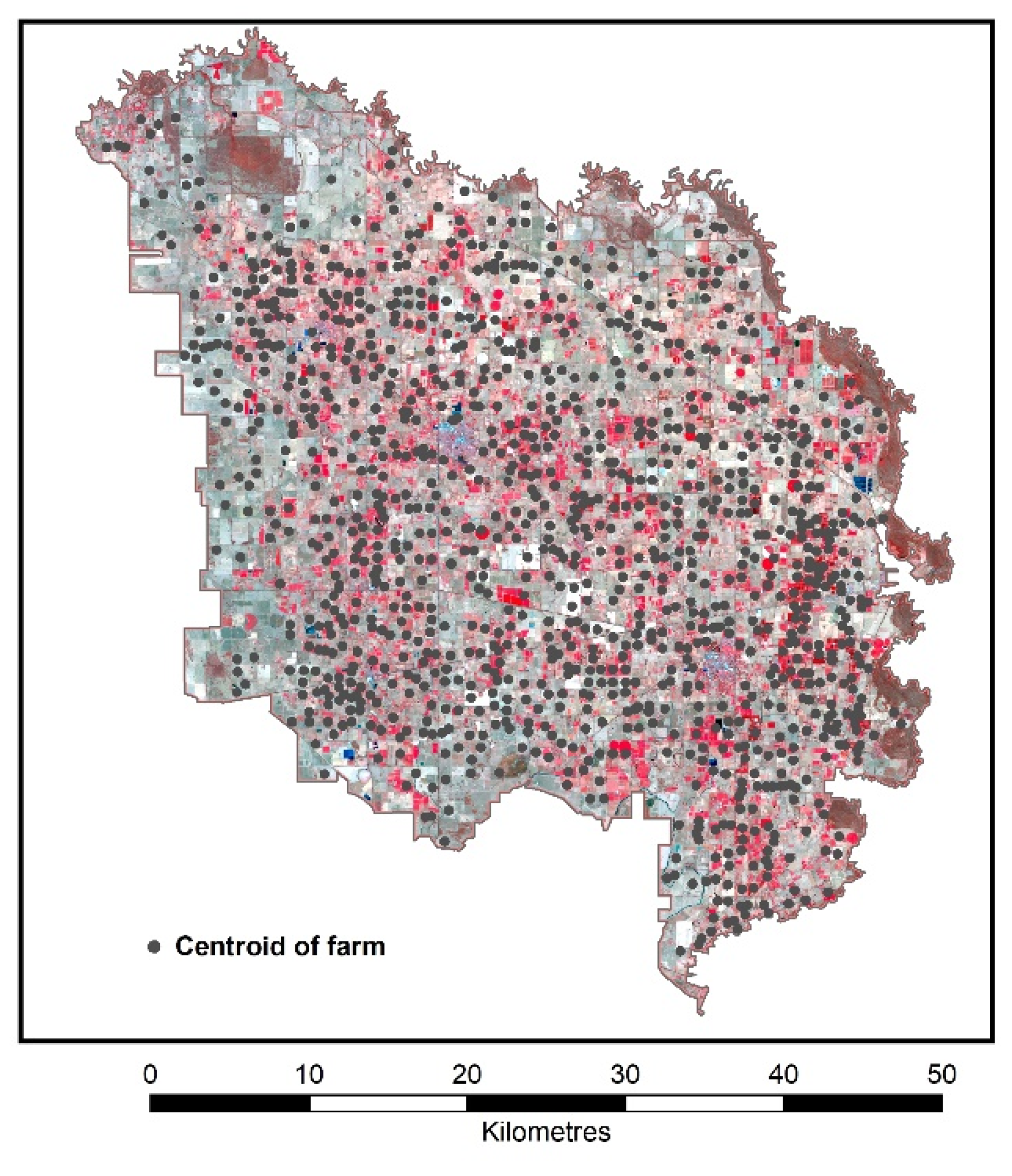
Validation was carried out on the pixels aggregated to the extent of irrigation water delivery licences. Water delivery for each license has been linked to spatial unit consisting of one or more paddocks. These units hereinafter are referred to as farms. The mapped results of irrigated landcover were compared with the actual irrigation deliveries to farms. Information on irrigation water supplies at farm level was sourced from the Victorian Water Register (VWR), a state-wide irrigation water database (https://waterregister.vic.gov.au/). Figure 4 shows the location of farms which have been included in the validation process. In this figure, the locations of farms have been shown by farm centroids instead of farm boundaries due to privacy reason.

3. Results

3.1. Distribution of Input Measures

The classification process takes two variables as inputs in both approaches – ‘optical’ and ‘thermal’. NDVI is one variable, which is a common measure used in both approaches, as shown in Figure 5A. Though the NDVI ranges between 0 and ≥ 0.8 in CGID, the notable areas are those with NDVI ≥ 0.4 shown as shades of green. These areas are predominantly under perennial horticulture, perennial pastures, or summer crops. The NDVI distribution appears patchy and irregular mainly due to the widely varying sizes of agricultural properties ranging between under 2 ha and over 1000 ha.

The values of STR in CGID range between 0 and ≥ 10 (Figure 5B). However, the notable areas are those with STR values of 2 and over, indicating the presence of substantial surface moisture. Here the distinction must be made between potential irrigation areas, which are exclusively agricultural properties, and the riverine zone of native vegetation where the source of surface moisture is not irrigation.

Figure 5C shows the distribution of NDWI in CGID. All NDWI values above zero indicate presence of surface water. In addition to a few large water bodies like Waranga Basin in the south-central part, farm dams of varying sizes are shown across the district. The areas with surface water have been excluded while evaluating STR values.

The ‘Ts-Ta’ as an input variable for thermal approach of classification is largely driven by the satellite-derived surface temperature (Ts), moderated by air temperature (Ta). The spatial variation of Ta in CGID was within 3°- 4°C (Figure 5D). It ranged between under 21°C and about 24°C, increasing from south-east to north-west direction (Figure 5D). On the other hand, Ts ranged between 26° and over 40°C. Relatively cooler surfaces were with < 34°C, roughly spread in patches but largely contiguous in the riverine areas in the east (Figure 5E).

The distribution of Ts-Ta in CGID ranged between 0° and 24°C (Figure 5F). Here, the relatively cooler areas appear more pronounced as compared to those in Ts.

Visual comparison of the Ts-Ta map (Figure 5F) with that of STR (Figure 5B), shows marked similarities. Locations of high surface moisture (i.e., high STR and low Ts-Ta) appear to be the same. Similarly, the dry surface areas of the two maps correspond well.

3.2. Thresholds for Pixel Classification

The Figure 6A,B show the identification of pixels as per optical and thermal approaches. Using Equation (9), the iteration process provided threshold for NDVI as 0.425, for STR as 1.425 and for Ts-Ta as 14.85°C. In each case, pixels have been divided into four classes. Pixels within Sector Four (refer to Figures 3A and 3B) have been identified as ‘irrigated’ crop or pasture.

3.3. Irrigated Landcover Classification

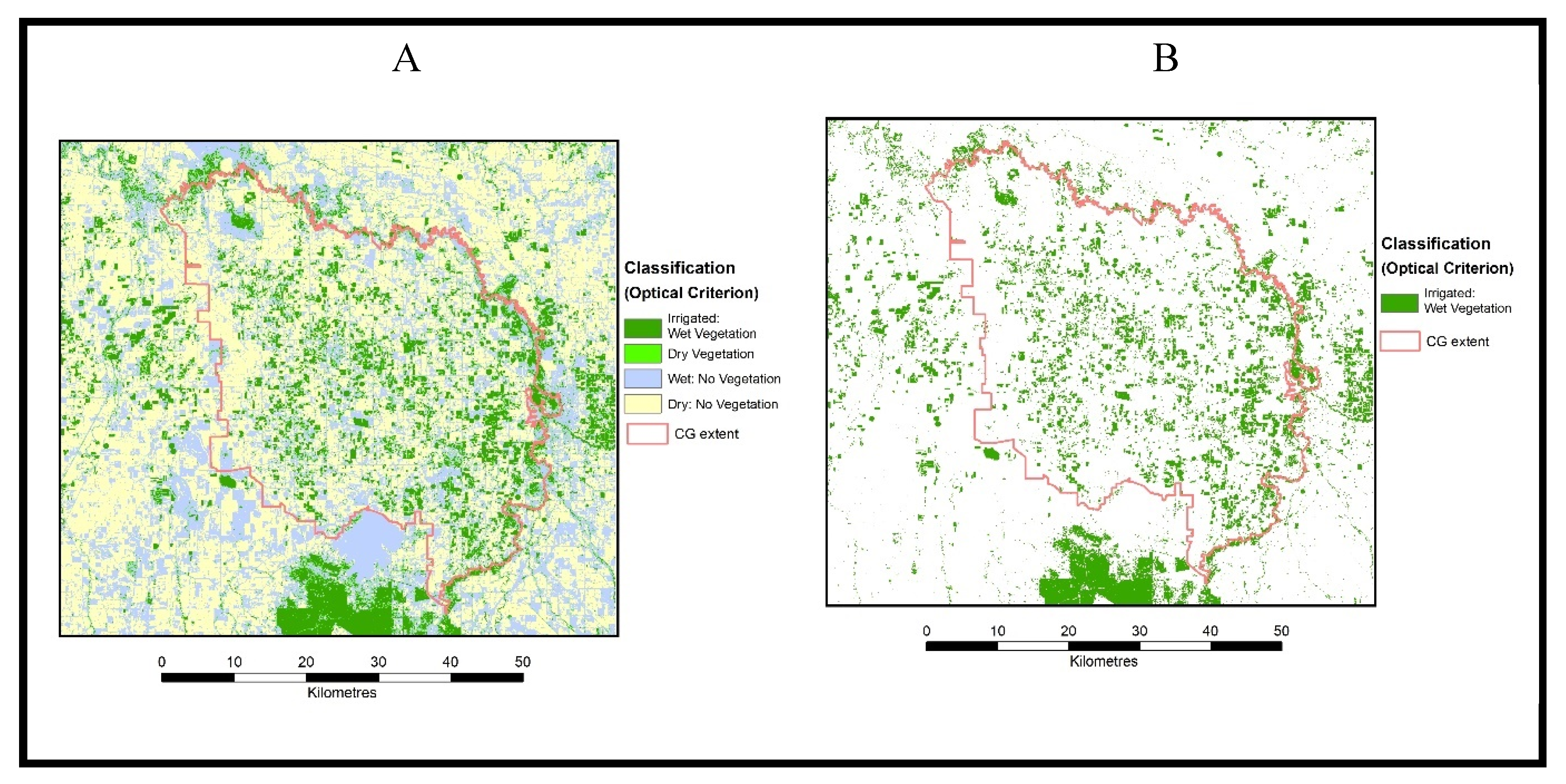
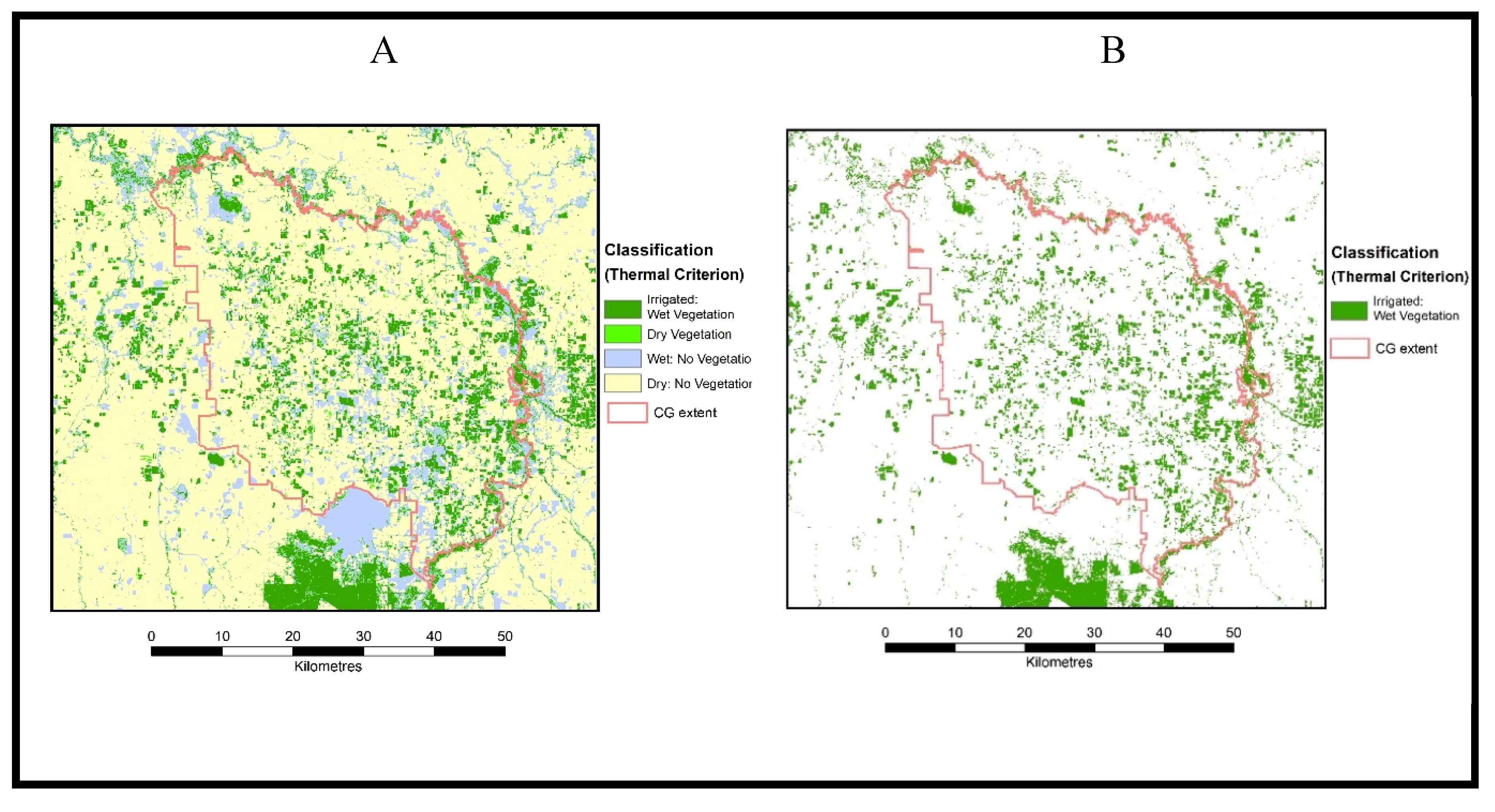
The Figure 7 shows the results of the irrigated landcover classification for optical approach. Figure 7A shows the four classes as identified in Figure 6A. Figure 7B is the map of irrigated landcover class only. Figure 8 shows the results of the irrigated landcover classification based on thermal approach where Figure 8A shows the four classes as identified in Figure 6B. Figure 8B is the map of irrigated landcover class only.

The visual comparison of the two maps of irrigated landcover (Figure 7B and Figure 8B) shows minor differences. The map of optical approach (Figure 7B) has identified slightly more pixels as irrigated in comparison to the map of thermal approach (Figure 8B)

3.4. Validation of Irrigated Landcover

As stated earlier, validation of irrigated land cover classification has been carried out at farm level. Farms ≥10 ha in size were selected for validation. A farm was considered as ‘irrigated’ (‘Reference’) based on a substantive amount of water delivery (≥0.1 ML per ha) to that farm during the timeframe of the summer season (December to February). No or negligible amount of water delivery (<0.1 ML per ha) was taken as the absence of irrigation on a farm. These reference farms were compared with the classification results for accuracy.

As per the classification, a farm was considered ‘irrigated’ provided a substantial proportion of pixels (≥25%) within that farm belonged to Sector 4 (Wet and active vegetation; Refer Figure 3 and Figure 6). This criterion was uniformly applied to both optical and thermal approaches.

Table 2 and Table 3 provide classification accuracy for the two approaches. The calculation of confusion matrix resulting into producer’s and user’s accuracies followed standard procedure [49,50]. Though the overall accuracy is high in both cases, the optical approach (97.6%) performed slightly better than the thermal approach (93.9%). The user’s accuracy for irrigated landcover was noticeably higher in case of optical approach (98.3%) as compared to that of thermal approach (88%). However, there is very little difference between the two approaches as per producer’s accuracy for irrigated landcover (96.2% for optical and 97.1 for thermal).

4. Discussion

The feasibility of using STR along with NDVI (optical approach) to map irrigated landcover has been confirmed by a high-level overall accuracy assessment (97.6%). These results of irrigated landcover by optical approach found to be comparable with those of a parallel process that used Ts-Ta along with NDVI (thermal approach). However, there was a noticeable difference in the user’s accuracy for the ‘irrigated’ class between the two approaches (88% thermal to 98.3% optical). This could have occurred due to the difference in the spatial resolution of a variable for surface moisture. STR is based on Band 7 of Landsat 8 which has 30m resolution, whereas Band 11 used in Ts-Ta is 100m resolution though resampled to 30m [51].

The threshold-based classification used in this study is an example of a simple and operational approach for routine monitoring of irrigated landcover. The initial threshold for NDVI (0.4) was on the assumption that, in an agriculture enterprise, vegetation with NDVI < 0.4 is unlikely to be a managed crop or pasture. In the case of STR and Ts-Ta, the initial threshold taken was the median pixel value of the variable, which was based on the experience from the previous studies in the region [46,47,52]. These initial thresholds and the related assumptions should be field tested further to ascertain the strengths and weaknesses of this approach in different landscapes and at different times.

The classification method used in this study assumes that the main source of surface moisture is irrigation and rainfall does not have any significant impact. As stated earlier, the summers in the study area are generally dry. The long-term average of rainfall during the three months of summer is 101.8mm (Figure 2). The study period (December 2020 to February 2021) was, however, drier with a total of 80.6mm. In case of high rainfall situations, there will be a requirement of season-wide vegetation as well as STR analysis of the known irrigated and dryland farms vis-à-vis rainfall records to make the desired adjustments to thresholding method.

This study used a single image as a representative of summer season. This is in accordance with a previous study in the irrigation regions of Victoria, Australia, which found the use of single ‘midseason’ image adequate to assess maximum crop cover because of strong temporal stability in NDVI response [53]. However, for further studies, there is a scope to test temporal aggregates of image-based variables from multiple sources including Landsat-8/9 and Sentinel-2.

This study is a formal affirmation of using STR as a substitute of Ts-based measures for irrigated landcover classification. The basis of this affirmation is the formal comparison of optical approach with thermal approach implemented in a key irrigation district. This opens the opportunity of utilising the widely available optical sensors for irrigated landcover investigations.

5. Conclusions

The satellite-derived surface moisture (STR, Ts) and vegetation status (NDVI) are appropriate measures to distinguish between irrigated and non-irrigated pixels within farmlands. The use of STR, which is based on Band 7 of Landsat-8 (optical spectral range), with NDVI demonstrated successful mapping of irrigated landcover for the summer season of 2020-21 in CGID. The results of this optical approach of classification are found to be comparable with those of thermal approach where Ts-Ta is used with NDVI for classification. These results have broader implications in terms of irrigated landcover assessment, as the use of satellite imagery in these applications may not necessarily be limited to sensors with either microwave or thermal bands. The impact of this is a greater freedom, both spatially and temporally, to develop this information.