Understanding the Boundless Potential of Infinite Numbers in Mathematics

Budee U Zaman

doi:10.20944/preprints202404.0792.v2

Preprint

Article

Understanding the Boundless Potential of Infinite Numbers in Mathematics

This version is not peer-reviewed.

Budee U Zaman^*

This version is not peer-reviewed.

Downloads

161

Views

Comments

Submitted:

12 April 2024

Posted:

15 April 2024

You are already at the latest version

Abstract

In this article, we discuss the concept of infinity (∞), infinitesimals □ , and a new mathematical operation that expands calculations into the realm of the infinite. This breakthrough allows for the computation of infinite numbers, leading to new possibilities for mathematical research and practical applications. By introducing infinite numbers, numerous advantages arise, such as accurately representing limits, divergences in integrals and infinite series, and extending calculations to infinity. This mathematical advancement opens doors to exploring uncharted territories, offering valuable insights and breakthroughs.

Keywords:

infinite series

;

infinity

;

infinitesimals

Subject:

Computer Science and Mathematics - Algebra and Number Theory

This preprints belongs to the Topic

Fuzzy Number, Fuzzy Difference, Fuzzy Differential: Theory and Applications

1. Introduction

The idea of infinity has always fascinated mathematicians, urging them to delve into the endless and expansive realm of numbers. Historically, infinity was seen as an elusive boundary, something that couldn’t be precisely calculated. But new discoveries have defied these constraints, bringing forth the groundbreaking notion of infinite numbers and infinitesimals.

The concepts of infinity and infinitesimals, focusing on a revolutionary mathematical operation that pushes computation into the infinite realm. This new capability not only reveals the secrets of infinite numbers but also has the potential to transform mathematical research and practical applications.

With the power of infinite numbers, we can overcome usual limitations, accurately express boundaries, navigate differences in integrals and infinite series with great precision, and push calculations to the edge of infinity. This incredible progress doesn’t just solve old math problems but also opens up new areas to explore, uncovering valuable knowledge and making breakthroughs.

Join us as we embark on this exhilarating exploration of the infinite, where mathematical boundaries blur and new vistas of discovery await [1,2,3,4,5,6]

2. Infinity

2.1

Odd, even and 0.999….

In mathematics, we often encounter intriguing concepts that challenge our intuition. Let’s explore some of these concepts, including infinite sets, contradictions, and the equality

1 = 0.999 \dots

2.1.1. Infinite Sets

Consider the set of integers and the set of odd integers. If the number of integers is infinite and equal to the number of odd integers, we encounter a contradiction. This leads us to contemplate the nature of infinity and the properties of different types of infinite sets.

\begin{matrix} number of integers & = \infty \\ number of integers & = number of odd + number of even \\ number of odd & = number of even \\ number of odd & = \frac{1}{2} \times number of integers \end{matrix}

2.1.2. The Curious Case of $1 = 0.999 \dots$

The equality

1 = 0.999 \dots

may seem strange at first glance. However, there are numerous ways to prove this statement. One approach is to consider the infinite decimal expansion of

0.999 \dots

and its relationship to the number 1.

Mathematics is filled with fascinating concepts that challenge our understanding of the world. By exploring topics such as infinite sets and numerical equalities, we can deepen our mathematical knowledge and appreciation.

3. Point, Length, Area, Volume

A 1m length consists of infinitely many points. Points of a 2m length are twice as many as points of a 1m length. A 1m² area is composed of 1m horizontal and 1m vertical.

1 m^{2} = 1 m \times 1 m

. A 1m³ volume is composed of 1m² area and 1m height.

1 m^{3} = 1 m^{2} \times 1 m

This is an example of infinity.

1 = Unit.

\infty = i n f i n i t y .

□=Infinitesimal.

\infty \times □ = 1

\infty \times \infty = \infty^{2}

□ \times □ = □^{2}

4. The Decimal and the +ve Integer

The number of positive decimals and the number of positive integers are the same.

\begin{matrix} 0.00, & 0.10, & 0.20, & 0.30, & \dots, & 0.80, & 0.90, \\ 0.01, & 0.11, & 0.21, & 0.31, & \dots, & 0.81, & 0.91, \\ 0.02, & 0.12, & 0.22, & 0.32, & \dots, & 0.82, & 0.92, \\ \dots & 0.031, & 0.131, & 0.231, & 0.331, & \dots, & 0.831, & 0.931, \\ \dots \end{matrix}

0.01

corresponds to the 10,

0.21

corresponds to the 12, and

0.931

corresponds to the 139.

4.1. The Sum of ∞ Sequence

The arithmetic sequence sum formula can be used to compute the sequence of nature number if the number of positive integers is unit ∞.

\sum (n a t u r e n u m b e r)) = \frac{\infty \times (2 \times 1 + (\infty - 1) \times 1)}{2} = \frac{\infty^{2} + \infty}{2}

Sum of first decimal is 4.5 \times \frac{\infty}{10}

Sum of \sec ond decimal is 0.45 \times \frac{\infty}{10}

4.5 \times \frac{\infty}{10} + 0.45 \times \frac{\infty}{10} + 0.045 \times \frac{\infty}{10} + \dots = 4.999 \dots 5 \times \frac{\infty}{10}

\begin{matrix} \sum decimal & = \frac{5 \times \infty - 5}{10} \\ = \frac{5 (\infty - 1)}{10} \\ = \frac{\infty - 1}{2} \\ Sec ond method of the decimal sequence sum : \\ If the formula of arithmetic sequence sum is used : \\ \sum (decimal) & = \frac{\infty \times (2 \times □ + (\infty - 1) \times □)}{2} \\ = \frac{\infty + 1}{2} \end{matrix}

Two results have difference as 1.

This difference between both parts of the picture is gray.

The first method did not include one. If the first method includes 1, the sum is

\frac{\infty + 1}{2}

\sum (natural number) = \sum (decimal) \times \infty

4.2. The Calculus

If the number of positive integers is denoted as ∞, then the number of real numbers is

2 \times \infty^{2}

This is often used as a basis for real numbers rather than natural numbers. If the number of real number is unit ∞, then number of nature number is

\frac{1}{2}

The table below shows Calculate the value of a few infinite number. Unit is the positive real number.

Table 1. Mathematical Expressions

Expression	Result
Number of positive real numbers	∞
Number of natural numbers	1
$\sum (natural number)$	$\frac{\infty + 1}{2}$
$\sum (natural {number)}^{2}$	$\frac{2 \infty^{2} + 3 \infty + 1}{6}$
$\int (positive real number)$	$\frac{\infty^{2}}{2}$
$\int (positive real {number)}^{2}$	$\frac{\infty^{3}}{3}$
$lim \frac{1}{x}$	□
$lim \frac{1}{x^{2}}$	$□^{2}$

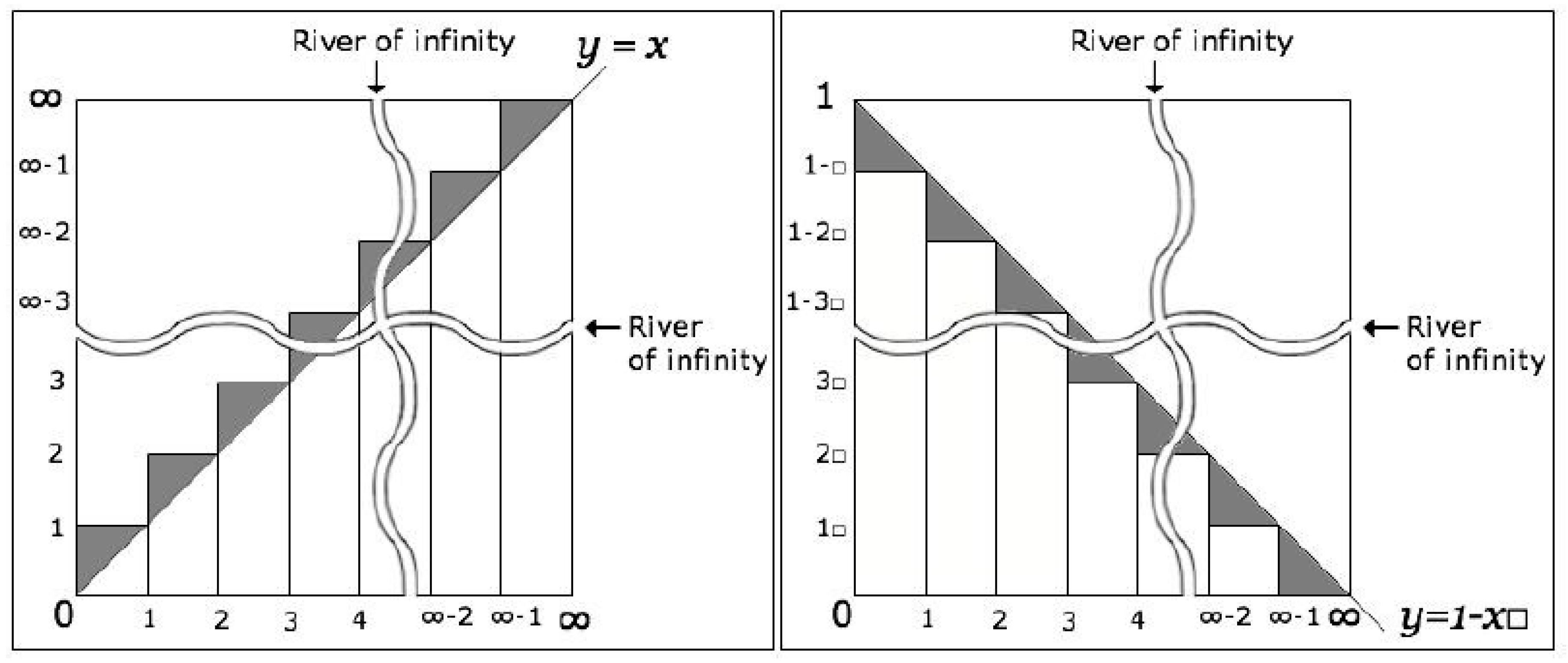
It becomes feasible for the integral representation to diverge. It becomes feasible for the infinite sequence representation to diverge. It becomes feasible to represent the exact limit precisely.

The ratio of the difference between □ and

□^{2}

is ∞. This is comparable to the ratio that separates 1 from ∞. The number of relatives per unit was represented by an infinite integer.

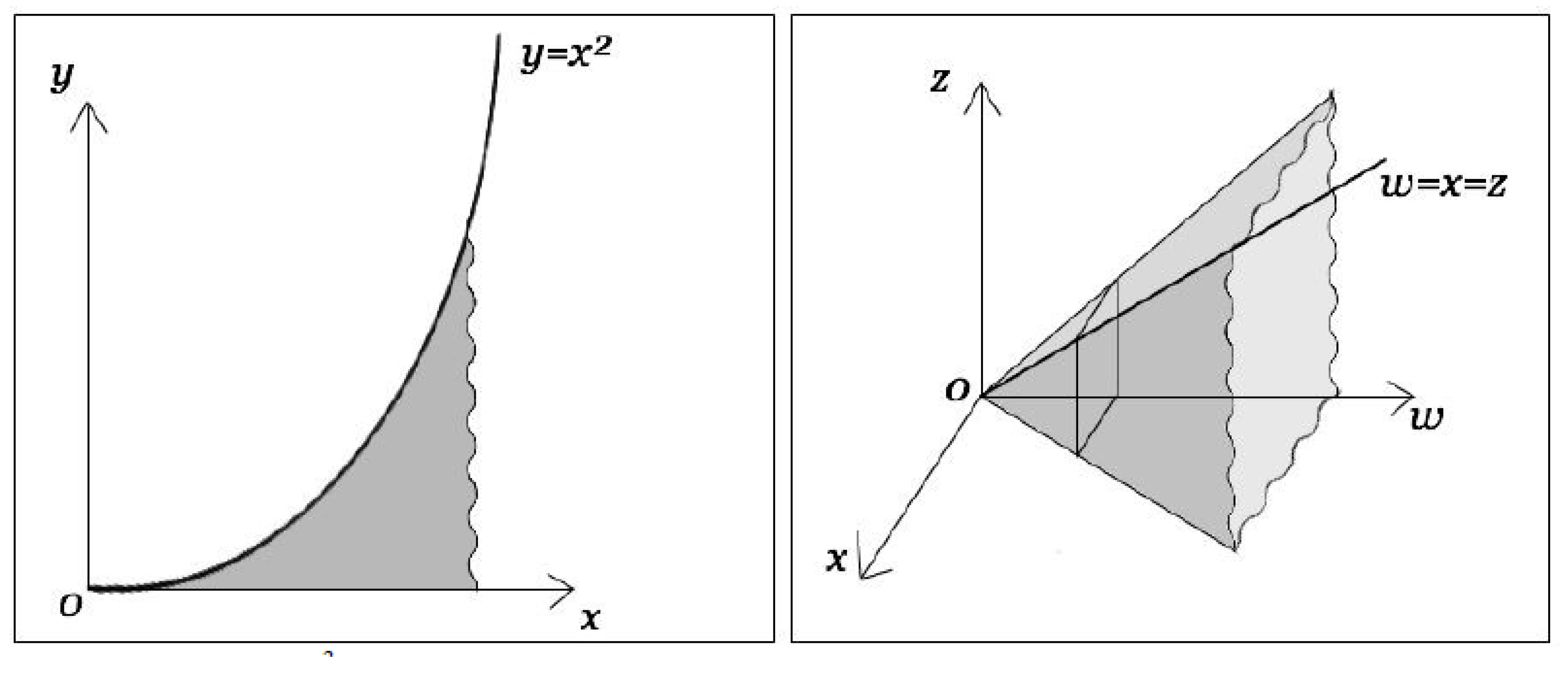
The integral of

x^{2}

\frac{x^{3}}{3}

The three-dimensional coordinates function

(w = x = z)

forms the shape of a quadrangular pyramid.

The dimensions of an infinite pyramid are

\frac{\infty^{3}}{3}

. The following two types are used to determine this:

\frac{1}{3}

is the size of the quadrangular pyramid, and

\infty^{3}

is the size of the three-dimensional.

x \times z

increases in the w-axial direction.

If x=z, then

x \times z = x^{2}

. Calculus leads to the infinite number.

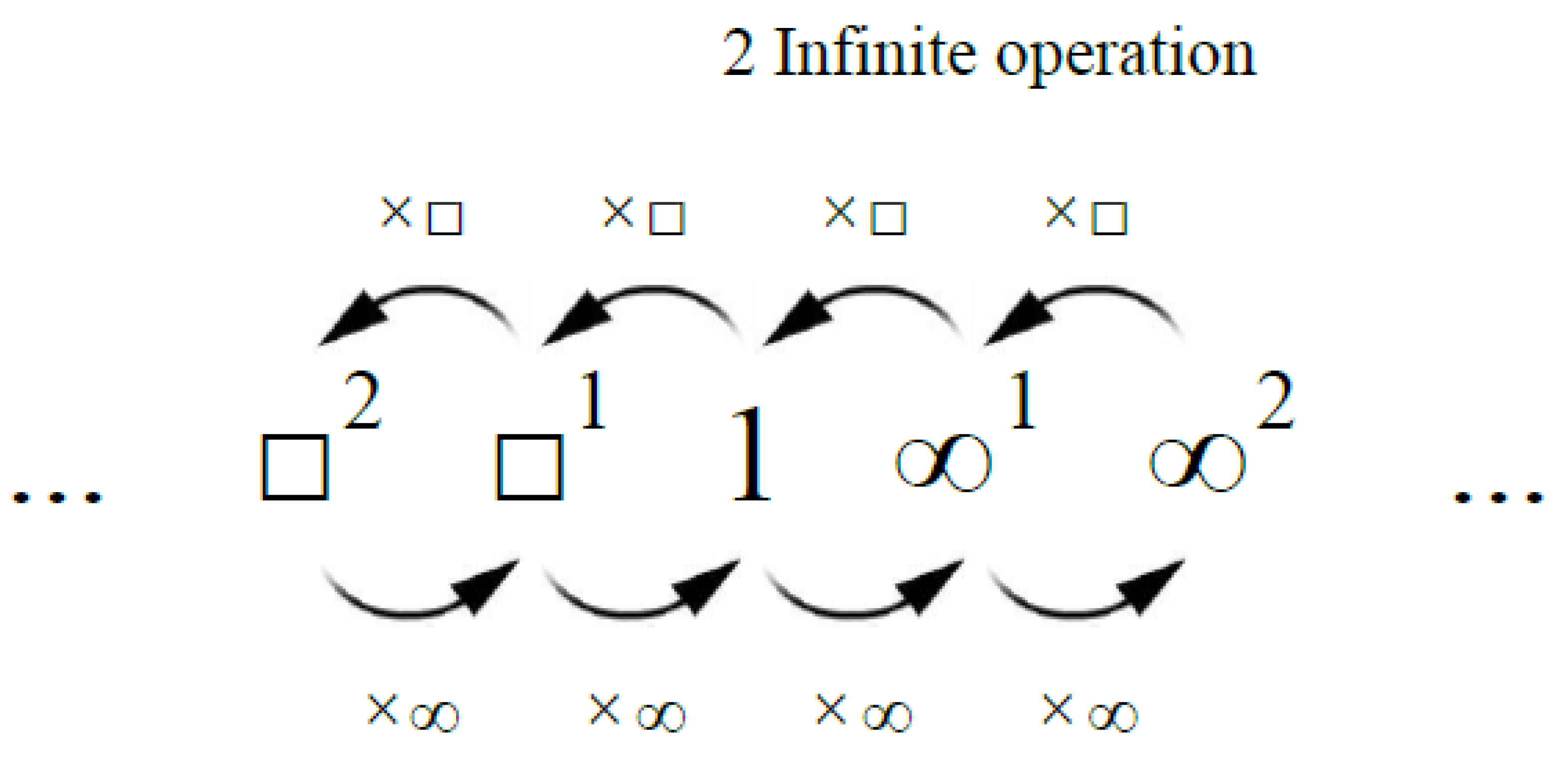
5. Infinite Degrees of Real Numbers

In your classification, you’ve defined infinite degrees for real numbers. Let’s represent a real number as x.

Degree 0:

If x is a real number, then its infinite degree 0 is denoted as

x \times \infty^{0}

Degree 1:

If x is a real number, then its infinite degree 1 is denoted as

x \times \infty^{1}

Degree 2:

If x is a real number, then its infinite degree 2 is denoted as

x \times \infty^{2}

Relationships:

$x \times \infty^{1}$ is larger than $x \times \infty^{0.5}$ .
$x \times \infty^{0}$ is smaller than $x \times \infty^{0.5}$ .

Multiplication of real numbers A and B is:

A \times \infty^{0} \times B \times \infty^{0} = A \times B \times \infty^{0}

Multiplication of infinite numbers A and B is:

A \times \infty^{1} \times B \times \infty^{2} = A \times B \times \infty^{3}

The

\infty^{0}

were omitted from the multiplication of real numbers.

5.1. $B u d e e B_{1}$

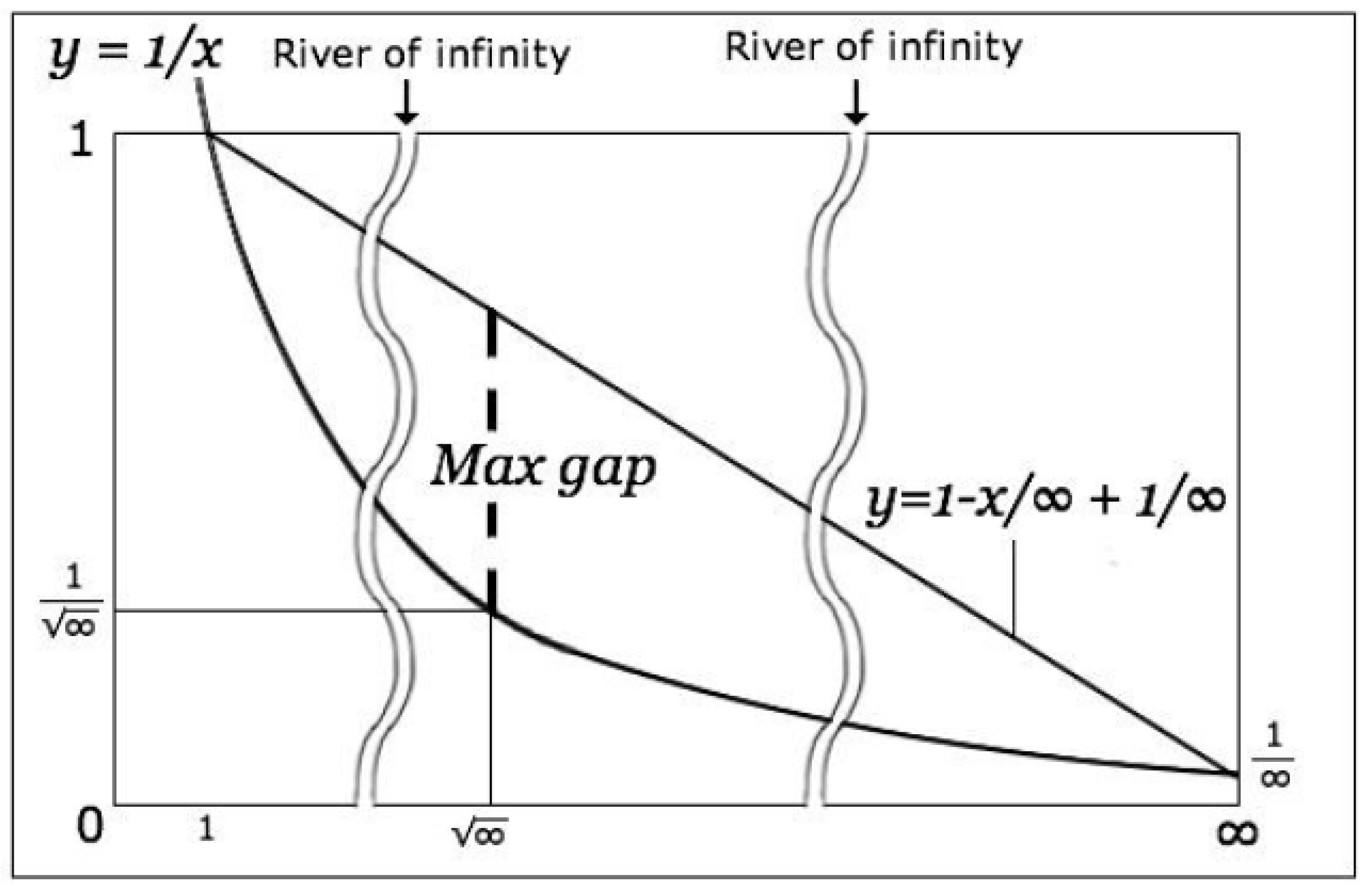
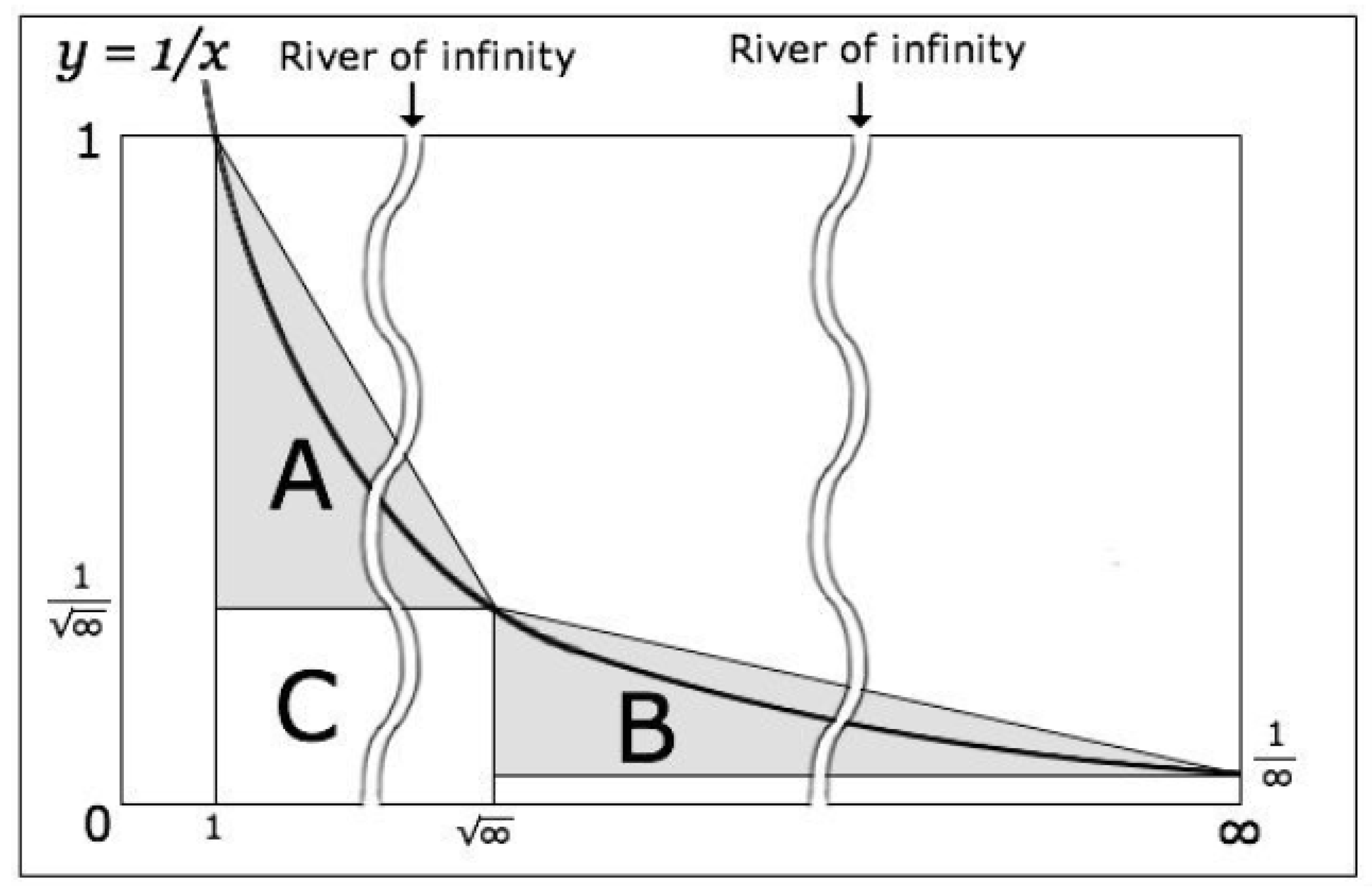
The limit of the sequence as

\frac{1}{\infty}

is smaller than any positive real number. If one wants to change the infinite degree, it requires the operation of an infinite number. The sequence is represented as

y = \frac{1}{x}

, called

B_{1}

. The infinite degree of

\sum B_{1}

is smaller than 1.

The sum of the 99th element of the sequence

B_{1}

is about 5.17. From the 100th element until the ∞th element, draw the straight line, and the area of the territory is:

(\frac{1}{100} - □) \times (\frac{\infty - 100}{2}) + □ \times (\infty - 100) + 5.17 \dots = \frac{\infty}{200} - 50 \times □ + 5.17 \dots

(1)

The sum of

\sum B_{1}

is smaller than

\frac{\infty}{200}

The element’s 10000th computation result is approximately

\frac{\infty}{20000}

, and

Σ B_{1}

is smaller than this.

Σ B_{1}

is smaller when calculating the type of natural possibility element.

Σ B_{1}

infinite degree is less than 1.

The functions

f_{a} (x)

and

f_{b} (x)

are given by:

\begin{matrix} f_{a} (x) & = 1 - \frac{x}{\infty} + \frac{1}{\infty} \\ f_{b} (x) & = \frac{1}{x} \end{matrix}

The biggest gap between the functions occurs at

x = \sqrt{\infty}

The given expressions are as follows:

A area is

\frac{\sqrt{\infty} - 2 + \frac{1}{\sqrt{\infty}}}{2}

B area is

\frac{\sqrt{\infty} - 2 + \frac{1}{\sqrt{\infty}}}{2}

C area is 1.

The area under B is

1 - \frac{1}{\sqrt{\infty}}

The sum is

\sqrt{\infty}

\sum B_{1}

is smaller than.

Infinite degree of

\sum B_{1}

are smaller than

0.5

, or same.

5.2. Real Number, Rational Number, Irrational Number

The real number will be able to define with two kinds. The first one is represented by natural numbers + decimal number. It was the small conceptual real number. The second one is defined as including the rational number and the irrational number. It was the great conceptual real number. The nature number that express the rational number and the small real number are the same. The problem is between

0 - 1

. The number of the decimal number is ∞, The number of the rational number which is the possibility of showing with

\frac{1}{x}

is ∞. When includes

\frac{2}{x}

\frac{3}{x}

,…, the number of the rational number is bigger number of the decimal number. The rational number uses

\frac{x}{y}

two numbers. The number of the rational number is maximum

\infty^{2}

. But less than

\infty^{2}

, because the rational number is duplicated.

The number

\frac{1}{3}

is stated using the ’/’ operator. The Calculation is not finished technically. A tiny real number like

\frac{1}{3}

or 0.3333 cannot exist. not be able to express without (…).

The real numbers, as defined in mathematics, encompass both rational and irrational numbers. This definition is broad and lacks clear boundaries. For the function

f (x) = \frac{1}{x}

, if x tends to infinity, the value is denoted as □.

\frac{1}{\infty - 1} = □ + □^{2} + □^{3} + \dots

This value is expressed with all infinite degrees which are smaller than 0.

∞ and □ are relative numbers. The infinite number expresses a proportion about an infinite unit. In the decimal system, ∞ grows 5 times faster than the binary system.

\frac{1}{3}

is not a recurring decimal in the ternary numeral system.

6. Error of Differential

The differential of

x^{2}

\frac{d y}{d x} = 2 x + d x

This

d x

is denoted as □. It appears as a similar small value in the sum of an infinite sequence.

The reason for this occurrence is standardized at the minimum unit. This differential standardizes at □ unit.

The sum of an infinite sequence standardizes at the integer unit.

The shape of the error resembles a staircase.

This value cannot be ignored as it becomes very large in calculations involving infinity. However, using

□^{2}

d x

can reduce the error value.

□^{3}

□^{\infty}

, and

□^{\infty^{\infty^{\infty}}}

are also viable options.

The same conclusion applies to integrals.

7. Example of the infinite number

Example one For $ζ$

\sum ζ = ζ (1) + ζ (2) + ζ (3) + ζ (4) + \dots

\infty = \frac{1}{1^{1}} + \frac{1}{1^{2}} + \frac{1}{1^{3}} + \frac{1}{1^{4}} + \dots

1 = \frac{1}{2^{1}} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + \dots

\frac{1}{2} = \frac{1}{3^{1}} + \frac{1}{3^{2}} + \frac{1}{3^{3}} + \frac{1}{3^{4}} + \dots

\frac{1}{3} = \frac{1}{4^{1}} + \frac{1}{4^{2}} + \frac{1}{4^{3}} + \frac{1}{4^{4}} + \dots

\dots = \dots

\sum ζ (x) - \sum ζ (1) = \infty - □

Example two For $\frac{1}{x}$

1 = {(\infty - 0)}^{0} \times □^{1} + {(\infty - 1)}^{0} \times □^{1} + {(\infty - 2)}^{0} \times □^{1} + \dots

\frac{1}{2} = {(\infty - 0)}^{1} \times □^{2} + {(\infty - 1)}^{1} \times □^{2} + {(\infty - 2)}^{1} \times □^{2} + \dots

\frac{1}{3} = {(\infty - 0)}^{2} \times □^{3} + {(\infty - 1)}^{2} \times □^{3} + {(\infty - 2)}^{2} \times □^{3} + \dots

\frac{1}{4} = {(\infty - 0)}^{3} \times □^{4} + {(\infty - 1)}^{3} \times □^{4} + {(\infty - 2)}^{3} \times □^{4} + \dots

\dots = \dots

Example Three

\begin{matrix} {(1 + □)}^{1} & = 1 + 1 □ \\ {(1 + □)}^{2} & = 1 + 2 □ + 1 □^{2} \\ {(1 + □)}^{3} & = 1 + 3 □ + 3 □^{2} + 1 □^{3} \\ {(1 + □)}^{4} & = 1 + 4 □ + 6 □^{2} + 4 □^{3} + 1 □^{4} \\ {(1 + □)}^{5} & = 1 + 5 □ + 10 □^{2} + 10 □^{3} + 5 □^{4} + 1 □^{5} \\ {(1 + □)}^{6} & = 1 + 6 □ + 15 □^{2} + 20 □^{3} + 15 □^{4} + 6 □^{5} + 1 □^{6} \end{matrix}

8. Infinite Expontial Infinity

The multiplication of 0 can make Everything disappear. 0 is similar to

□^{\infty^{\infty^{\infty}}}

but not 0.

The inverse of

□^{\infty^{\infty^{\infty}}}

\infty^{\infty^{\infty^{\infty}}}

□^{\infty^{\infty^{\infty}}}

\infty^{\infty^{\infty^{\infty}}} = 1 .

If inverse of 0 define @, then

0 \times @

=1.

@ to remove the paradox which occurs with multiplication operation of 0.

$1 \times 0 = 0$ , $1 / 0 = @$ .
All the inverse operation becomes possible.
But now, $@ \times 0 = @^{2}$ and $0 \times 0 = 0^{2}$ was made.

If we define

@^{2} = @

, then it becomes a notion of infinity currently used in mathematics. 0 and @ are difficult because they remove data. Any further operations will not be able to be accomplished. In order for an operation to continue continuously,

0^{2}

is necessary. But what is

0^{2}

? Is it necessary? If some number has the power of God, it will be @.

9. Conclusions

In end, the concept of infinity opens up a significant realm of possibilities for know-how the continuum hypothesis and resolving paradoxes within mathematics. By embracing the limitless, we are able to navigate thru the complexities of mathematical reasoning and explore new interpretations that go beyond traditional obstacles. The perception of limitless numbers presents a bridge to traverse the river of infinity, supplying insights into profound questions consisting of the nature of the continuum. Moreover, the apparently paradoxical equality of "1 = 0.999..." reveals resolution in the realm of limitless decimals, highlighting the nuanced and captivating nature of mathematical principles when viewed via the lens of infinity. In embracing the countless, we uncover new avenues for exploration and discovery in the wealthy tapestry of mathematical idea.

References

Zaman, B.U. Amazing The Sum of Positive and Negative Prime Numbers are Equal. Authorea Preprints 2023. [CrossRef]
Zaman, B.U. Natural Number Infinite Formula and the Nexus of Fundamental Scientific Issues. Technical report, EasyChair, 2023. [CrossRef]
Zaman, B.U. New Prime Number Theory. Authorea Preprints 2023. [CrossRef]
Zaman, B.U. The Philosophical and Mathematical Implications of Division by 0 2023.
Zaman, B.U. Rethinking Number Theory, Prime Numbers as Finite Entities and the Topological Constraints on Division in a Real Number Line. Authorea Preprints 2023. [CrossRef]
Zaman, B.U. The Two Couriers Problem and Diverse Approaches to Division by Zero. Technical report, EasyChair, 2023.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

161

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Understanding the Boundless Potential of Infinite Numbers in Mathematics

Abstract

Keywords:

Subject:

1. Introduction

2. Infinity

2.1

2.1.1. Infinite Sets

2.1.2. The Curious Case of 1 = 0 . 999 …

3. Point, Length, Area, Volume

4. The Decimal and the +ve Integer

4.1. The Sum of ∞ Sequence

4.2. The Calculus

5. Infinite Degrees of Real Numbers

Degree 0:

Degree 1:

Degree 2:

Relationships:

5.1. B u d e e B 1

5.2. Real Number, Rational Number, Irrational Number

6. Error of Differential

7. Example of the infinite number

8. Infinite Expontial Infinity

9. Conclusions

References

MDPI Initiatives

Important Links

Subscribe

2.1.2. The Curious Case of $1 = 0.999 \dots$

5.1. $B u d e e B_{1}$