Covers of Finitely Generated Acts over Monoids

1. Introduction and Preliminaries

Let S be a monoid. By a right S-act we mean a non-empty set A together with an action $A\times S\to A$ given by $(a,s)\mapsto as$ such that for all $a\in A,s,t\in S,a1=a$ and $a\left(st\right)=\left(as\right)t.$ We refer the reader to [1,7,9] for all undefined terms concerning acts over monoids.

Mahmoudi and Renshaw introduced coessential epimorphisms and covers of cyclic S-acts in [9], gave a description of coessential epimorphisms in terms of congruence classes and a method of constructing covers from left unitary submonoids, and defined a strongly flat cover, Condition $\left(P\right)$ cover, projective cover and provided a necessary and sufficient condition for a cyclic S-act to have a strongly flat cover, Condition $\left(P\right)$ cover and projective cover. Now we restrict our attention to these notions.

Let S be a monoid. A right S-act B is called a cover of a right S-act A if there exists an epimorphism $f:B\to A$ such that for any proper subact C of B the restriction ${f|}_C$ is not an epimorphism. Moreover, we call an S-epimorphism $f:B\to A$ coessential in [9] if for each S-act C and each S-map $g:C\to B$, if $fg$ is an epimorphism, then g is an epimorphism. And we shall say that an act B together with an S-epimorphism $f:B\to A$ is a X-cover of A if B satisfies property X and f is coessential. It is easy to see that $f:B\to A$ is a cover of A if and only if it is a coessential epimorphism. Let $\mathcal{X}$ be a class of right S-acts. We assume that $\mathcal{X}$ is closed under isomorphisms, i.e., if $A\in \mathcal{X}$ and $B\cong A$, then $B\in \mathcal{X}$.

The concept of cover used in [5] is slightly different from that given above. (Enochs’ notion) For a right S-act A, an S-act $X\in \mathcal{X}$ is called an $\mathcal{X}$-cover of A if there is a homomorphism $\phi :X\to A$ such that

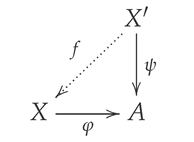
(1) for any homomorphism $\psi$: $X^{\prime }\to A$ with $X^{\prime }\in \mathcal{X}$, there is a homomorphism f: $X^{\prime }\to X$ with $\psi =\phi f$. In other words, the following diagram commutes;

(2) If an endomorphism $f:X\to X$ is such that $\phi =\phi f$, then f must be an automorphism.

If (1) holds, we call $\phi$: $X\to A$ an $\mathcal{X}$-precover.

Recall that an S-act $A_S$ is called strongly flat if the tensor functor $A\otimes -$ preserves pullbacks and equalizers. An S-act $A_S$ is said to satisfy Condition $\left(P\right)$ if for all $a,a^{\prime }\in A,s,s^{\prime }\in S$ such that $as=a^{\prime }{s}^{\prime }$, then there exist $a^{\prime \prime }\in A,u,v\in S$ with $a=a^{\prime \prime }u,a^{\prime }=a^{\prime \prime }v$ and $us=v{s}^{\prime }$. And recall that an S-act $A_S$ satisfies Condition $\left(E\right)$ if $as=a{s}^{\prime }$ for $a\in A,s,s^{\prime }\in S$, implies that there exist $a^{\prime }\in A,u\in S$ such that $a=a^{\prime }u$ and $us=u{s}^{\prime }$. It is well known that an act A is strongly flat if and only if it satisfies Condition $\left(P\right)$ and Condition $\left(E\right)$. We are principally concerned with finitely generated S-acts here and with the concepts of strongly flatness and Condition $\left(P\right)$ and in these cases there are useful characterizations.

A monoid S is called right reversible if for all $s,t\in S$, there exist $p,q\in S$ such that $ps=qt$. A monoid S is called left collapsible if for all $s,t\in S$, there exists $u\in S$ such that $us=ut$. A submonoid T of S is said to be left unitary if and only if whenever $t,ts\in T$ then $s\in T$.

Throughout this paper, S denotes a monoid, $A=\langle a_1,a_2,\cdots ,a_n\rangle ={\displaystyle \bigcup _{i=1}^n}{a}_{i}S$ is said that A is a n-generated right S-act and $I=\{1,2,\cdots ,n\}$. And ${\displaystyle \coprod _{i=1}^n}{a}_{i}S$ will denote a coproduct of cyclic subacts $a_{i}S$ for all $i\in I$. We shall deal exclusively with right S-acts and simply refer to them as S-acts. We shall also consistently write our maps on the left so that $gf$ means f followed by g.

The main results here are descriptions of finitely generated acts and coproducts in Section 2, and we provide a necessary and sufficient condition for a finitely generated S-act to have a cover in Section 3. Next in Section 4 we concentrate on strongly flat covers, Condition $\left(P\right)$ covers and projective covers, and the main conclusions extend some known results in [9]. In Section 5 we study Enochs’ notion of cover in the category of acts over monoids and focus on $\mathcal{X}$-precovers, where $\mathcal{X}$ is a class of S-acts closed under isomorphisms. Basic results on covers of acts over monoids can be found in [3,4,6,11].

2. Finite Generation and Coproducts

This section aims to describe the finite generation and coproduct of S-acts. A subset U of an S-act A is a generating set for A if for any $a\in A$, there exist $u\in U$, $s\in S$ such that $a=us$. In other words, U is a set of generating elements for $A_S$ if $\langle U\rangle :={\displaystyle \bigcup _{u\in U}^{ }}uS=A_S$, where $uS=\{us\mid s\in S\}$. An S-act A is said to be finitely generated (resp. cyclic) if it has a finite (resp. one-element) generating set. Further details may be found, for example, in [7].

Proposition 2.1. 

Let S be a monoid and $A={\displaystyle \bigcup _{i=1}^n}{A}_i$ be S-act, $A_i$ is a subact of A. For every $i\in I$, $A_i$ is finitely generated, then A is finitely generated.

Proof. 

Let $A_i=\langle X_i\rangle$. Then $A=\langle {\displaystyle \bigcup _{i=1}^n}{X}_i\rangle$. □

Proposition 2.2. 

Let S be a monoid and $A={\displaystyle \bigcup _{i=1}^n}{A}_i$ an S-act, $A_i$ are subacts of A for $i\in I$. And for $i\ne j\in I$, suppose that $A_i\bigcap A_j$ is either finitely generated or empty. If A is finitely generated, then $A_i$ for all $i\in I$, is finitely generated.

Proof. 

Let $I=\{1,2\}$, it is clear by Lemma 5.3 of [10]. If $I_1=\{1,2,\cdots ,n-1\}$ the assertion is hold, that is, for $i\ne j\in I_1$, $A_i\bigcap A_j$ is either finitely generated or empty, if A is finitely generated, then $A_i,i\in I$, is finitely generated. Assume that $I=\{1,2,\cdots ,n\}=I_1\bigcup \left\{n\right\}$. If $A_i\bigcap A_j=\varnothing$, $i\ne j\in I$, obviously. Otherwise, take $j=n$, for $i\in I_1$, $A_i\bigcap A_n$ is finitely generated, by Proposition 2.1, $\left({\displaystyle \bigcup _{i\in I_1}^{ }}{A}_i\right)\bigcap A_n$ is finitely generated. Since $A=\left({\displaystyle \bigcup _{i\in I_1}^{ }}{A}_i\right)\bigcup A_n$ is finitely generated, ${\displaystyle \bigcup _{i\in I_1}^{ }}{A}_i$ and $A_n$ are finitely generated. By assumption, $A_i$, $i\in I_1$, is finitely generated. Therefore, for all $i\in I$, $A_i$ is finitely generated. □

Corollary 2.1. 

Let S be a monoid. S-act $A={\displaystyle \coprod _{i=1}^n}{A}_i$ is finitely generated if and only if S-act $A_i$ is finitely generated.

It is important for monoids to consider the covers of finitely generated acts. Now we first aim to investigate the cover of coproducts of acts.

Proposition 2.3. 

Suppose that $f_i:B_i\to A_i,i\in I$ are a family of S-morphisms, where $I=\{1,2,\cdots ,n\}$. Let $B={\displaystyle \coprod _{i=1}^n}{B}_i$, $A={\displaystyle \coprod _{i=1}^n}{A}_i$, and $f:B\to A$ satisfies ${f|}_{B_i}=f_i$. Then $f:B\to A$ is a cover of A if and only if $f_i:B_i\to A_i$ are covers of $A_i$ for all $i\in I$.

Proof. Sufficiency. Since $f_i:B_i\to A_i$, $i\in I$ are a family of epimorphisms, it is clear that $f:B\to A$ is epimorphic. Assume that f is not coessential, that is, there exists a proper subact $\overline{B}$ of B such that ${f|}_{\overline{B}}$ is epimorphic. Therefore, there is $j\in I$ such that $B_j^{\prime }=B_j\bigcap \overline{B}$ is a proper subact of $B_j$. Thus, $f_j{|}_{B_j^{\prime }}$ is not epimorphism since $f_j:B_j\to A_j$ is a coessential epimorphism, so there exists $a_j\in A_j$ such that $f_j\left(b_j^{\prime }\right)\ne a_j$ for all $b_j^{\prime }\in B_j^{\prime }$. However, by the surjectivity of ${f|}_{\overline{B}}$, we obtain that $f\left(\overline{b}\right)=a_j$ for some $\overline{b}\in \overline{B}$. Thus there exists $k\in I$ such that $\overline{b}\in B_k$, $k\ne j$. Then $a_j=f\left(\overline{b}\right)\in A_k$ which contradicts $a_j\in A_j$.

Necessity. Let $f:{\displaystyle \coprod _{i=1}^n}{B}_i\to {\displaystyle \coprod _{i=1}^n}{A}_i$ be a coessential epimorphism. Then we obtain that $f_i:B_i\to A_i$ are a family of epimorphisms for all $i\in I$. To show that $f_i$ are coessential for all $i\in I$, assume that there exists a map $f_j:B_j\to A_j$ such that $f_j$ is not coessential, where $j\in I$. Then $f_j{|}_{C_j}:C_j\to A_j$ is an epimorphism for some proper subact $C_j$ of $B_j$. Thus ${f|}_{\left({\displaystyle \coprod _{i\ne j}^{ }}{B}_i\right){\displaystyle \coprod _{ }^{ }}{C}_j}:\left({\displaystyle \coprod _{i\ne j}^{ }}{B}_i\right){\displaystyle \coprod _{ }^{ }}{C}_j\to {\displaystyle \coprod _{i=1}^n}{A}_i$ is an epimorphism. But $\left({\displaystyle \coprod _{i\ne j}^{ }}{B}_i\right){\displaystyle \coprod _{ }^{ }}{C}_j$ is a proper subact of ${\displaystyle \coprod _{i=1}^n}{B}_i$ and by assumption ${f|}_{\left({\displaystyle \coprod _{i\ne j}^{ }}{B}_i\right){\displaystyle \coprod _{ }^{ }}{C}_j}$ is not epimorphic, a contradiction. So $f_i:B_i\to A_i$ are a family of coessential epimorphisms for all $i\in I$. □

Now we concentrate on covers of finitely generated of S-acts and we begin with some notations. For an element a of a right S-act A we denote by $R\left(a\right)$ the set $\{s\in S:as=a\}$, the submonoid of right identities of a, and it is clear that $R\left(a\right)$ is a left unitary submonoid of S. We denote by $r(a,b)$ the set $\left\{\right(s,t)\in S\times S:as=bt\}$. In particular, $r\left(a\right)=r(a,a)=\left\{\right(s,t)\in S\times S:as=at\}$, the right annihilator congruence ${\rho }_a$ of a. It is clear that $aS$ is isomorphic to $S/{\rho }_a$ under the S-isomorphism $as\mapsto \left[s\right]$, where $\left[s\right]$ denote the class of $s\in S$ with respect to an equivalence relation $\rho$.

Lemma 2.1 

([7], Proporsition III.13.14). Let $A_S$ be a finitely generated S-act. If $A_S$ satisfies Condition $\left(P\right)$, then $A_S$ is a coproduct of cyclic subacts.

Let S be a monoid and $A={\displaystyle \coprod _{i=1}^n}{A}_i$, where $A_i,i\in I$ are right S-acts. Then A is strongly flat (resp. satisfies Condition $\left(P\right)$) if and only if $A_i$ is strongly flat (resp. satisfies Condition $\left(P\right)$) for every $i\in I$. The following results turn out very helpful in the following section.

Proposition 2.4. 

If the finitely generated S-act $A=\langle a_1,\cdots ,a_n\rangle$ is strongly flat(resp. satisfis Conditon (P)), then $R\left(a_i\right)$ is a left collapsible(resp. right reversible) submonoid of S.

Proof. 

Let A satisfy Conditon $\left(P\right)$. By Lemma 2.1, $a_{i}S$ satisfies Conditon $\left(P\right)$ for $i\in I$. Thus $R\left(a_i\right)$ is right reversible. And in a similar way we obtain that $R\left(a_i\right)$ is a left collapsible submonoid of S if A is strongly flat. □

Proposition 2.5. 

Let T be a submonoid of a monoid S and A a right S-act, $a\in A$. If $r\left(a\right)=T\times T$, then $T=R\left(a\right)$.

Proof. 

Since $r\left(a\right)=\left\{\right(s,t)\in S\times S|as=at\}=T\times T$, for any $t\in T$ and $1\in T$, then $(1,t)\in T\times T=r\left(a\right)$. Thus $a=at$, that is, $t\in R\left(a\right)$. Therefore $T\subseteq R\left(a\right)$. It is clear that $R\left(a\right)\subseteq T$. □

Lemma 2.2. 

Let S be a monoid and P a left collapsible(resp. right reversible) submonoid of S, $A=\langle a_1,\cdots ,a_n\rangle$ is n-generated. If $r\left(a_i\right)=P\times P$, then $R\left(a_i\right)$ is left collapsible(resp. right reversible) and ${\displaystyle \coprod _{i=1}^n}{a}_{i}S$ is strongly flat(resp. satisfies Condition (P)).

Proof. 

Since $r\left(a_i\right)=P\times P$, $P=R\left(a_i\right)$ by Proposition 2.5 and so $R\left(a_i\right)$ is left collapsible(resp. right reversible). Notice that in either case, P is right reversible and so defined by $bs=bt$ if and only if there exists $p,q\in P$ with $ps=qt$. Notice that $b=a_i$. In fact, if $a_{i}s=a_{i}t$ then there exist $p,q\in P$ with $ps=qt$ and so $bs=bt$. Conversely, if $bs=bt$, then there are $p,q\in P$ with $ps=qt$ and $a_i=a_{i}p=a_{i}q$ from $P\subseteq R\left(a_i\right)$. So $a_{i}s=a_{i}ps=a_{i}qt=a_{i}t$ and hence $b=a_i$. It is clear that $a_{i}S$ satisfies Condition $\left(P\right)$. Then ${\displaystyle \coprod _{i=1}^n}{a}_{i}S$ satisfies Condition $\left(P\right)$. If in addition P is left collapsible, then ${\displaystyle \coprod _{i=1}^n}{a}_{i}S$ is strongly flat. □

It is clear that any cover of a cyclic right S-act is cyclic by Lemma 2.3 of [9]. The following theorem concerns the covers of n-generated right S-acts.

Theorem 2.1. 

Let $f:B_S\to A_S$ be a cover of $A_S$. Then $B_S$ is n-generated if and only if $A_S$ is n-generated.

Proof. Necessity. Assume that B is n-generated, $\overline{B}=\{b_1,b_2,\cdots ,b_n\}$ is a generating set of B. Since $f:B\to A$ is an epimorphism, A is generated by n elements. Now we are ready to prove n is the smallest. Suppose that $A=\langle y_1,\cdots ,y_k\rangle$, $k<n$. Then $f\left(z_i\right)=y_i$, $i=1,\cdots ,k$. Therefore $B={\displaystyle \bigcup _{i=1}^k}{z}_{i}S$, which contradicts that B is n-generated. Thus, A is n-generated.

Sufficiency. Suppose $A=\langle a_1,\cdots ,a_n\rangle$. Since f is an epimorphism, there exists $b_i\in B$ such that $f\left(b_i\right)=a_i,i=1,2,\cdots ,n.$ Take $C={\displaystyle \bigcup _{i=1}^n}{b}_{i}S$, clearly $C\subseteq B$ and $f\left(C\right)=A$. By the definition of cover, we have $C=B$. Therefore B is generated by n elements. Now we are ready to prove a result that n is the smallest. If $B=\langle x_1,\cdots ,x_k\rangle ,k<n$, and $f\left(B\right)=A$, we have A is generated by $f\left(x_i\right),i=1,2,\cdots ,k$, a contradiction. □

Let $A={\displaystyle \bigcup _{i=1}^n}{A}_i$ be n-generated and $B={\displaystyle \coprod _{i=1}^n}{B}_i$. The following Proposition 2.6 shows that $f:B\to A$ is a cover of A implies that $f_i:B_i\to A_i,i\in I$, are a family of covers of $A_i$.

Proposition 2.6. 

Let $A={\displaystyle \bigcup _{i=1}^n}{A}_i,B={\displaystyle \coprod _{i=1}^n}{B}_i$. Let $f_i:B_i\to A_i,i\in I$, be a family of S-morphisms, and $f:B\to A$ satisfies ${f|}_{B_i}=f_i$. Then $f:B\to A$ is a cover of A implies $f_i:B_i\to A_i,i\in I$, are a family of covers of $A_i$.

Proof. 

If $A_i\bigcap A_j=\varnothing$ for any $i,j\in I$, it is clear by Proposition 2.3. Otherwise, suppose $a\in A_i\bigcap A_j,i\ne j,i,j\in I$. Since f is an epimorphism, for $a\in A_i$, there exists $b\in B_i$ such that $f\left(b\right)=f_i\left(b\right)=a$. If $a\in A_j$, we have $f\left(b\right)=f_j\left(b\right)=a$ for some $b\in B_j$. But $B_i\bigcap B_j=\varnothing$, a contradiction. Therefore $A_i\bigcap A_j=\varnothing$, we obtain that $A={\displaystyle \coprod _{i=1}^n}{A}_i$. By Proposition 2.3, $f:B\to A$ is a cover of A implies that $f_i:B_i\to A_i$ are covers of $A_i$. □

Coversely, if B is n-generated and A is a disjoint union of n subacts, the argument always holds in Proposition 2.7.

Proposition 2.7. 

Suppose that $B={\displaystyle \bigcup _{i=1}^n}{B}_i$, $A={\displaystyle \coprod _{i=1}^n}{A}_i$, $f_i:B_i\to A_i$, $i\in I$ are a family of S-morphisms, and $f:B\to A$ satisfies ${f|}_{B_i}=f_i$. Then $f:B\to A$ is a cover of A if and only if $f_i:B_i\to A_i$ are a family of covers of $A_i$ for every $i\in I$.

Proof. 

Let $f:B\to A$ be a cover of A. If there exist $i,j\in I$ such that $B_i\bigcap B_j\ne \varnothing$, that is, $f\left(b_i\right)=f\left(b_j\right)=a$, where $b_i\in B_i,b_j\in B_j,a\in A$, then ${f|}_{(B_i\setminus \left\{b_i\right\})\bigcup \left({\displaystyle \bigcup _{k\ne i}^{ }}{B}_k\right)}:(B_i\setminus \left\{b_i\right\})\bigcup \left({\displaystyle \bigcup _{k\ne i}^{ }}{B}_k\right)\to {\displaystyle \coprod _{i=1}^n}{A}_i$ is an epimorphism, a contradiction. So f is one-to-one. Assume $b\in B_i\bigcap B_j$. Then $f\left(b\right)=f_i\left(b\right)\in A_i$, and $f\left(b\right)=f_j\left(b\right)\in A_j$ which contradicts $A_i\bigcap A_j=\varnothing$. Hence $B_i\bigcap B_j=\varnothing$ or the element in $B_i\bigcap B_j$ has no image under the action of f. If the latter, then ${f|}_{B\setminus (B_i\bigcap B_j)}:B\setminus (B_i\bigcap B_j)\to A$ is an epimorphism, a contradiction. Therefore, $B={\displaystyle \coprod _{i=1}^n}{B}_i$. Conversely, let $f_i:B_i\to A_i$ be a family of covers of $A_i$, we obtain the same result $B={\displaystyle \coprod _{i=1}^n}{B}_i$. By Proposition 2.3, $f:B\to A$ is a cover of A if and only if $f_i:B_i\to A_i$ are a family of covers of $A_i$. □

Remark 2.1. 

From the above several propositions it is shown that if A and B are the union(coproduct) of nS-acts $A_i$ and $B_i$, respectively, then $f:B\to A$ is a cover of A if and only if $f_i:B_i\to A_i$ are a family of covers of $A_i$ for $i\in \{1,2,\cdots ,n\}$.

Let S be a monoid and X an S-act. We say that X is Noetherian if every congruence on X is finitely generated, and we say that a monoid S is Noetherian if it is Noetherian as an S-act over itself.

Proposition 2.8. 

Let S be a Noetherian monoid and $f:B\to A$ be a cover. Then A is Noetherian if and only if B is Noetherian.

Proof. 

Let $f:B\to A$ be a cover of A. If B is Noetherian. By Lemma 7.6 of [2], then B is finitely generated, and so is A by Theorem 2.1. All finitely generated S-acts over a Noetherian monoid are Noetherian, thus A is Noetherian. Coversely, it is obvious. □

3. Covers of Finitely Generated Acts

Let S be a monoid and $\rho ,\sigma$ right congruences on S. In Mahmoudi and Renshaw [9], it is proved that a cyclic act $S/\rho$ has a cover $S/\sigma$ if and only if $\sigma \subseteq \rho$ and for all $u\in {\left[1\right]}_{\rho }$, $uS\cap {\left[1\right]}_{\sigma }\ne \varnothing$. The next there propositions are needed to get the result.

Proposition 3.1. 

Let S be a monoid. Then $A^{\prime }=\langle a_1^{\prime },a_2^{\prime },\cdots ,a_n^{\prime }\rangle$ is isomorphic to a finitely generated subact of $A=\langle a_1,a_2,\cdots ,a_n\rangle$ if and only if there exist $u_i,u_p\in S$, such that $r(a_i^{\prime },a_p^{\prime })=r(a_i{u}_i,a_p{u}_p)$ for any $i,p\in \{1,2,\cdots ,n\}$.

Proof. 

Let $f:A^{\prime }\to A$ be an S-monomorphism and $I=\{1,2,\cdots ,n\}$. For $a_i^{\prime }\in A^{\prime }$, there is $u_j\in S$ such that $f\left(a_i^{\prime }\right)=a_j{u}_j\in a_{j}S\subseteq A$, $i,j\in I$. Since f is a monomorphism, then $j=i$. Thus, we have $f\left(a_i^{\prime }\right)=a_i{u}_i$ for some $a_i\in \{a_1,\cdots ,a_n\}$ and $u_i\in S$. And so $f\left(a_i^{\prime }s\right)=a_i{u}_{i}s$ for any $s\in S$. Let $a_i^{\prime }s=a_p^{\prime }t$, $i,p\in I,s,t\in S$. Then $a_i{u}_{i}s=a_p{u}_{p}t$. In addition, suppose that $a_i{u}_{i}s=a_p{u}_{p}t$, and we have $a_i^{\prime }s=a_p^{\prime }t$ since f is monomorphic. Therefore $r(a_i^{\prime },a_p^{\prime })=r(a_i{u}_i,a_p{u}_p)$.

Conversely, the mapping $f:A^{\prime }\to A$ defined by $a_i^{\prime }s\mapsto a_i{u}_{i}s$ is well-defined and f is an S-monomorphism. □

Lemma 3.1. 

Let S be a monoid and $u_i\in S$. Consider the S-monomorphism $f:\langle a_1^{\prime },a_2^{\prime },\cdots ,a_n^{\prime }\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ given by $f\left(a_i^{\prime }s\right)=a_i{u}_{i}s$, $s\in S$. Then f is onto if and only if $u_{i}S\bigcap R\left(a_i\right)\ne \varnothing$ for every $i\in I$.

Proof. 

Since f is an S-epimorphism. For any $a_i\in \{a_1,\cdots ,a_n\}$, there exist $a_p^{\prime }\in \{a_1^{\prime },\cdots ,a_n^{\prime }\}$ and $m\in S$ such that $f\left(a_p^{\prime }m\right)=a_i$. And since $f\left(a_p^{\prime }m\right)=a_p{u}_{p}m$, it follows that $a_i=a_p{u}_{p}m\in a_{p}S$, namely $a_{i}S\subseteq a_{p}S$, a contradiction. Thus $p=i$ and so $a_i=a_i{u}_{i}m$, hence $u_{i}S\bigcap R\left(a_i\right)\ne \varnothing$.

Conversely, since $u_{i}S\bigcap R\left(a_i\right)\ne \varnothing$, there exists $s\in S$ such that $a_i=a_i{u}_{i}s$ for every $i\in I$. So $f\left(a_i^{\prime }s\right)=a_i{u}_{i}s=a_i$. It is easy to see that f is an epimorphism. □

Lemma 3.2. 

Let S be a monoid, $B=\langle b_1,b_2,\cdots ,b_n\rangle$ and $A=\langle a_1,a_2,\cdots ,a_n\rangle$. If $f:B\to A$ is a coessential epimorphism then there exists $u_i\in S$ such that $g:B^{\prime }\to B$, $b_i^{\prime }s\mapsto b_i{u}_{i}s$, is isomorphic, where $B^{\prime }=\langle b_1^{\prime },b_2^{\prime },\cdots ,b_n^{\prime }\rangle$. And $f^{\prime }:B^{\prime }\to A$ given by $f\left(b_i^{\prime }s\right)=a_{i}s$ is a coessential S-epimorphism. In particular, $r(b_i^{\prime },b_p^{\prime })\subseteq r(a_i,a_p)$.

Proof. 

Since $f:B\to A$ is a coessential epimorphism, it follows that A and B are n-generated. For any $a_i\in \{a_1,\cdots ,a_n\}$, there exist $b_i\in \{b_1,\cdots ,b_n\}$ and $u_i\in S$ such that $f\left(b_i{u}_i\right)=a_i$. Suppose that $g:B^{\prime }\to B$ given by $f\left(b_i^{\prime }s\right)=b_i{u}_{i}s$ is a monomorphism whose composite with f is clearly onto. Since B is a cover of A, $B^{\prime }\cong B$ and so $f^{\prime }:B^{\prime }\to A$, $b_i^{\prime }s\mapsto a_{i}s$, is a coessential S-epimorphism. It then follows that $r(b_i^{\prime },b_p^{\prime })\subseteq r(a_i,a_p)$. □

We now present a fundamental theorem that yields the main result of this section.

Theorem 3.1. 

Let S be a monoid and $A=\langle a_1,a_2,\cdots ,a_n\rangle$ a n-generated S-act. The map $f:\langle b_1,b_2,\cdots ,b_n\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ given by $b_{i}s\mapsto a_{i}s$ is a coessential epimorphism if and only if $r(b_i,b_j)\subseteq r(a_i,a_j)$, $i,j\in I$, and for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\left(b_i\right)\ne \varnothing$.

Proof. 

Let $b_{i}s=b_{j}t$ for $b_i,b_j\in \{b_1,b_2,\cdots ,b_n\}$, $s,t\in S$ and $i,j\in I$. Then $a_{i}s=a_{j}t$ because f is well-defined. Hence $r(b_i,b_j)\subseteq r(a_i,a_j)$. For $a_i\in \{a_1,a_2,\cdots ,a_n\}$, there exist $b_j\in \{b_1,\cdots ,b_n\}$ and $u_j\in S$ such that $f\left(b_j{u}_j\right)=a_i\in a_{i}S$, but $f\left(b_j{u}_j\right)=a_j{u}_j\in a_{j}S$, we obtain $a_{i}S\subseteq a_{j}S$, a contradiction. Therefore $j=i$ and so $f\left(b_i{u}_i\right)=a_i$. Since $f:\langle b_1,b_2,\cdots ,b_n\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ is a coessential epimorphism, by Lemma 3.2, there is a subact $\langle b_1^{\prime },b_2^{\prime },\cdots ,b_n^{\prime }\rangle$ such that $\langle b_1^{\prime },b_2^{\prime },\cdots ,b_n^{\prime }\rangle \cong \langle b_1,b_2,\cdots ,b_n\rangle$ and ${f|}_{\langle b_1^{\prime },b_2^{\prime },\cdots ,b_n^{\prime }\rangle }:\langle b_1^{\prime },b_2^{\prime },\cdots ,b_n^{\prime }\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ is a coessential epimorphism. So we have $b_i=b_i^{\prime }m$ for some $m\in S$. And since $g:\langle b_1^{\prime },b_2^{\prime },\cdots ,b_n^{\prime }\rangle \to \langle b_1,b_2,\cdots ,b_n\rangle$ is isomorphic by Lemma 3.2, it follows that $b_i{u}_{i}m=b_i$, thus $u_{i}S\bigcap R\left(b_i\right)\ne \varnothing$ as required.

Conversely, if the given conditions hold, then clearly f is well-defined. Let B be an S-subact of $\langle b_1,b_2,\cdots ,b_n\rangle$ and suppose that ${f|}_B$ is onto. Then for $a_i\in \{a_1,a_2,\cdots ,a_n\}$, there exists $b_p{u}_p\in B$ such that $f\left(b_p{u}_p\right)=a_i$ and we obtain $p=i$, so $f\left(b_i{u}_i\right)=a_i$. However $f\left(b_i{u}_i\right)=a_i{u}_i$, and hence $u_i\in R\left(a_i\right)$. By assumption, there exists $m\in S$ such that $b_i=b_i{u}_{i}m$, in the sense that $b_{i}s=\left(b_i{u}_{i}m\right)s=\left(b_i{u}_i\right)\left(ms\right)\in BS\subseteq B$ for an arbitrary $s\in S$. So $\langle b_1,b_2,\cdots ,b_n\rangle \subseteq B$, that is, $\langle b_1,b_2,\cdots ,b_n\rangle =B$, and f is a cover. □

If $n=1$, we can easily obtain the Theorem 2.7 in [9].

Theorem 3.2. 

Let S be a monoid and $A=\langle a_1,a_2,\cdots ,a_n\rangle$ a n-generated S-act. If the natural map $f:{\displaystyle \bigcup _{i=1}^n}{S}_i\to A$ is a coessential epimorphism, where $S_i\cong S$. Then $R\left(a_i\right),i\in I$, is a subgroup of S.

Proof. 

Since $f:{\displaystyle \bigcup _{i=1}^n}{S}_i\to {\displaystyle \bigcup _{i=1}^n}{a}_{i}S$ is a coessential epimorphism. Then for an arbitrary element $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\left(1\right)\ne \varnothing$. And $R\left(1\right)=\{t\in S|1t=1\}=\{1\}$. We can verify that $u_i{s}_i=1$ for $s_i\in S$. Moreover, $a_i=a_i{u}_i$, it is easy to see that $a_i{s}_i=a_i{u}_i{s}_i=a_i$ and so $s_i\in R\left(a_i\right)$. Consequently, $R\left(a_i\right)$ is a subgroup of S. □

Proposition 3.2. 

Let S be a monoid. Then the map $f:{\displaystyle \bigcup _{i=1}^n}{S}_i\to {\displaystyle \bigcup _{i=1}^n}{a}_{i}S$ is a coessential epimorphism, where $S_i\cong S$, if and only if $R\left(a_i\right),i\in I$, is a subgroup of S and $r(1_i,1_p)\subseteq r(a_i,a_p)$ for $i,p\in I$.

Proof. 

Let $f:{\displaystyle \bigcup _{i=1}^n}{S}_i\to {\displaystyle \bigcup _{i=1}^n}{a}_{i}S$, $s\mapsto a_{i}s$, be a coessential epimorphism. Let $1_{i}s=1_{p}t$ for $s,t\in S$ and $i,p\in I$. We have $a_{i}s=a_{i}s$ since f is well-defined. By Theorem 3.2, $R\left(a_i\right)$ is a subgroup of S.

Conversely, suppose that $R\left(a_i\right)$ is a subgroup of S. For any $u_i\in R\left(a_i\right)$, there exists $u_i^{-1}\in R\left(a_i\right)$ such that $u_i{u}_i^{-1}=\left\{1\right\}$. Thus $u_{i}S\bigcap R\left(1\right)\ne \varnothing$. In addition, since $r(1_i,1_p)\subseteq r(a_i,a_p)$ for $i,p\in I$, we can verify that f is a coessential epimorphism by Theorem 3.1. □

Proposition 3.3. 

Let S be a right simple semigroup with a 1 adjoined and $B=\langle b_1,b_2,\cdots ,b_n\rangle$, $A=\langle a_1,a_2,\cdots ,a_n\rangle$. If $r(b_i,b_p)\subseteq r(a_i,a_p)$ for $i,p\in I$ and $R\left(b_i\right)\ne \left\{1\right\}$. Then $f:B\to A$ given by $b_{i}s\mapsto a_{i}s$ is a coessential epimorphism.

Proof. 

Since $R\left(b_i\right)\ne \left\{1\right\}$, we can verify that $R\left(b_i\right)\subseteq S\setminus \left\{1\right\}=T$, where T is a right simple semigroup. So $tT=T$ for every $t\in T$. Then for $u_i\in R\left(a_i\right)$, $u_{i}T\bigcap R\left(b_i\right)=T\bigcap R\left(b_i\right)=R\left(b_i\right)\ne \varnothing$. It is easy to see that f is a coessential epimorphism since $r(b_i,b_p)\subseteq r(a_i,a_p)$. □

Remark 3.1. 

It follows from the above that covers of finitely generated S-acts need not be unique. If S is a group then every n-generated S-act has ${\displaystyle \bigcup _{i=1}^n}{S}_i$ as a cover, where $S_i\cong S$. And so proper n-generated S-acts do not have unique covers. In fact, if the map $\langle b_1,b_2,\cdots ,b_n\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ is onto, then $\langle b_1,b_2,\cdots ,b_n\rangle$ is trivially a cover of $\langle a_1,a_2,\cdots ,a_n\rangle$.

4. $\mathbf{N}$-Generated Flat Covers

In Mahmoudi and Renshaw [9] it is proved that an equivalent characterization of a cyclic act having flat properties covers, such as strongly flat, Condition $\left(P\right)$, projective. The next theorems are to investigate flatness covers of n-generated S-acts.

Theorem 4.1. 

Let S be a monoid. Then the n-generated S-act $A=\langle a_1,a_2,\cdots ,a_n\rangle$ has a strongly flat cover B if and only if $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ and $R\left(a_i\right)$ contains a left collapsible submonoid R such that for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$.

Proof. 

Suppose that A has a strongly flat cover B. By Theorem 2.1, $B=\langle b_1,b_2,\cdots ,$$b_n\rangle$. Then by Theorem 3.1 we can assume that $R=R\left(b_i\right)\subseteq R\left(a_i\right)$ and that for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$. Moreover, since B is strongly flat, $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ by Lemma 2.1 and R is left collapsible by Proposition 2.4.

Conversely, suppose that $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ and R is a left collapsible submonoid of $R\left(a_i\right)$ such that for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$. Define $r\left(b_i\right)=R\times R$, then $R\subseteq R\left(b_i\right)$ and further $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ is strongly flat by Lemma 2.2. Define a map $f:\langle b_1,b_2,\cdots ,b_n\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ given by $b_{i}s\mapsto a_{i}s$ and note that f is a well-defined S-epimorphism. To see this, first notice that if f is well-defined, then it is clearly an S-map which is onto. Since $R\subseteq R\left(a_i\right)$, it is easy to see that $R\times R\subseteq r\left(a_i\right)$ but $r\left(b_i\right)=R\times R$ and hence $r\left(b_i\right)\subseteq r\left(a_i\right)$. And $r(b_i,b_j)\subseteq r(a_i,a_j)$ for any $i\ne j,i,j\in I$, is not necessary to consider because $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$. Further, for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$ so f is coessential by Theorem 3.1. □

We can easily obtain the Theorem 3.2 of [9] if $n=1$ in Theorem 4.1.

Example 4.1. 

Let S be a left cancellative monoid. Then n-generated S-act $A=\langle a_1,a_2,\cdots ,a_n\rangle$ has a strongly flat cover if and only if $R\left(a_i\right)$, $i\in I$, is a subgroup of S and in this case ${\displaystyle \bigcup _{i=1}^n}{S}_i$ is a strongly flat cover of A, where $S_i\cong S$. First notice that the only strongly flat cover of a n-generated S-act(assuming that it has one) is then ${\displaystyle \bigcup _{i=1}^n}S$. Notice also that not all finitely generated S-acts need have a strongly flat cover(see, for example, Remark 3.6 in [9]).

Theorem 4.2. 

Let S be a monoid. Then the n-generated S-act $A=\langle a_1,a_2,\cdots ,a_n\rangle$ has a $\left(P\right)$-cover B if and only if $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ and $R\left(a_i\right)$ contains a right reversible submonoid R such that for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$.

Proof. 

Suppose that A has a $\left(P\right)$-cover, $B=\langle b_1,b_2,\cdots ,b_n\rangle$. Then by Theorem 3.1 we can assume that $R=R\left(b_i\right)\subseteq R\left(a_i\right)$ and that for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$. Moreover, since B satisfies Condition $\left(P\right)$, $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ by Lemma 2.1 and R is right reversible by Proposition 2.4.

Conversely, suppose that $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ and R is a right reversible submonoid of $R\left(a_i\right)$ such that for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$. Define $r\left(b_i\right)=R\times R$, then $R\subseteq R\left(b_i\right)$ and further $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$ satisfies Condition $\left(P\right)$ by Lemma 2.2. Define a map $f:\langle b_1,b_2,\cdots ,b_n\rangle \to \langle a_1,a_2,\cdots ,a_n\rangle$ given by $b_{i}s\mapsto a_{i}s$ and note that f is a well-defined S-epimorphism. Since $R\subseteq R\left(a_i\right)$, it follows that $R\times R\subseteq r\left(a_i\right)$ but $r\left(b_i\right)=R\times R$ and hence $r\left(b_i\right)\subseteq r\left(a_i\right)$. And $r(b_i,b_j)\subseteq r(a_i,a_j)$ for any $i\ne j,i,j\in I$, is not necessary to consider because $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S$. Further, since for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$, then f is coessential by Theorem 3.1. □

Similarly, if $n=1$, we can easily obtain the Theorem 4.2 of [9].

Proposition 4.1. 

Let S be a group. Then every n-generated S-act $A(A\ne S)$ has at least two $\left(P\right)$-covers but only has a unique strongly flat cover.

Proof. 

Let $A=\langle a_1,a_2,\cdots ,a_n\rangle$. Since S is a group, then all S-acts satisfy condition $\left(P\right)$ and so in particular A is a $\left(P\right)$-cover of itself. But $R\left(a_i\right),i\in I$, is a subgroup of S, thus ${\displaystyle \bigcup _{i=1}^n}{S}_i$ is a cover of A by Proposition 3.2, where $S_i\cong S$. While the latter part follows immediately from the Example 4.1. □

Lemma 4.1 

([8], Corollary 3.8). A right S-act $P_S$ is projective if and only if $P={\displaystyle \coprod _{i\in I}^{ }}{P}_i$ where $P_i\cong e_{i}S$ for idempotents $e_i\in S$, $i\in I$.

Theorem 4.3. 

Let S be a monoid and $A=\langle a_1,a_2,\cdots ,a_n\rangle$ a n-generated S-act. Then the following are equivalent:

$\left(1\right)$A has a projective cover;

$\left(2\right)$ There exits a submonoid R of $R\left(a_i\right)$ which has a left zero element and for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$.

$\left(3\right)$ The submonoid $R\left(a_i\right)$ of S has a minimal right ideal generated by an idempotent.

Proof. (1)⇒(2) Let $B=\langle b_1,b_2,\cdots ,b_n\rangle$ be a projective cover of A. Then by Theorem 3.1, take $R=R\left(b_i\right)$, for all $u_i\in R\left(a_i\right)$, $u_{i}S\bigcap R\ne \varnothing$. Moreover by Lemma 4.1 there exists $e_i\in E\left(S\right)$ with $B={\displaystyle \coprod _{i=1}^n}{b}_{i}S\cong {\displaystyle \coprod _{i=1}^n}{e}_{i}S$ and thus obviously $e_i\in R\left(e_i\right)$ and $R\left(e_i\right)=R\left(b_i\right)$. If $u_i\in R\left(e_i\right)$, then $e_i{u}_i=e_i$ and so $e_i$ is a left zero element of $R\left(b_i\right)$.

(2)⇒(3) Assume that $z\in R$ is a left zero element of R and consider the right ideal $zR\left(a_i\right)$ of $R\left(a_i\right)$. If this is not minimal, then there exists $u_i\in R\left(a_i\right)$ with $zuR\left(a_i\right)\ne zR\left(a_i\right)$. By assumption there exists $s\in S$ with $u_{i}s\in R\subseteq R\left(a_i\right)$, and since $R\left(a_i\right)$ is a left unitary submonoid, then $s\in R\left(a_i\right)$. Since z is a left zero element of R, $z=z\left(u_{i}s\right)\in z{u}_{i}R\left(a_i\right)$ and so $zR\left(a_i\right)=z{u}_{i}R\left(a_i\right)$, which is a contradiction. Therefore the submonoid $zR\left(a_i\right)$ of $zR\left(a_i\right)$ is a minimal right ideal generated by an idempotent.

(3)⇒(1) Suppose that $e_i\in E\left(S\right)$ with $e_{i}R\left(a_i\right)$ is a minimal right ideal of $R\left(a_i\right)$. Clearly ${\displaystyle \coprod _{i=1}^n}{e}_{i}S$ is projective. Define the map $f:{\displaystyle \coprod _{i=1}^n}{e}_{i}S\to {\displaystyle \bigcup _{i=1}^n}{a}_{i}S$ by $f\left(e_{i}s\right)=a_{i}s$. Then f is well defined since if $e_{i}s=e_{j}t$, $i,j\in I$ and $s,t\in S$, then $i=j$ and $a_{i}s=a_i{e}_{i}s=a_i{e}_{i}t=a_{i}t$. In addition, it is also coessential since if $u_i\in R\left(a_i\right)$, then $e_i{u}_{i}R\left(a_i\right)=e_{i}R\left(a_i\right)$ by the minimality of $e_{i}R\left(a_i\right)$, and so $e_i=e_i{u}_{i}t$ for some $t\in R\left(a_i\right)$. But then $u_{i}t\in R\left(e_i\right)$ and so $u_{i}S\bigcap R\left(e_i\right)\ne \varnothing$. Hence the result follows by Theorem 3.1. □

If $n=1$ in Theorem 4.3, we can get the Theorem 5.2 in [9].

5. $\mathcal{X}$-Precovers

In this section we study Enochs’ notion of cover [1] in the category of acts over monoids and focus on $\mathcal{X}$-precovers and $\mathcal{X}$-covers, where $\mathcal{X}$ will be a class of S-acts closed under isomorphisms. For example, we denote the class of all projective S-acts by $\mathcal{P}$. Clearly the concept of cover by Enochs’ is slightly different from that the coessential cover.

Proposition 5.1. 

Let S be a monoid and let $\mathcal{X}$ satisfy the property that $X\in \mathcal{X}\iff X\otimes M\in \mathcal{X}$ for ${ }_S{M}_S\in S$-act-S. If A has an $\mathcal{X}$-precover, then $A\otimes M$ has an $\mathcal{X}$-precover.

Proof. 

Let $g:C\to A$ be $\mathcal{X}$-precover of A. Define $g\otimes 1:C\otimes M\to A\otimes M$ to be the obvious induced map. Let $X\otimes M\in \mathcal{X}$ and let $h\otimes 1:X\otimes M\to A\otimes M$. Now, by the hypothesis, $X\in \mathcal{X}$, so, since C is an $\mathcal{X}$-precover of A, there exists $f\in$ Hom${ }_S(X,C)$ such that $gf=h$. So define $f\otimes 1:X\otimes M\to C\otimes M$ to be the induced map, and clearly $(g\otimes 1)(f\otimes 1)=gf\otimes 1=h\otimes 1$. Thus, $A\otimes M$ has an $\mathcal{X}$-precover. □

Proposition 5.2. 

Let A be an S-act and $\mathcal{X}$ a class of S-acts. Any retract of any act satisfying $\mathcal{X}$ satisfies $\mathcal{X}$. Then the $\mathcal{X}$-precover of A, if it exists, is the $\mathcal{X}$-precover of the retract of A.

Proof. 

Please see the following diagram

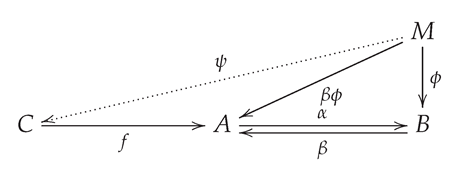
Let $f:C\to A$ be the $\mathcal{X}$-precover and B the retract of A. Then $\alpha :A\to B$ and $\beta :B\to A$ satisfy $\alpha \beta =1_B$. For S-map $\varphi :M\to B$, $M\in \mathcal{X}$, by the $\mathcal{X}$-precover property, there exists an S-map $\psi :M\to C$ such that $f\psi =\beta \varphi$. We claim that $\alpha f\psi =\alpha \beta \varphi =1_B\varphi =\varphi .$ Hence, $\alpha f:C\to B$ is the $\mathcal{X}$-precover of B. □

Proposition 5.3. 

Let $\mathcal{X}$ be a class of acts and $D\in \mathcal{X}$. Consider the following commutative diagram of S-acts: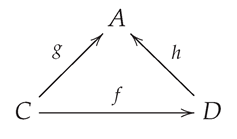

If $g:C\to A$ is an $\mathcal{X}$-precover of S-act A, then $h:D\to A$ is also a $\mathcal{X}$-precover of A.

Proof. 

Let $\psi :M\to A$ be an S-homomorphism for $M\in \mathcal{X}$. By the $\mathcal{X}$-precover property, there exists an S-map $\varphi :M\to C$ such that $g\varphi =\psi$. Hence, $hf\varphi =\psi$ from $hf=g$. So $h:D\to A$ is a $\mathcal{X}$-precover of A. □

Theorem 5.1. 

Let $\mathcal{X}$ be a class of S-acts and $f:A\to B$ be a monomorphism. Consider the following commutative diagram of S-acts: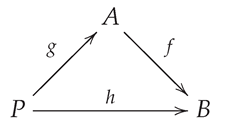

If $h:P\to B$ is an $\mathcal{X}$-precover of B, then $g:P\to A$ is an $\mathcal{X}$-precover of A.

Proof. 

For every S-map $h^{\prime }:P^{\prime }\to A$, where $P^{\prime }\in \mathcal{X}$. Since $h:P\to B$ is an $\mathcal{X}$-precover of B, there exists an S-map $\phi :P^{\prime }\to P$ with $fg\phi =h\phi =f{h}^{\prime }$. Then $g\phi =h$ since f is a monomorphism, and we are done. □

Dually, if $f:A\to B$ is an S-epimorphism, we obtain the following Theorem 5.2.

Theorem 5.2. 

Let S be a monoid and $\mathcal{P}$ the class of all projective S-acts. Let $f:A\to B$ be an S-epimorphism. Consider the following commutative diagram of S-acts:

If $g:P\to A$ is a $\mathcal{P}$-precover of A, then $h:P\to B$ is a $\mathcal{P}$-precover of B.

Proof. 

Let $g:P\to A$ be $\mathcal{P}$-precover of A and $f:A\to B$ an S-epimorphism. To show that $h:P\to B$ is a $\mathcal{P}$-precover of B, we assume that any S-map $\phi :P^{\prime }\to B$, where $P^{\prime }\in \mathcal{P}$. By assumption, there exists $\psi :P^{\prime }\to A$ such that $f\psi =\phi$. Since $g:P\to A$ is a $\mathcal{P}$-precover of A, we obtain that $g\varphi =\psi$ for some $\varphi :P^{\prime }\to P$. So $\phi =f\psi =fg\varphi =h\varphi$. Therefore, $h:P\to B$ is a $\mathcal{P}$-precover of B. □

Remark 5.1. 

It is clear that if $g:P\to A$ is an $\mathcal{X}$-cover of A, then $h:P\to B$ is an $\mathcal{X}$-cover of B in Theorem 5.2. A question that could be brought up is whether Theorem 5.2 is valid for free S-acts. It is easy to answer this question positively.

Theorem 5.3. 

Let S be a monoid and $\mathcal{X}$ a class of S-acts. If $A\in \mathcal{X}$ is an $\mathcal{X}$-precover of B and $C\in \mathcal{X}$ is an $\mathcal{X}$-precover of A. Then C is an $\mathcal{X}$-precover of B.

Proof. 

Suppose that $f:A\to B$ is an $\mathcal{X}$-precover of B and $g:C\to A$ is an $\mathcal{X}$-precover of A. For any S-map $h:P\to B$, for $P\in \mathcal{X}$, there is an S-map $\phi :P\to A$ with $f\phi =h$ since $f:A\to B$ is an $\mathcal{X}$-precover of B. Similarly, because $g:C\to A$ is an $\mathcal{X}$-precover of A, we have $g\psi =\phi$ for some S-map $\psi :P\to C$. Thus, we can verify that $h=f\phi =\left(fg\right)\psi$. So $fg:C\to B$ is an $\mathcal{X}$-precover of B, that is, C is an $\mathcal{X}$-precover of B. □

Proposition 5.4. 

Let S be a monoid and B a right S-act. Let $\mathcal{X}$ be a class of S-acts closed under factor acts. If $f:A\to B$ is a $\mathcal{X}$-precover for B, then $f^{\prime }:A/\rho \to B$ is a $\mathcal{X}$-precover for B, where $\rho \subseteq ker\left(f\right)$ is a congruence on A.

Proof. 

Let $\rho$ be a congruence on A contained in $ker\left(f\right)$ and $A\in \mathcal{X}$. First note that $A/\rho \in \mathcal{X}$. By Homomorphism Theorem for acts, there exists a homomorphism $f^{\prime }:A/\rho \to B$, defined by $f^{\prime }\left(a\rho \right)=f\left(a\right)$, with $f^{\prime }\pi =f$, where $\pi :A\to A/\rho$. For each morphism $h:C\to B$ with $C\in \mathcal{X}$, there exists a morphism $g:C\to A$ such that $fg=h$. Thus $f^{\prime }\left(\pi g\right)=h$, that is, $f^{\prime }:A/\rho \to B$ is a $\mathcal{X}$-precover for B. □

Proposition 5.5. 

Let $\mathcal{X}$ be a class of S-acts which is closed under subacts. And suppose that all subacts of B have $\mathcal{X}$-covers. If $A\in \mathcal{X}$ and $f:A\to B$ is an $\mathcal{X}$-precover and C is a proper subact of B. Then there exists an S-subact $A^{*}$ of A and a homomorphism $g:A^{*}\to C$ such that it is an $\mathcal{X}$-cover of C.

Proof. 

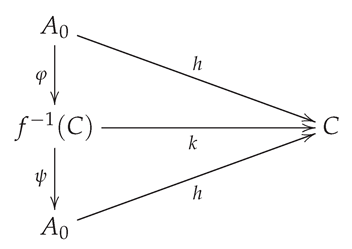
By assumption, we note that $f^{-1}\left(C\right)\in \mathcal{X}$. Thus $k:f^{-1}\left(C\right)\to C$ is an $\mathcal{X}$-precover of C. Let $h:A_0\to C$ be an $\mathcal{X}$-cover of C. Then we have the commutative diagram such that $k\phi =h$ and $h\psi =k$, and so $h\psi \phi =h$. Since h is an $\mathcal{X}$-cover of C, it follows that $\psi \phi$ is an automorphism of $A_0$. Thus $\phi$ is monomorphism. Take $A^{*}=\phi \left(A_0\right)\cong A_0$ is an S-subact of A, then $g=h\psi :A^{*}\to C$ is an $\mathcal{X}$-cover of C. □

6. Conclusions

Based on the covers of cyclic S-acts over monoids(see [9]), we have introduced the projective covers (resp. strongly flat covers, $\left(P\right)$-covers) of the finitely generated S-acts over monoids in this work. Then we pose the following questions for consideration:

1.What is the equivalent conditions of the Condition $\left(P^{\prime }\right)$-cover and $\left(P{F}^{\prime \prime }\right)$-cover of the finitely generated S-acts?

2.What is the flat covers of finitely presented S-acts?