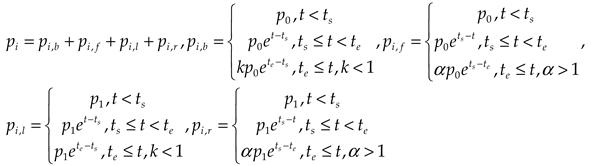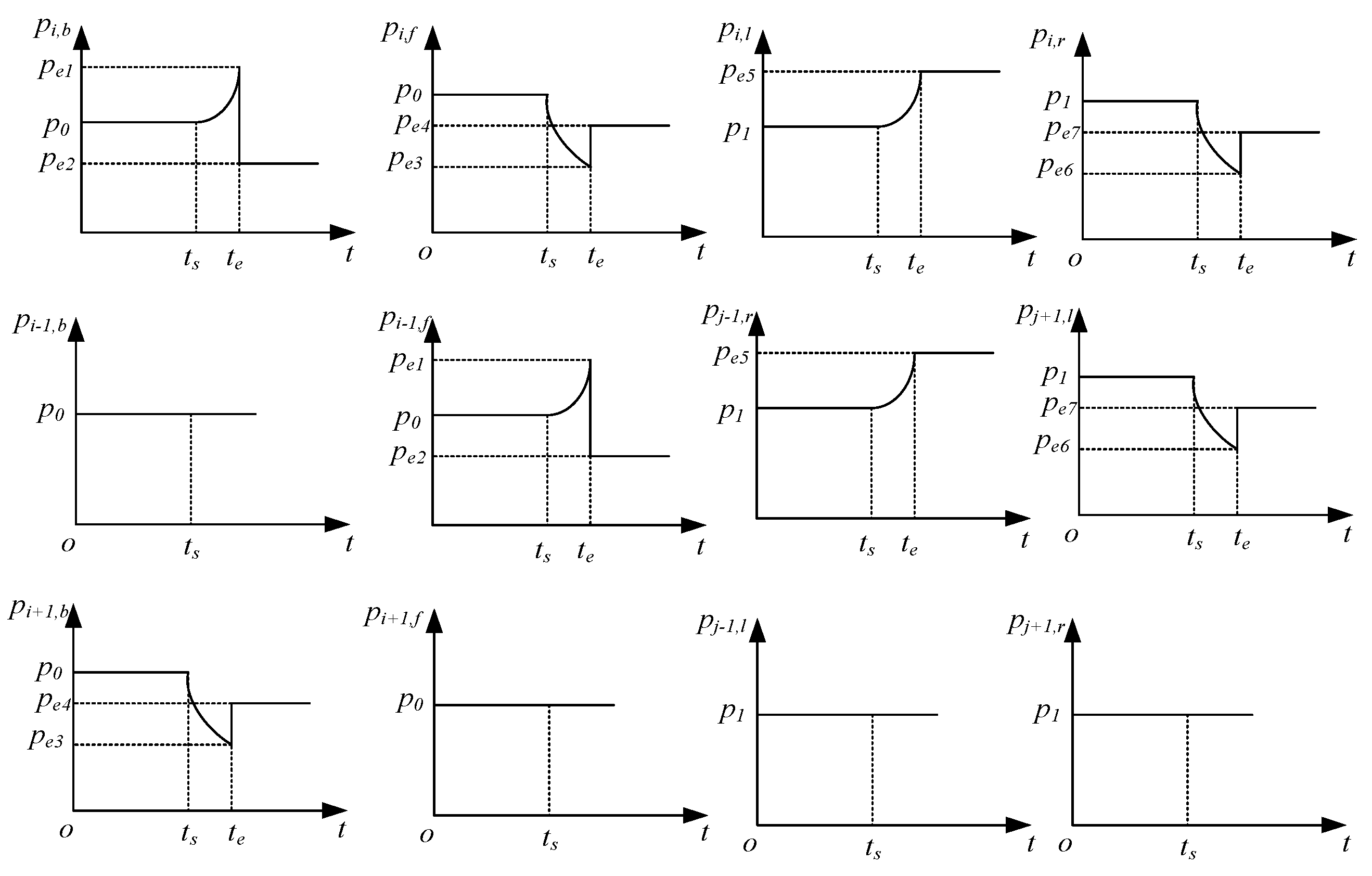Disturbance Propagation Model of Luggage Drifting Motion Based on Nonlinear Pressure in Typical Passenger Corridors of Transportation Hubs

In current transportation hubs, it is a common phenomenon that passengers travel with necessary wheeled-luggage or suitcases. Due to the fact that most luggage occupies certain space within dense passenger crowds with giant mass inertia, its abnormal motions, such as drifting, frequently trig unavoidable local disturbances and turbulence in surrounding pedestrian flows, further increasing security risk. While, current researches primarily concentrate on examining the impact of luggage on crowd evacuation efficiency through scenario-based experiments and analyzing the spatial characteristics of crowd distribution in surveillance videos. There still lacks of the dynamic disturbance mechanisms and crowd stability associated with the combined motion of passengers and luggage. Therefore, this study considers the luggage-laden passenger as a deformable particle, the resulting disturbance on surrounding non-luggage passengers is analyzed and quantified into a nonlinear pressure term. Subsequently, the disturbance propagation model of passenger-luggage is developed by adapting the classical Aw-Rascle traffic flow model with incorporation of the pressure term. Simulation experiments of disturbances caused by luggage drifting and retrograding validate that the proposed propagation model aligns with real-world situations in transportation hubs. Quantitively, when luggage-laden passenger drifted left, the disturbing force of left side crowd can reach a peak of 238N in the passenger density of 3.0 p/m2, and the maximum difference between the left and right sides disturbing force can reach 153N. Furthermore, it is recommended that the proposed model can be applied to crowd flow analysis and risk assessment.

Keywords:

Luggage-laden passenger

;

passenger-luggage flow

;

disturbance propagation dynamics

;

luggage drifting disturbance

Subject:

Computer Science and Mathematics - Applied Mathematics

1. Introduction

In recent decades, the advancement of modern public transportation systems, such as metros and railways, has led to increasingly crowded transportation hubs teeming with a vast number of passengers carrying luggage, trolley cases, or suitcases [1]. Given that luggage serves as a moving obstacle with relatively large mass inertia to surrounding passengers, the presence of luggage- laden passengers can heavily impact the evacuation efficiency during security emergencies such as fires and stampedes in transportation hubs [2].

Numerous studies focusing on luggage and passengers have uncovered the notable impact that luggage-laden passengers have on emergency evacuation processes. Though filed observations, studies found that the walking speed of a luggage-laden passenger has a distinct reduction compared to the ones without carrying luggage [3,4,5]. Davis et al. [6] discovered that the luggage size actually affect the crowd distribution in building plane though investigating the passenger flow in airport terminals. Jahedinia et al. [7] studied the particular flow characteristics in the mixture of non-luggage-laden passengers and luggage-laden passengers according to the collected data in a real case, and also considered the influence of different percentages of discarded luggage in crowded areas.

The influence of wheeled luggage or trolley cases on the movement of surrounding passengers is complex. Factors such as the proportion and size of luggage, passenger density, and the nature of luggage's abnormal motions are crucial considerations. Zhang et al.[8] introduced a modified social model to simulate different categories of pedestrians, and found that the presence of luggage led much more collision and friction to pedestrians. Besides, the traffic flow models have been applied to dense crowd modeling. In [9], a modified AW-Rascle model was proposed to describe the crowd convergence mechanism, and the internal pressure is positively corelated to the velocity and density. However, since luggage is one moving obstacle, the luggage-laden passengers and surrounding passengers cannot be regarded as the same medium in a macroscopic view, and their interaction mechanism cannot be described by the conventional fluid model.

Moreover, the literature [10] showed that the sway amplitude of luggage-laden passenger increases especially in highly dense pedestrian flow. As the wheeled luggage follows its owner with the help of pulleys, the luggage will maintain a certain motion inertia during the movement. When its owner makes a sudden turn or sways the suitcase will be driven by the passenger to turn, but the motion of the luggage has a certain lag following the passenger, which probably causes luggage drifting. A luggage drifting motion interferes with the expected movement of other passengers, and this crowd disturbance spreads around and dissipate with the increase of time and distance. Therefore, the mechanism of disturbance of luggage drifting on the crowd and the disturbance propagation dynamics are ongoing challenging issues on passenger crowd safety, and are the primary focuses of this paper.

The main contributions of the study are the following: (1) we propose a dynamic disturbance propagation model of abnormal luggage states based on the conservation law of fluids dynamic and Aw-Rascle model; (2) Considering the collision between passengers, a disturbance effect of luggage on the surrounding passengers is transferred into a nonlinear pressure term based on contact model and pressure characteristic analysis. (3) Experiments are designed to validate the effectiveness of our model quantitively, the disturbing force of left side crowd can reach a peak of 238N in the passenger density of 3.0

p / m^{2}

, and the maximum difference between the left and right sides disturbing force can reach 153N.

The outline of this paper is as follows: in Section 2, we conduct the literature survey of related works; in Section 3, we propose the disturbance dynamics model for luggage-laden passenger; in Section 4, the mechanism of the disturbance on surrounding passenger is studied, and we further propose the disturbance propagation model in passenger-luggage flow; in Section 5, simulation experiments of the disturbance propagation induced by luggage ’s retrograding and drifting movement are conducted based on the scenarios occurred in a straight corridor and L-shaped corridor of transportation hub respectively.

2. Related Works

2.1. Impact of Carried Luggage on Pessenger Crowd

Carrying luggage, baggage and suitcases is one of the prominent features of pedestrians in the transportation hubs like railway station [11]. Since the luggage occupies tangible space and its motion is not entirely synchronized with its owner, its presence can somehow impede the smooth flow of other passengers in the vicinity [1].

Currently, crowd distribution analysis is utilized to assess the impact of carried luggage on overall crowd dynamics. Fu et al. [12] analyzed the temporal features, passing performance, spatial distribution and crowd danger of the pedestrian trajectories from video recordings, and concluded that the average passing time of merging flow in Y-shaped corridor increases with the increasing number of pedestrian carrying luggage. Shi et al. [13] considered the boundary distance, interpersonal distance and distance headway to describe the distribution of pedestrians in the crowd with luggage. They found that luggage would enhance the distance headway for the whole crowd. Jian et al. [14] designed a series of experiments of luggage-laden pedestrian in the stairs of transportation terminals to study the influences of luggage on the longitudinal movement of crowd. Deng et al. [15] experimentally investigated the flow of luggage-carrying pedestrian through a bottleneck in both normal and emergency situations. Based on pedestrian trajectories, a dual-peaks spatial distribution of pedestrians was observed when no pedestrian carries luggage or when all pedestrians carry luggage. Huang et al.[16] performed the experiment of one-dimensional luggage-laden pedestrian movement. It is found that the average distance headway of pedestrians was obviously enlarged and the acceleration reduced when pedestrian switched their direction due to the presence of luggage.

Nevertheless, the aforementioned studies quantified the impact of carried luggage on crowd dynamics by conducting scenario-based experiments. These experiments analyzed the spatial and temporal distributions of crowds, as well as motion characteristics, comparing conditions with and without luggage-laden pedestrian. However, few prior studies focused on the quantitative analysis of luggage-laden passengers. Only a limited number of research endeavors have explored the impact mechanisms of wheeled luggage on crowd dynamics. In this paper, we define the luggage and its carrier as a combined particle, modeling the influence of this combination on crowd dynamics through a detailed force analysis.

2.2. Disturbance Propagation in Crowd Flow

Due to the factors of physical environment disturbance, object disturbance and individual behavior mutation, a crowd flow will change from a stable and orderly state to a chaotic and unstable state[17]. The redistribution of crowd density and fluctuation in velocity propagate instability within the crowd, heightening the risk of stampedes. This underscores the importance of accurately quantifying crowd disturbances. Wei et al. [18] improved the social force model by introducing the disturbance fluctuation force to describe the state change of pedestrian flow during evacuation and provided the mathematical expression of disturbing force. Researchers have recently made noteworthy progress with attracting attention to quantifying disturbances from a force perspective [19,20,21].

An internal disturbance can lead to result in varying degrees of dynamic propagation within the crowd flow. Lu [22] applied the wave theory to the study of crowded pedestrians which were regarded as a continuum, and disturbances in the crowd could propagate in the form of waves. Qin et al. [23]designed a distributed parameter system to describe the disturbed crowd dynamic based on the mass conservation law. Hanseler at el. [24] described the simultaneous and potentially conflicting propagation of multiple pedestrian group based on the continuum theory of pedestrian and cell transmission model. Wang et al. [25] proposed an extended car-following model to describe the dynamic features of mixed traffic with pedestrians walking on adjacent lane, and used the reductive perturbation method to analyze the nonlinear stability of the car flow model. Ma et al. [17] studied the stampede at the 2010 German music festival from a perspective of flow pattern, and the result showed that the force generated by the physical contact between pedestrians led to the unsteady crowd movement. The amplified and diffused energy of the disturbance ultimately led to the severe turbulences and stampedes.

Research achievements in both crowd dynamics and traffic flow above indicate that disturbances of certain intensity can induce congestion, even when density and flow are far from saturation. This is because that the evolution of traffic flow, as well as crowd flow, transitions from free flow to crowded flow in a complex process characterized by strong nonlinearity. It is significant for passenger crowd safety and management to consider the spatial and temporal features of disturbance and the impact of disturbance on crowd stability. In our previous study, the panic propagation dynamics [26] and the disturbance propagation model for abnormal behavior of pedestrian were proposed [27]. In this study, we further propose the disturbance propagation model of the abnormal motions of luggage.

3. Disturbance Dynamics Model of Luggage-laden Passenger

3.1. Dynamic Pressure between Luggage-Laden and Non-Luggage Passengers

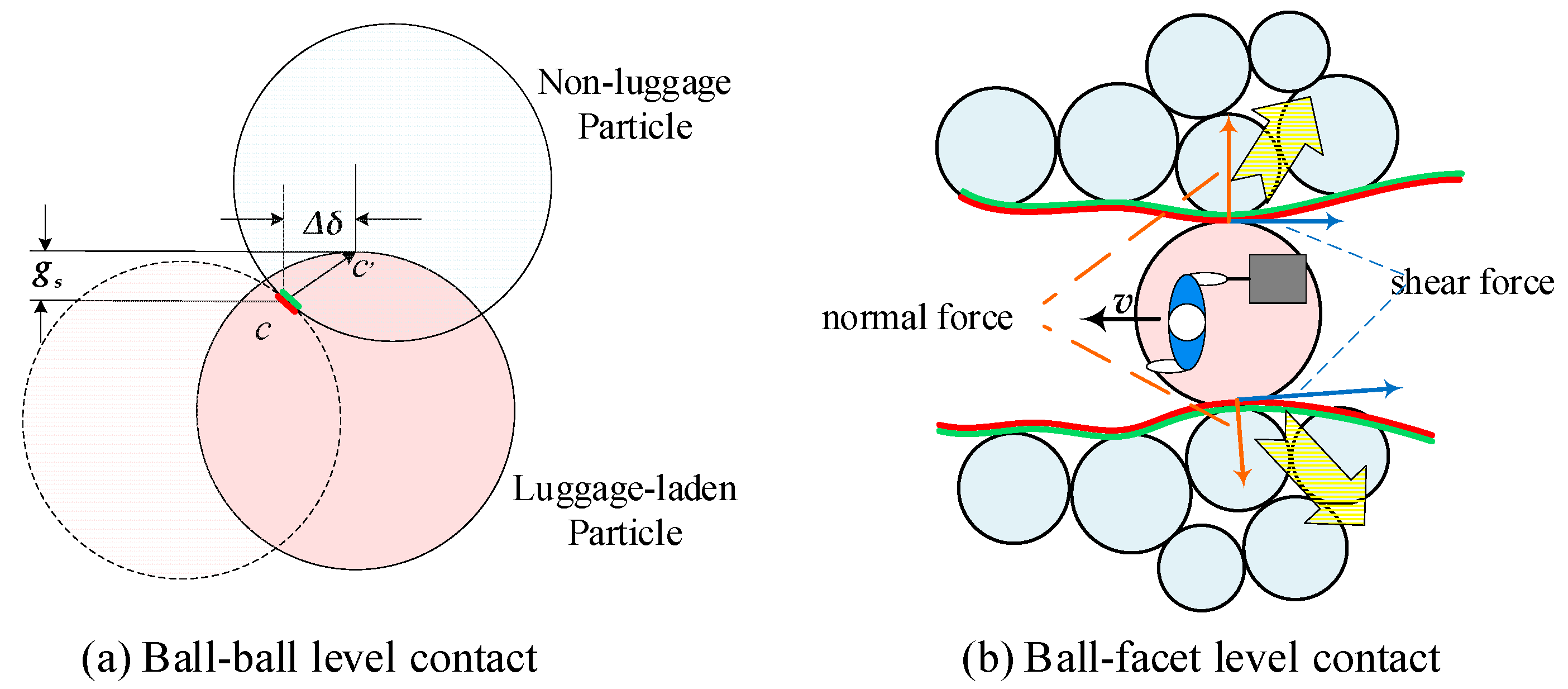
In dense pedestrian flow, the incomplete pursuit movement of luggage relative to its owner led the neighboring passengers avoid the luggage autonomously, which can be described from the perspective of contact force or pressure. In the field of rock mechanics, the interactions of granular material are modeled by varying contact models using the discrete element method (DEM)[28]. Analogously, the pressure between luggage-laden passengers and non-luggage passengers can be regarded as the contact force between particles of two different sizes. Dissimilarly, for simplicity and emphasizing the dynamic pressure of two different media, non-luggage passengers with a certain range are assembled into one particle, while every luggage-laden passenger is treated as a separate particle, as shown in Figure 1.

A common model for studying the contact force between circular particles is the contact stiffness model, which primarily consist of the linear contact model [28] and Hertz-Mindlin contact model [29]. As rigorous non-linear model of elasto-plastic contact model deformation are time-consuming in numerical simulation, and it is unnecessary to fully represent the actual collision deformation of pedestrian particles [30]. In this study, we employ the linear contact model to simulate the contact force between luggage-laden passengers and the surrounding ones.

In a contact stiffness model, although particles are regarded as rigid bodies, overlap between particles and a certain degree of collision deformation are permitted due to the interpersonal distance in real crowd. Figure 2 (a) illustrates the ball-ball level contact of luggage-laden passenger and non-luggage passenger. In the linear contact model, the simplest relation between the elastic force and displacement is linear [31]. The contact force in contact position

C

is composed of linear force

F^{l}

and dashpot force

F^{d}

, that is:

F_{c} = F^{l} + F^{d}

(1)

The linear component provides linear elastic and frictional properties, while the damped component provides viscous property. Linear force and dashpot force can both be resolved into shear and normal forces. The linear force is generated by a linear spring with constant normal stiffness

k_{n}

and shear stiffness

k_{s}

, and the dashpot force is generated by a damper with a normal and shear critical damping ratio of

β_{n}

and

β_{s}

, respectively. That is:

\{\begin{cases} F^{l} = {F_{n}}^{l} + {F_{s}}^{l}, \\ F^{d} = F_{n}^{d} + F_{s}^{d}, \\ {F_{n}}^{l} = k_{n} g_{s}, \\ {F_{s}}^{l} = k_{s} Δ δ, \\ F_{n}^{d} = - β_{n} Δ v_{n}, \\ F_{s}^{d} = - β_{s} Δ v_{s} \end{cases}

(2)

where the subindex s and n represent shear and normal direction respectively.

g_{s}

is the surface gap of the two particles.

Δ δ

is the relative displacement increment at the contact.

Δ v_{n}

and

Δ v_{s}

are the relative velocity increment of normal and shear direction respectively.

In a real scenario, the disturbance effect of luggage-laden passengers on the left and right sides of passengers is more significant. For this reason, when only one passenger carries luggage in a passenger flow, passengers of one side can be considered equivalent to a face., as shown in Figure 2 (b). Then the ball-ball level contact force is extended to the ball-facet level by elongating the contact surface. The left-side disturbing force of normal direction can be modeled in Equation (3), where

x_{n} (t)

is the overlap of normal direction in time

t

, and

Δ v (ρ, t)

is the normal velocity of the luggage-laden passenger relative to the crowd on the left, which can be described by Equation (4), where

n_{l e f t}

is the unit vector from the luggage in luggage-laden passenger to the crowd on the left at time t,

ν_{l e f t} (ρ)

is the velocity of left-side crowd of luggage-laden passenger particle with crowd density

ρ

. The values of

ν_{l} (ρ)

in different scenarios of transportation hubs are shown in Table 1.

F_{n_l e f t} (ρ, t) = {F_{n}}^{l} + {F_{n}}^{d} = - k_{n} x_{n} (t) - β_{n} Δ v (ρ, t)

(3)

Δ v (ρ, t) = (ν_{i} - ν_{l} (ρ)) n_{l e f t}

(4)

The left-side disturbing force of tangent direction is

F_{s_l e f t} (t)

F_{s_l e f t} (ρ, t) = - k_{s} x_{s} (t) - β_{s} ν_{s_l e f t} (t)

(5)

where,

x_{s} (t)

is the overlap of tangent direction in time t.

ν_{s_l e f t} (t)

is the tangent velocity of the luggage-laden passenger relative to the left-side crowd, which can be expressed by Equation (6):

ν_{s_l e f t} (t) = r ω \times n_{l e f t}

(6)

where,

r

and

ω_{i}

are the radius and the spin angular velocity of luggage respectively. Thus, when the luggage-laden passenger crosses the crowd, its disturbing force on the crowd of left side is:

F_{d ι s t u r b_l e f t} (ρ, t) = F_{s_l e f t} (ρ, t) + F_{n_l e f t} (ρ, t)

(7)

3.2. Disturbing Effect of Luggage Drifting Motion

Section 3.1 elucidates the dynamic disturbance caused by passengers carrying luggage on the surrounding passengers under relatively smooth flow conditions. The disturbing force primarily exhibits a linear relationship with displacement and velocity. However, when trampling and stampede occur in transportation hubs, wheeled luggage tends to drifting with the accelerating turn of its owner or even being abandoned during escape, and further exert turbulence on over-congested crowd. Since these abnormal motions of luggage have a sudden nature, and pedestrians can resist slight interference and readjust themselves to the balanced state, therefore, the linear pressure in Section 3.1 is not sufficiently realistic. In [27], the main inter-impacting pressure of pedestrian fall behavior was analyzed along longitudinal axis. Herein, the disturbing effects of both horizontal and vertical are quantified.

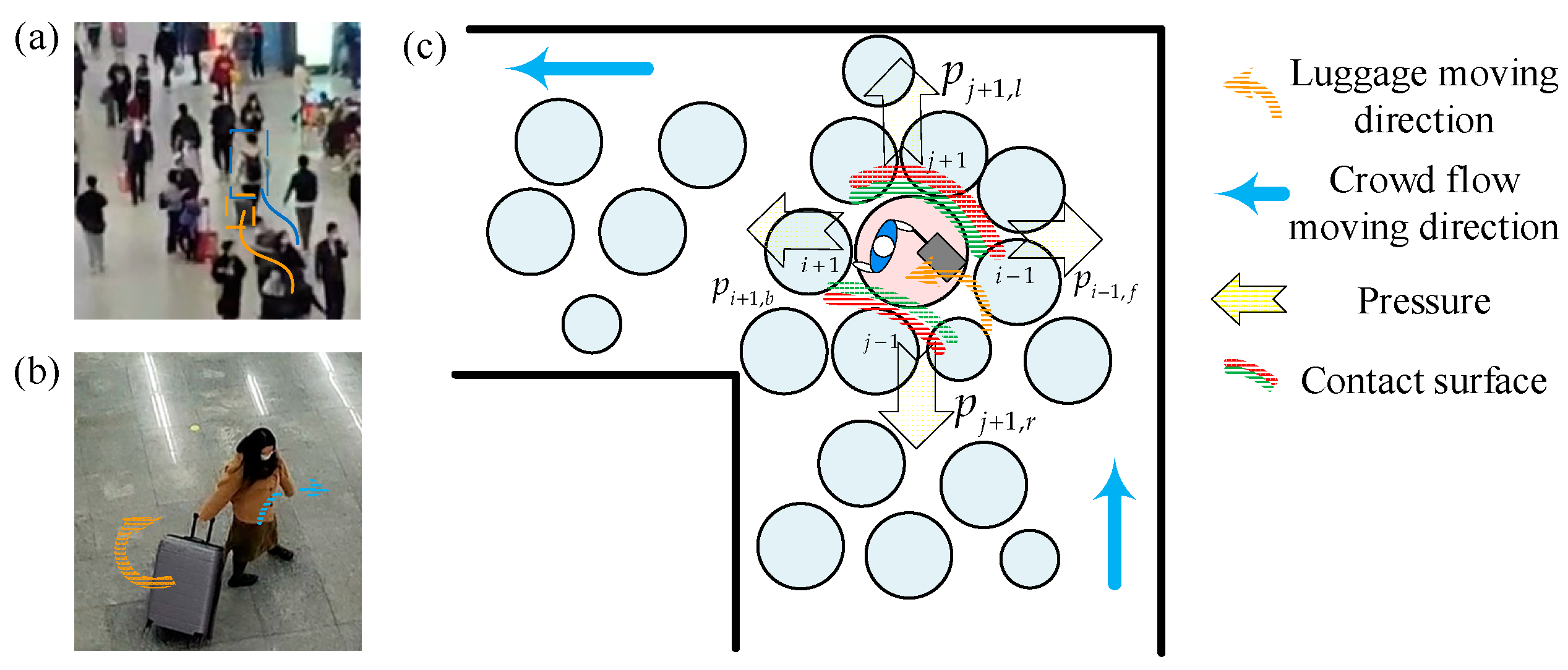
We consider luggage drifting left (or right) as an abnormal motion and describe it disturbing effect by analyzing its pressure characteristics. As shown in Figure 3 (c), When luggage abruptly drifting left, it affects the passengers i+1, i-1, j+1, j-1. The right side pressure of passengers on the left side of the luggage

p_{j - 1, r}

increases, while the left side pressure of passengers on the left side on the luggage

p_{j - 1, l}

remains unchanged. The luggage disturbing force of left side

p_{i, l}

and

p_{j - 1, r}

constitute a pair of interacting forces. The

p_{j + 1, l}

(the left side pressure of passengers on the right side of the luggage), with a opposite trend to

p_{j - 1, r}

, decays firstly and back to the balance value as the completion of turning and the movement of crowd. The luggage disturbing force of right side

p_{i, r}

and

p_{j + 1, l}

constitute a pair of interacting forces, too. As the luggage drifting increases the time that luggage-laden passenger stays in the disturbed position, the front pressure of luggage

p_{i, f}

and the rear pressure

p_{i, b}

will firstly decays and climbs to stable values, respectively. Therefore, the dynamics pressure of luggage drifting can be expressed non-linearly as follows (also shown in Figure 4):

(a) As to luggage

i

(8)

Where

p_{0}

is stable pressure value of

p_{i, f}

and

p_{i, f}

p_{l}

is stable pressure value of

p_{i, l}

and

p_{i, r}

t_{s}

is the moment that luggage start drifting, and

t_{e}

is the moment that luggage-laden passenger leaves the left side passengers.

(b) As to front passengers:

p_{i + 1} = p_{i + 1, b} + p_{i + 1, f}, p_{i + 1, b} = \{\begin{matrix} p_{0}, t < t_{s} \\ \begin{array}{l} p_{0} e^{t_{s} - t}, t_{s} \leq t < t_{e} \\ α p_{0} e^{t_{s} - t_{e}}, t_{e} \leq t, α > 1 \end{array} \end{matrix} p_{i + 1, f} = p_{0},

(9)

p_{i - 1} = p_{i - 1, b} + p_{i - 1, f}, p_{i - 1, f} = \{\begin{matrix} p_{0}, t < t_{s} \\ p_{0} e^{t - t_{s}}, t_{s} \leq t < t_{e} \\ k p_{0} e^{t_{e} - t_{s}}, t_{e} \leq t, k < 1 \end{matrix}, p_{i - 1, b} = p_{0}

(10)

(d) As to left side passengers:

p_{j - 1} = p_{j - 1, l} + p_{j - 1, r}, p_{j - 1, r} = \{\begin{matrix} p_{1}, t < t_{s} \\ p_{1} e^{t - t_{s}}, t_{s} \leq t < t_{e} \\ p_{1} e^{t_{e} - t_{s}}, t_{e} \leq t, k < 1 \end{matrix}, p_{j - 1, l} = p_{1}

(11)

(e) As to right side passengers:

p_{j + 1} = p_{j + 1, l} + p_{j + 1, r}, p_{j + 1, r} = p_{1}, p_{j + 1, l} = \{\begin{matrix} p_{1}, t < t_{s} \\ p_{1} e^{t_{s} - t}, t_{s} \leq t < t_{e} \\ α p_{1} e^{t_{s} - t_{e}}, t_{e} \leq t, α > 1 \end{matrix}

(12)

4. The Disturbance Propagation Model based on AR-Rascle Model in Crowd Flow

4.1. Disturbance of Luggage-Laden Passenger Particle on Surrounding Passengers

When a luggage-laden passenger encounters a sudden abnormal events, such as a rapid change in speed, abrupt turns, discarding suitcases, falls, seeking assistance for medical emergencies, brawls, or violent terrorist attacks, these unpredictable incidents can generate disturbing forces that disturb the balanced flow of the crowd. With reference to the form of pressure term of AR traffic flow model [33], the crowd flow pressure term under abnormal state is established, which can be expressed by Equation (13).

P = f (ρ, γ, ξ) = ρ^{γ} \cdot ξ

(13)

where,

ρ

is the crowd density,

γ

is the pressure coefficient,

ξ

is disturbance intensity.

γ

is used to reflect the resistance ability of the crowd under internal pressure. Hence, we define

γ

as the ratio of the disturbing force of luggage-laden passengers and their self-drive forces. The self-drive forces of pedestrians can refer to the social force model proposed by Helbing[34], or human centroid force[35]. Herein, we introduce desire force from the classic social force model, then

γ

is:

γ = \frac{p}{f_{d e s i r e}}

(14)

f_{d e s i r e} = m_{i} \frac{ν_{i}^{0} (t) e_{i}^{0} (t) - v_{i} (t)}{τ_{i}}

(15)

where

m_{i}

is the mass of passenger,

ν_{i}^{0}

is the desire velocity in a certain direction

e_{i}^{0}

v_{i}

is the velocity of passenger, and

τ_{i}

is the relaxation term. Note that, if luggage is drifting, then the pressure term is given by Equation (9)-(12). If not, we have:

p = F_{d ι s t u r b_l e f t} (or, F_{d ι s t u r b_r i g h t})

(16)

γ > 1

, the non-luggage passengers are squeezed stronger than their own control, prone to unsafe incidents. In [36], the pressure distribution around the disturbance source is assumed to follow a normal distribution. Thus, the disturbance intensity

ξ

of x axis can be expressed by:

ξ_{x} = ξ_{0} \cdot \frac{1}{\sqrt{2 π t}} e^{- \frac{{(x - a)}^{2}}{2 t}}

(17)

Thus, the pressure term of horizontal direction is:

P_{h} (ρ, γ, ξ) = ρ^{γ} \cdot ξ_{x} = ρ^{γ} \cdot ξ_{0} \cdot \frac{1}{\sqrt{2 π t}} e^{- \frac{{(x - a)}^{2}}{2 t}}

(18)

In AR traffic flow model, the pressure describes how an “average” driver would response to a variation of the density of cars in a limiting space. In this study, the pressure term is employed to describe the impact of disturbance on surrounding pedestrians caused by abnormal luggage motion.

4.2. Disturbance Propagation Model based on Aw-Rascle Model

The propagation of disturbance on passenger crowd follows the mass conservation law of the macroscopic hydrodynamic model [9], that is:

\frac{\partial ρ}{\partial t} + \frac{\partial (ρ v_{h})}{\partial x} + \frac{\partial (ρ v_{l})}{\partial y} = 0

(19)

where,

v_{h}

is the velocity of horizontal direction, and

v_{l}

is the velocity of lateral direction. Besides, the rear crowd can adjust their movement by directly observing the abnormal motion of luggage-laden passenger, while the front crowd cannot. This reflects the anisotropy of disturbance propagation in crowds. Thus, to describe the process of disturbance propagation, Aw-Rascle model [33,37], one typical anisotropic traffic flow model is employed. The classic Aw-Rascle model can be expressed by the following two Equation (20) (21):

\frac{\partial (v_{h} + P_{h})}{\partial t} + v_{h} \frac{\partial (v_{h} + P_{h})}{\partial x} = s_{1} = \frac{1}{τ} (V_{e h} - v_{h})

(20)

\frac{\partial (v_{l} + P_{l})}{\partial t} + u \frac{\partial (v_{l} + P_{l})}{\partial y} = s_{2} = \frac{1}{τ} (V_{e l} - v_{l})

(21)

where

τ

is the relaxation time,

V_{e h}

and

V_{e l}

are the equilibrium velocity of horizontal and lateral direction respectively.

s_{1}

and

s_{2}

are the relaxation term, and the

P_{h}

and

P_{l}

are the respectively refer to the horizontal and lateral pressure components. We replace the pressure term of Aw-Rascle model by the pressure term of crowd interior disturbance in Equation (18), then we have:

\frac{\partial (v_{h} + P_{ξ h})}{\partial t} + v_{h} \frac{\partial (v_{h} + P_{ξ h})}{\partial x} = \frac{1}{τ} (V_{e h} - v_{h})

(22)

\frac{\partial (v_{l} + P_{ξ l})}{\partial t} + u \frac{\partial (v_{l} + P_{ξ l})}{\partial y} = \frac{1}{τ} (V_{e l} - v_{l})

(23)

In the propagation process of disturbance, motion damping will be encountered. Due to the damping effect, energy is absorbed by passengers in the process of disturbance propagation until all the energy is dissipated. This phenomenon is called the damping wave elimination effect of crowds. The damping wave elimination of the crowd is carried out along the direction of the speed of the disturbance.

To simulate the damping effect of crowds, it is reasonable to add the damping wave elimination terms to construct a disturbance propagation model in (22) and (23), are:

S x = - ρ μ_{0} μ f (x)

(24)

S y = - ρ μ_{0} v f (x)

(25)

where

ρ

is the density of crowd,

μ_{0} μ

μ_{0} v

reflect the loss of disturbance during propagation. The damping distribution function is approximated by linear damping function:

f (x) = \frac{x - x_{s}}{x_{e} - x_{s}}

(26)

where,

x_{s}, x_{e}

are the horizontal coordinates of the start and end of the wave elimination zone respectively.

Multiply both sides of Equation (22) by density and add the damping wave elimination term, we obtain:

ρ \frac{\partial (v_{h} + P_{ξ h})}{\partial t} + ρ v_{h} \frac{\partial (v_{h} + P_{ξ h})}{\partial x} - ρ μ_{0} μ f (x) = ρ \frac{1}{τ} (V_{e h} - v_{h})

(27)

For vertical direction, similarly, we obtain:

ρ \frac{\partial (v_{l} + P_{ξ l})}{\partial t} + ρ u \frac{\partial (v_{l} + P_{ξ l})}{\partial y} - ρ μ_{0} v f (x) = ρ \frac{1}{τ} (V_{e l} - v_{l})

(28)

Equations (27) and (28) are the dynamic model for the disturbance propagation of a luggage-laden passenger.

5. Case Study and Discussion

5.1. Experiment Parameters Initialization

According to the combination characteristics of passengers and their luggage, the simulation models of passenger and luggage are established in Pathfinder2022 software. The model of passengers and luggage is shown in Figure 5. In [38], the mass of passenger and luggage were both assumed to conform to the normal distribution. The mass of adult passenger ranges [38,85]kg with a mean of 85kg and a standard deviation of 7.8kg. The mass of luggage ranges [5,25]kg with a mean of 16kg and a standard deviation of 2.3kg. Then, we set the passenger mass and luggage mass to 58kg and 16kg respectively. 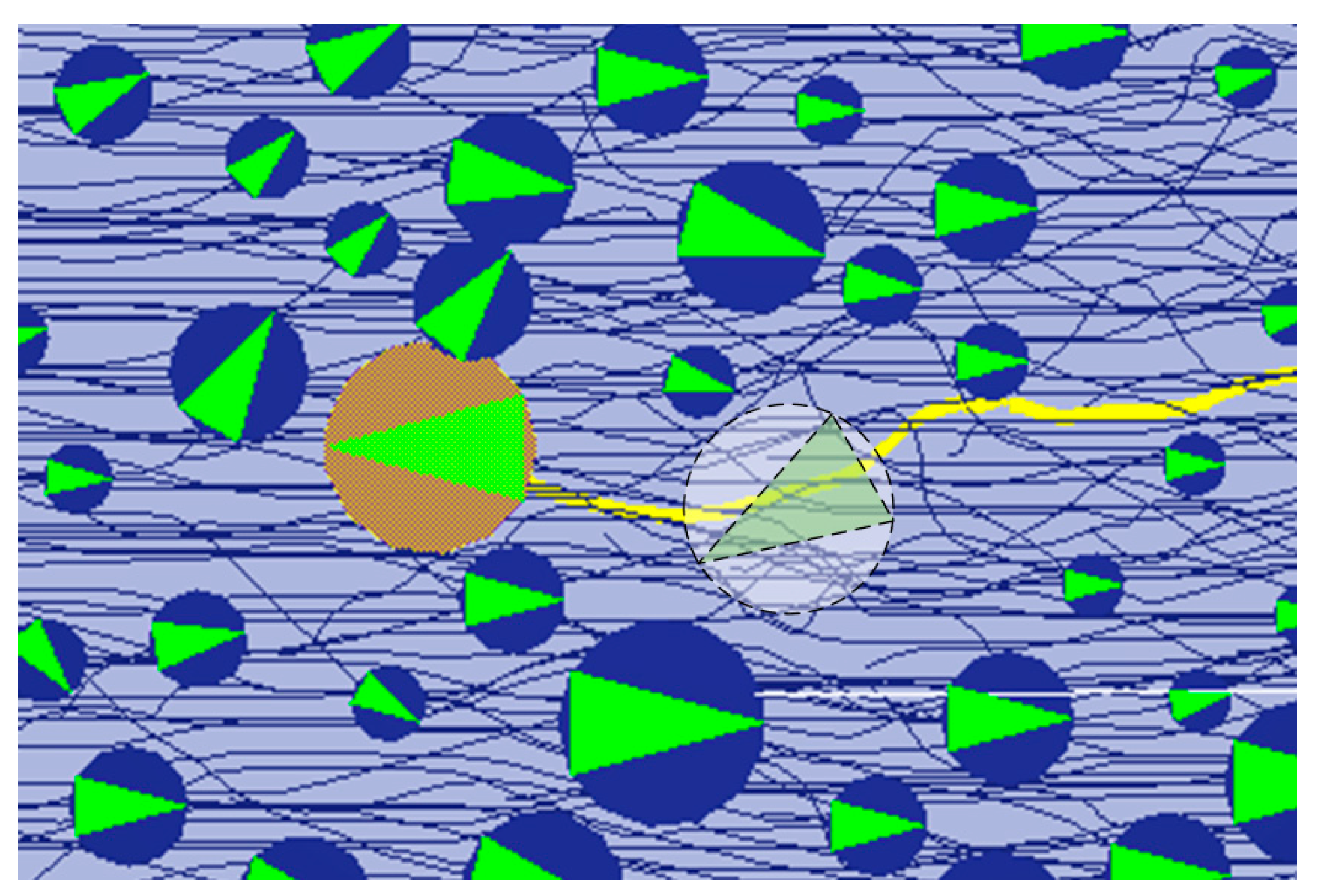As shown in Figure 6, we used the blue circles with green triangle to represent non-luggage passengers and their motion direction in a crowd, and used the brown circles with green triangle to represent luggage-laden passengers.

The related parameters of the simulation and their values are set in Table 2.

5.2. Case 1: Luggage Drifting Disturbance Propagation in a L-Shaped Corridor

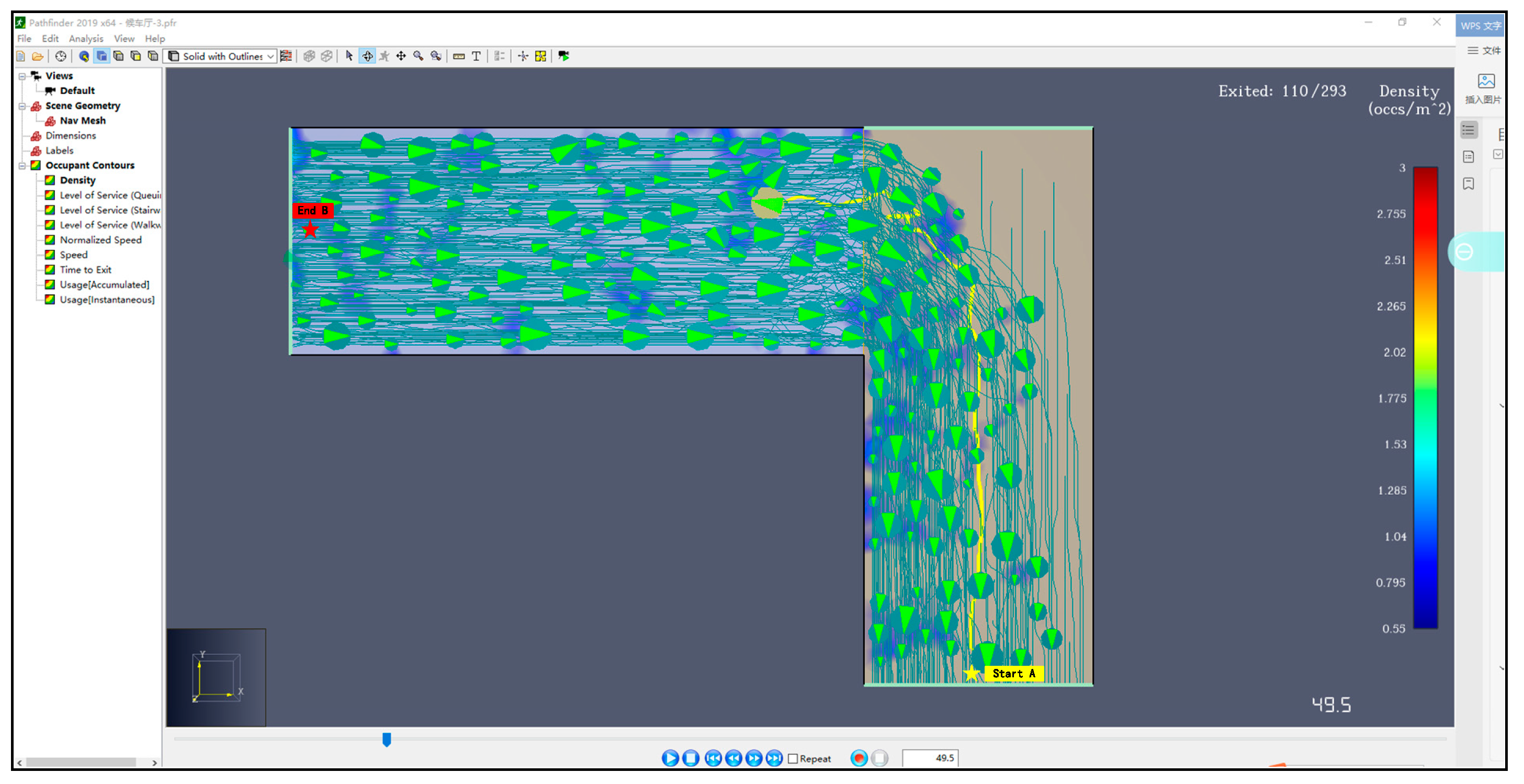
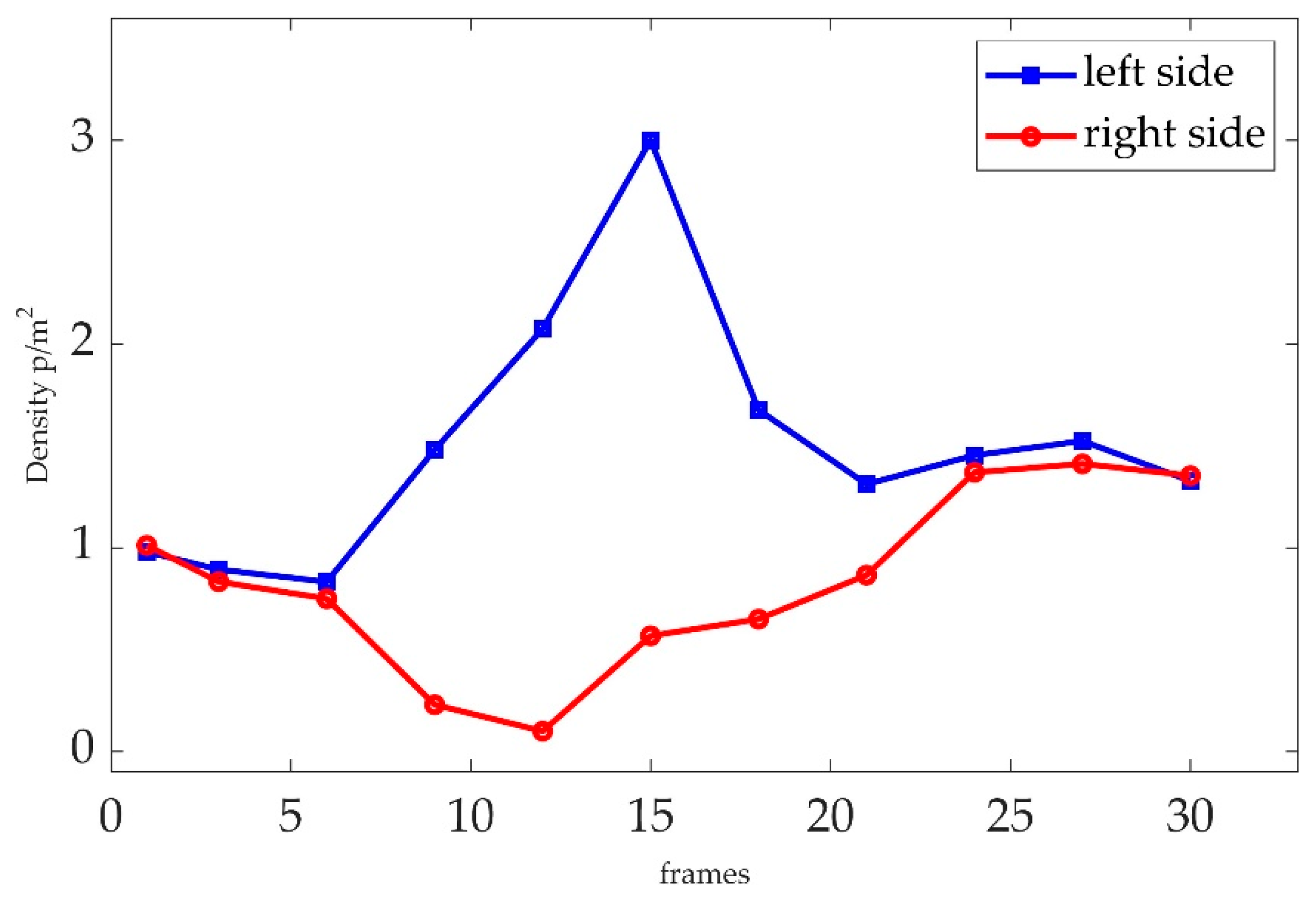
A sudden turn by a luggage-laden passenger is usually accompanied by a drifting of wheeled luggage, which is common seen in transportation hubs, especially in L-shaped corridors, with much more potential risk. Therefore, a typical L-shaped corridor in Shanghai Hongqiao railway station in China, with 10m width, was established in the Pathfinder2022 software. In Figure 7, a luggage-laden passenger made a sudden turn in a L-shaped corridor and caused luggage drifting. The crowd density and the disturbing force in the both side of the luggage-laden passenger were collected respectively. At the 5^th frame of the compared scenario video the difference of left side and right side disturbing force was 153N. 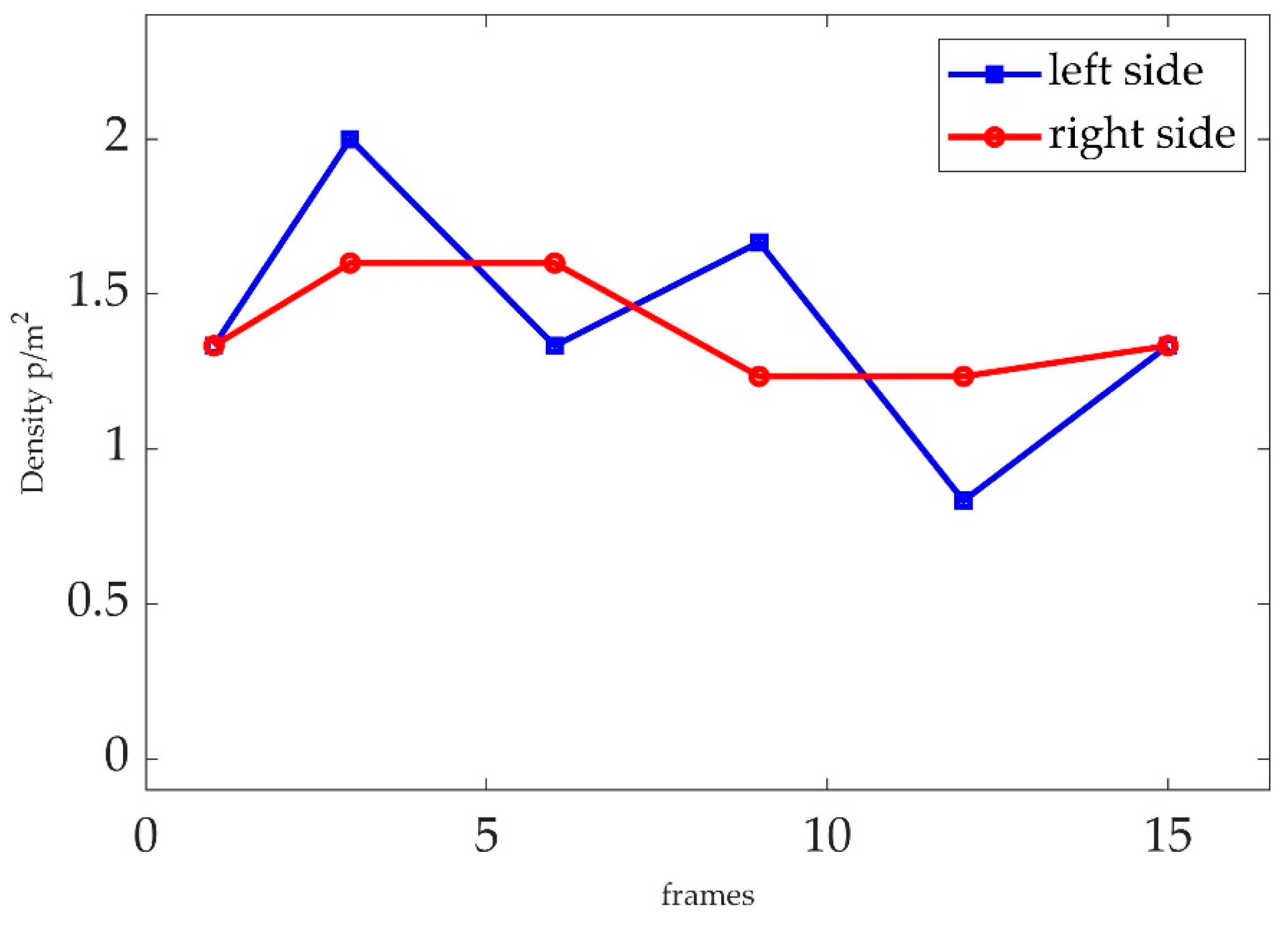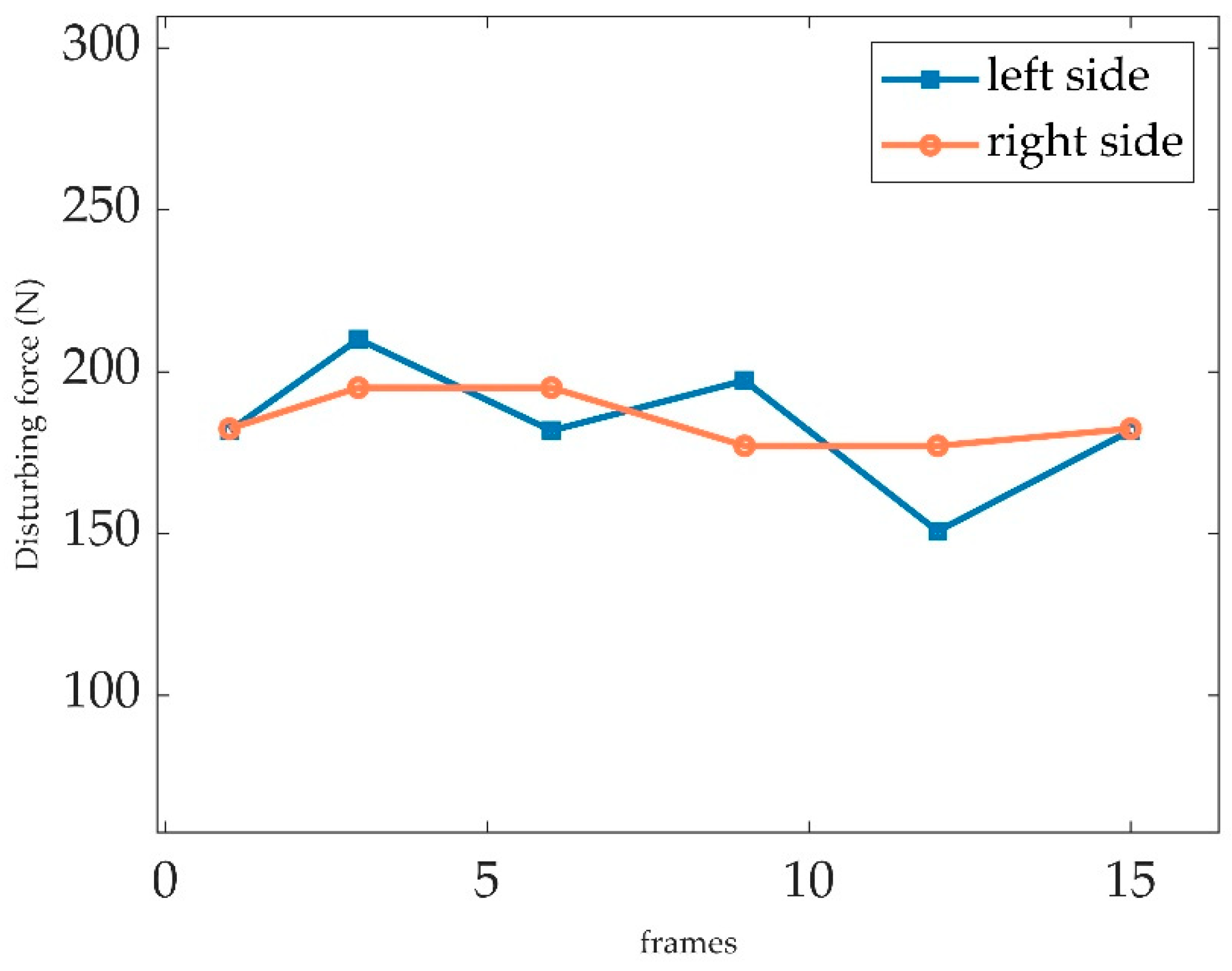At the 6^th frame of the video, when the luggage-laden passenger started turning left, the disturbing force of surrounding passengers in the left increased and reached to the peak of 238 approximately, while the disturbing force in the right side declined. With the completion of passenger turning, the passenger's left side disturbing force dropped and the right-side disturbing force rose and the passenger's left and right-side disturbing force is in a relatively balanced state. When the luggage suddenly drifted to the left, the passengers on the left side of the luggage would gather because of the obstruction of the luggage, thus increasing the density. After the completion of the passenger's turn, the crowd gradually readjusted its density on both sides back to the balanced value.

Figure 7. A luggage-laden passenger made a sudden turn in a L-shaped corridor.

Figure 8. Crowd density of luggage-laden passenger particle in both side with key frames.

Figure 9. Disturbing force of luggage-laden passenger particle in both side with key frames.

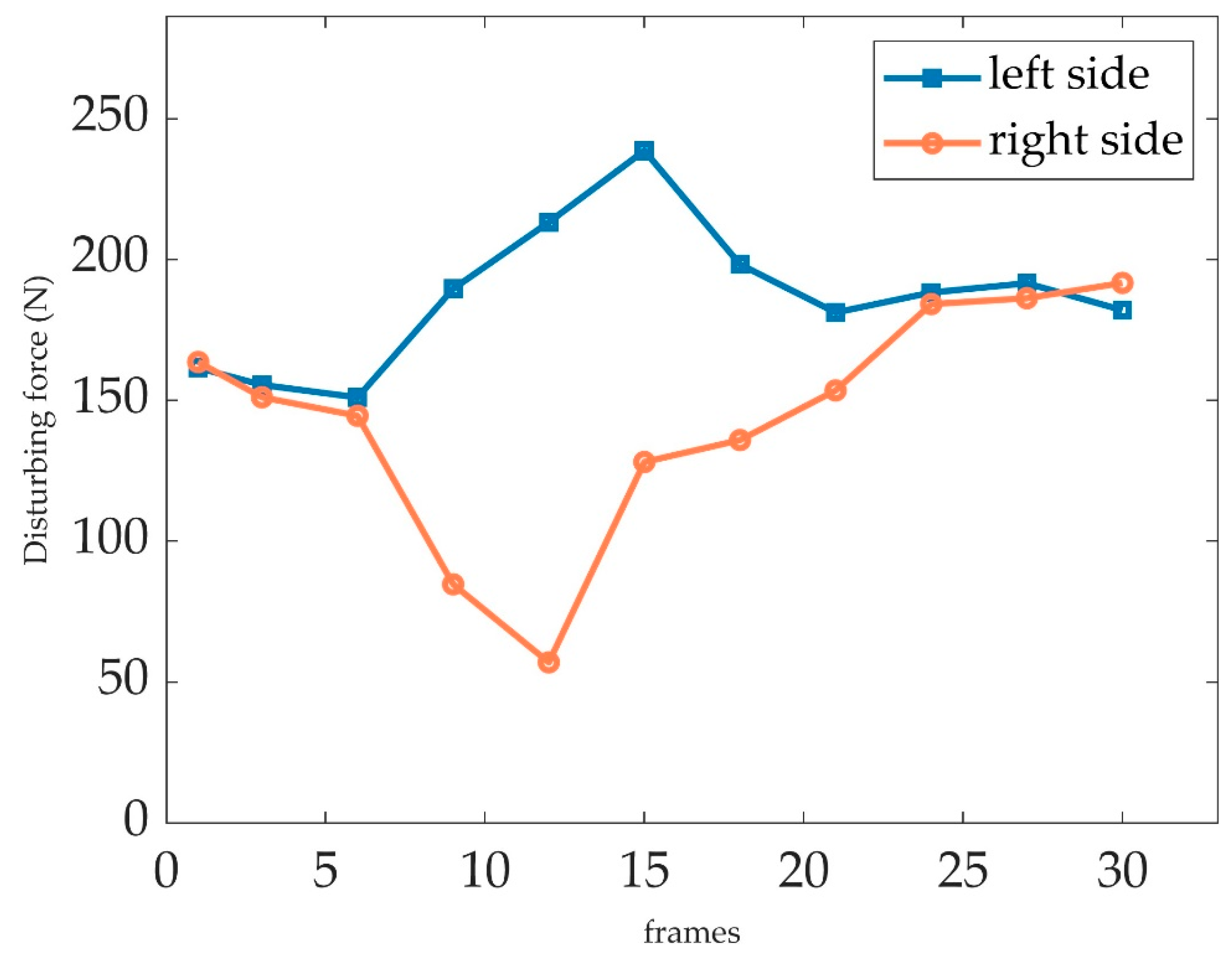
5.3. Case 2: Luggage Retrograding Disturbance Propagation in a Straight Corridor

To further verify the effectiveness of the proposed disturbance propagation model, the retrograding movement of a luggage-laden passenger was considered as the disturbance source in the forward-moving crowd. In the Pathfinder 2022 software, a

20 m \times 25 m

hallway is created as the experiment scenario. As shown in Figure 10, when the luggage-laden passenger crossed the channel in an opposite direction marking with a yellow curve, the normal movement of passed and surrounding passengers was disturbed consequently, which manifests as deviating from the previous forward direction and avoiding luggage-laden passenger. And the disturbance would continue to propagate further. The densities of the both side surrounding pedestrians in this process are shown in Figure 11, and the disturbing force to the both side surrounding pedestrians is shown in Figure 12. In Figure 12 ,

F_{d i s t u r b - r}, F_{d i s t u r b - l}

are the magnitude of the disturbing force of right side and left side respectively, with a slight fluctuation in time but are roughly equal as the trajectory of the luggage-laden passenger is approximately straight.

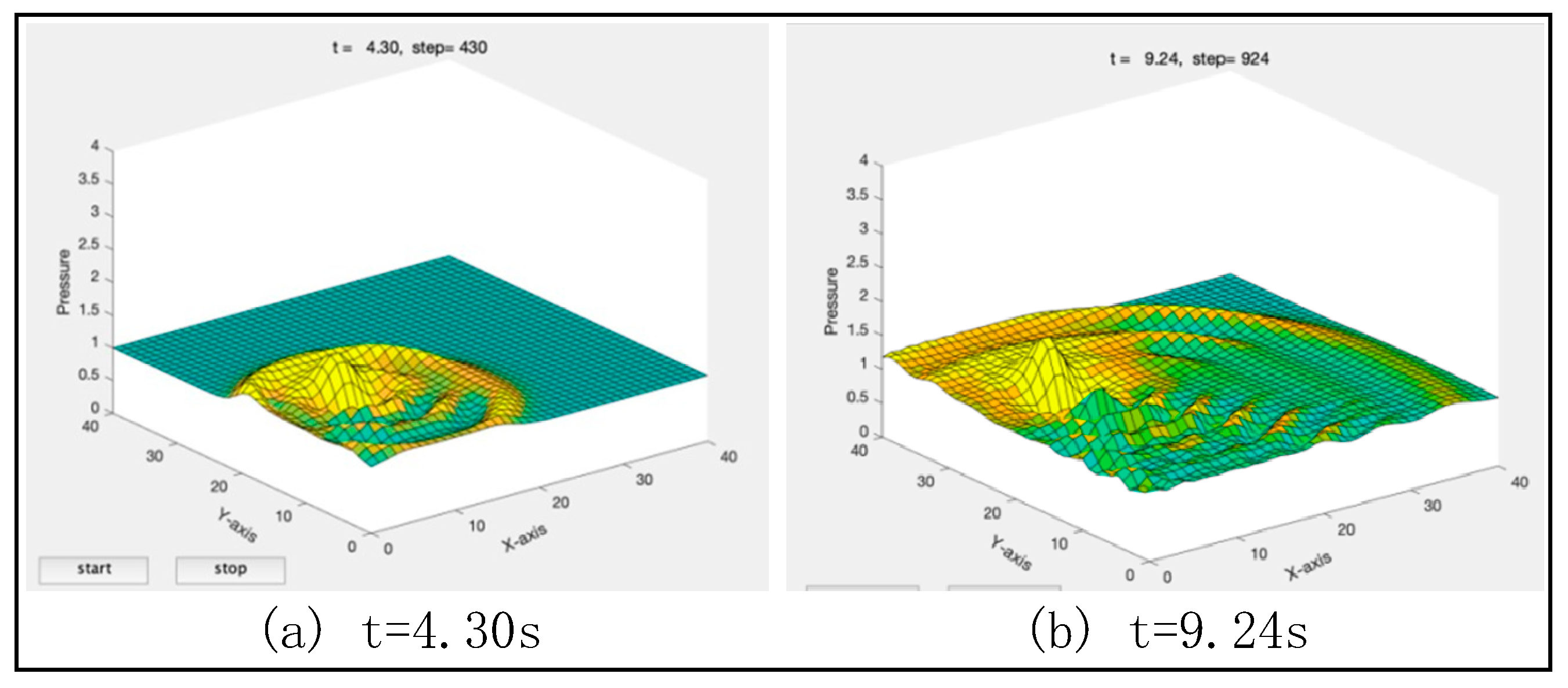
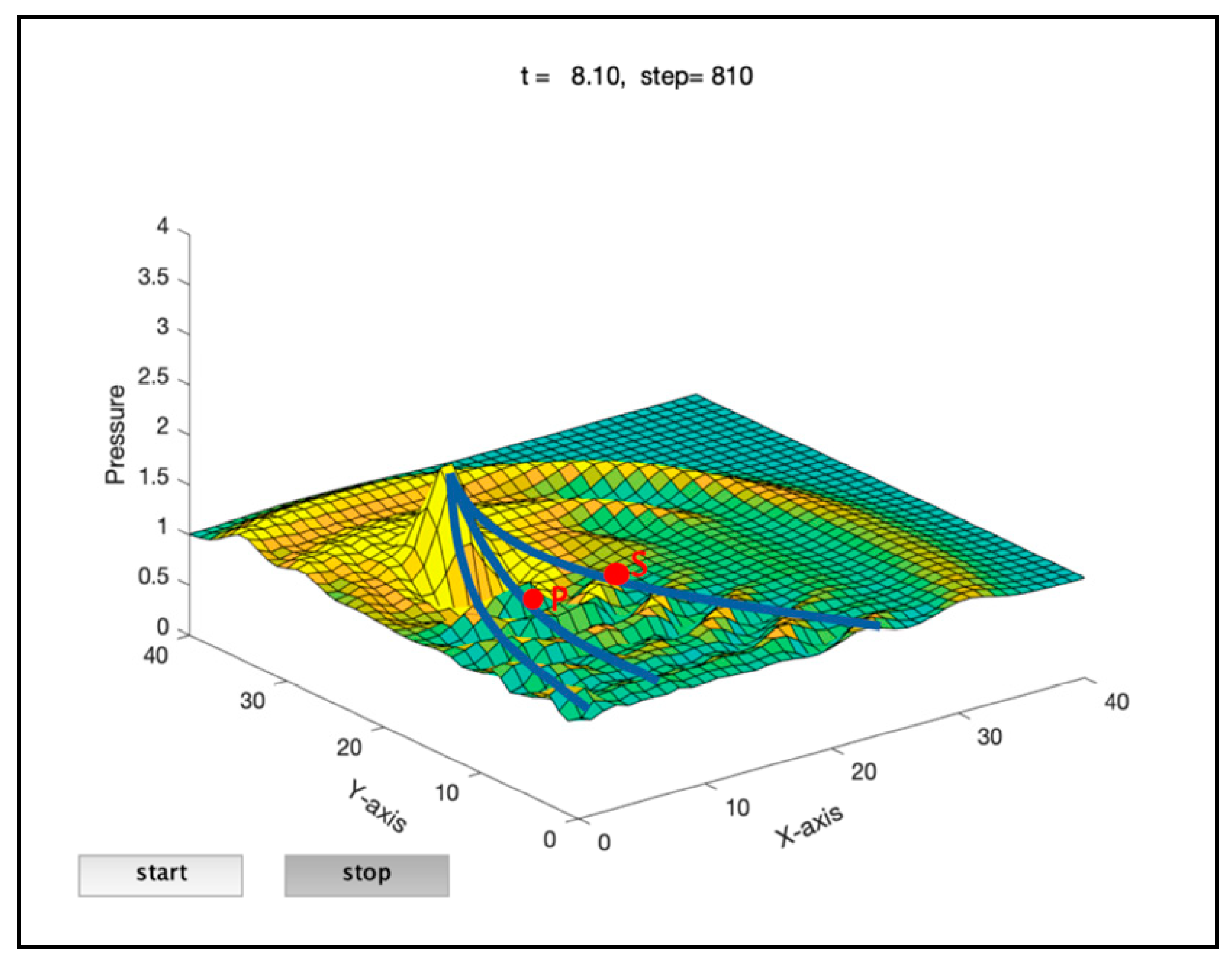
In this experiment, the pressure of the crowd was collected and visualized in MATLAB R2019b. As depicted in Figure 13 (a), when the luggage was advancing and causing a disturbance within the crowd, the propagation of the disturbance consistently intensified, displacing surrounding passengers at an angle towards the rear. The peak of the disturbance wave would form on the rear side of the luggage's motion direction, aligning with the direction of the luggage's disturbing force on the surrounding passengers. Consequently, the dissemination of the disturbance caused by a luggage to the surrounding passengers progressed in a manner consistent with the direction of the disturbing force. In addition, a low-disturbance area was formed behind the luggage.

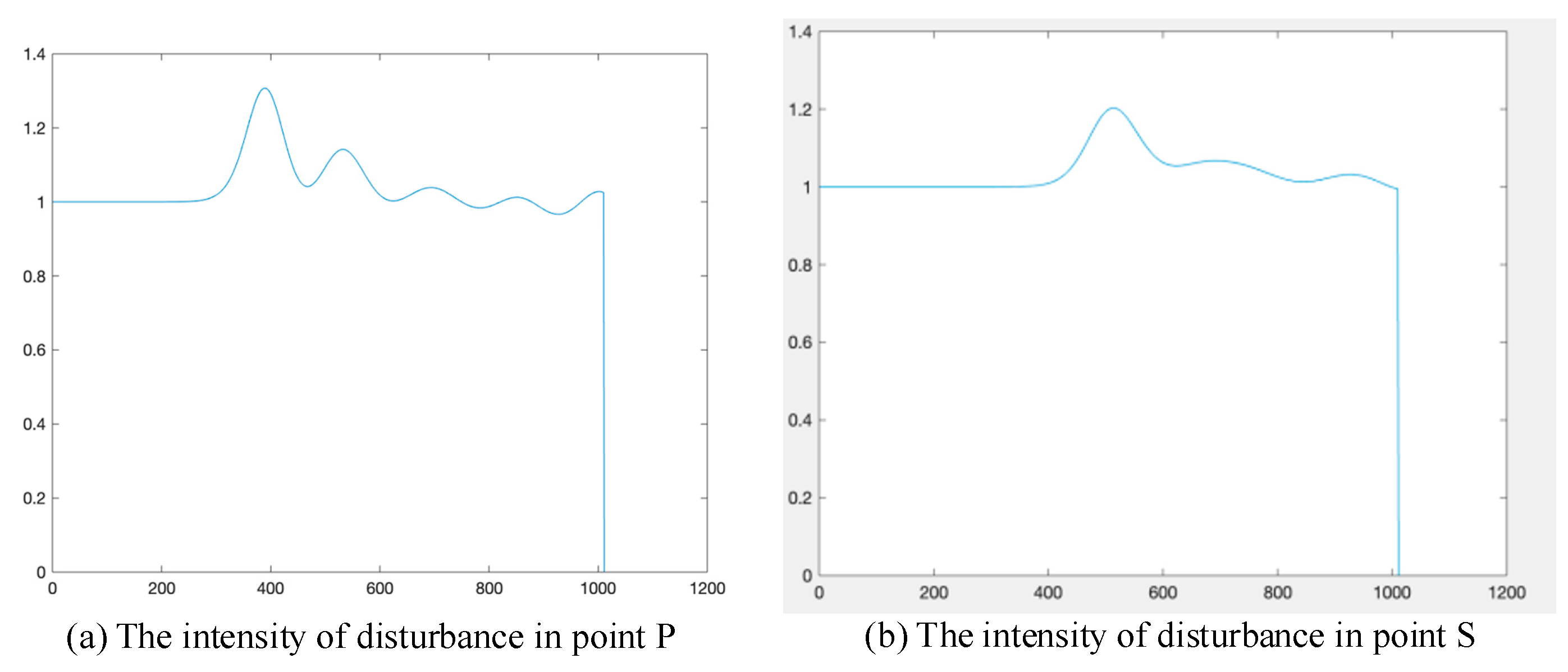
Next, the change in the intensity of the disturbance directly behind the luggage as well as the side rear will be discussed. As shown in Figure 14, points P and S were chosen to represent the front and side rear, respectively. In Figure 15(a), when the luggage-laden passenger particle was passing through point P, the pressure of P was greater than that of point S, with reaching a peak at 400^th frame. As the luggage-laden passenger particle moved away from point P, the pressure at point P oscillated at the frequency of the disturbance propagation and decays. The pressure at point S reaches the maximum at the 500^th frame and remained at about 1, which was maintained in a low equilibrium state with a long fluctuation time and a small fluctuation threshold. This is because disturbances at different moments will be superimposed at point S, making its fluctuation frequency longer. As it was too far from the trigger point of the disturbance, the initial pressure was less than the intensity of point P, but because of the propagation and superposition of disturbance, the pressure attenuation speed was slower than that of point P.

6. Conclusions

In this study, we proposed a dynamics propagation model of luggage drifting motion based on nonlinear pressure and Aw-Rascle model to quantitatively analyze the disturbance of luggage-laden passengers. To verify the proposed model, experiments of luggage drifting and retrograding were conducted in simulations. It was proven that the proposed model can keep consistent with the real-world situation:

(1) During the process of the luggage drifting to the left, the disturbing force exerted on the passengers to its left remains weak. On the right side of the luggage, the disturbing force transits from weak to strong, and then reverts to weak again.

(2) In the case that luggage-laden passenger moves against the flow, the disturbance propagated to the surrounding passengers advance in alignment with the direction of the disturbing force, and a low-disturbance zone is formed behind the luggage.

(3) In our quantitative results of luggage drifting show that the disturbing force of left side passengers upped to 238N and a maximum difference of 153N between left side and right side.

Further research involving more realistic and complex disturbance quantification, as well as model calibration using measured data, is recommended. This effort can enhance pedestrian flow modeling and facilitate crowd management in transportation hubs.

Author Contributions

Conceptualization, methodology, software, validation, formal analysis and investigation, resources, data curation, writing—original draft preparation, B.W., R.Z. and C.L.; writing—review and editing, R.Z. and E.S.W., and visualization, B.W. and Y.M.; supervision and project administration, R.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (No. 72374154).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Xu, D., J. Wang, J. Liu, Y. Wang and J. Jiang, 2023. A simulation study on the impact of abandoned trolley cases on pedestrian evacuation. KSCE Journal of Civil Engineering, 27(3): 1340-1349. [CrossRef]
Zhang, K., S. Yang, L. He and Y. Long, 2017. Research on emergency evacuation of passengers with luggage from bus station. China Safety Science Journal（CSSJ）, 27(1): 30-35. [CrossRef]
Yugendar, P. and K.V.R. Ravishankar, 2018. Crowd behavioural analysis at a mass gathering event. Journal of KONBiN, 46: 20 - 25. [CrossRef]
Laxman, K.K., R. Rastogi and S. Chandra, 2010. Pedestrian flow characteristics in mixed traffic conditions. Journal of Urban Planning and Development-asce, 136: 23-33. [CrossRef]
Tang, J., L. Yang and K. Liu, 2021. Simulation of safety evacuation of personnel at construction site based on bim technology. In: Proceedings of the 24th International Symposium on Advancement of Construction Management and Real Estate, J. TangL. Yang and K. Liu (Eds.). Springer Singapore, Singapore: pp: 1165-1175.
Davis, D.G. and J.P. Braaksma, 1988. Adjusting for luggage-laden pedestrians in airport terminals. Transportation Research Part A: General, 22(5): 375-388. [CrossRef]
Jahedinia, F., M. Bagheri, A. Naderan and Z. Bahramian, 2023. Simulation of luggage-laden passengers’ behavior in the evacuation process based on a floor field ca model case study: Tehran metro-rail transfer corridor. SIMULATION, 99(7): 681-701. [CrossRef]
Zhuang, Y., A. Schadschneider, H. Cheng and L. Yang, 2018. Estimating escalator vs stairs choice behavior in the presence of entry railing: A field study. KSCE Journal of Civil Engineering, 22(12): 5203-5214. [CrossRef]
Zhao, R., D. Wang, Y. Wang, C. Han, P. Jia, C. Li and Y. Ma, 2021. Macroscopic view: Crowd evacuation dynamics at t-shaped street junctions using a modified aw-rascle traffic flow model. IEEE Transactions on Intelligent Transportation Systems, 22(10): 6612-6621. [CrossRef]
Xiaofei, L., Experimental study on the effect of luggage type on pedestrian movement characteristics in stairs. Master Dissertation, Southwest Jiaotong University, 2022-05-17.
Fang, Z., W. Lv, L.-X. Jiang, Q. Xu and W. Song, 2015. Observation, simulation and optimization of the movement of passengers with baggage in railway station. International Journal of Modern Physics C, 26: 1550124. [CrossRef]
Fu, L.B., Y.Q. Chen, H.G. Qin, Q.Y. Chen, Y.J. He and Y.Q. Shi, 2023. Dynamics of merging flow involving luggage-laden pedestrians in a y-shaped corridor: An experimental study. Physica A, 628. [CrossRef]
Shi, Z.G., J. Zhang, X.X. Ren and W.G. Song, 2020. Quantifying the impact of luggage on pedestrian walking and running movements. Safety Science, 130. [CrossRef]
Shi, D., J. Ma, Q. Luo, X. Li, J. Chen and P. Lin, 2021. Fundamental diagrams of luggage-laden pedestrians ascending and descending stairs. Physica A: Statistical Mechanics and its Applications. [CrossRef]
Deng, Q., Z. Fu, T. Li, J. Ma and L. Luo, 2021. Effect of luggage-carrying on pedestrian flow through bottleneck: An experimental study. Transportmetrica A: Transport Science, 18: 1734 - 1753. [CrossRef]
Huang, S., R. Wei, S. Lo, S. Lu, C. Li, C. An and X. Liu, 2019. Experimental study on one-dimensional movement of luggage-laden pedestrian. Physica A: Statistical Mechanics and its Applications, 516: 520-528. [CrossRef]
Ma, J., W.G. Song, S.M. Lo and Z.M. Fang, 2013. New insights into turbulent pedestrian movement pattern in crowd-quakes. Journal of Statistical Mechanics: Theory and Experiment, 2013(02): P02028. [CrossRef]
Wei, J., W. Fan, Y. Guo, J.S. Hu and Y. Fang, 2020. An extended social force model for pedestrian evacuation under disturbance fluctuation force. International Journal of Modern Physics C. [CrossRef]
Wang, X., Z. Zhang, Y. Wang, J. Yang and L. Lu, 2022. A study on safety evaluation of pedestrian flows based on partial impact dynamics by real-time data in subway stations. Sustainability, 14(16): 10328-10347. [CrossRef]
Guo, Y., S. Ma, F. Wei, L. Lu, F. Sun and J. Wang, 2022. Analysis of behavior characteristics for pedestrian twice-crossing at signalized intersections based on an improved social force model. Sustainability, 14(4): 2003-2020. [CrossRef]
Zeng, W., H. Nakamura and P. Chen, 2014. A modified social force model for pedestrian behavior simulation at signalized crosswalks. Procedia - Social and Behavioral Sciences, 138: 521-530. [CrossRef]
Lu, C.X., 2006. Analysis on the wave of pedestrians. China Safety Science Journal（CSSJ）(02): 30-34+146. [CrossRef]
Qin, W., B. Cui and X. Lou, 2019. Tracking control of disturbed crowd dynamic system using unit sliding mode control and feedback linearization. Nonlinear Dynamics, 98(3): 2247-2260. [CrossRef]
Flurin, S.H., B. Michel, F. Bilal and M. Thomas, 2014. A macroscopic loading model for time-varying pedestrian flows in public walking areas. Transportation Research Part B: Methodological, 69: 60-80. [CrossRef]
Wang, P., G. Yu, X. Wu and Y. Wang, 2017. Linear and nonlinear stability analysis of an extended car-following model considering pedestrians on adjacent lane. Nonlinear Dynamics, 88(1): 777-789. [CrossRef]
Zhao, R., Q. Hu, Q. Liu, C. Li, D. Dong and Y. Ma, 2020. Panic propagation dynamics of high-density crowd based on information entropy and aw-rascle model. IEEE Transactions on Intelligent Transportation Systems, 21(10): 4425-4434. [CrossRef]
Li, C., R. Zhao, Y. Wang, P. Jia, W. Zhu, Y. Ma and M. Li, 2023. Disturbance propagation model of pedestrian fall behavior in a pedestrian crowd and elimination mechanism analysis. IEEE Transactions on Intelligent Transportation Systems: 1-11. [CrossRef]
Cundall, P.A. and O.D.L. Strack, 1979. A discrete numerical model for granular assemblies. Geotechnique, 29: 47-65. [CrossRef]
Mindlin, R.D., 2021. Compliance of elastic bodies in contact. Journal of Applied Mechanics, 16(3): 259-268. [CrossRef]
Pasha, M., S. Dogbe, C. Hare, A. Hassanpour and M. Ghadiri, 2014. A linear model of elasto-plastic and adhesive contact deformation. Granular Matter, 16(1): 151-162. [CrossRef]
Maio, F.D. and A.D. Renzo, 2005. Modelling particle contacts in distinct element simulations: Linear and non-linear approach. Chemical Engineering Research & Design, 83: 1287-1297. [CrossRef]
X, L., Study on the human crowd characteristics and trampling and crowd risk in railway station. Doctor Dissertation, Beijing Jiaotong university, 2020-.
Aw, A. and M. Rascle, 2000. Resurrection of "second order" models of traffic flow. SIAM Journal on Applied Mathematics, 60(3): 916-938. [CrossRef]
Helbing, D., I. Farkas and T. Vicsek, 2000. Simulating dynamical features of escape panic. Nature, 407(6803): 487-490. [CrossRef]
Zhao, R., Y. Wang, P. Jia, W. Zhu, C. Li, Y. Ma and M. Li, 2023. Abnormal behavior detection based on dynamic pedestrian centroid model: Case study on u-turn and fall-down. IEEE Transactions on Intelligent Transportation Systems, 24(8): 8066-8078. [CrossRef]
Zhao, R., Q. Liu, Q. Hu, D. Dong, C. Li and Y. Ma, 2021. Lyapunov-based crowd stability analysis for asymmetric pedestrian merging layout at t-shaped street junction. IEEE Transactions on Intelligent Transportation Systems, 22(11): 6833-6842. [CrossRef]
Rascle, M., 2002. An improved macroscopic model of traffic flow: Derivation and links with the lighthill-whitham model. Mathematical and Computer Modelling, 35(5): 581-590. [CrossRef]
Zhang, B.S., 2021. Experimental study on the influence of baggage weight on evacuation speed. Fire Science and Technology, 40(06): 837-842.

Figure 1. Particle diagram of passengers and luggage.

Figure 2. Diagram of a linear contact model. Note, pink disk represents luggage-laden particle, and blue disk represents non-luggage particle.

Figure 3. Illustration of luggage drifting motion and passengers’ pressure when luggage drifting. (a) The greater sway amplitude of luggage-laden passenger, with higher probability to drift. (b)Big drift angles caused by a slight turn at high speed. (c) Diagram of the pressure of surrounding passengers in case of luggage drifting.

Figure 4. Schematic diagram of the luggage case steering pressure characteristics.

Figure 5. Passenger and luggage model in a simulation (Pathfinder2022 software).

Figure 6. Schematic illustration of particles in simulation (Pathfinder2022 software).

Figure 10. Simulation of a passenger carrying luggage went against the crowd.

Figure 11. Crowd density of luggage-laden passenger particle in both side.

Figure 12. Disturbing force of luggage-laden passenger particle in both side.

Figure 13. Contact pressure distribution during a luggage retrograding.

Figure 14. Contact pressure distribution of point P and S in a passenger crowd at the moment of t=8.10s.

Figure 15. The change of the contact pressure in point P and S caused by luggage retrograding in a passenger crowd.

Table 1. Density-velocity of crowd in key areas[32].

Key areas in transportation hubs	$ν_{l} (ρ)$
Entrance of corridor	$v (ρ) = - 0.3657 ρ + 1.6721$
Middle of corridor	$v (ρ) = 0.806 e^{- 0.206 ρ}$
Exit of corridor	$v (ρ) = 0.0239 ρ^{2} - 0.0121 ρ + 1.3195$
Down stairs	$v (ρ) = 0.7909 e^{- 0.189 ρ}$
Up stairs	$v (ρ) = 0.8394 e^{- 0.212 ρ}$
Platform queuing area	$v (ρ) = 1.3016 e^{- 0.549 ρ}$

Table 2. Parameter setting in simulation.

Category	Parameters and their description	Value
Non-luggage passengers particle	Initial density $ρ_{sp}$ （ped /m²）	Variable
	Desire velocity $v_{s p}^{0} ρ$ （m/s）	Variable
	Initial velocity $v_{s p} (ρ)$ （m/s）	1.2m/s
	Particle radius $r_{s p}$ （m）	1.1m
	Particle mass $m_{sp}$ （kg）	64.08
Contact	Fraction coefficient μ	0.3
	Normal stiffness k_n	$1203.90$
	Initial shear stiffness k_s	$920.65$
	Normal damping coefficient $β_{n}$	$β_{n} (ρ, k_{n})$
	Shear damping coefficient $β_{s}$	$β_{s} (ρ, k_{s})$
Luggage-laden passengers particle	Initial density ρ（ped /m²）	Variable
	Desire velocity $v^{0}$ （m/s）	Variable
	Initial velocity $v (ρ)$ （m/s）	1.2m/s
	Particle radius $r$ （m）	0.75
	Particle radius m（kg）	74

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Disturbance Propagation Model of Luggage Drifting Motion Based on Nonlinear Pressure in Typical Passenger Corridors of Transportation Hubs

Abstract

Keywords:

Subject:

1. Introduction

2. Related Works

2.1. Impact of Carried Luggage on Pessenger Crowd

2.2. Disturbance Propagation in Crowd Flow

3. Disturbance Dynamics Model of Luggage-laden Passenger

3.1. Dynamic Pressure between Luggage-Laden and Non-Luggage Passengers

3.2. Disturbing Effect of Luggage Drifting Motion

4. The Disturbance Propagation Model based on AR-Rascle Model in Crowd Flow

4.1. Disturbance of Luggage-Laden Passenger Particle on Surrounding Passengers

4.2. Disturbance Propagation Model based on Aw-Rascle Model

5. Case Study and Discussion

5.1. Experiment Parameters Initialization

5.2. Case 1: Luggage Drifting Disturbance Propagation in a L-Shaped Corridor

5.3. Case 2: Luggage Retrograding Disturbance Propagation in a Straight Corridor

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe