1. Introduction

2. Results and Discussion

2.1. Analysis of the Reactivity Indices at the Ground State (GS) of the Reagents

The reactivity indices [5,6] for Cp 1 and the cyanoethylene series 4 computed at the GS are gathered in Table 2. Computational details are given in Supplementary Material. The B3LYP/6-31G(d) computational method was used because the original reactivity scales were established at that level [5,6]. Analysis of the electronic chemical potentials [39] μ of the regents allows establishing the polar character of an organic reaction, as well as the direction of the flux of the electron density unambiguously, which enable the classification of polar reactions [40]. The electronic chemical potential μ of Cp 1, −3.01 eV, is above those of the cyanoethylene series 4, between −4.70 (1CN) and −7.04 (4CN) eV, indicating that in these polar reactions the electron density will flux from Cp 1 towards these cyanoethylenes, being classified as P-DA reactions of forward electron density flux (FEDF) [40,41].

Cp 1 presents an electrophilicity ω index [4] of 0.83 eV and a nucleophilicity N index [8] of 3.37 eV, being classified as a moderate electrophile and a strong nucleophile. Consequently, Cp 1 will participate in P-DA reactions only as a good nucleophile. On the other hand, ethylene 6 presents an electrophilicity ω index of 0.73 eV and a nucleophilicity N index of 1.87 eV, being classified as a marginal electrophile and a marginal nucleophile. Consequently, ethylene 6 will never participate in a P-DA reaction. The non-polar Diels-Alder (N-DA) reaction of Cp 1 with ethylene 6 is classified within MEDT as a null electron density flux (NEDF) reaction [41].

The electrophilicity ω index of cyanoethylene series 4 ranges from 1.74 eV (1CN) to 5.95 eV (4CN), while the nucleophilicity N index ranges from 1.25 eV (1CN) to 0.00 eV (4CN). Note that the nucleophilicity N index for 4CN is exactly 0.00 eV because this molecule was chosen as the reference for the empirical nucleophilicity N scale [6,9]. Thus, while 1CN is located on the borderline between moderate electrophiles, the other cyanoethylenes are clearly classified as strong electrophiles; note that the tri- and tetracyanoethylenes 3CN and 4CN, with ω > 4.0 eV, are classified as superelectrophiles, a behavior that accounts for their high reactivity in polar processes [9] (see Table 1). On the other hand, all cyanoethylenes are classified as marginal nucleophiles. Consequently, this cyanoethylene series will participate towards Cp 1 in P-DA reactions of forward FEDF [41]. Both electrophilic and nucleophilic properties of this series vary with the number of cyano groups on the ethylene.

Along a polar cycloaddition reaction involving non-symmetric species such as 1CN, 2CN or 3CN, the most favorable reaction path involves the two-center interaction with the most electrophilic center of these cyanoethylenes [15]. In this sense, the analysis of the electrophilic P_k⁺ Parr functions [42] of the cyanoethylene series is a valuable tool to characterize the most electrophilic center of these molecules (see Figure 2 and Table 3).

Table 3. Gas-phase B3LYP/6-31G(d) electrophilic P_k⁺ Parr functions and local electrophilicity ω_k indices at the C1 and C2 carbons of the cyanoethylene series 4.

Table 3. Gas-phase B3LYP/6-31G(d) electrophilic P_k⁺ Parr functions and local electrophilicity ω_k indices at the C1 and C2 carbons of the cyanoethylene series 4.

	Pk+		ωk		Δωk
	C1	C2	C1	C2
1CN	0.63	0.20	1.10	0.34	0.76
2cCN	0.35	0.35	0.98	0.98	0.00
2tCN	0.33	0.33	1.01	1.01	0.00
2CN	0.74	0.10	2.28	0.30	1.98
3CN	0.46	0.22	2.03	0.94	1.09
4CN	0.32	0.32	1.91	1.91	0.00

Analysis of the electrophilic P_k⁺ Parr functions at the C1 and C2 carbons of the cyanoethylene series 4 indicates that the two ethylene carbons gather more than 60 % of the total amount of spin density in these molecules; i.e. the two carbons will accumulate more than 60 % of the electron density transferred to these ethylene derivatives via the GEDT in these P-DA reactions. As expected, the symmetrically substituted ethylenes 2cCN, 2tCN and 4CN present identical electrophilic P_k⁺ Parr functions at the two carbons, while the non-symmetrically substituted 1CN, 2CN and 3CN present a non-symmetrical electrophilic activation; in the three cases, the less substituted carbon present the higher electrophilic P_k⁺ Parr function (see Table 3).

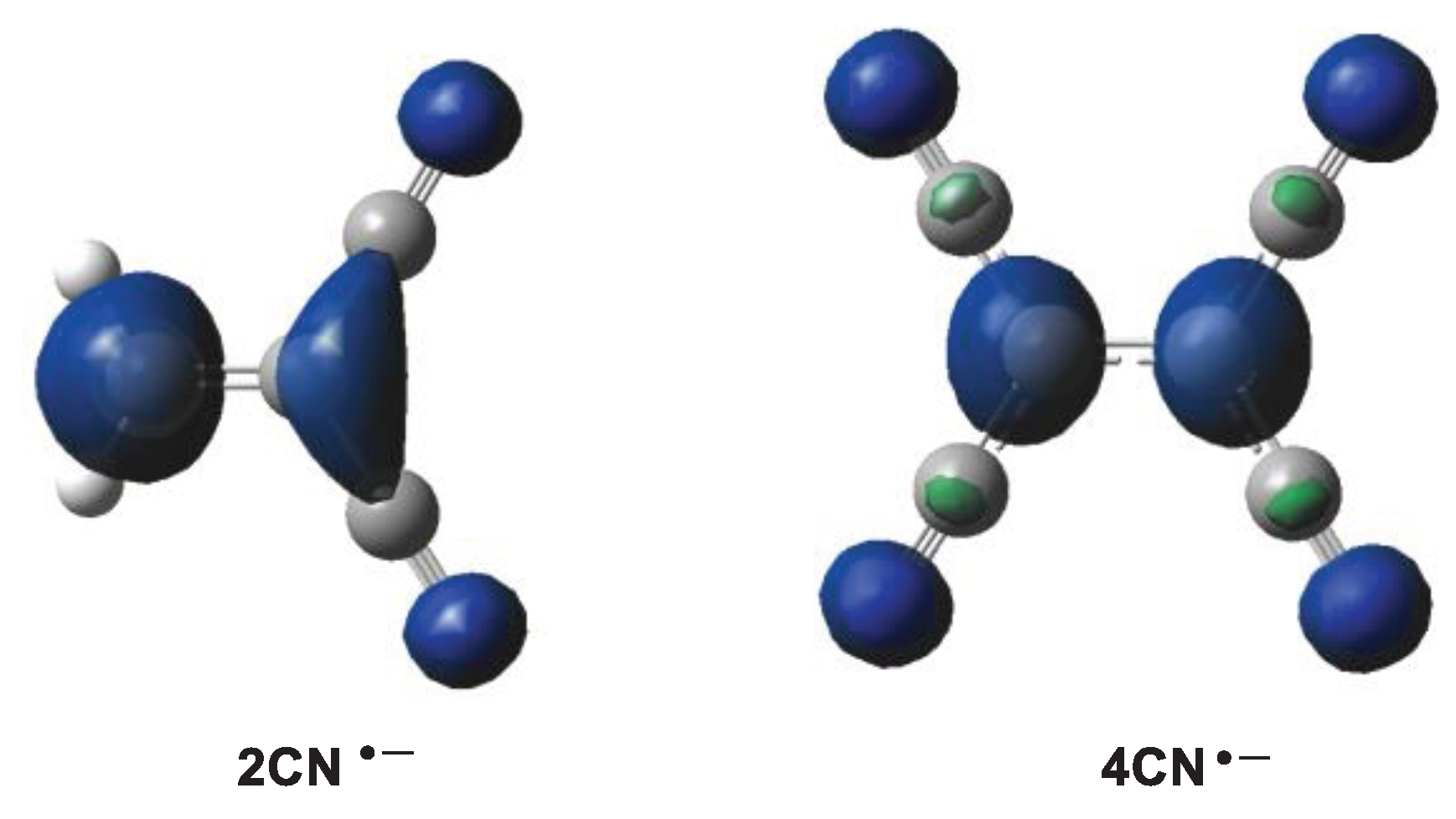
Figure 2. 3D representations of the Mulliken atomic spin densities of the radical anions of 2CN and 4CN.

Figure 2. 3D representations of the Mulliken atomic spin densities of the radical anions of 2CN and 4CN.

Analysis of the local electrophilicity ω_k indices [43] at the C1 and C2 carbons of these cyanoethylenes allows obtaining some appealing conclusions (see Table 3): i) while the symmetrically substituted ethylenes 2cCN, 2tCN and 4CN present identical electrophilic activation at the two ethylene carbons, predicting synchronous TSs, the non-symmetrically substituted 1CN, 2CN and 3CN present different electrophilic activation, predicting asynchronous TSs [15]; ii) at the non-symmetrically substituted 1CN, 2CN and 3CN cyanoethylenes, the less substituted C1 carbon presents the higher electrophilic activation, indicating that this carbon will be the preferred center to participate in the two-center interaction with the C6 carbon of the nucleophilic Cp 1 [15]; and finally, iii) the local electrophilicity at the C1 carbon of 2CN, ω_k = 2.28 eV, is higher than that at the C1 carbon of 3CN, ω_k = 2.03 eV, despite the more electrophilic character of 3CN than 2CN. Note that the two C1 and C2 carbons of the symmetrically substituted 2cCN and 2tCN are electrophilically activated by ca. ω_k = 1.0 eV each one.

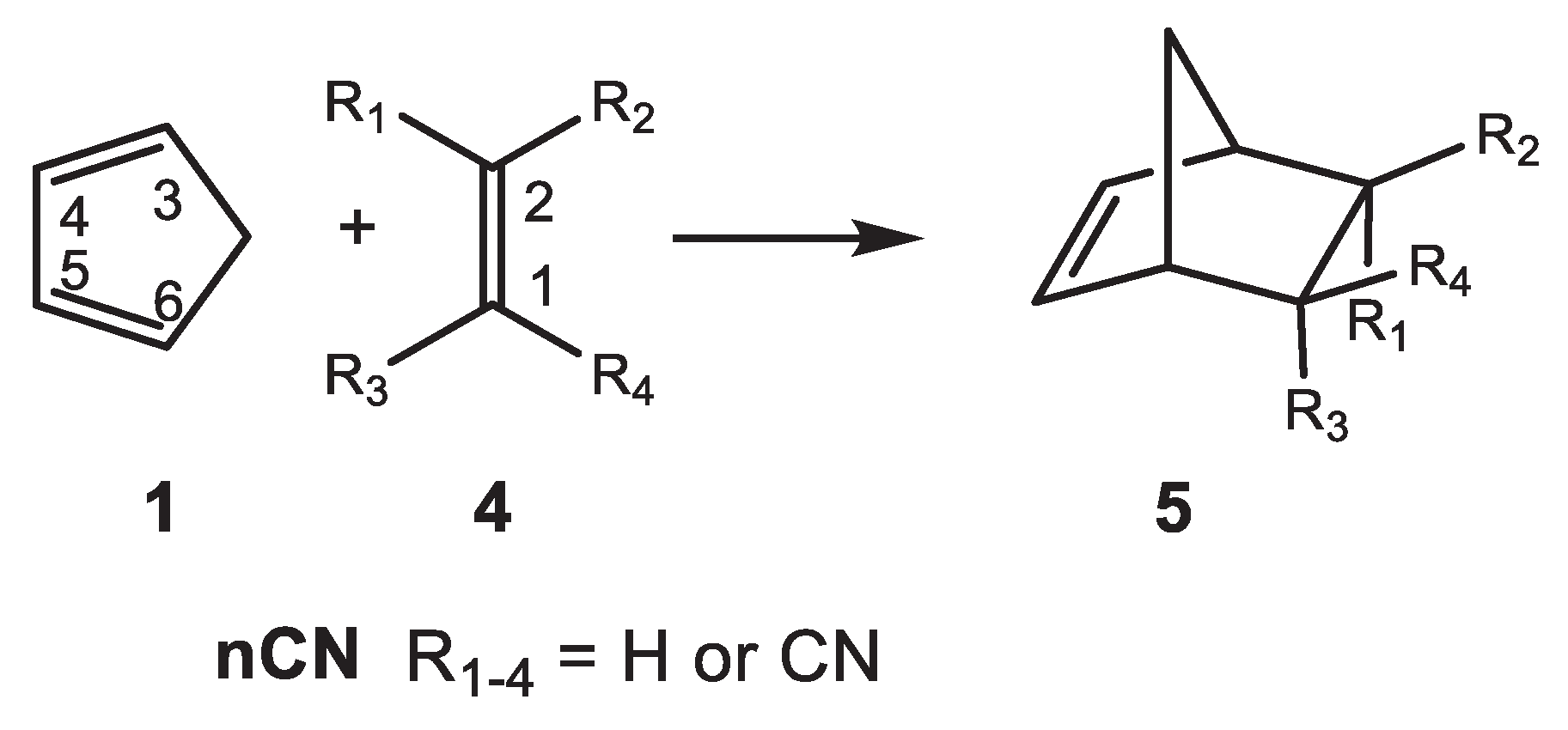
2.2. Study of the P-DA Reactions of Cp 1 with the Cyanoethylene Series 4

For the non-symmetrically substituted cyanoethylenes 1CN, 2CN and 3CN, two stereoisomeric reaction paths are feasible; only the endo approach mode was studied herein (see Scheme 3). A detailed analysis of the potential energy surfaces is found in reference 15. The M06-2X/6-311G(d,p) relative Gibbs free energies of TSs and CAs in dioxane are given in Table 4, while complete thermodynamic data are given in Table S3 in Supplementary Material.

The activation Gibbs free energies range from 25.9 (TS-1CN) to 12.7 (TS-4CN) kcal mol^-1. Note that the non-polar (N-DA) reaction of Cp 1 with ethylene 6 displays a very high activation Gibbs free energy of 29.8 kcal mol^-1 (see Table 4). These DA reactions are exergonic in the narrow range between –12.7 (CA-1CN) and –14.9 (CA-4CN) kcal mol^-1.

Table 4. M06-2X/6-311G(d,p) relative Gibbs free energies (ΔG in kcal mol^-1), computed at 293.15 K and 1 atm in dioxane, of TSs and CAs involved in the DA reactions of Cp 1 with ethylene 6 and the cyanoethylene series 4. The computed relative reaction rate constants k_r, with respect the reaction with ethylene 6, is also included.

Table 4. M06-2X/6-311G(d,p) relative Gibbs free energies (ΔG in kcal mol^-1), computed at 293.15 K and 1 atm in dioxane, of TSs and CAs involved in the DA reactions of Cp 1 with ethylene 6 and the cyanoethylene series 4. The computed relative reaction rate constants k_r, with respect the reaction with ethylene 6, is also included.

Reagent	TS	ΔG	kr	Product	ΔG
Ethylene 6	TS-Et	29.8	1.00E+00	CA-Et	-12.8
1CN	TS-1CN	25.9	8.09E+02	CA-1CN	-12.7
2cCN	TS-2cCN	22.3	3.91E+05	CA-2cCN	-13.8
2tCN	TS-2tCN	22.0	6.54E+05	CA-2tCN	-14.5
2CN	TS-2CN	18.2	4.45E+08	CA-2CN	-13.0
3CN	TS-3CN	15.9	2.31E+10	CA-3CN	-14.9
4CN	TS-4CN	12.7	5.62E+12	CA-4CN	-14.9

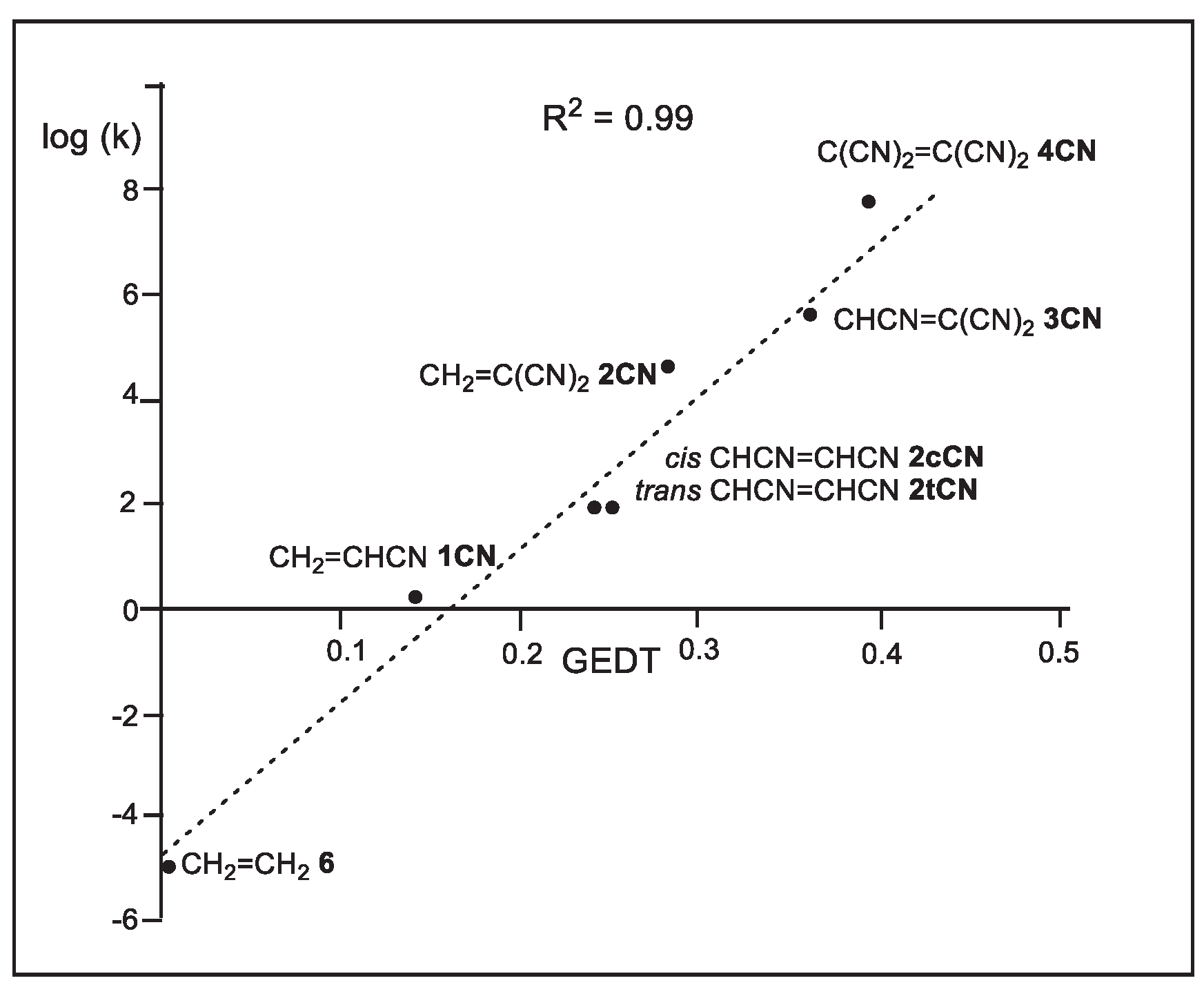
A representation of the activation Gibbs free energies versus the number of cyano groups on the ethylene shows a very good linear correlation with a coefficient of determination R² = 0.94 (see Figure S4 in Supplementary Material). This graph shows that the presence of the cyano group on the ethylene is additive, and has a marked effect on the kinetics of the reactions, in clear agreement with the experimental outcomes observed by Sauer et al. (see Table 1).

Using the Eyring-Polanyi equation [44], the relative reaction rate constants k_r of the P-DA reactions between Cp 1 and the cyanoethylene series 4, with respect to that with ethylene 5, were computed (see Table 4). The relative reaction rate constants k_r range from 8.09·10² (1CN) to 5.62·10¹² (4CN). Thus, the P-DA reaction involving the superelectrophilic tetracyanoethylene 4CN is 10¹² faster than the N-DA reaction of Cp 1 with ethylene 6. A representation of the logarithm of the experimental relative reaction rate constants log(k_rexp), with respect to the N-DA reactions of Cp 1 with ethylene 6, versus the logarithm of the computed relative reaction rate constants log(k_rcomp) shows a complete linear correlation with an R² =1.00 (see Figure S5 in Supplementary Material

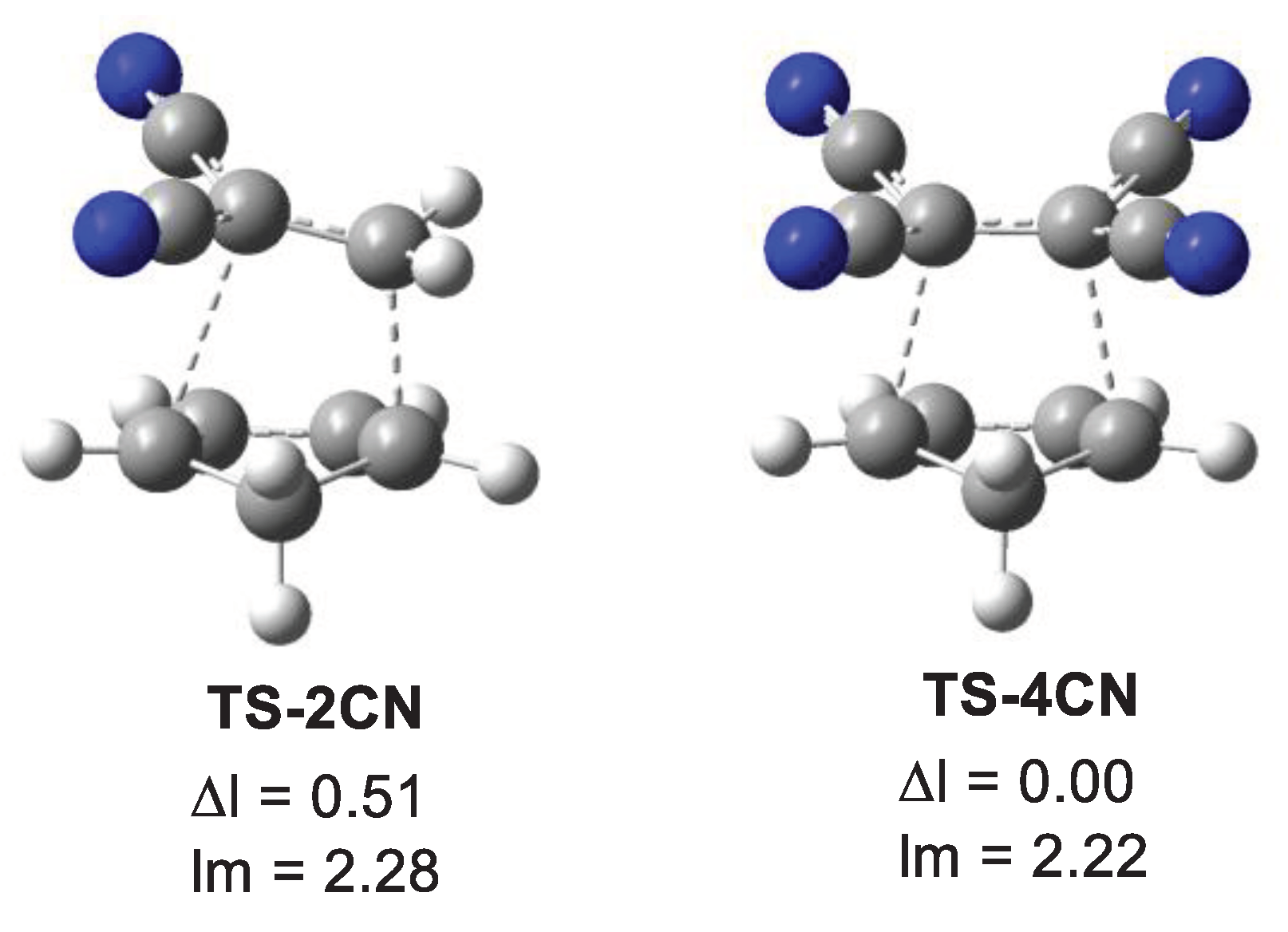
The main geometrical parameters at the gas phase TSs, i.e. the distances between the two pairs of C1−C6 and C2−C3 interacting centres, together with the geometrical asynchronicity, Δl, and the average of the two C−C distances, lm, are given in Table 5. Geometrical data in dioxane are gathered in Table S4 in Supplementary Material; they show no significant changes compared to the gas phase parameters. The geometries of two representative TSs are given in Figure 3, while the geometries of all TSs are given in Figure S6 in Supplementary Material. Some appealing conclusions can be obtained from the geometrical data given in Table 5: i) from a geometrical point of view, the TSs can be classified as synchronous and asynchronous TSs, depending on the evolution of the new C−C single bond formation; ii) while the synchronous TSs, Δl = 0.0 Å, come from the symmetrically substituted ethylenes, asynchronous TSs, Δl > 0.2 Å, come from the non-symmetrically substituted ethylenes; iii) interestingly, the average of the two C1−C6 and C2−C3 distances at all TS, including TS-Et, is 2.24 Å (see lm in Table 5). This behavior indicates that all TSs have a comparable advanced/early character. Considering that the C−C single bond formation takes place in the short range of 2.0-1.9 Å [17], these geometrical parameters indicate that formation of the first C−C single bond has not yet started in any of the TSs (see later). This behavior is consistent with Woodward's 1942 proposal that electron transfer occurs before the formation of the new C-C single bonds [13].

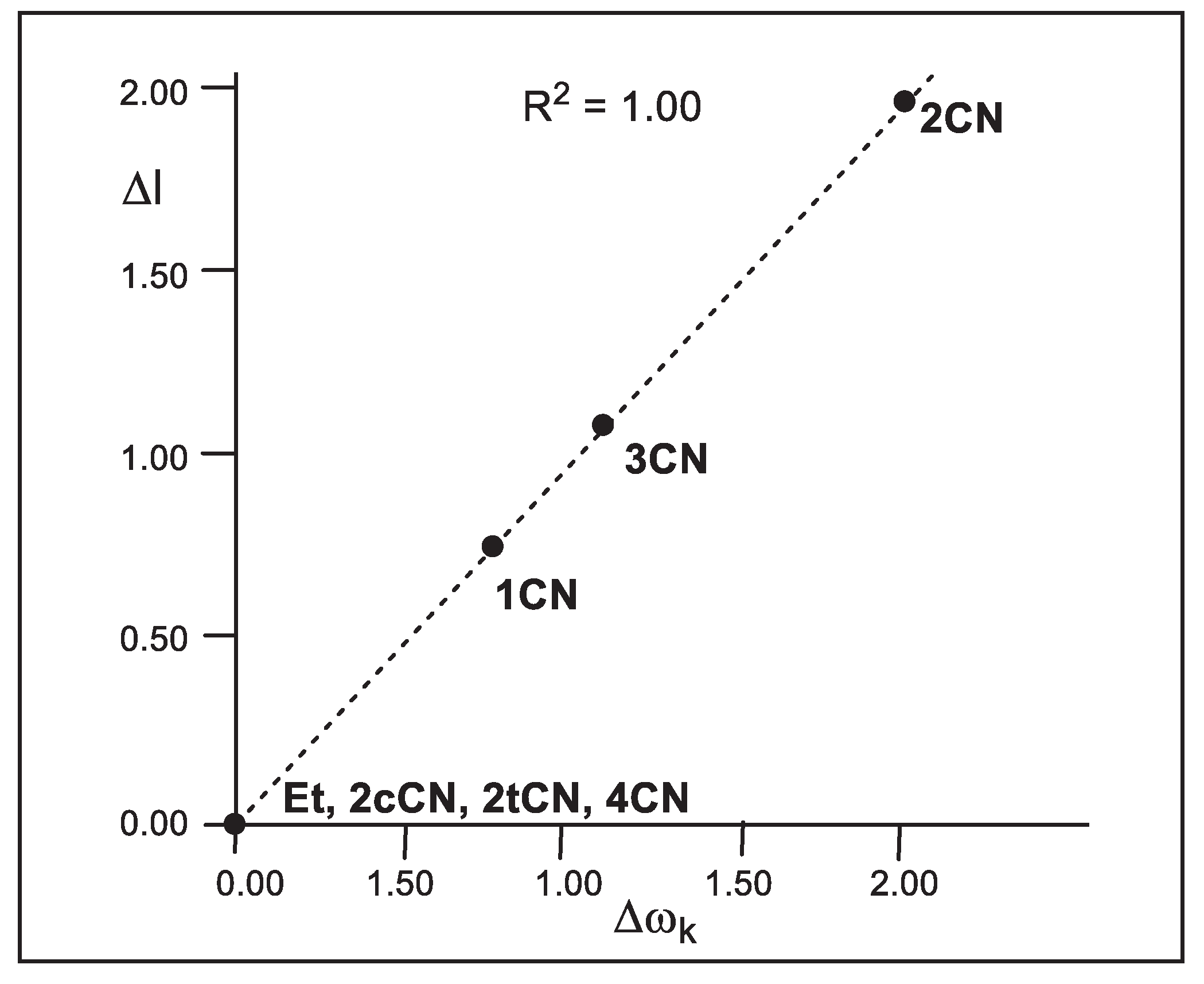
As Figure 4 shows, a complete linear correlation between the geometrical asynchronicity, Δl, of the TSs and the difference of the local electrophilicity ω_k indices of the C1 and C2 carbons of the cyanoethylenes, Δω_k, is established for the first time; R² =1.00. Thus, the symmetrically substituted cyanoethylenes 2cCN, 2tCN and 4CN with Δω_k = 0.00 eV yield synchronous TSs, while non-symmetrically substituted cyanoethylenes 1CN, 2CN and 3CN with Δω_k > 0.76 eV yield asynchronous TSs. This excellent relationship indicates that the different electrophilic activation of the two C1 and C2 carbons of the electrophilic ethylenes caused by the EW substitution controls the asynchronicity of the C−C single bond formation in these P-DA reactions.

Analysis of GEDT at the TSs permits to quantify the polar character of these DA reactions [17]. The GEDT values computed at the seven TSs in gas phase are given in Table 5. GEDT values in dioxane are displayed in Table S4 in Supplementary Material and show no significant changes compared to the gas-phase values. As expected, the GEDT value at TS-Et is negligible, 0.03 e, as a consequence of the marginal electrophilic character of ethylene 5 (see Table 2). Consequently, the corresponding DA reaction has a non-polar character, being classified as NEDF [41]. The presence of a cyano group in 1CN notably increases the GEDT at TS-1CN to 0.14 e. The addition of cyano groups at the ethylene moiety markedly increases the GEDT at the corresponding TSs, reaching a maximum value at TS-4CN with a GEDT = 0.42 e. These P-DA reactions are classified as FEDF [40,41], in agreement with the previous reactivity indices prediction (see Section 2.1). The presence of at least two cyano groups makes the corresponding DA reaction very polar (see Table 5). It is worth mentioning that GEDT values obtained from an NPA analysis do not significantly vary with the charge partitioning method because of its formal definition (see Computational Details). For instance, gas-phase GEDT values computed with Bader charges show no significant variation (see in Table S4 and the linear regression in Figure S7 in Supplementary Material).

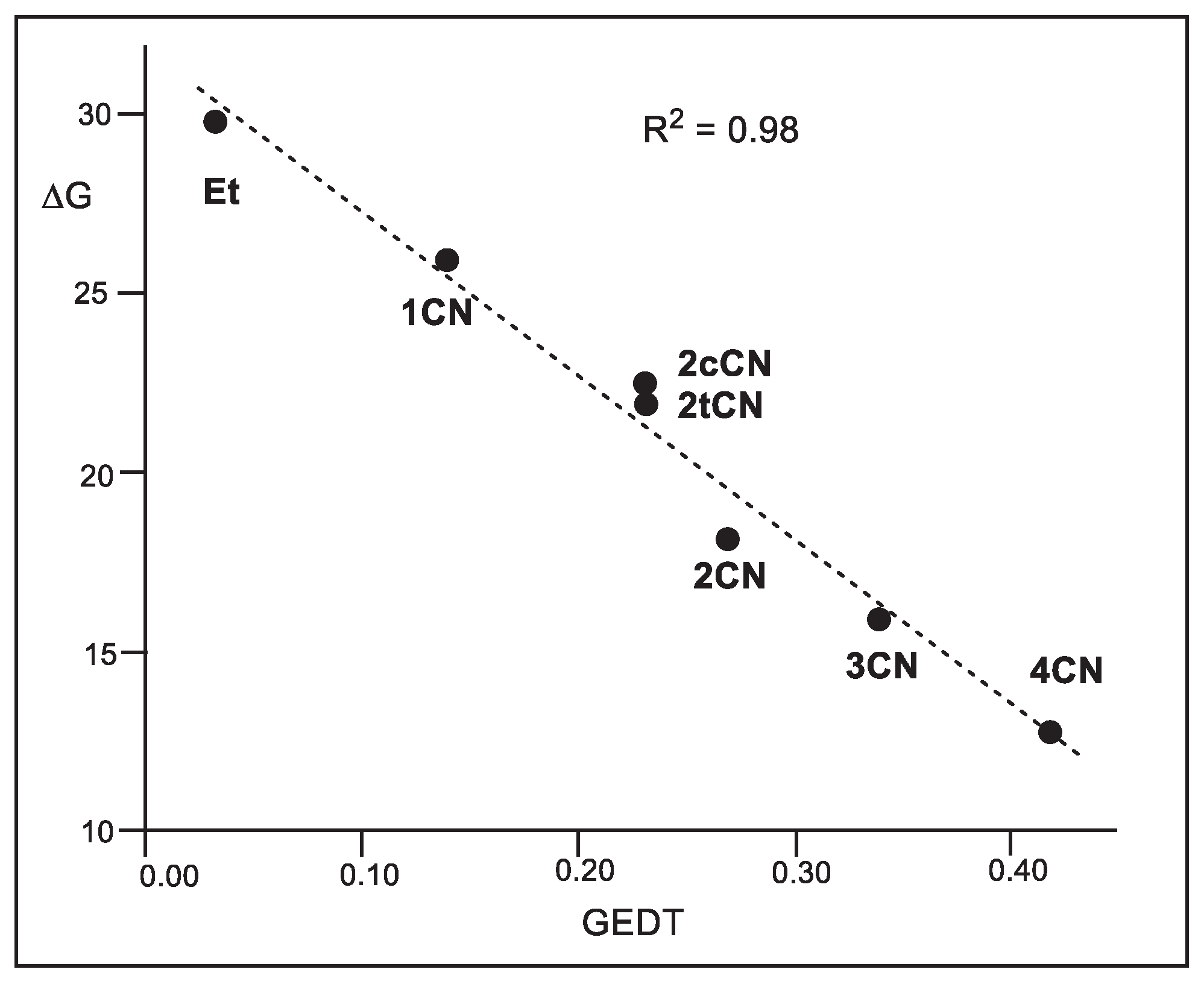
A representation of the activation Gibbs free energies of these P-DA reactions versus the computed GEDT values at the corresponding TSs also shows a very good linear correlation with an R² = 0.98 (see Figure 5). This linear correlation, that has been found in numerous organic reactions, shows the significant role of the polar character of the reactions, measured by the computed GEDT values, in reaction rates.

It is worth noting that although geminal 2CN is less electrophilic than vicinal 2cCN and 2tCN, the reaction of 2CN is more polar and has a higher reaction rate (see Figure 5). This finding points out, once again, the relevant role of GEDT in reaction rates, and indicates that asynchronous processes are generally preferred over synchronous ones due to a more favorable two-center interaction (see later).

Finally, ELF and QTAIM topological analyses of the electronic structures of the reagents and TSs were performed. The corresponding analyses are given in Supplementary Material. ELF analysis of the reagents indicates that the cyano substitution on the ethylene does not cause any remarkable changes in the C−C double bond region at the GS of these substituted ethylenes. On the other hand, ELF analysis of the TSs indicates that while the low polar TS-1CN and TS-2cCN and TS-2tCN shows a great similitude to the non-polar TS-Et, the highly polar TS-2CN, TS-3CN and TS-4CN show the presence of the pseudoradical centers demanded for the subsequent C−C single bond formation [17]. Both ELF and QTAIM analyses of the electron density at the TSs indicate that formation of the C−C single bonds has not started yet in any of them, thus rejecting the concept of concerted TSs.

2.3. IQA Analysis of the TSs of the P-DA Reactions of the Cyanoethylene Series 4

In order to determine the role of the GEDT caused by the cyano substitution on the ethylene in the experimental acceleration observed by Sauer et al. (see Table 1), a topological IQA [35] energy partitioning was carried out at the seven TSs in gas-phase. For this purpose, an Interacting Quantum Fragments (IQF) approach [45] was adopted, considering relative IQA energies at both interacting frameworks as defined Supplementary Material. The relative total, intra- and interatomic IQA energies of each TS fragment are given in Table 6, while total values are given in Table S5 in Supplementary Material.

Table 6 shows that the stabilization of the ethylene framework with the number of cyano groups, ΔE_tot(nCN) < 0, is stronger than the Cp destabilization, ΔE_tot(Cp) > 0, justifying the decrease of the activation energies along this cyanoethylene series. In addition, while the increase of the cyano substitution in the ethylene generally increases E_intra(X) in the two interacting frameworks and V_inter(Cp), a huge decrease of the interatomic V_inter(nCN) energies, by between −16.0 (1CN) and −102.0 (4CN) kcal mol^-1, is observed (see the differences between V_inter(nCN) and V_inter(Et)).

Table 6. M06-2X/6-311G(d,p) gas-phase relative total E_tot(X), intra-atomic E_intra(X) and interatomic V_inter(X) IQA energies, in kcal mol^-1, of the cyclopentadiene and ethylene frameworks at the TSs with respect to the separated reagents. The sum of the relative total IQA energies of the two interacting moieties, E_tot(Cp+Et), yields the activation energy. Standard deviations are given with respect to the N-DA reaction of Cp 1 with ethylene 6, in kcal mol^-1.

Table 6. M06-2X/6-311G(d,p) gas-phase relative total E_tot(X), intra-atomic E_intra(X) and interatomic V_inter(X) IQA energies, in kcal mol^-1, of the cyclopentadiene and ethylene frameworks at the TSs with respect to the separated reagents. The sum of the relative total IQA energies of the two interacting moieties, E_tot(Cp+Et), yields the activation energy. Standard deviations are given with respect to the N-DA reaction of Cp 1 with ethylene 6, in kcal mol^-1.

		Eintra(X)	Vinter(X)	Etot(X)	Etot(Cp+Et)
TS-Et	Cp	34.6	-26.8	7.8	15.6
	Et	33.1	-25.3	7.8
TS-1CN	Cp	37.8	-19.9	17.9	11.0
	1CN	34.4	-41.3	-6.9
TS-2cCN	Cp	42.3	-13.6	28.7	8.1
	2cCN	49.4	-70.0	-20.6
TS-2tCN	Cp	41.8	-13.2	28.6	6.9
	2tCN	46.5	-68.2	-21.7
TS-2CN	Cp	41.2	-10.0	31.2	4.0
	2CN	29.3	-56.5	-27.2
TS-3CN	Cp	46.1	-4.4	41.7	1.9
	3CN	54.8	-94.6	-39.8
TS-4CN	Cp	51.9	1.3	53.2	-1.5
	4CN	72.6	-127.3	-54.7
Standard deviation	Cp	10.0	18.2	28.1
	nCN	20.4	58.1	39.3

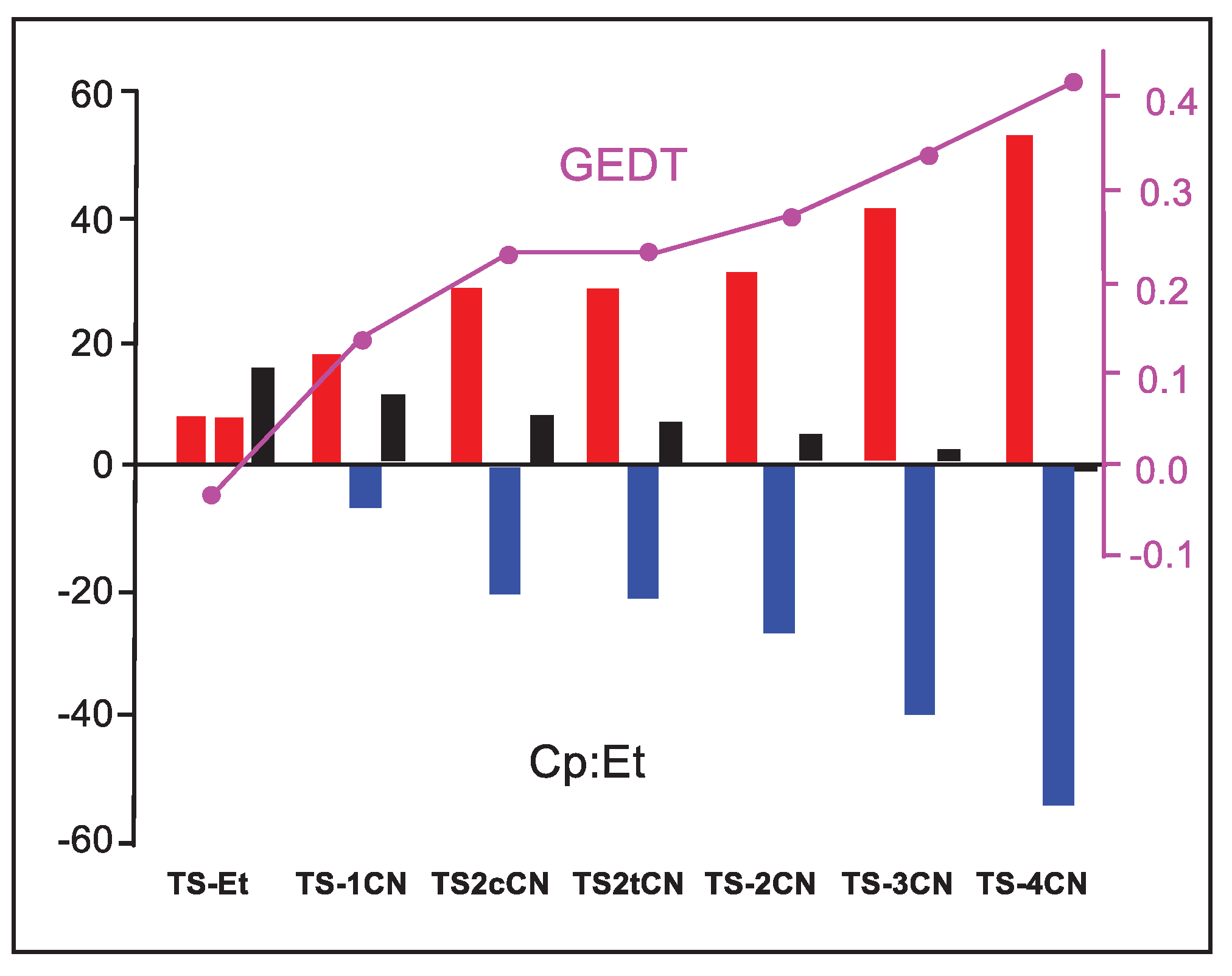
Figure 6 shows a graphical representation of the IQF E_tot(X) energy of the Cp and Et frameworks at the seven TSs and the E_tot(Cp+Et), which corresponds to the activation energies of these DA reactions. As can be observed, both E_tot(X) are positive and unfavorable in the N-DA reaction with ethylene 6. However, along the cyanoethylene series 4, the IQF energies associated with the Cp framework increase while those of the ethylene derivatives become more negative, i.e. more stabilizing. This stabilization reaches such an extent that, in TS-4CN, the stabilization of the ethylene framework overcomes the destabilization of the Cp one, and the corresponding relative energy of TS-4CN becomes negative. These behaviors are a consequence of the GEDT that takes place at the TSs (see Figure 6), that while it destabilizes the nucleophile Cp for making it lose electron density, it stabilizes the electrophile nCN as it gains electron density.

Consequently, the strong stabilization of the cyanoethylene framework at the TSs with the cyano substitution, by between 14.7 (1CN) and 62.5 (4CN) kcal mol^-1 with respect to the N-DA reaction of Cp 1 with ethylene 6, accounts for the decrease of the activation energies associated with the P-DA reactions between Cp 1 and the cyanoethylene series 4.

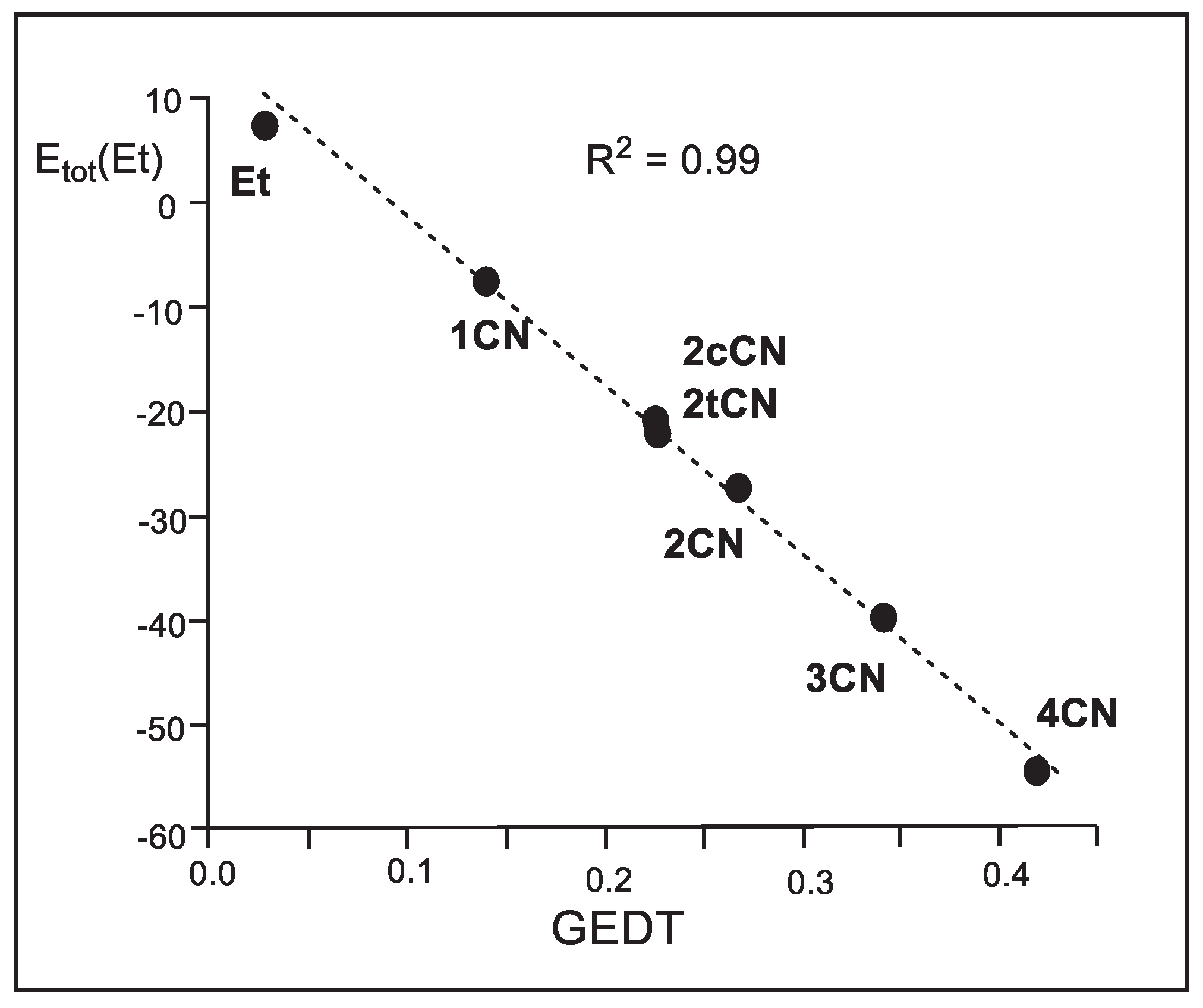
A representation of the logarithm of the experimental reaction rate constant k versus the stabilization of the ethylene frameworks at the TSs shows an excellent linear correlation with an R² = 0.95 (see Figure S8 in Supplementary Material). This figure shows the close relationship between the experimentally observed acceleration in this series of P-DA reactions and the decrease in activation energy resulting from the electronic stabilization of the ethylene framework. Furthermore, a representation of E_tot(Et) versus the GEDT computed at the TSs shows an excellent linear correlation with an R² = 0.99 (see Figure 7).

These linear correlations allow establishing, for the first time, that the electronic stabilization of the ethylene framework, resulting from the GEDT process taking place in polar reactions, is responsible for the increase of the reaction rate observed in these polar reactions [18]. Note that the N-DA reaction of ethylene 6, which presents a GEDT = 0.03 e, fits in the top left corner in the linear regression in Figure 7.

Figure 7. Plot of the gas-phase M06-2X/6-311G(d,p) relative total IQA atomic energies of the ethylene framework (E_tot(Et) in kcal mol^-1) vs. the GEDT (in average number of electrons, e) for the DA reactions of Cp 1 with ethylene 6 and the cyanoethylene series 4.

Figure 7. Plot of the gas-phase M06-2X/6-311G(d,p) relative total IQA atomic energies of the ethylene framework (E_tot(Et) in kcal mol^-1) vs. the GEDT (in average number of electrons, e) for the DA reactions of Cp 1 with ethylene 6 and the cyanoethylene series 4.

As the energy factor that changes the most with the cyano substitution is V_inter(Et), in order to gain a more detailed insight into the stabilization of the ethylene derivatives, the interatomic interactions between the Cp and ethylene frameworks, V_inter(Cp,Et), were considered separately from the interactions that take place within each of them, V’_inter(X). The corresponding energies, together with the standard deviations with respect to the N-DA reaction of ethylene 6 as the reference, are given in Table 7.

The standard deviation values indicate that the most drastic changes with the cyano substitution take place in decreasing the interatomic interactions occurring inside the ethylene fragment (see the standard deviation of V’_inter(Et) in Table 7). This effect overcomes the changes in the interatomic interactions between the fragments, V_inter(Cp,Et), which also become more stabilizing as the polar character of the reaction increases.

These findings confirm that the stabilization of the electrophilic reagent in P-DA reactions is the most relevant consequence of the GEDT, thus being responsible for the increase of reaction rates with the increase of the polar character [17].

Table 7. M06-2X/6-311G(d,p) gas-phase total interatomic interactions between the two Cp and Et fragments, V_inter(Cp,Et), and relative total interatomic energies within the two Cp and Et frameworks, V’_inter(X), in kcal mol^-1. Relative energies are given with respect to the separated reagents. Standard deviations are given with respect to the N-DA of Cp 1 with ethylene 6, in kcal mol^-1.

Table 7. M06-2X/6-311G(d,p) gas-phase total interatomic interactions between the two Cp and Et fragments, V_inter(Cp,Et), and relative total interatomic energies within the two Cp and Et frameworks, V’_inter(X), in kcal mol^-1. Relative energies are given with respect to the separated reagents. Standard deviations are given with respect to the N-DA of Cp 1 with ethylene 6, in kcal mol^-1.

	Vinter(Cp,Et)	V’inter(Cp)	V’inter(Et)
TS-Et	-153.7	50.0	51.5
TS-1CN	-160.4	60.4	38.9
TS-2cCN	-167.7	70.3	13.7
TS-2tCN	-168.7	71.1	16.2
TS-2CN	-165.5	72.8	26.3
TS-3CN	-174.1	82.6	-7.6
TS-4CN	-187.3	94.8	-33.6
Deviation	18.9	27.5	48.7

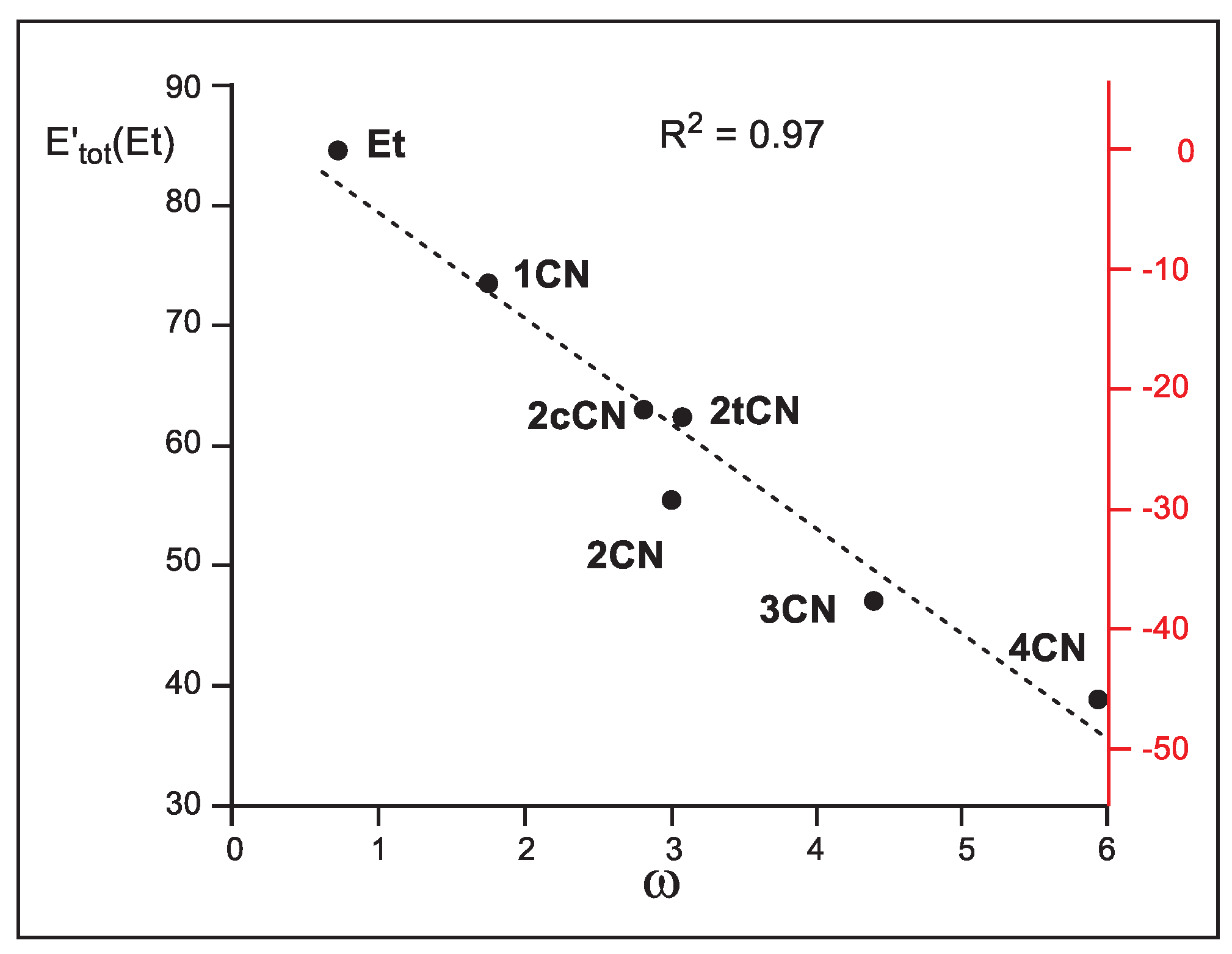
Finally, in 1999, Parr proposed the electrophilicity index ω as a measure of the electronic stabilization of a species when it acquires a certain amount of electron density from the environment [4]. Thus, when the sum of the relative intra-atomic E_intra(Et) and interatomic V’_inter(Et) IQA energies, i.e. E’_tot(Et), are represented versus the corresponding Parr’s electrophilicity ω indices (see Table 2), a very good linear correlation is obtained; R² = 0.97 (see Figure 8). The E’_tot(Et) in the N-DA reaction between Cp 1 and ethylene 6 is very unfavorable, 84.6 kcal mol^-1. The inclusion of the cyano groups stabilize the ethylene framework at the TSs by between 11.3 (1CN) and 45.7 (4CN) kcal mol^-1 as a consequence of the GEDT taking place at the polar TSs (see Figure 8). Consequently, this graph supports Parr’s proposal [4,46]; the higher the electrophilicity ω index, the higher the ethylene stabilization at the polar TSs. Given that the ethylene stabilization via the GEDT is the main factor responsible for the decrease of activation energies, as shown above, this linear correlation also validates Parr’s electrophilicity ω index as a solid predictor of reactivity in polar cycloaddition reactions.

3. Computational Methods

4. Conclusions

References

1. Ingold, C.K. Significance of tautomerism and of the reactions of aromatic compounds in the electronic theory of organic reactions. J. Chem. Soc. 1933, 1120-1127. [CrossRef]
2. Lapworth, A. Replaceability of Halogen Atoms by Hydrogen Atoms, Nature, 1925, 115, 625.
3. Carey, F.A.; Sundberg, R.J. Advanced Organic Chemistry, Part A: Structure and Mechanisms. Springer, New York, 2008.
4. Parr, R.G.; Szentpaly, L.v.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922-1924. [CrossRef]
5. Parr, R.G.; Yang, W. Density functional theory of atoms and molecules. Oxford University Press, New York, 1989.
6. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the conceptual density functional indices to organic chemistry reactivity. Molecules 2016, 21, 748. [CrossRef]
7. Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R.Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 2002, 58, 4417-4423. [CrossRef]
8. Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615-4624. [CrossRef]
9. Domingo, L.R.; Ríos-Gutiérrez, M. In Application of Reactivity Indices in the Study of Polar Diels–Alder Reactions. Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, Ed. Shubin Liu. WILEY-VCH GmbH. 2022, Vol. 2, pp. 481-502.
10. Diels, O.; Alder, K. Synthesen in der hydroaromatischen Reihe. Justus Liebigs Ann. Chem. 1928, 460, 98-122. [CrossRef]
11. Carruthers, W. In Some Modern Methods of Organic Synthesis. 2nd ed.; Cambridge University Press: Cambridge, UK, 1978.
12. Carruthers, W. In Cycloaddition Reactions in Organic Synthesis. Pergamon: Oxford, UK, 1990.
13. Woodward, R.B. The mechanism of the Diels-Alder reaction. J. Am. Chem. Soc., 1942, 64, 3058–3059.
14. Sauer, J.; Wiest, H.; Mielert, A. Eine Studie der Diels-Alder-Reaktion, I. Die Reaktivität von Dienophilen gegenüber Cyclopentadien und 9.10-Dimethyl-anthracen. Chem. Ber. 1964, 97, 3183–3207. [CrossRef]
15. Domingo, L.R.; M. J. Aurell, Pérez, P.; Contreras, R. Origin of the synchronicity on the transition structures of polar Diels-Alder reactions. Are these reactions [4+2] processes?. J. Org. Chem. 2003, 68, 3884–3890. [CrossRef]
16. Jones, G.O.; Guner, V.A.; Houk, K.N. Diels-Alder Reactions of Cyclopentadiene and 9,10-Dimethylanthracene with Cyanoalkenes: The Performance of Density Functional Theory and Hartree-Fock Calculations for the Prediction of Substituent Effects. J. Phys. Chem. A 2006, 110, 1216-1224. [CrossRef]
17. Domingo, L.R. A new C-C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415-32428. [CrossRef]
18. Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels-Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3583. [CrossRef]
19. Arnó, M.; Zaragozá, R.J.; Domingo, L.R. Lewis acid induced [2+2] Cycloadditions of Silyl Enol Ethers with α,β-Unsaturated Esters. A DFT Analysis. Eur. J. Org. Chem. 2005, 3973-3979. [CrossRef]
20. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A Molecular Electron Density Theory Study of the Reactivity and Selectivities in [3+2] Cycloaddition Reactions of C,N-Dialkyl Nitrones with Ethylene Derivatives. J. Org. Chem. 2018, 83, 2182-2197. [CrossRef]
21. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Unveiling the Lewis Acid Catalysed Diels–Alder Reactions Through the Molecular Electron Density Theory. Molecules 2020, 25, 2535. [CrossRef]
22. Domingo, L.R.; Pérez, P. Understanding the Higher–Order Cycloaddition Reactions of Heptafulvene, Tropone and its Nitrogen Derivatives with Electrophilic and Nucleophilic Ethylenes inside the Molecular Electron Density Theory. New J. Chem. 2022, 46, 294-308.
23. Domingo, L.R.; Seif, A.; Mazarei, E.; Zahedi, E.; Ahmadi, T.S. A Molecular Electron Density Theory (MEDT) study of the role of halogens (X2= F2, Cl2, Br2 and I2) on the aza-Michael-addition reactions. New J. Chem. 2020, 44, 19002-19012. [CrossRef]
24. Chamorro, E.; Duque-Norena, M.; Gutiérrez-Sanchez, N.; Rincon, E.; Domingo, L.R. A close look to the oxaphosphetane formation along the Wittig reaction: A [2+2] cycloaddition? J. Org. Chem. 2020, 85, 6675-6686. [CrossRef]
25. Domingo, L.R.; Aurell, M.J. Unveiling the Electrophilic Aromatic Substitution Reactions of Pyridine Derivatives with Nitronium Ion through Molecular Electron Density Theory. New. J. Chem. 2023, 47, 5193-5202. [CrossRef]
26. Domingo, L.R. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules 2016, 21, 1319. [CrossRef]
27. Fukui, K. In Molecular Orbitals in Chemistry, Physics, and Biology, New York, 1964.
28. Kitaura, K.; Morokuma, K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325-340. [CrossRef]
29. Morokuma, K.; Kitaura, K. In Chemical Applications of Atomic and Molecular Electrostatic Potentials, New York, Plenum., 1981, pp. 215–242.
30. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization n atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397–5403. [CrossRef]
31. Bader, R.F.W.: Tang, Y.H.; Tal, Y.; Biegler-König, F.W. Properties of atoms and bonds in hydrocarbon molecules. J. Am. Chem. Soc. 1982, 104, 946–952. [CrossRef]
32. Bader, R.F.W. Atoms in Molecules: A Quantum Theory. Oxford University Press, Oxford, New York, 1994.
33. Krokidis, K.; Noury, S.; Silvi, B. Characterization of Elementary Chemical Processes by Catastrophe Theory. J. Phys. Chem. A. 1997, 101, 7277−7282. [CrossRef]
34. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. How does the global electron density transfer diminish activation energies in polar cycloaddition reactions? A Molecular Electron Density Theory study. Tetrahedron 2017, 73, 1718-1724. [CrossRef]
35. Blanco, M.A.; Martín Pendás, A.; Francisco, E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [CrossRef]
36. Ríos-Gutiérrez, M.; Falcioni, F.; Domingo, L.R.; Popelier, P.L.A. A Combined BET and IQA-REG Study of the Activation Energy of non-polar zw-type [3+2] Cycloaddition Reactions. Phys. Chem. Chem. Phys. 2023, 25, 10853–10865. [CrossRef]
37. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Why is Phenyl Azide so Unreactive in [3+2] Cycloaddition Reactions? Demystifying Sustmann’s Paradigmatic Parabola. Org. Chem. Front. 2023, 10, 5579–5591. [CrossRef]
38. Domingo, L.R.; Pérez, P.; Ríos-Gutiérrez, M.; Aurell, M.J. A Molecular Electron Density Theory Study of Hydrogen Bond Catalysed Polar Diels–Alder Reactions of α,β-unsaturated Carbonyl Compounds. Tetrahedron Chem. 2024, 10, 100064.
39. Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [CrossRef]
40. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A Molecular Electron Density Theory Study of the Reactivity of Tetrazines in Aza-Diels-Alder Reactions. RSC Adv. 2020, 10, 15394–15405. [CrossRef]
41. Domingo, L.R.; Ríos-Gutiérrez, M. A Useful Classification of Organic Reactions Bases on the Flux of the Electron Density. Sci. Rad. 2023, 2, 1.
42. Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [CrossRef]
43. Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 2002, 58, 4417–4423. [CrossRef]
44. Evans, M.G.; Polanyi, M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. [CrossRef]
45. Triestram, L.; Falcioni, F.; Popelier, P.L.A. Interacting Quantum Atoms and Multipolar Electrostatic Study of XH···π Interactions. ACS Omega 2023, 8, 34844–34851. [CrossRef]
46. Chattaraj, P.K.; Roy, D.R. Update 1 of: Electrophilicity Index. Chem. Rev. 2007, 107, PR46–PR74. [CrossRef]
47. Zhao, Y.; Truhlar, D. G.The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215-245.
48. Hehre, M.J.; Radom, L.; Schleyer, P.V.R.; Pople, J. Ab initio Molecular Orbital Theory. Wiley: New York, NY, USA, 1986.
49. Tomasi, J.; Persico, M. Molecular interactions in solution: And overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [CrossRef]
50. Simkin, B.Y.; Sheikhet, I.I. Quantum Chemical and Statistical Theory of Solutions–Computational Approach. Ellis Horwood: London, UK, 1995.
51. Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [CrossRef]
52. Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [CrossRef]
53. Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [CrossRef]
54. Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [CrossRef]
55. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [CrossRef]
56. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016.
57. Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, 6th ed.; Semichem Inc.: Shawnee Mission, KS, USA, 2016.
58. Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [CrossRef]
59. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comp. Chem. 2012, 33, 580-592. [CrossRef]
60. AIMAll (Version 19.10.12), Keith, T.A. TK Gristmill Software, Overland Park KS, USA, 2019 (aim.tkgristmill.com).