Evolutionary Game Analysis on Cooperative Behavior of Major Projects’ Technology Innovation Subjects under General Contracting Mode

1. Introduction

Major infrastructure projects (hereafter referred to as major projects) refer to large-scale public projects with large investment scale, long implementation cycle and extremely complex technology, which have far-reaching impacts on economic and social development and ecological and environmental protection [1]. Major projects are huge in volume and scale, and face increasing challenges in technology due to highly uncertain engineering environments, diversified engineering requirements and increasingly stringent engineering objectives [2]. Different from general projects, major projects play a key role in improving people's well-being and promoting economic development [4]. Therefore, technological innovation is an inevitable choice when facing the difficult problems of major projects construction. Major projects' technology innovation refers to the process of integrating the technological innovation results of various innovation subjects guided by engineering demand [6]. Major projects' technology innovation involves many fields and has obvious complexity. The key to achieving a breakthrough in major projects' technology innovation lies in collaborative innovation by various subjects in the innovation process [7]. However, technological collaborative innovation can easily lead to conflicts between interests and resources, breed opportunistic behavior, thus reducing the efficiency of cooperation, and ultimately not conducive to the output of innovation results [8]. Only when the technological innovation behavior of each innovation subject in major projects is consistent can the overall innovation be realized.

On major projects' technology innovation, scholars at home and abroad have achieved rich research results. Ozorhon and Oral [10] found through research that project complexity, government innovation support policies and environmental pressure are the main driving forces to promote construction project innovation. On account of the complexity and uncertainty of major projects' technology innovation, organization and coordination of the process of technology innovation is essential. Major projects' technology innovation involves multiple fields, requiring owners to integrate resources such as manpower, capital [11] and stakeholder cooperation [12] , organize and coordinate well, and provide a favorable environment for innovation alliances that can carry out technological innovation activities [13]. However, due to their large-scale, infrastructure projects are characterized by temporary organization, complexity, diversity of innovation entities and uncertainty of technology, all of which make it easy to form innovation islands [14]. A favorable cooperative relationship can not only promote successful technological innovation, but it also lay a trust foundation for knowledge transfer. Trust is regarded as an important prerequisite for improving the effectiveness of knowledge transfer [15]. With the deepening of research, innovation networks and ecosystems are gradually being introduced into the major projects' technology innovation process. The traditional innovation paradigm is no longer suitable for major projects with high innovation complexity due to unclear powers and responsibilities and inefficient information exchange [16]. A compact innovation network should be formed among the participants [17] in which each participant can carry out technological innovation activities and jointly create value [18]. However, participants may have different goals for and plans from major projects' technology innovation, so the leaders of the innovation ecosystem should play a coordinating role [19]. Because major projects' technology innovation is a process in which many innovation subjects participate together, each innovation subject will have different goals, inconsistent interests, unequal status and asymmetric information, all of which will affect their behavior choices. Previous studies have also shown that a reasonable distribution ratio of innovation income, high trust among members, and optimal government incentives and punishment measures can promote the behavior of innovation subjects that promotes the success of cooperative innovation [18]. Ma et al. [20] constructed an evolutionary game model of cooperation network of green building technology innovation to study the influence of policies, including subsidies, taxation and intellectual property protection, on the decision-making behavior and network structure of green building enterprises. In addition to the above research perspectives, few scholars studied the behavior choices of innovation subjects from the perspectives of R&D cost, default cost and distribution ratio of green innovation benefits [21] , and cooperation intention and sharing level [22].

Government-industry-university-research institute co-operation is a vital part of the main body of major projects' technology innovation. Zan et al. [23] aimed to analyze the cooperative relationship between enterprises and research institutions and the influence of government policies on the stability of industry-university-research cooperation by constructing an innovation model of industry-university-research cooperation. The results are helpful to strengthen the stability of industry-university-research cooperation innovation and provide reference for the government to formulate effective policies.

A favorable reputation is conducive to improving enterprise effort levels and realizing pareto improvement of earnings [24]. Since the 1980s, many scholars have begun to study the mechanism of reputation. As a kind of implicit incentive mechanism, Fama [25] first proved that under the assumption of complete market mechanism, implicit incentives cannot completely replace explicit incentives. Kreps [26] studied the incentive effect of reputation through repeated game model. By constructing KMRW reputation model, he found that reputation and other implicit incentive mechanisms can achieve the purpose of motivating agents. Shi et al. [27] studied the dual reputation incentive mechanism in major engineering prefabrication and found that the introduction of reputation incentive mechanism under certain conditions can better coordinate the cooperative relationship between owners and prefabricators and prevent agent moral hazard. Li et al. [28] showed that reputation effect helps to improve the effort level of the agent and the income of the principal, and helps the principal and the agent to establish a long-term stable cooperative relationship. Therefore, reputation plays a sure role in promoting cooperative innovation.

To sum up, the existing literature shows that much research has been conducted on major projects' technology innovation and the behavior choice of technological innovation subjects, mainly reflected in the following: Firstly, the research on major projects' technology innovation by domestic and foreign scholars mainly focused on driving and hindering factors, innovation networks and ecosystems, and most of these studies used qualitative in nature. Secondly, when studying the behavior choice of technological innovation subjects, most scholars chose cooperation income and its distribution coefficient, innovation cost, etc. Thirdly, in the selection of technological innovation subjects, most scholars chose two or three parties from government, owners, industry-university-research institutes and enterprises. Compared with the existing research, this paper is original in that it: (1) selects the general contractor and subcontractor as the research objects to study the evolution process of different behavior strategies under the general contracting mode; and (2) introduces the reputation factor into the model, and studies the influence of reputation effect on the sustainable development of innovation subjects. In addition, this paper also studies the influence of reputation benefit on the decision-making behavior of innovation subjects.

The rest of this paper is arranged as follows: Problem description and assumptions are explained in Section 2. In Section 3, the expected function under different selection behaviors of the general contractor and subcontractor is constructed and the replicated dynamic equation is established. In addition, the influence of different factors on the choice behavior of both parties is also analyzed. Section 4 describes the numerical simulation results of various factors. Finally, research conclusions and suggestions are provided in Section 5.

2. Problem Description and Assumptions

2.1. Problem Description

The general contracting mode of an engineering construction project, such as the Changsha Maglev F-rail Technology Innovation Project, is a formal contract adopted by the owner to achieve the project goal. The evolutionary game model is based on the bounded rationality of decision makers and take the maximization of their own interests as the decision goal. Its nature is consistent with the research on cooperative behavior of major projects' innovation subjects. Therefore, based on the game theory, this paper studies the general contractor and subcontractor as the main body. Because the general contractor and subcontractor meet the bounded rationality assumption, they often cannot find the optimal strategies at the beginning of the game; therefore, both parties need to play many games and adjust in the continuous game to find the optimal strategies.

2.2. Model Assumptions

To analyze the technological innovation behavior between the general contractor and subcontractor, some assumptions are listed below.

Assumptions 1: In the process of technological innovation, both the general contractor and subcontractor have two opposing strategies, which are active collaborative innovation, negative collaborative innovation. This paper assumes that x(0≤x≤1) represents the probability that the general contractor adopts active collaborative innovation strategy and y(0≤y≤1) represents the probability that the subcontractor adopts active collaborative innovation strategy. General contractors' active collaborative innovation means actively participating in the collaborative technological innovation construction of major projects and being willing to carry out efficient collaborative innovation with subcontractors. Negative collaborative innovation means that they are unwilling to carry out collaborative innovation with subcontractors, but only want to obtain technological knowledge and the final innovation results of subcontractors. Subcontractors' active collaborative innovation means that they actively participate in technology research and development and collaborative innovation; whereas negative collaborative innovation refers to low willingness to participate in innovation of major projects and unwillingness to devote themselves to technology research and development.

Assumptions 2: The basic income of the general contractor engaging in a certain technology innovation project is R₁, and part of the technological collaborative innovation content is handed over to the subcontractor by adopting the general contracting mode. Assuming that the general contractor and subcontractor sign a technological collaborative innovation contract, the subcontractor's contract basic income is R₂.

Assumptions 3: The total benefit of collaborative innovation between the general contractor and subcontractor is M, and the technological income generated in the collaborative process is η_iV_i(i=1,2), where η_i and V_i(i=1,2) represent the technical innovation output coefficient and knowledge and technical value of the general contractor and subcontractor. Because the general contractor is in a dominant position throughout the process of collaborative technology innovation, it has the right to distribute the total output benefit of collaborative innovation, and the assumption λ(0<λ<1) indicates the distribution ratio of collaborative innovation benefit of the subcontractor. In order to solve the model, it is assumed that when one party adopts negative collaborative innovation strategy, its collaborative innovation will produce total benefits M=0.

Assumptions 4: The of collaborative innovation in major projects has the characteristics of dynamic replacement, which is characterized by the dynamic changes between temporary alliances or permanent organizations, and the technological achievements of collaborative innovation are finally transferred to the general contractor after the contract contents signed in the early stage are satisfied. Because the innovative technological achievements cannot be completely transformed, this paper assumes that the conversion rate of technological achievements is β(0<β<1).

Assumptions 5: When the general contractor and subcontractor carry out technological innovation, they need to invest their own innovation costs C_i(i=1,2). According to the reality, the innovation subjects have the ability to absorb the existing knowledge and technology, which will lead to a reduction in the number of trial-and-error operations during the process of innovation; this will, in turn, reduce the innovation cost. It is assumed that α₁ and α₂ represent the spillover technology absorption capacity of the general contractor and subcontractor, so the reduced innovation cost can be expressed as α_iC_i(i=1,2).

Assumptions 6: When there is negative collaborative innovation by one of the innovation subjects, there is "free rider" behavior. The concept "free rider" means that the general contractor or subcontractor unwilling to carry out collaborative innovation with the other subject, but only want to "enjoy the benefits" and absorb the knowledge and technology of the other side in the innovation process. Suppose that the income obtained by absorbing each other's knowledge and technology is ρ_iV_j(i,j=1,2,i≠j), where ρ_i(i=1,2) and V_j(j=1,2) indicate the subjects' learning ability and knowledge value respectively, and ρ_i>V_j(i,j=1,2,i≠j). If negative collaborative innovation is discovered, it will cause certain reputation loss to the offending innovation subjects. Assuming that the probability of being discovered is p, the lost reputation gain is $S_i=\frac{1}{2}pq{b}_i^2$ (i=1,2), in which the reputation discount coefficient is q, and b_i is the negative level, which is used to indicate the cooperative willingness of the subjects in the process of cooperation. The smaller b_i is, the stronger the cooperative willingness; otherwise, cooperative willingness will be lower.

3. Model Construction and Solution

3.1. Model Building

Based on Section 2.2, the income payment matrix of collaborative innovation between the general contractor and subcontractor is shown in Table 1.

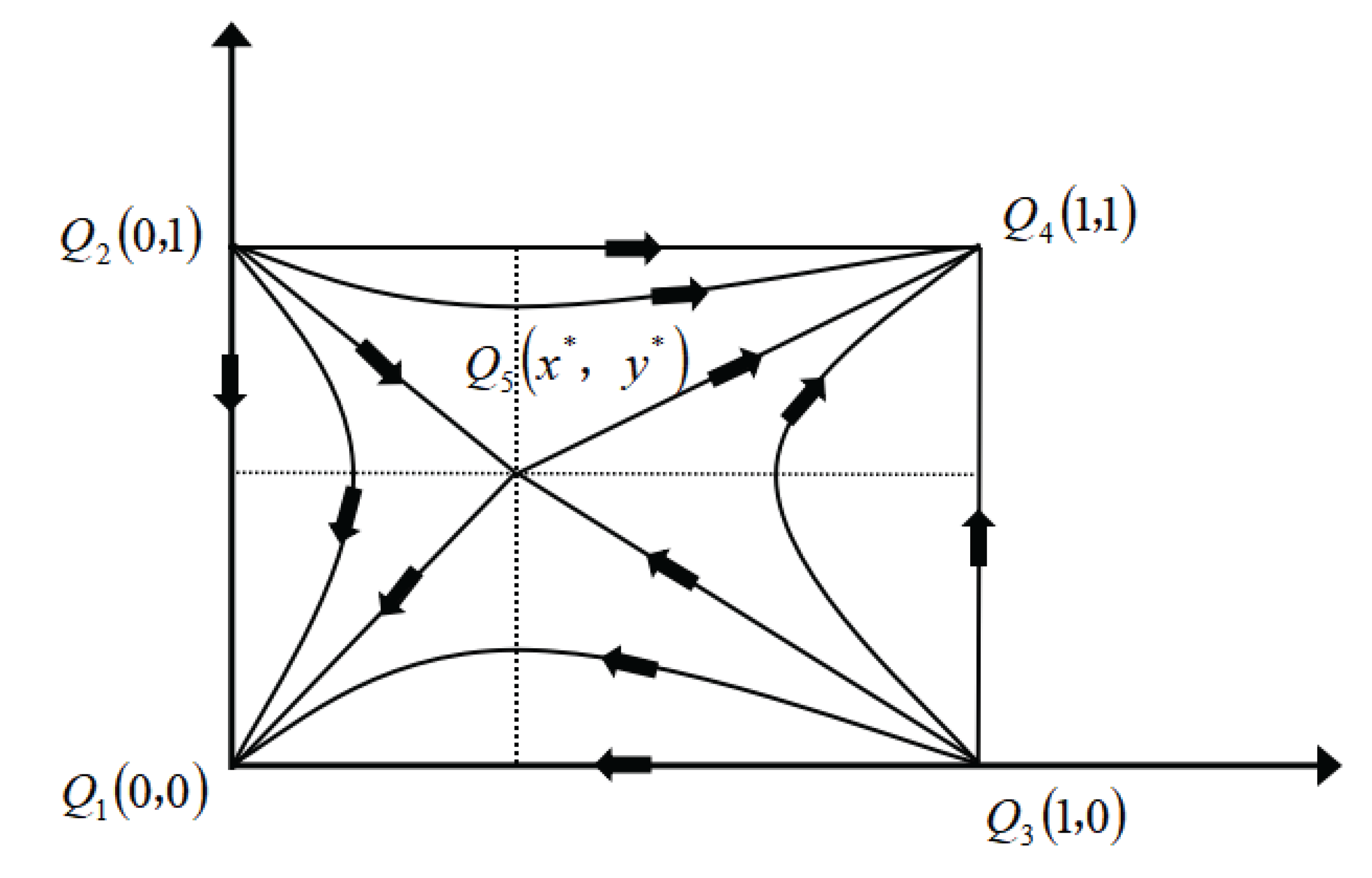
3.2. Model Analysis

According to the game theory and expected income formula, the expected income of the general contractor and subcontractor can be expressed respectively as E₁, and E₂. Based on Table 1, we can get the expected income of the general contractor under active collaborative innovation can be expressed as

$$E_{11}=y\left[\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1\right]+R_1+{\eta }_1{V}_1-\left(1-{\alpha }_1\right)C_1-{\rho }_2{V}_1$$

(1)

and the expected income of the general contractor under negative collaborative innovation can be expressed as

$$E_{12}=y{\rho }_1{V}_2+R_1-\frac{1}{2}pq{b}_1^2$$

(2)

The average expected income of the general contractor is

$$\begin{gathered} E_1=xy\left[\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2\right]+y{\rho }_1{V}_2+ \\ x\left[{\eta }_1{V}_1-\left(1-{\alpha }_1\right)C_1-{\rho }_2{V}_1+\frac{1}{2}pq{b_1}^2\right]+R_1-\frac{1}{2}pq{b_1}^2 \end{gathered}$$

(3)

According to the research content of Galor and Weil [29], the replication dynamic equation when the general contractor chooses active collaborative innovation strategy can be expressed as

$$\frac{dx}{dt}=x\left(1-x\right)\left[\begin{array}{c}y\left(1-\lambda +\beta \right)M+y\left({\rho }_2{V}_1-{\rho }_1{V}_2\right)\\ +{\eta }_1{V}_1+\frac{1}{2}pq{b}_1^2-\left(1-{\alpha }_1\right)C_1-{\rho }_2{V}_1\end{array}\right]$$

(4)

By the same token, the expected income of the subcontractor under the active collaborative innovation is

$$E_{21}=x\left(\lambda M+{\rho }_1{V}_2\right)+R_2+{\eta }_2{V}_2-\left(1-{\alpha }_2\right)C_2-{\rho }_1{V}_2$$

(5)

The expected income of the subcontractor under negative collaborative innovation is

$$E_{22}=x{\rho }_2{V}_1+R_2-\frac{1}{2}pq{b}_2^2$$

(6)

The average expected income of the subcontractor is

$$\begin{gathered} E_2=xy\left[\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1\right]+x{\rho }_2{V}_{21}+R_2-\frac{1}{2}pq{b_2}^2 \\ y\left[{\eta }_2{V}_2-\left(1-{\alpha }_2\right)C_2-{\rho }_1{V}_2+\frac{1}{2}pq{b_2}^2\right] \end{gathered}$$

(7)

The replication dynamic equation when the subcontractor chooses active collaborative innovation strategy can be expressed as

$$\frac{dy}{dt}=y\left(1-y\right)\left[\begin{array}{c}x\lambda M+x\left({\rho }_1{V}_2-{\rho }_2{V}_1\right)+{\eta }_2{V}_2\\ +\frac{1}{2}pq{b}_2^2-\left(1-{\alpha }_2\right)C_2-{\rho }_1{V}_2\end{array}\right]$$

(8)

Therefore, we can get a two-dimensional system of dynamic evolution of the general contractor and subcontractor, which can be expressed as Equation (9).

$$\left\{\begin{array}{c}\frac{dx}{dt}=x\left(1-x\right)\left[\begin{array}{c}y\left(1-\lambda +\beta \right)M+y\left({\rho }_2{V}_1-{\rho }_1{V}_2\right)+{\eta }_1{V}_1\\ +\frac{1}{2}pq{b}_1^2-\left(1-{\alpha }_1\right)C_1-{\rho }_2{V}_1\end{array}\right]\\ \frac{dy}{dt}=y\left(1-y\right)\left[x\lambda M+x\left({\rho }_1{V}_2-{\rho }_2{V}_1\right)+{\eta }_2{V}_2+\frac{1}{2}pq{b}_2^2-\left(1-{\alpha }_2\right)C_2-{\rho }_1{V}_2\right]\end{array}\right.$$

(9)

Let $\frac{dx}{dt}=0$ and $\frac{dy}{dt}=0$; the local equilibrium points of two-dimensional dynamical system can be obtained, which are Q₁(0,0), Q₂(0,1), Q₃(1,0), Q₄(1,1), Q₅(x^*,y^*), where

$$\begin{gathered} x^{*}=\frac{2{\rho }_1{V}_2+2\left(1-{\alpha }_2\right)C_2-pq{b}_2^2-2{\eta }_2{V}_2}{2\left(\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1\right)} \\ {y}^{*}=\frac{2{\rho }_2{V}_1+2\left(1-{\alpha }_1\right)C_1-pq{b}_1^2-2{\eta }_1{V}_1}{2\left[\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2\right]} \end{gathered}$$

According to Friedman's method [30], the stability analysis of Jacobian matrix of a two-dimensional continuous dynamical system can obtain the evolutionary stability strategies of the system. The Jacobian matrix of the above two-dimensional dynamical system is

$$J=\left|\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right|=\left|\begin{array}{cc}\frac{\left(dx/dt\right)}{dx}& \frac{\left(dx/dt\right)}{dy}\\ \frac{\left(dy/dt\right)}{dx}& \frac{\left(dy/dt\right)}{dy}\end{array}\right|$$

(10)

where

$$\begin{gathered} \frac{\left(dx/dt\right)}{dx}=\left(1-2x\right)\left[y\left(1-\lambda +\beta \right)M+y{\rho }_2{V}_1-y{\rho }_1{V}_2+{\eta }_1{V}_1+\frac{1}{2}pq{b}_1^2-\left(1-{\alpha }_1\right)C_1-{\rho }_2{V}_1\right] \\ \frac{\left(dx/dt\right)}{dy}=x\left(1-x\right)\left[\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2\right] \\ \frac{\left(dy/dt\right)}{dx}=y\left(1-y\right)\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1 \\ \frac{\left(dy/dt\right)}{dy}=\left(1-2y\right)\left[x\lambda M+x{\rho }_1{V}_2-x{\rho }_2{V}_1+{\eta }_2{V}_2+\frac{1}{2}pq{b}_2^2-\left(1-{\alpha }_2\right)C_2-{\rho }_1{V}_2\right] \end{gathered}$$

The stability of equilibrium points can be determined by the sign of the determinant and trace of the Jacobian matrix. When DetJ>0 and TrJ<0, the equilibrium points are evolutionary stable strategies. In order to ensure that x^*, y^* are all on the R={(x,y)|0≤x≤1,0≤y≤1} plane, the above assumptions must meet

$$\begin{gathered} {\eta }_i{V}_i+\frac{1}{2}pq{b}_i^2-\left(1-{\alpha }_i\right)C_i-{\rho }_j{V}_i<0，\left(i,j=\mathrm{1,2}\mathrm{且}i\ne j\right) \\ \lambda M-{\rho }_2{V}_1+{\eta }_2{V}_2+\frac{1}{2}pq{b}_2^2-\left(1-{\alpha }_2\right)C_2>0 \\ \left(1-\lambda +\beta \right)M-{\rho }_1{V}_2+{\eta }_1{V}_1+\frac{1}{2}pq{b}_1^2-\left(1-{\alpha }_1\right)C_1>0 \end{gathered}$$

There are five local equilibrium points in the system, Q₁(0,0), Q₂(0,1), Q₃(1,0), Q₄(1,1) and Q₅(x^*,y^*), and the stability of each equilibrium point is shown in Table 2.

From Table 2, for the asymptotic stable point Q₁(0,0), Q₄(1,1), the evolution strategies are {negative collaborative innovation, negative collaborative innovation}, and {active collaborative innovation, active collaborative innovation}. Q₂(0,1) and Q₃(1,0) are the instability points for the system to converge different strategies, and Q₅(x^*,y^*) is the saddle point. Figure 1 shows the phase distribution of cooperative evolutionary game between the general contractor and subcontractor.

From the curve trend in Figure1, when the initial state is located on the upper right corner of the broken line connection, the system will gradually converge to the asymptotic stable point Q₄(1,1), at which time the general contractor and subcontractor will choose the active collaborative innovation strategy. Similarly, when located in the lower left corner of the broken line connection, the system will gradually converge towards the asymptotic stable point Q₁(0,0), at which time the general contractor and subcontractor will choose the negative collaborative innovation. Which asymptotic stable point the system evolves towards depends on the regional area Q₂Q₅Q₃Q₄(S₁) and the size of the regional area Q₂Q₅Q₃Q₁(S₂). When S₁ is the larger area, the greater is the probability that both parties will move towards {active collaborative innovation, active collaborative innovation}. However, when S₂ is the larger area, the greater is the probability that both parties will move towards {negative collaborative innovation, negative collaborative innovation}. The area Q₂Q₅Q₃Q₁(S₂) can be expressed as

$$S_2=\frac{1}{2}\left(x^{*}+y^{*}\right)=\frac{2{\rho }_1{V}_2+2\left(1-{\alpha }_2\right)C_2-pq{b}_2^2-2{\eta }_2{V}_2}{\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1}+\frac{2{\rho }_2{V}_1+2\left(1-{\alpha }_1\right)C_1-pq{b}_1^2-2{\eta }_1{V}_1}{\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2}$$

(11)

The main factors affecting the change of the area Q₂Q₅Q₃Q₁(S₂) are discussed below.

Proposition 1:

The influence of income distribution coefficient of the total output of collaborative innovation on the final decision-making of the general contractor and subcontractor depends on specific conditions.

Proof: It can be derived from Equation (11) that

$$\frac{\partial S_2}{\partial \lambda }=\frac{M\left[2{\rho }_2{V}_1+2\left(1-{\alpha }_1\right)C_1-pq{b}_1^2-2{\eta }_1{V}_1\right]}{{\left[\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2\right]}^2}-\frac{M\left[2{\rho }_1{V}_2+2\left(1-{\alpha }_2\right)C_2-pq{b}_2^2-2{\eta }_2{V}_2\right]}{{\left(\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1\right)}^2}$$

(12)

According to the above, the distribution coefficient of $\frac{\partial S_2}{\partial \lambda }$ and the total yield of collaborative innovation is not a monotonic function, and the value of $\frac{\partial S_2}{\partial \lambda }$ should be determined according to the specific situation; that is, the final evolution result of the system depends on the size of the income distribution coefficient. When $\frac{\left[2{\rho }_2{V}_1+2\left(1-{\alpha }_1\right)C_1-pq{b}_1^2-2{\eta }_1{V}_1\right]}{{\left[\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2\right]}^2}>\frac{\left[2{\rho }_1{V}_2+2\left(1-{\alpha }_2\right)C_2-pq{b}_2^2-2{\eta }_2{V}_2\right]}{{\left(\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1\right)}^2}$,$\frac{\partial S_2}{\partial \lambda }$ is an increasing function of λ, that is, with the increase of λ, the probability of the system evolving in Q₁(0,0) direction increases. Similarly, when $\frac{\partial S_2}{\partial \lambda }$ is a decreasing function of λ, the probability of the system evolving in Q₄(1,1) direction increases with the increase of λ. In the process of collaborative innovation, because the general contractor has the right to distribute the total output income of collaborative innovation, general contractors cannot unilaterally reduce the income of subcontractors to improve their own income. When subcontractors are not satisfied with the distribution of benefits, they will tend to choose negative collaborative innovation strategy, which is not conducive to the promotion of a collaborative innovation process.

Proposition 2:

The stronger the absorptive capacity of spillover technology of the general contractor and subcontractor, the more likely the two parties will choose the active collaborative innovation strategy.

Proof: It can be derived from Equation (11) that

$$\left\{\begin{array}{c}\frac{\partial S_2}{\partial {\alpha }_1}=\frac{-2C_1}{\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2}<0\\ \frac{\partial S_2}{\partial {\alpha }_2}=\frac{-2C_2}{\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1}<0\end{array}\right.$$

(13)

Therefore, $\frac{\partial S_2}{\partial {\alpha }_i}$ (i=1,2) is a monotone decreasing function of α_i. The area of S₂ decreases with the increase of α_i, that is, the probability of the system evolving in the direction of Q₄(1,1) increases. When the innovation subjects have strong absorptive ability of spillover technology; that is, the innovation subjects can reduce the trial-and-error in the innovation process by absorbing the existing technological innovation achievements into the collaborative innovation process. This can reduce the innovation cost and increase its own income, thus prompting the innovation subjects to more likely choose the active collaborative innovation strategy.

Proposition 3:

The greater the probability of negative collaborative innovation being discovered, the more likely the general contractor and subcontractor choose active collaborative innovation strategy.

Proof: It can be derived from Equation (11) that

$$\frac{\partial S_2}{\partial p}=\frac{-q{b}_2^2}{\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1}+\frac{-q{b}_1^2}{\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2}<0$$

(14)

Therefore, $\frac{\partial S_2}{\partial p}$ is a monotone decreasing function of p. The area of S₂ decreases with the increase of p, that is, the more likely the system evolve in the direction of Q₄(1,1). From the above assumptions, we can get that the innovation subjects' choice of negative collaborative innovation behavior will not only cause losses to the present interests, but will also have a negative impact on the future interests. That is to say, the greater the potential loss of reputation caused by negative behavior of innovation subjects, the more likely those subjects will tend to choose active collaborative innovation strategies to maximize their own interests. In the end, sustainable development is achieved.

Proposition 4:

The greater the reputation discount coefficient, the more likely the general contractor and subcontractor choose the active collaborative innovation.

Proof: It can be derived from Equation (11) that

$$\frac{\partial S_2}{\partial q}=\frac{-p{b}_2^2}{\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1}+\frac{-p{b}_1^2}{\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2}<0$$

(15)

According to $\frac{\partial S_2}{\partial q}<0$, S₂ is a monotone decreasing function of q. The area of S₂ decreases with the increase of q, that is, the more likely the system evolve in the direction of Q₄(1,1). When the reputation discount coefficient increases; that is, when the reputation benefit lost by the innovation subjects due to the negative collaborative innovation strategy increases, the probability of the innovation subjects choosing active collaborative innovation strategy increases.

Proposition 5:

The lower the cost of innovation, the more likely the general contractor and subcontractor will choose active collaborative innovation.

Proof: It can be derived from Equation (11) that

$$\left\{\begin{array}{c}\frac{\partial S_2}{\partial C_1}=\frac{2\left(1-{\alpha }_1\right)}{\left(1-\lambda +\beta \right)M+{\rho }_2{V}_1-{\rho }_1{V}_2}>0\\ \frac{\partial S_2}{\partial C_2}=\frac{2\left(1-{\alpha }_2\right)}{\lambda M+{\rho }_1{V}_2-{\rho }_2{V}_1}>0\end{array}\right.$$

(16)

According to the Equation (16), S₂ is the increment function of C_i(i=1,2); that is, with an increase in innovation cost, the area of S₂ will increase accordingly. Inversely, when the innovation cost decreases, the area of S₂ will decrease, and the probability of the system evolving towards point Q₄(1,1) will increase. In the process of innovation, based on the assumption that the innovation subjects display bounded rationality, the innovation subjects take the maximization of their own interests as the innovation goal. When the innovation cost is reduced, the innovation subjects can obtain more benefits from technological innovation, and at this time, the innovation subjects will be more inclined to choose active collaborative innovation, thus promoting the development of technological innovation.

4. Numerical Simulation

4.1. Parameter Assignment of Related Variables

In Section 3.2, the influences of various factors on the system evolution process are discussed. To further analyze the rule of the general contractor and subcontractor choosing active collaborative innovation strategy, this paper uses the software MATLAB 2018a to conduct numerical simulation. To make the conclusion not lose generality, and by referring to previous research and combining with the actual situation, relevant variable parameters were assigned. The specific values reflect the relative size of each ability of the game subject, but do not represent the real amount. This paper assumes that at the initial stage of cooperation, the attitude of the two parties is neutral, that is, the negative level b_i(i=1,2) of both parties remains at 0.5. Due to the basic income of the both parties has no influence on the subsequent analysis, this paper assigns the basic income of zero. The related variable parameters are shown in Table 3.

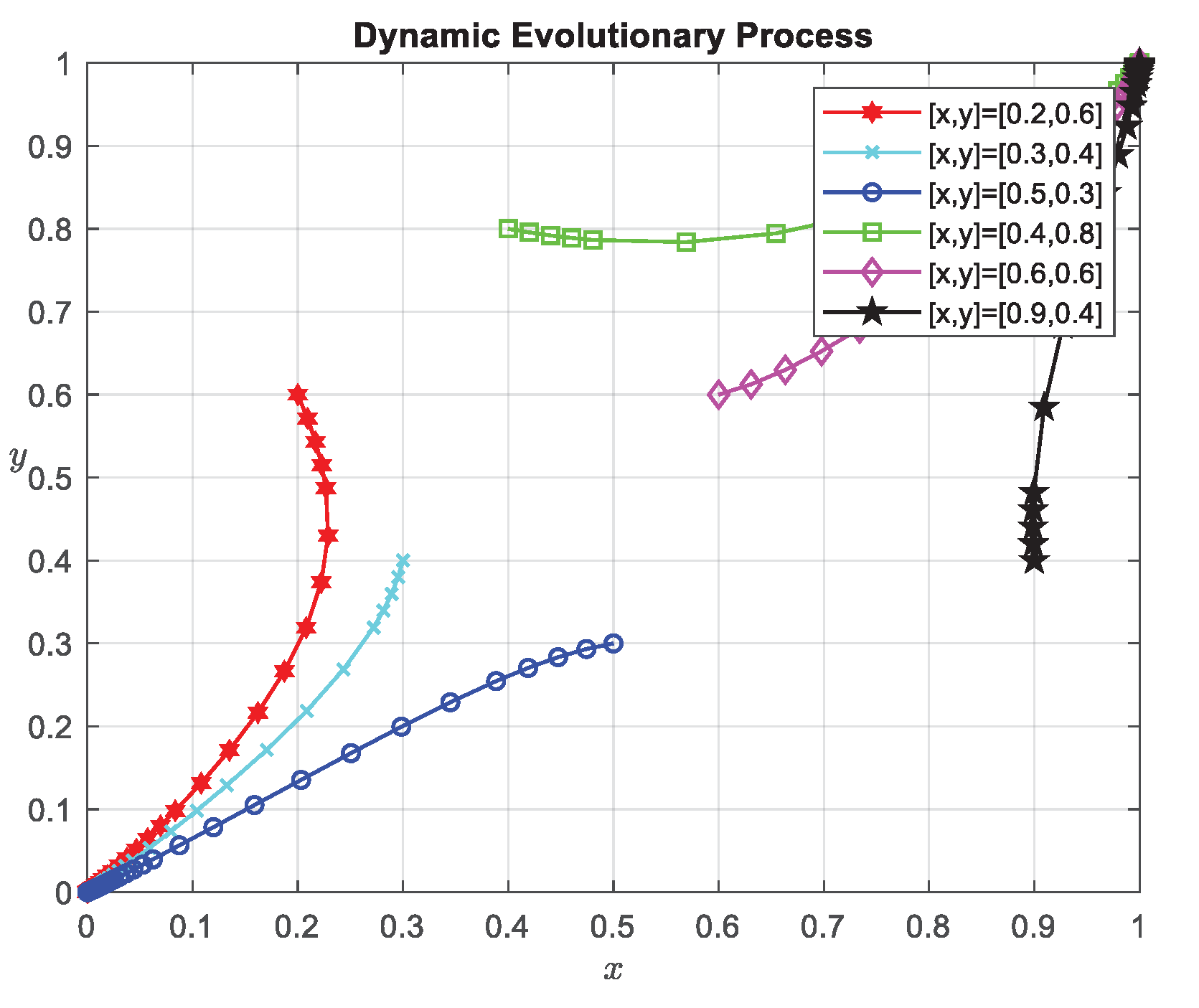
4.2. Influence of Initial Probability on System Evolution Process

To investigate the influence of the initial probability of selecting active collaborative innovation on the system evolution process, six groups of data are randomly selected for numerical simulation. Figure 2 shows that system evolution results under different probabilities. It can be concluded from Figure 2 that there are two stability strategies, (0, 0) and (1, 1); namely, {negative collaborative innovation, negative collaborative innovation} and {active collaborative innovation, active collaborative innovation}.

In the process of collaborative innovation, the collaborative innovation relationship between the two parties in the game is established on the basis of not damaging their own interests. From the above assumptions, it can be seen that when one party chooses the negative collaborative innovation strategy, there will be a "free rider" behavior; that is, it can get some of the benefits from the active party without reciprocal benefits flowing to the active party, thus damaging the interests of the active party. At this time, the active convenience will cause a change in strategy choice, that is, from active collaborative innovation to negative collaborative innovation, and will achieve a strategic stability at this time. When both parties of the game tend to choose an active collaborative innovation strategy, the interests of both parties are maximized. Under the assumption of bounded rationality, both parties aim at maximizing their own interests, so when both parties choose active strategies, they will not change the existing strategies; thus, forming a strategic stability.

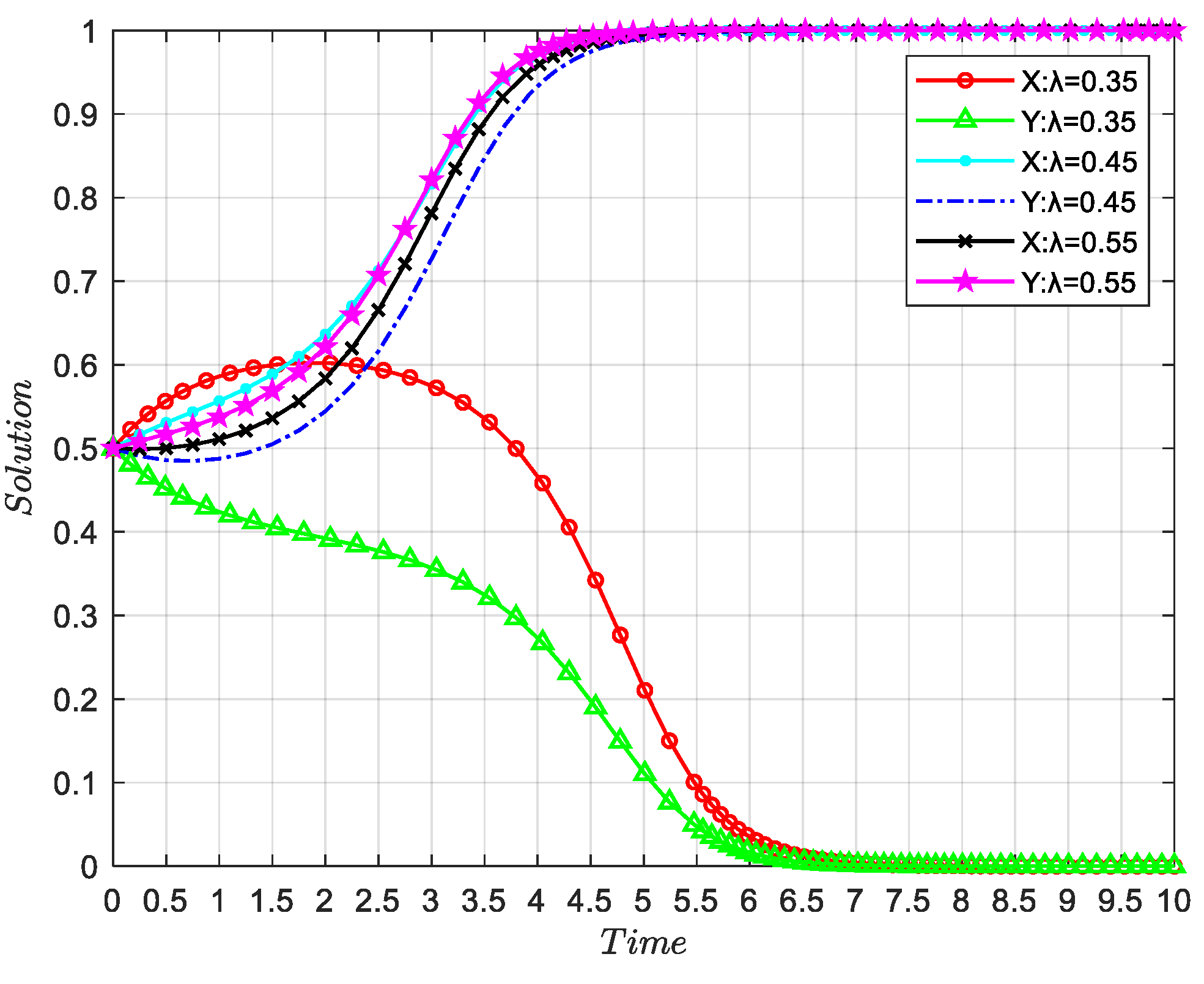
4.3. The Influence of λ on the Evolution Results of Both Parties

As the general contractor occupies a dominant position in the collaborative innovation process, it has the right to distribute the benefits of collaborative innovation. Therefore, to maximize its own interests, the general contractor may make unfair income distribution behavior. From the previous deduction, it can be concluded that there is a specific threshold for the income distribution ratio of collaborative innovation. When the distribution ratio is relatively low, the interests of collaborative innovation of subcontractors will be damaged, and they will gradually tend to choose negative collaborative innovation in the game process, which is not conducive to the promotion of technological collaborative innovation. Assuming that the income distribution ratio of collaborative innovation in this paper is 0.35, 0.45 and 0.55 the specific simulation results are shown in Figure 3.

The Figure 3 numerical simulation results verify the correctness of Proposition 1, and it can be concluded that there is a threshold between 0.35 and 0.45 in the income distribution ratio of collaborative innovation between the two parties in the game. When the income distribution ratio is less than the threshold, the system evolves towards negative collaborative innovation, whereas when it is greater than the threshold, it will evolve towards active collaborative innovation. The larger the income distribution ratio, the faster the system evolves and the shorter the time required to reach the stable strategy. From the perspective of sustainable development, the general contractor cannot unilaterally push down the income of the subcontractor to promote its own interests. This would cause the subcontractor to choose negative collaborative strategies, which is not conducive to the development of major engineering technology innovation. When distributing benefits, the general contractor should fully consider the benefits of partners, and rationally distribute the benefits of collaborative innovation without losing fairness, which can promote both parties to better evolve towards active cooperation, thus maximizing of their own interests and achieving sustainable development.

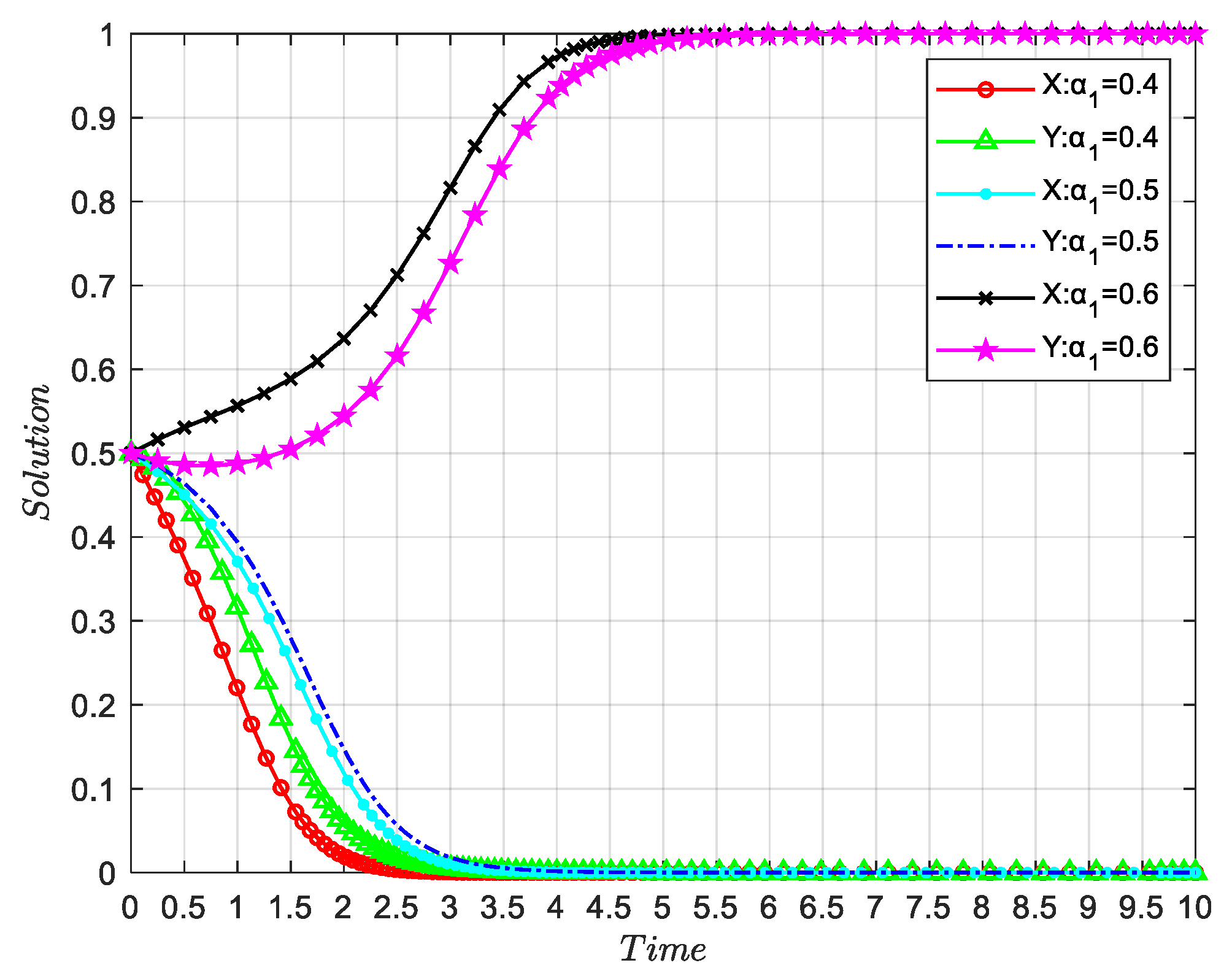
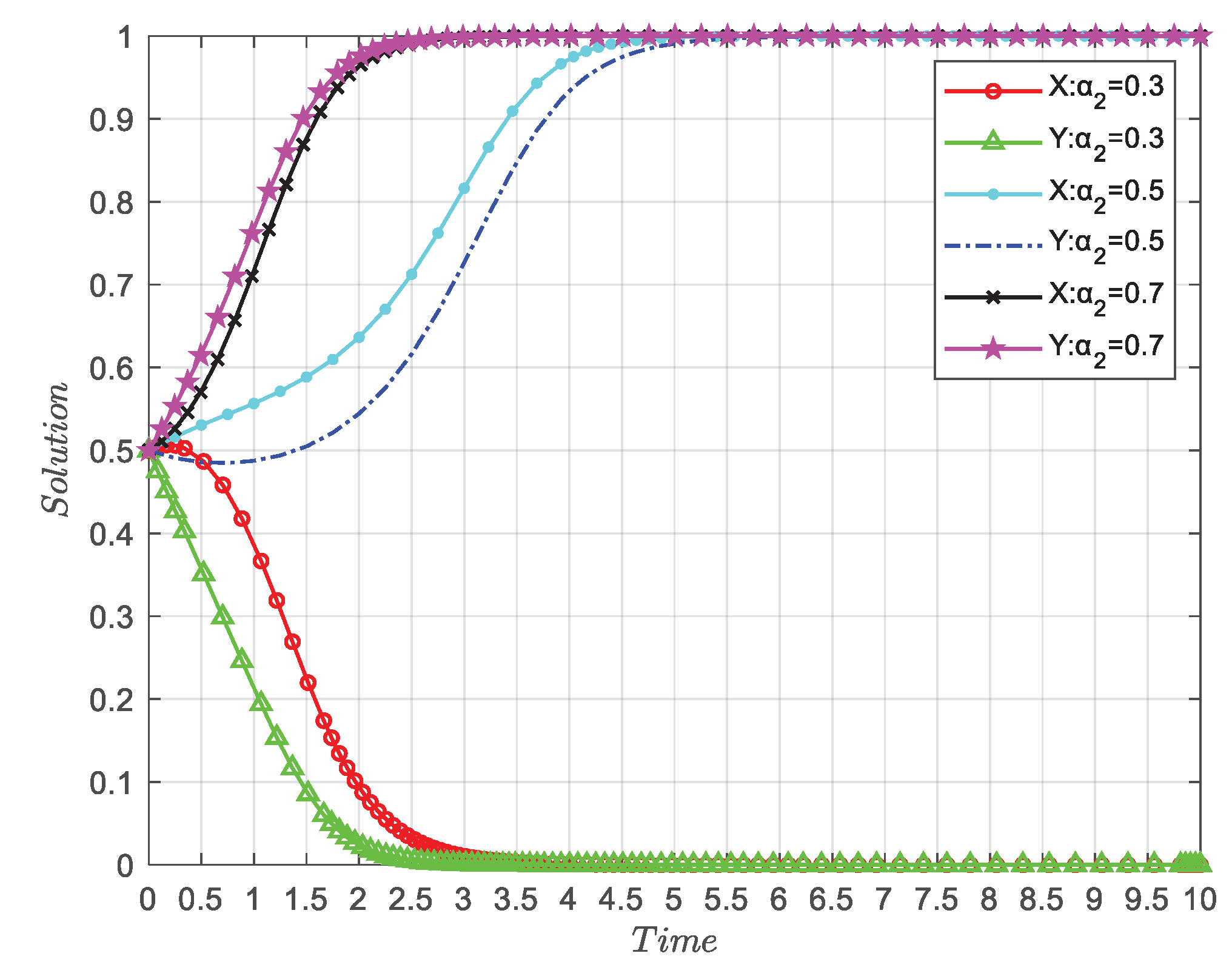
4.4. The Influence of α_i(i=1,2) on the Evolution Results of Both Parties

In the process of major projects' technology innovation, and based on the existing relevant research results, the innovation subjects can acquire valuable theoretical knowledge and technology for technological innovation, thus avoiding some mistakes or unnecessary experimentation in the innovation process. This knowledge acquisition subsequently reduces the innovation cost and improves income. Because neither contractor can absorb existing knowledge and technology completely, this paper selects the general contractor's spillover technology absorption capacity coefficients as 0.4, 0.5 and 0.6, and the subcontractor's spillover technology absorption capacity coefficients as 0.3, 0.5 and 0.7. The system evolution tracks are shown in Figure 4 and Figure 5.

By comparing the results in Figure 4 and Figure 5, it can be found that there are differences between the both parties in the threshold of spillover technology absorption capacity. The threshold of the former is between [0.5,0.6], while the threshold of the latter is between [0.3,0.5]. Therefore, it can be concluded that the spillover technology absorption capacity has different influences on different game players, and the game players will not change the existing innovation strategies when the cost reduction is small.

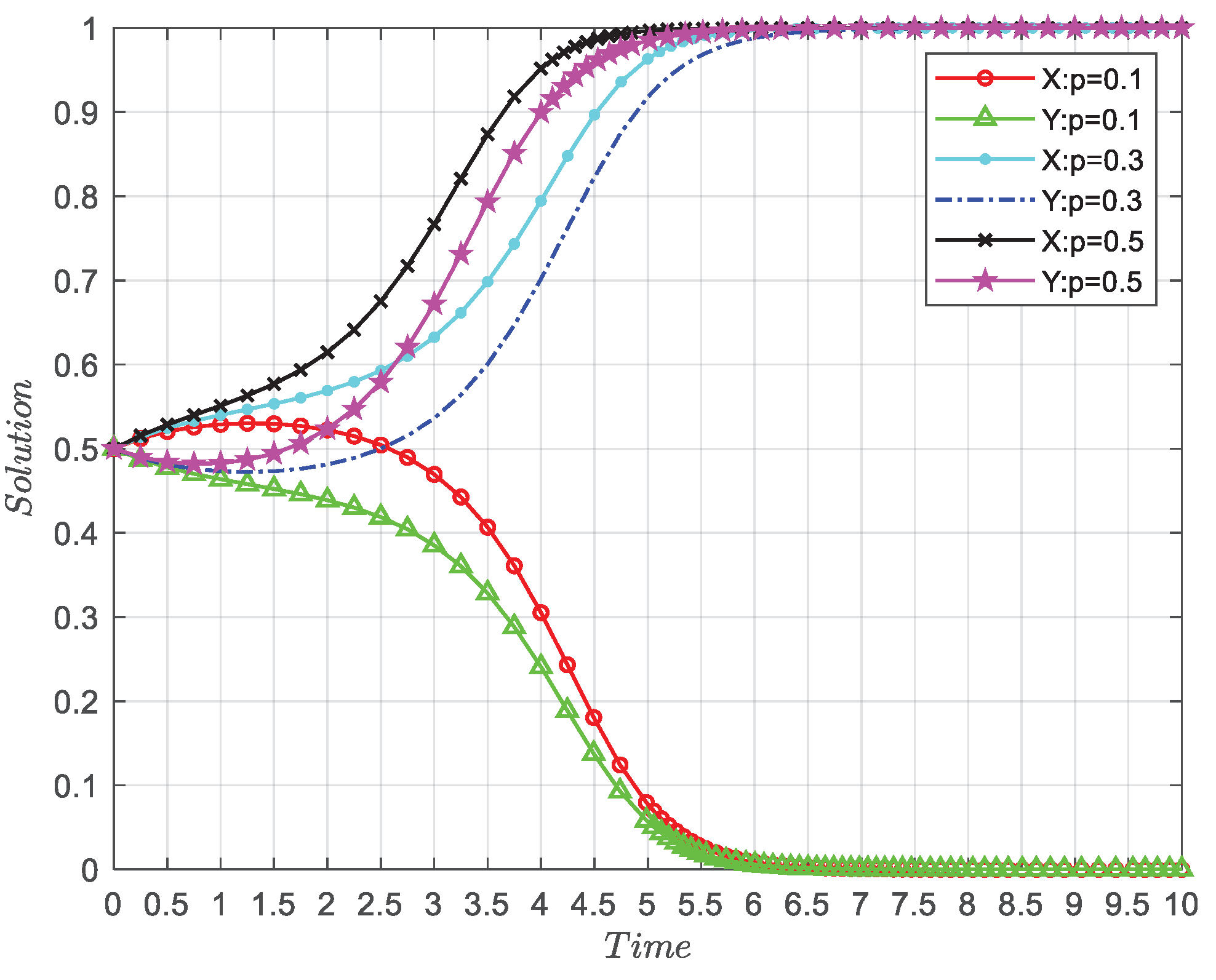
4.5. The Influence of p on Evolution Results of Both Parties

Major projects' constructions are related to the national economy and people's livelihood, and have extensive and high social attention. Negative cooperative behavior will not only bring negative impacts on project quality and progress, but it will also weaken the reputation of construction participants, and affect the promotion of projects' constructions and the development of construction participants. This paper assumes that the probability of negative collaborative innovation being discovered is 0.1, 0.3 and 0.5 and further analyzes the choice of evolutionary strategies of both parties in the game under different supervision, and obtains Figure 6.

Numerical simulation results show that the probability of active collaborative innovation will increase with the increase of the probability of negative collaborative innovation being discovered. According to Figure 6, when the probability is less than 0.3; that is, when the outside world gives less supervision to the participants in major projects' constructions, the participants will tend to choose negative cooperative behavior. At this time, the opportunistic motivation is strong, and the probability of collaborative innovation gradually tends to zero. When the general contractor and subcontractor realize that the external supervision is strong and has a great impact on their income, the collaborative innovation motivation of both parties becomes strong, and the system will develop in the direction of active collaborative innovation. Because major projects often have a great impact on social and economic development and improving people's lives, and considering the social benefits of major projects' constructions, it is necessary to implement appropriate supervision on the construction participants in the construction process to promote the development of technological innovation and the advancement of projects' construction process.

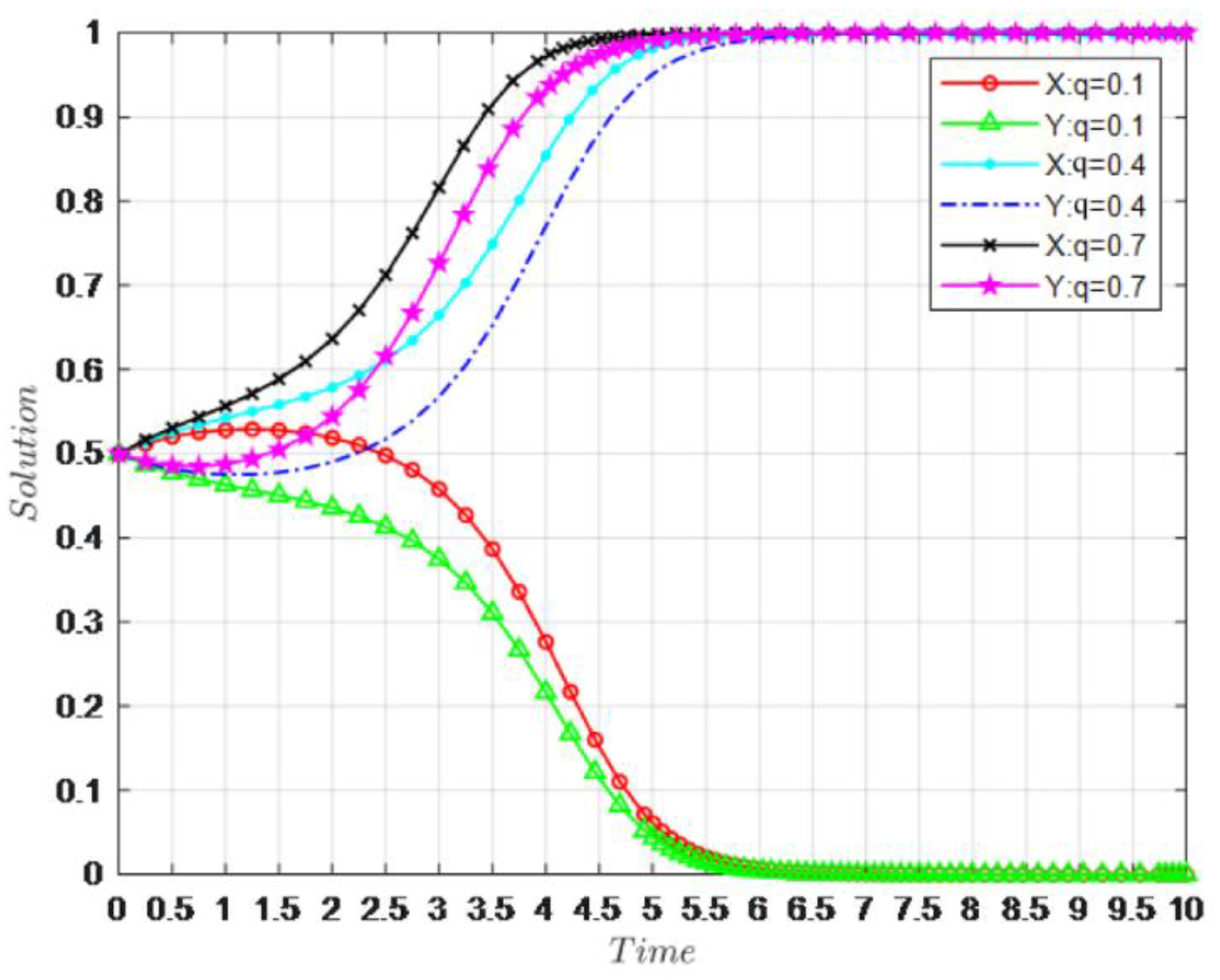
4.6. The Influence of q on Evolution Results of Both Parties

According to the above analyses, the larger the reputation discount coefficient, the greater the probability that the game players choose active collaborative innovation, and the more likely it is to lead to the evolution of the system in the direction of active collaborative innovation. This paper assumes that the reputation discount coefficients are 0.3, 0.4 and 0.5 respectively, and investigates the evolution process of active collaborative innovation strategy chosen by game players under different reputation influence degrees. The simulation results are shown in Figure 7. The results in Figure 7 verify the correctness of Proposition 4. At the same time, it can be concluded that the larger the reputation discount coefficient, the faster the system evolves towards active collaborative innovation.

Major projects have social influence beyond general projects and have great influence on national economic and social development. Enterprises participating in major projects' technology innovation and becoming the main body of their core technological innovation will significantly enhance their brand value and market influence. In the general contractor game, to maximize their own interests, the game subjects will inevitably choose negative and slack cooperative behaviors that pay the least cost and obtain the maximum benefits. Once the negative cooperative behavior is detected, there will be damage to its market reputation and reduced market share, which probably will produce a negative impact on its future development. When the game players realize that the reputation loss caused by negative behavior is too large, to improve influence in the industry and realize the sustainable development strategy, they will have greater enthusiasm for cooperative innovation.

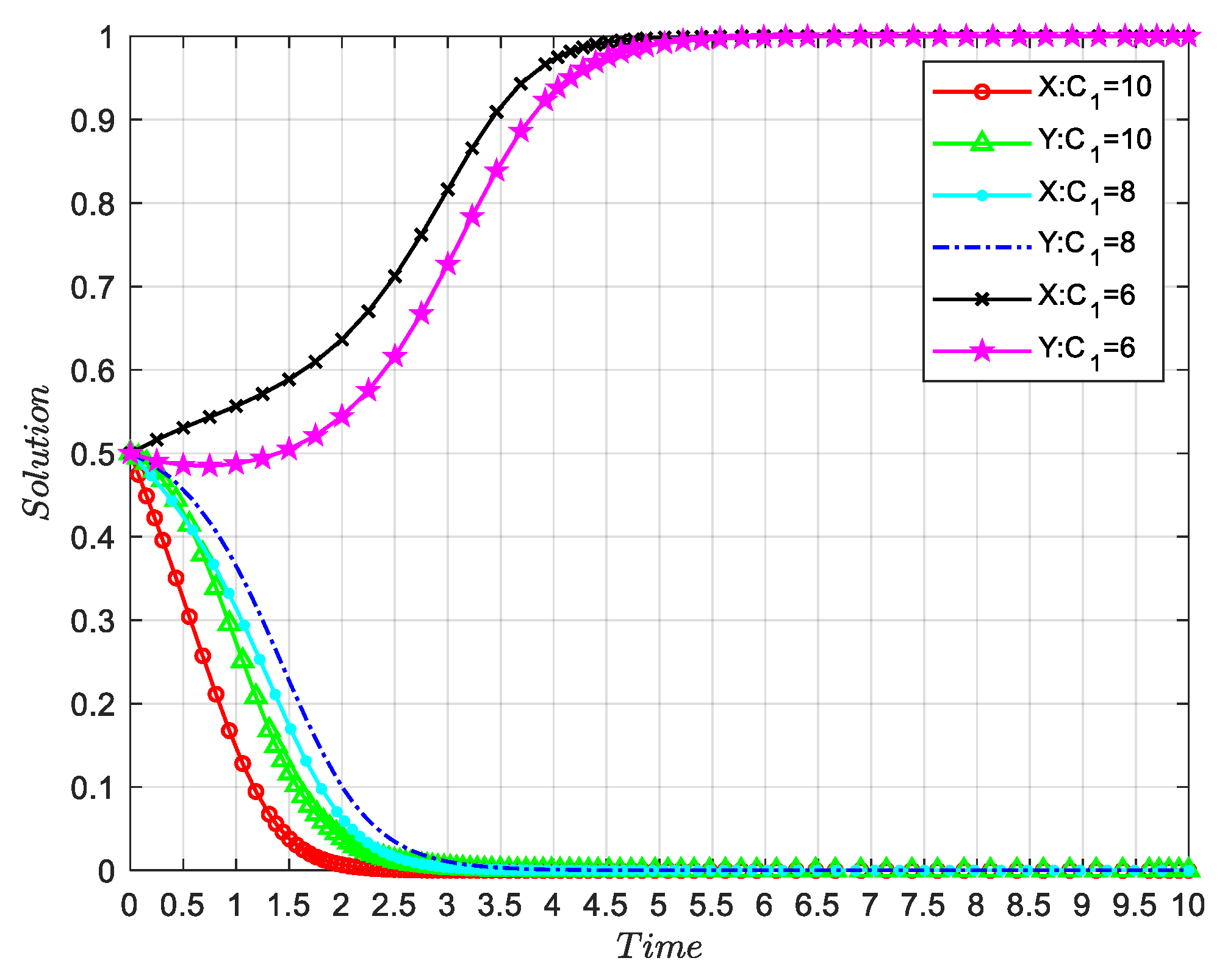
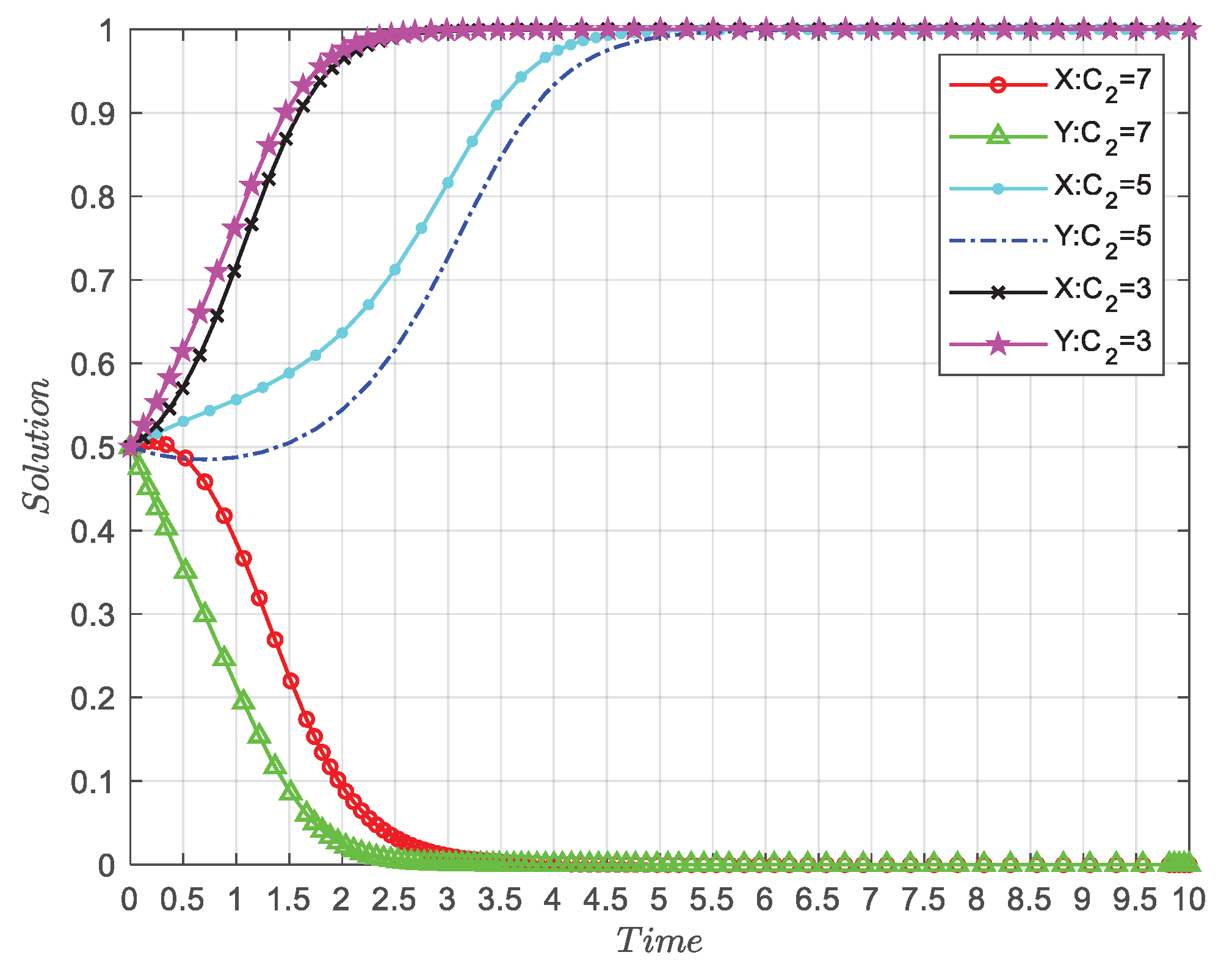
4.7. The Influence of C_i(i=1,2) on the Evolution Results of Both Parties

Different from general projects, major projects have the characteristics of long investment cycle, complex technology and large investment in R&D and innovation, which undoubtedly increases the cost and difficulty of innovation. In this paper, the influence of innovation cost on the evolution process of the system is considered, and the relative size of innovation cost of the game subjects is changed for simulation analysis under the condition that the relevant parameters are unchanged. The results are shown in Figure 8 and Figure 9.

The numerical simulation results in Figure 8 and Figure 9 also verify Proposition 5. When the innovation cost is too high, part of the profits is absorbed by the cost, which leads to the cost pressure on the general contractor and subcontractor becoming greater under the same income regime. The greater the risk they bear, the lower their profits, which makes them adjust their strategies and choose negative collaborative innovation behavior when they constantly play games; and the greater the innovation cost, the faster the evolution speed of the system towards negative cooperative behavior.

5. Research Conclusions and Suggestions

This paper constructs a collaborative innovation evolutionary game model of major projects' technology innovation subjects (the general contractor and subcontractor) by using the idea and method of evolutionary games, incorporates the reputation factor into the model, and considers the evolution process of game subjects' behavior under different factors on the basis of cooperation. The results show that:

First, there is a specific threshold for the income distribution ratio of collaborative innovation cooperation between subjects. If the income distribution ratio is slightly biased towards the subcontractor, it is more conducive to the evolution of the innovation subject in the direction of active collaborative innovation. Conversely, when the income distribution ratio is biased towards the general contractor, the innovation subject will finally choose negative collaborative innovation in the process of a continuous game, which is not conducive to the development of major engineering technology innovation and the advancement of engineering construction progress. The complexity characteristics of major projects make the innovation participants work together to complete all the innovation work, and reasonable benefit distribution is conducive to the development of technological innovation.

Second, the reduction of innovation cost will actively promote the evolution of both parties in the game towards active collaborative innovation, and the lower the innovation cost, the shorter the time for both parties of the game to reach evolutionary stability. Because major projects have the characteristics of high technical complexity and long investment cycle, the higher innovation costs will make the innovation subject bear huge cost pressure and risk, which will affect the decision-making of both parties in the game. In addition, the absorptive capacity of spillover technology of innovation subject will also affect the decision-making of each innovation subject. The stronger the absorptive capacity of an innovation subject, the greater the possibility that the system will evolve towards active collaborative innovation.

Third, on the basis of reputation effect, the probability of negative behavior being discovered is considered; that is, the attention given by the outside to major projects and technological innovations. It is found that when the probability of reputation discount coefficient and negative collaborative innovation is higher, the participants in major projects' technology innovation will choose active collaborative innovation strategies, and the larger the value, the shorter the time required for system evolution and stability. Due to their special social attributes, high-level supervision of major projects is necessary, and properly improving the supervision level can promote the evolution of active cooperation between the two parties.

The following suggestions are put forward:

(1)

Government can balance the problems in the income distribution by means of financial subsidies and innovation incentives. Major projects are the symbol of economic development, which can not only enhance China's comprehensive national strength and international status, but also accelerate China's modernization process. Because general contractors are in a dominant position in the construction process, unfairness will inevitably appear in the distribution of benefits, thus damaging the interests of subcontractors and leading them to choose negative cooperative behaviors. The behavior of participants in major project construction has an important impact on project quality and project cycle, so it is necessary to distribute the income reasonably, and the government should take financial means to balance the unfair distribution when necessary.

(2)

Participants in major projects should actively strengthen themselves and enhance their innovation ability. The innovation ability of participants will directly affect the promotion of major projects' technology innovation process. In the process of technological innovation, innovation cost is one of the important factors that restrict innovation enthusiasm, and innovation subjects are unwilling to bear huge cost pressure. Therefore, the innovation subjects should strive to improve the innovation ability, because the stronger the innovation ability, the lower the innovation cost. In addition, due to the large number of participants in major projects' technology innovation, in the early stage of project construction, the innovation ability of participants should be included in the assessment criteria when building a cooperative team with strong innovation abilities.

(3)

We propose to increase public participation in major projects' innovations. Major projects not only play an important role in the development of national economy, but also have a far-reaching impact on the public. For example, the completion of the Three Gorges Dam project not only solved the flood problem in the upper reaches of the Yangtze River, but also effectively alleviated the shortage of electricity in our society. Improving public participation can not only make the public perceive the social benefits brought by the construction of major projects, but to a certain extent they can also play a supervisory role on the participants in major projects and technological innovation. In addition, the government can also set up effective reward and punishment measures to improve the enthusiasm of public participation, and then promote the development of major projects and technological innovation.

• This study reveals the role of the general contractor and subcontractor in the process of major projects' technological innovation behavior decision-making, and refers to both development of major projects and technological innovation. However, this paper is from the theoretical point of view, and lacks engineering construction and technological innovation data, so there will be differences between the research conclusions and actual major projects. In addition, this paper selects only a few of the major projects' technology innovation influencing factors for research. In spite of these limitations, this research can act as a comprehensive reference point for more for in-depth studies.