SALOS - A UWB Single Anchor Indoor Localization System based on a Statistical Multipath Propagation Model

Among others, UWB-based multi anchor localization systems have been established for industrial indoor localization systems. However, multi anchor systems have high costs and installation effort. By exploiting the multipath propagation of the UWB signal, the infrastructure and thus the costs of conventional systems can be reduced. Our UWB Single Anchor Localization System (SALOS) successfully pursues this approach. The idea behind SALOS is to create a localization system with a sophisticated signal modeling. Therefore, neither measured reference like fingerprinting nor training is required for position estimation. Although SALOS has been implemented and tested successfully already in an outdoor scenario with multipath propagation, it has not yet been evaluated in indoor environment with challenging and hardly predictable multipath propagation. For this purpose, we have developed new algorithms for the existing hardware mainly a three-dimensional statistical multipath propagation model for arbitrary spatial geometries. The signal propagation between the anchor and predefined candidate points for the tag position is modeled in path length and complex-valued receive amplitudes. For position estimation, these modeled signals are combined to multiple sets and compared to UWB measurements via a similarity metric. In the end, a majority decision of multiple position estimates is performed. For evaluation, we implement SALOS in a modular fashion and install the system in a building. For a fixed grid of 20 positions, SALOS is evaluated in terms of position accuracy. The system results in correct position estimations for more than 73% of the measurements.

Keywords:

single anchor localization

;

indoor localization

;

UWB

;

channel impulse response

;

multipath propagation model

;

optimal anchor positioning

;

signal processing

;

DW1000

Subject:

Computer Science and Mathematics - Signal Processing

1. Introduction

Indoor localization is an ongoing research field with a plurality of solutions starting from light-based approaches [1], acoustics [2], or camera-based solutions [3] and ending with radio-based approaches. One key factor of success is performance and costs. Radio-based approaches with satisfactory performance often require costly infrastructure [4]. One approach in recent years is the reduction of costs by introducing single anchor localization systems.

Single anchor localization is a technique that aims to estimate the position of a target node in a wireless network using one single reference node, called the anchor [5]. This technique reduces costs and complexity of conventional multi-anchor systems, which require multiple reference nodes and synchronization among them [4]. However, single anchor localization also faces many challenges, such as the limited information available from one anchor, the multipath propagation of the wireless signals, and the non-line-of-sight conditions. To overcome these challenges, different approaches have been proposed, such as moving mobile anchors [6,7], integration of external inertial measurement units (IMU) [8], applying advanced signal processing [9] and optimization methods [10,11], as well as exploiting multipath signals [12,13].

In this paper, we review the state-of-the-art of single anchor localization and present our re-imagined novel system, SALOS, which is an ultra-wideband (UWB) single anchor indoor localization system based on a statistical multipath propagation model. The idea of SALOS is to estimate positions based on measurements only by comparison with modeled signals as reference. In [14], we have already shown with a rudimentary structure for SALOS that our approach to outdoor localization works with little multipath. For indoor use with massive multipath, we had to fundamentally re-develop the system. Figure 1 shows the structure of SALOS with the single processing steps from top to down. The main part is the modeling of sets of expected receive signals for possible tag positions namely the candidate points (CP), only based on the transmitted signal shape and the expected environment. Modeling is particularly challenging because the integrated low-cost hardware, namely Qorvo’s DW1000 RF chip, only provides on the hardware-side, post-processed receive signals, which are not physically correct. The set of these modeled receive signals is compared with the measured signal by a similarity metric to estimate the corresponding most likely position of the tag. The most likely positions for multiple sets of modeled signals are evaluated via majority decision. This decision results in a overall candidate point, which will be the final estimated position for the measurement. Following this setup, no further external information is needed, such as priori positions, IMU measurements or multiple antennas.

The contributions of the paper are:

We design a modular approach of a single anchor localization system called SALOS.
We present a three-dimensional multipath propagation model for arbitrary spatial geometries to construct receive signals with statistic variation of amplitude and phase.
With these distinct modeled signals, we employ a straightforward algorithm and similarity metric to estimate the tag’s position.
We evaluate the position accuracy of SALOS for a real indoor environment and publish the measurements and modeled datasets for free download.

The paper is organized as follows: Section 2 provides a review of related work on UWB-based localization systems with minimal infrastructure. A three-dimensional multipath propagation model is derived in Section 3. We explore UWB signal propagation in a multipath environment, resulting in modeled signals with statistical variation of amplitude and phase. Section 4 describes localization with SALOS in detail, including anchor placement, signal processing of the measured signal with distance measurement, and position estimation. The evaluation setup, the metrics, and results for assessing SALOS localization performance are available in Section 5. The paper concludes with a summary and a discussion of future work with potential research directions.

2. Related Work

With SALOS — our novel UWB-based single anchor localization system — we consider approaches for localization systems with minimal infrastructure and especially single anchor systems as related. Starting with Bluetooth which has low costs we will proceed with UWB systems and finally compare related work to our approach.

The radio technology Bluetooth offers localization capabilities with minimal infrastructure. In [8], Ye et al. analyze angle estimation together with signal strength for distance estimation and IMU data for indoor localization. Since version 5.1, the Bluetooth standard offers direction finding via an optional constant tone extension enabling low-cost localization for devices such as smartphones [15,16]. However, multipath propagation in indoor environments remains a problem for narrowband radio technologies such as Bluetooth [16].

To address multipath propagation or even apply it for localization we need higher bandwidth and short pulses. UWB communication systems meet these requirements. While SALOS works with active tag UWB nodes, the multipath assisted MA-RTI system from [17] follows a passive approach. The system tracks objects by incorporating multipath propagation, without nodes on the objects for localization. The approach is a good example how multipath propagation can help to improve accuracy or reduce costs.

In [18], Ge et al. propose a single anchor localization system combines time difference of arrival (TDoA) and multiple antennas to calculate the phase difference of arrival (PDoA) for indoor localization. Wang et al. propose a model that estimates the distance also via TDoA, and the angle-of-arrival (AoA) for every tag’s candidate position. However, their approach requires an anchor with multiple antennas [19]. In [20] and [21], Rzymowski et al. and Groth et al. proposed utilizing of an electronically steerable parasitic array radiator (ESPAR) antenna for single anchor localization. Grosswindhager et al. present single anchor localization with commercially off-the-shelf available UWB radios [22]. In order to better evaluate the multipath propagation, the received signal is artificially split up by using several antennas. Wang et al. propose a single anchor localization with UWB signals, using time-of-flight, and angle-of-arrival approaches in [23]. Although a single anchor is deployed, it is equipped with a circular antenna array including multiple of Qorvo’s DW1000 RF chips. All these systems try to handle multipath propagation by high bandwidth signals and estimating the most possible direction of the tag and distance to the tag via the received signal strength and multiple or special antennas.

In [24], Meissner et al. was the first to propose a two-dimensional single anchors localization systems and evaluate it via simulations. The idea is to exploit signal reflection on walls to calculate matching virtual anchors, which replace the requirement for physical anchors. We are inspired by this approach and use the virtual anchors concept in our modeling.

To the best of our knowledge, there are only few works that do not depend on multiple UWB radios, external information e.g. as IMUs, or multiple installed antennas. In [25], Mohammadmoradi et al. implement their system also with Qorvo’s DW1000 RF chip. They extract statistical features from the stored receive signal samples for usage in fingerprinting algorithms, needing for initialization a training measurement set.

Compared to this, in this paper we propose a novel approach that only employs information extracted from the DW1000’s measured UWB receive signal, modeled reference data and without prior training. Therefore, our approach does not require special or multiple antennas, it works with the default antennas. In addition, we present a modular framework for the algorithmic implementation, enabling distributed computation on different machines and commissioning as a live system. Insights from our proposed signal processing and modeling of the multipath propagation of SALOS can be adapted to other approaches (e.g. radio technologies) that depend on multiple antennas in the future.

3. Construction of Receive Signals with a Three-Dimensional Multipath Model

With SALOS, we introduce a localization system that does not require any recorded measurement data like fingerprints as a reference. In our approach, the reference data for position estimation is modeled artificially. The multipath propagation of the transmit signal affects the UWB receive signals, which are the basis for our measurements. We explain the propagation of the signal to the receiver in Section 3.1. We introduce the correlation between the tag and anchor position and the receive signal in Section 3.2 which is the basis for our position estimation. We present details of our multipath model in Section 3.3 including the geometric model, the creation of complex-valued amplitude multi-path components, and the complete modeling of the receive signals.

3.1. UWB Signal Propagation in Multipath Environments

The position estimation accuracy of SALOS depends on the artificial reference data. To model realistic UWB receive signals as a reference, we require a deep understanding of signal propagation in environments. Therefore, we discuss the signal propagation from a UWB signal from an anchor to a tag and the resulting receive signal.

UWB is characterized by a spectrum with a minimum bandwidth of

B \approx 500

MHz at a center frequency

f_{c} > 3.1

GHz [26]. We communicate in UWB low-band at

f_{c} = 3.4944

GHz with

B = 499.2

MHz, namely the IEEE 802.15.4-2011 standard channel 1 [27].

The transmit signal in the time domain is a sinc pulse multiplied with the carrier signal, so

x (t)

is defined as a cosine wave of frequency

f_{c}

, which is weighted with a sinc-function with zeros in the range of

T_{\sin c} = 1 / B

around t = 0:

\begin{matrix} x (t) = \sqrt{P_{Tx}} \cdot \frac{sin (π \cdot t / T_{\sin c})}{π \cdot t / T_{\sin c}} \cdot cos (2 π \cdot f_{c} \cdot t), \end{matrix}

(1)

where

P_{Tx}

is the transmit power. Figure 2 plots

x (t)

in time and frequency domain as

X (f)

In the following, we assume an omnidirectional radiation pattern of the transmitting and receiving antennas. We selected this pattern because similar antenna patterns are installed in the actual implementation of SALOS. The receiver

R x

receives

x (t)

multiple times following both the direct path and reflections on walls or obstacles, as signal echoes. Figure 3 sketches this scene.

In general, each propagation results in a number I of signal echos resulting from I paths. Each of the paths is characterized by several parameters:

τ_{i}

the transmission delay of the signal echo at

R x

{\underset{̲}{a}}_{i}

the complex amplitude of the signal echo, and

n_{i}

the number of reflections while passing the corresponding i-th path. Delay

τ_{i} = d_{i} / c_{0}

is the fraction of the path length

d_{i}

and the speed of light

c_{0} \approx 3 \cdot 10^{8} \frac{m}{s}

. The amplitude

{\underset{̲}{a}}_{i}

results from transmit power

P_{T x}

, the gain of antenna of

T x

- and

R x

-side (

G_{T x}, G_{R x}

). Furthermore, the power is reduced by the Friis’ propagation path losses

P_{P L, i}

[28]:

\begin{matrix} P_{P L, i} = {(\frac{4 π d_{i} f_{c}}{c_{0}})}^{2}, \end{matrix}

(2)

where

f_{c}

is the center frequency of the transmission signal

x (t)

With every of the

n_{i}

reflections, material and angle-dependent reflection losses occur. Additionally, the signal echo experiences a phase shift of

180^{\circ}

and thus the sign of its echo’s amplitude changes [29]. The channel impulse response (CIR)

h (t)

depicts the multipath’s influence on the transmission:

\begin{matrix} h (t) = \sum_{i = 0}^{I - 1} {(- 1)}^{n_{i}} {\underset{̲}{a}}_{i} \cdot δ (t - τ_{i}) \end{matrix}

(3)

The signal

y (t)

R x

is the superposition of all I signal echos with:

\begin{matrix} y (t) & = x (t) * h (t) \end{matrix}

(4)

\begin{matrix} = \sum_{i = 0}^{I - 1} {(- 1)}^{n_{i}} {\underset{̲}{a}}_{i} \cdot \frac{sin (π \cdot (t - τ_{i}) / T_{\sin c})}{π \cdot (t - τ_{i}) / T_{\sin c}} \cdot cos (2 π \cdot f_{c} \cdot (t - τ_{i})) . \end{matrix}

(5)

Eq. (4) ff. represents the receive signal in a multipath environment. We derive the correlation between the tag and anchor position and the receive signal in the next section.

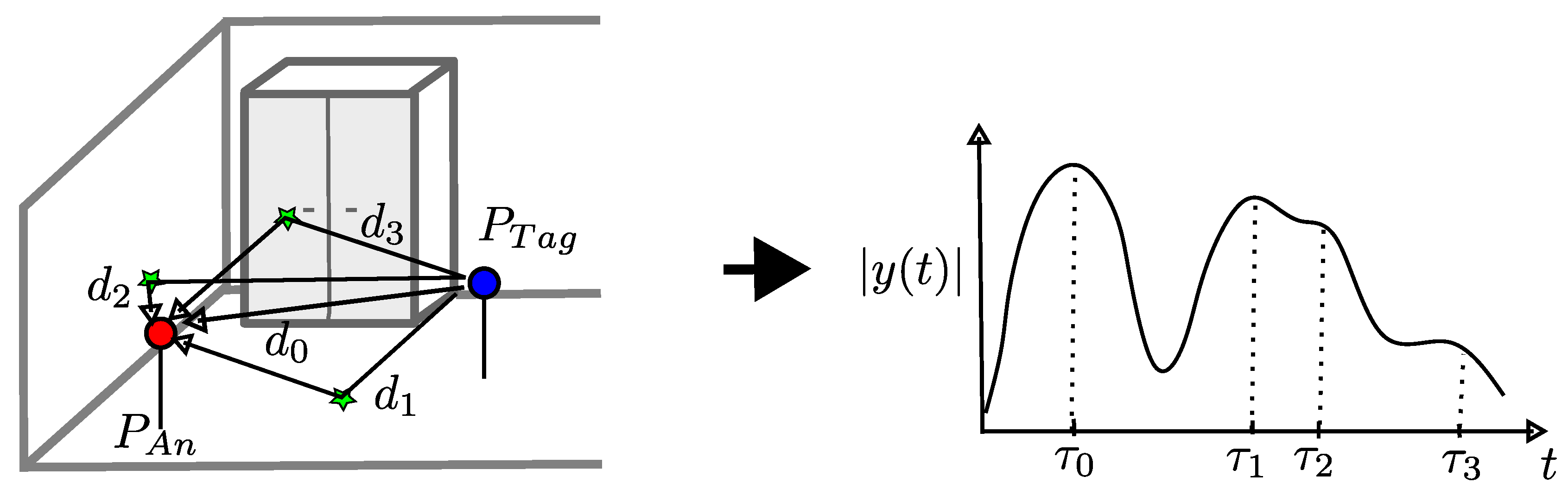
3.2. Correlation between Anchor and Tag Positions and UWB Signals

To enable optimal analysis of the receive signal for tag position estimation, it is necessary to consider the correlation between the tag position

P_{Tag}

and signal

y (t)

. In general, the paths of the received signal echoes depend on three factors: the anchor position

P_{An}

, the spatial geometry, and the

P_{Tag}

. For SALOS, the anchor is at a fixed position

P_{An}

within the spatial geometry, which is also assumed to be static meaning the anchor position and spatial geometry remain unchanged and known.

Thus, changes in the receive signal and its origin’s multipath propagation result solely from changes of the position of the tag

P_{Tag}

, as shown in Figure 4. This means that

y (t)

is correlated or mapped to

P_{Tag}

. To reverse the correlation and reconstruct

P_{Tag}

from

y (t)

, the mapping needs to be bijective: In this case the

y (t)

of each considered

P_{Tag}

is unambiguous and is mapped to exact one

P_{Tag}

. If ambiguity occurs and the

y (t)

for multiple tag positions cannot be distinguished additional external information is needed.

To ensure clear localization in SALOS, we aim for bijective mapping for a specific set of CPs in which the tag is placed later on. In order to fulfill this condition, for initialization the optimal anchor position

P_{An}

is selected in such a way that the receive signals are unambiguous at all CPs see [13]. We discuss the positioning of the anchor in Section 4. The following section describes the modeling of receive signals.

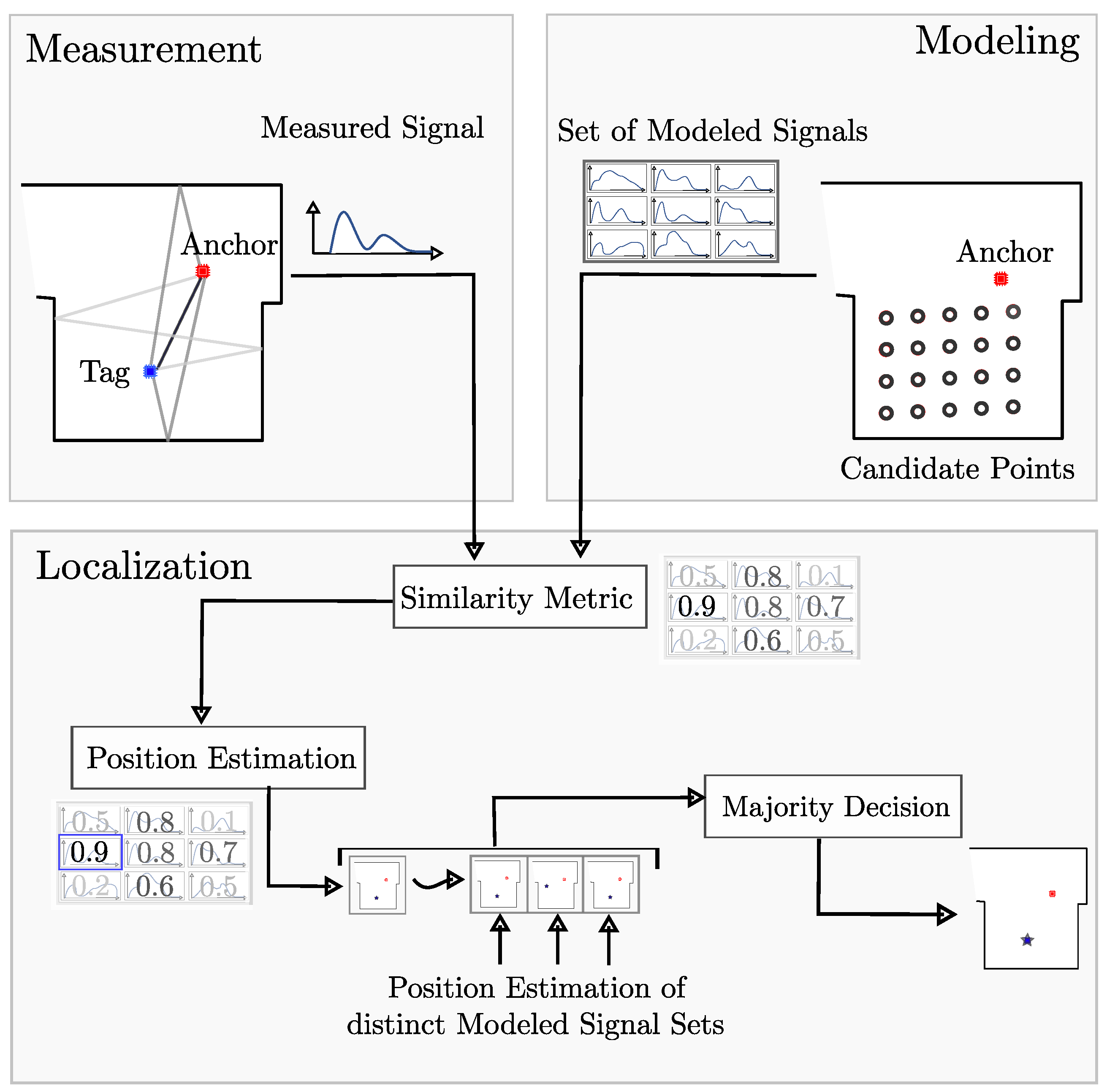
3.3. Modeling of Receive Signals Based on a Given Spatial Geometry

For constructing sets of suitable artificial reference data, a realistic modeling of receive signal is needed. To accurately model receive signals for arbitrary placed sensor nodes in a spatial geometry, following eq. (4), we need the original transmit signal

x (t)

and the modeled CIR

\hat{h} (t)

, including estimated transmission delays

\hat{τ}

and amplitudes

{{\hat{\underset{̲}{a}}}_{i}}

for all signal echoes. First, we introduce a three-dimensional geometric model to calculate all signal echoes including individual

\hat{τ}

in a multipath scenario in Section 3.3.1. Then, we extend our model with estimates for the complex-valued amplitudes

{\hat{\underset{̲}{a}}}

in Section 3.3.2. In the end, we show how the modeled receive signal is formed, see Section 3.3.3.

3.3.1. Three-Dimensional Multipath Model for Transmission Delay Estimation

To estimate the echoes’ transmission delays, we designed a multipath propagation model for arbitrary three-dimensional spatial geometries. Figure 5 depicts the estimated signal echo paths for a given set of tag and anchor nodes on a floor.

General Overview: The three-dimensional spatial geometry contains multiple reflective surfaces (e.g., walls, ground, ceiling, furniture and obstacles). We model the multipath propagation for each combination of anchor and tag position inside the geometry. With it, We calculate the respective path lengths and the reflection at the surfaces. Therefore we assumed that the materials of the surfaces have no noticeable influence on the transmission delay of the echoes.

The following description outlines the modeling for paths with exact

R_{\max} = 1

reflection illustrated in Figure 6, before the model is expanded to signal echoes with more reflections at the end of this section. Note: In the following, we distinguish between the infinite plane and the finite surface inside the plane.

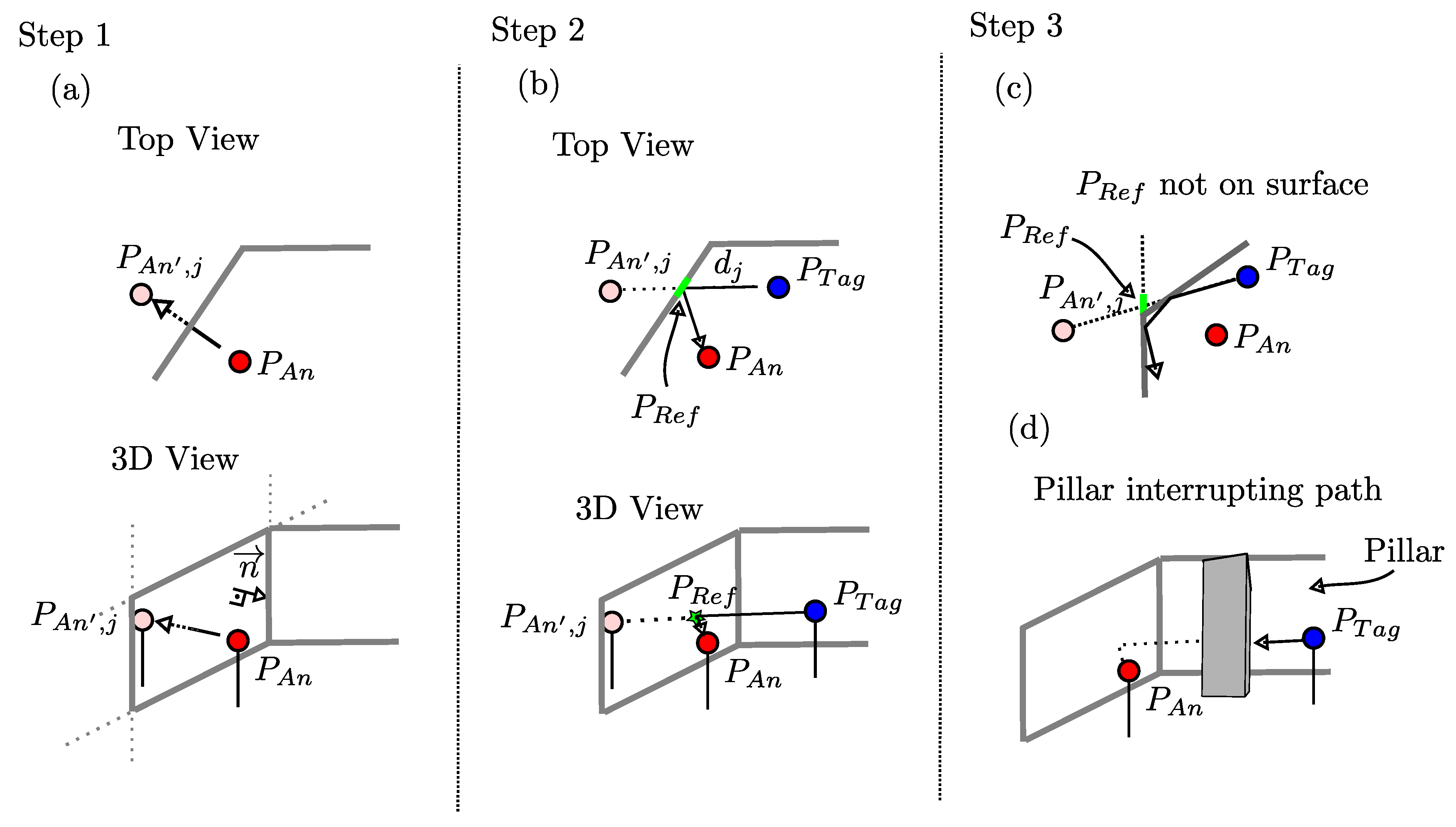
Step 1. Determining the position of virtual anchors: For modeling the signal echo paths, we determine the position of so-called virtual anchors, a reference point in the spatial geometry, to calculate the reflection path length between the anchor and the tag, and the reflection. For the j-th surface ( $j = 1, . . ., J$ ), the virtual anchor is the mirroring of the anchor on that surface. The mirroring of the anchor at position $P_{An}$ on a plane is to be computed in two iterations as shown in Figure 6 (a). First, determine the origin of the normal of the plane passing through the anchor position $P_{An}$ . Then determine the route ( $Δ$ x, $Δ$ y, $Δ$ z) between the origin of the normal and the anchor itself. The virtual anchor of the j-th surface is on the other side of this plane located at position $P_{{An}^{'}, j} = P_{An} - 2 \cdot (Δ x, Δ y, Δ z)$ . Overall for a spatial geometry with J walls J virtual anchors result.

Note: For the calculation of a valid virtual anchor it is not necessary that the origin of the normal is inside the surface.

Step 2. Calculation of the echo path: To model the multipath propagation delay accurately, a single parameter per path is needed, namely the path length $d_{j}$ for the generation of $h (t)$ . We calculate the point $P_{Ref}$ where the reflection occurs for validity check of the path. These steps are sketched in Figure 6 (b).

Due to geometry, the path length

d_{j}

is identical to the distance between the virtual anchor and the tag:

\begin{matrix} d_{j} = d_{ℓ 2} (P_{Tag} - P_{{An}^{'}, j}), \end{matrix}

(6)

where

d_{ℓ 2} (\cdot)

represents the Euclidean distance. For the point

P_{Ref}

where the reflection occurs, we draw a line between the virtual anchor and the tag. The intersection between the plane or the surface and the line is equal to

P_{Ref}

. The resulting path leads from

P_{Tag}

over

P_{Ref}

P_{An}

Step 3. Check path for validity: Not all paths created in the way described above are valid and thus distort the modeled receive signal. The first case occurs, if the reflection $P_{Ref}$ happens in the plane but outside the surface. Figure 6 (c) sketches the case where the $P_{Ref}$ is on the plane but not on the surface resulting in an invalid path.

The second case is, if a given surface (an obstacle e.g. a pillar) is interrupting the signal echo path, as shown in Figure 6 (d). With a single reflection, the path divides into two straight lines: One from

P_{An}

to the

P_{Ref}

and the second from

P_{Ref}

P_{Tag}

. For both lines, we check, if one of the remaining surfaces

k \neq j

intersects with any line. First, we check if there is an intersection with any surface’s plane. If this is true, the respective intersection is tested, if it is inside the plane’s surface. If this is the case for at least one line and one surface, the path becomes invalid.

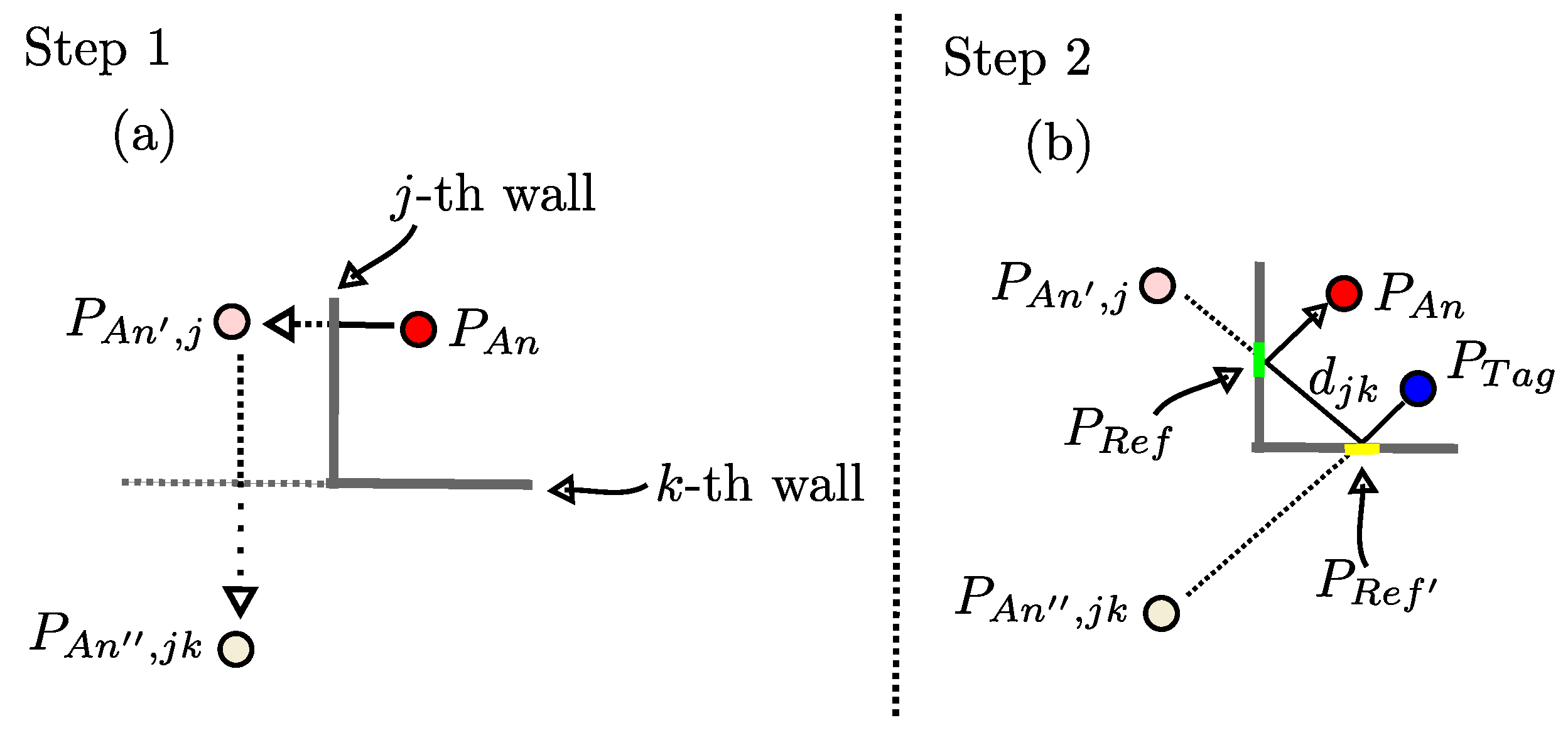
Expansion of the modeling for $R_{\max} \geq 2$ :

The exclusive integration of paths with a single reflection does not adequately represent reality. Also, paths with multiple reflections need to be taken into account. To model such paths, we apply the above steps for paths with more than a single reflection e.g.(

R_{\max} \geq 2

). The change is that additional mirroring occurs in step 1 and that the validity checks in step 2 are expanded for the path calculation.

In step 1, except mirroring the original anchor, we mirror the j-th virtual anchor at all remaining surfaces with

k \neq j

resulting in 2^nd-order virtual anchor at

P_{{An}^{''}, j k}

. Figure 7 (a) shows how additional virtual anchors are created for additional reflections in the paths.

So, overall two reflection points result. On the line

P_{{An}^{''}, j k}

P_{Tag}

P_{{Ref}^{'}}

is its intersection with the k-th wall.

P_{Ref}

is the intersection of the line

P_{{An}^{'}}

P_{{Ref}^{'}}

with the j-th wall. The path length of the corresponding signal path is

d_{j k} = d_{ℓ 2} (P_{Tag} - P_{{An}^{''}, j k})

. Figure 7 (b) depicts the path determination in step 2.

Finally, in step 3, this time three lines, namely

P_{An}

P_{Ref}

P_{Ref}

P_{{Ref}^{'}}

and

P_{{Ref}^{'}}

P_{Tag}

, are checked for interruption of the surface as mentioned above.

Knowing all I valid paths and their respective lengths

{d_{i}} = {d_{j}}

, the needed characterization parameters

\hat{τ_{i}} = d_{i} / c_{0}

are determinable. The estimated delays are not only needed for modeling the receive signal. Also, they are included for the upcoming statistical amplitude analysis.

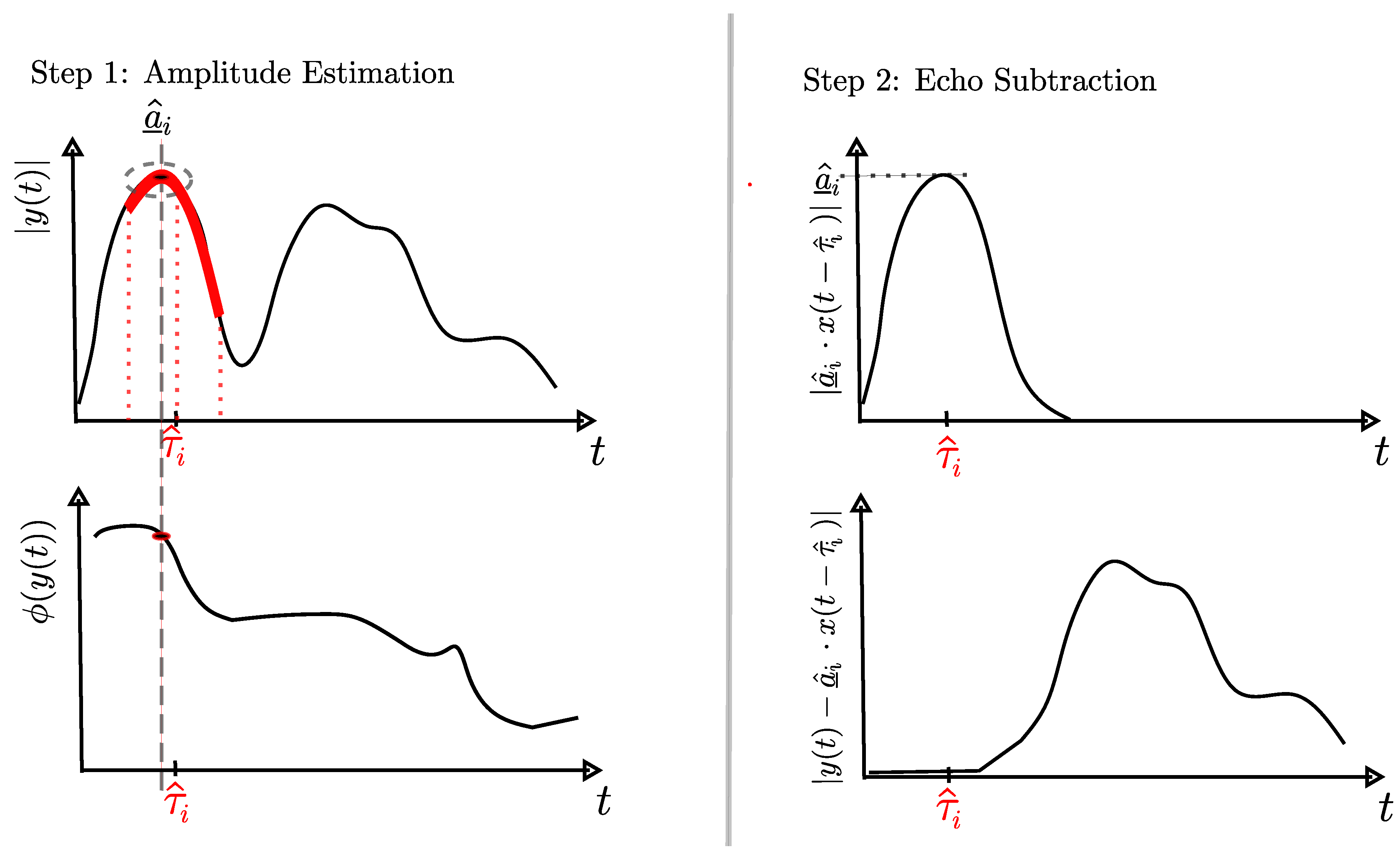
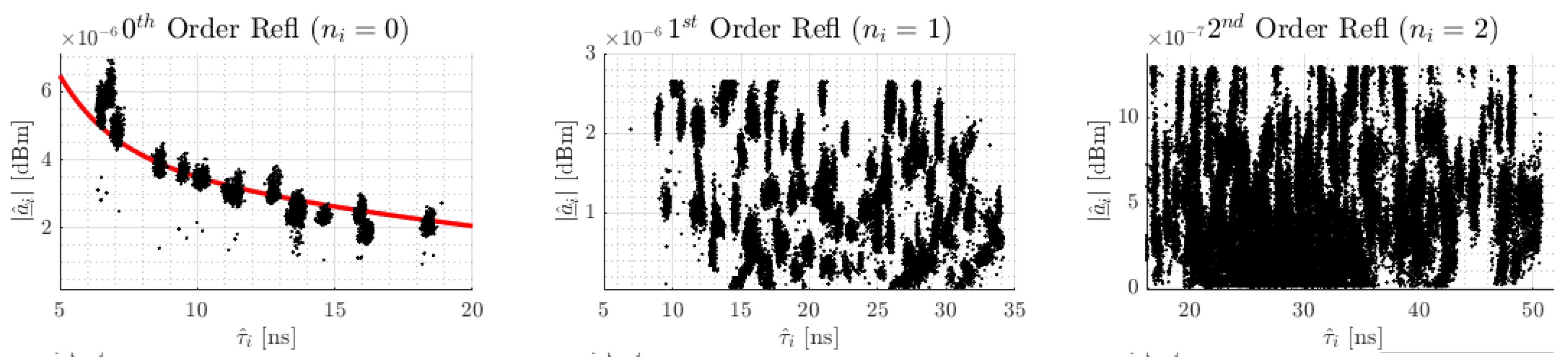
3.3.2. Statistical Analysis of the Amplitude for Estimation

According to eq. (4), to realistically model the receive signal we need transmission delay

\hat{τ}

and amplitude

{\underset{̲}{a}}_{i}

of each signal echo. Compared to

\hat{τ}

, the modeling of the complex amplitude

{\underset{̲}{a}}_{i}

is more challenging [22], as it is influenced by external factors such as material- and angle-dependent reflection coefficients and hardware-specific factors such as the automatic gain control (AGC) and the analog-to-digital converter (ADC) [27]. Also, the characteristics of the interference between two signal echoes is a further challenge which, under the given circumstances, makes it extremely difficult to trace back to specific amplitudes [30]. So, for SALOS we will model the amplitude randomized. In the following, we analyze the distribution statistically and identify important factors of the result. Based on them, we describe the chosen randomized modeling of the amplitude.

Note: In the following, we call the direct path without reflection the 0^th (reflection) order path. The paths with 1 or 2 reflection points are called the 1^st and 2^nd (reflection) order paths.

Analysis of amplitude’s characteristics and influence on modeling: For the analysis of amplitude’s characteristics, we recorded around 600 signal measurements for 20 tag and anchor position combinations, resulting in around 12,000 measurements. For these measurements, we determine the transmission delay of all signal echoes of the 0^th, 1^st, and 2^nd reflection orders following Section 3.3.1.

We estimate the complex amplitude

{\underset{̲}{a}}_{i}

of the signal echoes iteratively in magnitude

| {\underset{̲}{a}}_{i} |

and phase

ϕ ({\underset{̲}{a}}_{i})

. To analyze the amplitude with decreasing receive power, we consider the 0^th order signal echo first, then the reflections of the 1^st order with increasing transmission delay, and finally, the signal echoes of the 2^nd order also with increasing transmission delay. The following steps are identical for all echoes, as shown in Figure 8. First, we determine the analysis interval

[\hat{τ_{i}} - 1 ns, \hat{τ_{i}} + 1 ns]

, to compensate discrepancies between the measurement setup and modeling of up to 30 cm (

= 1

ns). Within this interval, we find the highest magnitude of the measured signal. For this maximum, we save the amplitude in magnitude and phase as

{\hat{\underset{̲}{a}}}_{i}

. If there was no maximum in the interval, but only a continuous curve, we save the complex amplitude at

\hat{τ_{i}}

. Finally, we subtract the shaped signal echo

{\hat{\underset{̲}{a}}}_{i} \cdot x (t - \hat{τ_{i}})

from the measured signal and process this difference further with the next signal echo.

Note: The following analysis is intended to provide an overview of the amplitudes for the given model. For a more realistic characterization of the amplitude, the distribution must be examined more closely. But here, indicators are enough for us to accurately model the complex amplitude successfully for the artificial receive signals.

We classify the amplitudes according to 0^th (around 12,000 values), 1^st (around 60,000 values), and 2^nd order (around 120,000 values) reflections. For analysis, we divide the complex values into phase and magnitude.

With few deviations, the phase estimations of the 0^th,1^st and 2^nd order reflections are located in the interval

[0, 2 π]

. There is no correlation between transmission delay and phase value, therefore these phases are considered independent of the transmission delay.

The results of the magnitude estimation are shown in Figure 9. From left to right, it depicts the magnitude estimations for all 0^th,1^st and 2^nd order signal echoes with respect to the estimated transmission delay

\hat{τ}

. As expected following Friis’ path loss model in eq. (2), the direct path shows an exponential decay of the magnitude with increasing distance between the sensor nodes. The red line in the plot depicts the exponential fitting with respect to the path losses. Table 1 lists the resulting fitting. The magnitudes of the 1^st and 2^nd order reflection are independent of the transmission delay. For them, the distribution of the magnitude is randomly between 0 and a maximum value: 1^st order maximum at

2.7 \cdot 10^{- 6}

dBm, 2^nd order maximum at

1.3 \cdot 10^{- 6}

dBm. We do not know the reason for this random distribution, but we take the corresponding maximum values as characteristics for modeling in our approach.

Based on the given characteristics, we determine random numbers for the magnitude and phase of each signal echo. Each phase is assumed to be uniformly distributed with

ϕ (\hat{{\underset{̲}{a}}_{i}}) \in U ([0, 2 π])

. In general, for magnitude modeling, we assume the 0^th order signal echoes to match the fitting described above. The magnitudes of 1^st and 2^nd order are normally distributed with

| \hat{{\underset{̲}{a}}_{i}} | \in N (μ, σ)

. For this, we determine mean

μ

and standard deviation

σ

based on the given sets of magnitudes. For these magnitudes, we also limit the random numbers upwards and downwards. If one of the random numbers is outside this range, the number is rolled again until the magnitude is within the range. The description of the random modeling for the 0^th, 1^st and 2^nd order reflections is listed in Table 1:

At this point, modeling for the transmission delays and the complex-valued amplitude were presented. Now the construction of the modeled receive signals and the allocation to signal sets for reference follows.

3.3.3. Modeling of the Receive Signals Sets for Reference

As mentioned above, to model accurately artificial receive signals we need the UWB transmit signal

x (t)

as well as a realistic CIR. With the given estimates for

{\hat{\underset{̲}{a}}}_{i}

and

\hat{τ_{i}}

, we construct the CIR

\hat{h} (t)

. Following eq. (4), with respect to the CP of the tag,

\hat{h} (t)

becomes

h_{CP} (t)

and the modeled signal

y_{CP} (t)

is calculated by convolution of

x (t)

and

h_{CP} (t)

\begin{matrix} y_{CP} (t) & = x (t) * h_{CP} (t) \end{matrix}

(7)

\begin{matrix} = \sum_{i = 0}^{I - 1} \underset{{\hat{\underset{̲}{a}}}_{i}}{\underset{︸}{| {\hat{\underset{̲}{a}}}_{i} | \cdot e^{j \cdot ϕ ({\hat{\underset{̲}{a}}}_{i})}}} \cdot x (t - \hat{τ_{i}}) \end{matrix}

(8)

The random amplitudes are crucial for the final shape of the modeled signals. Figure 10 shows at the top left a measured signal for a known spatial geometry, tag, and anchor position. The other receive signals shown are modeled based on the same setup with varying estimations of the complex amplitudes

{\hat{\underset{̲}{a}}}_{i}

. The respective correlation coefficient is given in the plot titles. While the shape at the top right seems to fit well, the modeled signals in the bottom row differ significantly from the measured one. This results only from the miss-modeled CIRs.

A good variance within the modeling increases the probability of correctly estimating the corresponding measured signal. For this, we create sets of

N_{CP}^{y (t)}

different randomly modeled signals per CP. These sets serve as reference data for SALOS.

After the description of SALOS’ modeling for the artificial reference data, the next section depicts how the localization with majority decision is done.

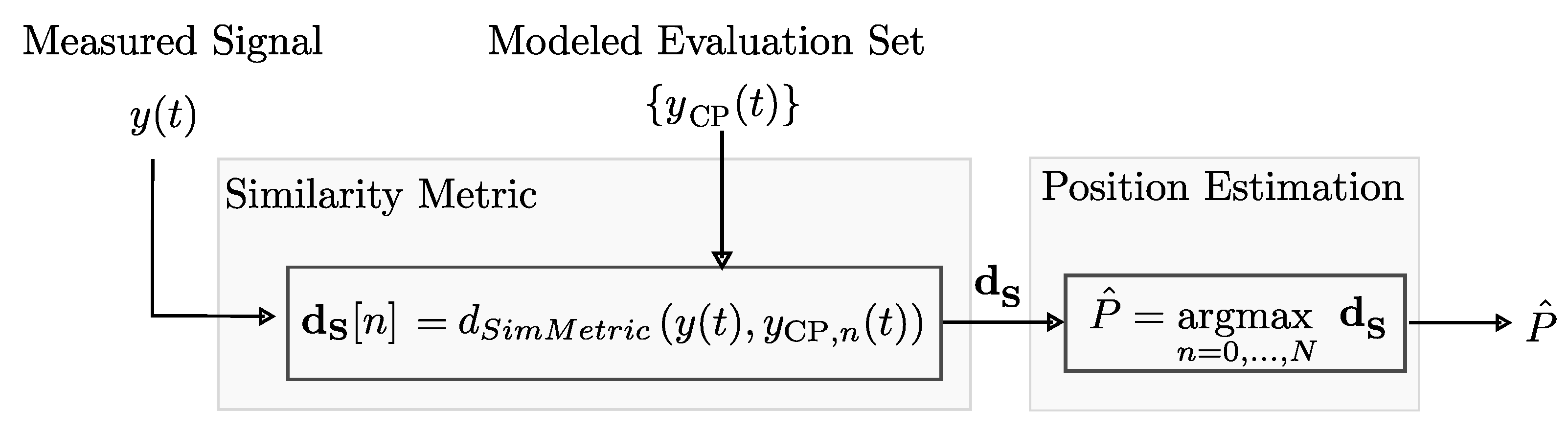
4. Localization Algorithm

The implementation of the localization algorithm in relation to the underlying input data and hardware is decisive for the accuracy of the system. Based on the modeled receive signal set, we design the localization algorithm and its implementation with Qorvo’s DW1000 UWB RF chip, integrated for measurement. In the first step, we derive the optimal anchor position for a given spatial geometry in Section 4.1. The DW1000 provides a raw UWB receive signal, which needs some processing as shown in Section 4.2. Finally we depict the localization algorithm based on the comparison of a measured receive signal and the modeled signal set in Section 4.3.

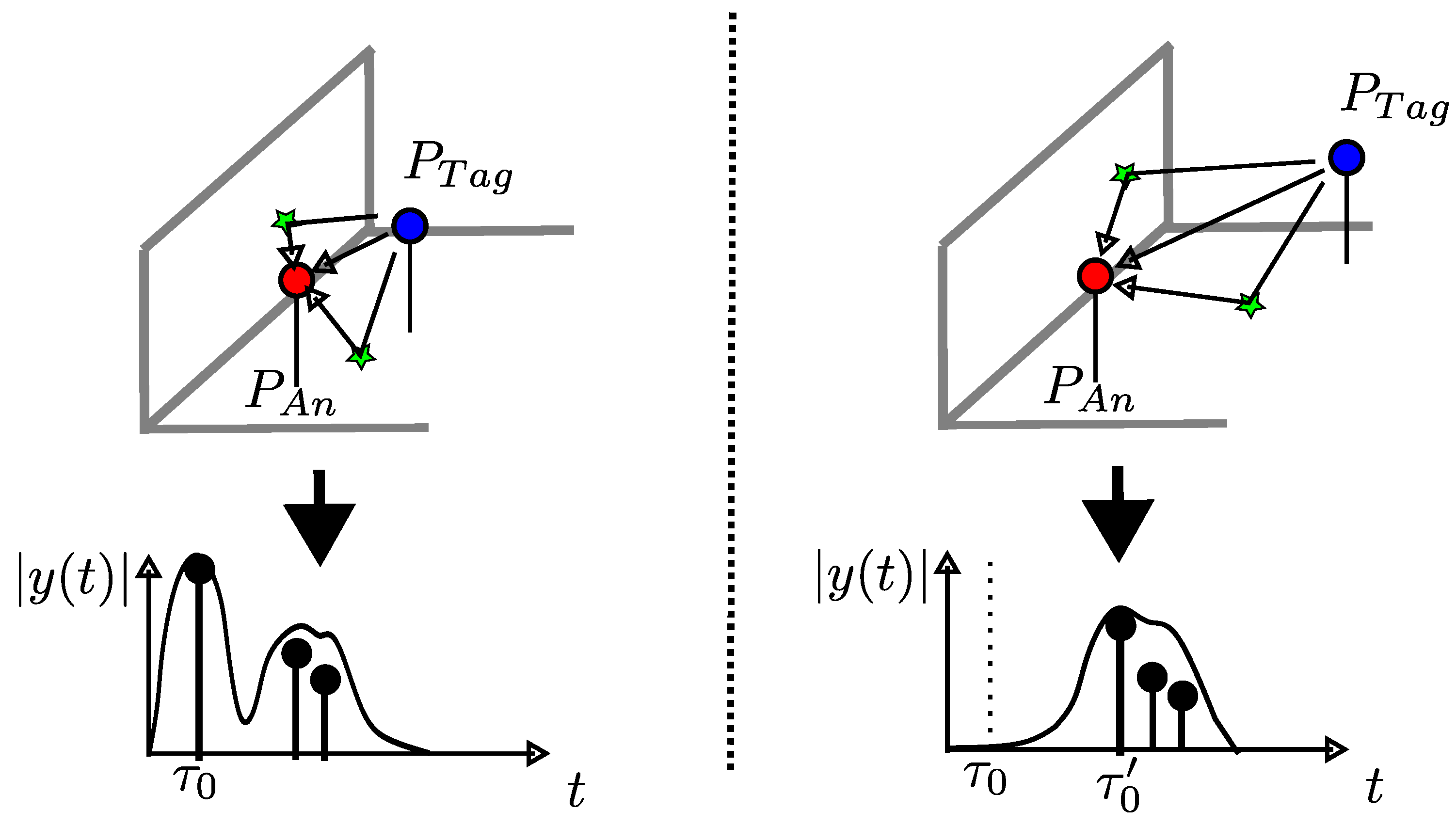
4.1. Optimal Position of the Anchor

In Section 3.2 we define, that all tag positions must result in unambiguous CIRs with respect to our chosen anchor position to avoid the need of additional assumptions, information or sensors. To place the anchor with respect to this case, in our previous work [13] we introduced the effective length of CIRs

ℓ_{e}

as a measure of the analyzed time interval to achieve unambiguity of CIRs.

In general two conditions for an anchor position are derived for optimization:

A valid anchor position results in unambiguous CIRs for all tag positions.
The optimal anchor position achieves the unambiguity of all CIRs with the shortest effective length $[0, ℓ_{e}]$ .

We always consider the optimal anchor position.

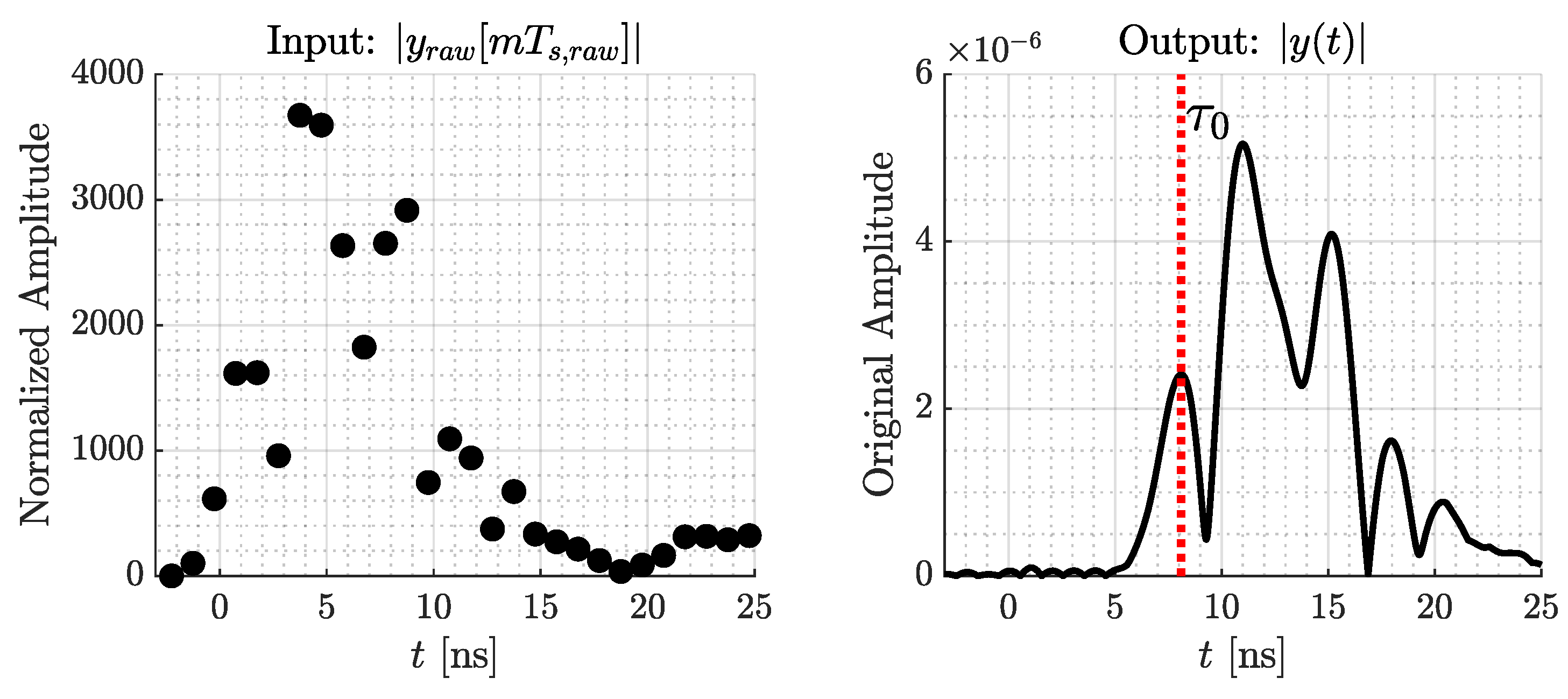
4.2. Signal Processing of Qorvo’s DW1000 Raw Measurements

The UWB receive signal measurement serves as input for the localization algorithm. This is realized by transmission via Qorvo’s DW1000 RF chip. But the DW1000 does not provide the measurement as needed, e.g. without distance information and accurate amplitude, therefore we process the signal after recording.

We apply a two-way ranging (TWR) for estimating the distance

d_{0}

between anchor and tag, which is described in Appendix A.

d_{0}

correlates to the transmission delay of the direct path with

τ_{0} = d_{0} / c_{0}

c_{0} \approx 3 \cdot 10^{8}

is speed of light. Additionally, we read the receive signal from the final message of TWR. In the following

y_{raw} [m T_{s, raw}]

is this DW1000’s measured signal with M samples,

m = [0, . . ., M - 1]

. The sample time is

T_{s, raw} \approx 1

ns. Since

y_{r a w} [m T_{s, raw}]

is a time-shifted, normalized, discrete, baseband-version of

y (t)

, we need further signal processing to recover

y (t)

. We describe the signal processing in this section.

The DW1000 marks the beginning of the first signal echo with the help of a leading-edge algorithm. The resolution of this marker is in the range of

1 / 64

ns, achieved by oversampling. With the transmission delay

τ_{0}

, we are able to create a matching time axis for the measurement.

Also, the DW1000 stores the measured receive signal strength (RSS) of the signal

P_{Rx}

in dBm. With

P_{Rx}

, we reconstruct the original output level of

y (t)

Finally, we interpolate the signal to estimate the data gaps between the samples. For interpolation, we convolve it with a sinc-function with zero crossings spaced at

T_{s, raw}

. Therefore, our processed signal is

y (t)

\begin{matrix} y (t) = \underset{Output Level Reconstruction}{\underset{︸}{\frac{10^{(\frac{P_{Rx}}{10})}}{\sum_{m = 0}^{M - 1} {| y_{raw} [m T_{s, raw}] |}^{2}}}} \cdot \underset{Interpolation}{\underset{︸}{\sum_{m = 0}^{M - 1} y_{raw} [m T_{s, raw}] * \frac{\sin (π t / T_{s, raw})}{π t / T_{s, raw}}}} . \end{matrix}

(9)

Figure 11 depicts the input and output of our signal processing.

For real implementation, we realize the interpolation with a discrete sinc-function in the range of

- 10

ns to 10 ns with a sample time of

T_{S} = 1 / 64

ns. Following eq. (9), this results in

y [k T_{S}]

with K samples indicated by

k = 0, . . ., K - 1

. In the following, this processed measurement is called the measured signal.

After modeled and measured signal are prepared, we focus on the position estimation based on the similarity between the measured and modeled signals.

4.3. Majority-Based Position Estimation

In SALOS, we compare the measured signal

y (t)

with sets of modeled signals

{y_{CP} (t)}

to find the most likely CP for position estimate. For determining this estimate for the given signals, a proper similarity metric focusing on the shape of the signals is needed. Otherwise the signal echo positions and therefore the multipath propagation lose importance.

The position estimation of SALOS is divided into two steps. First, the most similar modeled receive signal for the measured signal is determined. It indicates the most probable tag position. This is done for multiple sets of modeled signals. In the second step, the position estimations of the distinct signal sets are evaluated via majority decision to finally estimate the tag’s position.

For signal comparison, we implement the discrete cross-correlation as a similarity metric. Note: Each modeled signal

{y_{CP} (t)}

is also sampled with

T_{S} \approx 1 / 64

ns and consist of K samples with

k = 0, . . ., K - 1

. The time axis of the measured and modeled signal is identical.

d_{S} [n]

is the correlation coefficient between

y [k T_{S}]

and

y_{CP, n} [k T_{S}]

of the n-th CP with:

\begin{matrix} d_{S} [n] = \frac{1}{K - 1} \sum_{k = 0}^{K - 1} (\frac{y [k T_{s}] - μ (y [k T_{s}])}{σ (y [k T_{s}])}) (\frac{y_{CP, n} [k T_{s}] - μ (y_{CP, n} [k T_{s}])}{σ (y_{CP, n} [k T_{s}])}), \end{matrix}

(10)

where

μ (\cdot)

is the vector’s mean value and

σ (\cdot)

its variance. The more similar the signals are, the higher the correlation coefficient.

We estimate the position using the nearest neighbor concept: The best position estimate

\hat{P}

among the CPs also has the most similar modeled signal:

\begin{matrix} \hat{P} = \underset{n = 0, . . ., N - 1}{arg max} d_{S} . \end{matrix}

(11)

As mentioned in Section 3.3,

N_{CP}^{y (t)}

signals are modeled randomized for each CP. If

N_{CP}

is the number of CPs, a complete modeled evaluation set includes

N_{CP}^{y (t)} \times N_{CP}

modeled signals. The overall structure of SALOS’ position estimation for one evaluation set is shown in Figure 12.

Increasing

N_{CP}^{y (t)}

leads to advantages and disadvantages of the comparison. On the one hand, there is a higher probability of modeling a signal with a realistic shape for a specific CP. But in general, increasing

N_{CP}^{y (t)}

also increases the probability for an unfavorable miss-modeling of a false CP’s signal. So, although the mapping from signal to tag position is bijectively (see Section 3.2), the random-based signal modeling leads to an ambiguous signal under an unfortunate seed. Larger sets are therefore not directly associated with an increasing number of correct position estimates.

To lower this influence on the position estimation, multiple independent modeled evaluation sets are created. For each of the set, the tag position

{\hat{P}}_{l}

is estimated as described above. The overall position estimation

{\hat{P}}_{MD}

is done by majority decision of these estimations:

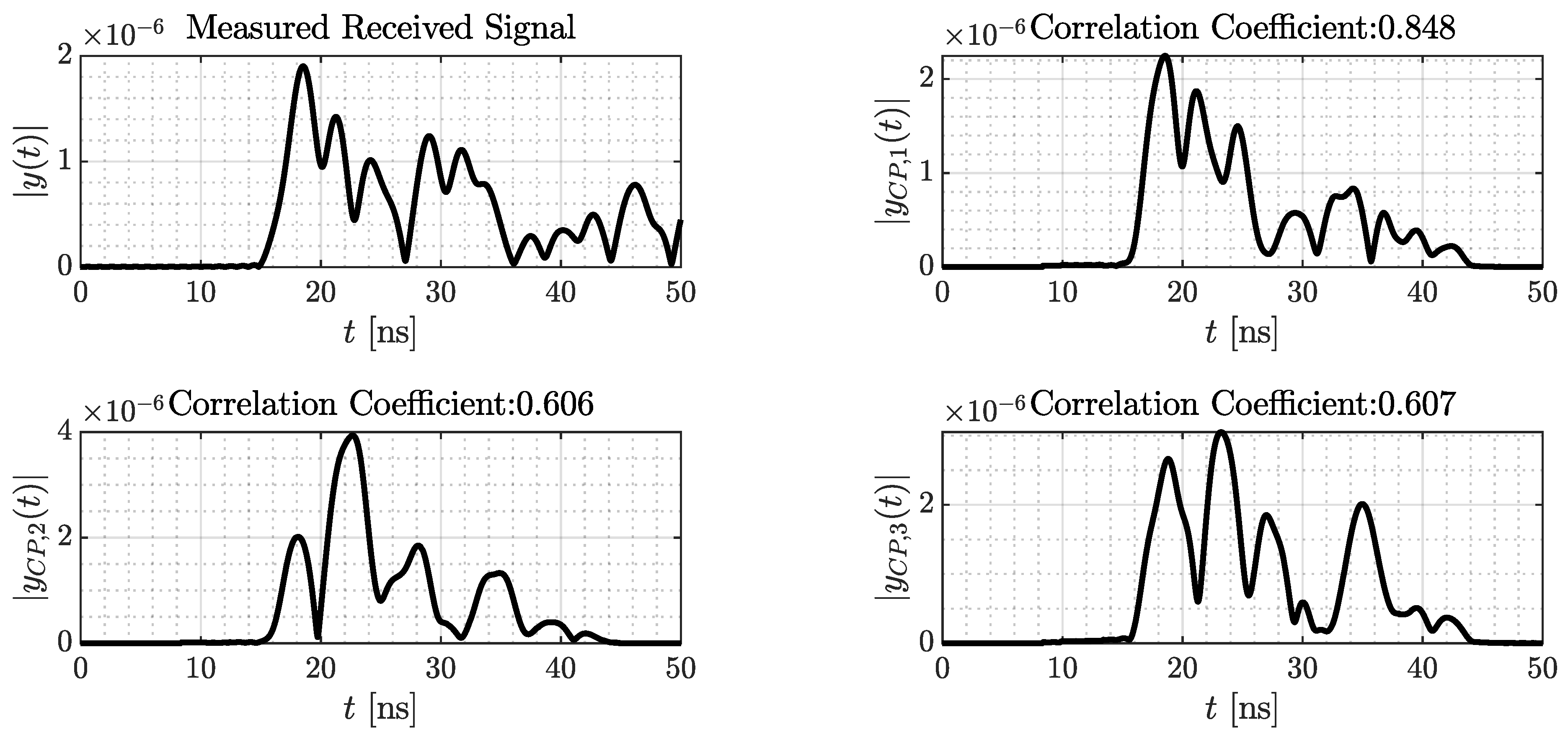
If a majority of the estimates are identical: In this case, this is also the position estimation ${\hat{P}}_{MD}$ .
If several positions are estimated equally often: Then the correlation coefficients of the corresponding estimates are compared. The highest coefficient indicates ${\hat{P}}_{MD}$ .

After position estimation, SALOS starts with the next measurement without changing the evaluation sets. So, only the DW1000 signal processing and the comparison itself need to be repeated per measurement. Note: We also implemented the described structure of SALOS modularily with real hardware. Appendix B describes the implementation details. We also provide the datasets of the modeled and measured signals for download at 1.

The evaluation of SALOS’ position estimation accuracy follows in the next section.

5. System Evaluation

Previously, we showed that position estimation is possible with SALOS in general. In this section, we will analyze to what extent the integration of a completely model-based reference influences the position estimation accuracy. Without proper accuracy, SALOS is not an alternative to established systems, despite hardware minimization. A valid evaluation of the position estimation accuracy is depending on a realistic setup and a comparison benchmark, as described in Section 5.1. The metric for evaluation and the resulting accuracy is shown in Section 5.2 and discussed in Section 5.3.

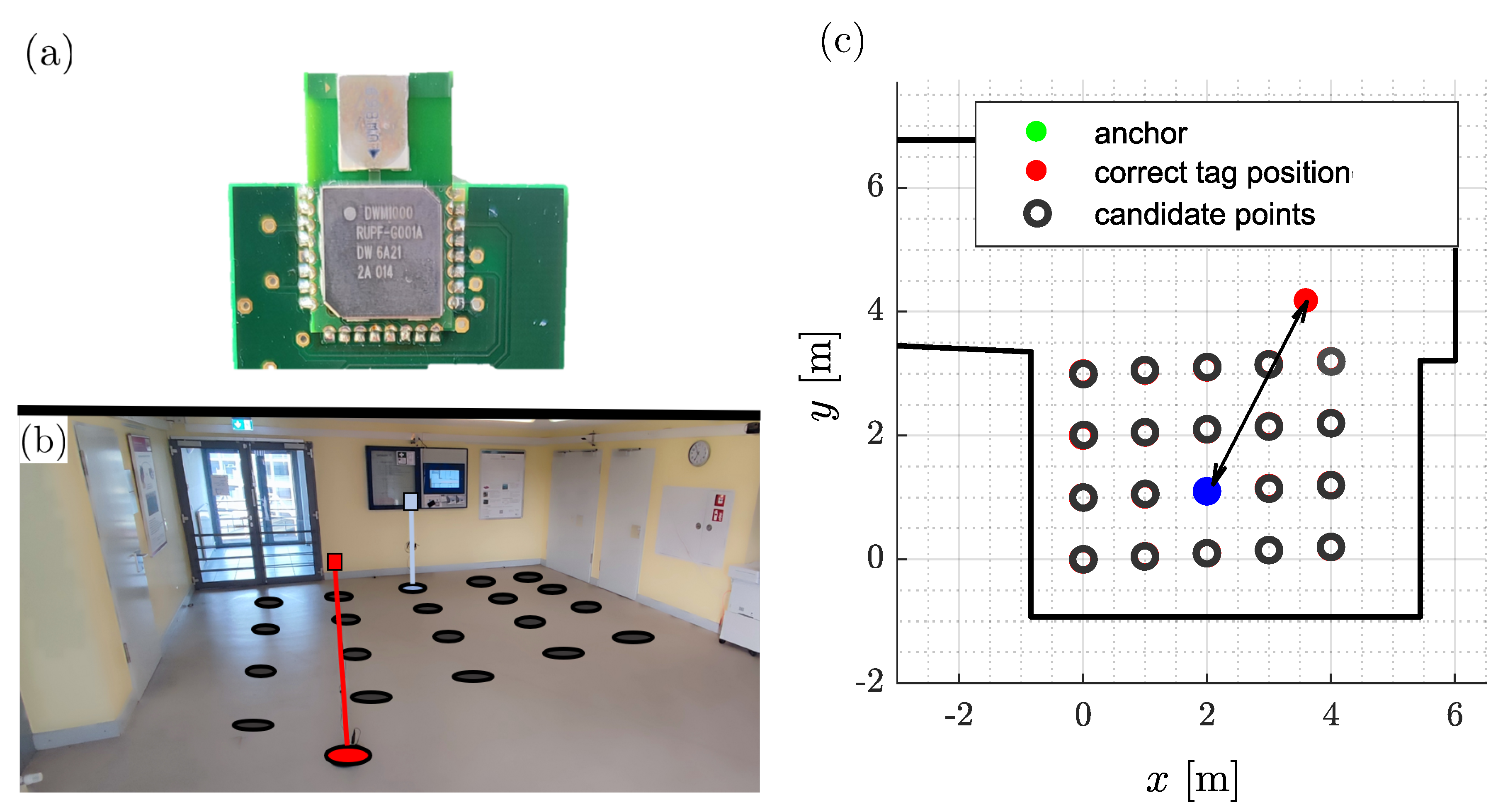
5.1. Evaluation Setup

The design of the evaluation setup significantly impacts the validity of position estimation accuracy results. Next, we will describe the implementation for evaluation covering the hardware, the environment and the comparison setups.

Sensor nodes equipped with Qorvo’s DW1000 RF chip serve as tags and anchors (see Figure 13 (a)). They are configured with the settings in Table 2. As described in Section 3.1, we will communicate on UWB channel 1 with a center frequency

f_{c}

of 3.4944 GHz and a bandwidth B of 499.2 MHz. We already depicted the corresponding transmit signal in Figure 2. The additional settings for pulse repetition and data rate as well as preamble settings are listed in Table 2 for completeness.

These devices will be deployed on a floor in a building for evaluation. A large corridor is an excellent choice for this purpose, since there is a large area for node placing which is characterized by various reflector materials and a non-rectangular spatial geometry. Note, we have measured and modeled the geometry in three dimensions. Figure 13 (b) depicts the corridor.

Figure 13 (c) depicts the footprint of the area including the anchor position and the 20 selected tag positions. Additionally, the anchor position and the 20 tag positions are listed in Table 3. The tag positions cover an area of approx.

3 m \times 4 m

. This grid results from previously recorded measurements of other localization systems. The anchor has been optimally placed with respect to these 20 positions (see Section 4.1).

Overall, we measure 500 receive signals at the 20 tag positions each. Since the anchor results in an effective length of

ℓ_{e} \approx 40

ns, we compare the first 40 ns of both, the measured and modeled signals. For each measured signal a position is estimated resulting in

10.000

estimations to evaluate.

The modeled CPs are identical with the chosen tag positions. Figure 13 (c) also illustrates this set. For each CP, the signal echo paths are modeled with

n_{i} \leq R_{\max} \leq 2

reflections per path. A higher number of paths increases processing complexity, e.g. for a six-sided spatial geometry,

6 + 30

paths with maximum 2 reflections result, while there are additional 150 paths with exact 3 reflections. Considering the signal echoes passing through those paths, further tests showed us, that the receive signal strength of these echoes is too low compared to paths with

R_{\max} \leq 2

. This results from additional reflection losses and in general longer reflection paths following eq. (2). Including these echoes in the modeling acts as an additional source of noise that degrades the system. So, we only include paths with

R_{\max} \leq 2

reflections, to reduce the complexity for calculation and therefore processing time.

Choosing this set of CPs results in the optimal setup to evaluate the position estimation accuracy of SALOS. We construct four evaluation sets including 50 modeled signals per CP. This results in

N_{CP}^{y (t)} \times N_{CP} = 50 \times 20 = 1, 000

modeled signals per set.

We compare the SALOS estimation accuracy with two randomized estimations as a benchmark for evaluation. For the first, we calculate the distance between each tag position and all CPs (see Figure 13 (c)). The histogram of the resulting distances represents guessing the CPs without any information, e.g., randomly. This is the scenario when none of the modeled information is matching. The second distribution covers randomized position estimations for CPs with a similar distance to the anchor as the correct estimate. This scenario is when the distance estimation is correct, but none of the modeled multipath information is useful. These randomized estimations set the lower threshold of accuracy to indicate the amount of information modeled.

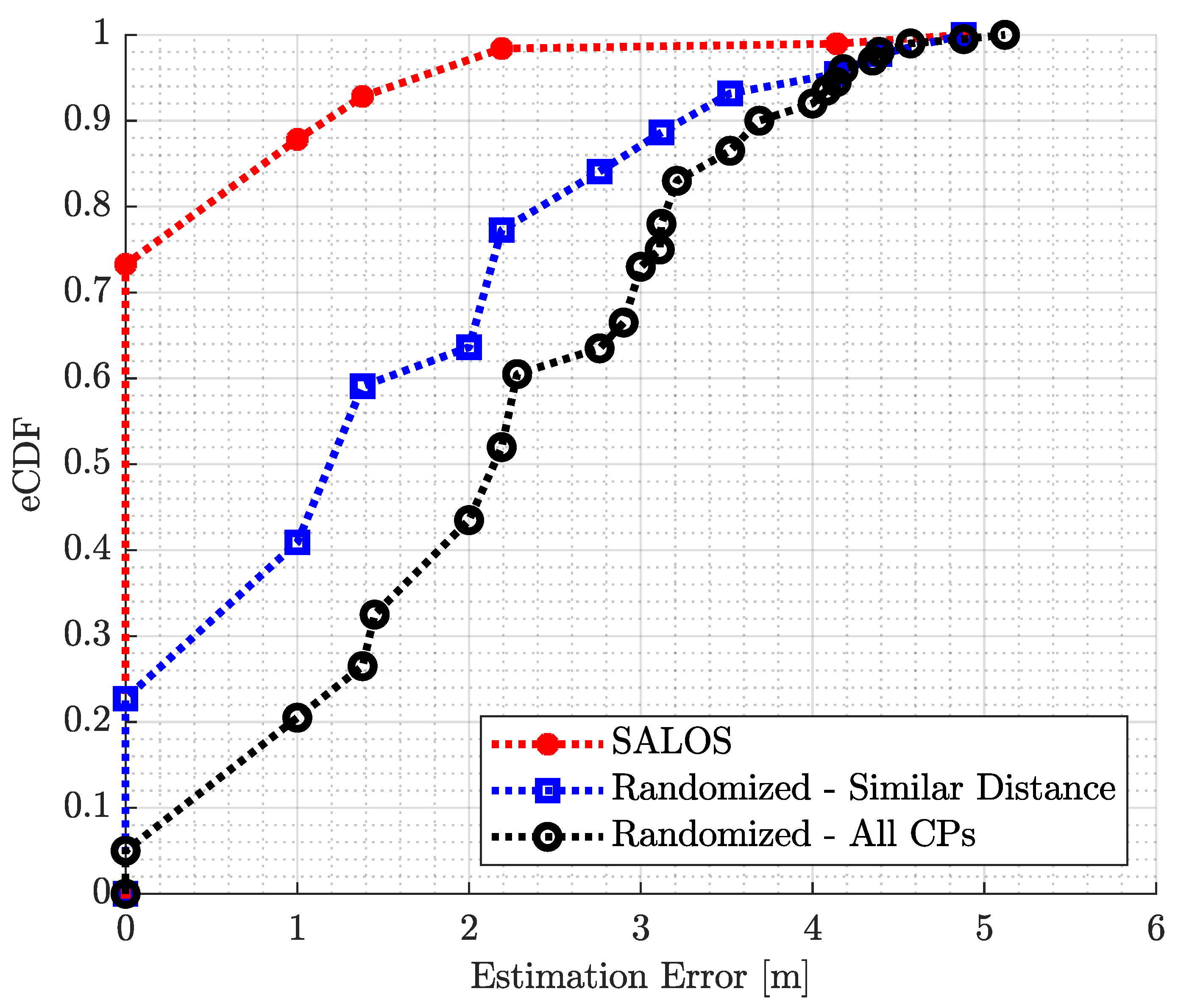
5.2. Evaluation of the Position Estimation Accuracy

For evaluation of the estimation accuracy, we calculate the estimation error based on the Euclidean distance

d_{ℓ 2} (P_{Tag}, {\hat{P}}_{Tag})

between the actual tag position

P_{Tag} = [x, y, z]

and the estimated position

{\hat{P}}_{Tag} = [\hat{x}, \hat{y}, \hat{z}]

for each measured signal:

\begin{matrix} d_{ℓ 2} (P_{Tag}, {\hat{P}}_{Tag}) = \sqrt{{(x - \hat{x})}^{2} + {(y - \hat{y})}^{2} + {(z - \hat{z})}^{2}} . \end{matrix}

(12)

The resulting position estimation errors are presented as empirical cumulative distribution functions (eCDF). The eCDFs of SALOS’ estimation errors and of the randomized estimations’ errors are shown in Figure 14.

The black eCDF depicts the position errors for the set, including any CP. For the blue eCDF, the distance estimate is integrated as a preselection of CP. While the overall random set makes a total correct decision of 5 % for all 20 CPs, the inclusion of the distance estimate in the random selection increases the number of correct decisions to around 23 %. Both graphs increase linearly then. The completely random selection achieves an estimation error of a maximum of 1 m in 21 % and an error of a maximum of

2.2

m in 52 %. With a reduced number of CPs, the position estimation achieves the accuracy of 1 m in 41 % of the cases, the

2.2

m in 77 % of the position estimates. The maximum estimation error is

5.12

m for the black eCDF and

4.88

m for the blue eCDF.

The red eCDF shows the result of the SALOS position estimation. A total of 7327 measurements and thus around 73 % of the positions are correctly estimated by incorporating SALOS’ modeled multipath propagation. Almost 88 % of the estimates have a maximum deviation of 1 m. More than 9840 of the 10000 measurements were traced back to the correct position with an accuracy of

2.2

m. The maximum estimation error is

4.88

m, like the blue eCDF.

5.3. Discussion

The motivation behind SALOS is to improve a single anchor localization system through sophisticated signal modeling. With modeled receive signals as reference measurements, we achieve position estimation without further external information.

With a pure random estimation, we achieve 5% (one out of 20) correct position estimations. With the help of the line-of-sight signal distance estimation the accuracy is improved to 23%. With our approach with multipath signal modeling, the accuracy increases to 73%. So, the number of correct position estimates is improved by a factor of

3.17

and

14.5

respectively, which demonstrates the significant advancement of the modeling.

There are certain positions with high estimation errors. These are positions that have a strong first-order reflection in the area of the glass door shown in Figure 13 (c). Although we do not consider wall material in our model, this effect is a strong indicator to consider glass walls in the 3D model.

After discussion of the evaluation results, we conclude this work with a summary and a view on future tasks regarding SALOS.

6. Conclusions and Future Work

In this paper, we presented SALOS, a modular model-based UWB system for indoor single-anchor localization. SALOS is a novel approach that reduces the infrastructure and costs of conventional multi-anchor systems by exploiting the multipath propagation of the UWB signal. We developed new algorithms for SALOS, such as the three-dimensional multipath model creating artificial receive signal models as reference for localization, and the majority decision-based position estimation. We evaluated SALOS on a floor in a building with 20 distinct tag positions and achieved correct position estimations for more than 73 % of the measurements. Our results demonstrate the feasibility and accuracy of SALOS for indoor localization. Especially, the influence of the realistic modeled receive signals is shown in the results. However, SALOS also faces some challenges, such as the placement of the anchor, the sensitivity to environmental changes, and the scalability to larger areas.

Therefore, we suggest some possible improvements in future work for SALOS. To maximize the multipath diversity and coverage, we will optimize the anchor placement, which includes both position and orientation. Also, we will adapt the multipath model and the artificial signal models to accommodate dynamic and heterogeneous environments. Additionally, our approach needs optimization for real-time operation with high update rates. We will conduct experiments with multiple tags to scale up the system and improve reliability and redundancy. We need to evaluate the system performance in different indoor settings and compare it with other state-of-the-art systems, like UWB multi-anchor systems, and Bluetooth AoA systems.

In the future, we plan to explore techniques, such as machine learning, deep learning, and cooperative localization, to see if and how much they could enhance the system’s capabilities and performance. The concept of SALOS can be extended to work with multiple antennas as depicted in the related work section. We hope that our work will inspire more research and innovation in the field of UWB single-anchor indoor localization.

Supplementary Materials

The materials are available online at https://git.mylab.th-luebeck.de/sven.ole.schmidt/salos-2024.

Author Contributions

Conceptualization, S.O.S. and H.H.; methodology, S.O.S. and H.H.; software, S.O.S. and F.J.; validation, S.O.S., M.C. and F.J.; formal analysis, S.O.S.; investigation, S.O.S.; resources, S.O.S.; data curation, S.O.S. and F.J.; writing—original draft preparation, S.O.S.; writing—review and editing, S.O.S., M.C., F.J. and H.H.; visualization, S.O.S. and F.J.; supervision, H.H.; project administration, H.H.; funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.

Funding

This publication is a result of the research of CoSA Center of Excellence.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

We provide the measurement data in the following repository https://git.mylab.th-luebeck.de/sven.ole.schmidt/salos-2024.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

ADC	analog-to-digital converter
AGC	automatic gain control
AoA	angle-of-arrival
CIR	channel impulse response
CP	candidate point
eCDF	empirical cumulative distribution function
ESPAR	electronically steerable parasitic array radiator
IMU	inertial measurement unit
MQTT	message queuing telemetry transport protocol
PDoA	phase difference of arrival
RF	radio frequency
RSS	receive signal strength
SALOS	single anchor localization system
TDoA	time difference of arrival
TWR	two-way-ranging
UWB	ultra-wideband
3D	three-dimensional

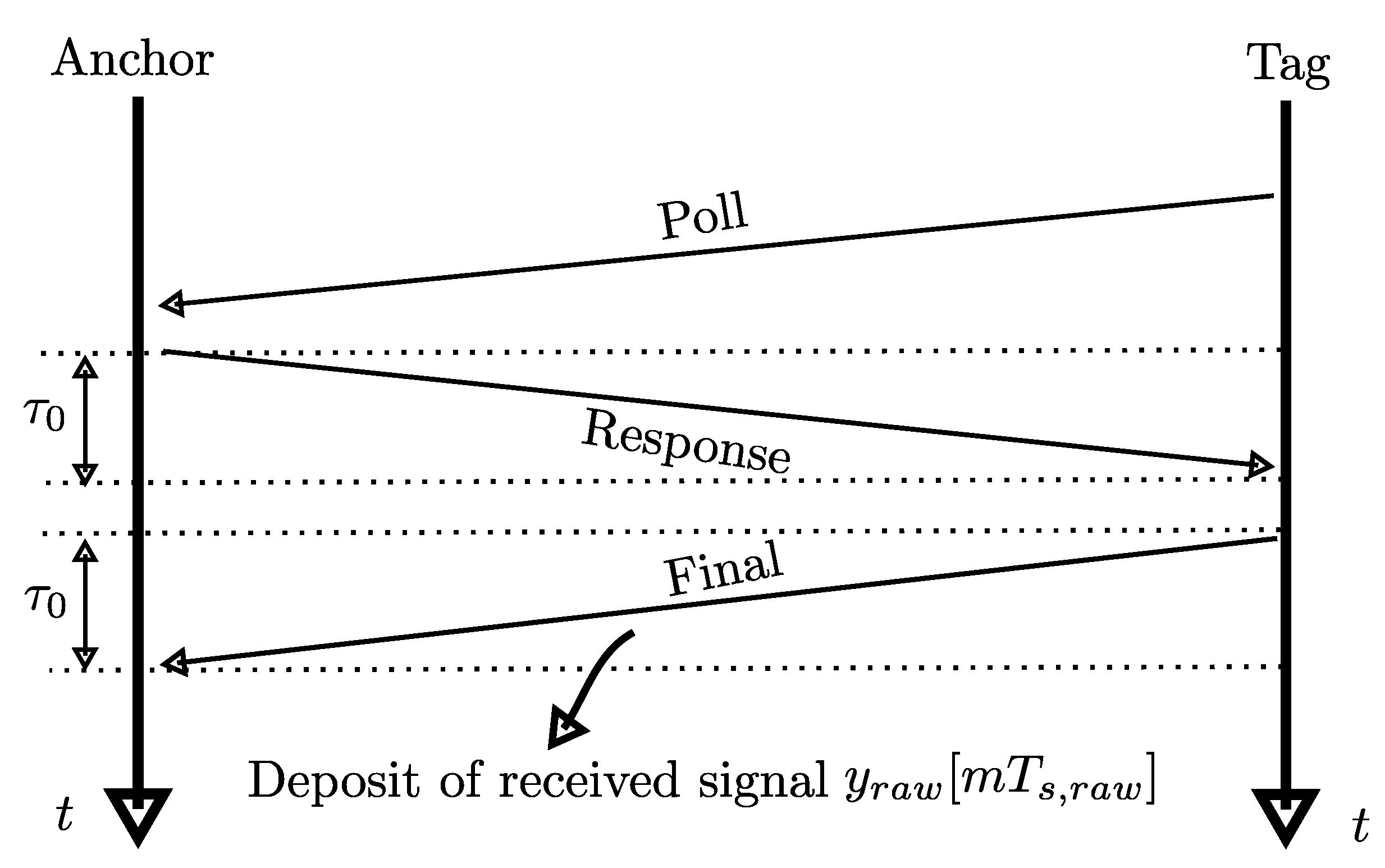
Appendix A DW1000 Distance Estimation via Two-Way-Ranging

For distance estimation, we implemented the two-way ranging method provided by the DW1000 described in [31]. Figure A1 sketches the message exchange necessary for this. After an initial synchronization, the anchor receives a

P o l l

message from the tag to start the TWR. The anchor responds with a

R e s p o n s e

message, to which the tag responds with a

F i n a l

message. The time interval between sending the

R e s p o n s e

and receiving the

F i n a l

message is twice the Time of Flight

τ_{0}

including the duration of the tag’s processing, which is known to the anchor.

Figure A1. Two-way ranging for distance estimation based on the DW1000 RF chip.

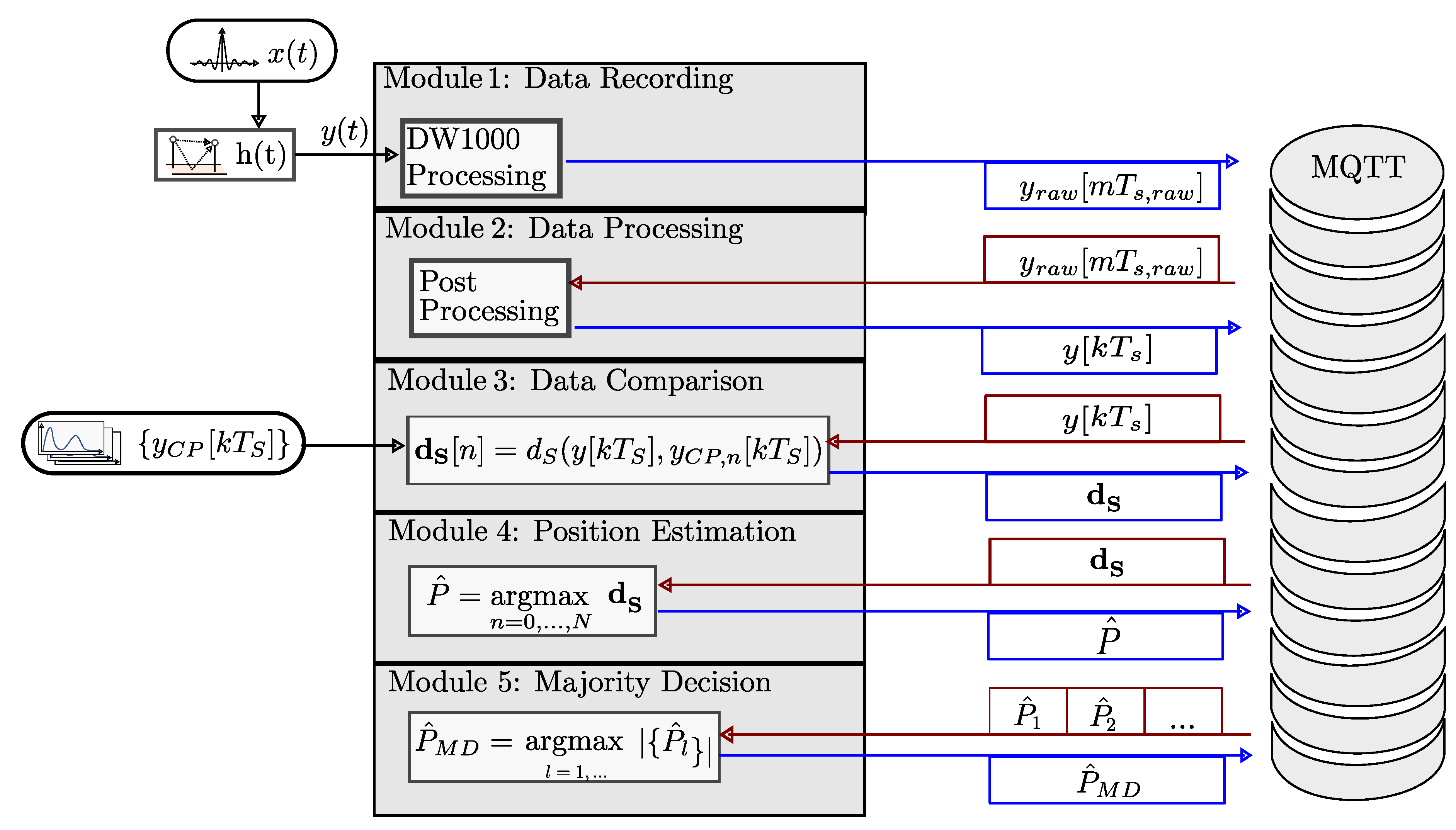
Appendix B The Modular Live-Streaming Structure of SALOS

The setup shown in the previous sections allows SALOS to be implemented using the DW1000 RF chip. The system can be operated live through the commissioning and the continuous data recording. To achieve a sufficiently high update interval for the position estimate, it is advisable to carry out the processing steps in parallel. In addition, the scalability of the system must be guaranteed, which is required by a large number of CPs and several tag sensor nodes. Since clearly separate processing steps result, the processing is divided into modules.

Figure A2. Block diagram of the MQTT-based modular live-implementation.

Figure A2 shows the selected structure. SALOS was divided into four modules that communicate with each other via the message queuing telemetry transport protocol (MQTT). MQTT is a lightweight communication protocol specifically designed to efficiently transfer messages between devices with limited resources. At the center is an MQTT broker that serves as a data hub. The modules take on at least one of two roles. The publisher stores data with a topic (e.g. SALOS/DW1000Data/Tag1/) on the data hub. The format of the data is selected flexibly since the data is not interpreted on the broker. We have decided on a binary format for the data because in contrast to ASCII characters, the transmission speed is increased [32]. The subscriber is able to subscribe to topics freely. Including a wildcard character # subscribes to all subtopics of one topic (e.g. SALOS/DW1000Data/# orders a subscription to all subtopics in the main topic SALOS/DW1000Data/). When data is stored on a subscribed topic, the data will be sent to him immediately when it arrives. The modules take on one or even both roles at the same time, which makes it easy to implement continuous data processing. With this communication protocol, new modules or external viewers are integrated without great effort. Note: The broker has no memory, so only the latest message of a topic is available for retrieval.

So, the modules of SALOS are exchangeable and scalable via live usage without intersecting the overall system. The data recording by the sensor node with built-in DW1000 RF chip are placed in Module 1, described in Section 4.2. In module 2, the receive signals are post-processed (cf. also Section 4.2). The application of the chosen similarity metric (see Section 4.3) including the stored receive signals of the CPs (as generated in Section 3.3.1) is in module 3. In the 4th and last module, the position of the tag is estimated using the similarity metric’s results (also covered in Section 4.3).

References

Rahman, A.M.; Li, T.; Wang, Y. Recent advances in indoor localization via visible lights: A survey. Sensors 2020, 20, 1382. [Google Scholar] [CrossRef] [PubMed]
Liu, M.; Cheng, L.; Qian, K.; Wang, J.; Wang, J.; Liu, Y. Indoor acoustic localization: A survey. Human-centric Computing and Information Sciences 2020, 10, 1–24. [Google Scholar] [CrossRef]
Morar, A.; Moldoveanu, A.; Mocanu, I.; Moldoveanu, F.; Radoi, I.E.; Asavei, V.; Gradinaru, A.; Butean, A. A comprehensive survey of indoor localization methods based on computer vision. Sensors 2020, 20, 2641. [Google Scholar] [CrossRef] [PubMed]
Leugner, S.; Hellbrück, H. Lessons learned: Indoor Ultra-Wideband localization systems for an industrial IoT application. Technical report, Technische Universität Braunschweig, Braunschweig, 2018. [CrossRef]
Meissner, P.; Witrisal, K. Multipath-assisted single-anchor indoor localization in an office environment. 2012 19th International Conference on Systems, Signals and Image Processing (IWSSIP). IEEE, 2012, pp. 22–25.
Han, G.; Jiang, J.; Zhang, C.; Duong, T.Q.; Guizani, M.; Karagiannidis, G.K. A survey on mobile anchor node assisted localization in wireless sensor networks. IEEE Communications Surveys & Tutorials 2016, 18, 2220–2243. [Google Scholar]
Shokry, A.; Elhamshary, M.; Youssef, M. DynamicSLAM: Leveraging human anchors for ubiquitous low-overhead indoor localization. IEEE Transactions on Mobile Computing 2020, 20, 2563–2575. [Google Scholar] [CrossRef]
Ye, F.; Chen, R.; Guo, G.; Peng, X.; Liu, Z.; Huang, L. A low-cost single-anchor solution for indoor positioning using BLE and inertial sensor data. IEEE Access 2019, 7, 162439–162453. [Google Scholar] [CrossRef]
Guerra, A.; Guidi, F.; Dardari, D. Single-anchor localization and orientation performance limits using massive arrays: MIMO vs. beamforming. IEEE Transactions on Wireless Communications 2018, 17, 5241–5255. [Google Scholar] [CrossRef]
Pelka, M.; Bartmann, P.; Leugner, S.; Hellbrück, H. Minimizing Indoor Localization Errors for Non-Line-of-Sight Propagation. International Conference on Localization and GNSS, 2018.
Cerro, G.; Ferrigno, L.; Laracca, M.; Miele, G.; Milano, F.; Pingerna, V. Uwb-based indoor localization: How to optimally design the operating setup? IEEE Transactions on Instrumentation and Measurement 2022, 71, 1–12. [Google Scholar] [CrossRef]
Witrisal, K.; Meissner, P.; Leitinger, E.; Shen, Y.; Gustafson, C.; Tufvesson, F.; Haneda, K.; Dardari, D.; Molisch, A.F.; Conti, A.; et al. High-accuracy localization for assisted living: 5G systems will turn multipath channels from foe to friend. IEEE Signal Processing Magazine 2016, 33, 59–70. [Google Scholar] [CrossRef]
Schmidt, S.O.; Cimdins, M.; Hellbrück, H. On the Effective Length of Channel Impulse Responses in UWB Single Anchor Localization. International Conference on Localization and GNSS, 2019.
Schmidt, S.O.; Cimdins, M.; Hellbrueck, H. SALOS - a UWB Single Anchor Localization System based on CIR-vectors - Design and Evaluation. International Conference for Indoor Positioning and Navigation (IPIN) 2022, 2022, pp. 1–16.
Pau, G.; Arena, F.; Gebremariam, Y.E.; You, I. Bluetooth 5.1: An analysis of direction finding capability for high-precision location services. Sensors 2021, 21, 3589. [Google Scholar] [CrossRef] [PubMed]
Zhuang, Y.; Zhang, C.; Huai, J.; Li, Y.; Chen, L.; Chen, R. Bluetooth localization technology: Principles, applications, and future trends. IEEE Internet of Things Journal 2022, 9, 23506–23524. [Google Scholar] [CrossRef]
Cimdins, M.; Schmidt, S.O.; John, F.; Constapel, M.; Hellbrück, H. MA-RTI: Design and Evaluation of a Real-World Multipath-Assisted Device-Free Localization System. Sensors 2023, 23. [Google Scholar] [CrossRef] [PubMed]
Ge, F.; Shen, Y. Single-Anchor Ultra-Wideband Localization System Using Wrapped PDoA. IEEE Transactions on Mobile Computing 2022, 21, 4609–4623. [Google Scholar] [CrossRef]
Wang, T.; Li, Y.; Liu, J.; Hu, K.; Shen, Y. Multipath-Assisted Single-Anchor Localization via Deep Variational Learning. IEEE Transactions on Wireless Communications 2024. [Google Scholar] [CrossRef]
Rzymowski, M.; Woznica, P.; Kulas, L. Single-Anchor Indoor Localization Using ESPAR Antenna. IEEE Antennas and Wireless Propagation Letters 2016, 15, 1183–1186. [Google Scholar] [CrossRef]
Groth, M.; Nyka, K.; Kulas, L. Fast Calibration-Free Single-Anchor Indoor Localization Based on Limited Number of ESPAR Antenna Radiation Patterns. 2023 17th European Conference on Antennas and Propagation (EuCAP), 2023, pp. 1–5. [CrossRef]
Großwindhager, B.; Rath, M.; Kulmer, J.; Bakr, M.S.; Boano, C.A.; Witrisal, K.; Römer, K. SALMA: UWB-based single-anchor localization system using multipath assistance. Proceedings of the 16th ACM Conference on Embedded Networked Sensor Systems, 2018, pp. 132–144.
Wang, T.; Zhao, H.; Shen, Y. An efficient single-anchor localization method using ultra-wide bandwidth systems. Applied Sciences 2019, 10, 57. [Google Scholar] [CrossRef]
Meissner, P.; Steiner, C.; Witrisal, K. UWB positioning with virtual anchors and floor plan information. 2010 7th Workshop on Positioning, Navigation and Communication. IEEE, 2010, pp. 150–156.
Mohammadmoradi, H.; Heydariaan, M.; Gnawali, O.; Kim, K. UWB-based single-anchor indoor localization using reflected multipath components. 2019 International Conference on Computing, Networking and Communications (ICNC). IEEE, 2019, pp. 308–312.
IEEE Standards Association. IEEE Standard for Low-Rate Wireless Networks–Amendment 1: Enhanced Ultra Wideband (UWB) Physical Layers (PHYs) and Associated Ranging Techniques, 2020.
Decawave Ltd 2017. DW1000 User Manual, 2017. Version 2.11.
Friis, H. A Note on a Simple Transmission Formula. Proceedings of the IRE 1946, 34, 254–256. [Google Scholar] [CrossRef]
Foerster, J. The effects of multipath interference on the performance of UWB systems in an indoor wireless channel. IEEE VTS 53rd Vehicular Technology Conference, Spring 2001. Proceedings (Cat. No.01CH37202), 2001, Vol. 2, pp. 1176–1180 vol.2. [CrossRef]
Schmidt, S.O.; Hellbrueck, H. Detection and Identification of Multipath Interference with Adaption of Transmission Band for UWB Transceiver Systems. International Conference for Indoor Positioning and Navigation (IPIN) 2021, 2021, pp. 1–16.
Decawave Ltd 2014. APS011 Application Note - Sources of error in DW1000 based two-way ranging (TWR) schemes, 2014. Version 1.1.
John, F.; Schmidt, S.O.; Hellbrück, H. Flexible Arbitrary Signal Generation and Acquisition System for Compact Underwater Measurement Systems and Data Fusion. OCEANS 2021: San Diego – Porto, 2021, pp. 1–6. [CrossRef]

1	https://git.mylab.th-luebeck.de/sven.ole.schmidt/salos-2024

Figure 1. General Structure of SALOS: Modeled receive signals are compared with measurements to estimate the tag’s position accurately.

Figure 2. Transmit Signal of UWB Channel 1 in Time and Frequency Domain.

Figure 3. Three-dimensional multipath environment including two walls, the ground and furniture.

Figure 4. Influence of the tag position

P_{Tag}

on the receive signal.

Figure 4. Influence of the tag position

P_{Tag}

on the receive signal.

Figure 5. Estimated signal echo paths of the proposed three-dimensional multipath propagation model.

Figure 6. Three-dimensional multipath modeling of signal echoes with single reflection paths.

Figure 7. Expansion of the modeling for signal echo paths with two reflections.

Figure 8. Process for iterative complex amplitude estimation

{\underset{̲}{\hat{a}}}_{i}

of i-th signal echo.

Figure 8. Process for iterative complex amplitude estimation

{\underset{̲}{\hat{a}}}_{i}

of i-th signal echo.

Figure 9. Results of the magnitude’s estimation

| {\hat{\underset{̲}{a}}}_{i} |

of the 0^th,1^st and 2^nd order signal echoes.

Figure 9. Results of the magnitude’s estimation

| {\hat{\underset{̲}{a}}}_{i} |

of the 0^th,1^st and 2^nd order signal echoes.

Figure 10. Shape of measured signal compared to three different modeled signals of the same tag position.

Figure 11. Signal processing steps for DW1000’s measurement

y_{raw} [m T_{s, raw}]

to the reconstructed

y (t)

Figure 11. Signal processing steps for DW1000’s measurement

y_{raw} [m T_{s, raw}]

to the reconstructed

y (t)

Figure 12. General Structure of position estimation for one evaluation set including

N_{CP}^{y (t)} \times N_{CP}

modeled signals.

Figure 12. General Structure of position estimation for one evaluation set including

N_{CP}^{y (t)} \times N_{CP}

modeled signals.

Figure 13. Evaluation Setup for SALOS: (a) Qorvo’s DW1000 RF Chip, equipped on sensor node. (b) Real indoor office corridor. (c) Evaluation set of CPs: original tag positions.

Figure 14. eCDF of position estimation errors for SALOS, as well as for a randomized positioning pick with and without including distance estimation.

Table 1. Distribution characterization of the amplitudes in magnitude and phase with respect to the reflection order.

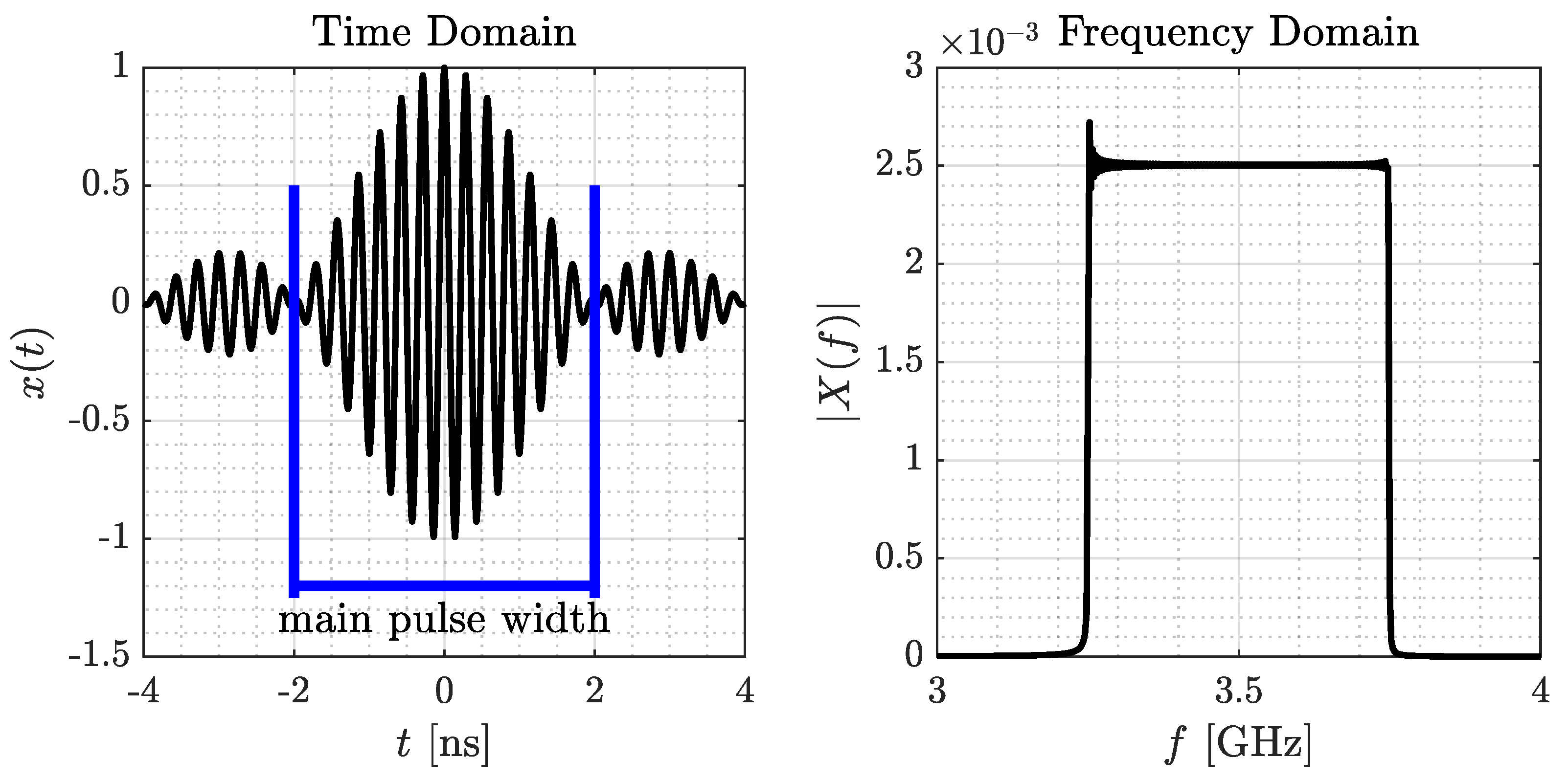
Order of Reflection	Magnitude $\| {\hat{\underset{̲}{a}}}_{i} \|$	Phase $ϕ ({\hat{\underset{̲}{a}}}_{i})$
0^th	$3.04 \cdot 10^{- 5} \cdot e^{- 5.22 \cdot 10^{8} \cdot τ_{i}} + 5.38 \cdot 10^{- 6} \cdot e^{- 4.81 \cdot 10^{7} \cdot τ_{i}}$	$U ([0, 2 π])$
1^st	$0 \leq N (1.24 \cdot 10^{- 6}, 7.46 \cdot 10^{- 7}) \leq 2.66 \cdot 10^{- 6}$	$U ([0, 2 π])$
2^nd	$0 \leq N (4.12 \cdot 10^{- 7}, 3.30 \cdot 10^{- 7}) \leq 1.30 \cdot 10^{- 6}$	$U ([0, 2 π])$

Table 2. Selected Settings of Qorvo’s DW1000 RF chip.

Setting	Value
UWB channel	1
Center frequency $f_{c}$	$3.4944$ GHz
Bandwidth B	$499.2$ MHz
Pulse repetition frequency	64
Preamble length	128
Preamble acquisition chunk size	8
Preamble code anchor and tag	9
Data rate	6.8 MBit/s

Table 3. Real tag and anchor positions.

Name	Coordinates $[x, y, z]$	Name	Coordinates $[x, y, z]$
$P_{T a g, 11}$	$[0.00, 0.00, 1.37]$	$P_{T a g, 31}$	$[0.00, 2.00, 1.37]$
$P_{T a g, 12}$	$[1.00, 0.05, 1.37]$	$P_{T a g, 32}$	$[1.00, 2.05, 1.37]$
$P_{T a g, 13}$	$[2.00, 0.10, 1.37]$	$P_{T a g, 33}$	$[2.00, 2.10, 1.37]$
$P_{T a g, 14}$	$[3.00, 0.15, 1.37]$	$P_{T a g, 34}$	$[3.00, 2.15, 1.37]$
$P_{T a g, 15}$	$[4.00, 0.20, 1.37]$	$P_{T a g, 35}$	$[4.00, 2.20, 1.37]$
$P_{T a g, 21}$	$[0.00, 1.00, 1.37]$	$P_{T a g, 41}$	$[0.00, 3.00, 1.37]$
$P_{T a g, 22}$	$[1.00, 1.05, 1.37]$	$P_{T a g, 42}$	$[1.00, 3.05, 1.37]$
$P_{T a g, 23}$	$[2.00, 1.10, 1.37]$	$P_{T a g, 43}$	$[2.00, 3.10, 1.37]$
$P_{T a g, 24}$	$[3.00, 1.15, 1.37]$	$P_{T a g, 44}$	$[3.00, 3.15, 1.37]$
$P_{T a g, 25}$	$[4.00, 1.20, 1.37]$	$P_{T a g, 45}$	$[4.00, 3.20, 1.37]$
$P_{A n}$	$[3.60, 4.17, 1.37]$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

132

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

SALOS - A UWB Single Anchor Indoor Localization System based on a Statistical Multipath Propagation Model

Abstract

Keywords:

Subject:

1. Introduction

2. Related Work

3. Construction of Receive Signals with a Three-Dimensional Multipath Model

3.1. UWB Signal Propagation in Multipath Environments

3.2. Correlation between Anchor and Tag Positions and UWB Signals

3.3. Modeling of Receive Signals Based on a Given Spatial Geometry

3.3.1. Three-Dimensional Multipath Model for Transmission Delay Estimation

3.3.2. Statistical Analysis of the Amplitude for Estimation

3.3.3. Modeling of the Receive Signals Sets for Reference

4. Localization Algorithm

4.1. Optimal Position of the Anchor

4.2. Signal Processing of Qorvo’s DW1000 Raw Measurements

4.3. Majority-Based Position Estimation

5. System Evaluation

5.1. Evaluation Setup

5.2. Evaluation of the Position Estimation Accuracy

5.3. Discussion

6. Conclusions and Future Work

Supplementary Materials

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

Appendix A DW1000 Distance Estimation via Two-Way-Ranging

Appendix B The Modular Live-Streaming Structure of SALOS

References

MDPI Initiatives

Important Links

Subscribe