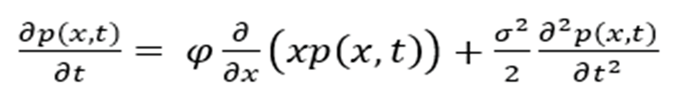Lower Bound for the Fokker Planck Kolmogorov (FPK) Probability Density Function Controller's Designed Parameter with FPK applications to Genetics

Ismail A. Mageed

doi:10.20944/preprints202402.1162.v1

Preprint

Review

Lower Bound for the Fokker Planck Kolmogorov (FPK) Probability Density Function Controller's Designed Parameter with FPK applications to Genetics

This version is not peer-reviewed.

Ismail A. Mageed^*

This version is not peer-reviewed.

Downloads

Views

Comments

Submitted:

20 February 2024

Posted:

20 February 2024

You are already at the latest version

Abstract

The hard open problem of finding the lower bound for the Fokker Planck Kolmogorov’s time-dependent controller parameter probability density function is addressed for the first time in literature in this work. This revolutionary exposition will put control theory and other related inter-disciplinary fields to a higher level towards contemporary control theory. Notably, based on the influential role of control theory in both engineering and industry, this paper will be of great value to all engineering and industry professionals who seek to know more about advanced trends within control theory settings. On the other remit of the spectrum, Fokker Planck Kolmogorov(FPK) equations are of high importance to physicists as well as mathematicians, based on their multiple applicability to multi-interdisciplinary fields of human knowledge, and beyond. So, this by default adds more taste and credibility to this study. Concluding thoughts are included at the end of the work along with a difficult outstanding problem and the direction of future work.

Keywords:

Fokker Planck Kolmogorov(FPK) equations

;

time-dependent controller’s designed parameter(TDCDP)

;

probability density function(PDF)

Subject:

Computer Science and Mathematics - Applied Mathematics

This preprints belongs to the Topic

Mathematical Modeling

1. Introduction

Complex stochastic systems are challenging to handle due to their extreme randomness and unpredictability. Variance is a statistical metric used to control unpredictability in Gaussian stochastic systems [1,2,3,4].

Stochastic systems with nonlinearities cannot be directly controlled using variance control approaches. This is because even in systems with Gaussian noise, non-Gaussian distributions of system variables are feasible [5].

Within some nonlinear systems, combined unpredictability and uncertainty may be too much for Gaussian processes to fully describe. In these circumstances, variance control approaches are useless [6].

The closed-loop system can be seen [7] as an Ornstein-Uhlenbeck process by applying the suggested control strategy.

d x_{t} = - φ x_{t} d t + σ d W_{t}

(1)

Here

x_{t}

is the system’s state,

φ

> 0

defines the controller’s designed parameter,

W_{t}

defines the Weiner process and

σ

is a positive real constant.

FPK reads:

(2)

p (x, t)

serves as the PDF with

x

to define the random variable of

x_{t} .

Equation (2)'s solution reads as PDF, namely

p (x, t) :

p (x, t) = \sqrt (\frac{φ}{π σ^{2} (1 - e^{- 2 φ t})}) e^{(- \frac{φ {(x - x_{0} e^{- φ t})}^{2}}{π σ^{2} (1 - e^{- 2 φ t})})}

(3)

A s t = 0, x_{0}

x_{t}

. Moreover,

φ (t) = \frac{W_{0} (- \frac{t σ^{2}}{r (t)} e^{- \frac{t σ^{2}}{r (t)}})}{2 t} + \frac{t σ^{2}}{2 r (t)}

(4)

r (t)

acts as a time-dependent variance function and

W_{0}

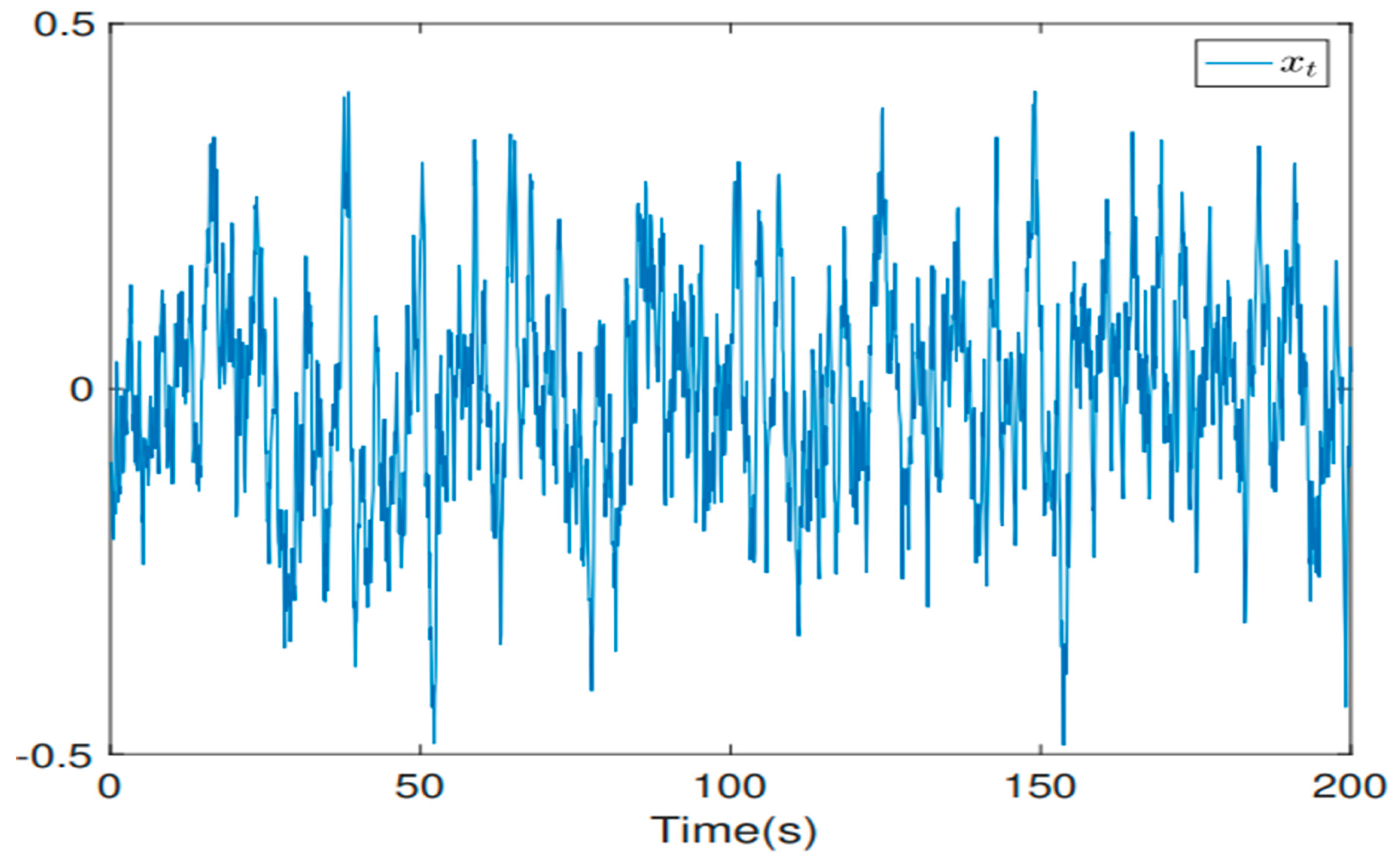
represents the Lambert W function [8]. The trajectory of the system in relation to the state

x_{t},

is shown in Figure 1 [7].

W_{0}

of (4) has the Taylor’s expansion [8]

W_{0} (z) = \sum_{n = 1}^{\infty} \frac{{(- n)}^{n - 1} z^{n}}{n!}

(5)

Where

z

is any complex number and it is satisfied when

z

is real. Also, for real values of

z

W_{0} (z)

satisfies:

\frac{d W_{0} (z)}{d z} = \frac{W_{0} (z)}{z (1 + W_{0} (z))}

(6)

The following theorem is essential to obtain the main results of section three.

Preliminary Theorem (PT) [9]

Let f be a function that is defined and differentiable on an open interval (c,d).

f^{'} (x) > (<) 0

\forall x \in (c, d)

, then f increases(decreases) on

(c, d)

(7)

This current paper contributes to:

Obtaining a first time ever, TDCDP’s lower bound, namely ${L B}_{φ (t)}$ .
Uncovering the significant temporal impact on ${L B}_{φ (t)} .$
A proposal for a challenging open problem.

This paper’s roadmap reads as: Section two is concerned with the methodology. Section three provides results and discussion. Section four highlights some FPK applications to genetics. Section five concludes with a tough open problem and research directions.

2. Methodology

Notably, a mathematical approach is undertaken to calculate the

{L B}_{φ (t)}

threshold based on the preliminary theorem(see Eqn (7)). More potentially, calculus and more advanced algebraic forms are utilized to uncover the lower bound of

φ (t) (c . f ., (4))

. Looking at the bigger picture, this discovery will lead to a contemporary control theory rather than being limited within the traditional classical frames.

More profoundly, some FPK applications to genetics are highlighted. Consequently, this consolidates the potential of FPK, not only to mathematical and physical setup, but also for medical related sciences. This will put the research community into more spacious frontiers of thoughtful innovation.

3. Results and discussion

Theorem 1

For

φ

(c.f., (4) and (5)), it holds that

φ (t) > (1 + \frac{t σ^{2}}{2 r (t)}) - \frac{1}{2 t} e^{\frac{t σ^{2}}{r (t)}}

(8)

Proof

Following (4) and (6),

φ (t) = (- \frac{1}{2 t} \sum_{n = 1}^{\infty} \frac{{(\frac{t σ^{2}}{r (t)})}^{n} e^{- \frac{n t σ^{2}}{r (t)}}}{n!} + \frac{t σ^{2}}{2 r (t)})

(9)

\frac{t σ^{2}}{2 r (t)} - \frac{1}{2 t} \sum_{n = 1}^{\infty} \frac{{(\frac{t σ^{2}}{r (t)})}^{n} e^{- \frac{n t σ^{2}}{r (t)}}}{n!}

(10)

> \frac{t σ^{2}}{2 r (t)} - \frac{1}{2 t} \sum_{n = 1}^{\infty} \frac{e^{- \frac{n t σ^{2}}{r (t)}}}{n!} (Since, e^{- \frac{n t σ^{2}}{r (t)}} < 1)

(11)

= (1 + \frac{t σ^{2}}{2 r (t)}) - \frac{1}{2 t} e^{\frac{t σ^{2}}{r (t)}}

(c.f., (8))

Notably, the obtained lower bound,

{L B}_{φ (t)}

= (1 + \frac{t σ^{2}}{2 r (t)}) - \frac{1}{2 t} e^{\frac{t σ^{2}}{r (t)}}

(c.f., (8)) is time dependent.

Numerical experiment

Let

r (t) = t^{2} σ^{2},

then,

{L B}_{φ (t)} = \frac{1}{2 t} (1 - e^{(\frac{1}{t})})

(12)

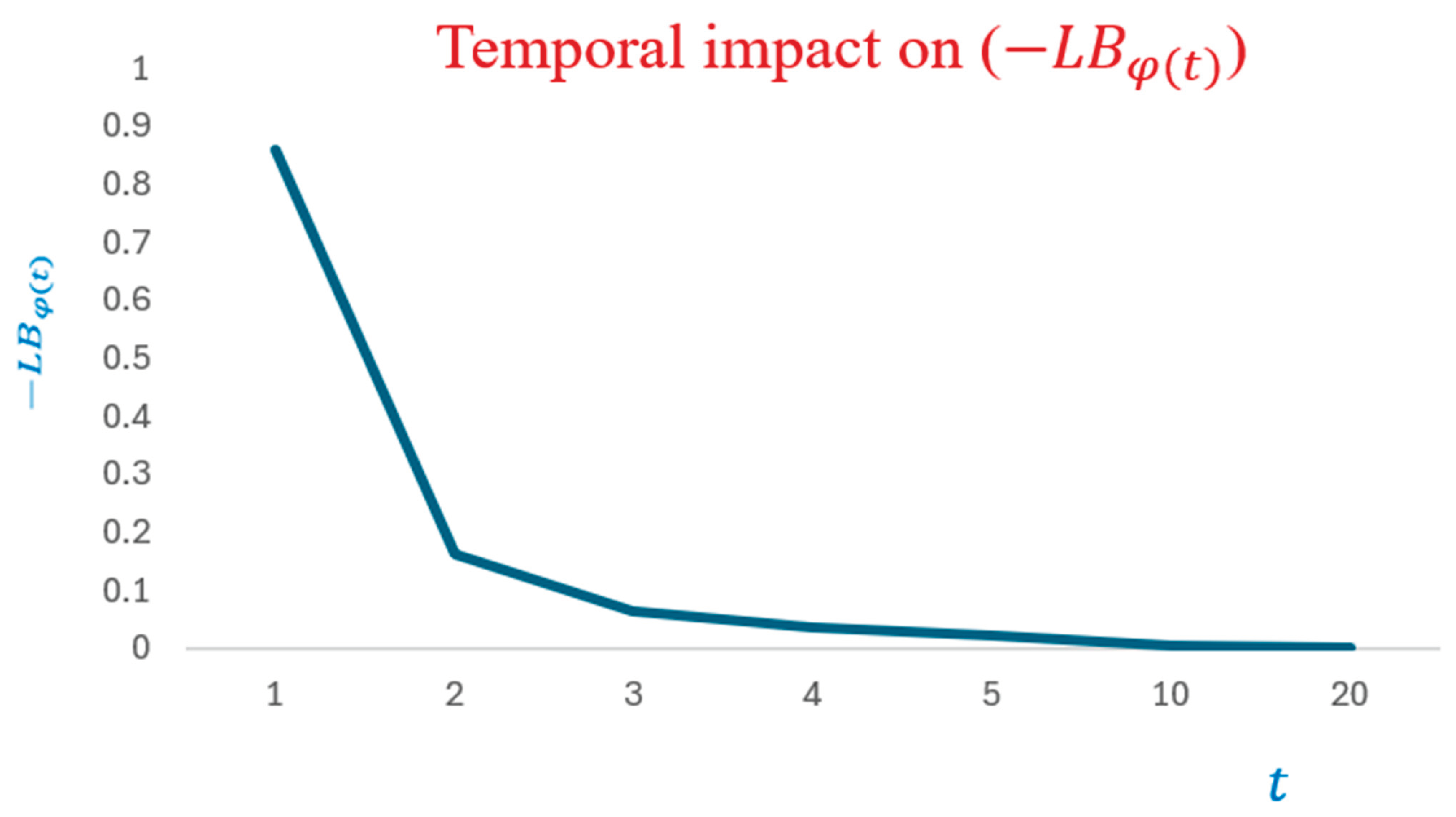
As illustrated by Figure 2, the progressive increase of time implies the increasability of

{L B}_{φ (t)}

. This reveals the temporal effect on

{L B}_{φ (t)}

. The following corollary validates the established experimental setup analytically.

Corollary 2

{L B}_{φ (t)} = \frac{1}{2 t} (1 - e^{(\frac{1}{t})})

of (12) is forever increasing in time.

Proof

We have

\begin{array}{l} \frac{\partial {L B}_{φ (t)}}{\partial t} & = - \frac{1}{2 t^{2}} (1 - e^{(\frac{1}{t})}) + \frac{1}{2 t} (\frac{1}{t^{2}} e^{(\frac{1}{t})}) \\ = - \frac{1}{2 t^{2}} (1 - e^{(\frac{1}{t})}) + \frac{1}{2 t} (\frac{1}{t^{2}} e^{(\frac{1}{t})}) \\ = - \frac{1}{2 t^{2}} + \frac{1}{2 t^{3}} e^{(\frac{1}{t})} + \frac{1}{2 t^{2}} e^{(\frac{1}{t})} \end{array}

> - \frac{1}{2 t^{2}} + \frac{1}{2 t^{3}} e^{(\frac{1}{t})} + \frac{1}{2 t^{2}} (Sin ce e^{(\frac{1}{t})} > 1 f o r a l l t > 0)

(13)

> 0

(14)

Engaging (14) and the Preliminary Theorem (PT), the required result follows.

4. FPK applications to genetics

In [10], an investigation was undertaken using Fokker-Planck equations to model gene regulatory networks in biology, focusing on the joint distribution of

m R N A

and

μ R N A

content in cells. It suggests that the presence of

μ R N A

increases the robustness of gene expression, leading to a smaller variation in

m R N A

density. The study uses theoretical formulas, dimensional analyses, and numerical simulations to explore the impact of different parameters and noise choices on gene expression levels.

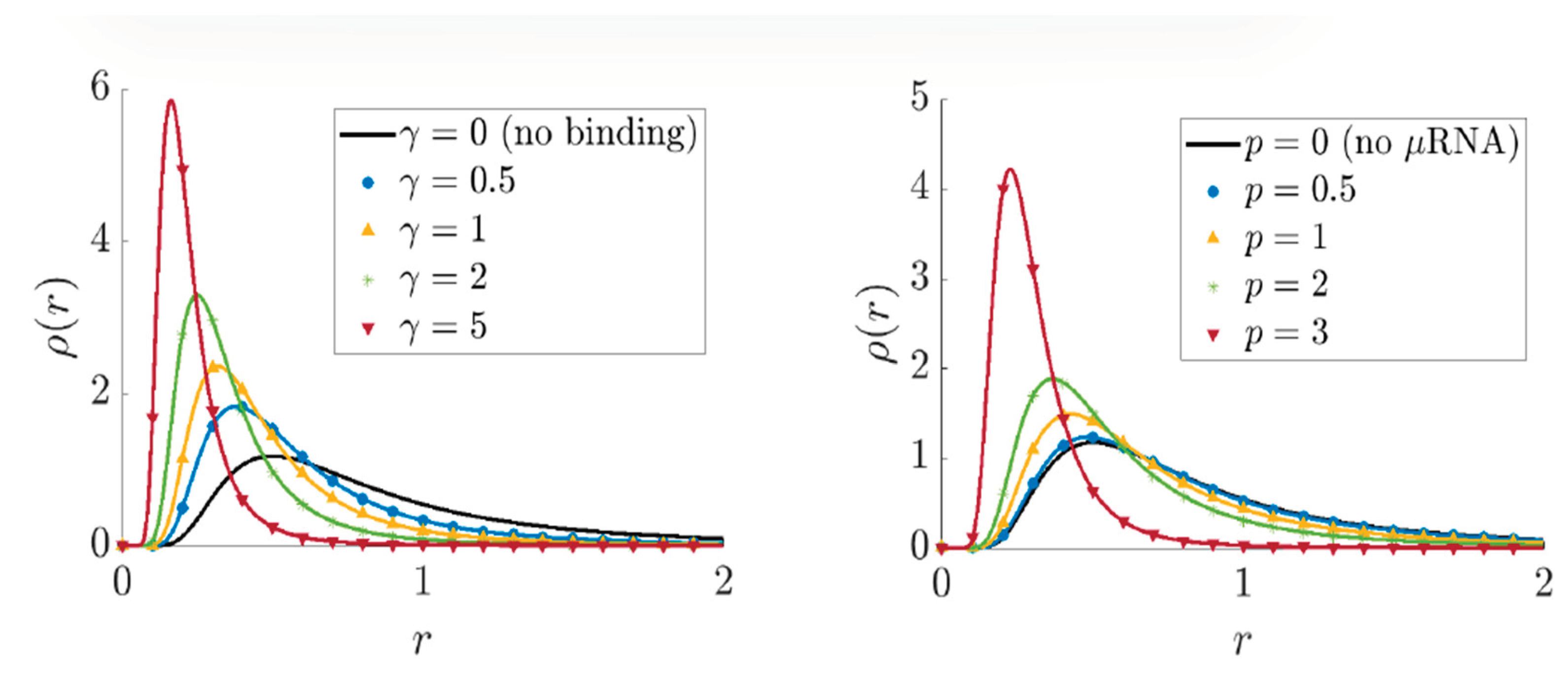
In the context of exploring gene expression [10], an exposition was undertaken to describe the process of evaluating cell-to-cell variation by computing specific quantities related to

m R N A

production and destruction. This involves numerical computations [10] using Gauss-Laguerre quadrature to approximate integrals against a gamma distribution, allowing for efficient analysis of the parameter space (

δ, γ, p

) and comparison of cell variation in different scenarios involving fast

m R N A

and free

m R N A

. The results are visualized through plots showing the relative cell-to-cell variation and explicit distributions for various parameter sets, aiding in understanding the qualitative behavior of gene expression under different conditions, as shown in Figure 3(c.f., [10]).

In [10], a new mathematical model based on the FPK equation was introduced to analyze how the presence of regulatory feed-forward loops involving

μ

RNA affects gene expression robustness in cells. By combining analytical formulas and numerical simulations, the researchers demonstrated that the presence of

μ

RNA can impact gene expression robustness, with the specific effect depending on the type of noise present in

m

RNA and

μ

RNA production processes. The study [10] also highlighted potential future research directions, such as parameter calibration from real-world data and further exploration of gene regulatory network complexities beyond the simplified model presented.

On the other side of the spectrum, the work in [11] investigated the innovative use of mathematics and biochemistry to study the formation of unique structures in DNA and

m

RNA near transcription, connecting them to neural networks. By applying statistical and stochastic methods, along with quantum principles, researchers can analyze the dynamics of these structures using Poisson spike trains and FPK stochastic differential equations. This approach [11] involves developing new multidimensional methods based on the Kolmogorov-Chentsov continuity theorem to understand the formation of specific DNA structures like G-quadruplexes and non-canonical bases during processes such as DNA methylation and in neural networks.

The Poisson spike train, is temporary in the context of the Hodgkin-Huxley model, commonly used in neural studies. This transient nature of the spike train is crucial for solving various Stochastic Differential Equations (SDE) and is depicted in Figure 4a,b (c.f., [11])of the research, showing different outcomes like damped oscillations, single spikes followed by transients, and sustained firing in simulations of the model.

The relationship between CpG islands and transcription initiation sites were extensively investigated [11], suggesting that the distribution of CpG islands around these sites follows a probability distribution. It also touches on the transient nature of DNA methylation, its impact on memory, and the involvement of additional dimensions in DNA methylation levels under changing environmental conditions. These insights are connected to the multidimensional time model applied to neural ion current models and the formation of non-canonical bases in DNA,

m

RNA, and RNA near transcription sites.

5. Conclusion and future research

In summary, the TDCDP’s lower bound, namely,

{L B}_{φ (t)}

is determined. More profoundly, a special case of,

{L B}_{φ (t)}

, was found to be forever increasing in time. Some FPK applications to genetics are introduced.

Here is a challenging open problem:

Can we solve the challenging open problem of finding the behavior of

{L B}_{φ (t)} = (1 + \frac{t σ^{2}}{2 r (t)}) - \frac{1}{2 t} e^{\frac{t σ^{2}}{r (t)}}

(c.f., (8))

Against time?

The proposed open challenge will be solved in the next phase of research, which will also look at further extensions of FPK theory to additional multidisciplinary areas of human knowledge.

References

Mageed IA, Yuyang Zhou, Y, Liu, Y, and Zhang Q, “ Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov(FPK) Equation to System Control, Modelling and Simulation”,In2023 28th International Conference on Automation and Computing (ICAC) 2023, 30th Aug- Sep 1. IEEE. [CrossRef]
Balci, I. M., & Bakolas, E. (2021, December). Covariance control of discrete-time gaussian linear systems using affine disturbance feedback control policies. In 2021 60th IEEE Conference on Decision and Control (CDC) (pp. 2324-2329). IEEE. [CrossRef]
Faulwasser, T., Ou, R., Pan, G., Schmitz, P., & Worthmann, K. (2023). Behavioral theory for stochastic systems? A data-driven journey from Willems to Wiener and back again. Annual Reviews in Control. [CrossRef]
Zhang, Q., & Zhou, Y. (2022). Recent advances in non-Gaussian stochastic systems control theory and its applications. International Journal of Network Dynamics and Intelligence, 111-119. [CrossRef]
A. Mageed, "Uniqeneness of The Time-Dependent Controller’s Designed Parameter (TDCDP) of Fokker Planck Kolmogorov(FPK) Probability Density Function(PDF) with Applications of Lambert W Function to Number Theory, Quantum Computing and Bitcoin Protocols," 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6. [CrossRef]
Chen, Y., Georgiou, T. T., & Pavon, M. (2021). Stochastic control liaisons: Richard sinkhorn meets gaspard monge on a schrodinger bridge. Siam Review, 63(2), 249-313. [CrossRef]
Capasso, V., & Capasso, V. (2021). Introduction to Continuous-Time Stochastic Processes. Springer International Publishing. [CrossRef]
Mageed, I.A, Threshold and Upper Bound for The Controller’s Designed Parameter of Fokker Planck Kolmogorov Probability Density Function with Applications to Cryptocurrency, The 2nd International Conference on Applied Mathematics, Informatics, and Computing Sciences (AMICS 2023), Ghent University, Belgium.
I. Mezo, Lambert W Function: Its Generalizations and Applications, Chapman and Hall/CRC: London, UK, (2022). [CrossRef]
Mageed, I. A., & Zhang, Q. (2023). Threshold Theorems for the Tsallisian and Rényian (TR) Cumulative Distribution Functions (CDFs) of the Heavy-Tailed Stable M/G/1 Queue with Tsallisian and Rényian Entropic Applications to Satellite Images (SIs). electronic Journal of Computer Science and Information Technology, 9(1), 41-47.
Degond, P., Herda, M., & Mirrahimi, S. (2020). A Fokker-Planck approach to the study of robustness in gene expression. arXiv preprint arXiv:2006.14985.
Fundator, M. (2021). APPLICATION OF MULTIDIMENSIONAL TIME MODEL TO DYNAMICAL RELATION OF POISSON SPIKE TRAINS IN NEURAL ION CURRENT MODELS AND FORMATION OF NON-CANONICAL BASES, ISLANDS, AND G-QUADRUPLEXES IN DNA, MRNA, AND RNA AT OR NEAR THE TRANSCRIPTION. [CrossRef]

Figure 1.

Figure 2. How time impacts

{L B}_{φ (t)}

Figure 2. How time impacts

{L B}_{φ (t)}

Figure 3. The comparison of marginal distributions of fast

μ R N A s

with free

m R N A

distributions for different parameters

p

and

γ

, where

δ

is fixed at 2. The left side shows how varying

γ

affects the distribution when

p

is set at 1.5, while the right side illustrates the impact of changing

p

when

γ

is set to 1. This analysis helps understand how different parameter values influence the distribution of fast

μ R N A s

compared to free

m

RNAs in the model being studied.

Figure 3. The comparison of marginal distributions of fast

μ R N A s

with free

m R N A

distributions for different parameters

p

and

γ

, where

δ

is fixed at 2. The left side shows how varying

γ

affects the distribution when

p

is set at 1.5, while the right side illustrates the impact of changing

p

when

γ

is set to 1. This analysis helps understand how different parameter values influence the distribution of fast

μ R N A s

compared to free

m

RNAs in the model being studied.

Figure 4. The possible patterns of transient Poisson spike trains in neural ion current models, particularly in the context of the Hodgkin-Huxley model. These transient spikes can manifest as damped oscillations, single spikes followed by transients, or sustained firing, providing insights into the behavior of neural systems under different current conditions. Understanding these transient spike train appearances is crucial for modeling and analyzing neural activity and stochastic processes in neuroscience research.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Lower Bound for the Fokker Planck Kolmogorov (FPK) Probability Density Function Controller's Designed Parameter with FPK applications to Genetics

Abstract

Keywords:

Subject:

1. Introduction

Preliminary Theorem (PT) [9]

2. Methodology

3. Results and discussion

Numerical experiment

4. FPK applications to genetics

5. Conclusion and future research

References

MDPI Initiatives

Important Links

Subscribe