The Infinite-Phased Root Parameter for the G1/M/1 Pointwise Stable Fluid Flow Approximation (PSFFA) Model of the Non-Stationary Ek/M/1 Queue with PSFFA Applications to Hospitals’ Emergency Departments

Dr Ismail A Mageed

doi:10.20944/preprints202402.1021.v1

Submitted:

18 February 2024

Posted:

19 February 2024

You are already at the latest version

Abstract

This paper provides a new discovery that adds to the contemporary theory of modelling of non-stationary queues, by capturing analytically the behavior of the root parameter, for the G1/M/1 PSFFA model of non-stationary Ek/M/1 queue. Additionally, it has been also revealed that the resulting root parameter reduces to the PSFFA model of non-stationary queue. Potential applications of PSFFA to Computer engineering are provided. Some challenging open problems are addressed combined with closing remarks and future research directions.

Keywords:

Hospital emergency departments

;

Non-stationary queue

;

PSFFA

;

state variable

;

k number of phases

Subject:

Computer Science and Mathematics - Probability and Statistics

I. Introduction

Customers' arrival processes in communication networks and other real-world queuing systems are frequently non-stationary, meaning they vary over time because of non-stationary input loads, routing and flow control modifications, and load sharing[1,2,3,4,5,6,7,8]. This is a critical factor to consider as communication networks grow and manage more complicated traffic kinds with different requirements for quality of service, which results in intermittent and non-stationary network traffic. Queuing theory addresses problems involving waiting, such standing in queue at a grocery store or bank, waiting for a computer to respond, expecting a piece of equipment to break, or waiting for public transportation.

In queuing theory, there are several ways to analyze dynamic arrival or service rates in systems. These methods include transient analysis, non-stationary analysis, applications of analysis methods, and simulations. It's critical to understand the distinction between transitory and non-stationary activity. Non-stationary behaviour is brought on by time-dependent arrival and/or service rates, whereas transient behaviour happens when the system is switching from one stationary load to another. To examine the behaviour of the system as a function of time, simulation methodologies entail executing several simulations and averaging the outcomes [1,2,3,4,5,6,7,8]. Nevertheless, rather than attempting to determine the transient behaviour analytically, researchers have concentrated on quantitatively identifying it, as it might be challenging to generate a closed form expression from the transform expression.

This current paper’s flowchart reads:

II. PSFFA

The PSFFA approach simulates the average number of consumers in the queue by using a non-linear differential equation. It has been demonstrated to be accurate and is based on steady state queueing relationships. This is a generalization of earlier fluid flow models and can be used for non-Markovian queues as well. Its advantages include being computationally efficient and simple to use, and it can serve as a basis for the development of dynamic network’s controllability [1].

Consider a single server queueing system with a non-stationary arrival mechanism. Assume that the underlying queue’s mean arrival and service rates are respectively,

λ (t)

and

μ (t)

. Define,

{(x}^{.} (t) = \frac{d x (t)}{d t}

), to be the state variable’s temporal change.

Let

f_{i n} (t)

and

f_{o u t} (t)

define the system’s temporal flow in and out, respectively.

x

(

t

) (c.f., [1]) reads:

x^{.} (t) = - f_{o u t} (t) + f_{i n} (t)

(1)

f_{o u t} (t)

reads:

f_{o u t} (t) = μ (t) ρ (t)

(2)

Moreover,

f_{i n} (t) = λ (t)

(3)

Therefore,

x^{.} (t) = - μ (t) ρ (t) + λ (t), 1 > ρ (t) = \frac{λ (t)}{μ (t)} > 0

(4)

In a stable queue(i.e.,

x^{.} (t) =

0),

x = G_{1} (ρ)

(5)

As

G_{1} (ρ)

is invertible, it reads:

ρ = G_{1}^{- 1} (x)

(6)

Consequently,

x^{.} (t) = - μ (t) (G_{1}^{- 1} (x (t))) + λ (t)

(7)

More specifically,

G 1 / M / 1

PSFFA models for both non-stationary

D / M / 1

and

E_{k} / M / 1

queues, respectively read as:

x^{.} (t) = - μ x (t) (1 - σ) + λ (t), = σ = e^{\frac{(σ - 1)}{ρ}} = σ_{D / M / 1}, ρ = \frac{λ}{μ}, σ (σ \in (0, 1))

(8)

x^{.} (t) = - μ x (t) (1 - σ) + λ (t), σ = {(\frac{k ρ}{k ρ + (1 - σ)})}^{k} = σ_{E_{k} / M / 1}, ρ = \frac{λ}{μ}, σ (1 > σ > 0)

(9)

III. UNLOCKING THE ROOT PARAMETER OF THE UNDERLYING QUEUE (c.f., (9))

Theorem 1

At an infinte phase,

σ_{E_{\infty} / M / 1}

=

σ_{D / M / 1}

Proof

Following (9),

σ = {(\frac{k ρ}{k ρ + (1 - σ)})}^{k}

Hence,

l n σ = k l n (\frac{k ρ}{k ρ + (1 - σ)}) = \frac{l n (\frac{k ρ}{k ρ + (1 - σ)})}{\frac{1}{k}}

(10)

Using Hopital’s rule,

\begin{array}{l} {l i m}_{k \to \infty} l n σ & = {l i m}_{k \to \infty} \frac{l n (\frac{k ρ}{k ρ + (1 - σ)})}{\frac{1}{k}} \\ = {l i m}_{k \to \infty} \frac{\frac{1}{(\frac{k ρ}{k ρ + (1 - σ)})} (\frac{ρ (k ρ + (1 - σ)) - k ρ^{2}}{{(k ρ + (1 - σ))}^{2}})}{- \frac{1}{k^{2}}} \\ = {l i m}_{k \to \infty} \frac{\frac{1}{(\frac{k ρ}{k ρ + (1 - σ)})} (\frac{ρ (k ρ + (1 - σ)) - k ρ^{2}}{{(k ρ + (1 - σ))}^{2}})}{- \frac{1}{k^{2}}} \\ = - (1 - σ) {l i m}_{k \to \infty} \frac{k}{(k ρ + (1 - σ))} = \frac{(σ - 1)}{ρ} \end{array}

(11)

Communicating (11) and (9), implies

σ_{E_{\infty} / M / 1} = σ_{D / M / 1}

(12)

V. SOME PSFFA APPLICATIONS TO HOSPITALS’ EMERGENCY DEPARTMENTS

In a dynamic queuing system, the PSFFA approach [9] is used to predict the length of the patient’s wait by calculating the average utilization rate and the expected number of patients served by the on-duty physicians. By streamlining the intricate link between utilization rate and queue length in a steady-state queuing system, this technique makes it possible to estimate the queue length at the conclusion of each session.

To overcome the nonlinear nature of the queue length function and enhance analysis and decision-making in patient queue management, a Minimum Error Area (MEA) approach is recommended.

The logic-based Bender decomposition (LBBD) method is used in the context of the scheduling problem discussed[9] to effectively handle the staffing and scheduling problems by iteratively optimizing the number of physicians required for each period and assigning work shifts to them.

The LBBD approach [9] involves a master problem focusing on staffing needs and a subproblem addressing scheduling, both formulated as Mixed Integer Programming (MIP) models. By iteratively solving these problems and incorporating logic-based Benders cuts, the algorithm aims to converge on the optimal solution for the primary MIP model, enhancing the efficiency and accuracy of the scheduling process.

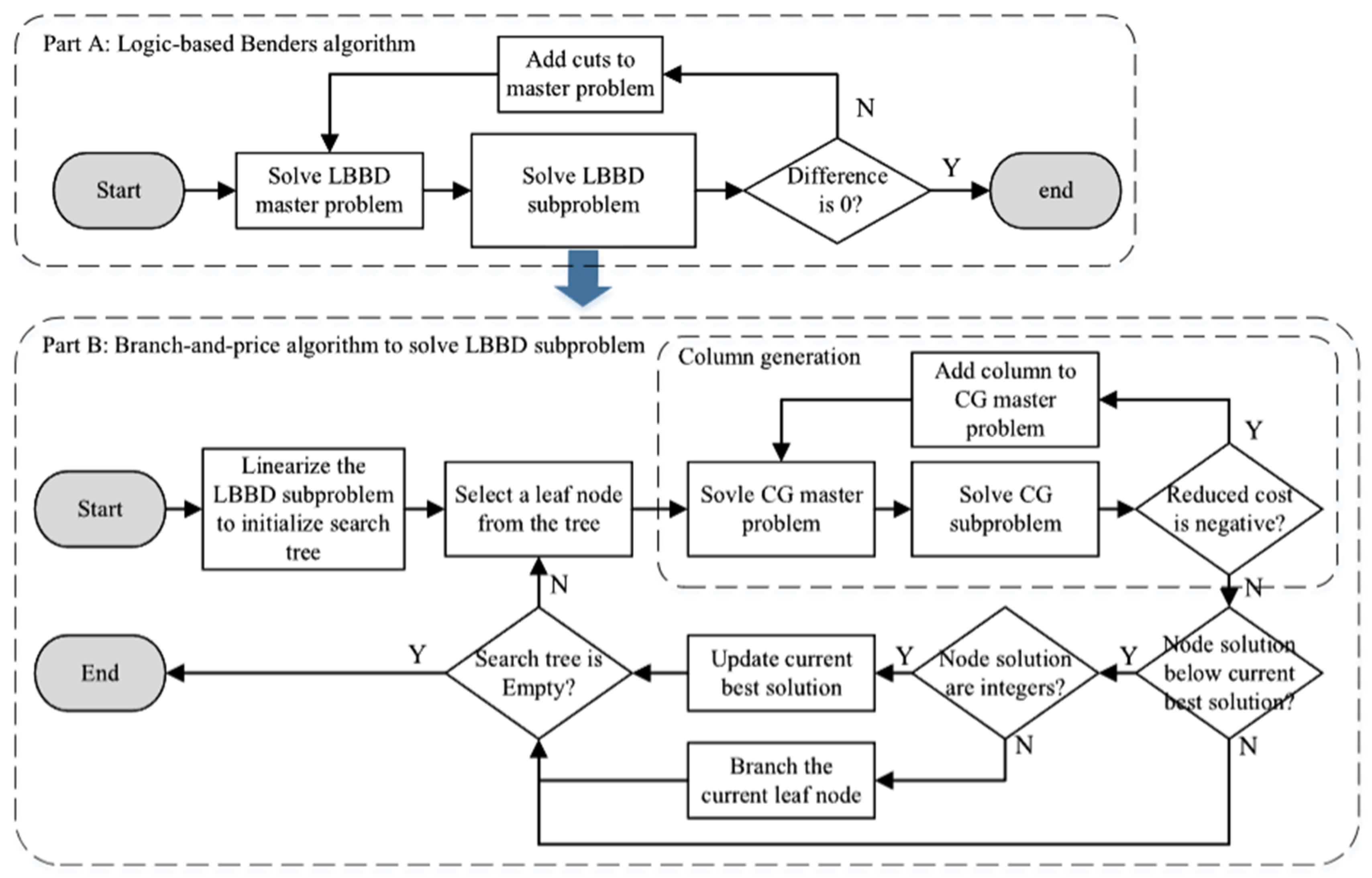
In the context of the scheduling problem [9], the flow chart of the logic-based Bender decomposition (LBBD) algorithm is depicted in Figure 1 (c.f., [9]). The LBBD algorithm alternates between solving a master problem, which focuses on determining the required number of physicians for each period to manage queue length, and a subproblem, which addresses the allocation of work shifts to individual physicians. This iterative process aims to optimize staffing decisions and scheduling assignments efficiently.

The proposed method[9] for physician scheduling in fever clinics during the COVID-19 pandemic results in an average weekly cost of $505.42, which is 9.75% lower than the current three-shift schedule cost of $560. Instance 8 shows the lowest total cost of $481, representing a 14.11% reduction. Additionally, the algorithm [9] helps manage patient queue lengths effectively, reducing the risk of cross-infection during peak periods compared to the existing schedule.

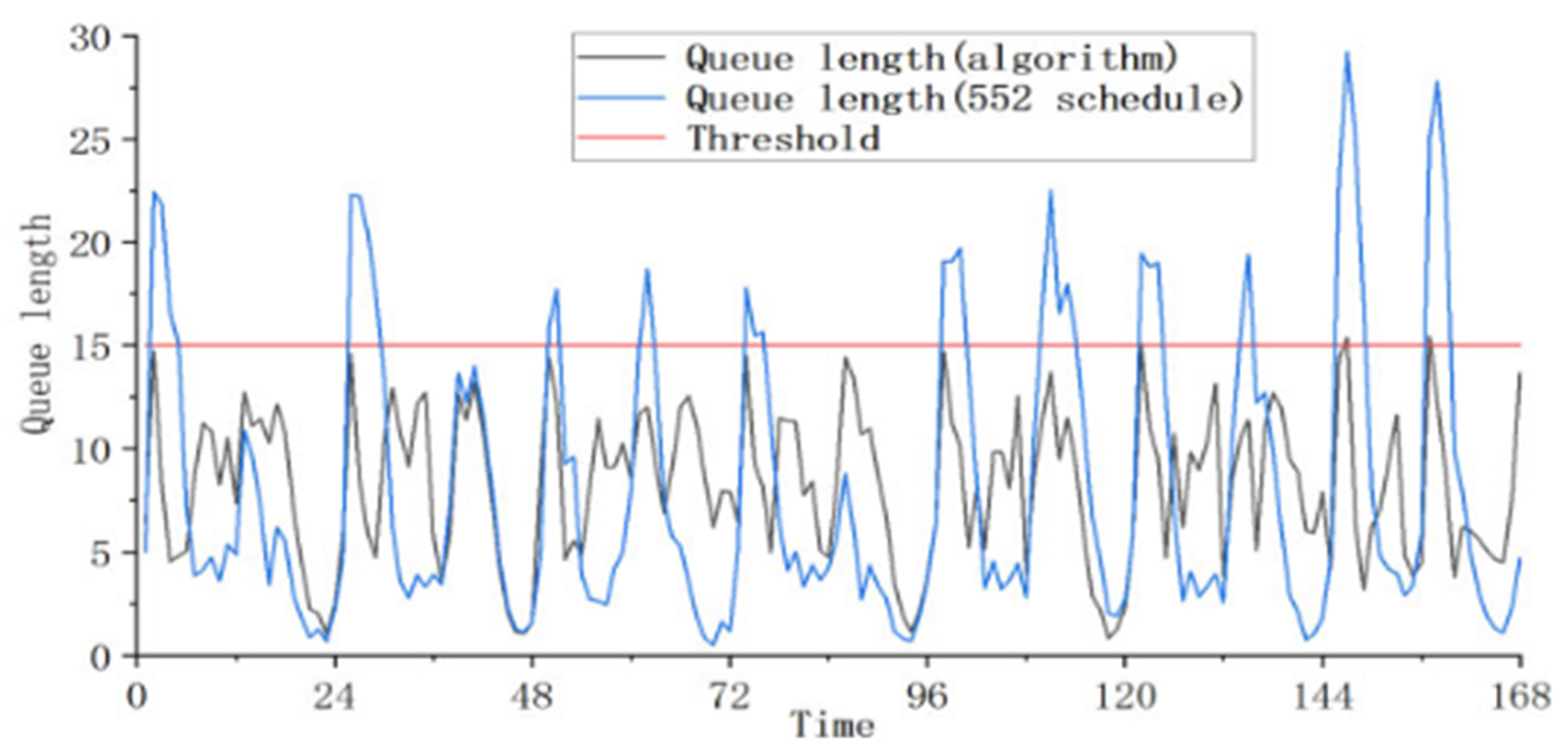
In the context of the study on physician scheduling in fever clinics during the COVID-19 pandemic, Figure 2 (c.f., [9]) shows that patient queue lengths frequently surpass the acceptable limit during peak hours at 9 a.m. and 9 p.m. This indicates potential overcrowding and increased risk of cross-infection during these peak periods under the current three-shift schedule used in the hospital. The proposed scheduling method aims to better match physician staffing with patient arrival rates, reducing queue lengths and improving service efficiency, especially during peak demand periods.

In summary, to effectively manage patient care during the Covid-19 pandemic, [9] addressed the significance of optimizing physician schedules in fever clinics. To efficiently address the scheduling problem, it presents a method that combines benders decomposition and column generation. It also introduces a mathematical model (MIP) to compute patient queue length. Comparing this method to the conventional three-shift schedule, the study demonstrates that it reduces physician costs and lengthens patient wait times. This makes it a viable option for handling high patient demand during serious pandemics.

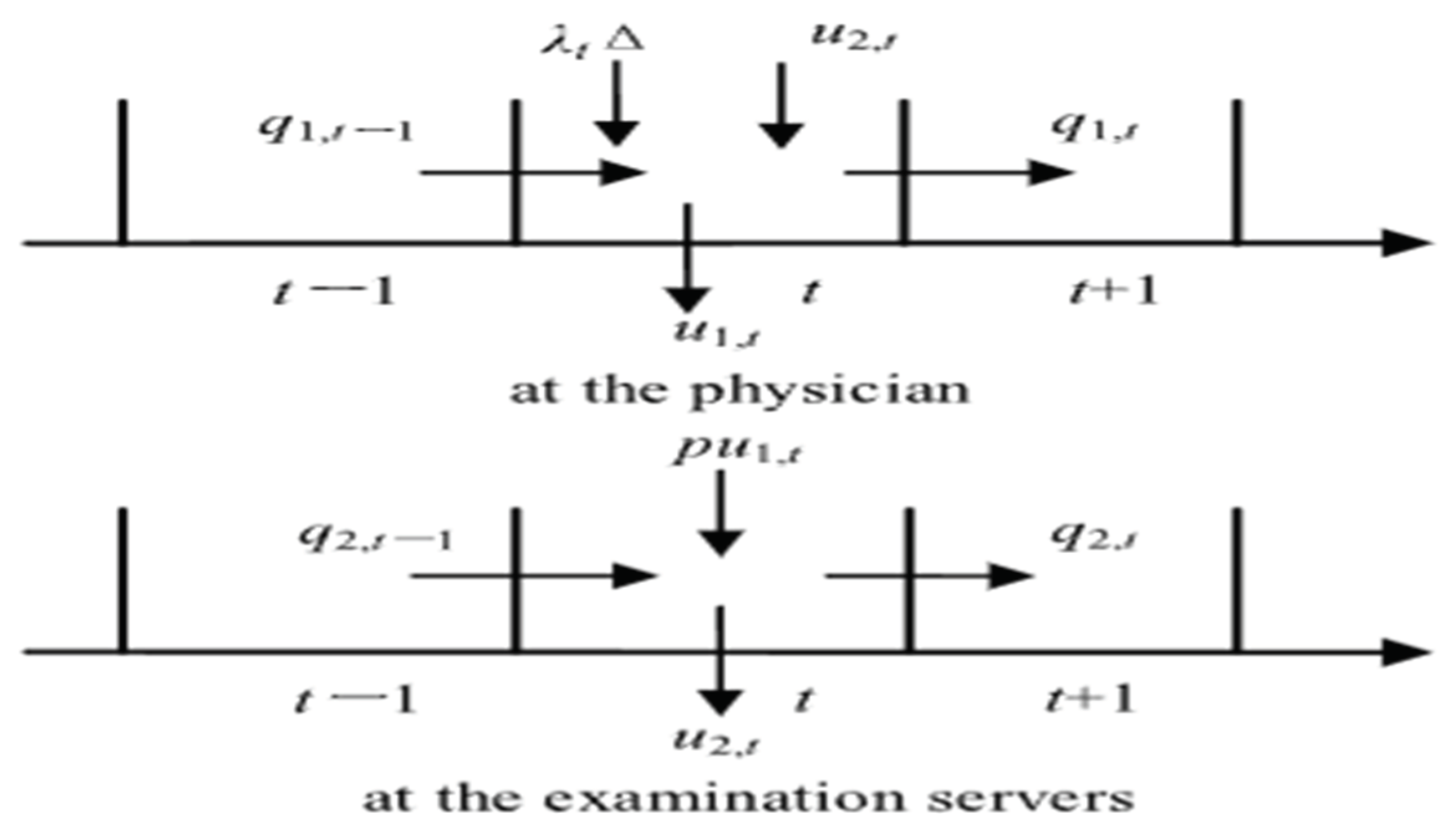
The Physician Scheduling for Fixed Appointment PSFFA model is extended by the authors to a queuing network with two stations, designated as station 1 and station 2, in the context of physician scheduling for emergency departments[10]. The system state at the end of each period in these stations is represented by symbols like

q_{1, t}

and

q_{2, t}

, where patients are serviced according to the First-Come- First-serve (FCFS) system, with no preference given to returning patients, and where patients are evaluated alongside newly arrived patients. In Figure 3(c.f., [10]), the balance of patients between the two stations over time is displayed, illustrating the fluid equilibrium of the queuing model.

In the context of solving physician scheduling problems, a Tabu Search (TS) algorithm is designed as a common method for addressing discrete optimization challenges, which iteratively explores neighborhood solutions, and updates based on specific criteria until a stopping condition is met. This approach has been successfully applied in physician scheduling, as demonstrated in previous studies, for a more detailed survey, consult[10].

VI. CONCLUSION, OPEN PROBLEMS AND FUTURE WORK

This paper is concerned with finding the analytic form for the root parameter of the

G 1 / M / 1

PSFFA model for

E_{k} / M / 1

queue at an infinte phase. More potentially, some PSFFA applications to hospital’s emergency departments are provided.

These are some emerging hard research questions:

Is it mathematically viable to solve the root equation

σ = {(\frac{k ρ}{k ρ + (1 - σ)})}^{k}, ρ = \frac{λ}{μ}, σ (1 > σ > 0)

(c,f., 9)

For the 1^st, 2^nd, 3^rd ..., 7^th phases? i.e., corresponding to

k = 1, 2, 3, . ., 7

Is $σ_{D / M / 1}$ (c.f., (8)) solvable?

Future work involves attempting to solve these research questions and searching PSFFA’s applicability to other multi-interdisciplinary fields of human knowledge.

References

x. Zhao et al, “A Queuing Network Model of a Multi-Airport System Based on Point-Wise Stationary Approximation,”, Aerospace, 2022, vol. 9, no. 7. [CrossRef]
V.B.Iversen, “ITU Teletraffic Engineering Handbook,”, Technical University of Denmark, 2021.
I. A. Mageed, and Q. Zhang, “Solving the open problem for GI/M/1 pointwise stationary fluid flow approximation model (PSFFA) of the non-stationary D/M/1 queueing system,” electronic Journal of Computer Science and Information Technology, vol. 1, no. 9,p. 1-6, 2023.
Q. Wu et al, “Time-dependent performance analysis of the 802.11p- based platooning communications under disturbance,” IEEE Transactions on Vehicular Technology , 2020, vol. 69, no. 12. [CrossRef]
N. Vuppalapati, et al, “Modeling & analysis of software defined networks under non-stationary conditions,” Peer-to-Peer Networking and Applications, 2021 vol. 14, no. 3. [CrossRef]
Y. Harold Robinson and E. Golden Julie, “ MTPKM: Multipart trust based public key management technique to reduce security vulnerability in mobile ad-hoc networks,”,Wireless Personal Communications, 2019, vol. 109, no. 2, p. 739-760. [CrossRef]
R. Liu et al, “Multiscale kernel based residual convolutional neural network for motor fault diagnosis under nonstationary conditions,”IEEE Transactions on Industrial Informatics, 2019, vol. 16, no. 6, p. 3797-3806. [CrossRef]
J.P. León et al, “A machine learning based Distributed Congestion Control Protocol for multi-hop wireless networks,” Computer Networks, 2023. [CrossRef]
Wang, C., Liu, R., & Wu, Z. (2023). Combining Benders Decomposition and Column Generation for Physician Scheduling in Fever Clinics During Covid-19 Pandemic. IEEE Transactions on Automation Science and Engineering. [CrossRef]
Wang, Z., Liu, R., & Sun, Z. (2022). Physician Scheduling for Emergency Departments Under Time-Varying Demand and Patient Return. IEEE Transactions on Automation Science and Engineering, 20(1), 553-570. [CrossRef]

Figure 1. Branch-and-Bound (BD) is used to solve a subproblem related to working costs and physician requirements, while Column Generation (CG) efficiently handles the complex scheduling by iteratively assigning physicians to shifts and determining the most valuable shifts to meet staffing needs. This approach streamlines the scheduling process by optimizing physician assignments and ensuring adequate coverage in fever clinics.

Figure 2. The management of patient queues during a severe pandemic using algorithmic scheduling.

Figure 3. In the context of the study on physician scheduling for emergency departments, the text refers to the fluid equilibrium within their queuing model. This equilibrium is depicted as essential for understanding the system state at different stations within the queuing network.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

The Infinite-Phased Root Parameter for the G1/M/1 Pointwise Stable Fluid Flow Approximation (PSFFA) Model of the Non-Stationary E_k/M/1 Queue with PSFFA Applications to Hospitals’ Emergency Departments