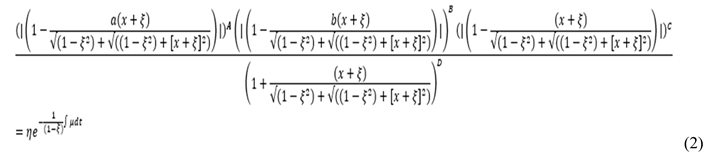Ismail’s Ratio Conquers New Horizons the Non-stationary M/G/1 Queue’s State Variable Closed Form Expression

Preprint

Article

Ismail’s Ratio Conquers New Horizons the Non-stationary M/G/1 Queue’s State Variable Closed Form Expression

Altmetrics

Downloads

125

Views

Comments

Dr Ismail A Mageed^*

This version is not peer-reviewed

Submitted:

07 February 2024

Posted:

09 February 2024

Read the latest preprint version here

Alerts

Abstract

This paper investigates the search for an exact analytic solution to the state variable of the non-stationary queue. Currently, the only known solution to this problem is through simulation. However, this study proposes a constant ratio

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

The field of transient/non-stationary analysis has limited literature, which can be categorized into simulation, transient analysis, analysis, and applications techniques. These categories encompass various approaches to studying systems that change over time, including simulations, analysing transient behaviour, and exploring non-stationary phenomena. In certain cases, mathematical transformations are employed to analysing non-stationary queueing systems. However, evaluating these expressions can be computationally complex. As a result, there has been a focus on numerically determining the transient behaviour of such systems instead of deriving closed form expressions.

The current exposition contributes to solving for first time ever, the longstanding unsolved problem of obtaining the state variable of the time varying

M / G / 1

queueing system.

The following flowchart shows how this paper is organized.

2. PSFFA

Therefore, the time varying

M / G / 1

queueing system’s PSFFA model [2,3,4,5] reads:

x^{.} = - μ (\frac{(x + 1) - \sqrt (x^{2} + 2 ξ x + 1)}{1 - ξ}) + λ

ξ = C_{s}^{2} = s q u a r e d c o e f f i c i e n t o f v a r i a t i o n

(1)

TVQSs’ life example [6] is depicted by Figure 1.

Figure 1.

3. Solving the non-stationary $M / G / 1$ queueing system’s PSFFA (c,f., (1))

Theorem 3.1.

Ismail’s ration,

β

solves (2.1), with a closed form expression to read as:

Proof

We have

x^{.} = - μ (\frac{(x + 1) - \sqrt (x^{2} + 2 ξ x + 1)}{1 - ξ}) + λ

ξ = C_{s}^{2}

(c.f., (1))

This translates to

\frac{d x}{((x + 1) - \sqrt (x^{2} + 2 ξ x + 1)) - β (1 - ξ))} = - \frac{μ d t}{(1 - ξ)}

β = \frac{λ (t)}{μ (t)} > 0

(2)

Let

x = \sqrt{(1 - ξ^{2})} c s c h y - ξ

, then

x^{.} = {- \sqrt{(1 - ξ^{2})} y}^{.} c o t h y c s c h y

. Thus, we have

\frac{- c o t h y c s c h y d y}{((c s c h y - c o t h y) - \frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}})} = - \frac{μ d t}{(1 - ξ)}

T h i s m e a n s

\frac{c o s h y d y}{- (1 + s i n h y - c o s h y) + \frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}} s i n h y) s i n h y} = - \frac{μ d t}{(1 - ξ)}

E q u i v a l e n t l y,

\frac{\frac{2}{\frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}}} (e^{3 y} + e^{y}) d y}{{[e}^{2 y} - \frac{e^{y}}{\frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}}} + [\frac{2}{(\frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}})} - 1]]} = - \frac{μ d t}{(1 - ξ)}

(3)

Define

\frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}} = ζ

[e^{2 y} + \frac{2 e^{y}}{ζ} - 1] = 0 ⟹

e^{y} = \frac{(\frac{1}{ζ} \pm \sqrt{(\frac{1}{ζ^{2}}} - 4 (\frac{2}{ζ} - 1))}{2} = \frac{(\frac{1}{ζ} \pm \sqrt{(\frac{1}{ζ^{2}}} - \frac{8}{ζ} + 4)}{2} = a, b

w h e r e

a = \frac{(\frac{1}{ζ} + \sqrt{(\frac{1}{ζ^{2}}} - \frac{8}{ζ} + 4)}{2}

b = \frac{(\frac{1}{ζ} - \sqrt{(\frac{1}{ζ^{2}}} - \frac{8}{ζ} + 4)}{2}

\frac{\frac{2}{ζ} (e^{3 y} + e^{y}) d y}{{[e}^{2 y} - \frac{e^{y}}{ζ} + [ζ - 1]] [e^{2 y} - 1]} = - \frac{μ d t}{(1 - ξ)}

(4)

\frac{\frac{2}{ζ} (e^{3 y} + e^{y})}{{[e}^{2 y} - \frac{e^{y}}{ζ} + [ζ - 1]] [e^{2 y} - 1]} = [\frac{A}{(e^{y} - a)} + \frac{B}{(e^{y} - b)} + \frac{C}{(e^{y} - 1)} + \frac{D}{(e^{y} + 1)}]

Hence, it is implied that:

- b A - a B + (1 - (a + b)) C - (a + b + 1) D = 0

(5)

∴ B = \frac{(1 - a) (C - D)}{(\frac{2}{ζ} + a)}

(6)

which implies

A =

\frac{2}{ζ} - \frac{(1 + \frac{2}{ζ}) C}{(\frac{2}{ζ} + a)} - \frac{(1 + \frac{2}{ζ} + 2 a) D}{(\frac{2}{ζ} + a)}

(7)

which yields

C = \frac{\frac{4}{ζ} (\frac{2}{ζ} + a) - [(1 + \frac{2}{ζ} + 2 a) - (a b - (a + b)) (\frac{2}{ζ} + a)] D}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}

(8)

b A + a B + a b C - a b D = 0

b [\frac{2}{ζ} - \frac{(1 + \frac{2}{ζ}) C}{(\frac{2}{ζ} + a)} - \frac{(1 + \frac{2}{ζ} + 2 a) D}{(\frac{2}{ζ} + a)}] + a [\frac{(1 - a) (C - D)}{(\frac{2}{ζ} + a)}] + a b C - a b D = 0

Therefore, we have

D = \frac{\frac{2 b}{ζ} + a (a b - \frac{b (1 + \frac{2}{ζ})}{(\frac{2}{ζ} + a)} + a [\frac{(1 - a)}{(\frac{2}{ζ} + a)}]) [\frac{\frac{4}{ζ} (\frac{2}{ζ} + a)}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}]}{(a b + b [\frac{(1 + \frac{2}{ζ} + 2 a)}{(\frac{2}{ζ} + a)}] + a [\frac{(1 - a)}{(\frac{2}{ζ} + a)}]) + a (a b - \frac{b (1 + \frac{2}{ζ})}{(\frac{2}{ζ} + a)} + a [\frac{(1 - a)}{(\frac{2}{ζ} + a)}]) [\frac{[(1 + \frac{2}{ζ} + 2 a) - (a b - (a + b)) (\frac{2}{ζ} + a)]}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}}

(9)

C = \frac{\frac{4}{ζ} (\frac{2}{ζ} + a) - [(1 + \frac{2}{ζ} + 2 a) - (a b - (a + b)) (\frac{2}{ζ} + a)] D}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}

(10)

A =

\frac{2}{ζ} - \frac{(1 + \frac{2}{ζ}) C}{(\frac{2}{ζ} + a)} - \frac{(1 + \frac{2}{ζ} + 2 a) D}{(\frac{2}{ζ} + a)}

B = \frac{(1 - a) (C - D)}{(\frac{2}{ζ} + a)}

(11)

This finally solves the complicated mathematical computations to

[\frac{A}{(e^{y} - a)} + \frac{B}{(e^{y} - b)} + \frac{C}{(e^{y} - 1)} + \frac{D}{(e^{y} + 1)}] d y = - \frac{μ d t}{(1 - ξ)}

I n t e g r a t i n g b o t h s i d e s

[A l n | (1 - a e^{- y}) | + B l n | (1 - b e^{- y}) | + C l n | (1 - e^{- y}) | - D l n (1 + e^{- y})] = - \frac{1}{(1 - ξ)} \int μ d t + l n η

f o r s o m e n o n - n e g a t i v e r e a l c o n s t a n t p a r a m e t e r η

O r

\frac{{| (1 - a e^{- y}) |}^{A} | {(1 - b e^{- y}) |}^{B} {| (1 - e^{- y}) |}^{C}}{{(1 + e^{- y})}^{D}} = η e^{- \int μ d t}

This transforms to the final required closed form solution:

\frac{{| (1 - a e^{- {c s c h}^{- 1} (\frac{x + ξ}{\sqrt (1 - ξ^{2})}))}) |}^{A} | {(1 - b e^{- {c s c h}^{- 1} (\frac{x + ξ}{\sqrt (1 - ξ^{2})}))}) |}^{B} {| (1 - e^{- {c s c h}^{- 1} (\frac{x + ξ}{\sqrt (1 - ξ^{2})}))}) |}^{C}}{{(1 + e^{- {c s c h}^{- 1} (\frac{x + ξ}{\sqrt (1 - ξ^{2})}))})}^{D}} = η e^{- \frac{1}{(1 - ξ)} \int μ d t}

By mathematical analysis, it is well known that

{c s c h}^{- 1} (\frac{x + ξ}{\sqrt (1 - ξ^{2})}) = l n (\frac{\sqrt (1 - ξ^{2}) + \sqrt ((1 - ξ^{2}) + {[x + ξ]}^{2})}{x + ξ})

,

x \neq - ξ

(we are allowed to assign

ξ \in [0, \infty))

Thus, one gets

\frac{{(| (1 - \frac{a (x + ξ)}{\sqrt (1 - ξ^{2}) + \sqrt ((1 - ξ^{2}) + {[x + ξ]}^{2})}) |)}^{A} {(| (1 - \frac{b (x + ξ)}{\sqrt (1 - ξ^{2}) + \sqrt ((1 - ξ^{2}) + {[x + ξ]}^{2})}) |)}^{B} {(| (1 - \frac{(x + ξ)}{\sqrt (1 - ξ^{2}) + \sqrt ((1 - ξ^{2}) + {[x + ξ]}^{2})}) |)}^{C}}{{(1 + \frac{(x + ξ)}{\sqrt (1 - ξ^{2}) + \sqrt ((1 - ξ^{2}) + {[x + ξ]}^{2})})}^{D}} = η e^{- \frac{1}{(1 - ξ)} \int μ d t}

where

a = \frac{(\frac{1}{ζ} + \sqrt{(\frac{1}{ζ^{2}}} - \frac{8}{ζ} + 4)}{2}

b = \frac{(\frac{1}{ζ} - \sqrt{(\frac{1}{ζ^{2}}} - \frac{8}{ζ} + 4)}{2}

\frac{(1 - β) (1 - ξ)}{\sqrt{1 - ξ^{2}}} = ζ

A =

\frac{2}{ζ} - \frac{(1 + \frac{2}{ζ}) C}{(\frac{2}{ζ} + a)} - \frac{(1 + \frac{2}{ζ} + 2 a) D}{(\frac{2}{ζ} + a)}

B = \frac{(1 - a) (C - D)}{(\frac{2}{ζ} + a)}

C = \frac{\frac{4}{ζ} (\frac{2}{ζ} + a) - [(1 + \frac{2}{ζ} + 2 a) - (a b - (a + b)) (\frac{2}{ζ} + a)] D}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}

D = \frac{\frac{2 b}{ζ} + a (a b - \frac{b (1 + \frac{2}{ζ})}{(\frac{2}{ζ} + a)} + a [\frac{(1 - a)}{(\frac{2}{ζ} + a)}]) [\frac{\frac{4}{ζ} (\frac{2}{ζ} + a)}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}]}{(a b + b [\frac{(1 + \frac{2}{ζ} + 2 a)}{(\frac{2}{ζ} + a)}] + a [\frac{(1 - a)}{(\frac{2}{ζ} + a)}]) + a (a b - \frac{b (1 + \frac{2}{ζ})}{(\frac{2}{ζ} + a)} + a [\frac{(1 - a)}{(\frac{2}{ζ} + a)}]) [\frac{[(1 + \frac{2}{ζ} + 2 a) - (a b - (a + b)) (\frac{2}{ζ} + a)]}{(\frac{2}{ζ}) + a + [a b - (a + b)] (\frac{2}{ζ} + a)}}

As required.

ξ

= 0, the derived solution reduces to the closed form solution of Time Varying

M / G / 1

queueing system.

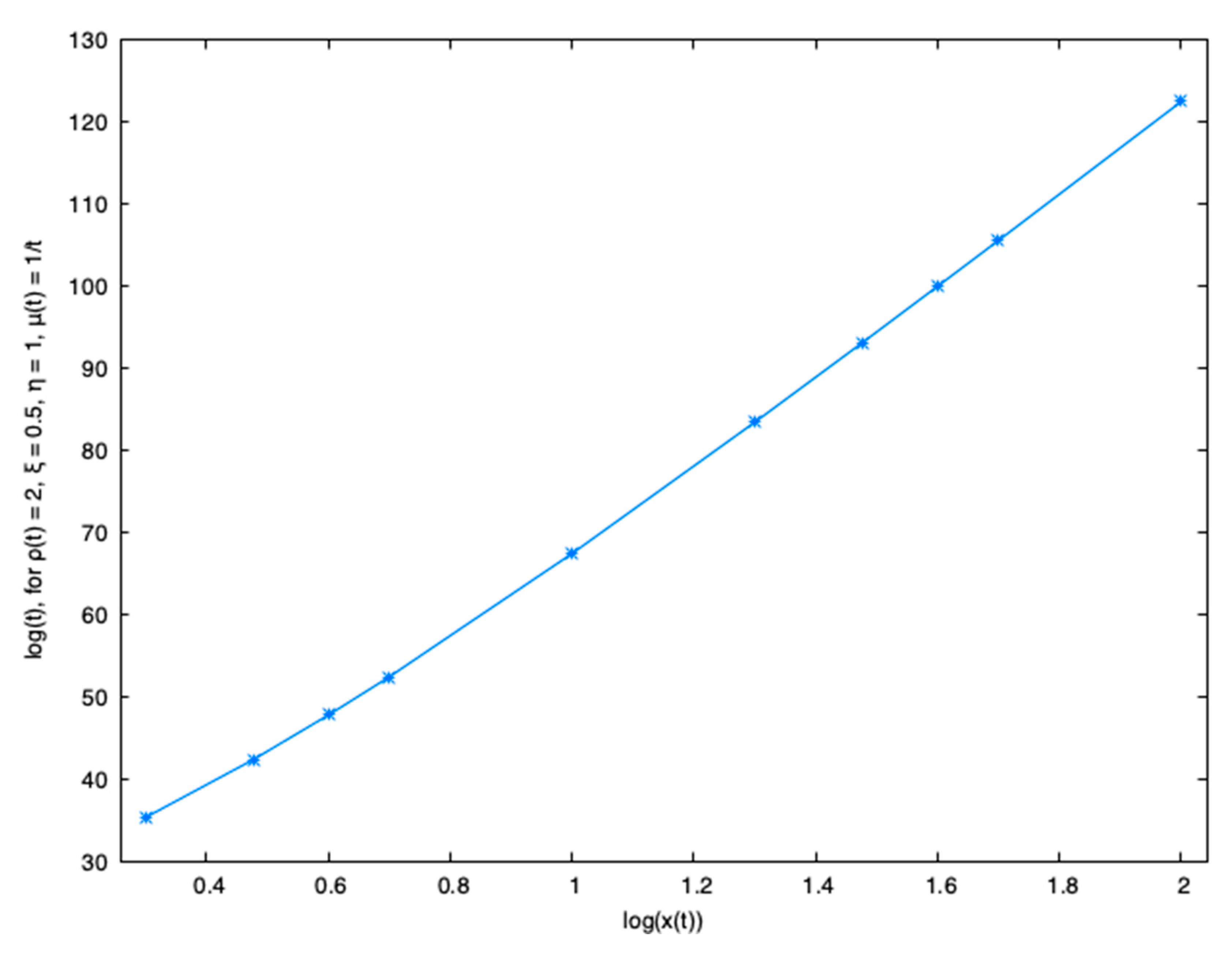
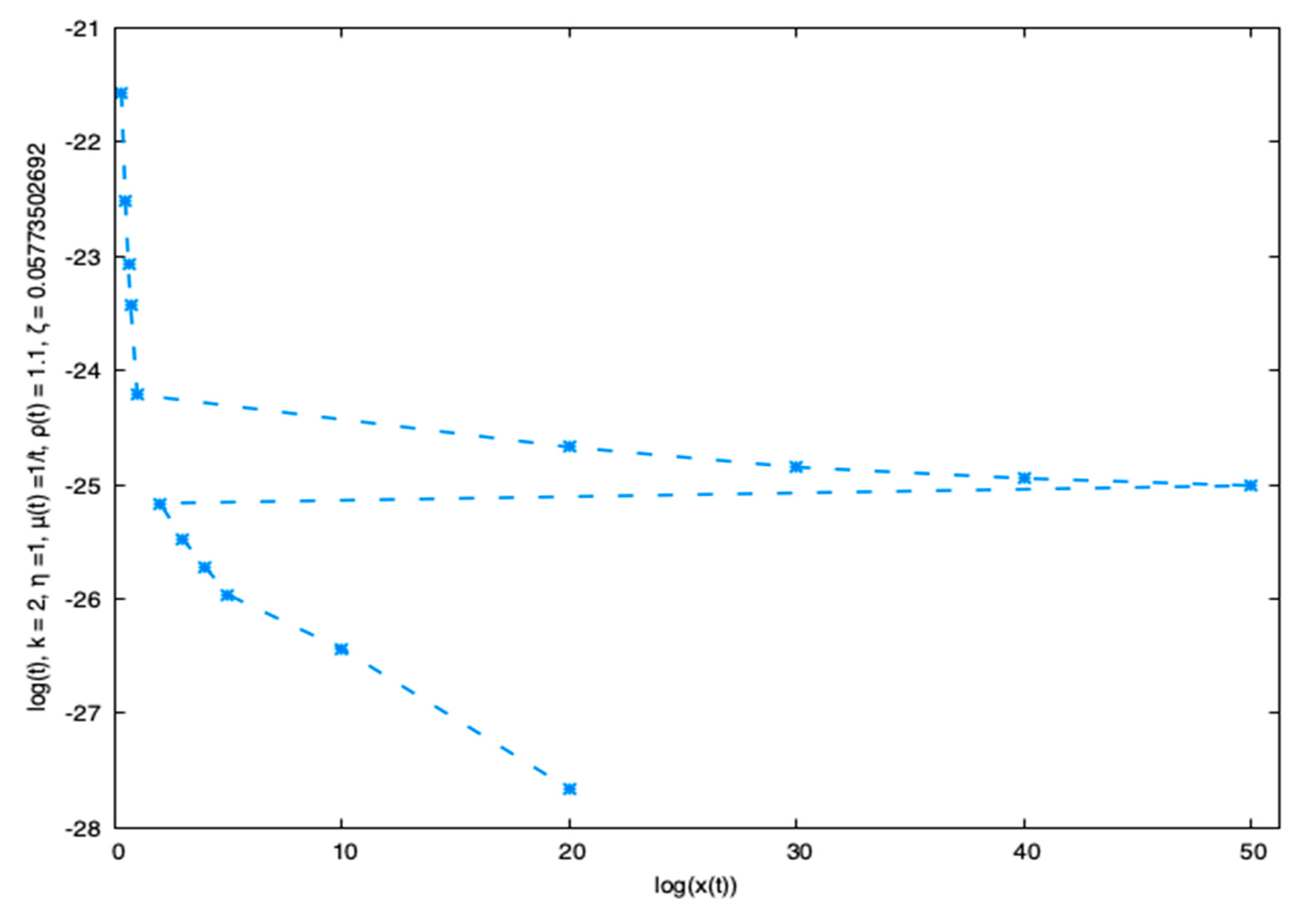
Numerical experiment

\frac{{(|(1 - \frac{a (x + ξ)}{\sqrt{1 - ξ^{2}} + \sqrt{(1 - ξ^{2}) + {[x + ξ]}^{2}}})|)}^{A} {(|(1 - \frac{b (x + ξ)}{\sqrt{1 - ξ^{2}} + \sqrt{(1 - ξ^{2}) + {[x + ξ]}^{2}}})|)}^{B} {(|(1 - \frac{(x + ξ)}{\sqrt{1 - ξ^{2}} + \sqrt{(1 - ξ^{2}) + {[x + ξ]}^{2}}})|)}^{C}}{{(1 + \frac{(x + ξ)}{\sqrt{1 - ξ^{2}} + \sqrt{(1 - ξ^{2}) + {[x + ξ]}^{2}}})}^{D}}

= η e^{- \frac{1}{(1 - ξ)} \int μ d t}

(c.f., Theorem(3.1))

Let

β = 2, ξ = 0.5 (i n s t a b i l i t y p h a s e f o r s t a b l e

M/G/1 queueuing system

), η = 1, μ (t) = \frac{1}{t}

. Hence,

ζ = 0

.2886751346,a =2.834830673, b = -6.298932288

A = 7.270191782, B = - 31.89121954, C = 107.0377732, D = - 62.65366597

\frac{{(| (1 - \frac{2.834830673 (x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{7.270191782} {(| (1 - \frac{(x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{107.0377732}}{{(1 + \frac{(x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})})}^{- 62.65366597} {(| (1 + \frac{6.298932288 (x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{31.89121954}}

= \frac{1}{t^{2}}

Hence,

t = \sqrt [\frac{{(| (1 + \frac{6.298932288 (x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{31.89121954} {(1 + \frac{(x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})})}^{- 62.65366597}}{{(| (1 - \frac{2.834830673 (x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{7.270191782} {(| (1 - \frac{(x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{107.0377732}}]

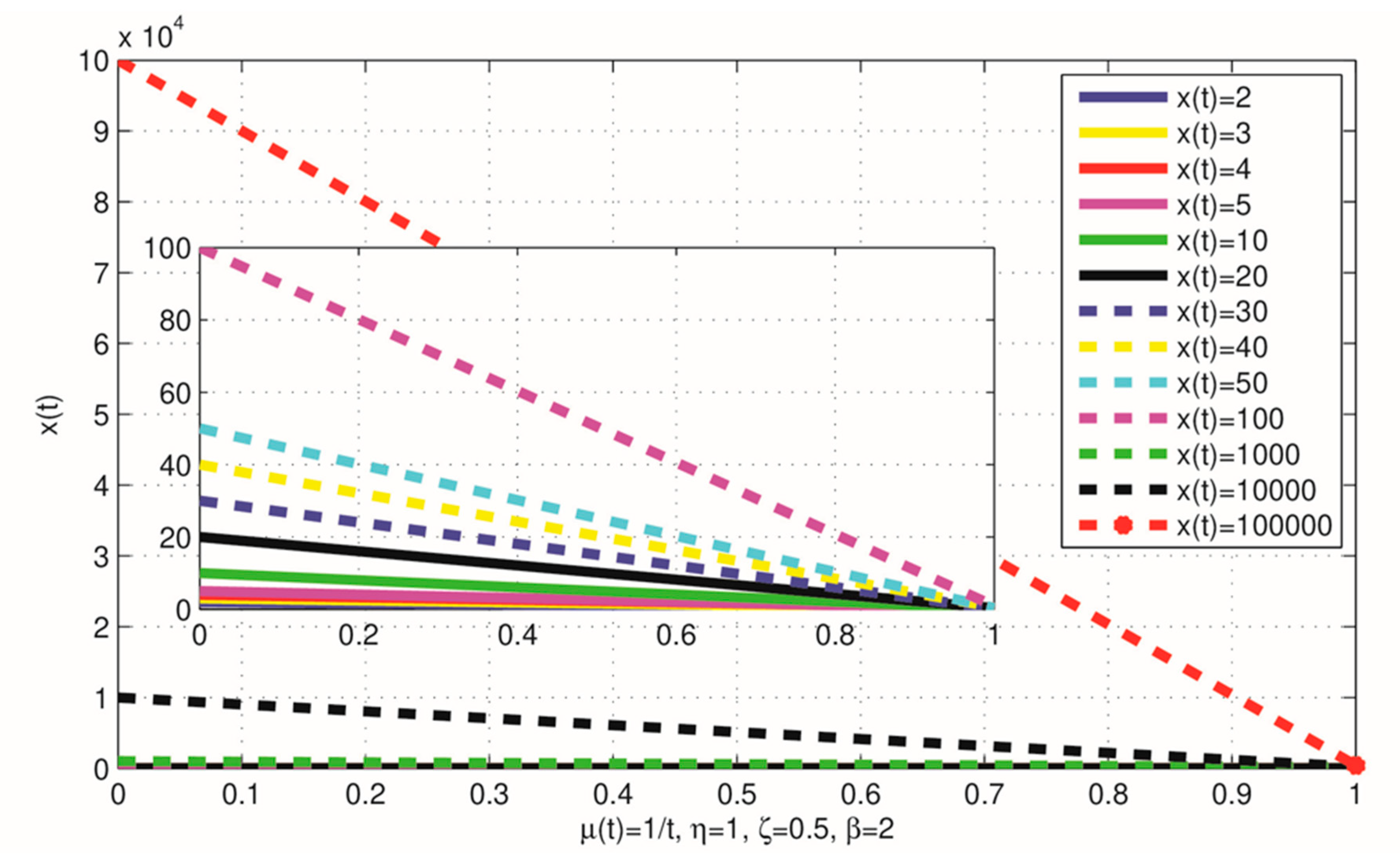
It is observed analytically that the assigned time increasing mean service rate,

μ (t) = \frac{1}{t} a n d

for sufficiently large number in the time varying

M / G / 1

queueing system, time will be increasing ultimately to approach infinity. This can be seen by Figure 2, Figure 3 and Figure 4.

Mathematically speaking, we have

{l i m}_{x (t) \to \infty} \sqrt [\frac{{(| (1 + \frac{6.298932288 (x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{31.89121954} {(1 + \frac{(x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})})}^{- 62.65366597}}{{(| (1 - \frac{2.834830673 (x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{7.270191782} {(| (1 - \frac{(x + 0.5)}{\sqrt (0.75) + \sqrt (0.75 + {[x + 0.5]}^{2})}) |)}^{107.0377732}}]

\sqrt [\frac{{(7.298932288)}^{31.89121954} {(2)}^{- 62.65366597}}{{(1.834830673)}^{7.270191782} {(0)}^{107.0377732}}]

\infty

4. Closing remarks with next phase of research

In this work, a challenging topic in queueing theory is examined; more precisely, the underlying queue’s state variable is determined. The article offers a solution to this issue by utilizing the non-stationary

M / G / 1

queue’s PSFFA analytic solution. Future work will concentrate on resolving open research issues and investigating applications of non-stationary queues in other scientific areas. The study also examines the effects of time and queueing parameters on the underlying queue’s performance.

References

x. Zhao et al, “A Queuing Network Model of a Multi-Airport System Based on Point-Wise Stationary Approximation,”, Aerospace, 2022, vol. 9, no. 7.
V.B.Iversen, “ITU Teletraffic Engineering Handbook,”, Technical University of Denmark, 2021.
I. A. Mageed, and Q. Zhang, “Solving the open problem for GI/M/1 pointwise stationary fluid flow approximation model (PSFFA) of the non-stationary D/M/1 queueing system,” electronic Journal of Computer Science and Information Technology, vol. 1, no. 9,p. 1-6, 2023.
A Mageed, D.I. Upper and Lower Bounds of the State Variable of M/G/1 PSFFA Model of the Non‐Stationary M/E_k/1 Queueing System. Preprints 2024, 2024012243. https://doi.org/10.20944/preprints202401.2243.v1.
Hu, L., Zhao, B., Zhu, J., & Jiang, Y. (2019). Two time-varying and state-dependent fluid queuing models for traffic circulation systems. European Journal of Operational Research, 275(3), 997–1019.
Roubos, A., Bhulai, S., & Koole, G. (2017). Flexible staffing for call centers with non-stationary arrival rates. Markov decision processes in practice, 487–503.

Figure 2.

Figure 3.

Figure 4.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Ismail’s Ratio Conquers New Horizons the Non-stationary M/G/1 Queue’s State Variable Closed Form Expression

Abstract

1. Introduction

2. PSFFA

3. Solving the non-stationary M / G / 1 queueing system’s PSFFA (c,f., (1))

4. Closing remarks with next phase of research

References

MDPI Initiatives

Important Links

Subscribe

3. Solving the non-stationary $M / G / 1$ queueing system’s PSFFA (c,f., (1))