2. ADM Formalism and Spacetime Foliations
At the core of the
Gravitas framework’s numerical subsystem is the
ADMDecomposition object, which plays a role analogous to the role played by the
MetricTensor object within
Gravitas’s symbolic subsystem [
1], and which allows one to represent a decomposition or “foliation” of a given differentiable Riemannian or pseudo-Riemannian manifold
into an ordered sequence of differentiable submanifolds
, where
, each of codimension-1 [
32,
33]. In the context of general relativity, the “ambient” manifold
is typically a pseudo-Riemannian/Lorentzian spacetime, and the submanifolds
are typically Riemannian spacelike hypersurfaces, ordered by a gauge-dependent “time” parameter [
34]. Mathematically, if
denotes the embedding of the submanifold
into the ambient manifold
, then the tangent bundle
on the submanifold
is included in the tangent bundle
on the ambient manifold
by means of the pushforward construction, whose cokernel/quotient is then the normal bundle
on the submanifold
, i.e. one has the following short exact sequence [
35,
36]:
In the above,
and
denote the tangent spaces of the manifolds
and
at points
and
, respectively;
designates the restriction of the tangent bundle
on the ambient manifold
to the submanifold
, i.e., more formally, it designates the pullback
of the tangent bundle
on the ambient manifold
to a corresponding vector bundle on the submanifold
;
denotes the normal space of the manifold
at the point
, i.e. the set of all vectors in the tangent space
of the ambient manifold
that are normal to every vector in the tangent space
of the submanifold
[
37]:
such that the normal bundle
is simply given by the quotient bundle:
and 0 designates the trivial (rank-0) vector bundle.
The metric tensor
on the ambient manifold
has the effect of splitting this exact sequence, thus guaranteeing that the restriction of the tangent bundle on the ambient manifold
to the submanifold
can be written as the following direct sum of tangent and normal bundles on the submanifold
:
This splitting allows one, in turn, to write the Levi-Civita connection
on the ambient manifold
as a sum of tangential and normal components, i.e. one has:
where
denotes an arbitrary tangent vector at the point
,
denotes an arbitrary vector field on the ambient manifold
,
denotes the space of smooth sections of the tangent bundle
(i.e. the space of vector fields definable on the ambient manifold
), the tangential component
denotes the orthogonal projection of the covariant derivative
onto the tangent bundle
, and the normal component
denotes the orthogonal projection of the covariant derivative
onto the normal bundle
. The induced Levi-Civita connection
on the submanifold
is then given by the orthogonal projection of the ambient Levi-Civita connection
onto the tangent bundle:
and the second fundamental form/extrinsic curvature tensor
K (a symmetric, vector-valued differential form taking values in the normal bundle
) is given by the orthogonal projection of the ambient Levi-Civita connection
onto the normal bundle [
36]:
i.e. one has, overall:
Returning now to the specific case of general relativity, in which our ambient manifold
is a Lorentzian spacetime, we proceed to define a universal “time function”
mapping each point/event to its corresponding coordinate time value; the submanifolds
are then given by the level surfaces of this universal time function, i.e:
We thus obtain a time-ordered sequence of purely spacelike hypersurfaces (each of codimension-1, with purely Riemannian signature)
which covers the entire ambient spacetime
:
If our ambient spacetime
is, moreover, globally hyperbolic, then these spacelike hypersurfaces are also strictly non-intersecting, i.e:
Henceforth, we shall denote the overall metric tensor on the ambient spacetime manifold
(assumed to be of dimension
n) by
g, and the “induced” metric tensor on the spacelike hypersurfaces
(assumed to be of dimension
) by
. Concretely,
ADMDecomposition represents such spacetime “foliations” by means of the ADM formalism first proposed by Arnowitt, Deser and Misner [
38,
39] (although the particular mathematical formulation of the
decomposition that
Gravitas uses is due to York [
40]), wherein one defines a metric tensor
on some “initial” spacelike hypersurface
, as well as the Lagrange multipliers
(a scalar field known as the
lapse function) and
(an
-dimensional vector field known as the
shift vector, with
, yet in which every such
depends upon all
n spacetime coordinates), which play the role of the gauge variables and consequently define how neighboring hypersurfaces are related to one another geometrically. More precisely, the lapse function
determines the proper time distance
between corresponding points on the spacelike hypersurfaces at coordinate time values
and
, as measured along the unit normal direction
to the hypersurface at
(i.e. the direction followed by normal observers):
whereas the shift vector (field)
determines how the spatial coordinates
get relabeled as one moves from the spacelike hypersurface at coordinate time value
to the spacelike hypersurface at coordinate time value
, i.e:
The overall line element/first fundamental form
for the ambient (spacetime)
MetricTensor object
is therefore given in terms of the components of the induced (spatial)
MetricTensor object
, the lapse function
and the components of the shift vector (field)
as:
with
ranging across all
(i.e across spatial coordinate indices only). Note that the spatial line element/first fundamental form
for the induced (spatial)
MetricTensor object
constituting the initial spacelike hypersurface of the Schwarzschild metric [
41], as developed independently by Droste [
42] (representing, for instance, an uncharged, non-rotating black hole with mass
M in Schwarzschild or spherical polar coordinates
) is given by:
whereas, for the initial spacelike hypersurface of the Kerr metric [
43] (representing, for instance, an uncharged, spinning black hole with mass
M and angular momentum
J in Boyer-Lindquist [
44] or oblate spheroidal coordinates
), the spatial line element is given instead by:
with
ranging across all
(i.e. across spatial coordinate indices only) in both cases. The corresponding
ADMDecomposition objects, including representations of both the induced/spatial and ambient/spacetime
MetricTensor objects, for the Schwarzschild and Kerr metrics are shown in
Figure 1, assuming the most general choice of gauge consisting of the lapse function
and the shift vector (field)
. By default, the most general forms of the ADM gauge variables are always assumed, and appropriate formal symbols are chosen for the various parameters of the decomposition (such as mass
M and angular momentum
J), as well as for the coordinates (such as time coordinate
t and radial coordinate
r), although these defaults may always be overridden by passing additional arguments to
ADMDecomposition, as illustrated in
Figure 2 for the case of modified shift vectors
(for Schwarzschild) and
(for Kerr).
Note that several other Cauchy surface geometries are built into
ADMDecomposition’s small (though continually growing) library of initial spacelike hypersurface configurations, including Cauchy initial data for the Reissner-Nordström metric [
45,
46], as developed independently by Weyl [
47] and Jeffery [
48] (representing, for instance, a charged, non-rotating black hole with mass
M and electric charge
Q in Schwarzschild or spherical polar coordinates
and the Kerr-Newman metric [
49,
50] (representing, for instance, a charged, spinning black hole with mass
M, angular momentum
J and electric charge
Q in Boyer-Lindquist or oblate spheroidal coordinates
), with spatial line elements given by:
and:
respectively, as shown in
Figure 3. Cosmological Cauchy initial data is also supported, such as for the Friedmann-Lemaître-Robertson-Walker or FLRW metric [
51,
52,
53,
54] (representing, for instance, a perfectly homogeneous and isotropic universe with scale factor
and curvature
k in spherical polar coordinates
), with spatial line element given by:
as shown in
Figure 4, both for the default choice of gauge with general lapse function
and general shift vector (field)
, and for the trivial choice of gauge with lapse function identically equal to 1 (i.e.
) and shift vector (field) identically equal to zero (i.e.
). In the above, as before,
and
represent spatial indices, and therefore range across
only.
In all that follows, we will use a bracketed “3” to indicate that a given object is restricted to spacelike hypersurfaces, with a bracketed “4” indicating instead that a given object is defined over the entire ambient spacetime (for instance,
denotes the covariant derivative operator on spacelike hypersurfaces, whose corresponding Christoffel symbols
are defined in terms of derivatives of the induced/spatial metric tensor
, while
denotes the covariant derivative operator on the ambient spacetime, whose corresponding Christoffel symbols
are defined in terms of derivatives of the overall spacetime metric tensor
); note that we use these particular numbers purely for illustrative purposes (since the formalism is often referred to as “
formalism”) - the objects themselves are defined within
Gravitas for arbitrary
n-dimensional spacetimes, which are then foliated into
-dimensional spacelike hypersurfaces. The future-pointing, timelike unit vector
that is normal to each spacelike hypersurface can now be computed as the spacetime contravariant derivative
of the distinguished time coordinate
t [
34]:
whereas the “time vector”
determines how corresponding points on neighboring hypersurfaces are related (and so, in particular, will differ from the normal vector
if the corresponding observer does not move in a normal direction to the hypersurfaces, which in turn corresponds to the case of a non-vanishing shift vector
):
In both of the above,
range across all
(i.e. across all spacetime coordinate indices).
Figure 5 and
Figure 6 show the components of the future-pointing unit normal vector
and of the future-pointing unit “time vector”
, computed directly from the respective
ADMDecomposition objects for the Schwarzschild and Kerr metrics, assuming a fully generic choice of gauge with lapse function
and shift vector
in both cases. Recall from the discussion above that the second fundamental form/extrinsic curvature tensor
K is simply the symmetric, vector-valued differential form given by the orthogonal projection ⊥ of the ambient/spacetime Levi-Civita connection
onto the normal bundle; we can express this in component form by taking the Lie derivative
of the spatial metric tensor
in the normal direction
[
55]:
i.e., in expanded form:
where
range across all
(i.e. across spatial coordinate indices only), as shown in
Figure 7 for the case of
ExtrinsicCurvatureTensor objects computed directly from the
ADMDecomposition objects for the Schwarzschild and Kerr metrics, assuming again a fully generic choice of gauge with lapse function
and shift vector
. Note that both the shift vector
and the extrinsic curvature tensor
are purely spatial objects, and so their indices are raised and lowered using the spatial metric tensor
rather than full spacetime metric tensor
, i.e:
for the case of the rank-1 shift vector/covector (field)
, and:
for the case of the rank-2 extrinsic curvature tensor (field)
K. Their covariant derivatives
(i.e. their derivatives along tangent vectors) are therefore represented in terms of the coefficients of the induced/spatial Levi-Civita connection
, i.e. the induced/spatial Christoffel symbols
, which are themselves represented in terms of partial derivatives of the spatial metric tensor
:
namely:
for the case of the rank-1 shift vector/covector (field)
, and:
for the case of the rank-2 extrinsic curvature tensor (field)
K. This is demonstrated in
Figure 8, in which all covariant derivatives of the
ExtrinsicCurvatureTensor object in lowered-index/covariant form (i.e.
, the default case), as well as all covariant derivatives of the
ExtrinsicCurvatureTensor object in raised-index/contravariant form (i.e.
) are computed for the
ADMDecomposition objects for the Schwarzschild and Kerr metrics, respectively, assuming generic gauge choice.
As stated previously, the orthogonal projection ⊤ of the ambient/spacetime Levi-Civita connection
onto the tangent bundle yields the induced/spatial Levi-Civita connection
, while the orthogonal projection ⊥ of the ambient/spacetime Levi-Civita connection
onto the normal bundle yields the symmetric (vector-valued) second fundamental form/extrinsic curvature tensor
K. The statement that this is necessarily the case is often referred to as the Gauss relation [
56], which asserts the following general relationship between (projections of) the ambient/spacetime Riemann tensor
and the induced/spatial Riemann tensor
(assuming that, as before, that
denotes the ambient/spacetime manifold and
denotes the induced/spatial submanifold):
or, in explicit (component-based) form:
where
designates the orthogonal projector, i.e. the projection operator in the normal direction
:
with
being the identity tensor (i.e. the Kronecker delta function). In the above,
range across all
(i.e. across all spacetime coordinate indices), while
range across all
(i.e. across spatial coordinate indices only), with
being the components of the ambient/spacetime Riemann tensor:
where
here ranges across all spacetime coordinate indices
,
being the components of the induced/spatial Riemann tensor:
where
here ranges across spatial coordinate indices
only, and with
being the ambient/spacetime Christoffel symbols, represented in terms of partial derivatives of the overall spacetime metric tensor
:
The Gauss equations necessarily hold identically for any
ADMDecomposition object computed directly from an (initial) spatial
MetricTensor object in the manner described previously, as illustrated in
Figure 9 for the cases of the Schwarzschild metric (representing, for instance, an uncharged, non-rotating black hole with mass
M in Schwarzschild or spherical polar coordinates
) and the Kerr metric (representing, for instance, an uncharged, spinning black hole with mass
M and angular momentum
J in Boyer-Lindquist or oblate spheroidal coordinates
), assuming a restricted choice of gauge consisting of the lapse function
and the modified shift vectors
(for Schwarzschild) and
(for Kerr). On the other hand, the Codazzi-Mainardi relation [
36,
56] asserts the following general relationship between (orthogonal projections of) the ambient/spacetime Ricci tensor and the covariant derivatives of the second fundamental form/extrinsic curvature tensor:
or, in explicit (component-based) form:
i.e., in expanded form:
with
ranging across all
(i.e. across all spacetime coordinate indices), while
range across all
(i.e. across spatial coordinate indices only). In the above,
designates the ambient/spacetime Ricci tensor, obtained through appropriate contraction of the ambient/spacetime Riemann tensor
(i.e.
), and
K designates the trace of the extrinsic curvature tensor
(i.e.
). Just as for the Gauss equations, the Codazzi-Mainardi equations also necessarily hold identically for any
ADMDecomposition object computed directly from an (initial) spatial
MetricTensor object in this way, as demonstrated in
Figure 10 for the cases of the Schwarzschild and Kerr metrics with a restricted choice of gauge consisting, as before, of the lapse function
and the modified shift vectors
(for Schwarzschild) and
(for Kerr). In some sense, the Gauss and Codazzi-Mainardi equations therefore represent a set of geometrical consistency conditions that must necessarily be satisfied in order for the hypersurfaces in the foliation to “plumb together” in some appropriate way.
In much the same vein as the Gauss and Codazzi-Mainardi equations above, it is also possible to relate the components of the ambient/spacetime Ricci tensor
and the induced/spatial Ricci tensor
; by making the time derivative of the extrinsic curvature tensor
the subject of these equations, one can then proceed to formulate them as a system of time evolution equations for the components of the extrinsic curvature tensor
(regarded here as the conjugate momenta of the components of the spatial metric tensor
, which are in turn regarded here as the dynamical variables of the theory):
i.e., in expanded form:
with
ranging across all
(i.e. across spatial coordinate indices only). Since these are purely geometrical identities relating components of
to components of
, these evolution equations necessarily hold identically for any
ADMDecomposition object computed from an (initial) spatial
MetricTensor object in the usual way, as shown in
Figure 11 for the cases of the Schwarzschild and Kerr metrics with the same restricted choice of gauge as before, consisting of the lapse function
and the modified shift vectors
(for Schwarzschild) and
(for Kerr). However, as we shall see shortly, once the Einstein field equations are used to replace the ambient/spacetime Ricci tensor terms
with stress-energy tensor terms
, these purely geometrical relations instead become bona fide evolution equations, describing how the components of the extrinsic curvature tensor
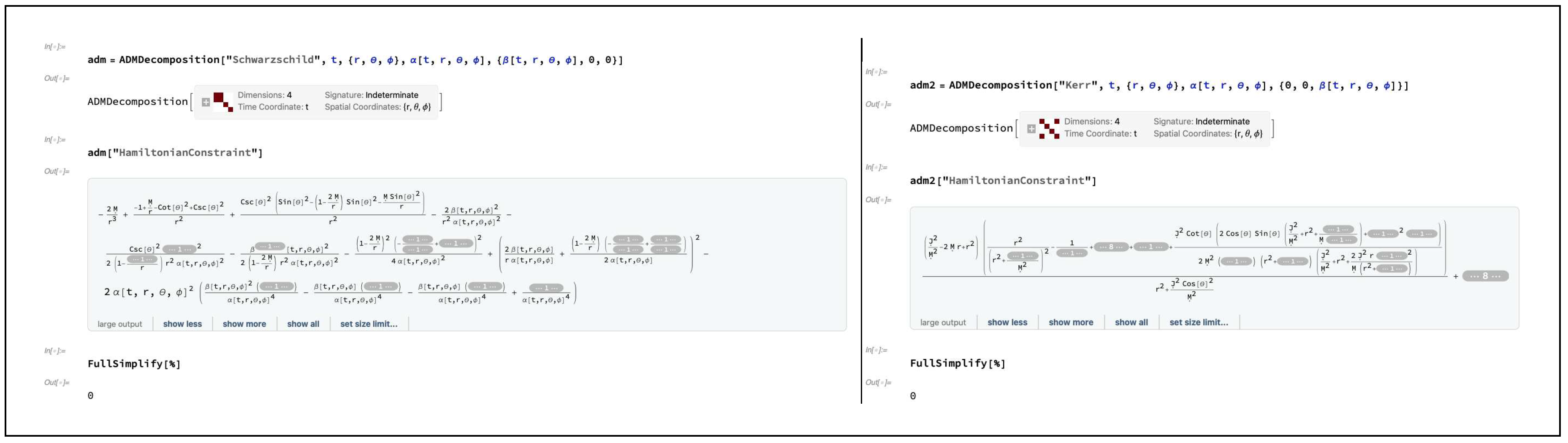
on spacelike hypersurfaces change as one moves forwards (or backwards) in time. By taking appropriate contractions of the Gauss equations, we also obtain a timelike projection of the contracted Bianchi identities, known as the Hamiltonian constraint
:
or, more succinctly:
with
ranging across all
(i.e. across spatial coordinate indices only), where we have used the definition of the ambient/spacetime Einstein tensor
:
with
here ranging across all
(i.e. across all spacetime coordinate indices), and where
and
denote the induced/spatial and ambient/spacetime Ricci scalars:
respectively. Likewise, one can obtain the corresponding spacelike projections of the contracted Bianchi identities by taking appropriate contractions of the Codazzi-Mainardi equations, thus yielding the so-called momentum constraints
(represented here in covector form):
i.e., in expanded form:
which, upon simplification again using the ambient/spacetime Einstein tensor
, become:
with
here ranging across all
(i.e. across spatial coordinate indices only). Just as with the evolution equations above, these forms of the Hamiltonian
and momentum
constraints are purely geometrical identities, and therefore vanish identically for any
ADMDecomposition object obtained from an (initial) spatial
MetricTensor object in the same way, as illustrated in
Figure 12 and
Figure 13, again for the cases of the Schwarzschild and Kerr metrics with modified shift vectors
and
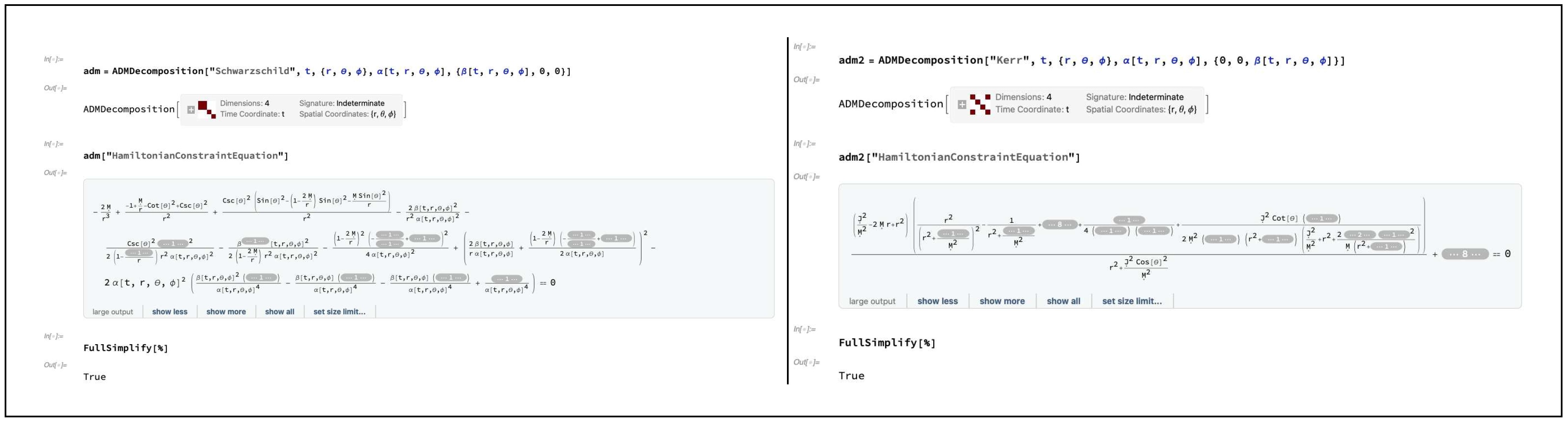
, respectively. The equations asserting that the Hamiltonian and momentum constraints vanish identically, i.e. that
and
, are consequently referred to as the Hamiltonian and momentum constraint equations, and they can be computed and verified directly within
Gravitas, as shown in
Figure 14 and
Figure 15. Much like the evolution equations, once the Einstein field equations are applied and used to transform the ambient/spacetime Einstein tensor terms
into stress-energy tensor terms
, the Hamiltonian and momentum constraint equations will cease to be purely geometrical identities and will instead become bona fide physical constraints on the evolution and choice of gauge. Indeed, in (for instance) the
-dimensional case, the ten independent Einstein field equations may be projected in the space-space directions (thus yielding the six evolution equations), the time-time direction (thus yielding the one Hamiltonian constraint equation) and the time-space/space-time directions (thus yielding the three momentum constraint equations), with the latter two corresponding to the four redundant degrees of freedom arising from the contracted Bianchi identities.
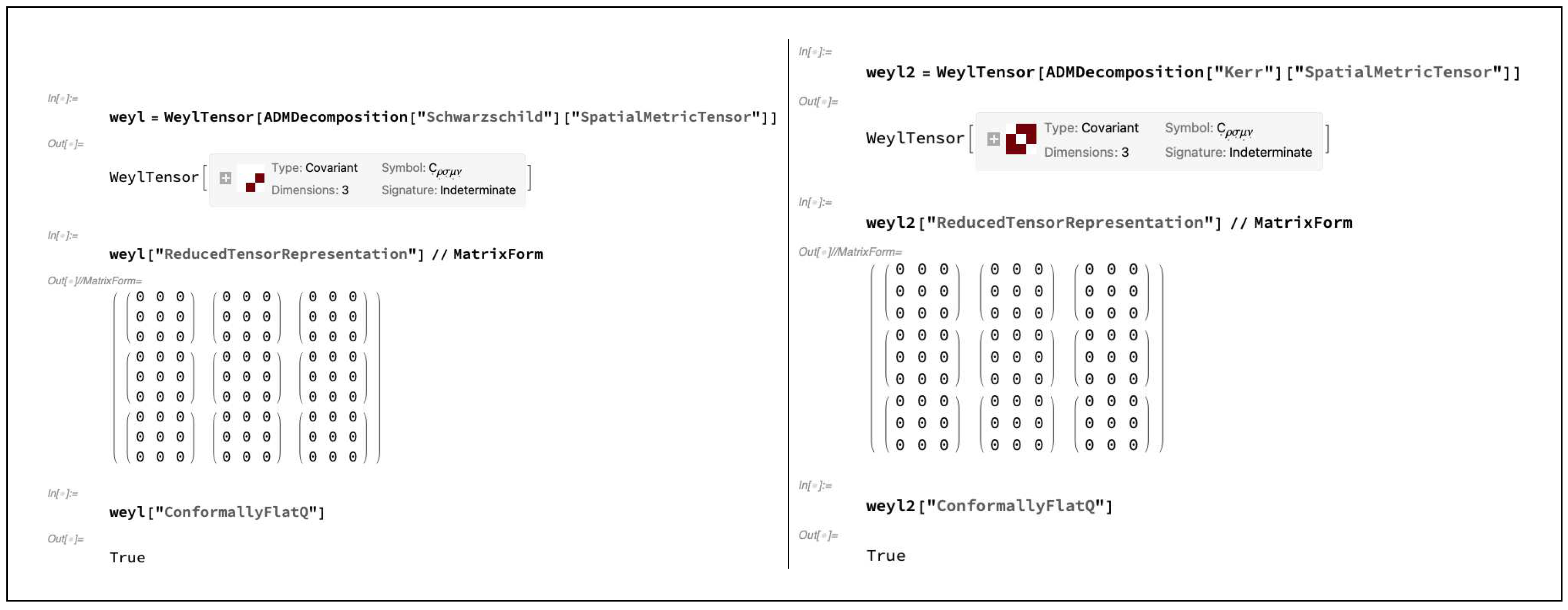
In all dimensions
, the vanishing of all components of the unique, trace-free, rank-4 Weyl tensor
[
57], obtained by subtracting out all trace components (i.e. all Ricci tensor components
) from the full Riemann tensor
via the Ricci decomposition theorem [
58]:
is both a necessary and sufficient condition for the underlying manifold
to be conformally-flat (by the Weyl-Schouten theorem [
59]), since the Weyl tensor
is invariant under all conformal transformations of the form
with real conformal factor
; the Weyl tensor
is also significant from a physical standpoint, since it governs the propagation of gravitational radiation within vacuum spacetimes. However, the fact that the Weyl tensor
vanishes identically in dimension
, as demonstrated in
Figure 16 for the cases of spatial
MetricTensor objects extracted from
ADMDecomposition objects for the Schwarzschild and Kerr metrics (with the most general choice of gauge, although this makes no difference to the spacelike hypersurface geometry) presents problems in the case of
decomposition and the ADM formalism, since it makes it more difficult to determine whether a given 3-dimensional spacelike hypersurface is conformally-flat (or, indeed, to extract gravitational wave data from 3-dimensional spacelike hypersurfaces directly); indeed, as seen here, the
WeylTensor objects will (incorrectly) report both manifolds to be conformally-flat in these cases. To this end, it is instructive instead to consider the rank-3 Cotton tensor
[
60], defined by:
i.e., in expanded form:
for which vanishing of all components
is both a necessary and sufficient condition for conformal-flatness in dimension
(in dimensions
, the vanishing of the Cotton tensor
is a necessary but not sufficient condition).
Figure 17 illustrates the use of the
CottonTensor function in
Gravitas to demonstrate that the spatial
MetricTensor object extracted from the
ADMDecomposition object is conformally-flat for the case of the Schwarzschild metric, but not for the Kerr metric (since it is provable that there do not exist any conformally-flat spatial slices of the Kerr metric [
61]). In fact, in the particular case of dimension
, one can simplify the Cotton tensor
even further by using the Hodge dual operation ★ in the associated Grassmann algebra to reduce the rank-3 Cotton tensor to the rank-2 Cotton-York tensor (density)
, defined by:
i.e., in expanded form:
where
designates the totally-antisymmetric Levi-Civita symbol of rank-3, and therefore the Cotton-York tensor (density)
is definable
only in three dimensions (in which, like the full Cotton tensor
, the vanishing of all components of the Cotton-York tensor
is both a necessary and sufficient condition for conformal-flatness).
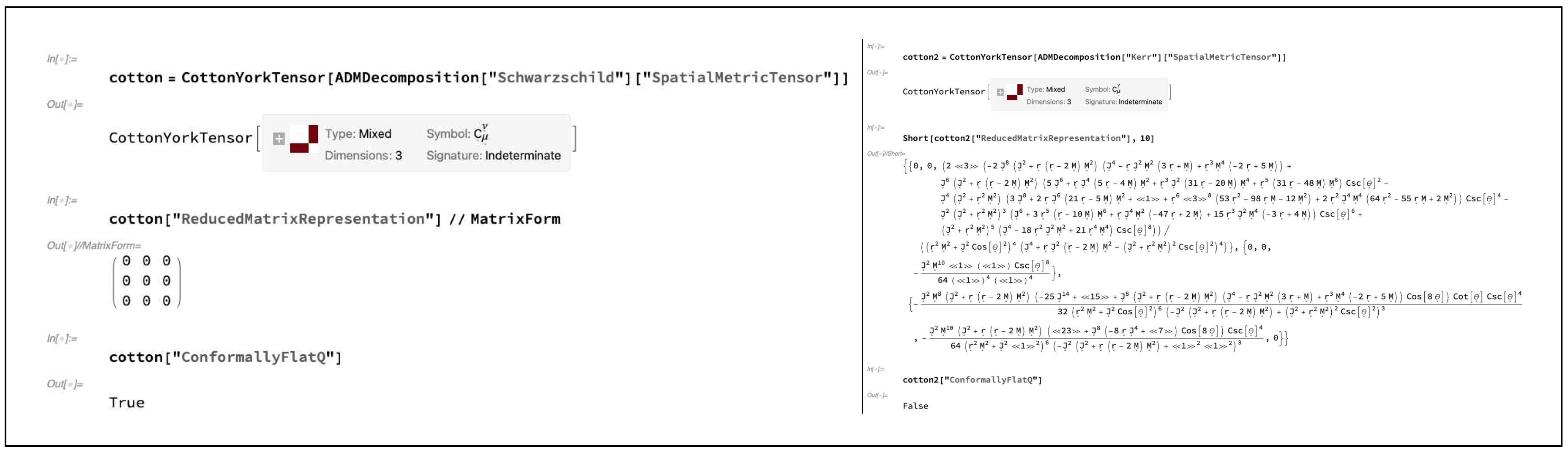
Figure 18 illustrates the use of the
CottonYorkTensor function in
Gravitas to demonstrate, once again, that the spatial
MetricTensor object extracted from the
ADMDecomposition object is conformally-flat in the Schwarzschild case but not in the Kerr case. The geometrical significance of the Cotton tensor
lies in its very simple transformation law under conformal rescalings of the form
with
, namely:
Figure 1.
On the left, the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , represented by its induced (spatial) and ambient (spacetime) MetricTensor objects in explicit covariant matrix form. On the right, the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , represented by its induced (spatial) and ambient (spacetime) MetricTensor objects in explicit covariant matrix form.
Figure 1.
On the left, the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , represented by its induced (spatial) and ambient (spacetime) MetricTensor objects in explicit covariant matrix form. On the right, the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , represented by its induced (spatial) and ambient (spacetime) MetricTensor objects in explicit covariant matrix form.
Figure 2.
On the left, the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1) in modified Schwarzschild or spherical polar coordinates , with lapse function and modified shift vector . On the right, the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum ) in modified Boyer-Lindquist or oblate spheroidal coordinates , with lapse function and modified shift vector .
Figure 2.
On the left, the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1) in modified Schwarzschild or spherical polar coordinates , with lapse function and modified shift vector . On the right, the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum ) in modified Boyer-Lindquist or oblate spheroidal coordinates , with lapse function and modified shift vector .
Figure 3.
On the left, the ADMDecomposition object for a Reissner-Nordström geometry (representing, for instance, a charged, non-rotating black hole with mass M and electric charge Q in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector . On the right, the ADMDecomposition object for a Kerr-Newman geometry (representing, for instance, a charged, spinning black hole with mass M, angular momentum J and electric charge Q in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector .
Figure 3.
On the left, the ADMDecomposition object for a Reissner-Nordström geometry (representing, for instance, a charged, non-rotating black hole with mass M and electric charge Q in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector . On the right, the ADMDecomposition object for a Kerr-Newman geometry (representing, for instance, a charged, spinning black hole with mass M, angular momentum J and electric charge Q in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector .
Figure 4.
On the left, the ADMDecomposition object for a Friedmann-Lemaître-Robertson-Walker or FLRW geometry (representing, for instance, a perfectly homogeneous and isotropic universe with scale factor and curvature k in spherical polar coordinates ) with lapse function and shift vector . On the right, the ADMDecomposition object for a Friedmann-Lemaître-Robertson-Walker or FLRW geometry (representing, for instance, a perfectly homogeneous and isotropic universe with scale factor and curvature k in modified spherical polar coordinates ) with trivial lapse function 1 and trivial shift vector .
Figure 4.
On the left, the ADMDecomposition object for a Friedmann-Lemaître-Robertson-Walker or FLRW geometry (representing, for instance, a perfectly homogeneous and isotropic universe with scale factor and curvature k in spherical polar coordinates ) with lapse function and shift vector . On the right, the ADMDecomposition object for a Friedmann-Lemaître-Robertson-Walker or FLRW geometry (representing, for instance, a perfectly homogeneous and isotropic universe with scale factor and curvature k in modified spherical polar coordinates ) with trivial lapse function 1 and trivial shift vector .
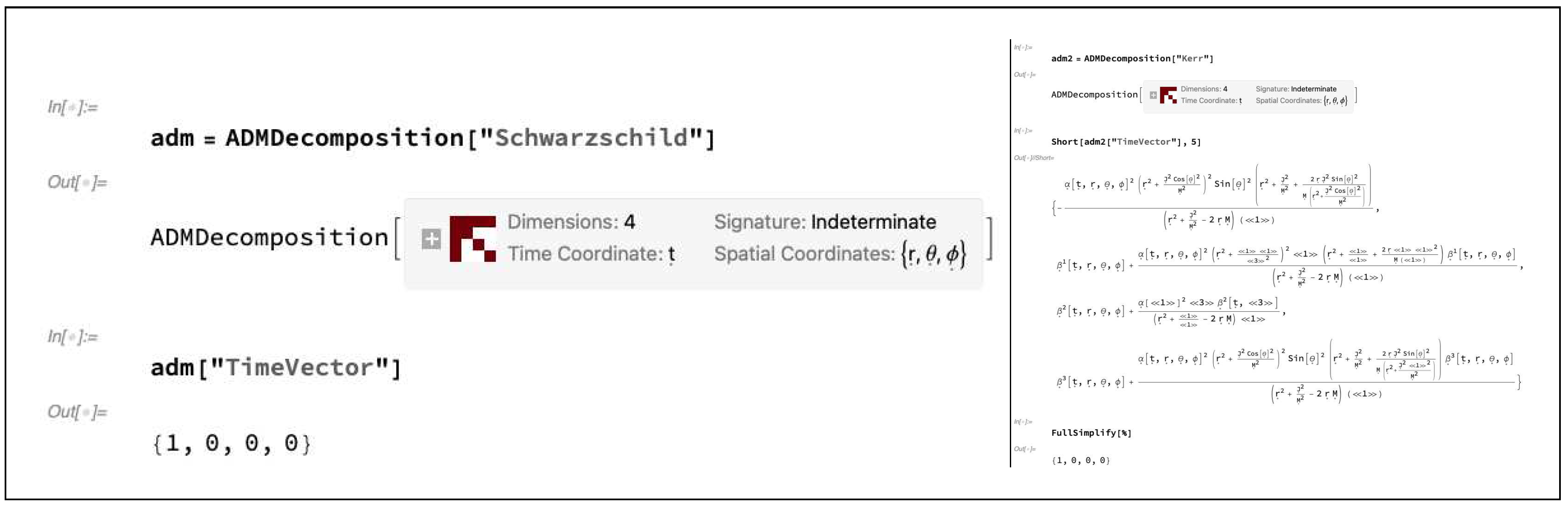
Figure 5.
On the left, the future-pointing, timelike unit vector normal to each spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector . On the right, the future-pointing, timelike unit vector normal to each spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector .
Figure 5.
On the left, the future-pointing, timelike unit vector normal to each spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector . On the right, the future-pointing, timelike unit vector normal to each spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector .
Figure 6.
On the left, the future-pointing unit “time vector” for each spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector . On the right, the future-pointing unit “time vector” for each spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector .
Figure 6.
On the left, the future-pointing unit “time vector” for each spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector . On the right, the future-pointing unit “time vector” for each spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector .
Figure 7.
On the left, the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , in explicit covariant matrix form, with both indices lowered/covariant (default). On the right, the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , in explicit contravariant matrix form, with both indices raised/contravariant.
Figure 7.
On the left, the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , in explicit covariant matrix form, with both indices lowered/covariant (default). On the right, the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , in explicit contravariant matrix form, with both indices raised/contravariant.
Figure 8.
On the left, the association of all covariant derivatives of the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , with both indices lowered/covariant (default). On the right, the association of all covariant derivatives of the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , with both indices raised/contravariant.
Figure 8.
On the left, the association of all covariant derivatives of the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , with both indices lowered/covariant (default). On the right, the association of all covariant derivatives of the ExtrinsicCurvatureTensor object computed from the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , with both indices raised/contravariant.
Figure 9.
On the left, the list of Gauss equations asserting the relationship between the components of the ambient/spacetime Riemann tensor and the components of the induced/spatial Riemann tensor for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically. On the right, the list of Gauss equations asserting the relationship between the components of the ambient/spacetime Riemann tensor and the components of the induced/spatial Riemann tensor for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically.
Figure 9.
On the left, the list of Gauss equations asserting the relationship between the components of the ambient/spacetime Riemann tensor and the components of the induced/spatial Riemann tensor for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically. On the right, the list of Gauss equations asserting the relationship between the components of the ambient/spacetime Riemann tensor and the components of the induced/spatial Riemann tensor for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically.

Figure 10.
On the left, the list of Codazzi-Mainardi equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the covariant derivatives of the extrinsic curvature tensor for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically. On the right, the list of Codazzi-Mainardi equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the covariant derivatives of the extrinsic curvature tensor for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically.
Figure 10.
On the left, the list of Codazzi-Mainardi equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the covariant derivatives of the extrinsic curvature tensor for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically. On the right, the list of Codazzi-Mainardi equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the covariant derivatives of the extrinsic curvature tensor for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically.
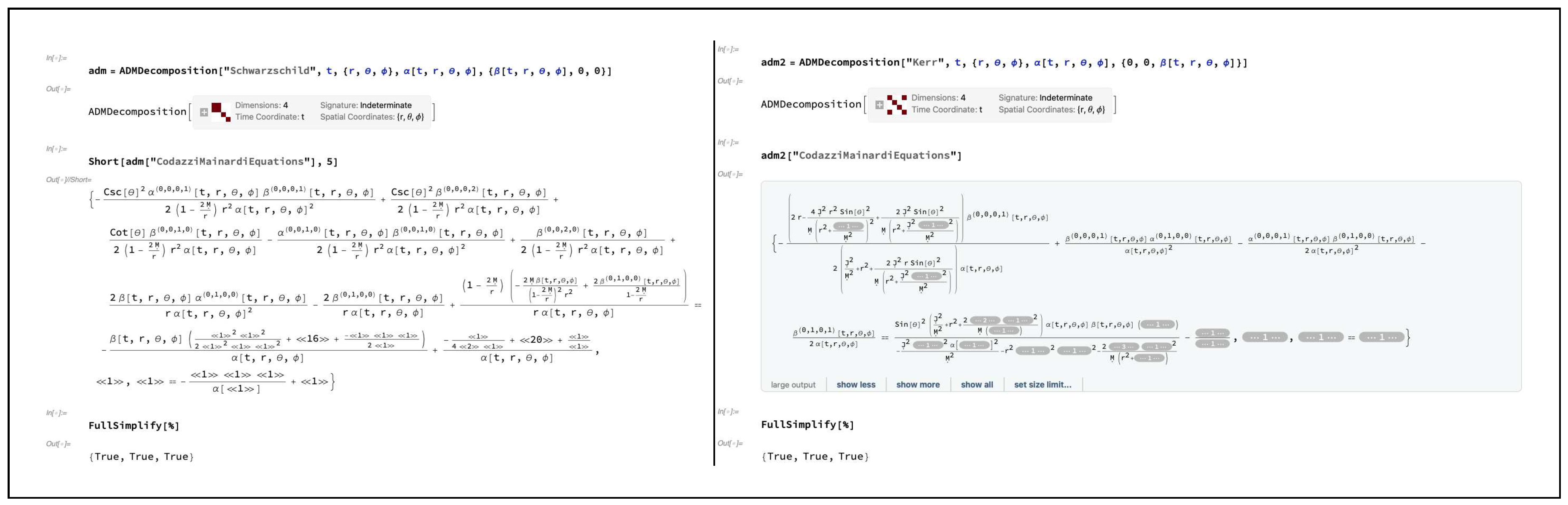
Figure 11.
On the left, the list of evolution equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the components of the induced/spatial Ricci tensor for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically. On the right, the list of evolution equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the components of the induced/spatial Ricci tensor for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically.
Figure 11.
On the left, the list of evolution equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the components of the induced/spatial Ricci tensor for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically. On the right, the list of evolution equations asserting the relationship between the components of the ambient/spacetime Ricci tensor and the components of the induced/spatial Ricci tensor for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all hold identically.
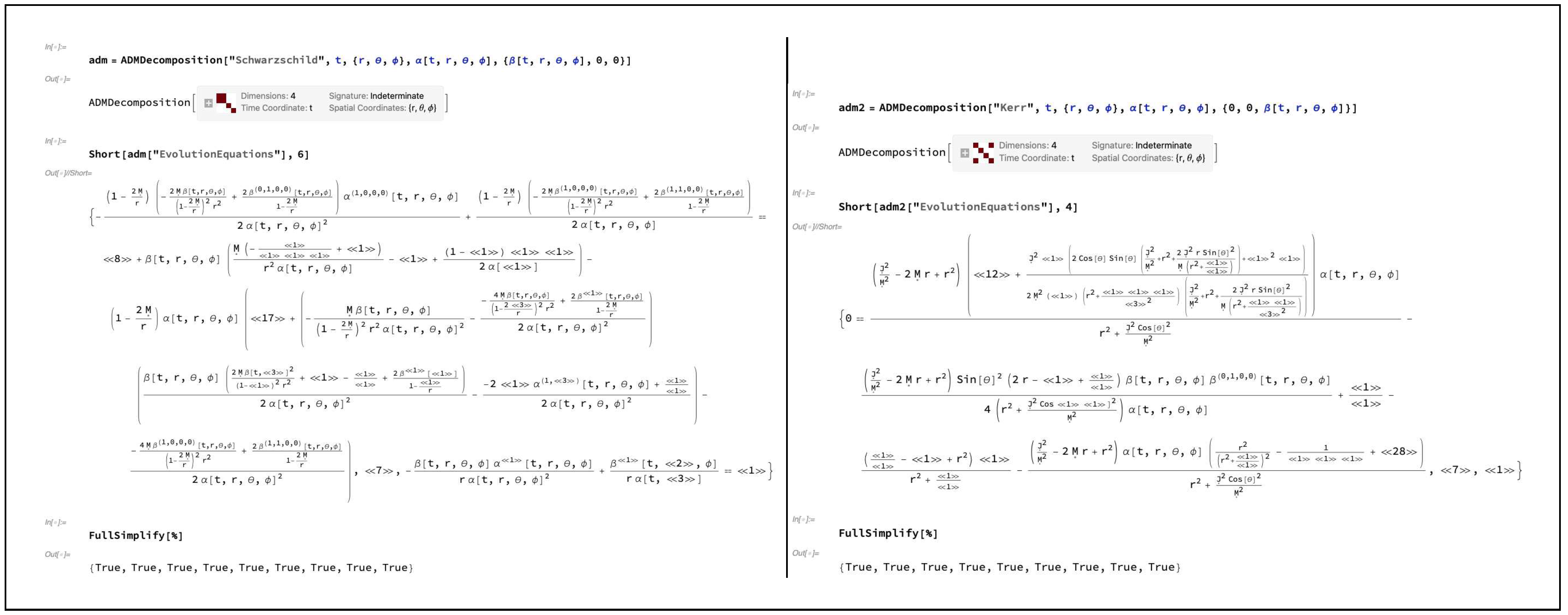
Figure 12.
On the left, the value of the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that it vanishes identically. On the right, the value of the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that it vanishes identically.
Figure 12.
On the left, the value of the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that it vanishes identically. On the right, the value of the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that it vanishes identically.
Figure 13.
On the left, the values of the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all vanish identically. On the right, the values of the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all vanish identically.
Figure 13.
On the left, the values of the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , together with a verification that they all vanish identically. On the right, the values of the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector , together with a verification that they all vanish identically.
Figure 14.
On the left, the condition required to guarantee that the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector vanishes, together with a verification that it holds identically. On the right, the condition required to guarantee that the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector vanishes, together with a verification that it holds identically.
Figure 14.
On the left, the condition required to guarantee that the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector vanishes, together with a verification that it holds identically. On the right, the condition required to guarantee that the Hamiltonian constraint obtained from contracting the Gauss equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector vanishes, together with a verification that it holds identically.
Figure 15.
On the left, the conditions required to guarantee that the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector vanish, together with a verification that they all hold identically. On the right, the conditions required to guarantee that the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector vanish, together with a verification that they all hold identically.
Figure 15.
On the left, the conditions required to guarantee that the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector vanish, together with a verification that they all hold identically. On the right, the conditions required to guarantee that the momentum constraints obtained from contracting the Codazzi-Mainardi equations for the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector vanish, together with a verification that they all hold identically.

Figure 16.
On the left, the WeylTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , illustrating that the Weyl tensor vanishes identically. On the right, the WeylTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , illustrating that the Weyl tensor vanishes identically.
Figure 16.
On the left, the WeylTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , illustrating that the Weyl tensor vanishes identically. On the right, the WeylTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , illustrating that the Weyl tensor vanishes identically.
Figure 17.
On the left, the CottonTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , illustrating that the hypersurface is conformally-flat. On the right, the CottonTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , illustrating that the hypersurface is not conformally-flat.
Figure 17.
On the left, the CottonTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , illustrating that the hypersurface is conformally-flat. On the right, the CottonTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , illustrating that the hypersurface is not conformally-flat.
Figure 18.
On the left, the CottonYorkTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , illustrating that the hypersurface is conformally-flat. On the right, the CottonYorkTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , illustrating that the hypersurface is not conformally-flat.
Figure 18.
On the left, the CottonYorkTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and shift vector , illustrating that the hypersurface is conformally-flat. On the right, the CottonYorkTensor object for the (initial) spacelike hypersurface of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and shift vector , illustrating that the hypersurface is not conformally-flat.
Figure 19.
On the left, the maximal slicing gauge condition on the lapse function of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the maximal slicing gauge condition on the lapse function of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 19.
On the left, the maximal slicing gauge condition on the lapse function of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the maximal slicing gauge condition on the lapse function of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 20.
On the left, the harmonic slicing gauge condition on the lapse function of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the harmonic slicing gauge condition on the lapse function of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole of mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 20.
On the left, the harmonic slicing gauge condition on the lapse function of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the harmonic slicing gauge condition on the lapse function of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole of mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 21.
On the left, the slicing gauge condition on the lapse function of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the slicing gauge condition on the lapse function of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole of mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 21.
On the left, the slicing gauge condition on the lapse function of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the slicing gauge condition on the lapse function of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole of mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 22.
On the left, the harmonic coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the harmonic coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 22.
On the left, the harmonic coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the harmonic coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 23.
On the left, the minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 23.
On the left, the minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 24.
On the left, the pseudo-minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the pseudo-minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 24.
On the left, the pseudo-minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector . On the right, the pseudo-minimal distortion coordinate gauge conditions on the shift vector of the ADMDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with lapse function and modified shift vector .
Figure 25.
On the left, the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is a non-exact solution to the vacuum ADM evolution equations, with eight additional field equations required. On the right, the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is a non-exact solution to the vacuum ADM evolution equations, with eight additional field equations required.
Figure 25.
On the left, the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is a non-exact solution to the vacuum ADM evolution equations, with eight additional field equations required. On the right, the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is a non-exact solution to the vacuum ADM evolution equations, with eight additional field equations required.

Figure 26.
On the left, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations. On the right, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations.
Figure 26.
On the left, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations. On the right, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations.

Figure 27.
On the left, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , illustrating that it does not vanish identically. On the right, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , illustrating that it does not vanish identically.
Figure 27.
On the left, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , illustrating that it does not vanish identically. On the right, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , illustrating that it does not vanish identically.
Figure 28.
On the left, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , illustrating that they do not vanish identically. On the right, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , illustrating that they do not vanish identically.
Figure 28.
On the left, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with zero cosmological constant , illustrating that they do not vanish identically. On the right, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with lapse function and modified shift vector , with non-zero cosmological constant , illustrating that they do not vanish identically.
Figure 29.
On the left, the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is an exact solution to the vacuum ADM evolution equations. On the right, the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is an exact solution to the vacuum ADM evolution equations.
Figure 29.
On the left, the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is an exact solution to the vacuum ADM evolution equations. On the right, the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , computed using SolveVacuumADMEquations, illustrating that this decomposition is an exact solution to the vacuum ADM evolution equations.
Figure 30.
On the left, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , together with a verification that they all hold identically. On the right, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , together with a verification that they all hold identically.
Figure 30.
On the left, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , together with a verification that they all hold identically. On the right, the list of vacuum ADM evolution equations, computed using the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , together with a verification that they all hold identically.
Figure 31.
On the left, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , together with a verification that it vanishes identically. On the right, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , together with a verification that it vanishes identically.
Figure 31.
On the left, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , together with a verification that it vanishes identically. On the right, the vacuum ADM Hamiltonian constraint, computed using the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , together with a verification that it vanishes identically.
Figure 32.
On the left, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , together with a verification that they all vanish identically. On the right, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , together with a verification that they all vanish identically.
Figure 32.
On the left, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with mass M in Schwarzschild or spherical polar coordinates ) with modified lapse function and vanishing shift vector , with zero cosmological constant , together with a verification that they all vanish identically. On the right, the list of vacuum ADM momentum constraints, computed using the VacuumADMSolution object for an ADM decomposition of a Kerr geometry (representing, for instance, an uncharged, spinning black hole with mass M and angular momentum J in Boyer-Lindquist or oblate spheroidal coordinates ) with modified lapse function and modified shift vector , with zero cosmological constant , together with a verification that they all vanish identically.
Figure 33.
On the left, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Minkowski geometry with lapse function and shift vector , in explicit contravariant matrix form. On the right, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and shift vector , in explicit contravariant matrix form.
Figure 33.
On the left, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Minkowski geometry with lapse function and shift vector , in explicit contravariant matrix form. On the right, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and shift vector , in explicit contravariant matrix form.
Figure 34.
On the left, the ADMStressEnergyDecomposition object for a perfect relativistic dust (representing an idealized dust distribution with density and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and shift vector , in explicit contravariant matrix form. On the right, the ADMStressEnergyDecomposition object for a perfect relativistic radiation distribution (representing an idealized distribution of radiation with pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and shift vector , in explicit contravariant matrix form.
Figure 34.
On the left, the ADMStressEnergyDecomposition object for a perfect relativistic dust (representing an idealized dust distribution with density and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and shift vector , in explicit contravariant matrix form. On the right, the ADMStressEnergyDecomposition object for a perfect relativistic radiation distribution (representing an idealized distribution of radiation with pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and shift vector , in explicit contravariant matrix form.
Figure 35.
On the left, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Minkowski geometry with lapse function and shift vector , in explicit contravariant matrix form. On the right, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and shift vector , in explicit contravariant matrix form.
Figure 35.
On the left, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Minkowski geometry with lapse function and shift vector , in explicit contravariant matrix form. On the right, the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and shift vector , in explicit contravariant matrix form.
Figure 36.
On the left, the relativistic energy density and relativistic momentum density of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the relativistic energy density and relativistic momentum density of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 36.
On the left, the relativistic energy density and relativistic momentum density of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the relativistic energy density and relativistic momentum density of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 37.
On the left, the relativistic Cauchy stress tensor and the corresponding stress tensor trace of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the relativistic Cauchy stress tensor and the corresponding stress tensor trace of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 37.
On the left, the relativistic Cauchy stress tensor and the corresponding stress tensor trace of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the relativistic Cauchy stress tensor and the corresponding stress tensor trace of the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 38.
On the left, the energy conservation equation for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the energy conservation equation for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 38.
On the left, the energy conservation equation for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the energy conservation equation for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 39.
On the left, the list of momentum conservation equations for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the list of momentum conservation equations for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 39.
On the left, the list of momentum conservation equations for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of a Schwarzschild geometry with lapse function and modified shift vector . On the right, the list of momentum conservation equations for the ADMStressEnergyDecomposition object for a perfect relativistic fluid (representing an idealized fluid with density , pressure P and spacetime velocity ) embedded within an ADM decomposition of an FLRW geometry with lapse function and modified shift vector .
Figure 40.
On the left, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required. On the right, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required.
Figure 40.
On the left, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required. On the right, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required.

Figure 41.
On the left, the list of ADM evolution equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations. On the right, the list of ADM evolution equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations.
Figure 41.
On the left, the list of ADM evolution equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations. On the right, the list of ADM evolution equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , together with a verification that they reduce down to a set of eight canonical field equations.

Figure 42.
On the left, the energy conservation equation obtained from the purely timelike projection of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant . On the right, the energy conservation equation obtained from the purely timelike projection of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant .
Figure 42.
On the left, the energy conservation equation obtained from the purely timelike projection of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant . On the right, the energy conservation equation obtained from the purely timelike projection of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant .

Figure 43.
On the left, the list of momentum conservation equations obtained from the purely spacelike projections of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant . On the right, the list of momentum conservation equations obtained from the purely spacelike projections of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a prefectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant .
Figure 43.
On the left, the list of momentum conservation equations obtained from the purely spacelike projections of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant . On the right, the list of momentum conservation equations obtained from the purely spacelike projections of the full continuity equations, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a prefectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant .

Figure 44.
On the left, the ADM Hamiltonian constraint, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , illustrating that it does not vanish identically. On the right, the ADM Hamiltonian constraint, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , illustrating that it does not vanish identically.
Figure 44.
On the left, the ADM Hamiltonian constraint, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , illustrating that it does not vanish identically. On the right, the ADM Hamiltonian constraint, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , illustrating that it does not vanish identically.
Figure 45.
On the left, the list of ADM momentum constraints, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , illustrating that they do not vanish identically. On the right, the list of ADM momentum constraints, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , illustrating that they do not vanish identically.
Figure 45.
On the left, the list of ADM momentum constraints, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic dust (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of dust) with lapse function and modified shift vector , with zero cosmological constant , illustrating that they do not vanish identically. On the right, the list of ADM momentum constraints, computed using the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic radiation distribution (representing a perfectly homogeneous and isotropic universe filled with an idealized distribution of radiation) with lapse function and modified shift vector , with zero cosmological constant , illustrating that they do not vanish identically.
Figure 46.
On the left, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic fluid (representing a perfectly homogeneous and isotropic universe filled with an idealized fluid) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required. On the right, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic fluid (representing a perfectly homogeneous and isotropic universe filled with an idealized fluid) with lapse function and modified shift vector , with non-zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required.
Figure 46.
On the left, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic fluid (representing a perfectly homogeneous and isotropic universe filled with an idealized fluid) with lapse function and modified shift vector , with zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required. On the right, the ADMSolution object for an ADM decomposition of an FLRW geometry equipped with a perfect relativistic fluid (representing a perfectly homogeneous and isotropic universe filled with an idealized fluid) with lapse function and modified shift vector , with non-zero cosmological constant , computed using SolveADMEquations, illustrating that this decomposition is a non-exact solution to the ADM evolution equations, with eight additional field equations required.

Figure 47.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices.
Figure 47.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices.
Figure 48.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 48.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by its final spatial hypergraph at coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.

Figure 49.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices.
Figure 49.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) with spatial coordinate information assigned to the vertices.

Figure 50.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 50.
On the left, a DiscreteHypersurfaceDecomposition object for a Schwarzschild geometry (representing, for instance, an uncharged, non-rotating black hole with numerical mass 1 in Schwarzschild or spherical polar coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned. On the right, a DiscreteHypersurfaceDecomposition object for a Kerr geometry (representing, for instance, an uncharged, spinning black hole with numerical mass 1 and numerical angular momentum in Boyer-Lindquist or oblate spheroidal coordinates with , and ), with a resolution of 400 vertices and a discretization scale of 1.2, represented by the evolution of its spatial hypergraphs for five time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 51.
The ADMDecomposition object for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates ) with trivial lapse function 1 and trivial shift vector , represented by its induced (spatial) and ambient (spacetime) MetricTensor objects in explicit covariant matrix form.
Figure 51.
The ADMDecomposition object for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates ) with trivial lapse function 1 and trivial shift vector , represented by its induced (spatial) and ambient (spacetime) MetricTensor objects in explicit covariant matrix form.
Figure 52.
The DiscreteHypersurfaceDecomposition object for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates with the radial boundary R of the domain set to be comparable to the Schwarzschild radii of the black holes, i.e. ) with the slicing condition and the minimal distortion coordinate conditions for the gauge, represented by the evolution of its spatial hypergraphs for six time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 52.
The DiscreteHypersurfaceDecomposition object for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates with the radial boundary R of the domain set to be comparable to the Schwarzschild radii of the black holes, i.e. ) with the slicing condition and the minimal distortion coordinate conditions for the gauge, represented by the evolution of its spatial hypergraphs for six time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 53.
The DiscreteHypersurfaceDecomposition object for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates with the radial boundary R of the domain set to be much larger than the Schwarzschild radii of the black holes, i.e. ) with the slicing condition and the minimal distortion coordinate conditions for the gauge, represented by the evolution of its spatial hypergraphs for six time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 53.
The DiscreteHypersurfaceDecomposition object for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates with the radial boundary R of the domain set to be much larger than the Schwarzschild radii of the black holes, i.e. ) with the slicing condition and the minimal distortion coordinate conditions for the gauge, represented by the evolution of its spatial hypergraphs for six time steps from coordinate time to coordinate time (colored based on extrinsic curvature) without any vertex coordinate information assigned.
Figure 54.
The outgoing gravitational wave strain for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates ) with the slicing condition and the minimal distortion coordinate conditions for the gauge, calculated from the real part of the , mode of the radial Weyl scalar , projected onto a sphere of radius .
Figure 54.
The outgoing gravitational wave strain for a Brill-Lindquist geometry (representing, for instance, a pair of uncharged, non-rotating black holes, initially at rest, each of mass M in Schwarzschild or spherical polar coordinates ) with the slicing condition and the minimal distortion coordinate conditions for the gauge, calculated from the real part of the , mode of the radial Weyl scalar , projected onto a sphere of radius .