Submitted:
17 January 2024
Posted:
17 January 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Related Work
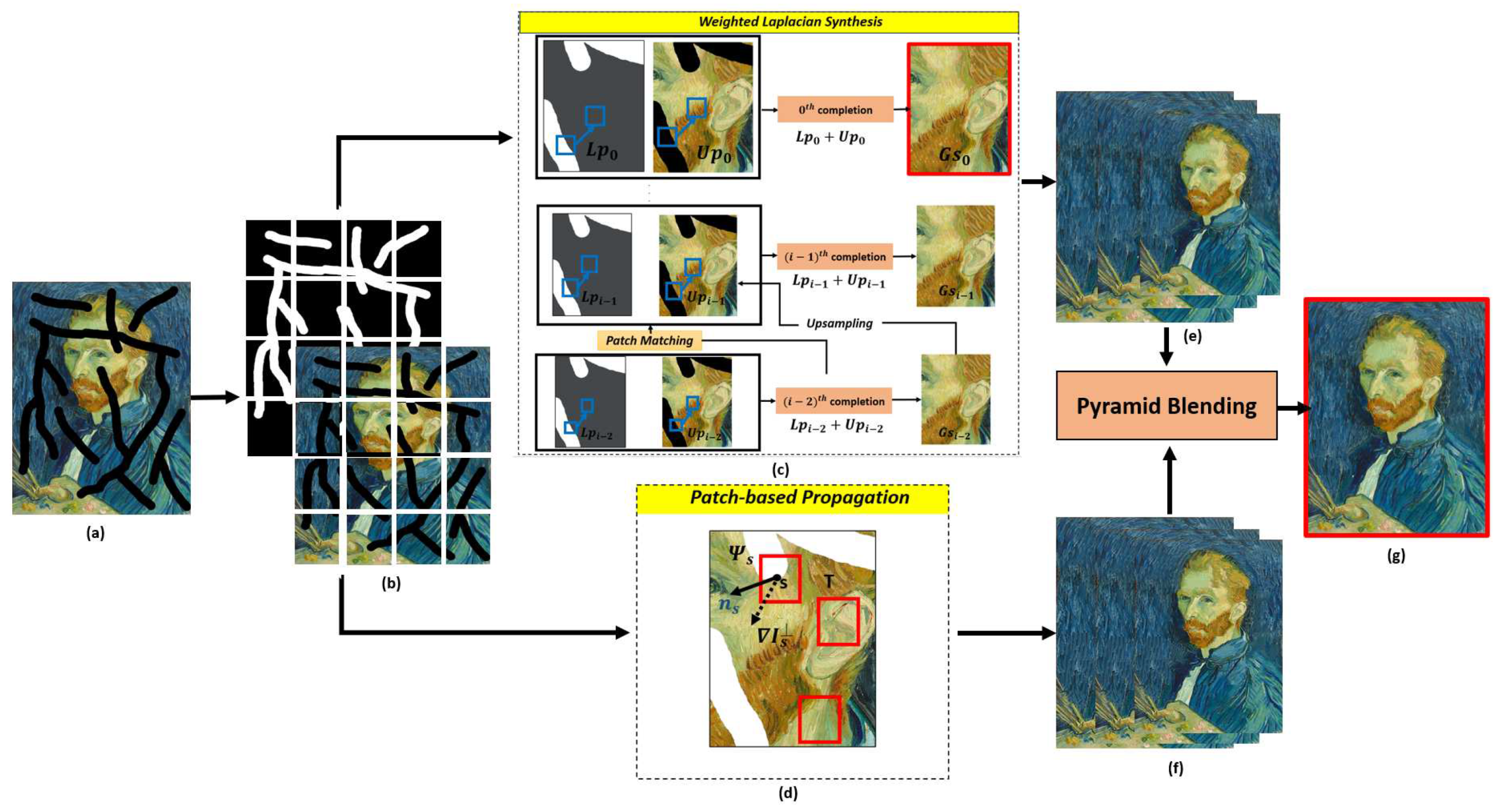
3. Methodology
3.1. Weighted Similarity-Confidence Laplacian Synthesis
3.2. Our Proposed Algorithm
| Algorithm 1: Weighted Similarity-Confidence Laplacian Synthesis |
|
|
| Segmentation |
| Divide the input image and its mask image into 16 multi-regions, each with a size of 400×400 pixels (Figure 2b). |
 |
4. Experimental Results
4.1. Qualitative Comparison
4.2. Quantitative Comparison
5. Discussion
6. Conclusions
References
- Criminisi, A.; Pérez, P.;Toyama, K. Object removal by exemplar-based inpainting. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2004.
- Efros, A. A.; Leung, T. K. Texture synthesis by non-parametric sampling. In Proceedings of the Seventh IEEE International Conference on Computer Vision, pp: 1033-1038, 1999.
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image inpainting. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, pp: 417-424, 2000.
- Darabi, S.; Shechtman, E.; Barnes, C.; Goldman, D. B. Image melding: Combining inconsistent images using patch-based synthesis. ACM Transactions on Graphics (TOG), 31(4), 82, 2012.
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T. S. Generative Image Inpainting with Contextual Attention. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
- Xiao, H.; Zhang, J.; Zhang, K.; Xiao, C. Deep Exemplar-Based Image Colorization. In International Conference on Computer Vision (ICCV), 2019.
- Yue, Z.; Zheng, Y. Artistic Style Transfer for Image Inpainting. IEEE Transactions on Image Processing, Volume 29, pp: 5142-5157, 2020.
- Zeng, Y.; Lin, Z.; Yang, J.; Zhang, J.; Shechtman, E.; Lu, H. High-resolution image inpainting with iterative confidence feedback and guided upsampling. European Conference on Computer Vision, pp. 1-17, 2020.
- Song, Y.; Yang, C.; Shen, Y.; Wang, P.; Huang, Q; Kuo, C. C. J. Spg-net: segmentation prediction and guidance network for image inpainting, arXiv:1805.03356, 2018.
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T. S. Generative image inpainting with contextual attention. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 5505–5514, 2018.
- Yi, Z.; Tang, Q.; Azizi, S.; Jang, D.; Xu, Z. Contextual residual aggregation for ultra high-resolution image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7508–7517, 2020.
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. ACM Transactions on Graphics (ToG), 36(4):1–14, 2017. [CrossRef]
- Ma, Y.; Liu, X.; Bai, S.; Wang, L.; Liu, A.; Tao, D.; Hancock, E. Region-wise generative adversarial image inpainting for large missing areas. arXiv:1909.12507, 2019.
- Li, J.; Wang, N.; Zhang, L.; Du, B.; Tao, D. Recurrent feature reasoning for image inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 7760–7768, 2020.
- Liu, G.; Reda, F. A.; Shih, K. J.; Wang, T. C.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), pp. 85–100, 2018.
- Telea, A. An image inpainting technique based on the fast marching method. J. Graph. Tools, vol. 9, no. 1, pp. 23–34, Jan. 2004. [CrossRef]
- Zuo, W.; Lin, Z. A generalized accelerated proximal gradient approach for total-variation-based image restoration. IEEE Trans. Image Processing, vol. 20, no. 10, pp. 2748–2759, Oct. 2011. [CrossRef]
- Dahl, J.; Hansen, P. C.; Jensen, S. H.; Jensen, T. L. Algorithms and software for total variation image reconstruction via first-order methods. Numerical Algorithms, vol. 53, no. 1, pp. 67–92, Jan. 2010. [CrossRef]
- Chan, T. F.; Shen, J. Nontexture inpainting by curvature-driven diffusions. Journal of Visual Communication and Image Representation, vol. 12, no. 4, pp. 436–449, Dec. 2001.
- Chan, T. F.; Kang, S. H.; Shen, J. Total variation denoising and enhancement of color images based on the CB and HSV color models. Journal of Visual Communication and Image Representation, vol. 12, no. 4, pp. 422–435, Dec. 2001. [CrossRef]
- Irawati, N. S.; Urano, Y.; Du, W. Image inpainting using orthogonal viewpoints and structure consistency in Manhattan World. In the 8th International Virtual Conference on Applied Computing and Information Technology (ACIT), 2021.
- Horikawa, E.; Irawati, N. S.; Du, W. Image inpainting using clustered planar structure guidance. In the 8th International Virtual Conference on Applied Computing and Information Technology (ACIT), 2021.
- Irawati, N. S.; Horikawa, E.; Du, W. Interactive image inpainting of large-scale missing region. IEEE Access, pp(99):1-1, 2021. [CrossRef]
- Irawati, N.S.; Du, W. Structure-texture consistent painting completion for artworks. IEEE Access (11), pp. 27369-27381, 2023.
- Urano, Y.; Sari, I.N.; Du, W. Image inpainting using automatic structure propagation with auxiliary line construction. 23rd ACIS International Summer Virtual Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD Summer), IEEE, pp. 107-112, Kyoto, Japan, 2022.
- Takarabe, J.; Sari, I.N.; Du, W. Depth map estimation of single-view image using smartphone camera for a 3 dimension image generation in augmented reality. Sixth International Symposium on Computer, Consumer and Control (IS3C), IEEE, pp. 167-170, Taichung, Taiwan, 2023.
- Masaoka, K.; Sari, I.N.; Du, W. Vanishing points detection with line segments of gaussian sphere. Sixth International Symposium on Computer, Consumer and Control (IS3C), IEEE, pp. 48-51, Taichung, Taiwan, 2023.
- Sari, I.N.; Masaoka, K.; Takarabe, J.; Du, W. High-resolution art painting completion using multi-region laplacian fusion. Sixth International Symposium on Computer, Consumer and Control (IS3C), IEEE, pp. 48-51, Taichung, Taiwan, 2023.
- Masaoka, K.; Sari, I. N.; Du, W. Edge-enhanced GAN with vanishing points for image inpainting. IEEE/ACIS International Summer Virtual Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing, 2022.
- Nazeri, K.; Joseph, E. Ng, T.; Qureshi, F. Z.; Ebrahimi, M. Edgeconnect: generative image inpainting with adversarial edge learning, arXiv:1901.00212, 2019.
- Liu, H.; Wan, Z.; Huang, W.; Song, Y.; Han, X.; Liao, J. PD-GAN: probabilistic diverse GAN for image inpainting. Conference on Computer Vision and Pattern Recognition (CVPR), 2021.
- Criminisi, A.; Perez, P.; Toyama, K. Region filling and object removal by exemplar-based image inpainting. IEEE Trans. Image Processing, vol. 13, no. 9, pp. 1200–1212, Sep. 2004.
- Sun, J.; Yuan, L.; Jia, J. Image completion with structure propagation. ACMTransactions on Graphic, 2005. [CrossRef]
- Chen, M.; Zhao, X.; Xu, D. Image inpainting for digital dunhuang murals using partial convolutions and sliding window method. Journal of Physics Conference Series, 1302(3):032040, 2019.
- Wang, H.; Li, Q.; Zou, Q. Inpainting of dunhuang durals by sparsely modeling the texture similarity and structure continuity. Journal on Computing and Cultural Heritage, 2018.
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A. A. Context encoders: feature learning by inpainting. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2536–2544, 2016.
- Chen, M.; Zhao, X.; Xu, D. Image inpainting for digital dunhuang murals using partial convolutions and sliding window method. Journal of Physics Conference Series, 1302(3):032040, 2019. [CrossRef]
- Wang, H.; Li, Q.; Zou, Q. Inpainting of dunhuang durals by sparsely modeling the texture similarity and structure continuity. Journal on Computing and Cultural Heritage, 2018.
- Lee, J. H.; Choi, I.; Kim, M. H. Laplacian patch-based image synthesis. IEEE Conference on Computer Vision and Pattern Recognition, 2016.
- Anmol, B.; Green, R. K. S.; Sachin, D. L. Spatially variant laplacian pyramids for multi-frame exposure fusion. Computer Vision and Image Processing, (pp.73-81), 2020.
- Wang, Z.; Bovik, A. C.; Lu, L. Why is image quality assessment so difficult. Proc. IEEE Int. Conf. Acoust. Speech Signal Processing,pp. 3313–3316, vol. 4, 2002.
- Qureshi, M. A.; Deriche, M.; Beghdadi, A.; Amin, A. A critical survey of state-of-the-art image inpainting quality assessment metric. Journal of Visual Communication and Image Representation, vol. 49, pp. 177–191, 2017. [CrossRef]
- Zhang, R.; Isola, P.; Efros, A. A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. IEEE International Conference Computer Vision and Pattern Recognition (CVPR), 2018.
- Ding, K.; Ma, K., Wang, S.; Simoncell, E. E. Image quality assessment: unifying structure and texture similarity. IEEE International Conference Computer Vision and Pattern Recognition (CVPR), 2020.

| Name | Criminisi [1] | Laplacian [39] | EdgeConnect [30] | Ours | ||||
|---|---|---|---|---|---|---|---|---|
| High | Low | High | Low | High | Low | High | Low | |
| Girl | 0.631 | 0.443 | 0.701 | 0.562 | 0.702 | 0.344 | 0.846 | 0.812 |
| Man | 0.642 | 0.531 | 0.719 | 0.407 | 0.745 | 0.307 | 0.897 | 0.808 |
| Scenery | 0.611 | 0.472 | 0.754 | 0.592 | 0.762 | 0.412 | 0.853 | 0.781 |
| Woman | 0.714 | 0.523 | 0.758 | 0.575 | 0.781 | 0.635 | 0.892 | 0.852 |
| Name | Criminisi [1] | Laplacian [39] | EdgeConnect [30] | Ours | ||||
|---|---|---|---|---|---|---|---|---|
| High | Low | High | Low | High | Low | High | Low | |
| Girl | 0.721 | 0.543 | 0.899 | 0.661 | 0.895 | 0.618 | 0.951 | 0.786 |
| Man | 0.792 | 0.601 | 0.872 | 0.644 | 0.834 | 0.562 | 0.932 | 0.888 |
| Scenery | 0.710 | 0.592 | 0.888 | 0.691 | 0.842 | 0.512 | 0.921 | 0.834 |
| Woman | 0.812 | 0.611 | 0.878 | 0.655 | 0.852 | 0.615 | 0.932 | 0.891 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).






