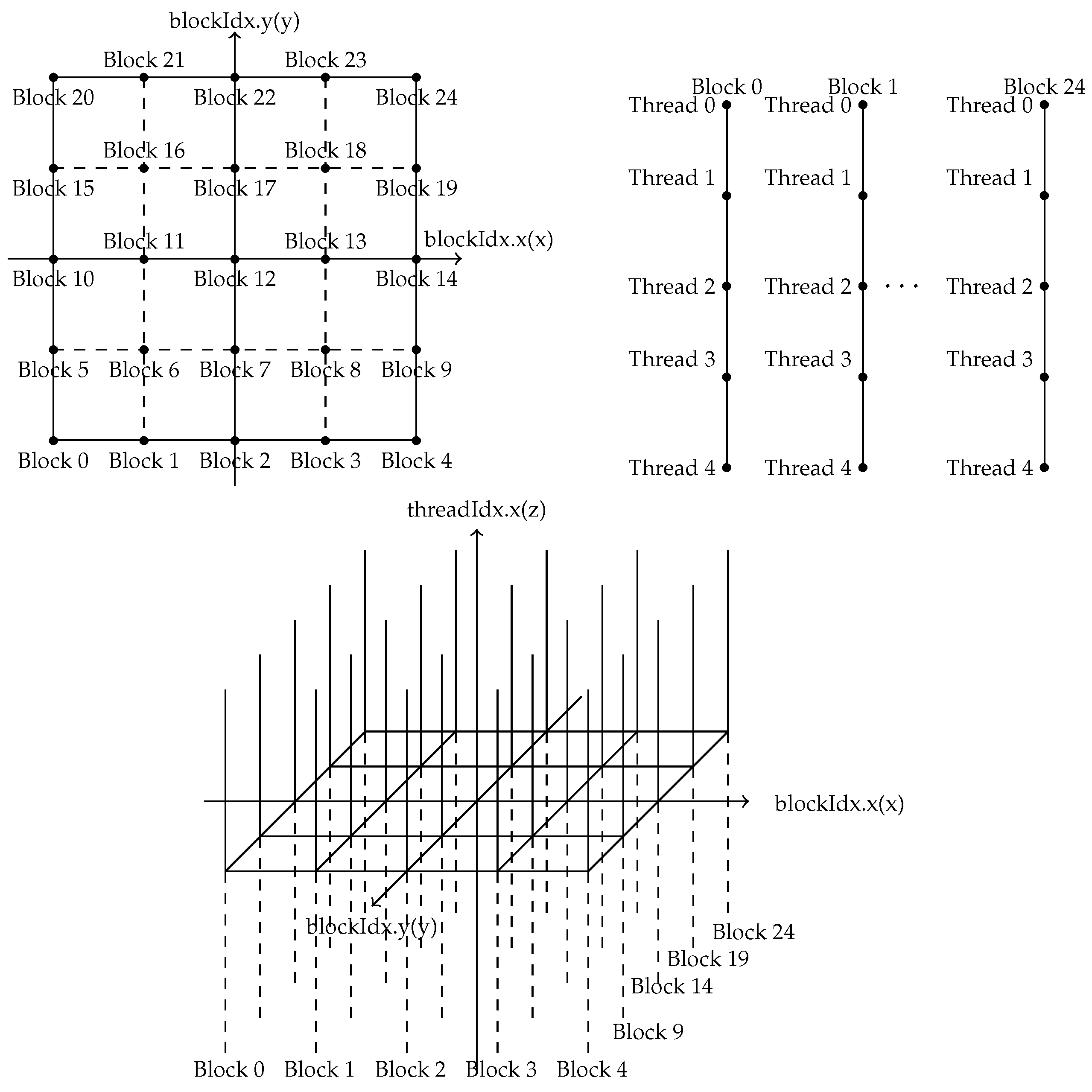An Algorithm Based on CUDA for Estimating Covering Functionals of Convex Bodies

Preprint

Article

An Algorithm Based on CUDA for Estimating Covering Functionals of Convex Bodies

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 January 2024

Posted:

16 January 2024

You are already at the latest version

Alerts

Abstract

In Chuanming Zong’s program to attack Hadwiger’s covering conjecture, which is a longstanding open problem from Convex and Discrete Geometry, it is essential to estimate covering functionals of convex bodies effectively. Recently, He et al. [J. Optim. Theory Appl. 2023, 196, 1036–1055.] and Yu et al. [Mathematics, 2023, 11, 2000] provided two deterministic global optimization algorithms having high computational complexity for this purpose. Since satisfactory estimations of covering functionals will be sufficient in Zong’s program, we propose a stochastic global optimization algorithm based on CUDA and provide an error estimation for the algorithm. The accuracy of our algorithm is tested by comparing numerical and exact values of covering functionals of convex bodies including the Euclidean unit disc, the three-dimensional Euclidean unit ball, the regular tetrahedron, and the regular octahedron. We also present estimations of covering functionals for the regular dodecahedron and the regular icosahedron.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

MSC: 52C17; 52B11; 52B10; 52A15; 52A20

1. Introduction

A compact convex subset K of

R^{n}

having interior points is called a convex body, whose boundary and interior are denoted by

bd K

and

int K

, respectively. Let

K^{n}

be the set of convex bodies in

R^{n}

. For each

K \in K^{n}

, let

c (K)

be the least number of translates of

int K

necessary to cover K. Regarding the least upper bound of

c (K)

K^{n}

, there is a long-standing conjecture:

Conjecture 1

(Hadwiger’s covering conjecture). For each

K \in K^{n}

, we have

c (K) \leq 2^{n};

equality holds if and only if K is a parallelotope.

Classical results related to this conjecture can be found in [1,2]. While extensive research has been conducted (see e.g., [3,4,5,6,7]), Conjecture 1 has only been conclusively resolved when

n = 2

For each

p \in Z^{+}

, set

[p] = \{i \in Z^{+} ∣ 1 \leq i \leq p\}

Let

K \in K^{n}

. A set having the form

λ K + x

, where

λ \in (0, 1)

and

x \in R^{n}

, is called a smaller homothetic copy of K. According to Theorem 34.3 in [1],

c (K)

equals the least number of smaller homothetic copies of K required to cover K. Clearly,

c (K) \leq p

for some

p \in Z^{+}

if and only if

Γ_{p} (K) < 1

, where

Γ_{p} (K) : = min \{γ > 0 ∣ \exists \{x_{i} ∣ i \in [p]\} \subseteq R^{n} s . t . K \subseteq ⋃_{i \in [p]} (γ K + x_{i})\} .

For each

p \in Z^{+}

, the map

\begin{matrix} Γ_{p} (\cdot) : K^{n} & \to [0, 1] \\ K & \mapsto Γ_{p} (K) \end{matrix}

is an affine invariant and is called the covering functional with respect to p. Let

K \in K^{n}

and

p \in Z^{+}

. A set C of p points satisfying

K \subseteq Γ_{p} (K) K + C,

is called a p-optimal configuration of K.

In [8], Chuanming Zong proposed the first program based on computers to tackle Conjecture 1 via estimating covering functionals. Two different algorithms have been designed for this purpose. The first one is introduced by Chan He et al. (cf. [9]) based on the geometric branch-and-bound method (cf. [10]). The algorithm is implemented in two parts. The first part uses geometric branch-and-bound methods to estimate

Γ (K, C)

, where

Γ (K, C) = min \{γ > 0 ∣ K \subseteq C + γ K\} .

The second part also uses geometric branch-and-bound methods to estimate

Γ_{p} (K)

. When

n \geq 3

, computing

Γ (K, C)

and

Γ_{p} (K)

in this way exhibits a significantly high computational complexity. The other is introduced by Man Yu et al. (cf. [11]) based on relaxation algorithm. Let

S \subseteq K

be a discretization of K,

P_{K}

be a set containing a p-optimal configuration of K, and

V \subseteq P_{K}

. They transformed the problem of covering S by smaller homothetic copies of K into a vertex p-center problem, and showed that the solution of the corresponding vertex p-center problem is a good approximation of

Γ_{p} (K)

by proving

Γ_{p} (S) - ε_{1} \leq Γ_{p} (K) \leq Γ_{p} (S) + ε_{2},

where

Γ_{p} (S) = min \{γ > 0 ∣ \exists \{x_{i} ∣ i \in [p]\} \subseteq R^{n} s . t . S \subseteq ⋃_{i \in [p]} (γ K + x_{i})\},

and

ε_{1}

and

ε_{2}

are two positive numbers satisfying

K \subseteq S + ε_{1} K and P_{K} \subseteq V + ε_{2} K .

Clearly, finer discretizations of K are required to obtain more accurate estimates of

Γ_{p} (K)

, which will lead to higher computational complexity.

In this paper, we propose an algorithm utilizes Compute Unified Device Architecture (CUDA) and stochastic global optimization methods to accelerate the process of estimating

Γ_{p} (K)

. CUDA is a parallel computing platform, particularly well-suited for handling large-scale computational tasks by performing many computations in parallel (cf. [12]). When discretizing convex bodies, CUDA provides a natural discretization method and enables parallel computation for all discretized points, thereby accelerating the execution of algorithms. As show in Section 2, when calculting

Γ (S, C)

for some

C \subseteq R^{n}

, we need to get the maximum dissimilarity between a point in S and its closest point in C. Reduction technique provided by CUDA, which typically involve performing a specific operation on all elements in an array (summation, finding the maximum, finding the minimum, etc., cf. [13]), enables efficient computation of

Γ (S, C)

. When facing large-scale optimization problems, stochastic algorithms have the capability to produce high-quality solutions in a short amount of time.

In Section 2, the problem of estimating

Γ_{p} (K)

is transformed to a minimization optimization problem, and an error estimation is provided. Using ideas mentioned in [9], an algorithm based on CUDA for

Γ_{p} (S)

is designed in Section 3. Results of computational experiments showing the effectiveness of our algorithm are presented in Section 4.

2. Covering Functional and Error Estimation

As in [9], we put

Q_{n} = {[- 1, 1]}^{n}

. For each

K \in K^{n}

, let

α (K) = max \{α > 0 ∣ \exists T \in A^{n} s . t . α Q_{n} \subseteq T (K) \subseteq Q_{n}\},

where

A^{n}

is the set of all nonsingular affine transformations on

R^{n}

. We can apply an appropriate affine transformation, if necessary, to ensure that

α (K) Q_{n} \subseteq K \subseteq Q_{n} .

Remark 1.

In general, it is not easy to calculate

α (K)

. If K is symmetric about the origin, then

1 α (K)

is the Banach-Mazur distance between K and

Q_{n}

. By Proposition 37.6 in [14], when K is the n-dimensional Euclidean unit ball

B_{2}^{n}

1 α (K) = \sqrt{n}

. For our purpose, it will be sufficient to choose an α, as large as possible, such that

α Q_{n} \subseteq K \subseteq Q_{n}

Definition 2

(cf. [11]). Let

K \in K^{n}

. For k,

c \in R^{n}

, the number

d (k, c) = min \{γ \geq 0 ∣ k \in γ K + c\} .

(1)

is called the dissimilarity of k and c.

K = B_{2}^{n}

, the dissimilarity between any two points is precisely the Euclidean distance between these two points. In general, the dissimilarity is not symmetric. If K is an n-dimensional convex polytope, the dissimilarity between any two points can be computed by Lemma 3.

Lemma 3.

Let

K \in K^{n}

be an n-dimensional convex polytope with

o \in int K

determined by

K = \{x \in R^{n} ∣ A x \leq B\},

(2)

where A is an m-by-n matrix and B is an n-dimensional column vector whose elements are all 1. For any

u, c \in R^{n}

, we have

d (u, c) = max_{1 \leq i \leq n} p_{i},

(3)

where

{(p_{i})}_{n \times 1} = A (u - c)

Proof.

Since K is bounded,

max_{1 \leq i \leq n} p_{i} \geq 0

. Let

γ_{0} = min \{γ \geq 0 ∣ u \in c + γ K\} .

For positive

γ

, we have

u - c \in γ K \Leftrightarrow \frac{1}{γ} (u - c) \in K \Leftrightarrow \frac{1}{γ} A (u - c) \leq B \Leftrightarrow A (u - c) \leq γ B .

Since

B = {(1, 1 \dots, 1)}^{T}

, we have

max_{1 \leq i \leq n} p_{i} \leq γ

, which implies that

max_{1 \leq i \leq n} p_{i} \leq γ_{0} = d (u, c) .

(4)

Since

p_{i} \leq max_{1 \leq j \leq n} p_{j}, \forall i \in [n]

, we have

A (u - c) \leq (max_{1 \leq i \leq n} p_{i}) B

. Thus

u - c \in (max_{1 \leq i \leq n} p_{i}) K,

which implies that

max_{1 \leq i \leq n} p_{i} \geq γ_{0} = d (u, c) .

(5)

The desired equality (3) follows from (4) and (5). □

Remark 4.

Clearly, each convex polytope K containing o in its interior can be represented as (2).

Let

i \geq 2

and

j \in [n]

be two integers. We denote by

p_{j} (x)

the j-th coordinate of a point

x \in R^{n}

and

S_{i} = \{(γ_{1}, \dots, γ_{n}) \in R^{n} ∣ γ_{j} \in \{- 1 + \frac{2 k}{i - 1} ∣ k \in [i - 1] \cup 0\}, \forall j \in [n]\} .

Lemma 5.

Q_{n} \subseteq S_{i} + \frac{1}{i - 1} Q_{n}

Proof.

Suppose that

x = (β_{1}, \dots, β_{n}) \in Q_{n}

. Let

y \in R^{n}

be the point satisfying

p_{j} (y) = \{\begin{matrix} \frac{⌊ β_{j} (i - 1) ⌋}{i - 1}, & ⌊ β_{j} (i - 1) ⌋ + i - 1 is even, \\ \frac{⌊ β_{j} (i - 1) ⌋ + 1}{i - 1}, & ⌊ β_{j} (i - 1) ⌋ + i - 1 is odd, \end{matrix} \forall j \in [n] .

Then

y \in S_{i}

. Let

j \in [n]

. If

⌊ β_{j} (i - 1) ⌋ + i - 1

is even, then

| β_{j} - p_{j} (y) | = \frac{β_{j} (i - 1) - ⌊ β_{j} (i - 1) ⌋}{i - 1} \leq \frac{1}{i - 1} .

Otherwise, we have

| β_{j} - p_{j} (y) | = \frac{| β_{j} (i - 1) - ⌊ β_{j} (i - 1) ⌋ - 1 |}{i - 1} \leq \frac{1}{i - 1} .

It follows that

{x - y}_{\infty} \leq \frac{1}{i - 1}

. Therefore

x \in y + \frac{1}{i - 1} Q_{n} \subseteq S_{i} + \frac{1}{i - 1} Q_{n} .

□

Theorem 6.

Let

α > 0

and

i \geq 2

be an integer. If

K \in K^{n}

satisfies

α Q_{n} \subseteq K \subseteq Q_{n}

, then

K \subseteq (S_{i} \cap (\frac{1 + α (i - 1)}{α (i - 1)} K)) + \frac{1}{i - 1} Q_{n} .

Proof.

By Lemma 5, we have

Q_{n} \subseteq S_{i} + \frac{1}{i - 1} Q_{n} .

It follows that

K \subseteq (S_{i} + \frac{1}{i - 1} Q_{n}) \cap K .

Let

x \in K

. There exists a point

p \in S_{i}

such that

x \in p + \frac{1}{i - 1} Q_{n} .

Thus

p \in x - \frac{1}{i - 1} Q_{n} \subseteq K + \frac{1}{i - 1} Q_{n} \subseteq K + \frac{1}{α (i - 1)} K = \frac{1 + α (i - 1)}{α (i - 1)} K .

Therefore, we have

x \in (S_{i} \cap (\frac{1 + α (i - 1)}{α (i - 1)} K)) + \frac{1}{i - 1} Q_{n} .

□

Let

α > 0

i \geq 2

be an integer, K be a convex body satisfying

α Q_{n} \subseteq K \subseteq Q_{n}

S = S_{i} \cap (\frac{1 + α (i - 1)}{α (i - 1)} K),

(6)

and

C \subseteq R^{n}

. Put

Γ (S, C) = inf \{γ > 0 ∣ S \subseteq C + γ K\},

and

Γ_{p} (S) = min \{Γ (S, C) ∣ C contains at most p points\} .

Proposition 7.

Let K, α, i, S be as above,

p \in Z^{+}

. Then

Γ_{p} (K) \leq Γ_{p} (S) + \frac{1}{α (i - 1)} .

(7)

Proof.

By Theorem 6, we have

K \subseteq S + \frac{1}{i - 1} Q_{n} \subseteq S + \frac{1}{α (i - 1)} K .

Let

C^{'}

be a p-element subset of

R^{n}

such that

S \subseteq C^{'} + Γ_{p} (S) K

. We have

K \subseteq S + \frac{1}{α (i - 1)} K \subseteq C^{'} + Γ_{p} (S) K + \frac{1}{α (i - 1)} K,

which completes the proof. □

3. An Algorithm Based on CUDA for $Γ_{p} (S)$

Let

K \in K^{n}

p \in Z^{+}

, and C be a set of p points. First, we use CUDA to get S defined by (6) and compute the minimum dissimilarity from each point in S to C. Then, we employ a CUDA-based reduction algorithm to get

Γ (S, C)

. Finally, we use different stochastic global optimization algorithms to estimate

Γ_{p} (S)

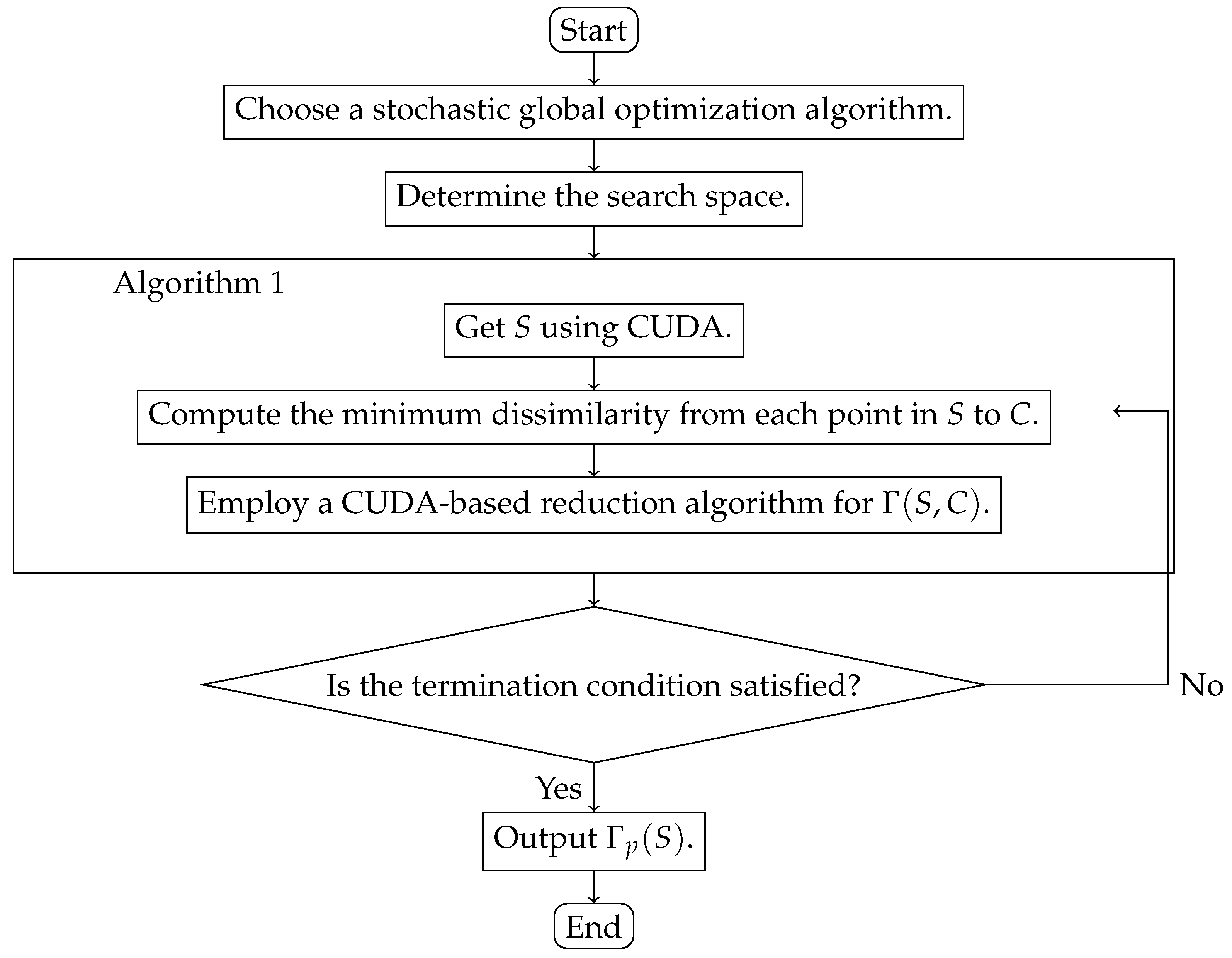
and select an appropriate optimization algorithm through comparison. Figure 1 shows the overall framework of the algorithm.

3.1. An Algorithm Based on CUDA for $Γ (S, C)$

CUDA organizes threads into a hierarchical structure consisting of grids, blocks, and threads. Grid is the highest-level organization of threads in CUDA, and a grid represents a collection of blocks. A block, identified by a unique block index within its grid, is a group of threads that can cooperate with each other and share data using shared memory. Threads are organized within blocks, and each thread is identified by a unique thread index within its block. The number of blocks and threads per block can be specified when launching a CUDA kernel. The grid and block dimensions can be one-dimensional, two-dimensional, or three-dimensional, depending on the problem to deal with. For more information about CUDA we refer to [15,16,17,18].

The organization of threads within blocks and grids provides a natural way to discretize

Q_{3}

. First, we discretize

[- 1, 1] \times [- 1, 1] \times 0

into a set P of (gridDim.x)×(gridDim.y) points. Each point p in P corresponds to a block

B_{p}

in CUDA. And

B_{p}

contains a collection of blockDim.x threads, each one of which corresponds to a point in

p + 0 \times 0 \times [- 1, 1]

. See Figure 2, where gridDim.x, girdDim.y, and blockDim.x are set to be 5.

Figure 1. The overall framework.

Let T be the set of all threads invoked by CUDA. Then the cardinality of T is

gridDim . x \times gridDim . y \times blockDim . x .

For

i \in [gridDim . x - 1] \cup 0

j \in [gridDim . y - 1] \cup 0

, and

k \in [blockDim . x - 1] \cup 0

, there is a thread

t : = t (i, j, k) \in T

indexed by

(j \times gridDim . x + i) \times blockDim . x + k,

which corresponds to the point

p_{t} = (- 1 + \frac{2 i}{gridDim . x - 1}, - 1 + \frac{2 j}{gridDim . y - 1}, - 1 + \frac{2 k}{blockDim . x - 1}) \in Q_{3} .

Put

S = \{t \in T ∣ p_{t} \in (1 + \frac{1}{α (gridDim . x - 1)}) K\},

where

α

is a positive number satisfying

α Q_{3} \subseteq K \subseteq Q_{3}

. For each

t \in S

, denote by

d (p_{t}, C)

the minimum dissimilarity from point

p_{t}

to C. I.e.,

d (p_{t}, C) = min \{d (p_{t}, c) ∣ c \in C\} .

t \notin S

, we set

d (p_{t}, C) = 0

. The CUDA thread corresponding to

t \in T

computes

d (p_{t}, C)

. Then a CUDA-based reduction algorithm will be invoked to get

{max}_{t \in T} d (p_{t}, C)

The idea of the reduction algorithm based on CUDA is to divide the original data into multiple blocks, then perform a local reduction operation on each block to obtain the local reduction result, and, finally, a global reduction operation is performed on the local reduction results to obtain the final reduction result (cf. [19]).

Algorithm 1 with parameters K, C, p, blockDim.x, gridDim.x, gridDim.y, and

α

calculates

Γ (S, C)

. It is more efficient than the geometric branch-and-bound approach proposed in [9]. For example, take

K = B_{2}^{3}

p = 6

\begin{matrix} C_{1} = { & (0.125, 0.125, 0.125), (- 0.125, - 0.125, - 0.125), (0.25, 0.25, 0.25), \\ (- 0.25, - 0.25, - 0.25), (0.5, 0.5, 0.5), (- 0.5, - 0.5, - 0.5), \\ (0.0375, 0.0375, 0.0375), (- 0.0375, - 0.0375, - 0.0375)}, and \\ C_{2} = { & (0, 0.57, - 0.38), (0.074, - 0.185, 0.618), (- 0.05, - 0.66, 0.13), \\ (0.32, - 0.25, - 0.58), (- 0.52, - 0.15, - 0.38), (- 0.587, 0.123, 0.22), \\ (0.662, - 0.024, 0.013), (0.136, 0.589, 0.319)} . \end{matrix}

Algorithm 1 yields good estimations of

Γ_{p} (S, C_{1})

and

Γ_{p} (S, C_{2})

much faster, see Table 1. Both algorithms run on a computer equipped with an AMD Ryzen 9 3900X 12-core processor and the NVIDIA A4000 graphics processor. For Algorithm 1, we take

gridDim . x = gridDim . y = blockDim . x = 1024

, and the accuracy is given by Proposition 7. For the geometric branch-and-bound algorithm, we set the relative accuracy

ε

to be

0.0001

(cf. [9] for the usage of the relative accuracy). The execution time of the geometric branch-and-bound approach exhibits substantial variability among different Cs, whereas the algorithm based on CUDA shows relatively consistent execution times across various cases.

Algorithm 1: An algorithm based on CUDA to compute

Γ (S, C)

Require:: a convex body K, a set C of p points in $R^{n}$ , a positive number $α$ , blockDim.x, gridDim.x and gridDim.y
Ensure:: $m a x$ as an estimation of $Γ (S, C)$
1:: Host and device allocate memory, initialize and copy host data to device
2:: $b i d \leftarrow blockIdx . y * gridDim . x + blockIdx . x$
3:: $t \leftarrow b i d * blockDim . x + threadIdx . x$
4:: $x [t] \leftarrow - 1 + 2 / (gridDim . x - 1) \cdot blockIdx . x$
5:: $y [t] \leftarrow - 1 + 2 / (gridDim . y - 1) \cdot blockIdx . y$
6:: $z [t] \leftarrow - 1 + 2 / (blockDim . x - 1) \cdot threadIdx . x$
7:: $p [t] \leftarrow (x [i d], y [i d], z [i d])$
8:: if $(p [t] \in (1 + \frac{1}{α (gridDim . x - 1)}) K$ then:
9:: Calculate $d (p [t], C)$ by Lemma 3
10:: $P [t] \leftarrow d (p [t], C)$
11:: else
12:: $P [t] \leftarrow 0$
13:: end if
14:: $s D a t a [threadIdx . x] \leftarrow P [t]$
15:: Using the reduction algorithm to find the maximum value
16:: $D d [blockIdx . x] \leftarrow s D a t a [0]$
17:: Copy the final reduction result to the host, $D [0] \leftarrow D d [blockIdx . x]$
18:: $m a x \leftarrow D [0]$
19:: return $m a x$

3.2. Different Stochastic Global Optimization Algorithms for $Γ_{p} (S)$

We choose to employ stochastic global optimization algorithms for several reasons. In the program proposed by Chuanming Zong (cf. [8]), after appropriately selecting a positive real number

β

and constructing a

β

-net

N

for

K^{n}

endowed with the Banach-Mazur metric, we only need to verify that

Γ_{2^{n}} (K) \leq c_{n}

holds for each

K \in N

, where

c_{n}

is a reasonably accurate estimate of the least upper bound of

Γ_{2^{n}} (K)

. For this purpose, we do not need to determine exact values of covering functionals of convex bodies in

N

. Stochastic global optimization algorithms demonstrate a low time complexity and high algorithmic efficiency. Moreover, based on the results presented in Table 4, it is evident that stochastic global optimization algorithms provide satisfactory estimates for covering functionals.

The NLopt (Non-Linear Optimization) library is a rich collection of optimization routines and algorithms, which provides a platform-independent interface for global and local optimization problems (cf. [20]). Algorithms in the NLopt library are partitioned into four categories: non-derivative based global algorithms, derivative based global algorithms, non-derivative based local algorithms, and derivative based local algorithms. We use several non-derivative based stochastic global algorithms here. All global optimization algorithms require bound constraints to be specified as optimization parameters (cf. e.g., [21]).

The following is the framework of a stochastic optimization algorithm based on NLopt.

Define the objective function and boundary constraints.
Declare an optimizer for NLopt.
Set algorithm and dimension.
Set termination conditions. NLopt provides different termination condition options including: value tolerance, parameter tolerance, function value stop value, iteration number, and time.

Proposition 8.

K \in K^{n}

K \subseteq Q_{n}

, and

(x + K) \cap K \neq \emptyset

, then

x \in 2 Q_{n}

Proof.

Suppose that

y \in (x + K) \cap K

. Then

z : = y - x \in K \subseteq Q_{n}

. Thus

\frac{1}{2} x = \frac{1}{2} y + \frac{1}{2} (- z) \in Q_{n},

which shows that

x \in 2 Q_{n}

. □

Remark 9.

By Proposition 8, when

K \subseteq Q_{n}

, we only need to search

2 Q_{n}

for points in a p-optimal configuration of K.

We utilized different stochastic global optimization algorithms to choose a more efficient one. Optimization algorithms under consideration include Controlled Random Search with local mutation (GN_CRS2_LM) (cf. [22]), evolutionary strategy (GN_ESCH) (cf. [23]), and evolutionary constrained optimization (GN_ISRES) (cf. [24]).

Algorithm 2: A stochastic optimization algorithm for

Γ_{p} (S)

based on NLopt.

Require:: K, C, p, blockDim.x, gridDim.x, gridDim.y, an estimation $Γ_{p} (K) \leq γ$ , lower bound LB and upper bound UB of the search domain
Ensure:: $m i n$ as an estimation of $Γ_{p} (S)$ .
1:: $F u n c t i o n M i n (u n s i g n e d n, c o n s t d o u b l e * x, d o u b l e * g r a d, v o i d * d a t a)$
2:: $begin$
3:: $x \leftarrow C$
4:: $m a x \leftarrow$ procedure( $K, C, p$ , blockDim.x, gridDim.x, gridDim.y) ▹Algorithm 1
5:: $end$
6:: $o p t e r \leftarrow n l o p t$ _ $c r e a t e (N L O P T$ _ $G N$ _ $C R S 2_L M, p \times n)$
7:: $o p t e r$ _ $s e t$ _ $l o w e r$ _ $b o u n d s (l b) \leftarrow$ LB
8:: $o p t e r$ _ $s e t$ _ $u p p e r$ _ $b o u n d s (u b) \leftarrow$ UB
9:: $n l o p t$ _ $s e t$ _ $m i n$ _ $o b j e c t i v e (o p t e r, M i n, N U L L)$
10:: $n l o p t$ _ $s e t$ _ $x t o l$ _ $r e l (o p t e r, t o l)$
11:: $m i n \leftarrow γ$
12:: $i \leftarrow 0$
13:: repeat
14:: $s t o p v a l \leftarrow m i n$
15:: $n l o p t$ _ $s e t$ _ $s t o p v a l (o p t e r, s t o p v a l)$
16:: $n l o p t$ _ $g e t$ _ $s t o p v a l (o p t e r)$
17:: $r e s u l t \leftarrow n l o p t$ _ $o p t i m i z e (o p t e r, x,$ &f_ $m i n)$
18:: if result then
19:: $m i n \leftarrow f$ _ $m i n$
20:: end if
21:: $i \leftarrow i + 1$
22:: until $i \geq 40$
23:: return $m i n$

Let p be a positive integer,

K = B_{2}^{3}

, LB=-2, UB=2, and

gridDim . x = gridDim . y = blockDim . x = 1024 .

Table 2 shows a comparison between these three stochastic algorithms. It can be seen that GN_CRS2_LM is better than the other ones.

4. Computational Experiments

All algorithms were coded in CUDA 12.2 and gcc 13.2.1. The computer’s graphics card is an NVIDIA RTX A4000.

4.1. Covering Functional of the Euclidean Unit Disc

Let

B_{2}^{2}

be the Euclidean unit disc. In this situation,

d (x, y)

is the Euclidean distance between x and y. The discretization of

Q_{2}

is performed using threadIdx.x for the x axis and blockIdx.x for the y axis. For a positive integer i, let

i = blockDim . x = gridDim . x

, then the values of threadIdx.x and blockIdx.x range from 0 to

i - 1

. Let

\begin{matrix} S_{i}^{2} = \{(x, y) ∣ x, y \in \{- 1 + \frac{2 k}{i - 1} ∣ k \in [i - 1] \cup \{0\}\}\} . \end{matrix}

It is clear that

\frac{\sqrt{2}}{2} Q_{2} \subseteq B_{2}^{2} \subseteq Q_{2} .

Let

S = S_{i}^{2} \cap (\frac{1 + \frac{\sqrt{2}}{2} (i - 1)}{\frac{\sqrt{2}}{2} (i - 1)} K) = S_{i}^{2} \cap (\frac{2 + \sqrt{2} (i - 1)}{\sqrt{2} (i - 1)} K) .

By Theorem 6, we have

B_{2}^{2} \subseteq S + \frac{1}{i - 1} Q_{2}

. By Corollary 3.1 in [9], there is a p-optimal configuration of

B_{2}^{2}

contained in

B_{2}^{2}

. Thus we can take

LB = - 1

and

UB = 1

. Proposition 7 shows that

Γ_{p} (B_{2}^{2}) \leq Γ_{p} (S) + \frac{\sqrt{2}}{i - 1} .

Numerical estimates of

Γ_{p} (B_{2}^{2})

are summarized in Table 3.

4.2. Covering Functionals of Three-Dimensional Convex Bodies

For each

K \in K^{3}

satisfying

α Q_{3} \subseteq K \subseteq Q_{3}

, let

i = gridDim . x = gridDim . y = blockDim . x

be a positive integer, then the values of threadIdx.x, blockIdx.x and blockIdx.y range from 0 to

i - 1

. Let

\begin{matrix} S_{i}^{3} : & = \{(x, y, z) ∣ x, y, z \in \{- 1 + \frac{2 k}{i - 1} ∣ k \in [i - 1] \cup 0\}\}, \end{matrix}

and

S = S_{i}^{3} \cap (\frac{1 + α (i - 1)}{α (i - 1)} K) .

By Theorem 6 and Proposition 7, we have

Γ_{p} (K) \leq Γ_{p} (S) + \frac{1}{α (i - 1)} .

(8)

4.2.1. Covering Functionals of $B_{2}^{3}$

By Remark 9, we set

LB = - 2

and

UB = 2

. Clearly,

\frac{\sqrt{3}}{3} Q_{3} \subseteq B_{2}^{3} \subseteq Q_{3} .

From (8), we have

Γ_{p} (B_{2}^{3}) \leq Γ_{p} (S) + \frac{\sqrt{3}}{i - 1} .

Numerical estimations of

Γ_{p} (B_{2}^{3})

for

p \in 4, 5, 6, 7, 8

are summarized in Table 4.

Table 4. Numerical estimations of

Γ_{p} (B_{2}^{3})

Table 4. Numerical estimations of

Γ_{p} (B_{2}^{3})

i	LB	UB	p	$Γ_{p} (S_{i})$	Ranges of $Γ_{p} (B_{2}^{3})$	Known Exact Value
1024	$- 2$	2	4	0.942359⋯	$\leq 0.9441 \dots$	0.943⋯[8]
1024	$- 2$	2	5	0.894146⋯	$\leq 0.8959 \dots$	0.894⋯[8]
1024	$- 2$	2	6	0.816220⋯	$\leq 0.8180 \dots$	0.816⋯[8]
1024	$- 2$	2	7	0.777139⋯	$\leq 0.7789 \dots$	0.778⋯[8]
1024	$- 2$	2	8	0.744846⋯	$\leq 0.7466 \dots$

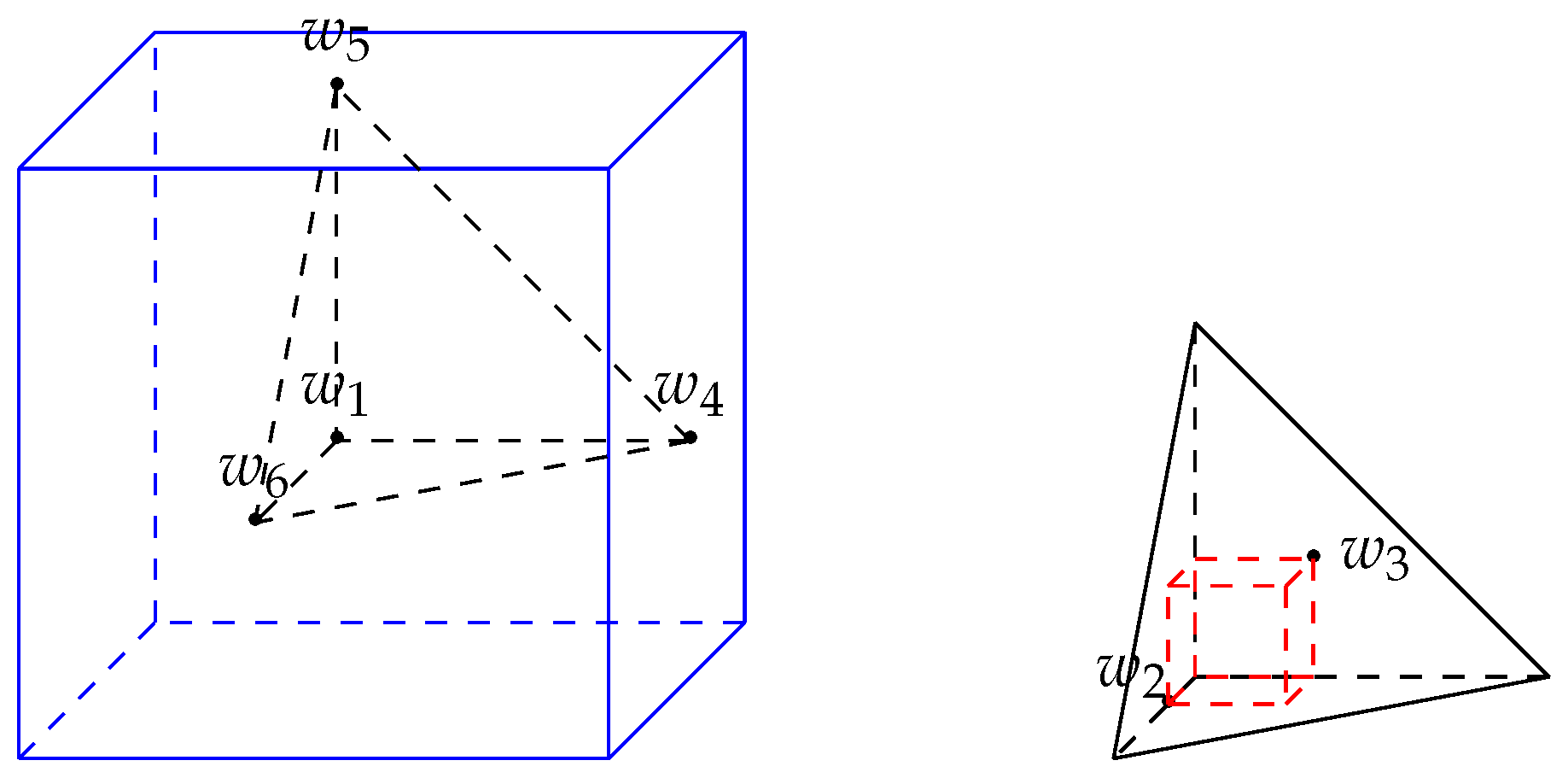
4.2.2. Covering Functional of the Regular Tetrahedron

Let

T = \{x \in R^{3} ∣ p_{i} (x) \geq 0 and \sum_{i \in [3]} p_{i} (x) \leq 1\} .

Thus T is a regular tetrahedron affinely equivalent to

T_{1} = \{x \in R^{3} ∣ p_{i} (x) \geq - \frac{1}{5} and \sum_{i \in [3]} p_{i} (x) \leq \frac{3}{5}\} .

Clearly,

T_{1} = \{x \in R^{n} ∣ A x \leq B\}

, where

A = [\begin{matrix} \frac{5}{3} & \frac{5}{3} & \frac{5}{3} \\ - 5 & 0 & 0 \\ 0 & - 5 & 0 \\ 0 & 0 & - 5 \end{matrix}] a n d B = [\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}] .

Let

v_{i} (x) = p_{i} (x) - p_{i} (c)

. Then

\begin{matrix} A [x - c] & = [\begin{matrix} \frac{5}{3} & \frac{5}{3} & \frac{5}{3} \\ - 5 & 0 & 0 \\ 0 & - 5 & 0 \\ 0 & 0 & - 5 \end{matrix}] \cdot [\begin{matrix} v_{1} (x) \\ v_{2} (x) \\ v_{3} (x) \end{matrix}] = [\begin{matrix} \frac{5}{3} (v_{1} (x)) + \frac{5}{3} (v_{2} (x)) + \frac{5}{3} (v_{3} (x)) \\ - 5 (v_{1} (x)) \\ - 5 (v_{2} (x)) \\ - 5 (v_{3} (x)) \end{matrix}] . \end{matrix}

By Lemma 3, the dissimilarity

d (x, c)

between x and c is given by

d (x, c) = max \frac{5}{3} v_{1} (x) + \frac{5}{3} v_{2} (x) + \frac{5}{3} v_{3} (x), - 5 v_{1} (x), - 5 v_{2} (x), - 5 v_{3} (x) .

It can be verified that

\frac{1}{5} Q_{3} \subseteq T_{1} \subseteq Q_{3},

see Figure 3, where

\begin{matrix} w_{1} = (- \frac{1}{5}, - \frac{1}{5}, - \frac{1}{5}), w_{2} = (- \frac{1}{5}, \frac{1}{5}, - \frac{1}{5}), w_{3} = (\frac{1}{5}, - \frac{1}{5}, \frac{1}{5}), \\ w_{4} = (1, - \frac{1}{5}, - \frac{1}{5}), w_{5} = (- \frac{1}{5}, - \frac{1}{5}, 1), and w_{6} = (- \frac{1}{5}, 1, - \frac{1}{5}) . \end{matrix}

By Remark 9, we take

LB = - 2

and

UB = 2

. By (8), we have

Γ_{p} (T) \leq Γ_{p} (S) + \frac{5}{i - 1} .

Numerical estimations of

Γ_{p} (T)

for

p \in 4, 5, 6, 7, 8

are summarized in Table 5.

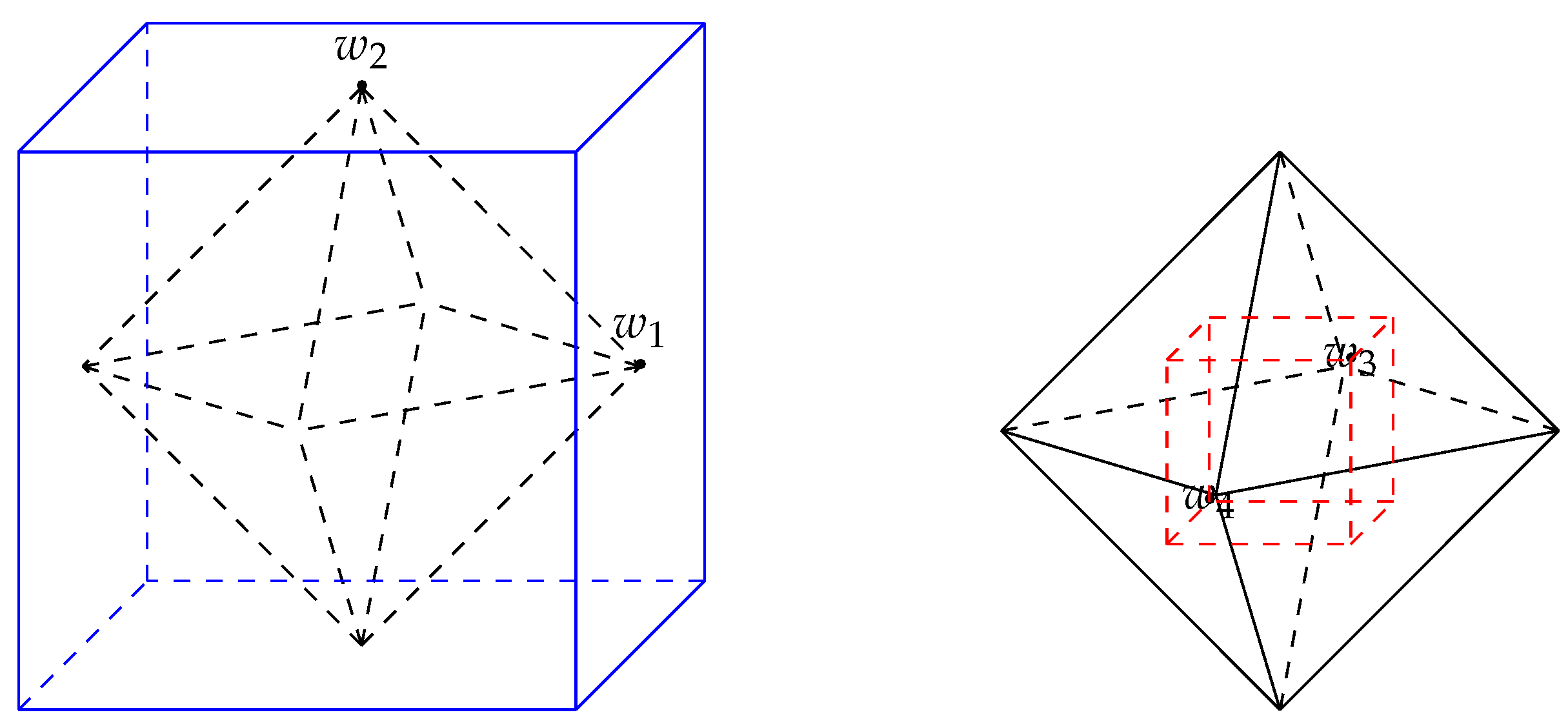
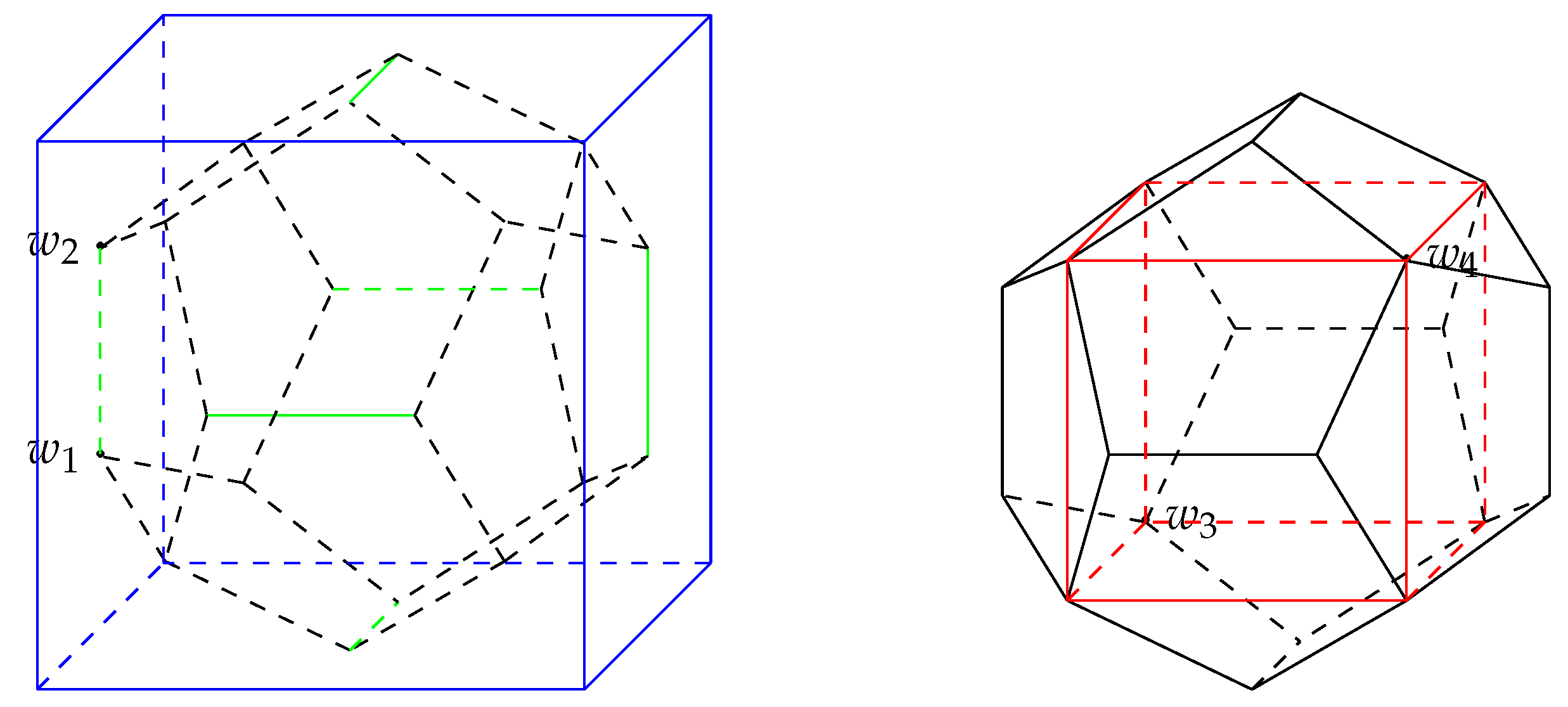
4.2.3. Covering Functional of the Regular Octahedron

Let

B_{1}^{3} = \{x \in R^{3} ∣ \sum_{i \in [3]} | p_{i} (x) | \leq 1\} .

Then

B_{1}^{3}

is a regular octahedron. By Lemma 3, the dissimilarity between x and c with respect to

B_{1}^{3}

is given by

d (x, c) = | v_{1} (x) | + | v_{2} (x) | + | v_{3} (x) | .

It can be verified that

\frac{1}{3} Q_{3} \subseteq B_{1}^{3} \subseteq Q_{3},

see Figure 4, where

w_{1} = (1, 0, 0), w_{2} = (0, 0, 1), w_{3} = (- \frac{1}{3}, - \frac{1}{3}, - \frac{1}{3}), and w_{4} = (\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) .

By Remark 9, we can set

LB = - 2

and

UB = 2

. From (8), we have

Γ_{p} (B_{1}^{3}) \leq Γ_{p} (S) + \frac{3}{i - 1} .

Numerical estimations of

Γ_{p} (B_{1}^{3})

for

p \in 6, 7, 8

are summarized in Table 6.

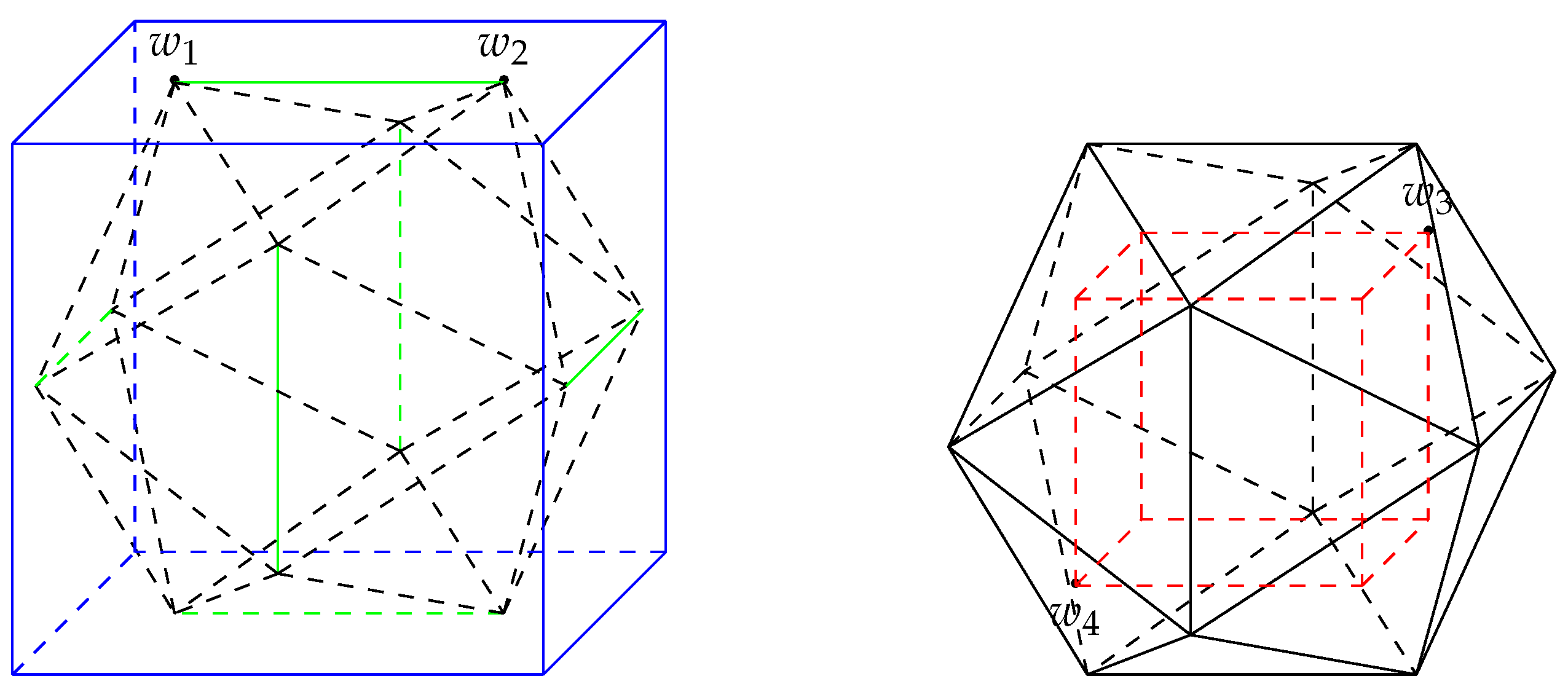
4.2.4. Covering Functional of the Regular Dodecahedron

Let P be the regular dodecahedron having the form

P = \{x \in R^{3} ∣ φ | p_{1} (x) | + | p_{2} (x) | \leq 1, φ | p_{2} (x) | + | p_{3} (x) | \leq 1, φ | p_{3} (x) | + | p_{1} (x) | \leq 1\},

where

φ = \frac{\sqrt{5} - 1}{2}

. By Lemma 3, the dissimilarity between x and c with respect to P is given by

\begin{matrix} d (x, c) = max { & φ v_{1} (x) + v_{2} (x), φ v_{1} (x) - v_{2} (x), - φ v_{1} (x) + v_{2} (x), - φ v_{1} (x) - v_{2} (x), \\ φ v_{2} (x) + v_{3} (x), φ v_{2} (x) - v_{3} (x), - φ v_{2} (x) + v_{3} (x), - φ v_{2} (x) - v_{3} (x), \\ φ v_{3} (x) + v_{1} (x), φ v_{3} (x) - v_{1} (x), - φ v_{3} (x) + v_{1} (x), - φ v_{3} (x) - v_{1} (x)} . \end{matrix}

It can be verified that

φ Q_{3} \subseteq P \subseteq Q_{3},

see Figure 5, where

w_{1} = (- 1, 0, φ - 1), w_{2} = (- 1, 0, 1 - φ), w_{3} = (- φ, - φ, - φ), and w_{4} = (φ, φ, φ) .

By Remark 9, we can set

LB = - 2

and

UB = 2

. From (8), we have

Γ_{p} (P) \leq Γ_{p} (S) + \frac{1}{φ (i - 1)} .

Numerical estimations of

Γ_{p} (P)

for

p \in 5, 6, 7, 8

are summarized in Table 7.

The estimate of

Γ_{8} (P)

is much better than that given in [27].

4.2.5. Covering Functional of the Regular Icosahedron

Let M be the regular icosahedron having the following form

\begin{matrix} \begin{matrix} M = {x \in R^{3} | φ |p_{1} (x)| & + φ |p_{2} (x)| + φ |p_{3} (x)| \leq 1, (φ - 1) | p_{1} (x) | + | p_{3} (x) | \leq 1, \\ | p_{1} (x) | + (φ - 1) | p_{2} (x) | \leq 1, | p_{2} (x) | + (φ - 1) | p_{3} (x) | \leq 1}, \end{matrix} \end{matrix}

where

φ = \frac{\sqrt{5} - 1}{2}

. By Lemma 3, the dissimilarity between x and c with respect to M is given by

\begin{matrix} \begin{matrix} d (x, c) = max {- φ v_{1} (x) + φ v_{2} (x) + φ v_{3} (x), - φ v_{1} (x) + φ v_{2} (x) - φ v_{3} (x), \\ φ v_{1} (x) + φ v_{2} (x) + φ v_{3} (x), φ v_{1} (x) + φ v_{2} (x) - φ v_{3} (x), - φ v_{1} (x) - φ v_{2} (x) + φ v_{3} (x), \\ φ v_{1} (x) - φ v_{2} (x) + φ v_{3} (x), φ v_{1} (x) - φ v_{2} (x) - φ v_{3} (x), - φ v_{1} (x) - φ v_{2} (x) - φ v_{3} (x), \\ (φ - 1) v_{1} (x) + v_{3} (x), (φ - 1) v_{1} (x) - v_{3} (x), (1 - φ) v_{1} (x) + v_{3} (x), (1 - φ) v_{1} (x) + v_{3} (x), \\ (φ - 1) v_{2} (x) + v_{1} (x), (φ - 1) v_{2} (x) - v_{1} (x), (1 - φ) v_{2} (x) + v_{1} (x), (1 - φ) v_{2} (x) + v_{1} (x), \\ (φ - 1) v_{3} (x) + v_{2} (x), (φ - 1) v_{3} (x) - v_{2} (x), (1 - φ) v_{3} (x) + v_{2} (x), (1 - φ) v_{3} (x) + v_{2} (x)} . \end{matrix} \end{matrix}

It can be verified that

\frac{1 + φ}{3} Q_{3} \subseteq M \subseteq Q_{3},

see Figure 6, where

\begin{matrix} w_{1} = (φ - 1, 0, 1), w_{2} = (1 - φ, 0, 1), \\ w_{3} = (- \frac{1 + φ}{3}, \frac{1 + φ}{3}, - \frac{1 + φ}{3}), and w_{4} = (\frac{1 + φ}{3}, - \frac{1 + φ}{3}, \frac{1 + φ}{3}) . \end{matrix}

By Remark 9, we take

LB = - 2

and

UB = 2

. By (8), we have

Γ_{p} (M) \leq Γ_{p} (S) + \frac{3}{(1 + φ) (i - 1)} .

Numerical estimations of

Γ_{p} (M)

for

p \in 4, 5, 6, 7, 8

are summarized in Table 8.

Compare to the estimate

Γ_{6} (M) \leq 0.873

given in [27], our estimate here is much better.

5. Conclusion

This paper proposes an algorithm based on CUDA for estimating covering functionals of three-dimensional convex polytopes, which is more efficient than the geometric branch-and-bound method presented in [9]. Theoretical accuracy of our algorithm is given by (8). Restrictions on the dimensions of each grid makes the implementation of our algorithm in higher dimensions difficult.

Author Contributions

Conceptualization, S.W.; methodology, X.H. and S.W.; software, X.H. ; validation, S.W. and L.Z.; writing–original draft preparation, X.H.; writing–review and editing, S.W. and L.Z.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the [National Natural Science Foundation of China] grant number [12071444] and the [Fundamental Research Program of Shanxi Province of China] grant numbers [202103021223191].

Data Availability Statement

Data sharing is not applicable, since no dataset was generated or analyzed during the current study.

Conflicts of Interest

The authors declare no conflict of interest.

References

Boltyanski, V.; Martini, H.; Soltan, P.S. Excursions into Combinatorial Geometry, Universitext; Springer: Verlag, Berlin/Heidelberg, Germany, 1997. [Google Scholar]
Martini, H.; Soltan, V. Combinatorial problems on the illumination of convex bodies. Aequationes Math. 1999, 57, 121–152. [Google Scholar] [CrossRef]
Bezdek, K. Classical Topics in Discrete Geometry, CMS Books in Mathematics/Ouvrages deMathématiques de la SMC; Springer: New York, 2010. [Google Scholar]
Brass, P.; Moser, M.; Pach, J. Research Problems in Discrete Geometry; Springer: New York, NY, USA, 2005. [Google Scholar]
Bezdek, K.; Khan, M.A. The geometry of homothetic covering and illumination. In Discrete Geometry and Symmetry; Springer: Cham, Switzerland, 2018; Volume 234, pp. 1–30. [Google Scholar]
Rogers, C.A.; Zong, C. Covering convex bodies by translates of convex bodies. Mathematika 1997, 44, 215–218. [Google Scholar] [CrossRef]
Papadoperakis, I. An estimate for the problem of illumination of the boundary of a convex body in E³. Geom. Dedicata 1999, 75, 275–285. [Google Scholar] [CrossRef]
Zong, C. A quantitative program for Hadwiger’s covering conjecture. Sci. China Math. 2010, 53, 2551–2560. [Google Scholar] [CrossRef]
He, C.; Lv, Y.; Martini, H.; Wu, S. A branch-and-bound approach for estimating covering functionals of convex bodies. J. Optimiz. Theory. App. 2023, 196, 1036–1055. [Google Scholar] [CrossRef]
Scholz, D. Deterministic Global Optimization: Geometric Branch-and-Bound Methods and their Applications; Springer: New York, 2012. [Google Scholar]
Yu, M.; Lv, Y.; Zhao, Y.; He, C.; Wu, S. Estimations of covering functionals of convex bodies based on relaxation algorithm. Mathematics 2023, 11, 2000. [Google Scholar] [CrossRef]
Han, T.D.; Abdelrahman, T.S. Hicuda: High-level GPGPU programming. IEEE T. Parall. Distr. 2011, 22, 78–90. [Google Scholar] [CrossRef]
Harris, M. Optimizing parallel reduction in CUDA. Available online: https://developer.download.nvidia.cn/assets/cuda/files/reduction.pdf.
Tomczak-Jaegermann, N. Banach-Mazur distances and finite-dimensional operator ideals. In Pitman Monographs and Surveys in Pure and Applied Mathematics; John Wiley & Sons, Inc.: New York, 1989; Volume 38. [Google Scholar]
Dind, K.; Tan, T.A. Review on general purpose computing on GPU and its applications in computational intelligence. CAAI Transactions on Intelligent Systems 2015, 10, 1–11. [Google Scholar]
Cheng, J.; Grossman, M.; Mckercher, T. Professional CUDA C Programming; John Wiley & Sons, Inc.: New York, 2014. [Google Scholar]
Ma, X.; Han, W. A parallel multi-swarm particle swarm optimization algorithm based on CUDA streams. In 2018 Chinese Automation Congress (CAC); IEEE: 2018; pp. 3002–3007.
Guide, D. CUDA C Programming Guide; NVIDIA, 2013.
Zhang, Y.; Chen, L.; An, X.; Yan, S. Study on performance optimization of reduction algorithm targeting GPU computing platform. Computer Science 2019, 46, 306–314. [Google Scholar]
Johnson, S.G. The NLopt Nonlinear-Optimization Package, 2010.
Tseng, L.Y.; Chen, C. Multiple trajectory search for large scale global optimization. In 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), IEEE: Hong Kong, 2008; pp. 3052–3059.
Wang, H.; Shao, H. System optimization strategy based on genetic algorithm and controlled random search. Control Theory and Applications 2000, 06, 907–910. [Google Scholar]
Hansen, N.; Ostermeier, A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef] [PubMed]
Branke, J.; Deb, K.; Miettinen, K.; Slowinski, R. Multi-objective Optimization: Interactive and Evolutionary Approaches; Springer: Verlag Berlin Heidelberg, 2008. [Google Scholar]
Abor, G.; Oth, F.T. Thinnest covering of a circle by eight, nine, or ten congruent circles. In Combinatorial and Computational Geometry; Cambridge University Press: Cambridge, UK, 2005; Volume 52, pp. 361–376. [Google Scholar]
Yu, M.; Gao, S.; He, C.; Wu, S. Estimations of covering functionals of simplices. Math. Inequal. Appl. 2023, 26, 793–809. [Google Scholar] [CrossRef]
Wu, S.; He, C. Covering functionals of convex polytopes. Linear. Algebra. Appl. 2019, 577, 53–68. [Google Scholar] [CrossRef]

Figure 2. Discretize

{[- 1, 1]}^{3}

with CUDA.

Figure 2. Discretize

{[- 1, 1]}^{3}

with CUDA.

Figure 3. Inscribed cube and circumscribed cube of the regular tetrahedron.

Figure 4. Circumscribed and inscribed cubes of the regular octahedron.

Figure 5. Inscribed cube and circumscribed cube of the regular dodecahedron.

Figure 6. Inscribed cube and circumscribed cube of the regular icosahedron.

Table 1. Comparison of results between the algorithm based on CUDA and the geometric branch-and-bound approach.

Algorithm	Algorithm 1	The geometric branch-and-bound approach
accuracy	$\frac{\sqrt{3}}{1023}$	0.0001
$Γ (S, C_{1})$	1.002750⋯	1.002089⋯
Time	42.258720 $m s$	32.594993 s
$Γ (S, C_{2})$	0.748103⋯	0.748099⋯
Time	42.232449 $m s$	0.303316 s

Table 2. Comparison between different stochastic algorithms.

Algorithm	GN_CRS2_LM	GN_ESCH	GN_ISRES
$Γ_{5} (B_{2}^{3})$	0.894120⋯	0.896774⋯	0.895573⋯
Time	3655 s	7863 s	35231 s
$Γ_{6} (B_{2}^{3})$	0.817386⋯	0.818881⋯	0.819020⋯
Time	3332 s	8036 s	34921 s

Table 3. Numerical estimations of

Γ_{p} (B_{2}^{2})

Table 3. Numerical estimations of

Γ_{p} (B_{2}^{2})

i	LB	UB	p	$Γ_{p} (S_{i})$	Ranges of $Γ_{p} (B_{2}^{2})$	Known Exact Value
1024	$- 1$	1	3	0.865850⋯	$\leq 0.8673 \dots$	0.866⋯[5]
1024	$- 1$	1	4	0.706002⋯	$\leq 0.7074 \dots$	0.707⋯[5]
1024	$- 1$	1	5	0.609076⋯	$\leq 0.6105 \dots$	0.609⋯[5]
1024	$- 1$	1	6	0.555575⋯	$\leq 0.5570 \dots$	0.555⋯[5]
1024	$- 1$	1	7	0.499461⋯	$\leq 0.5009 \dots$	0.5[25]
1024	$- 1$	1	8	0.444873⋯	$\leq 0.4463 \dots$	0.445⋯[25]

Table 5. Numerical estimations of

Γ_{p} (T)

Table 5. Numerical estimations of

Γ_{p} (T)

i	LB	UB	p	$Γ_{p} (S_{i})$	Ranges of $Γ_{p} (T)$	Known Exact Value or Estimations
1024	$- 2$	2	4	0.754079⋯	$\leq 0.7590 \dots$	$\frac{3}{4}$ [8]
1024	$- 2$	2	5	0.697766⋯	$\leq 0.7027 \dots$	$\frac{9}{13}$ [8]
1024	$- 2$	2	6	0.678219⋯	$\leq 0.6832 \dots$	$\frac{2}{3}$ [26]
1024	$- 2$	2	7	0.643850⋯	$\leq 0.6488 \dots$	$[\frac{3}{5}, \frac{7}{11}]$ [26]
1024	$- 2$	2	8	0.630140⋯	$\leq 0.6351 \dots$	$\leq \frac{8}{13}$ [26]

Table 6. Numerical estimations of

Γ_{p} (B_{1}^{3})

Table 6. Numerical estimations of

Γ_{p} (B_{1}^{3})

i	LB	UB	p	$Γ_{p} (S_{i})$	Ranges of $Γ_{p} (B_{1}^{3})$	Known Exact Value
1024	$- 2$	2	6	0.667671⋯	$\leq 0.6707 \dots$	$\frac{2}{3}$ [8]
1024	$- 2$	2	7	0.667666⋯	$\leq 0.6706 \dots$	$\frac{2}{3}$ [8]
1024	$- 2$	2	8	0.667657⋯	$\leq 0.6706 \dots$	$\frac{2}{3}$ [8]

Table 7. Numerical estimations of

Γ_{p} (P)

Table 7. Numerical estimations of

Γ_{p} (P)

i	LB	UB	p	$Γ_{p} (S_{i})$	Ranges of $Γ_{p} (P)$
1024	$- 2$	2	5	0.840639⋯	$\leq 0.8423 \dots$
1024	$- 2$	2	6	0.761430⋯	$\leq 0.7631 \dots$
1024	$- 2$	2	7	0.745951⋯	$\leq 0.7476 \dots$
1024	$- 2$	2	8	0.711539⋯	$\leq 0.7132 \dots$

Table 8. Numerical estimations of

Γ_{p} (M)

Table 8. Numerical estimations of

Γ_{p} (M)

i	LB	UB	p	$Γ_{p} (S_{i})$	Ranges of $Γ_{p} (M)$
1024	$- 2$	2	4	0.873606⋯	$\leq 0.8755 \dots$
1024	$- 2$	2	5	0.848224⋯	$\leq 0.8501 \dots$
1024	$- 2$	2	6	0.746998⋯	$\leq 0.7489 \dots$
1024	$- 2$	2	7	0.747460⋯	$\leq 0.7493 \dots$
1024	$- 2$	2	8	0.731832⋯	$\leq 0.7337 \dots$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Algorithm Based on CUDA for Estimating Covering Functionals of Convex Bodies

Abstract

1. Introduction

2. Covering Functional and Error Estimation

3. An Algorithm Based on CUDA for Γ p ( S )

3.1. An Algorithm Based on CUDA for Γ ( S , C )

3.2. Different Stochastic Global Optimization Algorithms for Γ p ( S )

4. Computational Experiments

4.1. Covering Functional of the Euclidean Unit Disc

4.2. Covering Functionals of Three-Dimensional Convex Bodies

4.2.1. Covering Functionals of B 2 3

4.2.2. Covering Functional of the Regular Tetrahedron

4.2.3. Covering Functional of the Regular Octahedron

4.2.4. Covering Functional of the Regular Dodecahedron

4.2.5. Covering Functional of the Regular Icosahedron

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3. An Algorithm Based on CUDA for $Γ_{p} (S)$

3.1. An Algorithm Based on CUDA for $Γ (S, C)$

3.2. Different Stochastic Global Optimization Algorithms for $Γ_{p} (S)$

4.2.1. Covering Functionals of $B_{2}^{3}$