Preprint
Article
Symmetry, Music and Water
Altmetrics
Downloads
795
Views
2366
Comments
0
This version is not peer-reviewed
Submitted:
16 January 2024
Posted:
17 January 2024
You are already at the latest version
Alerts
Abstract
There is a deep link existing between symmetry and nature that may be best apprehended by using group theory. In physics, giving a symmetry group is entirely equivalent to fix natural laws (Noether’s theorem). Within such a framework, it follows that all fundamental mechanical laws may be given by defining a group of symmetry operations belonging to the Gal(3,1) symmetry group having ten generators (3 + 3 + 3 + 1 = 10). The move to special relativity amounts simply to substitute another group ISO(3,1) to Gal(3,1) and having the same number of generators. In both cases, one immediately perceives that we live in universe with 3 dimensions of space and 1 dimension of time. A further progress could be made by looking for the symmetry group that leaves Maxwell’s equations invariant. The answer to this fundamental question is the group ISO(4,2)⊗U(2)⊗U(2) characterized by 23 generators : 15 = 10 + 5 for the conformal group ISO(4,2), 4 for U(2) and hence 8 = 4 + 4 for the compact part U(2)⊗U(2) that could be related to the existence of quantum physics besides relativity. As ISO(3,1) is a sub-group of ISO(4,2), the two numbers 4 and 2 suggests that, taking into account the existence of light besides matter, we live in an universe having 4 spacelike dimensions and 2 time-like dimensions. Here, it is proposed that, as music is characterized by a scale-invariant symmetry operation (transposition by octaves) and that as time may be perceived differently in shamanic trance for instance, the two “new” dimensions of our universe may be related to music and consciousness. Related to the fifth dimension of music, the notion of diapason linking physical frequencies to a musical note is revisited. It is thus proposed to adopt a new A4 = 429.62 Hz value based on universal physical constants of our universe and on the mass of the water molecule H₂O, the most abundant molecule in the universe. Demonstration is done that this new diapason is superior to other diapasons based on frequencies of 440 Hz or even 432 Hz
Keywords:
Subject: Arts and Humanities - Music
Introduction
Life appeared very early on Earth, around 4 billion years ago. Moreover, from one end of the world to the other, we agree that water is life. In fact, the utmost importance of water stems for the empirical fact that the three most abundant elements in the universe are hydrogen (92.8 at%), helium (7.1 at%) and oxygen (0.1 at%) [1]. As helium is a monoatomic gas, it follows that the water molecule, made up of two hydrogen atoms linked to the same oxygen atom (formula H₂O), is necessarily the most abundant molecule in the entire universe. Another crucial fact is that everything containing water has a shape. Hence the expression “Morphogenic Water”, forged a few years ago in order stressing this fundamental fact [2,3]. 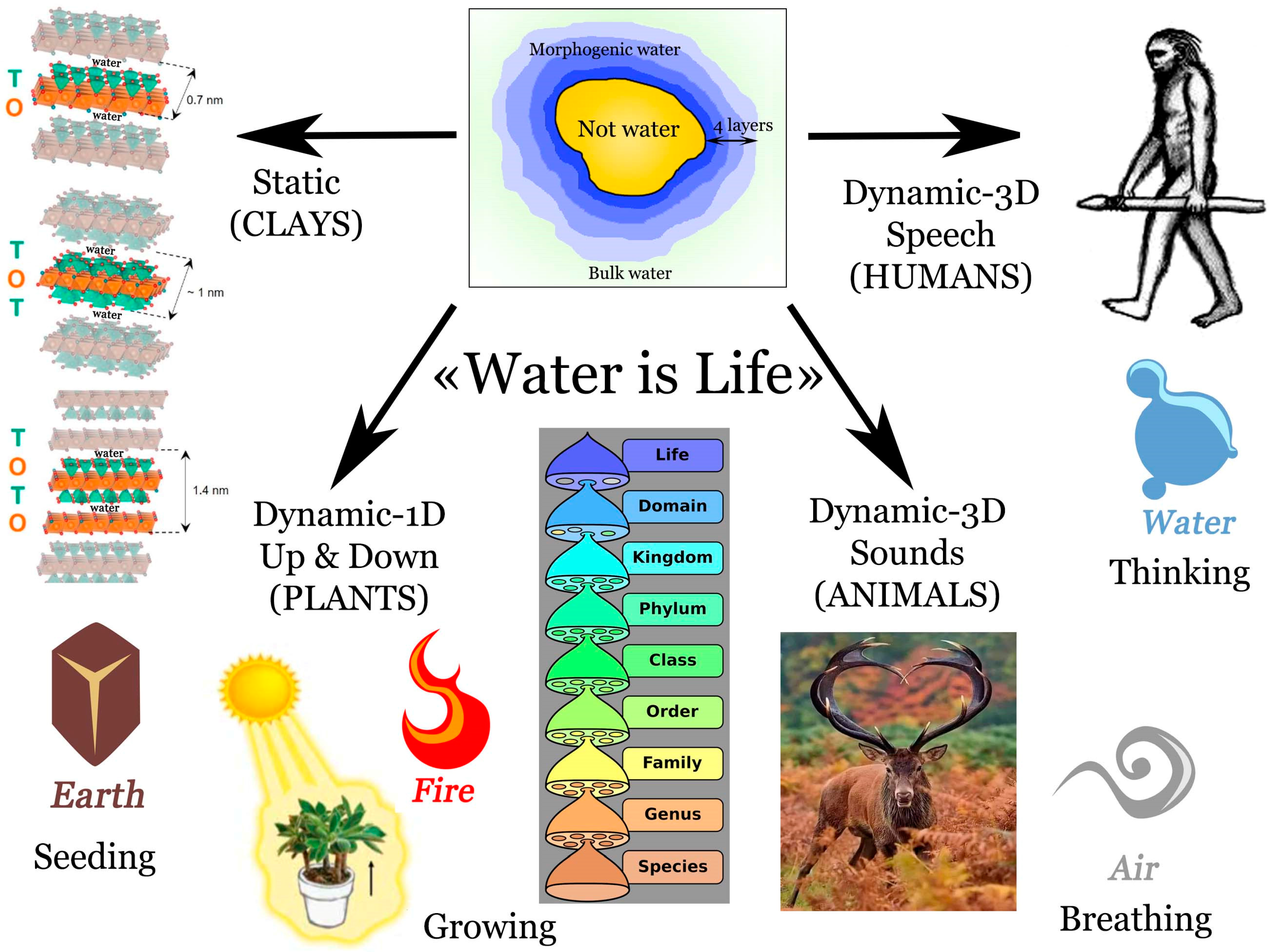As shown in Figure 1, four main types of morphogenic water may be readily identified in Nature. The very first class is when water is statically trapped between various aluminosilicate sheets forming what is called “clays” or “earth” according to Aristotle’s four elementary qualities [4]. The second class is organisms called “plants” that may be derived from the combined action of sun and water contained in earth. As sun is the ubiquitous source of energy on earth, we may refer to Aristotle’s second “fire” elementary quality. Here, water is moving up and down, i.e. only in one direction. The third class is obtained when plants are eaten by organisms capable of moving in three-dimensional space. These organisms are called “animals” and, unlike plants, which grow in silence, they can produce a range of sounds in the form of cries, grunts or chirps. As they have the ability to breathe form air, we may refer to Aristotle’s third “air” elementary quality. Finally, there’s the fourth class, corresponding to human beings, who can do everything that animals can do. What makes human special is that they are able to have a language structured in words and phrases, combined with a consciousness of existence that translates into highly elaborate and symbolic societal rituals. As three elementary qualities have already been attributed to clays, plants and animals, this leaves the fourth “water” for referring to consciousness. Theoretical reasons behind such an association have been discussed in depth elsewhere [5].
The human being with a cerebral cortex, Homo Sapiens, only appeared 300,000 years ago. One of the original features of Homo Sapiens was its ability to theorize about the external world around it. In contrast, an animal or plant doesn’t ask questions about its environment or its place in the universe. Of course, like a human being, an animal or plant acts according to its inner feelings. But the expression of this inner feeling translates into growth in the case of a plant, and movement in the case of an animal. In humans, there’s a third possibility: articulate verbal language. Both plants and animals have body language, so they can never lie. For animals, this should be obvious. But, for plants, one may wonder how a plant may have its own language. In fact, since the pioneering work of Chandra Bose, we know that plants are irritable [6], and such an irritability may be exploited after conversion of the vital electrical activity of a plant into musical notes [7]. So, both plants and animals are able to express their feelings as sounds. But, thanks to their verbal language, human beings are faced with a Cornelian choice: to tell the truth or to lie? This is because words are sounds plus something else which is called “meaning”.
- The seven frames of thought
Having explained what is “Morphogenic water”, we’re now going to look at the extent to which the concept of symmetry can help us bring some order into human thought. Indeed, when it comes to grasping the development of human thought in all its breadth, it’s very difficult to go back in time beyond ancient Egypt. Some may ask, quite rightly, why concern ourselves with very primitive ways of thinking when we have such a powerful modern science at our disposal. The answer to this question lies in the fact that modern science has completely overlooked the fact that a human being is not only made of matter. If this were the case, there would be no soul, no poetry, no art, no love in our existence. Once again, we come back to the need for alchemy between the material and spiritual sides of human nature. And the only common ground between matter and spirit is precisely that both can use numbers to express themselves. One quantitatively as a sum of units, the other more qualitatively as a division of a single unit. As this qualitative side of numbers is largely obscured in the modern scientific approach, I’ll start with a few reminders.
To begin with, there’s the number 0, which, for our Ancients, symbolized the entire universe in its unmanifested, latent, potential state. The symbol of the ouroboros, a snake biting its own tail, reflected this very well. However, another number, 1, could also play this role. But it described a manifest, real and visible state of this same universe. Here, the snake has stopped biting its own tail and can unfold in the form of an undulation that has no beginning and no end. In short, we have a unit, 1, and thus an essence for everything to come.
The number 2, on the other hand, was the number of discriminations. In other words, a manifestation of polarity, allowing us to differentiate between the head and tail of the cosmic serpent. This polarity is, of course, a source of instability. For if I’m on the right, the question arises: wouldn’t I be better off on the left? Hence the dissatisfaction, and hence the movement to try and regain the initial calm, which is of course impossible. For, if two appears, nothing can ever be the same again. Unit 1 has become polarized, and this polarization can no longer be undone.
However, if it’s impossible to return to 1, we can move forward in search of a compromise. Here we reach the number 3, which is the production number of all stable terrestrial things. The Egyptians engraved it in stone in the shape of a triangle (pyramids), while the Greeks founded philosophy on thesis, antithesis and synthesis. Nowadays, popular wisdom holds the saying: “Never 2 without 3”. The triangle is in fact the first creator of regular three-dimensional solid shapes such as the tetrahedron, octahedron and icosahedron.
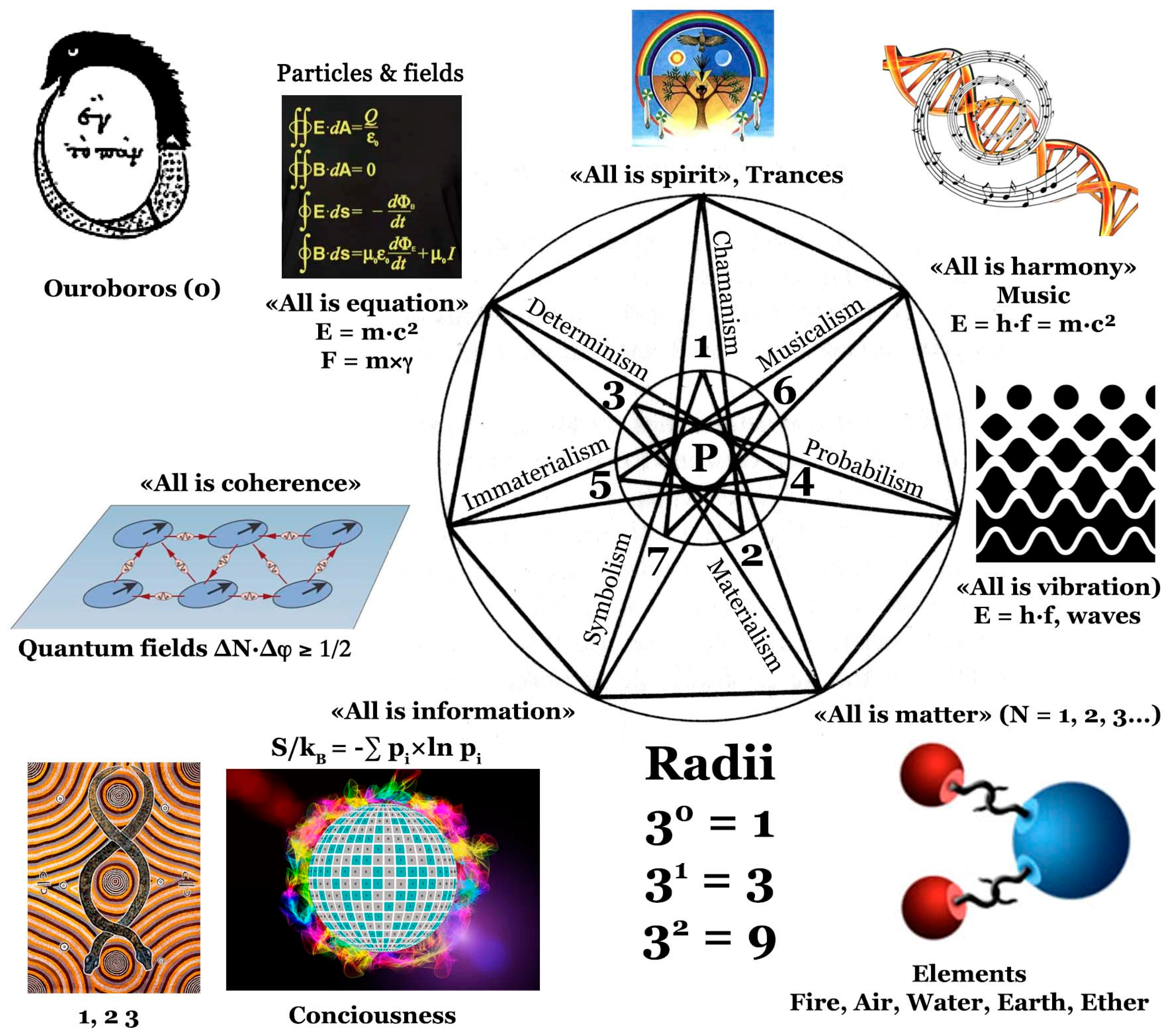
Now, let’s see what can be done with these first four integers: 0, 1, 2 and 3. The idea is to take the number 3, which represents stability, and consider its first three powers: 3⁰ = 1, 3¹ = 3 and 3² = 9. Next, we draw three concentric circles (A, B, C), the second of which (B) has triple the diameter of the first (A) and the third (C) has triple the diameter of the second (B). From any point on circle C, draw a tangent to circle A, crossing circle B at two points. From the second point, draw a new tangent to circle A, which will intersect circle C at another point other than the starting point. Repeat the same operation from this new point, and so on, until you have a double seven-pointed star (see Figure 2) [8].
The fact that such a construction is possible with a ruler and compass suggests that the number 7 must be important to human thought. Let’s see if this is indeed the case, by reviewing the different ways of thinking since human beings first pondered the “raison d’être” of things.
The most primitive frame of thought (shamanism) is undoubtedly linked to the idea that there are spirits in nature with whom it is possible to communicate via the shamanic trance. In fact, these altered states of consciousness are now being studied within a rigorous scientific framework [9].
The second frame of thought (materialism), can be linked to the idea that there are a number of fundamental elements in nature that account for the material variety of the universe. The exact nature of these fundamental elements varies from culture to culture. The emphasis here is on what can be seen, heard, touched, smelled or tasted. The third frame of thought (determinism) is linked to the idea that nothing happens by chance. Here, natural events are subject to a set of mathematical equations that enable us to accurately predict what will happen given a given set of initial conditions. We recognize here the framework of scientific thought developed from the seventeenth century onwards, mainly in Europe, which presupposes that, alongside matter, there is also light. We also know that, at the beginning of the twentieth century, this deterministic framework of thought proved totally inadequate to describe phenomena on the scale of a billionth of a meter (nanometer). Hence the birth of a fourth framework (probabilism) in which the deterministic equations of the macroscopic world are replaced by probabilistic equations from quantum physics.
However, the disadvantage of this fourth probabilistic framework is that every corpuscle of matter can be considered as a probability wave (wave/corpuscle duality). A fifth, more satisfactory framework of thought (immaterialism) has therefore been developed, based on quantum field theory. Here, there are no more waves or corpuscles, but only “quantum fields” which, depending on experimental conditions, can create particles or waves at will within a four-dimensional space-time, starting from a quantum vacuum that is the ultimate source of all reality.
The vast majority of physicists believe that this fifth framework is sufficient to describe all physical reality. However, a small minority believe that this framework also has its limitations, since it does not take into account symmetry operations of the “dilation” type, implying that the object under study remains invariant through change of scale. And, for such invariance to be ensured from the atomic to the macroscopic scale, it is necessary to introduce new so-called “scaling waves” that enable coherence to be preserved whatever the scale of observation [10]. The consequence of this state of affairs is the existence of “musical” laws in the vibratory organization of matter, hence the name “musicalism” for this sixth way of thinking.
Finally, recently, the existence of a seventh frame of thought has been proposed, symbolism, to account for the capacity of consciousness to manipulate information and give it meaning [11]. This framework is of course the most general, since it considers that everything is made up of information that can be stored both in the quantum vacuum and at the level of coherence domains that can appear when water undergoes the virtual excitations coming from this same quantum vacuum. From the point of view of symmetry, it’s worth noting that it’s possible to use group theory to validate different ways of thinking based on determinism. The idea here is to study the laws of nature and see which symmetry group can explain the mathematical form taken by these laws.
- Group theory
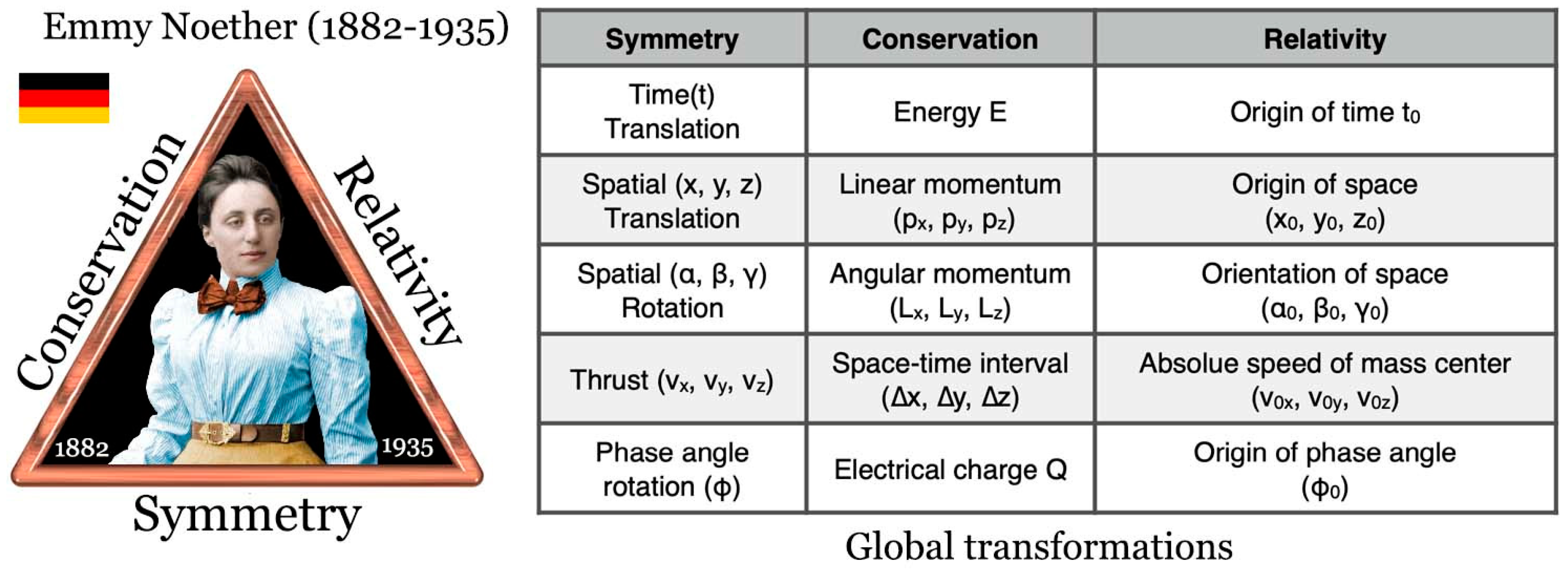
For the outer sensible world, we know that the world of elementary particles is totally ruled by symmetry considerations. Thus, when we try to marry quantum theory and general relativity, we end up with the idea that the notions of space, time, matter and electric charge don’t really exist. The only real entity is the vacuum, whether quantum or relativistic. Such a vacuum is a highly symmetrical medium that can be translated, rotated, expanded or contracted without changing its nature. All these operations form what is known as a symmetry group. What’s fascinating is that the simple fact of existence of a symmetry group is enough to define the form that physical laws will take. In other words, rather than making long and tedious measurements to empirically derive a law of nature, it’s better to look for symmetries. And, if symmetries are found, one may deduce the form that equations must take to remain invariant under the action of the symmetry group. Conversely, we can also start from a known physical law and look for the symmetry group that keeps the mathematical form of this law invariant. Modern physics has thus come to consider a number of symmetry groups acting either on the internal states of a quantum object, or on external states such as mass, velocity or spin. Each symmetry group containing a finite or infinite number of elements is defined by a finite number of generators, which can be combined to give an exhaustive list of all the elements making up the group. Moreover, when these generators depend on an infinitesimal parameter, Noether’s theorem [12] allows us to associate with each of them a physical quantity that will be conserved whatever the internal or external state of motion, as well as a quantity that will become unobservable.
Figure 3 summarized the fact that classical or quantum mechanics (first quantization) is equivalent to Galileo’s group Gal(3,1). The number 3 here means that this group operates in a 3-dimensional Euclidean (x, y, z) space, to which we add a fourth real parameter (t) playing the role of time. This group thus has 10 generators involving 3 spatial translations of infinitesimal distance (conservation of momentum), one temporal translation of infinitesimal duration (conservation of energy), 3 spatial rotations of infinitesimal angle (conservation of angular momentum) and 3 infinitesimal velocity changes called “thrusts” that may be considered as translations p → p + m·v in reciprocal linear momentum space. It follows that to fully characterize a corpuscle, we need to apply at least 3 labels to it: a mass m, an energy E and an angular momentum called “spin”. In the quantum version, we also demonstrate the existence of a selection rule prohibiting any quantum transition between states with different masses (conservation of mass). The laws of mechanics (Newton’s or Schrödinger’s equation, depending on whether the quantity of action involved is large or small), thermodynamics (first and second principles) and chemistry (conservation of mass) then derive from these great conservation laws imposed by the structure of Galileo’s group.
A trouble is then that the Gal(3,1) symmetry group is not able to describe electromagnetic phenomena. In other words, the famous Maxwell’s equations published in 1865 ruling electricity, magnetism and optics were not invariant through the symmetry operations of Gal(3,1). But, in May 1905 the French mathematician Henri Poincaré (1854–1912), communicating with his Dutch colleague H. A. Lorentz (1853– 1928), realized that the coordinate transformations leaving invariant Maxwell’s equations form another symmetry group, ISO(3,1), an acronym for “Inhomogeneous Special Orthogonal” group.
It is worth noticing that Poincaré’s ISO(3,1) symmetry group has seven infinitesimal generators in common with Gal(3,1): three spatial translations, three spatial rotations and one translation in time. The additional symmetries are three Lorentz’s boosts mixing each of the three space-coordinates with the time coordinate. This has the consequence of welding of space with time allowing only two Casimir invariants corresponding to the conservation of a single entity called mass-energy and another one named spin. In group-theory language, mass and energy now belong to the same irreducible representation of ISO(3,1). Whereas in the Gal(3,1) symmetry group, mass and energy belongs to different irreducible representations. Welding of space with time to form a 4D (4 = 3+1) space-time continuum noted M⁴ hereafter, is the reason for the existence of Einstein’s equation E = m·c².
However, just after the introduction of M⁴ Minkowski’s space, it was realized that Maxwell’s equations were in fact invariant under a larger Lie’s group, named the conformal group ISO(4,2). Here, five new generators are added to those defining ISO(3,1), one corresponding to dilatation in space and time and the four others to conformal symmetries that preserve angles between two arbitrary directions. The main consequence of existence of this new symmetry group is that the universe had better be considered as a 6D-continuum (6 = 4+2) with four space-like coordinates and two time-like coordinates. This meant that by specifying only four coordinates in M⁴ (x, y, z, t), some ambiguity remained. Consequently, one should also specify a fifth coordinate (s) setting the scale at which an observation is made. Such a fifth coordinate is crucial for living entities that could exist either as a single cell or as multicellular organisms able to grow in space and age in time. Concerning the second time-like coordinate of ISO(4,2) one may consider that any living entity is characterized by a birth date, a thing impossible in M⁴ where energy conservation implies that time, the conjugated variable to energy, has no origin (Noether’s thorem).
Basically, considering an hyper-surface in ISO(4,2), where an event is characterized by five coordinates (x, y, z, i·c·t, s), it becomes possible to speak of birth or death in an absolute sense. In other words, by combining the dilatation symmetry operation with translation and rotation symmetries, it is possible to build a quantum-mechanical proper time operator conjugated to mass. In a conformal space C⁵, it is thus meaningful to state that a given mass has appeared here (birthplace) at a precise time (birth date) and disappeared there (death place) at a posterior time (death date).
Moreover as ISO(4,2) implies the existence of a 6D-continumm, it follows that there is still a degree of freedom allowing discriminating between observable C⁵-hypersurfaces and other non-observable hypersurfaces. Hence, the idea that a sixth dimension allowing describing the information content in a V⁶ continuum. In fact, it was also realized that Maxwell’s equations were invariant under the symmetry operations of the highly symmetric ISO(4,2)⊗U(2)⊗U(2) group characterized by 6×5/2 + 22 + 22 = 23 generators. This new symmetry escaped notice for a long time because the eight integral-differential generators of U(2)⊗U(2) are associated with symmetry operations of a non-geometric nature. They are much harder to visualize than operations of the Lie algebra in the neighborhood of identity. The nature of these operators suggests again that it should exist a communication between all scales, from the smallest one to the largest and vice versa, whence non-locality and non-separability, which have been abundantly confirmed by experiments.
It follows from all these considerations that group theory fully validates our geometric construction of a regular seven-pointed star. The branch of shamanism and symbolism refers, of course, to the space V⁶, which unfolds in the group ISO(4,2) ⊗U(2) ⊗U(2). The musicalism branch to a hypersurface C⁵ in V⁶ reduced to the ISO(4,2) subgroup, and the immaterialism branch to the Minkowski subspace M⁴ deriving from the ISO(3,1) subgroup. The probabilism, determinism and materialism branches correspond to the symmetry group Gal(3,1), a subgroup of ISO(3,1). Probabilism takes into account the quantum aspect of nature that is ignored in determinism or materialism. Similarly, materialism breaks away from determinism as soon as we restrict ourselves to matter alone and ignore the existence of light.
- Pythagorean Music
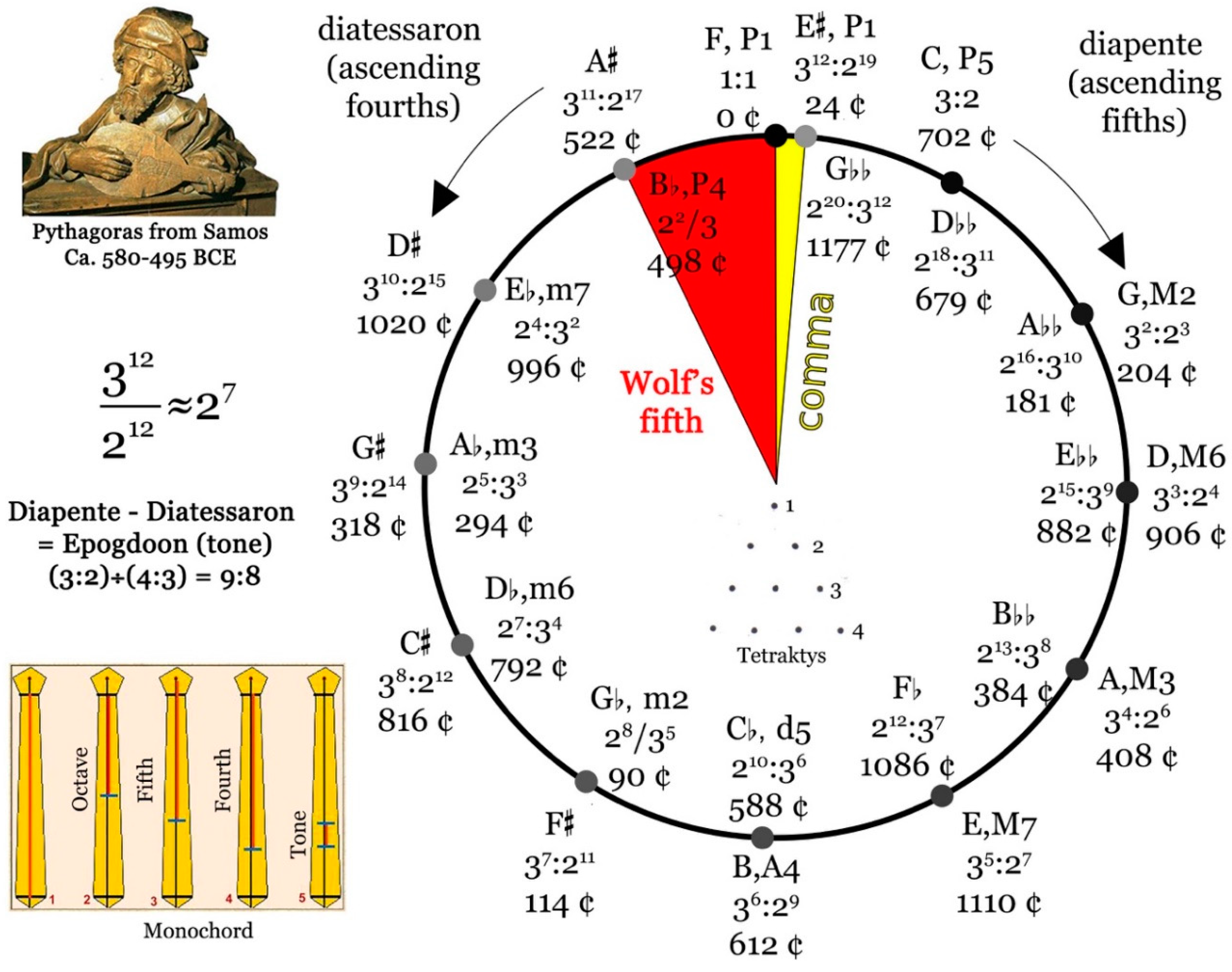
Here, we’ll explore the sixth framework of thought, musicalism, in more detail. This is because invariance by dilation symmetry is most clearly expressed in this framework. Moreover, music is another field of knowledge where symmetry plays a major role. Legend has it that the Greek mathematician Pythagoras, while on a walk, passed a blacksmith’s forge. He noticed that the note produced by the blacksmith’s hammer as it struck the anvil depended solely on the weight of the hammer. Thus, with a light hammer, the blacksmith produced a high-pitched sound, whereas with a heavier hammer, the sound appeared lower. Pythagoras soon came to the conclusion that the interval between two notes depended solely on the ratio between the masses of the hammers. For example, if we take three hammers weighing 2, 3 and 4 kg respectively, we find that the notes produced by the 2 and 4 kg hammers sound the same, although one is higher pitched than the other. This similarity between two different notes is due to the fact that the ratio between the masses of the hammers is 2, a whole number. The interval associated with the 2 and 3 kg hammers, on the other hand, corresponds to a ratio of 3/2. Although the two hammers do not produce the same sound, the sound produced by both hammers nevertheless produces a pleasing effect on the ear.
The philosophy of Pythagoras and his school was that everything in nature was expressed through integers or their ratios. One of their most important symbols was the tetraktys, a geometric figure representing the first 4 strictly positive integers in triangular form (Figure 4). The first point at the apex of the triangle represented the number 1, associated with the element fire. The next two points represented the number 2, associated with the element air. The three points below these two represented the number 3 and the element water. Finally, the four points forming the base of the triangle were associated with the number 4 and the element earth. The tetraktys thus had the property of also representing the decade, the number 10, but in a hidden way, since it was necessary to add the 4 numbers associated with the 4 elements, in order to obtain the secret value: 10 = 1 + 2 + 3 + 4. Only mathematicians, as the Pythagorean school of thought was known, were not only capable of understanding this after having followed the master’s teaching, but also of seeing the connection with music, thanks to the use of a monochord, a piece of wood on which a string was stretched that could be shortened at will by means of a movable bridge. Using this instrument and the human ear, it was found that strings shortened according to the ratios involving the four digits of the tetraktys produced sounds pleasing to the ear. In fact, string (1) shortened by half (2), generated the diapason (or octave) of ratio 2:1. The string (1) shortened by a third (3) generated the diapente (or fifth) corresponding to the ratio 3:2 (inverse of the ratio 2/3 = 1 - 1/3). Similarly, the string (1), shortened by a quarter, generated the diatessaron (or fourth) with ratio 4/3 (inverse of ratio 3/4 = 1 - 1/4). Through super-particular ratios of the form (n+1)/n, the tetraktys thus generated consonant chords that sounded very pleasing to the human ear. Finally, the difference between diapente and diatessaron gave rise to the Pythagorean epogdoon (tone or second). Accordingly, in Greek, the root “epi” means “above” and the root “ogdo” means “eight” and from mathematics : (3:2)÷(4:3) = (9:8).
From here, it was possible to define the Pythagorean “diton” (or major third) by superimposing two tones one on top of the other with a ratio (9:8)×(9:8) = (81:64). Being neither multiple nor super-particular, it was considered as “dissonant”. To arrive at the diatessaron from the diton, a Pythagorean limma (or diatonic semi-tone) with ratio (4:3)÷(81:64) = (256:243) had to be added. Thus, if we note C the fundamental note, D the note one epogdoon above C, E the note one epogdoon above D and F the note one limma above E, we define a first tetrachord C-D-E-F. By adding a new epogdoon, we obtain the diapente, since (4:3)×(9:8) = (3:2), noted G. Starting from this new note G, we could define an epogdoon above a note A, with ratio (3:2)×(9:8) = (27:16), then by adding a new epogdoon a note B with ratio (27:16)×(9:8) = (243:128). A limma was then added to arrive at the diapason, again noted C, since it corresponds to a double ratio of the starting note C, (243:128)×(256:243) = (2:1). The note G, diapente of C, thus generated its own tetrachord G-A-B-C, bringing us back to the pitch of the starting note. These two tetrachords (C-D-E-F) and (G-A-B-C), separated by a tone, could be used to construct a seven-notes scale (C-D-E-F-G-A-B) with the following sequence of intervals: (tone-tone-limma)-tone-(tone-tone-limma).
As shown below, such a Pythagorean construction is not unique and other constructions have proposed from antiquity up to the XXth century. In order to best compare different scales, it has been proven convenient to use a logarithmic scale where the octave is divided into 12×100 equal parts called cents (symbol ¢) [13]. Under these conditions, an octave with a ratio of 2:1 corresponds to 1200 cents. On such a logarithmic scale the difference ∆ measured in cents between two frequencies f₁ and f₂ is calculated using the relationship ∆ = 1200×log₂(f₁/f₂), with log₂ (x) = ln(x)/ln(2) where ln(x) is the natural logarithm. Now, if f₁ = p×f and f₂ = q×f, we may also use a p:q ratio: ∆ = 1200×log₂(p/q). The use of the logarithm function means that musicians add or subtract intervals expressed in cents, rather than multiplying or dividing frequencies expressed in hertz (Hz), as physicists do. The fact that the logarithm function transforms multiplication into addition and division into subtraction also makes comparisons and calculations much easier. Multiplying by 2 is equivalent to adding an interval of value 1, while dividing by 2 is equivalent to subtracting an interval of value 1. Now, if I add a fourth of ratio (4:3) to a fifth of ratio (3:2), I obtain a double frequency (4:3)×(3:2) = 2, i.e. an octave. Equivalently, if I use cents, I get 498¢ for the fourth plus 702¢ for the fifth, for a total of 1200¢, which also corresponds to the octave interval.
The Pythagorean method can also be used to understand the origin of notes altered by sharps or flats. The idea is to stack fifths with a ratio of 3:2 one on top of the other, starting from a fundamental note, in the hope of finding the starting note after transposing a certain number of octaves (Figure 4). Thus, starting from the note F, the first 5 iterations lead to the note E, which is one limma below the starting note. The sixth iteration generates B, the last note of the natural scale, while the seventh results in a note higher than the starting F, with a difference of one apotome (also called “chromatic semitone”), or around 114 ¢. As this note lies approximately between the F (0 ¢) and the G (204 ¢), we define the F sharp (F#) that will take us to the E# at the twelfth iteration of the 3:2 ratio. Unfortunately, this E# is still 23.5¢ too high in relation to the starting F, which defines the Pythagorean comma representing the gap between twelve fifths and seven octaves. As we can see, the cycle of fifths does not close in on itself, generating an infinite helix. If we try to force closure, we’ll have to shorten the twelfth fifth (A#-F) by a comma, generating a highly dissonant interval known as the “wolf fifth”. Symmetrically, we can proceed via a cycle of fourths with an inverse ratio of 4:3. The first iteration then leads to a note roughly halfway between the A and B of the fifths cycle. The difference, which is again one apotome with the note B, but downwards this time, defines B flat. In the Pythagorean scale, flats are therefore one Pythagorean comma lower than their conjoined sharps, giving the following order: F-G♭-F♯-G. Notes that differ by only one comma, such as G♭ and F♯, are said to be enharmonic.
It’s important to understand that the decision to create a scale based on seven musical notes was based on a purely numerological approach that had absolutely nothing to do with physiology or physics. Indeed, any interval involving prime factors greater than three, or involving irrational numbers, was rejected on principle. In particular, consonance was linked to having a super-particular ratio of the type (n+1/n) and not to the fact that the chord sounded pleasant to the ear. Thus, the sum of two consonances, diapason (2:1) plus diatessaron (4:3) corresponding to an eleventh chord of ratio (2:1)×(4:3) = (8:3), was considered dissonant, as it was neither a multiple nor a super-particular ratio.
This purely mathematical vision of music was not, of course, accepted by everyone, especially Aristoxenus of Taranto (375-335 AEC), who considered the eleventh chord to be completely consonant. He also considered that the diatessaron should be equal to two tones plus a semitone, and not two tones plus a limma as claimed by the Pythagoreans, so as to have exactly 6 tones or 12 semitones per octave. In this sense, Aristoxenus can be said to have been the precursor of the 12 equal semitones temperament used in music today, based on irrational numbers that were violently rejected by the Pythagoreans. Ptolemy of Alexandria (100-170) attempted to synthesize the two mathematical and empirical points of view, rejecting the dictatorship of tetraktys by considering super-particular ratios involving the number 5 as consonant, in order to render thirds acoustically pure. Among the new intervals accepted by Ptolemy were the right major third (5:4), the right minor third (6:5), the right minor tone (10:9) and the right diatonic semitone (16:15), all of which were considered dissonant by the Pythagoreans despite the fact that they were all super-particular and were perceived by the human ear as harmonious. However, since the numbers 2 and 5 are prime, it follows that a succession of thirds is no more capable of covering a whole number of diapasons than a succession of diapentes. It’s important to understand the intellectual stranglehold that Pythagorean mathematics had on medieval music. The ancient Greek philosophers were held in such high esteem by medieval academics that it was very difficult for them to accept other systems such as those defended by later philosophers like Aristoxenus or Ptolemy. The dogma imposed by tetraktys and the emphasis on super-particular relationships meant that the vast majority of medieval treatises advocated music that took the number 3 as the absolute limit of consonance, and imposed the exclusive use of the unison, octave, fifth and fourth in this preferred order. Thirds were considered dissonant not only numerologically, but also because the Pythagorean third (81:64), 22 cents above the pure acoustic third (5:4), sounded really bad to the ear. Although the situation began to change at the start of the Renaissance, Pythagorean dogma did not give way easily, since even in 1492, some authors continued to espouse Pythagorean doctrine. Eliminating the Pythagorean comma, which corresponds to an interval of 23¢ perfectly audible even to the unmusical ear, has always been an obsession for any self-respecting musician.
- Consonance and dissonance
What changed the game was the discovery that each musical note could be associated with a characteristic frequency of vibration. This was discovered independently between the 16th and 17th centuries by Galileo and Mersenne. It was also discovered that when a musical note was produced on a stringed or wind instrument, a complex sound was obtained corresponding to a certain fundamental frequency, as well as to a whole sequence of frequencies involving integer multiples of the fundamental frequency. The frequency component n×f is then called the nth harmonic. When certain harmonics are absent, or when the simple sine wave contained in a complex sound does not correspond to an integer multiple of the fundamental frequency (drum, gong...), we also speak of the nth partial. On a clarinet, for example, where only the odd-numbered harmonics are present, the first partial corresponds to the fundamental frequency and the second partial to the third harmonic.
The question that now arises is why two notes forming an octave interval sound so pleasant to the human ear, while two notes separated by a little less or a little more than an octave sound unpleasantly dissonant. With the first polyphonies appearing between 900 and 1300, the notion of consonance refers to the quality of sound produced when two notes are played simultaneously, regardless of context. During this period, there were only six consonant intervals: octave (2:1), fifth (3:2), fourth (4:3), octave augmented by a fifth (3:1), octave augmented by a fourth (8:3) and double octave (4:1). During this period, thirds and sixths were considered dissonant. Between 1300 and 1700, counterpoint appeared, in which certain notes were considered consonant in one context and dissonant in another.
Then, with the advent of the harmonic series, in the 18th century Rameau introduced the concept of the fundamental note, and an individual note is either consonant or dissonant in relation to this fundamental. Thirds and sixths thus became consonant intervals. Table 1 lists the 41 musical intervals that can be defined from the first sixteen harmonics of a fundamental note, in this case note C. The last column indicates, for a super-particular ratio of the type (n+1)/n, the name of the note associated with the nth harmonic. For other, non-super-particular ratios, the combination of intervals required to obtain such ratios is also indicated.
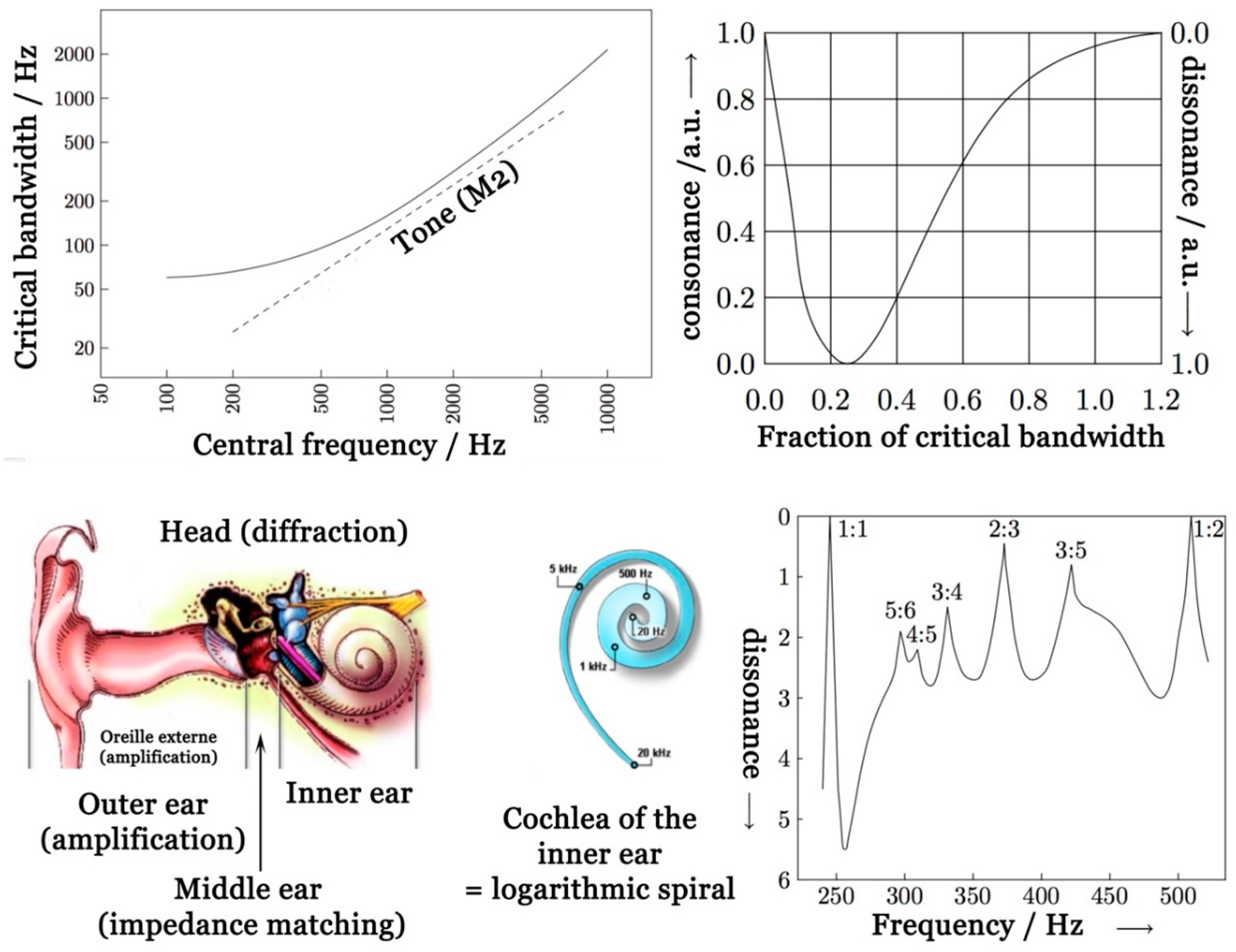
In the 19th century, Helmholtz (1821-1894) studied the structure of the human ear and concluded that dissonance arises from the first six partials being too close to each other, resulting in beats. In simple terms, this means that major seconds M2 and minor seconds m2 are the most dissonant intervals, with a difference of around 30-40 Hz, irrespective of the individual frequencies. For larger differences, the unpleasant sensation disappears and consonance is restored. Octave consonance then arises from the fact that all the partials of the higher note are present in those of the lower note.
Let’s take a look at the octave (ratio 2:1). Starting from note C, the first six partials are: C1 - C2 - G2 - C3 - E3 - G3. And, starting from the octave C2, we find: C2 - C3 - G3 - C4 - E4 - G4. Note that there are three common notes (C2, C3 and G3) and only octave relationships for the other notes. There are no conflicting notes of the m2 or M2 type, resulting in maximum consonance. Now let’s see what happens if we start with the fifth of C1, i.e. note G1. The partials here are: G1 - G2 - D3 - G3 - B3 - D4. Here we find two M2 conflicts: C3-D3 and D3-E3. The same phenomenon occurs with C1’s major sixth with partials: A1 - A2 - E3 - A3 - C#4 - E4, leading to two M2 conflicts with C1-partials (G2-A2 and G3-A3). Then comes C1’s fourth with partials: F1 - F2 - C2 - F3 - A3 - C4, leading to three M2 conflicts with C1-partials (F2-G2, F3-G3, G3-A3) and a single m2 conflict (E3-F3). For the minor third of C1, we have the series: E♭1 - E♭2 - B♭2 - E♭3 - G3 - B♭3, with one M2-type conflict with the C1-partials (B♭2-C3) and one m2-type conflict (E♭3-E3). The minor sixth of C1 has partials: A♭1 - A♭2 - E♭3 - A♭3 - C4 - E♭4, meanwhile, is characterized by three M2-type conflicts with C1-partials (G2-A♭2, E♭3-E3, G3-A♭3). As might be expected, C1’s second major gives the series: D1 - D2 -A2- D3 - F#3 - A3 with six M2-type conflicts with C1-partials (C1-D1, C2-D2, G2-A2, C3-D3, E3-F♯3, G3-A3) and one m2-type conflict (F♯3-G3). Finally, for C1’s second minor, we find the series: D♭1 - D♭2 - A♭2 - D♭3 - F3 - A♭3, with six m2-type conflicts with C1-partials (C1-D♭1, C2-D♭2, G2-A♭2, C3-D♭3, E3-F3, G3-A♭3) and one M2-type conflict (F3-G3).
These considerations of partials therefore enable us to classify our nine intervals in descending order of consonance: P8 (2:1) > P5 (3:2) ≈ M6 (5:3) > m3 (6:5) > P4 (4:3) > M3 (5:4) > m6 (8:5) > M2 (9:8) > m2 (16:15). These observations were confirmed in the 20th century via the notion of critical bandwidth that corresponds to the difference in frequency between two pure tones at which the sensation of “roughness” disappears and the tones sound smooth [14]. It was found that maximum dissonance is obtained with simple sinusoidal waves for a frequency deviation equal to a quarter of the critical bandwidth, with consonance becoming maximum when this same deviation becomes of the order of the critical bandwidth (Figure 5). For more complex sounds, it was assumed, as before, that the total dissonance is the sum of the dissonances caused by each pair of adjacent partials from the fundamental to the sixth harmonic. Note the very intense peaks for the unison (1:1), octave (1:2) and perfect fifth (2:3), and the less intense peaks for the minor third (5:6), major third (4:5), perfect fourth (3:4) and major sixth (3:5), in good agreement with the previous classification. The consequence of this notion of critical bandwidth is that if we consider a note with partials of 440, 860, 1203 and 1683 Hz and another with partials of 225, 440, 615 and 860 Hz, we will obtain a consonant sound despite the fact that the partials are not at the octave. It follows that consonant intervals can be obtained even when using frequencies with non-integer or even irrational frequency ratios.
- Riemann’s zeta-function
Once we understand the physiological importance of an interval between two notes, the problem arises of building a scale from the simplest possible frequency ratios. The first ratio after the 1:1 unison and the 2:1 octave is, of course, the 3:2 fifth. Generally speaking, as we have seen with the Pythagorean fifth cycle, the result is an infinite succession of notes. The same applies to the harmonic series, where there’s no need to limit yourself to the sixteenth harmonic. To obtain a musical scale from an infinite scale, each note characterized by a p:q ratio, must be transposed by a whole number m of octaves to arrive at a situation where 1 ≤ (p:q)/m ≤ 2. A musical scale is thus a finite succession of notes limited to a single octave.
For scales of equal temperament, it is usual consider that a full octave (2:1 ratio) corresponds to 12 intervals of 100¢, i.e. 1200¢ (12-EDO meaning 12-Equal Division of Octave). Of course, this raises the question of why 12 and not 41, 53 or 72 intervals? One answer is provided by the Pythagorean spiral of perfect fifths, which after 12 iterations of the ratio 3:2 covers roughly 7 octaves. But, again, this means overemphasizing Pythagoras. In strictly mathematical terms, the Pythagorean method seeks to solve the equation (3÷2)a = 2b, or 3a = 2(a+b). Since all integer powers of 3 are odd numbers, while all integer powers of 2 are even numbers, this equation has no solution. Another formulation is to look for a number b such that 2 = bn and 3/2 = bm. Moving on to logarithms, this is equivalent to solving the following equation:
Here 1/b is the average step of each interval. The aim is therefore to find two integers q2 and q3 such that q2×ln 3 = q3×ln 2, from which it will be possible to deduce a 1/ln b solution. Obviously, as we saw above, there is no such thing as an integer solution to such an equation, hence the existence of the various commas. But perhaps there are solutions very close to an integer. The degree of harmony can also be increased by solving equations:
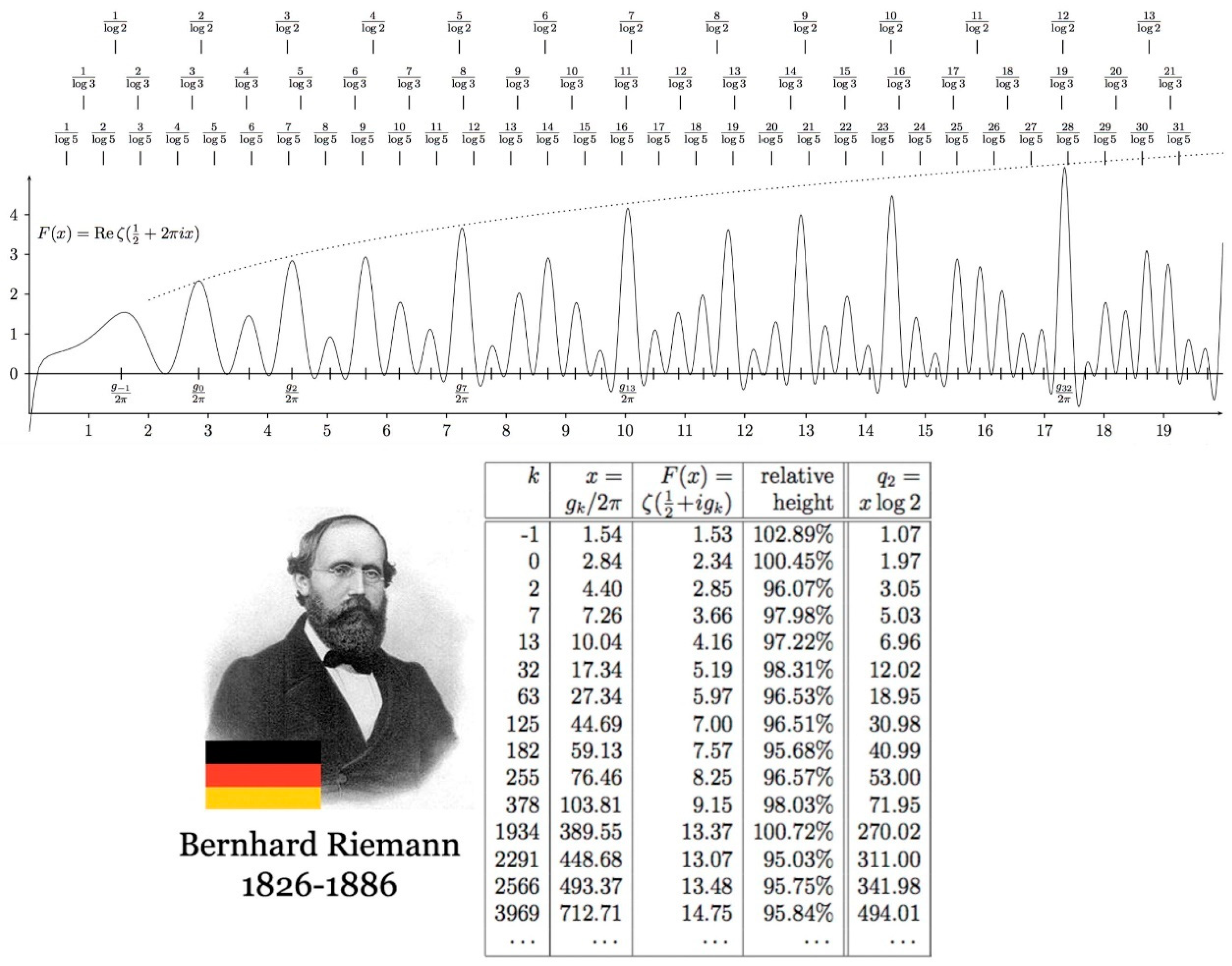
In fact, if we find two quasi-integers q2 and q3 as solutions to such an equation, we’ll also have as solutions the quasi-integers q4 = 2×q₂ and q6 = q2 + q3. There is in fact a graphical way of solving such equations (Figure 6). All you have to do is place markers on an x-axis for the values 1/ln 2, 2/ln 2, 3/ln 3, 4/ln 2... then just below the markers for the values 1/ln 3, 2/ln 3, 3/ln 3, 4/ln 4... and so on. The values of x = 1/ln b where there is quasi-coincidence of the markers are quasi-integers that are solutions to the equation posed. Now, is there a way of finding such coincidences more systematically, without using a graph? The idea here is to consider the following function F(x) [15]:
The choice of a cosine function is justified by the fact that the function f(x) = cos (2πx) has peaks f(x) = 1 for all integer values of x, while the σ factor ensures the convergence of the series. Here Re denotes the real part of a complex number and ζ is the Riemann zeta function defined on the plane of complex numbers. Now the problem of finding coincidences for ratios qn/ln n (n = 2, 3, 4, 5,...) has been reduced to finding the local maxima of the function Re[ζ(σ + 2πix)] as a function of x, for a fixed value of σ. Figure 6 shows the variation of this function for σ = ½ and the good correspondence that exists between coincidences and local maxima. Each of these maxima in fact happens to be very close to the so-called Gram points gk (k = -1, 0, 1, 2...) which are such that:
Im[ζ(σ + igk)] = 0 and Re[ζ(σ + igk)] ≠ 0
It therefore suffices to evaluate the Riemann zeta function at the level of its Gram points divided by 2π. The table given in Figure 6 thus lists all significant maxima up to the value x = 2000. The first 4 columns show the index k of the Gram point, its position and the value of F(x) in absolute value and in relative value with respect to the dotted curve, which gives an idea of the growth rate of these local maxima. The last column gives the quasi-integer qn for prime number n = 2. Values of qn for other prime numbers (5, 7, 11, 13…) are easily computed from the value of x: qn = x·ln n. As F(x) increases, the integers qn become closer to integer values, and the range where qn intervals correspond to a frequency ratio of type 1:n becomes better. We can see that the smallest prime numbers tend to give the best approximations to integers. Note that octaves are always well represented, even though this was not imposed at the outset, demonstrating the natural importance of the prime factor 2 in the perception of octaves, which has been noted since antiquity. The q2 column thus provides us with a sequence of integers for the optimal division of the octave into N intervals: N = 1, 2, 3, 5, 7, 12, 19, 31, 53, 72, 270, 311, 342 and 494.
Let us show, for the case N = 7, how to get ratios from the corresponding qn values. For this, we will restrict ourselves to the prime integers n = 2, 3 and 5. As here, x = 10.04, we may compute:
q2 = 10.04×ln 2 = 6.96 ≈ 7
q3 = 10.04×ln 2 = 11.03 ≈ 11
q5 = 10.04×ln 5 = 16.16 ≈ 16
The game here is to find a combination of quasi-integers q2, q3 and q5 capable of generating seven intervals numbered from 1 to 7. For instance, starting from note C (P1 = 1:1), the first degree could be obtained as:
2q3 - 3q2 = 2×11 - 3×7 = 22 -21 = 1
In order to find the ratio corresponding to a qn combination, each value of n present in the combination is elevated at the power of the qn coefficient, positive values corresponding to the numerator and negative values to the denominator. Here, for the major second, the q₃ coefficient is 2 while that of q₂ is -3, so that M2 = 3²:2³ = 9:8 (D). Here is what may be obtained for other intervals:
q₅ - 2q₂ = 16 - 2×7 = 16 - 14 = 2, i.e. M3 = 5¹:2² = 5:4 (E)
2q₂ - q₃ = 2×7 - 11 = 14 - 11 = 3, i.e. P4 = 2²:3¹ = 4:3 (F)
q₃ - q₂ = 11 - 7 = 4, i.e. P5 = 3¹:2¹ = 3:2 (G)
q₅ - q₃ = 16 - 11 = 5, i.e. M6 = 5¹:3¹ = 5:3 (A)
q₃ + q₅ -3q₂ = 11 + 16 - 3×7 = 27 - 21 = 6, i.e. M7 = (3¹×5¹):2³ = 15:8 (B)
q₂ = 7, i.e. P8 = 2¹:1 = 2:1 (C)
This is the seven-note major scale with the right intonation. To obtain the minor scale, we need to find another combination of quasi-integers for the second interval, for example:
q₂ + q₃ - q₅ = 7 + 11 - 16 = 18 - 16 = 2, or m3 = (2¹×3¹):5¹ = 6:5 (E♭, D♯)
For the minor seventh (sixth interval), we could have:
4q₂ - 2q₃ = 4×7 - 2×11 = 28 - 22 = 6, or m7 = 2⁴:3² = 16:9 (B♭, A♯))
For the sixth minor (fifth interval), we could take:
3q₂ - q₅ = 3×7 - 16 = 21 - 16 = 5, or m6 = 2³:5¹ = 8:5 (A♭, G♯)
Finally, for the second minor (first interval) we’d have:
4q₂ - q₃ - q₅ = 4×7 - 11 - 16 = 28 - 27 = 1, or m2 = 2⁴:(3¹×5¹) = 16:15 (D♭, C♯)
Note also the possibility of another ratio for the second major (first interval) since:
q₂ + q₅ - 2q₃ = 7 + 16 - 2×11 = 23 - 22 = 1, i.e. M2 = (2¹×5¹):3² = 10:9
The advantage of this method is that you can very well have ratios not included in Table 1. For example, the triton (third interval) can be obtained as follows:
2q₅ - 2q₃ - q₂ = 2×16 - 2×11 - 7 = 32 - 22 - 7 = 3, or TT = 5²:(3²×2¹) = 25:18 (F♯,G♭)
Of course, it is not mandatory to use a seven-notes scale. The value N = 2 means that the octave is split into just two parts. From Figure 6, we know that x = 2.84, hence q₂ = 2.84×ln 2 = 1.97 ≈ 2 and q₃ = 2.84×ln 3 = 3.12 ≈ 3. Here, with a single degree, two possibilities: q₃ - q₂ = 3 - 2 = 1, i.e. the perfect fifth P5 with ratio 3:2, or alternatively, 2q₂ - q₃ = 2×2 - 3 = 4 - 3 = 1, i.e. the perfect fourth P4 with ratio 4:3. Similarly, we could have chosen N = 5, i.e. x = 7.26 with q₂ = 7.26×ln 2 = 5.03 ≈ 5, q₃ = 7.26×ln 3 = 7.98 ≈ 8 and q₅ = 7.26×ln 5 = 11.69 ≈ 12. Hence the countless pentatonic scales used around the world. Here we recognize all five-note modal music including, in particular, most of the scales used in blues and jazz. The simplest one, derived from the natural major scale, is easily obtained as:
First degree: 2q₃ - 3q₂ = 2×8 - 3×5 = 16 - 15 = 1, i.e. M2 = 3²:2³ = 9:8
Second degree: q₅ - 2q₂ = 12 - 2×5 = 12 - 10 = 2, i.e. M3 = 5¹:2² = 5:4
Third degree: q₃ - q₂ = 8 - 5 = 3, i.e. P5 = 3:2
Fourth degree: q₅ - q₃ = 12 - 8 = 4, i.e. M6 = 5:3
So far, Riemann’s Zeta function simply reproduces what human beings have discovered empirically, at the cost of a great deal of more or less harmonious trials and errors. The main interest in this approach lies in microtonal music, where the octave is divided into more than 12 intervals. Thus, after the value N = 7, we find N = 12, N = 19 and N = 31. Not surprisingly, the astronomer Christian Huygens was the first to use a 19-tone equal-temperament scale (19-EDO) towards the end of the 17th century, providing a very good approximation of the right intonation and allowing modulation to other keys.
With q₃ = 27.34×ln 3 = 30.03 ≈ 30, the perfect fifth of ratio 3:2 corresponds here to the eleventh degree of the scale (q₃ - q₂ = 30 - 19 = 11), i.e. an interval that is less good than the approximation of the 12-DEO scale (). Huygens therefore also considered the case of a 31-EDO scale already studied in a musical treatise dated 1555 written by the Italian musician Nicola Vincentino and published in Rome under the title “L’antica musica ridotta alla moderna pratica”. Here, with q₃ = 44.69×ln 3 = 49.10 ≈ 49, the perfect fifth corresponds to the eighteenth degree of the scale (q₃ - q₂ = 49 - 31 = 18), i.e. an interval of , which is still not as good as the 12-EDO fifth. The main advantage of this scale is that it achieves an excellent approximation of the mesotonic fifth P5 = 696.6 ¢, allowing the entire mesotonic scale to be found. The musician Adriaan Fokker was an ardent advocate of such a 31-degree scale. However, to get the best approximation of the perfect fifth of ratio 3:2 = 701.96 ¢, it’s best to take the value N = 53, since with q₃ = 76.46×ln 3 = 84, the perfect fifth here corresponds to the thirty-one degree of the scale (q₃ - q₂ = 84 - 53 = 31), i.e. an interval of , which beats the 12-EDO fifth by a wide margin. In the Pythagorean version of this scale, the fifth is divided into 24 apotomes and 7 limmas, while the tone is divided into 31 + 31 - 53 = 9 units corresponding to 7 apotomes and 2 limmas. It should be noted that the Chinese musician King Fâng, who lived in the third century BC, had already observed that the fifty-fourth note of the Pythagorean cycle of fifths was very close to the first note. Similarly, Philolaos, a disciple of Pythagoras, imagined that a tone could be broken down into two minor semitones plus a Pythagorean comma, and considered that each minor semitone contained 4 commas. With 9 commas per tone and 4 commas per minor semitone, we obtain a total of 9×5 + 2×4 = 53 commas for the octave composed of 5 tones and 2 semitones. The mathematician Gérard Mercator (1620-1687) precisely calculated the numerical value of the ratio 353:284 = 3.62¢, hence the name “Mercator comma”. A division of the octave into 53 intervals was also envisaged by Isaac Newton.
However, the next approximation, N = 72, is even more interesting, as 72 is a multiple of 12, and the human ear is in tune to distinguish between the different degrees of such a scale, known as “moria” (Table 2). Note that the next integer in Figure 6 is N = 270, which gives intervals that are indistinguishable to the human ear, and therefore corresponds to scales of purely mathematical interest.
- The Tonnetz
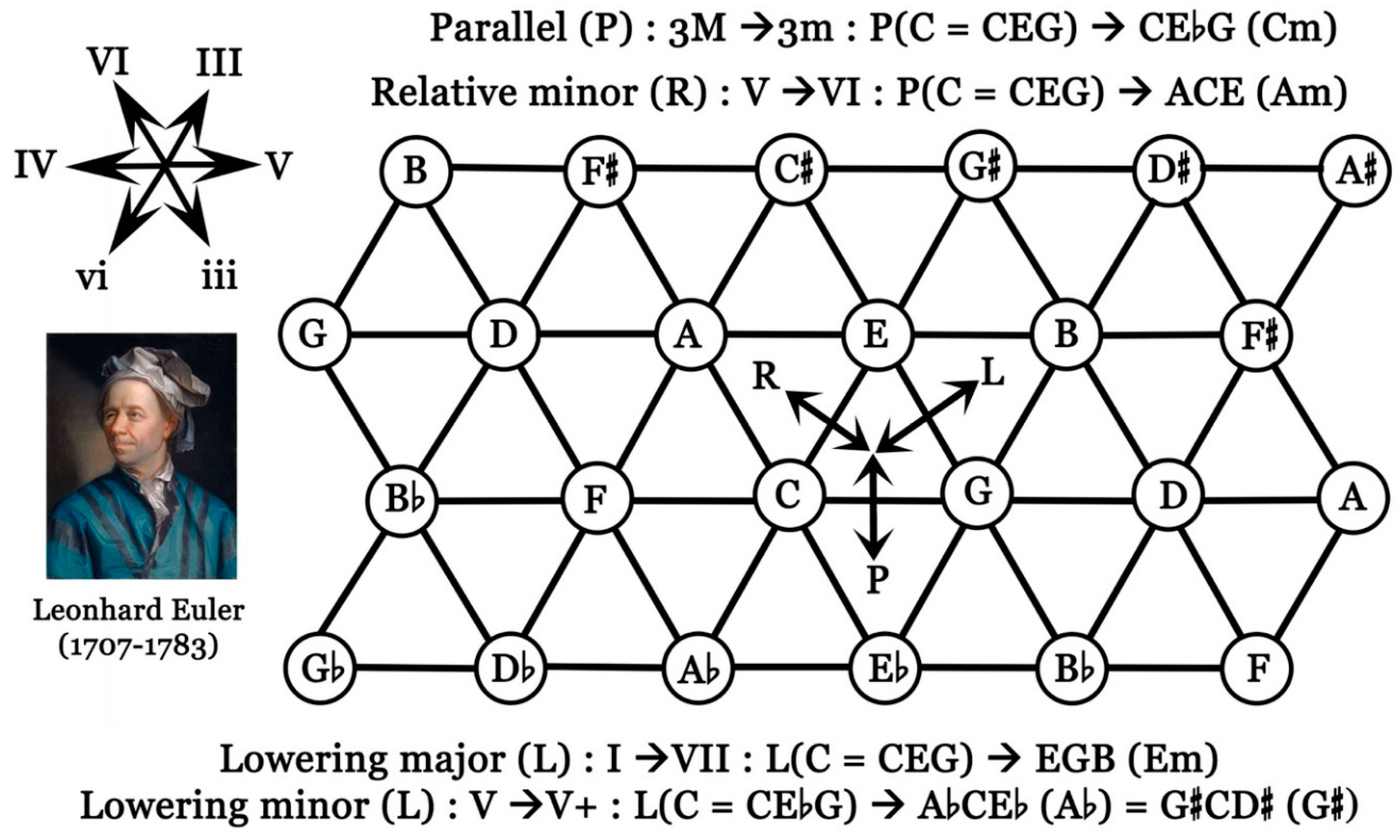
A chord corresponds a triad, i.e. to a set of 3 notes. A major chord is composed of a root, a major third and a fifth. A minor chord is made up of a root, a minor third and a fifth. In 1739, the mathematician Leonhard Euler (1707-1783) had the idea of representing tonal and harmonic relationships in music by means of a “tonal network” or “Tonnetz” in German. This was a diagram representing the tonal space of intonation in the form of a grid. In particular, this first version shows the relationships of fifths (ratio 3:2) and major thirds (ratio 5:4) between the degrees of the system. Thirty-five years later, in 1774, Euler provided a new version of this grid, this time called “Speculum musicum” or “Musical Mirror”, where the notes are aligned horizontally in fifths and vertically in major thirds. The Tonnetz was rediscovered in 1866 by Arthur von Oettingen (1836-1920), who conceived it with a theoretically infinite extension in all directions (ascending or descending fifths, to the right or left; ascending or descending major thirds, down or up) and minor thirds on the diagonals. Hugo Riemann (1849-1919) then extended the Tonnetz to equal temperament to infinity. Riemann defined three transformations: P (for “Parallel”), L (for “Leittonwechsel”) and R (for “Relative”). Figure 7 shows a modern version of this neo-Riemannian Tonnetz. Take, for example, a well-known harmonic chord progression such as: C - G - Am - F, as found in The Beatles’ “Let it Be” (1970) or Elton John’s “Can you feel the love tonight” (1994). If we refer to the Tonnetz, the transition from the C chord (C-E-G) to the G chord (G-B-D) corresponds to an LR-type movement. Then, the transition from the G chord (G-B-D) to the Am chord (A-C-E) corresponds to an RLR-type movement. Finally, the last passage from the Am chord (A-C-E) to the F chord (F-A-C) is an L-type movement, i.e. three L-type movements for three R-type movements. Thus, the neo-Riemannian Tonnetz is based on the parsimony of movements, i.e. “The rule of the shortest path”. Or, as Jean-Philippe Rameau put it: “You can only go from one note to another by the one closest to it”.
The Tonnetz may also be seen as a tessellation of the plane, i.e. a covering of the plane with geometric shapes (in this case, triangles). We call these periods the fundamental domains that allow us to see the Tonnetz as a topological object, in other words, a torus. Every piece of music therefore leaves a characteristic trace on the Tonnetz. As Table 3 shows, the symmetry operations of the Tonnetz form a group isomorphic to the dihedral group D12.
- The water diapason
From the above, we can see that music and science are closely related. Now, there’s a completely unsatisfactory point that needs to be considered. It’s well known that each musical note has a corresponding frequency, and that whole multiples of this frequency constitute the various harmonics. But the fact remains that it’s impossible to establish a correspondence between a musical note and a frequency, without the input of what we call a “diapason”. Without this crucial data, a musical note can correspond to any frequency. A diapason (from the Low Latin diapason, from the Greek dia pasôn khordôn, through all the strings) is therefore a device shaped as a tuning fork that produces a pure frequency corresponding to a perfectly sinusoidal wave, to which we arbitrarily associate a particular note, generally the note A4. This reference note is written between the second and third staff lines on a score. It corresponds to the open string of the violin and viola. This modern meaning of the word “diapason” corresponding to a tuning-fork, should not be confused with the Pythagorean diapason, synonym of “octave” (i.e. 2:1 ratio).
In 1936, the American National Standards Institute recommended that this A4 note be tuned to a frequency of 440 Hz. This standard was accepted by the International Organization for Standardization (ISO) in 1955 as ISO 16. It is now used as a reference frequency for tuning pianos, violins and other instruments. It’s worth noting that there’s no rational basis for choosing the 440 Hz frequency for the note A4. Between the 16th and 19th centuries, the frequency of this note ranged from 373 to 521 Hertz [16]. In 1859, France established its reference A4 note at 435 Hz at a temperature of 18°C. This was the first standardization on a national scale. In 1953, at the international conference in London, A4 = 440 Hertz became the reference for all orchestras worldwide. No one knows exactly what led to this precise value. One thing is certain, however. If the pitch is too high, it can affect the sound and vocal performance of singers. On the other hand, according to Hector Berlioz, wind instrument manufacturers were responsible for the constant rise in pitch between 1700 and 1858 (from 404 Hz to 457 Hz) [17]. This was to ensure maximum brilliance for flutes, oboes and clarinets. For stringed instruments (violins, violas, basses), this wasn’t too much of a problem, since all they had to do was stretch their strings a little more. The main malcontents were musicians playing bassoon, horn, trumpet or second oboe, who had to take their instruments to the maker to have the tube shortened...
Initiated by the French, the standardization of a A4-diapason was primarily a response to economic and commercial motivations. To be able to distribute fixed-tone instruments over increasingly vast territories, instrument makers needed to know which pitch to use to manufacture the instruments in large quantities. But while the A4 = 440 Hertz is now the standard, the musician or conductor is free to use any tuning fork. For example, musicians specializing in Baroque music use a pitch of 415 Hz, while symphony orchestras use pitches between 445 and 450 Hz. There is also much controversy on the Internet about the use of a 432 Hz pitch to produce music that is considered less aggressive and more serene than that produced at a 440 Hz pitch. A recent double-blind study involving 33 healthy volunteers has concluded that music tuned to 432 Hz was associated with a slight non-significant decrease in mean (systolic and diastolic) blood pressure values, as well as a marked decrease in mean heart rate (-4.79 bpm, p = 0.05) and a slight decrease in mean respiratory rate values (1 r.a., p = 0.06), compared to music tuned to 440 Hz [18]. Subjects were more focused on listening to music and more satisfied overall after sessions in which they listened to music tuned to A4 = 432 Hz. However, the results of the study suggest repeating the experiment with a larger sample and introducing randomized controlled trials covering more clinical parameters.
The theoretical arguments of those who defend the use of a diapason tuned at 432 Hz almost all appeal to more or less esoteric considerations, or else have recourse to numerology. As it happens, the number 432 is the product of 2⁴ = 16 by 3³ = 27. All that remains then is to find out how frequencies of 8 Hz or 144 Hz are natural (two numbers present in the famous Fibonacci series converging towards the golden number) and the “demonstration” is done... The weakness of such arguments becomes obvious when we consider that the number 8 = 2³ is common to both frequencies, since 432 = 8×54 and 440 = 8×55. Since we’re trying to discuss a difference of just 1 Hz after transposing 3 octaves downwards, all these numerological arguments must be rejected. If it gives you pleasure to use a 432 Hz pitch for listening to music, don’t hesitate for a second. But please don’t try to claim that it’s better than the 440 Hz tuning. After all, intellectual honesty dictates that all diapasons are basically equivalents. However, the same cannot be said for the way each one feels. Here, subjectivity reigns, and each human being is unique in his or her listening to music.
However, if one diapason is really better than other ones, the frequency of that diapason must be calculable and justifiable by means of the known laws of physics, through the judicious use of the universal physical constants of our universe. Here, we propose such a calculation, and then demonstrate with objective parameters that such an optimal diapason for playing music indeed exists. As explained before, arguments based on group theory applied to Maxwell’s equations, strongly suggest that our universe is not a 4-dimensional space-time continuum, but rather a five-dimensional space-time-scale hyper-surface embedded in a sixth-dimensional continuum of consciousness [13]. In this sixth framework of thought, called “musicalism” (see Figure 2), the choice of a diapason can no longer be arbitrary. For, the fifth dimension of scale implies that any living being can recognize itself from its constituent molecules (nanometer scale) to the meter scale via its 36×10¹² cells for a man, 28×10¹² cells for a woman and 17×10¹² cells for a child [19]. Given that 99.1 mol% of a cell is made up of water molecules [3], it follows that music can also influence our body water, our constituent cells and not just our ears.
In fact, in this fifth dimensional scale of the universe, masses must synchronize on a musical scale because energy can be expressed in two different, intrinsically equivalent ways. On the one hand, any mass m can be seen as energy according to the relation E = m·c², where c = 299,792,458 m·s⁻¹ is the propagation speed of light in a vacuum. On the other hand, according to quantum physics, all energy can be considered as a frequency f, according to the relation E = h·f, where h = 6.62606954×10⁻³⁴ J·s represents Planck’s quantum of action. If we accept that we’re talking about the same energy E in both cases, then it follows that m·c² = h·f, which means that any mass m can be associated with a characteristic frequency f. Now, for molecules, mass is expressed in Daltons (Da = g·mol⁻¹), which requires us to go through Avogadro’s constant, NA = 6.02214076×10²³ mol⁻¹, to get a mass expressed in kilograms (kg). Hence our fundamental relationship:
So, for a water molecule with a mass m = 18.01528 Da, we rigorously calculate a frequency f = 4.05767×10²⁵ Hz. It id at this point that the notion of scale invariance comes into play, coupling the world of the infinitely small with our macroscopic scale. In music, this scale invariance is expressed by the principle of octave identity, recognized since antiquity. At the frequency level, this principle corresponds to division or multiplication by a factor of 2. As the quantum frequencies of molecules are really very high, the most convenient is to use the logarithm function of base 2, noted log₂, which allows us writing:
log₂ f₀ = 76 + 1.575772681758021 + log₂ (m/Da)
⇒ f₀/2⁷⁶ (Hz) = 2.980951043045587×(m/Da)
⇒ f₀/2⁷⁶ (Hz) = 2.980951043045587×(m/Da)
Then, as m[H₂O] = 18.01528 Da, we should have f₀(H₂O) = 53.702667706758303 Hz. As this frequency is too low to correspond to a A4-diapason, we simply raise it by three octaves to arrive at the final result:
f₃(H₂O) = 53.702667706758303×2³ = 429.621341654066421 Hz
The interest of music produced with this A4 = 429.62 Hz water-based diapason, is that, via the scale waves involving the fifth dimension of our universe, we make our tens of trillions of body cells vibrate. We can therefore expect a very particular and objective feeling for this precise diapason in any living being having water as its basic constituent molecule.
- Spectrograms
From a practical point of view, some very famous pieces of classical music have been reproduced with this new tuning fork. So that everyone can form their own opinion, they can be listened to and downloaded from the website of composer Tommi Jack’s [20,21,22]. But using the water-based diapason at 429.62 Hz, also makes it possible to create entirely original music, by giving oneself a list of molecules and calculating the associated notes using the same method as that used for the water molecule. Thus, knowing the frequency f of these molecules calculated by means of their molecular mass, we can obtain the corresponding musical note based on the fact that there are exactly 1200 cents (¢) in an octave:
∆f(¢) = 1200×log₂(f/f₃) where f₃ = 429.62 Hz (A4)
A(0¢) A#(100¢) B(200¢) C(300¢) C#(400¢) D(500¢) D#(600¢) E(700¢) F(800¢) F#(900¢) G(1000¢) G#(1100¢) A(1200¢)
For example, let’s take the carbon dioxide molecule CO₂ with mass m = 44.009 Da. The associated quantum frequency is f = 2.981×44.009 = 131.19 Hz, or ∆f = -2054 ¢. Hence, going back 2 octaves: ∆f = 2400 - 2054 = 346 ¢. According to the table above, this difference corresponds to the note C increased by 46 ¢. Another choice would have been the note C# reduced by 54¢. But if you want to deviate as little as possible from the tempered scale, the best choice is the note C (+46¢). This is how to create entirely original “molecular” music, as soon as the composer has access to software and a high-quality sound bank. In this case, the use of software is imperative if we wish to maintain the cents deviation from the tempered scale, both in terms of the notes and the pitch of 429.62 Hz.
So far, so good. But now, how can we prove, objectively, that this computed diapason of 429.62 Hz is an optimal one? Here, the best is to choose a well-known musical piece and look at the frequency spectrum for a given diapason. For example, below is the frequency spectrum for Pachelbel’s canon composed around 1680 and harmonized with a 429.62 Hz pitch (Figure 8). We’ve also zoomed in on the richness of the sound generated at this pitch, associated with the water molecule. We then used other pitches (415 Hz, 432 Hz, 435 Hz, 439 Hz, 440 Hz and 442 Hz) to see the effect of changing pitch for the same composition using the same instruments.
Note that we have here a representation of the piece of music giving the frequencies (vertical scale graduated in Hertz) involved as a function of time (horizontal scale graduated in minutes and seconds). Such a representation is called a spectrogram. In addition to the spectrogram itself, we show, at the very top, in orange, how loudness varies (vertical scale graduated in decibels) as a function of time. There are two diagrams in each case, since we’re dealing here with stereo sound.
Now let’s see how to read a spectrogram. Figure 9 summarizes what you need to know. At the very bottom, we find the sound dynamics linked to low frequencies and corresponding to sound energy. The greater the dynamic range, the more yellow the color. Sound engineers refer here to the “light” contained in the sound, which can be strong or weak. Then, for higher frequencies above 5 kHz, we enter the realm of psychoacoustics, i.e. the presence of sound corresponding to red colors. Finally, beyond 10 kHz (typically), we find the “depth” of sound, corresponding to violet-tinged colors. Thanks to the spectrogram, it’s also possible to tell whether a sound has been compressed or not. If the sound has been compressed (in MP3 format, for example), there will be no frequencies above 15 kHz. We now have everything we need to see and understand the effect of the choice of pitch on a spectrogram.
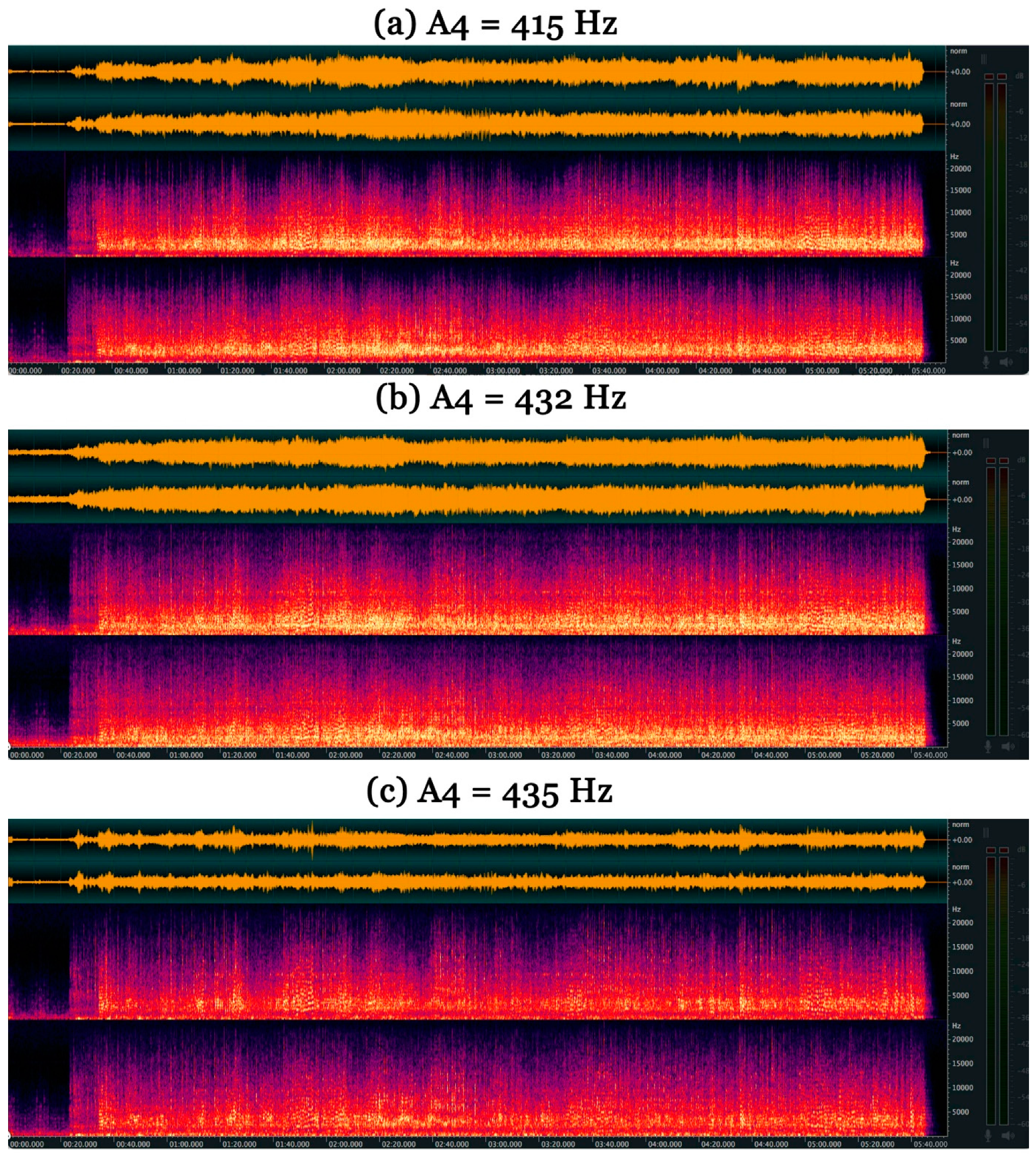
Thus, Figure 10 (top) shows the spectrogram of Pachelbel’s Canon using a pitch of 415 Hz for the musical rendering (German Baroque). Note that here all settings are identical, only the pitch has changed relative to Figure 8. We immediately notice that with this pitch, the sound has much less depth and that the light in the sound is much weaker, especially in the very low frequencies, below 1 kHz, where we see very little yellow color. This translates into a division by 2 of the sound intensity represented in orange. The sound has thus been considerably impoverished and weakened in relation to the pitch of the water molecule at 429.62 Hz.
Figure 10 also shows the spectrogram of the same Pachelbel canon with a pitch of 432 Hz (middle). Again, no other settings were changed. The result appears much better than with the 415 Hz pitch. However, it still lacks the richness of the 429.62 Hz diapason. Here too, the sound clearly lacks depth (black band around 20 kHz), even if we have recovered a fair amount of light at low frequencies. The problem here lies in the psychoacoustics of the sound, with a black band appearing between 7 and 8 kHz. This translates into a much-reduced sound intensity compared with the 429.62 Hz tuning fork, but still much better than with the 415 Hz tuning fork. This is obviously a pretty good diapason, but far from being optimal.
The last spectrogram in Figure 10 shows the effect of using a 435 Hz pitch for A4. As can be easily seen, the richness of the sound is much lower than at 432 Hz or 429.62 Hz pitch. Here, there is virtually no light left in the sound, with the appearance of a black band around 1 kHz, in addition to the black band between 7 and 8 kHz already observed with the 432 Hz tuning fork. The sound has also lost considerable depth, with many completely black zones above 10 kHz. The result is a considerably reduced sound intensity, even weaker than that obtained with the 415 Hz tuning fork. Remember that the 435 Hz pitch was the pitch recommended in France from 1853 onwards. Looking at the spectrogram, it’s easy to understand why no other country has followed France down this path, since it considerably impoverishes the sound.
Now, Figure 11a shows the spectrogram obtained, again for Pachelbel’s canon, with a pitch of 439 Hz, which was the official pitch of the Royal Philharmonic Orchestra in London. There’s greater depth of sound, but very little light below a frequency of 1 kHz. This weakened sound dynamic translates into a considerably reduced loudness, i.e. a factor of two compared with the French diapason at 435 Hz. In the light of these spectrograms, the advocates of the 432 Hz diapason were quite justified in extolling the virtues of their choice, which does indeed deliver less attenuated loudness and greater sonic richness. But today, with the new 429.62 Hz diapason, the 432 Hz tuning appears to be not an optimum choice, i.e. the least bad choice compared to the “historic” diapasons.
Obviously, it’s now time to consider the Pachelbel canon with a pitch of 440 Hz for A4 (Figure 11b), a standard that was accepted by the International Organization for Standardization (ISO) in 1955 as ISO 16. This standard is now used as a reference frequency in the tuning of pianos, violins and other instruments sold in the musical instrument trade. Note that the sound has good depth and plenty of light below a frequency of 1 kHz. On the other hand, as with the 432 Hz diapason, there are those two black bands between 7 and 8 kHz and around 20 kHz frequency. The result is a rather mediocre sound intensity, which appears much lower than that obtained with the 432 Hz diapason. Once again, this confirms the position of those in favor of the 432 Hz diapason. But these same proponents, in turn, have to capitulate to the A4 = 429.62 Hz pitch spectrogram.
We conclude this analysis of the effect of pitch by considering the orchestral pitch, set at 442 Hz for A4. Figure 11c shows the Pachelbel canon rendered with this latter pitch. Note that the two black bands present in music at 432 Hz or 440 Hz pitch have disappeared. This is obviously a very positive point. The result is a much stronger sound intensity. Nevertheless, the intensity remains slightly lower than that obtained with a 429.62 Hz tuning fork. The main reason for this seems to be the lack of light in the low frequencies below 1 kHz, where red largely dominates over yellow.
Following the study of these different spectrograms, it is possible to classify the different diapasons considered as follows:
429.62 Hz > 442 Hz > 432 Hz > 440 Hz > 415 Hz > 435 Hz > 439 Hz
Note that all these pitches are more or less arbitrary, with the exception of 429.62 Hz, which is the result of a rational calculation involving Planck’s quantum of action, the speed of light in vacuum, Avogadro’s constant and the average molar mass of a water molecule. These values are not arbitrary; they are fixed by Nature itself, not by human feeling. Remarkably, 429.62 Hz provides the richest spectrogram in terms of dynamics, psychoacoustics and sonic depth. It’s a win-win situation, with optimal sound intensity.
- Integrated Loudness (IL) and Loudness Range (LRA)
Of course, this classification could be criticized for its somewhat subjective nature. We have therefore also generated piano sounds for these different diapasons, and used the two concepts of Integrated Loudness (IL) and Dynamic Excursion Level (LRA). The first concept, IL gives a figure expressed in units known as LUFS (acronym for “Loadness Units relative to Full Scale”), with 1 LU = 1 dB. The aim here is to characterize the overall sound energy received by the human ear over the entire length of a piece of music. The value ranges from -30 LUFS for a whispering voice, through -16 LUFS for a scream, to the maximum value of 0 LUFS for a sound that becomes painful to listen to. In radio and television, for example, a standard has been set at -23 ± 1 LUFS to ensure that the sound level remains more or less stable whatever the program. In music, there is no standard, but to achieve a constant sound level without having to change the volume with each song, a sound level of between -20 LUFS and -16 LUFS is considered comfortable. This does not, of course, preclude the possibility of higher sound levels, in which case we leave it up to the listener to manually lower the volume of his or her listening system to achieve the optimum sound for his or her hearing. For example, in the case of our Pachelbel canon with a pitch of 429.62 Hz, we found IL = -8.71 LUFS.
One well-known way of increasing the sound level without having to touch any “volume” knob is to compress the music, i.e. to reduce its dynamic range, which has the effect of artificially increasing its integrated sound level. The problem here is to find, for a given piece of music, the right compromise between a song with a very wide dynamic range and therefore almost inaudible, and the same song with a very narrow dynamic range, which will certainly be much more powerful sonically, but also hopelessly flat and boring in terms of musical rendering. Hence the idea of a second parameter called the “Dynamic Excursion Indicator”, or LRA (acronym for “Loudness Range”). For the Pachelbel canon at a pitch of 429.62 Hz, we had LRA = 4.11 LU, a value indicating that there is little tension in the musical rendering. Indeed, below LRA = 4 LU, we have a gentle piece to listen to that encourages meditation, but which can also quickly become weary and boring. Above LRA = 5 LU, the track alternates between gentle moments and others that put you under tension. Finally, if 6 ≤ LRA ≤ 12 LU, we have a track where there are strong sonic differences between different sections of the song. This is what we’re looking for in classical music where, very often, we have LRA ≥ 9 LU. The same applies to ballads. For country-jazz music, we’ll typically have 6 ≤ LRA ≤ 8 LU. For rock or electronic music, we’re looking for an LRA around 5 LU. Finally, for Hip Hop or rap, we typically have LRA ≤ 5.
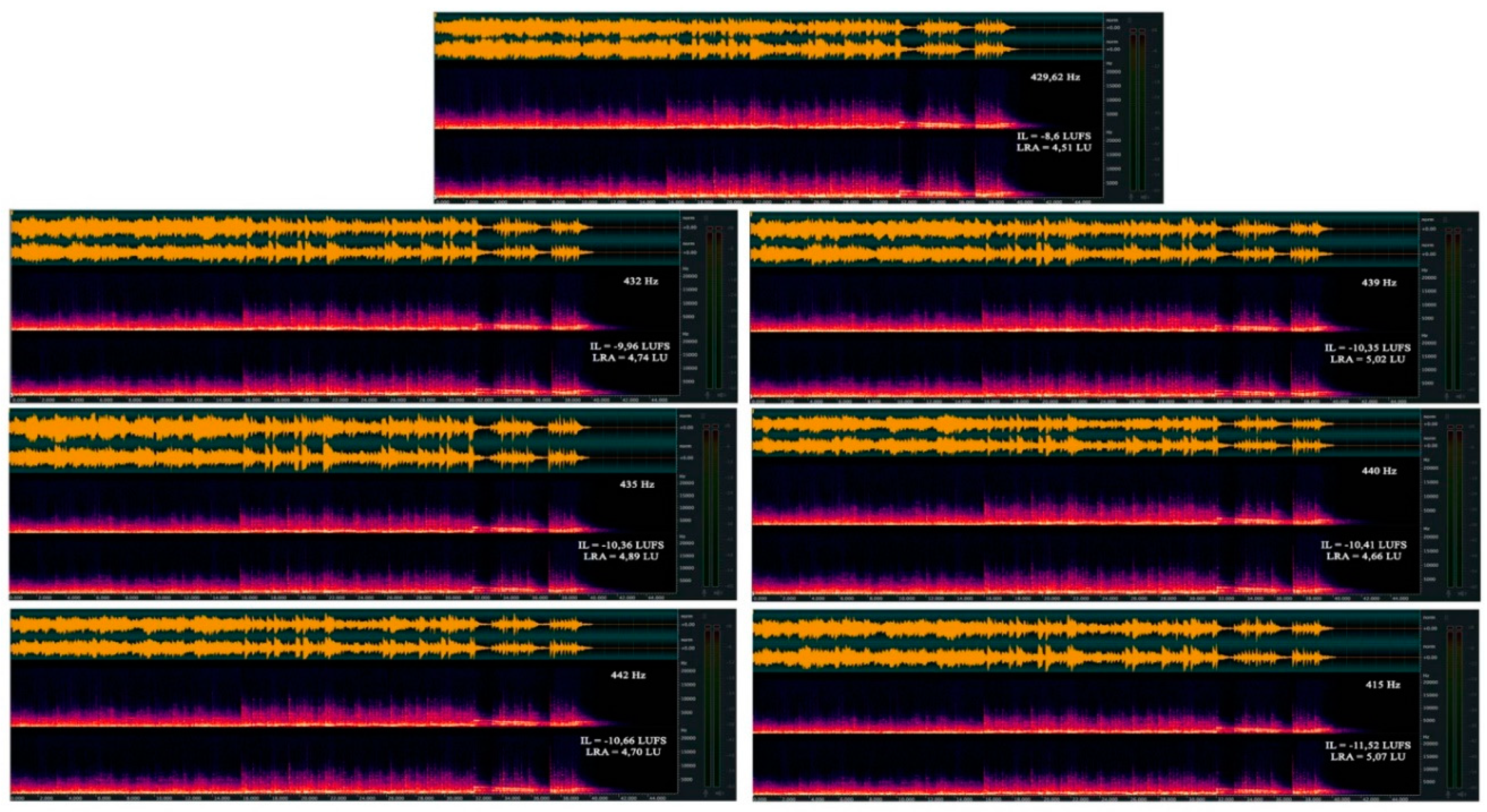
With this in mind, we generated the same piano sounds for the seven diapasons considered above, using the Pachelbel canon. Figure 12 shows the spectrograms obtained in each case. As we’re dealing here with a relatively simple sound, it’s rather difficult to establish a classification with the naked eye. Fortunately, software is available to calculate the Integrated Loudness (IL) and Dynamic Excursion Rating (DER) given for each pitch. Thus, based on the sound level, we obtain the following classification:
429.62 > 432 > 439 > 435 > 440 > 442 > 415
Note that we’re dealing here with non-compressed sound files. Consequently, what defines the sound level is frequency richness and the fact of having relative phases that reinforce rather than oppose each other. Remember that when two waves of the same frequency are in phase coincidence, they reinforce each other, resulting in maximum amplitude. Conversely, if there is phase opposition, they cancel each other out, giving zero sound amplitude. As a result, the 429.62 Hz pitch clearly stands out from the other pitches, with a sound level 1.36 LUFS above the 432 Hz pitch in second place. Note that this A4 = 432 Hz diapason stands out quite clearly (∆IL ≈ 0.4 LUFS) from the others (439 Hz, 435 Hz, 440 Hz, 442 Hz), which fit into a pocket handkerchief. As with the Pachelbel canon, the least frequency-rich and phase-coherent spectrogram is obtained with the German baroque pitch of 415 Hz, with a deviation of 0.86 LUFS from the orchestral pitch at 442 Hz.
Let’s now consider the dynamic excursion indicator (LRA), which gives the following ranking:
429.62 < 440 < 442 < 432 < 435 < 439 < 415
The 429.62 Hz diapason is again distinguished from the others by its narrower dynamic excursion range (∆LRA = 0.23 LU), closely followed (∆ = 0.15 LU) by the “official” 440 Hz pitch. In other words, it’s the 429.62 pitch that provides the least tension/relaxation contrast in the sound. Or, if you prefer, it’s at this pitch that the sound is the softest and least stressful. In contrast, the German Baroque pitch at 415 Hz is the most stressful. This is hardly surprising, given that classical music rarely seeks to lull the listener to sleep. On the contrary, strong contrasts are desired, to better highlight a particular voice or instrument. If this is the desired effect, the pitch based on the mass of the water molecule is not the right one for musical contrasts.
All of which goes to show that there really is something special with music composed at the pitch of the water molecule, at 429.62 Hz. The fact that it’s a diapason calculated using the laws of physics with universal constants, and not an empirical diapason based on musical feeling, gives it an interesting universality. Of course, we could have chosen any molecule other than the water molecule. As explained in the introduction, based the relative abundances of the atomic elements in the universe, it follows that the water molecule H₂O, should be the most abundant molecule in the entire universe. And, as everything containing water has a shape (hence the expression “Morphogenic Water”, recalling this fundamental fact), using the molar mass of this molecule to deduce an optimal and universal diapason seems perfectly logical.
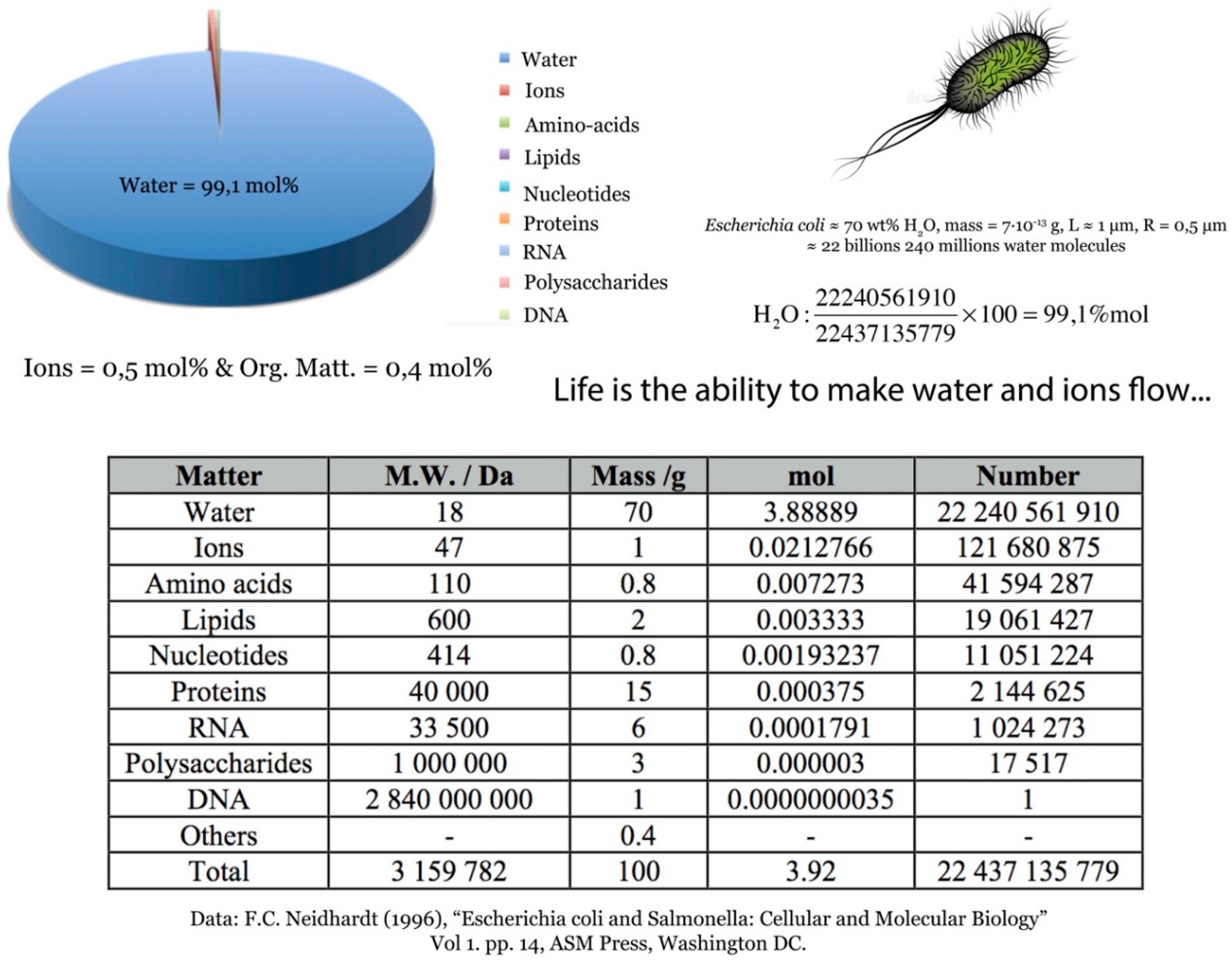
In order to better understand the deep link existing between life and water, one may refer to Figure 13. It shows that a single-celled living creature such as the bacterium Escherichia Coli, for its part, is 99.1 mol% water. So, here too, the choice of the water molecule as the universal diapason in biology, and not just in chemistry and physics, is obvious. Moreover, if we consider a human being, male or female, we find that the proportion of water molecules is 96.49 mol% in a man and 97.05 mol% in a woman (Table 4). And, as music was created by human beings for other human beings, the pitch of water at 429.62 Hz is once again a very natural choice. Obviously, much lower numbers would have been obtained if percentages have been expressed in wt% (mass of entities) and not in mol% (number of entities). This is what is usually done in most papers interested in water in biology. The trouble in dealing with mass is to mix two very different scales: the scale of macroscopic entities submitted to the force of gravitation (kilograms) with the scale of molecular entities submitted to the forces of diffusion (m²·s⁻¹). Such a practice being not logical, a better approach is then to count entities with integers that have no dimensional content. By using the scale-invariant mol% concept, one may treat on the same ground molecules as well as polymers, as here mass does not matter. Of course, such a practice in perfectly justified owing to the extraordinary small intrinsic value of the gravitational force relative to the electromagnetic force (10⁻³⁹:10⁻²) at the scale of a proton or a neutron [23].
Conclusion
In this study, we have tried to demonstrate that music can provide a completely rational and coherent framework for thinking, especially when it comes to choosing a diapason to transform any vibratory frequency into a musical note. We therefore recommend the use of a “scientific” diapason at 429.62 Hz, a value that can be calculated using the recognized laws of physics via a set of three universal constants (speed of light in vacuum c, quantum of action h and Avogadro number NA) and knowledge of the mass of a water molecule. We also demonstrated, through an analysis of spectrograms associated with different parameters for measuring sonic richness, that the choice of this diapason proved to be optimal compared with other choices of neighboring frequencies such as A4 = 432 Hz or A4 = 440 Hz. To date, dozens of musicians around the world have already chosen to use such a diapason in their musical performances with a wide variety of instruments. They all agree that making music at 429.62 Hz pitch greatly changes the experience for both them and the audience. We sincerely hope that this pitch will soon become a new musical standard in the world of music.
On a theoretical and scientific level, the reasons for such success can be traced back to the fact that Maxwell’s equations remain invariant when the symmetry operations of the ISO(4,2) group are applied. This is important, given that all living beings are at least 96% or more water, and that water, via its “coherence domains”, is highly sensitive to electromagnetic waves of all frequencies [5,24]. In particular, the fact that the ISO(4,2) symmetry group exhibits space-time dilatation operators helps us to understand how sound effects on the scale of the human ear can affect molecular processes taking place on the nanometer scale via scale resonance. These “scale waves” regulating the relative values of masses at different scales of observation are by no means new, since their existence was predicted as early as 1983 to explain the mass spectra of elementary particles [10]. What is new is the ability to relate them to the existence of the ISO(4,2) symmetry group.
With this study, we hope to have taken a decisive step towards ensuring that, in future, music will no longer be regarded only as an art, but also as a science with mathematical foundations as solid as those of physics, chemistry or molecular biology. Finally, since we know that music can also have therapeutic effects, we may hope that, in the not-too-distant future, agriculture and medicine will be enriched and enhanced by the systematic use of music at A4 = 429.62 diapason, in complement, of course, to the techniques that have been tried and tested since the advent of the scientific method.
References
- Available online: https://sciencenotes.org/composition-of-the-universe-element-abundance/.
- M. Henry (2021), Thermodynamics of Life. Substantia 5(1): 43-71. [CrossRef]
- M. Henry, « L’eau Morphogénique : Santé, Information et Champs de Conscience », Éditions Dangles, Escalquens (2020), EAN : 978 – 2 – 7033 – 1269 – 7.
- Aristotle, “De Generatione et Corruptione”, Book II, Chap. 3, translated by H. H. Joachim in W. D. Ross, ed., The Works of Aristotle, vol. 2 (Oxford: Oxford, 1930).
- M. Henry (2020), “Consciousness, Information, Electromagnetism and Water”, Substantia 4(1): 23-36. [CrossRef]
- Jagadis Chunder Bose, “Researches on irritability of plants”, Longmans, Green, and co, New York (1913).
- Jean Thoby, « Le Chant Secret des Plantes : Vibrations et émotions végétales », Rustica éditions, Paris (2022).
- François-Xavier Chaboche, « Vie et mystère des nombres », Éditions de Compostelle, Paris (1989), p. 155.
- Gosseries, M. Fecchio, A. Wolf, L. R. D. Sanz, C. Sombrun, A. Vanhaudenhuyse, S. Laureys, « Behavioural and brain responses in cognitive trance: A TMS-EEG case study », Clinical Neurophysiology, 131 (2020) 586-588.
- J. Sternheimer, « Musique des particules élémentaires », C. R. Acad. Sci. Paris, Ser. II, 297, 829-834 (1983).
- M. Henry, « Consciousness, Information, Electromagnetism and Water». Substantia 4(1): 23-36 (2020).
- Emmy Noether, “Invariante Variationsprobleme”, Königlich Gesellschaft der Wissenschaften Göttingen Nachrichten Mathematik-Physik Klasse (1918), 2, 235–267.
- J. Ellis, “On the musical scales of various nations”, J. Soc. Arts, 33 (1885) pp. 485-527.
- R. Plompt & W. J. M. Levelt, « Tonal consonance and critical bandwidth », J. Acoust. Soc. Am., 38 (1965) 548-560.
- Peter Buch, https://en.xen.wiki/images/b/b3/Zetamusic5.pdf.
- A.-E. Ceulemans, “Mezzo punto, tutto punto, tuono chorista: Les diapasons en Italie du Nord vers 1600”, Acta Musicologica, 82[2] (2010), pp. 237-261.
- Nicole Scotto di Carlo, « Les divas et le diapason », Médecine des Arts, 21 (1997), pp. 10-13.
- D. Calamassi, G.P. Pomponi, « Music Tuned to 440 Hz Versus 432 Hz and the Health Effects: A Double-blind Cross-over Pilot Study”, EXPLORE, 15[4], (2019), pp. 283-29.
- A. Hatton, E. D. Galbraith, N. S. C. Merleau, T. P. Miettinen, B. McDonald Smith and J. A. Shander “The human cell count and size distribution”, Proc. Natl. Acad. Sci. USA, 120[39] (2023) e2303077120, pp. 1-10.
- Album eau : https://tommijacks.bandcamp.com/album/eau-42962-hz-97-mol.
- Album eau vol. 2 : https://tommijacks.bandcamp.com/album/eau-429-62-hz-97-mol-vol-2.
- La de L’eau : https://tommijacks.bandcamp.com/album/la-de-leau.
- Yuval Ne’eman & Yoram Kirsh (1989), « The particle hunters », Cambridge University Press, Cambridge, Chap. 6, p. 127.
- Bono, E. Del Giudice, L. Gamberale, M. Henry, “Emergence of the Coherent Structure of Liquid Water”, Water, 4 (2012), pp. 510-532.
Figure 1.
The four main types of “morphogenic” water identified in nature and their association with Aristotle’s four elements theory.
Figure 1.
The four main types of “morphogenic” water identified in nature and their association with Aristotle’s four elements theory.
Figure 2.
The regular seven-pointed star of the seven frames of human thought.
Figure 3.
Noether’s theorem links any continuous symmetry operation to the great conservation principles of physics. Each symmetry also gives rise to a principle of relativity, meaning that a variable can take on an arbitrary value fixed by a given observer.
Figure 3.
Noether’s theorem links any continuous symmetry operation to the great conservation principles of physics. Each symmetry also gives rise to a principle of relativity, meaning that a variable can take on an arbitrary value fixed by a given observer.
Figure 4.
Cycles of ascending fifths (clockwise) or ascending fourths (counter-clockwise) generating the Pythagorean chromatic scale, with its two types of interval respectively short (limma = 90 ¢) and long (apotome = 114 ¢, defining the tone (204 = 114 + 90) and the comma (24 = 114 - 90). Intervals generated in relation to the fundamental note are also indicated with the conventions P = perfect, M = major, m = minor, A = augmented and d = diminished, 1 = unison, 2 = second, 3 = third, 4 = fourth, 5 = fifth, 6 = sixth and 7 = seventh. Tritone (TT) may be considered as A4 or d5.
Figure 4.
Cycles of ascending fifths (clockwise) or ascending fourths (counter-clockwise) generating the Pythagorean chromatic scale, with its two types of interval respectively short (limma = 90 ¢) and long (apotome = 114 ¢, defining the tone (204 = 114 + 90) and the comma (24 = 114 - 90). Intervals generated in relation to the fundamental note are also indicated with the conventions P = perfect, M = major, m = minor, A = augmented and d = diminished, 1 = unison, 2 = second, 3 = third, 4 = fourth, 5 = fifth, 6 = sixth and 7 = seventh. Tritone (TT) may be considered as A4 or d5.
Figure 5.
The basilar membrane of the human cochlea can be seen as a bandpass filter, letting through all frequencies within a certain frequency band and blocking all frequencies outside this band (bottom left). The figure at top left shows that the size of the critical bandwidth lies somewhere between a whole tone and a minor third for a large part of the audible range, and tends towards a major third for low frequencies. The figure at top right shows that dissonance appears maximum for a frequency deviation equal to a quarter of the critical bandwidth. Bottom right: the variation in consonance for an interval involving a complex sound with a fundamental frequency of 250 Hz and another sound with a higher frequency. Adapted from Plompt and Levelt (1965).
Figure 5.
The basilar membrane of the human cochlea can be seen as a bandpass filter, letting through all frequencies within a certain frequency band and blocking all frequencies outside this band (bottom left). The figure at top left shows that the size of the critical bandwidth lies somewhere between a whole tone and a minor third for a large part of the audible range, and tends towards a major third for low frequencies. The figure at top right shows that dissonance appears maximum for a frequency deviation equal to a quarter of the critical bandwidth. Bottom right: the variation in consonance for an interval involving a complex sound with a fundamental frequency of 250 Hz and another sound with a higher frequency. Adapted from Plompt and Levelt (1965).
Figure 6.
Generation of optimal ranges at N = 1, 2, 3, 5, 7, 12, 19, 31, 53, 72 and 270 degrees using Riemann’s zeta function. Note that 3 = 2+1, 5 = 2+3, 7 = 2+5, 12 = 7+5, 19 = 12+7 and 31= 12+19, 53 = 19+31+3, 72 = 19+53, reminiscent of the Fibonacci series converging on the golden number.
Figure 6.
Generation of optimal ranges at N = 1, 2, 3, 5, 7, 12, 19, 31, 53, 72 and 270 degrees using Riemann’s zeta function. Note that 3 = 2+1, 5 = 2+3, 7 = 2+5, 12 = 7+5, 19 = 12+7 and 31= 12+19, 53 = 19+31+3, 72 = 19+53, reminiscent of the Fibonacci series converging on the golden number.
Figure 7.
The Oettingen/Riemann Tonnetz derived from the “Speculum Musicum” of Leonard Euler (1774).
Figure 7.
The Oettingen/Riemann Tonnetz derived from the “Speculum Musicum” of Leonard Euler (1774).
Figure 8.
Top: Frequency spectrum of Johann Pachelbel’s canon harmonized at 429.62 Hz pitch. Bottom: Zoom into the frequency spectrum, showing the existence of a “light” in the sound.
Figure 8.
Top: Frequency spectrum of Johann Pachelbel’s canon harmonized at 429.62 Hz pitch. Bottom: Zoom into the frequency spectrum, showing the existence of a “light” in the sound.
Figure 9.
How to read a spectrogram.
Figure 10.
Spectrograms of the Pachelbel Canon for three A4 pitch values.
Figure 11.
Spectrograms of the Pachelbel Canon for three other A4 pitch values.
Figure 12.
Sound quantization of a sequence of piano notes for seven different diapasons.
Figure 13.
Main constituents of a single-celled living being such as the E. coli bacterium.
Table 1.
Harmonic series fn (n ≤ 16) and best approximation ratio (*) of equal-temperament scale. P1 = “Unisson (0 ¢)”, m2 = “Minor second (semi-tone, 100 ¢)”, M2 = “Major second (tone, 200 ¢)”, m3 = “Minor third (300 ¢)”, M3 = “Major third (400 ¢)”, P4 = “Perfect fourth (500 ¢)”, TT = “Tritone (600 ¢)”, P5 = “Perfect fifth (700 ¢)”, m6 = “Minor sixth (800 ¢)”, M6 = “Major sixth (900 ¢)”, m7 = “Minor seventh (1000 ¢)”, M7 = “Major seventh (1100 ¢)”, P8 = “Octave (1200 ¢). Intervals n2 (150 ¢), n3 (350 ¢), n6 (850 ¢) and n7 (1050 ¢) are “neutral”, i.e. cannot be qualified as having “minor” or “major” character.
Table 1.
Harmonic series fn (n ≤ 16) and best approximation ratio (*) of equal-temperament scale. P1 = “Unisson (0 ¢)”, m2 = “Minor second (semi-tone, 100 ¢)”, M2 = “Major second (tone, 200 ¢)”, m3 = “Minor third (300 ¢)”, M3 = “Major third (400 ¢)”, P4 = “Perfect fourth (500 ¢)”, TT = “Tritone (600 ¢)”, P5 = “Perfect fifth (700 ¢)”, m6 = “Minor sixth (800 ¢)”, M6 = “Major sixth (900 ¢)”, m7 = “Minor seventh (1000 ¢)”, M7 = “Major seventh (1100 ¢)”, P8 = “Octave (1200 ¢). Intervals n2 (150 ¢), n3 (350 ¢), n6 (850 ¢) and n7 (1050 ¢) are “neutral”, i.e. cannot be qualified as having “minor” or “major” character.
| Harmonic | Ratio | Cents (¢) | Interval Harmonic series |
| 1 | 1:1 | 0 | P1* C1 |
| 2 | 2:1 | 1200 | P8* C2 |
| 3 | 3:2 | 702 | P5 (+2¢)* G2 |
| 4 | 4:3 | 498 | P4 (-2¢)* C3 |
| 5 | 5:4 | 386 | M3 (-14 ¢)* E3 |
| 5 | 5:3 | 884 | M6 (-16 ¢)* (P4* ⊕ M3*) |
| 6 | 6:5 | 316 | m3+ (+16 ¢) G3 |
| 7 | 7:6 | 267 | m3- (-33 ¢) B♭3 |
| 7 | 7:5 | 582 | TT- (-18 ¢) (m3- ⊕ m3+) |
| 7 | 7:4 | 969 | m7- (-31 ¢) (TT- ⊕ M3*) |
| 8 | 8:7 | 231 | M2+ (+31 ¢) C4 |
| 8 | 8:5 | 814 | m6 (+14 ¢)* (TT- ⊕ M2+) |
| 9 | 9:8 | 204 | M2 (+4 ¢)* D4 |
| 9 | 9:7 | 435 | M3++ (+35 ¢) (M2* ⊕ M2+) |
| 9 | 9:5 | 1018 | m7+ (+18 ¢) (M2* + m6*) |
| 10 | 10:9 | 182 | M2- (-18 ¢) E4 |
| 10 | 10:7 | 617 | TT (+17 ¢)* (M2 ⊕ M3) |
| 11 | 11:10 | 165 | n2+ (+15 ¢) F♯4 |
| 11 | 11:9 | 347 | n3 (-3 ¢) (n2+ ⊕ M2-) |
| 11 | 11:8 | 551 | TT-- (-49 ¢) (n2+ ⊕ M3*) |
| 11 | 11:7 | 783 | m6- (-17 ¢) (n2+ ⊕ TT*) |
| 11 | 11:6 | 1050 | n7 (0¢) (n2+ ⊕ M6*) |
| 12 | 12:11 | 151 | n2 (+1 ¢) G4 |
| 12 | 12:7 | 933 | M6+ (+33 ¢) (m2++ ⊕ m6-) |
| 13 | 13:12 | 139 | n2- (-11 ¢) A4 |
| 13 | 13:11 | 289 | m3 (-11 ¢)* (n2- ⊕ M2---) |
| 13 | 13:10 | 454 | M3+++ (+54 ¢) (n2- ⊕ m3+) |
| 13 | 13:9 | 637 | TT+ (+37 ¢) (n2- ⊕ P4*) |
| 13 | 13:8 | 841 | n6 (-9 ¢) (n2- ⊕ P5*) |
| 13 | 13:7 | 1072 | n7+ (+22 ¢) (n2- ⊕ M6) |
| 14 | 14:13 | 128 | m2++ (+28 ¢) B♭4 |
| 14 | 14:11 | 418 | M3+ (+18 ¢) (m2++ ⊕ m3*) |
| 14 | 14:9 | 765 | m6-- (-35 ¢) (m2++ ⊕ TT+) |
| 15 | 15:14 | 119 | m2+ (+19 ¢) B4 |
| 15 | 15:13 | 248 | m3-- (-52 ¢) (m2+ ⊕ m2++) |
| 15 | 15:11 | 537 | P4+ (+37 ¢) (m2+ ⊕ M3+) |
| 15 | 15:8 | 1088 | M7 (-12 ¢)* (m2+ ⊕ m7-) |
| 16 | 16:15 | 112 | m2 (+12 ¢)* C5 |
| 16 | 16:13 | 360 | n3+ (+10 ¢) (m2* ⊕ m3--) |
| 16 | 16:11 | 649 | TT++ (+49 ¢) (m2* ⊕ P4+) |
| 16 | 16:9 | 996 | m7 (-4 ¢)* (m2* ⊕ M6*) |
Table 2.
Derivation of a 72-note scale from the limit 11 harmonic series. According to Figure 5, for this type of scale we have x = 103.81, i.e. q₂ = 103.81×ln 2 = 71.96 ≈ 72; q₃ = 103.81×ln 3 = 114. 05 ≈ 114; q₅ = 103.81×ln 5 = 167.08 ≈ 167; q₇ = 103.81×ln 7 = 202.01 ≈ 202; q₁₁ = 103.81×ln 11 = 248.93 ≈ 249. We can check that for simple ratios, we have q₇ - q₅ = 202 - 167 = 35 (ratio 7:5); q₃ - q₂ = 114 - 72 = 42 (ratio 3: 2); q₁₁ - q₇ = 249 - 202 (ratio 11:7) and q₅ - q₃ = 167 - 114 = 53 (ratio 5:3), according to this table. The same can be done for the other 68 compound ratios.
Table 2.
Derivation of a 72-note scale from the limit 11 harmonic series. According to Figure 5, for this type of scale we have x = 103.81, i.e. q₂ = 103.81×ln 2 = 71.96 ≈ 72; q₃ = 103.81×ln 3 = 114. 05 ≈ 114; q₅ = 103.81×ln 5 = 167.08 ≈ 167; q₇ = 103.81×ln 7 = 202.01 ≈ 202; q₁₁ = 103.81×ln 11 = 248.93 ≈ 249. We can check that for simple ratios, we have q₇ - q₅ = 202 - 167 = 35 (ratio 7:5); q₃ - q₂ = 114 - 72 = 42 (ratio 3: 2); q₁₁ - q₇ = 249 - 202 (ratio 11:7) and q₅ - q₃ = 167 - 114 = 53 (ratio 5:3), according to this table. The same can be done for the other 68 compound ratios.
| Interval | Degree | Ratio | Degree | Ratio | Degree | Ratio | Degree | Ratio | Degree | Ratio | Degree | Ratio |
| P1 | 0 | 1:1 | - | - | - | - | - | - | - | - | - | - |
| A1 | 1 | 81:80 | 2 | 45:44 | 3 | 33:32 | - | - | - | - | - | - |
| m2 | 4 | 25:24 | 5 | 21:20 | 6 | 35:33 | 7 | 15:14 | - | - | - | - |
| n2 | 8 | 27:25 | 9 | 12:11 | 10 | 11:10 | - | - | - | - | - | - |
| M2 | 11 | 10:9 | 12 | 9:8 | 13 | 25:22 | 14 | 8:7 | 15 | 81:70 | - | - |
| m3 | 16 | 7:6 | 17 | 33:28 | 18 | 25:21 | 19 | 6:5 | - | - | - | - |
| n3 | 20 | 40:33 | 21 | 11:9 | 22 | 99:80 | - | - | - | - | - | - |
| M3 | 23 | 5:4 | 24 | 44:35 | 25 | 14:11 | 26 | 9:7 | 27 | 35:27 | - | - |
| P4 | 28 | 21:16 | 29 | 33:25 | 30 | 4:3 | 31 | 27:20 | 32 | 15:11 | 33 | 11:8 |
| TT | 34 | 25:18 | 35 | 7:5 | 36 | 99:70 | 37 | 10:7 | 38 | 36:25 | - | - |
| P5 | 39 | 16:11 | 40 | 22:15 | 41 | 40:27 | 42 | 3:2 | 43 | 50:33 | 44 | 32:21 |
| m6 | 45 | 54:35 | 46 | 14:9 | 47 | 11:7 | 48 | 35:22 | 49 | 8:5 | - | - |
| n6 | 50 | 81:50 | 51 | 18:11 | 52 | 33:20 | - | - | - | - | - | - |
| M6 | 53 | 5:3 | 54 | 27:16 | 55 | 56:33 | 56 | 12:7 | 57 | 121:70 | - | - |
| m7 | 58 | 7:4 | 59 | 44:25 | 60 | 16:9 | 61 | 9:5 | - | - | - | - |
| n7 | 62 | 20:11 | 63 | 11:6 | 64 | 50:27 | - | - | - | - | - | - |
| M7 | 65 | 15:8 | 66 | 66:35 | 67 | 21:11 | 68 | 27:14 | - | - | - | - |
| d8 | 69 | 35:18 | 70 | 49:25 | 71 | 99:50 | - | - | - | - | - | - |
| P8 | 72 | 2:1 | - | - | - | - | - | - | - | - | - | - |
Table 3.
Cyclic group structure of the Tonnetz. The relative (R) minor of a major chord increases its fifth by a tone. The lowering (L) of a minor chord increases its fifth by a semi-tone. Starting from a C major chord, the same chord is recovered after twelve iterations of alternating operations R and L, meaning that (LR)¹² = 1, the identity. Moreover, the parallel (P) operation transforming a major chord in its minor form (lowering of the third by one semi-tone) may be expressed as: P = R(LR)³. As L(CEG) = EGB and L(EGB) = CEG, we also have L² = 1 and L(LR)L = RL = (LR)⁻¹. As the Dihedral D₁₂ group is of order h = 24 and may be generated according to D₁₂ = < a,b | a12=b2=1, bab=a-1 >, we see here that a = (LR) and b = L.
Table 3.
Cyclic group structure of the Tonnetz. The relative (R) minor of a major chord increases its fifth by a tone. The lowering (L) of a minor chord increases its fifth by a semi-tone. Starting from a C major chord, the same chord is recovered after twelve iterations of alternating operations R and L, meaning that (LR)¹² = 1, the identity. Moreover, the parallel (P) operation transforming a major chord in its minor form (lowering of the third by one semi-tone) may be expressed as: P = R(LR)³. As L(CEG) = EGB and L(EGB) = CEG, we also have L² = 1 and L(LR)L = RL = (LR)⁻¹. As the Dihedral D₁₂ group is of order h = 24 and may be generated according to D₁₂ = < a,b | a12=b2=1, bab=a-1 >, we see here that a = (LR) and b = L.
| Iteration | Relative minor of major chord | Lowering of minor chord |
| 1 | R(C = CEG) = ACE (Am) | L(Am) = FAC (F) |
| 2 | R(F) = DFA (Dm) | L(Dm) = B♭DF (B♭) |
| 3 | R(B♭) = GBD (Gm) | L(Gm) = E♭GB♭ (E♭) |
| 4 | R(E♭) = CE♭G (Cm) | L(Cm) = A♭CE♭ (A♭) |
| 5 | R(A♭) = FA♭C (Fm) | L(Fm) = D♭FA♭ (D♭) |
| 6 | R(D♭) = B♭D♭F (B♭m) | L(B♭m) = G♭B♭D♭ (G♭) |
| 7 | R(G♭) = E♭G♭B♭ (E♭m) | L(E♭m) = B♭E♭G♭ = BD♯F♯ (B) |
| 8 | R(B) = G♯BD♯ (G♯m) | L(G♯m) = EG♯B (E) |
| 9 | R(E) = C♯EG♯ (G♯m) | L(C♯m) = AC♯E (A) |
| 10 | R(A) = F♯AC♯ (F♯m) | L(F♯m) = DF♯A (D) |
| 11 | R(D) = BDF♯ (Bm) | L(Bm) = GBD (G) |
| 12 | R(G) = EGB (Em) | L(Em) = CEG (C) |
Table 4.
Average physical body composition for an adult Caucasian man and woman (20-29 years) living in the USA. IC = intracellular. EC = extracellular. Source : K. J. Ellis, « Reference man and woman more fully characterized », Biological Trace Element Research, G. N. Schrauzer Ed., The Humana Press Inc. (1990) pp. 385-400.
Table 4.
Average physical body composition for an adult Caucasian man and woman (20-29 years) living in the USA. IC = intracellular. EC = extracellular. Source : K. J. Ellis, « Reference man and woman more fully characterized », Biological Trace Element Research, G. N. Schrauzer Ed., The Humana Press Inc. (1990) pp. 385-400.
| Man | m / g | M / Da | Wt% | Mol% |
| Water (total) | 45 000 | 18.0 | 55.14 | 96.39 |
| Water (IC) | 24 900 | 18.0 | 30.51 | 53.33 |
| Water (EC) | 20 100 | 18.0 | 24.63 | 43.05 |
| Lipids | 19 800 | 600 | 24.26 | 1.27 |
| Proteins | 13 070 | 40 000 | 16.01 | 0.01 |
| Phosphates | 1 704 | 98,0 | 2.09 | 0.67 |
| Calcium | 1 230 | 40.1 | 1.51 | 1.18 |
| Glucides | 500 | 180.6 | 0.61 | 0.11 |
| Potassium | 149 | 39,1 | 0.18 | 0.15 |
| Sodium | 82 | 23,0 | 0.10 | 0.14 |
| Chloride | 77.5 | 35.5 | 0.09 | 0.08 |
| Total | 81 612.5 | - | 100.00 | 100.00 |
| Woman | m / g | M / Da | Wt% | Mol% |
| Water (total) | 30 900 | 18.0 | 52.32 | 97.49 |
| Water (IC) | 15 400 | 18.0 | 44.78 | 67.80 |
| Water (EC) | 15 500 | 18.0 | 19.61 | 29.69 |
| Lipids | 15 900 | 600 | 20.11 | 0.91 |
| Proteins | 9 270 | 40 000 | 11.73 | 0.01 |
| Phosphates | 1 372 | 98.0 | 1.74 | 0.48 |
| Calcium | 905.5 | 40.1 | 1.15 | 0.78 |
| Glucides | 500 | 180.6 | 0.63 | 0.10 |
| Potassium | 88.5 | 39.1 | 0.11 | 0.08 |
| Sodium | 63.5 | 23.0 | 0.08 | 0.10 |
| Chloride | 61.5 | 35.5 | 0.08 | 0.08 |
| Total | 59 061.0 | - | 100.0 | 100.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated