Prerpints.org logo
Preprint
Article

Conventional and Green Rubber Plasticizers Classified through the Nile Red [E(NR)] and Reichardt’s Polarity Scale [ET(30)]

This version is not peer-reviewed.

Submitted:

15 January 2024

Posted:

16 January 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
After a survey on polymer plasticization theories and conventional criteria to evaluate polymer-plasticizer compatibility through the solubility parameter, an attempt to create a polymer-plasticizers polarity scale through solvatochromic dyes has been made. Since the Reichardt’s ET(30) dye is insoluble in rubber hydrocarbon polymers like polyisoprene, polybutadiene and styrene-butadiene copolymers and is not also useful for the evaluation of the hydrocarbons and ester plasticizers, the Nile Red solvatochromic dye was instead used extensively and successfully for this class of compounds. A total of 53 different compounds were evaluated with the Nile Red dye and wherever possible also with the ET(33) Reichardt’s dye. A very good correlation was then found between the Nile Red scale E(NR) and the Reichardt’s ET(30) scale for this class of compounds focusing on diene rubbers and their typical hydrocarbons and new esters plasticizers. Furthermore, the E(NR) scale shows also a reasonable correlation with the total solubility parameter calculated according to the Van Krevelen method. Based on the above results, some conclusion was made about the compatibility between the diene rubbers and the conventional plasticizers as well as some new and green plasticizer proposed for the rubber compounds.
Keywords: 
rubbers
;  
plasticizers
;  
solvatochromic dyes
;  
Nile Red dye
;  
Reichardt dye ET(30)
;  
Reichardt dye ET(33)
;  
compatibility
;  
solubility parameter
Subject: 
Chemistry and Materials Science  -   Applied Chemistry

1. Introduction

Plasticizers are liquids at ambient temperature with relatively high molecular weight or, less frequently, low melting point solids which are added to a polymer matrix to change its viscoelastic properties [1,2,3,4,5,6,7,8,9]. The changes in the physical properties of the polymer matrix have many consequences starting from an improved processability, passing through an increased flexibility of the resulting polymer compound and leading to improved low temperature performances [1,2,3,4,5,6,7,8,9]. The latter result is achieved because the plasticizer is often a liquid characterized by a lower glass transition temperature (Tg) than the guest polymer matrix leading to a shift of the compound Tg toward lower temperatures. Indeed, the plasticizer efficiency is often measured by the degree of glass transition temperature shift toward lower temperatures of the resulting plasticized compound (Tgc) with respect to the glass transition of the raw polymer (Tgp) so that ΔTg = Tgp - Tgc [1,2,3,4,5,6,7,8,9]. However, the ΔTg is most pronounced in polymers with rigid chains (e.g. PVC) whereas the plasticizer causes a shift of the order of 100°-160°C. On the other hand, the effect of plasticizers on already flexible and rubber-like polymer is much less pronounced and limited to a ΔTg shift to just few tents of °C toward lower temperatures [1,2,3,4,5,6,7,8,9]. For rubbers already characterized by low glass transition temperature values (e.g. natural rubber Tg = -72°C or high cis-polybutadiene with Tg = -105°C), the plasticizer effect can cause a ΔTg ≈ -10°C [10,11]. For each given type of polymer or polymer blend, the efficiency of a plasticizer is measured by the degree of ΔTg it is able to cause with respect to another plasticizer. Furthermore, at least for polar polymers (and with a series of limitations) a simple relationship has been found: ΔTg = kn with k a proportionality constant and n the moles of plasticizer added, suggesting that the glass transition temperature shift is directly proportional by the amount of the plasticizer added [3]. On the other hand, for apolar polymers it holds a similar relationship: ΔTg = kϕ, where ϕ is the volume fraction of the plasticizer [3]. Another simple relationship for the determination of the compound glass transition is the following [8]:
1/Tgc = ω1/T1 + ω2/T2
where ω1 and ω2 are the weight fractions respectively of polymer and plasticizer while T1 and T2 values are the respective glass transition temperatures. Other relationships for the estimation of the glass transition of a plasticized compound can be found in ref. [8].
It is worth at this point to survey very shortly the three main theories of plasticization mechanism: the lubricity theory, the gel theory and the free volume theory. It is also interesting to note that the latter theory includes also the other two [1,2,3,4,5,6,7,8,9].
The lubricity theory [1,2,3,4,5,6,7,8,9] starts from the observation that in a pure polymer the resistance to deformation and flow derives from the intermolecular friction between adjacent polymer chains which are in direct contact. The introduction of the plasticizer molecules between the polymer chains facilitate the movement of the chain segments through a slippage mechanism provided by the lubricating action of the plasticizer.
The gel theory [1,2,3,4,5,6,7,8,9] represents a further step ahead with respect to the lubricity theory. It starts from the idea that in amorphous polymers the resistance to deformation derives from a model structure of the polymer intended as three-dimensional or honeycomb-type structure which can be defined also as a gel structure. Such a gel structure is conceived as derived from loose attachments or secondary forces which occur at rather regular intervals along the polymer chains and hence in the matrix. The introduction of a plasticizer in such honeycomb structure has the effect to break the loose attachments and to mask the center of forces by preventing the reformation of the three-dimensional macromolecular interaction. It is admitted that the masking action of the force centers derives from the fact that the polymer chain segments are solvated by the plasticizer. Solvation is always intended in a dynamic way so that each chain segment is solvated and de-solvated and sometimes the masking action is lost for a while. This implies an increased flexibility and flowability of the polymer chain and the resulting plasticized compound. Naturally, the chemical nature of each plasticizer exerts a different effect in the masking effect of the secondary force centers leading to the individual effect of each plasticizer.
The free volume theory [1,2,3,4,5,6,7,8,9] starts from the observation that the free volume in a polymer is a measure of the internal available space for the motion of the chain segments, the chain ends and the motion of the side groups of the chains. The free volume reaches the minimum value, say 2.5% of the volume of the given polymer body when it is cooled below its glass transition temperature. Indeed, below the Tg, because the limited free volume available the mentioned chains, ends and side groups movements are frozen and the polymer is in a glassy state. The increase of the motion of these moieties of the polymer can be achieved by heating, by the addition of a plasticizer (which being a low molecular weight molecule increases the number chain ends dramatically), by introducing branching or bulky side groups to the main polymer chain, by inserting more flexible chain segments into the main polymer chain. Thus, any action that leads to an increase in the free volume of a polymer is measurable by a shift of the glass transition toward lower temperatures. The simplest action which does not implies a chemical modification of the polymer, is just the physical addition of a plasticizer and is known as external plasticization to distinguish it from the internal plasticization which instead is due to the chemical modification of the polymer. It is evident that the free volume theory is the most convincing and includes all the notions of the lubricity and gel theories. In fact, the plasticizer fills the available free volume and creates extra free volume; the first molecular layer of plasticizer is adsorbed on the polymer chain segments and provides a certain degree of solvation shielding the force centers of interaction between chains and preventing polymer networking reformation on cooling. The excess of plasticizers molecules, not interacting directly with the polymer chain segments act as volume filler of the free volume created by the first layer of molecules solvating the chain segments and may provide a lubricating effect under deformation and flow. Additional discussion about the free volume theory and recent developments can be found in ref. [8].
The key practical problem in the use of plasticizers is the evaluation of the compatibility between the polymer, the polymer blend and the plasticizers. A general and updated survey can be found in ref. [9]. However, the most popular and accessible approach in the evaluating the polymer plasticizer compatibility involves the use of the solubility parameter either in rubber compounds [12] as well as in plastics [13].
The solubility parameter has been defined by Hildebrand and Scott [12] as:
δ = [(ΔHvap – RT)/Vm ]0.5
The evaporation enthalpy ΔHvap was taken as the parameter of the cohesion energy between molecules minus the thermal energy needed to separate them (RT) divided by the molar volume Vm. The Equation (2) can be re-written as:
δ = [(Ecoh) /Vm ]0.5
The cohesive energy Ecoh of a substance in a condensed state is defined as the increase in internal energy ΔU per mole of substance if all the intermolecular forces are eliminated.
Hansen [13] has shown that the solubility parameter proposed by Hildebrand and Scott does not take into account the contribution of polar forces and hydrogen bonding, therefore, a more complex solubility parameter has been proposed:
δ2 = δd2 + δp2 + δh2
derived from the contribution of three components of the cohesive energy:
Ecoh = Ed +Ep + Eh
respectively due to the contribution of dispersion and polar forces plus a hydrogen bonding contribution.
It is possible to calculate the solubility parameter and the solubility parameter components of almost all molecules and polymers by a group contribution method [14]. For this purpose, as explained by Van Krevelen [14] it is useful to introduce the molar attraction constant simply defined as:
φ = (Ecoh Vm )0.5
A set of equations has been proposed by Van Krevelen [14] for the calculation of the solubility parameter components using the molar attraction by a group contribution methodology:
δd = (∑φd)/ Vm
δp = (∑φp2 )0.5/ Vm
δh = [(∑Eh)/ Vm]0.5
The total solubility parameter can be calculated as follows:
δt = (δd2 + δp2 + δh2)0.5
It can be observed from equation (9) that the hydrogen bond parameter δh cannot be calculated from the molar attraction, but directly from the hydrogen bonding energy Eh [14]. There are numerous ways of evaluation of the solubility of a given polymer P in a given solvent S, Van Krevelen [14] suggests the criteria imposed by the following equation:
Δδ = [(δd,P - δd,S)2 + (δp,P - δp,S)2 + (δh,P – δh,S)2]0.5
To predict solubility:
Δδ ≤ 5
Alternatively, Hansen [13] has proposed a more sophisticated and relatively complex approach for the evaluation of the solubility of a polymer in a solvent.
A simpler and practical approach regards the direct adoption of the total solubility parameter δt eventually determined according to eq. (10), to evaluate the solubility between a polymer and a plasticizer or a solvent which conform to the criteria imposed by the following equation:
|Δδ| = (δt,P – δt,S) ≤ 3.0
a criteria proposed by Brydson [12].
Using the Van Krevelen methodology [14] in previous works we have calculated the solubility parameters of fullerenes [15] and their solubility in fatty acids esters and glycerides [16]. Similarly, it was through the calculated solubility parameters according to the Van Krevelen methodology [14] that it was calculated the compatibility between biodiesel and diene rubbers as well as other typical petroleum-derived plasticizers used in rubber compounding [17].
In the present work we wish to show an alternative or complementary approach to the solubility parameter to evaluate in a practical way the compatibility between a plasticizer and a polymer matrix (in particular a rubber polymer) by classifying also the plasticizers and the rubbers through the Reichardt’s polarity scale ET(30) or through a complementary scale. After all, the Reichardt’s polarity scale was also successfully applied for the first time in the selection of a bonding agent for a rocket propellant composite [18].

2. Materials and Methods

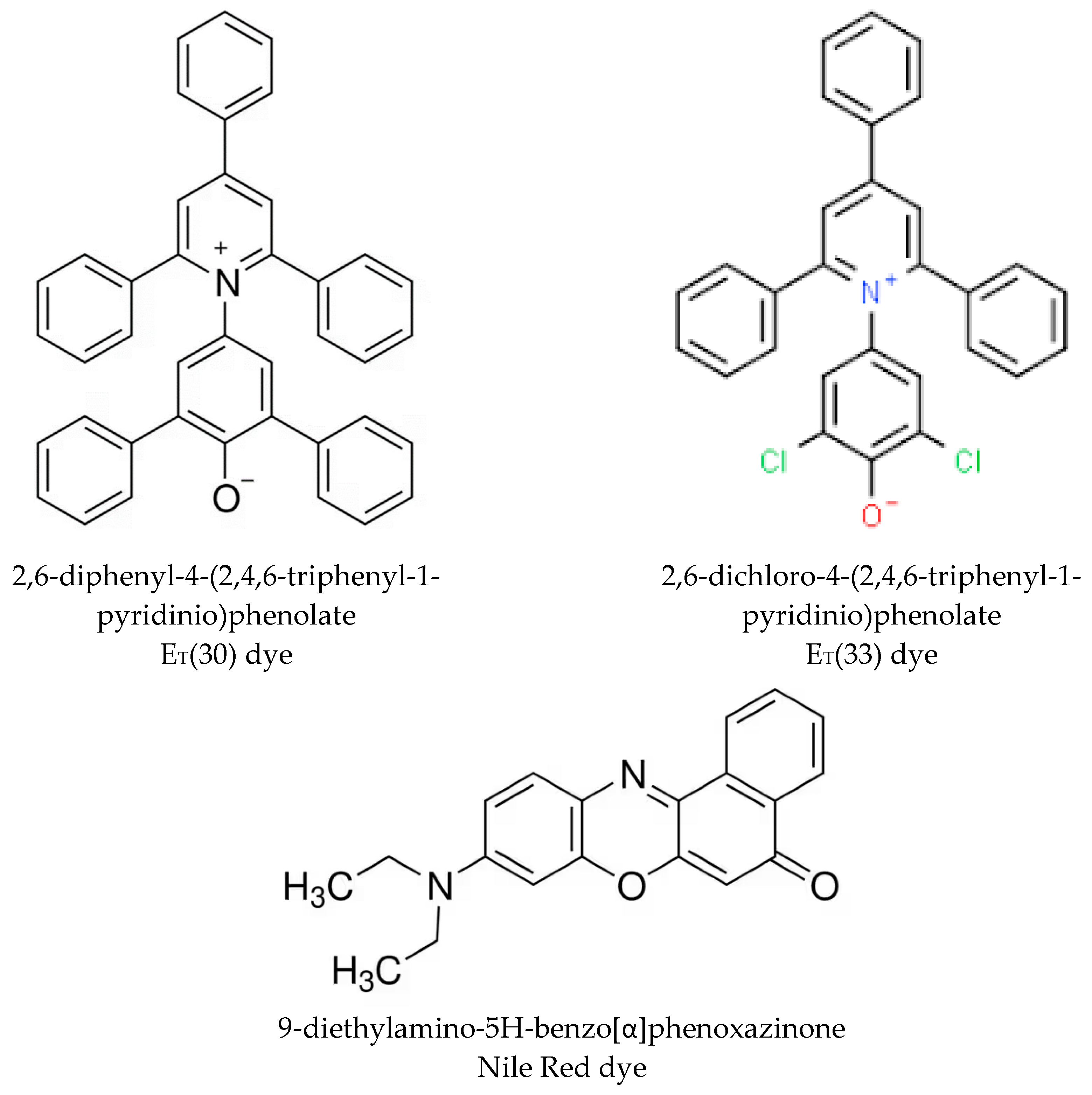
2.1. Materials

All plasticizers, solvent and polymers, unless otherwise stated were purchased from Merck-Aldrich (Germany-USA). The petroleum-based plasticizers or extenders used in the rubber (tire) industry were commercially available products sourced from the market of rubber chemicals and additives. Namely, these plasticizers are: T-DAE (= Treated Distillate Aromatic Extract), MES (= Mild Extract Solvate). Only the product Nytex BIO 6200 (a blend of naphthenic oil and fatty acids from renewable sources) was obtained from Nynas, Sweden. The methyl ester of rapeseed oil was a commercial biodiesel we used as rubber compound plasticizer in our earlier work [17]. Another commercially available plasticizer of this study was the methyl ester of coconut oil. These methyl esters are prepared on industrial scale by transesterification of the corresponding glycerides with methanol. Either the sunflower oil (high oleic content) and the soybean oil of the present work were industrial products obtained from the market of the rubber chemicals. There is a trend in the patent [19,20] and in the open literature e.g. [21] to adopt vegetable oils in tire treads as substitute of the petroleum-based plasticizers to make a greener tire. The most interesting vegetable oils appear to be the soybean [19] and the sunflower oil [20] including also a combination of both oils [21] as plasticizers in tire tread. Regarding the rubber samples, cis-1,4-polybutadiene (Europrene Neocis 60) was obtained from Versalis (Italy), the synthetic cis-1,4- polyisoprene sample was SKI-5PM produced by JSC Sterlitamak Petrochemical Plant (Russia) and the solution-styrene-butadiene rubber (S-SBR) was obtained from Arlanxeo (Germany). The S-SBR was the FX5000 grade characterized by 50% vinyl content and 20% styrene content. Epoxidized Natural Rubber (ENR-25) was supplied from Ekoprena (Malaysia). The nitrile rubber sample was sourced from Versalis (Italy) and it was the Europrene N3345 with 33% acrylonitrile content. All the other polymers including the liquid polymer samples were purchased from Merck-Aldrich (Germany-USA).
The solvatochromic dyes ET(30), and Nile Red whose chemical structures are shown in Scheme 1, were purchased from Merck-Aldrich (Germany-USA). The solvatochromic dye ET(33) was obtained from Fluka (Switzerland).

2.2. Determination of the maximum of absorbance with the solvatochromic dyes in liquid samples

For all plasticizers, solvents and liquid polymers, the dissolution of the minimal quantity of the selected solvatochromic dye was made in a beaker by stirring. For viscous liquids gentle heating was applied to accelerate the dissolution of the dye. The typical volume of each sample under analysis was 10 ml and the dye added much less than a spatula tip. Before making any spectrophotometric measurement on our Shimadzu UV2450 equipped with thermostated cells kept at 25°C, a back correction was made with the quartz cuvettes filled with the pure liquid sample under study. This operation is crucial especially with yellow or even brown liquid samples like for instance the plasticizers used in the tire industry. After the back correction step, the electronic absorption spectrum of the solvatochromic dye in the selected liquid was recorded using the reference cuvette filled with the reference liquid without any dye.

2.3. Determination of the maximum of absorbance with the solvatochromic dyes in solid thin film of polymer sample

Regarding the polymer thin films with the solvatochromic dye (typically Nile Red) embedded inside, the sample preparation has involved the following steps. The selected polymer or rubber cut in the smallest possible pieces was weighed in a flask (typically 500-600 mg) and dissolved in about 13 g of dichloromethane (CH2Cl2). Only for epoxidized natural rubber (ENR-25) and for nitrile rubber (Europrene N3345) it was necessary to use tetrahydrofuran (THF) as solvent instead of CH2Cl2. Once the polymer is fully dissolved, less than a tip of spatula of Nile Red was added to the solution and stirred till a complete dissolution of the dye. The resulting homogeneous solution was poured into an optical glass dish having a diameter of 11 cm and allowed the solvent to evaporate slowly and under a fume hood. After the complete evaporation of the solvent the resulting dyed polymer film in the dish was heated to 60°-70°C to permit the complete evaporation of any solvent trace. After cooling, the electronic absorption spectrum of the dyed polymer film was directly collected through the optical glass dish. Only in a couple of cases, i.e. with polystyrene and poly(lactic acid) it was possible to separate the polymer film from the glass dish as a free standing thin solid film. In the latter two cases the electronic absorption spectra were recorded directly on the free standing thin solid films.
The potential solvent effect was checked in the case of the polybutadiene. This polymer was dissolved both in CH2Cl2 and in THF. The resulting two different polymer films with Nile red dye were prepared on glass dish were analyzed spectrophotometrically getting the same absorption maximum value. Of course it is crucial the final “drying” step of the film under moderate heating to remove all the solvent traces which otherwise may affect the position of the absorption maximum.

3. Results

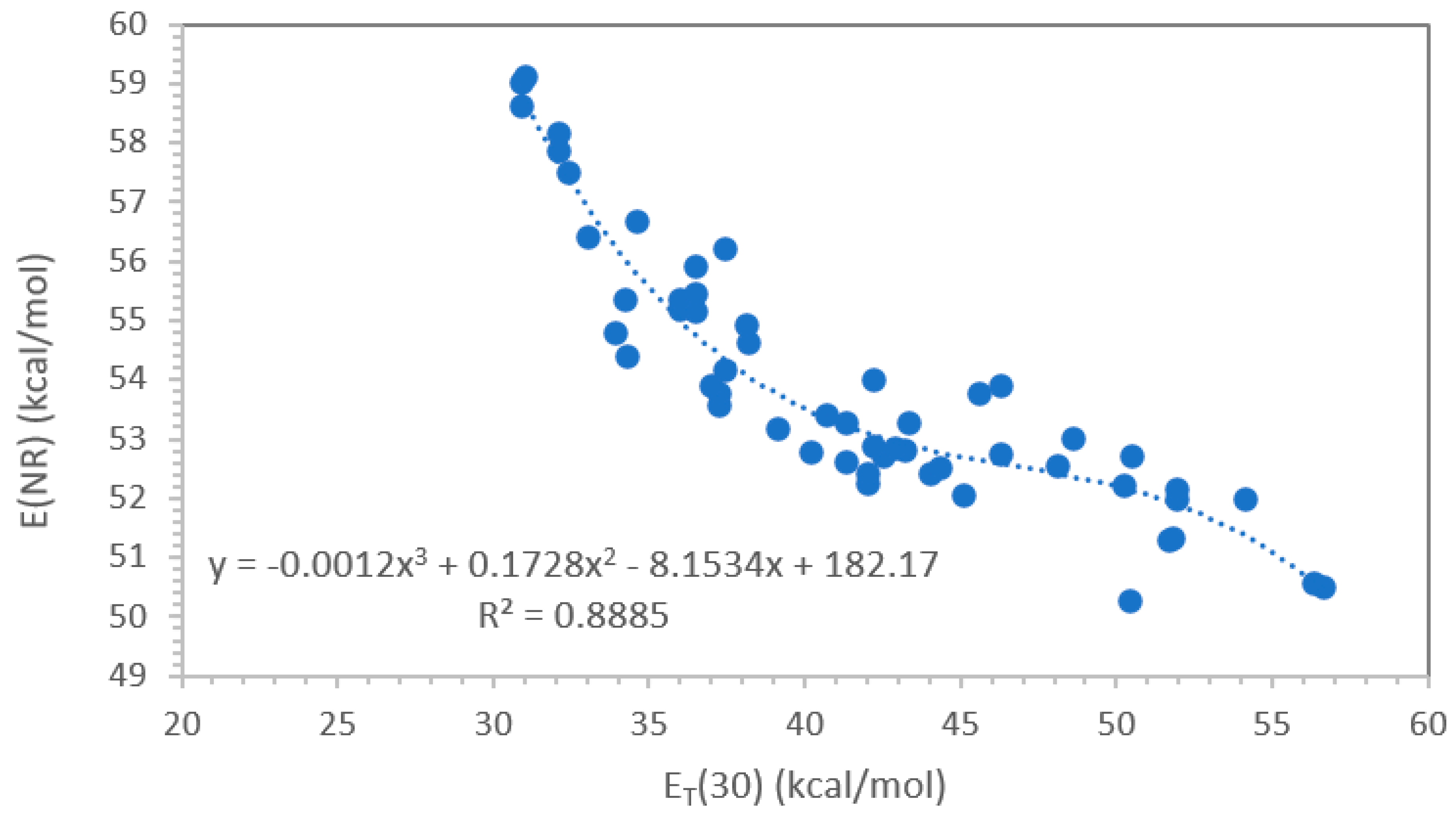
3.1. General aspects of Nile Red solvatochromic dye with respect to ET(30) dye.

The challenge of this work is to evaluate through a solvatochromic scale the potential compatibility between polymers and plasticizers with a special attention to rubber polymers and plasticizers used in the rubber and tire industry. This new approach could be a complementary and experimental way with respect to the evaluation and estimation of the solubility parameter of each component as done for example in a previous work [17] using the Van Krevelen methodology [14]. The key problem faced by the present work is represented by the fact that the fundamental Reichardt’s dye, the ET(30) of Scheme 1 is insoluble in hydrocarbons and it is not suitable also for esters plasticizers either for the relatively low solubility but also because the small residual acidity in the esters causes the protonation at the phenolate oxygen anion leading to the disappearance of the long wavelength solvatochromic charge transfer (CT) band [22]. Indeed, the ET(30) values of hydrocarbons were all determined through another complementary penta-t-butyl-substituted betaine dye called ET(45) [23] which is not easily accessible and furthermore it is sensitive to protonation exactly as the ET(30) dye. Thus, the Reichardt’s dye suitable for polar media with weak acidity is the ET(33) dye (see Scheme 1) [22] which in fact was adopted in the present work. The symmetrical chlorine substitution in ortho-position to the phenolate group, changes the pKa of the conjugated acid of the dye ET(33) by four orders of magnitude with respect to ET(30), make the former dye suitable for weakly acidic media [22]. Since the ET(30) but also the ET(33) values expressed in kcal/mol are both determined through the well-known equation [22,23]:
ET = 28591 λ-1
where λ is the maximum of absorption maximum of the long wavelength CT band of the pyridinium-N-phenolate betaine dye in a given liquid medium, the conversion from ET(33) value to ET(30) can be achieved through the following equation [22]:
ET(30) = 0.9953 ET(33) -8.1132
Despite the availability of ET(33), the potential measurement of the polarity in certain hydrocarbon-based plasticizers, in certain apolar polymers and in certain esters remains still unaffordable.
In a seminal paper belonging to this special issue of “Liquids” Acree and Lang [23] have shown an interesting and sophisticated approach which permits to estimate the ET(30) values of certain “difficult” substrates where the direct polarity measurement is hindered for a series of reasons, as in the present case for apolar polymers (e.g. rubbers and certain plasticizers).
An alternative to the above approach is to resume the solvatochromic dye known as Nile Red. The chemical structure of Nile Red is shown in Scheme 1 and the full chemical name of the dye is 9-diethylamino-5H-benzo[α]phenoxazinone [25]. It is a very stable fluorescent dye used for staining biological tissues being highly lipophilic [26]. Certain structural analogies between Nile Red and phenol blue are known since long time, comprised the interesting solvatochromic behavior of the former dye [26]. Indeed, Nile Red is not only soluble in hydrocarbons but also in fats where ET(30) is insoluble. In acid media Nile Red does not lose its solvatochromic behavior in contrast with the ET(30) dye [27]. In these instances Nile Red is completely complementary to ET(30) and it is the ideal dye for the present work where the substrates are apolar polymers (e.g. rubbers) hydrocarbons and ester plasticizers, but also triglycerides.
Deye, Berger and Anderson [27,28] have already made a systematic study of Nile Red in comparison to ET(30) dye, showing that with the former dye it is possible to measure the solvent polarity in much more liquids than those directly accessible by the ET(30), including fluorinated molecules and supercritical CO2. As in the case of ET(30), the electronic absorption maximum of Nile Red can be expressed in kcal/mol according to eq. (14), so that a E(NR) i.e. Nile Red scale for solvent has been constructed.
Figure 1 shows that correlation between E(NR) and ET(30) is not linear but quite complex, when considering all data available for any type of solvents (excluding the fluorinated molecules):
E(NR) = -0.0012 [ET(30)]3 + 0.1728 [ET(30)]2 -8.1534 [ET(30) ] + 182.17
with a correlation coefficient R2 = 0.888.
However, when considering only certain homogenous classes of solvents, for example non-HBD solvents, simpler and linear correlations are obtained as will be shown later.
It is also interesting to note that the attention toward the Nile Red dye as a solvatochromic probe alternative or complementary to ET(30) is steady either from a theoretical point of view but also by a practical point of view. The theoretical analysis focuses on the nature of the charge transfer transition of Nile Red which make it so sensitive as a probe. A twisted intramolecular charge transfer transition was advocated for this dye [29,30,31,32,33] and also the ground and excited dipole moments of the dye were estimated. The Nile Red dye is steady employed in many measurements ranging probing hydrocarbon liquids [34], absorption and fluorescence in a series of alcohols [35], analysis of green chemistry solvents polarity [36], study of anisotropic liquids [37], in zeolites [38], for the detection of lipid order heterogeneity in cells [39], detection of hydrogen bonding strength in microenvironments [40], limiting the numerous fields of current applications.

3.2. Determination of rubber and polymer polarity with Nile Red solvatochromic dye

As detailed in section 2.3 the micropolarity of the rubber polymers was determined with Nile Red solvatochromic dye either using model compounds or liquid polymers where the dye is soluble or using thin solid state polymer films where the dye was embedded in the polymer matrix with the aid of a solvent which was then removed completely. The basic idea of this latter approach derives from the seminal work of Dutta and coll. [41] who used Nile Red as micropolarity probe of plastics in polymethylmethacrylate (PMMA) and polyvinylalcohol films. We extended the same approach also to rubber polymers like cis-1,4-polyisoprene, cis-1,4-polybutadiene, the styrene-butadiene copolymer, epoxidized natural rubber and nitrile rubber. Furthermore, also the micropolarity of polystyrene and poly(lactic acid) films were studied, while for the PMMA it was adopted the E(NR) value found by Dutta et al. [41].
Table 1 reports the experimental E(NR) values for all the above mentioned rubbers and other liquids. In Table 1 the apolar compounds are at the top of the table and the most polar at the bottom of it.
Regarding the rubber and other polymer studied, the trend from apolar to polar compounds is absolutely logic starting with the liquid model compounds squalane and squalene (squalane is the liquid analogous of the ethylene-propylene copolymer while squalene can be considered a liquid model compound of natural rubber or cis-1,4-polyisoprene as discussed elsewhere [42]) as the most apolar, followed by the liquid polyisoprene and polybutadiene and then by the thin solid films of polybutadiene (BR) and polyisoprene (IR). The copolymer styrene-butadiene rubber (S-SBR) with 21% styrene content is found more polar than either BR and IR as expected. S-SBR shows the E(NR) values in the same range of polystyrene thin solid film and the petroleum-based rubber plasticizer T-DAE whose aromatic content is in the range of 20-25%.
As expected, polar polymers are appropriately positioned in the E(NR) scale with epoxidized natural rubber (ENR-25) showing an E(NR) value of 54.32 kcal/mol with respect to 57.55 kcal/mol of liquid IR and 56.82 kcal/mol of this solid film of IR.
Even more polar than ENR-25 are found polymethylmethacrylate (PMMA) and poly(lactic acid) (PLLA) both with E(NR) = 53.44 kcal/mol, followed by nitrile rubber (NBR) with 33% acrylonitrile (ACN) content and the Nile Red electronic transition at 53.07 kcal/mol. The most polar polymers (among those studied in the present work) were found two oligomers: polyethylene glycol (PEG-400) and polytetrahydrofuran liquid oligomer (polyTHF), both at 52.1 kcal/mol. Being oligomers, the latter two compounds have their micropolarity affected by the OH end groups which, of course, play an important role in affecting their polarity.

3.2. Determination of rubber plasticizers polarity with Nile Red solvatochromic dye

Treated-distillate aromatic extract (T-DAE) and mild extract solvate (MES) represent the most used petroleum-based plasticizers in rubber compounds since 2010 when the use of the distillate aromatic extract (DAE) was banned. T-DAE has an aromatic content in the range of 20-25% while the aromatic content of MES is limited to 10-15%. Unfortunately T-DAE is too dark to measure its E(NR) value but it was possible to do a measurement on it with the ET(33) dye. On the other hand, MES is much more clear in color than T-DAE and it was possible to make a measurement both with ET(33) and Nile Red dyes as summarized in Table 1. From these data, T-DAE results appropriately positioned in the Table 1 just between the S-SBR rubber and the polystyrene polymer. Surprisingly, the MES, which is prevalently aliphatic and naphthenic in its chemical nature results positioned not among the hydrocarbons in the top of Table 1 but rather in the upper-mid part of Table 1 sharing the same E(NR) value as biodiesel i.e. the methyl ester of fatty acids from rapeseed oil which instead it is appropriately positioned in the Table 1. Probably, there are components and impurities in the MES (which is a mixture of hydrocarbons) which affect its real polarity value. The presence of water and heteroatoms (e.g. N, S, Cl) may alter significantly the polarity in these industrial compounds.
As already stated in the section 2.1, there is trend to use as rubber plasticizers vegetable oils and the most popular are the soybean and the sunflower oils [19,20,21]. In Table 1 both oils were tested with the Nile Red dye and the soybean oil appears slightly less polar with E(NR) = 54.55 kcal/mol with respect to the sunflower oil high oleic having E(NR) = 54.13 kcal/mol. It is also interesting that a commercial product Nytex Bio 6200 which is a blend of petroleum-based naphthenic oil and fatty acids is classified in the E(NR) scale just in the middle between the soybean oil and the sunflower oil.
On the other hand, the methyl esters of fatty acids derived from rapeseed oil (biodiesel) or from coconut oil are slightly less polar than the triglycerides. In fact, for the methyl esters of fatty acids E(NR) = 54.7 kcal/mol while the triglycerides show E(NR) = 54.1-54.5 kcal/mol. Thus, at least in terms of compatibility with rubbers for tire application, based on the above data, there are no practical differences between the methyl esters of fatty acids and the triglycerides, as already disclosed some time ago [17].
In the past the phthalates were used as plasticizers for winter tire treads. However, at present there are a number of concerns regarding the environmental and health impact of phthalates [43,44,45] so that they are replaced by safer plasticizers. The typical plasticizers used in place of phthalates are adipates and sebacates. In our E(NR) scale, it is possible to see that the phthalates are located at E(NR) = 55.0-55.3 kcal/mol, although DOP (diethylhexylphthalate), the most used in the past, was found at 53.2 kcal/mol. It is interesting to note that the adipates are found at about 55 kcal/mol with diethylhexyladipate (DOA), the most common at 54.67 kcal/mol. The same comments apply to sebacates, that although more expensive than adipates, display similar E(NR) values adipates and DOA in particular.
Another trend regarding the substitution of DOP, involves the use of terephthalic acid derivatives, in particular, the use of dioctylterephthalate (DOTP) whose E(NR) in Table 1 was found at 54.27 kcal/mol, less polar, as expected, than DOP with 53.24 kcal/mol.
Tetrahydrofurfuryl alcohol (THFA) has been proposed as ideal alcohol from renewable sources. In fact, it derives from furfurol obtained from mineral acid treatment of biomasses. Then furfurol is fully hydrogenated to THFA. We have synthesized several esters of THFA as part of another project [46] and in Table 1 we are reporting the polarity values of the adipate, sebacate, oleate, laurate and pelargonate measured with the ET(33) dye; in the discussion section it will be shown how the ET(30) values correlate linearly with the E(NR) values, for the class of compounds considered in the present paper. The THFA esters appear too polar for a good compatibility with common rubbers such as IR, BR and S-SBR, but may be more than suitable as plasticizers for nitrile rubber (NBR) with E(NR) = 53.07 kcal/mol and 52-53 kcal/mol for the THFA esters.
Polyethylene glycol is used in certain rubber compound as compatibilizer aid between silica filler and rubber. The E(NR) value for PEG-400 was found at 52.15 kcal/mol while the E(NR) value of raw silica surface is not known but a work on modified silica surfaces reports E(NR) ≈ 48-7 – 52.6 kcal/mol [47]. Based on these data PEG-400 is really suitable to interact with silica surface. In Table 1 it is shown that also polytetrahydrofuran (polyTHF) oligomer is also a suitable liquid for the compatibilization of silica surface with rubber, since polyTHF shows the same E(NR) value as PEG-400. To reduce the polarity of PEG-400 is possible to esterificate the OH end groups of the glycol with oleic acid getting either PEG monooleate with E(NR) = 53.6 kcal/mol or PEG dioleate with 53.8 kcal/mol.

4. Discussion

4.1. Correlation between the E(NR) scale and the ET(30) scale

The results have shown that Nile Red is an excellent and complementary solvatochromic dye with respect to ET(30). Complementary because it is soluble in hydrocarbons and it is not sensitive to residual acidity which may be present in esters plasticizers. Furthermore, Nile Red is soluble also in the same solvents as ET(30) and ET(33). Without the use of Nile Red the present work could not have been made since we have dealt with hydrocarbon rubber polymers and plasticizers where ET(30) is insoluble or problematic but where also ET(33) has given problems. Furthermore, ET(33) is no more easily commercially available, while Nile Red it is due to the fact that it is used also as a staining dye for biological tissues and cells [26].
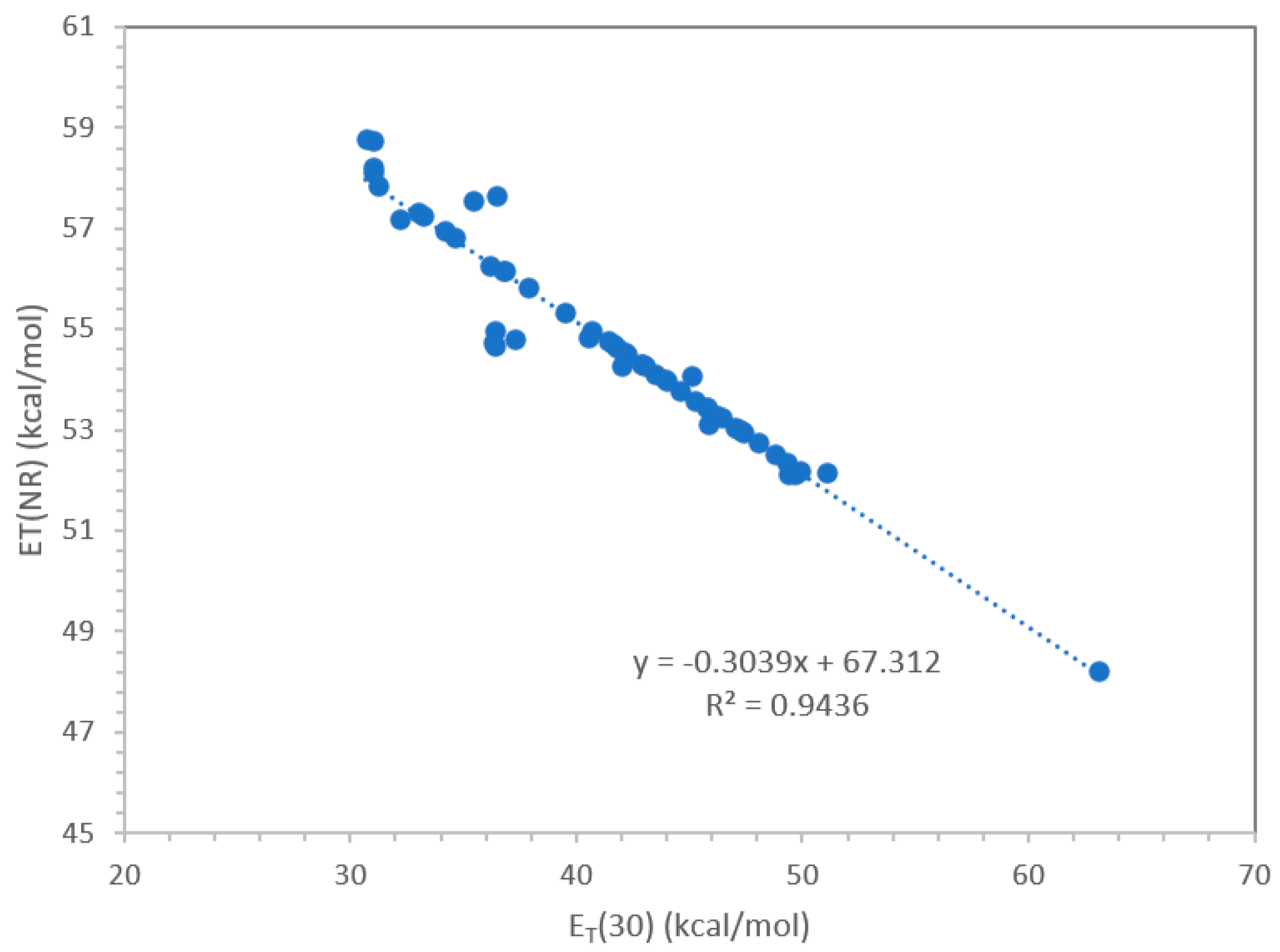
Preprints 96460 g002
Figure 2. Correlation between E(NR) and ET(30) using all the experimental data of Table 1.
Figure 2. Correlation between E(NR) and ET(30) using all the experimental data of Table 1.
Preprints 96460 g002
In this work 53 compounds either polymers or plasticizers were studied with Nile Red and wherever possible also with the ET(33) dye. The data in Table 1 obtained with the latter dye were changed into the ET(30) scale using the equation (15). Only in a couple of cases it was possible to use ET(30) dye directly. The experimental data of Table 1 where then put in a graph as shown in Figure 2, so that the following equation was obtained with a very good correlation coefficient R2 = 0.944:
E(NR) = -0.3039 ET(30) + 67.312
and the reverse equation:
ET(30) = [E(NR) – 67.312] / (-0.3039)
Eq. (17) was then used to calculate the E(NR) values which were not measured with Nile Red dye. The calculated values are shown in italic character in Table 1. Similarly, for the ET(30) values in Table 1 use was made of eq. (18) and the calculated values are shown in italic character as well.

4.2. Correlation between the solubility parameter δt and the E(NR) scale

In the introduction we have presented the classical approach to determine the compatibility between a polymer and a plasticizer. The classical approach implies the determination of the solubility parameter of both components, find these values in published tables (e.g. Hansen’s book [13]) or calculate by group increment the solubility parameter of each component through the Van Krevelen [14] or other similar approaches. Then, the solubility criteria are shown in the eq. (11-13).
It is interesting at this point to evaluate how the total solubility parameter δt correlates with the E(NR) scale. Our first approach was to use the Hansen solubility parameter δt derived from the data tabulated in ref. [13]. However, the correlation with the E(NR) values reported in Table 1 were not satisfactory.
The following step was to calculate the δt value for each solvent, plasticizer and polymer reported in Table 1 according to the Van Krevelen method [14]. The calculation results are shown in the last column in the right of Table 1. These calculated δt values were then put in a graph against the E(NR) values of Table 1 and the result is shown in Figure 2. Although the correlation coefficient R2 = 0.64 this time is not as good as the E(NR) vs ET(30) correlation shown in Figure 1, an evident trend can be observed so that at least a rough estimation of E(NR) can be derived from δt according to:
δt = -0.472 E(NR) + 43.33
In the correlation between the δt values of Table 1 and the E(NR) values we were forced to exclude the δt values of tetrahydrofurfuryl alcohol, ethyl lactate and the polymer polymethylmethacrylate (PMMA).
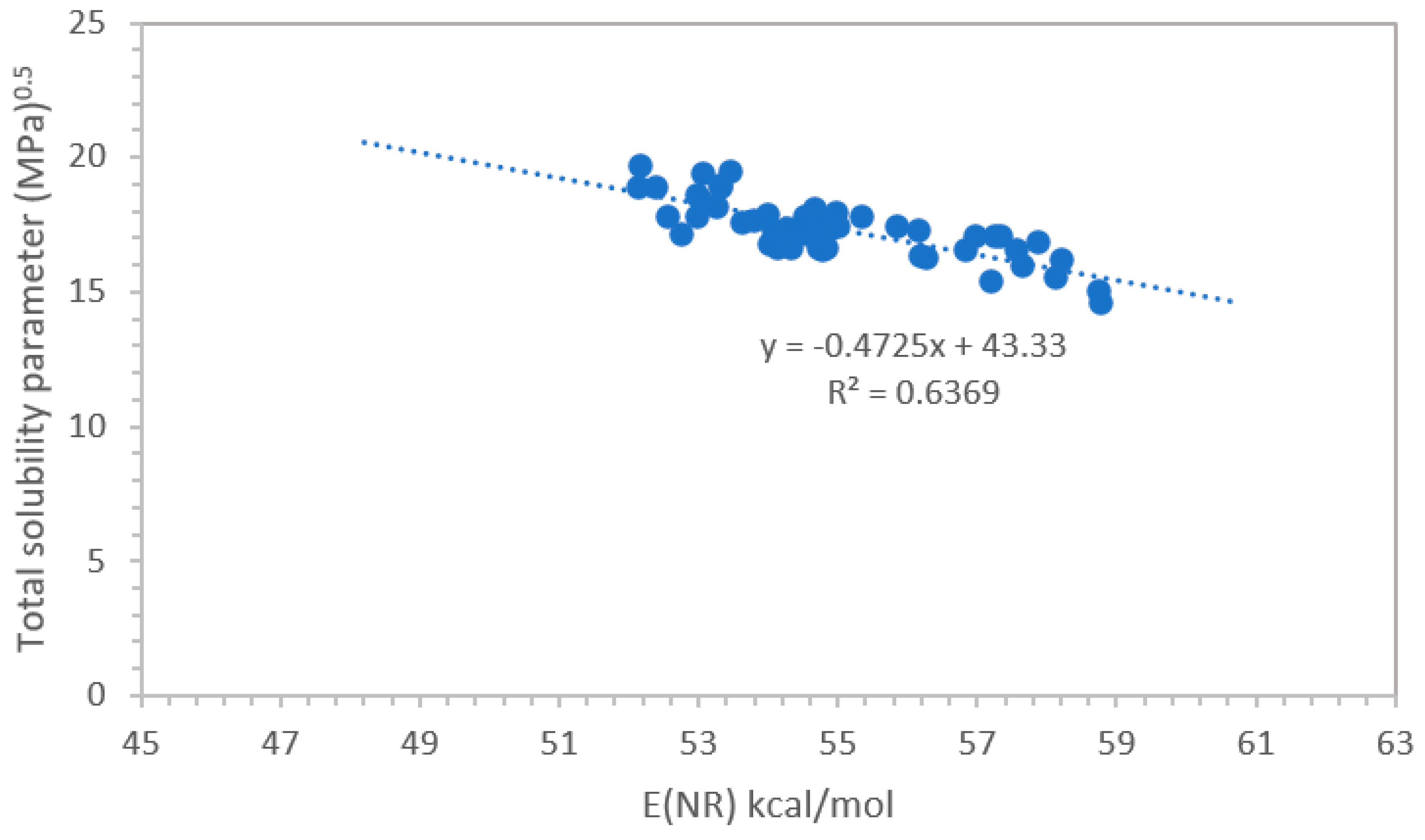
Preprints 96460 g003
Figure 2. Correlation between the solubility parameter δt and E(NR) scale.
Figure 2. Correlation between the solubility parameter δt and E(NR) scale.
Preprints 96460 g003

4.3. Some reflections on the diene rubber compatibility based on the E(NR) scale

The mail purpose of the present work, was to create a polarity scale for hydrocarbon rubbers and the conventional and new plasticizers. As shown in Table 1, it was possible to measure the E(NR) value of the key diene rubbers polyisoprene (IR), polybutadiene (BR) and the copolymer styrene-butadiene (S-SBR). From this measurement it turned out that either the liquid oligomers of IR and BR are adequate model compound of higher polymers IR and BR since very similar E(NR) values were measured. The same reasoning applies also for squalene as model compound of IR high polymer. Regarding the conventional hydrocarbon plasticizers of diene rubber, from Table 1 it is immediately evident that the T-DAE plasticizer with its relatively high aromatic content is fully compatible with S-SBR, since both compound share the same E(NR) value. Furthermore, it is also confirmed that T-DAE is also more compatible even with IR and BR than MES, which although less aromatic, evidently contains some structural feature which increases its polarity to the same level as biodiesel (the methyl ester of rapeseed oil tested previously with success as rubber compound plasticizer [17]).
The phthalate-based plasticizers used in the past in passenger winter tire treads result in the E(NR) scale less polar and more compatible with the diene rubber than the currently used ester plasticizers like adipates and sebacates.
“Green” plasticizers are those produced from renewable sources. Thus, emerging green plasticizers for the tire industry are soybean and sunflower oils as well as the semi-green blend of naphthenic oil with fatty acids (Nytex Bio 6200). As expected these green plasticizers are in the middle of Table 1 and probably the compatibility with the diene rubber like IR, BR and S-SBR is questionable. On the other hand, in Table 1 it is immediately evident that such mentioned green plasticizers have an excellent compatibility with more polar rubbers like epoxidized natural rubber (ENR) and nitrile rubber (NBR).
Tetrahydrofurfuryl alcohol (THFA) is considered a green alcohol fully derived from renewable sources. Thus, its esters with carboxylic acids also from renewable sources are 100% green. However, such esters of THFA are found all at the bottom of Table 1 suggesting an high level of polarity and poor compatibility with IR, BR and S-SBR. Instead the THFA esters are certainly suitable as plasticizers for the ENR and NBR.

5. Conclusions

The evaluation of the polymer-plasticizer compatibility through a ET(30) scale is hindered by the insolubility of the ET(30) dye in the hydrocarbon polymers like for instance IR, BR and S-SBR. Furthermore, ET(30) dye may have limited solubility in plasticizers and is sensitive to their weak acidity. In fact protonation of the ET(30) dye destroys the CT band of this solvatochromic dye. To circumvent such a situation, other authors [24] have proposed an interesting, original and sophisticated approach which permits to estimate the ET(30) values of certain “difficult” substrates where the direct polarity measurement is hindered. The alternative approach proposed in the present work is to use Nile red dye as solvatochromic dye. Nile red has the advantage to be soluble in hydrocarbons and in polar solvents and it is not sensitive toward protonation.
In Table 1 a series of 53 different compounds including rubbers, plasticizers, hydrocarbon solvents and even some polar polymers (like PMMA, PLLA, PEG-400 and polyTHF) were tested with the Nile Red probe. For the evaluation of liquids polarity, Nile Red was dissolved in the selected liquid and the spectrum recorded, while for polymers Nile Red was embedded in thin solid film of the selected polymer and the spectrum recorded on the solid state film. Wherever possible, the liquid or plasticizer was also evaluated with the ET(33) dye (seldom with the ET(30) dye) and the resulting value converted into the ET(30) scale through the eq. (15).
Thus, Table 1 in a certain number of cases reports both the E(NR) value and the ET(30) value. This has permitted to derive a correlation between E(NR) scale and ET(30) limited to the selected number of polymers and plasticizers as shown in Figure 1 and displayed by the eq. (17-18) with a very good correlation coefficient.
Furthermore, also the total solubility parameter δt as defined by the eq. (10) has been calculated for each compound according to the Van Krevelen method [14] and reported in Table 1. It was found also a reasonable correlation between the solubility parameter and the E(NR) scale as shown in Figure 2 and described by eq. (19).
Thus, with Nile red dye it is possible to study the polarity of hydrocarbon polymers (like rubbers) and plasticizers and to connect the results either with the Reichardt’s ET(30) scale and also with the total solubility parameter.

Author Contributions

This article was made by a single author.

Funding

This research received no external funding.

Data Availability Statement

This work will be available in the Researchgate website at the author’s page.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Sears, J.K.; Darby, J.R. The Technology of Plasticizers; J. Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
  2. Stepek, J.; Daoust, H. Additives for Plastics; Springer Science: New York, NY, USA, 1983; pp. 7–33. [Google Scholar]
  3. Tager, A. The Physical Chemistry of Polymers; Mir Publishers: Moscow, USSR, 1978; pp. 547–567. [Google Scholar]
  4. Cadogan, D.; Howick, C.J. Plasticizers. In Ullmann’s Encyclopedia of Industrial Chemistry, 5th ed.; Elvers, B., Arpe, H.J. et al., et al., Eds.; VCH: Weinheim, Germany, 1992; Volume A20, pp. 439–458. [Google Scholar]
  5. Sears, J.F.; Touchette, N.W. Plasticizers. In Concise Encyclopedia of Polymer Science and Engineering; Kroschwitz, J., Ed.; John Wiley & Sons: New York, NY, USA, 1999; pp. 734–744. [Google Scholar]
  6. Howick, C.J. Plasticizers. In Kirk-Othmer Encyclopedia of Chemical Technology, 5th ed.; Ley, C., Ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
  7. Godwin, A.D. Plasticizers. In Applied Plastics and Engineering Handbook; Kutz, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 487–502. [Google Scholar]
  8. Marcilla, A.; Breltràn, A. Mechanism of plasticizers action. In Handbook of Plasticizers, 4th ed; Wypich, G., Ed.; ChemTec Publishing: Toronto, ON, Canada, 2023; pp. 139–158. [Google Scholar]
  9. Wypich, A. Compatibility of plasticizers. In Handbook of Plasticizers, 4th ed.; Wypich, G., Ed.; ChemTec Publishing: Toronto, ON, Canada, 2023; pp. 159–180. [Google Scholar]
  10. Morris, G. Plasticizers. In Developments in Rubber Technology – 1; Whelan, A., Lee, K.S., Eds.; Elsevier Applied Science: London, UK, 1979; pp. 207–225. [Google Scholar]
  11. Crouter, B.G. Processing aids and plasticizers. In Developments in Rubber Technology – 4; Whelan, A., Lee, K.S., Eds.; Elsevier Applied Science: London, UK, 1987; pp. 119–158. [Google Scholar]
  12. Brydson, J.A. Rubber Chemistry; Applied Science Publishers Ltd.: London, UK, 1978. [Google Scholar]
  13. Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook; CRC press/Taylor & Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
  14. Van Krevelen, D.W. Properties of Polymers. Their correlation with chemical structure, their numerical estimation and prediction from additive group contributions, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
  15. Cataldo, F. On the solubility parameter of C60 and higher fullerenes. Fullerenes, Nanot Carbon Nanostruct 2009, 17, 79–84. [Google Scholar] [CrossRef]
  16. Cataldo, F. Solubility of fullerenes in fatty acids esters: a new way to deliver in vivo fullerenes. Theoretical calculations and experimental results”. In Medicinal Chemistry and Pharmacological Potential of Fullerenes and Carbon Nanotubes; Cataldo, F., Da Ros, T., Eds.; Springer Science: Dordrecht, The Netherlands, 2008; Chapter 13. [Google Scholar]
  17. Cataldo, F.; Ursini, O.; Angelini, G. Biodiesel as a plasticizer of a SBR-based tire tread formulation. ISRN Polym Sci. 2013, 2013, 340426. [Google Scholar] [CrossRef]
  18. Cataldo, F. Application of Reichardt’s solvent polarity scale (ET(30)) in the selection of bonding agents for composite solid rocket propellants. Liquids 2022, 2, 289–302. [Google Scholar] [CrossRef]
  19. Sandstrom, P.H.; Rodewald, S.; Ramanathan, A. Rubber composition and tire with component comprised of polyisoprene rubber and soybean oil. US Patent N°20140135424A1, 2014. assigned to Goodyear Tyre & Rubber Co.. [Google Scholar]
  20. Brunelet, T.; Dinh, M.; Favrot, J.M.; Labrunie, P.; Lopitaux, G.; Royet, J.G. Plasticizing system for rubber composition. US Patent N°7834074B2, 2004. assigned to Michelin Recherche et Technique SA. [Google Scholar]
  21. Mohamed, N.R.; Othman, N.; Shuib, R.K. Synergistic effect of sunflower oil and soybean oil as alternative processing oil in the development of greener tyre tread compound. J. Rubber Res. 2022, 25, 239–249. [Google Scholar] [CrossRef]
  22. Reichardt, C. Pyridinium-N-phenolate betaine dyes as empirical indicators of solvent polarity: some new findings. Pure Appl. Chem. 2008, 80, 1415–1432. [Google Scholar] [CrossRef]
  23. Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
  24. Acree, W.E., Jr.; Lang, A.S. Reichardt’s Dye-Based Solvent Polarity and Abraham Solvent Parameters: Examining Correlations and Predictive Modeling. Liquids 2023, 3, 303–313. [Google Scholar] [CrossRef]
  25. Davis, M.M.; Helzer, H.B. Titrimetric and Equilibrium Studies Using Indicators Related to Nile Blue A. Anal. Chem. 1966, 38, 451–461. [Google Scholar] [CrossRef]
  26. Green, F.J. The Sigma-Aldrich Handbook of Stains, Dyes and Indicators; Aldrich Chemical Company, Inc.: Milwaukee, WI, USA, 1990; pp. 519–520. [Google Scholar]
  27. Deye, J.F.; Berger, T.A.; Anderson, A.G. Nile Red as a solvatochromic dye for measuring solvent strength in normal liquids and mixtures of normal liquids with supercritical and near critical fluids. Anal. Chem. 1990, 62, 615–622. [Google Scholar] [CrossRef]
  28. Deye, J.F.; Berger, T.A.; Anderson, A.G. Errata Corrige. Anal. Chem. 1990, 62, 1552. [Google Scholar] [CrossRef]
  29. Ghoneim, N. Photophysics of Nile red in solution: steady state spectroscopy. Spectrochim Acta Part A Mol Biomol Spect 2000, 56, 1003–1010. [Google Scholar] [CrossRef]
  30. Dias Jr, L.C.; Custodio, R.; Pessine, F.B. Investigation of the Nile Red spectra by semi-empirical calculations and spectrophotometric measurements. Int. J. Quantum Chem. 2006, 106, 2624–2632. [Google Scholar] [CrossRef]
  31. Kawski, A.; Bojarski, P.; Kukliński, B. Estimation of ground-and excited-state dipole moments of Nile Red dye from solvatochromic effect on absorption and fluorescence spectra. Chem. Phys. Lett. 2008, 463, 410–412. [Google Scholar] [CrossRef]
  32. Guido, C.A.; Mennucci, B.; Jacquemin, D.; Adamo, C. Planar vs. twisted intramolecular charge transfer mechanism in Nile Red: new hints from theory. Phys. Chem. Chem. Phys. 2010, 12, 8016–8023. [Google Scholar] [CrossRef] [PubMed]
  33. Freidzon, A.Y.; Safonov, A.A.; Bagaturyants, A.A.; Alfimov, M.V. Solvatofluorochromism and twisted intramolecular charge-transfer state of the nile red dye. Int. J. Quantum Chem. 2012, 112, 3059–3067. [CrossRef]
  34. Yablon, D.G.; Schilowitz, A.M. Solvatochromism of Nile Red in nonpolar solvents. Appl. Spectrosc. 2004, 58, 843–847. [Google Scholar] [CrossRef] [PubMed]
  35. Zakerhamidi, M.S.; Sorkhabi, S.G. Solvent effects on the molecular resonance structures and photo-physical properties of a group of oxazine dyes. J. Lumin 2015, 157, 220–228. [Google Scholar] [CrossRef]
  36. Jessop, P.G.; Jessop, D.A.; Fu, D.; Phan, L. Solvatochromic parameters for solvents of interest in green chemistry. Green Chem. 2012, 14, 1245–1259. [Google Scholar] [CrossRef]
  37. Gilani, A.G.; Moghadam, M.; Zakerhamidi, M.S. Solvatochromism of Nile red in anisotropic media. Dyes Pigments 2012, 92, 1052–1057. [Google Scholar] [CrossRef]
  38. Sarkar, N.; Das, K.; Nath, D.N.; Bhattacharyya, K. Twisted charge transfer processes of Nile red in homogeneous solutions and in faujasite zeolite. Langmuir, 1994, 10, 326–329. [Google Scholar] [CrossRef]
  39. Kreder, R.; Pyrshev, K.A.; Darwich, Z.; Kucherak, O.A.; Mély, Y.; Klymchenko, A.S. Solvatochromic Nile Red probes with FRET quencher reveal lipid order heterogeneity in living and apoptotic cells. ACS Chem. Biol. 2015, 10, 1435–1442. [Google Scholar] [CrossRef]
  40. Cser, A.; Nagy, K.; Biczók, L. Fluorescence lifetime of Nile Red as a probe for the hydrogen bonding strength with its microenvironment. Chem. Phys. Lett. 2002, 360, 473–478. [Google Scholar] [CrossRef]
  41. Dutta, A.K.; Kamada, K.; Ohta, K. Spectroscopic studies of nile red in organic solvents and polymers. J. Photochem. Photobiol. A Chem. 1996, 93, 57–64. [Google Scholar] [CrossRef]
  42. Cataldo, F. Aminoxyl (nitroxyl or nitroxide) radical formation by the action of ozone on squalene containing secondary aromatic amine antioxidants. J. Vinyl Addit. Technol. 2022, 28, 379–389. [Google Scholar] [CrossRef]
  43. Mariana, M.; Castelo-Branco, M.; Soares, A.M.; Cairrao, E. Phthalates’ exposure leads to an increasing concern on cardiovascular health. J. Hazard Mater. 2023, 457, 131680. [Google Scholar] [CrossRef]
  44. Arrigo, F.; Impellitteri, F.; Piccione, G.; Faggio, C. Phthalates and their effects on human health: Focus on erythrocytes and the reproductive system. Compar. Biochem. Physiol. Part C Toxicol. Pharmacol. 2023, 270, 109645. [Google Scholar] [CrossRef]
  45. Luís, C.; Algarra, M.; Câmara, J.S.; Perestrelo, R. Comprehensive insight from phthalates occurrence: From health outcomes to emerging analytical approaches. Toxics 2021, 9, 157. [Google Scholar] [CrossRef]
  46. Cataldo, F. unpublished results.
  47. Moreno, E.M.; Levy, D. Role of the comonomer GLYMO in ORMOSILs as reflected by nile red spectroscopy. Chem. Mater. 2000, 12, 2334–2340. [Google Scholar] [CrossRef]
Preprints 96460 sch001
Scheme 1. The solvatochromic dyes used in the present work.
Scheme 1. The solvatochromic dyes used in the present work.
Preprints 96460 sch001
Preprints 96460 g001
Figure 1. Correlation between E(NR) and ET(30) using the data of ref.[27] and excluding the fluorinated molecules.
Figure 1. Correlation between E(NR) and ET(30) using the data of ref.[27] and excluding the fluorinated molecules.
Preprints 96460 g001
Table 1. Measured or calculated ET(30) and E(NR) values of plasticizers, rubber and polymers.
Table 1. Measured or calculated ET(30) and E(NR) values of plasticizers, rubber and polymers.
PLASTICIZER, SOLVENT OR
POLYMER		 ET(30) Kcal/mol E(NR) Kcal/mol References or notes on the ET(30) values References or notes on the E(NR) values Solubility parameter δt in (MPa)0.5 calc. according ref. [14]
isooctane 30.7 58.77 ref. [23] this work 14.6
n-hexane and cyclohexane 31.0 58.75 ref. [23] this work 15.1
tetradecane 31.0 58.21 ref. [23] this work 16.2
SQUALANE 31.0 58.12 estimated this work 15.6
decalin 31.2 57.87 ref. [23] this work 16.9
SQUALENE 36.5 57.64 this work fm ET(33) this work 16.0
Liquid cis-POLYISOPRENE (Liq-IR) 35.4 57.55 this work fm ET(33) this work 16.6
Liquid 1,2-POLYBUTADIENE 33.0 57.32 calculated (*) this work 17.1
Liquid cis-POLYBUTADIENE (Liq-BR) 33.2 57.25 calculated (*) this work 17.1
cyclohexene 32.2 57.19 ref. [23] this work 15.4
POLYBUTADIENE thin film (BR) 34.2 56.96 calculated (*) this work 17.1
POLYISOPRENE thin film (IR) 34.6 56.82 calculated (*) this work 16.6
Oleyl Oleate 36.2 56.27 this work fm ET(33) this work 16.3
S-SBR with styrene 21% & vinyl 50% 36.8 56.17 calculated (*) this work 17.4
T-DAE oil 36.8 56.2 this work fm ET(33) calculated (**) 17.3
POLYSTYRENE thin film 37.8 55.84 calculated (*) this work 17.5
di-n-butyl PHTHALATE 39.5 55.3 ref. [23] calculated (**) 17.8
dimethyl PHTHALATE 40.7 55.0 ref. [23] calculated (**) 18.0
Diisododecyl ADIPATE 36.4 54.98 this work fm ET(33) this work 17.5
Ethyl OLEATE 40.5 54.85 this work fm ET(30) this work 17.3
MES oil 37.3 54.83 this work fm ET(33) this work 16.7
Biodiesel fm rapeseed oil 41.4 54.77 calculated (*) this work 16.6
Diethylhexyl SEBACATE 36.3 54.76 this work fm ET(33) this work 17.0
Cocconut methyl ester 41.6 54.70 calculated (*) this work 16.7
dimethyl SEBACATE 41.8 54.7 this work fm ET(33) calculated (**) 18.1
Diethylhexyl ADIPATE (DOA) 36.4 54.67 calculated (*) this work 17.8
Dibutyl SEBACATE 42.3 54.5 this work fm ET(33) calculated (**) 17.8
Soybean oil 42.1 54.55 calculated (*) this work 17.2
Nytex BIO 6200 42.1 54.55 calculated (*) this work 16.7
Epoxidized Natural Rubber (ENR-25) 42.9 54.32 calculated (*) this work 17.2
Dioctylterephthalate (DOTP) 43.0 54.27 calculated (*) this work 17.4
Sunflower oil high oleic 43.5 54.13 calculated (*) this work 16.7
Ethyl PALMITATE 43.9 54.0 this work fm ET(30) calculated (**) 16.8
Diethyl AZELATE 45.1 54.08 this work fm ET(33) this work 17.3
methyl undecenoate 44.0 53.99 calculated (*) this work 17.9
PEG dioleate 44.6 53.79 calculated (*) this work 17.7
PEG monooleate 45.2 53.60 calculated (*) this work 17.6
Polymethylmethacrylate film (PMMA) 45.8 53.44 calculated (*) ref. [41]
Poly(Lactic acid) film (PLLA) 45.8 53.44 calculated (*) this work 19.5
Bis(THFA) ADIPATE 46.2 53.30 this work fm ET(33) calculated (**) 19.0
Ethyl levulinate 46.2 53.30 calculated (*) this work 18.9
Dioctylphthalate (ethylhexyl) (DOP) 46.4 53.24 calculated (*) this work 18.2
Nitrile Rubber with 33% ACN film 47.0 53.07 calculated (*) this work 19.4
Bis(THFA) SEBACATE 47.1 53.0 this work fm ET(33) calculated (**) 18.4
Bis(THFA) AZELATE 47.3 53.0 this work fm ET(33) calculated (**) 18.6
THFA OLEATE 47.4 53.0 this work fm ET(33) calculated (**) 17.8
THFA LAURATE (30°C) 48.0 52.8 this work fm ET(33) calculated (**) 17.2
THFA PELARGONATE (30°C) 49.3 52.4 this work fm ET(33) calculated (**) 18.9
Tetrahydrofurfuryl alcohol 49.9 52.2 this work fm ET(30) calculated (**)
L-(-) ethyl lactate 51.1 52.16 ref. [23] this work
Polyethylene glycol (PEG-400) 49.7 52.15 this work fm ET(30) this work 19.7
Polytetrahydrofuran (PolyTHF)low Mw 49.3 52.12 this work fm ET(30) this work 18.9
Water 63.1 48.21 ref. [23] this work
(*) Calculated with: E(NR) = -0.303 ET(30) + 67.31; (**) Calculated with: ET(30) = [E(NR) – 67.31] / -0.303 ; THFA = Tetrahydrofurfuryl.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

119

Views

33

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated