Enhancing Privacy in the Internet of Vehicles via Hyperelliptic Curve Cryptography

Preprint

Article

Enhancing Privacy in the Internet of Vehicles via Hyperelliptic Curve Cryptography

Altmetrics

Downloads

103

Views

126

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 January 2024

Posted:

08 January 2024

You are already at the latest version

Alerts

Abstract

The Internet of Things (IoT) is a technological paradigm that has gained significant momentum that last decade and, among others, enables the development of intelligent and interoperable device networks. In this respect, it has triggered the creation and evolution of VANETs (Vehicular Ad Hoc Networks), which are initially implemented in order to guarantee the safety of the drivers and the avoidance of traffic accidents. The drawback is that this fast evolution flags serious concerns as far as the privacy of users is concerned, while the population of attackers or entities that try to eavesdrop and intercept information has significantly increased. This imposes a serious risk for drivers moving across a Smart City. The research presented in this paper aims to evaluate privacy protection mechanisms in VANET environments, based on their efficiency and security level ensured, considering the fact that VANETs provide limited resources to users/drivers. Moreover, the usage of the elliptic curve cryptography in reduced resources environments is discussed. Finally, this paper compares the performance of three cryptographic algorithms, i.e., Elliptic Curve Cryptography (ECC), Hyperelliptic Curve Cryptography genus 2 (HECC-2) and HECC genus 3 (HECC-3), employed for an efficient authentication and safe message transmission mechanism in VANETs, targeting to extract conclusions related to the implementation of each cryptographic scheme in this specific application area.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction

The Internet of Things (IoT) is a state of the art paradigm that represents a set of networked hardware and software elements that connect and exchange data with other elements and systems over the Internet or other communications networks. A reflection of the IoT paradigm in the transportation domain is the Internet of Vehicles (IoV), which allows the vehicles and the respective road infrastructure to get interconnected and exchange data. The technologies that enable communication among vehicles (V2V) and between vehicles and road infrastructures (V2I) are getting quite popular and they introduce several research challenges. The IoV aims among others to enhance automation, efficiency and comfort in the transportation domain, and more importantly to strengthen the protection of drivers’ safety and the avoidance of car accidents that can often be fatal. At the same time, the evolution of 5G and 6G technology that support very high throughput and data rates, greatly facilitate the market penetration of the Internet of Vehicles.

However, the rapid evolution of IoV introduces high privacy-related risks, while the fact that the life of drivers and passengers may be jeopardized in case of successful malicious attacks over V2V or V2I communications, forces the need for extended security constraints to be addressed. Thus, the last years a lot of research initiatives focus on building a safer IoV communication environment, which has to be adapted to the limited environment that the engaged machine provide while communicating. Therefore, the security-related solutions in such environments need to be efficient, fast and limit the data traffic wherever possible.

The research presented in this paper elaborates on privacy preservation mechanisms for VANETs, using a simulated environment to deliver detailed evaluations.

The current paper focuses on evaluating the usage of Hyperelliptic Curve Cryptography (HECC) on IoT devices to strengthen the protection of privacy. The respective approach is exploited and tested in Internet of Vehicles environments, where HECC features such as increased security with small key, as well as speed in encryption/decryption are of prime importance. To evaluate the proposed approach, series of experiments have been executed using the ns-3 simulator and very interesting results have been obtained regarding the privacy preservation in IoV. Several evaluation metrics have been used in this respect, to allow for a thorough identification of the advantages and disadvantages of using HECC towards IoV privacy protection.

The rest of the paper is constructed as follows. Section 2 discusses the related state of the art literature regarding privacy protection in IoV environments. Section 3 elaborates on the related mathematical background regarding ECC, HECC genus 2 and HECC genus 3. Section 4 presents the approach proposed by this paper that aims to address specific elements of the IoV privacy protection problem. Section 5 presents the experimental evaluation findings obtained using various asymmetric and symmetric cryptographic protocols. Section 6 presents a device for encrypting and decrypting messages using ECC and AES using Arduino, a solution well suitable for IoV. Finally, section 7 concludes the paper and presents future plans towards the protection of privacy in IoV environments.

2. Related State of the Art

2.1. Authentication Schemes

With the continuous evolution of IoT and therefore IoV many schemes have been proposed to ensure secure and efficient communication in VANETs. Some of them are based solely on the authentication of users, others also address the processing and transmission of messages, while others try to improve the performance of the authentication of users and distribution of messages in the network. Firstly, schemes related to authentication are presented.

The EAAP scheme proposed by Azees, Vijayakumar, and Deborah [1] aims to provide efficient anonymous authentication for vehicles and RSUs in VANETs. It utilizes the bilinear-pairing cryptographic technique and distinguishes between authentication processes for vehicles and RSUs. The Trusted Authority (TA) provides parameters for certificate and signature generation to ensure secure authentication. Vehicles need to register with the TA and receive a “dummy” identifier (DID) that can link to their real identity. When a vehicle enters the network, it creates an anonymous certificate, signs it, and shares it with the necessary parameters. RSUs, on the other hand, receive their identifiers from the TA, register with the system, and generate anonymous certificates using a temporary secret key. The scheme is designed to be secure against authentication attacks and ensures location privacy, with the ability to detect and block malicious users from the network.

In the same year, Yanbing Liu et al. developed a dual authentication scheme called PPDAS [2], which employs encryption methods based on vehicle IDs and public key encryption. The scheme introduces the concept of vehicle reputation, where vehicles registered with the Trusted Authority communicate through the RSU. The vehicles generate pseudonyms that can only be deciphered by the RSU and the TA using bilinear pairing properties. Time stamps are used to prevent replay attacks, and the Message Authentication Code (MAC) technique is implemented to avoid message tampering attacks. The authentication process consists of two stages. Initially, vehicles send their pseudonyms, public keys, and time stamps to the TA via the RSU. The TA validates the time stamp and compares the calculated MAC code to the received code. Once successful, the first stage of validation is completed. The reputation of the vehicles is then checked based on confidence matrices and an average confidence level of the communicating pair. The second stage of authentication depends on the trust level of the vehicles. After communication is finished, vehicles evaluate each other and update the trust tables with the TA through the RSU.

In 2018, Hyo Jin Jo et al. [3] introduced a co-operative authentication scheme that involves the cooperation between vehicles and RSUs for secure message transmission. The scheme utilizes binary key trees for key management and authentication. Vehicles periodically validate received messages, authenticate themselves, and share the results with nearby vehicles, which in turn validate their results. This process allows for the confirmation of the messages’ authenticity within the network, while the RSU is responsible for revoking malicious or invalid users by disclosing group keys only to valid users and informing them about revoked vehicles through the Revocation List. This scheme improves the efficiency of recalling and sharing public keys in a vehicle network, as well as detecting malicious users. However, a drawback of these schemes is the increased network traffic and time delay caused by vehicles communicating with each other, the RSU, and a Trusted Authority (TA-CA) in certain cases.

2.2. Secure Message Dissemination

In 2021, Hassan Mistareehi et al. [4] proposed an architecture for secure messaging in vehicular cloud networks. The proposed architecture for secure messaging in vehicular cloud networks aims to enhance authentication and message propagation performance in highly dense areas. The scheme utilizes both symmetric and asymmetric encryption for key and message transfer. If a vehicle is out of range of a roadside unit (RSU), its message/request is transmitted to the RSU through nearby vehicles using the AODV algorithm. When a vehicle registers in a regional cloud, it receives a key pair and the RSU’s public key. Then, messages are authenticated using digital signatures and encrypted with an asymmetric manner, so that the RSU can receive and authenticate sensitive information from the vehicles. The RSU can group multiple messages and send them in large packets to the local cloud to avoid network congestion. Also, pseudonyms are used to maintain anonymity of vehicles and change when the number of vehicles in the area decreases with a technique that extends the logic of Mix-Zones. The scheme offers security against various attacks but does not consider the computational load on the RSU with increasing density.

In 2021, Mir Ali Rezazadeh Baee et al. proposed a scheme called ALI [5], that aims to provide message authentication and encryption in VANETs using Elliptic Curve cryptography. It utilizes the Elliptic Curve Qu-Vanstone (ECQV) scheme, which is based on Elliptic Curves, to propagate occasional keys of vehicles. For the exchange of symmetric encryption keys, the scheme employs ECIES, which utilizes Diffie-Hellman mechanism and a Hash-based Key Derivation Function (HKDF). The Trusted Authority (TA) passes the keys to vehicles and RSUs during registration using the ECQV scheme and encrypts the messages with ECIES for faster communication. Keys are valid for a predefined period, and upon expiration, users must request new keys from the TA. Communication between vehicles and the TA is done through RSUs, with encrypted identities. RSUs transmit a symmetric key to vehicles for encryption and to do that securely, the symmetric key is generated using the TA’s public key. The scheme requires, also, a daily handshake between vehicles and the TA to receive this public key and ensure key freshness. The scheme utilizes Elliptic Curve cryptography and provides efficient authentication, identity privacy, and network authentication. However, authentication of messages is done by vehicles themselves, which may cause delays due to limited computing power.

2.3. Secure Schemes That Distribute the Computational Load on the Network

In 2018, Amit Dua et al. [6] tried to group the vehicle authentication process using Cluster Heads. The vehicles are grouped based on criteria such as location, speed, and computing power and a so-called Cluster Head (CH) is elected within each group. The Trusted Authority authenticates the CH and assigns it a group ID (GID). Once the CH is authenticated, it becomes responsible for authenticating other vehicles in its region. The vehicles in the cluster receive the GID from the CH that they are assigned to and authenticate themselves using it. The vehicles then exchange a symmetric Session Key to facilitate further communication. Authentication and key exchange are based on Elliptic Curve cryptography, using the ElGamal technique. This authentication scheme provides confidentiality, authentication, and identity privacy, while being resistant to man-in-the-middle attacks. It also reduces computation times and improves the size and number of required messages.

Lastly, in 2022, Hassan Mistareehi and D. Manivannan [7] proposed a scheme combining group authentication with secure message dissemination in vehicular cloud networks. The scheme uses RSUs to verify message authenticity and integrity before distribution and can delegate leadership roles to vehicles, reducing computational load on RSUs. Vehicles entering the RSU’s area receive a certificate, validate it, and establish communication with the RSU. RSUs can select a Group Leader (GL) to manage authentication and message grouping for efficiency, similar to the approach of Cluster Heads presented by Amit Dua et al. [6]. GLs periodically send proof of leadership and their public key and operate like RSUs in their region of influence. Vehicles authenticate and exchange symmetric keys with the GL or RSU, using a series of Join and Accept messages that are encrypted using asymmetric encryption. RSUs verify messages and handle data dissemination. The Trusted Authority maintains a revocation list and key updates, while pseudonyms are also used to ensure location privacy and anonymity. The scheme enhances security and efficiency in vehicular networks, using various cryptographic techniques to prevent attacks.

3. Analysis of the ECC, HECC-2, HECC-3

3.1. Elliptic Curve Cryptography

The mathematicians Koblitz and Miller separately, proposed at the year 1985 a group of points coming from an elliptic curve that was defined on a finite field in order to make good advantage of the Discrete Logarithm Problem in Cryptography. Since in the points of the Elliptic Curve there cannot be exploited the property of the prime factors that the Number Field Sieve uses. The best method of solving the Discrete Logarithm in the Group is that of the square root complexity, something that makes the group suitable for cryptographic techniques [8].

In order to use the Curves for building the desirable group, initially the elements of the Group need to be defined as well as the respective process that will be used in order to define the Group. The Curve and inductively the points that define the Group are given by the subsequent equation:

E : y^{2} = x^{3} + A x + B, where : (A, B ϵ 𝕂)

(1)

Also, there should apply that the curve is non-singular, which means that the

- (4 A^{3} + 27 B^{3})

should not appear and the Finite Field 𝕂 to have a characteristic different from 2 and 3. So, the elements of the group consist of the points that define the curve, with the neutral element, to point to infinity.

At this part the process of Group is defined. As it is observed in the specific curves’ form, every element

P = (x_{0}, y_{0}),

has an inverse point, that is the 2nd point that line

x = x_{0}

intersects the curve, so

P^{'} = (x_{0}, - y_{0}^{'})

Figure 1. Elliptic Curve’s reverse point [8].

In order to define the process of Group, 2 points on the curve are used. Let P and Q. The line that is passing through the two points, intersects the curve in a 3rd point, the R. So, there can be defined the process P ⨁ Q that outputs the point R’, which stands for the reverse of R, since P, Q and R are collinearly (Figure 2 and Figure 3).

In order to utilize the Discrete Logarithm, there is defined the scalar multiplication as:

P ⟼ [n] P = P ⨁ P ⨁ P \dots ⨁ P for n times

(2)

So, it is obvious the presence of the Discrete Logarithm problem, where P is the generator element and n is the power (exponent) of the generator in order to build the Cyclic Group, with the desirable characteristics of the uniform distribution.

So, in the cryptographic systems based on Elliptic Curves (ECC), the element n that multiplies the generator P can be taken as the secret key of the user, while the result of the process is the public key. In order for an attacker to retrieve the secret key from the public key, they should solve the Discrete Logarithm problem in the Cyclic Group that was previously defined, something very difficult. From the other side, the process of scalar multiplication is easy and with various mathematics techniques can be calculated very efficiently. It is very important that the generator and the parameters of the curve are chosen with much attention, so that the Cyclic Group to have as an order a prime number. That is a bit difficult. However, in the elliptic curves there are now efficient ways to produce safe curves and generator parameters. It is proven that the order of the Cyclic Group is around

p + O (\sqrt{p})

[8], where p is the prime number that was chosen in order to define the Finite Field, so there can be an estimation of each curve’s security. More specifically, since the better algorithms solve the Discrete Logarithm have complexity

O (\sqrt{p}

) and let p have size n bits, then for ensuring 128-bit level security, the p has to have n/2 equal to 128, thus 256 bits.

The Elliptic Curve Cryptography is widely prevalent today with implementations in the field of cryptocurrencies, in collateral of security in systems that maintain limited processing power and memory, as occurs in embedded systems and in Internet of Things, in digital certificates and signatures. There has been extended research in the current object and there is an official data base that contains secure improvements in the calculations that are needed, with the result to be easily implementable in applications without the need to know the mathematics concepts that they define them. Moreover, they provide security with small key sizes, in comparison to the RSA.

However, the careful choice of the parameters that are needed can cause security gaps in the scheme that will be chosen for an application, if the engineer who chooses that does not know completely mathematical background and makes something wrong to that choice. Moreover, the Discrete Logarithm problem is not safe, it cannot withstand to Quantum Attacks. So, in future applications the Elliptic Curves are not enough to ensure safe modern networks.

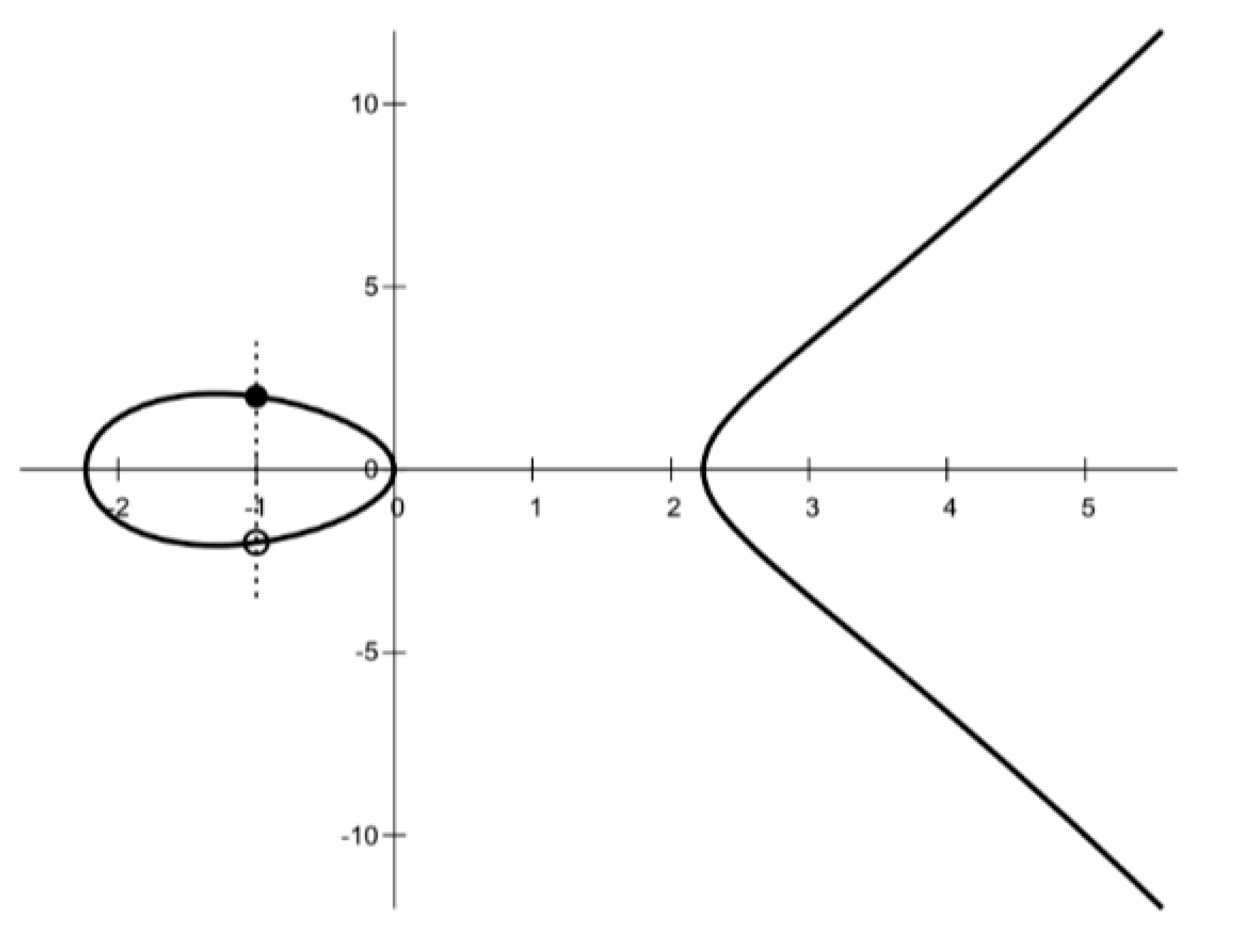
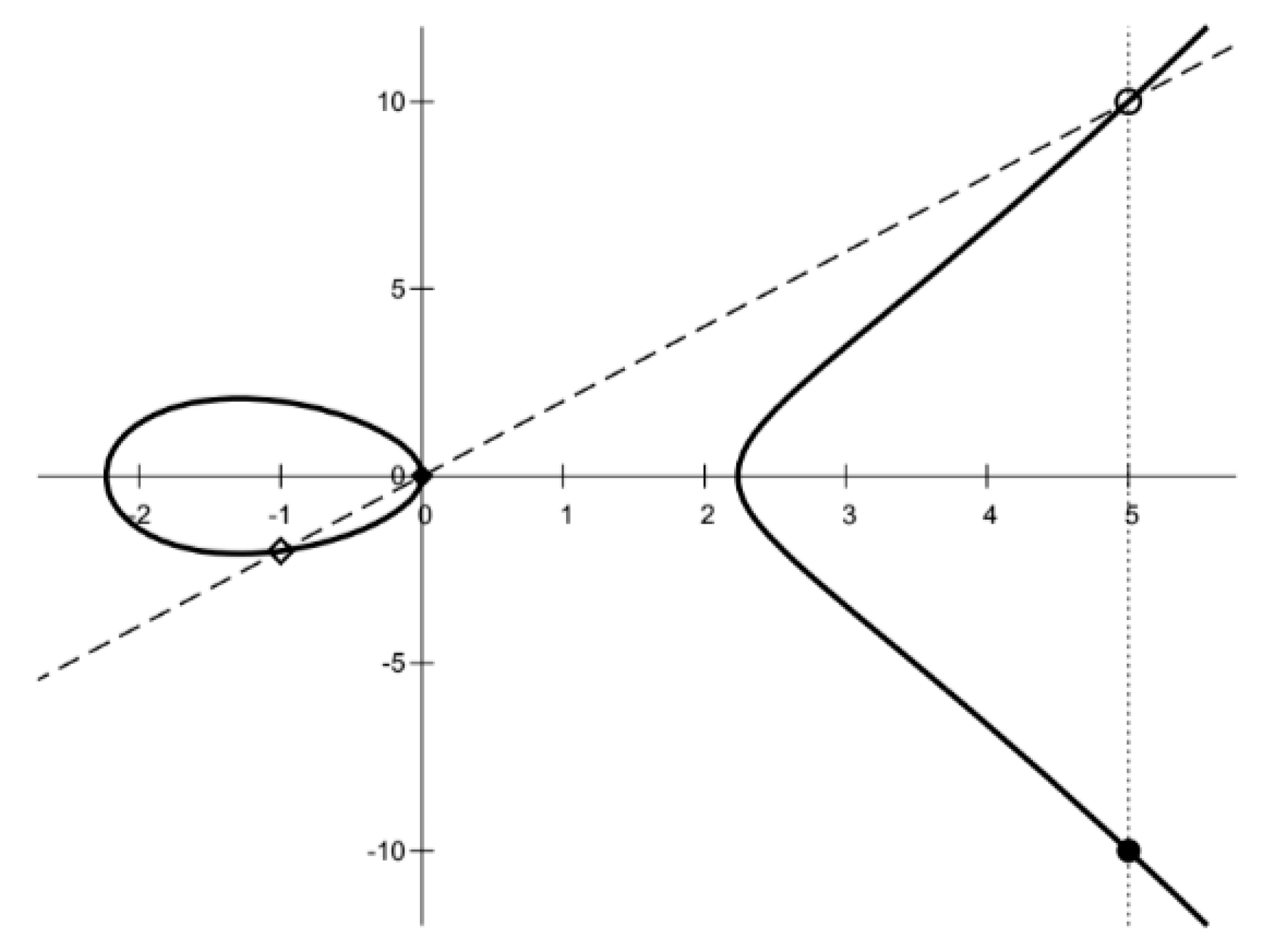
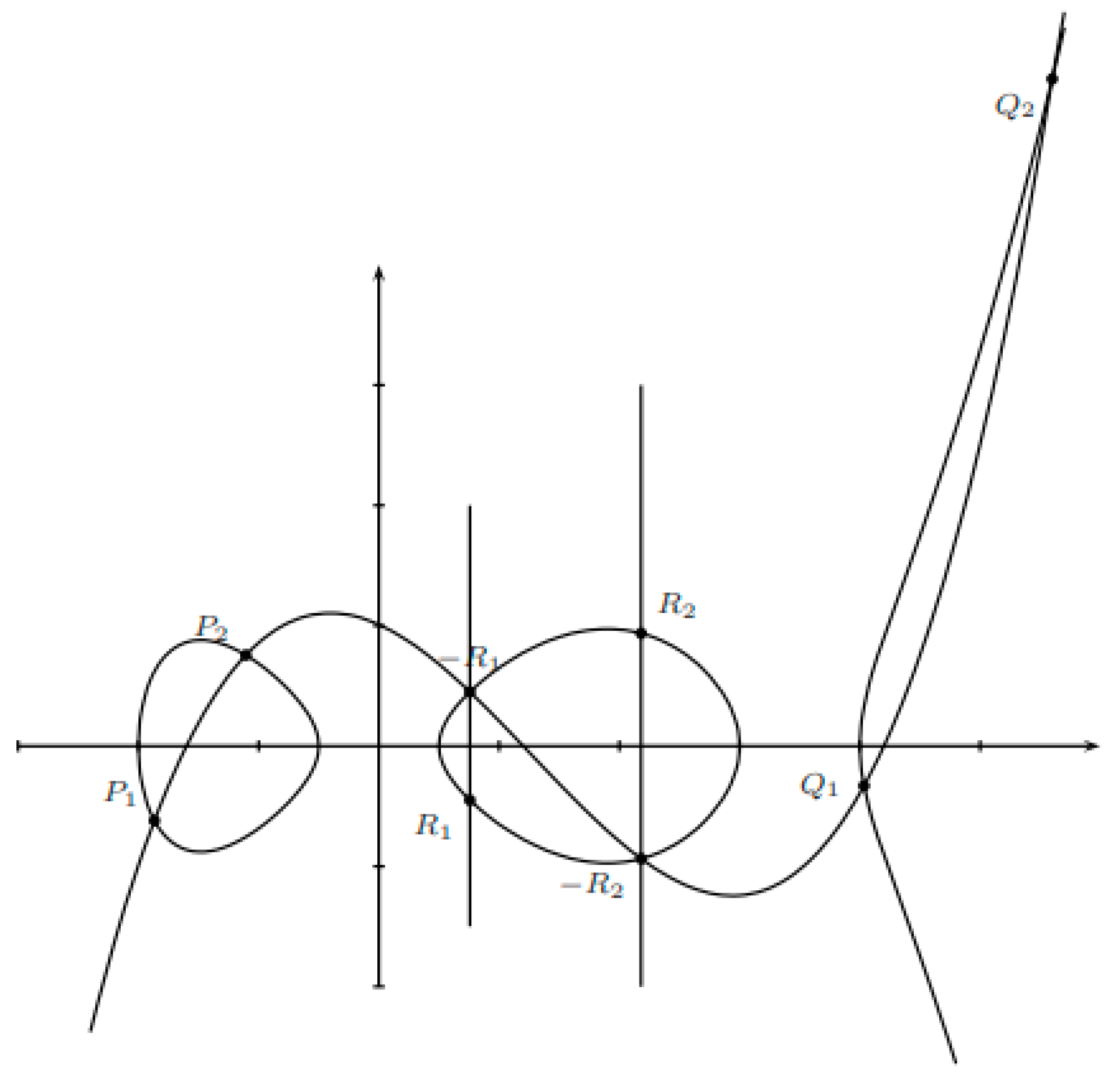
3.2. Hyperelliptic Curve Cryptography for Genus ≥ 2

Five years after the introduction of Elliptic Curves in Cryptography, Koblitz proposed the use of Jacobian Curves in order to produce a suitable Group. Elliptic Curves are a sub-category of the Hyperelliptic Curves, since they are of the ≥ 2 Hyperelliptic Curves for genus = 1.

In order to follow the equivalent procedure of enactment of a Cyclic Group based on Hyperelliptic Curves of genus ≥ 2 there is no need to simple consider as a group’s process the procedure that it was described previously, since now each line can intersect the curve in the

2 \cdot g + 1

points, where g is the curve’s genus [8].

Hyperelliptic Curves of genus g can be described by the following equation:

C : y^{2} + h (x) y = f (x), h, f ϵ K [x], \deg (f) = 2 g + 1, \deg (h) \leq g, f s i n g u l a r

(3)

As previously observed, the curve has to be non-singular which is guaranteed with the condition that no point does not zero both partial derivatives.

In order to build a Cyclic Group, the method that was proposed is to modify a set of points where the summation follows a function. For example, in a curve as in Figure 3, which is a curve of genus 2, the points

R_{1} = (x_{R 1}, y_{R 1})

and

{- R}_{1} = (x_{R 1}, y_{R 1})

belong in the curve

x = x_{R 1}

, so it can be assumed that

R_{1} ⨁ ({- R}_{1}) = 0

. Consequently, the points

P_{1}, P_{2}, Q_{1}, Q_{2}, {- R}_{1}, {- R}_{2}

follow a cubic function, so they are summed to zero. So, as an element there can be assumed the elements which are coming from the sum of two (generally 2 points, where g is the genus) points and the process between two points (or generally g) elements outputs as result the two more points where a cubic (or generally

g + 1

order) function

y = s (x)

intersects the Hyperelliptic Curve.

The class that was previously described is called Order of the Divisor Class

{P i c}_{c}^{o}

of the Curve. The Divisor class gets many shapes, however, the one that prevails for defining the Class and for developing the arithmetic is the Mumford representation. In that representation the elements of the Class are two polynomials

u (x)

and

v (x)

which follow the characteristics:

the $u$ is singular
$\deg (v) < \deg (u) \leq g (g e n u s)$
the $u$ divides precisely the polynomial $v^{2} + v h - f$

So, the polynomial u(x) can be expressed as following:

u (x) = \prod_{i = 1}^{r} (x - x_{i})

(4)

where the

x_{i}

is the coordinate of the points that are chosen to shape the element. More specifically for the

P_{i}

points that take part (support points) it has to apply that

P_{i} \neq P_{\infty}

P_{i} \neq - P_{j}

, for every

i \neq j

. This specific shape applies to the Class of Reduced Divisors, when the following exists:

r \leq g

. Since it was defined that the Class which frames the Cyclic Group, which is the interesting part, it is very significant to develop efficient algorithms for the calculation of the Class process that was described previously. Various algorithms have been built and optimized for the execution of this process, however, as it is easily viewed it is more difficult to calculate in regard to the one that was defined for Elliptic Curves. The fact which makes the Hyperelliptic Curves suitable to Cryptography fields is that in order to achieve a certain level of security, the Finite Field and the related Arithmetic that is needed, should take place in smaller numbers.

That happens because the elements of the Class consist from the

g

points and not from one point, the Class has size

p^{g}

, when the

p

is enough large. So, based on the calculation of the security level which was analyzed in Elliptic Curves section, a Hyperelliptic Curve of genus 2 can achieve 128-bit security level with a Finite Field of size 128-bit, while a Hyperelliptic Curve of genus 3 can achieve the same security level with 86-bit. It is observed that as the genus becomes bigger, the size of the Finite Field becomes smaller and so the keys that will be used can get smaller and achieve the same security level. Unfortunately, the Index Calculus attack, that is not possible to Elliptic Curves, can solve the Discrete Logarithm Problem in a reasonable time, when the genus becomes bigger. For that reason, the curves of genus equal or bigger than 4 are not used in Cryptography [9]. The curves of genus 2 are enough safe, however the curves of genus 3 are used but they are not as safe as Elliptic Curves.

The Hyperelliptic Curve cryptography is not as prevalent as occurs with the Elliptic Curves, so, there are no databases that have defined carefully the parameters of the Curves which need to be chosen. For that reason, it is not so easy to be used in Industry, since they are in a research level. Also, the algorithms whcih exist for calculating the level of a Class, as an output of the Reduced Divisor class is not efficient and this makes the process of producing security of Hyperelliptic Curves difficult concept.

Nevertheless, the small key size that are the outcome, and the improvement in their arithmetic, makes them significant interesting for systems with limited resources, such as embedded systems and the well-known VANETs (Vehicular Ad-hoc Networks). that’s why the current years this specific are has started to bring the attention of the scientific community.

4. Proposed Approach

Based on the related state of the art review, the security scheme presented by Hassan Mistareehi and D. Manivannan [7] with Group Leader clustering has been selected in the proposed approach to simulate secure message exchange scenarios on VANETs and has been extended to utilize ECC and HECC encryption algorithms and techniques to evaluate their performance. In this section, the tools and software used are presented, while the details of the implemented cryptographic algorithms, of the road traffic simulation, of the VANET communication implementation and of the developed energy consumption model are provided.

4.1. Tools & Software

Some well-known software tools were used to construct the simulation environment for the evaluation of the cryptographic methods on VANETs. The open-source software called Network Simulator 3 (NS-3)1 was used to simulate a sample VANET and also to handle the underlying network protocols. NS-3 provides an implementation of the WAVE protocol stack, or more formally the WiFi 802.11p IEEE standard and the IEEE 1609 standards. It also provides the routing algorithm designed for VANETs, AODV and ways for measuring the energy consumption on network devices in the simulation. Furthermore, to generate a realistic traffic scenario, another open-source tool, SUMO, was used. SUMO is widely used for simulating and analyzing road traffic, while it is also compatible with NS-3, using generated XML files that can be imported to NS-3 and create a VANET with realistic movement scenarios. Finally, to visualize the network, PyViz was used. NS-3 already supports PyViz and is providing an easy way to visualize the VANET using it.

4.2. Implementation of Cryptographic Techniques

The approach presented in [7] utilizes multiple cryptographic techniques to ensure security for vehicle communications on VANETs. In our simulation, we do not emphasize on pseudonym exchange and key updating/revocation, but mainly on the procedure of vehicle registration in an RSUs region, the procedure of choosing and informing a Group Leader in the network and finally, the procedure of a vehicle informing the RSU/GL about an important observed event in the region. Therefore, symmetric encryption is implemented using AES, while asymmetric encryption is implemented using ECC or HECC genus 2 or 3 using the ElGamal method2. However, ElGamal method requires the messages to be a cryptographic Group element, a reduced divisor. So, a method of mapping text to a reduced divisor is also needed to be implemented. Furthermore, ECDSA signatures and HEC ElGamal signatures are used, key generation and distribution is implemented using (H)ECQV, (Hyper)Elliptic Qu-Vanstone certificates. Since no open-source library for Hyperelliptic Curve Cryptography of genus 3 is provided in C++, one is implemented and analyzed in this paper.

As mentioned above, the stages of the approach in [7] that rely on symmetric encryption are implemented using AES, specifically, using the methods provided by the C++ library, Crypto++. AES is used with CBC mode of operation and with 16 bytes – 128 bits key and block sizes. Also, an Initialization Vector is used and is transmitted along with the symmetric key. To properly transmit the keys and IVs to the network as strings, the HexEncoder and HexDecoder methods of the library are used. Encrypted text outputs are always a multiple of 16 bytes since, by default, PKCS padding is used to handle input blocks.

Crypto++ additionally provides an API for executing ECC cryptographic operations (scalar multiplication, point addition etc.) and implemented methods for signing and verifying messages using ECDSA signatures. Curve secp256r3 and its parameters (base/generator element) is provided by Crypto++ and it is chosen for our simulation because it produces 256-bit keys and therefore 128-bit security level. ElGamal encryption/decryption is implemented using the ScalarMultiply, Add and Subtract methods of Crypto++ to produce the cypher text as the tuple

(a, b), w h e r e a = k \cdot G, b = k \cdot P + Μ

, where

k

is a random integer of Group order (256 bits),

G

is the generator element,

P

is the public key and

M

is the message encoded as an EC point. The plain text is received by calculating

M = b - x \cdot a

, where

x

is the private key. For encoding text as an EC Point, the Koblitz method is implemented [10]. Modular arithmetic is executed using the NTL library4 and given the plain text as an integer x that is less than the Group Order, the calculated EC Point

(x_{1}, y_{1})

x_{1} = x \cdot k + i

, where

k = 1000

and

1 \leq i \leq 999

. The

x_{1}

is calculated by the above equation until it is a quadratic residue5, i.e.,

y^{2} = x_{1} m o d n

has a solution. ECDSA signatures are generated using Signer class of Crypto++ and verification is executed using the Verifier class of Crypto++. Points are compressed so that only the

x

coordinate is transmitted along with one extra byte to reconstruct y coordinate properly.

Key-pair generation, distribution and validation is handled by the ECQV certificate scheme [11] for all three different asymmetric encryption algorithms. The scheme is adapted to match the requirements for Hyperelliptic Curve Cryptography. ECQV consists of 5 steps: ECQV_Setup, Cert_Request, Cert_Generate, Cert_PK_Extraction, Cert_Reception. At the ECQV_Setup step, the simulated node that acts as the Certificate Authority generates a key-pair

d_{C A}, Q_{C A}

. The public key

Q_{C A}

is considered to be known to every participating vehicle and RSU. At the Cert_Request step, a node that requests a valid certificate from the CA generates a key-pair

k_{U}, R_{U}

and sends the public key

R_{U}

to the CA along with its ID. At the Cert_Generate step, the CA receives the

R_{U}

from the node, it generates another key-pair

k, k * G

and then it computes

P_{U} = R_{U} + k \cdot G

and generates the certificate which include

P_{U}

. It also calculates

r = e \cdot k + d_{C A} (m o d n)

, where

= H a s h_{n} (C e r t)

and

n

is the Group Order. Finally, it sends the certificate and the parameter r to the node. At the Cert_PK_Extraction step, any node that wants to extract the public key from the certificate executes

Q_{U} = e \cdot P_{U} + Q_{C A}

. For the node that requested the certificate, at the Cert_Reception step, it computes its public as mentioned above and it also computes its private key

d_{U} = r + e \cdot k_{U} (m o d n)

, where

e = H a s h_{n} (C e r t)

and validates if

Q_{U} = d_{U} \cdot G

. For ECC, these operations are executed using the Crypto++ API for ECC operations including scalar multiplication and addition, while for Hashing, the SHA3-256 class of Crypto++ is used. Furthermore, for modular arithmetic the ModularArithmetic class is used that is initialized on

n

, the Group Order.

To implement the cryptographic operations for HECC of genus 2, libg2hec6, has been used. This is a C++ library that provides methods for generating and and performing operations on reduced divisors of Hyperelliptic Curves of genus 2, which are suitable for cryptographic operations. The methods are based on the algorithms of the Handbook of Elliptic and Hyperelliptic Curve Cryptography by Henri Cohen and Gerhard Frey [12]. It is based on NTL, a C++ library for number theory mathematics. For encryption/decryption using ElGamal and for HECQV certificates, the same operations are used as in ECC, but now the Group elements are the reduced divisors in Mumford representation. For signing and verifying messages, ElGamal signatures are used. The operations are similar to ECDSA, however methods were implemented from scratch. The produced signature is the tuple

(a, b)

, where

a = k \cdot g

and

b = \frac{m - x \cdot f (a)}{k} (m o d N)

, where

m

is the message as a reduced divisor,

x

is the private key

k

is a random integer in

[1, N)

N

is the Group Order,

g

is the generator element as a reduced divisor and

f

is a bijection of a reduced divisor in Mumford representation to an integer in

[1, N)

. The bijection used is

f (u) = (u_{1}^{2} + u_{2}^{2}) (m o d N)

, where

u_{1}

u_{2}

the coefficients of the u polynomial of the reduced divisor in Mumford representation.

The challenge in HECC is to choose secure Hyperelliptic Curve parameters for the cryptographic operations, since there is no given database of curves and parameters, like in ECC. Furthermore, general encoding and decoding techniques, that are needed for ElGamal encryption and signatures, to the Jacobian of the curves have not been established, so only algorithms for specific Hyperelliptic Curve families have been produced. For ElGamal signatures the Group Order needs to be known and to be prime or “almost” prime and the cofactor needs to be known as well. So, for the signatures of HECC genus 2 a curve was chosen from the “Construction of Secure Random Curves of Genus 2 over Prime Fields” by Gaudry and Schost [13]. Specifically:

y^{2} = f (x) σ τ ο F_{p} w i t h p = 5 \cdot 1024 + 8503491

(5)

with

f (x) = x^{5} + 2682810822839355644900736 x^{3} + 226591355295993102902116 x^{2} + 2547674715952929717899918 x + 4797309959708489673059350

(6)

is chosen which produces a Group of Order:

N = 249999999999941304386009994022094639661975160756

(7)

where

N

is a prime number of 128 bits. That means that the security level of the curve is at the 128-bit level and can be compared with secp256-r1 that is chosen for ECC operations.

To overcome the challenge of encoding text to the Jacobian of the curve, a technique proposed by Michel Sack and Nafissatou Diarra on 2018 [14] to encode integers as points to a specific family of Hyperelliptic Curves of arbitrary genus was used. In their paper, they provide code in Sage for executing their encoding techniques, which was translated to C++ using the NTL library. First of all, a different curve needs to be used and is produced by their algorithm for a given Finite Field of characteristic

p

. However,

p = 3 m o d 4

and

p = 7 m o d 8

. So, the characteristic of the Field is chosen as:

p = 340282366920938463463374607431768211223

(8)

which is 128-bit and produces a Group of Order close to 256-bits. The curve is then produced based on the algorithm [14] and is used for all cryptographic operations, except ElGamal signatures. Unfortunately, the exact Order of the curve is unknown. With [14], text is mapped to a point in the Hyperelliptic Curve and then 2 points are combined and a reduced divisor produced. Specifically, the

u

polynomial of the divisor is calculated as

u (x) = (x - x_{1}) \cdot (x - x_{2})

and the

v

polynomial is calculated as

v c = \frac{y_{1} - y_{2}}{x_{1} - x_{2}}

and

d = y_{1} - c \cdot x_{1}

Since in Mumford representation, the v polynomial can be constructed from the u polynomial it useful for a realistic simulation scenario to use divisor compression techniques. It is known that

u | v^{2} - f

, so based on the algorithm proposed by Henri Cohen and Gerhard Frey on their book [12], a compression technique is used and the divisors are transmitted only using 256 bits for the

u_{1}, u_{2}

coefficients and one more byte used for the reconstruction information of the

v

polynomial.

Finally, for HECC of genus 3, a new library was created to match the needs of the simulation. Based completely on libg2hec implementation 7and Cohen’s and Frey’s book [12], the curve and divisor classes were modified to match the required conditions for genus 3 curves and divisors. Most importantly, for Group operations, SAM, NAF and ML methods for scalar multiplication were used exactly as implemented in libg2hec since they are of arbitrary genus. For divisor “addition” and “doubling” Cantor’s algorithm can be used without modification since it is of arbitrary genus, however it is slow. Therefore, algorithms 14.52 and 14.53 for genus 3 divisor addition and doubling from the Handbook of Elliptic and Hyperelliptic Curve [12] were implemented. As for cryptographic techniques, the same methods as in HECC of genus 2 were used. What differs are the chosen curves and the encoding/decoding and bijection techniques, which are adapted for genus 3 divisors. For general cryptographic operations, excluding signatures, a Finite Field of:

p = 77371252455336267181195223

(9)

was used. Again,

p = 3 m o d 4

and

p = 7 m o d 8

, while

p

is an 86-bit integer which produces a Group Order of almost 256-bits. This Field is used by the algorithm of Michel Sack and Nafissatou Diarra [14] to produce a curve that will be used for the cryptographic operations. For signatures, since the Group Order needs to be known, based on the publication of Annegret Weng [15], curve:

y^{2} = x^{7} + x^{5} + 6218231719898953 \cdot x^{3} + 8683773159487505

(10)

was selected, where the Group Order is

N = 8 q

, where

q

is a prime number of 168 bits. Also, the bijection

f

used for ElGamal signatures is now modified to

f (u) = u_{1}^{2} + u_{2}^{2} + u_{2}^{2} (m o d N)

and for the encodings on the Jacobian, Michel Sack’s and Nafissatou Diarra’s algorithm [14] is used to map text to points in the HEC and then 3 points are combined to produce a valid reduced divisor of genus 3.

4.3. Simulation of Road Traffic

The implementation of the road traffic involved using the SUMO tool to convert a real-world area into an XML file for network generation and route planning. Random routes were generated for nodes, and a traffic simulation of 400 seconds was conducted, while spawning a vehicle every 0.5 seconds. This produced an XML file, which was then converted to a .tcl format suitable for NS-2 and NS-3 simulations using the trace exporter tool of SUMO. In the NS-3 simulation, 63 vehicles were introduced, with an additional manually added node serving as an RSU. To address issues that arise with all vehicles being present in the simulation since the start, precise entry and exit times were extracted from the .tcl file to control communication timing. Additionally, WAVE devices were installed on each node using appropriate NS-3 classes, with power and priority settings applied for packet transmissions.

4.4. Implementation of VANET Communication

The communication between vehicles and the Roadside Unit (RSU) to implement a secure scheme using desired cryptographic techniques was entirely carried out using NS-3 in C++, with the assistance of libraries like Crypto++, libg2hec, NTL, and g3hec, developed during the project and discussed in chapter 4.2. Specifically, communication was achieved through WAVE layer packets, extracting metrics without additional delay from processing higher network and application layers. Callback functions were installed to process incoming packets at nodes and take further actions based on the communication stage (Join, Accept, Extract_Symmetric, Receive GL Proof, Receive Vehicle Information based on [7]), such as sending a response packet if necessary. Responses were routed randomly within a 0-3 second window to better utilize bandwidth and avoid collisions. The RSU stores the status of all vehicles in the area, key pairs, CA information, and the public key of entering vehicles along with their certificates. It maintains the total number of vehicles that joined, the GL identifier, the exchanged symmetric keys with vehicles, and parameters of curves used for encryption. Vehicles store their own keys, CA, RSU and GL public keys if available, certificates, the status of the communication that is ongoing, symmetric keys, IV arrays, and curve parameters.

Communication starts with the RSU broadcasting its certificate every 2 seconds. All vehicles are initially in RECEIVE_CERT state. Upon RSU certificate receipt, vehicles verify it, get the RSU public key, store it, and send back a Join packet to the RSU, transitioning to RECEIVE_ACCEPT_KEY state. RSU processes the response, changing vehicle state first to RECEIVE_ACCEPT_KEY, then ON_SYMMETRIC_ENC after sending the ACCEPT response. Vehicle density increases after 120 seconds, leading to congestion. RSU randomly selects a Group Leader (GL), sends GL Proof of Leadership, the GL transitions to GROUP_LEADER_INFORM and then IS_GROUP_LEADER. Note: ECC and HECC do not allow encryption of the Proof of Leadership message, so the RSU provides to the GL its own certificate, signed with RSU’s public key. GL relays decrypted message to the network every 2 seconds. Existing and new vehicles follow Join and Accept process with the GL (using RECEIVE_ACCEPT_GL and ON_SYMM_GL states). Finally, vehicles transmit an INFORM message at random times once they receive a symmetric key. GL gathers Inform messages and sends them to the RSU.

4.5. Implementation of Energy Consumption Model

NS-3 provides methods for calculating the energy consumption on simulated nodes based on the energy that a real network device (WAVE interface) would consume while the vehicle is communicating with the network. Specifically, the WiFi Radio Energy Model of NS-3 was used to calculate how much the device’s battery is reduced after each transition of the WiFi state (Idle, CcaBusy, Tx, Rx, ChannelSwitch, Sleep, Off). Every WAVE network device is given 1000 Joules of battery at initialization for simulation purposes, since the difference in energy is the desired metric. After each major communication step that was mention in section 4.4, the remaining energy is subtracted from the energy level that was stored before the communication was executed and the energy consumption is calculated.

5. Experimental Evaluation

In the current section there is the presentation of the experimental results via the use of the three asymmetric cryptography algorithms that have been presented in section 3, i.e., ECC, HECC-2, HECC-3.

In the executed simulations, 63 vehicles have been used, as well as one RSU, which covered the entire area. Moreover, the messages were transmitted with the maximum capable energy and priority aiming at mitigating the collisions from simultaneous transmission and was chosen to realize a simple retreat of the responses up to 3 seconds. The period of time was big enough for real systems; however, it was used for better supervision of the communication. In addition, the measurements take place in cryptographic techniques. The specific technique increases the total time so, it increases the energy that is used in that period of time, since it is affected by the operational time. Thus, in some parts of the communication it is observed greater power usage than others.

In order to measure time the researchers used the following function: chrono::high_resolution_clock::now() at the beginning and in the end of each calculation. In the diagrams one can observe the mean time of the time durations and the energy. The measurement of the parameters took place via the calculation of byte buffer before it was transmitted to the node. So, in the measurements is not included the size of the header that the WAVE protocol adds.

The simulations took place in virtual environment Linux Ubuntu 20.04.6 with host Windows 10, 8 GB RAM available memory and 4 cores (Intel Core i5-10300H, clocked at 2.50 GHz.) There was also used the following open-source tools: NS-3.30, SUMO 1.16.0, NTL 5.5.

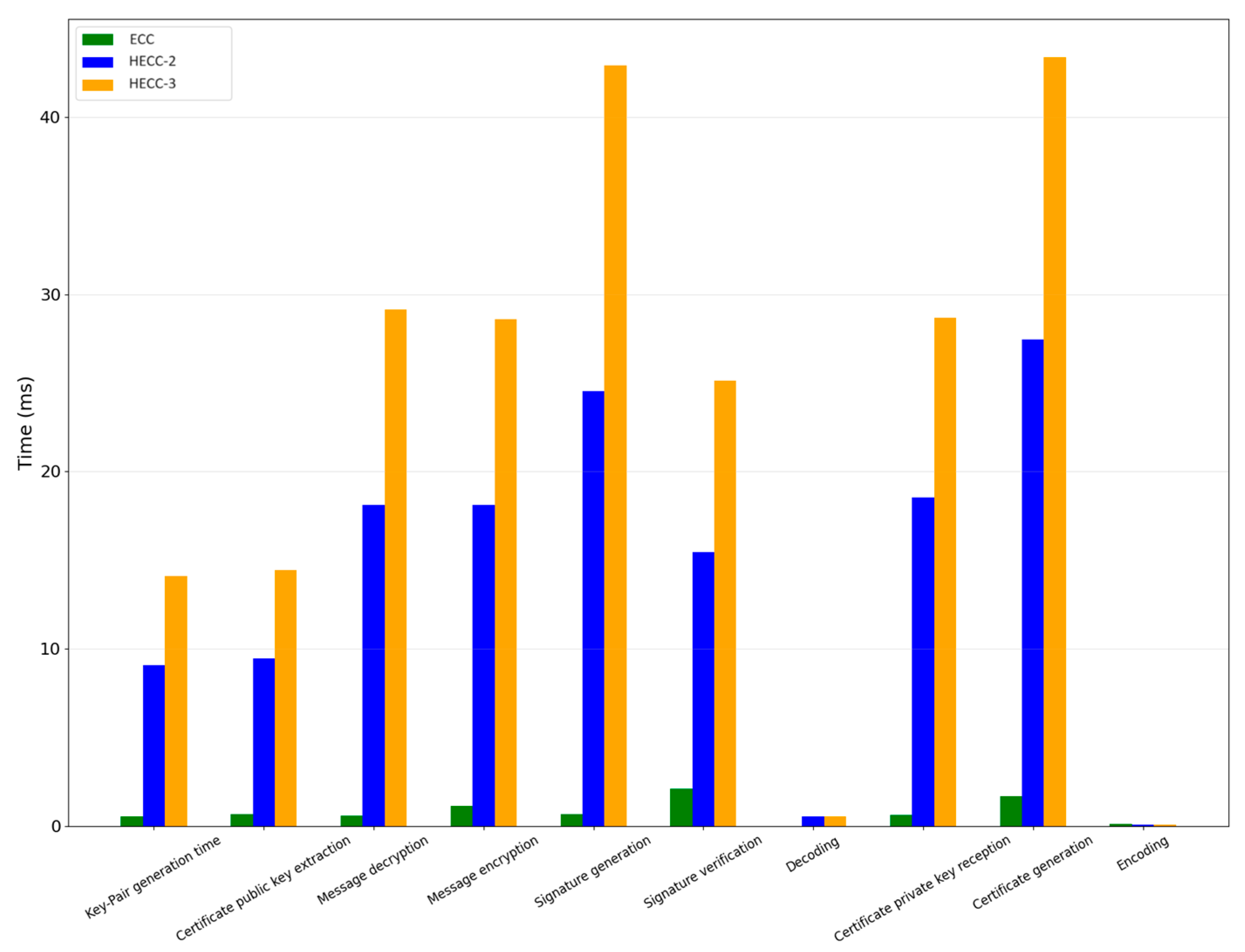
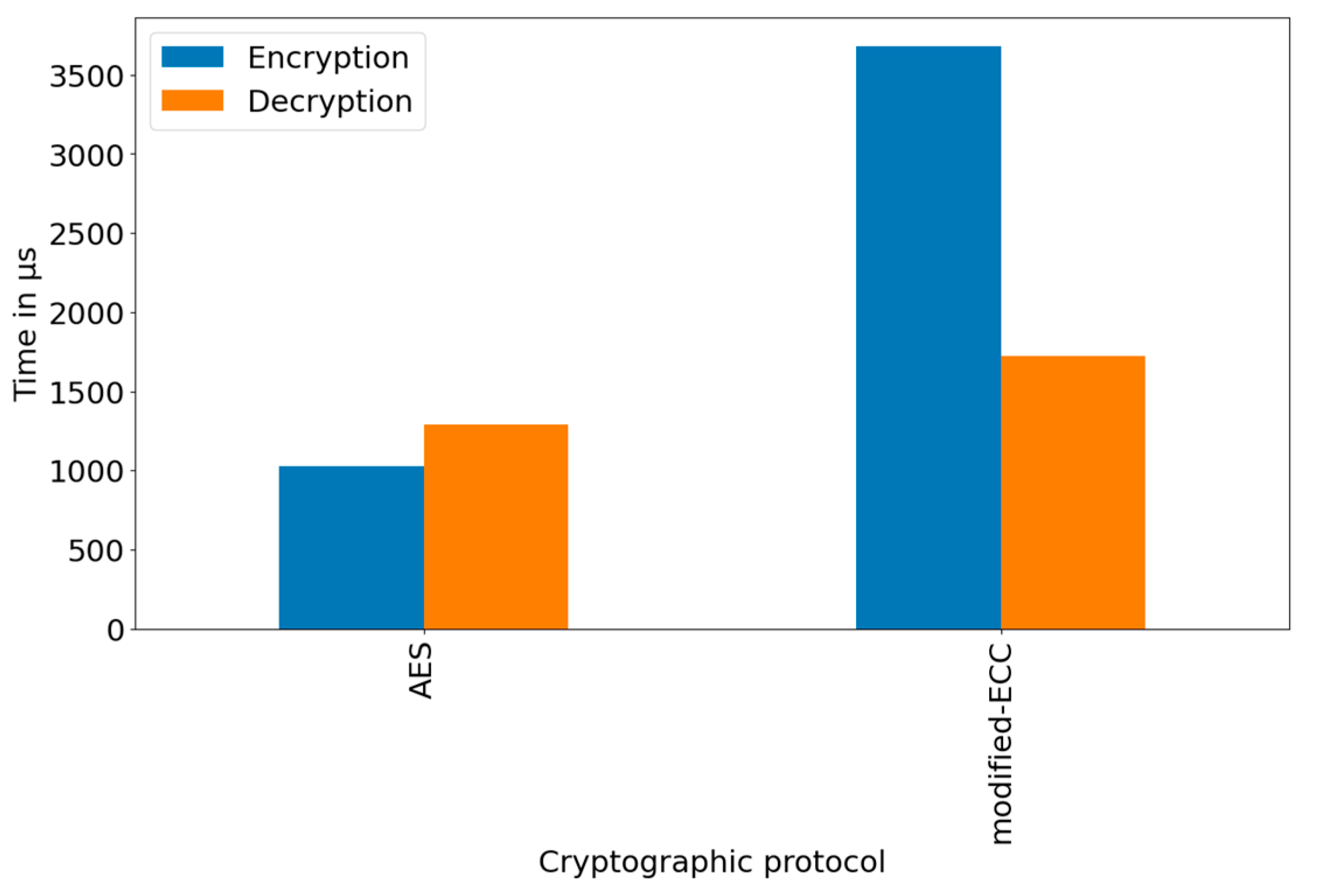
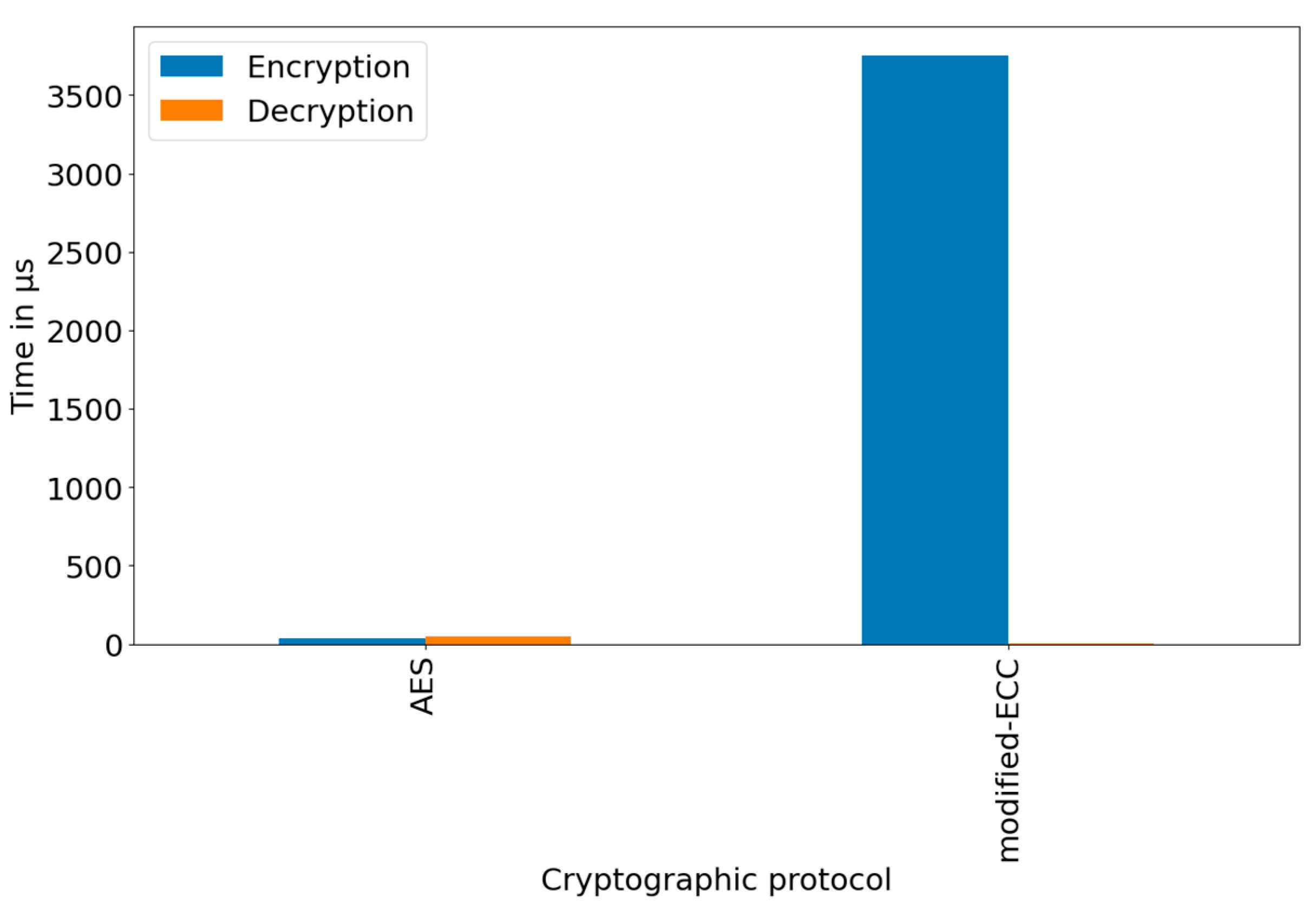
5.1. Duration of Cryptographic Operations

Initially, the execution times of the underlying cryptographic operations have been experimentally measured. In this respect, series of experiments have been conducted aiming to measure the durations of the following operations:

Key-pair generation
Certificate public key extraction
Message decryption
Message encryption
Signature generation
Signature verification
Decoding
Certificate private key reception
Certificate generation
Encoding

The respective results obtained regarding the durations of the operations aforementioned when adopting the three studied cryptographic approaches (i.e., ECC, HECC-2 and HECC-3) are presented in Figure 4.

As expected and as indicated in Figure 4, in principle, the ECC cryptographic operations are much shorter than the respective HECC operations. More specifically, for the same key size of 128 bits, the key production based on ECC is 16 times faster than in HECC genus 2, and 27 times faster than the key production duration in HECC genus 3.

Similar observations are made for the certificates generation extraction times and times based on the ECQV scheme. As indicated in Figure 4, the respective production and extraction carried out via the ECC is 15 times faster than the respective operations in HECC genus 2 and 25 times faster than that in HECC genus 3. It is easily observed that the production is the slowest process, then follows the secret key extraction process (Figure 4) and lastly is that of the public key extraction. More specifically it is 3 times faster than the production operation.

Regarding the durations of the encryption and decryption operations, the obtained results are similar. Therefore, as indicated in Figure 4, the encryption and decryption operations are much faster in ECC than the two other HECC approaches, i.e., 13 times faster than HECC genus 2 and 21 times faster than HECC genus 3.

Similarly, with respect to the signature generation duration, the ECC approach is much faster than the HECC genus 2 scheme, which in turn is faster than the HECC genus 3 approach, as indicated in Figure 4. The observations are similar also for the signature verification duration, as presented in Figure 4. More specifically, the signature validation time is 5.3 times faster in ECC than HECC-2 and 8.3 times faster than HECC-3. This is due to the fact that the curve employed for the signatures by HECC-2 corresponds to 84-bit security level, as opposed to the ECC curve that corresponds to 128-bit security level.

With regards to the message encoding and decoding operations’ durations, the encoding based on Koblitz algorithm that is employed by ECC is slower than the algorithms employed by HECC genus 2 and genus 3 [12], as indicated in Figure 4 (bars of encoding and decoding). More specifically, encoding via the use of ECC is about 38% slower than HECC-2 or HECC-3. As far as decoding time is concerned, this is about 50% faster in ECC than in HECC-2 or HECC-3.

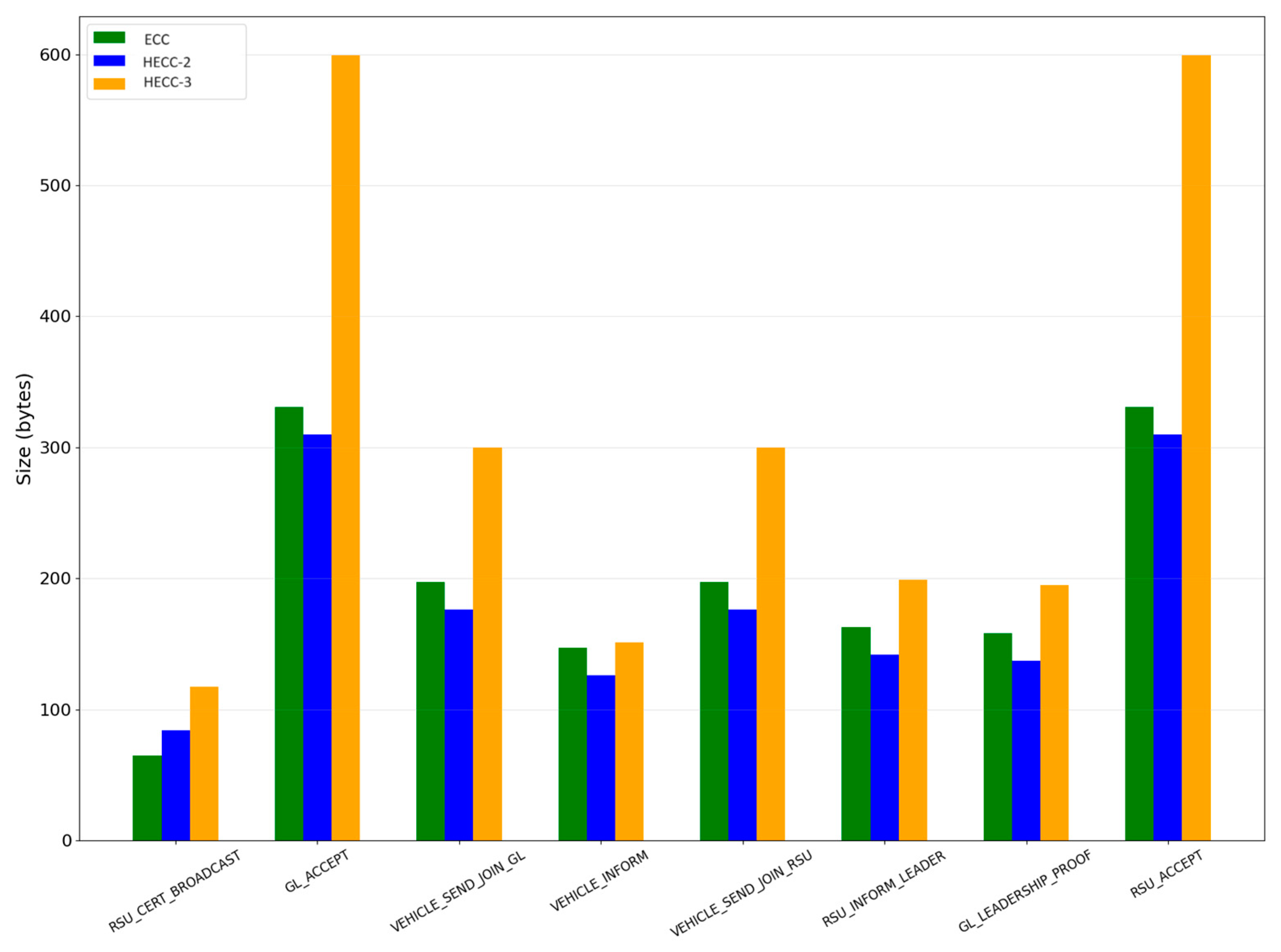
5.2. Size of Exchanged Messages

Concerning the simulation of the communication, the following types of messages have been used:

RSU_CERT_BROADCAST: The certificate that RSU transmits periodically.
VEHICLE_SEND_JOIN_RSU: The message “Join” that the vehicle sends to the RSU, when it needs to subscribe to the RSU’s area.
RSU_ACCEPT: The RSU’s response to the vehicle’s message “join”. It also contains the cryptographic symmetric key.
RSU_INFORM_LEADER: The message that RSU sends, in order to update a vehicle that a Group Leader was chosen. It brings the Proof of Leadership.
GL_LEADERSHIP_PROOF: The message that GL (Group Leader) broadcasts periodically, in order to prove that it is valid and invite the vehicles to “join” him.
VEHICLE_SEND_JOIN_GL: The message “Join” that the vehicle sends to the GL, when it needs to subscribe to the respective GL.
GL_ACCEPT: The GL’s response to the vehicle’s message “join”, also carrying the cryptographic symmetric key.
VEHICLE_INFORM: The message that a vehicle sends in order to update for its position. It was chosen typically as an updating message for the system evaluation.

Subsequently, the various messages’ size has been experimentally measured. In this respect, series of experiments have been conducted where the sizes of the types of messages mentioned in the previous list have been estimated. The respective results obtained are presented in Figure 5, for the three different algorithms of asymmetric cryptography studied.

As one may easily observe, the HECC genus 3 scheme results in the largest GL_LEADERSHIP_PROOF message size, whereas respective size for ECC is a bit smaller, and the HECC genus 2 is the smallest. As far as the size of the VEHICLE_SEND_JOIN_GL message is concerned, the HECC genus 3 scheme results in the largest size, while HECC genus 2 results in the smallest size of the respective message type.

Regarding the size of the GL_ACCEPT message the observations are similar, as the HECC genus 3 results in the largest size, while ECC corresponds to about half of the respective message size and HECC genus 2 results in the smallest size of this message over the three cryptographic schemes studied (Figure 5). As far as the VEHICLE_INFORM message size is concerned, the situation is similar for the ECC and HECC genus 3 schemes (about 150 Bytes), while the HECC genus 2 results in slightly smaller VEHICLE_INFORM messages of about 125 -130 Bytes.

Overall, as indicated in Figure 5, the messages exchanged using ECC or HECC-2 correspond to about the same size, whereas HECC-3 scheme results in messages of significantly larger size. This is more obvious for the GL_ACCEPT and RSU_ACCEPT messages. In general, the sizes of the messages are similar. If there was use of same level of signature for HECC-2 the respective messages would have been of the same size. In order to achieve the same size in genus 2, the idea was to use divisor compression. In HECC-3 it was tricky to use compression realizations, so there is the transmission of information containing the parameters of the Curve in RSU_CERT_BROADCAST. The latter action is more realistic, but it increases the transmitted information. It should be highlighted that the RSU_CERT_BROADCAST, GL_LEADERSHIP_PROOF and VEHICLE_INFORM messages were sent periodically, as is the case in non-simulated systems.

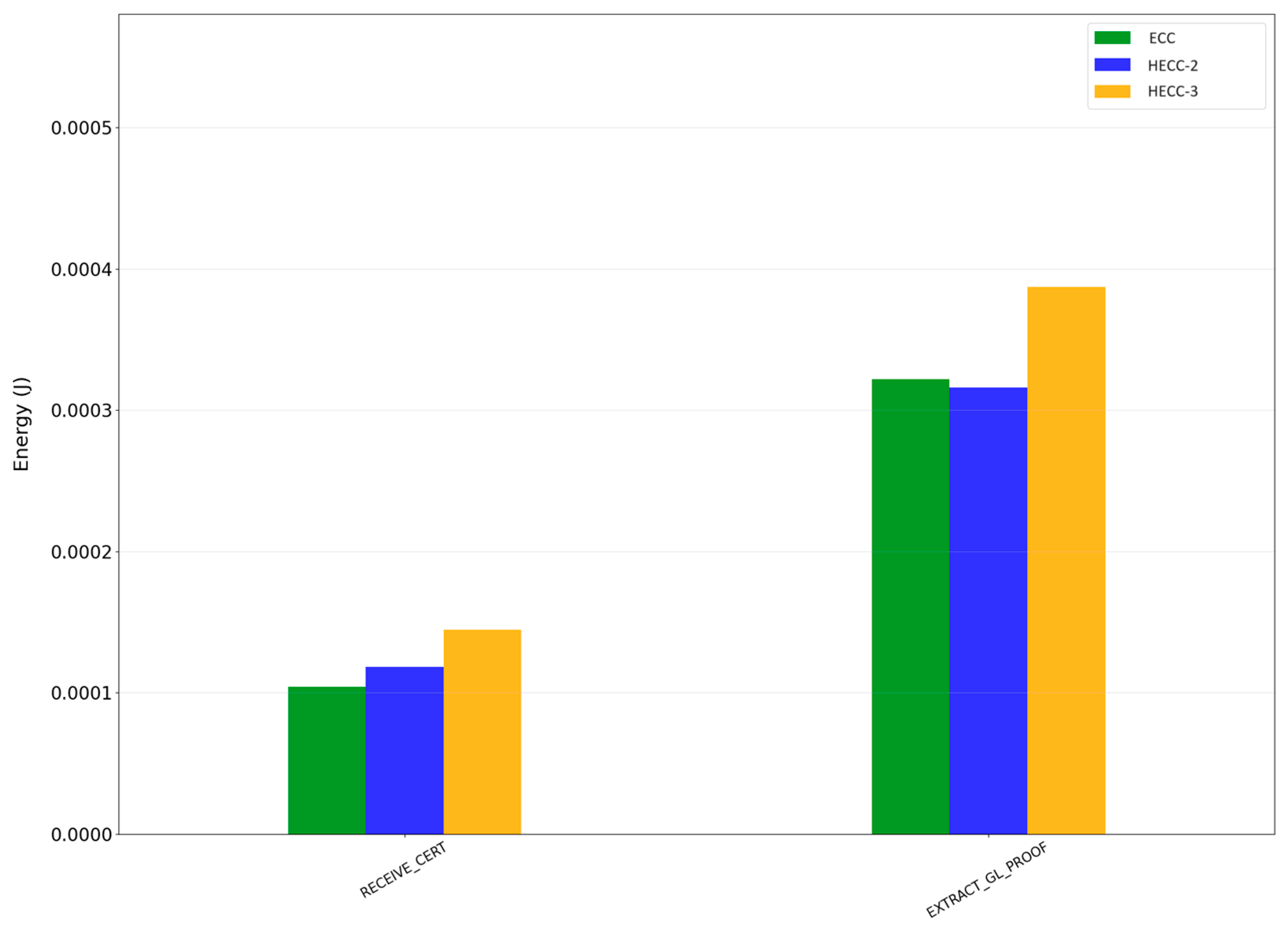
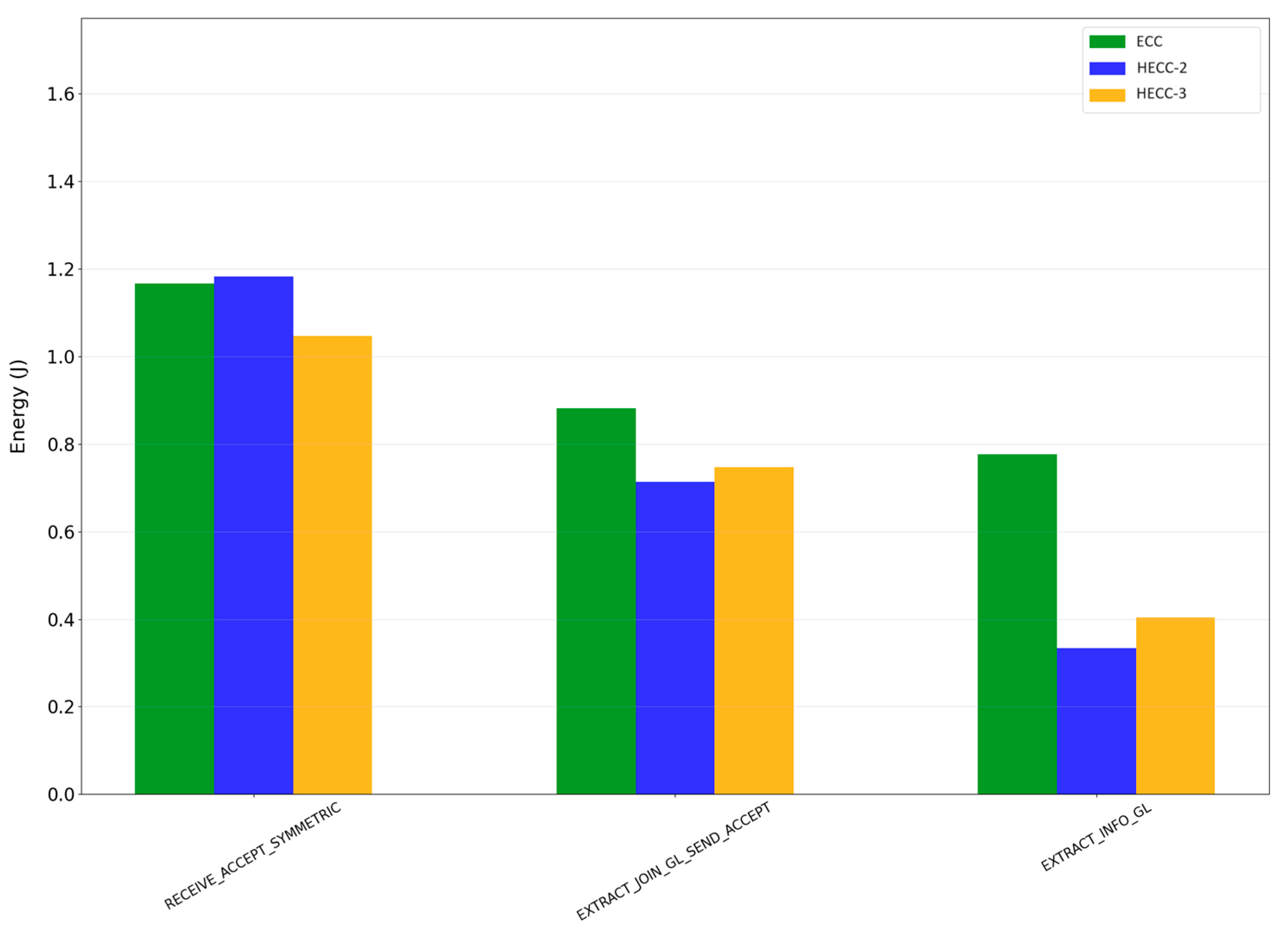
5.3. Energy Consumption

The energy consumption for the three cryptographic algorithms studied is depicted in Figure 6. The idea is that the ns-3 starts from a standard initial energy threshold and measures the depletion as the exchange of messages take place. The energy consumption metric is critical for the vehicle side, rather than on the infrastructure, given the respective resource constraints applicable. The respective energy consumption levels are the following:

RECEIVE_CERT: It just describes the procedure of receiving and the processing of the certificate of the RSU (process of very small-time duration).
EXTRACT_GL_PROOF: It describes the procedure of receiving and processing of the GL leader’s proof (process of very small-time duration).
RECEIVE_ACCEPT_SYMMETRIC: It describes the procedure of sending the message “Join” and receiving and processing of the “Accept” reception from the RSU.
EXTRACT_JOIN_SEND_ACCEPT: It describes the procedure of the “Join” message that GL received from a vehicle and the transmission of the “Accept” response.
EXTRACT_INFO_GL: It describes the procedure of extracting a message “Inform” that GL receives from a vehicle.

Subsequently, the energy consumption in very small-time procedure metric has been experimentally evaluated. In this respect, several experiments have been conducted to measure the previously mentioned levels and the respective results obtained are presented in Figure 6 and Figure 7, with regards to the average consumption of each level in Joules.

In Figure 6, one may observe that the energy consumption in RECEIVE_CERT is less than 200 μJ for all the studied schemes (ECC, HECC genus 2, HECC genus 3), while as far as the EXTRACT_GL_PROOF is concerned, the respective consumption lies between 300 μJ and 400 μJ. Figure 7 depicts the RECEIVE_ACCEPT_SYMMETRIC consumption, that lies between 1.1 Joules to 1.2 Joules for all three cryptographic schemes (ECC, HECC genus 2, HECC genus 3). The EXTRACT_ACCEPT_JOIN_GL_SEND_ACCEPT consumption is lower and lies between 0.6 Joules and 0.9 Joules, while the lowest consumption is related to EXTRACT_INFO_GL consumption that lies between 0.3 Joules and 0.7 Joules.

It is observed that the highest amount of energy is consumed by the HECC genus 3 for the very small-time procedures, whereas in the rest, the ECC consumes the most among the three. In principle, the energy consumption depends on the sizes of the messages, since large messages which require fragmentation, cause more state switches in the transmission device, thus leading to higher energy consumption. However, as the three studied algorithms have also been selected due to the small message sizes, and therefore in the WAVE level they do not demand fragmentation.

6. A Device for Message Encryption via Zigbee Network, Using AES or ECC

In the current section there is an analysis of a device implemented to secure messages over wireless network, and more specifically via the use of Xbee Zigbee modules. The whole construction was implemented via the use of Arduino MEGA 2560, an Arduino GIGA R1, a TFT screen connected to the Arduino, a voltage translator, a Xbee Zigbee, a USB splitter, a DC power supply and a USB keyboard.

6.1. AES Cryptographic Protocol

First, there is an introduction to AES algorithmic scheme, since ECC was analyzed in a previous section. The AES algorithm was originally proposed by Joan Daemen and Vincent Rijmen. The algorithm was selected as the mainstream encryption algorithmic scheme (Advanced Encryption Standard) by the famous NIST (National Institute of Standards and Technology) in 2001 [16]. There are many characteristics of AES scheme, that distinguish it from similar symmetric cryptographic schemes. These are described below:

AES scheme is a block cipher that makes use of the same key either for encryption or decryption period.
The unencrypted text block size is 16-bytes (128-bits)
The size of the key can be 128-bits, 192-bits or 256-bits
AES contains iterations, best known as rounds, related to the key sizes. These are the following: i) 10 rounds for 128-bits key size, ii) 12 rounds for 192-bits size and iii) 14 rounds for 256-bits size.
AES contains 4-levels: 1) SubByte, 2) ShiftRow, 3) MixColumn, 4) AddRoundKey. Those stages are taking place in a continuous logic and realized as rounds on a 4x4 bytes state array. The plaintext (the text to be encrypted) is fed in those rounds.

Below, there is an analysis of each level (stage) [16]:

The SubByte level is a byte substitution in a non-linear rationale, that is realized on every byte of the State array in an independent logic.
The ShiftRow Stage consists of four rows. The initial row is unshifted, while the rest 3 rows are moved in a circular logic over 1 to 3 bytes.
The MixColumns Stage makes use of the column-by-column for working the state. Every column is used as a polynomial consisting of four-terms in a GF(28). Then, undergoes a multiplication with a fixed a(x) modulo x4+1 polynomial.
The AddRoundKey part operates the States via the use of one of the sub-keys by realizing XOR computation. The latter is implemented between every byte of the sub-key and every byte of the State.

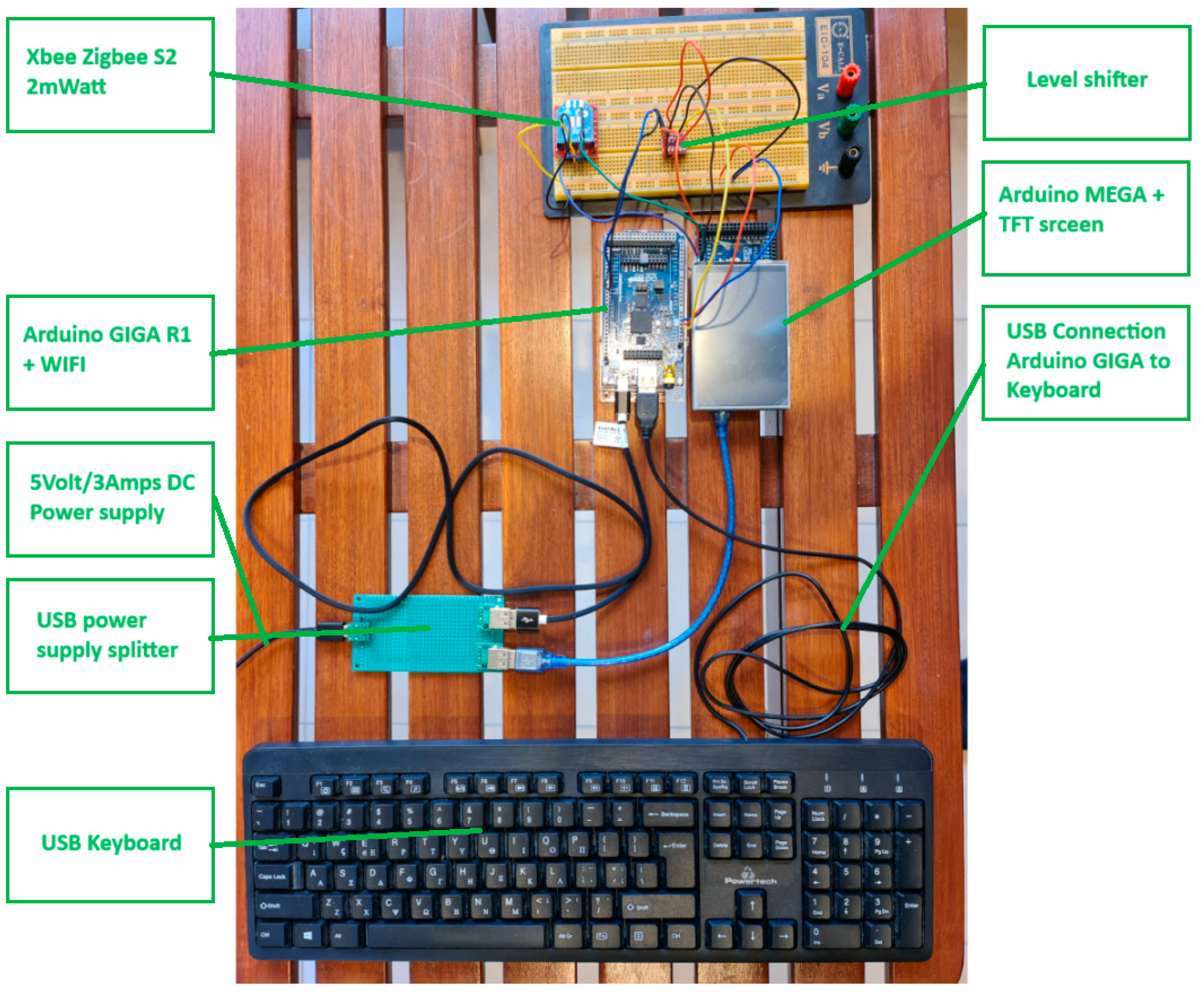
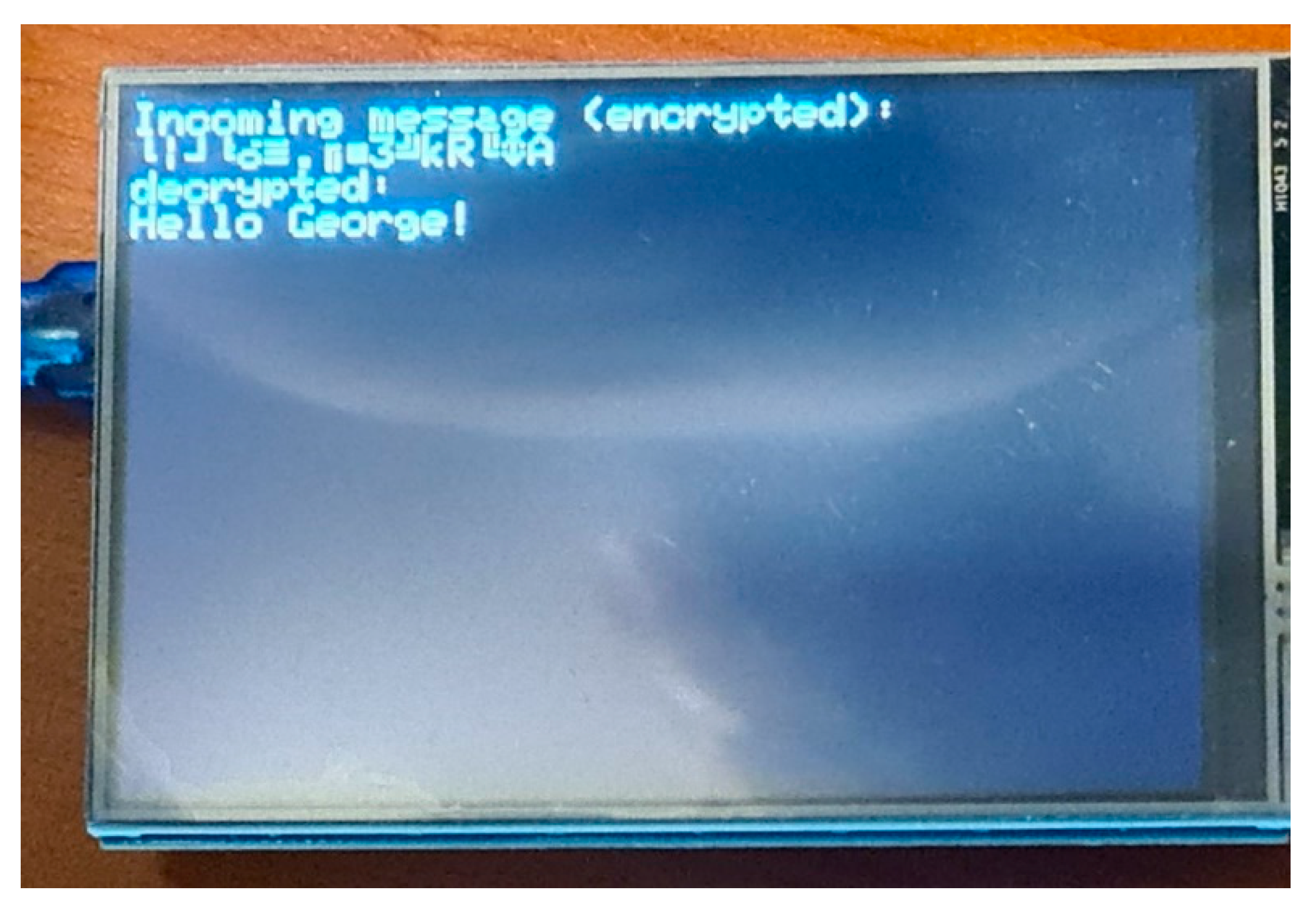
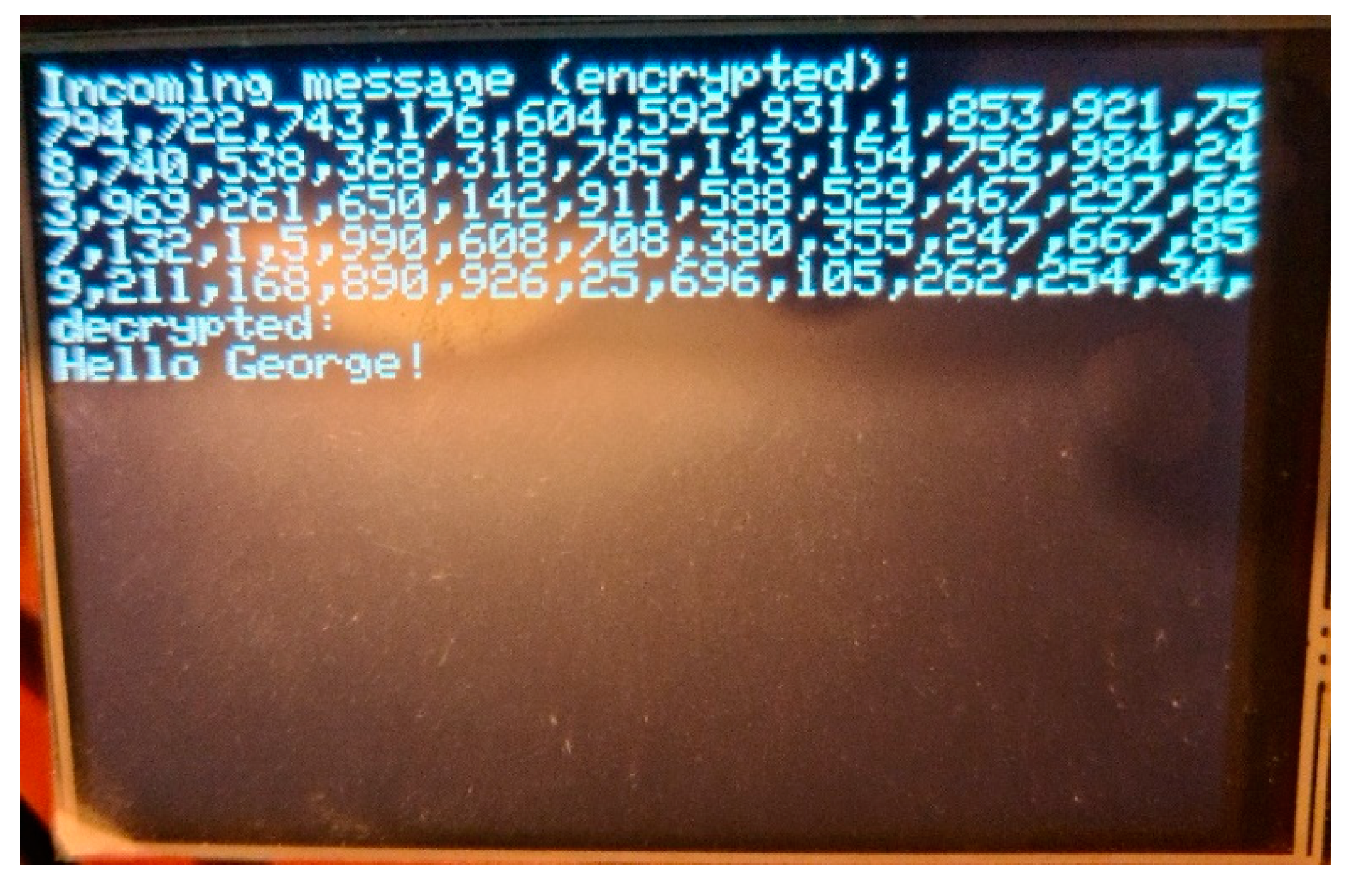
6.2. Presentation of the Message Encryption/Decryption Device

The experiments that took place they used 2 different algorithmic schemes. The first one was the AES and the second one was based on ECC transformed in order to encrypt and decrypt messages because ECC is not made initially to decrypt and encrypt text messages. The authors used the following github repositories: for AES: this AES library that suits Arduino8. and for ECC encryption/decryption of the messages the following library9.

An LCD 4” touch display shield, attached to the Arduino MEGA 2560 R3, and was used in order for the user to see the received messages and see the message they send. The characteristics of the display are the following10:

LCD Type: TFT
LCD Interface: SPI
LCD Controller: ILI9486
Touch Screen Type: Resistive
Touch Screen Controller: XPT2046
Colors: RGB, 65K colors
Resolution: 480x320 (Pixel)
Aspect Ratio: 8:5
I/O Voltage: 3.3 - 5V

So, the idea is that the user of each side picks an encryption key that have been shared with the other user in a safe channel, meaning that it could be shared in a for life conversation they had. Each user makes use of the same key in order to encrypt the messages they send to other side and decrypt the received messages in order to be able to read the plaintext.

We used Arduino GIGA R1, because it encompasses a USB interface, suitable for connecting the USB keyboard. The Arduino MEGA 2560 R3 is connected with the TFT screen, so that the users can see the received decrypted messages from the other side. Arduino MEGA 2560 R311 is a famous open-source solution for IoT experiments, using the ATmega2560 microcontroller. There is the capability of using the UART protocol it encompasses, and various I/O pins. Its 8-bit CPU is clocked at 16MHz.

Arduino GIGA R112 is an Arduino capable of doing IoT experiments which is significantly more powerful than the Arduino MEGA 2560. It uses the STM32H747XI dual Cortex-M7+M4 32bit low power Arm MCU clocked at 480Hz and 240 MHz respectively. It contains many I/O pins and many protocols (4 x UAR, 3 x I2C, 2 x SPI, CAN), 2Mbytes flash memory, and it operates at 3.3Volts both power and logic. The latter justifies the reason why a SparkFun Logic Level Converter - Bi-Directional 13was used in order for the two Arduino (MEGA 2560 and GIGA R1) to communicate between them. Arduino GIGA R1 was used, due to its USB interface, so that we could connect the USB keyboard to the device, in order to type messages.

A USB voltage splitter was used in order to supply with power the 2 Arduino, the voltage translator and the Xbee Zigbee S2 2mW. The Xbee Zigbee S2 2 mW 14(+3dBm) has a coverage of 120 meters at LoS. Zigbee protocol is a low-power solution for wireless data exchange at 250kbps maximum data rate. It operates at 3.3Volts@40mA. That’s why we need to use a voltage translator in order to be able to communicate with Arduino MEGA 2560 R3, that operates at 5 Volts. The whole construction was supplied by a 5Volts/3Amps DC power supply connected to the USB splitter inputs, as it is depicted in Figure 8 and Figure 9.

Figure 10 depicts the image of the one of the TFT screens while decrypting an incoming message, while using AES encryption protocol. While in Figure 11, one can observe the decrypting message when using the ECC scheme.

As far as the encryption/decryption times, we took some measurements, both for AES and ECC algorithmic schemes. Concerning AES scheme, the encryption time for message “Hello George!” took 1028 μsec and decryption time took 1292 μsec. As far as the ECC is concerned, for the message “Hello George!” the encryption took 3861 μsec or (3,861 microseconds) and the decryption took 1721 μsec (or 1,721 microseconds). Figure 12 show the print-screen from the terminal while encrypting and decrypting the message,

We used an oscilloscope in order to get the pulse-train of the plaintext (unencrypted message) (Figure 13) and the encrypted message (Figure 14), that is leaving Arduino MEGA 2560 R3 so that it can be fed to the Zigbee and transmitted wirelessly to the other end. As it is clear in Figure 13 that the pulse reaches 5 Volt. Of course, it is too difficult to catch the whole message because the pulse-train would be large to be fitted to the image. Also, the bit rate at which the Arduino receives or transmits messages it is fixed at 9600 bps on both mechanisms that were presented exhaustively in previous images.

Then we did the following: we used Arduino GIGA R1 in order to obtain the metrics, either using ECC or using AES. We did not connect the Arduino GIGA R1 to the mechanism that was presented before because the TFT screen could not be matched with the current Arduino. So, we just connect the Arduino GIGA R1 to the laptop in order to take the metrics via the Serial reading of the Arduino IDE platform. The encryption and decryption times for AES are depicted in Figure 15. Also, the times for encryption and decryption of the modified ECC are depicted in Figure 15. As it is observed the encryption time using AES and Arduino GIGA R1 took 34 μsec instead of 1028 μsec with Arduino MEGA 2560 R3. While the decryption time using the same cryptographic scheme and Arduino GIGA R1, took 50 μsec instead of 1292 μsec with Arduino MEGA 2560 R3. Again, by using ECC for encryption with Arduino GIGA R1 it took 3753 μsec instead of 3681 μsec with Arduino MEGA 2560 R3, whereas for the same cryptographic scheme for the decryption part and the Arduino GIGA R1 it took 2 μsec instead of 1721 μsec with Arduino MEGA 2560 R3. As it is more than clear Arduino GIGA R1 excels Arduino MEGA 2560 R3 in the most metrics concerning encryption/decryption for AES and ECC cryptographic schemes.

7. Conclusions and Plans for the Future

This paper introduced the usage of Hyperelliptic Curve Cryptography for enhancing privacy in IoV. This idea is quite new, as even though there are papers introducing various techniques on achieving IoV privacy, HECC has not been exploited yet. Series of experiments have been carried out in ns-3 simulator where an entire area of vehicles, RSUs and GLs had been established. The goal was to achieve the maximum privacy given various modelled attacks. The following cryptographic methods have been studied: ECC, HECC-2, HECC-3.

In this respect, several metrics have been measured to evaluate the proposed approach, such as the following: key-pair generation time, certificate public key generation, message decryption, message encryption, signature generation, signature verification, decoding, certificate private key reception, certificate generation, encoding. Additional evaluation metrics used include the size of the messages exchanged, the paper also studies the energy consumption for the message generation and exchange.

Moreover, the paper introduces an innovative approach for exchanging messages via Zigbee in the ISM (Industrial Scientific Medical) free band via the use of Arduino modules and appropriately constructed electronics. The proposed approach uses either AES or a modified version of ECC cryptographic methods. Evaluation metrics used also included the duration of encryption/decryption as far as the message exchange is concerned. The evaluation outcome indicates that AES is faster than the modified-ECC in decryption/encryption of messages in most of the metrics obtained, for both Arduino modules used.

The evaluation results indicate that in most of the metrics measured ECC demonstrates better results than HECC-2 and HECC-3. However, there are cases where HECC outperforms ECC, but they are limited. This occurs because ECC has been greatly improved the last years by the research community, and it delivers better results in most of the metrics. HECC on the other hand is not as mature and it is not optimized to run fast, although it uses smaller key sizes with respect to ECC for the same security level. Moreover, HECC includes involved the usage of very complex mathematics, and this is one reason why it is used less extensively than ECC. It is however expected, that if HECC is optimized in the future in C/C++ programming language or even in VHDL code, it will be able to demonstrate much better evaluation results, far better that ECC.

The proposed future extensions of the presented approach mainly focus on the improvement of the HECC performance. Initially their arithmetic can improve via the use of a modern library for modular arithmetic. The use of NTL 5.5, which is outdated, maybe produces delays in scalar multiplication. Moreover, it can be studied the use of special curves [17], in which have been proposed improvements in their arithmetic. It is concluded, that the best choice of the parameters can improve significantly the performance of HECC, as it is referred in the publication of Pelzl, Wollinger et.al. [18]. Apart from them, in case of the embedded systems, can also be used accelerators (such as FPGAs, ASICs) in real systems for improving their performance.

In addition, the choice of Hyperelliptic Curves in that specific scheme is limited by the existence of a general algorithm for coding messages targeting the curve. The algorithm [14] that was used is the most generalized algorithm that exists in literature and limits the choice of curve in specific curve families. It is important to study which of the family of curves is cryptographic appliable, meaning that they produce a class with an order “near” prime number. Because of this, fragmentation algorithms of points in Jacobian Hyperelliptic Curves can be used, in order to identify which are the most secure. Moreover, the generation of secure curves via the use of CM method will produce more choices of secure curves with known order, so that there could be used curves of the same security level and in signatures for better study and comparison.

Author Contributions

Conceptualization, G.R. and I.R.; methodology, G.R. and P.D.; software, P.D. and G.R.; validation, G.R., P.D. and I.R.; formal analysis, G.R. and P.D.; investigation, G.R. and P.D.; writing—original draft preparation, P.D. and G.R.; writing—review and editing, G.R. and I.R.; supervision, I.R.; project administration, I.R.; funding acquisition, I.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Azees, M.; Vijayakumar, P.; Deboarh, L.J. EAAP: Efficient anonymous authentication with conditional privacy-preserving scheme for vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2467–2476. [Google Scholar] [CrossRef]
Liu, Y.; Wang, Y.; Chang, G. Efficient privacy-preserving dual authentication and key agreement scheme for secure V2V communications in an IoV paradigm. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2740–2749. [Google Scholar] [CrossRef]
Jo, H.J.; Kim, I.S.; Lee, D.H. Reliable cooperative authentication for vehicular networks. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1065–1079. [Google Scholar] [CrossRef]
Mistareehi, H.; Islam, T.; Manivannan, D. A secure and distributed architecture for vehicular cloud. Internet Things 2021, 13, 100355. [Google Scholar] [CrossRef]
Baee, M.A.R.; Simpson, L.; Boyen, X.; Foo, E.; Pieprzyk, J. ALI: Anonymous lightweight inter-vehicle broadcast authentication with encryption. IEEE Trans. Dependable Secur. Comput. 2022. [Google Scholar]
Dua, A.; Kumar, N.; Das, A.K.; Susilo, W. Secure message communication protocol among vehicles in smart city. IEEE Trans. Veh. Technol. 2017; 67, 4359–4373. [Google Scholar]
Mistareehi, H.; Manivannan, D. A low-overhead message authentication and secure message dissemination scheme for vanets. Network 2022, 2, 139–152. [Google Scholar] [CrossRef]
Scheidler, R. An introduction to hyperelliptic curve arithmetic. 2015. [Google Scholar]
Alimoradi, R. A study of hyperelliptic curves in cryptography. Int. J. Comput. Netw. Inf. Secur. 2016, 8, 67. [Google Scholar] [CrossRef]
Bh, P.; Chandravathi, D.; Roja, P.P. Encoding and decoding of a message in the implementation of Elliptic Curve cryptography using Koblitz’s method. Int. J. Comput. Sci. Eng. 2010, 2, 1904–1907. [Google Scholar]
Campagna, M. SEC 4: Elliptic curve Qu-Vanstone implicit certificate scheme (ECQV). Standards for Efficient Cryptography, Version, 1. 2013. [Google Scholar]
Handbook of elliptic and hyperelliptic curve cryptography. Cohen, H.; Frey, G.; Avanzi, R.; Doche, C.; Lange, T.; Nguyen, K. and Vercauteren, F. (Eds.) CRC press: Boca Raton, FL, USA, 2005. [Google Scholar]
Gaudry, P.; Schost, É. Construction of secure random curves of genus 2 over prime fields. In Advances in Cryptology-EUROCRYPT 2004: International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2-6 May 2004; Proceedings 23 (pp. 239-256); Springer: Berlin/Heidelberg, Germany, 2 May 2004. [Google Scholar]
Seck, M.; Diarra, N. Unified Formulas for Some Deterministic Almost-Injective Encodings into Hyperelliptic Curves. Progress in Cryptology–AFRICACRYPT 2018: 10th International Conference on Cryptology in Africa, Marrakesh, Morocco, 7–9 May 2018; Proceedings 10 (pp. 183-202). Springer International Publishing: Berlin/Heidelberg, Germany, 7 May 2018. [Google Scholar]
Weng, A. A class of hyperelliptic CM-curves of genus three. J. -Ramanujan Math. Soc. 2001, 16, 339–372. [Google Scholar]
Hammod, D.N. June. Modified Lightweight AES based on Replacement Table and Chaotic System. In 2022 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA) (pp. 1-5). IEEE; 2022. [Google Scholar]
Pelzl, J.; Wollinger, T.; Paar, C. Special hyperelliptic curve cryptosystems of genus two: Efficient arithmetic and fast implementation. Embedded Cryptographic Hardware: Design and Security. 2004. [Google Scholar]
Pelzl, J.; Wollinger, T.; Guajardo, J.; Paar, C. Hyperelliptic curve cryptosystems: Closing the performance gap to elliptic curves (update). Cryptology ePrint Archive. 2003. [Google Scholar]

1	https://www.nsnam.org/about/what-is-ns-3/
2	https://en.wikipedia.org/wiki/ElGamal_encryption
3	https://neuromancer.sk/std/secg/secp256r1
4	https://libntl.org
5	https://en.wikipedia.org/wiki/Quadratic_residue
6	https://github.com/syncom/libg2hec/tree/master
7	https://github.com/syncom/libg2hec/tree/master
8	https://github.com/DavyLandman/AESLib
9	https://github.com/ShubhamAnnigeri/tinyECC-ArduinoIDE
10	https://grobotronics.com/display-4-touch-lcd-shield-for-arduino.html
11	https://store.arduino.cc/products/arduino-mega-2560-rev3
12	https://grobotronics.com/arduino-giga-r1-wifi.html?sl=en
13	https://www.sparkfun.com/products/12009
14	https://www.sparkfun.com/products/retired/10414

Figure 2. Group rule for the points of Elliptic Curve [8].

Figure 3. Hyperelliptic Curve of genus 2, with y2 = f(x) [8].

Figure 4. Duration of the various cryptographic operations (in ms).

Figure 5. Size of the messages exchanged during the ns-3 simulation (in Bytes).

Figure 6. Energy consumption in very small-time procedure.

Figure 7. Procedures’ energy consumption.

Figure 8. The various connections of the encryption/decryption device.

Figure 9. The entire construction for two users. Each side can receive and send messages to the other side which is encrypted and decrypted either via AES or ECC executed in Arduino MEGA 2560 R3 microcontroller.

Figure 10. Interface snapshot when a user receives a decrypted message in case the AES symmetric algorithmic scheme is used.

Figure 11. Interface snapshot when a user receives a decrypted message in case the ECC asymmetric algorithmic scheme is used.

Figure 12. Encryption and decryption times (in μsec) for Arduino MEGA 2560 R3 when either AES or modified-ECC cryptographic scheme is used.

Figure 13. The electrical signal of the plaintext message, as it is sent from the USB keyboard to the Arduino MEGA 2560, in order to be encrypted either by AES symmetric cryptographic scheme or the ECC asymmetric cryptographic scheme.

Figure 14. The electrical signal of the encrypted (by AES) message that is fed to the Zigbee (from the Arduino) in order to be then transmitted wirelessly by the Zigbee.

Figure 15. The encryption and decryption time in μsec of the message: “Hello George!” while using Arduino GIGA R1 when either AES or modified-ECC cryptographic scheme is used.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Enhancing Privacy in the Internet of Vehicles via Hyperelliptic Curve Cryptography

Abstract

1. Introduction

2. Related State of the Art

2.1. Authentication Schemes

2.2. Secure Message Dissemination

2.3. Secure Schemes That Distribute the Computational Load on the Network

3. Analysis of the ECC, HECC-2, HECC-3

3.1. Elliptic Curve Cryptography

3.2. Hyperelliptic Curve Cryptography for Genus ≥ 2

4. Proposed Approach

4.1. Tools & Software

4.2. Implementation of Cryptographic Techniques

4.3. Simulation of Road Traffic

4.4. Implementation of VANET Communication

4.5. Implementation of Energy Consumption Model

5. Experimental Evaluation

5.1. Duration of Cryptographic Operations

5.2. Size of Exchanged Messages

5.3. Energy Consumption

6. A Device for Message Encryption via Zigbee Network, Using AES or ECC

6.1. AES Cryptographic Protocol

6.2. Presentation of the Message Encryption/Decryption Device

7. Conclusions and Plans for the Future

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe