On the Sums over Inverse Powers of Zeroes of the Hurwitz Zeta-Function, and Some Related Properties of These Zeroes

Preprint

Article

On the Sums over Inverse Powers of Zeroes of the Hurwitz Zeta-Function, and Some Related Properties of These Zeroes

Altmetrics

Downloads

100

Views

Comments

Sekatski Serguei^*

This version is not peer-reviewed

Submitted:

31 December 2023

Posted:

02 January 2024

You are already at the latest version

Alerts

Abstract

Recently, we have applied the generalized Littlewood theorem concerning contour integrals of the logarithm of analytical function to find the sums over inverse powers of zeroes for the incomplete Gamma- and Riemann zeta- functions, polygamma functions, and elliptical functions. Here, the same theorem is applied to study such sums for the zeroes of the Hurwitz zeta-function , including the sum over the inverse first power of its appropriately defined non-trivial zeroes. We also study some related properties of the Hurwitz zeta-function zeroes. In particular, we show that for any natural N and small real epsilon, when z tends to n=0, -1, -2… we can find at least N zeroes of zeta in the - vicinity of 0 for sufficiently small epsilon, as well as one simple zero tending to 1, etc.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: 30E20; 30C15; 33B20; 33B99

1. Introduction

For any fixed complex

z \neq 0, - 1, - 2 \dots

, and Res>1, Hurwitz zeta – function is defined as

ζ (s, z) = \sum_{n = 0}^{\infty} \frac{1}{{(n + z)}^{s}}

(1)

and by analytic continuation for

Re s \leq 1

. The only one singularity of the function is the simple pole at s=1 with the residue one; see e.g. references [1,2,3,4,5] for the discussion of the main properties of this function. In practice, the following Hermite’s integral representation, valid for Rez>0 and

s \neq 1

is mostly used for such a continuation:

ζ (s, z) = \frac{1}{2} z^{- s} + \frac{z^{1 - s}}{s - 1} + 2 \int_{0}^{\infty} \frac{\sin (s \arctan (x / z))}{{(x^{2} + z^{2})}^{s / 2} (e^{2 π x} - 1)} d x,

(2)

and for Rez<0 the functional relation

ζ (s, z) = \frac{1}{z^{s}} + ζ (s, z + 1),

(3)

with its evident subsequent applications, like

ζ (s, z) = \frac{1}{z^{s}} + \frac{1}{{(z + 1)}^{s}} + ζ (s, z + 2)

, etc. are exploited.

The properties of the Hurwitz zeta-function were much studied due to its great importance in number theory and physics; for the latter see especially [6]. Of course, the question of the location of zeroes of Hurwitz zeta-function has also been much studied, which is not surprising given the celebrated Riemann hypothesis and the circumstance that

ζ (s, 1) = ζ (s)

. Probably the Theorem of Davenport and Heilbronn [7] remains the most interesting result here: they proved that for any rational or transcendent irrational

0 < z < 1

z \neq 1 / 2

, there are infinitely many zeroes of

ζ (s, z)

in any strip

1 < Re s (s, z) < 1 + ε

for any real positive

ε

; later on, the same was proven by Cassel for algebraic irrational z [8]. There are also a number of both analytic and numerical studies dealing with the (mainly real) zeroes of

ζ (s, z)

, see e.g. [9,10,11,12,13,14]. In particular, for real

0 < z \leq 1

, Spira [9] established the absence of zeroes to the right of

Re s \geq 1 + z

, the absence of zeroes for

| Im s | \geq 1

Re s < - 1

, and showed that for

| Im s | \leq 1

and

Re s \leq (- 4 x + 1 + 2 [1 - 2 x])

, the only zeroes are (analogues of) trivial zeroes, one in each interval

- 2 n - 4 x \pm 1

, n is an integer and

n \geq 1 - 2 x

. He also indicated the formula describing the number of zeroes of

ζ (s, z)

with

0 < Re s \leq T

N (z, T) = \frac{T}{2 π} \ln T - T (\frac{1 + \ln (2 π x)}{2 π}) + O (\ln T) .

(4)

(This relation was not explicitly proven by Spira; he limited himself with the statement that it can be proven by a method of Berndt [15]. The same formula was conjectured and tested numerically in [14]).

Nevertheless, despite these findings, the picture is far from being the fully clarified, so that the question concerning the sum over inverse powers of Hurwitz zeta-function zeroes seems remains quite actual. We study it, together with some related questions, in the present paper. Our method is mainly based on the generalized Littlewood theorem, and recently analogous studies were undertaken for the polygamma-, incomplete gamma- and Riemann zeta-functions [16], as well as elliptical functions [17]. These applications in itself follow our earlier applications to the Riemann zeta-function [18,19,20]; here we would like to underline that one of them has been highlighted in a recent Encyclopedia of mathematics entry [21]. By this reason, only very short discussion of the method itself is given below. All details can be found in the aforementioned papers, especially [16].

2. The generalized Littlewood theorem

The generalized Littlewood theorem concerning contour integrals of the logarithm of analytical function is stated as follows:

Theorem 1 (The Generalized Littlewood theorem).

Let C denote the rectangle bounded by the lines

x = X_{1}, x = X_{2}, y = Y_{1}, y = Y_{2}

where

X_{1} < X_{2}, Y_{1} < Y_{2}

and let f(z) be analytic and non-zero on C and meromorphic inside it, and let also g(z) be analytic on C and meromorphic inside it. Let F(z)=ln(f(z)) be the logarithm defined as follows: we start with a particular determination on

x = X_{2}

, and obtain the value at other points by continuous variation along y=const from

\ln (X_{2} + i y)

. If, however, this path would cross a zero or pole of f(z), we take F(z) to be

F (z \pm i 0)

according as to whether we approach the path from above or below. Let also

\tilde{F} (z) = \ln (f (z))

be the logarithm defined by continuous variation along any smooth curve fully lying inside the contour which avoids all poles and zeroes of f(z) and starts from the same particular determination on

x = X_{2}

. Suppose also that the poles and zeroes of the functions f(z), g(z) do not coincide.

Then

\int_{C} F (z) g (z) d z = 2 π i (\sum_{ρ_{g}} r e s (g (ρ_{g}) \cdot \tilde{F} (ρ_{g})) - \sum_{ρ_{f}^{0}} \int_{X_{1} + i Y_{ρ}^{0}}^{X_{ρ}^{0} + i Y_{ρ}^{0}} g (z) d z + \sum_{ρ_{f}^{p o l}} \int_{X_{1} + i Y_{ρ}^{p o l e}}^{X_{ρ}^{p o l e} + i Y_{ρ}^{p o l e}} g (z) d z)

(5)

where the sum is over all

ρ_{g}

which are poles of the function g(z) lying inside C, all

ρ_{f}^{0} = X_{ρ}^{0} + i Y_{ρ}^{0}

which are zeroes of the function f(z) both counted taking into account their multiplicities (that is the corresponding term is multiplied by m for a zero of the order m) and which lie inside C, and all

ρ_{f}^{p o l e} = X_{ρ}^{p o l e} + i Y_{ρ}^{p o l e}

which are poles of the function f(z) counted taking into account their multiplicities and which lie inside C. The assumption is that all relevant integrals on the right hand side of the equality exist.

Below, with the exception of the Section 4, we apply this Theorem for certain particular cases when the contour integral

\int_{C} F (z) g (z) d z

disappears (tends to zero) if the contour tends to infinity, that is when

X_{1}, Y_{1} \to - \infty, X_{2}, Y_{2} \to + \infty

. This means that eq. (1.1) takes the form

\sum_{ρ_{f}^{0}} \int_{- \infty + i Y_{ρ}^{0}}^{X_{ρ}^{0} + i Y_{ρ}^{0}} g (z) d z - \sum_{ρ_{f}^{p o l}} \int_{- \infty + i Y_{ρ}^{p o l e}}^{X_{ρ}^{p o l e} + i Y_{ρ}^{p o l e}} g (z) d z = \sum_{ρ_{g}}^{} r e s (g (ρ_{g}) \cdot F (ρ_{g})) .

(6)

3. Sums over inverse powers of zeroes for the Hurwitz zeta-function

3.1. General formulae

At the point s=1, the Hurwitz zeta-function possesses absolutely and uniformly converging Laurent expansion with the generalized Stieltjes constants [1,2,3,4,5]

γ_{n} (z) = \lim_{N \to \infty} (\sum_{k = 0}^{N} \frac{\ln^{n} (k + z)}{k + z} - \frac{\ln^{n + 1} (N + z)}{n + 1}) :

(7)

ζ (s, z) = \frac{1}{s - 1} + \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n!} γ_{n} (z) {(s - 1)}^{n} .

(8)

This expansion is evidently analogous to that of the Riemann zeta-function

ζ (s) = \frac{1}{s - 1} + \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n!} γ_{n} {(s - 1)}^{n}

. Here

γ_{0} : = γ

is Euler – Mascheroni constant.

Thus

(s - 1) ζ (s, z) = 1 - ψ (z) (s - 1) - γ_{1} (z) {(s - 1)}^{2} + \frac{1}{2} γ_{2} (z) {(s - 1)}^{3} + O ({(s - 1)}^{4}),

(9)

and this solves the problem of the sum of inverse powers of «zeroes minus one» in the same fashion as in our previous works [16,17]. We need just to add that the asymptotic of the Hurwitz zeta-function, similarly to the Riemann zeta-function, for large |s| is O(sln(s)) [1,2,3,4,5], so that we can use the generalized Littlewood theorem for

n \geq 3

Let us just a bit enlarge the scope of our elementary Lemma 1 from [16].

Lemma 1.

Let f(z) is be analytical function defined on the whole complex plane except possibly a countable set of points. Let also this function can be represented in some vicinity of the point z=0 by the Taylor expansion

f (z) = 1 + a_{1} z + a_{2} z^{2} + a_{3} z^{3} + a_{4} z^{4} + \dots

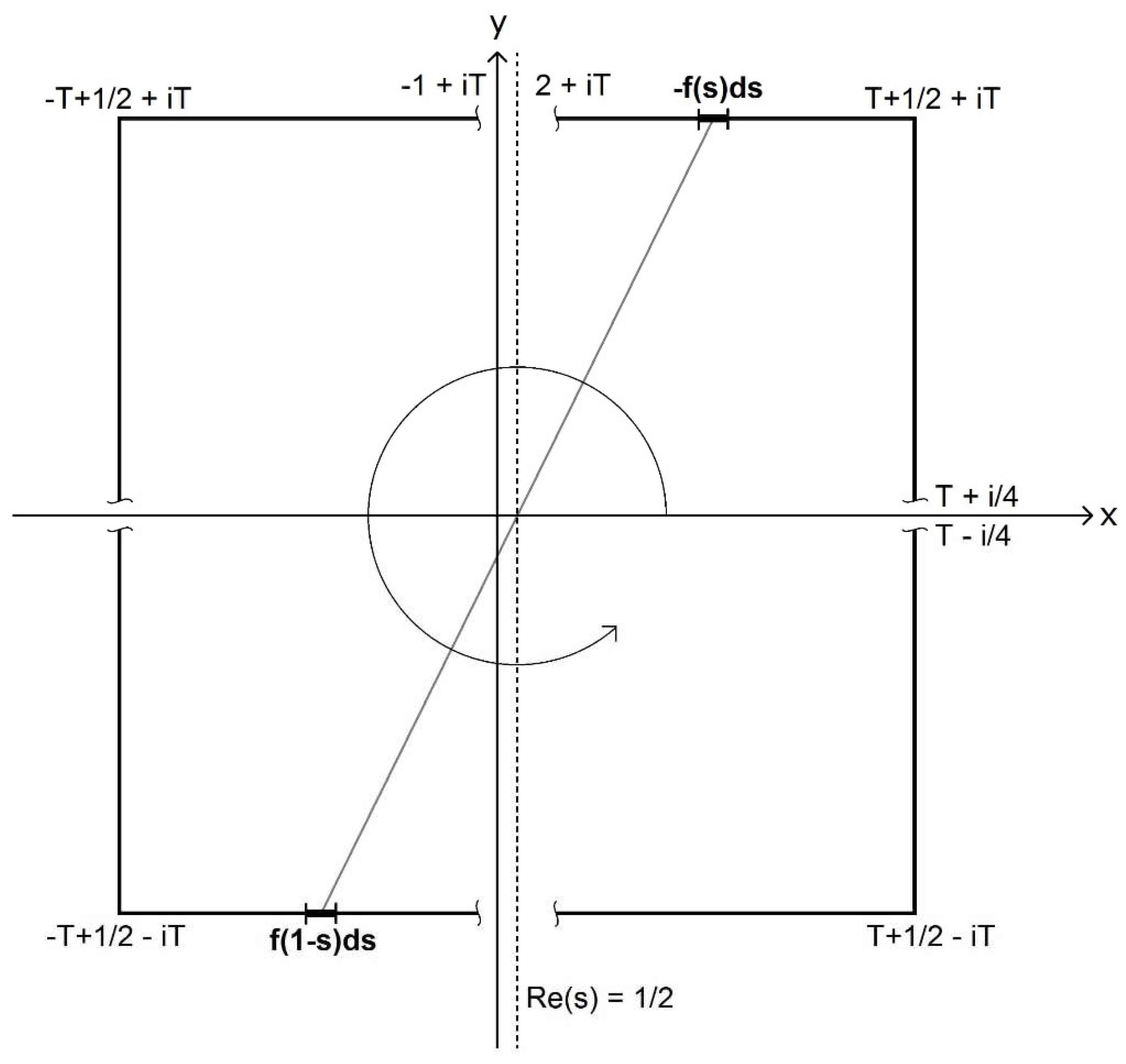
and contour integral

\int_{C} \frac{\ln (f (z))}{z^{3}} d z

tends to zero when contour C tends to infinity (see Theorem 1.1 for the details). Then for the sum over zeroes

ρ_{i, 0}

having order k_i and poles

ρ_{i, p o l e}

having order l_i of the function f(z), we have

\sum_{}^{} (\frac{k_{i}}{ρ_{i, 0}^{2}} - \frac{l_{i}}{ρ_{i, p o l e}^{2}}) = a_{1}^{2} - 2 a_{2},

(10)

\sum_{}^{} (\frac{k_{i}}{ρ_{i, 0}^{3}} - \frac{l_{i}}{ρ_{i, p o l e}^{3}}) = - a_{1}^{3} + 3 a_{1} a_{2} - 3 a_{3},

(11)

\sum_{}^{} (\frac{k_{i}}{ρ_{i, 0}^{4}} - \frac{l_{i}}{ρ_{i, p o l e}^{4}}) = a_{1}^{4} - 4 a_{1} a_{3} + 2 a_{2}^{2} - 4 a_{4} .

(12)

Proof:

We trivially have in some vicinity of the point z=0 the Taylor expansion

\ln (f (z)) = a_{1} z + (a_{2} - \frac{1}{2} a_{1}^{2}) z^{2} + (a_{3} - a_{1} a_{2} + \frac{1}{3} a_{1}^{3}) z^{3} + (a_{4} - \frac{1}{2} a_{2}^{2} + a_{1} a_{3} - \frac{1}{4} a_{1}^{4}) z^{4} + \dots

, and now the direct application of the Theorem 1 to the integrals

\int_{C} \frac{\ln (f (z))}{z^{n}} d z

with n=3, 4, 5 gives the statement of the lemma. □

Remark 1.

In such particular form, the Lemma is presented for the ease of application. Of course, this is possible to establish the difficult-to-use general relation between the coefficients of the Taylor expansions of the functions

f (z) = 1 + a_{1} z + a_{2} z^{2} + a_{3} z^{3} + a_{4} z^{4} + \dots

and

\ln (f (z)) = b_{1} z + b_{2} z^{2} + b_{3} z^{3} + b_{4} z^{4} + \dots

, and this actually has been done e.g. in [22]. For completeness, we reproduce here Lemma 2.1 from that work (given there for one particular function with the alternating signs in the Taylor expression, but this is not important. Note also the misprint in the formulation of the Lemma; the final formula in its proof is correct).

Lemma 2.

Let the function f(z) has the following Taylor expansion in the vicinity of z=0:

f (z) = 1 - \sum_{n = 1}^{\infty} a_{n} z^{n}

. Then

\ln (f (z)) = \sum_{n = 1}^{\infty} b_{n} z^{n}

where

b_{n} = - \sum_{j_{1} + 2 j_{2} + 3 j_{3} + \dots = n}^{} \frac{(j_{1} + j_{2} + j_{3} + \dots - 1)!}{j_{1}! j_{2}! j_{3}! \dots} a_{1}^{j_{1}} a_{2}^{j_{2}} a_{3}^{j_{3}} \dots

Proof.

\ln (f (z)) = - \sum_{m = 1}^{\infty} \frac{1}{m} {(\sum_{k = 1}^{\infty} a_{k} z^{k})}^{m} = - \sum_{m = 1}^{\infty} \frac{1}{m} \sum_{j_{1} + j_{2} + j_{3} + \dots = m}^{} \frac{m!}{j_{1}! j_{2}! \dots} z^{j_{1} + 2 j_{2} + 3 j_{3} + \dots} a_{1}^{j_{1}} a_{2}^{j_{2}} a_{3}^{j_{3}} \dots

= - \sum_{m = 1}^{\infty} \sum_{j_{1} + j_{2} + j_{3} + \dots = m}^{} \frac{(m - 1)!}{j_{1}! j_{2}! \dots} z^{j_{1} + 2 j_{2} + 3 j_{3} + \dots} a_{1}^{j_{1}} a_{2}^{j_{2}} a_{3}^{j_{3}} \dots

= - \sum_{n = 1}^{\infty} z^{n} \sum_{j_{1} + 2 j_{2} + 3 j_{3} + \dots = n}^{} \frac{(j_{1} + j_{2} + j_{3} + \dots - 1)!}{j_{1}! j_{2}! j_{3}! \dots} a_{1}^{j_{1}} a_{2}^{j_{2}} a_{3}^{j_{3}} \dots

□

Using Lemma 1 and just substituting the appropriate values of a_i into it, we obtain:

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{2}} = ψ^{2} (z) + 2 γ_{1} (z),

(13)

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{3}} = ψ^{3} (z) + 3 ψ (z) γ_{1} (z) - \frac{3}{2} γ_{2} (z),

(14)

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{4}} = ψ^{4} (z) + 2 ψ (z) γ_{2} (z) + 2 γ_{1}^{2} (z) + \frac{2}{3} γ_{3} (z) .

(15)

Here we substitute

γ_{0} (z) = - ψ (z)

[1,2,3,4,5], where

ψ (z)

is digamma function, see e.g. [3,4,5] for discussion of this function.

To find the sums

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{2}}

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{3}}

, etc. we also use our standard approach to write, if

z \neq 1 / 2;_{} 0, - 1, - 2, - 3 \dots

\frac{ζ (s, z)}{ζ (0, z)} = 1 + \frac{1}{ζ (0, z)} ζ' (0, z) s + \frac{1}{2 ζ (0, z)} ζ'' (0, z) s^{2} + \frac{1}{6 ζ (0, z)} ζ''' (0, z) s^{3} + O (s^{4})

(++)

(all derivatives in the paper are over the variable s), whence by the Lemma 1

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{2}} = 1 + \frac{{[\ln Γ (z) - \frac{1}{2} \ln 2 π]}^{2}}{{(1 / 2 - z)}^{2}} - \frac{ζ'' (0, z)}{1 / 2 - z},

(16)

\begin{array}{l} \sum_{z e r o e s_{} o f_{} ζ (0, z)} \frac{k_{i}}{ρ_{i}^{3}} = 1 - \frac{1}{{(1 / 2 - z)}^{3}} {(\ln Γ (z) - \ln 2 π)}^{3} + \frac{3}{2 {(1 / 2 - z)}^{2}} (\ln Γ (z) - \ln 2 π) ζ'' (0, z) \\ - \frac{1}{2 (1 / 2 - z)} ζ''' (0, z) \end{array},

(17)

\begin{array}{l} \sum_{z e r o e s_{} o f_{} ζ (0, z)}^{} \frac{k_{i}}{ρ_{i}^{4}} = 1 + \frac{1}{{(1 / 2 - z)}^{4}} {(\ln Γ (z) - \ln 2 π)}^{4} - \frac{2}{3 {(1 / 2 - z)}^{3}} (\ln Γ (z) - \ln 2 π) ζ''' (0, z) \\ + \frac{1}{2 {(1 / 2 - z)}^{2}} {[ζ'' (0, z)]}^{2} - \frac{ζ'''' (0, z)}{6 (1 / 2 - z)} \end{array},

(18)

Here we used the relations [1,2,3,4,5]

ζ (0, z) = \frac{1}{2} - z

(19)

and

ζ' (0, z) = \ln Γ (z) - \frac{1}{2} \ln 2 π,

(20)

readily following from the integral representation (1) and the second Binet’s integral formula

\ln Γ (z) = (z - 1 / 2) \ln z + \frac{1}{2} \ln (2 π) + 2 \int_{0}^{\infty} \frac{\arctan (x / z)}{e^{2 π x} - 1} d x

[3,4,5] for Rez>0. In these equations, 1 is the contribution of the simple pole at s=1.

Similarly, for any

p \neq 1

we have

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}} = \frac{1}{{(1 - p)}^{2}} + \frac{{[ζ' (s, z) |_{s = p}]}^{2}}{ζ^{2} (p, z)} - \frac{ζ'' (s, z) |_{s = p}}{ζ (p, z)},

(21)

provided

ζ (p, z) \neq 0

and

z \neq 0, - 1, - 2, - 3 \dots

, and analogously for the sums over larger inverse powers.

3.2. Behavior of the s-zeroes when z tends to infinity

The behavior of the sums over inverse powers of zeroes of the Hurwitz zeta-function when z tends to infinity is trivial and not interesting: all such sums tend to zero.

We know that for any

s \neq 1

z \to \infty

in the sector

\arg (z) \leq π - δ

with an arbitrary small positive fixed

δ

the following asymptotic holds [1,2]:

ζ (s, z) \sim \frac{z^{1 - s}}{s - 1} + \frac{1}{2} z^{- s} + \sum_{k = 1}^{\infty} \frac{B_{2 k}}{(2 k)!} {(s)}_{2 k - 1} z^{1 - s - 2 k} .

(22)

Here B_2k are Bernoulli numbers and Pochhammer symbol notation is employed. Corresponding asymptotics of the Hurwitz zeta-function derivatives were also much studied, see e.g. [23,24,25], with the main conclusion that the “naïve” differentiation of (22) suffices. Substitution of these asymptotics to (21) shows that for

z \to \infty

in the sector

\arg (z) \leq π - δ

with an arbitrary small positive fixed

δ

and any

p \neq 1

, the sum

\sum_{\begin{array}{l} z e r o e s_{} o f_{} s, \\ ζ (s, z) \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}}

tends to zero for any such p such that

ρ_{i} \neq p

The following technical details might be useful. We have

ζ' (s, z) \sim - \frac{\ln z \cdot z^{1 - s}}{s - 1} - \frac{z^{1 - s}}{{(s - 1)}^{2}} + o (z^{1 - s})

ζ'' (s, z) \sim \frac{\ln^{2} z \cdot z^{1 - s}}{s - 1} + \frac{2 \ln z \cdot z^{1 - s}}{{(s - 1)}^{2}} + \frac{2 z^{1 - s}}{{(s - 1)}^{3}} + o (z^{1 - s})

{(ζ' (s, z) / ζ (s, z))}^{2} \sim \ln^{2} z + \frac{2 \ln z}{s - 1} + \frac{1}{{(s - 1)}^{2}} + o (1)

;

ζ'' (s, z) / ζ (s, z) \sim \ln^{2} z + \frac{2 \ln z}{s - 1} + \frac{2}{{(s - 1)}^{2}} + o (1)

, and thus we have proven our statement for n=2. But indeed, the statement that all

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{n}}

n \geq 2

, for the Hurwitz zeta-function tend to zero for any p not equal to one or zero when z tends to infinity, follows just from the circumstance that the used “asymptotic function”

\frac{z^{1 - s}}{s - 1}

has no zeroes (and one simple pole at s=1), there is nothing to prove and study. (If we consider two terms of the asymptotic development, we do obtain one zero at s=1-2z, where

\frac{z^{1 - s}}{s - 1} + \frac{1}{2} z^{- s} = 0

- but clearly for any p,

\frac{1}{{(1 - 2 z - p)}^{n}} \to 0

when |z| tends to infinity, etc.).

For p=1 we have the same picture of disappearance of the sums provided the simple pole at z=1 is removed, see formulae (13 – 15). For n=2 we can illustrate this applying the known asymptotics

ψ (z) \sim \ln z + O (1 / z)

[3,4,5] and

γ_{1} (z) \sim - \frac{1}{2} \ln^{2} z + O (\ln z / z)

[26] when

z \to \infty

in the sector

\arg (z) \leq π - δ

with an arbitrary small positive fixed

δ

. We are unaware of the studies of the corresponding asymptotics for larger Stieltjes constants. They can be inferred from the requirement that the sum at question tends to zero. For example, from (17) we have

γ_{2} (z) \sim - \frac{1}{3} \ln^{3} z + o (\ln^{3} z)

This asymptotic behavior merely reflects the fact that there is no small in module s-zeroes when z tends to infinity except possibly the case of large by module negative real z, where the question should be studied separately.

3.3. Behavior of the s-zeroes when z tends to zero

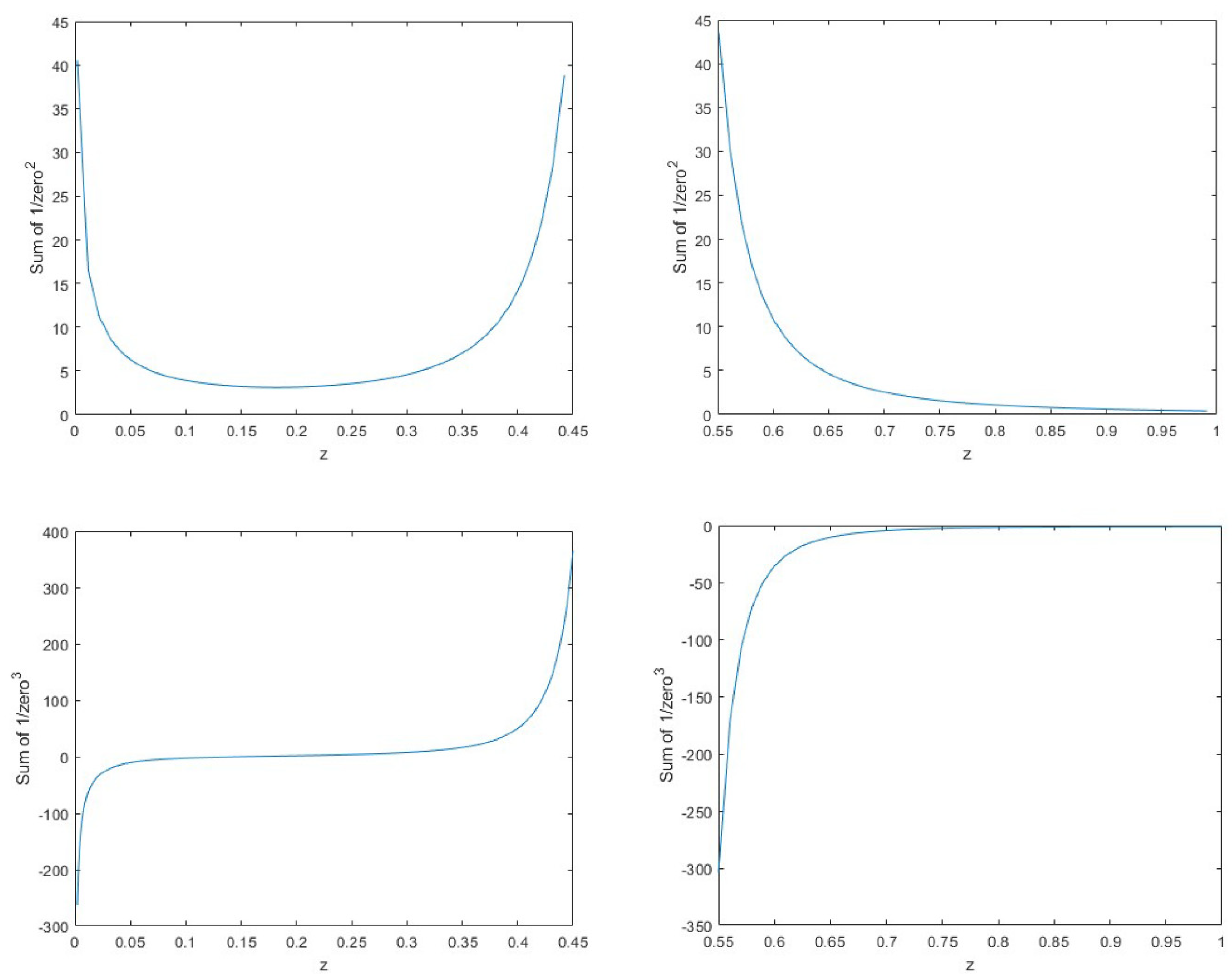
Quite the contrary, the behavior of the sums over inverse powers of zeroes (that is, of course, also the behavior of the zeroes themselves) is interesting and complicated when z tends to zero. Let us start with the analysis of

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{2}}

We know [3,4,5]

Γ (z) = \frac{1}{z} - γ + O (z)

. From

ζ^{(k)} (0, 1) = ζ^{(k)} (0) = O (1)

and

ζ (s, z) = \frac{1}{z^{s}} + ζ (s, z + 1)

, we have for small z

ζ^{(k)} (0, z) = {(- 1)}^{k} \ln^{k} z + ζ^{(k)} (0) + O (z)

(23)

(In particular, from (20)

ζ' (0, z) = - \ln z - \frac{1}{2} \ln 2 π - γ z + O (z^{2})

. Sf. also the paper of Deniger who showed that for real positive z,

ζ'' (0, z) = ζ'' (0) + γ_{1} z + \ln^{2} z + \sum_{n = 1}^{\infty} (\ln^{2} (z + n) - \ln^{2} n - 2 z \frac{\ln n}{n})

, the series converges absolutely and uniformly on any compact subset of R⁺ [27], and the result is analytically continued to all z except z=0, - 1, -2…). Thus from (23) it immediately follows that when

z \to 0

{(\ln Γ (z) - \frac{1}{2} \ln (2 π))}^{2} = \ln^{2} z + \ln (2 π) \cdot \ln z + \frac{1}{4} \ln^{2} (2 π) + O (z)

ζ'' (z) = \ln^{2} z + ζ'' (0) + O (z)

and thus the asymptotic of

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{2}}

with the O(z) precision is

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{2}} =

2 \ln^{2} z + 4 \ln (2 π) \cdot \ln z + 1 + \ln^{2} (2 π) - 2 ζ'' (0) + O (z)

. For completeness, we present the value of

ζ'' (0)

here (see e.g. [27]):

ζ'' (0) = \frac{1}{2} (- \ln^{2} 2 π - \frac{π^{2}}{12} + γ^{2} + γ_{1}) ≃ - 2.006

. Thus

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{2}} = 2 \ln^{2} z + 4 \ln (2 π) \cdot \ln z + 1 + 2 \ln^{2} (2 π) + \frac{π^{2}}{6} - 2 γ^{2} - 2 γ_{1} + O (z) .

(24)

Certainly, this sum tends to the plus infinity so attesting the presence of s-zeroes tending to zero when

z \to 0

We have

ζ (s, z) = z^{- s} + ζ (s, 1 + z)

thus s-zeroes of

ζ (s, z)

are the solutions of the equation

z^{- s} = - ζ (s, 1 + z)

. In the first approximation, the “asymptotic equation” is

z^{- s} = \frac{1}{2}

whose solutions are

s = - \frac{\ln 2}{\ln (1 / z)} + \frac{2 π i n}{\ln (1 / z)}

, n is an arbitrary integer. The next approximation is given by

\exp (- \ln z (\frac{\ln 2}{\ln z} + δ s)) = \frac{1}{2} + \frac{1}{2} \ln 2 π \cdot \frac{\ln 2}{\ln z}

, so that

s_{0} = \frac{\ln 2}{\ln z} - \frac{\ln 2 π \cdot \ln 2}{\ln^{2} z} + o (\frac{1}{\ln^{2} z})

, and similarly for all complex solutions:

\exp (- \ln z (\frac{\ln 2}{\ln z} + δ s)) = \frac{1}{2} + \frac{1}{2} \ln 2 π \cdot (\frac{\ln 2}{\ln z} + \frac{2 n π i}{\ln z})

thus

s_{n} = \frac{\ln 2}{\ln z} - \frac{\ln 2 π \cdot \ln 2}{\ln^{2} z} + \frac{2 n π i}{\ln z} - \frac{2 n π i \cdot \ln 2 π}{\ln^{2} z} + o (\frac{1}{\ln^{2} z})

(25)

Here we used

ζ' (0) = - \frac{1}{2} \ln 2 π

. Of course, such series in the inverse powers of the logarithm converges extremely slowly. This is also clear that not all n, but only their finite number, are indeed the solutions for any concrete finite z.

To enrich our consideration, we invoke the Rouché’s theorem about zeroes of the sums of analytical functions, see e.g. [28]. The searched zeroes of the function

ζ (s, z) = z^{- s} + ζ (s, 1 + z)

can be seen as zeroes of the sum of the two functions:

ζ (s, z) = f (s, z) + g (s, z)

with

f (s, z) = z^{- s} - 1 / 2

and

g (s, z) = 1 / 2 + ζ (s, 1 + z)

, both holomorphic in the region |s|<1 (remind that we are working with the function of s here; z is just some complex number).

Theorem 2.

For an arbitrary large positive integer N and arbitrary small real

ε

, we can find such real value of

z_{0} (N, ε)

that the function

ζ (s, z)

with

| z | \leq z_{0}

has at least N zeroes in the area

| s | < ε

Proof.

Let

0 < | z | \leq 3 / 4

, say (with the upper limit we avoid the non-existence of the function

ζ (s, z)

for z=-1), and consider the following close area D: circle with its interior defined as

| s | \leq 1 - δ

for an arbitrary small fixed positive

δ < 1

. (The most interesting case is, of course,

| s | \leq ε

with an arbitrary small fixed positive

ε

). We evidently can select the (possibly with the very small module) value of z such that

i): there are no zeroes of the function $f (s, z) = z^{- s} - 1 / 2$ on $\partial D$ (i.e. on the circle $| s | = 1 - δ$ ; trivial), and
ii): on $\partial D$ $| f (s, z) | > | g (s, z |$ - because the module of $g (s, z) = 1 / 2 + ζ (s, 1 + z)$ is

bounded there (albeit can be very large when

δ

is small due to the presence of the pole at s=1) while

| z^{- s} |

is not.

Thus the Rouché’s theorem states that inside D the function

ζ (s, z)

has the same number of zeroes, taking into account their orders, as the function

f (s, z)

. The zeroes of the latter were described above. Taking smaller and smaller values of |z| we will get larger and larger numbers of zeroes of

ζ (s, z)

lying in D. □

The existence of such close to 0 s-zeroes is, in a sense, “predicted” by the counting formula (4), which states that the number of zeroes of

ζ (s, z)

logarithmically tends to infinity when

z \to 0

for any finite T. Note that the main asymptotic term of the sum (24) is exactly the sum of zeroes over the inverse squares of the solutions of the “asymptotic” equation

z^{- s} = \frac{1}{2}

, viz.

s = - \frac{\ln 2}{\ln (1 / z)} + \frac{2 π i n}{\ln (1 / z)}

. This case has been already considered by us for the roots of the equation

e^{z} = a

in [16], so we will not include its evident slight generalization here again and limit ourselves with the following remark.

Remark 2.

The application of the generalized Littlewood theorem to zeroes of

f (z) = e^{b z} - a = 0

, having for

a \neq 1

the Taylor expansion

\frac{f (z)}{1 - a} = 1 + \frac{b}{1 - a} z + \frac{b^{2}}{2 (1 - a)} z^{2} + O (z^{3})

, immediately gives

\sum_{}^{} \frac{k_{i}}{ρ_{i}^{2}} = \frac{b^{2}}{{(1 - a)}^{2}} - \frac{b^{2}}{1 - a}

- this can be written knowing nothing about the exact values of zeroes. Actually we know that they all are simple (and equal to

ρ_{n} = \frac{\ln a}{b} + \frac{2 π i n}{b}

provided

a \neq 0

, otherwise there are no zeroes) hence k_i can be omitted. If a=1 and

b \neq 0

, we have

\frac{f (z)}{b z} = 1 + \frac{1}{2} b z + \frac{1}{6} b^{2} z^{2} + \frac{1}{24} b^{3} z^{3} + \frac{1}{120} b^{4} z^{4} + O (z^{5})

thus

\sum_{}^{}' \frac{1}{ρ_{i}^{2}} = \frac{b^{2}}{4} - \frac{b^{2}}{3} = - \frac{b^{2}}{12}

. Here as usual the prime sign in the sum means that the value z=0 should be omitted during the summing. This is simply the statement

\sum_{n = - \infty}^{n = \infty} \frac{b^{2}}{{(2 π n i)}^{2}} = - \frac{b^{2}}{12}

(Basel problem solution). Quite similarly, exploiting eq. (12), we can establish

ζ (4) = \frac{π^{4}}{90}

[29], etc.

Just for curiosity, we can find the sum over the inverse second powers of the roots

ρ_{i}

of the equation

f (z) : = \exp (b z) - 1 - b z = 0

. We have

\frac{2 f (z)}{b^{2} z^{2}} = 1 + \frac{1}{3} b z + \frac{1}{12} b^{2} z^{2} + O (z^{3})

whence

\sum_{}^{}' \frac{1}{ρ_{i}^{2}} = \frac{b^{2}}{9} - \frac{b^{2}}{6} = - \frac{b^{2}}{18}

(can this be named “the general Basel problem”?). See also the discussion of the general problem concerning the sums over inverse powers of roots of the equation

f (z) = a

in [16].

In addition to those described above, there are also other s-zeroes of

ζ (s, z)

when z tends to zero, including that close to 1 (it is discussed below), zeroes with Res>1, which existence was proven by Davenport - Heilbronn [7] and Cassel [8], and infinitely many zeroes in the critical strip

0 \leq Re s \leq 1

, where the function

ζ (s)

is unbounded. There are also zeroes close to the trivial zeroes of the Riemann zeta-function lying at s=-2, -4, -6… To find such a zero at

s = - 2 k + δ

with small

| δ |

, we have the equation

ζ (- 2 k + δ, z) = z^{2 k - δ} + ζ (- 2 k + δ, 1 + z) = 0

, which solution is

δ \sim - \frac{z^{2 k}}{ζ' (2 k)}

, i.e.

s \sim - 2 k - \frac{z^{2 k}}{ζ' (2 k)} .

(26)

For the completeness, let us remind that

ζ' (- 2 k) = \frac{{(- 1)}^{k} ζ (2 k + 1) (2 k)!}{2^{2 k + 1} π^{2 k}}

[29].

The following simple proposition holds.

Proposition 1.

For any p with Rep<0 and p not equal to -2, -4-, -6… as well as any zero of

ζ (s, z)

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}} = \frac{1}{{(1 - p)}^{2}} + \frac{{[ζ' (p)]}^{2}}{ζ^{2} (p)} - \frac{ζ'' (p)}{ζ (p)} + O (z^{- Re p} \ln^{2} z) .

(27)

For any p with

Re p > 0

, and p not equal to 1 as well as any zero of

ζ (s, z)

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}} = \frac{1}{{(1 - p)}^{2}} + O (z^{Re p}) .

(28)

Proof.

From (21), we see, from

ζ (p, z) = \frac{1}{z^{p}} + ζ (p) + O (z)

, that in the vicinity of z=0 for p not equal to one,

ζ' (p, z) = - \frac{\ln z}{z^{p}} + ζ' (p) + O (z)

and

ζ'' (p, z) = \frac{\ln^{2} z}{z^{p}} + ζ'' (p) + O (z)

. Thus if Rep<0 and

p \neq - 2, - 4, - 6 \dots

, as well as any zero of

ζ (s, z)

, there is no peculiarities in the sum:

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}} = \frac{1}{{(1 - p)}^{2}} + \frac{{[ζ' (p)]}^{2}}{ζ^{2} (p)} - \frac{ζ'' (p)}{ζ (p)} + O (z^{- Re p} \ln^{2} z)

Re p > 0

p \neq 1

, as well as any zero of

ζ (s, z)

, asymptotically we have

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}} = \frac{1}{{(1 - p)}^{2}} + {(\frac{z^{- p} \ln z + ζ' (1 + z)}{z^{- p} + ζ (p, 1 + z)})}^{2} - \frac{z^{- p} \ln^{2} p + ζ'' (p, 1 + z)}{z^{- p} + ζ (p, 1 + z)} =

\frac{1}{{(1 - p)}^{2}} + {(\frac{\ln z + z^{p} ζ' (1 + z)}{1 + z^{p} ζ (p, 1 + z)})}^{2} - \frac{\ln^{2} p + z^{p} ζ'' (p, 1 + z)}{1 + z^{p} ζ (p, 1 + z)} =

\frac{1}{{(1 - p)}^{2}} + O (z^{Re p})

. □

Similar statements hold for larger powers of zeroes in the sums.

If p=1, we need to use formulae (13 – 15) and their analogues for larger n. For

z \to 0

the sum

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{2}} = ψ^{2} (z) + 2 γ_{1} (z)

becomes infinitely large attesting the presence of zero close to s=1 for the case. The asymptotics are well known:

ψ (z) = - \frac{1}{z} + O (1)

[3,4,5], while for the

γ_{1} (z)

we use the functional equation

γ_{1} (z) = γ_{1} (z + 1) - \frac{\ln z}{z}

(following again from

ζ (s, z) = \frac{1}{z^{s}} + ζ (s, z + 1)

) and

γ_{1} (1 + z) = O (1)

to write

γ_{1} (z) = - \frac{\ln z}{z} + O (1)

. Similarly,

γ_{l} (z) = \frac{{(- 1)}^{l} \ln^{l} z}{z} + γ_{l}

. Thus

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{2}} \sim \frac{1}{z^{2}} - 2 \frac{\ln z}{z} + O (1)

, so that we can deduce the existence of a zero at

s = 1 - z + z^{2} \ln z + O (z^{2})

when

z \to 0

. Asymptotics of all subsequent sums

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{n}}

are quite consistent with the existence of such single s-zero when z tends to zero.

Again, using Rouché’s theorem we can show that this zero is isolated and simple. Stronger versions of the theorem below can be proven, but for our purposes the following one seems enough.

Theorem 3.

For any z, such that

| z | > 0

and

| z | \leq 0.01

, say, the circle with its interior D

| s - 1 | \leq 0.1

contains only one simple s-zero of the Hurwitz zeta-function

ζ (s, z)

. This zero approaches 1 as

s = 1 - z + z^{2} \ln z + O (z^{2})

when z approaches zero.

Proof.

The consideration is with the holomorphic on the whole complex plane function

δ \cdot ζ (1 + δ, z)

, where

δ = s - 1

. We write

δ \cdot ζ (1 + δ, z) = f (δ) + g (δ)

with

f (δ) = \frac{δ}{z^{1 + δ}} + 1

and

g (δ) = δ ζ (1 + δ, 1 + z) - 1

. The numerical analysis readily shows that in the chosen area of s, z,

| g (δ) | = | δ ζ (1 + δ, 1 + z) - 1 | < 1

. It is also clear that the chosen circle D contains only one simple zero of the function f(s) (there exists only one simple solution of

δ = - z^{1 + δ}

) – viz., that which approaches 1 as

s = 1 - z + z^{2} \ln z + O (z^{2})

when z approaches zero. Finally, on the

\partial D

| f (δ) | = | \frac{δ}{z^{1 + δ}} + 1 | \geq | \frac{δ}{z^{1 + δ}} | - 1 \geq \frac{0.1}{{0.01}^{1 - 0.1}} - 1 > 5 > | g (δ) | . □

For small real positive z the existence of single simple zero tending to 1 as 1-z+z²lnz+O(z²) has been proven by Endo & Suzuki [10]. Note that for such z, Res<1 hence the series representation (1) cannot be used to search for its value.

3.4. Behavior of the s-zeroes when z tends to -n

Quite analogously, the sums over inverse powers of zeroes becomes infinitely large when

z \to - n

for any non-negative n, see (16 - 18). Again, from

ζ^{(k)} (0, 1) = O (1)

and

ζ (s, z) = \frac{1}{z^{s}} + ζ (s, z + 1)

, that is

ζ^{(k)} (s, z) = \frac{{(- 1)}^{k} \ln^{k} z}{z^{s}} + ζ^{(k)} (s, z + 1)

, we have by induction

(

ζ (s, z - n) = \frac{1}{{(z - n)}^{s}} + \frac{1}{{(z - n + 1)}^{s}} + \dots + \frac{1}{{(z - 1)}^{s}} + \frac{1}{z^{s}} + ζ (s, z + 1)

, etc.) that for any –n:

ζ^{(k)} (0, - n + z) = {(- 1)}^{k} \ln^{k} z + O (1)

. We have from (16) that for

s, δ \to 0

\sum_{z e r o e s_{} o f_{} ζ (s, - n + δ)}^{} \frac{k_{i}}{ρ_{i}^{2}} = 1 + \frac{\ln^{2} δ}{{(1 / 2 + n)}^{2}} - \frac{\ln^{2} δ}{1 / 2 + n} + o (\ln^{2} δ)

- the sum which again reflects the presence of s-zeroes tending to 0. And indeed we have for

z \to - n

n \geq 1

, the following “asymptotic equation”:

ζ (- n + δ) \sim n + δ^{- s} - \frac{1}{2} = 0

hence

δ^{- s} = - n + \frac{1}{2}

, which solutions are

s = \frac{\ln (- n + 1 / 2)}{\ln (1 / δ)} + \frac{(2 n + 1) π i}{\ln (1 / δ)} + O (\frac{1}{\ln^{2} δ})

, sf. the corresponding discussion for the case

z \to 0

. Note that when

n \neq 0

, we do not have real solutions any more, all zeroes are complex, and that the real part of the corresponding solutions for

n \geq 2

is positive contrary to the cases n=0, 1.

Quite similarly, when

z \to - n

for any non-negative n we have

ψ (- n + z) = - \frac{1}{z} + O (1)

and

γ_{l} (- n + z) = \frac{{(- 1)}^{l} \ln^{l} z}{z} + O (1)

and thus the same zero

s = 1 - δ + δ^{2} \ln δ + O (δ^{2})

also exists for the case. Also similarly to the case n=0, for

Re p > 0

p \neq 1

, asymptotically we have

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to - n \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{m}} \sim \frac{1}{{(1 - p)}^{m}}

. But when

z \to - n

, analogues of the simple zeroes, of course, do not lye any more in the close vicinity of s=-2, -4, -6.

Remark 3.

1. Using the Rouché’s Theorem, the theorems analogous to those two of the previous sub-section can be easily proven when

z \to - n

for any non-negative n either.

2. Note, that for the s-zero tending to 1 as 1-z+z²lnz+O(z²), existing when

z \to 0

, the sums

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0,_{} - 1,_{} - 2,_{} - 3 \dots \end{array}}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{n}}

for all

n \geq 2

are, of course, consistent with the only one such s-zero. Quite the contrary, for the s-zeroes tending to 0 when

z \to 0

, the sums

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0,_{} - 1,_{} - 2,_{} - 3 \dots \end{array}}^{} \frac{k_{i}}{ρ_{i}^{n}}

are inconsistent with the only one, or even some finite number of zeroes. For example, from

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{2}} = 2 \ln^{2} z + o (\ln^{2} z)

, supposing that there is only one zero we should anticipate

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{3}} = 2^{3 / 2} \ln^{3} z + o (\ln^{3} z)

(or

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{3}} = - 2^{3 / 2} \ln^{3} z + o (\ln^{3} z)

) and

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{4}} = 4 \ln^{3} z + o (\ln^{3} z)

, while from (17) we have

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{3}} = 3 \ln^{3} z + o (\ln^{3} z)

and from (18) -

\sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ z \to 0 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{4}} = \frac{37}{3} \ln^{4} z + o (\ln^{4} z)

4. The sums over inverse zeroes of the Hurwitz zeta-function

The sums

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i} - p}

cannot be directly obtained by our method because the contour integral

\int_{C}^{} \frac{\ln ζ (s, z)}{{(s - p)}^{2}} d s

does not tend to zero in the limit of infinitely large contours C; it diverges. But the same situation occurs for the Riemann zeta-function - however, the “symmetric” sum

\lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s), \\ | Im ρ | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p}

well exists: it is known that

\lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s), \\ | Im ρ | < T \end{array}}^{} \frac{k_{i}}{ρ_{i}} = - \frac{1}{2} γ - 1 + \frac{1}{2} \ln 4 π

[29], etc. Indeed, the existence of such sums over non-trivial zeroes readily follows from the counting function for such zeroes, the circumstance that their real parts are bounded (they all lie inside the critical strip), and the possibility to pair complex conjugate zeroes so obtaining

\frac{1}{σ + i T} + \frac{1}{σ - i T} = \frac{2 σ}{σ^{2} + T^{2}}

The Riemann xi-function

ξ (s) = \frac{1}{2} (s - 1) π^{- s / 2} Γ (1 + s / 2) ζ (s)

(29)

is entire, and its only zeroes are the non-trivial zeroes of

ζ (s)

[29], but in the frame of our method we still cannot use the integrals

\int_{C}^{} \frac{\ln ξ (s)}{{(s - p)}^{2}} d s

because the asymptotic of xi-function is O(slns). However, actually we can use this integral, and below we will demonstrate how.

First, with our approach we easily get

\sum_{z e r o e s_{} o f_{} ξ (s)}^{} \frac{k_{i}}{{(ρ_{i} - p)}^{2}} = - \frac{d}{d s} \frac{ξ'}{ξ} |_{s = p}

, and then formally integrate this relation obtaining

\lim_{T \to \infty} \sum_{\begin{array}{l} z e r o e s_{} o f_{} ξ (s), \\ | Im ρ | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} = - \frac{ξ'}{ξ} (p) + C_{1}

- provided, of course, that p is not equal to any non-trivial zero and the corresponding constant C₁ exists. To find the latter, we can use the value p=1/2 where evidently

\lim_{T \to \infty} \sum_{\begin{array}{l} z e r o e s_{} o f_{} ξ (s), \\ | Im ρ | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - 1 / 2} = 0

and

\frac{ξ'}{ξ} (1 / 2) = 0

either, hence C₁=0 and thus

\lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s), \\ | Im ρ | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} = - \frac{ξ'}{ξ} (p) .

(30)

But this actually suggests that the limit of the value of the contour integral

\int_{C}^{} \frac{\ln ξ (s)}{{(s - p)}^{2}} d s

for infinitely large contours C exists (and, in particular, it is equal to zero for p=1/2), and now we will analyze similar contour integrals directly.

Let us introduce the function

f (s) : = ζ (s) Γ (1 + s / 2)

which has the simple pole at s=1 and whose only zeroes are non-trivial zeroes of the Riemann zeta-function. We consider the contour integral

\int_{C}^{} \frac{\ln f (s)}{{(s - p)}^{2}} d s

dividing the contour C into two parts: left, where Res<1/2, and right, where Res>1/2, and summing “the paired symmetrical contributions”

- \ln (f (s)) d s

and

\ln (f (1 - s)) d s

, see Figure 1. We know

ζ (1 - s) = 2^{1 - s} π^{- s} \sin (\frac{π (1 - s)}{2}) Γ (s) ζ (s)

[29], so that for the function

Γ (1 + s / 2) ζ (s)

its “symmetric partner” (reflection

s \mapsto 1 - s

) is

Γ (3 / 2 - s / 2) ζ (1 - s)

. Now we use reflection and duplication rules for the gamma-function [3,4,5],

\sin (\frac{π (1 - s)}{2}) = \frac{π}{Γ (\frac{1 - s}{2}) Γ (\frac{1 + s}{2})}

and

Γ (s) = π^{- 1 / 2} 2^{s - 1} Γ (s / 2) Γ (1 / 2 + s / 2)

, to write

ζ (1 - s) = π^{- s + 1 / 2} \frac{Γ (s / 2)}{Γ (1 / 2 - s / 2)} ζ (s)

and

\frac{2}{s} π^{s - 1 / 2} ζ (1 - s) Γ (1 / 2 - s / 2) = Γ (1 + s / 2) ζ (s)

, or

\frac{2}{s} {(\frac{1}{2} - \frac{s}{2})}^{- 1} π^{s - 1 / 2} ζ (1 - s) Γ (3 / 2 - s / 2) = Γ (1 + s / 2) ζ (s)

. Thus

\ln [\frac{2}{s} {(\frac{1}{2} - \frac{s}{2})}^{- 1} π^{s - 1 / 2}] = - \ln [ζ (1 - s) Γ (3 / 2 - s / 2)] + \ln [Γ (1 + s / 2) ζ (s)]

: we explicitly expressed the difference of the ln(f(s)) for both “left and right parts of the contour”.

Figure 1. Illustrating the division of the contour C, using in the integral

\int_{C}^{} f (s) d s

, into left and right part by the vertical line Res=1/2. The integral value is then calculated by pairing the “symmetric contributions” at s and 1-s:

- f (s) d s + f (1 - s) d s

. The segments, removed from the consideration during the calculations (their contributions clearly tend to zero in the limit of infinitely large contours), are also shown.

Figure 1. Illustrating the division of the contour C, using in the integral

\int_{C}^{} f (s) d s

, into left and right part by the vertical line Res=1/2. The integral value is then calculated by pairing the “symmetric contributions” at s and 1-s:

- f (s) d s + f (1 - s) d s

. The segments, removed from the consideration during the calculations (their contributions clearly tend to zero in the limit of infinitely large contours), are also shown.

For the integral

\int_{C}^{} \frac{A (s)}{{(s - p_{1})}^{2}} d s

with the function A(s) such that A(s)=A(1-s) we have, by considering the contour integral as the sum of its left and right parts:

\int_{C}^{} \frac{A (s)}{{(s - p_{1})}^{2}} d s =

\int_{C / 2}^{} [\frac{A (s)}{{(s - p_{1})}^{2}} - \frac{A (s)}{{(1 - s - p_{1})}^{2}}] d s

. Here and below C/2 under the integral sign denotes the integration over “left half of the contour”, viz. the joined segments

[1 / 2 + i T, - T + 1 / 2 + i T]

[- T + 1 / 2 + i T, - T + 1 / 2 - i T]

and

[- T + 1 / 2 - i T, 1 / 2 - i T]

, see Figure 1. Evidently,

\int_{C / 2}^{} [\frac{A (s)}{{(s - p_{1})}^{2}} - \frac{A (s)}{{(s - p_{2})}^{2}}] d s

= \int_{C / 2}^{} \frac{A (s) (2 s - p_{1} - p_{2}) (p_{1} - p_{2})}{{(s - p_{1})}^{2} {(s - p_{2})}^{2}} d s = 0

for any p₁, p₂ and A(s) having asymptotic o(s), thus only the factor

\ln [\frac{2}{s} {(\frac{1}{2} - \frac{s}{2})}^{- 1} π^{s - 1 / 2}]

presented in the “left half of the contour”, viz. the joined segments

[1 / 2 + i T, - T + 1 / 2 + i T]

[- T + 1 / 2 + i T, - T + 1 / 2 - i T]

and

[- T + 1 / 2 - i T, 1 / 2 - i T]

, see Figure 1, contributes to the contour integral value. The contribution of

\ln [\frac{2 π^{- 1 / 2}}{s} {(\frac{1}{2} - \frac{s}{2})}^{- 1}]

, which is O(lns), tends to zero, so that only the term

\ln [π^{s - 1 / 2}] = (s - 1 / 2) \ln π

contributes. Its contribution is easy to calculate from the “symmetric” writing

\frac{2 π^{- 1 / 2}}{s} {(\frac{1}{2} - \frac{s}{2})}^{- 1} \times [π^{- s / 2} ζ (1 - s) Γ (3 / 2 - s / 2)] = [Γ (1 + s / 2) ζ (s) π^{s / 2}]

\int_{C}^{} \frac{\ln π^{s / 2}}{{(s - p)}^{2}} d s = 2 π i \cdot \frac{\ln π}{2}

Thus the generalized Littlewood theorem reads:

\frac{1}{2} \ln π = \lim_{T \to \infty} (- \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s), \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} + \frac{ζ'}{ζ} (p) + \frac{1}{2} ψ (1 / 2 + p) + \frac{1}{1 - p})

, and we have proven

\lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s), \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} = - \frac{1}{2} \ln π - \frac{ζ'}{ζ} (p) - \frac{1}{2} ψ (1 / 2 + p) + \frac{1}{1 - p}

(31)

Certainly, this is much easier to prove from (29) and (30), but the above consideration will guide us for the proof of the following Theorem.

Theorem 4.

Let m, n be positive integers and 0<m/n<1. We will name zeroes

ρ_{j}

of the Hurwitz zeta-function

ζ (s, \frac{m}{n})

with

Re ρ \leq - 1

trivial, and order them in the following way:

Re ρ_{1} \geq Re ρ_{2} \geq Re ρ_{3} \geq \dots

. The following formula holds for p not equal to 1 or any zero of the

ζ (s, \frac{m}{n})

\begin{array}{l} \lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} m / n), \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} = - \frac{1}{2} \ln π + \frac{1}{2} \ln (m / n) - \frac{ζ' (s, m / n)}{ζ (s, m / n)} (p) - \frac{1}{2} ψ (1 / 2 + p) + \frac{1}{1 - p} + \\ \sum_{\begin{array}{l} t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} m / n), \\ j = 1 \end{array}}^{\infty} [\frac{1}{ρ_{j} - p} + \frac{1}{2 j + p}] \end{array} .

(32)

Proof.

Our aim is to evaluate the contour integral

\int_{C}^{} \frac{\ln [ζ (s,_{} m / n) Γ (s / 2)]}{{(s - p)}^{2}} d s

in the limit of infinitely large contour C, and then to exclude the simple poles of

Γ (s / 2)

from the sums pertinent to the Hurwitz zeta-function. Clearly, due to the asymptotic of the functions which occur here, we can omit some finite segments of the contour, say

[- 1 + i T, 2 + i T]

[- 1 - i T, 2 - i T]

and

[T + i / 4, T - i / 4]

[- T + i / 4, - T - i / 4]

from the calculations: they contribute nothing in the limit at question.

First, we note that the results of Spira [9], briefly reviewed in the Introduction, show that except the “trivial zeroes”, all other zeroes of the function

ζ (s, z)

with real

0 < z \leq 1

are contained in the strip

- 1 < Re s < 1 + z

. They are complex-conjugated, and the counting function of zeroes eq. (4) implies the convergence of the “symmetric” sum

\lim_{T \to \infty} \sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s, z), \\ Re s > - 1,_{} | Im s | < T . \end{array}}^{} \frac{k_{i}}{ρ_{i} - p}

if p is not a zero. Another Spira result, that for

| Im s | \leq 1

and

Re s \leq (- 4 x + 1 + 2 [1 - 2 x])

, the only zeroes are (analogues of) trivial zeroes, one in each interval

- 2 n - 4 x \pm 1

, n is an integer and

n \geq 1 - 2 x

, guaranties the convergence of the sum

\sum_{\begin{array}{l} t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} z), \\ j = 1 \end{array}}^{\infty} [\frac{1}{ρ_{j} - p} + \frac{1}{2 j + p}]

We have the functional equation (Rademacher’s formula) [1,2,3,4,5]:

ζ (1 - s, \frac{m}{n}) = \frac{2 Γ (s)}{{(2 π n)}^{s}} \sum_{k = 1}^{n} [\cos (\frac{π s}{2} - \frac{2 π k m}{n}) ζ (s, \frac{k}{n})]

(33)

so that, using again reflection and duplication rules for the gamma-function, see above, we obtain:

ζ (1 - s, \frac{m}{n}) Γ (\frac{1 - s}{2}) = 2 Γ (s) Γ (\frac{1 - s}{2}) {(2 π n)}^{- s} \sum_{k = 1}^{n} \cos (\frac{π s}{2} - \frac{2 π k m}{n}) ζ (s, \frac{k}{n}) = 2 π^{- 1 / 2} 2^{s - 1} Γ (\frac{s}{2}) Γ (\frac{1 + s}{2}) Γ (\frac{1 - s}{2}) {(2 π n)}^{- s} \sum_{k = 1}^{n} \cos (\frac{π s}{2} - \frac{2 π k m}{n}) ζ (s, \frac{k}{n}) = π^{1 / 2} 2^{s} Γ (\frac{s}{2}) \frac{1}{\sin (π / 2 - π s / 2)} {(2 π n)}^{- s} \sum_{k = 1}^{n} \cos (\frac{π s}{2} - \frac{2 π k m}{n}) ζ (s, \frac{k}{n}) = π^{1 / 2} Γ (s / 2) {(π n)}^{- s} \sum_{k = 1}^{n} \frac{\cos (\frac{π s}{2} - \frac{2 π k m}{n})}{\cos (π s / 2)} ζ (s, \frac{k}{n}) = π^{1 / 2} Γ (s / 2) {(π n)}^{- s} \sum_{k = 1}^{n} [\cos (2 π k m / n) + \tan (π s / 2) \sin (2 π k m / n)] ζ (s, \frac{k}{n}) .

We write, supposing

ζ (s, m / n) \neq 0

\begin{array}{l} ζ (1 - s, \frac{m}{n}) Γ (\frac{1 - s}{2}) = π^{1 / 2} Γ (s / 2) {(π n)}^{- s} ζ (s, \frac{m}{n}) \times \\ \sum_{k = 1}^{n} [\cos (2 π k m / n) + \tan (π s / 2) \sin (2 π k m / n)] ζ (s, \frac{k}{n}) / ζ (s, \frac{m}{n}) \end{array}

(34)

That is, we have established the relation between the functions in the right and left parts of the contour in the contour integral

\int_{C}^{} \frac{\ln [ζ (s, m / n) Γ (s / 2)]}{{(s - p)}^{2}} d s

. From the previous consideration for the Riemann zeta-function, we know that only those factors in such a relation, whose logarithms asymptotically are at least O(s), are important for the integral value. Thus rather rough estimations suffice, and below in this Section the writing

f (s) \sim g (s)

means

f (s) = O (1) \cdot g (s)

for large

| s |

. We can use, for Res>1 (see the note in the beginning of the proof that we exclude certain finite segments of the contour from the consideration),

ζ (s, \frac{m}{n}) = \frac{n^{s}}{m^{s}} + ζ (s, 1 + \frac{m}{n})

, where

ζ (s, 1 + \frac{m}{n}) = O (1)

, and the circumstance that all trigonometrical functions appearing here are O(1) (for estimation of the

\tan (π s / 2)

remind that we exclude the segments

[T + i / 4, T - i / 4]

[- T + i / 4, - T - i / 4]

from the calculations; see again the note in the beginning of the proof). We get

ζ (1 - s, \frac{m}{n}) Γ (\frac{1 - s}{2}) \sim Γ (s / 2) {(π n)}^{- s} ζ (s, \frac{m}{n}) \times \sum_{k = 1}^{n} [\cos (2 π k m / n) + \tan (π s / 2) \sin (2 π k m / n)] \frac{m^{s}}{k^{s}}

, where finally in the sum only the term with k=1 is important:

ζ (1 - s, \frac{m}{n}) Γ (\frac{1 - s}{2}) \sim Γ (s / 2) {(π n / m)}^{- s} ζ (s, \frac{m}{n})

- because for any complex numbers a_k,

\sum_{k = 1}^{n} a_{k} \frac{m^{s}}{k^{s}} = a_{1} m^{s} \cdot \sum_{k = 2}^{n} \frac{a_{k}}{a_{1}} \frac{1}{k^{s}}

with

\ln (\sum_{k = 2}^{n} \frac{a_{k}}{a_{1}} \frac{1}{k^{s}}) = O (1)

; for our case definitely

a_{1} \neq 0

The application of the generalized Littlewood theorem to the “symmetric” contour integral

\int_{C}^{} \frac{\ln [{(π n / m)}^{- s / 2} ζ (s, m / n) Γ (s / 2)]}{{(s - p)}^{2}} d s

(compare again with the case of the Riemann zeta-function considered above) reads:

\begin{array}{l} \frac{1}{2} \ln π + \frac{1}{2} \ln (n / m) = \lim_{T \to \infty} (- \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} m / n), \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p}) + \frac{ζ' (s, m / n)}{ζ (s, m / n)} (p) + \frac{1}{2} ψ (1 / 2 + p) - \frac{1}{1 - p} - \\ \sum_{\begin{array}{l} t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} m / n), \\ j = 1 \end{array}}^{\infty} [\frac{1}{ρ_{j} - p} + \frac{1}{2 j + p}] \end{array}

and finally

\begin{array}{l} \lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} m / n), \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} = - \frac{1}{2} \ln π + \frac{1}{2} \ln (m / n) - \frac{ζ' (s, m / n)}{ζ (s, m / n)} (p) - \frac{1}{2} ψ (1 / 2 + p) + \frac{1}{1 - p} + \\ \sum_{\begin{array}{l} t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} m / n), \\ j = 1 \end{array}}^{\infty} [\frac{1}{ρ_{j} - p} + \frac{1}{2 j + p}] \end{array} .

□

Remark 4.

This is hardly doubtful that the formula analogous to (32) is applicable for the function

ζ (s, z)

for any real 0<z<1, not only rational z=m/n. However, the present author did not succeed to prove such more general version of the Theorem.

For m/n=1/2, where

ζ (s, 1 / 2) = (2^{s} - 1) ζ (s)

[29], the formula merely reflects the appearance of an additional factor

2^{s / 2}

multiplied on the “symmetrical” function

2 \sinh (\frac{s \ln 2}{2})

describing new (with respect to those of the Riemann zeta-function) zeroes

ρ_{n} = \pm \frac{2 π i n}{\ln 2}

of the function

ζ (s, 1 / 2)

2^{s} - 1 = 2^{s / 2} \cdot 2 \sinh (\frac{s \ln 2}{2})

. The contribution of this “disturbing” factor should be removed from

\frac{ζ'}{ζ} (p, 1 / 2)

during the calculation of

\lim_{T \to \infty} \sum_{\begin{array}{l} n o n - t r i v i a l_{} z e r o e s_{} o f_{} ζ (s,_{} 1 / 2), \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p}

Indeed, here we have an illustration how the sum over inverse zeroes of the function

f (z) = e^{b z} - a

, see Remark 2,

\lim_{T \to \infty} \sum_{\begin{array}{l} z e r o e s_{} o f_{} f (z) \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p}

should be found. We have

f (z) = e^{b z} - a = \sqrt{a} e^{b z / 2} (\frac{1}{\sqrt{a}} e^{b z / 2} - \sqrt{a} e^{- b z / 2}) = 2 \sqrt{a} e^{b z / 2} \sinh (b z / 2 - \frac{1}{2} \ln a)

, and the contribution of the factor

e^{b z / 2}

should be removed from

\frac{f'}{f} (p)

during the calculation of

\lim_{T \to \infty} \sum_{\begin{array}{l} z e r o e s_{} o f_{} f (z) \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p}

\lim_{T \to \infty} \sum_{\begin{array}{l} z e r o e s_{} o f_{} f (z) \\ | Im (ρ_{i}) | < T \end{array}}^{} \frac{k_{i}}{ρ_{i} - p} = - \frac{f'}{f} (p) + \frac{b}{2} = - \frac{b e^{b p}}{e^{b p} - a} + \frac{b}{2}

, or

\sum_{n = - \infty}^{\infty} \frac{1}{\frac{\ln a}{b} + \frac{2 π i n}{b} - p} = - \frac{b e^{b p}}{e^{b p} - a} + \frac{b}{2}

. Of course, also

\sum_{n = - \infty}^{\infty} \frac{1}{\frac{\ln a}{b} + \frac{2 π i n}{b} - p} = - \frac{b}{2} \tanh (\frac{b p}{2} - \frac{1}{2} \ln a)

; the terms with +n and -n should be paired when summing.

5. Some exact values for the sums considered

Formulae obtained in the paper solve the problem of the calculation of the sums of the inverse squares and larger powers of zeroes of the Hurwitz zeta-function, expressing them via the derivatives of this function at zero or the derivatives of the function

(s - 1) ζ (s, z)

at s=1, i.e via the generalized Stieltjes coefficients. But for the Hurwitz zeta-function, the specific question of the expression of the values of the derivatives at zero via the generalized Stieltjes coefficients, received a lot of attention, see e.g. [30,31,32] and references therein, especially in [30]. This is due to the existence of the functional equation (Rademacher’s formula) [1,2,3,4,5]: for rational positive z=m/n,

1 \leq m \leq n

ζ (s, \frac{m}{n}) = \frac{2 Γ (1 - s)}{{(2 π n)}^{1 - s}} \sum_{k = 1}^{n} [\sin (\frac{π s}{2} + \frac{2 π k m}{n}) ζ (1 - s, \frac{k}{n})],

(35)

and, of course, also

ζ (1 - s, \frac{m}{n}) = \frac{2 Γ (s)}{{(2 π n)}^{s}} \sum_{k = 1}^{n} [\cos (\frac{π s}{2} - \frac{2 π k m}{n}) ζ (s, \frac{k}{n})]

, written above as eq. (33).

Following the tradition, rather cumbersome expression of the second derivative of the Hurwitz zeta-function

ζ'' (0, \frac{m}{n})

via elementary functions (here we count gamma – function in this class) and the generalized Stieltjes coefficients

γ_{1} (\frac{k}{n}), γ_{2} (\frac{k}{n})

(more precisely, via the sums

\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n})

and

\sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n})

) are given in the Appendix. (The status of these formulae actually is similar to the status of the formulae following from the Taylor development analysis of other functional equations, as, say,

\sin x = \sin (x + 2 π)

\sin x = - \sin (x + π)

, that is

\sum_{k = 0}^{\infty} \frac{{(- 1)}^{k} {(2 π)}^{2 k + 1}}{(2 k + 1)!} = 0

\sum_{k = 0}^{\infty} \frac{{(- 1)}^{k} π^{2 k + 1}}{(2 k + 1)!} = 0

, and so on).

As a result, numerous expressions are known for many (mostly first) generalized Stieltjes coefficients

γ_{n} (z)

and their relations with the derivatives of the Hurwitz zeta-function at zero; see e.g. [29,30,31] and references therein; especially reach results and references can be found in Blagouchine’s paper [29]. Many of these results might be used for the calculations of the sums over zeroes considered here. For example, at least for the cases

\frac{m}{n} = {\frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{1}{3}, \frac{2}{3}, \frac{1}{6}, \frac{5}{6}}

the coefficients

γ_{1} (\frac{m}{n})

are known in close forms (see p. 100 of [31] and references therein), which immediately enables to write rather elegant expressions for the corresponding sums

\sum_{z e r o e s_{} o f_{} s}^{} \frac{k_{i}}{{(ρ_{i} - 1)}^{2}}

. For instance:

γ_{1} (1 / 4) = 2 π \ln Γ (1 / 4) - \frac{3 π}{2} \ln π - \frac{7}{2} \ln^{2} 2 - (3 γ + 2 π) \ln 2 - \frac{γ π}{2} + γ_{1} ≅ - 5.5181, γ_{1} (3 / 4) = - 2 π \ln Γ (1 / 4) + \frac{3 π}{2} \ln π - \frac{7}{2} \ln^{2} 2 - (3 γ - 2 π) \ln 2 + \frac{γ π}{2} + γ_{1} ≅ - 0.391381, etc

For the sums

\sum_{z e r o e s_{} o f_{} s}^{} \frac{k_{i}}{ρ_{i}^{2}}

, an interesting case appears for n=3. We know

\sum_{l = 1}^{m - 1} ζ'' (0, \frac{l}{m}) = - \frac{1}{2} \ln^{2} m - \ln m \cdot \ln 2 π

, formula (58) of [30]. Thus

ζ'' (0, 1 / 3) + ζ'' (0, 2 / 3) = - \frac{1}{2} \ln^{2} 3 - \ln 3 \cdot \ln 2 π

, and this enables to express the difference of sums over inverse square of zeroes of two Hurwitz zeta-functions in rather elegant form which does not include any generalized Stieltjes coefficient:

\begin{array}{l} \sum_{z e r o e s_{} ζ (s, 1 / 3)}^{} \frac{k_{i}}{ρ_{i}^{2}} - \sum_{z e r o e s_{} ζ (s, 2 / 3)}^{} \frac{k_{i}}{ρ_{i}^{2}} = 36 [\ln^{2} Γ (1 / 3) - \ln^{2} Γ (2 / 3) - \ln Γ (1 / 3) \cdot \ln 2 π + \ln Γ (2 / 3) \cdot \ln 2 π] + \\ \ln^{2} 3 + 6 \ln 3 \cdot \ln 2 π ≅ 2.2436 \end{array}

. This equality has been tested: numerical application of formula () gives

\sum_{z e r o e s_{} ζ (s, 1 / 3)}^{} \frac{k_{i}}{ρ_{i}^{2}} ≅ 5.9583

and

\sum_{z e r o e s_{} ζ (s, 2 / 3)}^{} \frac{k_{i}}{ρ_{i}^{2}} ≅ 3.7146

, so that the difference at question is around 2.2436 indeed.

The relation

ζ'' (0, p) + ζ'' (0, 1 - p) = - 2 (γ + \ln 2 π) \ln (2 \sin π p) + 2 \sum_{n = 1}^{\infty} \frac{\cos 2 π p n \cdot \ln n}{n}

(p. 575 of [30]) is also worthwhile to note: it enables to calculate

\sum_{z e r o e s_{} ζ (s, p)}^{} \frac{k_{i}}{ρ_{i}^{2}}

- \sum_{z e r o e s_{} ζ (s, 1 - p)}^{} \frac{k_{i}}{ρ_{i}^{2}}

for any positive rational p less than 1 without the recourse to any generalized Stieltjes coefficient and second derivatives of the Hurwitz zeta-function (but with recourse to the infinite series).

6. Numerical illustration

It seems really interesting and, we believe, illuminative, to see how s-zeroes of the function

ζ (s, z)

evolve when z moves from small real positive value to z=1/2 and then to z=1, sf. some data in this direction in [16]. As a prototype of such researches, we can indicate the very interesting papers by Kölbig [32,33] about the incomplete Riemann- and gamma-functions: it seems that the questions put forward by him there still remain unanswered. For example, the following questions about s-zeroes of the Hurwitz zeta-function arise. Do its “numerous” zeroes existing in the vicinity of s=0 for small z evolves to “false”

s_{k} = 2 π i n / \ln 2

zeroes of the function

ζ (s, 1 / 2)

when z increases from (almost) zero to 1/2? What happens with them after, when z further moves to 1 (i.e. only the Riemann zeta–function’s zeroes rest), and so on.

These questions evidently require extensive numerical researches and are not investigated in the present paper (however, see some simple observations in the end of the Section). Our aim is much more modest: just to exploit the circumstance that the above formulae are quite fit for numerical calculations due to the availability of the option to calculate derivatives of the Hurwitz zeta-function; e.g

hurwitzZeta(n, s, z) in MATLAB, which returns

\frac{d^{n} ζ (s, z)}{d s^{n}}

, or StieltjesGamma[n,a] in Matematica, which returns generalized Stieltjes coefficients

γ_{n} (a)

. (But caution: in Matematica, the function

ζ (s, z) = \sum_{n = 0}^{\infty} \frac{1}{{({(n + z)}^{2})}^{s / 2}}

is implemented as the Hurwitz zeta-function).

In Figure 2 we present the numerical results obtained exploiting the aforementioned hurwitzZeta(1, s, z) and hurwitzZeta(2, s, z) functions.

Our other numerical observations are the following. We confirm the presence of a small by module real negative zeroes of the Hurwitz zeta function when real

z \to 0

, the absence of small by module positive real zeroes for such a case, and the absence of small by module real zeroes when

z \to - 1, - 2, - 3

. For example, for z=10^-5

ζ (s, z) = 0

for s=-0.071; for z=10^-4,

ζ (s, z) = 0

for s=-0.094; for z=10^-3 - for

s=-0.135; for z=0.1 - for s=-0.623, and so on: we have tested that this zero moves to the first trivial zero of

ζ (s, z)

lying at s=-2 when z moves to ½. We also confirm the presence of small by module complex conjugate complex zeroes when

z \to 0

Finally, the presence of s-zero tending to 0 as

s \sim - \frac{2 δ}{\ln 2} + o (δ)

when

z = \frac{1}{2} + δ

with real

δ \to 0

(a trivial consequence of eqs. (16 - 18) in the vicinity of z=1/2), was also confirmed. We tested that it moves to the first trivial zero of

ζ (s, z)

lying at s=-2 when z moves to 1, and moves to the zero close to 1 when z moves to 0.

7. Discussion and conclusions

To finish, let us briefly discuss the question of the sum of inverse powers of zeroes of the Hurwitz zeta function as a function of z with fixed s. Unfortunately, as of today, such a question cannot be put forward for an arbitrary s, because for non-integer s, the expression

ζ (s, z) = \sum_{n = 0}^{\infty} \frac{1}{{(n + z)}^{s}}

simply is not a continuous function of z. For example (we follow J. Lewittes paper [35]),

\lim_{y \to 0 +} = \sum_{n = 0}^{\infty} {(\frac{1}{2} + i y + n)}^{- s} \neq \sum_{n = 0}^{\infty} {(\frac{1}{2} + n)}^{- s}

due to the discontinuity of the argument function, usually defined to be

- π \leq \arg (z) < π

, on the negative real axis. Thus some restrictions of the permissible z - values should be introduced for an arbitrary s, which makes our approach inapplicable. It seems that only the integer values of s larger than one, that is s=2, 3, 4…, where the function is determined by the absolutely convergent series on the whole complex plane, can be considered. Then this function is just the polygamma function, and the corresponding sums over inverse powers of zeroes were earlier considered in [17].

Also the following question seems natural to the present author. The aforementioned Theorem of Davenport and Heilbronn [7] was proven using Kronecker’s theorem about the Diophantine approximation and Rouché’s theorem for a specially (ingeniously) constructed function Z(s), which is quite close to

ζ (s, x)

and definitely has zeroes with Res >1, for all real rational

0 < x < 1

. Given that the rational numbers are everywhere in the segment

0 < x < 1

, and that the sums over zeroes

\sum_{z e r o e s_{} o f_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{n}}

are certainly continuous, may a (kind of) topological proof for non-rational x can be constructed? (Cassel’s generalization [8] is not topological). May zeroes with Res >1 “abruptly” disappear for all (or “topologically many”) non-rational values of x? It seems not. (Certainly, there is no problem that such zeroes “disappear” at certain isolated points as e.g. x=1/2: this means only that

\lim_{x \to 1 / 2} \sum_{\begin{array}{l} z e r o e s_{} o f_{} ζ (s,_{} x), \\ Re s > 1 \end{array}}^{} \frac{k_{i}}{ρ_{i}^{n}} = 0

for all n, and in principle, there is nothing surprising here). Similarly, we believe, some (a kind of) topological proof of the Theorem 4 for an arbitrary real

0 < z < 1

might be possible.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflict of interest

The author declares no conflict of interest.

Appendix A

In a sense, the question of expression of the derivatives

ζ' (0, \frac{m}{n}), ζ'' (0, \frac{m}{n})

via the generalized Stieltjes coefficients

γ_{1} (\frac{k}{n})

has been solved by J. Musser in his Thesis work [32]. However, his final formulae, see pp. 27 and 21, contain parameters C_l (“the coefficients of the Taylor expansion of

\cos (\frac{π s}{2} - \frac{2 π k m}{n}) \frac{2}{{(2 π n)}^{s}}

about s=1”) and are not fully explicit. Here we present the answer in the form similar to that given by Blagouchine [30], who has solved, in a sense, the inverse problem of expressing the generalized Stieltjes coefficients

γ_{1} (\frac{k}{n})

via

ζ' (0, \frac{m}{n}), ζ'' (0, \frac{m}{n})

Starting from (35), where m, n are natural numbers,

n \geq 1

and

1 \leq m \leq n

, we have with the O(s³) precision the following Laurent expansion:

\begin{array}{l} \frac{1}{2} - \frac{m}{n} + s ζ' (0, \frac{m}{n}) + \frac{s^{2}}{2} ζ'' (0, \frac{m}{n}) + O (s^{3}) = \frac{2}{2 π n} [1 + γ s + \frac{π^{2}}{12} s^{2}] [1 + s \ln (2 π n) - \frac{s^{2}}{2} \ln^{2} (2 π n)] \times \\ \sum_{k = 1}^{n} [\sin \frac{2 π k m}{n} + \frac{π s}{2} \cos \frac{2 π k m}{n} - \frac{π^{2} s^{2}}{8} \sin \frac{2 π k m}{n} - \frac{π^{3} s^{3}}{48} \cos \frac{2 π k m}{n}] [- \frac{1}{s} - ψ (\frac{k}{n}) + γ_{1} (\frac{k}{n}) s + \frac{1}{2} γ_{2} (\frac{k}{n}) s^{2}] \end{array} .

(A1)

The last factor in square brackets (that under the sum sign) is equal to

- \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) ψ (\frac{k}{n}) + [\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) - \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) ψ (\frac{k}{n})] s + [\frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) + \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) + \frac{π^{2}}{8} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) ψ (\frac{k}{n})] s^{2},

(A2)

O(1/s) term disappears due to evident

\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) = 0

, and the contribution

\frac{π^{3} s^{2}}{48} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) = 0

disappears as well. In addition to these two, below we will also use the summation rules

\sum_{k = 1}^{n} k \cos (\frac{2 π k m}{n}) = n

and

\sum_{k = 1}^{n} k \sin (\frac{2 π k m}{n}) = - \frac{n}{2} \cot \frac{π m}{n}

. All these classic rules are valid for m=1, 2, 3… n-1 and readily follow from the sine and cosine representation via

e^{\pm i x}

, the sum of geometric progression formula

\sum_{k = 1}^{n} e^{i k x} = \frac{e^{i k (n + 1)} - e^{i k}}{e^{i k} - 1}

, and differentiation.

Now we apply the following more complex but still quite known summation rules, which are Gauss’ identities

\sum_{k = 1}^{n - 1} \cos (\frac{2 π k m}{n}) ψ (\frac{m}{n}) = γ + n \ln (2 \sin \frac{m π}{n})

, whence

\sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) ψ (\frac{m}{n}) = n \ln (2 \sin \frac{m π}{n})

, and

\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) ψ (\frac{k}{n}) = \frac{π}{2} (2 m - n)

Thus, the third factor in A1 (that under the sum sign) is

\frac{π}{2} (n - 2 m) + [\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{1} (\frac{k}{m}) - \frac{π n}{2} \ln (2 \sin \frac{m π}{n})] s

+ [\frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) + \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) + \frac{π^{3}}{16} (2 m - n)] s^{2}

. Equating the O(s) terms should give the known

ζ' (0, \frac{m}{n}) = \ln Γ (\frac{m}{n}) - \frac{1}{2} \ln 2 π

. In such a way we obtain the summation rule

\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) = \frac{π}{2} (γ + \ln (2 π n)) (2 m - n) - \frac{π n}{2} (\ln π - \ln \sin \frac{m π}{n}) + n π \ln Γ (\frac{m}{n}),

(A3)

which is contained in the Theorem 2 of Blagouchine [30]. In the same theorem he presents also the sum

\sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) = n (γ + \ln (2 π n)) \ln (2 \sin \frac{m π}{n}) + \frac{n}{2} [ζ'' (0, \frac{m}{n}) + ζ'' (0, 1 - \frac{m}{n})] .

(A4)

(we added the term corresponding to k=n to his original sum). We will use this rule later on, but at this stage it is inapplicable due to the presence of second derivatives of the Hurwitz zeta-function.

Thus finally, the factor under the sum sign in (A1) is

\frac{π}{2} (n - 2 m) + [\frac{π}{2} (γ + \ln 2 π n) (2 m - n) - \frac{π n}{2} (\ln π - \ln \sin \frac{m π}{n}) + n π \ln Γ (\frac{m}{n}) - \frac{π n}{2} \ln (2 \sin \frac{m π}{n})] s

+ [\frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) + \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) + \frac{π^{3}}{16} (2 m - n)] s^{2}

, and we have with the O(s³) precision:

π n [(\frac{1}{2} - \frac{m}{n} + s ζ' (0, \frac{m}{n}) + \frac{s^{2}}{2} ζ'' (0, \frac{m}{n})] = [1 + γ s + \frac{π^{2}}{12} s^{2}] [1 + s \ln (2 π n) - \frac{s^{2}}{2} \ln^{2} (2 π n)] \times {[\frac{π}{2} (n - 2 m) + [\frac{π}{2} (γ + \ln 2 π n) (2 m - n) - \frac{π n}{2} \ln 2 π + n π \ln Γ (\frac{m}{n})] s + [\frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) + \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) + \frac{π^{3}}{16} (2 m - n)]} s^{2} .

(A5)

Now we compare the O(s²) terms. To simplify the appearance of the subsequent formulae, let us denote

C_{m n} = \frac{π}{2} (γ + \ln 2 π n) (2 m - n) - \frac{π n}{2} \ln 2 π + n π \ln Γ (\frac{m}{n})

. This gives

\begin{array}{l} \frac{1}{2} π n ζ'' (0, \frac{m}{n}) = \frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) + \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) + \frac{π^{3}}{16} (2 m - n) + \\ \frac{π}{2} (n - 2 m) (\frac{π^{2}}{12} - \frac{1}{2} \ln^{2} 2 π n) + C (m, n) (γ + \ln 2 π n) \end{array}

That is

\frac{1}{2} π n ζ'' (0, \frac{m}{n}) = \frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) + \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) + \frac{π^{3}}{16} (2 m - n) + \frac{π}{2} (n - 2 m) (\frac{π^{2}}{12} - \frac{1}{2} \ln^{2} 2 π n) + [\frac{π}{2} (γ + \ln 2 π n) (2 m - n) - \frac{π n}{2} \ln 2 π + n π \ln Γ (\frac{m}{n})] (γ + \ln 2 π n),

(A6)

which is our final formula. Remind that m=1, 2, 3, …n-1 here.

Remark 5.

Equation A5, together with the sum A4, can be used to estimate

\sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n})

\frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) = - \frac{π}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) γ_{1} (\frac{k}{n}) - \frac{π^{3}}{16} (2 m - n) + \frac{π n}{2} ζ'' (0, \frac{m}{n}) - \frac{π}{2} (n - 2 m) (\frac{π^{2}}{12} - \frac{1}{2} \ln^{2} 2 π n) - [\frac{π}{2} (γ + \ln 2 π n) (2 m - n) - \frac{π n}{2} \ln 2 π + n π \ln Γ (\frac{m}{n})] (γ + \ln 2 π n)

Thus

\frac{1}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) γ_{2} (\frac{k}{n}) = \frac{π n}{4} (ζ'' (0, \frac{m}{n}) - ζ'' (0, 1 - \frac{m}{n})) - \frac{π^{3}}{16} (2 m - n) - \frac{π}{2} [n (γ + \ln (2 π n)) \ln (2 \sin \frac{m π}{n})] - \frac{π}{2} (n - 2 m) (\frac{π^{2}}{12} - \frac{1}{2} \ln^{2} 2 π n) - [\frac{π}{2} (γ + \ln 2 π n) (2 m - n) - \frac{π n}{2} \ln 2 π + n π \ln Γ (\frac{m}{n})] (γ + \ln 2 π n) .

(A7)

It is easy to check up that the simplest example of n=2, m=1 gives correct triviality 0=0.

Finally, we would like to note that the Laurent series expansion of the Rademacher’s formula written in the form (33), and subsequent equating of the coefficients in front of the s terms may be used to prove the main Theorem 1 of [30]. We believe that the following short exposition still might be useful.

From (33), we have with O(s²) precision:

\begin{array}{l} - \frac{1}{s} - ψ (\frac{m}{n}) + γ_{1} (\frac{m}{n}) s = 2 [1 - s \ln 2 π n + \frac{s^{2}}{2} \ln^{2} 2 π n] [\frac{1}{s} - γ + (\frac{1}{2} γ^{2} + \frac{π^{2}}{12}) s] \times \\ [\sum_{k = 1}^{n} [\cos (\frac{2 π k m}{n}) + \frac{π}{2} \sin (\frac{2 π k m}{n}) s - \frac{π^{2}}{8} \cos (\frac{2 π k m}{n}) s^{2}] [\frac{1}{2} - \frac{k}{n} + (\ln Γ (\frac{k}{n}) - \frac{1}{2} \ln 2 π) s + \frac{1}{2} ζ'' (0, \frac{k}{m}) s^{2}] \end{array}

With the same precision, the last term in square brackets under the sign of sum is

\begin{array}{l} - \frac{1}{2} + [- \frac{π}{2 n} \sum_{k = 1}^{n} k \sin (\frac{2 π k m}{n}) + \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n})] s + \\ [\frac{1}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) ζ'' (0, \frac{k}{m}) + \frac{π}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n}) + \frac{π^{2}}{8}] s^{2} \end{array},

Thus

- \frac{1}{2 s} - \frac{1}{2} ψ (\frac{m}{n}) + \frac{1}{2} γ_{1} (\frac{m}{n}) s = [1 - s \ln 2 π n + \frac{s^{2}}{2} \ln^{2} 2 π n] [\frac{1}{s} - γ + (\frac{1}{2} γ^{2} + \frac{π^{2}}{12}) s] \times \begin{array}{l} {- \frac{1}{2} + [\frac{π}{4} \cot \frac{π m}{n} + \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n})] s + \\ [\frac{1}{2} \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) ζ'' (0, \frac{k}{m}) + \frac{π}{2} \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n}) + \frac{π^{2}}{8}] s^{2}} \end{array},

where the aforementioned summation rule for

\sum_{k = 1}^{n} k \sin (\frac{2 π k m}{n})

was used.

Equating of O(1) terms gives

- \frac{1}{2} ψ (\frac{m}{n}) = \frac{γ}{2} + \frac{1}{2} \ln 2 π n

+ \frac{π}{4} \cot \frac{π m}{n} + \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n})

, and then recalling

Γ (1 - z) Γ (z) = \frac{π}{\sin π z}

and pairing the terms with

\ln Γ (\frac{m}{n})

and

\ln Γ (1 - \frac{m}{n})

, we arrive to the standard [3,4,5]

ψ (\frac{m}{n}) = - γ - \ln 2 n - \frac{π}{2} \cot \frac{π m}{n} + 2 \sum_{k = 1}^{[\frac{n - 1}{2}]} \cos (\frac{2 π k m}{n}) \ln \sin (\frac{π k}{n}) .

(A8)

Equating of O(s²) terms leads to the Blagouchine’s first Theorem [30]:

γ_{1} (\frac{m}{n}) = [\sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) ζ'' (0, \frac{k}{m}) + π \sum_{k = 1}^{n} \sin (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n}) + \frac{π^{2}}{4}] + [\frac{π}{2} \cot \frac{π m}{n} + 2 \sum_{k = 1}^{n} \cos (\frac{2 π k m}{n}) \ln Γ (\frac{k}{n})] [- \ln 2 π n - γ] + - \frac{1}{2} \ln^{2} 2 π n - γ \ln 2 π n - (\frac{1}{2} γ^{2} + \frac{π^{2}}{12}) .

He then made also some additional manipulations: substituted

ζ'' (0, 1) = ζ'' (0) = γ_{1} + \frac{1}{2} γ^{2} - \frac{π^{2}}{24} - \frac{1}{2} \ln^{2} 2 π

, paired terms with

\frac{k}{m}

and

\frac{m - k}{m}

in the sums, used explicit form for

ζ'' (0, 1 / 2)

, etc.

Consideration of more terms in the aforementioned Taylor expansion will lead to the expressions of higher generalized Stieltjes coefficients

γ_{n} (\frac{m}{n})

via higher derivatives

ζ^{(m)} (0, \frac{m}{n})

(cf. also second part of [30]). In particular, due to the appearance of the values of the Riemann zeta function of odd integers in the Taylor expansion of

Γ (s)

, e.g.

Γ (s) = \frac{1}{s} - γ + (\frac{1}{2} γ^{2} + \frac{π^{2}}{12}) s + (- \frac{π^{2}}{12} γ - \frac{γ^{3}}{6} - \frac{1}{3} ζ (3)) s^{2} + O (s^{3})

, in such a way we may obtain probably not-without-the-interest expressions of

ζ (2 n + 1)

via the generalized Stieltjes coefficients

γ_{k} (\frac{m}{n})

and derivatives

ζ^{(k)} (0, \frac{m}{n})

References

Apostol, T. M. Hurwitz zeta function; Olver, Frank W. J., Lozier, Daniel M., Boisvert, Ronald F., Clark, Charles W., Eds.; NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, 2010. [Google Scholar]
NIST Digital Library of Mathematical Functions, DLMF: NIST Digital Library of Mathematical Functions, Chapter 25.
Erdélyi, A; Magnus, W; Oberhettinger, F; Tricomi, F.G. Higher Transcendental Functions. Vol. I; McGraw-Hill Book Company Inc.: New York-Toronto-London, 1953. [Google Scholar]
Abramowitz, M; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series; U.S. Government Printing Office: Washington, D.C., 1964. [Google Scholar]
Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th edition; Cambridge University Press: Cambridge, 1927. [Google Scholar]
Elizade, E. Ten Physical Applications of Spectral Zeta Functions, 2nd edition, Lecture Notes in Phys., vol. 855. Springer: Heidelberg, 2012.
Davenport, H.; Heilbronn, H. On the zeroes of certain Dirichlet series. J. London Math. Soc. 1936, 11, 181–185. [Google Scholar] [CrossRef]
Cassels, J.W.S. Footnote to a note of Davenport and Heilbronn. J. London Math. Soc. 1961, 36, 177–184. [Google Scholar] [CrossRef]
Spira, R. Zeroes of Hurwitz Zeta functions. Math. Comp. 1976, 30, 863–866. [Google Scholar] [CrossRef]
Endo, K.; Suzuki, Y. Real zeros of Hurwitz zeta-functions and their asymptotic behavior in the interval (0, 1). J. Math. Anal. Appl. 2019, 473, 624–635. [Google Scholar] [CrossRef]
Nakamura, T. Real zeros of Hurwitz-Lerch zeta functions in the interval (−1, 0). J. Math. Anal. Appl. 2016, 438, 42–52. [Google Scholar] [CrossRef]
Matsusaka, T. Real zeroes of the Hurwitz zeta-function. Acta Arith 2018, 183, 53–62. [Google Scholar] [CrossRef]
Nakamura, T. Real zeros of Hurwitz–Lerch zeta and Hurwitz–Lerch type of Euler–Zagier double zeta functions. Math. Proc. Camb. Phil. Soc. 2016, 160, 39–50. [Google Scholar] [CrossRef]
Frisk, H.; de Gosson, S. On the motion of zeroes of zeta functions. arXiv:math-ph/0102007v1.
B. C. Berndt, B.C. The number of zeroes for $ζ^{(k)} (s)$ . J. London Math. Soc. 1970, 2, 577–580. [Google Scholar] [CrossRef]
Sekatskii, SK. On the Use of the Generalized Littlewood Theorem Concerning Integrals of the Logarithm of Analytical Functions for Calculation of Infinite Sums and Analysis of Zeroes of Analytical Functions. Axioms, 2023; 12, 68. [Google Scholar]
Sekatskii, SK. On the Use of the Generalized Littlewood Theorem Concerning Integrals of the Logarithm of Analytical Functions to Elliptic Functions. Axioms, 2023; 15, 595. [Google Scholar]
Sekatskii, S.K.; Beltraminelli, S.; Merlini, D. On equalities involving integrals of the logarithm of the Riemann $ζ$ -function and equivalent to the Riemann hypothesis. Ukrainian Math. J. 2012, 64, 218–228. [Google Scholar] [CrossRef]
Sekatskii, S.K.; Beltraminelli, S.; Merlini, D. On Equalities Involving Integrals of the Logarithm of the Riemann $ζ$ -function with Exponential Weight which are Equivalent to the Riemann Hypothesis. Int. J. Analysis 2015. art. ID 980728. [Google Scholar] [CrossRef]
Sekatskii, SK; Beltraminelli, S. Some simplest integral equalities equivalent to the Riemann hypothesis. Ukrainian Math. J. 2022, 74, 1256–1263. [Google Scholar] [CrossRef]
Broughan, K.A. Equivalents of the Riemann Hypothesis, vol. 2 Encyclopedia of Mathematics and its Applications; Cambridge Univ. Press: Cambridge, 2017; p. 165. [Google Scholar]
Mezö, I.; Hoffman, M.E. Zeroes of digamma function and its Barnes G-function analogue. Int. Transform. Spec. Funct. 2017, 28, 846–858. [Google Scholar] [CrossRef]
Elizalde, E. An asymptotic expansion for the first derivative of the generalized Riemann zeta function. Math. Comput. 1986, 47, 347–350. [Google Scholar] [CrossRef]
Elizalde, E. A simple recurrence for the higher derivatives of the Hurwitz zeta function. J. Math. Phys. 1993, 34, 3222–3226. [Google Scholar] [CrossRef]
Seri, R. A non-recursive formula for the higher derivatives of the Hurwitz zeta function. J. Math. Anal. Appl. 2015, 424, 826–834. [Google Scholar] [CrossRef]
Coffey, M.W. The Stieltjes constants, their relation to the η_j coefficients, and representation of the Hurwitz zeta function. Analysis 2010, 30, 383–409. [Google Scholar] [CrossRef]
Deninger, C. On the analogue of the formula of Chowla and Selberg for the real quadratic fields. J. reine angew. Math. 1984, 351, 171–191. [Google Scholar]
Beardon, A.F. Complex Analysis. The argument principle in analysis and topology; John Wiles & Sons: Chichester, 1979. [Google Scholar]
Titchmarsh, E.C.; Heath-Brown, E. R. The theory of the Riemann Zeta-function; Clarendon Press: Oxford; UK, 1988. [Google Scholar]
Blagouchine, I.V. A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations. J. Numb. Theory. 2015, 148, 537–592. [Google Scholar] [CrossRef]
Blagouchine, I.V. Rediscovery of Malmsten’s integrals, their evaluation by contour integration methods with some related results. Ramanujan J. 2014, 35, 21–110. [Google Scholar] [CrossRef]
Musser, J. Higher derivatives of the Hurwitz Zeta function, 2011. Master Thesis & Specialists Projects, Paper 1093. http://digitalcommons.wku/theses/1093.
Kölbig, K.S. Complex zeros of an incomplete Riemann zeta function and of the incomplete gamma function. Math. Comp. 1970, 24, 679–696. [Google Scholar] [CrossRef]
Kölbig, K.S. On the zeros of the incomplete gamma function. Math. Comp. 1972, 26, 751–755. [Google Scholar] [CrossRef]
Lewittes, J. Analytic continuation of Eisenstein Series. Trans. Amer. Math. Soc. 1972, 171, 469–490. [Google Scholar] [CrossRef]

Figure 2. The values of

\sum_{z e r o e s_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{2}}

(up) and

\sum_{z e r o e s_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{3}}

(down).

Figure 2. The values of

\sum_{z e r o e s_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{2}}

(up) and

\sum_{z e r o e s_{} ζ (s, z)}^{} \frac{k_{i}}{ρ_{i}^{3}}

(down).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Sums over Inverse Powers of Zeroes of the Hurwitz Zeta-Function, and Some Related Properties of These Zeroes

Abstract

1. Introduction

2. The generalized Littlewood theorem

3. Sums over inverse powers of zeroes for the Hurwitz zeta-function

3.1. General formulae

3.2. Behavior of the s-zeroes when z tends to infinity

3.3. Behavior of the s-zeroes when z tends to zero

3.4. Behavior of the s-zeroes when z tends to -n

4. The sums over inverse zeroes of the Hurwitz zeta-function

5. Some exact values for the sums considered

6. Numerical illustration

7. Discussion and conclusions

Funding

Data Availability Statement

Conflict of interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe