1. Introduction
In physics the dimensions of a massive object can be ignored and can be treated as a pointlike object, i.e. a point particle. In electrostatic theory, point particles with electric charge are referred to as point charges. Two point charges, one with charge and the other one with charge separated by a distance d, constitute an electric dipole. An object with an electric dipole moment p is subject to a torque when placed in an external electric field E. In the context of viscous fluid dynamics and at the very heart of turbulent fluid flows are many interacting vortices that produce a chaotic and seemingly unpredictable velocity field. Gaining new insight into the complex motion of vortices and how they can lead to topological changes of flows is of fundamental importance in our strive to understand turbulence. One aim is to form an understanding of vortex interactions by investigating the dynamics of point vortex dipoles interacting with a hierarchy of vortex structures using idealized point vortex models [1]. The existence of dipoles describes vortex motion and can possibly lead to a better understanding of the turbulence problem. A fully lagrangian numerical method for simulation of 3D nonstationary flow of viscous and ideal incompressible fluid is developed in [2]. This method is based on the representation of a vortex field as a set of dipole particles. An introduced vector-function D describes density of dipole momentum. The equation for this function is in accordance with Navier-Stokes equations. The vorticity is equal to curl of dipole momentum density. Thus vortex field is always solenoidal. The dipole particles are generated at a body surface and are moving and interacting. The region where function D is essentially non-zero approximately coincides with the vortex region. Each dipole particle induces the velocity field which is equal to field of a point dipole at large distance from the particle. But near a particle the induced velocity field takes into account the particle volume and viscosity of the liquid. The method can be applied for simulation of ideal and viscous flows. The dynamics of a dipole without external strain using a long simulation time and a large box size has been studied in [3]. There numerical results are provided for a viscous dipole. In [3] from a practical point of view, the dipole field turns out to be generated from an impulse jet flow and, more generally, when an external forcing characterized by a net linear momentum, is present. Dipoles can originate from jets generated at a strait, or from the coupling between topography and the oscillating tide motion. Dipolar vortices are also self-propagating, which implies some consequences on the transport of mass and heat. For instance, a dipole can trap passive scalars such as phytoplankton [4] within its core, and thereafter transport it. Contrary to the single monopole which is known mathematically to converge towards a Lamb-Oseen vortex by viscous diffusion, this problem seems not to be settled in the case of the dipole. Numerical solutions have been computed by [5] starting with various initial conditions: an initial Lamb dipole, two Rankine vortices or elliptic Kirchhoff vortices, all giving at the end of the simulation a Lamb-like dipole. Finally the presence of a tail behind the dipole and the cause of its formation have been studied as a viscous symmetry breaking. This has been particularly put into evidence theoretically [6] or experimentally [7] in the presence of an external strain. Wang et al. [8] have examined globally dynamical stabilizing effects of the geometry of the domain at which the flow locates and of the geometry structure of the solutions with the finite energy to the three-dimensional 3D incompressible Navier Stokes and Euler systems. The global well-posedness for large amplitude smooth solutions to the Cauchy problem for 3D incompressible NS and Euler equations based on a class of variant spherical coordinates has been obtained, where smooth initial data is not axi-symmetric with respect to any coordinate axis in Cartesian coordinate system. In their work [8] they have considered such variant spherical coordinates with Dirichlet type boundary conditions and have proven existence, uniqueness and exponentially decay rate in time of the global strong solution to the initial boundary value problem for 3D incompressible NS equations for a class of the smooth large initial data and a class of the special bounded domain described by variant spherical coordinates. In the present work it has been determined that as the kinematic viscosity changes from the corresponding value at to the fully viscous case for the Periodic Navier Stokes equations (PNS) at the value the solution reaches a peak ( ) in . (third component of in Cartesian co-ordinates) Here in the viscous case there exists a dipole which is not centered at the center of the cell of the Lattice. This immediately implies that since the dipole by definition has an equal in magnitude positive and negative peak in the third component of velocity, then the dipole Riemann cut-off surface is covered by a closed surface which is the sphere and where a given cell of dimensions is circumscribed on a sphere of radius 1. For such a closed surface containing a dipole it necessarily follows that the flux at the surface of the sphere of wrt to surface normal is zero. In terms of mathematical analysis of the NS equations in a thin spherical shell, the convergence of the longitudinal velocity averaged in the radial direction across the shell to the strong solution to the two-dimensional NS equations on a sphere as the thickness of the shell converges to zero has been rigorously proved by Temam and Ziane. However a Dirichlet type impenetrability condition is used there with all three components of velocity(no gradients at the wall). In the present work a Neumann impenetrability condition is used with the gradient of the third component of velocity. Here at the six points where the sphere touches the cube walls, it has been determined that the velocities satisfy PNS and the function is Hölder continuous there . By using the spherical co-ordinate system in terms of Cartesian co-ordinates and using the chain rule the solution can be extended to all of the sphere. This is the first extension. In terms of pure rotation which signifies rotation of the sphere. Finally as a result in the present work, on the sphere with a Neumann boundary condition, (Here ) a non smooth solution [9] for exists which is Hölder continuous and it is proven that it is possible to extend Hölder continuity on the sphere uniquely to all of the interior of the Ball of radius one. Although non-uniqueness is proposed to occur for solutions in the interior of the ball for PNS equations there exists at least one solution there that is Hölder continuous.
2. Materials and Methods
Consider the incompressible 3D Navier-Stokes equations defined on the 3-Torus
. The PNS system is,
where
is velocity,
is pressure and
is the forcing function. Here
, where
,
, and
denote respectively the
x,
y and
z components of velocity. Introducing Poisson’s equation (see [10–12]), the second derivative
is set equal to the second derivative obtained in the
expression further below, as part of
, and
where the last three terms on rhs of Equation (
2) can be shown to be equal to
[13]. Along with equations below, the continuity equation in Cartesian co-ordinates is
. The one parameter group of transformations on a critical space of PNS is,
Next the right hand side of the group of transformations Equation (
3)are mapped to
variable terms. Here
and
are in the interval
∈
,
The double transformation here is used for notational clarity. Note that the original Navier-Stokes equations are preserved and rearranged in the following form,
where
are given in [14,15] and it has been shown there that this decomposition is valid and that on a volume of an arbitrarily small sphere embedded in each cell of the lattice centered at the central point of each cell of the 3-torus,
is negligible for the case of no viscosity(Euler equation) and for viscosity
the existence of a dipole occurs with the centre of the dipole occurring shifted away from the centre of the given cell. From this equation we can solve for
algebraically and differentiating wrt to
and using Poisson’s equation by setting the representation of each of the two partial derivatives wrt to
equal to each other we can obtain,
which is exactly the following equation,
where
is the external forcing vector and
is the velocity in each cell of the 3-Torus.
For the three forcing terms, set them equal to products of reciprocals of degenerate WeierstrassP functions shifted in spatial co-ordinates from the center
The
is the center of each cell of the lattice in
. Upon substituting the WeierstrassP functions and their reciprocals into Equation (
7) together with the forcing terms given by
(in Eq. (
8)), it has been determined that in the equation terms in it are multiplied by reciprocal
P functions that touch the centers of the cells of the lattice thus simplifying Eq(
7). The initial condition in
at
is instead of a product of reciprocal degenerate
P function for forcing, is a sum of these functions. The parameter
m in the
P function if chosen to be small gives a ball,
In the case when fluid region
has a connected boundary and certain smoothness conditions are fulfilled, Leray proved the solvability of the Navier Stokes equations in his famous paper [16]. The same result holds when the flux
of the velocity vector (all 3 components of velocity) across each connected component
of the boundary vanishes. This condition means that the flow region contains neither sources nor sinks.
Now continuing the analysis, the function
associated with
in [14,15] can be calculated as follows,
where
are pressure gradient derivative terms wrt to
and
z as functions of
t.
Solutions of Equation (
7) exist in the form
where the function
can be explicitly written as
where
is the corresponding eigenvalue associated with the solution of Eqs.(
7-
8). Setting the two functional forms for
equal to each other and solving the ordinary differential equation for
[see [14,15] , a LambertW function solution exists for
and the form of solution is a
W function multiplied by a JacobiSN complex valued function in
. [see [15]-chapter8]
It has recently been shown in [14] that the following PDE results on a suitable subspace of the solution space for
which holds on an epsilon ball about the center of each cell of the lattice and existing (to be shown) dipole center of a given cell of
,
3. Results
The solution in [14] occurs for large
and time
t. The solution was rescaled in
. (In the form
, where
is a large complex valued shift.) In [14] this was valid for
that is the Euler equations. In this paper the same shift occurs but as
approaches unity and given the reduced PNS equations the relationship in terms of the definition of the LambertW function as shown in Equation (
14) exists. The variable
is complexified. As a result the first derivative wrt to
can be written using the chain rule as,
Here it is assumed that
, where
is arbitrary large complex valued data in the complex norm in the complex space
. (The test value of the form of this function turns out to be
where
B is precisely determined to produce the Riemann surface further obtained and
,
where central point occurs for
and
is the dipole off center point for high viscosity. There are two
balls, one about the origin with associated low viscosity and one about the shifted away from origin dipole center associated with high viscosity). Also the variable
is the complexification of the
-component of velocity given by PNS equations on
. (recall one can use either
or
or
or
with a factor of
introduced. It can be shown that as
gets large
. Also note
for the viscous case)
The argument of the shifted Riemann surface obtained is derived from the definition of the LambertW function. The argument of the
W function which is a function of
, say
is set equal to
. It is precisely as follows,
When the logarithm terms are subtracted the other terms are put to the right hand side of the equation. Taking the exponential of both sides cancels the logarithm and leaves us with an exponential of a binomial in
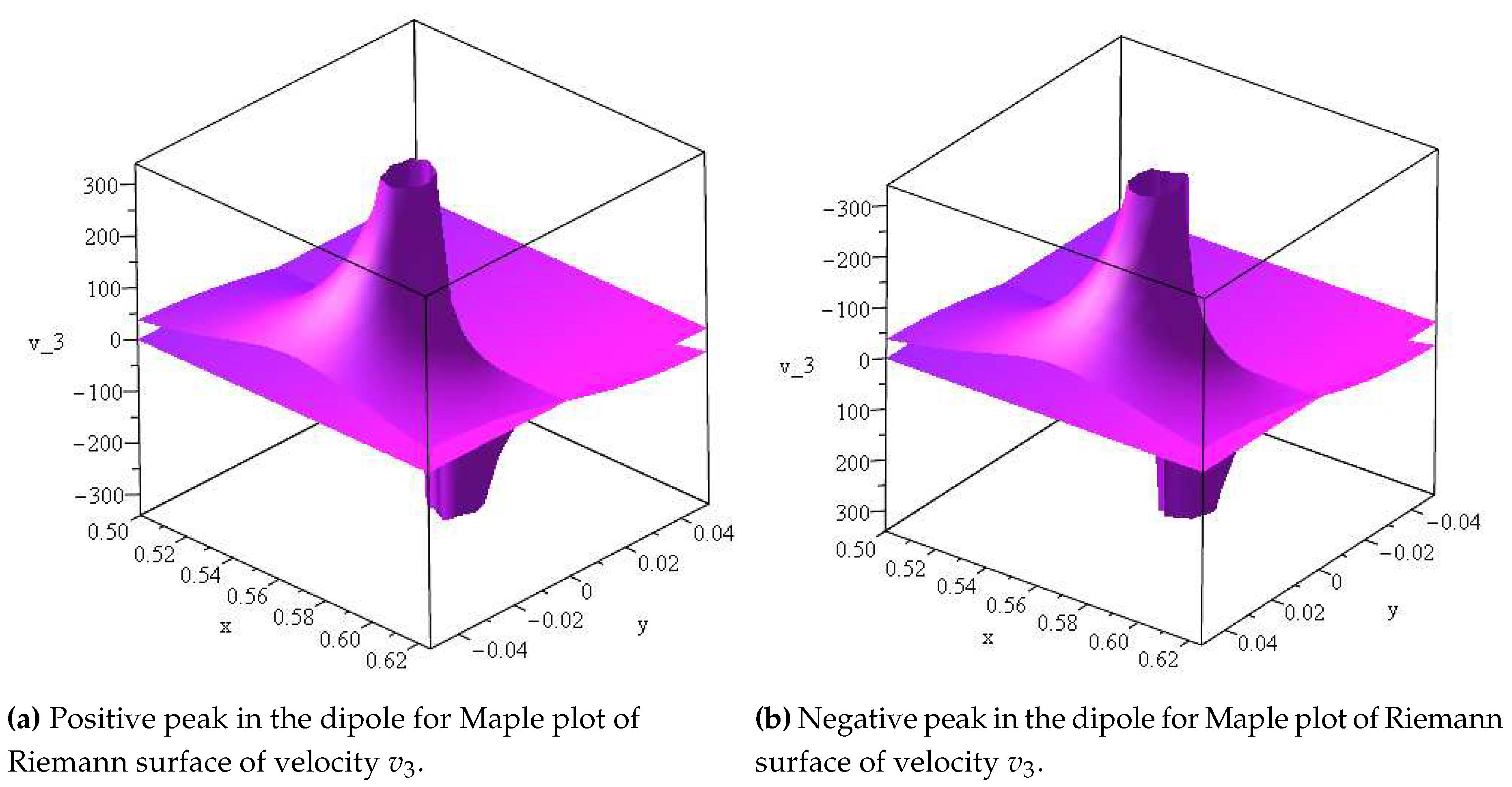
. Linearizing the exponential gives the dipoles in
Figure 2a,b. The "plot3d" command is used where four functions are plotted together, that is,
,
,
u and
v, where
. Here
w is the complex LambertW function associated with the viscous solution. One solves for
in terms of
.
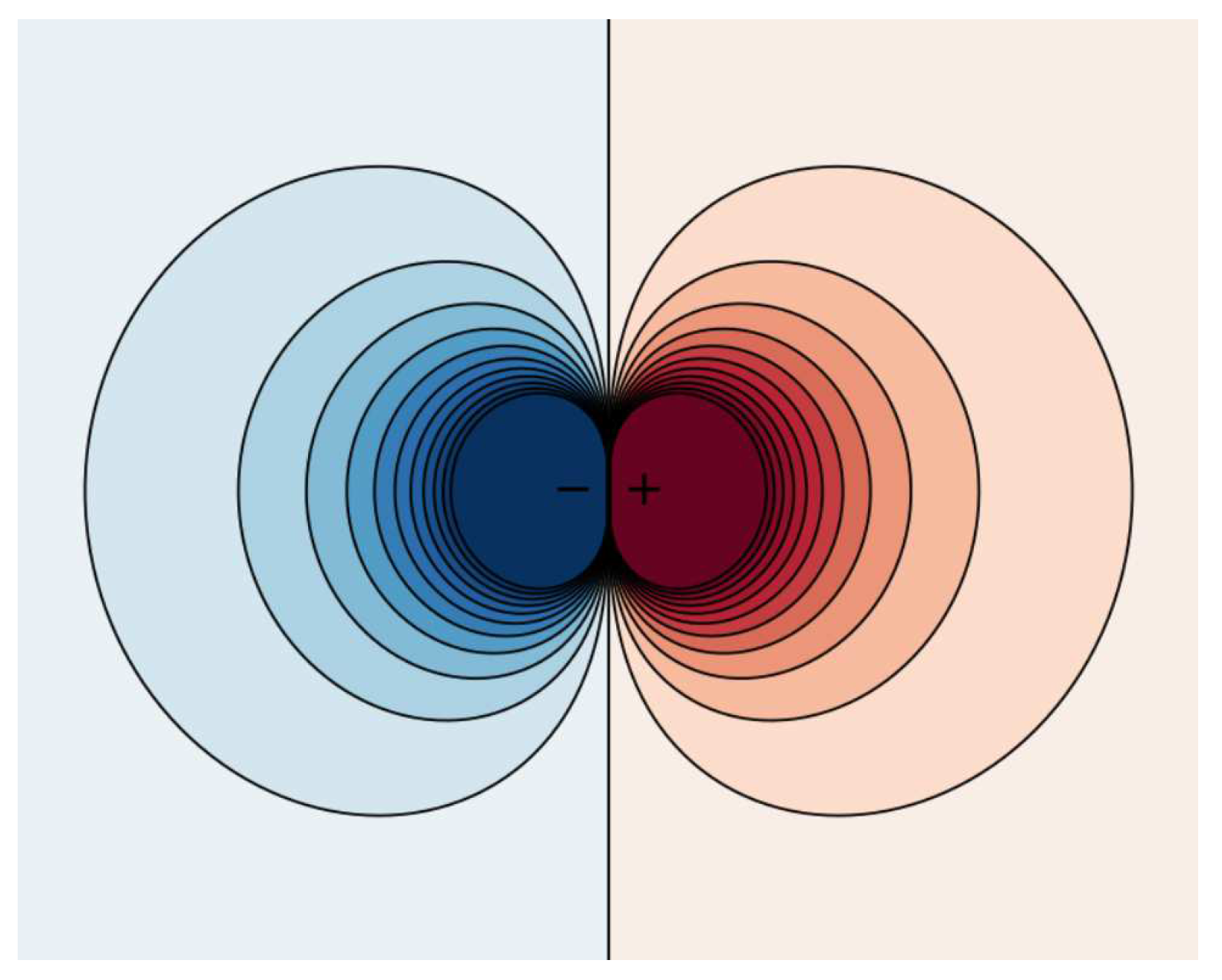
Figure 1.
A Dipole pair associated with a contour plot of -component velocity .
Figure 1.
A Dipole pair associated with a contour plot of -component velocity .
The command lines in Maple are:
Note that we use the following: Given a constant
c we can solve
simply by solving
which says
,
W is the LambertW function. The values are large in
for viscous flows but become physical when we divide by
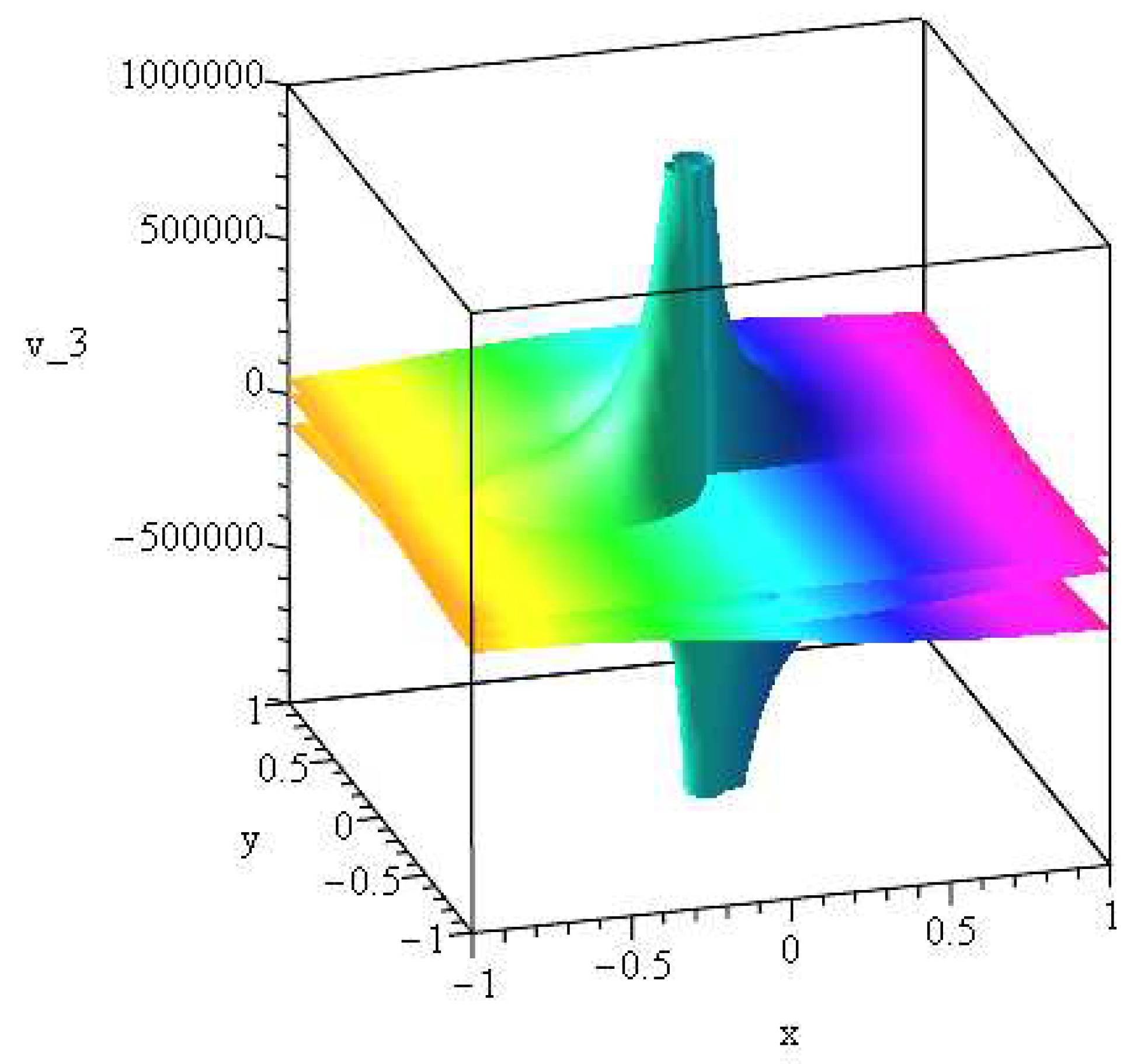
. In
Figure 3 the quantity is scaled down by dividing by an appropriate large
. Here the Riemann surface is centralized for small time
s and very small viscosity in comparison to the viscosity shown in
Figure 2a,b where an offset center exists of a dipole. For the (arbitrary) small viscosity this occurs near the center of the sphere. For low viscosity compared to the higher viscosity case, a finite time singularity occurs well before the higher viscous case. In the first command line of the previous program, taking the negative of both sides and then operating by the exponential function gives on the left side the argument of the LambertW function solution to the viscous problem.
The vanishing of the derivative of
wrt to
is connected to Rummer and Fet’s theory [17] of expressing the volume integral of the Laplacian on an epsilon ball, where in Eq(14) the following reduced PDE occurs when viscosity is included in the PNS equations and thus the reduced form obtained,
Here the viscosity term is not taken to be zero but the gradient of omitted term in the derivative of
wrt to
vanishes itself. This is due to the chain rule and the large shift in the initial condition in
. As a result dividing by viscosity
, the following equation is introduced,
Now it has been pointed out in chapter 8 of reference [14,15] that since
approaching 1 from the right of 1 provides us with a blowup at minus infinity from the right side of some
with linear graphs intersecting arbitrarily large
values at
, that it remains to show that the simplified equation, Equation (
15), with
introduced in place of the derivative term squared has a solution which is Hölder continuous and whose solution has a first derivative blowup from the left at blowup point
. This has already been shown in [14]. Taking
, we have full viscosity in the PNS problem as expected. In [14] the solution was in terms of a LambertW function and for zero viscosity. Here it is seen that as
goes from 0 to 1 that the the solution
has a derivative in
which approaches zero. In
Figure 1 and
Figure 2a,b the Riemann surfaces are obtained using Maple for the complexification of the solution in terms of the initial condition
and large
t determined. [also see [18] on how to obtain the Maple plots of general Riemann surfaces using the "charisma function" Note that
Figure 1 is a contour plot of the Riemann surface of
.]
In the foregoing analyses a matching of two solutions for
and hence
has been carried out. One solution is the extended solution in [14] in which a LambertW solution is obtained as a function of a linear combination of spatial and time variables respectively and particularly for the shifted large data
problem. The second solution is determined to be as in [15] which is the product of a JacobiSN function and a different form of a time dependent function. This is denoted as
. Equating the two forms of the
functions’ LambertW arguments obtained yields,
The incomplete elliptic integral EllipticE is defined as,
Differentiating twice and solving for
gives,
Here the constant
R and
is such that,
In particular
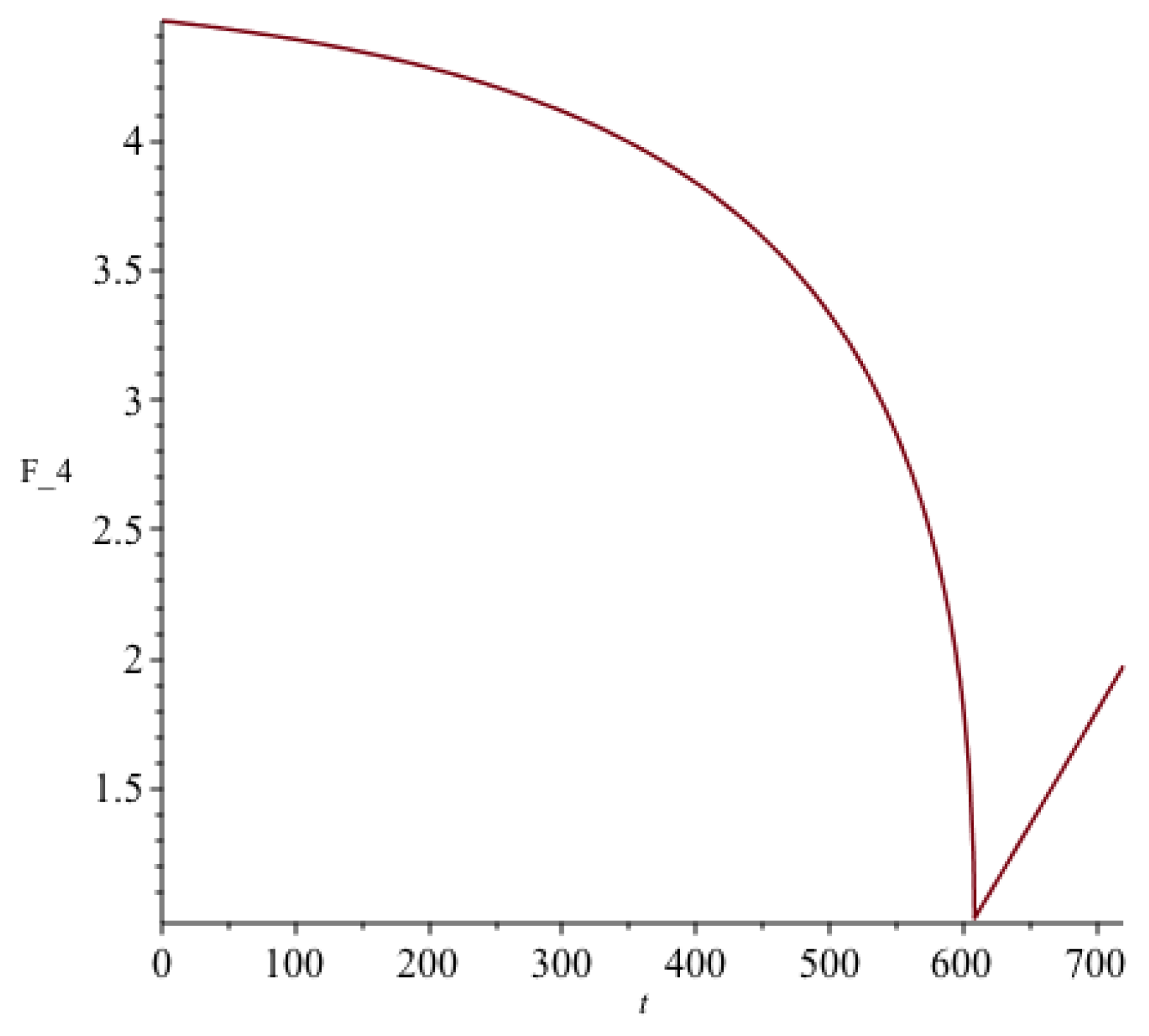
R is chosen to be extremely small and
is very large and as a benchmark test the values considered are,
where these values are substituted in the left side of Eq.(20). (C=1 is set in Equation (
10) for the function
) This temporal solution for the function
can be identified as a Hölder continuous function as shown in
Figure 4.
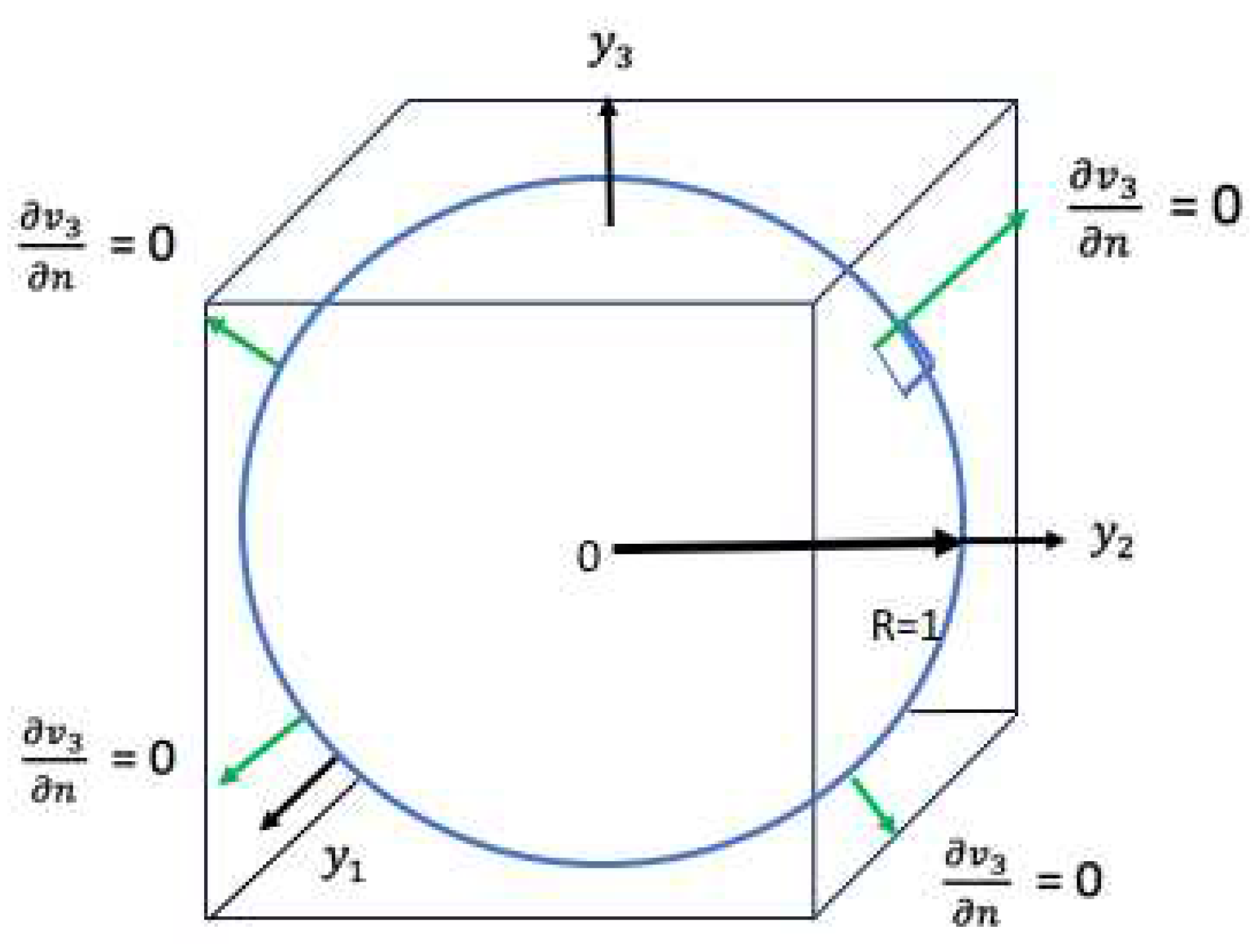
In the viscous case there exists a dipole which is not centered at the center of the cell of the Lattice. This immediately implies that since the dipole by definition has an equal in magnitude positive and negative peak in the third component of velocity, then the dipole Riemann cut-off surface is covered by a closed surface which is the sphere
and where a given cell of dimensions
is circumscribed on a sphere of radius 1. See
Figure 5. For such a closed surface containing a dipole it necessarily follows that the flux at the surface of the sphere of
wrt to
is zero. Finally as a result on the sphere a solution for
is obtained which is proven to be Hölder continuous and it is proven that it is possible to extend Hölder continuity on the sphere to all of the interior of the sphere.
Recalling the WeierstrassP function (
P) based
,
and
solutions in
,
and
co-ordinates,
The governing PDE at the boundary of
of the sphere is directly determined from Eqs.(
7-
8) and the zero flux condition since the sphere contains a dipole, where all the derivatives
,
are taken to be zero. The resulting PDE in Cartesian co-ordinates is,
Factoring out the derivative of
wrt to
s and taking the other factor to be zero, upon substituting
,
and
into Equation (
31) gives a solvable PDE. The corresponding equation has as inputs the functions
,
and
again respectively. Taking each of these functions to be Hölder continuous in
s results in a PDE that has no
s derivatives in it. Hence it can be easily shown that the resulting PDE has as solution a Hölder continuous function in
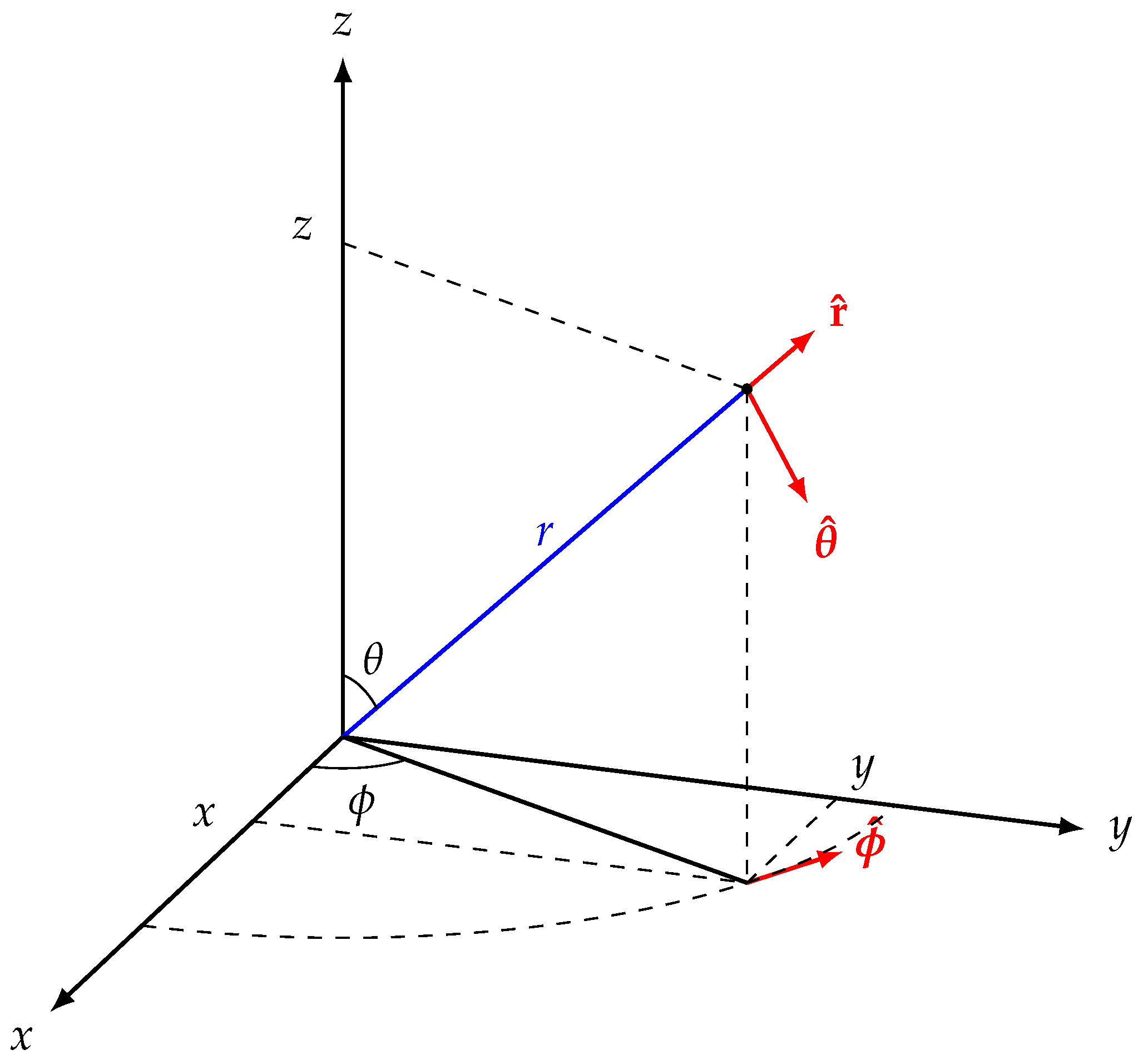
at six points where the surface of the sphere coincides with the boundary of a given open cube. This must be the solution on the sphere boundary which is therefore Hölder continuous. This follows since we have the following co-ordinate transformations between Cartesian and spherical co-ordinates,(see
Figure 6)
It is relatively straightforward to show by using the chain rule and the above transformations on the surface of the sphere that the new function in terms of is separable on the surface of the sphere and thus is in the same Hölder continuous form as the six points mentioned earlier that are known to be Hölder continuous in s there.