Prerpints.org logo
Preprint
Article

Beyond Traditional Assessment: A Fuzzy Logic-Infused Hybrid Approach to Equitable Proficiency Evaluation via Online Practice Tests

Altmetrics

Downloads

69

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 December 2023

Posted:

26 December 2023

You are already at the latest version

Alerts
Abstract
This article presents a hybrid approach to assessing students’ foreign language proficiency in a cyber-physical educational environment. It focuses on the advantages of integrated assessment of student knowledge by considering the impact of automatic assessment, learners’ independent work, and their achievements to date. An assessment approach is described using the mathematical theory of fuzzy functions, which are employed to ensure fair evaluation of students. The largest possible number of students, whose re-evaluation of test results will not affect the overall performance of the student group, is automatically determined. The study also models the assessment process in the cyber-physical educational environment through the formal semantics of calculus of context-aware ambients (CCA).
Keywords: 
Subject: Computer Science and Mathematics  -   Other

1. Introduction

Student assessment is an important aspect of the educational process that aims to measure the knowledge, skills, and achievements of students in the course of their studies. The development of modern education, along with traditional learning, also requires the use of new assessment models, which must provide flexibility in terms of the ways and forms of education, personalization, and the possibility of taking into account the individual characteristics of each student. The problem is becoming more relevant also in terms of reducing the degree of formal education, compared to hybrid forms and the use of virtual educational platforms [1].
Cyber-physical educational environments provide integration of virtual and physical components in the educational process. This model of education is used in various contexts, including in educational institutions, vocational training, distance learning, as well as for non-formal lifelong learning. Motivated by the advantages that these environments provide, teams from the Faculty of Mathematics and Informatics (FMI) of the University of Plovdiv are developing prototypes of cyber-physical educational platforms intended for training both university students and non-learners [2,3]. Assessment is a key feature of any such platform and the difficulties are related to the hybrid nature of learning – face-to-face, distance learning, self-study, project-based, etc.
The article presents a model for assessing students’ knowledge in a cyber-physical educational environment by using the mathematical theory of fuzzy sets. Modeling of processes and communication between intelligent components is realized through the formal semantics of Calculus of context-aware ambients (CCA). To test the presented model, data is used from the assessment of first-year students from FMI of the University of Plovdiv in their English language course.
The structure of the article is as follows: In the second section, the motivation and research related to the topic are discussed. The third part considers the possibilities of applying the theory of fuzzy sets to evaluate students and the CCA modeling of the process of assessment, and the fourth part comments on the findings of the research. The conclusion summarizes the results and points out perspectives for future studies.

2. Motivation and related works

Based on the definition of the National Science Foundation (NSF) [4], Cyber-Physical Systems (CPS) provide integration between computational, network, and physical processes. Embedded digital components and networks monitor and control physical processes, supplying continuous feedback and control. CPS integrate the dynamics of physical processes with those of software and networks, providing opportunities for modeling, design, and analysis techniques. These systems must ensure dynamic interaction with objects from the physical and virtual worlds, which requires the use of autonomous intelligent components. Thus, cyber-physical systems move into cyber-physical spaces, in which users are placed at the center of social interactions. In this sense, the cyber-physical-social space is a fusion of the physical space, cyberspace, and the social space. The evolution from CPS to CPSS [5] is a long process that involves solving challenges and problems of a different nature. These spaces have the potential to be adapted in all spheres of the modern world – in a ”smart city“, agriculture, animal husbandry, transport, medicine, tourism, and, of course, education.
The creation of educational cyber-physical platforms is a challenge, but also a necessity [6]. In these spaces, continuous blended (face-to-face and virtual) learning is possible, tailored to the personal characteristics of each student. An important component of these environments is the development of an appropriate test platform that provides opportunities for assessment and self-assessment of learners [7].
The Virtual-Physical Space (ViPS) is being developed by a team of the DeLC laboratory at the University of Plovdiv as a reference IoT-based architecture that can be adapted to different CPSS applications in different application areas [8]. In the field of higher education, the Virtual Education Space (VES) platform is being developed, which builds on the Distributed e-Learning Center (DeLC) educational platform. DeLC has been actively used in university education since 2004 and provides e-learning services and SCORM-based learning content [9]. Some of the strengths of the testing platform in DeLC are that it is user-friendly and employs metadata, which allows tests to be compiled based on different criteria, enables the use of photos and other visual components, provides an option to preview the test before being administered to students, and offers the option to set a time limit and different validity periods for each test.
An alternative platform used for e-tests at the Faculty of Mathematics and Informatics is DisPeL (Distributed e-Learning Platform), whose key elements are administration of the learning process and adaptability of the learning content [10]. DisPeL enhances the educational process by providing the following electronic services:
  • automation of the administrative process
  • maintaining an adaptive learning process
  • online review of student progress and assessment
  • supporting conventional testing and evaluation.
Due to its advantages and characteristics, the DisPeL test system has been successfully implemented in several universities in Bulgaria. By choosing the appropriate platform, the cyber-physical space allows to automatically process the learners’ scores and through fuzzy sets to make corrections leading to a fairer assessment. We have further illustrated that there is a limit on the number of students being re-evaluated which ensures that after correcting their grades, the mean and the variance of the group does not change statistically significantly. If this set of revised scores is increased, not only does a different distribution result, but also the corrected scores may not correspond to the actual knowledge of the learners.

3. Materials and Methods

The study was carried out in the context of study at FMI of the University of Plovdiv. All students study English as a foreign language for 160 or 200 academic hours in the first academic year depending on their major. Learners have seminars in English once a week and they are taught in groups of about 20 learners of a similar level of knowledge and skills in accordance with the European Framework of Reference for Languages (CEFR) [11]. Since grading is done through continuous assessment, besides the placement test, students at FMI sit for a Midterm and a Final test. Their final grades in English are formed at the end of the course on a six-point scale (2 is the lowest grade corresponding to Fail, and 6 is the highest grade – Excellent).

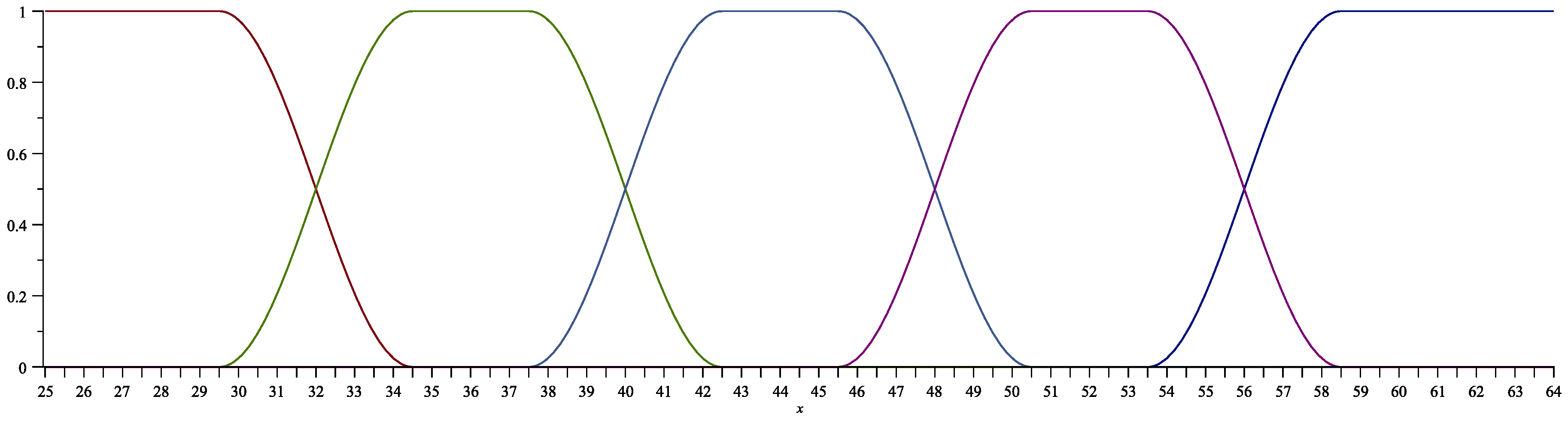
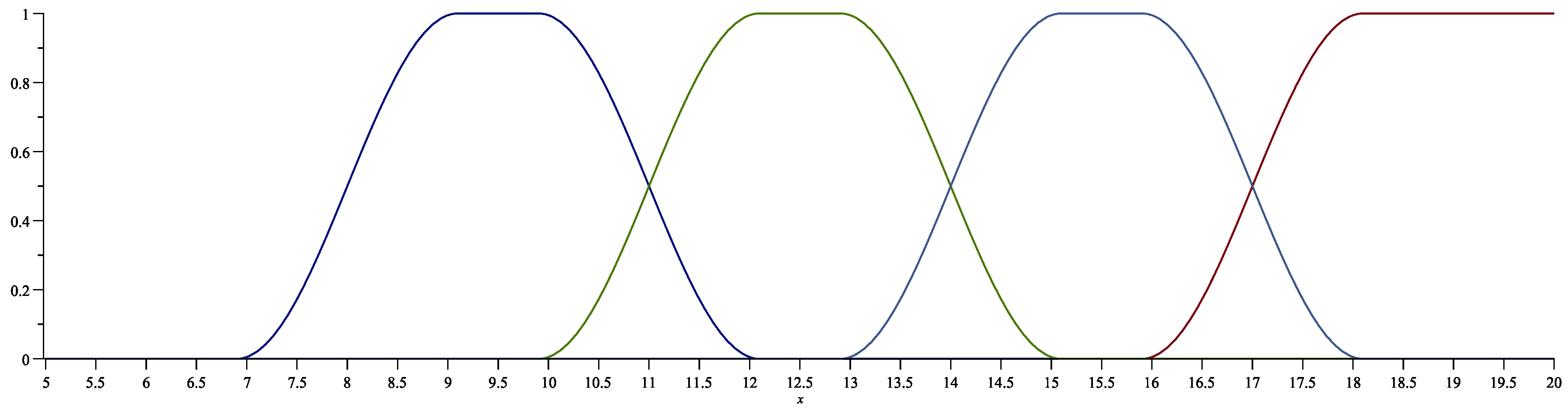
3.1. Application of the fuzzy set theory in student assessment

The standard evaluation of online practice tests at FMI of the University of Plovdiv is conducted by using the following grading system:
  • An Excellent 6 grade is awarded for test scores from 87 % to 100 %
  • A Very good 5 grade – from 75 % to 86 %
  • A Good 4 grade – from 62 % to 74 %
  • A Satisfactory 3 grade is from 50 % to 61 %
  • A Poor 2 grade is 49 % and below.
However, the fairness of marginal, “borderline” scores that determine whether a learner is assigned the higher or the lower grade can be viewed as questionable. It can be considered unjust for a learner to pass a test with 50 points out of 100, and for another one to fail the same exam with only a single point less than him/her. In an attempt to make students’ boundary grades more equitable, we have employed a fuzzy-set technique to change the grades of the borderline cases in two examination tests. Similar efforts have been described in [12] and [13], where fuzzy logic and fuzzy functions were applied to estimate learners’ tests with a view to allocate them a more objective grade.
The first exam considered is a Final test taken by 78 students at the end of the language course. It consists of 60 closed questions and one open, with a maximum score of 80 points, 20 of which are awarded for the open question. When test questions measure similar capability or expertise, they yield a large inner consistency reliability. If a test comprises various types of questions evaluating different kinds of capabilities and knowledge, Cronbach’s coefficient tends to be smaller as a consequence of the dissimilarity of the questions in the context of layout and content. For this reason, initially we need to decide what weight to assign on the open question to guarantee the reliability of the test; an erroneous choice can often prove discriminatory. The alpha coefficient of Cronbach can effortlessly be estimated by means of the formula:
α = k k − 1 1 − Sum   of   Item   Variances Test   Variances
The evaluated test item is 61 with sum of variances 50.91 , and the Test Variance is 179.45 . Inserting these numbers in (1), we get α = 0.72 , which means that the reliability is simply acceptable. The largest variance happens in the open question; consequently, we are searching for γ > 0 to multiply the scores of the open-ended question for α to become bigger. In case we choose γ = 0.2 , we obtain sum of the variances 12.92 , and the Test Variance is 114.99 . Implementing the new numbers in (1), we get α = 0.902 , therefore, the reliability is excellent.
Thus, the maximum score that a learner can receive is 64 (60 for the closed questions + 20 × 0.2 for the open one), i.e. the maximum points for the closed questions are 60, and the maximum score for the open one is 4. Using the standard grading of online practice tests at FMI, the results should be interpreted as follows: An Excellent 6 grade is from 56 to 64 points, a Very good 5 grade is from 48 to 55, a Good 4 grade is from 40 to 47, a Satisfactory 3 grade is from 32 to 39, and a Poor 2 grade is 31 points and below.
The second test is a Midterm Test, taken approximately in the middle of the language course. It was administrated to 36 students altogether. The test consists of 70 closed questions with 1 point awarded for a correct answer, and 3 open questions, the maximium points to which are 6 each. Thus, the overall maximum test points are 88 and the highest possible score for the open items is 18. The Cronbach’s alpha is 0.82 , meaning that the reliability of the test is good. There were no great differences in the variances of the different types of questions, that is why we will not search for a scaling coefficient to increase Cronbach’s alpha coefficient as we did for the first test. At first glance, the results of the second test appear to be worse when compared with the first one, because not a single test–taker has obtained the maximum points. Solely to simplify the calculations and the notations, in order to use one and the same function in the fuzzy sets technique, we scaled the results of the second test. Thus, we scaled the points to ensure that the maximum score obtained by a student in the second test would represent the maximum points of the test, i.e. the highest number of points, received by the students, was 80, therefore we scaled the results of all students with the factor 64 / 80 . Since the scores from the open question(s) are used for fuzzifying some of the test results, we scaled the 18 points from the results from the open questions in the second test by a factor of 20 / 18 in order to be able to use the same functions in the calculations.
Fuzzy logic, fuzzy sets, and fuzzy functions have been widely used since its introduction by Zadeh [13]. We would like to emphasize only several works that have a connection with our investigation in e–learning and e–testing: [14,15,16,17].
A classical technique for reevaluations of test results by fuzzy sets is to consider some borderline grades that need to be reassessed [14,15]. However, we will present a different approach. We will search for a maximum number of possible borderline grades to be fuzzified without changing the statistical distribution of the overall grade. We have considered five functions that stand for the fuzzy membership ones to the sets of marks. We would like to mention that in very recent years there has been a large increase of the usage of fuzzy logic in the evaluation of students’ performance [18,19,20,21,22,23,24,25,26,27,28].
Let f : R 3 → R and g : R 3 → R be two functions. We have specified five functions, which denote the bell-like functions of fuzzy membership to the sets of marks.
μ P o o r = 1 x < x 1 f ( x 1 , x 2 , x ) x 1 ≤ x < x 2 0 x 2 ≤ x ≤ x 9     μ S a t i s . = 0 x 0 ≤ x < x 1 g ( x 1 , x 2 , x ) x 1 ≤ x < x 2 1 x 2 ≤ x < x 3 f ( x 3 , x 4 , x ) x 3 ≤ x < x 4 0 x 4 ≤ x ≤ x 9
μ G o o d = 0 x 0 ≤ x < x 3 g ( x 3 , x 4 , x ) x 3 ≤ x < x 4 1 x 4 ≤ x < x 5 f ( x 5 , x 6 , x ) x 5 ≤ x < x 6 0 x 6 ≤ x ≤ x 9     μ V e r y G o o d = 0 x 0 ≤ x < x 5 g ( x 5 , x 6 , x ) x 5 ≤ x < x 6 1 x 6 ≤ x < x 7 f ( x 7 , x 8 , x ) x 7 ≤ x < x 8 0 x 8 ≤ x ≤ x 9
μ E x c e l l e n t = 0 x 0 ≤ x < x 7 g ( x 7 , x 8 , x ) x 7 ≤ x < x 8 0 x 8 ≤ x ≤ x 9
We can consider the following functions:
f ( a , b , x ) = cos a π a − b − π a − b 2 + 1 2 , g ( a , b , x ) = cos ( 2 a − b ) π a − b − π a − b 2 + 1 2
and we get a bell–shaped fuzzy function μ P o o r , μ S a t i s . , μ G o o d , μ V e r y G o o d , μ E x c e l l e n t , denoted by μ P , μ S , μ G , μ V , μ E , respectively.

3.2. The test construction

The test consists of several sections, each one aimed to check specific knowledge.
Criterion I (reproduction of information) is the lowest level in the cognitive domain, hence multiple choice questions (MCQ) are employed most frequently to determine whether students remember correctly the form of certain expressions, for example:
He kept explaining his point of view until he was ........... in the face but the inspectors were not impressed
a) 
red
b) 
blue
c) 
black
d) 
pink.
The test questions related to Criterion II usually incorporate multiple choice, True/False, or closed questions to match words or expressions with their definitions, synonyms, and antonyms, for example:
Choose the word which is a SYNONYM (a word with a similar meaning) to the capitalized word in the sentence:
The company was FOUNDED by two partners.
a) 
set up
b) 
discovered
c) 
reformed
d) 
destroyed
The test questions relating to Criterion III. (detection of errors in various contexts) are usually multiple choice ones to choose the part of the sentence which contains a spelling or grammar mistake and True or False to determine whether the sentences are free of lexical or grammatical errors or not. For example,
Choose the part of the sentence which contains a spelling or grammar mistake.
The money doesn’t smell.
a) 
the
b) 
money
c) 
doesn’t
d) 
smell
Criterion IV. (analysis of the lexical and grammatical items of a sentence) most often comprises MCQ to select a sentence which most accurately explains the meaning of another one, or to choose the correct grammatical form of a verb, or short-answer test items to write the most appropriate word(s)/ expression(s) or a grammatical form in a sentence. For instance,
Select the sentence which most accurately explains the meaning of the given one.
He was considered a nut and was ridiculed for standing out.
a) 
He was believed to be crazy so everyone mocked him because he wasn’t sitting down like the others.
b) 
The others made fun of him because he liked nuts more than anything else.
c) 
He wasn’t like the others so people thought he was out of his mind and praised him.
d) 
People thought he was a lunatic and laughed at him because he was different.
Finally, the test questions with reference to Criterion V. (text creation) usually instruct students to compose a text with a limited number of words to demonstrate specific knowledge or skills such as writing an email or a review of a product that they have bought, to explain and illustrate the meaning and use of idioms, etc. An example would be the following task:
WRITING: Your friend Kate had asked you to look after her cat while she was abroad but the cat disappeared. Write a short email (50-70 words) to her in which you:
  • Include a greeting;
  • Apologize and say that you lost her cat;
  • Explain how exactly it happened;
  • Say what you have done about it.
  • Close your email.

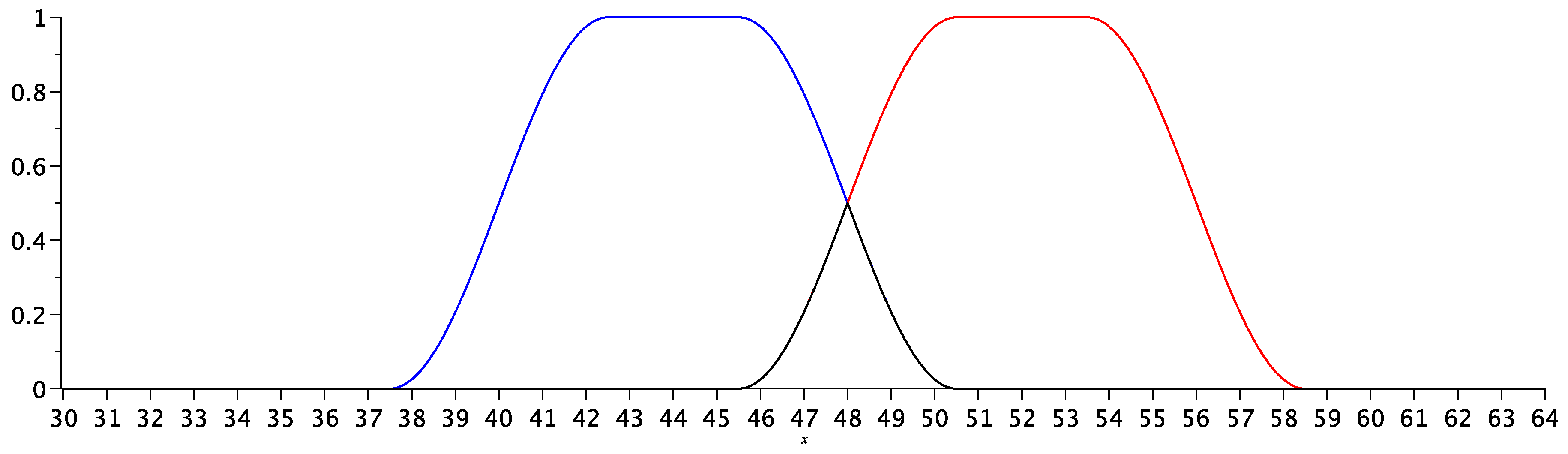
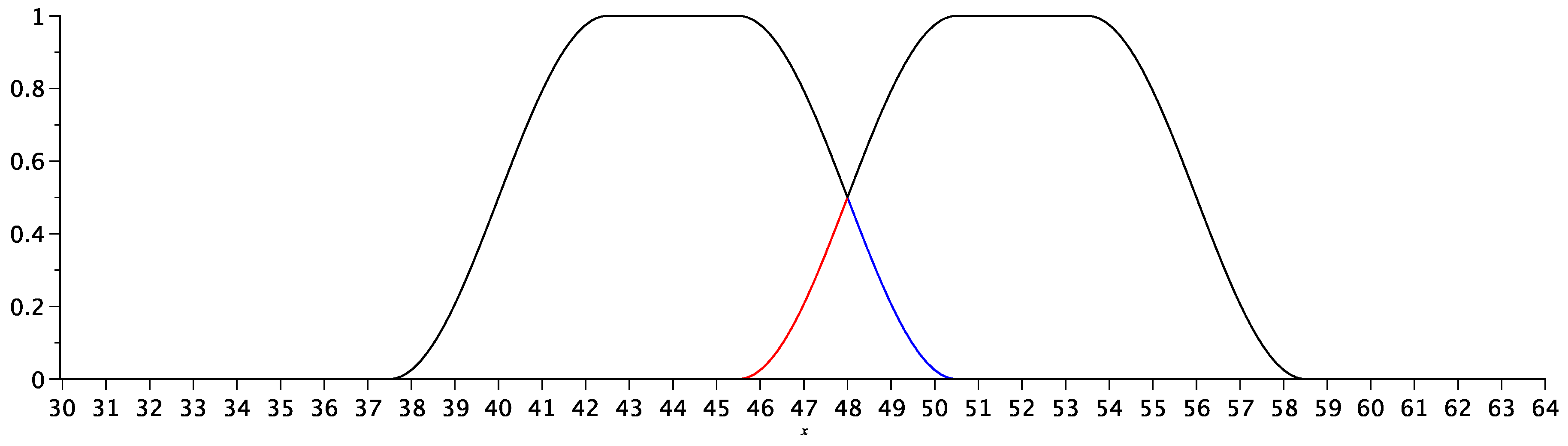
3.3. Illustration of the fuzzy logic usage in recalculating students’ marks

We illustrate the functions defined above in the case when x 0 = 0 , x 1 = 29.5 , x 2 = 34.5 , x 3 = 37.5 , x 4 = 42.5 , x 5 = 45.5 , x 6 = 50.5 , x 7 = 53.5 , x 8 = 58.5 , x 9 = 64 (Figure 1).
Therefore, a student with 41 overall points belongs to the set of Satisfactory grades with a degree 0.21 and to the class of Good grades with a degree 0.79 and to the other sets: Poor, Very good or Excellent grades with a degree 0. A student with an overall score of 44 points belongs to the set of Good grades with a degree 1 and to the other sets: Poor, Satisfactory, Very good, or Excellent mark with a degree 0.
In case the points a learner has received in a test do not belong definitely to a given set, we need to choose a different criterion, which depends on the learner’s result, in order to decide which grade to assign him/her, and that will be the learner’s result on the open items. In addition, we once again divided the learners’ marks into 5 groups: Poor (from y 0 to y 1 points), Satisfactory (from y 2 to y 3 ), Good (from y 4 to y 5 ), Very good (from y 6 to y 7 ), and Excellent (from y 8 to y 9 ), and we also defined their membership functions μ , which we will denote by ν P , ν S , ν G , ν V and ν E
We illustrate the defined above functions in the case y 0 = 0 , y 1 = 6.9 , y 2 = 9.1 , y 3 = 10.4 , y 4 = 12.6 , y 5 = 13.4 , y 6 = 15.6 , y 7 = 16.4 , y 8 = 18.6 , y 9 = 20 (Figure 2).
The norms for executing set procedures of union (AND), intersection (OR), and complement (NOT) that concern us the most are given below.
For Union, we look at the degree of membership for each set and pick the lower one of the two, that is: μ A ∪ B = min ( μ A , μ B ) (Figure 3).
For Intersection, we inspect the degree of membership for each set and choose the larger of the two, that is μ A ∩ B = max ( μ A , μ B ) (Figure 4).
The Fuzzy Associative matrix (Table 1) provides an appropriate manner to immediately integrate the input relations in order to get the fuzzified output results [14] or [29]. The input values for the scores of the open-ended items are at the upper section of the matrix and the input values for the total results of the test are down left in the matrix. We have used the conventional Bulgarian grading scale.
Let us review a learner with a total result of 49 points and a mark on the open-ended item of 19 points. He or she belongs to the set of Very Good marks with a degree μ V e r y G o o d ( 49 ) = 0.79 and to the set of Good grades with a degree μ E x c e l l e n t ( 49 ) = 0.21 . Normally, he/she will be assessed with Very good (5). Nevertheless, the crossing of the two marks – the total points together with the points of the open question, denotes the following: He or she belongs to the set μ V e r y G o o d ∩ ν E x c e l l e n t with 0.79 degree; to μ G o o d ∩ ν E x c e l l e n t with 0.21 degree; to the set μ V e r y G o o d ∩ ν V e r y G o o d with 0.005 degree, and to the set μ G o o d ∩ ν V e r y G o o d with a degree 0.005 of the matrix in Table 1. Consequently, we can assign him or her Excellent (6).
In accordance with [14] and [29], we have to recalculate the mark for each learner, whose test score does not belong definitely to a given set. For this purpose, we can consider the table, in which the function F returns the minimums of μ and ν . The highest membership grade that is obtained from the table stands for the corrected mark from the matrix (Table 2).
Now, by way of illustration, let a student have a total test score of 57 points and open question result of 18 points ( p = 57 and q = 18 ). As shown in Table 3, after the fuzzification, the student will be marked with Excellent (6), which coincides with the traditional evaluation.
If we analyze another learner that has received 42 points (which corresponds to Good (4) in the traditional scoring system) and 17 points for the open-ended item, it is seen from Table 4 that after the correction that particular learner should get a higher mark, namely Very Good (5).
To recalculate the test results, we only need to input the test scores and MapleSoft 2016.0 automatically chooses the scores to be fuzzified and calculates the fuzzified grades.
We define two parameters ε > 0 and δ > 0 and we specify that x 0 = 0 , x 1 = 32 − ε , x 2 = 32 + ε , x 3 = 40 − ε , x 4 = 40 + ε , x 5 = 48 − ε , x 6 = 48 + ε , x 7 = 56 − ε , x 8 = 56 + ε , x 9 = 64 , y 0 = 0 , y 1 = 8 − δ , y 2 = 8 + δ , y 3 = 11 − δ , y 4 = 11 + δ , y 5 = 14 − δ , y 6 = 14 + δ , y 7 = 17 − δ , y 8 = 17 + δ , y 9 = 20 .
As a result, Maple returns that when ε = 2.6 and δ = 1.5 , the two distributions do not differ statistically and ε + δ = 4.1 is the largest possible sum. In this case, we have changed 46 marks. When we fuzzify the grades with ε = 2.7 and δ = 1.5 , the two distributions differ statistically. We acquire 56 marks to be changed as follows: by increasing the set of fuzzified marks we only add new students, whose marks will be reevaluated. That is why we have listed in Table 5 the 56 fuzzified marks as follows (the information below is organized in this order: [classical test grade, classical open question grade], student’s number in the list, test score, open question score, fuzzified grade, classical grade). We have used a bold font for the 10 new students that were added by increasing ε = 2.6 to ε = 2.7 .
At any stage of the calculations, Maple tests the Standard T-Test with Paired Samples. In the case of ε = 2.6 and δ = 1.5 we get that we should accept the hypothesis that the distributions have equal means and in the case ε = 2.7 , δ = 1.5 , Maple returns that we should reject the hypothesis that the two distributions have equal means.
We will analyze the fuzzified grades in the Discussion below in order to justify that we have obtained fairer marks in the first case and less equitable marks in the second one.
In the second exam the students have received the following scores:
Overall points [78, 76, 80, 63, 67, 61, 68, 75, 13, 72, 74, 76, 72, 79, 70, 58, 57, 66, 66, 59, 74, 67, 36, 35, 75, 38, 36, 52, 47, 55, 25, 47, 73, 35, 31, 70] and points on the open questions [15, 14, 15, 7, 6, 8, 9, 13, 0, 13, 13, 14, 11, 15, 15, 3, 9, 11, 8, 9, 13, 12, 0, 3, 14, 0, 0, 6, 7, 8, 0, 3, 13, 0, 0, 7]. Compared with the results from the first test – overall points [57, 74, 58, 58, 22, 65, 19, 70, 21, 63, 42, 42, 62, 42, 63, 23, 47, 62, 66, 74, 59, 56, 69, 59, 67, 55, 48, 41, 52, 46, 42, 37, 53, 61, 58, 30, 35, 69, 63, 66, 54, 41, 48, 47, 50, 63, 56, 41, 50, 56, 45, 36, 60, 43, 69, 55, 70, 77, 71, 74, 24, 66, 54, 43, 49, 59, 53, 42, 54, 60, 62, 56, 35, 59, 71, 53, 61, 52] and points on the open question [18, 20, 19, 19, 7, 18, 0, 20, 0, 17, 14, 16, 14, 16, 18, 10, 8, 20, 16, 19, 16, 16, 20, 14, 20, 18, 18, 0, 14, 7, 9, 0, 8, 13, 20, 9, 0, 12, 16, 18, 18, 13, 19, 15, 17, 19, 8, 15, 20, 19, 16, 0, 16, 15, 20, 20, 19, 20, 20, 20, 10, 19, 19, 0, 0, 0, 16, 10, 14, 14, 18, 18, 7, 19, 17, 16, 16, 6]), it is perceived that the results from the second test from the open questions are much lower than those from the first one.
When we fuzzify the grades with ε = 2.4 and δ = 1.2 , the two distributions will differ statistically. We get 18 grades to be modified, without changing the distributions of the overall marks before and after the fuzzification.

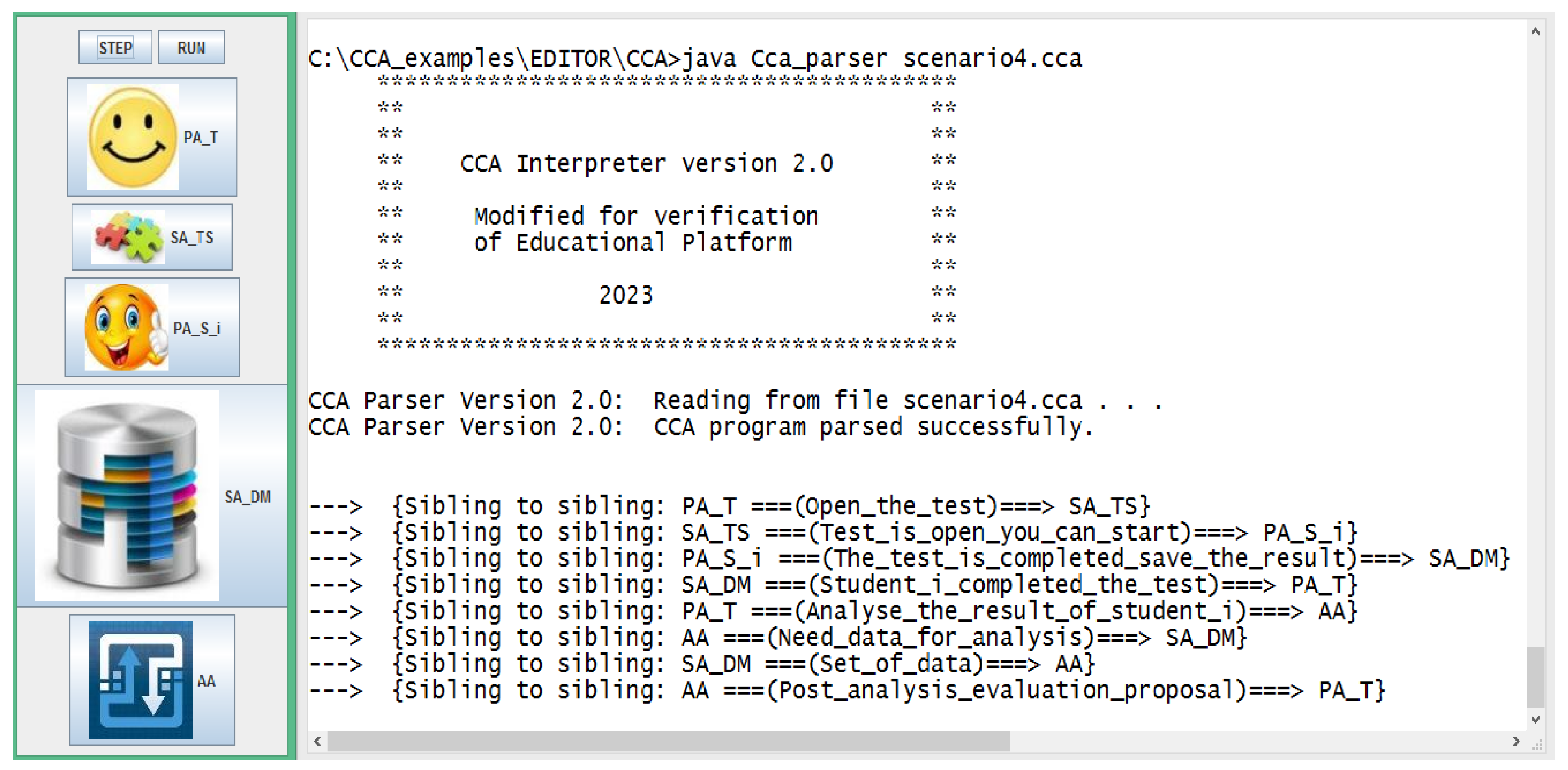
3.4. CCA modeling of the assessment process in a cyber-physical educational environment

Ambient-oriented modeling ( A O M ) is a type of computational process, in the context of which interactions between objects from the physical and the virtual worlds play a major role. The Calculus of Context-aware Ambients ( C C A ) formalism models the system’s ability to respond to changes in the surrounding space [30]. A C S A environment is an identity that is used to describe an object or a component – a process, device, location, etc. Each environment has a name, boundaries, and can contain other environments within itself, as well as be included in another environment. There are three possible relationships between any two environments – parent, child, and relative. Each environment can communicate with the environments around it and environments can exchange messages with each other. The process of exchanging messages is done using the handshaking process. In the notation, “ : : ” is a symbol for relative environments; “ ↑ ” and “ ↓ ” are parent and child symbols; “ < > ” means sending, and “ ( ) ” means receiving a message. An environment can be mobile, i.e. it can move within its surroundings. With C C A , there are two movement options: in and out, which allow environments to move from one location to another. In C C A , four syntactic categories can be distinguished:
  • processes P
  • capabilities M
  • locations α
  • context expressions k.
As we have already pointed out, the concept of ambients is an abstraction of the limited space where some computation is performed. Ambients are mobile and can build ambient hierarchies. Through these hierarchies, any entity in a cyber-physical system can be modeled, regardless of its nature (physical, logical, mobile, or static), as well as the environment (or context) of that entity. In addition, an ambient contains a process representing its capabilities, i.e. the actions that this ambient is allowed to perform, as well as mobility capabilities, contextual capabilities, and communication capabilities.
Due to its dynamic and hybrid nature, the process of assessing student knowledge in the context described in the previous section can be modeled using the mathematical notation of C C A . The cyber-physical educational environment is, by its nature, a multi-agent system that implements processes and services through interaction between various intelligent agents. Each component of the environment is served by one or more specialist assistants, and users are represented in the platform by their personal assistants. Each such intelligent environment component can be represented by a separate C C A ambient. Let us consider the following ambients:
  • PA_T – a personal assistant to the teacher;
  • PA_Si – a personal assistant of the i-th student;
  • SA_TS – a specialist assistant serving the Test System in the Education space
  • SA_DM – a specialist assistant providing services related to the use of data from the Data Module
  • SA_SB – a specialist assistant supporting interaction with Student Books component
  • AA – an analytical assistant that provides services related to information analysis by using the described fuzzy set approach.
We will model the processes of these ambients according to the hybrid approach described above.
The instructor, through their personal assistant, sends a message to the assistant of the test system requesting to open the test for all students. After a student completes the test, their score is recorded in the Data Module, and the teacher receives information about it. The instructor’s personal assistant communicates with the A A ambient with a request to analyze the results of that student according to the considered approach and in consequence receives a proposal for an assessment, which he/she sends to the student’s virtual student book. The process of this ambient is represented by (2).
P P A _ T ≡ S A _ T S : : < Open   the   test > . 0 | S A _ D M : : ( Student i completed   the   test ) . 0 | A A : : < Analyze   the   results   of   student i > . A A : : ( Post − analysis   evaluation   proposal ) . S A _ S B : : < Record   the   grade   of   student i > . 0 )
After receiving a request to open the test from the teacher’s personal assistant PA_T, the SA_TS ambient sends information to the students’ personal assistants. This communication with the i-th student is modeled in (3).
P S A _ T S ≡ P A _ T : : ( Open   the   test ) . S A _ S i : : < Test   is   open ,   you   can   start > . 0
As soon as the student finishes working on the test, his/her personal assistant sends a message to the specialist assistant of the data module SA_DM with a request to record the results obtained. The ambient process is represented by (4).
P P A _ S i ≡ S A _ T S : : ( Test   is   open ,   you   can   start ) S A _ D M : : < The   test   is   complete ,   save   the   result > . 0
The specialist assistant of the data module SA_DM records the results of the students and sends information to the teacher. When it receives a request from the A A ambient, it selects the requested data and sends it for analysis. The process of this ambient is represented in (5).
P S A _ D M ≡ P A _ S i : : ( The   test   is   complete ,   save   the   result ) P A _ T : : < Student i completed   the   test > . 0 | A A : : ( Need   data   for   analysis ) . A A : : < Set   of   data > . 0
The A A ambient analyzes the results of the conducted test after a request from the teacher’s personal assistant. To access a particular set of data, it sends a request to the SA_DM ambient. The process is presented in (6).
P A A ≡ P A _ T : : ( Analyze   the   results   of   student i ) . 0 | S A _ D M : : < Need   data   for   analysis > . 0 | S A _ D M : : ( Set   of   data ) . P A _ T : : < Post - analysis   evaluation   proposal > . 0
The closing stage of the implementation of the process is the recording of the final assessment of the students in the administrative system of the virtual student book (SA_SB).
The c c a P L programming language is a computer-readable version of the C C A syntax. The interpreter of this language enables testing and verification of the modeled scenario (Figure 5).

4. Results and Discussion

We will analyze the fuzzified marks in this section in order to justify that we have obtained fairer marks regardless of the fact that the two distributions differ statistically.
From practical experience, we can verify the use of practice tests can be an effective tool for both student evaluation and learning. By combining tests with open and closed questions and using the fuzzy set technique to correct the results, we achieve more accurate assessment, which helps to a certain extent to avoid the possibility of randomly selected answers, which is a well known risk when administering tests. To justify the ethics and credibility of changing borderline grades, we will explain why we consider it fair to apply changes to the grades when the two distributions after the fuzzification do not differ statistically, and vice versa – that it would not be equitable to make alterations when the two distributions differ statistically.
Let us take as an example the grades of student № 35 from the list of the test takers [4, 6], 35, 42.0, 20, 5, 4. Initially, he had obtained the grade Good (4) with 42 out of 64 points. Inspecting his test, it becomes obvious that he has some knowledge gaps referring to grammar usage, for example his use of Present Perfect tense is rather inconsistent because in some cases he uses it correctly but in others he confuses it with Past Simple tense. However, he has grasped the use of Present Simple and Present Continuous tenses and has completed all the tasks involving those two tenses appropriately. On the other hand, the student has received the maximum of 20 points for the open question – his answer is coherent, logical, with a clear structure, and his thesis is supported by a relevant example. Moreover, from our observations as teachers of this particular student, we can affirm that he is diligent and hard-working and he puts a lot of effort in his work. Therefore, we are convinced that it would be unfair to assess his test with the lower grade – Good 4, but he well deserves the grade of Very good 5, obtained after the process of fuzzification when the two distributions do not differ statistically.
Next, we will consider the instance when delta is larger, in the case of which new students are added, whose grades will be automatically revised. As the hypothesis test shows, a great number of the distributions of assessments are statistically different from the classical evaluation and we will justify that the changes in the assessments that occur in this case can be assumed as unfair.
Now, let us regard another example of a student whose grade would be unjust to alter (when the two distributions differ statistically). Let us review the results, for instance, of a student who is number 6 in the list: [5, 6], 6, 50.6, 18, 6, 5. His original grade, based on the standard grading system, is Very good 5. Although he has obtained a considerably high score on the open question, the mistakes made on the MCQ are quite sporadic, for instance, in certain cases, he has applied a grammar rule correctly, while in others he hasn’t, or the student has selected the appropriate preposition from a list of options in a closed question and then has used it incorrectly in his written text, which suggests a random choice of answers in the test. Consequently, we believe that it would be improper to correct his grade to the maximum possible score.
On the other hand, ambient-oriented CCA modeling makes it possible to describe in a unified way different objects from the physical and the virtual worlds. The development of cyber-physical educational platforms is a labor-intensive, long, and expensive process, which is why the preliminary modeling of the main processes and services in the space is of particular importance. In the context of the need to assess students’ knowledge in the cyber-physical educational space, CCA modeling provides abundant opportunities for preliminary verification, testing, and process analysis.

5. Conclusions

The article discusses a hybrid approach to assessing students’ foreign language knowledge in a cyber-physical educational environment. The presented assessment approach, through the use of the mathematical theory of fuzzy functions, ensures a fair assessment of students, which motivates them to take tests conscientiously in order to get the most out of them.
Ambient-oriented CCA modeling provides ample opportunities for preliminary testing, verification, and analysis of the base scenarios related to both student assessment and provision of the entire learning process in the cyber-physical educational space.

6. Patents

Not applicable.

Author Contributions

Formal analysis: T.G., V.I. and B.Z.; Methodology: T.G., V.I. and B.Z. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The datasets used and/or analyzed during the current study are available from the corresponding author on a request.

Acknowledgments

This study is financed by the European Union-NextGenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project DUECOS BG-RRP-2.004-0001-C01.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Morales-Salas, R.E.; Infante-Moro, J.C.; Gallardo-Pérez, J. Evaluation of virtual learning environments. A management to improve. International Journal of Educational Research and Innovation 2020, 2020, 126–142. [Google Scholar] [CrossRef]
  2. Stoyanov, S.; Glushkova, T.; Stoyanova-Doycheva, A.; Krasteva, I. The virtual education space: Concept, architecture, application. Informatics and Education 2021, 36, 47–54. [Google Scholar] [CrossRef]
  3. Todorov, J.; Krasteva, I.; V., I.; Doychev, E. BLISS-A CPSS-like Application for Lifelong Learning. IEEE International Symposium on INnovations in Intelligent SysTems and Applications, INISTA 2019 - Proceedings, 2019, p. Article number 8778363. [CrossRef]
  4. National Science Foundation (US). Cyber-Physical Systems (CPS), 2008. Available online: https://www.nsf.gov/pubs/2008/nsf08611/nsf08611.htm (accessed on 20 December 2023).
  5. Wang, X.; Yang, J.; Han, J.; Wang, W.; Wang, F.Y. Metaverses and DeMetaverses: From digital twins in CPS to parallel intelligence in CPSS. IEEE Intelligent Systems 2022, 37, 97–102. [Google Scholar] [CrossRef]
  6. Gürdür Broo, D.; Boman, U.; Törngren, M. Cyber-physical systems research and education in 2030: Scenarios and strategies. Journal of Industrial Information Integration 2021, 21, 100192. [Google Scholar] [CrossRef]
  7. National Academies of Sciences, Engineering, and Medicine.. A 21st century cyber-physical systems education, 2017. Available online: https://nap.nationalacademies.org/catalog/23686/a-21st-century-cyber-physical-systems-education (accessed on 20 December 2023).
  8. Stoyanov, S.; Stoyanova-Doycheva, A.; Glushkova, T.; Doychev, E. Virtual physical space – An architecture supporting internet of things applications. 2018 20th International Symposium on Electrical Apparatus and Technologies (SIELA), Bourgas, Bulgaria, 2018, p. Article number 8447156. [CrossRef]
  9. Stoyanov, S.; Glushkova, T.; Stoyanova-Doycheva, A.; Todorov, J.; Toskova, A. A Generic Architecture for Cyber-Physical-Social Space Applications. Intelligent Systems: Theory, Research and Innovation in Applications. Studies in Computational Intelligence 2020, 864, 319–343. [Google Scholar] [CrossRef]
  10. Rahnev, A.; Pavlov, N.; Golev, A.; Stieger, M.; Gardjeva, T. New electronic education services using the Distributed E–Learning Platform (DisPeL). International Electronic Journal of Pure and Applied Mathematics (IEJPAM) 2014, 7, 63–72. [Google Scholar] [CrossRef]
  11. Council of Europe. Common European framework of reference for languages: Learning, teaching, assessment. Cambridge, U.K: Press Syndicate of the University of Cambridge, 2011. Available online: https://rm.coe.int/CoERMPublicCommonSearchServices/DisplayDCTMContent?documentId=0900001680459f97 (accessed on 20 December 2023).
  12. Ivanova, V.; Zlatanov, B. Application of fuzzy logic in online test evaluation in English as a foreign language at university level. AIP Conference Proceedings 2019, 2172, 040009. [Google Scholar] [CrossRef]
  13. Zadeh, L. Fuzzy Sets. Information and Control 1965, 8, 338–353.
  14. Fahad, S.; Shah, A. Intelligent testing using fuzzy logic: Applying fuzzy logic to examination of students. Innovations in E-learning, Instruction Technology, Assessment, and Engineering Education 2007, pp. 95–98. [CrossRef]
  15. Gokmena, G.; Akinci, T.; Tektau, M.; Onat, N.; Kocyigit, G.; Tektau, N. Evaluation of student performance in laboratory applications using fuzzy logic. Procedia Social and Behavioral Sciences 2010, 2, 902–909. [Google Scholar] [CrossRef]
  16. Dias, S.; Diniz, J. FuzzyQoI model: A fuzzy logic-based modelling of users’ quality of interaction with a learning management system under blended learning. Computers & Education 2013, 69, 38–59. [Google Scholar] [CrossRef]
  17. Troussas, C.; Krouska, A.; Sgouropoulou, C. Collaboration and fuzzy–modeled personalization for mobile game–based learning in higher education. Computers & Education 2020, 144, 103698. [Google Scholar] [CrossRef]
  18. Aldana-Burgos, L.; Gaona-García, P.; Montenegro-Marín, C. A Fuzzy Logic Implementation to Support Second Language Learning Through 3D Immersive Scenarios. Smart Innovation, Systems and Technologies 2023, 320, 501–511. [Google Scholar] [CrossRef]
  19. Nandwalkar, B.; Pardeshi, S.; Shahade, M.; Awate, A. Descriptive Handwritten Paper Grading System using NLP and Fuzzy Logic. International Journal of Performability Engineering 2023, 19, 273–282. [Google Scholar] [CrossRef]
  20. Brimzhanova, S.; Atanov, S.; Moldamurat, K.; Baymuhambetova, B.; Brimzhanova, K.; Seitmetova, A. An intelligent testing system development based on the shingle algorithm for assessing humanities students’ academic achievements. Education and Information Technologies 2022, 27, 10785–10807. [Google Scholar] [CrossRef] [PubMed]
  21. Doz, D.; Cotič, M.; Felda, D. Random Forest Regression in Predicting Students’ Achievements and Fuzzy Grades. Mathematics 2023, 11, 4129. [Google Scholar] [CrossRef]
  22. Doz, D.; Felda, D.; Cotič, M. Demographic Factors Affecting Fuzzy Grading: A Hierarchical Linear Regression Analysis. Mathematics 2023, 11, 1488. [Google Scholar] [CrossRef]
  23. Doz, D.; Felda, D.; Cotič, M. Assessing Students’ Mathematical Knowledge with Fuzzy Logic. Education Sciences 2022, 12, 266. [Google Scholar] [CrossRef]
  24. Doz, D.; Felda, D.; Cotič, M. Combining Students’ grades and Achievements on the National assessment of Knowledge: A fuzzy Logic Approach. Axioms 2022, 11, 359. [Google Scholar] [CrossRef]
  25. Doz, D.; Felda, D.; Cotič, M. Using Fuzzy Logic to Assess Students’ Mathematical Knowledge. in Proc. Nauka i obrazovanje – izazovi i perspektive, 2022, pp. 263–278. [CrossRef]
  26. Özseven, B.E.; Çağman, N. A Novel Student Performance Evaluation Model Based on Fuzzy Logic for Distance Learning. International Journal of Multidisciplinary Studies and Innovative Technologies 2022, 6, 29–37. [Google Scholar] [CrossRef]
  27. Özseven, B.E.; Çağman, N. A novel evaluation model based on fuzzy logic for distance learning. [CrossRef]
  28. Sobrino, A. Fuzzy Logic and Education: Teaching the Basics of Fuzzy Logic through an Example (by Way of Cycling). Education Sciences 2013, 3, 75–97. [Google Scholar] [CrossRef]
  29. Ivanova, V.; Zlatanov, B. Implementation of fuzzy functions aimed at fairer grading of students’ tests. Education Sciences 2019, 8, 214. [Google Scholar] [CrossRef]
  30. Siewe, F.; Zedan, H.; Cau, A. The calculus of context-aware ambients. Journal of Computer and System Sciences 2011, 77, 597–620. [Google Scholar] [CrossRef]
Preprints 94383 g001
Figure 1. Plots of μ P o o r , μ S a t i s . , μ G o o d , μ V G o o d and μ E x c e l l e n t .
Figure 1. Plots of μ P o o r , μ S a t i s . , μ G o o d , μ V G o o d and μ E x c e l l e n t .
Preprints 94383 g001
Preprints 94383 g002
Figure 2. Plots of ν P o o r , ν S a t i s . , ν G o o d , ν V G o o d and ν E x c e l l e n t .
Figure 2. Plots of ν P o o r , ν S a t i s . , ν G o o d , ν V G o o d and ν E x c e l l e n t .
Preprints 94383 g002
Preprints 94383 g003
Figure 3. Plots of μ A , μ B and μ A ∩ B = min ( μ A , μ B ) .
Figure 3. Plots of μ A , μ B and μ A ∩ B = min ( μ A , μ B ) .
Preprints 94383 g003
Preprints 94383 g004
Figure 4. Plots of intersection μ A ∪ B = max ( μ A , μ B ) .
Figure 4. Plots of intersection μ A ∪ B = max ( μ A , μ B ) .
Preprints 94383 g004
Preprints 94383 g005
Figure 5. Testing and verification using the c c a P L interpreter and animator
Figure 5. Testing and verification using the c c a P L interpreter and animator
Preprints 94383 g005
Table 1. Fuzzy Associative matrix.
Table 1. Fuzzy Associative matrix.
ν P o o r ν S a t i s f . ν G o o d ν V e r y G o o d ν E x c e l l e n t
μ P o o r 2 2 3 3 4
μ S a t i s f . 2 3 3 4 4
μ G o o d 2 3 4 5 5
μ V e r y G o o d 3 4 5 5 6
μ E x c e l l e n t 3 4 5 6 6
Table 2. The different combinations of the minimums of μ and ν , computed by means of F.
Table 2. The different combinations of the minimums of μ and ν , computed by means of F.
F ( μ P ( p ) , ν P ( q ) ) F ( μ P ( p ) , ν S ( q ) ) F ( μ P ( p ) , ν G ( q ) ) F ( μ P ( p ) , ν V G ( q ) ) F ( μ P ( p ) , ν E ( q ) )
F ( μ S ( p ) , ν P ( q ) ) F ( μ S ( p ) , ν S ( q ) ) F ( μ S ( p ) , ν G ( q ) ) F ( μ S ( p ) , ν V G ( q ) ) F ( μ S ( p ) , ν E ( q ) )
F ( μ G ( p ) , ν P ( q ) ) F ( μ G ( p ) , ν S ( q ) ) F ( μ G ( p ) , ν G ( q ) ) F ( μ G ( p ) , ν V G ( q ) ) F ( μ G ( p ) , ν E ( q ) )
F ( μ V ( p ) , ν P ( q ) ) F ( μ V ( p ) , ν S ( q ) ) F ( μ V ( p ) , ν G ( q ) ) F ( μ V ( p ) , ν V G ( q ) ) F ( μ V ( p ) , ν E ( q ) )
F ( μ E ( p ) , ν P ( q ) ) F ( μ E ( p ) , ν S ( q ) ) F ( μ E ( p ) , ν G ( q ) ) F ( μ E ( p ) , ν V G ( q ) ) F ( μ E ( p ) , ν E ( q ) )
Table 3. The fuzzified learner’s mark when p = 57 , q = 18 .
Table 3. The fuzzified learner’s mark when p = 57 , q = 18 .
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0.005 0.21
0 0 0 0.005 0.79
Table 4. The fuzzified learner’s mark when p = 42 , q = 17 .
Table 4. The fuzzified learner’s mark when p = 42 , q = 17 .
0 0 0 0 0
0 0 0 0.02 0.02
0 0 0 0.5 0.49
0 0 0 0 0
0 0 0 0 0
Table 5.  
Table 5.  
[ 4 , 6 ] , 1 , 42.6 , 18 , 5 , 4 [ 6 , 6 ] , 2 , 58.0 , 20 , 6 , 6 [4, 6], 3, 42.80, 19, 5, 4
[4, 6], 4, 42.80, 19, 5, 4 [ 5 , 6 ] , 6 , 50.6 , 18 , 6 , 5 [ 5 , 6 ] , 8 , 54.0 , 20 , 6 , 5
[ 5 , 5 ] , 10 , 49.4 , 17 , 5 , 5 [ 2 , 5 ] , 11 , 30.8 , 14 , 3 , 2 [2, 5], 12, 29.20, 16, 3, 2
[5, 5], 13, 50.80, 14, 5, 5 [2, 5], 14, 29.20, 16, 3, 2 [ 5 , 6 ] , 15 , 48.6 , 18 , 6 , 5
[ 4 , 2 ] , 17 , 40.6 , 8 , 2 , 4 [ 4 , 6 ] , 18 , 46.0 , 20 , 5 , 4 [5, 5], 19, 53.20, 16, 5, 5
[6, 6], 20, 58.80, 19, 6, 6 [ 4 , 5 ] , 21 , 46.2 , 16 , 4 , 4 [ 5 , 5 ] , 24 , 47.8 , 14 , 5 , 4
[ 4 , 6 ] , 26 , 40.6 , 18 , 5 , 4 [ 3 , 6 ] , 27 , 33.6 , 18 , 4 , 3 [ 4 , 2 ] , 28 , 41.0 , 0 , 2 , 4
[ 4 , 5 ] , 29 , 40.8 , 14 , 4 , 4 [ 4 , 2 ] , 30 , 40.4 , 7 , 2 , 4 [3, 3], 31, 34.80, 9, 3, 3
[ 5 , 2 ] , 33 , 46.6 , 8 , 3 , 4 [ 5 , 4 ] , 34 , 50.6 , 13 , 5 , 5 [ 4 , 6 ] , 35 , 42.0 , 20 , 5 , 4
[ 5 , 5 ] , 39 , 50.2 , 16 , 5 , 5 [ 4 , 6 ] , 41 , 39.6 , 18 , 5 , 3 [ 2 , 4 ] , 42 , 30.6 , 13 , 3 , 2
[ 3 , 6 ] , 43 , 32.8 , 19 , 4 , 3 [ 5 , 6 ] , 46 , 47.8 , 19 , 6 , 4 [ 5 , 2 ] , 47 , 49.6 , 8 , 3 , 5
[ 3 , 6 ] , 49 , 34.0 , 20 , 4 , 3 [ 4 , 6 ] , 50 , 40.8 , 19 , 5 , 4 [ 3 , 5 ] , 51 , 32.2 , 16 , 4 , 3
[ 5 , 5 ] , 53 , 47.2 , 16 , 5 , 4 [ 2 , 5 ] , 54 , 31.0 , 15 , 3 , 2 [ 3 , 6 ] , 56 , 39.0 , 20 , 4 , 3
[ 5 , 6 ] , 57 , 54.80 , 19 , 6 , 5 [ 5 , 6 ] , 59 , 55.0 , 20 , 6 , 5 [ 6 , 6 ] , 60 , 58.0 , 20 , 6 , 6
[5, 6], 62, 50.80, 19, 6, 5 [ 3 , 6 ] , 63 , 38.8 , 19 , 4 , 3 [ 5 , 2 ] , 65 , 49.0 , 0 , 3 , 5
[ 4 , 5 ] , 67 , 40.2 , 16 , 4 , 4 [ 3 , 3 ] , 68 , 34.0 , 10 , 3 , 3 [4, 5], 69, 42.80, 14, 4, 4
[ 5 , 5 ] , 70 , 48.8 , 14 , 5 , 5 [ 5 , 6 ] , 71 , 47.6 , 18 , 6 , 4 [ 4 , 6 ] , 72 , 41.6 , 18 , 5 , 4
[ 2 , 2 ] , 73 , 29.4 , 7 , 2 , 2 [ 6 , 6 ] , 75 , 57.4 , 17 , 6 , 6 [ 4 , 5 ] , 76 , 40.2 , 16 , 4 , 4
[ 5 , 5 ] , 77 , 48.2 , 16 , 5 , 5 [ 5 , 2 ] , 78 , 47.2 , 6 , 3 , 4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated