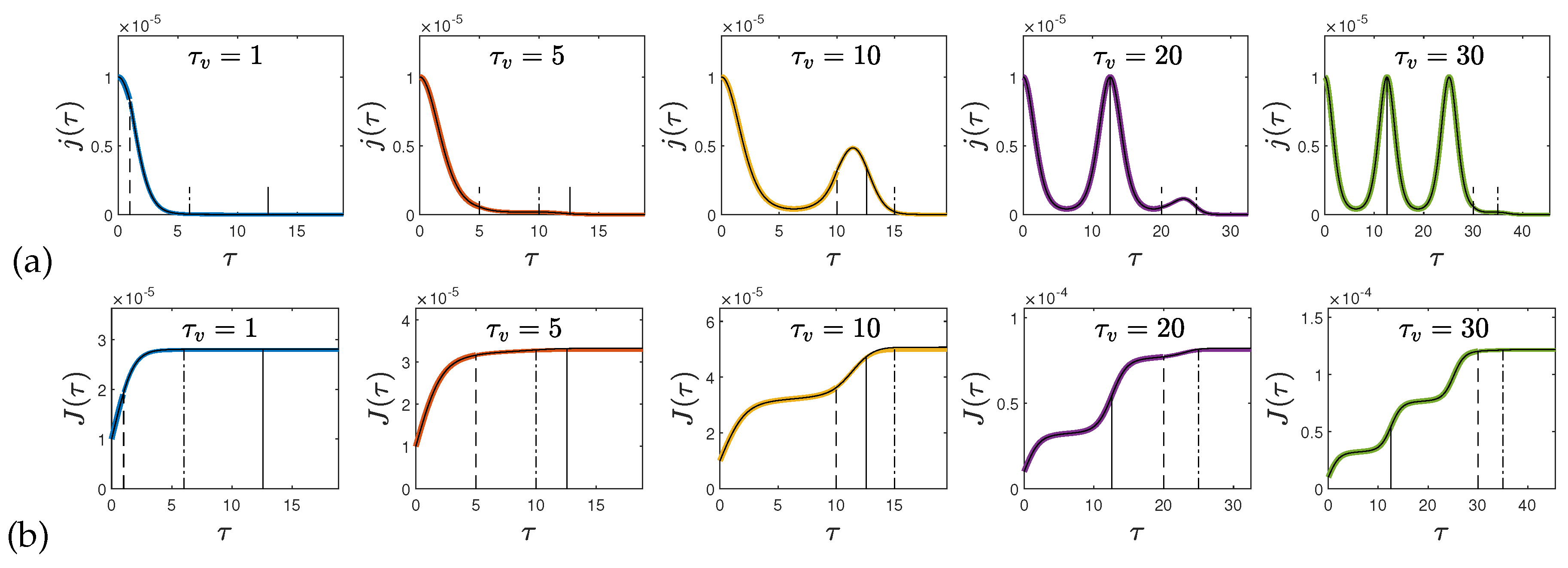Preprint

Article

On the Analytical Solution of the Sirv-Model for the Temporal Evolution of Epidemics for General Time-Dependent Recovery, Infection and Vaccination Rates

Altmetrics

Downloads

115

Views

Comments

A peer-reviewed article of this preprint also exists.

Martin Kröger^*

Reinhard Schlickeiser

Martin Kröger^*

Reinhard Schlickeiser

This version is not peer-reviewed

This preprints belongs to the Collection

Preprints on COVID-19 and SARS-CoV-2

Submitted:

23 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts

Abstract

The susceptible-infected-recovered/removed-vaccinated (SIRV) epidemics model is an important generalization of the SIR epidemics model as it accounts quantitatively for the effects of vaccination campaigns on the temporal evolution of epidemics outbreaks. Additional to the time-dependent infection ($a(t)$) and recovery ($\mu (t)$) rates, regulating the transitions between the compartments $S\to I$ and $I\to R$, respectively, the time-dependent vaccination rate $v(t)$ accounts for the transition between the compartments $S\to V$ of susceptible to vaccinated fractions. An accurate analytical approximation is derived for arbitrary and different temporal dependencies of the rates which is valid for all times after the start of the epidemics for which the cumulative fraction of new infections $J(t)\ll 1$. As vaccination campaigns automatically reduce the rate of new infections by transferring susceptible to vaccinated persons, the limit $J(t)\ll 1$ is even better fulfilled than in the SIR-epidemics model. The comparison of the analytical approximation for the temporal dependence of the rate of new infections $\jt(t)=a(t)S(t)I(t)$, the corresponding cumulative fraction $J(t)$, and $V(t)$, respectively, with the exact numerical solution of the SIRV-equations for different illustrative examples proves the accuracy of our approach. The considered illustrative examples include the cases of stationary ratios with a delayed start of vaccinations, and an oscillating ratio of recovery to infection rate with a delayed vaccination at constant rate. The proposed analytical approximation is self-regulating as the final analytical expression for the cumulative fraction $\jinf $ after infinite time allows us to check the validity of the original assumption $J(t)\le \jinf \ll 1$.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

The susceptible-infected-recovered/removed-vaccinated (SIRV) epidemic model [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] is an important generalization of the simpler susceptible-infected -recovered/removed (SIR) epidemic model [23,24,25,26,27] as it accounts for the effects of vaccination campaigns on a considered population, while the original SIR model does not take into account vaccination campaigns. In the SIRV model the time-dependent infection (

a (t)

), recovery (

μ (t)

) and vaccination (

v (t)

) rates regulate the transitions between the compartments

S \to I

I \to R

and

S \to V

, respectively. Two important key parameters of the SIRV pandemic model are the ratios

k (t) = μ (t) / a (t)

of the recovery to infection rate and

b (t) = v (t) / a (t)

of the vaccination to infection rate. Existing analytical solutions to the SIRV equations [2,28] have adopted originally stationary values of the ratios

k (t) = k_{0}

and

b (t) = b_{0}

, allowing for arbitrary time-dependent infection rates

a (t)

so that the recovery and vaccination rates have the same time dependence as the infection rate. Here we apply the recently developed analytical approach for the solution of the SIR-epidemics model [29] to the SIRV-epidemics model. For all times after the start of the epidemic, for which the cumulative fraction of infected persons

J (t) ≪ 1

is much less then unity, an accurate analytical approximative solution of the SIRV equations is possible for general and arbitrary time dependences of the infection (

a (t)

), recovery (

μ (t)

) and vaccination (

v (t)

) rates. As vaccination campaigns automatically reduce the rate of new infections by transferring susceptible persons directly to vaccinated persons, who then no longer can get infected, the limit

J ≪ 1

is even better fulfilled than in the SIR-epidemics model.

Of high interest, especially from the medical and public health care points of view, are the rate of new infections

\overset{˚}{J} (t)

and its corresponding cumulative number

J (t)

, defined by

\overset{˚}{J} (t) = a (t) S (t) I (t), J (t) = J (t_{0}) + \int_{t_{0}}^{t} d ξ \overset{˚}{J} (ξ),

(1)

respectively, after the start of the pandemic outburst at time

t_{0}

, as the hospitalization and death rates are directly proportional to

\overset{˚}{J} (t)

. Forecasts of the hospitalization and death rates are essential in order to prepare a community for an upcoming pandemic outburst by introducing non-pharmaceutical interventions and/or vaccination campaigns at an optimized time.

The organization of the manuscript is as follows. In Sect. 2 we introduce the starting SIRV-model equations both in terms of the real time t and the reduced time

τ = \int_{t_{0}}^{t} d ξ a (ξ)

. It is beneficial for the analysis to express the SIRV-equations in a form directly involving the observable quantities such as rate of new infections

j (τ) = S (τ) I (τ)

, the cumulative fraction of infections

J (τ) = J (0) + \int_{0}^{τ} d x j (x) = η + \int_{0}^{τ} d x j (x) = 1 - S (τ) - V (τ) = R (τ) + I (τ)

and the cumulative fraction of vaccinated persons

V (τ)

. As shown in Sect. 3 the SIRV-equations in this form allow an approximate analytical solution in the limit of small cumulative fractions

J ≪ 1

. The approximate solution can be written both as function of the real and the reduced time. In Sect. 4 the approximate solutions are compared with the earlier obtained analytical results for the special case of stationary ratios between the recovery to infection rate and the vaccination to infection rate, respectively. In Sects. 5 and 6 we investigate two applications which were inaccessible to analytical treatment before. The considered applications include the cases of stationary ratios with a delayed start of vaccinations (Sect. V), and an oscillating ratio of recovery to infection rate with a delayed vaccination at constant rate (Sect. VI). Here the analytical approximations are compared with the exact numerical solution of the SIRV-equations for these two applications in order to test the accuracy of the analytical approach. A summary and conclusion (Sect. VII) completes the manuscript.

2. SIRV model

The original SIRV-equations read [1]

\begin{matrix} \frac{d S}{d t} & = & - a (t) S I - v (t) S, \end{matrix}

(2)

\begin{matrix} \frac{d I}{d t} & = & a (t) S I - μ (t) I, \end{matrix}

(3)

\begin{matrix} \frac{d R}{d t} & = & μ (t) I, \end{matrix}

(4)

\begin{matrix} \frac{d V}{d t} & = & v (t) S, \end{matrix}

(5)

obeying the sum constraint

S (t) + I (t) + R (t) + V (t) = 1

(6)

at all times

t \geq t_{0}

after the start of the wave at time

t_{0}

with the initial conditions

I (t_{0}) = η, S (t_{0}) = 1 - η, R (t_{0}) = 0, V (t_{0}) = 0,

(7)

where

η

is positive and usually very small,

η ≪ 1

Recently, it has been demonstrated [30] that the SIRV equations (2) -() can be expressed as

\begin{matrix} b (τ) & = & \frac{\frac{d V}{d τ}}{1 - V (τ) - J (τ)}, \end{matrix}

(8)

\begin{matrix} I (τ) & = & \frac{j (τ)}{1 - V (τ) - J (τ)}, \end{matrix}

(9)

and

\begin{matrix} k (τ) = 1 - V (τ) - J (τ) - \frac{d}{d τ} ln [\frac{j (τ)}{1 - V (τ) - J (τ)}] \end{matrix}

(10)

in terms of the reduced time

τ = \int_{t_{0}}^{t} d ξ a (ξ),

(11)

and the ratios

k (τ) = \frac{μ (τ (t))}{a (τ (t))}, b (τ) = \frac{v (τ (t))}{a (τ (t))} .

(12)

The great advantage of the SIRV equations written in the form (8)–(10) is the direct involvement of observable and monitored quantities, such as the rate of new infections

j (τ) = S (τ) I (τ)

, the cumulative fraction of new infections

J (t) = J (τ) = J (0) + \int_{0}^{τ} d x j (x) = η + \int_{0}^{τ} d x j (x) = 1 - S (τ) - V (τ) = R (τ) + I (τ)

and the cumulative fraction of vaccinated persons

V (t) = V (τ)

. This has enabled the determination [30] of the time variation of the ratios

k (t)

and

b (t)

from past Covid-19 mutant waves. For completeness we note the SIRV equations (2)–(5) in terms of the reduced time (11)

\begin{matrix} \frac{d S}{d τ} & = & - S I - b (τ) S, \end{matrix}

(13)

\begin{matrix} \frac{d I}{d τ} & = & S I - k (τ) I, \end{matrix}

(14)

\begin{matrix} \frac{d R}{d τ} & = & k (τ) I, \end{matrix}

(15)

\begin{matrix} \frac{d V}{d τ} & = & b (τ) S, \end{matrix}

(16)

\begin{matrix} 1 & = & S (τ) + I (τ) + R (τ) + V (τ) . \end{matrix}

(17)

In the following we will derive approximate analytical solutions of the four nonlinear differential equations (13)–(16) in the limit of small

J (τ) ≪ 1

and prove its accuracy by comparing with the exact numerical solutions of these equations for a number of illustrative examples of the reduced time dependence of the ratios

k (τ)

and

b (τ)

. As will be demonstrated the proposed analytical approximation is self-regulating as the final analytical expression for the cumulative fraction

J_{\infty} = {lim}_{t \to \infty} J (t)

after infinite time allows us to check the validity of the original assumption

J (t) = J (τ) \leq J_{\infty} ≪ 1

3. Approximative analytical solutions

3.1. Solution in the limit of small $J ≪ 1$

Initially at reduced time

τ = 0

the cumulative number of new infections is extremely small. In the limit

J (τ) \leq J_{\infty} ≪ 1

, where

J_{\infty} = J (τ = \infty)

, also at later times we use the approximations

1 - J (τ) ≃ 1 - J_{\infty}

to obtain for Eq. (8)

b (τ) ≃ \frac{\frac{d V}{d τ}}{1 - J_{\infty} - V (τ)} = \frac{d}{d τ} ln {[1 - J_{\infty} - V (τ)]}^{- 1},

(18)

With the initial condition

V (0) = 0

for arbitrary but given dependencies

b (τ)

, Eq. (18) immediately integrates to

V (τ) ≃ (1 - J_{\infty}) [1 - e^{- \int_{0}^{τ} d x b (x)}],

(19)

which approaches

V_{\infty} = V (\infty) = 1 - J_{\infty}

after infinite time.

Likewise, in the same limit

J \leq J_{\infty} ≪ 1

Eq. (10) becomes

k (τ) ≃ 1 - J_{\infty} - V (τ) - \frac{d}{d τ} ln [\frac{j (τ)}{1 - J_{\infty} - V (τ)}] = (1 - J_{\infty}) e^{- \int_{0}^{τ} d x b (x)} - \frac{d}{d τ} ln [\frac{j (τ) e^{\int_{0}^{τ} d x b (x)}}{1 - J_{\infty}}],

(20)

where we inserted Eq. (19). With the initial condition

j (0) = η (1 - η)

Eq. (20) integrates to

j (τ) ≃ η (1 - η) exp \int_{0}^{τ} d x [(1 - J_{\infty}) e^{- \int_{0}^{x} d y b (y)} - k (x) - b (x)] .

(21)

Because of the adopted smallness

J_{\infty} ≪ 1

we simplify the approximative solution (21) in the following as

j (τ) ≃ η (1 - η) exp \int_{0}^{τ} d x [e^{- \int_{0}^{x} d y b (y)} - k (x) - b (x)] .

(22)

but we keep the

J_{\infty}

in the solution (19) in order not to violate the restriction

J (τ) + V (τ) \leq J_{\infty} + V_{\infty} \leq 1

In terms of the real time in this early time limit the approximative solution (19) and (22) read

V (t) ≃ (1 - J_{\infty}) [1 - e^{- \int_{t_{0}}^{t} d ξ v (ξ)}],

(23)

and

\overset{˚}{J} (t) ≃ a (t) η (1 - η) exp [\int_{0}^{t} d ξ [a (ξ) e^{- \int_{t_{0}}^{ξ} d y v (y)} - μ (ξ) - v (ξ)]],

(24)

respectively.

3.2. Comparison with the SIR model limit

The SIR model corresponds to the limit of no vaccinations

v = b = 0

, corresponding to

V = 0

. In this limit the solutions (22) and (24) reduce to

j_{SIR} (τ) ≃ η (1 - η) e^{\int_{0}^{τ} d x [1 - k (x)]}

(25)

and

{\overset{˚}{J}}_{SIR} (t) ≃ a (t) η (1 - η) e^{\int_{0}^{t} d ξ [a (ξ) - μ (ξ]},

(26)

respectively, in perfect agreement with the earlier derived Eqs. (15) and (17) of ref. [29].

3.3. Properties of the approximative solution (22)

The approximative solution (22) is predominantly determined by the reduced time variation of the ratios

k (τ)

and

b (τ)

. For the first and second time derivatives of the solution (22) we obtain

\begin{matrix} \frac{d j}{d τ} & = & η (1 - η) [e^{- \int_{0}^{τ} d y b (y)} - k (τ) - b (τ)] exp \int_{0}^{τ} d x [e^{- \int_{0}^{x} d y b (y)} - k (x) - b (x)], \end{matrix}

(27)

\begin{matrix} \frac{d^{2} j}{d τ^{2}} & = & η (1 - η) ({[e^{- \int_{0}^{τ} d y b (y)} - k (τ) - b (τ)]}^{2} - \frac{d k}{d τ} - \frac{d b}{d τ} - b (τ) e^{- \int_{0}^{τ} d y b (y)}) exp \int_{0}^{τ} d x [e^{- \int_{0}^{x} d y b (y)} - k (x) - b (x)] . \end{matrix}

(28)

Consequently, extrema of the rate of new infections occur at reduced times

τ_{E}

determined by

k (τ_{E}) + b (τ_{E}) = e^{- \int_{0}^{τ_{E}} d y b (y)} .

(29)

As the right-hand side of this Eq. is smaller or equal than unity no extrema of infections occur for a sum of variations

k (τ) + b (τ) > 1

(30)

greater than unity at all times. As both rates are semi-positive the condition (30) for no extrema in the rate iof new infections is fulfilled if either the vaccination rate

v (t) > a (t)

is greater than the infection rate and/or the recovery rate

μ (t) > a (t)

is greater than the infection rate.

In the case of reduced time intervals where

k (τ) + b (τ) < 1,

(31)

we obtain

{[\frac{d^{2} j}{d τ^{2}}]}_{τ_{E}} = - η (1 - η) ({[\frac{d k}{d τ}]}_{τ_{E}} + {[\frac{d b}{d τ}]}_{τ_{E}} + b^{2} (τ_{E}) + b (τ_{E}) k (τ_{E})) exp [\int_{0}^{τ_{E}} d x (e^{- \int_{0}^{x} d y b (y)} - k (x) - b (x))],

(32)

so that the extrema are maxima if

{[\frac{d k}{d τ}]}_{τ_{E}} + {[\frac{d b}{d τ}]}_{τ_{E}} + b^{2} (τ_{E}) + b (τ_{E}) k (τ_{E}) > 0

(33)

is positive. Alternatively, the extrema are minima if

{[\frac{d k}{d τ}]}_{τ_{E}} + {[\frac{d b}{d τ}]}_{τ_{E}} + b^{2} (τ_{E}) + b (τ_{E}) k (τ_{E}) < 0

(34)

is negative. Note that there can be multiple minima and maxima depending on the reduced time variation of the ratios

k (τ)

and

b (τ)

. The extreme values of the rate of new infections in the case

τ_{E} < τ_{c}

are given by

j_{E} (τ_{E} \leq τ_{c}) = η (1 - η) e^{\int_{0}^{τ_{E}} d x [e^{- \int_{0}^{x} d y b (y)} - k (x) - b (x)]} .

(35)

3.4. Cumulative fraction

Integrating the rate of new infections (22) provides us with the corresponding cumulative fraction

J (τ \leq τ_{c}) = η + η (1 - η) \int_{0}^{τ} d z exp [\int_{0}^{z} d x (e^{- \int_{0}^{x} d y b (y)} - k (z) - b (z))] .

(36)

For general reduced time variations

k (τ)

and

b (τ)

the integral in Eq. (36) can be reasonably well approximated evaluated using the method of steepest descent [31,32] by expanding the argument in the exponential function in Eq. (36) to second order in z around its (possible multiple) minimum values

τ_{m}

h (z) = - \int_{0}^{z} d x (e^{- \int_{0}^{x} d y b (y)} - k (z) - b (z)) ≃ h (τ_{m}) + \frac{{(z - τ_{m})}^{2}}{2 h_{m}^{^{''}}},

(37)

where

h_{m}^{''} = {[\frac{d^{2} h (z)}{d z^{2}}]}_{τ_{m}} .

(38)

With this expansion we obtain for the cumulative fraction (36)

J (τ \leq τ_{c}) ≃ η + η (1 - η) \sum_{m} \sqrt{\frac{π}{2 h_{m}^{^{''}}}} e^{- h (τ_{m})} [\erf (\sqrt{\frac{h_{m}^{^{''}}}{2}} (τ - τ_{m})) + \erf (\sqrt{\frac{h_{m}^{^{''}}}{2}} τ_{m})],

(39)

where the sum of m accounts for possible multiple minima and

\begin{matrix} h (τ_{m}) & = & \int_{0}^{τ_{m}} d x [k (x) + b (x) - e^{- \int_{0}^{x} d y b (y)}], \\ h_{m}^{''} & = & {[\frac{d k}{d τ}]}_{τ_{m}} + {[\frac{d b}{d τ}]}_{τ_{m}} + b^{2} (τ_{m}) + b (τ_{m}) k (τ_{m}) . \end{matrix}

(40)

For a minimum the second derivative

h_{m}^{''} > 0

has to be positive. The minima occur at times given by

k (τ_{m}) + b (τ_{m}) = e^{- \int_{0}^{τ_{m}} d y b (y)},

(41)

and, as discussed before, see Eqs. (29)–(31) only for reduced time intervals where the sum

k (τ) + b (τ) < 1

is less than unity.

4. Special case: stationary ratios

We first consider the approximative solutions (19) and (22) in the special case of stationary ratios

\begin{matrix} k (τ) & = & k_{0}, \\ b (τ) & = & b_{0}, \end{matrix}

(42)

considered before [1]. We readily obtain

V (τ) = (1 - J_{\infty}) [1 - e^{- b_{0} τ}],

(43)

and

j (τ) = η (1 - η) exp [\frac{1 - e^{- b_{0} τ}}{b_{0}} - (k_{0} + b_{0}) τ] .

(44)

Provided

k_{0} + b_{0} < 1

the rate of new infections (44) attains its maximum value at the reduced time

τ_{m} = - \frac{ln (k_{0} + b_{0})}{b_{0}} .

(45)

The maximum rate of new infections then is

j_{\max} = j (τ_{m}) = η (1 - η) {(k_{0} + b_{0})}^{\frac{k_{0} + b_{0}}{b_{0}}} e^{\frac{1 - (k_{0} + b_{0})}{b_{0}}} .

(46)

Equations (45) and (46) agree exactly with Eqs. (98) and (100) derived before [1].

4.1. Cumulative fraction

Integrating Eq. (44) yields for the cumulative fraction

J (τ) = η + η (1 - η) H (τ),

(47)

with the integral

H (τ) = \int_{0}^{τ} d x exp [\frac{1 - e^{- b_{0} x}}{b_{0}} - (k_{0} + b_{0}) x] = b_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1}{b_{0}}} \int_{\frac{e^{- b_{0} τ}}{b_{0}}}^{\frac{1}{b_{0}}} d y y^{\frac{k_{0}}{b_{0}}} e^{- y},

(48)

where we substituted

y = e^{- b_{0} x} / b_{0}

. The integral (48) can be expressed as the difference of two lower incomplete gamma functions

γ (s, x) = \int_{0}^{x} t^{s - 1} e^{- t} d t = Γ (s) - Γ (s, x),

(49)

yielding

H (τ) = b_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1}{b_{0}}} [γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}}) - γ (1 + \frac{k_{0}}{b_{0}}, \frac{e^{- b_{0} τ}}{b_{0}})],

(50)

so that the cumulative fraction (47) is given by

J (τ) = η + η (1 - η) b_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1}{b_{0}}} [γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}}) - γ (1 + \frac{k_{0}}{b_{0}}, \frac{e^{- b_{0} τ}}{b_{0}})] .

(51)

For infinitely large times the fraction (51) approaches the final value

J_{\infty} = J (τ = \infty) = η + η (1 - η) b_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1}{b_{0}}} γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}}) .

(52)

Equations (51) and (52) agree exactly with the earlier derived Eqs. (A10) and (102) of ref. [1], using a different approach.

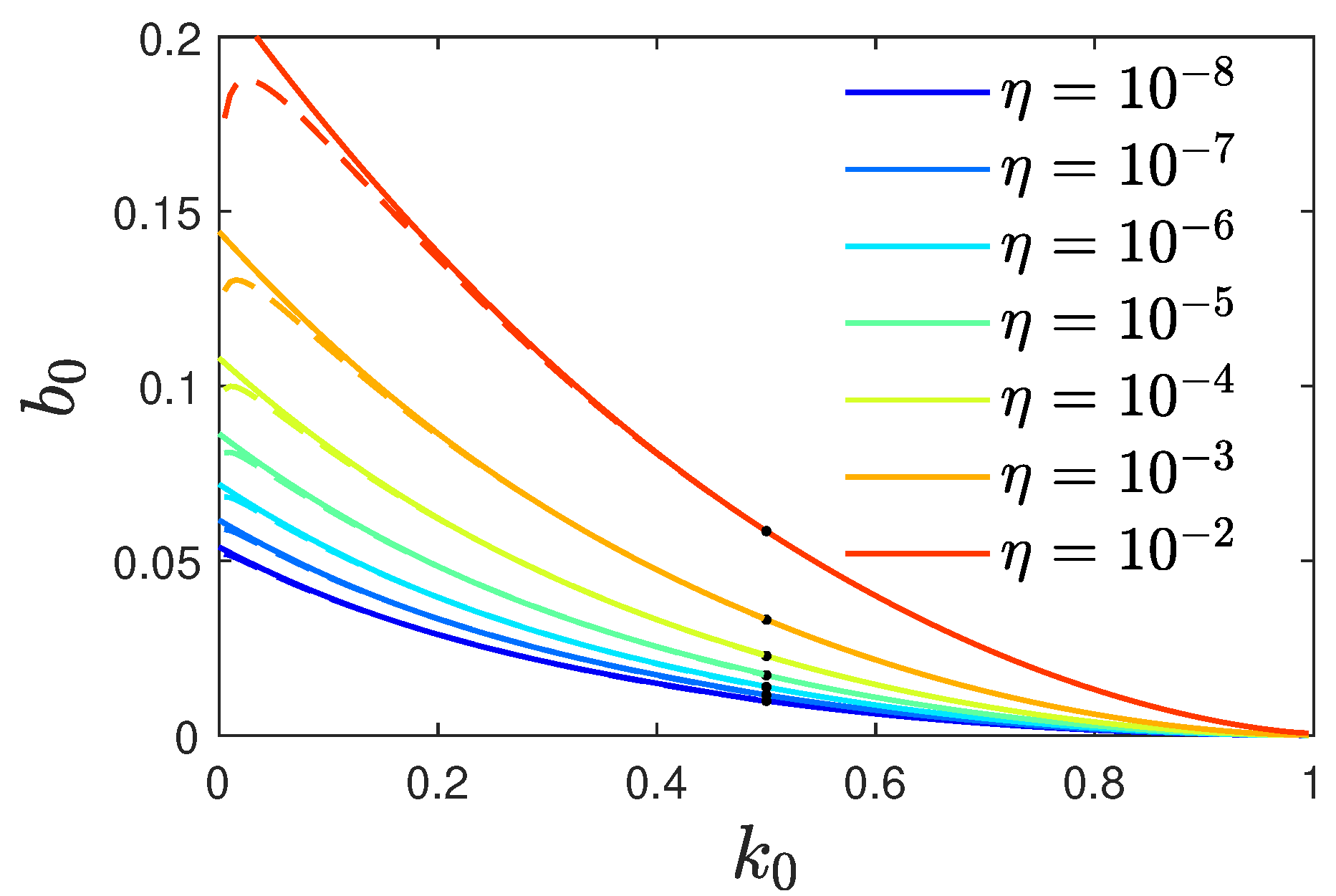
Because the analytical approximations were derived in the limit

J \leq J_{\infty} ≪ 1

, for consistency we have to require

J_{\infty} < 1

for the values of

k_{0}

and

b_{0}

for which our approximation holds. In Figure 1 we calculate the required values of

k_{0}

and

b_{0}

fulfilling

J_{\infty} < 1

using Eq. (52). The required values depend on the initial condition encoded by

η

, and are located above the line shown in this figure. For sufficiently large

k_{0}

J_{\infty} < 1

for any ratio

b_{0}

, while at low recovery to infection ratios

k_{0}

, the vaccination to infection rate must be significant to ensure

J_{\infty} < 1

. The regime of

b_{0}

close to zero is numerically difficult to evaluate using Eq. (52).

4.2. Limit $b_{0} ≪ 1$

In the limit of small

b_{0} ≪ 1

we use relation (49) and the asymptotic expansion (Eq. 6.5.32 in [33]) of the upper incomplete gamma function for large arguments

x ≫ 1

Γ (s, x ≫ 1) ≃ x^{s - 1} e^{- x} [1 + \frac{s - 1}{x} + \frac{(s - 1) (s - 2)}{x^{2}} + \dots],

(53)

to obtain for

γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}}) ≃ Γ (1 + \frac{k_{0}}{b_{0}}) - b_{0}^{\frac{k_{0}}{b_{0}}} e^{- \frac{1}{b_{0}}} [1 + k_{0} + k_{0} (k_{0} - 1) + \dots]

(54)

The fraction (52) then becomes

J_{\infty} (b_{0} ≪ 1) ≃ η + η (1 - η) [Γ (1 + \frac{k_{0}}{b_{0}}) b_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1}{b_{0}}} - [1 + k_{0} + k_{0} (k_{0} - 1) + \dots]]

(55)

Using Stirling’s (Eq. 6.1.37 in [33]) formula for the gamma function

Γ (x + 1) \sim \sqrt{2 π x} {(x / e)}^{x} [1 + {(12 x)}^{- 1}]

for large x, Eq. (55) becomes,

J_{\infty} (b_{0} ≪ 1) ≃ η + η (1 - η) [\sqrt{\frac{2 π k_{0}}{b_{0}}} k_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1 - k_{0}}{b_{0}}} (1 + \frac{b_{0}}{12 k_{0}}) - [1 + k_{0} + k_{0} (k_{0} - 1) + \dots]]

(56)

For values of

b_{0} < k_{0} < 1

the fraction (56) to leading orders is given by

J_{\infty} (b_{0} ≪ 1) ≃ η + η (1 - η) [\sqrt{2 π k_{0} / b_{0}} e^{(1 - k_{0}) / b_{0}} k_{0}^{k_{0} / b_{0}} - 1] .

(57)

Because one has to require

J_{\infty} \leq 1

, or equivalently,

ln (J_{\infty}) \leq 0

, Eq. (57) turns into an inequality for

b_{0}

, that can be written in terms of the principal branch

W_{0}

of Lambert’s W-function, because

(x / b_{0}) - ln b_{0} = ln y

is solved for any

x \geq 0

and y by

x / W_{0} (x y)

, leading to

b_{0} \geq \frac{2 (1 - k_{0} + k_{0} ln k_{0})}{W_{0} (\frac{{(1 + η)}^{2} [1 - k_{0} + k_{0} ln (k_{0})]}{π k_{0} η^{2}})} .

(58)

This inequality (58) ensures

J_{\infty} \leq 1

. Along with the information contained in Eq. (52), it is visualized in Figure 1.

5. Stationary ratios with delayed start of vaccinations

As first new application of our results we discuss the case of stationary ratio

k (τ) = k_{0}

for all reduced times and the influence of a stationary ratio

b (τ)

starting at the delayed reduced time

τ_{v} > 0

, i.e.,

\begin{matrix} k (τ) & = & k_{0}, \\ b (τ) & = & b_{0} Θ (τ - τ_{v}) \end{matrix}

(59)

where

Θ (x < 0) = 0

and

Θ (x \geq 1)

denotes the step function. We then obtain for Eq. (19), i.e., in the limit

J ≪ 1

V = 0

for

τ < τ_{V}

and

V (τ \geq τ_{v}) = (1 - J_{\infty}) [1 - e^{- b_{0} (τ - τ_{v})}] .

(60)

Likewise the rate (22) becomes the SIR-rate [29]

j (0 \leq τ < τ_{v}) = η (1 - η) e^{(1 - k_{0}) τ}

(61)

at times without vaccination and

j (τ \geq τ_{v}) = η (1 - η) exp [(1 - k_{0}) τ_{v} + \frac{1 - e^{- b_{0} (τ - τ_{v})}}{b_{0}} - (k_{0} + b_{0}) (τ - τ_{v})]

(62)

at later times. While the SIR-rate (61) is exponentially increasing in reduced time, the rate (62) has a maximum value

\begin{matrix} j_{\max} = j (τ_{m}) & = & η (1 - η) exp [(1 - k_{0}) τ_{v} + \frac{1 - e^{- b_{0} (τ_{m} - τ_{v})}}{b_{0}} - (k_{0} + b_{0}) (τ_{m} - τ_{v})] \\ = & η (1 - η) {(k_{0} + b_{0})}^{\frac{k_{0} + b_{0}}{b_{0}}} exp [(1 - k_{0}) τ_{v} + \frac{1 - (k_{0} + b_{0})}{b_{0}}], \end{matrix}

(63)

provided

k_{0} + b_{0} < 1

, the rate of new infections attains its maximum at the reduced time

τ_{m} = τ_{v} - \frac{ln (k_{0} + b_{0})}{b_{0}} .

(64)

We first note that for

τ_{v} = 0

the rates (62) and (63) correctly reproduce the earlier results (44) and (46). We emphasize that the delayed start of the vaccinations increases both the maximum time of the rate of infections and the maximum rate of new infections. Compared to the case of no delay in the start of vaccinations (

τ_{v} = 0

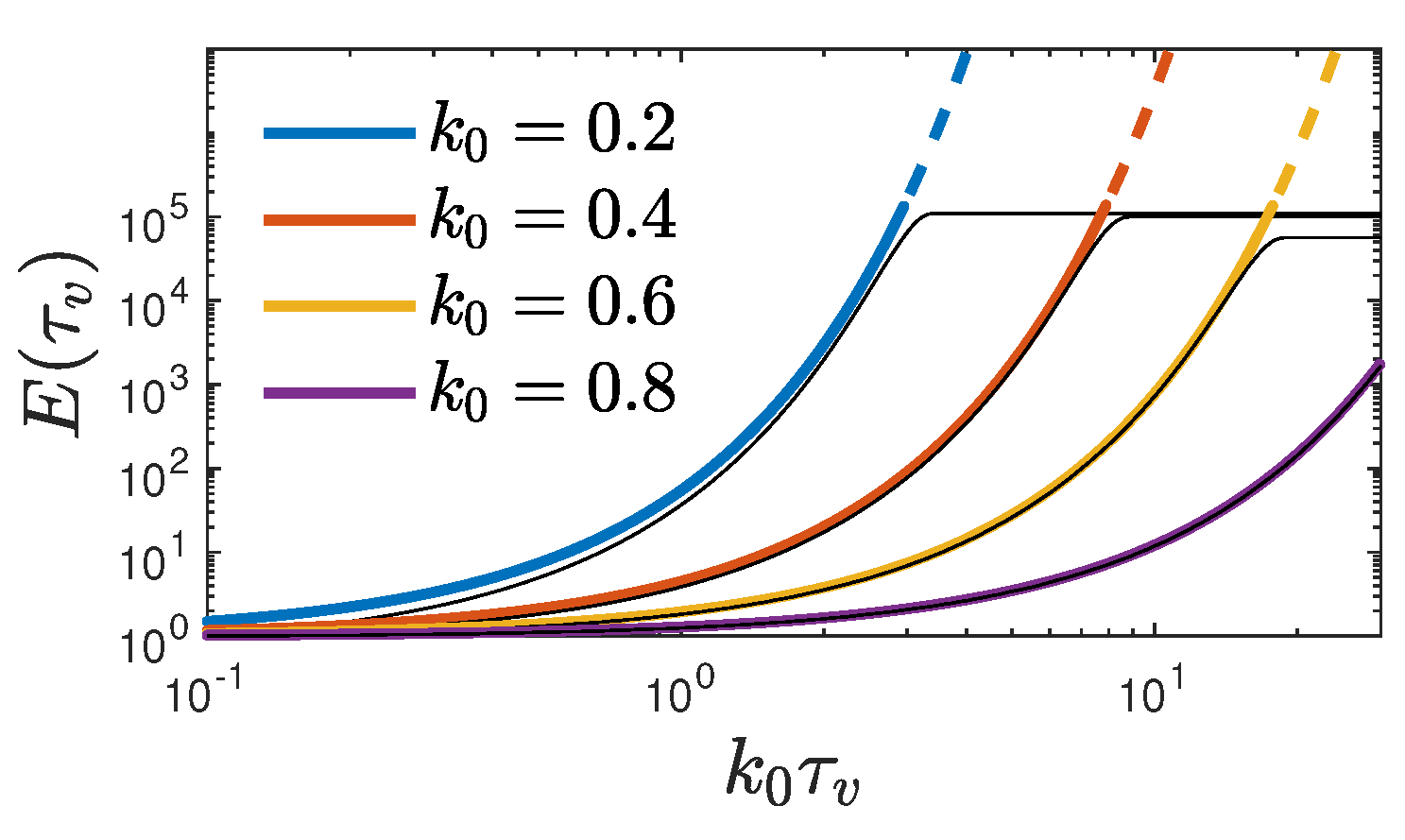
) we introduce the enhancement factor for the maximum rate

E (τ_{v}) = \frac{j_{\max} (τ_{v})}{j_{\max} (τ_{v} = 0)} = e^{(1 - k_{0}) τ_{v}},

(65)

shown in Figure 2, which is independent of the vaccination rate and determined by the values of

k_{0}

and

τ_{v}

. Apparently, this exponential enhancement solely results from the new infections before the vaccinations start. While the enhancement factor increases exponentially over a wide range of

k_{0} τ_{v}

, in accord with Eq. (65), it numerically reaches a plateau as

k_{0} τ_{v}

approaches infinity, whose height increases with decreasing

η

. This is a clear indications that for large values of the enhancement factor a regime is reached where no longer

J (τ_{m})

is much smaller than unity so that the analytical approximation no longer holds. This explanation is supported by the cumulative fraction at large times (68) (see below) being directly proportional to the enhancement factor (65).

Integrating the rates of new injections (61) and (63) yields for the cumulative fraction

J (0 \leq τ < τ_{v}) = η + \frac{η (1 - η)}{1 - k_{0}} [e^{(1 - k_{0}) τ} - 1],

(66)

and

J (τ \geq τ_{v}) = η + \frac{η (1 - η)}{1 - k_{0}} [e^{(1 - k_{0}) τ_{v}} - 1] + η (1 - η) b_{0}^{\frac{k_{0}}{b_{0}}} e^{(1 - k_{0}) τ_{v} + \frac{1}{b_{0}}} [γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}}) - γ (1 + \frac{k_{0}}{b_{0}}, \frac{e^{- b_{0} (τ - τ_{v})}}{b_{0}})] .

(67)

For infinite large times the fraction (67) approaches the final value

\begin{matrix} J_{\infty} = J (τ = \infty) & = & η + \frac{η (1 - η)}{1 - k_{0}} [e^{(1 - k_{0}) τ_{v}} - 1] + η (1 - η) b_{0}^{\frac{k_{0}}{b_{0}}} e^{(1 - k_{0}) τ_{v} + \frac{1}{b_{0}}} γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}}) \\ = & \frac{η (1 - η)}{1 - k_{0}} E (τ_{v}) [1 + (1 - k_{0}) b_{0}^{\frac{k_{0}}{b_{0}}} e^{\frac{1}{b_{0}}} γ (1 + \frac{k_{0}}{b_{0}}, \frac{1}{b_{0}})] + \frac{η (η - k_{0})}{1 - k_{0}} . \end{matrix}

(68)

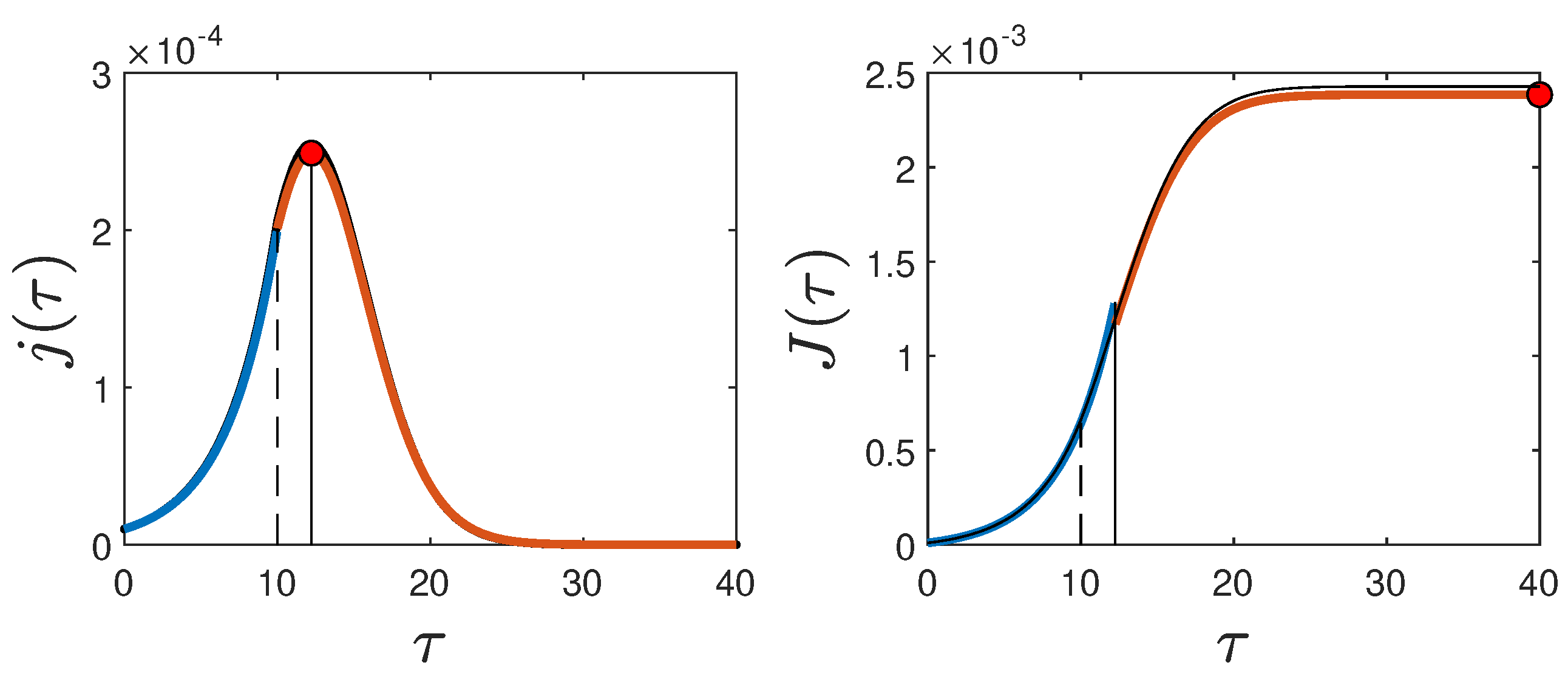
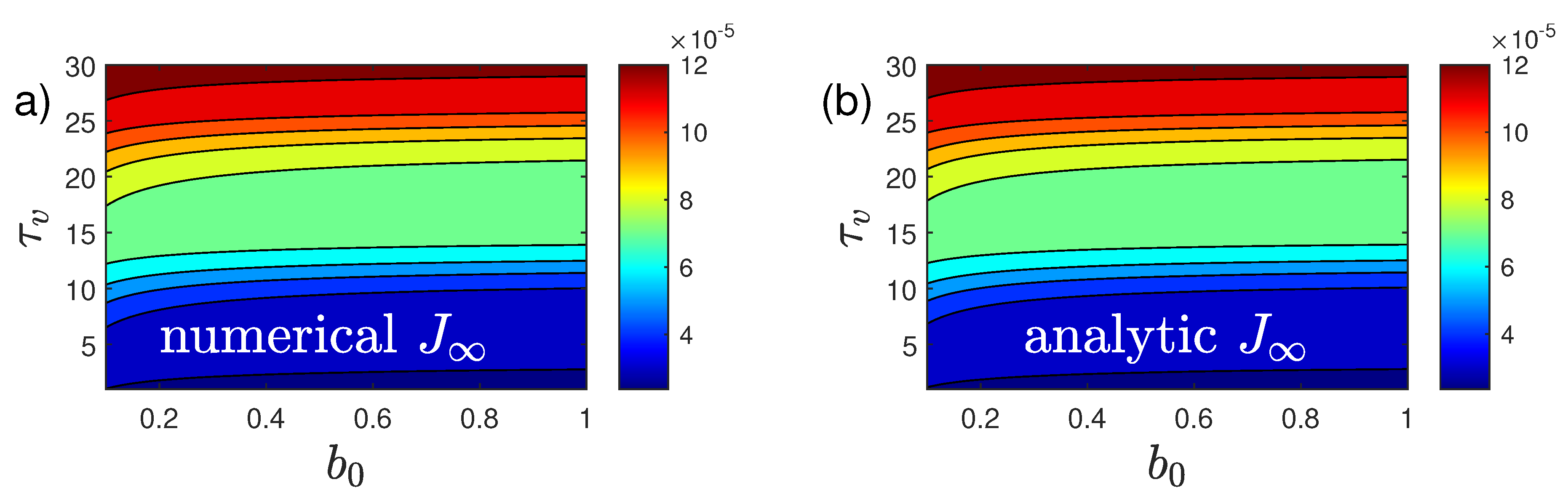
An example showing all quantities calculated analytically in this section, along with the numerical solution for a case with

J_{\infty} ≪ 1

(Figure 1), is given in Figure 3.

6. Oscillating ratio k with delayed vaccinations at constant rate $b_{0}$

As second application we investigate the influence of delayed vaccinations with constant rate on the earlier discussed SIR-application [29] with an oscillating k ratio and delayed vaccination ratio b,

\begin{matrix} k (τ) & = & 1 + α sin (β τ), \end{matrix}

(69)

\begin{matrix} b (t) & = & b_{0} Θ (τ - τ_{v}), \end{matrix}

(70)

with constant values

α

and

β

. As noted before [29] the oscillating ratio (69) represents a series of repeating pandemic outbursts with equal amplitudes in the rate of new infections. We then obtain for Eq. (19)

V = 0

for

τ < τ_{V}

and

V (τ \geq τ_{v}) = 1 - e^{- b_{0} (τ - τ_{v})} .

(71)

Likewise the rate (22) becomes the SIR-rate [29]

j (0 \leq τ \leq τ_{v}) = η (1 - η) e^{\frac{α}{β} [cos (β τ) - 1]}

(72)

at times without vaccination, and

j (τ \geq τ_{v}) = η (1 - η) exp \{\frac{α}{β} [cos (β τ) - 1] + \frac{1 - e^{- b_{0} (τ - τ_{v})}}{b_{0}} - (1 + b_{0}) (τ - τ_{v})\}

(73)

at later times. In Figure 4-a we show the rate of new infections (72)–(73) in the case

α = 0.8

and

β = 0.5

for several values of the starting time of vaccinations

τ_{v}

and the vaccination rate

b_{0} = 0.2

. We also compare in each case the analytical approximations with the exact rates of new infections from solving the SIRV equations numerically.

For the corresponding cumulative fractions one finds [29]

J (τ \leq τ_{v}) = η + η (1 - η) e^{- \frac{α}{β}} [τ I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n β} sin (n β τ)]

(74)

in terms of an infinite series of the modified Bessel function of the first kind

I_{n} (z)

, and

J (τ \geq τ_{v}) = η + η (1 - η) e^{- \frac{α}{β}} \{M (τ) + τ_{v} I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n β} sin (n β τ_{v})\},

(75)

with the integral

M (τ) = \int_{τ_{v}}^{τ} d x e^{\frac{α}{β} cos (β x) - (1 + b_{0}) (x - τ_{v}) + \frac{1 - e^{- b_{0} (x - τ_{v})}}{b_{0}}} = \int_{0}^{τ - τ_{v}} d y e^{\frac{α}{β} cos [β (y + τ_{v})] + g (y)},

(76)

where we substituted

y = x - τ

and introduced the function

g (y) = \frac{1 - e^{- b_{0} y}}{b_{0}} - (1 + b_{0}) y .

(77)

This function (77) has the following asymptotic behaviors for small and large values of

b_{0} y

, i.e.

g (y) ≃ \{\begin{matrix} - b_{0} y (1 + \frac{y}{2}), & for y ≪ b_{0}^{- 1}, \\ \frac{1}{b_{0}} - (1 + b_{0}) y, & d for y ≫ b_{0}^{- 1} . \end{matrix}

(78)

In the following we therefore approximate the function (77) as

g (y) ≃ g_{A} (y)

with

g_{A} (y) = - b_{0} y (1 + \frac{y}{2}) Θ [b_{0}^{- 1} - y] + [\frac{1}{2 b_{0}} - (1 + b_{0}) y] Θ [y - b_{0}^{- 1}] .

(79)

With this approximation we calculate the integral (76). For values of

τ \leq τ_{v} + b_{0}^{- 1}

we obtain

\begin{matrix} M (τ - τ_{v} \leq b_{0}^{- 1}) & ≃ & \int_{0}^{τ - τ_{v}} d y e^{\frac{α}{β} cos [β (y + τ_{v})] - b_{0} y (1 + \frac{y}{2})} \\ = & \int_{0}^{τ - τ_{v}} d y [I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} I_{n} (\frac{α}{β}) cos [n β (y + τ_{v})]] e^{- b_{0} y (1 + \frac{y}{2})} \\ = \sqrt{\frac{π}{2 b_{0}}} e^{\frac{b_{0}}{2}} & \{I_{0} (\frac{α}{β}) [\erf (\sqrt{\frac{b_{0}}{2}} (τ - τ_{v} + 1)) - \erf \sqrt{\frac{b_{0}}{2}}] + 2 \sum_{n = 1}^{\infty} I_{n} (\frac{α}{β}) e^{- \frac{n^{2} β^{2}}{2 b_{0}}} W_{n} (τ)\}, \end{matrix}

(80)

with

\begin{matrix} W_{n} (τ) & = & \sqrt{\frac{2 b_{0}}{π}} e^{- b_{0} / 2} e^{\frac{n^{2} β^{2}}{2 b_{0}}} \int_{0}^{τ - τ_{v}} d y cos [n β (y + τ_{v})] e^{- b_{0} y (1 + \frac{y}{2})} \\ = & ℜ \{e^{ı n β (τ_{v} - 1)} [\erf (\sqrt{\frac{b_{0}}{2}} (τ - τ_{v} + 1) - \frac{ı n β}{\sqrt{2 b_{0}}}) - \erf (\sqrt{\frac{b_{0}}{2}} - \frac{ı n β}{\sqrt{2 b_{0}}})]\} \end{matrix}

(81)

in terms of error functions with complex arguments. The real part in Eq. (81) is calculated in detail in Appendix A providing

\begin{matrix} W_{n} (τ) & = & cos [n β (τ_{v} - 1)] [\erf (\sqrt{\frac{b_{0}}{2}} (τ - τ_{v} + 1)) - \erf \sqrt{\frac{b_{0}}{2}}] \\ + \frac{e^{- \frac{b_{0}}{2} {(τ - τ_{v} + 1)}^{2}}}{π \sqrt{2 b_{0}} (τ - τ_{v} + 1)} \{cos [n β (τ_{v} - 1)] - cos n β τ\} - \frac{e^{- \frac{b_{0}}{2}}}{π \sqrt{2 b_{0}}} \{cos [n β (τ_{v} - 1)] - cos n β τ_{v}\} \\ + \frac{2 e^{- \frac{b_{0}}{2} {(τ - τ_{v} + 1)}^{2}}}{π} \sum_{m = 1}^{\infty} \frac{e^{- \frac{m^{2}}{4}} \{\sqrt{2 b_{0}} (τ - τ_{v} + 1) [cos [n β (τ_{v} - 1)] - cosh (\frac{m n β}{\sqrt{2 b_{0}}}) cos n β τ] + m sinh (\frac{m n β}{\sqrt{2 b_{0}}}) sin n β τ\}}{m^{2} + 2 b_{0} {(τ - τ_{v} + 1)}^{2}} \\ - \frac{2 e^{- \frac{b_{0}}{2}}}{π} \sum_{m = 1}^{\infty} \frac{e^{- \frac{m^{2}}{4}} \{\sqrt{2 b_{0}} [cos [n β (τ_{v} - 1)] - cosh (\frac{m n β}{\sqrt{2 b_{0}}}) cos n β τ_{v}] + m sinh (\frac{m n β}{\sqrt{2 b_{0}}}) sin n β τ_{v}\}}{m^{2} + 2 b_{0}} . \end{matrix}

(82)

Likewise, in the alternative case

τ \geq τ_{v} + b_{0}^{- 1}

we find

\begin{matrix} M (τ - τ_{v} \geq b_{0}^{- 1}) & ≃ & \int_{0}^{b_{0}^{- 1}} d y e^{\frac{α}{β} cos [β (y + τ_{v})] - b_{0} y (1 + \frac{y}{2})} + e^{\frac{1}{2 b_{0}}} \int_{b_{0}^{- 1}}^{τ - τ_{v}} d y e^{\frac{α}{β} cos [β (y + τ_{v})] - (1 + b_{0}) y} \\ = & \sqrt{\frac{π}{2 b_{0}}} e^{\frac{b_{0}}{2}} \{I_{0} (\frac{α}{β}) [\erf (\sqrt{\frac{b_{0}}{2}} (\frac{1}{b_{0}} + 1)) - \erf \sqrt{\frac{b_{0}}{2}}] + 2 \sum_{n = 1}^{\infty} I_{n} (\frac{α}{β}) e^{- \frac{n^{2} β^{2}}{2 b_{0}}} W_{n} (τ_{v} + \frac{1}{b_{0}})\} \\ + e^{\frac{1}{2 b_{0}}} \int_{b_{0}^{- 1}}^{τ - τ_{v}} d y [I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} I_{n} (\frac{α}{β}) ℜ e^{ı n β (y + τ_{v})}] e^{- (1 + b_{0}) y} . \end{matrix}

(83)

The remaining integrals can be evaluated with the help of

\int_{b_{0}^{- 1}}^{τ - τ_{v}} d y e^{- (1 + b_{0}) y} = \frac{e^{- \frac{1 + b_{0}}{b_{0}}} - e^{- (1 + b_{0}) (τ - τ_{v})}}{1 + b_{0}},

(84)

and

\begin{matrix} ℜ \int_{b_{0}^{- 1}}^{τ - τ_{v}} d y e^{ı n β (y + τ_{v}) - (1 + b_{0}) y} & = & \frac{1}{n^{2} β^{2} + {(1 + b_{0})}^{2}} [(n β sin n β τ - (1 + b_{0}) cos n β τ) e^{- (1 + b_{0}) (τ - τ_{v})} \\ - (n β sin n β (τ_{v} + \frac{1}{b_{0}}) - (1 + b_{0}) cos n β (τ_{v} + \frac{1}{b_{0}})) e^{- \frac{1 + b_{0}}{b_{0}}}] . \end{matrix}

(85)

Consequently, Eq. (83) becomes

\begin{matrix} M (τ - τ_{v} \geq b_{0}^{- 1}) & ≃ & \sqrt{\frac{π}{2 b_{0}}} e^{\frac{b_{0}}{2}} \{I_{0} (\frac{α}{β}) [\erf (\sqrt{\frac{b_{0}}{2}} (\frac{1}{b_{0}} + 1)) - \erf \sqrt{\frac{b_{0}}{2}}] + 2 \sum_{n = 1}^{\infty} I_{n} (\frac{α}{β}) e^{- \frac{n^{2} β^{2}}{2 b_{0}}} W_{n} (τ_{v} + \frac{1}{b_{0}})\} \\ + e^{\frac{1}{2 b_{0}}} I_{0} (\frac{α}{β}) \frac{e^{- \frac{1 + b_{0}}{b_{0}}} - e^{- (1 + b_{0}) (τ - τ_{v})}}{1 + b_{0}} + 2 e^{\frac{1}{2 b_{0}}} \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n^{2} β^{2} + {(1 + b_{0})}^{2}} \times \\ [(n β sin n β τ - (1 + b_{0}) cos n β τ) e^{- (1 + b_{0}) (τ - τ_{v})} - (n β sin [n β (τ_{v} + \frac{1}{b_{0}})] - (1 + b_{0}) cos [n β (τ_{v} + \frac{1}{b_{0}})]) e^{- \frac{1 + b_{0}}{b_{0}}}] . \end{matrix}

(86)

For the cumulative fraction (75) we obtain

J (τ_{v} \leq τ \leq τ_{v} + b_{0}^{- 1}) = η + η (1 - η) e^{- \frac{α}{β}} \{τ_{v} I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n β} sin (n β τ_{v}) + M (τ - τ_{v} \leq b_{0}^{- 1})\},

(87)

and

J (τ \geq τ_{v} + b_{0}^{- 1}) = η + η (1 - η) e^{- \frac{α}{β}} \{τ_{v} I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n β} sin (n β τ_{v}) + M (τ - τ_{v} \geq b_{0}^{- 1})\},

(88)

by inserting Eq. (83) and (86), respectively. Hence the cumulative fraction after infinite time is given by

\begin{matrix} J_{\infty} & = & η + η (1 - η) e^{- \frac{α}{β}} {τ_{v} I_{0} (\frac{α}{β}) + 2 \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n β} sin (n β τ_{v}) \\ + \sqrt{\frac{π}{2 b_{0}}} e^{\frac{b_{0}}{2}} [I_{0} (\frac{α}{β}) [\erf (\sqrt{\frac{b_{0}}{2}} (\frac{1}{b_{0}} + 1)) - \erf \sqrt{\frac{b_{0}}{2}}] + 2 \sum_{n = 1}^{\infty} I_{n} (\frac{α}{β}) e^{- \frac{n^{2} β^{2}}{2 b_{0}}} W_{n} (τ_{v} + \frac{1}{b_{0}})] \\ + e^{\frac{1}{2 b_{0}}} I_{0} (\frac{α}{β}) \frac{e^{- \frac{1 + b_{0}}{b_{0}}}}{1 + b_{0}} + 2 e^{- \frac{1 + 2 b_{0}}{2 b_{0}}} \sum_{n = 1}^{\infty} \frac{I_{n} (\frac{α}{β})}{n^{2} β^{2} + {(1 + b_{0})}^{2}} [(1 + b_{0}) cos [n β (τ_{v} + \frac{1}{b_{0}})] - n β sin [n β (τ_{v} + \frac{1}{b_{0}})]]}, \end{matrix}

(89)

which is compared in Figure 5 with the numerical values. It is sufficient to evaluate the sums up to

n = m = 50

; with this setting the calculation of a

J_{\infty}

value lasts only a fraction of a second.

7. Summary and conclusions

The dynamical equations of the susceptible-infected-recovered/removed-vaccinated (SIRV) epidemics model play an important role to predict and/or analyze the temporal evolution of epidemics outbreaks accounting quantitatively for the influence of vaccination campaigns. Additional to the time-dependent infection (

a (t)

) and recovery (

μ (t)

) rates, regulating the transitions between the compartments

S \to I

and

I \to R

, respectively, the time-dependent vaccination (

v (t)

accounts for the transition between the compartments

S \to V

of susceptible to vaccinated fractions. Here apparently for the first time a new accurate analytical approximation is derived for arbitrary and different but given temporal dependences of the infection, recovery and vaccination rates, which is valid for all times after the start of the epidemics for which the cumulative fraction of new infections

J (t) ≪ 1

is much less than unity. As vaccination campaigns automatically reduce the rate of new infections by transferring susceptible persons to vaccinated persons, who then no longer can get infected, the limit

J ≪ 1

is even better fulfilled than in the SIR-epidemics model which does not account for vaccinations. The proposed analytical approximation is self-regulating as the final analytical expression for the cumulative fraction

J_{\infty}

after infinite time allows to check the validity of the original assumption

J (t) \leq J_{\infty} ≪ 1

, thus indicating the allowed range of parameter values describing the temporal dependence of the ratios

k (t) = μ (t) / a (t)

and

b (t) = v (t) / a (t)

The comparison of the analytical approximation for the temporal dependence of the rate of new infections

\overset{˚}{J} (t) = a (t) S (t) I (t)

, the corresponding cumulative fraction of new infections

J (t) = J (t_{0}) + \int_{t_{0}}^{t} d x j (x)

,and the fraction of vaccinated persons

V (t)

, respectively, with the exact numerical solution of the SIRV-equations for two different and interesting applications proves the accuracy of the analytical approach. These two applications were not accessible to analytical treatment before. The considered applications include the cases of stationary ratios with a delayed start of vaccinations, and an oscillating ratio of recovery to infection rate with a delayed vaccination at constant rate. The excellent agreement of the analytical approximations with the exact numerical solution of the SIRV-equations for these two applications proves the accuracy of the analytical approach. In the first case the effect of a delayed start of vaccinations on the maximum rate of new infections and on the final cumulative fraction of infected persons is quantitatively calculated demonstrating the importance of an early start of vaccinations during a new epidemic outburst. Moreover, the new analytical approximation agrees favorably well with the earlier obtained analytical approximation [28] for the case of stationary ratios between the recovery to infection rate and the vaccination to infection rate, respectively, implying that the time dependence of the three rates

a (t)

μ (t)

, and

v (t)

is the same.

Data Availability Statement

The data that support the findings of this study are available within the article.

Appendix A Reduction of the function W n (τ)

In order to reduce the function

W_{n} (τ)

introduced in Eq. (81) we use for the error function with complex argument their infinite series representation (Eq. 7.1.29 in [33])

\erf (X + ı Y) = \erf X + \frac{e^{- X^{2}}}{2 π X} [1 - cos 2 X Y + ı sin 2 X Y] + \frac{2}{π} e^{- X^{2}} \sum_{m = 1}^{\infty} \frac{e^{- \frac{m^{2}}{4}}}{m^{2} + 4 X^{2}} [f_{m} (X, Y) + ı g_{m} (X, Y)],

(A1)

with

\begin{matrix} f_{m} (X, Y) & = & 2 X - 2 X cosh (m Y) cos (2 X Y) + m sinh (m Y) sin (2 X Y), \\ g_{m} (X, Y) & = & 2 X cosh (m Y) sin (2 X Y) + m sinh (m Y) cos (2 X Y) \end{matrix}

(A2)

and the properties

f_{m} (X, - Y) = f_{m} (X, Y)

and

g_{m} (X, - Y) = - g_{m} (X, Y)

. After straightforward but tedious algebra one obtains for general real values of A, B and C for

\begin{matrix} ℜ [e^{ı A} \erf (C - ı B)] & = & cos (A) \erf (C) + \frac{e^{- C^{2}}}{2 π C} [(1 - cos 2 B C) cos A + sin (2 B C) sin A] \\ + \frac{2 e^{- C^{2}}}{π} \sum_{m = 1}^{\infty} \frac{e^{- \frac{m^{2}}{4}}}{m^{2} + 4 C^{2}} [f_{m} (C, B) cos A + g_{m} (C, B) sin A] \\ = & cos (A) \erf (C) + \frac{e^{- C^{2}}}{2 π C} [cos A - cos (A + 2 B C)] \\ + \frac{2 e^{- C^{2}}}{π} \sum_{m = 1}^{\infty} \frac{e^{- \frac{m^{2}}{4}}}{m^{2} + 4 C^{2}} {2 C [cos A - cosh (m B) cos (A + 2 B C)] \\ + m sinh (m B) sin (A + 2 B C)} . \end{matrix}

(A3)

Applying Eq. (A3) to the two error functions in Eq. (81) then yields Eq. (82). For A, B, C equally distributed in the range

[0, 10]

, the first term

cos (A) \erf (C)

in Eq. (A3) contributes on average about 97% to the full expression. This feature can be used to write down a simplified expression for

W_{n} (τ)

References

Schlickeiser, R.; Kröger, M. Analytical modeling of the temporal evolution of epidemics outbreaks accounting for vaccinations. Physics 2021, 3, 386–426. [CrossRef]
Babaei, N.A.; Özer, T. On exact integrability of a COVID-19 model: SIRV. Math. Meth. Appl. Sci. 2023, 1, 1–18.
Rifhat, R.; Teng, Z.; Wang, C. Extinction and persistence of a stochastic SIRV epidemic model with nonlinear incidence rate. Adv. Diff. Eqs. 2021, 2021, 200.
Ameen, I.; Baleanu, D.; Ali, H.M. An efficient algorithm for solving the fractional optimal control of SIRV epidemic model with a combination of vaccination and treatment. Chaos Solit. Fract. 2020, 137, 109892. [CrossRef]
Oke, M.; Ogunmiloro, O.M.; Akinwumi, C.T.; Raji, R.A. Mathematical Modeling and Stability Analysis of a SIRV Epidemic Model with Non-linear Force of Infection and Treatment. Commun. Math. Appl. 2019, 10, 717–731.
Liu, X.D.; Wang, W.; Yang, Y.; Hou, B.H.; Olasehinde, T.S.; Feng, N.; Dong, X.P. Nesting the SIRV model with NAR, LSTM and statistical methods to fit and predict COVID-19 epidemic trend in Africa. BMC Public Health 2023, 23. [CrossRef]
Mahayana, D. Lyapunov Stability Analysis of Covid-19 SIRV Model. 2022 IEEE 18th Int. Colloquium on Signal Processing & Applications (CSPA 2022). IEEE; Univ Teknologi Mara; IEEE Control Syst Soc; IEEE Control Syst Soc Malaysia Chapter, IEEE, 2022, pp. 287–292. [CrossRef]
Petrakova, V.S.; Shaydurov, V.V. SIRV-D Optimal Control Model for COVID-19 Propagation Scenarios. J. Siber. Fed. Univ. Math. Phys. 2023, 16, 87–97.
Zhao, Z.; Li, X.; Liu, F.; Jin, R.; Ma, C.; Huang, B.; Wu, A.; Nie, X. Stringent Nonpharmaceutical Interventions Are Crucial for Curbing COVID-19 Transmission in the Course of Vaccination: A Case Study of South and Southeast Asian Countries. Healthcare 2021, 9. [CrossRef]
Smith, D.K.; Lauro, K.; Kelly, D.; Fish, J.; Lintelman, E.; McEwen, D.; Smith, C.; Stecz, M.; Ambagaspitiya, T.D.; Chen, J. Teaching Undergraduate Physical Chemistry Lab with Kinetic Analysis of COVID-19 in the United States. J. Chem. Educ. 2022, 99, 3471–3477. [CrossRef]
Huntingford, C.; Rawson, T.; Bonsall, M.B. Optimal COVID-19 Vaccine Sharing Between Two Nations That Also Have Extensive Travel Exchanges. Front. Public Health 2021, 9. [CrossRef]
Marinov, T.T.; Marinova, R.S. Adaptive SIR model with vaccination: simultaneous identification of rates and functions illustrated with COVID-19. Sci. Rep. 2022, 12. [CrossRef]
Beenstock, M.; Felsenstein, D.; Gdaliahu, M. The joint determination of morbidity and vaccination in the spatiotemporal epidemiology of COVID-19. Spatial Spatial-Tempor. Epidem. 2023, 47. [CrossRef]
Haas, F.; Kröger, M.; Schlickeiser, R. Multi-Hamiltonian structure of the epidemics model accounting for vaccinations and a suitable test for the accuracy of its numerical solvers. J. Phys. A 2022, 55. [CrossRef]
Li, X.; Li, X.; Zhang, Q. Time to extinction and stationary distribution of a stochastic susceptible-infected-recovered-susceptible model with vaccination under Markov switching. Math. Popul. Stud. 2020, 27, 259–274. [CrossRef]
Cai, C.R.; Wu, Z.X.; Guan, J.Y. Behavior of susceptible-vaccinated-infected-recovered epidemics with diversity in the infection rate of individuals. Phys. Rev. E 2013, 88. [CrossRef]
Widyaningsih, P.; Nugroho, A.A.; Saputro, D.R.S. Susceptible Infected Recovered Model with Vaccination, Immunity Loss, and Relapse to Study Tuberculosis Transmission in Indonesia. Int. Conf. Sci. Appl. Sci. (ICSAS 2018); Suparmi, A.; Nugraha, D., Eds. Sebelas Maret Univ, Amer. Inst. Physics, 2018, Vol. 2014, AIP Conf. Proc. [CrossRef]
Chapman, J.D.; Evans, N.D. The structural identifiability of susceptible-infective-recovered type epidemic models with incomplete immunity and birth targeted vaccination. Biomed. Signal Process. Control 2009, 4, 278–284. [CrossRef]
Wang, J.; Zhang, R.; Kuniya, T. A reaction-diffusion Susceptible-Vaccinated-Infected-Recovered model in a spatially heterogeneous environment with Dirichlet boundary condition. Math. Comp. Simul. 2021, 190, 848–865. [CrossRef]
Khader, M.M.; Adel, M. Numerical Treatment of the Fractional Modeling on Susceptible-Infected-Recovered Equations with a Constant Vaccination Rate by Using GEM. Int. J. Nonlin. Sci. Numer. Simul. 2019, 20, 69–75. [CrossRef]
Dai, Y.; Zhou, B.; Jiang, D.; Hayat, T. Stationary distribution and density function analysis of stochastic susceptible-vaccinated-infected-recovered (SVIR) epidemic model with vaccination of newborns. Math. Meth. Appl. Sci. 2022, 45, 3401–3416. [CrossRef]
Kiouach, D.; El-idrissi, S.E.A.; Sabbar, Y. The impact of Levy noise on the threshold dynamics of a stochastic susceptible-vaccinated-infected-recovered epidemic model with general incidence functions. Math. Meth. Appl. Sci. 2023. [CrossRef]
Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700. [CrossRef]
Kendall, D.G. Deterministic and stochastic epidemics in closed populations. Proc. Third Berkeley Symp. on Math. Statist. and Prob. 1956, 4, 149. [CrossRef]
Wu, W.; Teng, Z. Periodic wave propagation in a diffusive SIR epidemic model with nonlinear incidence and periodic environment. J. Math. Phys. 2022, 63, 122701.
Zhang, S.P.; Yang, Y.R.; Zhou, Y.H. Traveling waves in a delayed SIR model with nonlocal dispersal and nonlinear incidence. J. Math. Phys. 2018, 59, 011513.
Wu, W.; Zhang, L.; Teng, Z. Wave propagation in a nonlocal dispersal SIR epidemic model with nonlinear incidence and nonlocal distributed delays. J. Math. Phys. 2020, 61, 061512.
Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the temporal evolution of epidemics: Part B. Semi-time case. J. Phys. A 2021, 54, 175601. [CrossRef]
Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the not too late temporal evolution of epidemics for general time-dependent recovery and infection rates. Covid 2023, 3, 1781–1796.
Schlickeiser, R.; Kröger, M. Key epidemic parameters of the SIRV model determined from past COVID-19 mutant waves. Covid 2023, 3, 592–600.
Morse, P.M.; Feshbach, H. Methods of Theoretical Physics, Part I; McGraw-Hill, New York, 1953.
Mathews, J.; Walker, R.L. Mathematical Methods in Physics, 2nd ed.; Benjamin, Menlo Park, California, 1970.
Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publ., New York, 1970.

Figure 1. Required lower limiting values of

b_{0}

versus

k_{0}

, fulfilling

J_{\infty} \leq 1

using Eq. (52), for various initial

η

(solid lines). Within the

(k_{0}, b_{0})

-region above a certain solid line,

J_{\infty} < 1

, while the exact numerical solution features

J_{\infty} \leq 1

for any choice of

k_{0}

and

b_{0}

. The regime

b_{0} ≪ 1

is numerically difficult to evaluate using Eq. (52); beyond

k_{0} > 1 / 2

(marked by black dots), we use the explicit Eq. (58). For

k_{0} < 1 / 2

, the Eq. (58) is shown as dashed line, highlighting the region of

k_{0}

where Eq. (58) cannot be used.

Figure 1. Required lower limiting values of

b_{0}

versus

k_{0}

, fulfilling

J_{\infty} \leq 1

using Eq. (52), for various initial

η

(solid lines). Within the

(k_{0}, b_{0})

-region above a certain solid line,

J_{\infty} < 1

, while the exact numerical solution features

J_{\infty} \leq 1

for any choice of

k_{0}

and

b_{0}

. The regime

b_{0} ≪ 1

is numerically difficult to evaluate using Eq. (52); beyond

k_{0} > 1 / 2

(marked by black dots), we use the explicit Eq. (58). For

k_{0} < 1 / 2

, the Eq. (58) is shown as dashed line, highlighting the region of

k_{0}

where Eq. (58) cannot be used.

Figure 2. The enhancement factor

E (τ_{v})

as function of

k_{0} τ_{v}

for various

k_{0}

. Analytical result (65) (colored) compared with the numerical result (black) for

b_{0} = 0.5

and

η = 10^{- 5}

. Note the double-logarithmic representation. The dashed parts of the analytic results highlight the regimes for which Eq. (65) cannot be used anymore, as

J_{\infty}

(68) exceeds unity.

Figure 2. The enhancement factor

E (τ_{v})

as function of

k_{0} τ_{v}

for various

k_{0}

. Analytical result (65) (colored) compared with the numerical result (black) for

b_{0} = 0.5

and

η = 10^{- 5}

. Note the double-logarithmic representation. The dashed parts of the analytic results highlight the regimes for which Eq. (65) cannot be used anymore, as

J_{\infty}

(68) exceeds unity.

Figure 3. Example for Section 5 using

k_{0} = 0.7

b_{0} = 0.1

τ_{v} = 10

, and

η = 10^{- 5}

. Numerical solution (solid black curve) for (a)

j (τ)

and (b)

J (τ)

. In (a) the analytical expressions (61) (blue) and (62) (red) had been added. The vertical lines are at

τ = τ_{v}

(dashed) and

τ = τ_{m}

(solid) according to Eq. (64). The filled red circle corresponds to Eq. (63). In (b) the analytical expressions are taken from Eqs. (66) (blue) and (67) (red), while the red circle marks the analytical expression for

J_{\infty}

according to Eq. (68).

Figure 3. Example for Section 5 using

k_{0} = 0.7

b_{0} = 0.1

τ_{v} = 10

, and

η = 10^{- 5}

. Numerical solution (solid black curve) for (a)

j (τ)

and (b)

J (τ)

. In (a) the analytical expressions (61) (blue) and (62) (red) had been added. The vertical lines are at

τ = τ_{v}

(dashed) and

τ = τ_{m}

J_{\infty}

according to Eq. (68).

Figure 4. (a) Perfect agreement between the analytical solutions (72) and (73) (colored) with the numerical solutions (black) for different values of

τ_{v} = 1, 5, 10, 20, 30

(see figure legends) at

α = 0.8

β = 0.5

b_{0} = 0.2

, and

η = 10^{- 5}

. For times

τ < τ_{v}

, the analytical solution is insensitive to

τ_{v}

, and branches from this curve at

τ = τ_{v}

. The vertical black lines are at

τ = τ_{v}

(dashed) and

τ = 2 π / β

(solid), and

τ = τ_{v} + b_{0}^{- 1}

(dot-dashed). (b) Corresponding cumulative

J (τ)

. Numerical solution (black) together with the analytical Eqs. (74) and (87) - (88) (colored).

Figure 4. (a) Perfect agreement between the analytical solutions (72) and (73) (colored) with the numerical solutions (black) for different values of

τ_{v} = 1, 5, 10, 20, 30

(see figure legends) at

α = 0.8

β = 0.5

b_{0} = 0.2

, and

η = 10^{- 5}

. For times

τ < τ_{v}

, the analytical solution is insensitive to

τ_{v}

, and branches from this curve at

τ = τ_{v}

. The vertical black lines are at

τ = τ_{v}

(dashed) and

τ = 2 π / β

(solid), and

τ = τ_{v} + b_{0}^{- 1}

(dot-dashed). (b) Corresponding cumulative

J (τ)

. Numerical solution (black) together with the analytical Eqs. (74) and (87) - (88) (colored).

Figure 5.

J_{\infty}

as function of

b_{0}

and

τ_{v}

. Remaining parameters as in Fig Figure 4, i.e.,

α = 0.8

β = 0.5

, and

η = 10^{- 5}

. (a) The numerical result, (b) The analytic result using Eq. (89).

Figure 5.

J_{\infty}

as function of

b_{0}

and

τ_{v}

. Remaining parameters as in Fig Figure 4, i.e.,

α = 0.8

β = 0.5

, and

η = 10^{- 5}

. (a) The numerical result, (b) The analytic result using Eq. (89).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Analytical Solution of the Sirv-Model for the Temporal Evolution of Epidemics for General Time-Dependent Recovery, Infection and Vaccination Rates

Abstract

1. Introduction

2. SIRV model

3. Approximative analytical solutions

3.1. Solution in the limit of small J ≪ 1

3.2. Comparison with the SIR model limit

3.3. Properties of the approximative solution (22)

3.4. Cumulative fraction

4. Special case: stationary ratios

4.1. Cumulative fraction

4.2. Limit b 0 ≪ 1

5. Stationary ratios with delayed start of vaccinations

6. Oscillating ratio k with delayed vaccinations at constant rate b 0

7. Summary and conclusions

Data Availability Statement

Appendix A Reduction of the function W n (τ)

References

MDPI Initiatives

Important Links

Subscribe

3.1. Solution in the limit of small $J ≪ 1$

4.2. Limit $b_{0} ≪ 1$

6. Oscillating ratio k with delayed vaccinations at constant rate $b_{0}$