Shared Protentions in Multi-Agent Active Inference

In this paper, we unite concepts from Husserlian phenomenology, the active inference framework in theoretical biology, and category theory in mathematics to develop a comprehensive framework for understanding social action premised on shared goals. We begin with an overview of Husserlian phenomenology, focusing on aspects of inner time consciousness, namely, retention, primal impression, and protention. We then review active inference as a formal approach to modeling agent behavior, based on variational (approximate Bayesian) inference. Expanding upon Husserl’s model of time consciousness, we consider collective goal-directed behavior, emphasizing shared protentions among agents and their connection to the shared generative models of active inference. This integrated framework aims to formalize shared goals in terms of shared protentions, and to thereby shed light on the emergence of group intentionality. Building on this foundation, we incorporate mathematical tools from category theory; particularly, sheaf and topos theory, to furnish a mathematical image of individual and group interactions within a stochastic environment. Specifically, we employ morphisms between polynomial representations of individual agent models, allowing predictions not only of their own behaviors but also those of other agents and environmental responses. Sheaf and topos theory facilitate the construction of coherent agent worldviews and provides a way of representing consensus or shared understanding. We explore the emergence of shared protentions, bridging the phenomenology of temporal structure, multi-agent active inference systems, and category theory. Shared protentions are highlighted as pivotal for coordination and achieving common objectives. We conclude by acknowledging the intricacies stemming from stochastic systems and uncertainties in realizing shared goals.

Keywords:

Subject: Computer Science and Mathematics - Mathematical and Computational Biology

1. Introduction

This paper proposes to understand collective action driven by shared goals by formalizing core concepts from phenomenological philosophy—notably Husserl’s phenomenological descriptions of the consciousness of inner time—using mathematical tools from category theory under the active inference approach to theoretical biology. This project falls under the rubric of computational phenomenology [1] and pursues initial work [2,3] that proposed an active inference version of (core aspects of) Husserl’s phenomenology. Our specific contribution in this paper will be to extend the core aspects of Husserl’s description of time consciousness to group action, and to propose a formalization of this extension.

In detail, we unpack the notion of shared goals in a social group by appealing to the construct of protention (or real-time, implicit anticipation) in Husserlian phenomenology. We propose that individual-scale protentions can be communicated (explicitly or implicitly) to other members of a social group, and we argue that, when properly augmented with tools from category theory, the active inference framework allows us to model the resulting shared protentions formally, in terms of a shared generative model. To account for multiple agents in a shared environment, we extend our model to represent the interaction of agents having different perspectives on the social world, enabling us to model agents that predict behavior—both their own and that of their companions, as well as the environment’s response to their actions. We utilize sheaf-theoretic and topos-theoretic tools, from category theory, to construct coherent representations of the world from the perspectives of multiple agents, with a focus on creating "internal universes" (topoi) that represent the beliefs, perceptions, and predictions of each agent. In this setting, shared protentions are an emergent property—and possibly a necessary property—of any collective scale of self-organization, i.e., self-organization where elements or members of an ensemble co-organize themselves.

We begin by reviewing aspects of Husserlian temporal phenomenology, with a particular focus on the notions of primal impression, retention, and protention. These provide us with a conceptual foundation to think scientifically about the phenomenology of the emergence of shared goals in a community of interacting agents. We cast these shared goals in terms of the protentional (or future oriented) aspects of immediate phenomenological experience; in particular, what we call "shared protentional goals." We then formalize this neo-Husserlian construct with active inference, which allows for the representation and analysis of oneself and another’s generative models—and their interactions with their environment. By using tools from category theory, namely, polynomial morphisms and hom polynomials, we are able to design agent architectures that implement a form of recursive cognition and prediction of other agents’ actions and environmental responses. Finally, we propose a method for gluing together the internal universes of multiple agents, using topoi from category theory, allowing for a more robust representation and analysis of individual and group interactions within a stochastic environment. We use these tools to construct what we call a "consensus topos", which represents the understanding of the world that is shared among the agents. This consensus topos may be considered the mathematical object representing the external world, providing a unified framework for analyzing social action based on shared goals. Our integrative approach provides some key first steps towards a computational phenomenology of collective action under a shared goal, which may help us naturalize group intentionality more generally, and better understand the complex dynamics of social action.

2. From the phenomenology of time consciousness to co-construction and shared goals

2.1. Overview of Husserlian phenomenology of inner time consciousness

This section provides an examination of the intricate (but informal) descriptive study of the conscious perception of internal time that was proposed by the originator of the discipline of phenomenology, Husserl [1,4,5,6]. In philosophy, the term "phenomenology" is used in a technical sense, to denote a specific kind of philosophical discourse, namely: the descriptive study of the dynamics, structure, and contents of first-person, conscious experience. (The term is also used, less formally, to denote the descriptions that result from such an exercise, and more generally, to denote the way in which some thing discloses itself to a conscious subject.) Husserl himself defined phenomenology as a systematic effort to offer precise descriptions of the essential or necessary properties that pertain to various kinds of first person experience, by virtue of them being the kind of experience that they are. Thus, we can think of phenomenology as an informal counterpart to mathematics, interested in the "essence" or essential properties of certain kinds of experience. Here, we focus on Husserl’s description of inner time consciousness, and interpretations thereof—keeping in mind, of course, that Husserl scholarship is an active field of philosophical research, and that any given interpretation will be subject to dispute. In what follows, we mainly draw from Husserl’s early lectures on time consciousness [4] and intersubjectivity [7], and on formal approaches to Husserl [2,3]

Husserl argues that the consciousness of inner time is the fundamental form of consciousness, acting as the background against which all other forms of conscious experience are situated and unfold. What Husserl calls the "constitution" of objects of experience (i.e., their disclosure to a perceiving subject) always presupposes the consciousness of time as a background condition [4,8,9]. Crucially, much like other thinkers of the time, like Bergson [10] and James [11], Husserl observes that the consciousness of time exhibits a form of "temporal thickness": on this view, the way in which objects are experienced always evinces a kind of temporal depth. That is, any given experiential "now" carries with it a dimension of the just-passed and the just-yet-to-come. Husserl posits that the stream of conscious experience consists mostly of raw sensations or sensory data that arise in a basic, unprocessed state: these are called "primal impressions." Husserl refers to this primal stratum of sensory experience as the "hyletic" data of consciousness (derived from the Greek term for matter, hyle) [4]. This data is then "formatted," so to speak, in accordance with the cognitive principles governing the awareness of internal time.

In this context, "retention" refers to the aspect of time awareness that preserves the previous state or path of the temporal object, in a particular manner: as "living" and contributing to the present "now" of perception. Husserl describes retentions using the metaphor of "sediment" that accumulates over time. What Husserl calls "protention," in contrast, refers to the element of time consciousness that looks ahead, so to speak, and anticipates the immediate future state or path of a temporal object. Retention and protention are both distinguished from the explicit recollection of a past event, and the explicit imagining of a possible future event.

Husserl contends that our experience of temporally extended objects consists in a flow of anticipation (via protention), and fulfillment/frustration by new primal impressions, which may or may not conform with what was predicted to happen. Our inner time-consciousness consists of a dynamic process that anticipates what will be experienced next, based on what has just been experienced. Thus, the flow of time consciousness is composed in a series of structured impressions. Primal impression, retention, and protention interact to shape the temporal flow of conscious experience. Retentions and protentions create a framework of sorts that structure the ebb and flow of conscious experience, which in turn affects how we perceive and anticipate events. The temporal thickness of experience, on this view, consists in the protented aspects of experience interacting with "sedimented" retentions.

2.2. Shared protentions

Through the analysis of the phenomenological components of temporal consciousness, we can access a valuable understanding of how individuals develop collective objectives and expectations, and how these are incorporated into the previously mentioned mathematical models. Indeed, missing from the above account is intersubjectivity and the sharing of goals by agents in a shared life world. Husserl himself devoted much energy to thinking about intersubjectivity [7]. Zooming out to the broader literature, the concept of sharing of goals or beliefs can be understood through several interrelated perspectives. Group members may possess shared beliefs about the past, as well as aligned expectations about the future that are not explicitly expressed, but that naturally coincide due to shared experiences or comprehension [12]. We would equate these shared ways of anticipating and smoothly coping with the world as being premised on a set of "shared protentions." Assuming the plausibility of such a neo-Husserlian concept, group members can be seen as actively and implicitly aligning their beliefs and expectations, through dialogue and interaction, thereby enhancing their ability to predict each other’s actions and intentions [13], and thereby coming to perceive and act in the world in similar ways. Thus, shared retentions and protentions might arise collectively within the group, as shared styles of appraising and engaging with the social world—extending beyond the individual agent’s subjective experience, and leading to a shared implicit comprehension that surpasses and encompasses individual viewpoints.

We might consider protentions to be "shared" in several senses. A shared protention might refer to isomorphic protentions, implicitly shared among agents that are not in direct interaction or communication. Another sense of shared protention might be a belief that can be ascribed to an ensemble per se, for example, the protentions of a social group might be understood as arising from interactions between individual agents of a common cultural background, each with their own, distinct, individual-level protentions. In the following analysis, we propose to formally model these shared temporal structures, which involve resonant cognitive models and communication, and which impact the decision-making and behavior of agents within a social group.

3. An overview of active inference

Here we provide a brief overview of active inference, oriented towards application in the setting of shared protentional goals (for a more complete overview of active inference see [14,15,16]; and for its application to modeling phenomenological experience, aka "computational phenomenology," see [17]).

Active inference is a mathematical account of the behavior of cognitive agents, modeling the action-perception loop in terms of variational (approximate Bayesian) inference. A generative model is defined, encompassing beliefs about the relationship between (unobservable) causes (s)—whose temporal transitions depend upon action (u)—and (observable) effects (o), formalized as [18]:

P (o_{τ}, s_{τ}, u_{τ} | s_{τ - 1}) = \underset{l i k e l i h o o d}{\underset{︸}{P (o_{τ} | s_{τ})}} \underset{p r i o r}{\underset{︸}{P (s_{τ} | s_{τ - 1}, u_{τ}) P (u_{τ})}}

This probabilistic model contains a Markov blanket in virtue of certain conditional independencies—implicit in the above factorization—that individuate the observer from the observed (e.g., the agent from her environment). Agents can then be read as minimizing a variational free energy functional of (approximate Bayesian) beliefs over unobservable causes or states Q(s), given by:

\begin{matrix} Q (s_{τ}, u_{τ}) = arg {min}_{Q} F \end{matrix}

(1)

\begin{matrix} F = E_{Q} [ln \underset{p o s t e r i o r}{\underset{︸}{Q (s_{τ}, u_{τ})}} - ln \underset{l i k e l i h o o d}{\underset{︸}{P (o_{τ} | s_{τ}, u_{τ})}} - ln \underset{p r i o r}{\underset{︸}{P (s_{τ}, u_{τ})}}] \end{matrix}

(2)

\begin{matrix} = \underset{d i v e r g e n c e}{\underset{︸}{D_{K L} [Q (s_{τ}, u_{τ}) | | P (s_{τ}, u_{τ} | o_{τ})]}} - \underset{l o g e v i d e n c e}{\underset{︸}{ln P (o_{τ} | m)}} \end{matrix}

(3)

\begin{matrix} = \underset{c o m p l e x i t y}{\underset{︸}{D_{K L} [Q (s_{τ}, u_{τ}) | | P (s_{τ}, u_{τ})]}} - \underset{a c c u r a c y}{\underset{︸}{E_{Q} [ln P (o_{τ} | s_{τ}, u_{τ})]}} \end{matrix}

(4)

Agents interact with the environment, updating their beliefs to minimize variational free energy. The variational free energy provides an upper bound on the log evidence for the generative model (a.k.a., marginal likelihood), which can be understood in terms of optimizing Bayesian beliefs to provide a simple but accurate account of the sensorium (i.e., minimizing complexity while maximizing accuracy). This is sometimes referred to as self-evidencing [19]

Priors over action are based on the free energy expected following an action; such that the most likely action an agent commits to can be expressed as a softmax function of expected free energy:

\begin{matrix} P (u) = σ (- γ \cdot G (u)) \end{matrix}

(5)

(6)

\begin{matrix} G (u) = E_{Q_{u}} [ln Q (s_{τ + 1} | u) - ln Q (s_{τ + 1} | o_{τ + 1}, u) - ln P (o_{τ + 1} | c)] \end{matrix}

(7)

(8)

\begin{matrix} = \underset{e x p e c t e d i n f o r m a t i o n g a i n}{\underset{︸}{E_{Q_{u}} [ln Q (s_{τ + 1} | o_{τ + 1}, u) - ln Q (s_{τ + 1} | u)]}} - \underset{e x p e c t e d v a l u e}{\underset{︸}{E_{Q_{u}} [ln P (o_{τ + 1} | c)]}} \end{matrix}

(9)

\begin{matrix} = \underset{r i s k}{\underset{︸}{D_{K L} [Q (o_{τ + 1} | u) | | P (o_{τ + 1} | c)]}} \underset{a m b i g u i t y}{\underset{︸}{- E_{Q_{u}} [ln Q (o_{τ + 1} | s_{τ + 1}, u)]}} \end{matrix}

(10)

(3)

Here, G(

π

) is the expected free energy for policy u and

γ

is a precision parameter influencing the stochasticity of action selection. Effectively, actions are selected based on their expected value, which is the expected log likelihood of preferred observations, and their epistemic value, representing the expected information gain. The expected free energy can also be rearranged in terms of risk and ambiguity; namely, the divergence between anticipated and preferred outcomes, and the imprecision of outcomes, given their causes. Comparison of equations (2) and (3) show that risk is analogous to expected complexity while ambiguity can be associated with expected inaccuracy. In summary, agents engage with their world by updating beliefs about the hidden or latent states causing observations while, at the same time, acting to solicit observations that minimize expected free energy; namely, minimize risk and ambiguity.

4. Active inference and time consciousness

We have previously [1] framed Husserl’s descriptions of time consciousness in terms of (Bayesian) belief updating, while further work proposed a mathematical reconstruction of the core notions of Husserl’s phenomenology of time consciousness—retention, primal impression, protention, and the constitution of disclosure of objects in the flow of time consciousness—using active inference [2] See also [20] for related work. Active inference foregrounds a manner in which previous experience updates an agent’s (Bayesian) beliefs, and thereby underwrite behaviors and expectations, leading to a better understanding of the world.

Descriptions of temporal thickness from Husserl’s phenomenology are highly compatible with generative modeling in active inference agents. To connect the phenomenological ideas reviewed above with active inference, consider again how active inference agents update their beliefs about the world based on the temporal flow structure. In active inference, agents continuously update their posterior beliefs by integrating new observations with their existing beliefs. This belief updating involves striking a balance between maintaining the agent’s current beliefs and learning from new information. Retention and primal impressions relate to the fact that, in active inference, all past knowledge contributes to shaping beliefs about the present state of the world. In short, active inference effectively bridges prior experiences with current expectations. In this setting, retentions are formalized as the encoding of new information about the world under a generative model. Primal impressions are formalized as the new data that agents sample over time, forcing an agent to update its beliefs about the world, leading to a better understanding of the environment and allowing for more effective information and preference-seeking behavior. Thus, the consciousness of inner time can be modeled as active inference: where prior beliefs (sedimented retentions) are intermingled with ongoing sensory information (primal impression), and contextualized by an unfolding, implicit and future-oriented anticipation of what will be sensed next (protention).

4.1. Mapping Husserlian phenomenology to active inference models

As illustrated in Table 1, and previously explored in [1], Active inference comprehensively maps to Husserlian phenomenology: observations represent the hyletic data; namely, sensory information that sets perceptual boundaries but is not directly perceived. The hidden states correspond to the perceptual experiences; namely, the data infers that are inferred from the sensory input. The likelihood and prior transition matrices are associated with the idea of sedimented knowledge. These matrices represent the background understanding and expectations that scaffold perceptual encounters. The preference matrix evinces a similarity to Husserl’s notions of fulfillment or frustration. It represents the expected results or preferred observations. The initial distributions represent the prior beliefs of the agent that are shaped by previous experiences. In particular, the habit matrix resonates with Husserlian notions of horizon and trail set. Collectively, these aspects of the generative model entail prior expectations and the possible course of action.

Table 1. Parameters used in the general model under the active inference framework and their phenomenological mapping.

Parameter	Description	Phenomenological Mapping
$o \in O$	Observations that capture the sensory information received by the agent	Represents the hyletic data, setting perceptual boundaries but not directly perceived
$s \in S$	Hidden states that capture the causes for the sensory information – the latent or worldly states	Corresponds to perceptual experiences, inferred from sensory input
$P (o \| s) = C a t (A)$	Likelihood matrix that captures the mapping of observations to (sensory) states	Associated with sedimented knowledge, representing background understanding and expectations
$P (s \| s_{- 1}, μ) = C a t (B)$	Transition matrix that captures the mapping for how states are likely to evolve	Linked to sedimented knowledge, shaping perceptual encounters
$P (o_{+ 1} \| c) = C a t (C)$	Preference matrix that captures the preferred observations for the agent, which drive their actions	Similar to Husserl’s notions of fulfillment or frustration, representing expected results or preferences
$P (s_{0}) = C a t (D)$	Initial distribution that captures the priors over the hidden states	Represents prior beliefs, shaped by previous experiences and current expectations
$P (μ) = C a t (E)$	Habit matrix that captures the prior expectations for initial actions	Connected to Husserlian notions of horizon and trail set, symbolizing prior expectations
$π$	Policy matrix that captures the potential policies that guide the agent’s actions, driving the evolution of the B matrix	Symbolizes the possible course of action, influenced by background information and values

4.2. An active inference approach to shared protentions

Active inference often involves agents making inferences about each other’s mental states by attributing cues to underlying causes [21]. The emergence of communication and language in collective or federated inference provides a concrete example of how these cues become standardized across agents[22]. Individuals agents leverage their beliefs to discern patterns of behavior and belief updating in others. This entails a state of mutual predictability that can be seen as a communal or group-level reduction of (joint) free energy [21,23]. When agents are predictable to each other, they can anticipate each other’s actions in a complementary fashion—in a way that manifests as generalized synchrony [24]. This is similar to how language emerges in federated inference, as a tool for minimizing free energy across agents in a shared econiche [25].

As agents in a group exhibit similar behaviors, they generate observable cues in the environment (e.g., an elephant path through a park) that guide other agents towards the same generative models, and nudge agents towards the same behavior. This has been discussed in terms of "deontic value", which scores the degree to which an agent’s observing some behavior will cause that agent to engage in that behavior [25]. Alignment can thus be achieved by agents that share similar enough goals, and exist in similar enough environments, thereby reinforcing patterns of behavior and epistemic foraging for new information [21,25]. Individual agents perceive the world, link observable "deontic cues" to the latent states and policies that cause them, and observe others, using these cues to engage in situationally appropriate ways with the world. These deontic cues might range from basic road markings to intricate semiotics or symbols such as language [26].

Consider, for example, someone wearing a white lab coat. You and the person wearing the lab coat share some similarities which lead you to believe the coat means the same thing to them and you. You know lab coats are generally worn for scientific or medical purposes (sedimented retentions scaffolded by the cognitive niche). The person wearing the labcoat is standing in a street near a hospital building. From all these cues, without ever wearing a labcoat yourself, or being a doctor, you can make a pretty good guess that this individual is a doctor.

Similarly, gathering interoceptive cues to infer one’s own internal states can enable individuals to make sense of other people’s behavior and allow them to infer the internal states of another [27,28]. Within a multi-agent system, the environment is complex, encompassing both abiotic and social niches. The abiotic niche is the physical and inanimate components of the environment, whereas the social niche comprises the interactions and observations resulting from the activities of other agents. This differentiation underscores that the environment is not exclusively shaped by agents, but rather is shaped by an intricate self-sustaining interaction between living and non-living things. This suggests that agents not only acquire knowledge about their environment to efficiently understand and navigate it, but they are also acquiring knowledge about others and, implicitly, themselves in tandem. These ideas provide some framing for the core question that will concern us presently: How should we model such shared protentions? To model shared protentions effectively, the use of category theory becomes a key epistemological resource. The mathematical precision and structural complexity of category theory provide a sophisticated framework for comprehending the cohesive behaviors of agents in regard to shared objectives or future perspectives. It explores fundamental relationship among the things like the characteristics of agent interaction, goals, protentions, and the organization of their environmental resources. This theoretical framework allows for a formal and scalable understanding of shared protentions, highlighting the interconnections and relational dynamics between individuals in a complex setting.

5. Category-theoretic description of shared protentions in Active Inference ensembles

We have reviewed active inference based approaches to time consciousness and in particular the construct of a shared protention. Here, we propose a category theoretic formulation of shared protentions—among an ensemble of active inference agents [29], combining two main ideas: first, a notion of agent derived from categorical systems theory [30], whose boundary (or Markov blanket) is described using polynomial functors; second, the concept of sheaf, to account for agents with shared beliefs that may thus be “glued together”.

We do not pretend to give a detailed mathematical exposition of either of these concepts here, and instead refer the interested reader to [31] on polynomial interaction and [32] on the basic ideas of sheaf theory. For our purposes, it will be sufficient to know some basic concepts from set theory (the notions of disjoint union and intersection), and the basic definitions of category and functor, which we now review.

Categories capture the mathematical essence of composition, the process by which many parts make a whole. A category

X

is thus determined by a collection of objects, denoted

X_{0}

, and, for each pair

(a, b)

of objects, a set

X (a, b)

of morphisms from a to b. We denote such a morphism by

f : a \to b

, and say it has sourcea and targetb. Morphisms with compatible source and target may be composed, so that

f : a \to b

and

g : b \to c

yield

g \circ f : a \to c

, and each object a is assigned an identity morphism,

i d_{a} : a \to a

. The morphisms of a category are required to satisfy two axioms: unitality, saying

f \circ i d_{a} = f = i d_{b} \circ f

; and associativity

h \circ (g \circ f) = (h \circ g) \circ f

, meaning we can simply write

h \circ g \circ f

for consecutive composition. A basic example of a category is the category

Set

, whose objects are sets X and whose morphisms

f : X \to Y

are functions

f (x) = y

A functor is a morphism between categories. If we think of a category as like “a set where there may be relationships (morphisms) between points”, then a functor is like a function which preserves the structure of those relationships. Formally, if

C

and

D

are categories, then a functor

F : C \to D

is a mapping

F_{0} : C_{0} \to D_{0}

along with a family of functions

F_{a, b} : C (a, b) \to D (F_{0} a, F_{0} b)

, indexed by the objects

a, b

C

; one typically drops the subscripts and infers them from the context. These mappings must satisfy the axioms of functoriality:

F (g \circ f) = F (g) \circ F (f)

and

F (i d_{a}) = i d_{F a}

, for all morphisms

f, g

and objects a in

C

. Each object a in a category

C

induces a functor

C (a, -) : C \to Set

, which maps each object b to the set

C (a, b)

of morphisms

a \to b

, and which sends each morphism

g : b \to c

to the function

g \circ (-) : C (a, b) \to C (a, c)

which acts by post-composition,

f \mapsto g \circ f

. Beyond these “representable” functors, both polynomial functors and sheaves are also special kinds of functor.

5.1. `Polynomial’ generative models

At school, we learn about polynomial functions, such as

f (x) = x^{2} + 3 x + 2

; a polynomial functor is to this concept precisely what a functor is to a function. Formally, one merely changes the variables, coefficients and exponents in the expression from numbers to sets1. In an expression such as

y^{A} + B y + C

, we interpret the exponential

y^{A}

as the representable functor

X \mapsto X^{A} : = Set (A, X)

B y

as the product functor

X \mapsto B \times X

, and + as the disjoint union of sets, so that all together, the expression encodes the functor

X \mapsto X^{A} + B \times X + C

Every polynomial can be written in the form of a sum (disjoint union) of representable functors,

\sum_{i : I} y^{p [i]}

, for some indexing set I and collection of exponents

{p [i]}

; for example, we can write

B y

\sum_{b : B} y^{1}

, where 1 is the 1-element set

{*}

. Therefore, we will henceforth summarize the data of a polynomial p as

p = \sum_{i : p (1)} y^{p [i]}

where we now write

p (1)

for the indexing set.

The mathematics of polynomial functors supplies a perhaps surprisingly rich formalism for describing interacting systems such as intelligent agents. We can think of a polynomial p as describing the `interface’ or `boundary’ of such a system: each element i of

p (1)

represents a possible shape or configuration that the system may adopt, or the possible actions that it may take; and each exponent

p [i]

represents the set of possible `inputs’ that it may expect (such as sense-data), having adopted configuration i.

Because the type of expected sense-data may depend on the configuration adopted (just as you don’t expect to `see` when you close your eyes), this generalizes the usual notion of a Markov blanket in active inference to something more dynamical. We can thus model an active inference agent with boundary polynomial p as predicting the activity of its boundary p. That is to say, we collect the exponent sets

p [i]

together into their disjoint union

Σ p : = \sum_{i : p (1)} p [i]

and then understand the agent as predicting a distribution over the whole set

Σ p

. This amounts to predicting both its configurations

i : p (1)

(hence, its actions) and, compatibly, its sense-data in each

p [i]

. If we restrict each

p [i]

to be the same (so there is no dependence of sense-data on configuration), then we can recover the standard Markov blanket: if we set

p [i] = S

to be the sense-data and

p (1) = A

the actions, then

\sum_{a : A} S = A \times S

Being a category-theoretic formalism, one doesn’t just have objects (polynomials), but also morphisms between them: these encode the data of how agents with polynomial interfaces may interact; in particular, they encode how systems may be `nested’ within each other. Thus, a morphism

φ : p \to q

encodes how a system with boundary p may be nested within a system with boundary q, and consists of a pair

(φ_{1}, φ^{♯})

of a `forwards’ function

φ_{1} : p (1) \to q (1)

(that encodes how p-configurations or p-actions are translated into q-configurations) and a family of `backwards’ functions

φ_{i}^{♯} : q [φ_{1} (i)] \to p [i]

(that encodes dually how q-sense-data is translated into p-sense-data). Polynomials and their morphisms collect into a category,

Poly

Now, a morphism

p \to q

represents simply nesting a p-system within a q-system; but often, as here, we wish to consider how multiple agents form a coherent collective, which means we need a way to encode multiple agents’ polynomials as a single polynomial. For this, we can use the tensor of polynomial functors,

p \otimes p^{'}

, which places the two interfaces p and

p^{'}

"side by side". Formally, we define

p \otimes p^{'}

as the polynomial

\sum_{i : p (1)} \sum_{j^{'} : p^{'} (1)} y^{p [i] + p^{'} [j]}

. With this definition, we can understand a morphism

p \otimes p^{'} \to q

as representing how systems p and

p^{'}

come together to form a system with boundary q.

This is not yet enough for our purposes; we also wish to model systems that recursively predict the beliefs of other agents in their environment. Behaviorally, this means predicting how the other agents are going to act, given their perceptions—which in turn means predicting the patterns of interaction within the environment. And, formally, this means ’internalizing’ these patterns into a single polynomial.

Thus, given polynomials p and q, we can define the corresponding hom polynomial

[p, q] : = \sum_{φ : Poly (p . q)} y^{\sum_{i : p (1)} q [φ_{1} (i)]}

The set of configurations of

[p, q]

is the set of morphisms

p \to q

, so to adopt a

[p, q]

-configuration is to adopt a particular pattern of interaction.

Dually, the “sense-data” associated to a particular pattern of interaction

φ

is given by the configurations of the `inner’ system p and, for each such configuration

i : p (1)

, the corresponding sense-data

q [φ_{1} (i)]

for the outer system q in the configuration implied by i via

φ

A prediction over

[p, q]

is thus a prediction over the set

Σ [p, q] = \sum_{φ : Poly (p . q)} \sum_{i : p (1)} q [φ_{1} (i)]

that is, a distribution over patterns of interaction

Poly (p, q)

, inner configurations

p (1)

and outer sense data

\sum_{i} q [φ (i)]

. By way of example, if we assume that the outer system q is `closed’ (with no further external environment), then that is to say that it has the trivial interface

q = y

with only one configuration (`being’) and no non-trivial sense-data. A morphism

p \to y

corresponds to a function2

p (1) \to \sum_{i} p [i]

, which encodes how the environment responds with sense-data, given the p-system’s actions. Thus, a prediction over

[p, y]

is a prediction of the environment’s response, along with a prediction of "how to act".

We can use this idea to extend the standard formalism of active inference agents’ internal generative models, by saying that a polynomial generative model for a solitary system with boundary p is a probability kernel (conditional probability distribution)

γ : X ⇝ Σ [p, y]

for some choice of internal state space X, along with a prior distribution on X. This means that, for each

x : X

, we obtain a distribution over

p (1) \times Poly (p, y)

: a belief about actions to take, along with a belief about how the environment will respond with sense-data.

When the system of interest is not solitary, however, it may sensibly imagine its environment to include other agents: thus, the "outer system" no longer has the trivial form y, but may itself be modelled as using a hom polynomial

[\otimes_{j} q_{j}, y]

, where the

q_{j}

are the polynomials representing the other agents. Thus, its generative model is extended to a probability kernel of the form

X ⇝ \sum [p, [\otimes_{j} q_{j}, y]]

. It is possible to prove an isomorphism of polynomials

[p, [q, r]] ≅ [p \otimes q, r]

, and so this model is equivalent to one of the form

X ⇝ \sum [\otimes_{j} p_{j}, y]

Such an agent thus predicts not only its actions, but those of its companion agents, along with how the environment will respond to all of them. The foregoing isomorphism can be repeated to arbitrary levels of nesting, and thus constitutes a starting point for a formal "theory of mind"; and indeed, a starting point for an account of agents that model each other’s protentions.

5.2. A sheaf-theoretic approach to multi-agent systems

In the preceding section, we described how an ensemble of agents may predict each other’s behavior by instantiating a family of polynomial generative model. However, there is nothing in that formalism which pushes the agents’ beliefs to be in any way compatible: they need not share protentions. Indeed, a true collective of agents should be a group of agents that have `overlapping’ world models, sufficiently cohesive to promote the development of common intentions among individuals

In order to describe agents with such shared beliefs, we propose upgrading the formalism using the mathematical tools of sheaf and topos theory. Sheaves are in some sense the canonical structure for distributed data [32], and tools from sheaf theory allow us to describe agents that communicate in order to reach a consensus [33].

In more detail, a sheaf over a topological space constitutes a systematic method of keeping track of how `local’ data or qualities, defined on open subsets, can be reliably concatenated to represent a `global’ situation. This attribute renders them highly valuable in comprehending the varied and potentially contradictory convictions, perspectives, and forecasts of individual agents within a multi-agent system. Sheaves enable the depiction of both the diversity and agreement among various agents’ perspectives on the environment, and their ability to alter over time is crucial for adjusting and reacting to system modifications. Sheaves formalize the concept of “shared experience” among agents, which is essential for reaching a consensus on the structure of the external world.

Mathematically, a sheaf F is an assignment of data sets to a space X, such that the assignment “agrees on overlaps”, meaning that, if we consider overlapping subsets U and V of X, then

F (U)

and

F (V)

agree on the overlap

U \cap V

. A little more formally, if we consider there to be a morphism

U \to U^{'}

whenever

U^{'} \subseteq U

, we obtain a category

O (X)

whose objects are (open) subsets of X and whose morphisms are such (`opposite’) inclusions. Then a sheaf F is a functor

O (X) \to Set

such that, whenever U and V cover W (as when

W = U \cap V

) so that there are morphisms

ι_{U} : U \to W

and

ι_{V} : V \to W

O (X)

, then, if

u \in U

and

v \in V

, there is a unique

w \in W

such that

F (ι_{U}) (u) = w = F (ι_{V}) (v)

. The category of sheaves on X forms a subcategory

Sh (X)

of the category of functors

O (X) \to Set

Now, a space such as X is itself an object of a category of spaces

Spc

, whose morphisms are the appropriate kind of functions between spaces (e.g., continuous functions between topological spaces), and when

Spc

has enough structure (such as when it is a topos), there is an equivalence between

Sh (X)

and the category

Spc / X

of bundles over X, whose objects are morphisms

π_{E} : E \to X

Spc

and whose morphisms

f : π_{E} \to π_{F}

are functions

f : E \to F

such that

π_{E} = π_{F} \circ f

. We can use this equivalence3 to lift the models of the previous section to the world of sheaves, as we now sketch.

A bundle

π_{E} : E \to X

thus may itself be seen as representing a type (or collection) of data that varies over the space X; for each

x \in X

, there is a fibre

E_{x}

encoding the data relevant to x. In this way, each polynomial

Σ p = \sum_{i : p (1)} p [i]

yields a `discrete’ bundle

\sum_{i : p (1)} p [i] \to p (1)

which maps

(i, x)

to i. But the polynomials of the preceding section are in no way related to another ambient spatial structure: for instance, one might expect that the internal space X of an agent’s generative model

X ⇝ Σ p

is structured as a model of the agent’s external environment, which is likely spatial; likewise, the type of available configurations

p (1)

may itself depend on where in the environment the agent finds itself (consider that we might suppose this X to encode also task-relevant information).

This suggests that the agent’s configuration space

p (1)

should itself be bundled over X, so that the polynomial p takes the form

\sum_{i} p [i] \to p (1) \to X

as a morphism—or rather, as an object in

Spc / X

. In order for this to make sense, we need to be able to instantiate the category

Poly

Spc / X

, rather than

Set

: but this is possible if

Spc

has enough structure4, as we have assumed. Then, we can define a spatial generative model on the interface p over X to be a probability kernel

X ⇝ p

Spc / X

, i.e. that makes the following diagram commute, along with a prior on X:

(11)

Such a kernel must therefore be a stochastic section of the bundle

π_{p (1)} \circ p

; and with it, an agent can make predictions according to where it believes itself to be in its configuration space, compatibly with the structure of that space.

Now in this spatially-enhanced setting, we may recapitulate the polynomial theory-of-mind of the preceding section, and suppose that each agent j is equipped with a spatial generative model of the form

X_{j} ⇝ Σ [\otimes_{i} p_{i}, y]

. If we additionally suppose that the collection of agents’ model spaces

{X_{j}}

covers a (perhaps-larger) space Z, then we can in turn ask whether it is possible to glue these models

X_{j} ⇝ Σ [\otimes_{i} p_{i}, y]

together accordingly, to form a “sheaf of world models” W.

If it is possible, then we may say that the agents inhabit a shared universe — and thus, with appropriate generative models, may be said to share protentions. Conversely, if it is not possible, then we may ask: what is the obstruction? In this case, there must be some disagreement between the agents. But sheaf theory supplies tools for overcoming such disagreements [34,35], and thus to communicate to reach a consensus [33]; even if the disagreements are fundamental, it is usually possible to derive dynamics that will yield as close to a sheaf as possible [36]. In future work, we hope to apply these methods to multi-agent active inference model, in order to demonstrate this consensus-building.

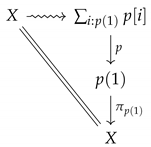
5.2.1. A note on toposes

Sheaves collect into categories called toposes. A topos is a category that has both spatial and logical structure [37], allowing for the expression of logical propositions and deductions within it. Topos theory, extending beyond sheaf theory, provides a more holistic and abstract framework. Each topos is like a “categorified space”, and comes with an internal logic and language, whose expressions are relative to the space that the topos models, thereby enabling a more profound exploration of the conceptual structures within these spaces. In this way, each topos can be thought of as a `universe’, where the truth of propositions may depend on where they are uttered. For example, the topos

Spc / X

assumed above represents “the universe of the space X”, known as the “little topos” or “petit topos” of X.

The tools of sheaf theory naturally extend to toposes. Thus, in the foregoing discussion, we considered a collection of agents with internal world models

{X_{j}}

, which in turn induce toposes

Spc / X_{j}

that we may consider gluing into a “shared universe”

Spc / W

according to their topology or interaction pattern. Perhaps, in the end, we may consider this shared universe to be the agents’ understanding of their actual universe, socially constructed.

6. Closing Remarks

Our paper introduces the integration of Husserlian phenomenology, active inference in theoretical biology, and category theory. We have formalized collective action and shared goals using mathematical tools of increasing generalization. We were able to anchor this formalism in phenomenology by delving into Husserl’s phenomenology of inner time consciousness, emphasizing retention, primal impression, and protention. We then proposed these concepts could be connected in the formation of shared goals in social groups. With a short overview of active inference, we cast the action-perception loop of cognitive agents as variational inference, furnishing an isomorphic construct to time consciousness. Building on this introduction, we were able to review the relationship between Husserl’s time consciousness and active inference established in a previous paper, showing how past experiences and expectations influence present behavior and understanding. We then proceeded to leverage a category theory to model shared protentions among active inference agents, using concepts like polynomial functors and sheaves. These sophisticated tools were necessary to account for the complexity of shared protentions, leveraging existing tools of category theory. Our paper achieves a conceptual and mathematical image of the interconnection among agents, enabling them to coordinate in large groups across spatiotemporal scales. It dissolves the boundaries between externalist and internalist perspectives by demonstrating the intrinsic connections of perceptions extended in time. This formalization elucidates how agents co-construct their world and interconnect through this process, offering a novel approach to understanding collective action and shared goals.

References

Albarracin, M.; Pitliya, R.J.; Ramstead, M.J.; Yoshimi, J. Mapping husserlian phenomenology onto active inference. arXiv preprint arXiv:2208.09058, 2022. [Google Scholar]
Yoshimi, J. The Formalism. In Husserlian Phenomenology; Springer, 2016; pp. 11–33.
Yoshimi, J. Husserlian phenomenology: A unifying interpretation; Springer, 2016.
Husserl, E. The phenomenology of internal time-consciousness; Indiana University Press, 2019.
Andersen, H.K.; Grush, R. A brief history of time-consciousness: historical precursors to James and Husserl. Journal of the History of Philosophy 2009, 47, 277–307. [Google Scholar] [CrossRef]
Poleshchuk, I. From Husserl to Levinas: the role of hyletic data, affection, sensation and the other in temporality. In From Husserl to Levinas; 2009; pp. 1000–1030. [Google Scholar]
Husserl, E. The phenomenology of intersubjecitvity. Hamburg: Springer. Search in, 1973. [Google Scholar]
Sokolowski, R. The formation of Husserl’s concept of constitution; Vol. 18, Springer Science & Business Media, 2013.
Hoerl, C. Husserl, the absolute flow, and temporal experience. Philosophy and Phenomenological Research 2013, 86, 376–411. [Google Scholar] [CrossRef]
Bergson, H. Matière et mémoire; République des Lettres, 2020.
James, W. Principles of Psychology 2007.; Cosimo, 2007.
Laroche, J.; Berardi, A.M.; Brangier, E. Embodiment of intersubjective time: relational dynamics as attractors in the temporal coordination of interpersonal behaviors and experiences. Frontiers in psychology 2014, 5, 1180. [Google Scholar] [CrossRef] [PubMed]
Benford, S.; Giannachi, G. Temporal trajectories in shared interactive narratives. Proceedings of the sigchi conference on human factors in computing systems, 2008, pp. 73–82.
Smith, R.; Friston, K.J.; Whyte, C.J. A step-by-step tutorial on active inference and its application to empirical data. Journal of mathematical psychology 2022, 107, 102632. [Google Scholar] [CrossRef] [PubMed]
Parr, T.; Pezzulo, G.; Friston, K.J. Active inference: the free energy principle in mind, brain, and behavior; MIT Press, 2022.
Friston, K.; Da Costa, L.; Sajid, N.; Heins, C.; Ueltzhöffer, K.; Pavliotis, G.A.; Parr, T. The free energy principle made simpler but not too simple. Physics Reports 2023, 1024, 1–29. [Google Scholar] [CrossRef]
Ramstead, M.J.; Seth, A.K.; Hesp, C.; Sandved-Smith, L.; Mago, J.; Lifshitz, M.; Pagnoni, G.; Smith, R.; Dumas, G.; Lutz, A. ; others. From generative models to generative passages: A computational approach to (neuro) phenomenology. In Review of Philosophy and Psychology; 2022; pp. 1–29. [Google Scholar]
Çatal, O.; Nauta, J.; Verbelen, T.; Simoens, P.; Dhoedt, B. Bayesian policy selection using active inference. arXiv preprint arXiv:1904.08149, 2019. [Google Scholar]
Hohwy, J. The self-evidencing brain. Noûs 2016, 50, 259–285. [Google Scholar] [CrossRef]
Bogotá, J.D.; Djebbara, Z. Time-consciousness in computational phenomenology: a temporal analysis of active inference. Neuroscience of Consciousness 2023, 2023, niad004. [Google Scholar] [CrossRef] [PubMed]
Veissière, S.P.; Constant, A.; Ramstead, M.J.; Friston, K.J.; Kirmayer, L.J. Thinking through other minds: A variational approach to cognition and culture. Behavioral and brain sciences 2020, 43, e90. [Google Scholar] [CrossRef] [PubMed]
Friston, K.; Parr, T.; Heins, C.; Constant, A.; Friedman, D.; Isomura, T.; Fields, C.; Verbelen, T.; Ramstead, M.; Clippinger, J.; Frith, C.D. Federated inference and belief sharing. University College London Queen Square Institute of Neurology 2023. [Google Scholar] [CrossRef] [PubMed]
Ramstead, M.J.; Hesp, C.; Tschantz, A.; Smith, R.; Constant, A.; Friston, K. Neural and phenotypic representation under the free-energy principle. Neuroscience & Biobehavioral Reviews 2021, 120, 109–122. [Google Scholar]
Gallagher, S.; Allen, M. Active inference, enactivism and the hermeneutics of social cognition. Synthese 2018, 195, 2627–2648. [Google Scholar] [CrossRef] [PubMed]
Constant, A.; Ramstead, M.J.; Veissière, S.P.; Friston, K. Regimes of expectations: an active inference model of social conformity and human decision making. Frontiers in psychology 2019, 10, 679. [Google Scholar] [CrossRef] [PubMed]
Constant, A.; Ramstead, M.J.; Veissiere, S.P.; Campbell, J.O.; Friston, K.J. A variational approach to niche construction. Journal of the Royal Society Interface 2018, 15, 20170685. [Google Scholar] [CrossRef] [PubMed]
Ondobaka, S.; Kilner, J.; Friston, K. The role of interoceptive inference in theory of mind. Brain and cognition 2017, 112, 64–68. [Google Scholar] [CrossRef] [PubMed]
Seth, A. Being you: A new science of consciousness; Penguin, 2021.
St Clere Smithe, T. Polynomial Life: The Structure of Adaptive Systems. Electronic Proceedings in Theoretical Computer Science; Open Publishing Association: Cambridge, UK, 2022; Volume 372, pp. 133–148. [Google Scholar] [CrossRef]
Myers, D.J. Categorical Systems Theory (Draft); (Draft), 2022.
Spivak, D.I.; Niu, N. Polynomial Functors: A General Theory of Interaction; (In press), 2021.
Robinson, M. Sheaves Are the Canonical Data Structure for Sensor Integration. Information Fusion 2017, 36, 208–224, [arxiv:math.AT/1603.01446v3]. [Google Scholar] [CrossRef]
Hansen, J.; Ghrist, R. Opinion Dynamics on Discourse Sheaves. arXiv, 2020; [arxiv:math.DS/2005.12798]. [Google Scholar]
Hansen, J. Laplacians of Cellular Sheaves: Theory and Applications. PhD thesis, University of Pennsylvania, 2020.
Abramsky, S.; Carù, G. Non-Locality, Contextuality and Valuation Algebras: A General Theory of Disagreement. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2019, 377, 20190036. [Google Scholar] [CrossRef]
Hansen, J.; Ghrist, R. Learning Sheaf Laplacians from Smooth Signals. ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019. [CrossRef]
Shulman, M. Homotopy Type Theory: The Logic of Space. New Spaces for Mathematics and Physics, 2017, [arxiv:math.CT/1703.03007].

	*Supported by VERSES.
1	This replacement may be seen to generalize polynomial functions if we note that a number such as 3 may be seen to stand for a set ${, , *}$ of the same cardinality.
2	Strictly speaking, a section of the bundle $\sum_{i p (1)} p [i] \to p (1)$ .
3	To see one direction of the equivalence, observe that, given a bundle $π_{E} : E \to X$ , we can obtain a sheaf by defining $F (U)$ to be the pullback of $π_{E}$ along the inclusion $U ↪ X$ .
4	It must be locally Cartesian closed, which it will be if it is a topos.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer